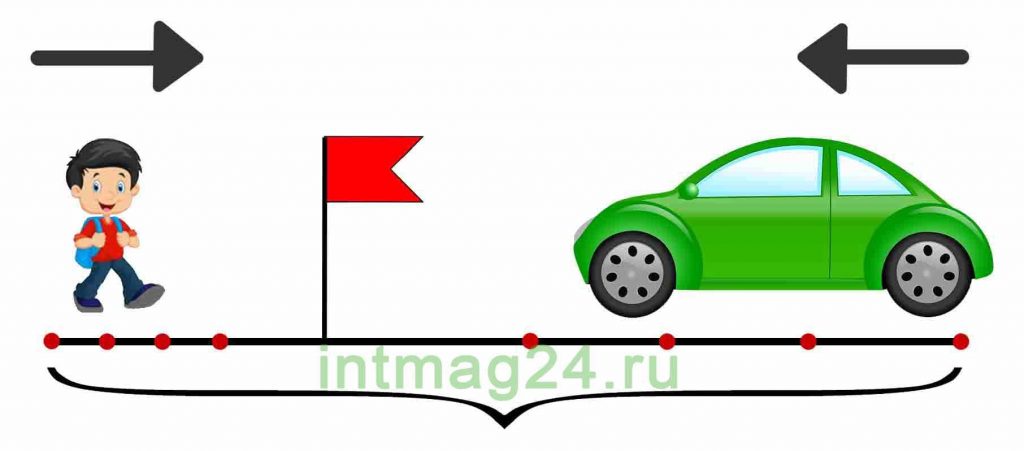
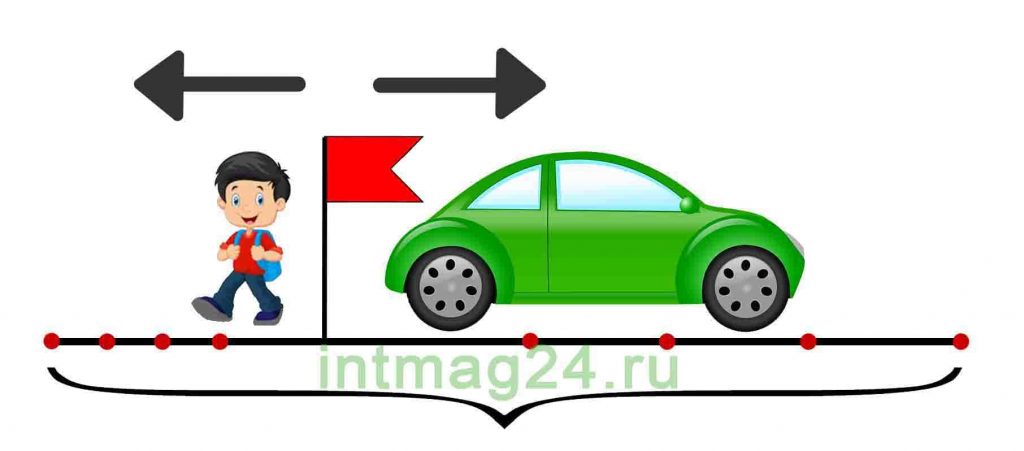
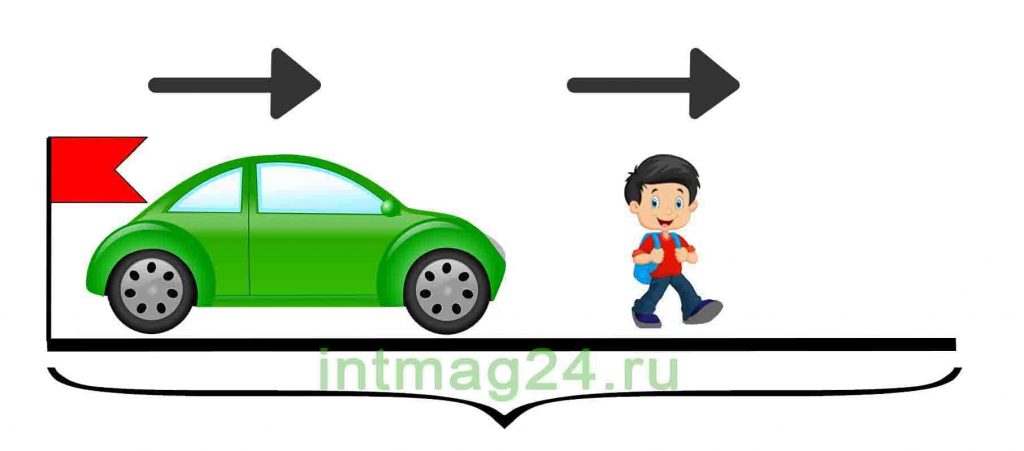
Задачи на движение навстречу друг другу (встречное движение) — один из трех основных видов задач на движение.
Если два объекта движутся навстречу друг другу, то они сближаются:
Чтобы найти скорость сближения двух объектов, движущихся навстречу друг другу, надо сложить их скорости:
Скорость сближения больше, чем скорость каждого из них.
Скорость, время и расстояние связаны между собой формулой пути:
Рассмотрим некоторые задачи на встречное движение.
Задача 1
Два велосипедиста выехали навстречу друг другу. Скорость одного из низ 12 км/ч, а другого — 10 км/ч. Через 3 часа они встретились. Какое расстояние было между ними в начале пути?
Решение:
Условие задач на движение удобно оформлять в виде таблицы:
|
v, км/ч |
t, ч |
s, км |
|
|
I велосипедист |
12 |
3 |
? |
|
II велосипедист |
10 |
3 |
? |
1) 12+10=22 (км/ч) скорость сближения велосипедистов
2) 22∙3=66 (км) было между велосипедистами в начале пути.
Ответ: 66 км.
Задача 2
Два поезда идут навстречу друг другу. Скорость одного из них 50 км/ч, скорость другого — 60 км/ч. Сейчас между ними 440 км. Через сколько часов они встретятся?
Решение:
|
v, км/ч |
t, ч |
s, км |
|
|
I поезд |
60 |
? |
? |
|
II поезд |
50 |
? |
? |
1) 60+50=110 (км/ч) скорость сближения поездов
2) 440:110=4 (ч) время, через которое поезда встретятся.
Ответ: через 4 ч.
Задача 3.
Два пешехода находились на расстоянии 20 км друг от друга. Они вышли одновременно навстречу друг другу и встретились через 2 часа. Скорость одного пешехода 6 км/ч. Найти скорость другого пешехода.
|
v, км/ч |
t, ч |
s, км |
|
|
I пешеход |
6 |
2 |
? |
|
II пешеход |
? |
2 |
? |
1) 20:2=10 (км/ч) скорость сближения пешеходов
2) 10-6=4 (км/ч) скорость другого пешехода.
Ответ: 4 км/ч.
— простые задачи на скорость, время и расстояние;
— задачи на встречное и противоположное движение;
— задачи на движение в одном направлении (на сближение и удаление);
— решение задач на движение по реке.
Скорость, время и расстояние: определения, обозначения, формулы
скорость = расстояние: время — формула нахождения скорости;
время = расстояние: скорость — формула нахождения времени;
расстояние = скорость · время — формула нахождения расстояния.
Скорость – это расстояние, пройденное за единицу времени: за 1 секунду, за 1 минуту, за 1 час и так далее.
Пример обозначения: 7 км/ч (читается: семь километров в час).
Если весь путь проходится с одинаковой скоростью, то такое движение называется равномерным.
На сайте представлены калькуляторы онлайн, с помощью которых можно перевести скорость, время и расстояние в другие единицы измерения:
1.Конвертер единиц измерения скорости
2.Конвертер единиц измерения времени
3.Конвертер единиц измерения расстояния (длины)
Примеры простых задач.
Задача 1.
Автомобиль проехал 180 км за 2 часа. Чему равна скорость автомобиля?
Решение: 180:2=90 (км/ч.)
Ответ: Скорость автомобиля равна 90 км/ч.
Задача 2.
Автобус проехал путь в 240 км со скоростью 80 км/ч. Сколько времени ехал автобус?
Решение: 240:80=3 (ч.)
Ответ: Автобус проехал 3 часа.
Задача 3.
Грузовик ехал 5 часов со скоростью 70 км/ч. Какое расстояние проехал грузовик за это время?
Решение: 70 · 3 = 350 (км)
Ответ: Грузовик за 5 часов проехал 350 км.
Задачи на встречное движение
В таких задачах два объекта движутся навстречу друг другу.
Задачи на встречное движение можно решать двумя способами:
1. Найти значения скорости, времени и расстояния для каждого объекта.
2. Найти скорость сближения объектов (как сумму их скоростей), общие время и расстояние. Скорость сближения — это расстояние, пройденное двумя объектами навстречу друг другу за единицу времени.
Задача 4.
Из двух пунктов навстречу друг другу одновременно выехали два поезда и встретились через 3 часа. Первый поезд ехал со скоростью 80 км/ч, а второй – со скоростью 70 км/ч. На каком расстоянии друг от друга находятся пункты?
Решение:
Первый способ. Найти расстояние, которое проехал каждый автобус, и сложить полученные данные:
80*3=240 (км) – проехал 1й автобус, 70*3=210 (км) – проехал 2й поезд,
240+210=450 (км) – проехали два поезда.
Второй способ. Найти скорость сближения поездов, то есть на сколько сокращалось расстояние между ними каждый час; а затем найти расстояние:
80+70=150 (км/ч), 150*3=450 (км).
Ответ: города находятся на расстоянии 450 км.
Задача 5.
Из двух городов навстречу друг другу одновременно выехали два автобуса. Первый автобус ехал со скоростью 80 км/ч, а второй – со скоростью 70 км/ч. Какое расстояние будет между ними через 2 часа, если расстояние между городами 450 км?
Решение:
Первый способ. Определить, сколько километров проехал каждый автобус и найти расстояние, которое осталось проехать:
80*2=160 (км)-проехал 1й автобус, 70*2=140 (км)-проехал 2й автобус,
160+140=300 (км)-проехали два автобуса, 450-300=150 (км)-осталось проехать.
Второй способ. Найти скорость сближения автобусов и умножить ее на время в пути.
80*70=150 (км/ч) – скорость сближения; 150*2=300 (км) – проехали два автобуса; 450-300=150 (км) – осталось проехать.
Ответ: Через 2часа расстояние между автобусами будет 150 км.
Задачи на движение в противоположных направлениях
В таких задачах два объекта движутся в противоположных направлениях, отдаляясь друг от друга. В таком типе задачи используется скорость удаления. Задачи на движение в противоположных направлениях также можно решить двумя способами:
1. Найти значения скорости, времени и расстояния для каждого объекта.
2. Найти скорость удаления объектов (как сумму их скоростей), общие время и расстояние. Скорость удаления — это расстояние, которое увеличивается за единицу времени между двумя объектами, двигающимися в противоположных направлениях.
Задача 6.
Два автомобиля выехали одновременно из одного и того же пункта в противоположных направлениях. Скорость первого автомобиля 100 км/ч, скорость второго – 70 км/ч. Какое расстояние будет между автомобилями через 4 часа?
Решение:
Первый способ. Определить расстояние, которое проехал каждый автомобиль и найти сумму полученных результатов:
1) 100 · 4 = 400 (км) – проехал первый автомобиль
2) 70 · 4 = 280 (км) – проехал второй автомобиль
400 + 280 = 680 (км)
Второй способ. Найти скорость удаления, то есть значение увеличения расстояния между автомобилями за каждый час, а затем скорость удаления умножить на время в пути.
100 + 70= 170 км/ч – это скорость удаления автомобилей.
170 · 4 = 680 (км)
Ответ: Через 4 часа между автомобилями будет 680 км.
Задача 7.
Из двух населённых пунктов, расстояние между которыми 40 км, вышли в противоположных направлениях два туриста. Первый турист шёл со скоростью 4 км/ч, а второй — 5 км/ч. Какое расстояние между туристами будет через 5 часов?
Решение:
Первый способ. Определить сколько километров прошёл каждый из туристов за 5 часов, сложить полученные результаты, а затем к полученному расстоянию прибавить расстояние между населенными пунктами.
1) 4 · 5 = 20 (км) – прошёл первый турист;
2) 5 · 5 = 25 (км) – прошёл второй турист;
3) 20 + 25 = 45 (км);
4) 45 + 40 = 85 (км).
Второй способ. Найти скорость удаления пешеходов, затем найти пройденное расстояние, к полученному результату прибавить расстоянием между населёнными пунктами.
4 + 5 = 9 (км/ч);
9 · 5 = 45 (км);
45 + 40 = 85 (км);
Ответ: Через 5 часов расстояние между пешеходами будет 85 км.
Задачи на движение в одном направлении
В таких задачах два объекта движутся в одном направлении с разной скоростью, при этом они сближаются друг с другом или отдаляются друг от друга. Соответственно находится скорость сближения или скорость удаления объектов.
Формула нахождения скорости сближения или удаления двух объектов, которые движутся в одном направлении: из большей скорости вычесть меньшую.
Задача 8.
Из города выехал автомобиль со скоростью 40 км/ч. Через 4 часа вслед за ним выехал второй автомобиль со скоростью 60 км/ч. Через сколько часов второй автомобиль догонит первый?,
Решение:
Задачу можно решить с помощью уравнения.
В этом случае скорость первого автомобиля 40 км/час, время в пути на 4 часа больше, чем время второго автомобиля (или t+4). Скорость второго автомобиля 60 км/час, время в пути – t. Расстояние оба автомобиля проехали одинаковое. Поэтому можно составить уравнение: 40*(t+4)=60*t. Отсюда получаем t=8 (часов) – время в пути второго автомобиля, за которое он догонит первый.
Решение задачи без использования уравнения.
Так как на момент выезда второго автомобиля из города первый уже был в пути 4 часа, то за это время он успел удалиться от города на: 40 · 4 = 160 (км).
Второй автомобиль движется быстрее первого, значит, каждый час расстояние между автомобилями будет сокращаться на разность их скоростей: 60 — 40 = 20 (км/ч) – это скорость сближения.
Разделив расстояние между автомобилями на скорость их сближения, можно узнать, через сколько часов они встретятся: 160 : 20 = 8 (ч)
Ответ: Второй автомобиль догонит первый через 8 часов.
Задача 9.
Из двух посёлков между которыми 5 км, одновременно в одном направлении вышли два пешехода. Скорость пешехода, идущего впереди, 4 км/ч, а скорость пешехода, идущего позади 5 км/ч. Через сколько часов после выхода второй пешеход догонит первого?
Решение: Так как второй пешеход движется быстрее первого, то каждый час расстояние между ними будет сокращаться. Значит можно определить скорость сближения пешеходов: 5 — 4 = 1 (км/ч).
Оба пешехода вышли одновременно, значит расстояние между ними равно расстоянию между посёлками (5 км). Разделив расстояние между пешеходами на скорость их сближения, узнаем через сколько второй пешеход догонит первого: 5 : 1 = 5 (ч)
Ответ: Через 5 часов второй пешеход догонит первого.
Задача 10.
Два автомобиля выехали одновременно из одного и того же пункта в одном направлении. Скорость первого автомобиля 80 км/ч, а скорость второго – 40 км/ч.
1) Чему равна скорость удаления между автомобилями?
2) Какое расстояние будет между автомобилями через 3 часа?
3) Через сколько часов расстояние между ними будет 200 км?
Решение:
1) 80 — 40 = 40 (км/ч) — скорость удаления автомобилей друг от друга.
2) 40 · 3 = 120 (км) – расстояние между ними через 3 часа./
3) 200 : 40 = 5 (ч) – время, через которое расстояние между автомобилями станет 200 км.
Ответ:
1) Скорость удаления между автомобилями равна 40 км/ч.
2) Через 3 часа между автомобилями будет 120 км.
3) Через 5 часов между автомобилями будет расстояние в 200 км.
Задачи на движение по реке
Рассмотрим задачи, в которых речь идёт о движении объекта по реке. Скорость любого объекта в стоячей воде называют собственной скоростью этого объекта.
Чтобы узнать скорость объекта, который движется по течению реки, надо к собственной скорости объекта прибавить скорость течения реки. Чтобы узнать скорость объекта, который движется против течения реки, надо из собственной скорости объекта вычесть скорость течения реки.
Задача 11.
Лодка движется по реке. За сколько часов она преодолеет расстояние 120 км, если ее собственная скорость 27 км/ч, а скорость течения реки 3 км/ч?
Решение:
1) лодка движется по течению реки.
27 + 3 = 30 (км/ч) – скорость лодки по течению реки.
120 : 30 = 4 (ч) – проплывет путь.
2) лодка движется против течения реки.
27 — 3 = 24 (км/ч) — скорость лодки против течения реки
120 : 24 = 5 (ч) – проплывет путь.
Ответ:
1) При движении по течению реки лодка потратит 4 часа на путь.
2) При движении против течения реки лодка потратит 5 часов на путь.
Итак, для решения задач на движение:
- Основная формула:S=ν*t;
- Нужно сделать чертеж, который поможет определить тип задачи.
- Все цифры нужно привести в единые единицы измерения: длина и время
Заключение.
Решая много задач по данной теме, ученик обязательно научится быстро ориентироваться в понятиях «скорость», «время» и «расстояние» и быстро решать задачи всех типов.
Весь курс начальной школы (за 1-4 классы) в краткой форме на сайте edu.intmag24.ru. С помощью курса можно быстро повторить основные моменты и правила по предметам: русский язык, математика, окружающий мир.
Для решения более сложных задач на движение посмотрите, как составлять схемы и таблицы данных для наглядного представления и структурирования данных.
Содержание:
- § 1 Формула одновременного движения
- § 2 Задачи на встречное движение
- § 3 Задачи на движение вдогонку
- § 4 Задачи на движение в противоположных направлениях
- § 5 Задачи на движение с отставанием
- § 6 Краткие итоги по теме урока
§ 1 Формула одновременного движения
С формулами одновременного движения мы сталкиваемся при решении задач на одновременное движение. Умение решать ту или иную задачу на движение зависит от некоторых факторов. Прежде всего, необходимо различать основные типы задач.
Задачи на одновременное движение условно делятся на 4 типа: задачи на встречное движение, задачи на движение в противоположных направлениях, задачи на движение вдогонку и задачи на движение с отставанием.
Основными компонентами этих типов задач являются:
пройденный путь – S, скорость — ʋ, время – t.
Зависимость между ними выражается формулами:
S = ʋ · t, ʋ = S : t, t = S : ʋ.
Помимо названных основных компонентов при решении задач на движение мы можем столкнуться с такими компонентами, как: скорость первого объекта — ʋ1, скорость второго объекта – ʋ2, скорость сближения – ʋсбл., скорость удаления – ʋуд., время встречи – tвстр., первоначальное расстояние – S0 и т.д.
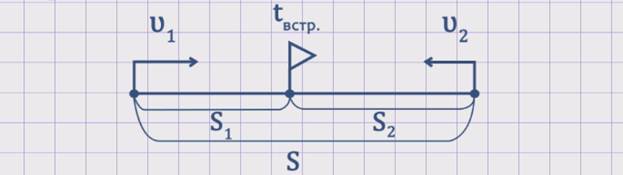
§ 2 Задачи на встречное движение
При решении задач данного типа применяются следующие компоненты: скорость первого объекта — ʋ1; скорость второго объекта — ʋ2; скорость сближения – ʋсбл.; время до встречи – tвстр.; путь (расстояние), пройденный первым объектом – S1; путь (расстояние), пройденный вторым объектом — S2; весь путь, пройденный обоими объектами – S.
Схема к задачам такого типа выглядит следующим образом:
Зависимость между компонентами задач на встречное движение выражается следующими формулами:
1.первоначальное расстояние между объектами можно вычислить по следующим формулам: S = ʋсбл. · tвстр. или S = S1 + S2;
2.скорость сближения находится по формулам: ʋсбл. = S : tвстр. или ʋсбл. = ʋ1 + ʋ2;
3.время встречи вычисляется следующим образом:
tвстр. = S : ʋсбл., tвстр. = S1 : ʋ1 или tвстр. = S2 : ʋ2.
Рассмотрим применение данных формул на примере следующей задачи.
Два теплохода плывут навстречу друг другу. Скорости теплоходов 35 км/ч и 28 км/ч. Через какое время они встретятся, если расстояние между ними 315 км?
ʋ1 = 35 км/ч, ʋ2 = 28 км/ч, S = 315 км, tвстр. = ? ч.
Чтобы найти время встречи, необходимо знать первоначальное расстояние и скорость сближения, так как tвстр. = S : ʋсбл. Поскольку расстояние известно по условию задачи, найдем скорость сближения. ʋсбл. = ʋ1 + ʋ2 = 35 + 28 = 63 км/ч. Теперь можем найти и искомое время встречи. tвстр. = S : ʋсбл = 315 : 63 = 5 ч. Получили, что теплоходы встретятся через 5 часов.
§ 3 Задачи на движение вдогонку
При решении задач данного типа применяются следующие компоненты: скорость первого объекта – ʋ1; скорость второго объекта — ʋ2; скорость сближения – ʋсбл.; время до встречи – tвстр.; путь (расстояние), пройденный первым объектом – S1; путь (расстояние), пройденный вторым объектом – S2; первоначальное расстояние между объектами – S.
Схема к задачам такого типа выглядит следующим образом:
Зависимость между компонентами задач на движение вдогонку выражается следующими формулами:
1.Первоначальное расстояние между объектами можно вычислить по следующим формулам:
S = ʋсбл. · tвстр.илиS = S1 — S2;
2.скорость сближения находится по формулам: ʋсбл. = S : tвстр. или ʋсбл. = ʋ1 — ʋ2;
3.Время встречи вычисляется следующим образом:
tвстр. = S : ʋсбл., tвстр. = S1 : ʋ1 или tвстр. = S2 : ʋ2.
Рассмотрим применение данных формул на примере следующей задачи.
Тигр погнался за оленем и догнал его через 7 минут. Каково первоначальное расстояние между ними, если скорость тигра равна 700 м/мин, а скорость оленя — 620 м/мин?
ʋ1 = 700 м/мин, ʋ2 = 620 м/мин, S = ? м, tвстр. = 7 мин.
Чтобы найти первоначальное расстояние между тигром и оленем, необходимо знать время встречи и скорость сближения, так как S =tвстр. · ʋсбл. Поскольку время встречи известно по условию задачи, найдем скорость сближения. ʋсбл. = ʋ1 — ʋ2 = 700 – 620 = 80 м/мин. Теперь можем найти и искомое первоначальное расстояние. S =tвстр. · ʋсбл = 7 · 80 = 560 м. Получили, что первоначальное расстояние между тигром и оленем составляло 560 метров.
§ 4 Задачи на движение в противоположных направлениях
При решении задач данного типа применяются следующие компоненты: скорость первого объекта – ʋ1; скорость второго объекта – ʋ2; скорость удаления – ʋуд.; время в пути – t.; путь (расстояние), пройденный первым объектом – S1; путь (расстояние), пройденный вторым объектом – S2; первоначальное расстояние между объектами – S0; расстояние, которое будет между объектами через определенное время – S.
Схема к задачам такого типа выглядит следующим образом:
Зависимость между компонентами задач на движение в противоположных направлениях выражается следующими формулами:
1.Конечное расстояние между объектами можно вычислить по следующим формулам:
S = S0 + ʋуд.· tили S = S1 + S2 + S0; а первоначальное расстояние – по формуле: S0 = S — ʋуд. · t.
2.Скорость удаления находится по формулам:
ʋуд. = (S1 + S2) : t илиʋуд. = ʋ1 + ʋ2;
3.Время в пути вычисляется следующим образом:
t = (S1 + S2) : ʋуд., t = S1 : ʋ1или t = S2 : ʋ2.
Рассмотрим применение данных формул на примере следующей задачи.
Два автомобиля выехали из автопарков одновременно в противоположных направлениях. Скорость одного – 70 км/час, другого – 50 км/час. Какое расстояние будет между ними через 4 часа, если расстояние между автопарками составляет 45 км?
ʋ1 = 70 км/ч, ʋ2 = 50 км/ч, S0 = 45 км, S = ? км, t = 4 ч.
Чтобы найти расстояние между автомобилями в конце пути, необходимо знать время в пути, первоначальное расстояние и скорость удаления, так как S = ʋуд. · t+ S0Поскольку время и первоначальное расстояние известны по условию задачи, найдем скорость удаления. ʋуд. = ʋ1 + ʋ2 = 70 + 50 = 120 км/ч. Теперь можем найти и искомое расстояние. S = ʋуд. · t+ S0 = 120 · 4 + 45 = 525 км. Получили, что через 4 часа между автомобилями будет расстояние в 525 км
§ 5 Задачи на движение с отставанием
При решении задач данного типа применяются следующие компоненты: скорость первого объекта – ʋ1; скорость второго объекта – ʋ2; скорость удаления – ʋуд.; время в пути – t.; первоначальное расстояние между объектами – S0; расстояние, которое станет между объектами через определенное количество времени – S.
Схема к задачам такого типа выглядит следующим образом:
Зависимость между компонентами задач на движение с отставанием выражается следующими формулами:
1.Первоначальное расстояние между объектами можно вычислить по следующей формуле: S0 = S — ʋуд.· t; а расстояние, которое станет между объектами через определенное время, — по формуле: S = S0 + ʋуд. · t;
2.Скорость удаления находится по формулам: ʋуд.= (S – S0) : t или ʋуд. = ʋ1 — ʋ2;
3.Время вычисляется следующим образом: t = (S – S0) : ʋуд.
Рассмотрим применение данных формул на примере следующей задачи:
Из двух городов в одном направлении выехали две машины. Скорость первой – 80 км/ч, скорость второй – 60 км/ч. Через сколько часов между машинами будет 700 км, если расстояние между городами 560 км?
ʋ1 = 80 км/ч, ʋ2 = 60 км/ч, S = 700 км, S0 = 560 км, t = ? ч.
Чтобы найти время, необходимо знать первоначальное расстояние между объектами, расстояние в конце пути и скорость удаления, так как t = (S – S0) : ʋуд. Поскольку оба расстояния известны по условию задачи, найдем скорость удаления. ʋуд. = ʋ1 — ʋ2 = 80 – 60 = 20 км/ч. Теперь можем найти и искомое время. t = (S – S0) : ʋуд = (700 – 560) : 20 = 7ч. Получили, что через 7 часов между машинами будет 700 км.
§ 6 Краткие итоги по теме урока
При одновременном встречном движении и движении вдогонку расстояние между двумя движущимися объектами уменьшается (до встречи). За единицу времени оно уменьшается на ʋсбл., а за все время движения до встречи оно уменьшится на первоначальное расстояние S. Значит, в обоих случаях первоначальное расстояние равно скорости сближения, умноженной на время движения до встречи: S = ʋсбл. · tвстр.. Разница лишь в том, что при встречном движении ʋсбл. = ʋ1 + ʋ2, а при движении вдогонку ʋсбл. = ʋ1 — ʋ2.
При движении в противоположных направлениях и с отставанием расстояние между объектами увеличивается, поэтому встреча не произойдет. За единицу времени оно увеличивается на ʋуд., а за все время движения оно увеличится на значение произведения ʋуд.· t. Значит, в обоих случаях расстояние между объектами в конце пути равно сумме первоначального расстояния и произведения ʋуд.· t. S = S0 + ʋуд.· t.Разница лишь в том, что при противоположном движении ʋуд. = ʋ1 + ʋ2, а при движении с отставанием ʋуд. = ʋ1 — ʋ2.
Список использованной литературы:
- Петерсон Л.Г. Математика. 4 класс. Часть 2. / Л.Г. Петерсон. – М.: Ювента, 2014. – 96 с.: ил.
- Математика. 4 класс. Методические рекомендации к учебнику математики «Учусь учиться» для 4 класса / Л.Г. Петерсон. – М.: Ювента, 2014. – 280 с.: ил.
- Зак С.М. Все задания к учебнику математики для 4 класса Л.Г. Петерсон и комплекту самостоятельных и контрольных работ. ФГОС. – М.: ЮНВЕС, 2014.
- CD-ROM. Математика. 4 класс. Сценарии уроков к учебнику к 2 части Петерсон Л.Г. – М.: Ювента, 2013.
Использованные изображения:
Задачи на встречное движение
Рассмотрим задачи, в которых речь идёт о встречном движении. В таких задачах два каких-нибудь объекта движутся навстречу друг другу. Задачи на встречное движение можно решать двумя способами.
Задача 1. Два автомобиля выехали одновременно из двух населённых пунктов и встретились через 4 часа. Первый автомобиль ехал со скоростью 100 км/ч, а второй — со скоростью 70 км/ч. На каком расстоянии друг от друга находятся населённые пункты?
Решение: Из условия задачи известны скорость каждого автомобиля и время, которое автомобили были в пути. Значит, можно найти расстояние, которое проехал каждый автомобиль до встречи. Для этого нужно скорость умножить на время:
1) 100 · 4 = 400 (км) — проехал первый автомобиль,
2) 70 · 4 = 280 (км) — проехал второй автомобиль.
Найдя сумму полученных результатов, узнаем расстояние между населёнными пунктами:
400 + 280 = 680 (км).
Данную задачу можно решить и другим способом. Каждый час расстояние между автомобилями сокращалось на 170 километров (100 + 70), 170 км/ч — это скорость сближения автомобилей. За 4 часа они проехали расстояние:
Таким образом, задачу на встречное движение можно решить двумя способами:
| 1-й способ: | 2-й способ: |
|---|---|
| 1) 100 · 4 = 400 (км) | 1) 100 + 70 = 170 (км/ч) |
| 2) 70 · 4 = 280 (км) | 2) 170 · 4 = 680 (км) |
| 3) 400 + 280 = 680 (км) |
Ответ: Населённые пункты находятся на расстоянии 680 км.
Задача 2. Из двух посёлков навстречу друг другу вышли одновременно два пешехода. Скорость первого пешехода 4 км/ч, а скорость второго пешехода 5 км/ч. Какое расстояние будет между пешеходами через 5 часов после выхода, если расстояние между посёлками 70 км?
Решение: Сначала можно определить сколько километров прошёл каждый из пешеходов за 5 часов, для этого скорость пешеходов умножим на 5:
1) 4 · 5 = 20 (км) — прошёл первый пешеход,
2) 5 · 5 = 25 (км) — прошёл второй пешеход.
Затем можно найти общий путь, пройденный двумя пешеходами за 5 часов:
Теперь можно найти расстояние между пешеходами, отняв от общего расстояния между посёлками 45 уже пройденных километров:
У данной задачи есть и второй вариант решения. Можно сначала найти скорость сближения пешеходов:
Затем найти пройденное расстояние, умножив скорость сближения (9 км/ч) на время движения пешеходов (5 ч):
А теперь, для нахождения расстояния между пешеходами, вычесть пройденное расстояние (45 км) из общего:
Таким образом, данная задача имеет два варианта решения:
| 1-й способ: | 2-й способ: |
|---|---|
| 1) 4 · 5 = 20 (км) | 1) 4 + 5 = 9 (км/ч) |
| 2) 5 · 5 = 25 (км) | 2) 9 · 5 = 45 (км) |
| 3) 20 + 25 = 45 (км) | 3) 70 — 45 = 25 (км) |
| 4) 70 — 45 = 25 (км) |
Ответ: Через 5 часов расстояние между пешеходами будет 25 км.
Как решать задачи на движение на ЕГЭ по математике 2019
Классическим примером текстовой задачи, которая может встретиться вам на ЕГЭ, является задача на движение. Эти задачи довольно разнообразны и включают в себя: задачи на движение навстречу, задачи на движение вдогонку, задачи на движение по реке. И поэтому вопрос, как же решать задачи на движение, иногда ставят учеников в тупик.
Научиться решать такие задачи довольно легко, для этого нужно знать алгоритм, состоящий всего из 3 шагов.
Формула, которую обязательно нужно знать, и секрет, как ее легко запомнить
Для решения любой задачи на движение вам обязательно нужно знать всего одну формулу, которая вам уже давно известна:И уметь правильно выражать из этой формулы скорость и время:Многие ученики путаются при записи этих формул, допуская ошибки. Чтобы раз и навсегда запомнить формулы нахождения расстояния, скорости и времени, просто нарисуй треугольник. В верхнем углу треугольника напиши S, а внизу — V и t. Проведи горизонтальную черту между ними. Теперь мы можем закрыть рукой ту величину, которую нам нужно найти, и увидим формулу нахождения этой величины. Например, нам нужно найти расстояние. Закрываем рукой S, и на нашем рисунке останется V t – это и есть формула нахождения расстояния. Или нам нужно найти время. Закрываем рукой t, и на нашем рисунке остается – формула нахождения времени. Нужно найти скорость? Закрываем рукой V, получаем – формулу нахождения скорости. Главное запомнить, что S должна быть в верхнем углу. Это можно сделать, например, с помощью ассоциации, что S похожа на змею, а змея – хозяйка горы, поэтому она на вершине. Вот как выглядит такой магический треугольник:
3 простых шага решения задачи на движение
Чтобы правильно решить задачу на движение нужно:
- Определить неизвестное и составить таблицу на основании условия задачи.
- Составить уравнение на основании таблицы.
- Вернуться к условиям задачи и записать правильный ответ.
Давайте подробнее разберем каждый шаг:
- Вначале нам нужно внимательно прочитать условие задачи и определить, что же взять за переменную Х. Чаще всего в задачах на движение удобнее всего за переменную Х обозначить скорость. Если же скорость нам прямо дана в условиях задачи, то за переменную Х обозначаем время. Если в условиях задачи прямо указаны значения и скорости, и времени, тогда за переменную Х берем расстояние. Затем из условий задачи определить все, что нам известно и занести в таблицу.
- На основании полученной таблицы составляем уравнение и решаем его. После решения уравнения не торопимся записывать ответ. Ведь нахождение Х – это не всегда ответ к исходной задаче. Такую ошибку совершают многие ученики: фактически правильно решив задачу, они записывают неправильный ответ.
- После решения уравнения возвращаемся к условиям задачи и смотрим, что же требовалось найти. Находим неизвестное и записываем ответ.
Задачи на движение бывают разными. В таких задачах участники движения могут двигаться навстречу друг другу, вдогонку, они могут двигаться по реке (против течения или по течению). Каждая из этих задач имеет особенности решения, о которых мы поговорим ниже и разберем на примерах.
Задачи на движение вдогонку: примеры с решением
При решении задачи, по условия которой оба участника движения двигаются в одном направлении, как правило, сравнивается время их движения. Необходимо запомнить правила:
- Если время движения сравнивается (то есть присутствуют слова больше/меньше), то мы приравниваем время и прибавляем слагаемое. То есть чтобы получить большее время, мы прибавляем к меньшему времени что-то еще (из условий задачи).
- Если условия задачи содержат общее время, то дроби, выражающее время, складываются.
Давайте разберем, как работают эти правила при решении задач.
Задача 1
Велосипедист и автомобилист одновременно выехали из пункта А в пункт Б, расстояние между которыми равно 50 км. Известно, что скорость автомобилиста на 40 км/ч больше, чем у велосипедиста, в результате чего автомобилист приехал в пункт Б на 4 часа раньше. Найдите скорость велосипедиста.
1. Необходимо определить, что взять за переменную Х и составить таблицу. Вспоминаем, что удобнее всего за Х обозначить скорость в том случае, если она прямо не указано в условиях задачи.
В нашем случае скорость в условиях задачи не указана, поэтому скорость велосипедиста обозначаем за Х.
Составляем таблицу, данные для которой берем из условий задачи.
Итак, расстояние (S) нам известно – 50 км, скорость велосипедиста – х, скорость автомобилиста на 40 км/ч больше, значит она равна х + 40. Чтобы определить время вспоминаем формулу t = S / V и подставляем в нее наши значения. Время, затраченное велосипедистом, получится 50 / х, а время, затраченное автомобилистом — 50 / (х + 40).2. На основании таблицы и условий задачи необходимо составить уравнение.
Из условий задачи нам известно, что автомобилист приехал раньше велосипедиста на 4 часа (смотрим наше первое правило). Это значит, что велосипедист затратил на 4 часа больше времени, чем автомобилист. Следовательно,
50 / (х + 40) + 4 = 50 / х
Решаем полученное уравнение, для этого приводим наши дроби к одному знаменателю:
50х + 4х (х + 40) – 50 (х+40) / х (х + 40) = 0
(50х + 4х 2 + 160х – 50х – 2000) / х (х+40) = 0
(4х 2 + 160х – 2000) / (х 2 + 40х) = 0
Умножим обе части уравнение на х 2 + 40х:
4х 2 + 160х – 2000 = 0
Разделим обе части уравнения на 4:
х 2 + 40х – 500 = 0
D = 40 2 – 4 * 1 * (-500) = 3600
Далее находим корни уравнения:
х2 = — 50
3. Возвращаемся к условиям задачи и вспоминаем, что же требовалось найти.
Нам нужно было определить скорость велосипедиста, которую мы обозначили за Х.
Скорость велосипедиста должна быть положительна, поэтому х2 не подходит по смыслу задачи. Следовательно, нас интересует только х1 и скорость велосипедиста равна 10 км/ч.
Задача 2
Велосипедист выехал с постоянной скоростью из города А в город Б, расстояние между которыми равно 80 км. На следующий день он поехал обратно, при этом его скорость была на 2 км/ч больше прежней. По пути велосипедист останавливался и отдыхал 2 часа. В итоге на возвращение из города Б в город А у него ушло времени столько же, сколько на путь из города А в город Б. Найдите скорость велосипедиста на пути из города А в город Б.
1. Обозначим скорость велосипедиста на пути из города А в город Б как переменную Х.
Из условий задачи: расстояние — 80 км, скорость велосипедиста во второй день – х. Его скорость во второй день была на 2 км/ч больше, чем в первый день, т.е. в первый день она была ниже, следовательно, скорость велосипедиста в первый день равна х – 2. Определим затраченное велосипедистом время на путь по формуле t = S / V. Тогда время, затраченное в первый день на путь равно 80 / х, во второй день — 80 / (х + 2).2. На основании таблицы и условий задачи составим уравнение.
Из условий задачи нам известно, что во второй день велосипедист останавливался и отдыхал 2 часа, следовательно, в пути он провел на 2 часа меньше (смотрим наше первое правило). Также нам известно, что общее затраченное велосипедистом время в первый и во второй дни равно. Следовательно:
80 / (х + 2) + 2 = (80 / х)
Решаем полученное уравнение, для чего приводим дроби к общему знаменателю:
(80х + 160 – 80х – 2х (х+2)) / х (х + 2) = 0
Умножаем обе части уравнения на х (х + 2):
160 – 2х 2 + 4х = 0
— 2х 2 — 4х + 160 = 0
Делим обе части уравнения на -2:
D = 2 2 – 4 * 1 * (-80) = 4 + 320 = 324
Тогда корни уравнения равны:
3. Возвращаемся к условиям задачи. Нам необходимо было найти скорость велосипедиста на пути из города А в город Б, которую мы обозначали за Х.
Скорость должна быть положительна, поэтому х2 = — 10 не подходит по смыслу задачи. Следовательно, скорость велосипедиста равна 8.
Задачи на движение навстречу: примеры с решением
Главное, что нужно помнить о движении навстречу: скорости участников движения складываются.
В тех случаях, когда нам неизвестно общее расстояние, то есть мы не можем его определить из условий задачи и из составленных уравнений, данное расстояние следует принимать за единицу.
Примеры решения задач на движение навстречу:
Задача 1
Из города А в город Б выехал автомобилист, через 3 часа навстречу ему выехал мотоциклист со скоростью 60 км/ч. Автомобилист и мотоциклист встретились на расстоянии 350 км от города А. Расстояние между городами А и Б равно 470 км. Найдите скорость автомобилиста.
1. Обозначим скорость автомобилиста как Х.
Автомобилист и мотоциклист встретились на расстоянии 350 км от города А. Следовательно, автомобилист проехал 350 км, а мотоциклист 470 – 350 = 120 км.
Составим таблицу:2. Составим уравнении на основании таблицы и условий задачи.
Из условий задачи известно, что автомобилист ехал на 3 часа дольше, чем мотоциклист (пользуемся первым правилом, которое разбирали при решении задач на движение вдогонку). Следовательно:
Решаем полученное уравнение:
3. Возвращаемся к условиям задачи. Нам необходимо было найти скорость автомобилиста, которую мы обозначали за Х. Следовательно, скорость автомобилиста равна 70 км/ч.
Задача 2
Из городов А и Б одновременно навстречу друг другу выехали автомобилист и велосипедист. Автомобилист приехал в город А на 6 часов раньше, чем велосипедист приехал в город Б. Встретились они через 4 часа после начала движения. Сколько времени затратил автомобилист на путь из города Б в город А?
1. Время автомобилиста обозначим как Х.
Примем расстояние между городами А и Б за единицу. Остальные данные берем из условий задачи.
Составим таблицу:2. Составим уравнение на основании таблицы и условий задачи.
Известно, что велосипедист и автомобилист встретились через 4 часа после начала движения и в сумме преодолели все расстояние от города А до города Б. То есть все расстояние от города А до города Б было преодолено за 4 часа.
Вспоминаем, что при движении навстречу скорости движения участников складываются. Подставим в формулу пути известные нам данные:
((1 / х) + (1 / (х — 6))) * 4 = 1
Решаем полученное уравнение:
(4 / х) + (4 / (х — 6)) = 1
Приводим дроби к одному знаменателю:
(4х — 24 + 4х — х 2 + 6х) / (х (х — 6)) = 0
Делим обе части уравнения на х (х — 6), при условии, что х > 6:
-х 2 + 14х — 24 = 0
Умножим обе части уравнение на -1:
х 2 — 14х + 24 = 0
Находим дискриминант нашего квадратного уравнения:
D = 14 2 – 4 * 1 * 24 = 100
Находим корни уравнения:
х2 2 + 40х – 40х – 200 = 0
3. Возвращаемся к условию задачи. Нам необходимо было найти собственную скорость катера, которую мы обозначили за Х. Так как скорость не может быть отрицательной, то х1 = -15 противоречит условию задачи. Следовательно, собственная скорость катера равна 15 км/ч.
Задача 2
Моторная лодка вышла в 9:00 из пункта А в пункт Б, расстояние между которыми 30 км. Пробыв в пункте Б 3 часа, моторная лодка повернула назад и вернулась в пункт А в 20:00. Найдите скорость течения реки, если известно, что собственная скорость моторной лодки 8 км/ч.
1. Обозначим скорость течения реки за х. Остальные данные берем из условия задачи.
Составим таблицу:2. Составим уравнение.
Нам известно, что моторная лодка начала свое движение в 9:00, а закончила в 20:00, а также в течение этого времени пробыла без движения во время стоянки – 3 часа. Таким образом, общее время движения будет 20 – 9 – 3 = 8 часов. Когда речь идет об общем времени движения, то нам нужно сложить время движения по течению и время движения против течения (пользуемся вторым правилом, которое разбирали при решении задач на движение вдогонку). Получаем:
30 / (8+х) + 30 / (8-х) = 8
Решаем полученное уравнение. Для этого приводим дроби к общему знаменателю:
(30 (8+х) + 30 (8-х) – 8 (8-х) (8+х)) / (8-х) (8+х) = 0
Умножаем обе части уравнения на (8-х) (8+х):
240 + 30х + 240 – 30х – (64 – 8х) (8+х) = 0
480 – 512 – 64х + 64х – 8х 2 = 0
3. Возвращаемся к условию задачи. Нам необходимо было найти скорость течения, которую мы обозначили за х. Так как скорость не может быть отрицательной, то х1 = -2 противоречит условию задачи. Следовательно, скорость течения равна 2 км/ч.
Итак, мы разобрались, как решать задачи на движения. В ЕГЭ 2019 помимо задач на движение могут содержаться и другие текстовые задачи: на смеси и сплавы, на работу, на проценты. О том, как их решать, вы можете узнать на нашем сайте.
Задачи на движение
Задачи на движение (скорость, время и расстояние) являются одной из основных типов задач по математике, которые должен уметь решать каждый школьник. В данной статье рассмотрены все типы задач на движение:
— простые задачи на скорость, время и расстояние;
— задачи на встречное и противоположное движение;
— задачи на движение в одном направлении (на сближение и удаление);
— решение задач на движение по реке.
Скорость, время и расстояние: определения, обозначения, формулы
скорость = расстояние: время — формула нахождения скорости;
время = расстояние: скорость — формула нахождения времени;
расстояние = скорость · время — формула нахождения расстояния.
Скорость – это расстояние, пройденное за единицу времени: за 1 секунду, за 1 минуту, за 1 час и так далее.
Пример обозначения: 7 км/ч (читается: семь километров в час).
Если весь путь проходится с одинаковой скоростью, то такое движение называется равномерным.
На сайте представлены калькуляторы онлайн, с помощью которых можно перевести скорость, время и расстояние в другие единицы измерения:
Примеры простых задач.
Задача 1.
Автомобиль проехал 180 км за 2 часа. Чему равна скорость автомобиля?
Решение: 180:2=90 (км/ч.)
Ответ: Скорость автомобиля равна 90 км/ч.
Задача 2.
Автобус проехал путь в 240 км со скоростью 80 км/ч. Сколько времени ехал автобус?
Решение: 240:80=3 (ч.)
Ответ: Автобус проехал 3 часа.
Задача 3.
Грузовик ехал 5 часов со скоростью 70 км/ч. Какое расстояние проехал грузовик за это время?
Решение: 70 · 3 = 350 (км)
Ответ: Грузовик за 5 часов проехал 350 км.
Задачи на встречное движение
В таких задачах два объекта движутся навстречу друг другу.
Задачи на встречное движение можно решать двумя способами:
1. Найти значения скорости, времени и расстояния для каждого объекта.
2. Найти скорость сближения объектов (как сумму их скоростей), общие время и расстояние. Скорость сближения — это расстояние, пройденное двумя объектами навстречу друг другу за единицу времени.
Задача 4.
Из двух пунктов навстречу друг другу одновременно выехали два поезда и встретились через 3 часа. Первый поезд ехал со скоростью 80 км/ч, а второй – со скоростью 70 км/ч. На каком расстоянии друг от друга находятся пункты?
Решение:
Первый способ. Найти расстояние, которое проехал каждый автобус, и сложить полученные данные:
80*3=240 (км) – проехал 1й автобус, 70*3=210 (км) – проехал 2й поезд,
240+210=450 (км) – проехали два поезда.
Второй способ. Найти скорость сближения поездов, то есть на сколько сокращалось расстояние между ними каждый час; а затем найти расстояние:
80+70=150 (км/ч), 150*3=450 (км).
Ответ: города находятся на расстоянии 450 км.
Задача 5.
Из двух городов навстречу друг другу одновременно выехали два автобуса. Первый автобус ехал со скоростью 80 км/ч, а второй – со скоростью 70 км/ч. Какое расстояние будет между ними через 2 часа, если расстояние между городами 450 км?
Решение:
Первый способ. Определить, сколько километров проехал каждый автобус и найти расстояние, которое осталось проехать:
80*2=160 (км)-проехал 1й автобус, 70*2=140 (км)-проехал 2й автобус,
160+140=300 (км)-проехали два автобуса, 450-300=150 (км)-осталось проехать.
Второй способ. Найти скорость сближения автобусов и умножить ее на время в пути.
80*70=150 (км/ч) – скорость сближения; 150*2=300 (км) – проехали два автобуса; 450-300=150 (км) – осталось проехать.
Ответ: Через 2часа расстояние между автобусами будет 150 км.
Задачи на движение в противоположных направлениях
В таких задачах два объекта движутся в противоположных направлениях, отдаляясь друг от друга. В таком типе задачи используется скорость удаления. Задачи на движение в противоположных направлениях также можно решить двумя способами:
1. Найти значения скорости, времени и расстояния для каждого объекта.
2. Найти скорость удаления объектов (как сумму их скоростей), общие время и расстояние. Скорость удаления — это расстояние, которое увеличивается за единицу времени между двумя объектами, двигающимися в противоположных направлениях.
Задача 6.
Два автомобиля выехали одновременно из одного и того же пункта в противоположных направлениях. Скорость первого автомобиля 100 км/ч, скорость второго – 70 км/ч. Какое расстояние будет между автомобилями через 4 часа?
Решение:
Первый способ. Определить расстояние, которое проехал каждый автомобиль и найти сумму полученных результатов:
1) 100 · 4 = 400 (км) – проехал первый автомобиль
2) 70 · 4 = 280 (км) – проехал второй автомобиль
400 + 280 = 680 (км)
Второй способ. Найти скорость удаления, то есть значение увеличения расстояния между автомобилями за каждый час, а затем скорость удаления умножить на время в пути.
100 + 70= 170 км/ч – это скорость удаления автомобилей.
170 · 4 = 680 (км)
Ответ: Через 4 часа между автомобилями будет 680 км.
Задача 7.
Из двух населённых пунктов, расстояние между которыми 40 км, вышли в противоположных направлениях два туриста. Первый турист шёл со скоростью 4 км/ч, а второй — 5 км/ч. Какое расстояние между туристами будет через 5 часов?
Решение:
Первый способ. Определить сколько километров прошёл каждый из туристов за 5 часов, сложить полученные результаты, а затем к полученному расстоянию прибавить расстояние между населенными пунктами.
1) 4 · 5 = 20 (км) – прошёл первый турист;
2) 5 · 5 = 25 (км) – прошёл второй турист;
3) 20 + 25 = 45 (км);
4) 45 + 40 = 85 (км).
Второй способ. Найти скорость удаления пешеходов, затем найти пройденное расстояние, к полученному результату прибавить расстоянием между населёнными пунктами.
4 + 5 = 9 (км/ч);
9 · 5 = 45 (км);
45 + 40 = 85 (км);
Ответ: Через 5 часов расстояние между пешеходами будет 85 км.
Задачи на движение в одном направлении
В таких задачах два объекта движутся в одном направлении с разной скоростью, при этом они сближаются друг с другом или отдаляются друг от друга. Соответственно находится скорость сближения или скорость удаления объектов.
Формула нахождения скорости сближения или удаления двух объектов, которые движутся в одном направлении: из большей скорости вычесть меньшую.
Задача 8.
Из города выехал автомобиль со скоростью 40 км/ч. Через 4 часа вслед за ним выехал второй автомобиль со скоростью 60 км/ч. Через сколько часов второй автомобиль догонит первый?,
Решение:
Задачу можно решить с помощью уравнения.
В этом случае скорость первого автомобиля 40 км/час, время в пути на 4 часа больше, чем время второго автомобиля (или t+4). Скорость второго автомобиля 60 км/час, время в пути – t. Расстояние оба автомобиля проехали одинаковое. Поэтому можно составить уравнение: 40*(t+4)=60*t. Отсюда получаем t=8 (часов) – время в пути второго автомобиля, за которое он догонит первый.
Решение задачи без использования уравнения.
Так как на момент выезда второго автомобиля из города первый уже был в пути 4 часа, то за это время он успел удалиться от города на: 40 · 4 = 160 (км).
Второй автомобиль движется быстрее первого, значит, каждый час расстояние между автомобилями будет сокращаться на разность их скоростей: 60 — 40 = 20 (км/ч) – это скорость сближения.
Разделив расстояние между автомобилями на скорость их сближения, можно узнать, через сколько часов они встретятся: 160 : 20 = 8 (ч)
Ответ: Второй автомобиль догонит первый через 8 часов.
Задача 9.
Из двух посёлков между которыми 5 км, одновременно в одном направлении вышли два пешехода. Скорость пешехода, идущего впереди, 4 км/ч, а скорость пешехода, идущего позади 5 км/ч. Через сколько часов после выхода второй пешеход догонит первого?
Решение: Так как второй пешеход движется быстрее первого, то каждый час расстояние между ними будет сокращаться. Значит можно определить скорость сближения пешеходов: 5 — 4 = 1 (км/ч).
Оба пешехода вышли одновременно, значит расстояние между ними равно расстоянию между посёлками (5 км). Разделив расстояние между пешеходами на скорость их сближения, узнаем через сколько второй пешеход догонит первого: 5 : 1 = 5 (ч)
Ответ: Через 5 часов второй пешеход догонит первого.
Задача 10.
Два автомобиля выехали одновременно из одного и того же пункта в одном направлении. Скорость первого автомобиля 80 км/ч, а скорость второго – 40 км/ч.
1) Чему равна скорость удаления между автомобилями?
2) Какое расстояние будет между автомобилями через 3 часа?
3) Через сколько часов расстояние между ними будет 200 км?
Решение:
1) 80 — 40 = 40 (км/ч) — скорость удаления автомобилей друг от друга.
2) 40 · 3 = 120 (км) – расстояние между ними через 3 часа./
3) 200 : 40 = 5 (ч) – время, через которое расстояние между автомобилями станет 200 км.
Ответ:
1) Скорость удаления между автомобилями равна 40 км/ч.
2) Через 3 часа между автомобилями будет 120 км.
3) Через 5 часов между автомобилями будет расстояние в 200 км.
Задачи на движение по реке
Рассмотрим задачи, в которых речь идёт о движении объекта по реке. Скорость любого объекта в стоячей воде называют собственной скоростью этого объекта.
Чтобы узнать скорость объекта, который движется по течению реки, надо к собственной скорости объекта прибавить скорость течения реки. Чтобы узнать скорость объекта, который движется против течения реки, надо из собственной скорости объекта вычесть скорость течения реки.
Задача 11.
Лодка движется по реке. За сколько часов она преодолеет расстояние 120 км, если ее собственная скорость 27 км/ч, а скорость течения реки 3 км/ч?
Решение:
1) лодка движется по течению реки.
27 + 3 = 30 (км/ч) – скорость лодки по течению реки.
120 : 30 = 4 (ч) – проплывет путь.
2) лодка движется против течения реки.
27 — 3 = 24 (км/ч) — скорость лодки против течения реки
120 : 24 = 5 (ч) – проплывет путь.
Ответ:
1) При движении по течению реки лодка потратит 4 часа на путь.
2) При движении против течения реки лодка потратит 5 часов на путь.
Итак, для решения задач на движение:
- Основная формула:S=ν*t;
- Нужно сделать чертеж, который поможет определить тип задачи.
- Все цифры нужно привести в единые единицы измерения: длина и время
Заключение.
Решая много задач по данной теме, ученик обязательно научится быстро ориентироваться в понятиях «скорость», «время» и «расстояние» и быстро решать задачи всех типов. Получить карточки с задачами разных видов можно по ссылке.
Задачи на движение
Задачи на движение начинают проходить в 5 классе и решают все оставшиеся учебные годы вплоть до 11 класса. В ЕГЭ по математике вы найдете задачи на движение в задании 11, в котором собраны все текстовые задачи. Рассмотрим как надо решать задачи на движение из ЕГЭ. Но сначала немного теории.
Как решать задачи на движение
Решение задач на движение подчиняется четкому алгоритму, который состоит из нескольких этапов:
- Анализ данных.
- Составление таблицы.
- Составление уравнения.
- Решение уравнения.
Остановимся подробно на каждом пункте:
1. Первое, с чего нужно начать — медленно и вдумчиво прочитать условие задачи, то есть проанализировать данные.
Чтобы наглядно представить задачу, необходимо сделать рисунок и отобразить на нем все известные по условию задачи величины.
2. Второй шаг — составить таблицу по условию задачи, внести в таблицу известные величины и ввести неизвестные.
Таблица состоит из трех столбцов S, v и t (путь, скорость и время) и нескольких строк. При заполнении каждой строки сначала выбираем и заполняем тот столбец, информация о котором дана в задаче. Еще один столбец записываем в роли неизвестного (чаще всего, это то, что требуется найти в задаче). В третью, оставшуюся колонку вписываем связь характеристик из двух уже заполненных столбцов по формуле:
В таблице получается столько строчек, сколько каждый из объектов задачи действовал (то есть, перемещался) или мог бы действовать.
3. Следующий шаг — при помощи сделанного рисунка и заполненной таблицы составить уравнение или систему уравнений.
По окончании заполнения таблицы оказывается, что есть часть информации, которая не вошла в таблицу. Эта информация характеризует те значения величин в колонках, которые вычисляются в третью очередь, то есть по формуле. На основании этой информации и данных из третьей колонки составляем уравнение.
4. Решить полученное уравнение и прийти к ответу.
Когда уравнение составлено, последний шаг — это решить его, и, в конце концов, получить ответ.
Будьте внимательны, если за неизвестное вы приняли не то, что требуется найти в задаче. В этом случае следует выразить то, что нужно найти через полученное решение уравнения.
Если, решив уравнение, вы получили несколько ответов, то следует отобрать только имеющие смысл решения. Помните, что путь, скорость и время не могут быть отрицательными.
Примеры решения
Два велосипедиста одновременно отправляются в 60-километровый пробег. Первый едет со скоростью на 10 км/ч большей, чем второй, и прибывает к финишу на 3 часа раньше второго. Найдите скорость велосипедиста, пришедшего к финишу вторым.
В задаче требуется найти скорость второго, более медленного, велосипедиста. Примем его скорость за x. Заполним таблицу:
| v, км/ч | t, ч | S, км | |
| Первый велосипедист | x + 10 | 60 | |
| Второй велосипедист | x | 60 |
В условии задачи сказано, что первый велосипедист прибыл к финишу на 3 часа раньше второго. На основании этого составим уравнение:
Получаем два корня, x1 = 10 и x2 = –20. Второй корень не подходит, так как скорость не может быть отрицательной.
Виды задач на движение
Движение навстречу друг другу, движение в противоположных направлениях
Если два объекта движутся навстречу друг другу, то они сближаются:
При движении в противоположном направлении объекты удаляются:
В обоих случаях объекты как бы «помогают» друг другу преодолеть общее для них расстояние, «действуют сообща». Поэтому чтобы найти их совместную скорость (это и будет скорость сближения или удаления), нужно складывать скорости объектов:
Движение друг за другом (вдогонку)
При движении в одном направлении объекты также могут как сближаться, так и удаляться. В этом случае они как бы «соревнуются» в преодолении общего расстояния, «действуют друг против друга». Поэтому их совместная скорость будет равна разности скоростей.
Если скорость идущего впереди объекта меньше скорости объекта, следующего за ним, то они сближаются. Чтобы найти скорость сближения, надо из большей скорости вычесть меньшую:
Если объект, идущий впереди, движется с большей скоростью, чем идущий следом за ним, то они удаляются. Чтобы найти скорость удаления, надо из большей скорости вычесть меньшую:
При движении навстречу друг другу и движении в противоположных направлениях скорости складываем.
При движении в одном направлении скорости вычитаем.
Задачи на движение по кругу
При движении по кругу объекты могут:
- сближаться, если скорость догоняющего больше скорости догоняемого. Скорость сближения будет равна ;
- отдаляться, если скорость догоняющего меньше скорости догоняемого. Скорость удаления будет равна .
При этом пройденные расстояния измеряются длиной круговой трассы, равной S.
- Если два объекта начинают движение по кругу из одной и той же точки, то в момент первой встречи более быстрый объект пройдет расстояние на один круг больше.
- Если два объекта начинают движение по кругу из разных точек, расстояние между которыми равно S0, то в момент первой встречи догоняющий объект пройдет на S0 км большее расстояние, чем догоняемый.
- Если через определенное время t первый объект опережает второй на m кругов, то разница пройденных объектами расстояний будет равна m · S: S1 – S2 = m · S.
Задачи на движение мимо объекта
В задачах на движение мимо объекта обязательно присутствуют протяженные тела — поезда, туннели, корабли и т. п. Зачастую движущимся объектом является поезд.
Если поезд длиной L движется мимо точечного объекта (столба, светофора, человека), то он проходит расстояние, равное его длине L:
При этом, если точечный объект (пешеход, велосипедист) тоже движется, то совместная скорость равна сумме скоростей, если поезд и объект двигаются в разных направлениях (как в пункте 1), и равна разности скоростей, если они двигаются в одном направлении (как в пункте 2).
Если поезд длиной L1 движется мимо протяженного объекта (туннеля, лесополосы) длиной L2, то он проходит расстояние, равное сумме длин самого поезда и протяженного объекта:
S = L1 + L2 = v0 · t.
При этом, если протяженный объект (например, другой поезд) тоже движется, то совместная скорость равна сумме скоростей, если оба объекта двигаются в разных направлениях, и равна разности скоростей (из большей вычитается меньшая), если они двигаются в одном направлении.
Задачи на движение по течению и против течения
В задачах на движение помимо собственной скорости плывущего тела нужно учитывать скорость течения.
При движении по течению скорость течения прибавляется к скорости плывущего тела: v = v0 + vтеч.
При движении против течения скорость течения отнимается от скорости плывущего тела: v = v0 – vтеч.
Задачи на движение из ЕГЭ по математике (профильный уровень)
Задача 1.
Из одной точки круговой трассы, длина которой равна 44 км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 112 км/ч, и через 48 минут после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч.
Решение: Пусть скорость второго автомобиля равна v км/ч. За 4/5 часа первый автомобиль прошел на 44 км больше, чем второй, отсюда имеем:
112 ∙ = v ∙ = v ∙ + 44 ⇔ 4 ∙ v = 112 ∙ 4 – 44 ∙ 5 ⇔ v = 57.
Следовательно, скорость второго автомобиля была равна 57 км/ч.
Ответ: 57 км/ч.
Задача 2.
Из пункта A круговой трассы выехал велосипедист, а через 10 минут следом за ним отправился мотоциклист. Через 2 минуты после отправления он догнал велосипедиста в первый раз, а еще через 3 минуты после этого догнал его во второй раз. Найдите скорость мотоциклиста, если длина трассы равна 5 км. Ответ дайте в км/ч.
Решение:
До первой встречи велосипедист провел на трассе 1/5 часа, а мотоциклист 1/30 часа. Пусть скорость мотоциклиста равна v км/ч, тогда скорость велосипедиста равна
Тогда если скорость велосипедиста – это 1 единица отношения, то скорость мотоциклиста – это 6 единиц отношения.
Так как они едут в одном направлении, их общая скорость 5 единиц отношения.
∙5 ед.отн. = 5
Таким образом, скорость мотоциклиста была равна 120 км/ч.
Ответ: 120 км/ч.
Задача 3
Часы со стрелками показывают 3 часа ровно. Через сколько минут минутная стрелка в девятый раз поравняется с часовой?
Решение: Скорость движения минутной стрелки 12 делений/час (под одним делением здесь подразумевается расстояние между соседними цифрами на циферблате часов), а часовой ― 1 деление/час. До девятой встречи минутной и часовой стрелок минутная должна сначала 8 раз «обогнать» часовую, то есть пройти 8 кругов по 12 делений. Пусть после этого до четвертой встречи часовая стрелка пройдет L делений. Тогда общий путь минутной стрелки складывается из найденных 96 делений, ещё 3 изначально разделяющих их делений (поскольку часы показывают 3 часа) и последних L делений. Приравняем время движения для часовой и минутной стрелок:
, отсюда , отсюда и .
Ответ: через 9 минут.
Задача 4
Из одной точки круговой трассы, длина которой равна 14 км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 80 км/ч, и через 40 минут после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч.
Решение:
Данную задачу можно интерпретировать (представить её, как задачу на линейное движение): Два автомобиля одновременно начинают движение в одном направлении. Скорость первого равна 80 км/ч. Через 40 минут он опережает второго на 14 км (т. к. сказано, что на один круг). Найти скорость второго. Очень важно в заданиях на движение представить сам процесс этого движения.
Сравнение так же производим по расстоянию.
За x принимаем искомую величину ― скорость второго. Время движения 40 минут (2/3 часа) для обоих. Заполним графу «расстояние»:
| v | t | S | |
| 1 | 80 | 2/3 | |
| 2 | x | 2/3 |
Расстояние, пройденное первым, больше расстояния, который прошёл второй на 14 км.
80 ∙ больше, чем x ∙ больше, чем x ∙ на 14.
80 ∙ = x ∙ = x ∙ + 14;
– – = x ∙ ;
Скорость второго автомобиля 59 (км/ч).
Ответ: 59 км/ч.
Задача 5
Из пункта A в пункт B, расстояние между которыми 75 км, одновременно выехали автомобилист и велосипедист. Известно, что за час автомобилист проезжает на 40 км больше, чем велосипедист. Определите скорость велосипедиста, если известно, что он прибыл в пункт B на 6 часов позже автомобилиста. Ответ дайте в км/ч.
Решение:
Пусть v км/ч – скорость велосипедиста, тогда скорость автомобилиста равна v + 40 км/ч. Велосипедист был в пути на 6 часов больше, отсюда имеем:
Таким образом, скорость велосипедиста была равна 10 км/ч.
Ответ: 10 км/ч.
Прямолинейное движение: равномерное и равноускоренное
Задачи ЕГЭ по кодированию генетического кода
Как решать текстовые задачи по математике ЕГЭ
Как решать задачи на вероятность
Как решать экономические задачи егэ по математике профильный уровень
Сочинение на тему: Автор и его герой в поэме «Василий Теркин». Движение сюжета поэмы
http://yourrepetitor.ru/kak-reshat-zadachi-na-dvizhenie-na-ege-po-matematike-2019/
Содержание
- Главная > Памятка
- Задачи на движение в одном направлении
- Скачать:
- Предварительный просмотр:
Рассмотрим задачи, в которых речь идёт о встречном движении. В таких задачах два каких-нибудь объекта движутся на встречу друг другу. Задачи на встречное движение можно решать двумя способами.
Задача 1. Два автомобиля выехали одновременно из двух населённых пунктов и встретились через 4 часа. Первый автомобиль ехал со скоростью 100 км/ч, а второй – со скоростью 70 км/ч. На каком расстоянии друг от друга находятся населённые пункты?
Решение: Из условия задачи известны скорость каждого автомобиля и время, которое автомобили были в пути. Значит, можно найти расстояние, которое проехал каждый автомобиль до встречи. Для этого нужно скорость умножить на время:
1) 100 · 4 = 400 (км) – проехал первый автомобиль
2) 70 · 4 = 280 (км) – проехал второй автомобиль
Найдя сумму полученных результатов, узнаем расстояние между населёнными пунктами:
400 + 280 = 680 (км)
Данную задачу можно решить и другим способом. Каждый час расстояние между автомобилями сокращалось на 170 километров (100 + 70), 170 км/ч – это скорость сближения автомобилей. За 4 часа они проехали расстояние:
Таким образом, задачу на встречное движение можно решить двумя способами:
| 1-й способ: | 2-й способ: |
| 1) 100 · 4 = 400 (км) | 1) 100 + 70 = 170 (км/ч) |
| 2) 70 · 4 = 280 (км) | 2) 170 · 4 = 680 (км) |
| 3) 400 + 280 = 680 (км) |
Ответ: Населённые пункты находятся на расстоянии 680 км.
Задача 2. Из двух посёлков навстречу друг другу вышли одновременно два пешехода. Скорость первого пешехода 4 км/ч, а скорость второго пешехода 5 км/ч. Какое расстояние будет между пешеходами через 5 часов после выхода, если расстояние между посёлками 70 км?
Решение: Сначала можно определить сколько километров прошёл каждый из пешеходов за 5 часов, для этого скорость пешеходов умножим на 5:
1) 4 · 5 = 20 (км) – прошёл первый пешеход
2) 5 · 5 = 25 (км) – прошёл второй пешеход
Затем можно найти общий путь, пройденный двумя пешеходами за 5 часов:
Теперь можно найти расстояние между пешеходами, отняв от общего расстояния между посёлками 45 уже пройденных километров:
У данной задачи есть и второй вариант решения. Можно сначала найти скорость сближения пешеходов:
Затем найти пройденное расстояние, умножив скорость сближения (9 км/ч) на время движения пешеходов (5 ч):
А теперь, для нахождения расстояния между пешеходами, вычесть пройденное расстояние (45 км) из общего:
Таким образом, данная задача имеет два варианта решения:
| 1-й способ: | 2-й способ: |
| 1) 4 · 5 = 20 (км) | 1) 4 + 5 = 9 (км/ч) |
| 2) 5 · 5 = 25 (км) | 2) 9 · 5 = 45 (км) |
| 3) 20 + 25 = 45 (км) | 3) 70 — 45 = 25 (км) |
| 3) 70 — 45 = 25 (км) |
Ответ: Через 5 часов расстояние между пешеходами будет 25 км.
Главная > Памятка
| Информация о документе | |
| Дата добавления: | |
| Размер: | |
| Доступные форматы для скачивания: |
Памятка «Учимся решать задач на движение»
В задачах на движение рассматриваются три взаимосвязанные величины:
S — расстояние (пройденный путь),
t — время движения и
V — скорость – расстояние, пройденное за единицу времени.
Расстояние – это произведение скорости на время движения
Скорость — это частное от деления расстояния на время движения
Время – это частное от деления расстояния на скорость движения
Задачи на встречное движение
Если два тела одновременно движутся навстречу друг другу, то расстояние между ними постоянно изменяется на одно и то же число, равное сумме расстояний, которые проходят тела за единицу времени.
Скорость сближения – это сумма скоростей, движущихся навстречу друг другу тел. V сближ. = 1V + 2V
Пример 1. Два велосипедиста одновременно выехали навстречу друг другу из двух посёлков и встретились через 3 часа. Первый велосипедист ехал со скоростью 12 км/ч, а второй – 14 км/ч. На каком расстоянии находятся посёлки?
V сближ. = 1V + 2V
1) 12 • 3 = 36 (км) – проехал первый велосипедист до встречи
2) 14 • 3 = 42 (км) – проехал второй велосипедист до встречи
3) 36 + 42 = 78 (км)
1) 12 + 14 = 26 (км/ч) – скорость сближения
Ответ : расстояние между посёлками 78 км.
Пример 2. Из двух городов навстречу друг другу выехали две машины. Скорость первой – 80 км/ч, скорость второй – 60 км/ч. Через, сколько часов машины встретятся, если расстояние между городами 280 км?
V сближ. = 1V + 2V
1) 80 + 60 = 140 (км/ч) – скорость сближения
2) 280 : 140 = 2 (ч)
Ответ : машины встретятся через 2 часа.
Пример 3. Из двух городов, расстояние между которыми 340 км, выехали одновременно навстречу друг другу две машины. Скорость первой – 80 км/ч. С какой скоростью ехала вторая машина, если встретились они через 2 часа?
2V = V сближ. — 1V
1) 340 : 2 = 170 (км/ч) – скорость сближения
2) 170 – 80 = 90 (км/ч)
Ответ : 90 км/ч. скорость второй машины
Задачи на движение в противоположных направлениях
Если два тела одновременно движутся в противоположных направлениях, то расстояние между ними постепенно увеличивается.
Скорость удаления – это расстояние, которое проходят тела за 1 ч при движении в противоположных направлениях. V удал. = 1V + 2V
Пример 1. Два лыжника одновременно вышли из пункта А в противоположных направлениях. Первый лыжник шёл со скоростью 12 км/ч, а второй – 14 км/ч. На каком расстоянии друг от друга они будут через 3 ч?
1)12 • 3 = 36 (км) – расстояние, которое прошёл первый лыжник за 3 ч
2)14 • 3 = 42 (км) – расстояние, которое прошёл второй лыжник за 3 ч
1)12 + 14 = 26 (км/ч) – скорость удаления
Ответ: через 3 ч они будут друг от друга на расстоянии 78 км.
Пример 2. Из города в противоположных направлениях выехали две машины. Скорость первой – 80 км/ч, скорость второй – 60 км/ч. Через сколько часов расстояние между машинами будет 280 км?
1) 80 + 60 = 140 (км/ч) – скорость удаления
2) 280 : 140 = 2 (ч)
Ответ: через 2 часа расстояние между машинами будет 280 км
Пример 3. Из города одновременно в противоположных направлениях выехали две машины. Скорость первой – 80 км/ч. С какой скоростью ехала вторая машина, если через 2 часа расстояние между ними было 340 км?
1) 340 : 2 = 170 (км/ч) – скорость удаления машин
2) 170 – 80 = 90 (км/ч)
Ответ: скорость второй машины 90 км/ч.
Задачи на движение в одном направлении
Пример 1. Автомобиль за 2 ч проехал 192 км. Следующие 3 ч он двигался со скоростью на 6 км/ч меньше. Сколько всего километров проехал автомобиль?
1)192 : 2 = 96 (км/ч) – первая скорость
2)96 – 6 = 90 (км/ч) – вторая скорость
3)90 • 3 = 270 (км) – второе расстояние
4)192 + 270 = 462 (км)
Пример 2. Из двух пунктов, расстояние между которыми 24 км, одновременно вышел спортсмен и выехал велосипедист. Скорость спортсмена 6 км/ч., а скорость велосипедиста 18 км/ч..
1).Через сколько часов велосипедист догонит спортсмена?
2).На каком расстоянии от пункта В велосипедист догонит спортсмена?
3). На сколько километров путь велосипедиста больше пути спортсмена?


V приближ. = 2V -1V , где 2V ֺ > 1V
1). 18 – 6 = 12 (км /ч.) – скорость приближения велосипедиста и спортсмена
2). 24 : 12 = 2 (ч.) – время, через которое велосипедист догонит спортсмена.
3). 6 ●2 = 12 (км) – расстоянии, на котором велосипедист догонит спортсмена.
Ответ: через 2 часа; 12 км.
Пример 3. За какое время мотоцикл догонит грузовой автомобиль, если расстояние между ними 45 км, а скорость мотоцикла больше скорости грузовика на 15 км/ч?
Цель: закрепить умение решать задачи на встречное движение.
Карточки можно использовать и для индивидуальной, и для парной работы.
Скачать:
| Вложение | Размер |
|---|---|
| zadachi_na_vstrechnoe_dvizhenie_4_klass.docx | 14.58 КБ |
Предварительный просмотр:
1. Из двух деревень одновременно вышли навстречу друг другу две группы туристов. Одна группа шла со скоростью 3 км/ч, а другая 4 км/ч. Встретились они через 2 ч. Чему равно расстояние между деревнями?
2. С двух полярных станций одновременно навстречу друг другу выехали две собачьи упряжки. Одна упряжка двигалась со скоростью 14 км/ч, а скорость другой 12 км/ч. Через сколько часов упряжки встретятся, если расстояние между полярными станциями 52 км?
3. Два лыжника вышли одновременно навстречу друг другу из двух разных пунктов, расстояние между которыми
66 км. Скорость первого 12 км/ч. С какой скоростью ехал второй лыжник, если они встретились через 3 часа?
1. Из двух городов одновременно вылетели навстречу друг другу два голубя. Они встретились через 5 ч. Скорость одного голубя 62 км/ч, а второго 68 км/ч. Узнай расстояние между городами.
2. Два пешехода вышли одновременно из двух деревень навстречу друг другу. Один шёл со скоростью 5 км/ч, скорость другого 4 км/ч. Через сколько часов они встретятся, если расстояние между деревнями 36 км?
3. Два пловца поплыли одновременно навстречу друг другу с двух разных концов бассейна, длина которого 100 метров. Первый плыл со скоростью 20 м/мин. С какой скоростью плыл второй пловец, если они встретились через 2 минуты?
1.Из двух посёлков одновременно выехали навстречу друг другу велосипедист и мотоциклист. Они встретились через 4 ч. Скорость велосипедиста 15 км/ч, а мотоциклиста 57 км/ч. Узнай расстояние между посёлками.
2. Две многоножки ползли навстречу друг другу. Скорость одной 2 дм/мин, а скорость второй 3 дм/мин. Через сколько минут они встретятся, если первоначальное расстояние между ними было 15 дм?
3. Две ласточки одновременно вылетели навстречу друг другу. Одна летит со скоростью 23 м/с. С какой скоростью летит вторая ласточка, если первоначальное расстояние между ними 920 м и встретились они через 20 секунд?
1.От двух пристаней одновременно навстречу друг другу отошли катер и лодка. Они встретились через 6 ч. Скорость лодки 8 км/ч, а скорость катера 35 км/ч. Узнай расстояние между пристанями.
2.Дв пчелы вылетели из ульев одновременно навстречу друг другу. Одна пчела летела со скоростью 8 м/с, скорость другой 7 м/с. Через сколько секунд пчёлы встретятся, если расстояние между ульями 135 м?
3. Автомобиль и автобус выехали одновременно из двух городов навстречу друг другу. Скорость автомобиля 90 км/ч. Расстояние между городами 1600 км. С какой скоростью шёл автобус, если они встретились через 10 часов?
1. Две водомерки отправились одновременно с противоположных концов пруда навстречу друг другу. Они встретились через 3 минуты. Одна водомерка плыла со скоростью 48 м/мин, а другая со скоростью 40 м/мин. Узнай расстояние между берегами пруда.
2. С двух станций, расстояние между которыми равно 320 км, вышли одновременно два товарных поезда. Один поезд проходил 29 км, а другой 35 км. Через сколько часов эти поезда встретятся?
3. Расстояние между сёлами 48 км. Из них вышли одновременно навстречу друг другу два пешехода. Скорость одного пешехода 3 км/ч. С какой скоростью шёл второй пешеход, если они встретились через 6 часов?
1. От двух городов одновременно отошли навстречу друг другу товарный и пассажирский поезда. Товарный поезд шёл со скоростью 56 км/ч, а пассажирский со скоростью 74 км/ч. Каково расстояние между городами, если поезда встретились через 4 ч?
2.От двух раковин два рака ползут навстречу друг другу. Скорость первого 18 м/мин, а скорость второго 20 м/мин. Через сколько минут раки встретятся, если расстояние между раковинами равно 114 м?
3. От двух причалов, расстояние между которыми 90 км, одновременно вышли навстречу друг другу две лодки. Первая шла со скоростью 8 км/ч. С какой скоростью шла вторая лодка, если они встретились через 5 часов?
1. Две группы туристов вышли одновременно навстречу друг другу из двух сёл. Расстояние между сёлами 27 км. Одна группа шла со скоростью 4 км/ч. С какой скоростью шла вторая группа, если они встретились через 3 часа?
2. Теплоход и катер отошли от двух пристаней одновременно навстречу друг другу. Скорость теплохода 30 км/ч, скорость катера 25 км/ч. Через сколько часов суда встретятся, если расстояние между пристанями равно 330 км?
3. Две гремучие змеи выползли одновременно из своих укрытий навстречу друг другу и встретились через 5 минут. Скорость одной змеи 48 м/мин, а скорость другой 53 м/мин. Каково расстояние между укрытиями змей?
1.Два мотоциклиста выехали одновременно навстречу друг другу из двух городов. Расстояние между городами 465 км. Первый мотоциклист ехал со скоростью 80 км/ч. С какой скоростью ехал второй мотоциклист, если они встретились через 3 часа?
2. Две медузы плыли навстречу друг другу. Скорость одной 50 м/мин, а скорость другой 55 м/мин. Через сколько минут они встретятся, если первоначальное расстояние между ними было 315 метров?
3. Две девочки вышли одновременно навстречу друг другу из своих домов. Они встретились через 8 минут. Одна шла со скоростью 60 м/мин, а другая со скоростью 70 м/мин. Какое расстояние между домами девочек?