где xвых – выходная величина; xвх.i – i-я входная величина; a, b, c, … – коэффициенты, не зависящие от xвых и xвх.i, t – время.
Переменные x, описывающие систему, представляют собой функции времени и делятся на входные и выходные так, чтобы входные являлись причиной изменения выходных. Коэффициенты a, b, c, … описывают свойства системы.
Система называется стационарной, если коэффициенты a, b, c, … не зависят от времени, и нестационарной, если хотя бы один из них от времени зависит.
Система является нелинейной, если хотя бы один из коэффициентов a, b, c, … зависит от xвых или xвх..
Если система имеет одну выходную переменную, т.е. описывается одним уравнением вида (4.1), то она называется одномерной. Многомерные системы имеют более одной выходной величины и описываются системой уравнений вида (4.1).
Порядком рассматриваемой системы называется наивысший порядок производной в ее дифференциальном уравнении (или системе дифференциальных уравнений).
Левая часть уравнения (4.1) описывает собственное движение системы – изменение ее состояния в отсутствие внешних воздействий. Правая часть описывает влияние внешних воздействий на состояние системы.
Уравнение (4.1) относится только к системам без запаздывания. Для систем с запаздыванием хотя бы одна из величин xвых или xвх. должна быть представлена как функция с запаздывающим аргументом:
xвых(t – τ) или xвх(t – τ),
где τ – время запаздывания, характеризующее «отставание» той или иной функции.
Например, для объекта регулирования первого порядка без запаздывания с одной регулируемой величиной x уравнение (4.1) запишется как
Для
устойчивости САР с запаздыванием по
критерию Найквиста необходимо и
достаточно, чтобы при изменении частоты
от 0 до +
годограф Найквиста не охватывал точку
с координатами (-1, j0).
Годограф Найквиста
для САР с запаздыванием строится
следующим образом.
Сначала
строят годограф Найквиста для САР без
запаздывания, заменив в выражении (3) p
на j.
Годограф Найквиста для САР без запаздывания
приведен на рисунке 3 (кривая
).
Затем каждый вектор, соответствующий
частоте
,
поворачивается на угол.
И так для всех частот от 0 до +.
В итоге получается годограф Найквиста
для САР с запаздыванием
.
jQ()
P()
-1
Рисунок
3 – Годографы Найквиста для САР
без
запаздывания ()
и с запаздыванием ()
2.1.3 Построение области устойчивости
Область устойчивости
для САР с запаздыванием строится на
основе критерия Михайлова.
На
границе устойчивости годограф Михайлова
проходит через начало координат, причем
так, что весь остальной ход годограф
Михайлова соответствует условию
устойчивости. Так как при прохождении
годографа Михайлова через начало
координат
= 0, то уравнения
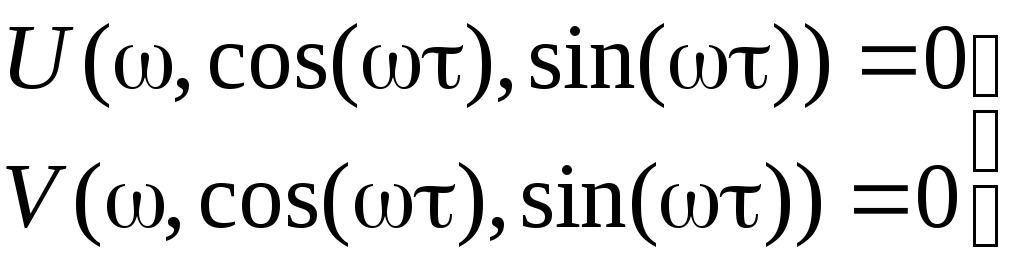
определяют
границу области устойчивости по одному
параметру. Область устойчивости
изображается либо на плоскости двух
параметров, либо в пространстве
параметров, входящих в коэффициенты
уравнений (10). Пример области устойчивости
для САР с запаздыванием приведен на
рисунке 4. Внутри очерченной этими
границами области в какой-либо точке
проверяется весь ход годографа Михайлова,
чтобы убедиться, что выделенная область
является областью устойчивости.
Рисунок 4 – Область
устойчивости
2.1.4 Определение критического времени запаздывания
Для
определения критического значения
времени запаздывания используется
критерий Найквиста. Критическое время
запаздывания
–
это время, при котором САР с запаздыванием
будет находиться на границе устойчивости.
В этом случае годограф Найквиста
будет проходить через точку (-1, j0),
что показано на рисунке 5.
Это
значит, что при некоторой частоте
. (11)
Отсюда
имеем, что
. (12)
Рисунок
5 – Годограф Найквиста для САР с
запаздыванием
на границе устойчивости
Рисунок
6 – Графическое определение
критического
времени запаздывания
Графическое
определение
приведено на рисунке 6. В этом случае
строится годограф Найквиста
,
а затем проводится окружность единичного
радиуса с центром в начале координат.
Через точку пересечения годографа
Найквиста и единичной окружности
проводится радиус. Угол, образуемый
этим радиусом и линией -,
представляет
значение
. (13)
Зная
угол
и значение частоты
,
соответствующей точке пересечения по
выражению (12), определяют
.
2.2 Оценка качества регулирования сар с запаздыванием
Для
САР с запаздыванием используются такие
же оценки качества регулирования, что
и для САР без запаздывания, которые
приведены в методических указаниях
[5]. Отличие состоит только в определении
времени регулирования
и интегральных оценок качества
регулирования.
Кривые
переходного процесса для САР без
запаздывания (кривая 1) и с запаздыванием
(кривая 2) приведены на рисунке 7, где
,
– соответственно время регулирования
для САР без запаздывания и с запаздыванием.

1 2
y
t

Рисунок
7 –
Кривые переходного процесса для САР
с запаздыванием и без запаздывания
Как
видно из графиков на рисунке 7, время
регулирования для САР с запаздыванием
. (14)
Интегральная
оценка для САР c
запаздыванием определяется в соответствии
со схемой на рисунке 8.

II
I


Рисунок
8 –
Схема определения интегральной оценки
для САР с запаздыванием
В
отличие от САР без запаздывания, для
которой интегральная оценка определяется
выражением
(15)
и
равна площади криволинейной трапеции
I,
для САР с запаздыванием
, (16)
где
первое слагаемое характеризует площадь
прямоугольника, ограниченного временем
чистого запаздывания .
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Расчет времени запаздывания сигналов, проходящих через фильтр нижних частот
Уточнение формулы для определения времени запаздывания при прохождении апериодических сигналов через фильтр нижних частот (ФНЧ). Рассматриваются оценки времени запаздывания и устанавливается его связь с корнями характеристического полинома и передаточной функцией цепи.
Авторы: А. Е. Завьялов, М. В. Соклакова, Э. П. Чернышев
Направление: Электротехника
Ключевые слова: Время запаздывания, фильтр нижних частот, фазочастотная характеристика, передаточная функция
Открыть полный текст статьи

























