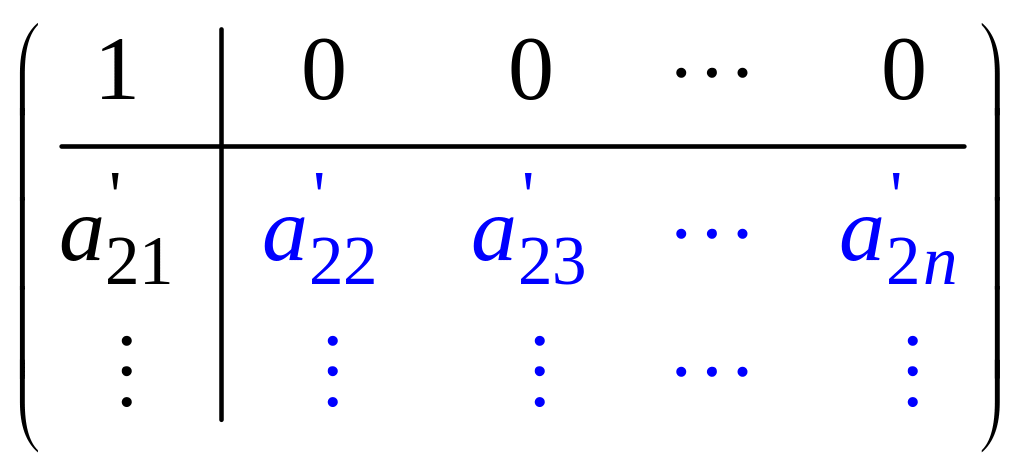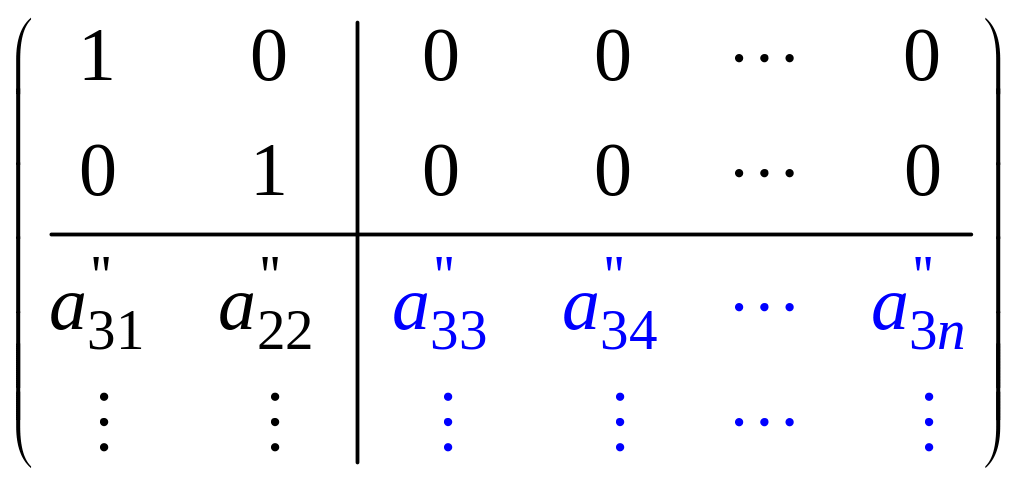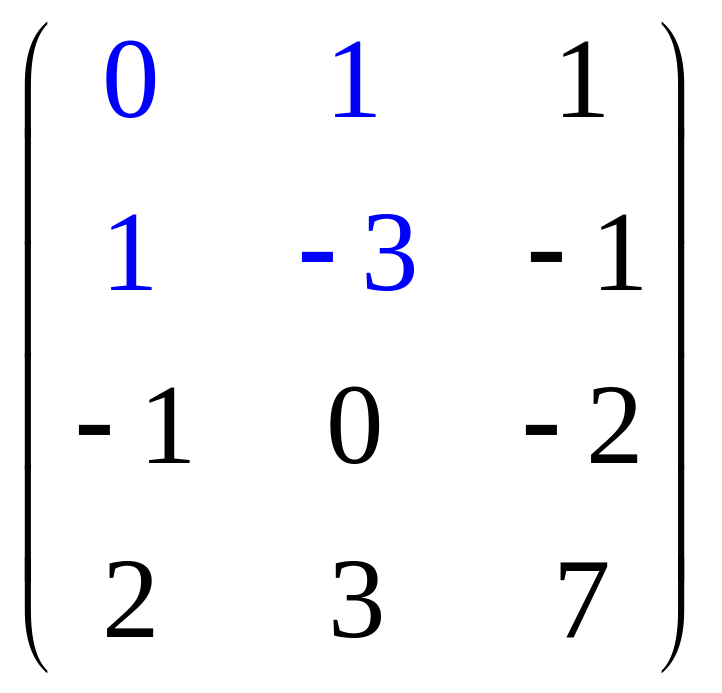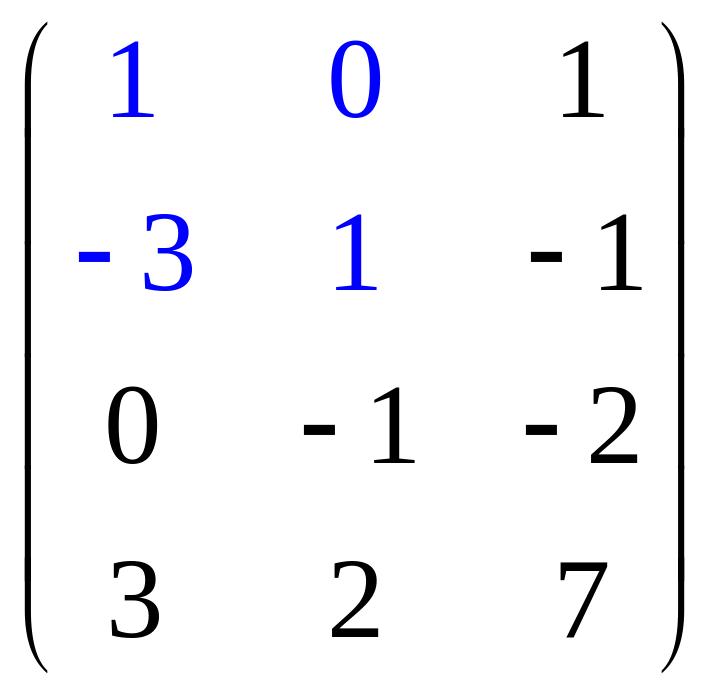Как найти все базисные миноры - Исправление недочетов и поиск решений вместе с Examum.ru

Ранг матрицы и базисный минор матрицы

Пусть — матрица размеров mtimes n , а — натуральное число, не превосходящее и : kleqslantmin{m;n} . Минором k-го порядка матрицы называется определитель матрицы k-го порядка, образованной элементами, стоящими на пересечении произвольно выбранных строк и столбцов матрицы . Обозначая миноры, номера выбранных строк будем указывать верхними индексами, а выбранных столбцов — нижними, располагая их по возрастанию.

Пример 3.4. Записать миноры разных порядков матрицы

$A=begin{pmatrix}1&2&1&0\ 0&2&2&3\ 1&4&3&3end{pmatrix}!.$

Решение. Матрица имеет размеры 3times4 . Она имеет: 12 миноров 1-го порядка, например, минор $M_{2}^{3}=det(a_{32})=4$ ; 18 миноров 2-го порядка, например, $M_{23}^{12}=begin{vmatrix}2&1\2&2end{vmatrix}=2$ ; 4 минора 3-го порядка, например,

$M_{{134}}^{{123}}= begin{vmatrix}1&1&0\0&2&3\ 1&3&3 end{vmatrix}=0.$

В матрице размеров mtimes n минор r-го порядка называется базисным, если он отличен от нуля, а все миноры (r+1)-ro порядка равны нулю или их вообще не существует.

Рангом матрицы называется порядок базисного минора. В нулевой матрице базисного минора нет. Поэтому ранг нулевой матрицы, по определению полагают равным нулю. Ранг матрицы обозначается operatorname{rg}A .

Пример 3.5. Найти все базисные миноры и ранг матрицы

$A=begin{pmatrix}1&2&2&0\0&2&2&3\0&0&0&0end{pmatrix}!.$

Решение. Все миноры третьего порядка данной матрицы равны нулю, так как у этих определителей третья строка нулевая. Поэтому базисным может быть только минор второго порядка, расположенный в первых двух строках матрицы. Перебирая 6 возможных миноров, отбираем отличные от нуля

$M_{12}^{12}= M_{13}^{12}= begin{vmatrix}1&2\0&2 end{vmatrix}!,quad M_{24}^{12}= M_{34}^{12}= begin{vmatrix}2&0\2&3end{vmatrix}!,quad M_{14}^{12}= begin{vmatrix}1&0\0&3end{vmatrix}!.$

Каждый из этих пяти миноров является базисным. Следовательно, ранг матрицы равен 2.

Замечания 3.2

1. Если в матрице все миноры k-го порядка равны нулю, то равны нулю и миноры более высокого порядка. Действительно, раскладывая минор (k+1)-ro порядка по любой строке, получаем сумму произведений элементов этой строки на миноры k-го порядка, а они равны нулю.

2. Ранг матрицы равен наибольшему порядку отличного от нуля минора этой матрицы.

3. Если квадратная матрица невырожденная, то ее ранг равен ее порядку. Если квадратная матрица вырожденная, то ее ранг меньше ее порядка.

4. Для ранга применяются также обозначения operatorname{Rg}A,~ operatorname{rang}A,~ operatorname{rank}A .

5. Ранг блочной матрицы определяется как ранг обычной (числовой) матрицы, т.е. не обращая внимания на ее блочную структуру. При этом ранг блочной матрицы не меньше рангов ее блоков: operatorname{rg}(Amid B)geqslantoperatorname{rg}A и , поскольку все миноры матрицы (или ) являются также минорами блочной матрицы .

Теоремы о базисном миноре и о ранге матрицы

Рассмотрим основные теоремы, выражающие свойства линейной зависимости и линейной независимости столбцов (строк) матрицы.

Теорема 3.1 о базисном миноре. В произвольной матрице каждый столбец {строка) является линейной комбинацией столбцов (строк), в которых расположен базисный минор.

Действительно, без ограничения общности предполагаем, что в матрице размеров mtimes n базисный минор расположен в первых строках и первых столбцах. Рассмотрим определитель

$D=left|begin{array}{ccc|c}a_{11}&cdots&a_{1r}&a_{1k}~\ ~vdots&ddots &vdots&vdots~\ ~a_{r1}&cdots&a_{rr}&a_{rk}~\hline ~a_{s1}&cdots&a_{sr}&a_{sk}end{array}right|,$

который получен приписыванием к базисному минору матрицы соответствующих элементов s-й строки и k-го столбца. Отметим, что при любых 1leqslant sleqslant m и 1leqslant kleqslant n этот определитель равен нулю. Если sleqslant r или kleqslant r , то определитель содержит две одинаковых строки или два одинаковых столбца. Если же s>r и k>r , то определитель равен нулю, так как является минором (r+l)-ro порядка. Раскладывая определитель по последней строке, получаем

$a_{s1}cdot D_{r+11}+ldots+ a_{sr}cdot D_{r+1r}+a_{sk}cdot D_{r+1,r+1}=0,$

где $D_{r+1,j}$ — алгебраические дополнения элементов последней строки. Заметим, что $D_{r+1,r+1}ne0$ , так как это базисный минор. Поэтому

$a_{sk}=lambda_1cdot a_{s1}+ldots+lambda_rcdot a_{sr}$ , где $lambda_j=-frac{D_{r+1,j}}{D_{r+1,r+1}},~j=1,2,ldots,r.$

Записывая последнее равенство для s=1,2,ldots,m , получаем

$begin{pmatrix}a_{1k}\vdots\a_{mk}end{pmatrix}= lambda_1cdot! begin{pmatrix}a_{11}\vdots\a_{m1}end{pmatrix}+ldots lambda_rcdot! begin{pmatrix}a_{1r}\vdots\a_{mr}end{pmatrix}!.$

т.е. -й столбец (при любом 1leqslant kleqslant n ) есть линейная комбинация столбцов базисного минора, что и требовалось доказать.

Теорема о базисном миноре служит для доказательства следующих важных теорем.

Условие равенства нулю определителя

Теорема 3.2 (необходимое и достаточное условие равенства нулю определителя). Для того чтобы определитель был равен нулю необходимо и достаточно, чтобы один из его столбцов {одна из его строк) был линейной комбинацией остальных столбцов (строк).

В самом деле, необходимость следует из теоремы о базисном миноре. Если определитель квадратной матрицы n-го порядка равен нулю, то ее ранг меньше , т.е. хотя бы один столбец не входит в базисный минор. Тогда этот выбранный столбец по теореме 3.1 является линейной комбинацией столбцов, в которых расположен базисный минор. Добавляя, при необходимости, к этой комбинации другие столбцы с нулевыми коэффициентами, получаем, что выбранный столбец есть линейная комбинация остальных столбцов матрицы. Достаточность следует из свойств определителя. Если, например, последний столбец A_n определителя det(A_1~A_2~cdots~A_n) линейно выражается через остальные

$A_n=lambda_1cdot A_1+lambda_2cdot A_2+ldots+lambda_{n-1}cdot A_{n-1},$

то прибавляя к A_n столбец A_1 , умноженный на (-lambda_1) , затем столбец A_2 , умноженный на (-lambda_2) , и т.д. столбец $A_{n-1}$ , умноженный на $(-lambda_{n-1})$ , получим определитель $det(A_1~cdots~A_{n-1}~o)$ с нулевым столбцом, который равен нулю (свойство 2 определителя).

Инвариантность ранга матрицы при элементарных преобразованиях

Теорема 3.3 (об инвариантности ранга при элементарных преобразованиях). При элементарных преобразованиях столбцов (строк) матрицы ее ранг не меняется.

Действительно, пусть operatorname{rg}A=r . Предположим, что в результате одного элементарного преобразования столбцов матрицы получили матрицу . Если было выполнено преобразование I типа (перестановка двух столбцов), то любой минор (r+l)-ro порядка матрицы либо равен соответствующему минору (r+l)-ro порядка матрицы , либо отличается от него знаком (свойство 3 определителя). Если было выполнено преобразование II типа (умножение столбца на число lambdane0 ), то любой минор (г+l)-ro порядка матрицы либо равен соответствующему минору (r+l)-ro порядка матрицы , либо отличается от него множителем (свойство 6 определителя). Если было выполнено преобразование III типа (прибавление к одному столбцу другого столбца, умноженного на число Lambda ), то любой минор (г+1)-го порядка матрицы либо равен соответствующему минору (г+1) -го порядка матрицы (свойство 9 определителя), либо равен сумме двух миноров (r+l)-ro порядка матрицы (свойство 8 определителя). Поэтому при элементарном преобразовании любого типа все миноры (r+l)-ro порядка матрицы равны нулю, так как равны нулю все миноры (г+l)-ro порядка матрицы . Таким образом, доказано, что при элементарных преобразованиях столбцов ранг матрицы не может увеличиться. Так как преобразования, обратные к элементарным, являются элементарными, то ранг матрицы при элементарных преобразованиях столбцов не может и уменьшиться, т.е. не изменяется. Аналогично доказывается, что ранг матрицы не изменяется при элементарных преобразованиях строк.

Следствие 1. Если одна строка (столбец) матрицы является линейной комбинацией других ее строк (столбцов), то эту строку (столбец) можно вычеркнуть из матрицы, не изменив при этом ее ранга.

Действительно, такую строку при помощи элементарных преобразований можно сделать нулевой, а нулевая строка не может входить в базисный минор.

Следствие 2. Если матрица приведена к простейшему виду (1.7), то

operatorname{rg}A=operatorname{rg}Lambda=r,.

Действительно, матрица простейшего вида (1.7) имеет базисный минор r-го порядка.

Следствие 3. Любая невырожденная квадратная матрица является элементарной, другими словами, любая невырожденная квадратная матрица эквивалентна единичной матрице того же порядка.

Действительно, если — невырожденная квадратная матрица n-го порядка, то operatorname{rg}A=n (см. п.З замечаний 3.2). Поэтому, приводя элементарными преобразованиями матрицу к простейшему виду (1.7), получим единичную матрицу Lambda=E_n , так как operatorname{rg}A=operatorname{rg}Lambda=n (см. следствие 2). Следовательно, матрица эквивалентна единичной матрице E_n и может быть получена из нее в результате конечного числа элементарных преобразований. Это означает, что матрица элементарная.

Теорема 3.4 (о ранге матрицы). Ранг матрицы равен максимальному числу линейно независимых строк этой матрицы.

В самом деле, пусть operatorname{rg}A=r . Тогда в матрице имеется линейно независимых строк. Это строки, в которых расположен базисный минор. Если бы они были линейно зависимы, то этот минор был бы равен нулю по теореме 3.2, а ранг матрицы не равнялся бы . Покажем, что — максимальное число линейно независимых строк, т.е. любые строк линейно зависимы при p>r . Действительно, образуем из этих строк матрицу . Поскольку матрица — это часть матрицы , то operatorname{rg}Bleqslant operatorname{rg}A=r<p . Значит, хотя бы одна строка матрицы не входит в базисный минор этой матрицы. Тогда по теореме о базисном миноре она равна линейной комбинации строк, в которых расположен базисный минор. Следовательно, строки матрицы линейно зависимы. Таким образом, в матрице не более, чем линейно независимых строк.

Следствие 1. Максимальное число линейно независимых строк в матрице равно максимальному числу линейно независимых столбцов:

$operatorname{rg}A=operatorname{rg}A^T.$

Это утверждение вытекает из теоремы 3.4, если ее применить к строкам транспонированной матрицы и учесть, что при транспонировании миноры не изменяются (свойство 1 определителя).

Следствие 2. При элементарных преобразованиях строк матрицы линейная зависимость (или линейная независимость) любой системы столбцов этой матрицы сохраняется.

В самом деле, выберем любые столбцов данной матрицы и составим из них матрицу . Пусть в результате элементарных преобразований строк матрицы была получена матрица , а в результате тех же преобразований строк матрицы была получена матрица . По теореме 3.3 operatorname{rg}B'=operatorname{rg}B . Следовательно, если столбцы матрицы были линейно независимы, т.е. k=operatorname{rg}B (см. следствие 1), то и столбцы матрицы также линейно независимы, так как k=operatorname{rg}B' . Если столбцы матрицы были линейно зависимы (k>operatorname{rg}B) , то и столбцы матрицы также линейно зависимы (k>operatorname{rg}B') . Следовательно, для любых столбцов матрицы линейная зависимость или линейная независимость сохраняется при элементарных преобразованиях строк.

Замечания 3.3

1. В силу следствия 1 теоремы 3.4 свойство столбцов, указанное в следствии 2, справедливо и для любой системы строк матрицы, если элементарные преобразования выполняются только над ее столбцами.

2. Следствие 3 теоремы 3.3 можно уточнить следующим образом: любую невырожденную квадратную матрицу, используя элементарные преобразования только ее строк (либо только ее столбцов), можно привести к единичной матрице того же порядка.

В самом деле, используя только элементарные преобразования строк, любую матрицу можно привести к упрощенному виду Lambda (рис. 1.5) (см. теорему 1.1). Поскольку матрица невырожденная (det{A}ne0) , то ее столбцы линейно независимы. Значит, столбцы матрицы Lambda также линейно независимы (следствие 2 теоремы 3.4). Поэтому упрощенный вид Lambda невырожденной матрицы совпадает с ее простейшим видом (рис. 1.6) и представляет собой единичную матрицу Lambda=E (см. следствие 3 теоремы 3.3). Таким образом, преобразовывая только строки невырожденной матрицы, ее можно привести к единичной. Аналогичные рассуждения справедливы и для элементарных преобразований столбцов невырожденной матрицы.

Ранге произведения и суммы матриц

Теорема 3.5 (о ранге произведения матриц). Ранг произведения матриц не превышает ранга множителей:

operatorname{rg}(Acdot B)leqslant min{operatorname{rg}A,operatorname{rg}B}.

В самом деле, пусть матрицы и имеют размеры mtimes p и ptimes n . Припишем к матрице матрицу C=ABcolon,(Amid C) . Разумеется, что operatorname{rg}Cleqslantoperatorname{rg}(Amid C) , так как — это часть матрицы (см. п.5 замечаний 3.2). Заметим, что каждый столбец C_j , согласно операции умножения матриц, является линейной комбинацией столбцов A_1,A_2,ldots,A_p матрицы A=(A_1~cdots~A_p):

$C_{j}=A_1cdot b_{1j}+A_2cdot b_{2j}+ldots+A_{p}cdot b_{pj},quad j=1,2,ldots,n.$

Такой столбец можно вычеркнуть из матрицы (Amid C) , при этом ее ранг не изменится (следствие 1 теоремы 3.3). Вычеркивая все столбцы матрицы , получаем: operatorname{rg}(Amid C)=operatorname{rg}A . Отсюда, operatorname{rg}Cleqslantoperatorname{rg}(Amid C)=operatorname{rg}A . Аналогично можно доказать, что одновременно выполняется условие , и сделать вывод о справедливости теоремы.

Следствие. Если невырожденная квадратная матрица, то operatorname{rg}(AB)= operatorname{rg}B и operatorname{rg}(CA)=operatorname{rg}C , т.е. ранг матрицы не изменяется приумножении ее слева или справа на невырожденную квадратную матрицу.

Теорема 3.6 о ранге суммы матриц. Ранг суммы матриц не превышает суммы рангов слагаемых:

operatorname{rg}(A+B)leqslant operatorname{rg}A+operatorname{rg}B.

Действительно, составим матрицу (A+Bmid Amid B) . Заметим, что каждый столбец матрицы A+B есть линейная комбинация столбцов матриц и . Поэтому operatorname{rg}(A+Bmid Amid B)= operatorname{rg}(Amid B) . Учитывая, что количество линейно независимых столбцов в матрице не превосходит operatorname{rg}A+operatorname{rg}B , а operatorname{rg}(A+B)leqslant operatorname{rg}(A+Bmid Amid B) (см. п.5 замечаний 3.2), получаем доказываемое неравенство.

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

Содержание:

Формулировка теоремы о базисном миноре
Примеры решения задач

Формулировка теоремы о базисном миноре

Теорема

Столбцы матрицы $A$,
входящие в базисный минор, образуют линейно независимую
систему. Любой столбец матрицы $A$ линейно выражается через остальные столбцы
из базисного минора.

В матрице $A$ размеров
$m times n$
минор
$r$-го порядка называется базисным, если он отличен от нуля,
а все миноры
$(r + 1)$-ro порядка равны нулю или их вообще не существует.

Следствие. Если все столбцы матрицы
$A$ линейно выражаются через
$r$ столбцов
$A_{i 1}, A_{i 2}, ldots, A_{i r}$, которые образуют
линейно независимую систему, то ранг матрицы
$operatorname{rang} A=r$ .

Примеры решения задач

Пример

Задание. Найти все базисные миноры и ранг матрицы:

$$A=left(begin{array}{llll}1 & 2 & 2 & 0 \ 0 & 2 & 2 & 3 \ 0 & 0 & 0 & 0end{array}right)$$

Решение. Все миноры третьего порядка данной матрицы равны нулю, так как у этих
определителей
третья строка будет нулевой. Поэтому базисным может быть только минор второго порядка, который будет состоять из
элементов первых двух строк матрицы. Перебираем всевозможные миноры второго порядка, состоящие из элементов указанных строк:

$$M_{12}^{12}=left|begin{array}{cc}1 & 2 \ 0 & 2end{array}right|=1 cdot 2-0 cdot 2=2-0=2 neq 0$$
$$M_{13}^{12}=left|begin{array}{cc}1 & 2 \ 0 & 2end{array}right|=1 cdot 2-0 cdot 2=2-0=2 neq 0$$
$$M_{14}^{12}=left|begin{array}{cc}1 & 0 \ 0 & 3end{array}right|=1 cdot 3-0 cdot 0=3-0=3 neq 0$$
$$M_{23}^{12}=left|begin{array}{ll}2 & 2 \ 2 & 2end{array}right|=0$$
$$M_{24}^{12}=left|begin{array}{cc}2 & 0 \ 2 & 3end{array}right|=2 cdot 3-2 cdot 0=6-0=6 neq 0$$
$$M_{34}^{12}=left|begin{array}{cc}2 & 0 \ 2 & 3end{array}right|=2 cdot 3-2 cdot 0=6-0=6 neq 0$$

Таким образом, пять минор являются ненулевыми и каждый из них — базисный. Следовательно, так как порядок базисных миноров равен
двум, то и ранг матрицы равен двум: $operatorname{rang} A=2$ .

Ответ. Базисные миноры $M_{12}^{12}, M_{13}^{12}, M_{14}^{12}, M_{24}^{12}, M_{34}^{12} ;$ rang $A=2$ .

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Источник

В данной публикации мы рассмотрим теорему о базисном миноре (формулировка и следствия). Также разберем пример задачи для демонстрации ее применения на практике.

Формулировка теоремы
Пример задачи

Формулировка теоремы

В произвольной матрице A столбцы/строки, входящие в состав базисного минора M (называются “базисными”), линейно независимы. Каждый столбец/строка матрицы является линейной комбинацией базисных столбцов/строк.

Допустим, дана матрица A размером mxn. Базисным называется ненулевой минор M порядка r, при этом все миноры более старшего порядка (r+1 и выше) равняются нулю или их вовсе нет. Это значит, что r равняется меньшему из чисел m или n.

Из теорему о базисном миноре следует:

Линейно независимые столбцы/строки матрицы, число которых равно рангу данной матрицы, являются базисными.
Ранг любой матрицы равняется максимальному количеству содержащихся в ней линейно независимых строк/столбцов.

Пример задачи

Давайте найдем всем базисные миноры матрицы A, представленной ниже, а также определим ее ранг.

Решение:

1. Выполним элементарные преобразования над матрицей, чтобы упростить ее. Для начала разделим третью строку на 2 и переставим ее с первой местами.

2. Отнимем из третьей строки первую.

3. Получаем матрицу с нулевой строкой, что означает, что все миноры третьего порядка равняются нулю.

4. Таким образом, базисными в нашем случае могут быть только ненулевые миноры второго порядка, состоящие из первой и второй строк полученной матрицы.

Ответ:
Все рассчитанные миноры отличны от нуля, значит, все они являются базисными. Ранг матрицы равен двум (rang A = 2), так как все миноры более высокого (третьего) порядка равны нулю.

Источник

Рассмотрим
некоторую, не обязательно квадратную,
матрицу А. Выберем какие-нибудь s номеров
строк i₁,
i₂,
,
i_s
и s номеров столбцов j₁,
j₂,
,
j_s,
причём i₁<i₂<<i_s
и j₁<j₂<<j_s.

Определение.
Минором порядка s матрицы А называется
детерминант матрицы порядка s, образованный
элементами, расположенными на пересечении
выбранных строк и столбцов, т.е. число

Определение.
В матрице А размеров

минор порядка r называется базисным,
если он отличен от нуля, а все миноры
порядка r+1 равны нулю или миноров порядка
r+1 вообще нет, т.е. r совпадает с меньшим
из чисел m или n.

Определение.
Строки и столбцы, на пересечении которых
расположен базисный минор, называются
базисными
строками и столбцами.

Определение.
Рангом матрицы
А называется наивысший порядок отличных
от нуля миноров этой матрицы и обозначается

.

Свойства
ранга матрицы и базисного минора.

Ранг
матрицы А размеров

не превосходит меньшего из её размеров.
rangA=0
тогда и только тогда, когда
Для
квадратной матрицы А порядка n rangA= n
тогда и только тогда, когда А –
невырожденная.
Базисные
строки (столбцы) матрицы А линейно
независимы.
Теорема
о
базисном
миноре.
В произвольной матрице каждый столбец
(строка) является линейной комбинацией
базисных столбцов (строк).
Теорема
о
ранге
матрицы.
Ранг матрицы А равен максимальному
числу линейно независимых столбцов
(строк) в этой матрице.
где
n – число столбцов матрицы А или строк
матрицы B.
rang(A^TA)=rang
A.
rang(AB)=
rang
A,
если B
– квадратная матрица и

Элементарные
преобразования
матриц.

Отбрасывание
нулевой строки (столбца).
Умножение
всех элементов строки (столбца) на
число, не равное нулю.
Изменение
порядка строк (столбцов) матрицы.
Прибавление
к каждому элементу одной строки (столбца)
соответствующих элементов другой
строки (столбца), умноженных на любое
число.
Транспонирование
матрицы.

Теорема.
Ранг матрицы не изменяется при элементарных
преобразованиях.

Определение.
Матрицы А и B
называются эквивалентными
(АB),
если матрица B
получена из матрицы А в результате
элементарных преобразований.

3.7 Нахождение ранга матрицы

Алгоритм
Гаусса
вычисления
ранга
матрицы.

Если
все

то rangA = 0.
Выбираем
элемент матрицы

Помещаем его в левый верхний угол
матрицы и делим первую строку матрицы
на

С помощью элементарных преобразований
обращаем все элементы первой строки в
нули:

.

Если
в части матрицы, выделенной синим
цветом, все

то rangA = 1.
Если
хотя бы один элемент в области, выделенной
синим цветом, отличен от нуля, алгоритм
повторяем. Перестановкой строк и
столбцов матрицы выбранный элемент

помещаем на место второго элемента
второй строки; делим всю вторую строку
матрицы на этот элемент; элементы второй
строки, начиная с третьего, обращаем в
нули. Получим матрицу вида:

Если
в части этой матрицы, выделенной синим
цветом,

то rang A = 2.

Если
хотя бы один элемент

в этой области, то алгоритм повторяем.

После
r
шагов получим матрицу ранга r
вида:

Пример.
Определить ранг и базисный минор матрицы:

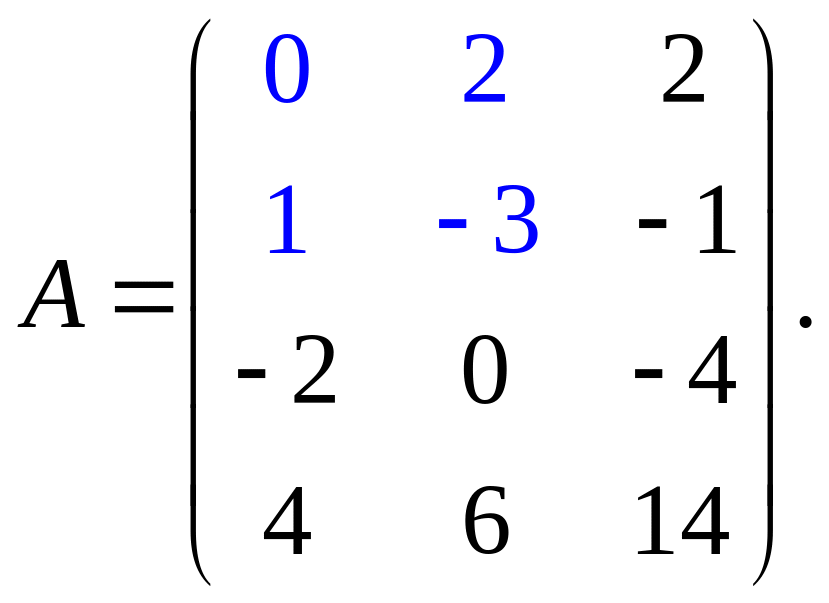
Решение.
Выполним следующие преобразования:
первую, третью и четвертую строки поделим
на 2, затем поменяем местами первый и
второй столбцы:


.

Из
третьего столбца вычтем первый, потом
из него же вычтем второй, умноженный на
два:



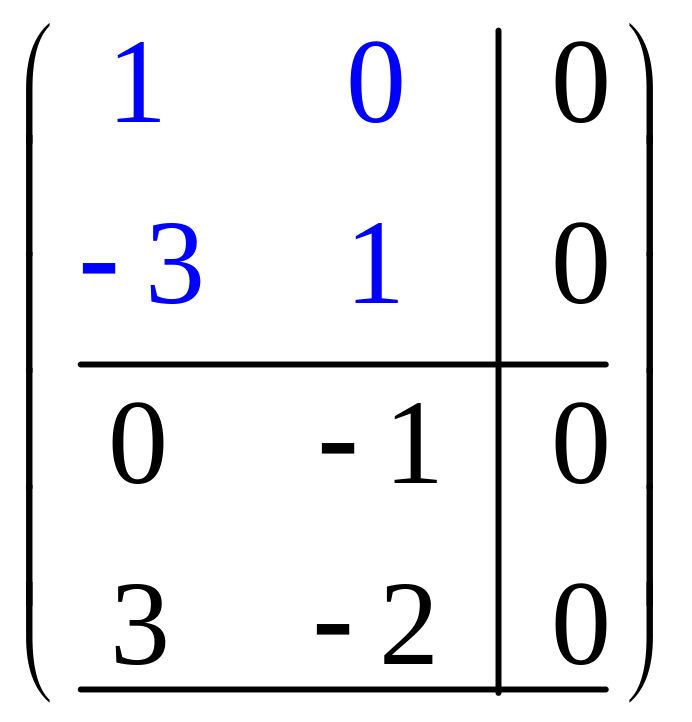
Очевидно,
что ранг последней (а, значит, и исходной)
матрицы равен 2.

Для
того, чтобы определить базисный минор
в исходной матрице, нам необходимо
выделить базисные строки и столбцы. Для
последней матрицы базисный минор выделен
синим цветом. Проходя все действия в
обратном порядке, определим базисный
минор исходной матрицы.

Метод
окаймляющих
миноров.

Определение.
Минор M₁
называется окаймляющим
для минора М, если М получается из M₁вычёркиванием
одной крайней строки (первой или
последней) и одного крайнего столбца.

Теорема.
Если в матрице А размеров

имеется
минор порядка r, не равный нулю, а все
его окаймляющие миноры порядка r+1 равны
нулю, то rang A =r.

Пример.
Для предыдущего
примера:

Вычисляем
минор второго порядка:

Выбираем
миноры третьего порядка, в которые
входят строки и столбы, дающие предыдущий
минор. Таких миноров всего два:

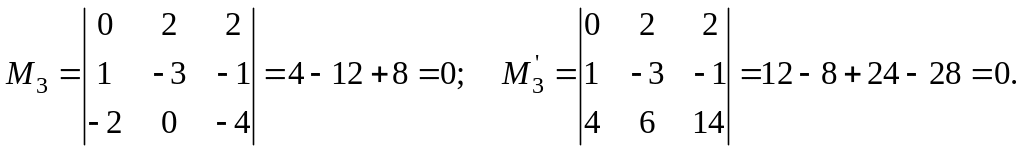
Так
как оба этих минора равны нулю, то ранг
матрицы равен 2 (то есть порядку минора
M₂).

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Онлайн калькуляторы

На нашем сайте собрано более 100 бесплатных онлайн калькуляторов по математике, геометрии и физике.

Справочник

Основные формулы, таблицы и теоремы для учащихся. Все что нужно, чтобы сделать домашнее задание!

Заказать решение

Не можете решить контрольную?!
Мы поможем! Более 20 000 авторов выполнят вашу работу от 100 руб!

Теорема о базисном миноре

Следствие. Определитель -го порядка равен нулю тогда и только тогда, когда его строки (столбцы) линейно зависимы.

Теорема о базисном миноре матрицы служит для доказательства таких важных теорем:

Теорема 1. Линейно независимые строки (столбцы) матрицы, количество которых равно рангу матрицы, являются базисными строками (столбцами).

Теорема 2. (Теорема о ранге матрицы). Для любой матрицы ее ранг равен максимальному количеству ее линейно независимых строк (столбцов).

Примеры решения задач

Понравился сайт? Расскажи друзьям!

Источник