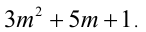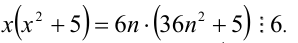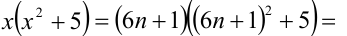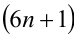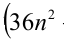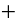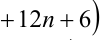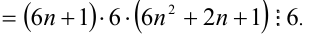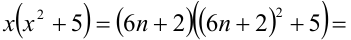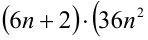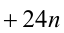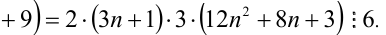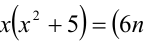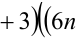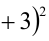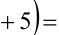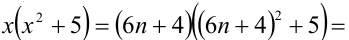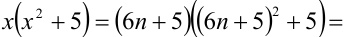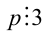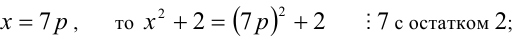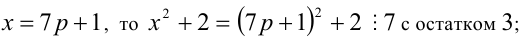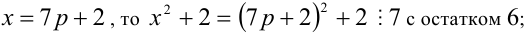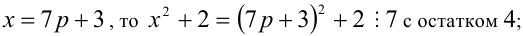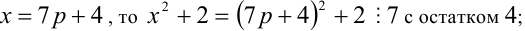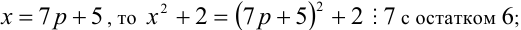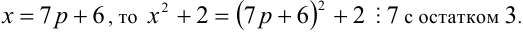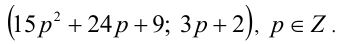Как найти все целые числа при делении

Метод анализа остатков

В основе метода анализа остатков, который используется при решении ряда задач с целочисленными неизвестными, лежит формула деления с остатком. Суть метода состоит в рассмотрении случаев различных остатков от деления на заданное число, что позволяет в конечном итоге решить поставленную задачу.

В первых трёх примерах, приведённых ниже, в явном виде ищутся остатки от деления одних целых чисел на другие.

Пример №19.

Найти частное и остаток от деления числа (— 23) на 7.

Решение:

Согласно формуле деления с остатком, получаем:

— 23 = — 4 • 7 + 5 , т.е. частное равно — 4, а остаток равен 5.

Пример №20.

Найти сумму остатков, получающихся при делении числа 7263544587435873 на 2, 4, 5, 9, 10, 25.

Решение:

Используя признаки делимости нацело на числа 2,4,5,9,10 и 25, находим остатки:

• остаток от деления на 2 равен 1;
• остаток от деления на 4 равен 1;
• остаток от деления на 5 равен 3;
• остаток от деления на 9 равен 0;
• остаток от деления на 10 равен 3;
• остаток от деления на 25 равен 23.

Суммируя остатки 1 + 1+3+0+3+23, получаем в ответе 31.

Пример №21.

Пусть остаток от деления натурального числа m на 7 равен 3. Найти остаток от деления на 7 числа

Решение:

Из условия следует, что число m имеет вид: 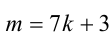. Тогда

Таким образом, остаток от деления числа 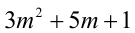на 7 равен 1.

Пример №22.

Доказать, что при любых целых X число 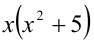делится нацело на 6.

Решение:

Разобьём множество всех целых X на 6 групп в зависимости от остатка при делении на 6, т.е. рассмотрим 6 случаев:

1) Пусть 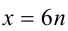, тогда

2) Пусть 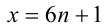, тогда

3) Пусть 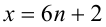, тогда

4) Пусть 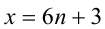, тогда

5) Пусть 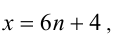тогда

6) Пусть 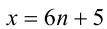, тогда

Таким образом, мы рассмотрели все целые числа X и доказали, что всегда (в каждом из шести случаев) выражение 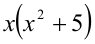кратно 6.

Замечание. Эту задачу можно было решить иначе. Преобразуем данное в условии задачи выражение:

Каждое из двух слагаемых делится нацело на 6 (первое как произведение трёх последовательных целых чисел), поэтому их сумма кратна 6.

Пример №23.

Учительница принесла в класс счётные палочки. Дети раскладывали их в пакетики. Когда разложили по 2 палочки в каждый пакетик, то осталась 1 лишняя палочка. Затем разложили по 13 штук в пакетик, и тогда осталось 7 лишних палочек. Когда же палочки разложили по 9 штук в пакетик, то лишних не осталось. Сколько, самое меньшее, было счётных палочек?

Решение:

Пусть всего было n счётных палочек. Тогда условия задачи приводят к системе

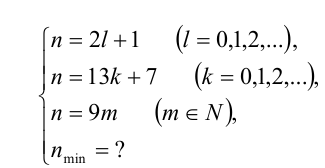
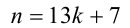
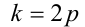
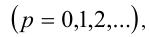
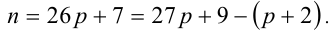
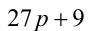
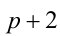
Таким образом, требуется найти наименьшее натуральное нечётное число п , делящееся на 9 и дающее при делении на 13 остаток 7. Заметим, что в силу нечётности число k должно быть чётным, т.е. причём меньшему n соответствует меньшее р , но тогда имеем Поскольку числа п и делятся нацело на 9, то, следовательно, число также должно быть кратно 9 (и при этом быть минимальным). Наименьшее целое неотрицательное р , для которого выполняются эти условия, равно 7, откуда находим

Ответ: самое меньшее — 189 счётных палочек.

Пример №24.

После деления некоторого двузначного числа на сумму его цифр получается 7 и в остатке 6. После деления этого же двузначного числа на произведение его цифр в частном получается 3 и в остатке 11. Найти это двузначное число.

Решение:

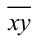
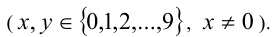
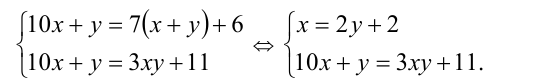
Обозначим — искомое число Тогда, по условию, имеем систему уравнений

Решая систему методом подстановки, находим единственное решение, удовлетворяющее всем условиям задачи: x= 8, y = 3 . Ответ: 83.

Пример №25.

Целые числа m, n,k не делятся нацело на 3. Доказать, что число 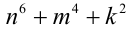делится на 3.

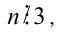
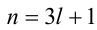
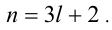
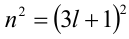
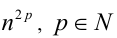
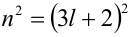
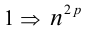
Доказательство. Если то возможны два случая: и . В первом случае — делится на 3 с остатком 1, а значит, , также делится на 3 с остатком 1. Аналогично во втором случае: делится на 3 с остатком делится на 3 с остатком 1. Таким образом, если целое число не делится нацело на 3, то его квадрат (любая чётная степень) при делении на 3 дают остаток 1. Но тогда сумма трёх таких чётных степеней кратна 3.

Пример №26.

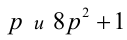
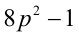
Доказать, что если — простые числа, то — тоже простое число.

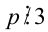
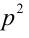
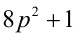
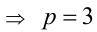
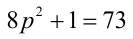
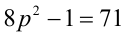
Доказательство. Если , то остаток от деления на 3 равен 1. Но тогда делилось бы на 3, что противоречит условию. Следовательно, , тогда действительно — простое число, и при этом тоже является простым.

Пример №27.

Решить уравнение в целых числах

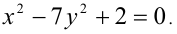
Решение:

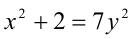
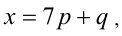
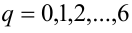
Перепишем уравнение в виде: . Заметим, что правая часть уравнения при любом целом Y делится нацело на 7. Выясним, какие остатки при делении на 7 даёт левая часть данного уравнения. Для этого разобьём множество всех целых X на 7 групп в зависимости от остатка при делении на 7: где , и рассмотрим каждый из этих случаев в отдельности.

1) Если

2) если

3) если

4) если

5) если

6) если

7) если

Итак, правая часть уравнения делится на 7 нацело (т.е. с остатком 0), а левая часть при этом — с остатками 2, 3, 4, 6. Однако равные числа при делении на одно и то же целое число 7 должны давать одинаковые остатки. Полученное противоречие говорит о том, что данное уравнение не имеет решений в целых числах.

Пример №28.

Найти все пары целых чисел (x;y), удовлетворяющие уравнению

и доказать, что для каждой такой пары сумма 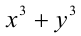является нечётным числом.

Решение:

Заметим, что левая часть уравнения кратна 3, следовательно, и правая часть должна делиться на 3 нацело. Разобьём множество всех целых y на три группы в зависимости от остатка при делении на 3:

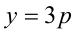
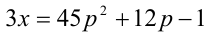
1) Если , то уравнение примет вид . Это равенство невозможно, так как его левая часть кратна 3, а правая — нет.

2) Если 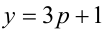, то получим аналогичную ситуацию.

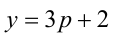
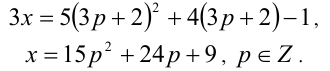
3) Наконец, если , то, подставляя в уравнение, получим

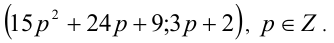
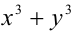
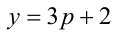
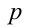
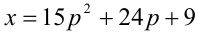
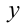
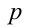
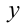
Следовательно, общий вид решений:Осталось показать, что — нечётно. В самом деле, если чётно, то — чётно и, значит, — нечётно. Если, наоборот, — нечётно, то также нечётно, а значит, — чётно. Таким образом, числа и , а значит и их кубы, имеют всегда разную чётность, поэтому их сумма есть нечётное число.

Ответ:

Пример №29.

Решить в целых числах уравнение

Решение:

Так как произвольное целое число представимо в виде , или где , а

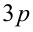
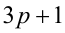
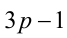
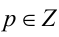
то любое число в кубе или делится нацело на 9, или даёт при делении на 9 в остатке 1 или 8. Аналогично, так как 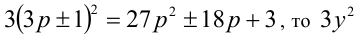даёт при делении на 9 остаток 0 или 3. Итак, правая часть уравнения может делиться на 9 с остатками 2 или 5, а левая — 0, 1 или 8. Следовательно, уравнение не имеет решений в целых числах.

Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:

Предмет математика

Эти страницы возможно вам будут полезны: