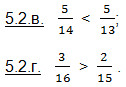При решении неравенств вы должны свободно владеть понятием числового неравенства, знать, что такое решение неравенства, что значит решить неравенство, помнить свойства неравенств. То же относится и к системам числовых неравенств. Все эти сведения вы можете найти в любом пособии для поступающих в вузы.
Напомним свойства числовых неравенств.
1. Если а > b , то b < а; наоборот, если а < b, то b > а.
2. Если а > b и b > c, то а > c. Точно так же, если а < b и b < c, то а < c.
3. Если а > b, то а + c > b+ c (и а – c > b – c). Если же а < b, то а + c < b+ c (и а – c < b – c). Т. е. к обеим частям неравенства можно прибавлять (или из них вычесть) одну и ту же величину.
4. Если а > b и c > d, то а + c > b + d; точно так же, если а < b и c < d, то а + c < b + d, т. е. два неравенства одинакового смысла можно почленно складывать.
Замечание.
Два неравенства одинакового смысла нельзя почленно вычитать друг из друга, так как результат может быть верным, но может быть и неверным. Например, если из неравенства 11 > 9 почленно вычесть неравенство 3 > 2, то получим верное неравенство 8 > 7. Если из неравенства 11 > 9 почленно вычесть неравенство 7 > 2, то полученное неравенство будет неверным.
5. Если а > b и c < d, то а – c > b – d; если а < b и c > d, то а – c < b – d, т.е. из одного неравенства можно почленно вычесть другое неравенство противоположного смысла, оставляя знак того неравенства, из которого вычиталось другое.
6. Если а > b и m – положительное число, то m а > m b и 
, т.е. обе части неравенства можно умножить или разделить на одно и то же положительное число ( знак неравенства остаётся тем же ).
Если же а > b и n – отрицательное число, то n а < n b и 
, т.е. обе части неравенства можно умножить или разделить на одно и то же отрицательное число, но при этом знак неравенства нужно переменить на противоположный.
7. Если а > b и c > d , где а, b, c, d > 0, то а c > b d и если а < b и c < d, где а, b, c, d > 0, то аc < bd, т.е. неравенства одного смысла на множестве положительных чисел можно почленно перемножать.
Следствие. Если а > b, где а, b > 0, то а2 > b2, и если а < b, то а2 < b2, т.е. на множестве положительных чисел обе части неравенства можно возводить в квадрат.
8. Если а > b, где а, b > 0, то 
и если а < b , то 
.
Виды неравенств и способы их решения
1. Линейные неравенства и системы неравенств
Пример 1. Решить неравенство 
.
Решение:
.
Ответ: х < – 2.
Пример 2. Решить систему неравенств 
Решение:
.
Ответ: (– 2; 0].
Пример 3. Найти наименьшее целое решение системы неравенств
Решение:
Ответ: 
2. Квадратные неравенства
Пример 4. Решить неравенство х2 > 4.
Решение:
х2 > 4 (х – 2)∙(х + 2) > 0.
Решаем методом интервалов.
Ответ:
3. Неравенства высших степеней
Пример 5. Решить неравенство (х + 3)∙(х2 – 2х + 1) > 0.
Решение:
Ответ: 
.
Пример 6. Найти середину отрезка, который является решением неравенства 4х2 – 24х + 24 < 4у2, где 
.
Решение:
Область определения неравенства: 
.
С учётом области определения 4х2 – 24х + 24 < 4у2 будет равносильно неравенству
Решаем методом интервалов.
Решение неравенства: 
.
Середина отрезка: 
.
Ответ: 
.
4. Рациональные неравенства
Пример 7. Найти все целые решения, удовлетворяющие неравенству 
.
Решение:
Методом интервалов:
Решение неравенства: 
.
Целые числа, принадлежащие полученным полуинтервалам: – 6; – 5; – 4; 1.
Ответ: – 6; – 5; – 4; 1.
5. Иррациональные неравенства
Помните! Начинать решение иррациональных неравенств нужно с нахождения области определения.
Пример 8. Решить неравенство 
.
Решение:
Область определения: 
.
Так как арифметический корень не может быть отрицательным числом, то 
.
Ответ: 
.
Пример 9. Найти все целые решения неравенства 
.
Решение:
Область определения 
.
– быть отрицательным не может, следовательно, чтобы произведение было неотрицательным достаточно потребовать выполнения неравенства 
, при этом учитывая область определения. Т.е. исходное неравенство равносильно системе 
.
Целыми числами из этого отрезка будут 2; 3; 4.
Ответ: 2; 3; 4.
Пример 10. Решить неравенство 
.
Решение:
Область определения: 
Преобразуем неравенство: 
. С учётом области определения видим, что обе части неравенства — положительные числа. Возведём обе части в квадрат и получим неравенство, равносильное исходному.
т.е. 
, и этот числовой отрезок включён в область определения.
Ответ: .
Пример 11. Решить неравенство 
.
Решение:
Раскрываем знак модуля.
Объединим решения систем 1) и 2): 
.
Ответ: .
6. Показательные, логарифмические неравенства и системы неравенств
Пример 12. Решите неравенство 
.
Решение:
.
Ответ: 
.
Пример 13. Решите неравенство 
.
Решение:
.
Ответ: 
.
Пример 14. Решите неравенство 
.
Решение:
Ответ: 
.
Пример 15. Решите неравенство 
.
Решение:
Ответ: 
.
Задания для самостоятельного решения
Базовый уровень
Целые неравенства и системы неравенств
1) Решите неравенство 2х – 5 ≤ 3 + х.
2) Решите неравенство – 5х > 0,25.
3) Решите неравенство 
.
4) Решите неравенство 2 – 5х ≥ – 3х.
5) Решите неравенство х + 2 < 5x – 2(x – 3).
6) Решите неравенство 
.
7) Решите неравенство (х – 3) (х + 2) > 0.
Решить систему неравенств 
9) Найдите целочисленные решения системы неравенств 
.
10) Решить систему неравенств 
.
11) Решить систему неравенств 
12) Найти наименьшее целое решение неравенства 
13) Решите неравенство 
.
14) Решите неравенство 
.
15) Решите неравенство 
.
16) Решите неравенство 
.
17) Найдите решение неравенства 
, принадлежащие промежутку 
.
18) Решить систему неравенств 
19) Найти все целые решения системы 
Рациональные неравенства и системы неравенств
20) Решите неравенство 
.
21) Решите неравенство 
.
22) Определите число целых решений неравенства 
.
23) Определите число целых решений неравенства 
.
24) Решите неравенство 
.
25) Решите неравенство 2x<16 .
26) Решите неравенство 
.
27) Решите неравенство 
.
28) Решите неравенство 
.
29) Найдите сумму целых решений неравенства 
на отрезке [– 7, 7].
30) Решите неравенство 
.
31) Решите неравенство 
.
Иррациональные неравенства
32) Решите неравенство 
.
33) Решите неравенство 
34) Решите неравенство 
.
Показательные, логарифмические неравенства и системы неравенств
35) Решите неравенство 
.
36) Решите неравенство 
.
37) Решите неравенство 
.
38) Решите неравенство 
.
39) Решите неравенство 
.
40) Решите неравенство 49∙7х < 73х + 3.
41) Найдите все целые решения неравенства 
.
42) Решите неравенство 
.
43) Решите неравенство 
.
44) Решите неравенство 7x+1-7x<42 .
45) Решите неравенство log3(2x2+x-1)>log32 .
46) Решите неравенство log0,5(2x+3)>0 .
47) Решите неравенство 
.
48) Решите неравенство 
.
49) Решите неравенство 
.
50) Решите неравенство logx+112>logx+12 .
51) Решите неравенство logx9<2.
52) Решите неравенство 
.
Повышенный уровень
53) Решите неравенство |x-3|>2x.
54) Решите неравенство 2│х + 1| > х + 4.
55) Найдите наибольшее целое решение неравенства 
.
56) Решить систему неравенств 
57) Решить систему неравенств 
.
58) Решите неравенство 
.
59) Решите неравенство 25•2x-10x+5x>25 .
60) Решите неравенство 
.
Ответы
1) х ≤ 8; 2) х < – 0,05; 3) х ≥ 5; 4) х ≤ 1; 5) х > –2; 6) х < 11; 7) 
; (-2;0]; 9) – 1; 10) х ≥ 7,5; 11)
; 12) 1; 13)
; 14) х ≤ – 0,9; 15) х < – 1; 16) х < 24; 17)
; 18) 
; 19) 3, 4, 5;
20) (0; 2); 21) (0; 1,5); 22) 3; 23) 6; 24) (–1; 1,5); 25) х < 4; 26)
; 27) (– 3; 17); 28)
; 29) – 10; 30) (0; + ∞); 31)
; 32) [1;17); 33) x > 17; 34) х ≥ 2; 35)
; 36) х < 2; 37) х > 0; 38) х ≤ 3; 39) х > – 3,5; 40) х > – 0,5; 41) 0, 1, 2, 3, 4, 5; 42) х < 3; 43) 
; 44) х < 1; 45) 
; 46) (– 1,5; – 1); 47) х < 0; 48)
; 49) 
; 50) х > 0; 51) 
; 52) 
; 53) х < 1; 54)
; 55) – 1; 56) 
; 57) [3,5; 10]; 58) (0, 1); 59) (0; 2); 60)
.
Слайд 1
7. Методы решения уравнений и неравенств в целых числах Выполнила: ученица 11 «А» класса Устименко О.Д. Учитель математики: Кукса Б.И. 2014г. МОУ — СОШ № 3 г. Можайск Презентация на тему:
Слайд 2
7.1. Линейные уравнения Метод прямого перебора Использование неравенств Использование отношения делимости Метод «спуска» Использование формул 7.2. Нелинейные уравнения Метод разложения на множители Вынесение общих множителей за скобку Применение формул сокращенного умножения Использование параметра Метод решения относительно одной переменной выделение целой части Метод «спуска» метод конечного «спуска» Параметризация уравнения Функционально-графический метод 7.3. Неравенства Использование области определения Использование монотонности Использование ограниченности 7.4. Уравнения и неравенства Уравнение с одной неизвестной Показательные уравнения Неравенства Уравнения, содержащие функцию «целая часть числа» [ x ]
Слайд 3
Пример 74. В клетке сидят кролики и фазаны. Всего у них 18 ног. Узнать сколь- ко в клетке тех и других. Укажите все решения. Решение. Пусть х – количество кроликов , у – количество фазанов, тогда имеем уравнение 4 x + 2y = 18 или 2x + y = 9 Если х =1, то у=7. Если х=2, то у=5. Если х = 3, то у = 3. Если х = 4, то у = 1. При х = 5 получаем 2 ∙ 5 = 10 > 9. Ответ: (1 ;7), (2;5), (3;3), (4;1). 7.1. Линейные уравнения Метод прямого перебора
Слайд 4
Использование неравенств Пример 75. Решить в натуральных числах уравнение 5х + 8у = 39 Решение. Для уменьшения перебора вариантов рассмотрим неравенства 5х = 39 – 8у ≥ 0 8у = 39 – 5х ≥ 0 у ≤ 4 х ≤ 7 Проведем перебор по неизвестной у. Если у = 1, то х = 6,2 не является натуральным числом. Если у = 2, то х = 4,6 не является натуральным числом. Если у = 3, то х = 3. Если у = 4, то х = 1,4 не является натуральным числом. Ответ: (3; 3)
Слайд 5
Использование отношения делимости Пример 76. Имеются контейнеры двух видов: по 130 кг и 160 кг. Сколько было контейнеров первого и сколько второго вида, если вместе они весят 3 тонны? Укажите все решения Решение. Обозначим количество контейнеров первого вида через х , второго – через у . Получаем уравнение 130х + 160у = 3000 или 13х + 16у = 300. Далее имеем : 13х + 13у + 3у = 13 ∙ 23 + 1, 3у — 1 = 13 ∙ (23 — х — у). Отсюда следует, что разность 3у — 1 делится на 13. Если 3у — 1 = 0, то у не является натуральным числом. Если 3у — 1 = 13, то у не является натуральным числом. Если 3у — 1 = 26, то у = 9 и х = 12. Если 3у — 1 = 39, то у не является натуральным числом. Если 3у — 1 = 52, то у не является натуральным числом. Если 3у — 1 = 65, то у = 22 но 16 ∙ 22 = 352 > 300. Ответ: 12 контейнеров по 130 кг и 9 по 160 кг.
Слайд 6
Метод «спуска» Пример 79. Решить в целых числах уравнение 5х — 7у = 3. Решение. Выразим из уравнения то не- известное, коэффициент при котором меньше по модулю: Дробь должна быть равна целому числу. где z – целое число. Тогда 2у + 3 = 5 z . Из последнего уравнения выразим то неизвестное, коэффициент при котором меньше по модулю, и проделаем аналогичные преобразования: Дробь должна быть целым числом. Обозначим , г де t – целое число . Отсюда z = 2t — 3. Последовательно возвращаемся к неизвестным x и y . y = 3∙(2t — 3) — t = 5t — 9, x = y + z = 5t — 9 + 2t — 3 = 7t — 12. Ответ: x = 7t — 12, y = 5t — 9, где t Z . Положим ,
Слайд 7
Использование формул Теорема. Уравнение a 1 x 1 + a 2 x 2 + … + a n x n = b разрешимо в целых числах тогда и только тогда, когда d │ b , где d = НОД ( a 1, a 2 ,…, a n ). Теорема. Пусть уравнение ax + by= c разрешимо в Z и пара ( x 0 ; y 0 ) является частным решением этого уравнения. Тогда множеством всех решений в Z данного уравнения является множество пар ( x; y ) , где Следствие. Пусть а и b взаимно просты и ( x 0 y 0 ) какое-нибудь решение уравнения ax + by = c (*) Тогда формулы x = x 0 — b ∙ t , y = y 0 + a ∙ t при t є Z дают все решения уравнения (*).
Слайд 8
Пример 81. (МГУ, 1969). Остаток от деления некоторого натурального числа n на 6 равен 4, остаток от деления n на 15 равен 7. Чему равен остаток от деления n на 30? Решение. Из условия задачи следует, что существует натуральное число k такое, что n = 6k + 4. 2 k — 5l = 1. (*) Для решения этого уравнения найдем какое-нибудь частное решение в целых (не обязательно неотрицательных) числах. Подбором в качестве такого частного решения можно взять, например, k = -2 , l = -1 . Согласно следствия уравнение (*) имеет решения k = -2 +5t, l = -1 + 2t, где t є Z. Чтобы числа k и l были неотрицательными, параметр t должен принимать натуральные значения. Теперь имеем n = 6 ∙ (5t — 2) +4 = Ответ: 22. Аналогично имеем , n = 15l + 7, где l є N. Исключая из этих двух равенств n , получим уравнение 30t — 8 = 30(t — 1) + 22.
Слайд 9
Пример 83. Решить в целых числах уравнение 127 x — 52y + 1 = 0. Решение. Преобразуем отношение коэффициентов при неизвестных. Прежде всего, выделим целую часть неправильной дроби Правильную дробь заменим равной ей дробью Тогда получим Проделаем такие же преобразования с полученной в знаменателе неправильной дробью . Повторяя те же рассуждения для дроби , получим
Слайд 10
Мы получили выражение, которое называется конечной цепной или непрерывной дробью. Отбросив последнее звено этой цепной дроби – одну пятую, превратим получающуюся при этом новую цепную дробь в простую и вычтем ее из исходной дроби Приведем полученное выражение к общему знаменателю и отбросим его 127 ∙ 9 — 52 ∙ 22 + 1 = 0. 127 x -52y + 1 = 0 x = 9, y = 22 x = 9 +52t , y = 22 + 127 t , где t є Z . Ответ: x = 9 +52t , y = 22 + 127 t , где t є Z .
Слайд 11
7.2. Нелинейные уравнения Метод разложения на множители вынесение общих множителей за скобку Пример 84. Решить в целых числах уравнение 2 x 3 + xy — 7 = 0 . Решение. Приведем данное уравнение к виду x(2x 2 + y) = 7 Так как 7= 1 ∙ 7 = 7 ∙ 1 = -1 ∙ (-7) = -7 ∙ (-1), то рассмотрим четыре системы уравнений: Из каждой системы получаем решения. Ответ: (1; 5); (-1; -9); (7; -97); (-7; -99).
Слайд 12
Применение формул сокращенного умножения Пример 85. Найти все пары натуральных чисел, разность квадратов которых равна 55. Решение. Запишем условие задачи в виде уравнения n 2 — k 2 = 55 или (n — k)(n + k) = 55. Так как n + k > 0 , то n — k > 0 , причем n + k > n — k. Поскольку 55 = 1 ∙ 55 = 5 ∙ 11 то возможны два случая Решая эти уравнения, получим два ответа: n = 28, k = 27 и n = 8, k = 3. Ответ: (28; 27); (8; 3).
Слайд 13
Использование параметра Пример 88. Решить в целых числах уравнение 2 x 2 — 2yx + 9x + y = 2. Решение. Перепишем уравнение в виде 2 x 2 — x(2y — 9) + y — 2 + a = a и разложим левую часть уравнения на множители как квадратный трехчлен относительно х . Находим дискриминант D = 4y 2 — 44y + 97 — 8a. Очевидно, если , 97 — 8a = 121 , то дискриминант будет полным квадратом. При этом a = -3 и Отсюда x 1 = 0,5 и x 2 = y — 5 . Уравнение принимает вид (2x — 1)(x — y + 5) = -3 . Рассмотрите самостоятельно решение последнего уравнения. Ответ: (1; 9); (-1; 3); (2; 8); (0; 2).
Слайд 14
Метод решения относительно одной переменной выделение целой части Пример 89. (МГУ, 1997). Найти все пары целых чисел x и у, удовлетворяющие уравнению 3xy + 14x + 17y + 71 = 0. Решение. Выразим из данного уравнения у через х: При этом следует отметить, что величина 3x + 17 ≠ 0 (так как x – целое число). Выделим из дроби в правой части этого равенства правильную алгебраическую дробь (у которой степень числителя меньше степени знаменателя): Умножим обе части последнего равенства на 3:
Слайд 15
Метод «спуска» метод конечного «спуска» Пример 96. Решить в целых числах уравнение 2x 2 — 5y 2 = 7. Решение. Так как 2x 2 – четное число, а 7 – нечетное, то 5y 2 должно быть нечетным, т.е. у – нечетное. Пусть , y = 2z + 1, где z є Z , тогда данное уравнение можно переписать в виде x 2 — 10z 2 — 10z = 6. Отсюда видно, что x должно быть четным. Пусть , x = 2m , тогда последнее уравнение примет вид 2m 2 — 5z(z + 1) = 3 , что невозможно, так как число z(z + 1) – четно, а разность двух четных чисел не может быть равна нечетному числу. Таким образом, данное уравнение не имеет решений в целых числах. Ответ: нет решений.
Слайд 16
Поскольку числа 3у и 14 – целые, то 3x +17 должно быть делителем числа 25 : 3x + 17 = ±1; ±5; ±25 – всего 6 возможностей. Отсюда для x получаем три возможных значения: –4, –6, –14 (в остальных трех случаях x не является целым). Соответствующие значения у равны –3, –13, –5. Ответ: (-4; -3); (-6; -13); (-14; -5). Замечание. В данном примере суть выделения целой части состоит в избавлении переменной x из числителя (сравните с примером 77). В решении был использован прием домножения обеих частей равенства на коэффициент при x в знамена- теле. Этот прием домножения также удобно использовать при решении уравнений методом разложения на множители.
Слайд 17
Параметризация уравнения Пример 99. Решить в целых числах уравнение x 3 + y 3 + z 3 = 2 . Решение. Положим x = a + b, y = a — b. Так как x 3 + y 3 = 2a 3 + 6ab 2 , то исходное уравнение принимает вид 2a 3 + 6ab 2 + z 3 = 2. Положив a = 1, получим z 3 = -6b 2 . Считаем теперь b = 6t 2 Отсюда x = 1 + 6t 2 , y = 1 -6t 2 , z = -6t 2 . Таким образом, получено бесконечное множество решений исходного уравнения, соответствующих целочисленным значениям параметра t . Ответ: x = 1 + 6t 2 , y = 1 -6t 2 , z = -6t 2 , где t є Z
Слайд 18
Функционально-графический метод Пример 100. (МИОО 2010). Найти все пары натуральных k и n таких, что k < n и ( n ) k = ( k ) n . Решение. 1 . Преобразуем исходное равенство: k ln n = n ln k 2.
Слайд 19
откуда следует k = 1 или , k = 2, причем для каждого k может найтись не более одного значения n , удовлетворяющего уравнению в паре с этим значением k . 3. В случае k = 1 из данного уравнения получаем n = 1, ч то не соответствует условию k < n . 4. В случае k = 2 получаем уравнение , n 2 = 2 n , решение которого легко находится подбором: n = 4, причем в силу выше- сказанного это единственное решение n > e . Ответ: k = 2 , n = 4 .
Слайд 20
7.3. Неравенства Использование области определения Пример 102. (МГУ, 1973). Найти все целые числа x , удовлетворяющие неравенству Решение. Допустимые значения x определяются системой неравенств Подставляем последовательно найденные значения x в неравенство, предварительно его упростив.
Слайд 21
1. x = 1. Тогда 2. х = 2. Тогда 3. х = 3. Тогда Ответ: 2; 3.
Слайд 22
Использование монотонности Пример 103. (МГУ, 1976). Найти все целые z , удовлетворяющие неравенству Решение. Допустимые значения z определяются из системы Заметим, что левая часть неравенства увеличивается с ростом z , а правая – уменьшается. Это обстоятельство позволяет упростить перебор. В силу сделанного выше замечания, необходимости в проверке значений z = 3, 4, 5, 6 нет. Эти числа решениями не являются. Ответ: -1, 0, 1.
Слайд 23
Использование ограниченности Пример 104. (МГУ, 1996). Найти все целочисленные решения неравенства Решение. Целые решения будем искать из двух ограничений системы Первое неравенство выполняется при x = 3, 4, 5, 6. Но из этих значений исходному неравенству удовлетворяет только x = 3 . При x = 0, 1, 2 первое неравенство не выполняется. При x = -1 выполняется как первое не- равенство, так и исходное неравенство. При x = -2 первое неравенство не выполняется. При остальных значениях x = -3, -4, … первое неравенство не разрешимо, так как левая часть неравенства x(x 2 — 5) ≥ 3 будет отрицательной. Ответ: -1; 3.
Слайд 24
Метод интервалов Пример 105. (МГУ, 1972). Определить, сколько целочисленных решений имеет неравенство Решение. Методом интервалов по 2 n определяем решения (см. рис. 2): Дальше подбором находим n = ± 2, ± 3, ±4 или n = ±8, ±9,±10, ±11, ±12. Ответ: 16 решений.
Слайд 25
7.4. Уравнения и неравенства Уравнение с одной неизвестной Пример 107. Может ли квадратное уравнение ax 2 + bx + c = 0 с целыми коэффициентами иметь дискриминант, равный 23? Первое решение. Рассмотрим уравнение b 2 — 4ac = 23. Так как 23 – нечетное число, а 4 ac – четное, то b 2 и, следовательно, b – нечетное число, т.е . b = 2k — 1, k є Z . Тогда (2k — 1) 2 — 4ac = 23; 4(k 2 — k -ac) = 22. Последнее уравнение не имеет решений, так как 22 не делится на 4. Второе решение. Перепишем уравнение b 2 — 4ac = 23 в виде b 2 — 25 = 4ac — 2 и разложим обе части уравнения на множители: (b — 5)(b + 5) = 2(2ac — 1). (*) Так как в правой части уравнения – число четное, то и в левой – тоже четное, следовательно, b — 5 и b + 5 одновременно четные (докажите), т.е. b — 5 =2m, b — 5 = 2k. Левая часть уравнения (*) делится на 4 , а правая – нет, поэтому уравнение b 2 -4ac = 23 не имеет решений в целых числах. Третье решение. Перепишем уравнение b 2 -4ac = 23 в виде b 2 = 4ac + 23 или b 2 = 4(ac + 5) + 3. Получили, что квадрат натурального числа при делении на 4 дает остаток 3 , что невозможно (докажите). Ответ: не может.
Слайд 26
Показательные уравнения Теорема. Если остаток от деления a 1 на b равен r 1 , а остаток от деления a 2 на b равен r 2 , то остаток от деления a 1 +a 2 на b равен остатку от деления r 1 + r 2 на b . Опорная задача. Докажите, что оста- ток от деления на 3 числа 5 k равен 1 , если k четно, и 2 , если k нечетно.
Слайд 27
Неравенства Пример 121. (МИОО 2010). Найти все пары (x; y) целых чисел, удовлетворяющие системе неравенств : Решение. Выделяя полные квадраты, получаем: Из первого и второго неравенства системы: Подставляя x = 12 в систему, получаем: Ответ: (12; -8).
Слайд 28
Уравнения, содержащие функцию «целая часть числа» [ x ] Целой частью числа x называется наибольшее целое число, не превосходящее х . Свойства целой части числа: 1) Из равенства [y] = n следует, что a) n – целое число; б) y = n + α , где 0 ≤ α < 1; в) 0 ≤ y — n < 1. 2) Если [ u ] = [ v ] то u = m + α , v = m+ β , где 0 ≤ α < 1 и 0 ≤ β <1 , поэтому u — v = α — β и -1 < u — v < 1. 3 ) Если [ x + y ] = x то x – целое число и 0 ≤ y < 1. 4) Если n – целое число, то [ n + x ] = n + [ x ].
На чтение 3 мин. Просмотров 8.2k.
Рассмотрим что такое числовое неравенство, числовые неравенства имеют следующие свойства.
Свойства числовых неравенств
- Если при сравнении чисел a и b разность a-b – положительное число, то a > b.
- Если при сравнении чисел a и b разность a-b – отрицательное число, то a < b.
Строгие и нестрогие числовые неравенства:
- Если неравенства записываются знаками < или > , то их называют строгими неравенствами.
- Если неравенства записывают знаками ≤ или ≥, то их называют нестрогими неравенствами.
Как решать числовое неравенство
Примеры.
1. Сравните числа а и b по их разности.
а) a-b=-7. Решение. Так как разность a-b – отрицательное число, то a < b.
б) a-b=4,5. Решение. Так как разность a-b – положительное число, то a > b.
в) a-b=0. Решение. Так как разность a-b равна нулю, то a=b.
2. Сравните данные числа.
а) 0,099 и 0,1. Решение. Десятичные дроби сравниваются поразрядно: из двух чисел больше то, которое содержит больше единиц высшего разряда.
0,099 < 0,1, так как 0 < 1 (сравнили десятые доли чисел).
б) -5,43 и -5,6. Решение. -5,43 > -5,6, так как из двух отрицательных чисел больше то, модуль которого меньше.
так как из двух дробей с одинаковыми знаменателями больше та, числитель которой больше, а меньше та, числитель которой меньше.
так как из двух дробей с одинаковыми числителями больше та, знаменатель которой меньше, а меньше та, знаменатель которой больше.
Решение. Приведем дроби к общему знаменателю. Получаем:
Теперь сравниваем дроби с одинаковыми знаменателями. Получаем:
3. Записать в виде двойного неравенства: 6 < 12 и 12 < 15.
Решение. 6 < 12 < 15. Читают: двенадцать больше шести и меньше пятнадцати.
4. Выписать все целые числа, удовлетворяющие двойному неравенству:
— 4 ≤ х < 3. Решение: -4; -3; -2; -1; 0; 1; 2.
5. Задания для самостоятельного решения.
5.1 Сравните с нулем разность чисел а и b, если
а) a < b; б) a > b; в) a=b.
5.2. Сравните данные числа.
а) -2,467 и -2,476; б) 8,98 и 8,899;
5.3. Выписать все целые числа, удовлетворяющие двойному неравенству:
а) -5 ≤ х < 1; б) -3 < x ≤ 3; в) 4 < x < 9; г) -8 ≤ x ≤ -4.
Ответы на решение числовых неравенств
5.1.а. a-b < 0;
5.1.б. a-b > 0;
5.1.в. a-b=0.
5.2.а. -2,467 > -2,476;
5.2.б. 8,98 > 8,899;
5.3.а -5; -4; -3; -2; -1; 0;
5.3.б. -2; -1; 0; 1; 2; 3;
5.3.в. 5; 6; 7; 8;
5.3.г. -8; -7; -6; -5; -4.
ответы
ваш ответ
Можно ввести 4000 cимволов
отправить
дежурный
Нажимая кнопку «отправить», вы принимаете условия пользовательского соглашения
похожие темы
похожие вопросы 5
Сколько целых решений имеет неравенство -18
Для того, чтобы определить сколько целых решений имеет неравенство — 18 < х < 174 выполним следующие действия.
Алгоритм решения задачи
- вспомним определение целого числа;
- выясним входят ли концы отрезка в решение неравенства;
- найдем число отрицательных решений неравенства;
- найдем число положительных решений неравенства;
- найдем количество целых решений неравенства.
Определение целого числа
Давайте вспомним определение целого числа в математике.
Натуральные числа, противоположные им числа и 0 называются целыми числами.
Теперь выясним входят ли концы отрезка в решение неравенства.
Знаки в заданном неравенстве — 18 < х < 174 строгие и при изображении этих точек на координатной прямой они будут выколотыми и не будут являться решением неравенства.
Найдем количество целых решений неравенства — 18 < х < 174
Чтобы посчитать число целых решений неравенства можно поступить двумя способами:
1) выписать все целые числа удовлетворяющие неравенству и сосчитать их;
2) методом логических рассуждений вычислить число отрицательных решений, число положительных решений и не забыть про ноль.
Давайте решим наше задание вторым способом.
Рассмотрим отрезок (- 18; 0). На нем целых чисел, удовлетворяющих нашему неравенству будет 17 (так как -18 не входит и число 0 мы посчитаем отдельно).
0 будем считать за 1 решение неравенства.
Рассмотрим отрезок (0; 174). На нем целых чисел, удовлетворяющих неравенству 173.
Сложим число всех найденных решений на каждом из рассмотренных отрезков и получим:
102. Сколько целых чисел удовлетворяют неравенству x 2 — x — 30 < 0?
Решебник по алгебре за 9 класс (А.Г. Мордкович, Л.А. Александрова, Т.Н. Мишустина и др., 2010 год),
задача №102
к главе «Неравенства и системы неравенств».
Выделите её мышкой и нажмите CTRL + ENTER
Большое спасибо всем, кто помогает делать сайт лучше! =)
Нажмите на значок глаза возле рекламного блока, и блоки станут менее заметны. Работает до перезагрузки страницы.
математика — Неравенство в целых числах
По стройте область , заданную этими неравенствами , и посмотрите.
Область я построил, получается очень узкий и с вершинами имеющими большие координаты (-80; -60); (60; 40); (0; 0) и по графику точки не удается посчитать. Должен быть аналитический метод решения.
2 ответа
Количество точек на границе треугольника подсчитывается просто, и оно равно $%60$%. Далее, нетрудно подсчитать площадь этого треугольника — либо по общей формуле, через определитель, либо разбивая прямоугольник $%[-80;60]times[-60;40]$% на несколько фигур, включая исследуемый треугольник, площадь которых легко вычисляется. Получается значение площади $%S=200$%. Далее можно применить известную формулу Пика, согласно которой площадь многоугольника в узлах целочисленной решётки равна $%B+Gamma/2-1$%, где $%B$% — число внутренних целочисленных точек многоугольника, а $%Gamma$% — число граничных. Мы знаем, что $%Gamma=60$%, откуда $%B=200-60/2+1=171$%. В задаче нужно подсчитать значение $%B+Gamma$%, и оно равно $%231$%.
Имеет смысл рассмотреть другое решение, на формулу Пика не опирающееся. Оно состоит в следующем. Будем использовать уже введённые обозначения $%A(0;0)$%, $%B(60;40)$%, $%C(-80;-60)$%. Построим прямоугольник $%CDBE$%, где $%D(-80;40)$%, $%E(60;-60)$%. В прямоугольнике имеется ровно $%(140+1)(100+1)$% точек (далее под точками понимаются целочисленные), и из них $%21$% лежит на диагонали $%BC$%. Поэтому выше и ниже неё лежат по $%frac12((140+1)(100+1)-21)=7100$% точек. Нас не интересует то, что лежит ниже диагонали, поэтому имеем $%21+7100$% точек. Из них мы вычитаем то, что лежит выше диагонали $%AC$% в прямоугольнике с указанной диагональю; это будет $%frac12((80+1)(60+1)-21)=2460$%, а также аналогичное количество для диагонали $%AC$%, которое равно $%frac12((60+1)(40+1)-21)=1246$%. Наконец, надо вычесть ещё точки прямоугольника с диагональю $%AD$%, не считая его правой и нижней границ, а это $%80cdot40=3200$%. В итоге получается $%21+7100-2460-1240-3200=231$%.
отвечен 22 Ноя ’13 18:59
Все множество, которое удовлетворяет даной системе, есть внутренняя часть треугольника (с границей) АВС, где А(0;0); В(60;40); С(-80;-60). Треугольник очень «худенький» и «длинный», т.к. растояние от точки А до прямой ВС равно $%5x-7y-20=0$% равно $%20/ sqrt=2,32..$%, т.е. точек там не так уж и много во внутренней части. На отрезке АВ лежат точки $%(3t; 2t), t<=20, t>=0$%, т.е. 21 точка. На отрезке АС $%(4t; 3t), t>=-20, t<=0$%, т.е. 21 точка. На отрезке BС $%(-80+7t; -60+5t), t<=20, t>=0$%, т.е. 21 точка. Осталось как-то оценить внутренние точки.
отвечен 22 Ноя ’13 14:48
Спасибо. Но точки на прямой найти не очень сложно, главная проблема определить количесиво целых решений внутри треугольника.
Можно попробовать сделать так: решить в целых числах совокупность неравенства 3y/2<=x<=4+7y/5 и 4y/3<=x<=4+7y/5. В первом неравенстве рассматривать значения у кратные 10 (общий знаменатель выражений 3у/2 и 7у/5). Аналогично для второго неравенства, только значения у, кратные 15.
Исходя из этих соображений, у меня получается количество целых пар 64. Хотелось бы, чтобы кто-нибудь проверил, если не сложно. Заранее спасибо.