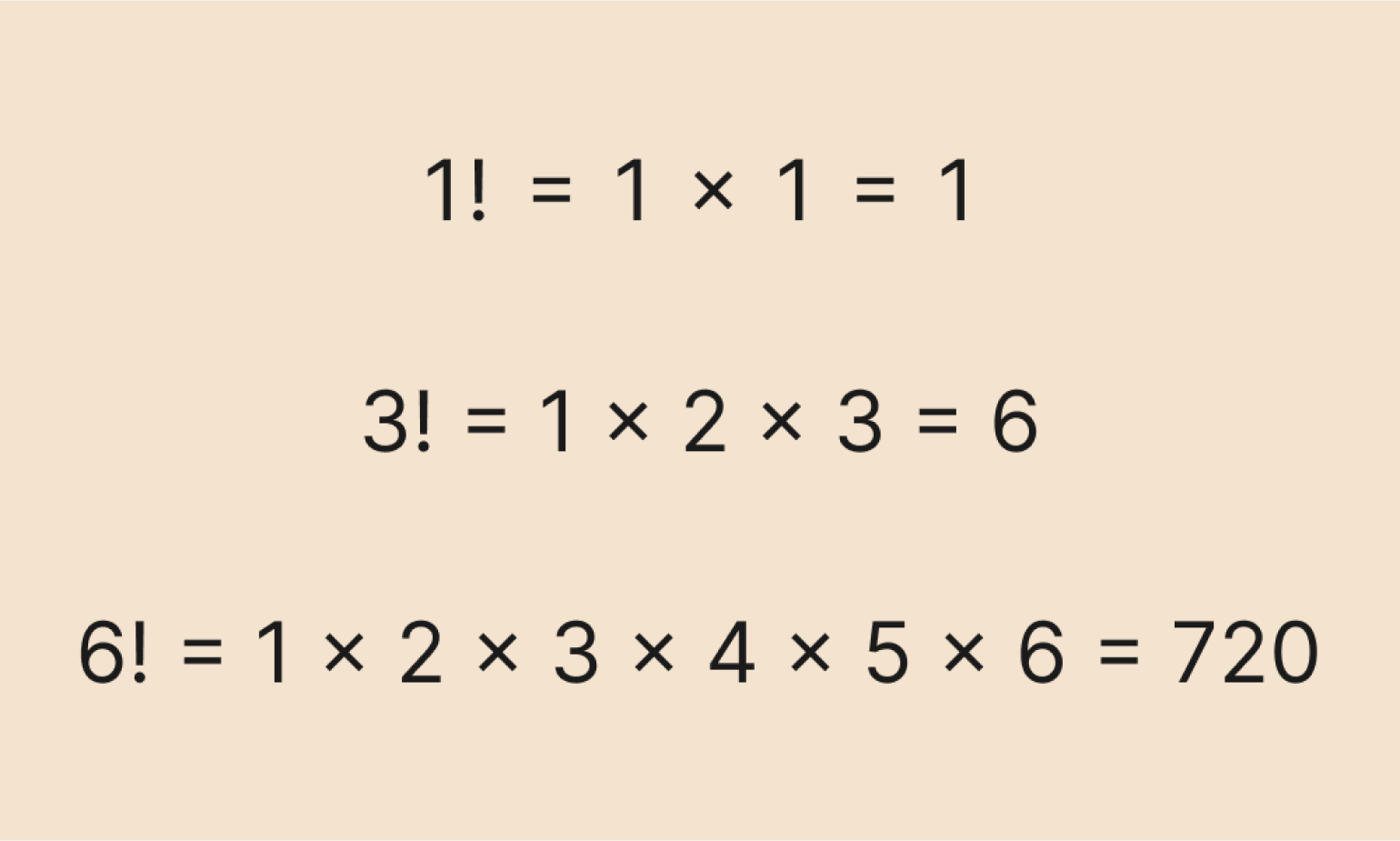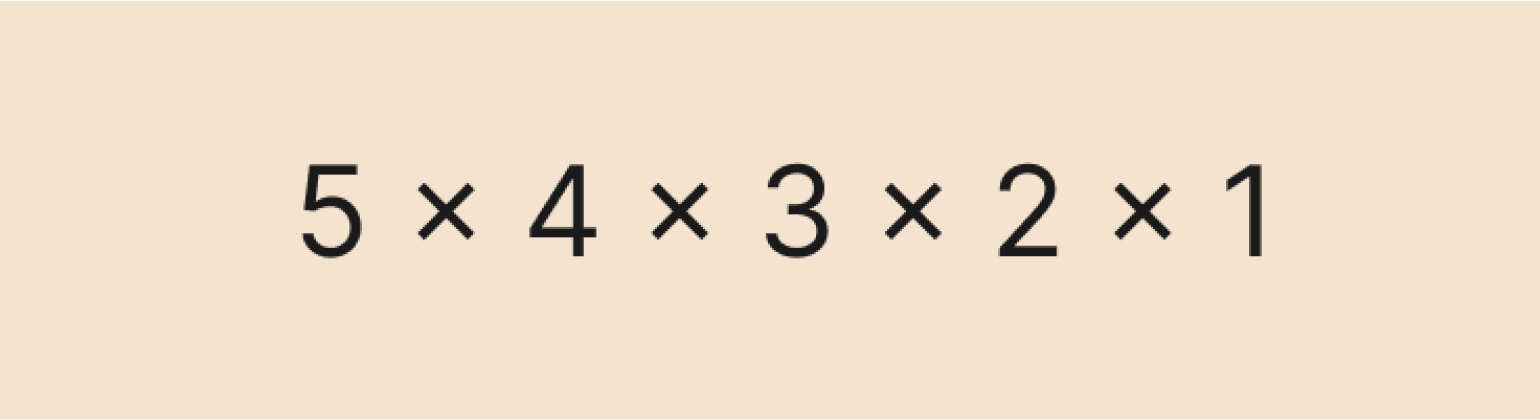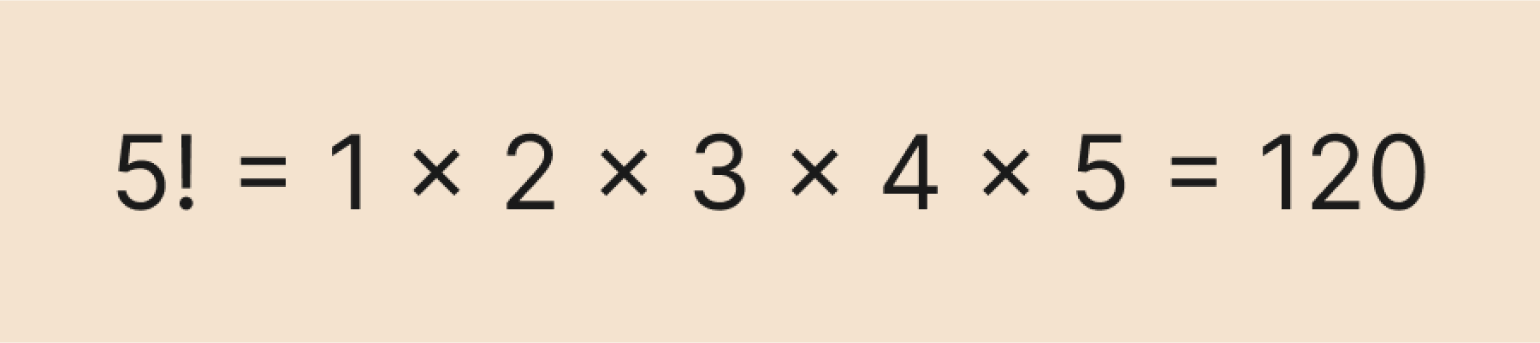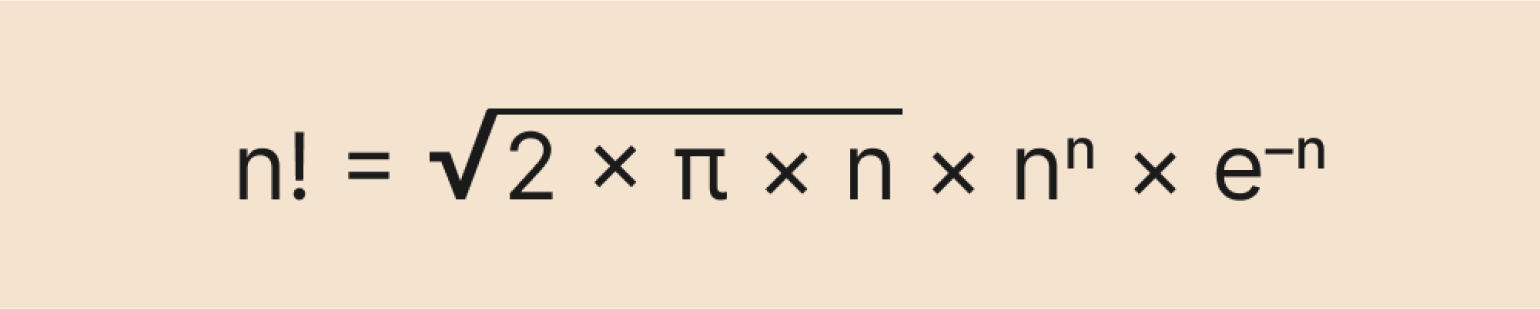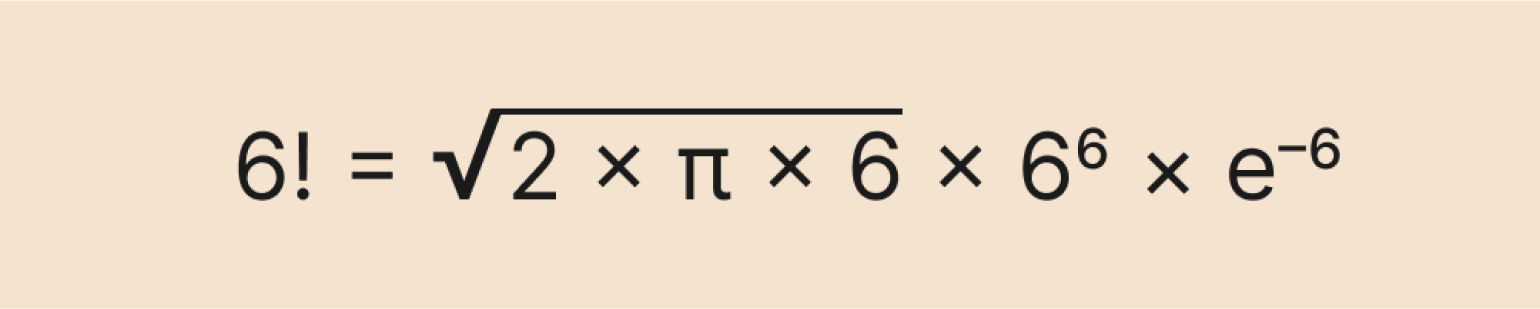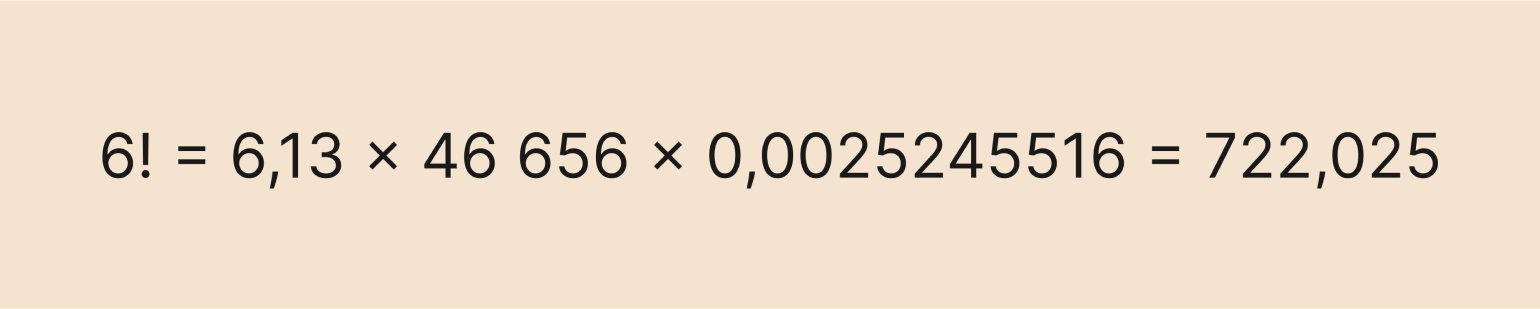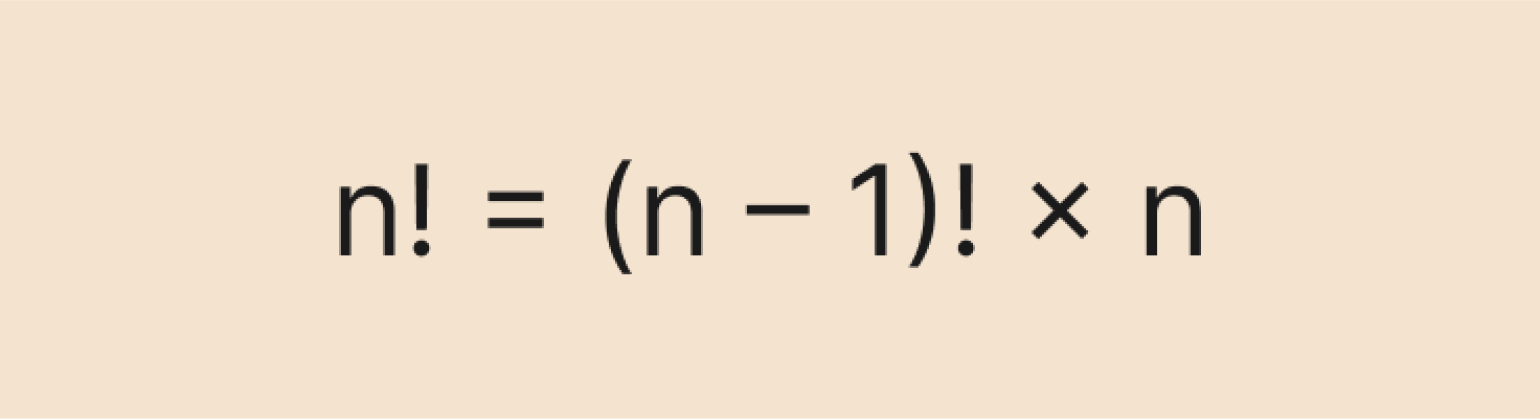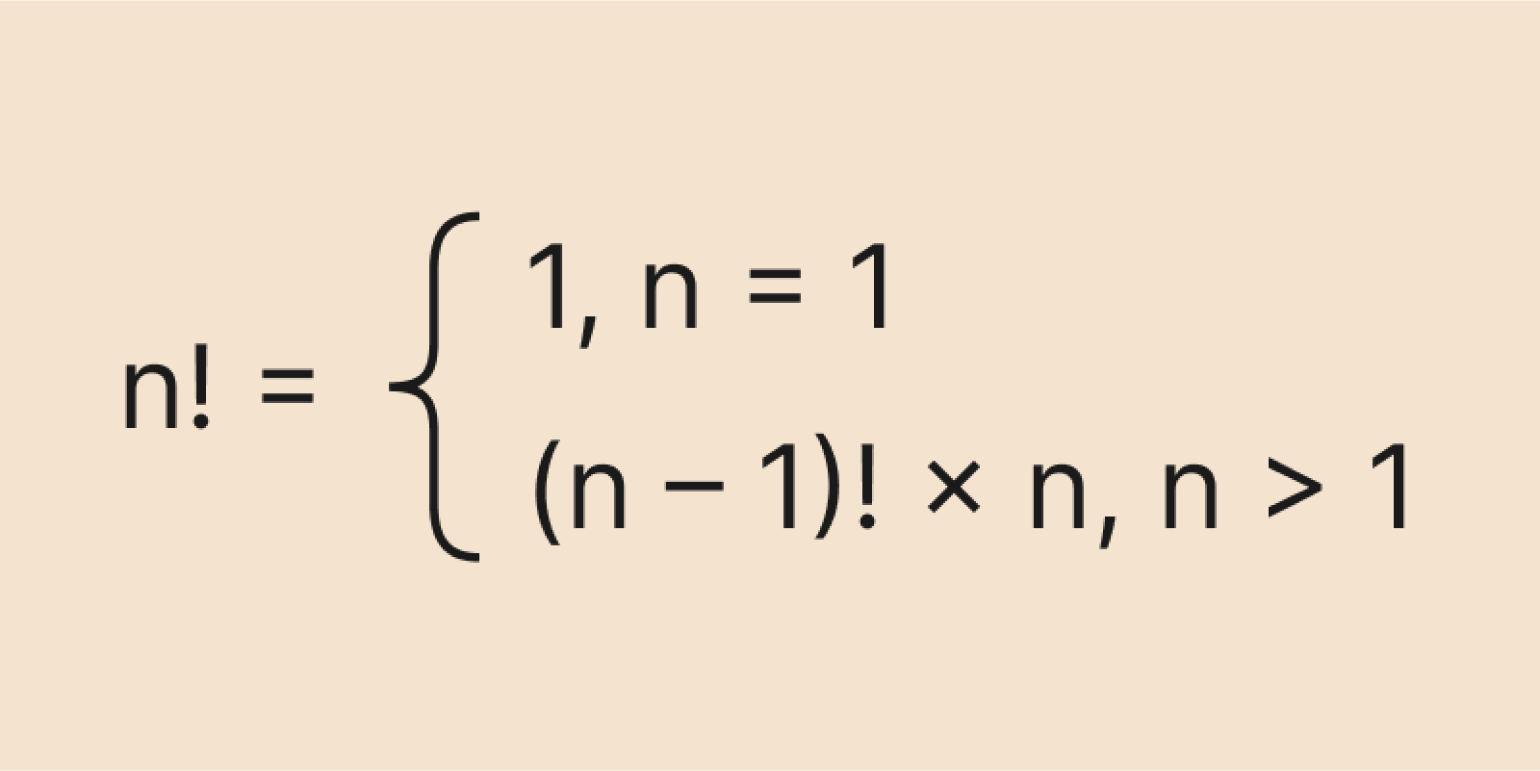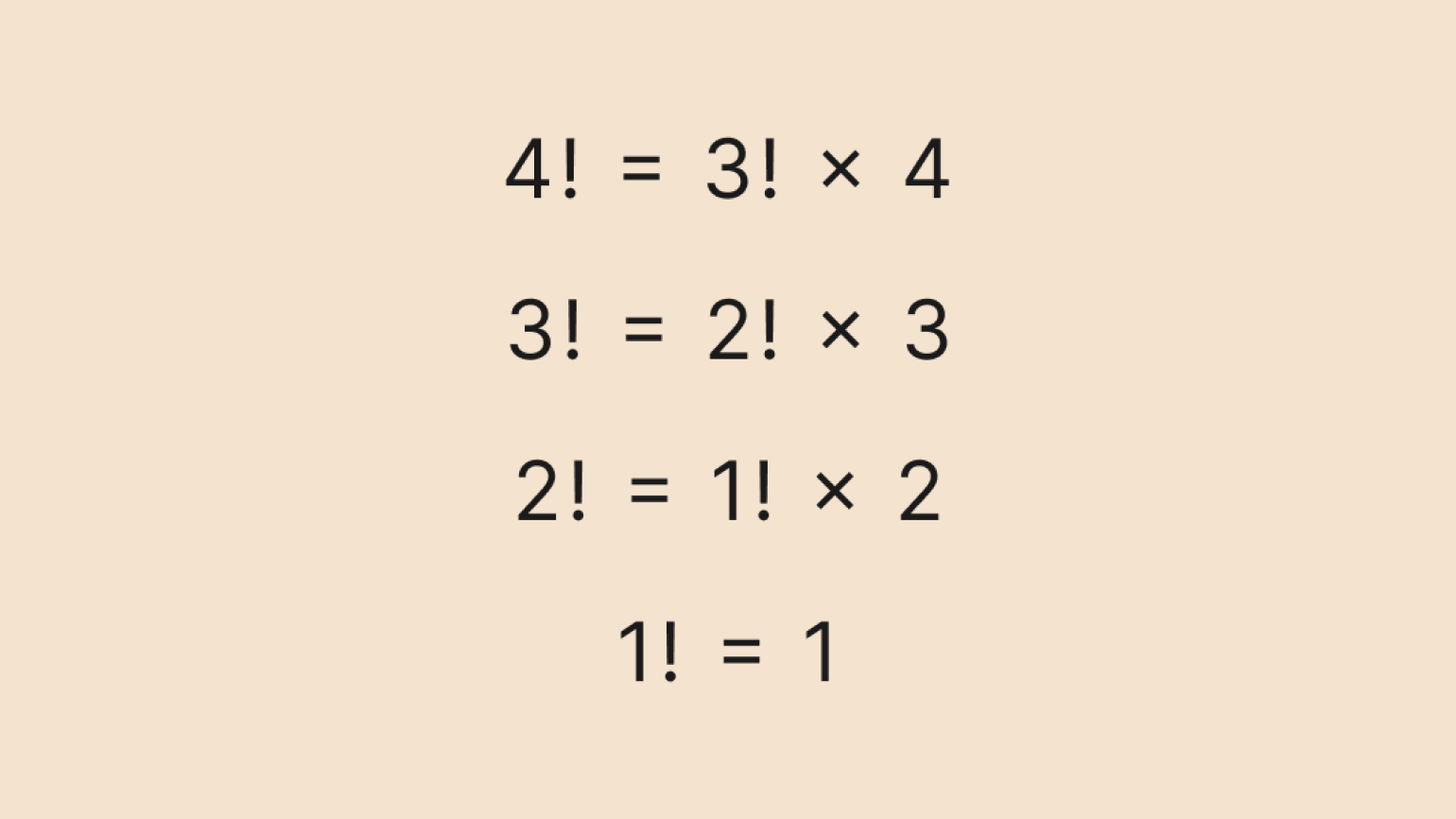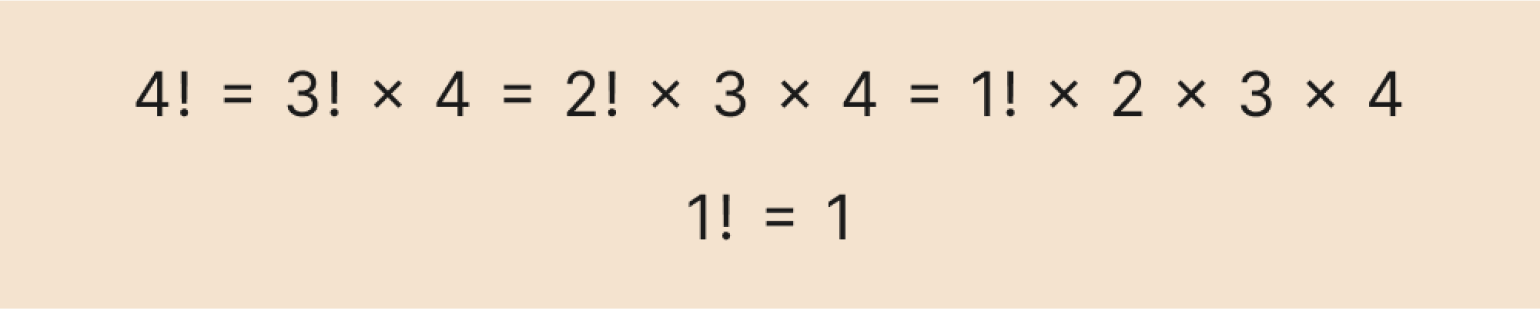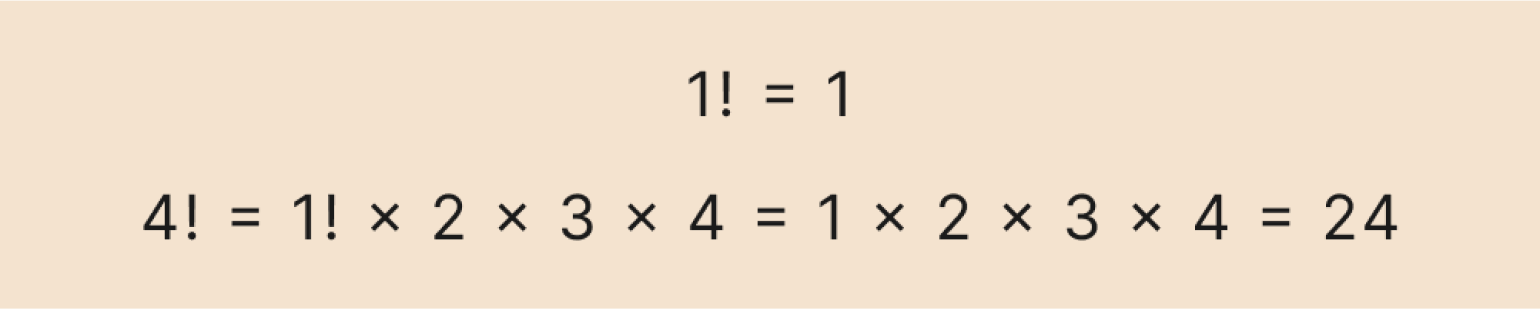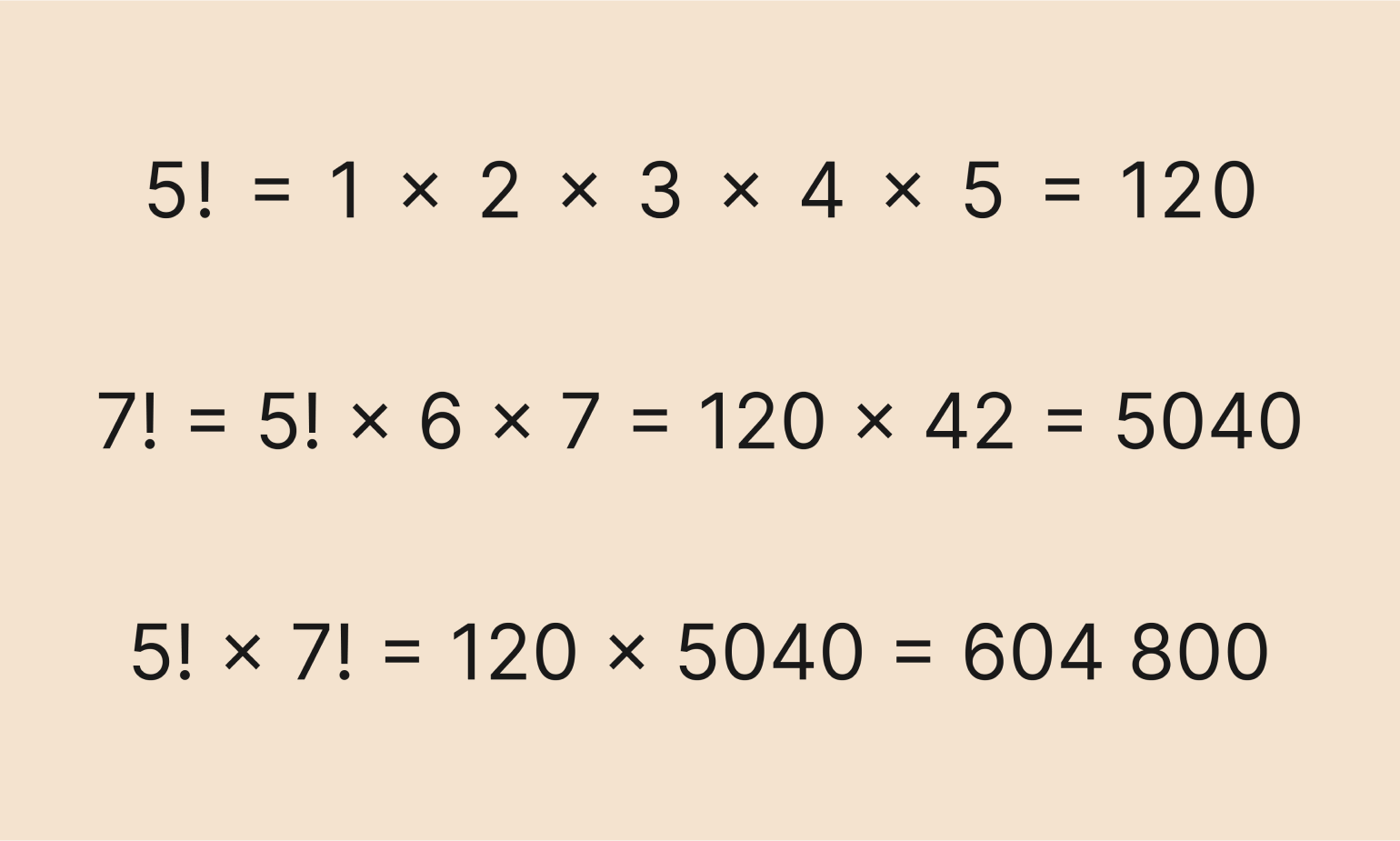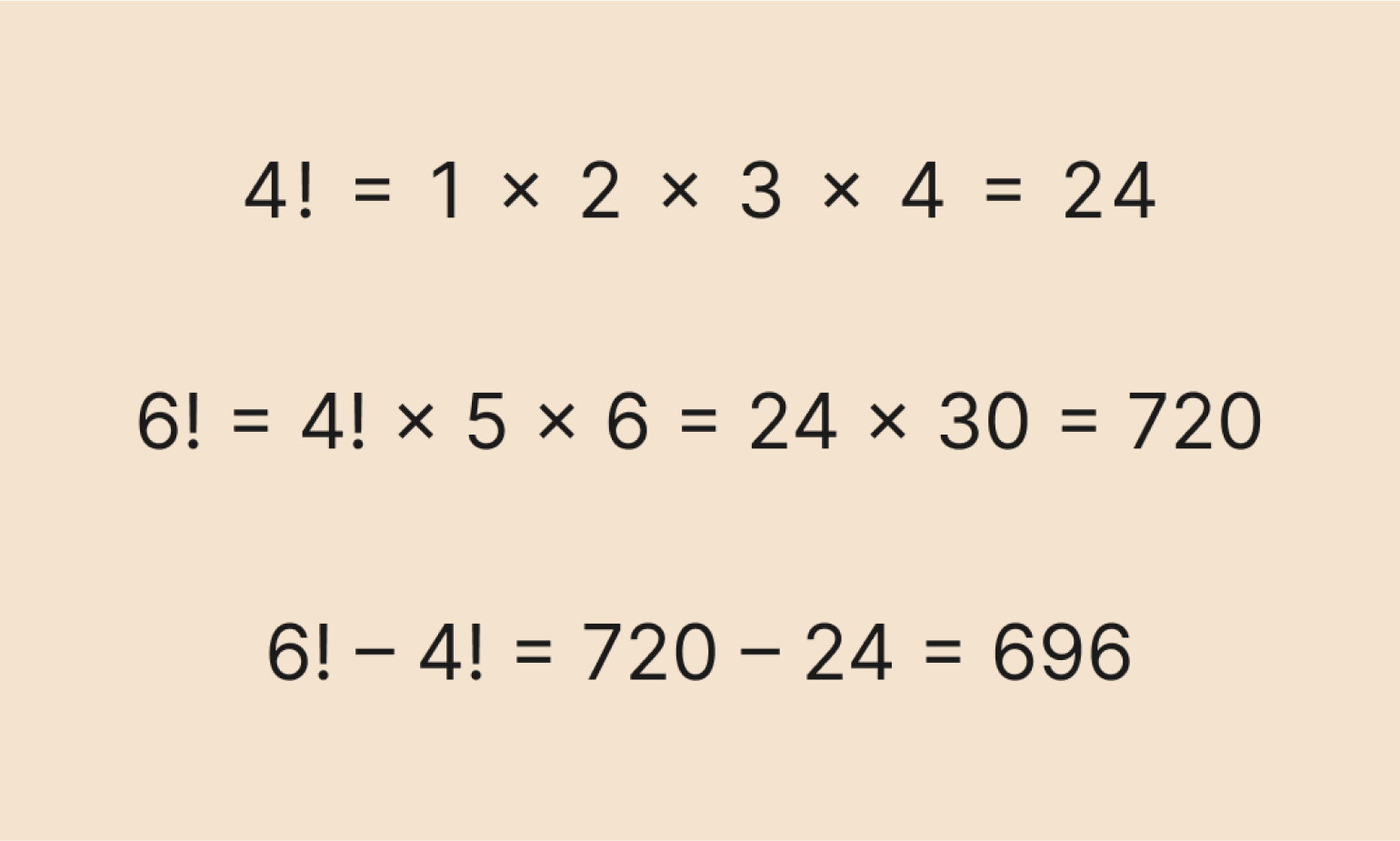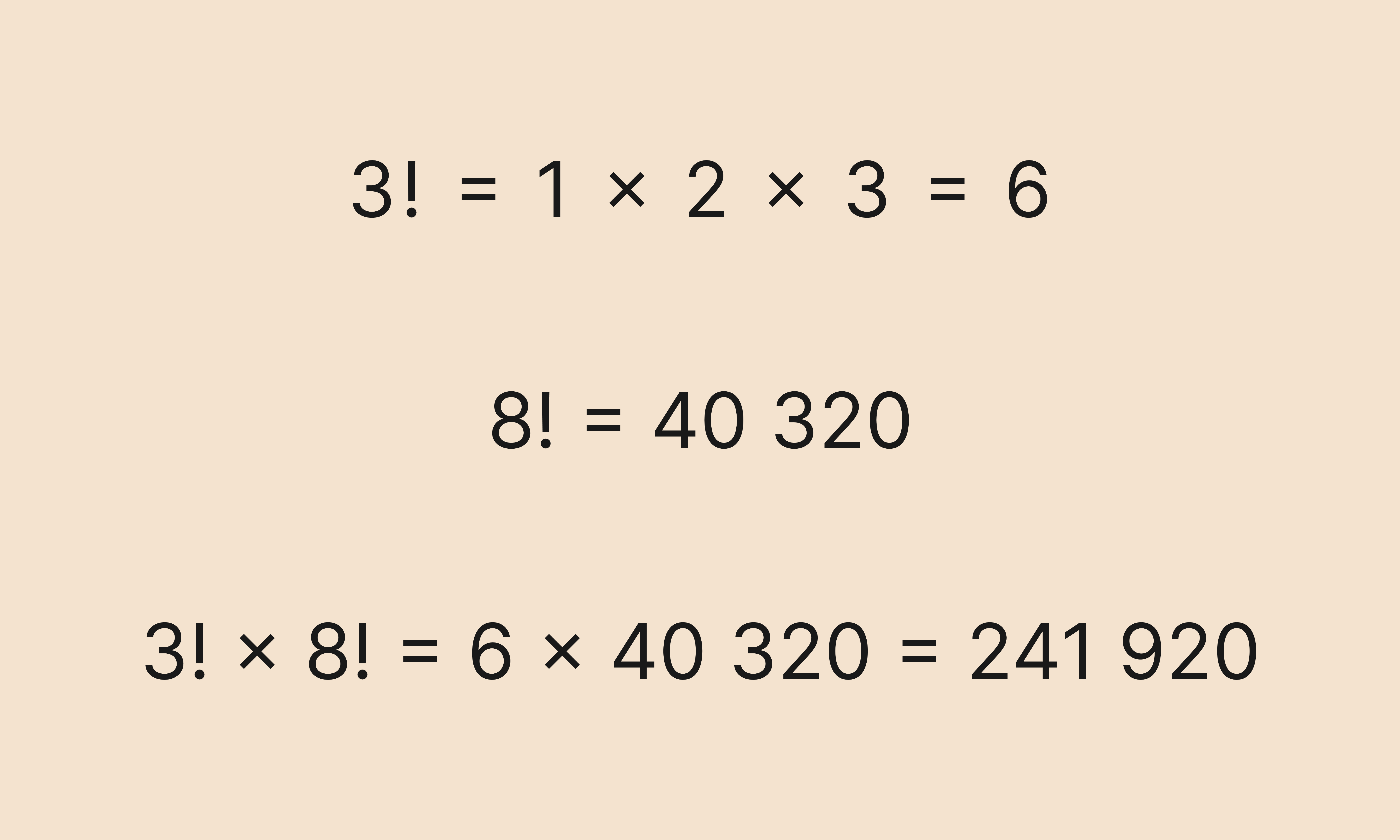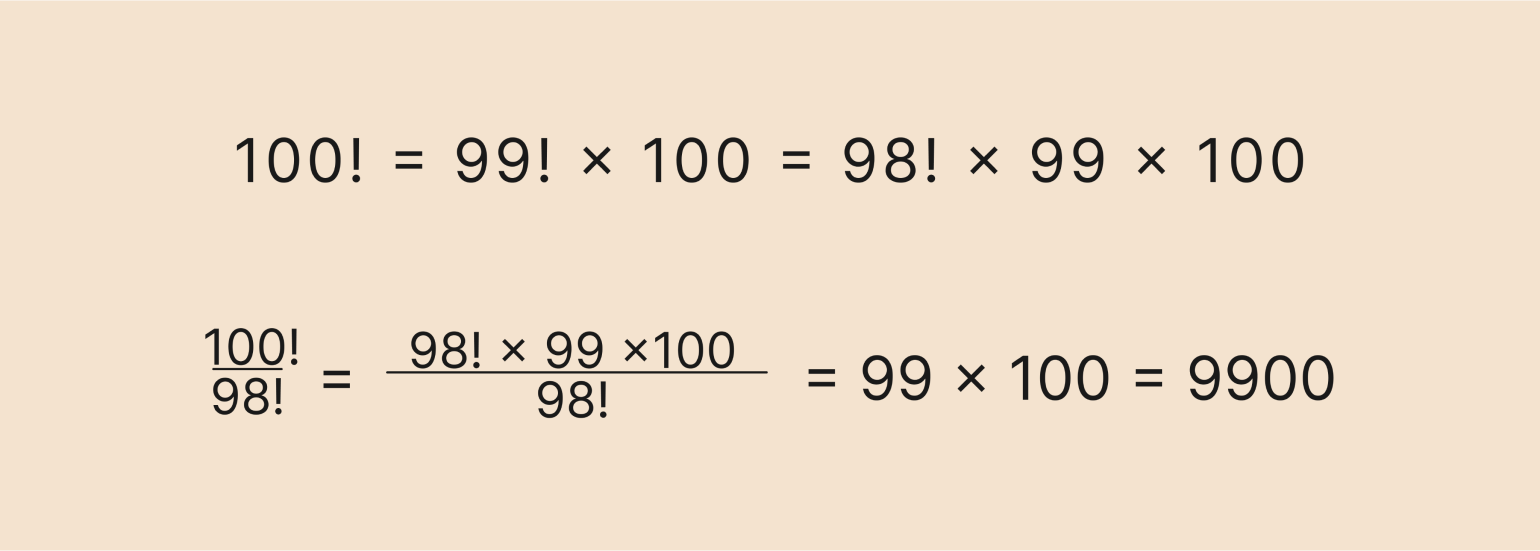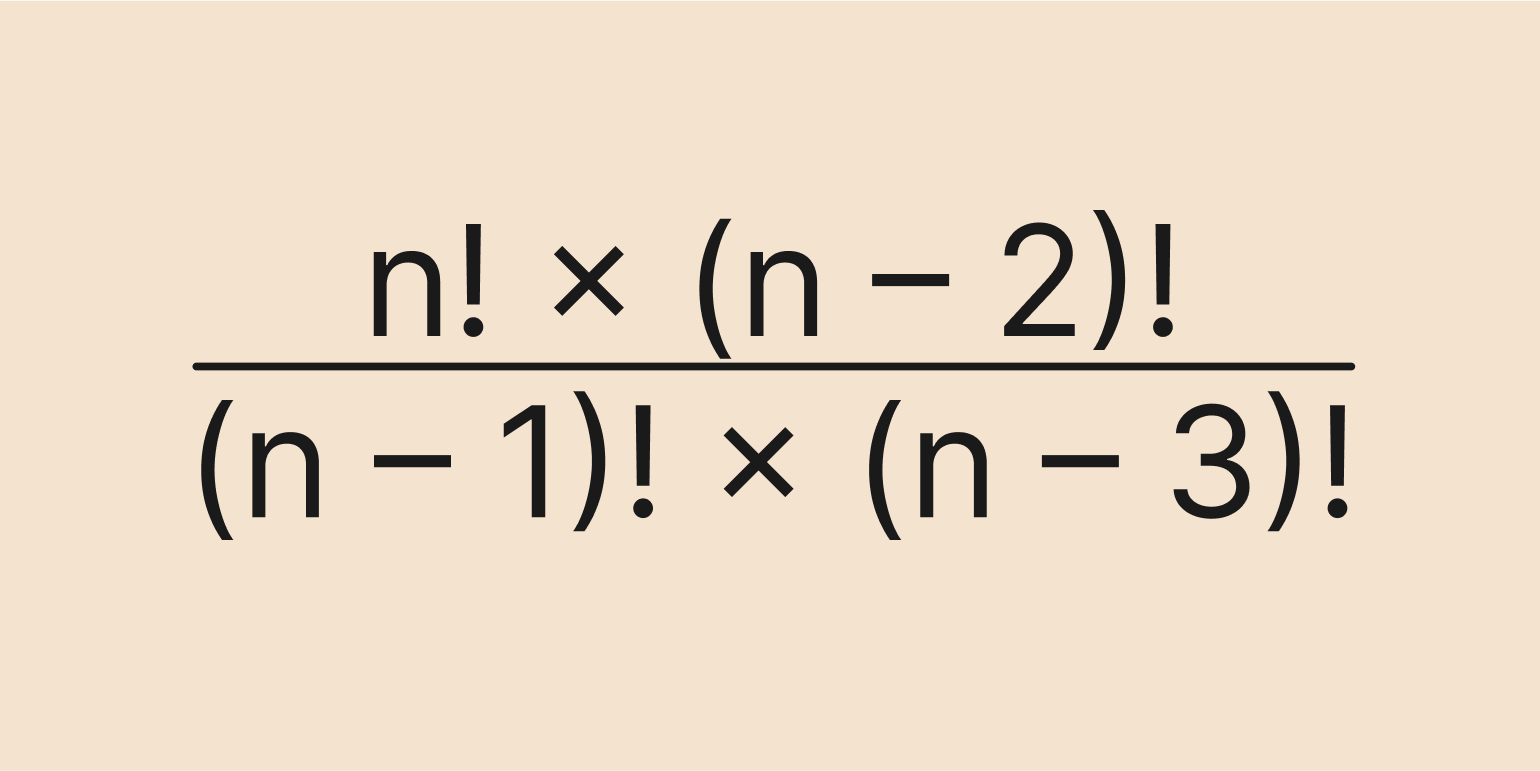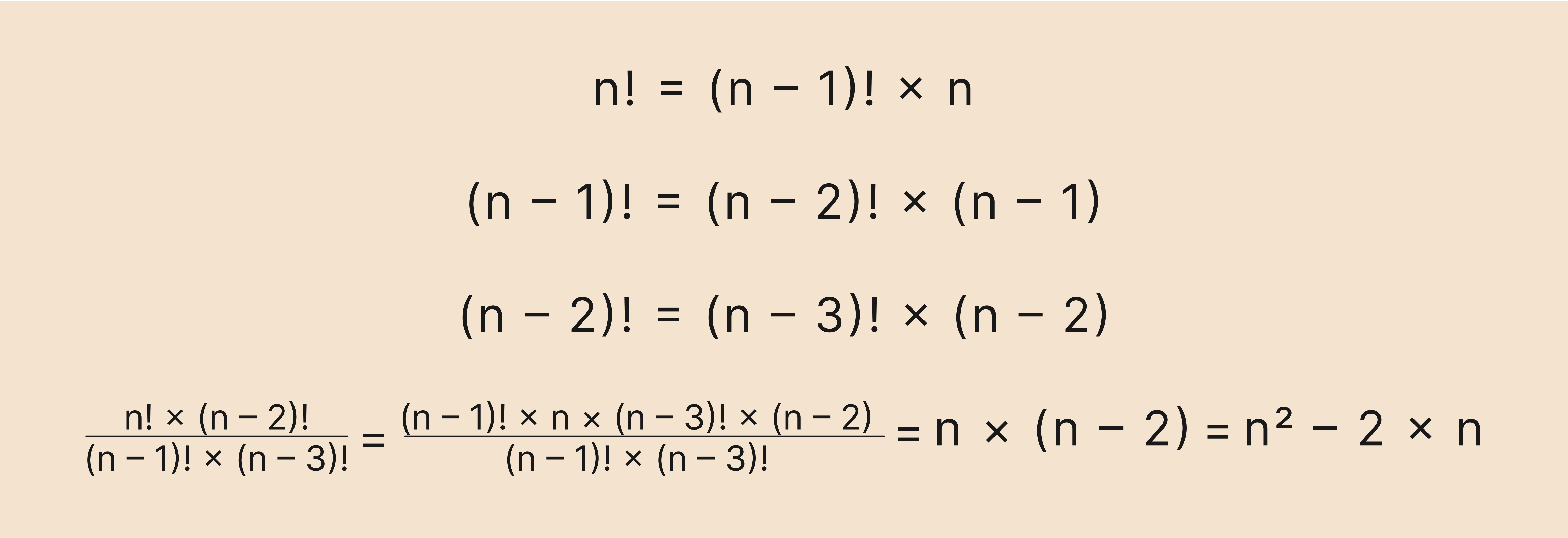Improve Article
Save Article
Like Article
Improve Article
Save Article
Like Article
Given a number n, count the total number of divisors of n!.
Examples:
Input : n = 4
Output: 8
Explanation:
4! is 24. Divisors of 24 are 1, 2, 3, 4, 6,
8, 12 and 24.Input : n = 5
Output : 16
Explanation:
5! is 120. Divisors of 120 are 1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 24 30, 40, 60 and 12
A Simple Solution is to first compute the factorial of the given number, then count the number of divisors of the factorial. This solution is not efficient and may cause overflow due to factorial computation.
A better solution is based on Legendre’s formula. Below are the step:
- Find all prime numbers less than or equal to n (input number). We can use Sieve Algorithm for this. Let n be 6. All prime numbers less than 6 are {2, 3, 5}.
- For each prime number, p find the largest power of it that divides n!. We use Legendre’s formula for this purpose.
The value of largest power that divides n! is ⌊n/p⌋ + ⌊n/(p2)⌋ + ⌊n/(p3)⌋ + ……
Let these values be exp1, exp2, exp3,… Using the above formula, we get the below values for n = 6.- The largest power of 2 that divides 6!, exp1 = 4.
- The largest power of 3 that divides 6!, exp2 = 2.
- The largest power of 5 that divides 6!, exp3 = 1.
- The result is (exp1 + 1) * (exp2 + 1) * (exp3 + 1) … for all prime numbers, For n = 6, the values exp1, exp2, and exp3 are 4 2 and 1 respectively (computed in above step 2). So our result is (4 + 1)*(2 + 1) * (1 + 1) = 30
Below is the implementation of the above idea.
C++
#include<bits/stdc++.h>
using namespace std;
typedef unsigned long long int ull;
vector<ull> allPrimes;
void sieve(int n)
{
vector<bool> prime(n+1, true);
for (int p=2; p*p<=n; p++)
{
if (prime[p] == true)
{
for (int i=p*2; i<=n; i += p)
prime[i] = false;
}
}
for (int p=2; p<=n; p++)
if (prime[p])
allPrimes.push_back(p);
}
ull factorialDivisors(ull n)
{
sieve(n);
ull result = 1;
for (int i=0; i < allPrimes.size(); i++)
{
ull p = allPrimes[i];
ull exp = 0;
while (p <= n)
{
exp = exp + (n/p);
p = p*allPrimes[i];
}
result = result*(exp+1);
}
return result;
}
int main()
{
cout << factorialDivisors(6);
return 0;
}
Java
import java.util.*;
class GFG
{
static Vector<Integer> allPrimes=new Vector<Integer>();
static void sieve(int n){
boolean []prime=new boolean[n+1];
for(int i=0;i<=n;i++)
prime[i]=true;
for (int p=2; p*p<=n; p++)
{
if (prime[p] == true)
{
for (int i=p*2; i<=n; i += p)
prime[i] = false;
}
}
for (int p=2; p<=n; p++)
if (prime[p])
allPrimes.add(p);
}
static long factorialDivisors(int n)
{
sieve(n);
long result = 1;
for (int i=0; i < allPrimes.size(); i++)
{
long p = allPrimes.get(i);
long exp = 0;
while (p <= n)
{
exp = exp + (n/p);
p = p*allPrimes.get(i);
}
result = result*(exp+1);
}
return result;
}
public static void main(String []args)
{
System.out.println(factorialDivisors(6));
}
}
Python3
allPrimes = [];
def sieve(n):
prime = [True] * (n + 1);
p = 2;
while(p * p <= n):
if (prime[p] == True):
i = p * 2;
while(i <= n):
prime[i] = False;
i += p;
p += 1;
for p in range(2, n + 1):
if (prime[p]):
allPrimes.append(p);
def factorialDivisors(n):
sieve(n);
result = 1;
for i in range(len(allPrimes)):
p = allPrimes[i];
exp = 0;
while (p <= n):
exp = exp + int(n / p);
p = p * allPrimes[i];
result = result * (exp + 1);
return result;
print(factorialDivisors(6));
C#
using System;
using System.Collections;
class GFG
{
static ArrayList allPrimes = new ArrayList();
static void sieve(int n)
{
bool[] prime = new bool[n+1];
for(int i = 0; i <= n; i++)
prime[i] = true;
for (int p = 2; p * p <= n; p++)
{
if (prime[p] == true)
{
for (int i = p*2; i <= n; i += p)
prime[i] = false;
}
}
for (int p = 2; p <= n; p++)
if (prime[p])
allPrimes.Add(p);
}
static int factorialDivisors(int n)
{
sieve(n);
int result = 1;
for (int i = 0; i < allPrimes.Count; i++)
{
int p = (int)allPrimes[i];
int exp = 0;
while (p <= n)
{
exp = exp + (n / p);
p = p * (int)allPrimes[i];
}
result = result * (exp + 1);
}
return result;
}
public static void Main()
{
Console.WriteLine(factorialDivisors(6));
}
}
PHP
<?php
$allPrimes = array();
function sieve($n)
{
global $allPrimes;
$prime = array_fill(0, $n + 1, true);
for ($p = 2; $p * $p <= $n; $p++)
{
if ($prime[$p] == true)
{
for ($i = $p * 2; $i <= $n; $i += $p)
$prime[$i] = false;
}
}
for ($p = 2; $p <= $n; $p++)
if ($prime[$p])
array_push($allPrimes, $p);
}
function factorialDivisors($n)
{
global $allPrimes;
sieve($n);
$result = 1;
for ($i = 0; $i < count($allPrimes); $i++)
{
$p = $allPrimes[$i];
$exp = 0;
while ($p <= $n)
{
$exp = $exp + (int)($n / $p);
$p = $p * $allPrimes[$i];
}
$result = $result * ($exp + 1);
}
return $result;
}
echo factorialDivisors(6);
?>
Javascript
<script>
let allPrimes = [];
function sieve(n)
{
let prime = new Array(n+1);
for(let i = 0; i <= n; i++)
prime[i] = true;
for (let p = 2; p * p <= n; p++)
{
if (prime[p] == true)
{
for (let i = p*2; i <= n; i += p)
prime[i] = false;
}
}
for (let p = 2; p <= n; p++)
if (prime[p])
allPrimes.push(p);
}
function factorialDivisors(n)
{
sieve(n);
let result = 1;
for (let i = 0; i < allPrimes.length; i++)
{
let p = allPrimes[i];
let exp = 0;
while (p <= n)
{
exp = exp + parseInt(n / p, 10);
p = p * allPrimes[i];
}
result = result * (exp + 1);
}
return result;
}
document.write(factorialDivisors(6));
</script>
Time Complexity: (O(n * log(logn))
Auxiliary Space: O(n)
This article is contributed by Shashank Mishra ( Gullu ). This article is reviewed by team GeeksforGeeks.
Please write comments if you find anything incorrect, or you want to share more information about the topic discussed above.
Last Updated :
13 Feb, 2023
Like Article
Save Article
Делители факториала
По заданному натуральному числу N необходимо вычислить количество натуральных чисел, которые являются делителями N! (факториала числа N).
Например, при N=4, N!=4⋅3⋅2⋅1=24. Это число имеет следующие делители: 1,2,3,4,6,8,12,24. Таким образом, искомое количество составляет 8.
Напишите программу, которая по натуральному N находит количество делителей его факториала.
Ввод 4
Вывод 8
n = int(input())
d=1
factorial = 1
while n > 1:
factorial *= n
n -= 1
numb = factorial
count_of_dividers = 2
for i in range(numb - 1, 1, -1):
if (numb % i == 0):
count_of_dividers += 1
print(count_of_dividers)
Программа выполняется долго…
#статьи
- 19 май 2023
-
0
Что такое факториал и как его вычислить
Статья, после которой вы начнёте щёлкать факториалы как орешки.
Иллюстрация: Катя Павловская для Skillbox Media
Любитель научной фантастики и технологического прогресса. Хорошо сочетает в себе заумного технаря и утончённого гуманитария. Пишет про IT и радуется этому.
Даже если вы уже давно окончили школу, факториалы всё равно могут доставить немало приятных флешбэков — например, если вы обучаетесь программированию и знакомитесь с задачками на рекурсию или комбинаторику. Поэтому мы решили максимально просто объяснить, что такое факториал, как его вычислять и зачем он вообще нужен.
Эта статья будет полезна как опытным программистам, которые хотят освежить знания, так и тем, кто ещё учится: школьникам, студентам и совсем зелёным джунам.
Содержание:
- Что такое факториал
- Для чего он нужен
- Основные свойства и формулы
- Шпаргалка: таблица факториалов
- Решаем задачи на факториалы
- Что запомнить
Факториал числа n — это произведение всех натуральных чисел от единицы до n. Обозначается факториал символом восклицательного знака: !.
Это определение из учебника, и оно пока звучит сложновато — неясно, зачем эти факториалы вообще нужны и как они могут пригодиться в науке и технике. Но об этом чуть позже — для начала давайте посмотрим на примеры факториалов:
Чтобы вычислить их, нам нужно перемножить все числа от единицы до числа, стоящего под знаком факториала — так гласит определение. Получаем выражения:
Ещё в математическом определении сказано, что факториал не может быть отрицательным или дробным — то есть вот такие факториалы вычислить нельзя:
Факториалы незаменимы там, где нужно быстро посчитать количество комбинаций и сочетаний разных предметов. В математике этому посвящён даже целый раздел — комбинаторика. Её методы используют много где: от лингвистики до криптографии и анализа ДНК. И во всех этих сферах факториал помогает упрощать сложные вычисления.
Разберём на примере, как это работает.
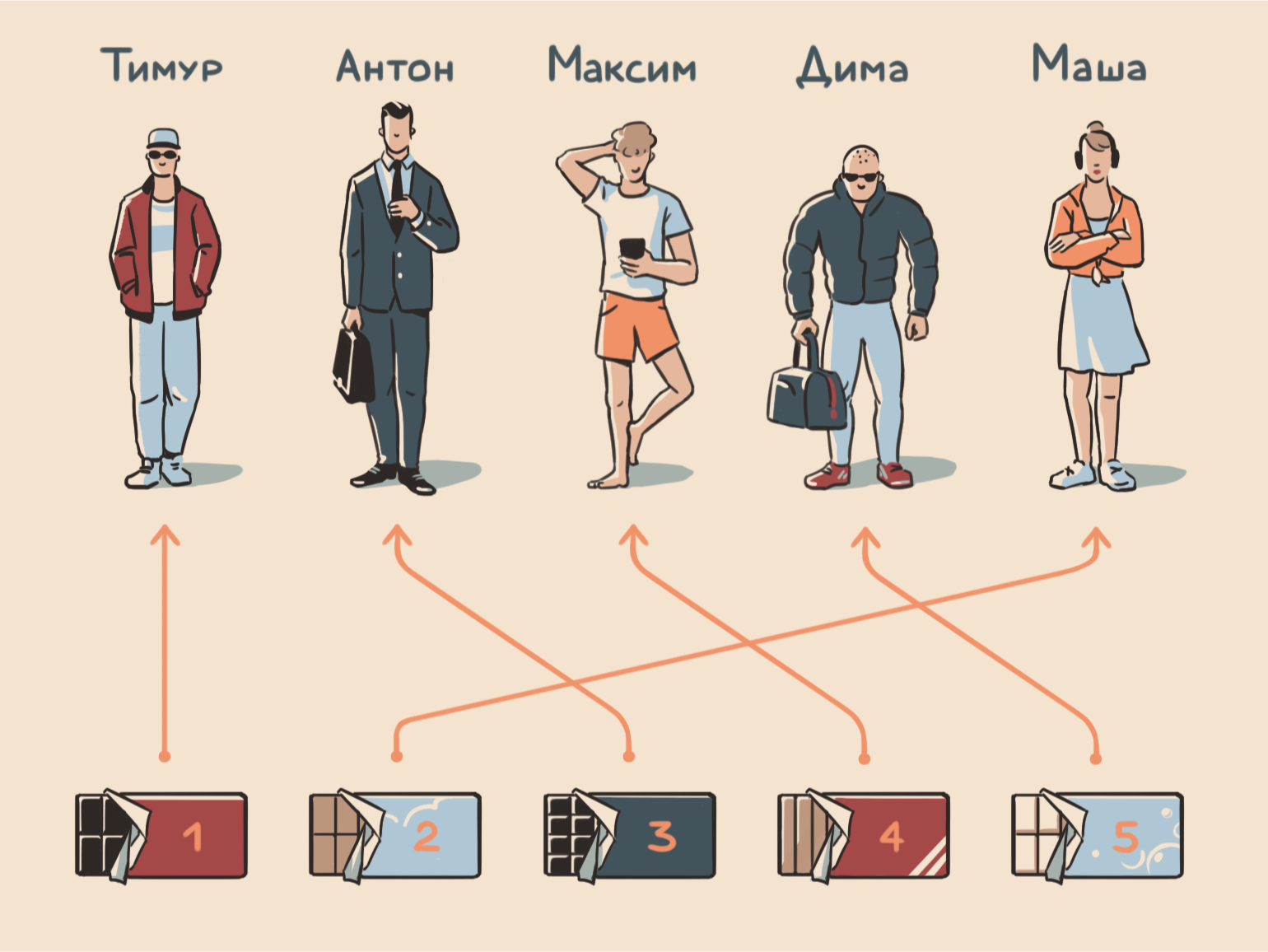
Допустим, у вас есть пять шоколадок и вы решили раздать их пяти друзьям — каждому по одной. Задача — выяснить, сколько существует способов раздать эти шоколадки. Начинаем размышлять:
- первую шоколадку можно отдать одному из пяти друзей;
- вторую — одному из четырёх друзей, потому что один уже получил свою шоколадку;
- третью — одному из трёх, потому что двое уже наслаждаются своими шоколадками;
- четвёртую — одному из двух;
- пятую — последнему другу.
Получается, что способов раздать первую шоколадку — 5, вторую — 4, третью — 3, четвёртую — 2, а пятую — всего 1. По правилам математики, чтобы выяснить общее количество всех вариантов, нужно перемножить их между собой. Ну а кто мы такие, чтобы с этими правилами спорить?
Смотрим на выражение выше и понимаем: ведь оно идеально вписывается в определение факториала — произведение натуральных чисел от одного до n (в нашем случае n равно 5). Следовательно, это выражение можно коротко и изящно записать в виде факториала:
Выходит, что всего способов раздать пять шоколадок пяти друзьям существует 120. Вот как может выглядеть один из них:
Конечно, в жизни вам вряд ли придётся считать количество способов раздать друзьям шоколадки. Но, например, в статистике, теории вероятностей, матанализе и программировании факториалы используют сплошь и рядом. Так что, если видите себя в будущем на матмехе или, на худой конец, в IT, то лучше познакомиться с ними хотя бы бегло.
Так как факториалы используются в разных областях математики, свойств у них довольно много — каждая область привносит какие-то свои методы вычислений. Одно из свойств вы уже знаете: факториал — это всегда целое положительное число. Вот ещё несколько, которые стоит запомнить:
- Факториал нуля равен единице — 0! = 1.
- Факториал единицы тоже равен единице: 1! = 1.
- Рекурсия: n! = (n – 1)! × n. Это основное свойство факториалов, о нём мы чуть подробнее поговорим дальше.
Мы видим, что каждое свойство описывается какой-то формулой — и некоторые из этих формул могут быть весьма полезны. Они позволяют нам находить факториалы проще и быстрее, чем простым перемножением натуральных чисел. Разберём эти формулы тоже.
Чтобы вычислить факториал, не используя так много операций умножения, придумали формулу Стирлинга. Вот как она выглядит:
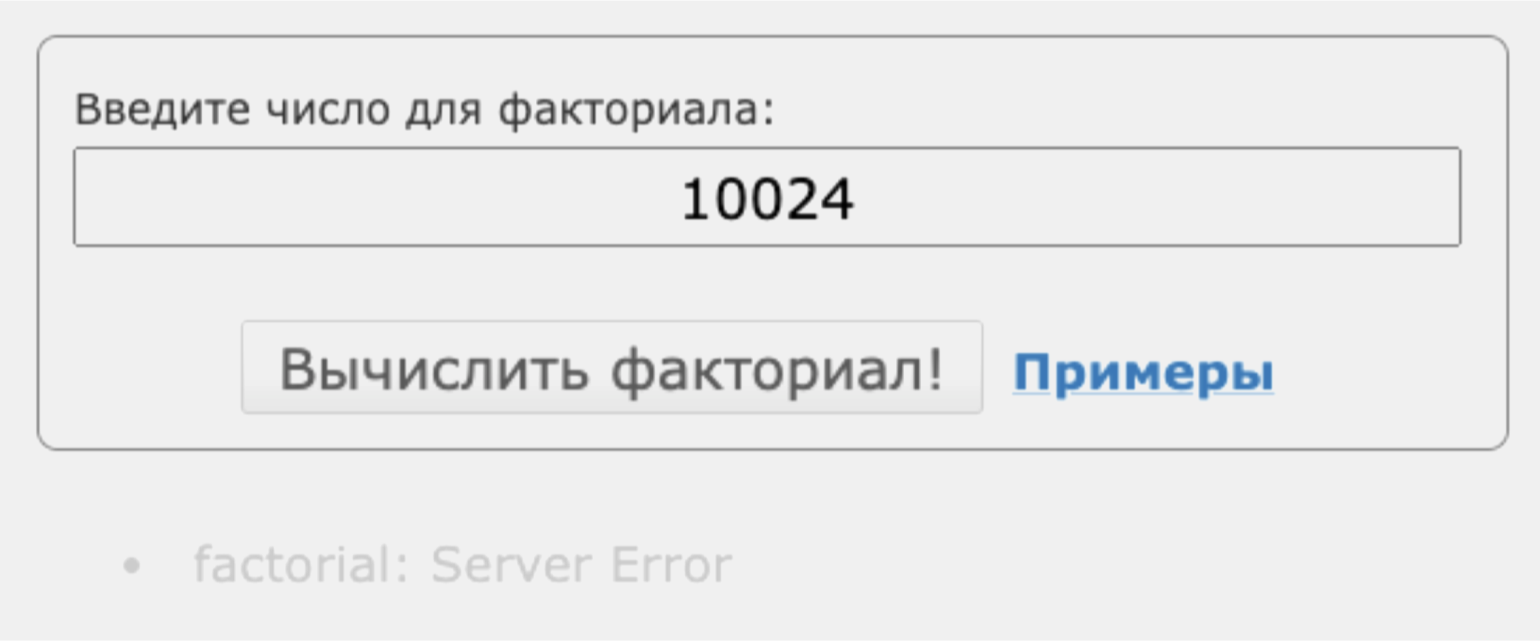
Выглядит страшно, но на самом деле она очень полезная. Её используют, когда хотят приблизительно узнать факториал большого числа. Обычным способом это будет сделать сложно даже мощному компьютеру — например, попробуйте посчитать в онлайн-калькуляторе факториал числа 10 024 (спойлер: это может занять несколько часов и даже дней).
Скришнот: «Контрольная работа РУ — калькуляторы онлайн» / Skillbox Media
Давайте попробуем вычислить факториал числа 6 по этой формуле:
Число e примерно равно 2,71, а π — 3,14. Подставляем их в выражение и получаем ответ:
Получили приближённое значение настоящего факториала, который равен 720. Но можно сделать ответ и более точным. Для этого нужно добавить больше знаков после запятой всем переменным — например, если взять 20 знаков, то ответ будет таким:
Это уже больше похоже на правду. Хотя погрешность всё равно есть.
Рекуррентная формула позволяет вычислить факториал числа n, основываясь на факториале предыдущего числа — (n – 1). Выглядит она так:
В целом рекуррентная формула не приносит нам большой пользы, так как всё равно приходится вычислять факториал предыдущего числа. Если он равен какому-то большому числу (например, 100), то использование формулы теряет смысл — слишком уж много вычислений это потребует.
Рекуррентная формула основана на главном свойстве факториалов — рекурсии: n! = (n – 1)! × n. Это свойство особенно полезно при решении задач по комбинаторике: так мы можем быстро сокращать факториалы и упрощать выражения.
Однако рекуррентная формула хорошо подходит для алгоритмов — в частности, для программирования. Мы можем задать начальное значение: например, что 0! = 1 или 1! = 1, а затем считать следующие факториалы по формуле:
Получим алгоритм для вычисления факториалов. Не очень эффективный, но простой.
Давайте вычислим по этой формуле факториал числа 4. Сначала распишем рекуррентную формулу до базового значения — факториала числа 1:
Можно записать это и в сокращённом виде:
Теперь последовательно подставляем значение факториала, которое мы уже знаем, и вычисляем результат:
Получили ответ — 24. Ничего сложного, просто перемножаем числа.
Кстати, всю эту формулу можно обернуть в реально работающую функцию на языке Python:
def factorial(n): # Определяем функцию if n == 0 or n == 1: # Базовый случай return 1 else: # Рекуррентный случай return factorial(n-1) * n # Вызываем эту же функцию, но с меньшим аргументом print(factorial(4)) # Печатаем факториал 4 # Вывод: # 24
Можете попробовать запустить её в онлайн-интерпретаторе и посмотреть, как работает. Тут есть один нюанс: Python не даст вам посчитать факториал числа больше 998, так как у него есть ограничение на количество вызовов функции — в программировании это называется глубиной рекурсии.
Чтобы быстро находить, чему равен факториал, можно запомнить или сохранить в заметки вот такую табличку. Она рассчитана всего на 12 чисел, но для большинства учебных задач этого хватит.
| 1! | 1 |
| 2! | 2 |
| 3! | 6 |
| 4! | 24 |
| 5! | 120 |
| 6! | 720 |
| 7! | 5040 |
| 8! | 40 320 |
| 9! | 362 880 |
| 10! | 3 628 800 |
| 11! | 39 916 800 |
| 12! | 479 001 600 |
С теорией вроде разобрались — теперь попробуем решить несколько задач с факториалами, чтобы закрепить знания на практике.
Задача: перемножить два факториала.
Решение:
Сперва нужно вычислить значения факториалов, а затем перемножить полученные значения:
Обратите внимание: во второй строке мы применили рекуррентную формулу, чтобы быстрее вычислить факториал числа 7.
Задача: вычесть из одного факториала другой.
Решение:
Используем тот же подход, что и в предыдущей задаче: сначала вычисляем факториалы, а затем получаем ответ на всё выражение.
Вроде бы ничего сложного, главное — не запутаться в умножении.
Задача: умножить один факториал на другой:
Решение:
Вычисляем факториалы, потом перемножаем их значения:
Во второй строке мы воспользовались таблицей выше и быстро нашли значение факториала от числа 8.
Задача: сократить дробь и вычислить её значение.
Решение:
Здесь мы воспользуемся рекуррентной формулой для вычисления факториала и разложим верхний факториал на множители:
В первой строке мы применили рекуррентную формулу два раза, а во второй — просто сократили одинаковые факториалы в числителе и в знаменателе.
Задача: сократить дробь.
Решение:
Хотя здесь нет конкретных чисел, но принцип решения остаётся таким же: используем рекуррентную формулу и сокращаем одинаковые значения в числителе и знаменателе.
Главное — не запутаться и правильно применить рекуррентную формулу.
- Факториал — это произведение всех натуральных чисел от 1 до данного числа. Например, факториал числа 5 будет равен 1 × 2 × 3 × 4 × 5 = 120.
- Его используют во многих областях науки — например, комбинаторике, теории вероятностей и математическом анализе.
- Помимо стандартной формулы для вычисления факториала можно использовать формулы Стирлинга и рекуррентную формулу.
- Формула Стирлинга нужна для того, чтобы посчитать факториал без большого числа операций умножения.
- Рекуррентная формула позволяет вычислить факториал на основе предыдущего факториала.

Научитесь: Профессия Data Scientist
Узнать больше
Вот проблема, которую я недавно пытался решить: дано целое число n, каковы все его делители?
Делитель, также известный как фактор или множитель, — это такое целое число m, на которое n делится без остатка. Например, делителями числа 12 являются 1, 2, 3, 4, 6 и 12.
В итоге я написал кое-что с помощью itertools, и в моем коде используется несколько интересных моментов из теории чисел. Я не знаю, буду ли я возвращаться к нему снова, но я надумал написать эту статью, потому что мои попытки решить озвученный выше вопрос перетекли в довольно забавное упражнение.
Простейший подход
Если мы хотим найти все числа, которые делят n без остатка, мы можем просто перебрать числа от 1 до n:
def get_all_divisors_brute(n):
for i in range(1, int(n / 2) + 1):
if n % i == 0:
yield i
yield n
На деле нам нужно дойти только до n/2, потому что все, что больше этого значения, гарантировано не может быть делителем n — если вы разделите n на что-то большее, чем n/2, результат не будет целым числом.
Этот код очень прост, и для малых значений n он работает достаточно хорошо, но он довольно неэффективен и медлителен в других случаях. По мере увеличения n время выполнения линейно увеличивается. Можем ли мы сделать лучше?
Факторизация
В моем проекте я работал в основном с факториалами. Факториал числа n, обозначаемый n! — это произведение всех целых чисел от 1 до n включительно. Например:
8! = 8 × 7 × 6 × 5 × 4 × 3 × 2 × 1
Поскольку факториалы состоят преимущественно из небольших множителей, я решил попробовать получить список делителей, определив сначала наименьшие из них. В частности, я искал простые множители, то есть те, которые также являются простыми числами. (Простое число — это число, единственными делителями которого являются оно само и 1. Например, 2, 3 и 5 являются простыми, а 4 и 6 — нет).
Вот функция, которая находит простые делители числа n:
def get_prime_divisors(n):
i = 2
while i * i <= n:
if n % i == 0:
n /= i
yield i
else:
i += 1
if n > 1:
yield n
Это похоже на предыдущую функцию, использующую перебор делителей: мы продолжаем пробовать множители, и если находим подходящий, то делим на него. В противном случае мы проверяем следующее число. Это довольно стандартный подход к поиску простых множителей.
Теперь мы можем использовать этот метод для получения факторизации числа, то есть для его записи в виде произведения простых чисел. Например, факторизация числа 8! выглядит следующим образом:
8! = 2^7 × 3^2 × 5 × 7
Вычисление такой факторизации относительно эффективно, особенно для факториалов, так как, поскольку все простые множители очень малы, вам не нужно делать много делений.
В теории чисел есть утверждение, называемое основной теоремой арифметики, которое гласит, что простые факторизации (разложения) уникальны: для любого числа n существует только один способ представить его в виде произведения простых множителей. (Я не буду приводить здесь доказательство, но вы можете найти его в Википедии).
Это дает нам способ находить делители путем перебора всех комбинаций простых множителей. Простые множители любого m делителя числа n должны входить в подмножество простых множителей n, иначе m не делило бы число n.
Переход от факторизации к делителям
Для начала разложим исходное число на простые множители с указанием «кратности», то есть мы должны получить список всех множителей и количество раз, которое каждый из них встречается в факторизации:
import collections
def get_all_divisors(n):
primes = get_prime_divisors(n)
primes_counted = collections.Counter(primes)
...
Затем, давайте продолжим и возведем каждое простое число во все степени, которые могут появиться в возможном делителе n.
def get_all_divisors(n):
...
divisors_exponentiated = [
[div ** i for i in range(count + 1)]
for div, count in primes_counted.items()
]
Например, для 8! представленный код выдаст нам следующее:
[
[1, 2, 4, 8, 16, 32, 64, 128], // 2^0, 2^1, ..., 2^7
[1, 3, 9], // 3^0, 3^1, 3^2
[1, 5],
[1, 7],
]
Затем, чтобы получить делители, мы можем использовать довольно удобную функцию itertools.product, которая принимает на вход итерабельные объекты и возвращает все возможные упорядоченные комбинации их элементов. В нашем случае она выбирает по одному числу из каждого списка с возведениями в степень, а затем, перемножая их вместе, мы получаем очередной делитель n.
import itertools
def calc_product(iterable):
acc = 1
for i in iterable:
acc *= i
return acc
def get_all_divisors(n):
...
for prime_exp_combination in itertools.product(*divisors_exponentiated):
yield calc_product(prime_exp_combination)
Таким образом, мы находим все делители n (хотя, в отличие от предыдущих функций, они не отсортированы).
Собираем все вместе
Сложив все это, мы получим следующую функцию для вычисления делителей n:
import collections
import itertools
def get_prime_divisors(n):
i = 2
while i * i <= n:
if n % i == 0:
n /= i
yield i
else:
i += 1
if n > 1:
yield n
def calc_product(iterable):
acc = 1
for i in iterable:
acc *= i
return acc
def get_all_divisors(n):
primes = get_prime_divisors(n)
primes_counted = collections.Counter(primes)
divisors_exponentiated = [
[div ** i for i in range(count + 1)]
for div, count in primes_counted.items()
]
for prime_exp_combination in itertools.product(*divisors_exponentiated):
yield calc_product(prime_exp_combination)
print(list(get_all_divisors(40320))) # 8!
Такая реализация очень эффективна, особенно когда у вас много маленьких простых множителей, как в случае с факториалами, с которыми я работал. Я не знаю, насколько хорошо она покажет себя в общем случае, и, если вы занимаетесь серьезными научными вычислениями, я уверен, что вы легко найдете уже реализованные и оптимизированные алгоритмы для такого рода вещей.
Загрузить PDF
Загрузить PDF
Число называется делителем (или множителем) другого числа в том случае, если при делении на него получается целый результат без остатка.[1]
Для малого числа (например, 6) определить количество делителей довольно легко: достаточно выписать все возможные произведения двух целых чисел, которые дают заданное число. При работе с большими числами определить количество делителей становится сложнее. Тем не менее, если вы разложите целое число на простые множители, то легко сможете определить число делителей с помощью простой формулы.
-
1
Запишите заданное целое число вверху страницы. Вам понадобится достаточно места для того, чтобы расположить ниже числа дерево множителей. Для разложения числа на простые множители можно использовать и другие методы, которые вы найдете в статье Как разложить число на множители.
- Например, если вы хотите узнать, сколько делителей, или множителей имеет число 24, запишите
вверху страницы.
- Например, если вы хотите узнать, сколько делителей, или множителей имеет число 24, запишите
-
2
Найдите два числа (помимо 1), при перемножении которых получается заданное число. Таким образом вы найдете два делителя, или множителя данного числа. Проведите от данного числа две ветки вниз и запишите на их концах полученные множители.
-
3
Поищите простые множители. Простым множителем называется такое число, которое делится без остатка лишь на само себя и на 1.[2]
Например, число 7 является простым множителем, так как оно делится без остатка лишь на 1 и 7. Для удобства обводите найденные простые множители кружком.- Например, 2 является простым числом, поэтому обведите
кружком.
- Например, 2 является простым числом, поэтому обведите
-
4
Продолжайте раскладывать составные (не простые) числа на множители. Проводите следующие ветки от составных чисел до тех пор, пока все множители не станут простыми. Не забывайте обводить простые числа кружками.
-
5
Представьте каждый простой множитель в степенной форме. Для этого подсчитайте, сколько раз встречается каждый простой множитель в нарисованном дереве множителей. Это число и будет степенью, в которую необходимо возвести данный простой множитель.[3]
-
6
Запишите разложение числа на простые множители. Первоначально заданное число равно произведению простых множителей в соответствующих степенях.
- В нашем примере
.
Реклама
- В нашем примере
-
1
-
2
Подставьте в формулу величины степеней. Будьте внимательны и используйте степени при простых множителях, а не сами множители.
-
3
Сложите величины в скобках. Просто прибавьте 1 к каждой степени.
-
4
Перемножьте полученные величины. В результате вы определите количество делителей, или множителей данного числа
.
Реклама
Советы
- Если число представляет собой квадрат целого числа (например, 36 является квадратом числа 6), то оно имеет нечетное количество делителей. Если же число не является квадратом другого целого числа, количество его делителей четно.
Реклама
Похожие статьи
Об этой статье
Эту страницу просматривали 121 121 раз.