I am given a string and i need to find all possible letter combinations of this string. What is the best way I can achieve this?
example:
abc
result:
abc
acb
bca
bac
cab
cba
i have nothing so far. i am not asking for code. i am just asking for the best way to do it? an algorithm? a pseudocode? maybe a discussion?
K Mehta
10.3k4 gold badges45 silver badges76 bronze badges
asked Jul 29, 2011 at 15:50
2
Do you want combinations or permutations? For example, if your string is «abbc» do you want to see «bbac» once or twice?
If you actually want permutations you can use std::next_permutation and it’ll take care of all the work for you.
answered Jul 29, 2011 at 15:53
Mark BMark B
94.8k10 gold badges109 silver badges186 bronze badges
2
If you want the combinations (order independant) You can use a combination finding algorithm such as that found either here or here. Alternatively, you can use this (a java implementation of a combination generator, with an example demonstrating what you want.
Alternatively, if you want what you have listed in your post (the permutations), then you can (for C++) use std::next_permutation found in <algorithm.h>. You can find more information on std::next_permutation here.
Hope this helps. 
answered Jul 29, 2011 at 15:55
Thomas RussellThomas Russell
5,8204 gold badges31 silver badges68 bronze badges
In C++, std::next_permutation:
std::string s = "abc";
do
{
std::cout << s << std::endl;
} while (std::next_permutation(s.begin(), s.end()));
answered Jul 29, 2011 at 15:54
Peter AlexanderPeter Alexander
53.1k13 gold badges119 silver badges168 bronze badges
Copied from an old Wikipedia article;
For every number k, with 0 ≤ k < n!, the following algorithm generates a unique permutation on sequence s.
function permutation(k, s) {
for j = 2 to length(s) {
swap s[(k mod j) + 1] with s[j]; // note that our array is indexed starting at 1
k := k / j; // integer division cuts off the remainder
}
return s;
}
answered Jul 29, 2011 at 16:00
QwerkyQwerky
18.1k6 gold badges44 silver badges80 bronze badges
Статьи / Python
Встроенный модуль itertools в Python — простой инструментарий, позволяющий генерировать полный список возможных комбинаций из заданного набора символов. Как с этим работать и справляться — далее в статье.
Что ж, в преддверии Нового года KOTOFF.net вновь расправляет крылья.
И сразу к делу. Рассмотрим всего 3 функции и их различия.
1. Нахождение всевозможных комбинаций из набора символов
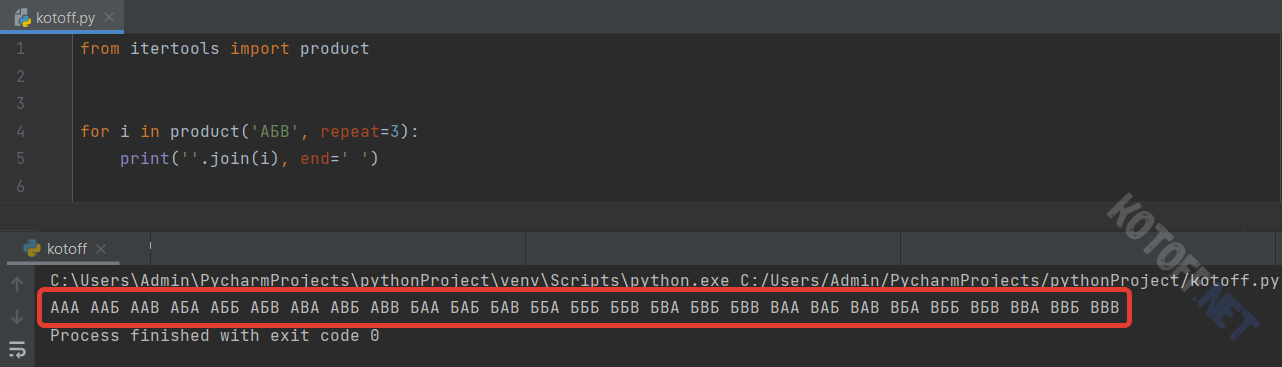
Допустим, у нас есть некий алфавит из трёх букв (А, Б, В), и из него необходимо составить максимальное количество трёхзначных слов (комбинаций). Причём в данном случае буквы могут повторяться. Алфавит короткий, однако у нас получится составить целых 27 слов. На каждую позицию приходится по 3 варианта букв, соответственно, общее количество комбинаций можно посчитать так: nk (n — количество доступных символов в степени k — длина конечной комбинации). Для нашего случая: 33 = 27
Теперь импортирую itertools и сгенерирую всё то, что выше считали руками, но теперь уже с помощью функции product():
from itertools import product
for i in product('АБВ', repeat=3):
print(''.join(i), end=' ')Функция принимает два параметра (набор символов и длина конечного объекта). С помощью join() получили строковое представление полученной комбинации.
Можно добавить в цикл некий фильтр (условие). Например, сделаю так, чтобы комбинируемые слова начинались только с «X» и заканчивались на «YZY»:
Попробуем сгенерировать всевозможные автомобильные номера для одного региона. Способ, конечно, не особо рациональный, но для примера сгодится:
from itertools import product
import re
chars = '0123456789АВЕКМНОРСТУХ'
reg = '[АВЕКМНОРСТУХ]{1}d{3}[АВЕКМНОРСТУХ]{2}'
for i in product(chars, repeat=6):
if re.fullmatch(reg, ''.join(i)):
print(''.join(i))Кстати, если добавить в цикл счётчик, то в итоге получим цифру 1.728.000 (12*10*10*10*12*12). Именно столько номеров формата x000xx можно наклепать для одного региона 
2. Перестановка символов в наборе
В отличие от предыдущего примера, теперь мы не можем использовать по несколько раз один и тот же символ. Можем только переставлять их местами. Принцип подсчёта количества комбинаций остаётся тот же: необходимо перемножить количество вариантов символов на каждую позицию слова между собой. Но поскольку по мере составления слова на каждую последующую позицию символов будет оставаться всё меньше и меньше, то и формула также меняется на: n! / (n-k)! (n — количество доступных символов, k — длина слова). Если n = k, то можно использовать упрощённую формулу: n! (факториал числа n).
В питоне для таких целей используется функция permutations(). Принимает тоже два параметра: набор символов и длину генерируемой комбинации:
from itertools import permutations
for i in permutations('АБВ'):
print(''.join(i))Из трёх букв будет сгенерировано 6 различных слов с неповторяющимися символами (1! = 1 * 2 * 3 = 6)
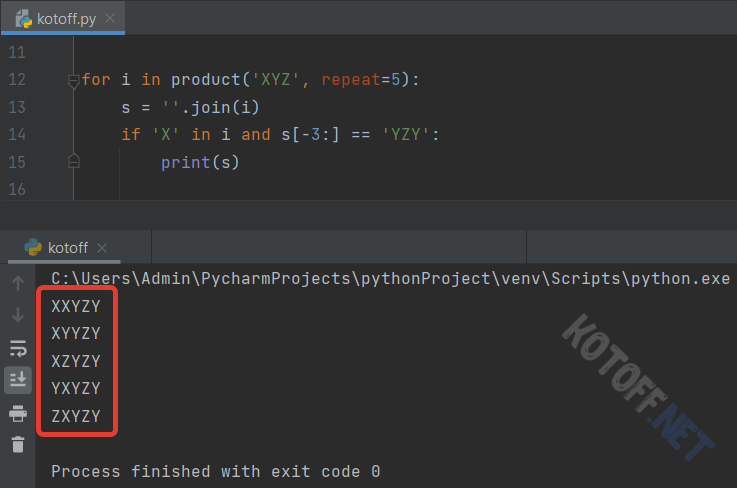
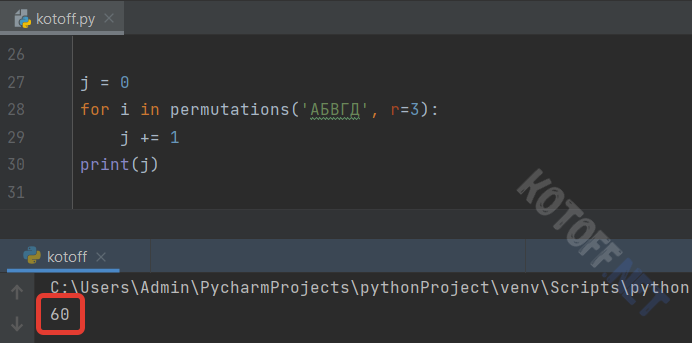
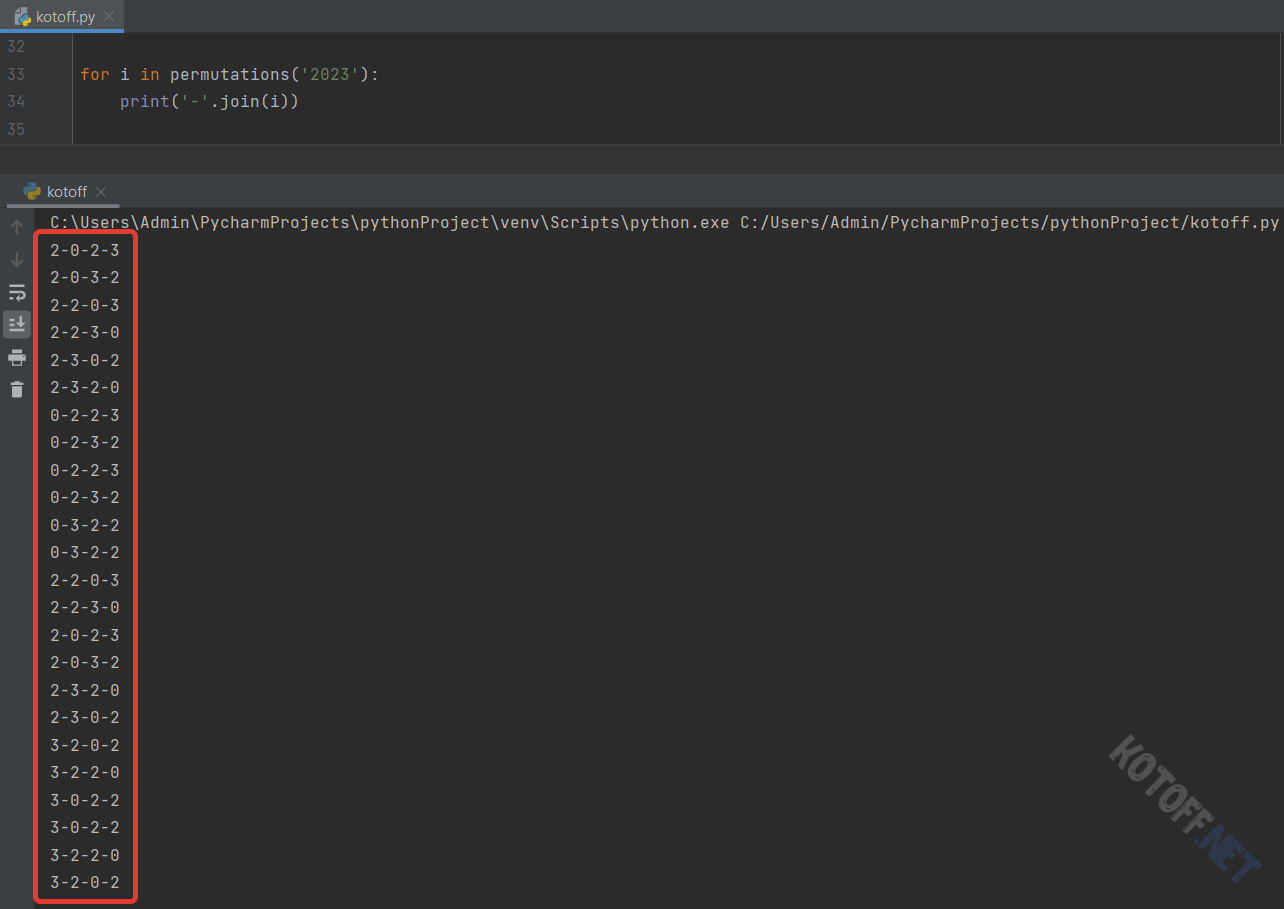
Попробуем составить трёхзначные слова в 5-символьном алфавите (5! / (5-3)! = 120 / 2 = 60):
Кстати, если в заданном «алфавите» есть повторяющиеся символы, то они будут повторяться и в комбинациях:
3. Сочетания без повторений
А если нужно составить не комбинации, а отдельные неповторяющиеся сочетания? Например, есть 6 человек. Вопрос: какими способами их можно разбить по парам? Опять же, пользуемся формулой: n! / (n-k)! / k! (n — количество доступных объектов/символов, k — количество сочетаний). Соответственно, существует 6! / (6-2)! / 2! = 720 / 24 / 2 = 15 вариантов разбиения этих 6 персон по парам.
Теперь реализуем эту задачу на питоне с помощью функции combinations(). Принимает она два параметра — список и кол-во сочетаний:
from itertools import combinations
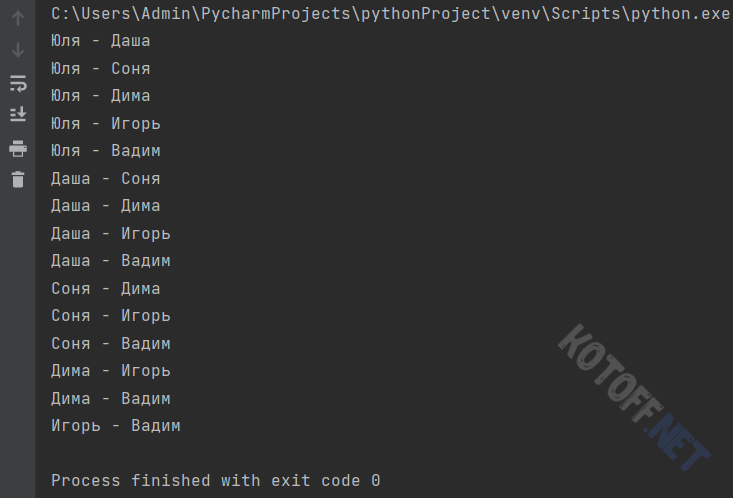
for i in combinations(['Юля', 'Даша', 'Соня', 'Дима', 'Игорь', 'Вадим'], 2):
print(' - '.join(i))Результат работы программы будет таков:
На этом, пожалуй, на сегодня всё. С наступающим! 
Если я правильно понял, вам нужны размещения без повторений. Их можно сгенерировать, например, так:
static void Main(string[] args)
{
var chars = new HashSet<char>(new [] { 'a', 'b', 'c', 'd' });
foreach (var s in GetAllPermutations(chars, 3)) // 3 -- длина
Console.WriteLine(s);
}
static IEnumerable<string> GetAllPermutations(HashSet<char> chars, int n)
{
if (n == 0)
yield return "";
foreach (var c in chars.ToList())
{
chars.Remove(c);
foreach (var s in AddAllFrom(chars, n - 1))
yield return c + s;
chars.Add(c);
}
}
Результат:
abc
abd
acd
acb
adb
adc
bcd
bca
bda
bdc
bac
bad
cda
cdb
cab
cad
cbd
cba
dab
dac
dbc
dba
dca
dcb
Поскольку функция GetAllPermutations возвращает ленивый энумератор, вы можете получить только часть результатов, применив LINQ-операторы наподобие .Take(10). Но моя функция не является чистой: во время энумерации изменяется состояние множества chars. (Этот же эффект не даст обходить одну и ту же последовательность дважды одновременно.) Для того, чтобы сделать функцию чистой, необходимо инкапсулировать изменяемые данные. Получается следующее:
static void Main(string[] args)
{
var chars = new[] { 'a', 'b', 'c', 'd' };
var seq = GetAllPermutations(chars, 3).Take(10);
foreach (var s in seq) // 3 -- длина
Console.WriteLine(s);
}
static IEnumerable<string> GetAllPermutations(IEnumerable<char> chars, int n)
{
HashSet<char> curr = new HashSet<char>(chars);
foreach (var s in GetAllPermutationsRec(n))
yield return s;
}
static IEnumerable<string> GetAllPermutationsRec(int n, HashSet<char> curr) // not pure!
{
if (n == 0)
yield return "";
foreach (var c in curr.ToList())
{
curr.Remove(c);
foreach (var s in GetAllPermutationsRec(n - 1))
yield return c + s;
curr.Add(c);
}
}
|
magnum1992 44 / 44 / 19 Регистрация: 22.05.2011 Сообщений: 156 Записей в блоге: 5 |
||||
|
1 |
||||
Как найти все возможные комбинации букв в слове?27.01.2014, 19:02. Показов 11026. Ответов 9 Метки нет (Все метки)
Допустим есть слово ПОРТ. Нужно получить все возможные комбинации букв из этого слова 3-х и 4-х значные. Т.е. получится 4!*3!*2! 3-х значных наборов и столько же 4-х значных. Так вот в чем вопрос есть ли алгоритм который и составляет эти самые комбинации?
Но знаю что это совсем никудышный вариант. Особенно смущает наличие тут рандома.
0 |
|
290 / 289 / 108 Регистрация: 04.09.2010 Сообщений: 638 |
|
|
27.01.2014, 20:10 |
2 |
|
0 |
|
44 / 44 / 19 Регистрация: 22.05.2011 Сообщений: 156 Записей в блоге: 5 |
|
|
28.01.2014, 09:24 [ТС] |
3 |
|
Алгоритм Нарайаны я думаю в моей задаче не подходит так как он ищет перестановки только в конкретном слове, а у меня например должно быть так:
0 |
|
16 / 16 / 5 Регистрация: 18.05.2012 Сообщений: 39 |
|
|
28.01.2014, 12:29 |
4 |
|
Тебе нужно допилить этот алгоритм. Алгоритм должен получать все возможные наборы из 4 и 3 букв. Наборы букв не дублируются.
0 |
|
44 / 44 / 19 Регистрация: 22.05.2011 Сообщений: 156 Записей в блоге: 5 |
|
|
28.01.2014, 13:50 [ТС] |
5 |
|
Тебе нужно допилить этот алгоритм. Скорее нужно не допилить алгоритм, а написать другой который будет искать эти самые наборы.
0 |
|
kesean 290 / 289 / 108 Регистрация: 04.09.2010 Сообщений: 638 |
||||
|
28.01.2014, 15:09 |
6 |
|||
|
Решение
Скорее нужно не допилить алгоритм, а написать другой Скорее нужно не изобретать велосипед, а использовать то, что нам деды завещали
0 |
|
44 / 44 / 19 Регистрация: 22.05.2011 Сообщений: 156 Записей в блоге: 5 |
|
|
28.01.2014, 16:30 [ТС] |
7 |
|
kesean, Не могли бы вы пояснить код?
0 |
|
kesean 290 / 289 / 108 Регистрация: 04.09.2010 Сообщений: 638 |
||||
|
28.01.2014, 16:59 |
8 |
|||
1 |
|
44 / 44 / 19 Регистрация: 22.05.2011 Сообщений: 156 Записей в блоге: 5 |
|
|
29.01.2014, 16:07 [ТС] |
9 |
|
Все модернизировал большое спасибо.
0 |
|
0 / 0 / 0 Регистрация: 14.02.2016 Сообщений: 3 |
|
|
10.03.2019, 21:20 |
10 |
|
У меня 16 букв (KLMNOPQRSTUVWXYZ). Сколько комбинацией можно по 32.
0 |
Доброго времени суток, читатель, хочу представить вам алгоритм перебора любой последовательности, для начала поставим задачу.
Задача: перебрать все возможные сочетания букв латинского алфавита, длинной от 1 до 3 символов
Решение:
На первый взгляд самым простым выходом было бы сделать рекурсивный вызов, в данном частном случае когда идет речь о строках не более 3 символов, такое решение будет самое быстрое в реализации, примеров с рекурсией я приводить не стану, но варианты с рекурсией не всегда подходят в меру своего ресурсопотребления.
Самым простым вариантом без рекурсии, если задача очень проста и не требует универсальности решения, являются вложенные циклы. Этот вариант прост в реализации, когда речь идет о переборе, например строк длиной не более 2-3 символов, 3 вложенных цикла портят читаемость кода, а если нам нужно не 3 а 30 символов, 30 вложений %)
И, наконец, мы дошли до начинки, как можно перебрать все варианты сочетания всех букв, расширим задачу до всех букв с учетом регистра и все цифры (a-zA-Z0-9).
«Все гениальное — просто», среди читателей этой статьи найдется не мало людей, которым будет достаточно назвать один термин, который лег в основу реализации данного алгоритма, но есть и такие, которым нужно все разжевать, поэтому я приведу код, который это делает на языке программирования PHP, а термин этот «Системы счисления»
«Системы счисления» — почти идеально подходят для перебора таких последовательностей, за исключением того, что система счисления воспринимается как число, в результате этого выпадают значения с первым нулевым элементом, т.е если рассматривать десятичную систему счисления, то после 99 идет 100 101 101…, а в строковом представлении после 99 должно идти 000 001 002. Ну и, наконец, сам алгоритм:
// Формируем рабочую систему (a-zA-Z0-9)
$work = array(0,1,2,3,4,5,6,7,8,9);
// буквы нижнего регистра
for($i = 97; $i <= 122; $i++){
$work[] = chr($i);
}
// буквы верхнего регистра
for($i = 65; $i <= 90; $i++){
$work[] = chr($i);
}
// проверим, что получилось, если нужно
//print_r($work);
// Теперь можно приступать к решению нашего примера
// перебор будет в одном цикле, без рекурсии, и перебирать мы будем не буквы, а цифры
// параметры перебора
$min_length = 1;
$max_length = 3; // поставим 3, чтобы хватило памяти для массива $result
// определяем порядковый номер минимального значения длинной строки $min_length
$min = str_to_dec(str_repeat($work[sizeof($work)- 1], $min_length-1), $work)+1;
// определяем порядковый номер максимального значения длинной строки $max_length
$max = str_to_dec(str_repeat($work[sizeof($work)- 1], $max_length), $work);
// предварительно определить количество возможных значений перебора можно следующим образом
// столько же итераций совершит цикл
$size = $max - $min +1;
$result = array();
for($i = $min; $i <= $max; $i++ )
{
$result[] = dec_to_str($i, $work);
}
// $result = массив, содержащий все возможные значения длинной строки от $min_length до $max_length
print_r($result);
// для ускорения выполнения всего перебора , цикл от min до max можно разбить на несколько циклов
// и запустить их к примеру с помощью pcntl_fork
// методы
/**
* переводит строки из системы счисления $work в десятичную систему
* другими словами находит порядковый номер строки в списке вариаций сочетаний
* при неизменном массиве $work, каждая последовательность будет иметь свой уникальный порядковый номер
* и не будет повторяться
*/
function str_to_dec($s, $sys)
{
$sys = array_flip($sys);
$j = -1;
$result = 0;
for($i = strlen($s)-1; $i >= 0; $i--)
{
$j++;
$result += ($sys[$s[$j]]+1) * pow(sizeof($sys), $i);
}
return $result;
}
/**
* переводит число $int (десятичная система) в систему исчисления $work
*/
function dec_to_str($i, $work)
{
$r = sizeof($work);
$w = '';
while($i > 0)
{
$t = $i % $r;
if($t == 0){
$w .= $work[$r-1];
$i = $i / $r -1;
} else {
$w .= $work[$t-1];
$i = ($i - $t) / $r;
}
}
return strrev($w);
}Данный вариант перебора использовался мною для перебора массива большой вложенности, предварительно модифицирован под конкретную задачу, но принцип оставался тем же.
Первоначально задача стояла перебрать строго заданную последовательность символов, но решение пришло более универсальное. Данная реализация была опубликована только на моем личном сайте тут, с нетерпением жду отзывов от достопочтенной публики.


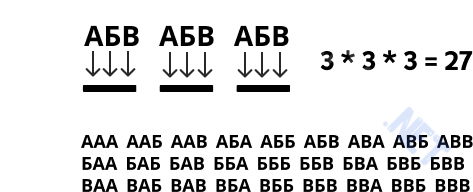



 Сообщение было отмечено NickoTin как решение
Сообщение было отмечено NickoTin как решение
 :
: