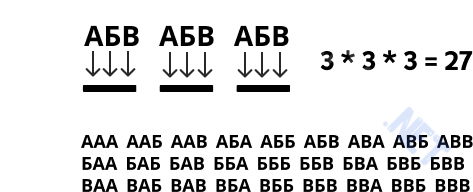Статьи / Python
Встроенный модуль itertools в Python — простой инструментарий, позволяющий генерировать полный список возможных комбинаций из заданного набора символов. Как с этим работать и справляться — далее в статье.
Что ж, в преддверии Нового года KOTOFF.net вновь расправляет крылья.
И сразу к делу. Рассмотрим всего 3 функции и их различия.
1. Нахождение всевозможных комбинаций из набора символов
Допустим, у нас есть некий алфавит из трёх букв (А, Б, В), и из него необходимо составить максимальное количество трёхзначных слов (комбинаций). Причём в данном случае буквы могут повторяться. Алфавит короткий, однако у нас получится составить целых 27 слов. На каждую позицию приходится по 3 варианта букв, соответственно, общее количество комбинаций можно посчитать так: nk (n — количество доступных символов в степени k — длина конечной комбинации). Для нашего случая: 33 = 27
Теперь импортирую itertools и сгенерирую всё то, что выше считали руками, но теперь уже с помощью функции product():
from itertools import product
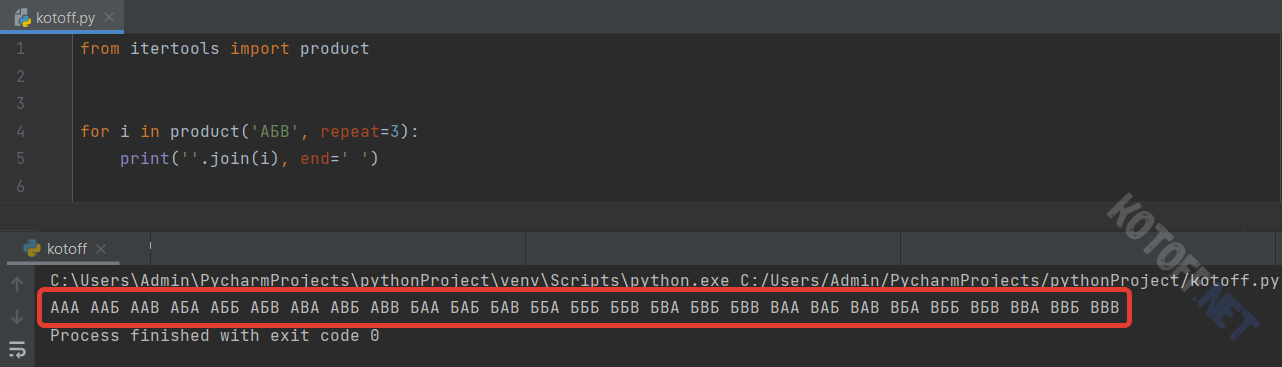
for i in product('АБВ', repeat=3):
print(''.join(i), end=' ')Функция принимает два параметра (набор символов и длина конечного объекта). С помощью join() получили строковое представление полученной комбинации.
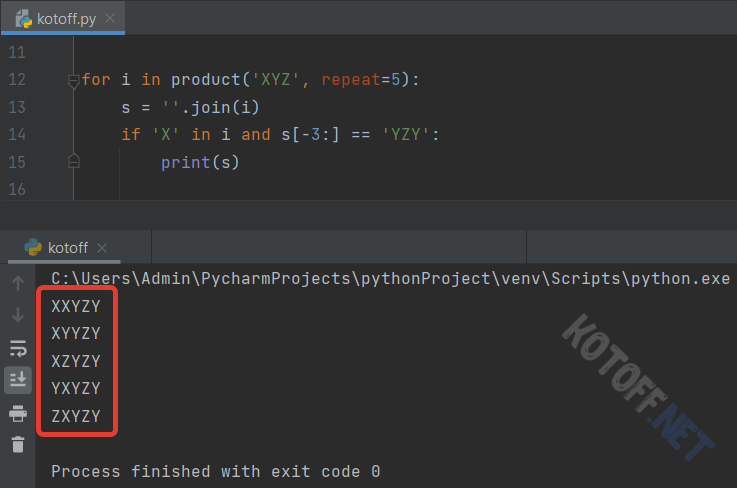
Можно добавить в цикл некий фильтр (условие). Например, сделаю так, чтобы комбинируемые слова начинались только с «X» и заканчивались на «YZY»:
Попробуем сгенерировать всевозможные автомобильные номера для одного региона. Способ, конечно, не особо рациональный, но для примера сгодится:
from itertools import product
import re
chars = '0123456789АВЕКМНОРСТУХ'
reg = '[АВЕКМНОРСТУХ]{1}d{3}[АВЕКМНОРСТУХ]{2}'
for i in product(chars, repeat=6):
if re.fullmatch(reg, ''.join(i)):
print(''.join(i))Кстати, если добавить в цикл счётчик, то в итоге получим цифру 1.728.000 (12*10*10*10*12*12). Именно столько номеров формата x000xx можно наклепать для одного региона 
2. Перестановка символов в наборе
В отличие от предыдущего примера, теперь мы не можем использовать по несколько раз один и тот же символ. Можем только переставлять их местами. Принцип подсчёта количества комбинаций остаётся тот же: необходимо перемножить количество вариантов символов на каждую позицию слова между собой. Но поскольку по мере составления слова на каждую последующую позицию символов будет оставаться всё меньше и меньше, то и формула также меняется на: n! / (n-k)! (n — количество доступных символов, k — длина слова). Если n = k, то можно использовать упрощённую формулу: n! (факториал числа n).
В питоне для таких целей используется функция permutations(). Принимает тоже два параметра: набор символов и длину генерируемой комбинации:
from itertools import permutations
for i in permutations('АБВ'):
print(''.join(i))Из трёх букв будет сгенерировано 6 различных слов с неповторяющимися символами (1! = 1 * 2 * 3 = 6)
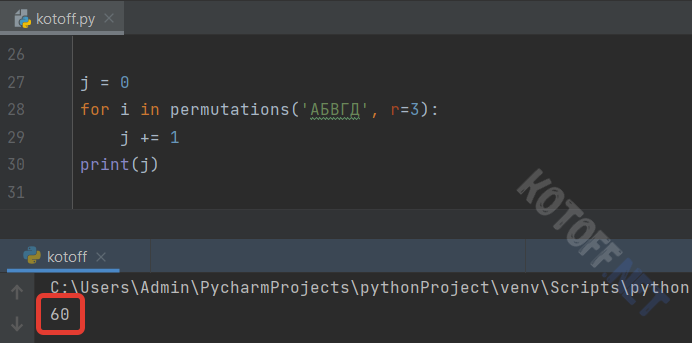
Попробуем составить трёхзначные слова в 5-символьном алфавите (5! / (5-3)! = 120 / 2 = 60):
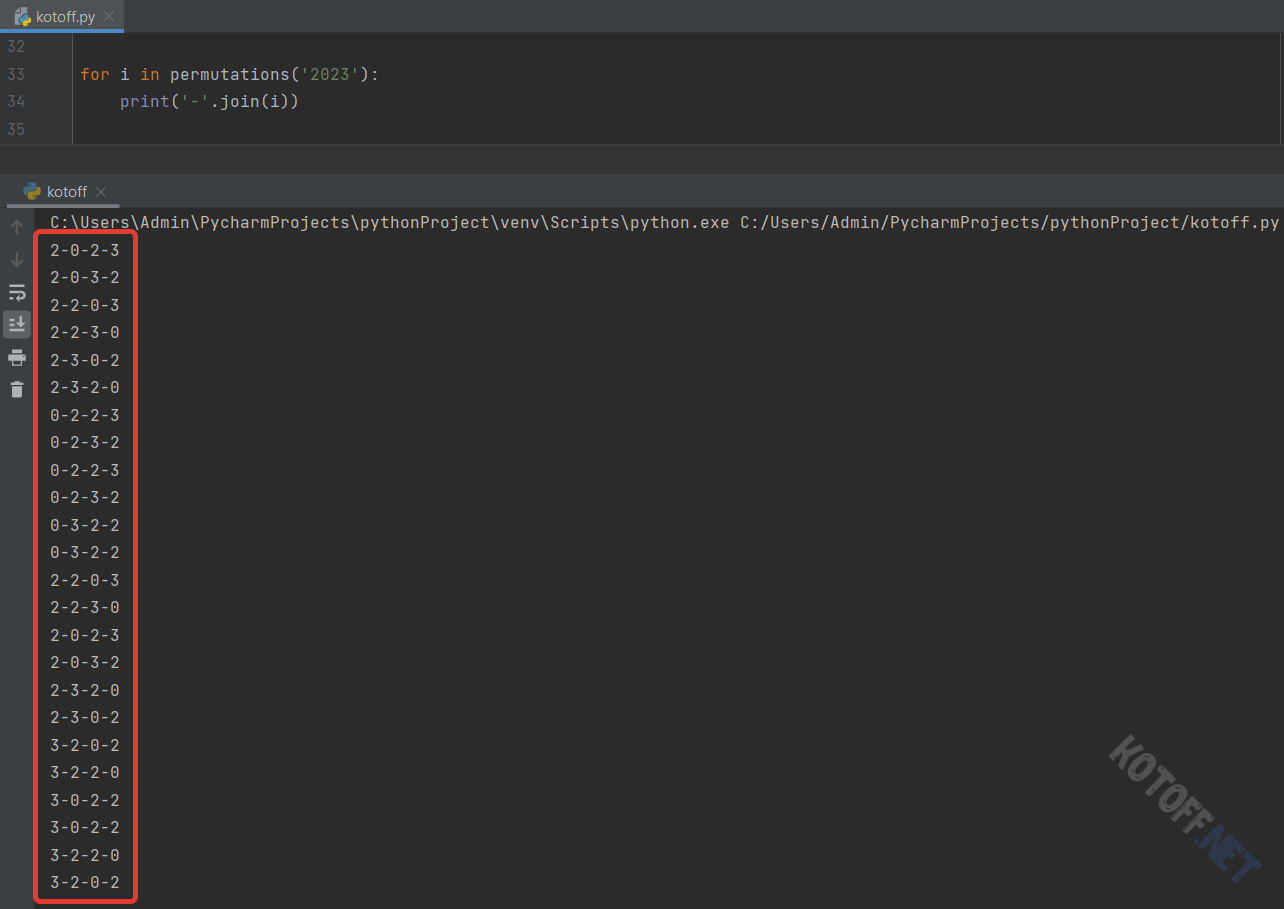
Кстати, если в заданном «алфавите» есть повторяющиеся символы, то они будут повторяться и в комбинациях:
3. Сочетания без повторений
А если нужно составить не комбинации, а отдельные неповторяющиеся сочетания? Например, есть 6 человек. Вопрос: какими способами их можно разбить по парам? Опять же, пользуемся формулой: n! / (n-k)! / k! (n — количество доступных объектов/символов, k — количество сочетаний). Соответственно, существует 6! / (6-2)! / 2! = 720 / 24 / 2 = 15 вариантов разбиения этих 6 персон по парам.
Теперь реализуем эту задачу на питоне с помощью функции combinations(). Принимает она два параметра — список и кол-во сочетаний:
from itertools import combinations
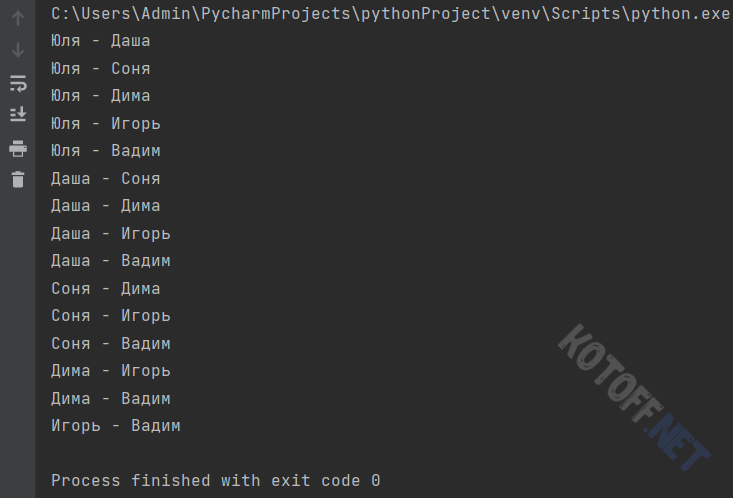
for i in combinations(['Юля', 'Даша', 'Соня', 'Дима', 'Игорь', 'Вадим'], 2):
print(' - '.join(i))Результат работы программы будет таков:
На этом, пожалуй, на сегодня всё. С наступающим! 
Пример рекурсивной генерации на Python. Функция берёт текущую комбинацию, и вставляет в неё очередной элемент (с номером idx) во все возможные места, а также пропускает данный элемент (второй вызов gencomb)
def gencombs(comb, lst, idx):
if idx >= len(lst):
print(comb)
else:
for i in range(len(comb),-1, -1):
gencombs(comb[:i] + [lst[idx]] + comb[i:], lst, idx + 1)
gencombs(comb, lst, idx + 1)
gencombs([],"abc", 0)
['a', 'b', 'c']
['a', 'c', 'b']
['c', 'a', 'b']
['a', 'b']
['b', 'a', 'c']
['b', 'c', 'a']
['c', 'b', 'a']
['b', 'a']
['a', 'c']
['c', 'a']
['a']
['b', 'c']
['c', 'b']
['b']
['c']
[]
Есть массив:
array(
0 => 'один',
1 => 'два',
3 => 'три',
4 => 'четыре',
5 => 'пять',
6 => 'шесть'
);
Как можно найти все возможные неповторяющиеся комбинации из этих слов?
Т.е. например нужно получить подобное:
array(
0 => array('один', 'два', 'три', 'четыре', 'пять', 'шесть'),
1 => array('один', 'два', 'три', 'четыре', 'пять'),
3 => array('один', 'два', 'три', 'четыре'),
4 => array('один', 'два', 'три'),
5 => array('один', 'два'),
6 => array('один'),
7 => array('один', 'три', 'четыре', 'пять', 'шесть'),
8 => array('два', 'три', 'четыре', 'пять', 'шесть'),
9 => array('четыре', 'пять', 'шесть'),
//и т.д.
);Голову сломал уже всю. Не могу сообразить.

При игре Wordle поиск правильных букв обычно определяется первыми словами. Чем эффективнее первое слово, тем больше подсказок мы можем получить, чтобы правильно написать букву. Обычно у каждого свои предпочтения.
Для тех из вас, кто не знает, Wordle — это ежедневная игра в слова, созданная Джошем Уордлом, в которой каждый день вам предстоит разгадывать новую словесную головоломку. Для получения дополнительной информации вы можете получить https://www.nytimes.com/games/wordle/index.html.
В этом посте я буду искать решение с использованием Python для получения наилучшего первого слова. Здесь буду использовать основные статистические методы, чтобы всем было легко их понять.
Я разделю эту статью на 4 части, а именно:
- Поиск по первому слову
- В поисках второго слова
- Найдите сочетание первого и второго слов
- Ищите наиболее оптимальную комбинацию.
Поиск по первому слову
Я использовал dataset из книги Дональда Э. Кнута «Искусство компьютерного программирования» (TAOCP). Dataset содержит слова на английском языке, состоящие из 5 букв (в соответствии с ограничением букв в мире), в общей сложности 5757 слов.
ЦИТАТА: Приведенный выше набор данных взят у проф. Дональда Э. Кнута, почетного профессора искусства компьютерного программирования в Стэнфордском университете.
Первое, что я сделал, это импортировал зависимости и загрузил файл набора данных.
import pandas as pd
import numpy as np
import math
words = []
with open('sgb-words.txt') as f:
words = [line.rstrip() for line in f]Набор данных содержит следующие данные.
which
there
their
about
would
...
pupalПервая обработка выполняется путем удаления одних и тех же букв в каждом слове. Это необходимо для того, чтобы мы могли получить слово из 5 разных букв. Метод заключается в следующем:
distinct_words = []
for word in words:
distinct_words.append(list(set(word)))Результат будет таким.
[['w', 'h', 'i', 'c'],
['t', 'h', 'e', 'r'],
['t', 'h', 'e', 'i', 'r'],
['a', 'b', 'o', 'u', 't'],
['w', 'o', 'u', 'l', 'd'],
...
['p', 'u', 'a', 'l']]После этого мы можем получить вес каждой буквы. Метод довольно прост, а именно путем сложения каждой буквы, и результаты представлены в виде словаря. Вес будет определять, как часто появляется буква, чем чаще появляется буква, тем больше вес буквы.
letter_counter = {}
for word in distinct_words:
for letter in word:
if letter in letter_counter:
letter_counter[letter] += 1
else:
letter_counter[letter] = 0Результат мы увидим ниже:
{'h': 790,
'w': 500,
'i': 1538,
'c': 919,
'e': 2657,
't': 1461,
'r': 1798,
'u': 1067,
'a': 2180,
'o': 1682,
'b': 668,
'l': 1433,
'd': 1099,
's': 2673,
'f': 501,
'g': 650,
'k': 573,
'n': 1218,
'y': 867,
'p': 894,
'v': 308,
'm': 793,
'q': 52,
'j': 87,
'x': 137,
'z': 120}Если мы отсортируем результат будет таким:
>>> {key: val for key, val in sorted(letter_counter.items(), key = lambda x: x[1], reverse = True)}
{'s': 2673,
'e': 2657,
'a': 2180,
'r': 1798,
'o': 1682,
'i': 1538,
't': 1461,
'l': 1433,
'n': 1218,
'd': 1099,
'u': 1067,
'c': 919,
'p': 894,
'y': 867,
'm': 793,
'h': 790,
'b': 668,
'g': 650,
'k': 573,
'f': 501,
'w': 500,
'v': 308,
'x': 137,
'z': 120,
'j': 87,
'q': 52}Из этих результатов видно, что 5 букв, которые появляются чаще всего это буквы s, e, a, r и o. Кроме того, это результат выраженный в процентах.
>>> values = letter_counter.values()
>>> total = sum(values)
>>> percent = [value * 100. / total for value in values]
>>> for i, letter in enumerate(letter_counter.keys()):
... print("{}: {}".format(letter, percent[i]))
h: 2.962685167822989
w: 1.8751171948246765
i: 5.767860491280705
c: 3.4464654040877556
e: 9.964372773298331
t: 5.479092443277705
r: 6.742921432589537
u: 4.00150009375586
a: 8.17551096943559
o: 6.307894243390212
b: 2.505156572285768
l: 5.374085880367523
d: 4.121507594224639
s: 10.024376523532721
f: 1.878867429214326
g: 2.4376523532720795
k: 2.148884305269079
n: 4.567785486592912
y: 3.2514532158259892
p: 3.3527095443465216
v: 1.1550721920120008
m: 2.973935870991937
q: 0.19501218826176636
j: 0.3262703918994937
x: 0.5137821113819614Далее нам нужно найти только слово, в котором буква имеет наибольший вес. Метод заключается в следующем:
word_values = []
for word in distinct_words:
temp_value = 0
for letter in word:
temp_value += letter_counter[letter]
word_values.append(temp_value)
words[np.argmax(word_values)]И результат arose. Если посмотреть на приведенные выше данные, можно увидеть, что в слове arose есть буквы, которые имеют большой вес. Таким образом, на основе статистических результатов можно сделать вывод, что слово arose — лучшее слово для использования в первом слове Wordle.
Но достаточно ли первого слова?
Иногда нам нужно еще одно слово, чтобы получить достаточно подсказок. Поэтому мы поищем другое слово.
В поисках второго слова
После того, как мы получили первое слово, следующим шагом будет получение списка слов, не содержащих букв в первом слове. Например, первое слово, которое мы получаем — arose. Таким образом, список слов в наборе данных не может содержать буквы a, r, o, s и e. Если есть слово, содержащее эти буквы, то оно будет удалено из списка. Метод заключается в следующем.
result_word = []
first_word_list = list(set(best_word))for word in words:
in_word = False
i = 0
while i < len(first_word_list) and not in_word:
if first_word_list[i] in word:
in_word = True
i += 1
if not in_word:
result_word.append(word)И результат таков.
['which',
'think',
'might',
'until',
...
'biffy']Количество слов сократилось до 310 слов с прежних 5757 слов. Осталось всего около 5% слов.
Следующим шагом будет повторение процесса, аналогичному поиску по первому слову. Полный код выглядит следующим образом:
import pandas as pd
import numpy as np
import math
def best_words(words):
distinct_words = []
for word in words:
distinct_words.append(list(set(word)))
letter_counter = {}
for word in distinct_words:
for letter in word:
if letter in letter_counter:
letter_counter[letter] += 1
else:
letter_counter[letter] = 0
word_values = []
for word in distinct_words:
temp_value = 0
for letter in word:
temp_value += letter_counter[letter]
word_values.append(temp_value)
return word_values
def get_best_word(words, word_values):
return words[np.argmax(word_values)]
def remove_word_contain_letters(words, first_word):
result_word = []
first_word_list = list(set(first_word))
for word in words:
in_word = False
i = 0
while i < len(first_word_list) and not in_word:
if first_word_list[i] in word:
in_word = True
i += 1
if not in_word:
result_word.append(word)
return result_word
words = []
with open('sgb-words.txt') as f:
words = [line.rstrip() for line in f]
word_values = best_words(words)
first_word = get_best_word(words, word_values)
second_words = remove_word_contain_letters(words, first_word)
second_values = best_words(second_words)
second_word = get_best_word(second_words, second_values)
print(first_word) # first word
print(second_word) # second wordИ результаты первого и второго слова — arose и unity.
Из приведенного выше метода можно сделать вывод, что слова arose и unity лучшие слова для начала игры в Wordle. Однако, если мы посмотрим на статистику по количеству букв в предыдущем посте, то можно увидеть, что буквы u и y не входят в топ-10 наиболее часто используемых букв. Это указывает на то, что слова arose и unity могут быть не самыми оптимальными словами.
Найдите сочетание первого и второго слов
В этом разделе мы обсудим, как можно получить два слова, буквы которых — это все буквы, которые встречаются чаще всего.
Нам нужно только повторить процесс, который мы уже проделывали раньше. Если в предыдущем процессе мы использовали только первое слово, с лучшим значением, то теперь мы также используем второе лучшее слово в качестве первого слова, чтобы получить больше вариаций в результатах.
Шаги следующие
Первый — вычислить значение для всех слов, а затем отсортировать слова по значению.
values = best_words(words)
values_index = np.argsort(values)[::-1]После этого мы будем искать первое и второе слова, как и раньше. Разница в том, что мы продолжим цикл, чтобы найти первый и второй цикл комбинации слов, чтобы получить слова, которые имеют наилучшие значения.
best_val = 0
best_word_list = []
top_words = sorted(values, reverse=True)
for i, idx in enumerate(values_index):
best_word = words[idx]
second_words = remove_word_contain_letters(words, best_word)
second_values = best_words(second_words)
second_best_word = get_best_word(second_words, second_values)
temp_value = 0
for letter in second_best_word:
temp_value += letter_counter[letter]
if temp_value + top_words[i] >= best_val:
best_val = temp_value + top_words[i]
print(best_word, second_best_word, top_words[i] + temp_value)И результат таков.
arose unity 17141
tears doily 17388
stare doily 17388
tares doily 17388
rates doily 17388
aster doily 17388
tales irony 17507
taels irony 17507
stale irony 17507
least irony 17507
tesla irony 17507
steal irony 17507
slate irony 17507
teals irony 17507
stela irony 17507
store inlay 17507
lores antic 17559
...
laird stone 17739
adorn tiles 17739
radon tiles 17739
tonal rides 17739
talon rides 17739
lined roast 17739
intro leads 17739
nitro leads 17739
nodal tries 17739Из этих результатов первый столбец — первое слово, второй столбец — второе, а третий столбец — это сумма значений первого и второго слова.
Если вы посмотрите на результаты выше, слова arose и unity не являются сочетанием слов с наибольшей ценностью. Кроме того, есть много словосочетаний которые получают значение 17739. Если вы обратите внимание на все буквы в словосочетании, которое получают это значение, именно 10 букв встречаются чаще всего в наборе данных. Таким образом, можно сделать вывод, что комбинация слов, получившее значение 17739, является наивысшей комбинацией слов, которую мы можем получить.
Но какое сочетание слов является наиболее оптимальным?
Чтобы получить ответ на этот вопрос нам нужно знать вес букв в зависимости от их размещения.
Ищите наиболее оптимальную комбинацию
Теперь мы будем искать более оптимальное словосочетание, которое будет первым и вторым словом в игре Wordle. Далее нам нужно рассчитать веса букв для каждой позиции. Метод заключается в следующем.
letter_list =['r', 'o', 'a', 's', 't', 'l', 'i', 'n', 'e', 's']
letter_value = {}
for letter in letter_list:
letter_counter = {}
for i in range(len(letter_list)//2):
loc_counter = 0
for j in range(len(words)):
if words[j][i] == letter:
loc_counter += 1
letter_counter[str(i)] = loc_counter
letter_value[letter] = letter_counterПеременная letter_list состоит из букв, которые встречаются чаще всего. После этого мы посчитаем, сколько вхождений этих букв в начале слова и так далее из всех слов в наборе данных.
Содержимое letter_value следующее
{'r': {'0': 268, '1': 456, '2': 475, '3': 310, '4': 401},
'o': {'0': 108, '1': 911, '2': 484, '3': 262, '4': 150},
'a': {'0': 296, '1': 930, '2': 605, '3': 339, '4': 178},
's': {'0': 724, '1': 40, '2': 248, '3': 257, '4': 1764},
't': {'0': 376, '1': 122, '2': 280, '3': 447, '4': 360},
'l': {'0': 271, '1': 360, '2': 388, '3': 365, '4': 202},
'i': {'0': 74, '1': 673, '2': 516, '3': 284, '4': 45},
'n': {'0': 118, '1': 168, '2': 410, '3': 386, '4': 203},
'e': {'0': 129, '1': 660, '2': 397, '3': 1228, '4': 595}}Эти результаты объясняют, что, например, буква r появляется как первая буква 268 раз, как вторая буква 456 раз и так далее… Таким образом, мы можем получить значение каждой позиции.
Далее мы рассчитаем вес словосочетания, которое мы получили ранее, используя letter_value. Метод заключается в следующем:
result_list = []
for i in range(len(best_word_list)):
word_value = 0
for word in best_word_list[i]:
for j, letter in enumerate(word):
if letter in letter_value:
word_value += letter_value[letter][str(j)]
result_list.append(word_value)И вот результат.
for i in range(len(result_list)):
print(best_word_list[i], result_list[i])
=== result ===
['arose', 'unity'] 3219
['tears', 'doily'] 5507
['stare', 'doily'] 4148
['tares', 'doily'] 6565
...
['lined', 'roast'] 4983
['intro', 'leads'] 4282
['nitro', 'leads'] 4831
['nodal', 'tries'] 5910Чтобы получить более оптимальную комбинацию значений, мы можем ввести следующий синтаксис:
result_index = np.argsort(result_list)[::-1]
best_word_list[result_index[0]]И лучшее словосочетание это toned и rails.
Наконец, это полный код первого поиска слов в Wordle с использованием серии Python.
import pandas as pd
import numpy as np
import math
def best_words(words):
distinct_words = []
for word in words:
distinct_words.append(list(set(word)))
letter_counter = {}
for word in distinct_words:
for letter in word:
if letter in letter_counter:
letter_counter[letter] += 1
else:
letter_counter[letter] = 0
word_values = []
for word in distinct_words:
temp_value = 0
for letter in word:
temp_value += letter_counter[letter]
word_values.append(temp_value)
return word_values
def get_best_word(words, word_values):
return words[np.argmax(word_values)]
def remove_word_contain_letters(words, first_word):
result_word = []
first_word_list = list(set(first_word))
for word in words:
in_word = False
i = 0
while i < len(first_word_list) and not in_word:
if first_word_list[i] in word:
in_word = True
i += 1
if not in_word:
result_word.append(word)
return result_word
words = []
with open('sgb-words.txt') as f:
words = [line.rstrip() for line in f]
distinct_words = []
for word in words:
distinct_words.append(list(set(word)))
letter_counter = {}
for word in distinct_words:
for letter in word:
if letter in letter_counter:
letter_counter[letter] += 1
else:
letter_counter[letter] = 0
word_values = best_words(words)
first_word = get_best_word(words, word_values)
second_words = remove_word_contain_letters(words, first_word)
second_values = best_words(second_words)
second_word = get_best_word(second_words, second_values)
values = best_words(words)
values_index = np.argsort(values)[::-1]
best_val = 0
best_word_list = []
top_words = sorted(values, reverse=True)
for i, idx in enumerate(values_index):
best_word = words[idx]
second_words = remove_word_contain_letters(words, best_word)
second_values = best_words(second_words)
second_best_word = get_best_word(second_words, second_values)
temp_value = 0
for letter in second_best_word:
temp_value += letter_counter[letter]
if temp_value + top_words[i] >= best_val:
best_val = temp_value + top_words[i]
best_word_list.append([best_word, second_best_word])
letter_list =['r', 'o', 'a', 's', 't', 'l', 'i', 'n', 'e', 's']
letter_value = {}
for letter in letter_list:
letter_counter = {}
for i in range(len(letter_list)//2):
loc_counter = 0
for j in range(len(words)):
if words[j][i] == letter:
loc_counter += 1
letter_counter[str(i)] = loc_counter
letter_value[letter] = letter_counter
result_list = []
for i in range(len(best_word_list)):
word_value = 0
for word in best_word_list[i]:
for j, letter in enumerate(word):
if letter in letter_value:
word_value += letter_value[letter][str(j)]
result_list.append(word_value)
result_index = np.argsort(result_list)[::-1]
print(best_word_list[result_index[0]])Можно сделать вывод, что слова toned и rails являются лучшими сочетаниями слов для начала игры Wordle. В дополнение к тому факту, что буквы в словесной комбинации являются буквами, которые чаще всего встречаются в наборе данных, буквы также размещаются в позиции, которая имеет наибольшее значение.
Ответ может быть не полностью оптимальным, поскольку он опирается только на статистические данные без учета других соображений.
Purpose
You’re saying combinations, but combinations are semantically unordered, what you mean, is you intend to find the intersection of all ordered permutations joined by spaces with a target list.
To begin with, we need to import the libraries we intend to use.
import re
import itertools
Splitting the string
Don’t split on characters, you’re doing a semantic search for words exclusive of strange characters.
Regular expressions, powered by the re module are perfect for this. In a raw
Python string, r'', we use the regular expression for the edge of a word, b, around any alphanumeric character (and _), w, of number greater than or equal to one, +.
re.findall returns a list of every match.
re_pattern = r'bw+b'
silly_string = 'alpha beta charlie, delta&epsilon foxtrot'
words = re.findall(re_pattern, silly_string)
Here, words is our wordlist:
>>> print words
['alpha', 'beta', 'charlie', 'delta', 'epsilon', 'foxtrot']
Creating the Permutations
Continuing, we prefer to manipulate our data with generators to avoid unnecessarily materializing data before we need it and holding large datasets in memory. The itertools library has some nice functions that neatly suit our needs for providing all permutations of the above words and chaining them in a single iterable:
_gen = (itertools.permutations(words, i + 1) for i in xrange(len(words)))
all_permutations_gen = itertools.chain(*_gen)
listing all_permutations_gen with list(all_permutations_gen) would give us:
[(‘alpha’,), (‘beta’,), (‘charlie’,), (‘delta’,), (‘epsilon’,),
(‘foxtrot’,), (‘alpha’, ‘beta’), (‘alpha’, ‘charlie’), (‘alpha’,
‘delta’), (‘alpha’, ‘epsilon’), (‘alpha’, ‘foxtrot’), (‘beta’,
‘alpha’), (‘beta’, ‘charlie’), (‘beta’, ‘delta’), (‘beta’, ‘epsilon’),
(‘beta’, ‘foxtrot’), (‘charlie’, ‘alpha’), (‘charlie’, ‘beta’),
(‘charlie’, ‘delta’), (‘charlie’, ‘epsilon’), (‘charlie’, ‘foxtrot’),
(‘delta’, ‘alpha’), (‘delta’, ‘beta’), (‘delta’, ‘charlie’), (‘delta’,
‘epsilon’), (‘delta’, ‘foxtrot’), (‘epsilon’, ‘alpha’), (‘epsilon’,
‘beta’), (‘epsilon’, ‘charlie’), (‘epsilon’, ‘delta’), (‘epsilon’,
‘foxtrot’), (‘foxtrot’, ‘alpha’), (‘foxtrot’, ‘beta’), (‘foxtrot’,
‘charlie’), (‘foxtrot’, ‘delta’), (‘foxtrot’, ‘epsilon’), (‘alpha’,
‘beta’, ‘charlie’), (‘alpha’, ‘beta’, ‘delta’), …
If we materialized the generator in a list instead of a set, printing the first 20 items would show us:
>>> print all_permutations[:20] # this only works if you cast as a list instead
['alpha', 'beta', 'charlie', 'delta', 'epsilon', 'foxtrot', 'alpha beta', 'alpha charlie', 'alpha delta', 'alpha epsilon', 'alpha foxtrot', 'beta alpha', 'beta charlie', 'beta delta', 'beta epsilon', 'beta foxtrot', 'charlie alpha', 'charlie beta', 'charlie delta', 'charlie epsilon']
But that would exhaust the generator before we’re ready. So instead, now we get the set of all permutations of those words
all_permutations = set(' '.join(i) for i in all_permutations_gen)
Checking for Membership of any Permutations in Target List
So we see with this we can now search for an intersection with the target list:
>>> target_list = ["zero","omega virginia","apple beta charlie"]
>>> all_permutations.intersection(target_list)
set([])
And in this case, for the examples given, we get the empty set, but if we have a string in the target that’s in our set of permutations:
>>> target_list_2 = ["apple beta charlie", "foxtrot alpha beta charlie"]
>>> all_permutations.intersection(target_list_2)
set(['foxtrot alpha beta charlie'])