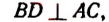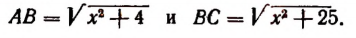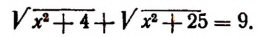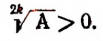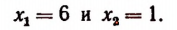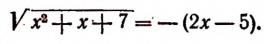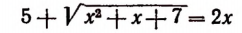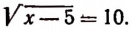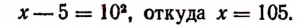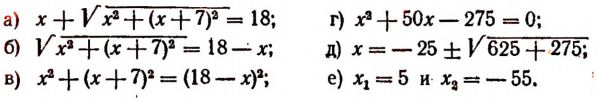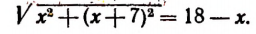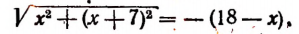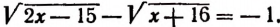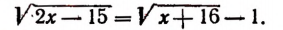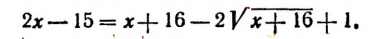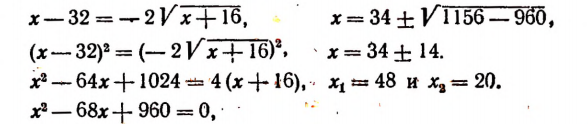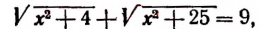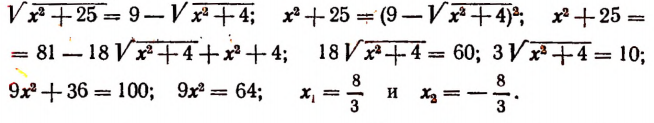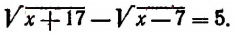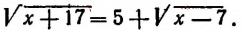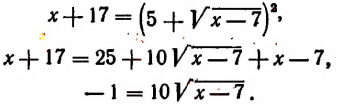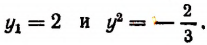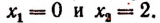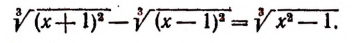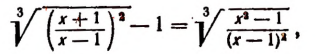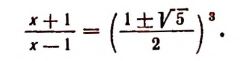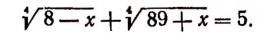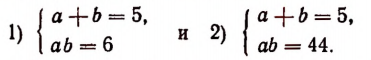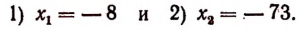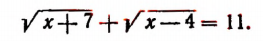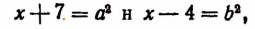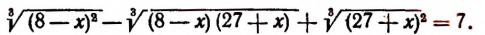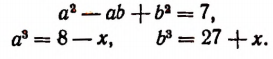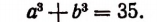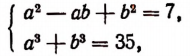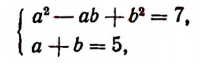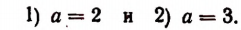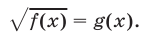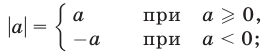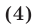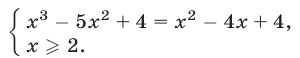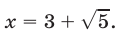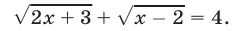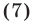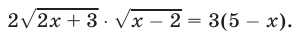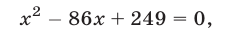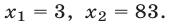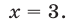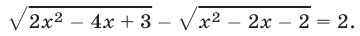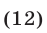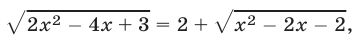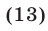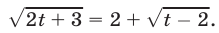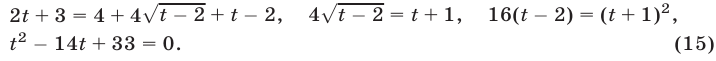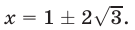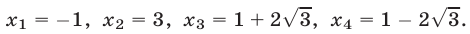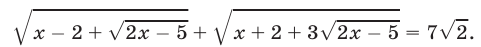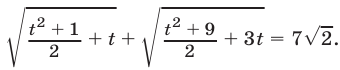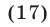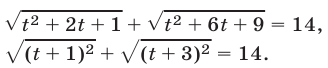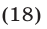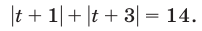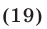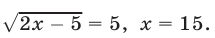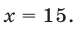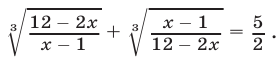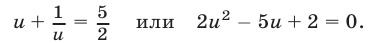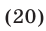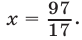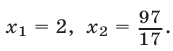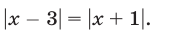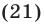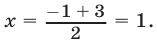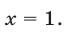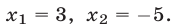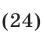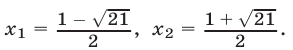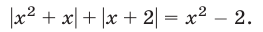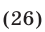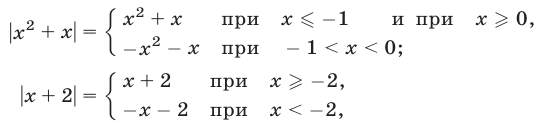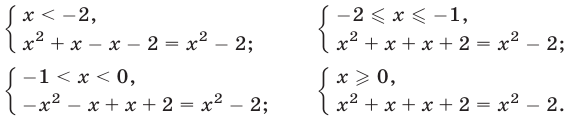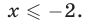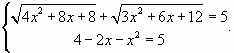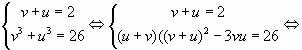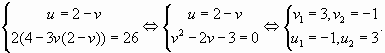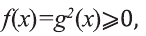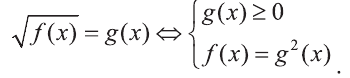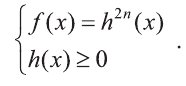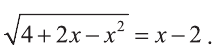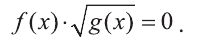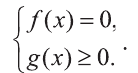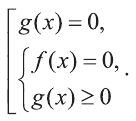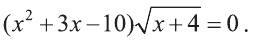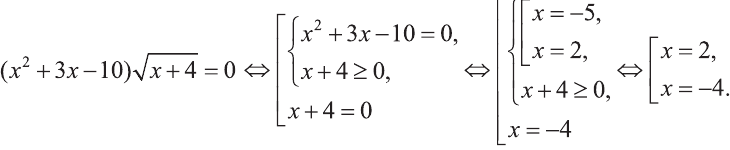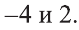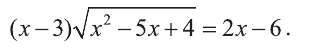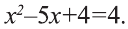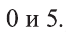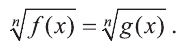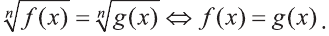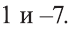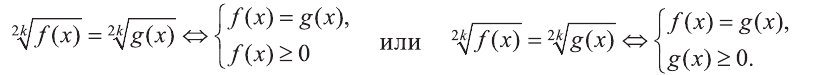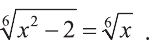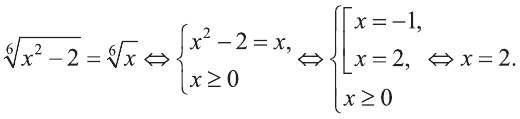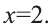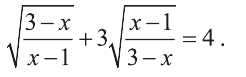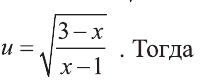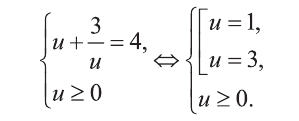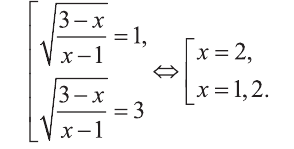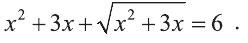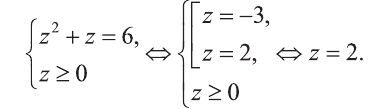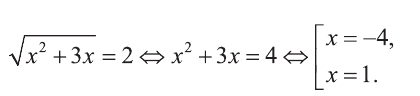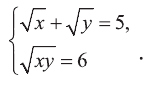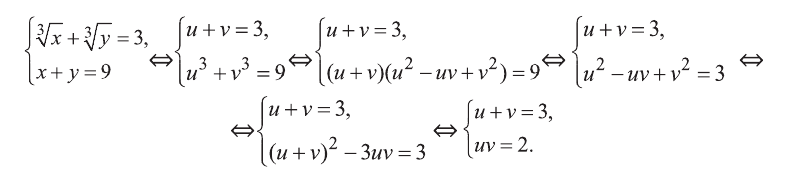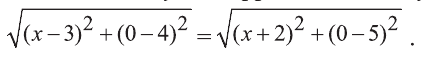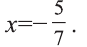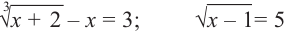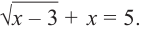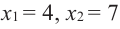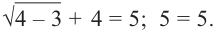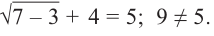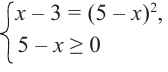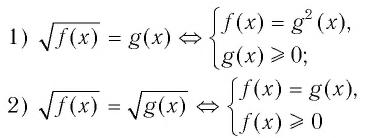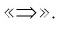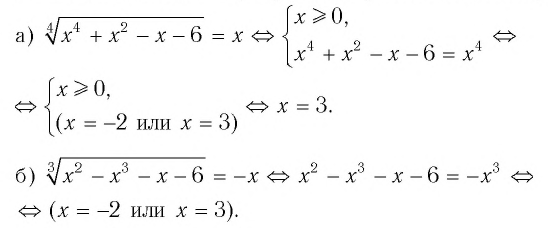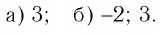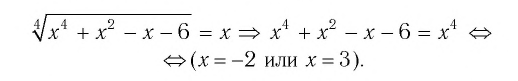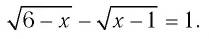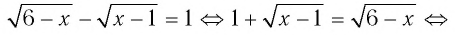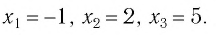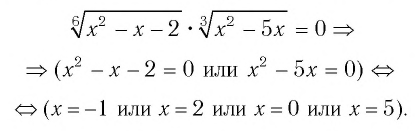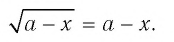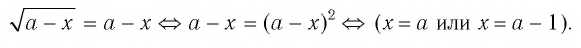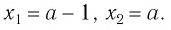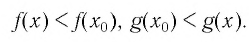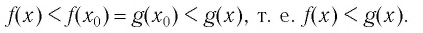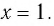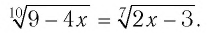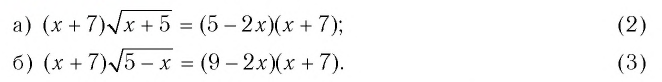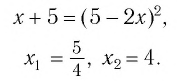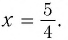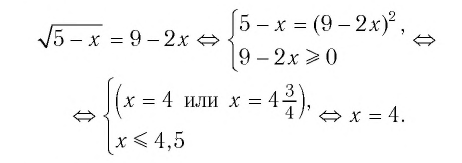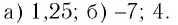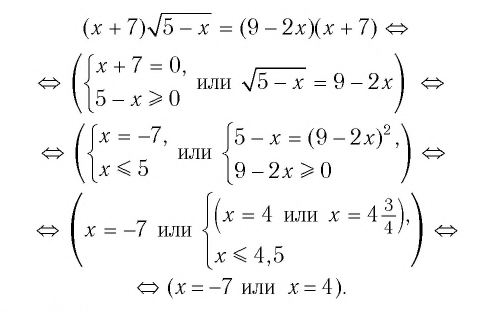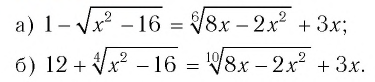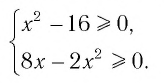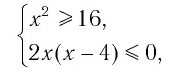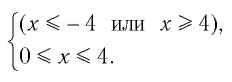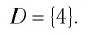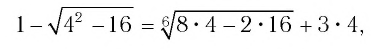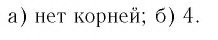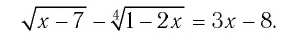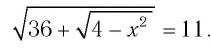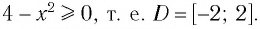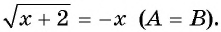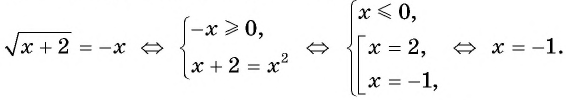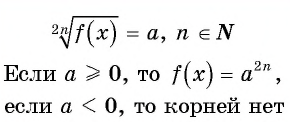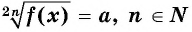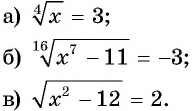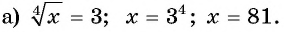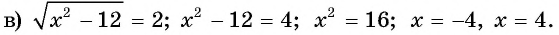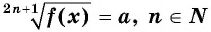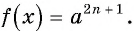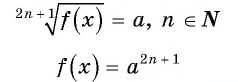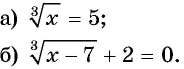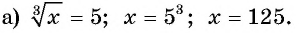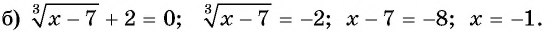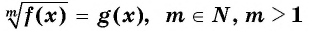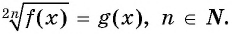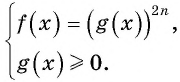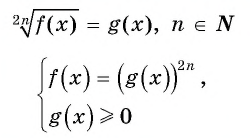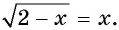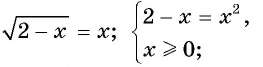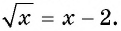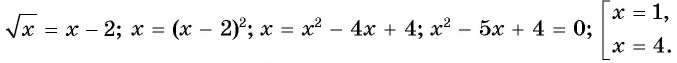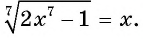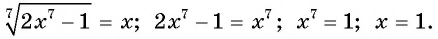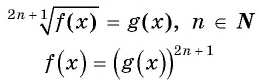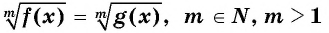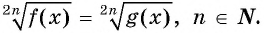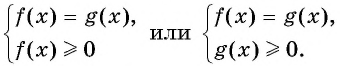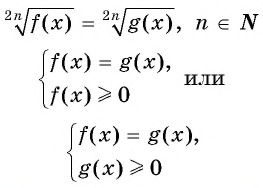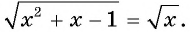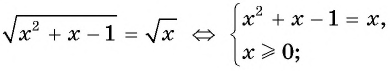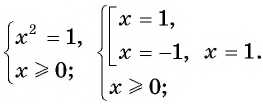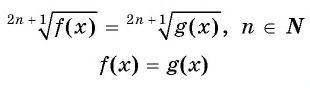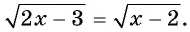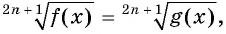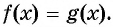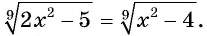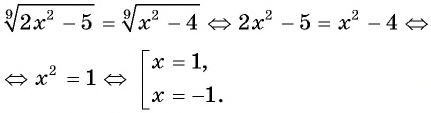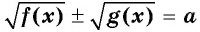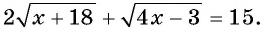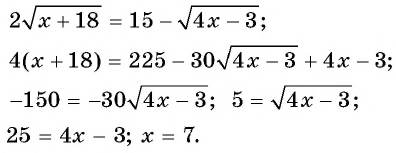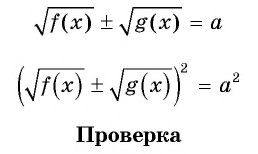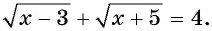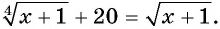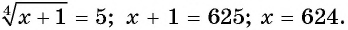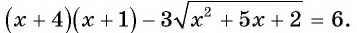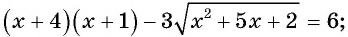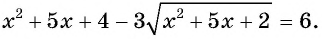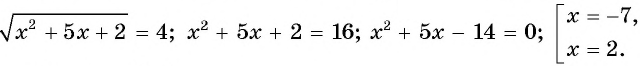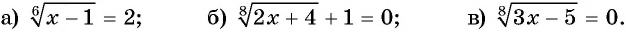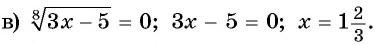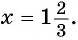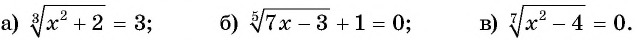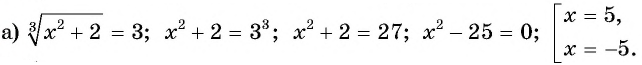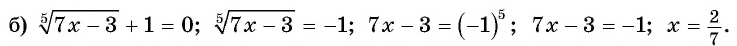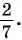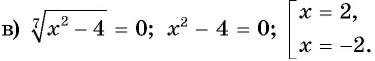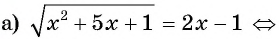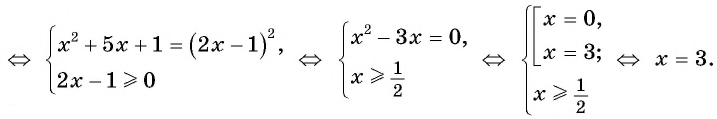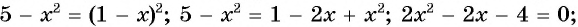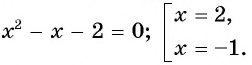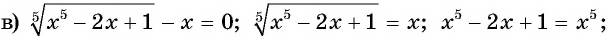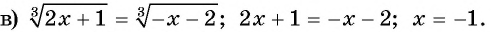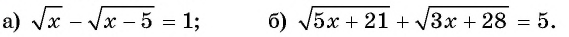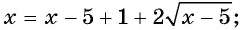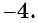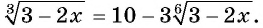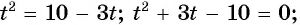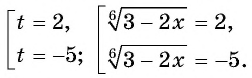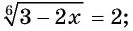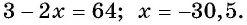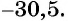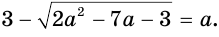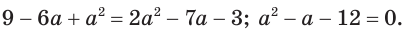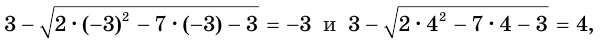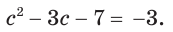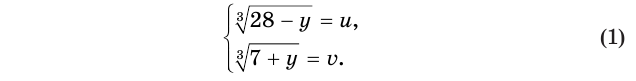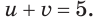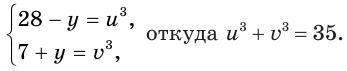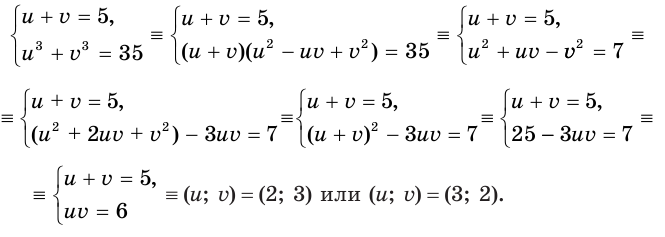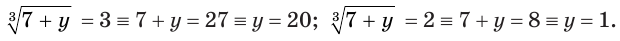Что такое иррациональные уравнения?
Не секрет же, что большинство чисел можно представить в виде обыкновенной дроби с натуральными числами в числителе и знаменателе?
Например, число 7 – это (frac{21}{3})
Иррациональные числа не такие. Их невозможно представить в виде дроби. Они странные.
Гиппас создал античным математикам множество проблем: их теории о том, что все в мире соизмеримо целым числам, рушились одна за другой. И они боялись.
Но мы будем смелыми 🙂
Сначала разберемся, что такое рациональные уравнения, а потом научимся находить решение иррациональных уравнений.
Итак, что из себя представляют рациональные уравнения, а что – иррациональные:
- ( 3cdot (x+1)=x) – как думаешь, какое это? Тут сложение, умножение, нет корней, и степеней никаких – рациональное!
- ( 3cdot (x+1)=sqrt{x}) – вот тебе и корень из переменной, значит уравнение НЕ рациональное (или иррациональное);
- ( 3cdot (x+1)=frac{1}{x}) – а это – рациональное;
- ( 3cdot (x+1)={{x}^{2}}) – тут вот степень, но она с целым показателем степени (( 2)– целое число) – значит, это тоже рациональное уравнение;
- ( 3cdot (x+1)={{x}^{-1}}) – даже уравнение с отрицательным показателем степени тоже является рациональным, ведь, по сути, ( {{x}^{-1}}) – это ( frac{1}{x});
- ( 3cdot (x+1)={{x}^{0}}) – тоже рациональное, т.к. ( {{x}^{0}}=1);
- ( 3cdot (x+1)={{x}^{frac{1}{2}}}) – а с ним поосторожнее, степень-то дробная, а по свойству корней ( {{x}^{frac{1}{2}}}=sqrt{x}), как ты помнишь, корня в рациональных уравнениях не бывает.
Надеюсь, теперь ты сможешь различить, к какому виду относится то или иное уравнение.
Дадим oпределение:
Иррациональными уравнениями называются уравнения, в которых переменная содержится под знаком корня или знаком возведения в дробную степень.
А вот как это выглядит: ( sqrt{x}); ( {{x}^{frac{1}{3}}}).
Но только отличать рациональное от иррационального недостаточно, тебе же решать их надо! Вся сложность в корнях, так?
Так избавься от них, вот и все дела!
Если еще не догадался, как, то я подскажу: просто возведи в нужную степень обе части уравнения, а потом решай его как простое рациональное уравнение.
Но проверяй все корни! Позже ты поймешь, почему делать это необходимо.
Как рациональные уравнения решать помнишь? Если забыл, то советую почитать «Рациональные уравнения».
Если читать лень, напомню вкратце. Для верного решения рациональных уравнений, ты должен придерживаться следующего алгоритма:
Пример №3
( sqrt{12-x}=x)
После возведения обеих частей в квадрат имеем:
( 12-x={{x}^{2}}), упрощаем и решаем квадратное уравнение по теореме Виета
( {{x}^{2}}+{x}-12=0)
( left[ begin{array}{l}{{x}_{1}}=3\{{x}_{2}}=-4end{array} right.)
У нас два корня, пробуем их подставить в исходное для проверки.
Подставляем ( 3), ( sqrt{9}=3), ( 3=3) – подходит.
Подставим ( -4), получим ( sqrt{16}=-4)…
Но ведь ( 4ne -4)! Что же получается, ( -4) – посторонний корень.
Заговор какой-то!
Думаю, интрига затянулась, настало время объяснить, почему получаются какие-то посторонние корни.
Опять объяснять буду на примере:
( -2ne 2), но если мы возведем в квадрат обе части, ( {{(-2)}^{2}}={{(2)}^{2}}), ( 4=4).
Ну как тебе фокус? 🙂
То же самое получается и в нашем примере с иррациональным уравнением, в результате преобразования мы можем найти все корни, но могут примешаться и посторонние.
Их надо отфильтровать проверкой, проверив, будет ли соблюдаться равенство исходного уравнения при их подстановке.
А если взять не вторую, а третью степень:
( {{(-2)}^{3}}ne {{(2)}^{3}})
( -8ne 
Пример №4 (метод уединения радикала)
( sqrt{2x+1}+sqrt{x}=1)
В этом примере есть два подкоренных выражения и число ( 1).
Чтобы избавиться от корня, нужно обе части возвести в квадрат, но, прежде чем сделать это, перенесем ( sqrt{x}) в правую часть.
( sqrt{2x+1}=1-sqrt{x})
«Зачем?» – спросишь ты.
Дело в том, что, если возводить в квадрат в таком виде, упрощать придется дольше, не веришь – попробуй сам, а я, пожалуй, избавлю себя от расписывания этого 🙂
Теперь возводим в квадрат обе части и упрощаем.
( sqrt{2x+1}=1-sqrt{x})
( 2x+1=1-2sqrt{x}+x)
( x=-2sqrt{x})
Понял, в чем сложность?
Этот метод решения математики называют «метод уединения радикала».
Радикал (выражение с корнем) надо уединить в одной стороне уравнения. Но уединять и возводить в степень придется не один раз.
Чтобы избавиться от корней и получить нормальное (рациональное 🙂 ) уравнение, придется выполнять множество замысловатых махинаций, которые заключаются в уединении и возведении в степень.
С другой стороны, можно заметить, что на определенной стадии решения становится без дальнейших упрощений понятно, что в уравнении, например, нет решений.
Например…
Корни степени больше 2
Ты спросишь: а что всё про квадратные корни? Как же быть с остальными степенями?
Спрошу в ответ: а чем они отличаются?
Отличие, на самом деле, есть. Но важна не конкретная степень корня, а четность этой степени.
Корни четной степени
Корни ( displaystyle 2), ( displaystyle 4), ( displaystyle 6), и т.д. степеней очень похожи друг на друга, и принцип решения уравнений с ними абсолютно одинаковый. Дело в том, что корень четной степени можно всегда привести к квадратному (вспоминаем тему «Корень и его свойства»!):
( displaystyle sqrt[4]{x}=sqrt{sqrt{x}};text{ }sqrt[6]{x}=sqrt{sqrt[3]{x}};text{ }sqrt[2k]{x}=sqrt{sqrt[k]{x}})
Например:
( displaystyle sqrt[4]{A}=Btext{ }Leftrightarrow text{ }left{ begin{array}{l}A={{B}^{4}}\Bge 0end{array} right.)
Корни нечетной степени
С нечетными степенями (( displaystyle 3), ( displaystyle 5), …) все намного проще!
Дело в том, что корень нечетной степени можно извлекать из любого числа! (И снова, если ты этого не знал, вспомни тему «Корень и его свойства»!)
Что это значит?
Теперь никаких дополнительных условий, никаких ограничений – просто возводим все в нужную степень и решаем:
( displaystyle begin{array}{l}sqrt[3]{A}=Btext{ }Leftrightarrow text{ }A={{B}^{3}}\sqrt[5]{A}=Btext{ }Leftrightarrow text{ }A={{B}^{5}}end{array})
Примеры:
- ( displaystyle sqrt[5]{2-x}=-2)
- ( displaystyle sqrt[4]{3+2{x}-{{x}^{2}}+{{x}^{4}}}=x)
- ( displaystyle sqrt[3]{{{x}^{3}}+3x+5}=x)
- ( displaystyle sqrt[3]{6+{{x}^{2}}-{{x}^{3}}}=1-x)
Ответы:
План урока:
Иррациональные уравнения
Простейшие иррациональные уравнения
Уравнения с двумя квадратными корнями
Введение новых переменных
Замена иррационального уравнения системой
Уравнения с «вложенными» радикалами
Иррациональные неравенства
Иррациональные уравнения
Ранее мы рассматривали целые и дробно-рациональные уравнения. В них выражение с переменной НЕ могло находиться под знаком радикала, а также возводиться в дробную степень. Если же переменная оказывается под радикалом, то получается иррациональное уравнение.
Приведем примеры иррациональных ур-ний:
Заметим, что не всякое уравнение, содержащее радикалы, является иррациональным. В качестве примера можно привести
Это не иррациональное, а всего лишь квадратное ур-ние. Дело в том, что под знаком радикала стоит только число 5, а переменных там нет.
Простейшие иррациональные уравнения
Начнем рассматривать способы решения иррациональных уравнений. В простейшем случае в нем справа записано число, а вся левая часть находится под знаком радикала. Выглядит подобное ур-ние так:
где а – некоторое число (константа), f(x) – рациональное выражение.
Для его решения необходимо обе части возвести в степень n, тогда корень исчезнет:
Получаем рациональное ур-ние, решать которые мы уже умеем. Однако есть важное ограничение. Мы помним, что корень четной степени всегда равен положительному числу, и его нельзя извлекать из отрицательного числа. Поэтому, если в ур-нии
n – четное число, то необходимо, чтобы а было положительным. Если же оно отрицательное, то ур-ние не имеет корней. Но на нечетные n такое ограничение не распространяется.
Пример. Решите ур-ние
Решение. Справа стоит отрицательное число (– 6), но квадратный корень (если быть точными, то арифметический квадратный корень) не может быть отрицательным. Поэтому ур-ние корней не имеет.
Ответ: корней нет.
Пример. Решите ур-ние
Решение. Теперь справа стоит положительное число, значит, мы имеем право возвести обе части в квадрат. При этом корень слева исчезнет:
x– 5 = 62
х = 36 + 5
х = 41
Ответ: 41.
Пример. Решите ур-ние
Решение. Справа стоит отрицательное число, но это не является проблемой, ведь кубический корень может быть отрицательным. Возведем обе части в куб:
х – 5 = (– 6)3
х = – 216 + 5
х = – 211
Ответ: – 211.
Конечно, под знаком корня может стоять и более сложное выражение, чем (х – 5).
Пример. Найдите решение ур-ния
Решение. Возведем обе части в пятую степень:
х2 – 14х = 25
х2 – 14х – 32 = 0
Получили квадратное ур-ние, которое можно решить с помощью дискриминанта:
D = b2– 4ac = (– 14)2 – 4•1•(– 32) = 196 + 128 = 324
х1 = (14 – 18)/2 = – 2
х2 = (14 + 18)/2 = 16
Итак, нашли два корня: (– 2) и 16.
Ответ: (– 2); 16.
Несколько более сложным является случай, когда справа стоит не постоянное число, а какое-то выражение с переменной g(x). Алгоритм решения тот же самый – необходимо возвести в степень ур-ние, чтобы избавиться от корня. Но, если степень корня четная, то необходимо проверить, что полученные корни ур-ния не обращают правую часть, то есть g(x), в отрицательное число. В противном случае их надо отбросить как посторонние корни.
Пример. Решите ур-ние
Решение. Возводим обе части во вторую степень:
х – 2 = (х – 4)2
х – 2 = х2 – 8х + 16
х2 – 9х + 18 = 0
D = b2– 4ac = (– 9)2 – 4•1•18 = 81 – 72 = 9
х1 = (9 – 3)/2 = 3
х2 = (9 + 3)/2 = 6
Получили два корня, 3 и 6. Теперь проверим, во что они обращают правую часть исходного ур-ния (х – 4):
при х = 3 х – 4 = 3 – 4 = – 1
при х = 6 6 – 4 = 6 – 4 = 2
Корень х = 3 придется отбросить, так как он обратил правую часть в отрицательное число. В результате остается только х = 6.
Ответ: 6.
Пример. Решите ур-ние
Решение. Здесь используется кубический корень, а потому возведем обе части в куб:
3х2 + 6х – 25 = (1 – х)3
3х2 + 6х – 25 = 1 – 3х + 3х2 – х3
х3 + 9х – 26 = 0
Получили кубическое ур-ние. Решить его можно методом подбора корня. Из всех делителей свободного коэффициента (– 26) только двойка обращает ур-ние в верное равенство:
23 + 9•2 – 26 = 0
8 + 18 – 26 = 0
0 = 0
Других корней нет. Это следует из того факта, что функция у = х3 + 9х – 26 является монотонной.
Заметим, что если подставить х = 2 в левую часть исходного ур-ния 1 – х, то получится отрицательное число:
при х = 2 1 – х = 1 – 2 = – 1
Но означает ли это, что число 2 НЕ является корнем? Нет, ведь кубический корень вполне может быть и отрицательным (в отличие от квадратного). На всякий случай убедимся, что двойка – это действительно корень исходного уравнения:
Ответ: 2.
Уравнения с двумя квадратными корнями
Ситуация осложняется, если в ур-нии есть сразу два квадратных корня. В этом случае их приходится убирать последовательно. Сначала мы переносим слагаемые через знак «=» таким образом, чтобы слева остался один из радикалов и ничего, кроме него. Возводя в квадрат такое ур-ние, мы избавимся от одного радикала, после чего мы получим более простое ур-ние. После получения всех корней надо проверить, какие из них являются посторонними. Для этого их надо просто подставить в исходное ур-ние.
Пример. Решите ур-ние
Решение. Перенесем вправо один из корней:
Возведем обе части в квадрат. Обратите внимание, что левый корень при этом исчезнет, а правый – сохранится:
Теперь снова перемещаем слагаемые так, чтобы в одной из частей не осталось ничего, кроме корня:
Поделим на 4:
Снова возведем ур-ние в квадрат, чтобы избавиться и от второго корня:
(2х – 4)2 = 13 – 3х
4х2 – 16х + 16 = 13 – 3х
4х2 – 13х + 3 = 0
D = b2– 4ac = (– 13)2 – 4•4•3 = 169 –48 = 121
х1 = (13 – 11)/8 = 0,25
х2 = (13 + 11)/8 = 3
Имеем два корня: 3 и 0,25. Но вдруг среди них есть посторонние? Для проверки подставим их в исходное ур-ние. При х = 0,25 имеем:
Получилось ошибочное равенство, а это значит, что 0,25 не является корнем ур-ния. Далее проверим х = 3
На этот раз получилось справедливое равенство. Значит, тройка является корнем ур-ния.
Ответ: 3
Введение новых переменных
Предложенный метод последовательного исключения радикалов плохо работает в том случае, если корни не квадратные, а имеют другую степень. Рассмотрим ур-ние
Последовательно исключить корни, как в предыдущем примере, здесь не получится (попробуйте это сделать самостоятельно). Однако помочь может замена переменной.
Для начала перепишем ур-ние в более удобной форме, когда вместо корней используются степени:
х1/2 – 10х1/4 + 9 = 0
Теперь введем переменную t = x1/4. Тогда х1/2 = (х1/4)2 = t2. Исходное ур-ние примет вид
t2– 10t + 9 = 0
Это квадратное ур-ние. Найдем его корни:
D = b2– 4ac = (– 10)2 – 4•1•9 = 100 – 36 = 64
t1 = (10 – 8)/2 = 1
t2 = (10 + 8)/2 = 9
Получили два значения t. Произведем обратную замену:
х1/4 = 1 или х1/4 = 9
Возведем оба ур-ния в четвертую степень:
(х1/4)4 = 14 или (х1/4)4 = 34
х = 1 или х = 6561
Полученные числа необходимо подставить в исходное ур-ние и убедиться, что они не являются посторонними корнями:
В обоих случаях мы получили верное равенство 0 = 0, а потому оба числа, 1 и 6561, являются корнями ур-ния.
Пример. Решите ур-ние
х1/3 + 5х1/6 – 24 = 0
Решение. Произведем замену t = x1/6, тогда х1/3 = (х1/6)2 = t2. Исходное ур-ние примет вид:
t2 + 5t – 24 = 0
Его корни вычислим через дискриминант:
D = b2– 4ac = 52 – 4•1•(– 24) = 25 + 96 = 121
t1 = (– 5 – 11)/2 = – 8
t2 = (– 5 + 11)/2 = 3
Далее проводим обратную заменуx1/6 = t:
х1/6 = – 8 или х1/6 = 3
Первое ур-ние решений не имеет, а единственным решением второго ур-ния является х = 36 = 729. Если подставить это число в исходное ур-ние, то можно убедиться, что это не посторонний корень.
Ответ: 729.
Замена иррационального уравнения системой
Иногда для избавления от радикалов можно вместо них ввести дополнительные переменные и вместо одного иррационального ур-ния получить сразу несколько целых, которые образуют систему. Это один из самых эффективных методов решения иррациональных уравнений.
Пример. Решите ур-ние
Решение. Заменим первый корень буквой u, а второй – буквой v:
Исходное ур-ние примет вид
u + v = 5 (3)
Если возвести (1) и (2) в куб и квадрат соответственно (чтобы избавиться от корней), то получим:
х + 6 = u3 (4)
11 – х = v2 (5)
Ур-ния (3), (4) и (5) образуют систему с тремя неизвестными, в которой уже нет радикалов:
Попытаемся ее решить. Сначала сложим (4) и (5), ведь это позволит избавиться от переменной х:
(х + 6) + (11 – х) = u3 + v2
17 = u3 + v2 (6)
из (3) можно получить, что v = 5 – u. Подставим это в (6) вместо v:
17 = u3 + v2 (6)
17 = u3 + (5 – u)2
17 = u3 + u2– 10u + 25
u3 + u2 – 10u + 8 = 0
Получили кубическое ур-ние. Мы уже умеем решать их, подбирая корни. Не вдаваясь в подробности решения, укажем, что корнями этого ур-ния являются числа
u1 = 1; u2 = 2; u3 = – 4
подставим полученные значения в (4):
x + 6 = u3 (5)
x + 6 = 13 или х + 6 = 23 или х + 6 = (– 4)3
x + 6 = 1 или х + 6 = 8 или х + 6 = – 64
х = – 5 или х = 2 или х = – 70
Итак, нашли три возможных значения х. Но, конечно же, среди них могут оказаться посторонние корни. Поэтому нужна проверка – подставим полученные результаты в исходное ур-ние. При х = – 5 получим
Корень подошел. Проверяем следующее число, х = 2:
Корень снова оказался верным. Осталась последняя проверка, для х = – 70:
Итак, все три числа прошли проверку.
Ответ: (– 5); 2; (– 70).
Уравнения с «вложенными» радикалами
Порою в ур-нии под знаком радикала стоит ещё один радикал. В качестве примера приведем такую задачу:
При их решении следует сначала избавиться от «внешнего радикала», после чего можно будет заняться и внутренним. То есть в данном случае надо сначала возвести обе части равенства в квадрат:
Внешний радикал исчез. Теперь будем переносить слагаемые, чтобы в одной из частей остался только радикал:
Хочется поделить полученное ур-ние (1) на х, однако важно помнить, что деление на ноль запрещено. То есть, если мы делим на х, то мы должны наложить дополнительное ограничение х ≠ 0. Случай же, когда х всё же равен нулю, мы рассматриваем отдельно. Для этого подставим х = 0 сразу в исходное ур-ние:
Получили верное рав-во, значит, 0 является корнем. Теперь возвращаемся к (1) и делим его на х:
Возводим в квадрат и получаем:
х2 + 40 = (х + 4)2
х2 + 40 = х2 + 8х + 16
8х = 24
х = 3
И снова нелишней будет проверка полученного корня:
Корень подошел.
Ответ: 0; 3.
Иррациональные неравенства
По аналогии с иррациональными ур-ниями иррациональными неравенствами называют такие нер-ва, в которых выражение с переменной находится под знаком радикала или возводится в дробную степень. Приведем примеры иррациональных нер-в:
Нет смысла решать иррациональные нер-ва, если есть проблемы с более простыми, то есть рациональными нер-вами, а также с их системами. Поэтому на всякий случай ещё раз просмотрите этот и ещё вот этот уроки.
Начнем с решения иррациональных неравенств простейшего вида, у которых в одной из частей стоит выражение под корнем, а в другой – постоянное число. Достаточно очевидно, что нер-во вида
Может быть справедливым только тогда, когда
То есть, грубо говоря, нер-ва можно возводить в степень. Однако при этом могут возникнуть посторонние решения. Дело в том, что нужно учитывать и тот факт, что подкоренное выражение должно быть неотрицательным в том случае, если степень корня является четной. Таким образом, нер-во
при четном n можно заменить системой нер-в
Пример. При каких значениях x справедливо нер-во
Решение. С одной стороны, при возведении нер-ва в квадрат мы получим такое нер-во:
х – 2 < 9
х < 11
Однако подкоренное выражение должно быть неотрицательным, то есть
х – 2 ⩾ 0
x⩾2
Итак, мы получили, что 2 ⩽ х < 11. Напомним, что традиционно решения нер-в записывают с помощью промежутков. Поэтому двойное нер-во 2 ⩽ х < 11 мы заменим на равносильную ему запись х∈[2; 11).
Ответ: х∈[2; 11).
Пример. Решите нер-во
Решение. Возведем нер-во в четвертую степень:
6 – 2х ⩾ 24
6 – 2х ⩾ 16 (1)
– 2х ⩾ 10
х ⩽ – 5 (знак нер-ва изменился из-за того, что мы поделили его на отрицательное число)
Получили промежуток х∈(– ∞; – 5). Казалось бы, надо записать ещё одно нер-во
6 – 2х ⩾ 0 (2)
чтобы подкоренное выражение было неотрицательным. Однако сравните (1) и (2). Ясно, что если (1) выполняется, то справедливым будет и (2), ведь если какое-то выражение больше или равно двум, то оно автоматически будет и больше нуля! Поэтому (2) можно и не решать.
Ответ: х∈(– ∞; – 5)
Теперь посмотрим на простейшие нер-ва с корнем нечетной степени.
Пример. Найдите решение нер-ва
Решение. Всё очень просто – надо всего лишь возвести обе части в куб:
х2 – 7x< 23
x2– 7x– 8 < 0
Получили неравенство второй степени, такие мы уже решать умеем. Напомним, что сначала надо решить ур-ние
x2– 7x– 8 = 0
D = b2– 4ac = (– 7)2 – 4•1•(– 
х1 = (7 – 9)/2 = – 1
х2 = (7 + 9)/2 = 8
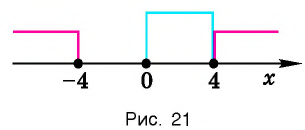
Далее полученные точки отмечаются на координатной прямой. Они разобьют ее на несколько промежутков, на каждом из которых функция у =x2– 7x– 8 сохраняет свой знак. Определить же этот самый знак можно по направлению ветвей параболы, которую рисует схематично:
Видно, что парабола располагается ниже оси Ох на промежутке (– 1; 8). Поэтому именно этот промежуток и является ответом. Нер-во строгое, поэтому сами числа (– 1) и 8 НЕ входят в ответ, то есть для записи промежутка используются круглые скобки.
Обратите внимание: так как в исходном нер-ве используется корень нечетной (третьей) степени, то нам НЕ надо требовать, чтобы он был неотрицательным. Он может быть меньше нуля.
Ответ: (– 1; 8).
Теперь рассмотрим более сложный случай, когда в правой части нер-ва стоит не постоянное число, а некоторое выражение с переменной, то есть оно имеет вид
Случаи, когда n является нечетным числом, значительно более простые. В таких ситуациях достаточно возвести нер-во в нужную степень.
Пример. Решите нер-во
Решение.Слева стоит кубический корень, а возведем нер-во в третью степень (при этом мы используем формулу сокращенного умножения):
7 – х3< (1 – х)3
7 – х3< 1 – 3x + 3x2– х3
3х2 – 3х – 6 > 0
x2– х – 2 > 0
И снова квадратное нер-во. Найдем нули функции записанной слева, и отметим их на координатной прямой:
x2– х – 2 = 0
D = b2– 4ac = (– 1)2 – 4•1•(– 2) = 1 + 8 = 9
х1 = (1 – 3)/2 = – 1
х2 = (1 + 3)/2 = 2
Нер-во выполняется при х∈(– ∞; – 1)⋃(2; + ∞). Так как мы возводили нер-во в нечетную степень, то больше никаких действий выполнять не надо.
Ответ: (– ∞; – 1)⋃(2; + ∞).
Если в нер-ве
стоит корень четной степени, то ситуация резко осложняется. Его недостаточно просто возвести его в n-ую степень. Необходимо выполнение ещё двух условий:
f(x) > 0 (подкоренное выражение не может быть отрицательным);
g(x) > 0 (ведь сам корень должен быть неотрицательным, поэтому если g(x)будет меньше нуля, то решений не будет).
Вообще говоря, в таких случаях аналитическое решение найти возможно, но это тяжело. Поэтому есть смысл решить нер-во графически – такое решение будет более простым и наглядным.
Пример. Решите нер-во
Решение. Сначала решим его аналитически, без построения графиков. Возведя нер-во в квадрат, мы получим
2х – 5 <(4 – х)2
2х – 5 < 16 – 8х + х2
х2 – 10х + 21 > 0(1)
Решением этого квадратного нер-ва будет промежуток (– ∞;3)⋃(7; + ∞). Но надо учесть ещё два условия. Во-первых, подкоренное выражение должно быть не меньше нуля:
2х – 5 ⩽ 0
2x⩽5
x⩽ 2,5
Во-вторых, выражение 4 – х не может быть отрицательным:
4 – х ⩾ 0
х ⩽ 4
Получили ограничение 2,5 ⩽ х ⩽ 4, то есть х∈[2,5; 4]. С учетом того, что при решении нер-ва(1) мы получили х∈(– ∞;3)⋃(7; + ∞), общее решение иррационального нер-ва будет их пересечением, то есть промежутком [2,5; 3):
Скажем честно, что описанное здесь решение достаточно сложное для понимания большинства школьников, поэтому предложим альтернативное решение, основанное на использовании графиков. Построим отдельно графики левой и правой части нер-ва:
Видно, что график корня находится ниже прямой на промежутке [2,5; 3). Возникает вопрос – точно ли мы построили график? На самом деле с его помощью мы лишь определили, что искомый промежуток находится между двумя точками. В первой график корня касается оси Ох, а во второй точке он пересекается с прямой у = 4 – х. Найти координаты этих точек можно точно, если решить ур-ния. Начнем с первой точки:
Итак, координата х первой точки в точности равна 2,5. Для нахождения второй точки составим другое ур-ние:
Это квадратное ур-ние имеет корни 3 и 7 (убедитесь в этом самостоятельно). Число 7 является посторонним корнем:
Подходит только число 3, значит, вторая точка имеет координату х = 3, а искомый промежуток – это [2,5; 3).
Ответ: [2,5; 3).
Ещё тяжелее случаи, когда в нер-ве с корнем четной степени стоит знак «>», а не «<», то есть оно имеет вид
Его тоже можно решить аналитически, однако мы для простоты рассмотрим только графическое решение.
Пример. Найдите решение нер-ва
Решение. Построим графики обеих частей:
Видно, что в какой-то точке графики пересекаются, после чего график корня будет лежать выше прямой у = 2 – х. Осталось найти точное значение точки, для чего можно составить ур-ние:
Корни квадратного ур-ния найдем через дискриминант:
Мы убедились, что иррациональные ур-ния и нер-ва являются довольно сложными. Для разных задач приходится использовать разные, не всегда стандартные методы решений. Зачем же их вообще надо решать? Оказывается, они часто возникают при геометрических расчетах. В частности, уравнение, описывающее зависимость расстояния между двумя точками от их координат, является иррациональным. Поэтому при решении многих физических задач, связанных с движением объектов в пространстве, возникает необходимость решать иррациональные ур-ния.
Также важно напомнить, что для поступления в ВУЗ по окончании 11 класса школьники сдают ЕГЭ. В задачах 13 и 15 очень попадаются именно иррациональные ур-ния и нер-ва. Поэтому, если вы желаете в будущем получить высшее образование по экономической (менеджер, аналитик, брокер, банкир), технической (инженер, программист) и тем более физико-математической специальности, то начинайте тренироваться уже сейчас!
Алгебра
План урока:
Иррациональные уравнения
Ранее мы рассматривали целые и дробно-рациональные уравнения. В них выражение с переменной НЕ могло находиться под знаком радикала, а также возводиться в дробную степень. Если же переменная оказывается под радикалом, то получается иррациональное уравнение.
Приведем примеры иррациональных ур-ний:
Заметим, что не всякое уравнение, содержащее радикалы, является иррациональным. В качестве примера можно привести
Это не иррациональное, а всего лишь квадратное ур-ние. Дело в том, что под знаком радикала стоит только число 5, а переменных там нет.
Простейшие иррациональные уравнения
Начнем рассматривать способы решения иррациональных уравнений. В простейшем случае в нем справа записано число, а вся левая часть находится под знаком радикала. Выглядит подобное ур-ние так:
где а – некоторое число (константа), f(x) – рациональное выражение.
Для его решения необходимо обе части возвести в степень n, тогда корень исчезнет:
Получаем рациональное ур-ние, решать которые мы уже умеем. Однако есть важное ограничение. Мы помним, что корень четной степени всегда равен положительному числу, и его нельзя извлекать из отрицательного числа. Поэтому, если в ур-нии
n – четное число, то необходимо, чтобы а было положительным. Если же оно отрицательное, то ур-ние не имеет корней. Но на нечетные n такое ограничение не распространяется.
Пример. Решите ур-ние
Решение. Справа стоит отрицательное число (– 6), но квадратный корень (если быть точными, то арифметический квадратный корень) не может быть отрицательным. Поэтому ур-ние корней не имеет.
Ответ: корней нет.
Пример. Решите ур-ние
Решение. Теперь справа стоит положительное число, значит, мы имеем право возвести обе части в квадрат. При этом корень слева исчезнет:
Пример. Решите ур-ние
Решение. Справа стоит отрицательное число, но это не является проблемой, ведь кубический корень может быть отрицательным. Возведем обе части в куб:
Конечно, под знаком корня может стоять и более сложное выражение, чем (х – 5).
Пример. Найдите решение ур-ния
Решение. Возведем обе части в пятую степень:
х 2 – 14х – 32 = 0
Получили квадратное ур-ние, которое можно решить с помощью дискриминанта:
D = b 2 – 4ac = (– 14) 2 – 4•1•(– 32) = 196 + 128 = 324
Итак, нашли два корня: (– 2) и 16.
Несколько более сложным является случай, когда справа стоит не постоянное число, а какое-то выражение с переменной g(x). Алгоритм решения тот же самый – необходимо возвести в степень ур-ние, чтобы избавиться от корня. Но, если степень корня четная, то необходимо проверить, что полученные корни ур-ния не обращают правую часть, то есть g(x), в отрицательное число. В противном случае их надо отбросить как посторонние корни.
Пример. Решите ур-ние
Решение. Возводим обе части во вторую степень:
х – 2 = х 2 – 8х + 16
D = b 2 – 4ac = (– 9) 2 – 4•1•18 = 81 – 72 = 9
Получили два корня, 3 и 6. Теперь проверим, во что они обращают правую часть исходного ур-ния (х – 4):
при х = 3 х – 4 = 3 – 4 = – 1
при х = 6 6 – 4 = 6 – 4 = 2
Корень х = 3 придется отбросить, так как он обратил правую часть в отрицательное число. В результате остается только х = 6.
Пример. Решите ур-ние
Решение. Здесь используется кубический корень, а потому возведем обе части в куб:
3х 2 + 6х – 25 = (1 – х) 3
3х 2 + 6х – 25 = 1 – 3х + 3х 2 – х 3
Получили кубическое ур-ние. Решить его можно методом подбора корня. Из всех делителей свободного коэффициента (– 26) только двойка обращает ур-ние в верное равенство:
Других корней нет. Это следует из того факта, что функция у = х 3 + 9х – 26 является монотонной.
Заметим, что если подставить х = 2 в левую часть исходного ур-ния 1 – х, то получится отрицательное число:
при х = 2 1 – х = 1 – 2 = – 1
Но означает ли это, что число 2 НЕ является корнем? Нет, ведь кубический корень вполне может быть и отрицательным (в отличие от квадратного). На всякий случай убедимся, что двойка – это действительно корень исходного уравнения:
Уравнения с двумя квадратными корнями
Ситуация осложняется, если в ур-нии есть сразу два квадратных корня. В этом случае их приходится убирать последовательно. Сначала мы переносим слагаемые через знак «=» таким образом, чтобы слева остался один из радикалов и ничего, кроме него. Возводя в квадрат такое ур-ние, мы избавимся от одного радикала, после чего мы получим более простое ур-ние. После получения всех корней надо проверить, какие из них являются посторонними. Для этого их надо просто подставить в исходное ур-ние.
Пример. Решите ур-ние
Решение. Перенесем вправо один из корней:
Возведем обе части в квадрат. Обратите внимание, что левый корень при этом исчезнет, а правый – сохранится:
Теперь снова перемещаем слагаемые так, чтобы в одной из частей не осталось ничего, кроме корня:
Снова возведем ур-ние в квадрат, чтобы избавиться и от второго корня:
(2х – 4) 2 = 13 – 3х
4х 2 – 16х + 16 = 13 – 3х
4х 2 – 13х + 3 = 0
D = b 2 – 4ac = (– 13) 2 – 4•4•3 = 169 –48 = 121
Имеем два корня: 3 и 0,25. Но вдруг среди них есть посторонние? Для проверки подставим их в исходное ур-ние. При х = 0,25 имеем:
Получилось ошибочное равенство, а это значит, что 0,25 не является корнем ур-ния. Далее проверим х = 3
На этот раз получилось справедливое равенство. Значит, тройка является корнем ур-ния.
Введение новых переменных
Предложенный метод последовательного исключения радикалов плохо работает в том случае, если корни не квадратные, а имеют другую степень. Рассмотрим ур-ние
Последовательно исключить корни, как в предыдущем примере, здесь не получится (попробуйте это сделать самостоятельно). Однако помочь может замена переменной.
Для начала перепишем ур-ние в более удобной форме, когда вместо корней используются степени:
х 1/2 – 10х 1/4 + 9 = 0
Теперь введем переменную t = x 1/4 . Тогда х 1/2 = (х 1/4 ) 2 = t 2 . Исходное ур-ние примет вид
Это квадратное ур-ние. Найдем его корни:
D = b 2 – 4ac = (– 10) 2 – 4•1•9 = 100 – 36 = 64
Получили два значения t. Произведем обратную замену:
х 1/4 = 1 или х 1/4 = 9
Возведем оба ур-ния в четвертую степень:
(х 1/4 ) 4 = 1 4 или (х 1/4 ) 4 = 3 4
х = 1 или х = 6561
Полученные числа необходимо подставить в исходное ур-ние и убедиться, что они не являются посторонними корнями:
В обоих случаях мы получили верное равенство 0 = 0, а потому оба числа, 1 и 6561, являются корнями ур-ния.
Пример. Решите ур-ние
х 1/3 + 5х 1/6 – 24 = 0
Решение. Произведем замену t = x 1/6 , тогда х 1/3 = (х 1/6 ) 2 = t 2 . Исходное ур-ние примет вид:
Его корни вычислим через дискриминант:
D = b 2 – 4ac = 5 2 – 4•1•(– 24) = 25 + 96 = 121
Далее проводим обратную заменуx 1/6 = t:
х 1/6 = – 8 или х 1/6 = 3
Первое ур-ние решений не имеет, а единственным решением второго ур-ния является х = 3 6 = 729. Если подставить это число в исходное ур-ние, то можно убедиться, что это не посторонний корень.
Замена иррационального уравнения системой
Иногда для избавления от радикалов можно вместо них ввести дополнительные переменные и вместо одного иррационального ур-ния получить сразу несколько целых, которые образуют систему. Это один из самых эффективных методов решения иррациональных уравнений.
Пример. Решите ур-ние
Решение. Заменим первый корень буквой u, а второй – буквой v:
Исходное ур-ние примет вид
Если возвести (1) и (2) в куб и квадрат соответственно (чтобы избавиться от корней), то получим:
Ур-ния (3), (4) и (5) образуют систему с тремя неизвестными, в которой уже нет радикалов:
Попытаемся ее решить. Сначала сложим (4) и (5), ведь это позволит избавиться от переменной х:
(х + 6) + (11 – х) = u 3 + v 2
из (3) можно получить, что v = 5 – u. Подставим это в (6) вместо v:
17 = u 3 + (5 – u) 2
17 = u 3 + u 2 – 10u + 25
u 3 + u 2 – 10u + 8 = 0
Получили кубическое ур-ние. Мы уже умеем решать их, подбирая корни. Не вдаваясь в подробности решения, укажем, что корнями этого ур-ния являются числа
подставим полученные значения в (4):
x + 6 = 1 3 или х + 6 = 2 3 или х + 6 = (– 4) 3
x + 6 = 1 или х + 6 = 8 или х + 6 = – 64
х = – 5 или х = 2 или х = – 70
Итак, нашли три возможных значения х. Но, конечно же, среди них могут оказаться посторонние корни. Поэтому нужна проверка – подставим полученные результаты в исходное ур-ние. При х = – 5 получим
Корень подошел. Проверяем следующее число, х = 2:
Корень снова оказался верным. Осталась последняя проверка, для х = – 70:
Итак, все три числа прошли проверку.
Уравнения с «вложенными» радикалами
Порою в ур-нии под знаком радикала стоит ещё один радикал. В качестве примера приведем такую задачу:
При их решении следует сначала избавиться от «внешнего радикала», после чего можно будет заняться и внутренним. То есть в данном случае надо сначала возвести обе части равенства в квадрат:
Внешний радикал исчез. Теперь будем переносить слагаемые, чтобы в одной из частей остался только радикал:
Хочется поделить полученное ур-ние (1) на х, однако важно помнить, что деление на ноль запрещено. То есть, если мы делим на х, то мы должны наложить дополнительное ограничение х ≠ 0. Случай же, когда х всё же равен нулю, мы рассматриваем отдельно. Для этого подставим х = 0 сразу в исходное ур-ние:
Получили верное рав-во, значит, 0 является корнем. Теперь возвращаемся к (1) и делим его на х:
Возводим в квадрат и получаем:
х 2 + 40 = (х + 4) 2
х 2 + 40 = х 2 + 8х + 16
И снова нелишней будет проверка полученного корня:
Иррациональные неравенства
По аналогии с иррациональными ур-ниями иррациональными неравенствами называют такие нер-ва, в которых выражение с переменной находится под знаком радикала или возводится в дробную степень. Приведем примеры иррациональных нер-в:
Нет смысла решать иррациональные нер-ва, если есть проблемы с более простыми, то есть рациональными нер-вами, а также с их системами. Поэтому на всякий случай ещё раз просмотрите этот и ещё вот этот уроки.
Начнем с решения иррациональных неравенств простейшего вида, у которых в одной из частей стоит выражение под корнем, а в другой – постоянное число. Достаточно очевидно, что нер-во вида
Может быть справедливым только тогда, когда
То есть, грубо говоря, нер-ва можно возводить в степень. Однако при этом могут возникнуть посторонние решения. Дело в том, что нужно учитывать и тот факт, что подкоренное выражение должно быть неотрицательным в том случае, если степень корня является четной. Таким образом, нер-во
при четном n можно заменить системой нер-в
Пример. При каких значениях x справедливо нер-во
Решение. С одной стороны, при возведении нер-ва в квадрат мы получим такое нер-во:
х ⩽ – 5 (знак нер-ва изменился из-за того, что мы поделили его на отрицательное число)
Получили промежуток х∈(– ∞; – 5). Казалось бы, надо записать ещё одно нер-во
чтобы подкоренное выражение было неотрицательным. Однако сравните (1) и (2). Ясно, что если (1) выполняется, то справедливым будет и (2), ведь если какое-то выражение больше или равно двум, то оно автоматически будет и больше нуля! Поэтому (2) можно и не решать.
Теперь посмотрим на простейшие нер-ва с корнем нечетной степени.
Пример. Найдите решение нер-ва
Решение. Всё очень просто – надо всего лишь возвести обе части в куб:
x 2 – 7x– 8 2 – 7x– 8 = 0
D = b 2 – 4ac = (– 7) 2 – 4•1•(– 
Далее полученные точки отмечаются на координатной прямой. Они разобьют ее на несколько промежутков, на каждом из которых функция у =x 2 – 7x– 8 сохраняет свой знак. Определить же этот самый знак можно по направлению ветвей параболы, которую рисует схематично:
Видно, что парабола располагается ниже оси Ох на промежутке (– 1; 8). Поэтому именно этот промежуток и является ответом. Нер-во строгое, поэтому сами числа (– 1) и 8 НЕ входят в ответ, то есть для записи промежутка используются круглые скобки.
Обратите внимание: так как в исходном нер-ве используется корень нечетной (третьей) степени, то нам НЕ надо требовать, чтобы он был неотрицательным. Он может быть меньше нуля.
Теперь рассмотрим более сложный случай, когда в правой части нер-ва стоит не постоянное число, а некоторое выражение с переменной, то есть оно имеет вид
Случаи, когда n является нечетным числом, значительно более простые. В таких ситуациях достаточно возвести нер-во в нужную степень.
Пример. Решите нер-во
Решение.Слева стоит кубический корень, а возведем нер-во в третью степень (при этом мы используем формулу сокращенного умножения):
И снова квадратное нер-во. Найдем нули функции записанной слева, и отметим их на координатной прямой:
D = b 2 – 4ac = (– 1) 2 – 4•1•(– 2) = 1 + 8 = 9
Нер-во выполняется при х∈(– ∞; – 1)⋃(2; + ∞). Так как мы возводили нер-во в нечетную степень, то больше никаких действий выполнять не надо.
стоит корень четной степени, то ситуация резко осложняется. Его недостаточно просто возвести его в n-ую степень. Необходимо выполнение ещё двух условий:
f(x) > 0 (подкоренное выражение не может быть отрицательным);
g(x) > 0 (ведь сам корень должен быть неотрицательным, поэтому если g(x)будет меньше нуля, то решений не будет).
Вообще говоря, в таких случаях аналитическое решение найти возможно, но это тяжело. Поэтому есть смысл решить нер-во графически – такое решение будет более простым и наглядным.
Пример. Решите нер-во
Решение. Сначала решим его аналитически, без построения графиков. Возведя нер-во в квадрат, мы получим
х 2 – 10х + 21 > 0(1)
Решением этого квадратного нер-ва будет промежуток (– ∞;3)⋃(7; + ∞). Но надо учесть ещё два условия. Во-первых, подкоренное выражение должно быть не меньше нуля:
Во-вторых, выражение 4 – х не может быть отрицательным:
Получили ограничение 2,5 ⩽ х ⩽ 4, то есть х∈[2,5; 4]. С учетом того, что при решении нер-ва(1) мы получили х∈(– ∞;3)⋃(7; + ∞), общее решение иррационального нер-ва будет их пересечением, то есть промежутком [2,5; 3):
Скажем честно, что описанное здесь решение достаточно сложное для понимания большинства школьников, поэтому предложим альтернативное решение, основанное на использовании графиков. Построим отдельно графики левой и правой части нер-ва:
Видно, что график корня находится ниже прямой на промежутке [2,5; 3). Возникает вопрос – точно ли мы построили график? На самом деле с его помощью мы лишь определили, что искомый промежуток находится между двумя точками. В первой график корня касается оси Ох, а во второй точке он пересекается с прямой у = 4 – х. Найти координаты этих точек можно точно, если решить ур-ния. Начнем с первой точки:
Итак, координата х первой точки в точности равна 2,5. Для нахождения второй точки составим другое ур-ние:
Это квадратное ур-ние имеет корни 3 и 7 (убедитесь в этом самостоятельно). Число 7 является посторонним корнем:
Подходит только число 3, значит, вторая точка имеет координату х = 3, а искомый промежуток – это [2,5; 3).
Ещё тяжелее случаи, когда в нер-ве с корнем четной степени стоит знак «>», а не « 1/2 = х – 3
Как решать иррациональные уравнения. Примеры.
Уравнения, в которых под знаком корня содержится переменная, называт иррациональными.
Методы решения иррациональных уравнений, как правило, основаны на возможности замены (с помощью некоторых преобразований) иррационального уравнения рациональным уравнением, которое либо эквивалентно исходному иррациональному уравнению, либо является его следствием. Чаще всего обе части уравнения возводят в одну и ту же степень. При этом получается уравнение, являющееся следствием исходного.
При решении иррациональных уравнений необходимо учитывать следующее:
1) если показатель корня — четное число, то подкоренное выражение должно быть неотрицательно; при этом значение корня также является неотрицательным (опредедение корня с четным показателем степени);
2) если показатель корня — нечетное число, то подкоренное выражение может быть любым действительным числом; в этом случае знак корня совпадает со знаком подкоренного выражения.
Пример 1. Решить уравнение
Возведем обе части уравнения в квадрат.
x 2 — 3 = 1;
Перенесем -3 из левой части уравнения в правую и выполним приведение подобных слагаемых.
x 2 = 4;
Полученное неполное квадратное уравнение имеет два корня -2 и 2.
Произведем проверку полученных корней, для этого произведем подстановку значений переменной x в исходное уравнение.
Проверка.
При x1 = -2 — истинно:
При x2 = -2- истинно.
Отсюда следует, что исходное иррациональное уравнение имеет два корня -2 и 2.
Пример 2. Решить уравнение .
Это уравнение можно решить по такой же методике как и в первом примере, но мы поступим иначе.
Найдем ОДЗ данного уравнения. Из определения квадратного корня следует, что в данном уравнении одновременно должны выполнятся два условия:
а) x — 90;
x9;
б) 1 — x0;
-x-1 ;
x1.
ОДЗ данного уранения: x.
Ответ: корней нет.
Пример 3. Решить уравнение=+ 2.
Нахождение ОДЗ в этом уравнении представляет собой достаточно трудную задачу. Возведем обе части уравнения в квадрат:
x 3 + 4x — 1 — 8= x 3 — 1 + 4+ 4x;
=0;
x1=1; x2=0.
Произведя проверку устанавливаем, что x2=0 лишний корень.
Ответ: x1=1.
Пример 4. Решить уравнение x =.
В этом примере ОДЗ найти легко. ОДЗ этого уравнения: x[-1;).
Возведем обе части этого уравнения в квадрат, в результате получим уравнение x 2 = x + 1. Корни этого уравнения:
x1 =
x2 =
Произвести проверку найденных корней трудно. Но, несмотря на то, что оба корня принадлежат ОДЗ утверждать, что оба корня являются корнями исходного уравнения нельзя. Это приведет к ошибке. В данном случае иррациональное уравнение равносильно совокупности двух неравенств и одного уравнения:
x + 10 и x0 и x 2 = x + 1, из которой следует, что отрицательный корень для иррационального уравнения является посторонним и его нужно отбросить.
Ответ:
Пример 5 . Решить уравнение+= 7.
Возведем обе части уравнения в квадрат и выполним приведение подобных членов, перенес слагаемых из одной части равенства в другую и умножение обеих частей на 0,5. В результате мы получим уравнение
= 12, (*) являющееся следствием исходного. Снова возведем обе части уравнения в квадрат. Получим уравнение (х + 5)(20 — х) = 144, являющееся следствием исходного. Полученное уравнение приводится к виду x 2 — 15x + 44 =0.
Это уравнение (также являющееся следствием исходного) имеет корни x1 = 4, х2 = 11. Оба корня, как показывает проверка, удовлетворяют исходному уравнению.
Замечание. При возведении уравнений в квадрат учащиеся нередко в уравнениях типа (*) производят перемножение подкоренных выражений, т. е. вместо уравнения•= 12, пишут уравнение = 12. Это не приводит к ошибкам, поскольку уравнения являются следствиями уравнений. Следует, однако, иметь в виду, что в общем случае такое перемножение подкоренных выражений дает неравносильные уравнения.
В рассмотренных выше примерах можно было сначала перенести один из радикалов в правую часть уравнения. Тогда в левой части уравнения останется один радикал и после возведения обеих частей уравнения в квадрат в левой части уравнения получится рациональная функция. Такой прием (уединение радикала) довольно часто применяется при решении иррациональных уравнений.
Пример 6. Решить уравнение-= 3.
Уединив первый радикал, получаем уравнение
=+ 3, равносильное исходному.
Возводя обе части этого уравнения в квадрат, получаем уравнение
x 2 + 5x + 2 = x 2 — 3x + 3 + 6, равносильное уравнению
4x — 5 = 3(*). Это уравнение является следствием исходного уравнения. Возводя обе части уравнения в квадрат, приходим к уравнению
16x 2 — 40x + 25 = 9(x 2 — Зх + 3), или
7x 2 — 13x — 2 = 0.
Это уравнение является следствием уравнения (*) (а значит, и исходного уравнения) и имеет корни. Первый корень x1 = 2 удовлетворяет исходному уравнению, а второй x2 =- не удовлетворяет.
Заметим, что если бы мы сразу, не уединив один из радикалов, возводили обе части исходного уравнения в квадрат нам бы пришлось выполнить довольно громозкие преобразования.
При решении иррациональных уравнений, кроме уединения радикалов используют и другие методы. Рассмотрим пример использования метода замены неизвестного (метод введения вспомогательной переменной).
Пример 7. Решить уравнение 2x 2 — 6x ++ 2 = 0.
Введем вспомогательную переменную. Пусть y =, где y0, тогда получим уравнение 2y 2 + y — 10 = 0;
y1 = 2; y2 = -. Второй корень не удовлетворяет условию y0.
Возвращаемся к x:
= 2;
x 2 — 3x + 6 = 4;
x 2 -3x + 2 = 0;
x1 = 1; x2 = 2. Проверкой устанавливаем, что оба корня являются корнями иисходного уравнения.
Ответ: x1 = 1; x2 = 2.
Пример 8. Решить уравнение+=
Положим= t, Тогда уравнение примет вид t +=откуда получаем следствие: 2t 2 — 5t + 2 = 0 Решая это квадратное уравнение, находим два корня: t1 = 2 t2 =. Задача сводится теперь к решению следующих двух уравнений:
= 2,(*)=(**)
Возводя обе части уравнения (*) в куб, получаем 12 — 2x = 8x — 8; x1 = 2.
Аналогично, решив (**), находим x2 =.
Оба найденных корня удовлетворяют исходному уравнению, так как в процессе решения мы использовали (кроме замены неизвестного) только преобразование вида [f(x) = g(x)][f n (x) = g n (x)], а при таком преобразовании, как было отмечено выше, получается равносильное уравнение.
Ответ: х1 = 2, x2 =.
Иррациональные уравнения в математике с примерами решения и образцами выполнения
Задача:
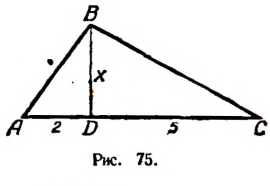
В треугольнике ABC (рис. 75):
AD = 2 см, DC = 5 см,
АВ + ВС = 9 см.
Найти BD.
Решение:
Пусть длина отрезка BD равна х см. Тогда
Получилось уравнение, в котором неизвестное входит в подкоренное выражение. Такое уравнение называется иррациональным. Решение этого уравнения приведено на странице 310.
Определение:
Уравнение, в котором неизвестное входит в какое-либо выражение, стоящее под знаком корня, называется иррациональным.
Во многих случаях иррациональное уравнение, как это ниже показано на примерах, может быть преобразовано в рациональное, являющееся его следствием. Но прежде чем показать это на примерах, мы изложим предварительные сведения, необходимые для понимания процесса решения иррациональных уравнений.
1. Всякий корень четной степени из положительного числа, входящий в иррациональное уравнение, мы будем считать, как и раньше, арифметическим. Поясним это. Если А > 0 и в иррациональное уравнение входит 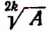
Принимая во внимание сказанное выше, мы должны считать, что, например, уравнение
не имеет корней. Действительно,
при
при
при 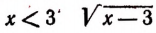
Таким образом, 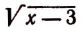
корней не имеет.
Было бы ошибкой считать число 4 корнем уравнения 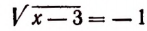
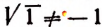
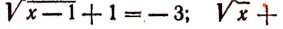
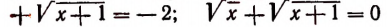
Теорема:
Если обе части уравнения А=В возвысить в квадрат, то полученное уравнение 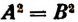
Решив это уравнение, убедимся, что его корнями будут числа 4 и — 6, т. е. только корни данного уравнения х + 1 = 5 и сопряженного ему уравнения х + 1 = —5 .
Как раз в этом и заключается смысл сформулированной выше теоремы.
Доказательство:
Уравнение 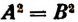
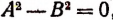
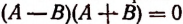
Следствие:
Из доказанной теоремы вытекает, что при переходе от уравнения А = В к уравнению 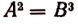
А = —В.
Если окажется, что уравнение А = — В не имеет корней, то не появляется и посторонних корней.
Иррациональные уравнения, содержащие только один радикал
Уединив корень, получим:
Возведем обе части этого уравнения в квадрат. В результате получим рациональное уравнение
Решив последнее уравнение, получим, что
Теперь необходимо проверить, являются ли числа 6 и 1 корня-ми данного уравнения. Проверка показывает, что число 6 является корнем уравнения 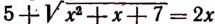
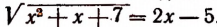
Итак, иррациональное уравнение
имеет лишь один корень, равный числу 6.
Возьмем еще одно уравнение, содержащее только один радикал, а именно:
Здесь корень уже уединен. Поэтому, возведя обе части уравнения в квадрат, получим:
Проверка показывает, что число 105 является корнем данного уравнения. Здесь мы не получили постороннего корня, потому что сопряженное уравнение, т. е. уравнение 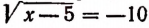
Примеры:
Проверка показывает, что оба числа 5 и —55 являются корнями уравнения
Значит, сопряженное уравнение, т. е. уравнение
корней не имеет.
Уравнения, содержащие два квадратных радикала
Пример:
Уединим один из корней:
Возведем в квадрат левую и правую части последнего уравнения:
Уединим один оставшийся корень:
Проверкой устанавливаем, что данное уравнение 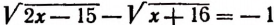
Пример:
В качестве второго примера решим уравнение
составленное по условиям задачи, поставленной в начале настоящей главы.
Легко убедиться, что оба числа 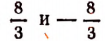
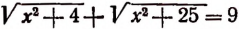
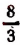
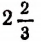
Пример:
Уединим один из корней:
Возведем в квадрат левую и правую части этого уравнения:
Последнее уравнение корней не имеет, ибо его левая часть есть отрицательное число, а правая часть ни при каком значении х не может быть числом отрицательным. Значит, и первоначальное уравнение корней не имеет.
Искусственные приемы решения иррациональных уравнений
Пример:
Примем 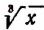
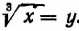
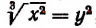
Отсюда
Приняв 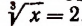
Приняв затем 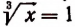
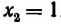
Пример:
Положим, что 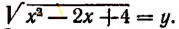
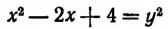
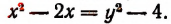
Освободившись от корня, получим:
Отсюда
Значение 
обозначили 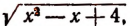
Взяв у = 2 и подставив это значение неизвестного у в уравнение 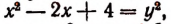
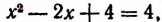
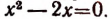
Числа 0 и 2 являются корнями первоначального уравнения. Других действительных корней данное уравнение не имеет.
Пример:
Подстановкой убеждаемся, что 1 не есть корень данного уравнения. Поэтому, разделив обе части уравнения на 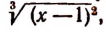
После сокращения последнее уравнение принимает вид:
Обозначив 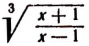
Составим производную пропорцию, воспользовавшись тем, что сумма членов первого отношения так относится к их разности, как сумма членов второго отношения к их разности. Получим, что
Способ решения иррационального уравнения с помощью системы рациональных уравнений
Решение всякого иррационального уравнения можно свести к решению соответствующей системы рациональных уравнений. Общий метод, позволяющий это сделать, покажем на примерах.
1. Решить уравнение
Пользуясь тем, что
и тем, что 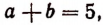
Отсюда 1) аb = 6 и 2) аb = 44.
Теперь остается решить две системы:
Первая система дает а = 2, b = 3 и а = 3, b = 2.
Вторая система действительных решений не имеет.
Пользуясь, например, уравнением 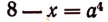
2. Решить уравнение:
или равносильную ей систему:
Отсюда а = 6.
Из уравнения 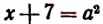
3. Решить уравнение:
Из последних двух равенств будем иметь:
илн равносильную ей систему:
Пользуясь уравнением 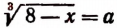
Дополнение к иррациональным уравнениям и примеры с решением
Уравнения, в которых переменная находится под знаком корня, называются иррациональными. Решение иррациональных уравнений сводится к переходу от иррационального уравнения к рациональному путем возведения обеих частей уравнения в степень, равную показателю степени корня. Если показатель степени четный, то необходимо либо предварительно выписывать ограничения: подкоренное выражение должно быть неотрицательным, выражение, равное арифметическому корню, также должно быть неотрицательным, т. к. в четную степень без приобретения посторонних корней можно возводить только неотрицательные выражения, либо делать проверку полученных решений.


Этот материал взят со страницы решения задач по математике:
Возможно вам будут полезны эти страницы:
Уравнения, содержащие знак модуля
1.Методы решения иррациональных уравнений, как правило, основаны на возможности замены (с помощью некоторых преобразований) иррационального уравнения рациональным уравнением, которое либо равносильно исходному иррациональному уравнению, либо является его следствием. Чаще всего обе части уравнения возводят в одну и ту же степень. При этом получается уравнение, являющееся следствием исходного.
При решении иррациональных уравнений необходимо учитывать следующее:
1) если показатель радикала — четное число, то подкоренное выражение должно быть неотрицательным; при этом значение радикала также является неотрицательным;
2) если показатель радикала — нечетное число, то подкоренное выражение может быть любым действительным числом; в этом случае знак радикала совпадает со знаком подкоренного выражения.
Рассмотрим уравнение вида
Если 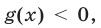
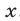
Если же 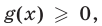
Замечание:
При решении уравнения (1) нет необходимости предварительно находить ОДЗ левой части (1), решая неравенство 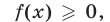
2.Из определения модуля (абсолютной величины) числа следует, что
1)
2)
3) если 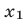
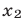
Пример:
Решение:
Уравнение (4) равносильно системе
Уравнение (5), равносильное каждому из уравнений 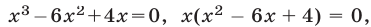
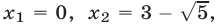
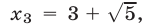
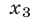
Ответ.
Пример:
Решение:
Возведя обе части уравнения (7) в квадрат, получим уравнение
равносильное (7), так как обе части уравнения (7) неотрицательны. Уравнение (8) равносильно уравнению
Возведя в квадрат обе части уравнения (9), получим уравнение
которое имеет корни
Заметим, что уравнение (11) является следствием уравнения (7), так как 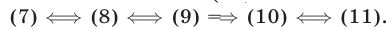
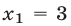
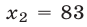
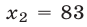
Ответ.
В рассмотренном примере можно было сначала перенести один из радикалов в правую часть уравнения (метод уединения радикала), а затем возвести обе части полученного уравнения в квадрат.
Воспользуемся этим приемом при решении следующего примера.
Пример:
Решение:
Применив метод уединения радикала, получим уравнение
равносильное уравнению (12).
Заметим, что нет необходимости находить ОДЗ уравнения (13), но следует обратить внимание на подкоренные выражения. Если ввести новое неизвестное (выполнить замену переменной), полагая 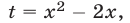
При 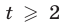
Корни 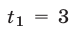
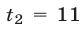
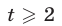
Если 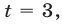
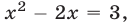
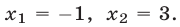
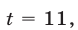
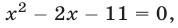
Ответ.
В примерах 1-3 был использован метод возведения обеих частей уравнения в квадрат. В отдельных случаях применяются другие приемы, которые могут оказаться более эффективными.
Пример:
Решение:
Положим 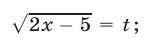
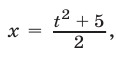
Уравнение (17) равносильно каждому из уравнений
Используя тождество 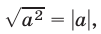
Так как 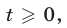
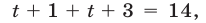
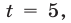
Ответ.
Пример:
Решение:
Полагая 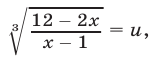
Уравнение (20) имеет корни 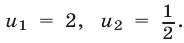
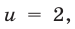
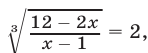
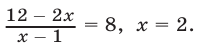
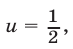
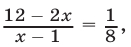
Оба найденных корня являются корнями исходного уравнения, так как в процессе решения было использовано (наряду с заменой неизвестного) только преобразование вида 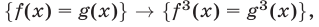
Ответ.
Пример:
Решение:
Так как 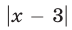
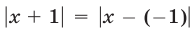
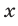
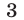
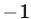
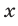
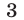
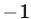
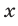
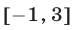
Ответ.
Пример:
Решение:
Полагая 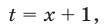
Если 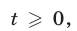
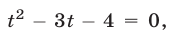
Поскольку при замене 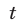
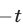
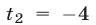

Ответ.
Пример:
Решение:
Положим 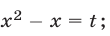
Решить уравнение (25) — значит найти все такие точки числовой оси 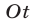
Пусть 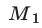
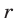
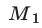
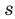
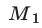
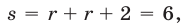
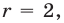
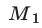
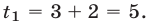
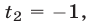
Таким образом, задача сводится к решению уравнений 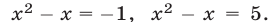
Ответ.
Пример:
Решение:
Функция 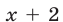
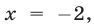
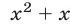

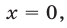
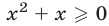
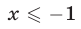
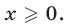
а уравнение (26), записанное без знака модуля на промежутках 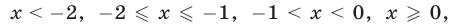
Первой из этих систем удовлетворяют все значения 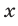
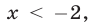

Ответ.
Решение иррациональных уравнений


Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:





















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
http://viripit.ru/Pag5_3.htm
http://lfirmal.com/irratsionalnyie-uravneniya-zadachi-s-resheniem/
Методы решения иррациональных уравнений
Разделы:
Математика
Я бы почувствовал настоящее
удовлетворение лишь в том случае,
если бы смог передать ученику гибкость ума,
которая дала бы ему в дальнейшем
возможность самостоятельно решать задачи.
У.У.Сойер.
Определение. Уравнение с одной
переменной называют иррациональным, если хотя бы
одна из функций или
содержит переменную под знаком
радикала.
При решении иррациональных уравнений
необходимо установить область допустимых
значений переменных, исходя из условия, что все
радикалы, входящие в уравнение, должны быть
арифметическими.
1. Метод пристального взгляда
Этот метод основан на следующем теоретическом
положении: “Если функция возрастает в области
определения и число входит в множество значений, то уравнение
имеет
единственное решение.”
Для реализации метода, основанного на этом
утверждении требуется:
а) Выделить функцию, которая фигурирует в
уравнении.
b) Записать область определения данной функции.
c) Доказать ее монотонность в области
определения.
d) Угадать корень уравнения.
t) Обосновать, что других корней нет.
f) Записать ответ.
Пример 1. .
Наличие радикалов четной степени говорит о том,
что подкоренные выражения должны быть
неотрицательными. Поэтому сначала найдем
область допустимых значение переменной .
Очевидно, что левая часть уравнения не
существует ни при одном значении неизвестного . Таким
образом, вопрос о решении уравнения снимается –
ведь нельзя же осуществить операцию сложения в
левой части уравнения, так как не существует сама
сумма. Каков же вывод? Уравнение не может иметь
решений, так как левая часть не существует ни при
одном значении неизвестного .
Пример 2.
Рассмотрим функцию .
Найдем область определения данной функции:
Данная функция является монотонно
возрастающей.
Для
эта функция будет принимать наименьшее значение
при , а
далее только возрастать.. Число 5 принадлежит
области значения, следовательно, согласно
утверждению .
Проверкой убеждаемся, что это действительный
корень уравнения..
2. Метод возведения обеих частей уравнений в
одну и ту же степень.
Теорема.
Если возвести обе части уравнения (1) в
натуральную степень , то уравнение
(2)
является следствием уравнения (1).
Доказательство. Если выполняется числовое
равенство , то по свойствам степени выполняется
равенство , т.е. каждый корень уравнения (1) является
и корнем уравнения (2), это значит, что уравнение (2)
является следствием уравнения (1).
Если ,
то справедливо и обратная теорема. В этом случае
уравнения (1) и (2) равносильны.
Если ,
равенство справедливо, если выполняется хотя бы
одно из равенств и
. Значит уравнения (1) и (2) в этом
случае не равносильны. Поэтому, если в ходе
решения иррационального уравнения
приходилось возводить обе его части в степень с
четным показателем, то могли появиться
посторонние корни. Чтобы отделить их, проверки
можно избежать, введя дополнительное требование . В этом
случае уравнение равносильно системе
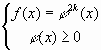
системе отсутствует требование ,
обеспечивающее существование корня степени , т.к. оно
было бы излишним в связи с равенством .
Пример 1.
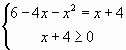
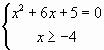
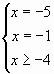
Ответ:
Если в уравнение входят несколько радикалов, то
их можно последовательно исключать с помощью
возведения в квадрат, получая в итоге уравнение
вида
При этом полезно учитывать область допустимых
значений исходного уравнения.
Пример 2.
Ответ:
3. Решение уравнений с использованием замены
переменной.
Введение вспомогательной переменной в ряде
случаев приводит к упрощению уравнения. Чаще
всего в качестве новой переменной используют
входящий в уравнение радикал. При этом уравнение
становится рациональным относительно новой
переменной.
Пример1.
Пусть тогда исходное уравнение примет вид:
,
корни которого и
Решая уравнение
, получаем
и
Ответ:
В следующих примерах используется более
сложная замена переменной.
Пример 2
Перенесем в левую часть все члены уравнения и
произведем дополнительные преобразования: .
Замена приводит уравнение к виду
корнями
которого являются и
Осталось решить совокупность двух уравнений:
Ответ:
4. Метод разложения на множители выражений,
входящих в уравнение.
Теорема.
Уравнение , определенное на всей числовой оси,
равносильно совокупности уравнений
Пример1.
При
уравнение принимает вид: которое равносильно
совокупности двух уравнений:
Ответ:
Выделить общий множитель часто бывает очень
трудно. Иногда это удается сделать после
дополнительных преобразований. В приведенном
ниже примере для этого рассматриваются попарные
разности подкоренных выражений.
Пример 2.
Если внимательно посмотреть на уравнение, то
можно увидеть, что разности подкоренных
выражений первого и третьего , а также второго и
четвертого членов этого уравнения равны одной и
той же величине
В таком случае далее следует воспользоваться
тождеством:
Уравнение примет вид:
или
Корень уравнения т.е. число
при подстановке в исходное
уравнение дает верное равенство.
Уравнение не имеет решений, так как его левая часть
положительна в своей области определения.
Ответ:
5. Метод выделения полных квадратов при решении
иррациональных уравнений.
При решении некоторых иррациональных
уравнений полезна формула
Пример 1.
Преобразуем уравнение следующим образом:
или
Обозначим и решим полученное уравнение
методом интервалов.
Разбирая отдельно случаи ,
находим,
что решениями последнего уравнения являются .
Возвращаясь к переменной , получаем неравенства
Ответ:
6. Метод оценки.
Этот способ применим в том случае, когда
подкоренные выражения представляют собой
квадратный трехчлен, не раскладывающийся на
линейные множители. Поэтому целесообразно
оценить левую и правую части уравнения.
Пример 1.
Оценим обе части уравнения:
,
,
Левая часть уравнения существует при всех
значениях переменной , не меньших 5, а правая – при всех
значениях, не больших 5, следовательно, уравнение
будет иметь решение, если обе части уравнения
одновременно равны 5, т. е. справедлива следующая
система:
Корнем второго уравнения системы является
число
Проверим, является ли это число корнем второго
уравнения:
.
Ответ:
Пример 2.
Для всех имеем
Используя неравенство Коши, можем записать:
причем равенство достигается при и
Таким образом, -корень исходного уравнения.
Ответ:
7. Иррациональные уравнения, содержащие
степени выше второй.
Если уравнение имеет вид то его можно решить , возводя
обе части этого уравнения в степень . Полученное
уравнение при нечетном
равносильно данному уравнению, а при
четном является
нго следствием, аналогично рассмотренному выше
случаю при
Пример 1
Возведем обе части уравнения в куб:
или
которое
равносильно совокупности двух уравнений:
Ответ:
При решении иррациональных уравнений очень
часто пользуются следующим приемом.
Если
то
В последнем равенстве заменяют на
и
получают
Далее легко избавиться от кубической
иррациональности , возводя обе части в куб.
Пример 2.
Здесь, очевидно,
Возведем в куб обе части уравнения, получим:
,
или
или
или
или
Проверка подтверждает, что это корень
уравнения.
Ответ:
Замечание.
Замена в конкретном примере левой части на
правую, вообще говоря , неправомерна –ведь нам
неизвестно ни одно значение , при котором это
уравнение превращается в верное числовое
равенство. Возможно, таких решений нет вообще.
Допуская в практических действиях такую замену,
мы фактически расширяем возможное множество
решений. Поэтому все найденные решения следует
проверять и только те, которые превращают
исходное уравнение в верное равенство, следует
записать в ответ.
От того, что школьник решит лишний десяток
задач, умнее и сообразительнее он не станет,
Результат обучения оценивается не количеством
сообщаемой информации, а качеством ее усвоения.
Это качество будет выше, если на один и тот же
пример посмотреть с разных сторон. Решение задач
разными способами способствует развитию
активного мышления учащихся. Хорошую почву для
этого дает решение примеров разными способами.
Пример 3. Способ 1.
(1)
Возведем обе части уравнения в куб:
Группируя, получаем:
Используя равенство (1) имеем:
или
или
или
корни которого
Ответ:
Способ 2.
Иногда полезно ввести не одну вспомогательную
переменную, а несколько, сводя исходное
уравнение к системе уравнений.
Пусть Тогда
Таким образом справедлива следующая система:
Возвращаясь к переменной находим
Ответ:
В следующем примере введение вспомогательной
переменной сводит исходное уравнение к
однородному.
Пример 4.
Положим
Тогда исходное уравнение примет вид:
Поскольку при котором переменная
обращается в нуль, не является решением
исходного уравнения ( в чем можно убедиться
подстановкой), делим обе части уравнения на
решая которое , находим:
Осталось решить уравнения и
Корнями этих уравнений являются числа
Ответ:
Пример 5.
Область допустимых значений задается
неравенством
Преобразуем уравнение следующим образом:
Один корень этого уравнения
Для решения второго уравнения положим
и решим
Корни этого уравнения
Последний корень не принадлежит указанному
промежутку, поэтому, решая уравнение , получим
Ответ :
8.02.2006
Уравнения, в которых неизвестное участвует под знаком корня называется иррациональным.
Содержание:
Рассмотрим методы решения некоторых видов иррациональных уравнений.
Рассмотрим простое иррациональное уравнение вида:
Пусть выражения f(х), g(x) принимают неотрицательные значения. Возводя обе части уравнения в квадрат, получим равносильное уравнение.
Так как
Значит, решение уравнения (1) осуществляется по правилу:
Аналогично уравнение вида 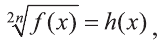
Пример:
Решите уравнение
Решение:
Возводя обе части уравнения в квадрат, получим равносильное уравнение 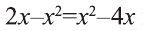
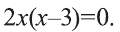
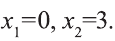
Уравнения вида
Для того чтобы произведение двух выражений обращалось в нуль, необходимо и достаточно равенство нулю, хотя бы одного из сомножителей.
Значит, для того чтобы 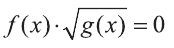
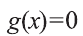
Этот факт мы кратко будем записывать так:
Пример:
Решите уравнение
Решение:
Ответ:
Пример:
Решите уравнение
Решение:
Данное уравнение приводится к виду 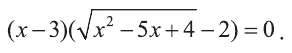
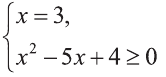
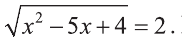
Ответ:
Уравнение вида
При решении таких уравнений сначала следует учесть четность-нечетность числа n, а затем привести его к равносильному уравнению.
Пусть n нечётно:
Например, уравнение 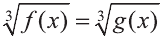
Пример:
Решите уравнение
Решение:
Ответ:
Пусть n четно, то есть n=2к. В этом случае данное уравнение равносильно каждой из систем:
На практике из данных систем выбирается то, которое легче решается.
Пример:
Решите уравнение
Решение:
Ответ:
IV Замена переменных.
Пример:
Решите уравнение
Решение:
Выполним замену
Найдем теперь корни данного уравнения.
Ответ: х=2 и х=1,2.
Пример:
Решите уравнение
Решение:
Выполним замену 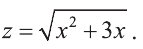
Найдем теперь корни данного уравнения
Ответ: х=4 и х=1.
Системы иррациональных уравнений
Решение систем, состоящих из иррациональных уравнений, опирается на известные нам методы сложения, подстановки и т.д. При этом следует учитывать области существования участвующих иррациональных выражений.
Пример:
Решите систему уравнений
Решение:
Данная система имеет решения
Пример:
Решите систему уравнений
Решение:
Обозначим 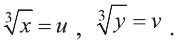
Эта система имеет решения 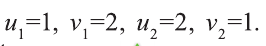

Пример:
Найдите точку С(х; 0), равноудаленную от точек А(3; 4) и В(-2; 5) плоскости.
Решение:
Из соотношения АС=ВС и формулы расстояния между двумя точками плоскости получим иррациональное уравнение
Делая равносильные преобразования, получим уравнение,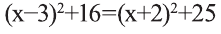
Пример:
Найдите точку на прямой у=3х, равноудаленную от точек А(-1;2) и В(3;—4) плоскости.
Решение:
По условию, ордината и абсцисса искомой точки удовлетворяет соотношению у=3х, поэтому она имеет координаты С(х;3х). Из соотношения АС=ВС и формулы расстояния между двумя точками плоскости получим иррациональное уравнение 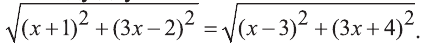
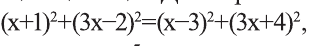
Значит, С(—5/7; -15/7) — искомая точка. Ответ: С(-5/7; -15/7).
Что называется иррациональным уравнением
Уравнение, содержащее переменную под знаком радикала (или в дробной степени) называется иррациональным уравнением.
Примеры:
При решении рациональных уравнений, как правило, применяют возведение в степень. При этом необходимо учитывать следующее:
- решение рационального уравнения ищут на множестве действительных чисел;
- для радикала четной степени берутся арифметические корни, для радикала нечетной степени — действительные значения;
- при возведении обеих частей уравнения в нечетную степень получается равносильное уравнение;
- При возведении в четную степень множество допустимых значений переменной нового уравнения может расширяться. Возможно, что некоторые корни нового уравнения могут не удовлетворять иррациональному уравнению. Поэтому при возведении в четную степень надо проверять, удовлетворяют ли полученные значения переменных заданному иррациональному уравнению.
Пример:
Решите уравнение
Решение:
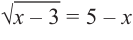
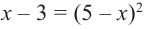
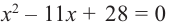
Проверка:
При 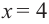
При 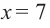
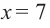
Ответ: {4}
Отметим, что решить уравнение 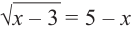
Определение иррационального уравнения
В этой лекции мы будем рассматривать уравнения, содержащие переменную (неизвестное) под знаком корня (радикала). Такие уравнения называют иррациональными.
Напомним на примерах два из возможных подходов к решению иррациональных уравнений.
Вычисление иррациональных уравнений
Первый подход состоит в замене исходного уравнения равносильным ему уравнением (системой или совокупностью уравнений и неравенств). Поскольку все равносильные уравнения имеют одни и те же решения, то при этом подходе проверка полученных значений переменной по условию исходного уравнения не является необходимой частью решения.
Например, при решении иррациональных уравнений часто пользуются следующими утверждениями о равносильности:
(вместо неравенства 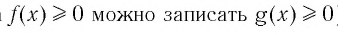
Второй подход состоит в замене исходного уравнения его следствием. Поскольку решений в уравнении-следствии (системе или совокупности) может быть больше, чем в исходном уравнении, то необходимой частью процесса решения является проверка полученных значений переменной по условию исходного уравнения.
Переход к следствию из данного уравнения при оформлении записи решения можно обозначать символом
Примеры с решением
Пример №1
Решить уравнение:
Пример №2
Способ 1 (сохранение равносильности).
Ответ:
Для уравнения а) покажем решение способом 2 (использование уравнения-следствия):
Проверка: при х = -2 получим 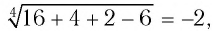
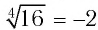
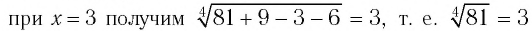
Пример №3
Решить уравнение
Решение:
Способ 1 (сохранение равносильности).
при любых допустимых значениях х обе части уравнения неотрицательны, поэтому, возведя их в квадрат, получим равносильное уравнение
Ответ: 2.
Способ 2 (использование уравнения-следствия).
Проверка: х=2 удовлетворяет исходному уравнению, а х=5 не удовлетворяет (убедитесь в этом).
Пример №4
Решить уравнение
Решение:
Способ 1 (сохранение равносильности).
Решив это уравнение и систему, получим
Ответ: -1; 2; 5.
Способ 2 (использование уравнения-следствия).
Проверка по условию исходного уравнения показывает, что 0 не является его корнем, так как при х = 0 выражение 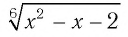
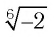
Пример №5
Решить уравнение с неизвестным х:
Решение:
Имеем (объясните почему):
Ответ: при любом значении 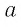
Пример №6
Решить уравнение 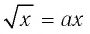
Решение:
Очевидно, что х = 0 — корень уравнения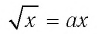
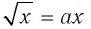
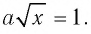
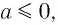
Ответ:
Решение иррациональных уравнений с использованием свойств функций
Уточним определение уравнения с одной переменной, данное в предыдущих классах.
Пусть 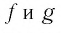
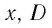
называется уравнением с переменной х, а множество D — областью определения этого уравнения (или областью допустимых значений переменной).
Переменную в уравнении называют также неизвестным. Корнем или решением уравнения 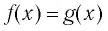
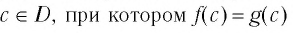
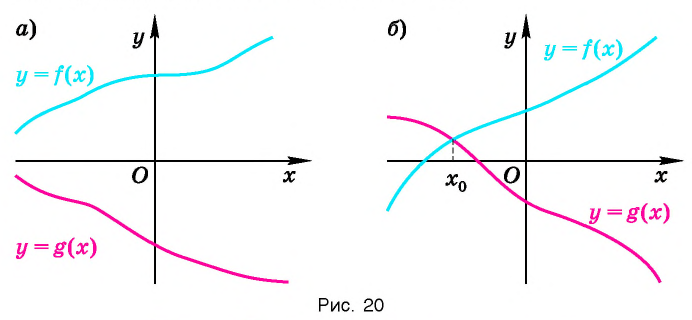
Теорема:
Уравнение
где 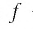
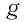
(Действительно, на рисунке 20, а, б видно, что графики возрастающей функции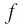
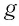
▲ Доказательство. Пусть 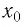
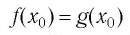
Если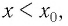
Следовательно,
Значит, никакое число 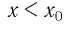
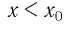
Замечание. Эта теорема справедлива и тогда, когда одна функция возрастающая (убывающая), а другая постоянная.
Приведем несколько примеров, где при решении иррациональных уравнений используются свойства возрастания и убывания функций.
Пример №7
Решить уравнение
Решение:
Способ 1.
Подбором находим, что 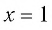
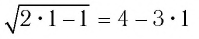
Так как функция 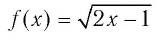
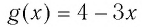
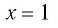
Ответ: 1.
Способ 2.
Возможно и другое решение:
Так как функция 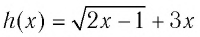
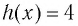
Пример №8
Решить уравнение
Решение:
Подбором находим, что число 2 — корень данного уравнения, поскольку 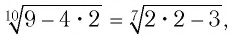
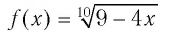
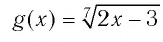
Ответ: 2.
▲ Иногда при решении иррациональных (и других) уравнений бывает полезно предварительно найти область определения уравнения.
Пример №9
Решить уравнение:
Решение:
а) Значение 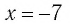
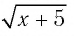
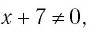
Решим это уравнение, переходя к уравнению-следствию:
Проверка показывает, что корнем уравнения (4) (а значит, и уравнения (2)) является значение
б) Очевидно, что значение 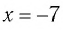
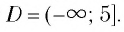
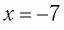
При 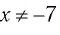
Решая это уравнение, получаем:
Ответ:
Решение уравнения (3) с помощью знаков равносильности можно записать так:
Пример №10
Решить уравнение:
Решение:
а) Поскольку функция 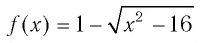
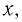
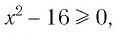
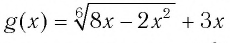
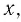
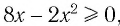
Решая эту систему, получаем равносильную ей систему:
откуда имеем
На рисунке 21 видно, что решением этой системы является только значение х = 4. Значит, область определения уравнения состоит из единственного числа 4, т. е.
Осталось проверить, является ли число 4 корнем данного уравнения. Подставив 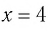
т. е. 1 = 12 — неверное числовое равенство, значит, 4 не является корнем данного уравнения.
б) Решение этого примера аналогично решению примера а). Выполните его самостоятельно.
Ответ:
Пример №11
Решить уравнение
Решение:
Область определения данного уравнения совпадает со множеством решений системы неравенств:
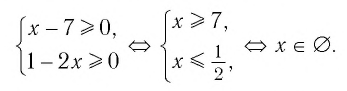
Ответ: нет корней.
Иногда при решении уравнений бывает полезно обратить внимание на наибольшее или наименьшее значения входящих в них функций.
Пример №12
Решить уравнение
Решение:
Область определения уравнения совпадает со множеством решений неравенства
Очевидно, что функция 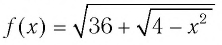
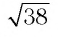
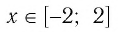
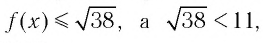
Ответ: нет решений. ▲
Напомним:
Уравнения, содержащие переменную под знаком корня, называются иррациональными.
При решении иррациональных уравнений не всегда удается от данного уравнения перейти к равносильному ему уравнению.
Например, решим уравнение
Первый способ.
Возведем обе части уравнения в квадрат, получим уравнение 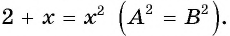
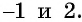
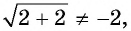
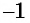
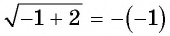
Посторонний корень уравнения (число 2) появился оттого, что уравнение 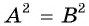
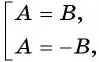
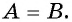
Второй способ.
Уравнение 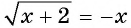
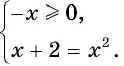
Третий способ.
Запишем уравнение 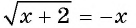
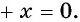
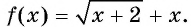
Рассмотрим некоторые виды иррациональных уравнений и методы их решения.
Уравнение вида=2n√f(x), где n∈N
Уравнение вида
Если 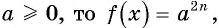
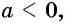
Пример №13
Решите уравнение:
Решение:
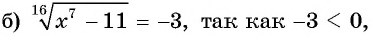
Ответ а) 81; б) нет корней; в) -4; 4.
- Заказать решение задач по высшей математике
Уравнение вида 2n+1√f(x)=a, где n∈N
Уравнение вида
Уравнение 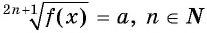
Пример №14
Решите уравнение:
Решение:
Ответ а) 125; б) -1.
Уравнение вида m√f(x)=g(x), m∈N, m>1
Уравнение вида
Пусть 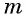
Рассмотрим способы решения уравнения вида
Первый способ.
Данное уравнение равносильно системе
Пример №15
Решите уравнение
Решение:
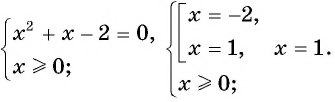
Второй способ.
Уравнение данного вида можно решить, возведя обе части уравнения в степень 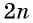
Пример №16
Решите уравнение
Решение:
Проверка: при 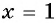
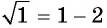
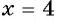
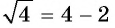
Если 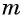
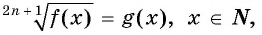
Пример №17
Решите уравнение
Решение:
Ответ: 1.
Уравнение вида m√f(x)=m√g(x), m∈N, m>1
Уравнение вида
Пусть 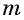
Рассмотрим способы решения уравнения вида
Первый способ.
Данное уравнение равносильно одной из систем
Пример №18
Решите уравнение
Решение:
Ответ: 1
Второй способ.
Уравнение этого вида можно решить, возведя обе части уравнения в степень 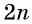
Пример №19
Решите уравнение
Решение:
Проверка: при 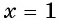
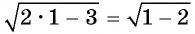
Ответ: нет корней.
Если 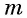
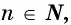
Пример №20
Решите уравнение
Решение:
Ответ: -1; 1.
Уравнение вида √f(x)±√g(x)=a
Уравнение вида
Первый способ.
Уравнение вида 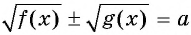
Пример №21
Решите уравнение
Решение:
Перенесем одно из слагаемых в правую часть, для того чтобы сократить преобразования.
Проверка: 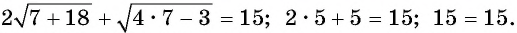
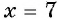
Ответ: 7.
Второй способ.
Некоторые уравнения этого вида можно решить, используя свойства функций.
Пример №22
Решите уравнение
Решение:
Функция 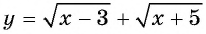
При 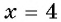
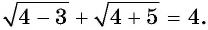
Ответ: 4.
Метод замены переменной
Пример №23
Решите уравнение
Решение:
Пусть 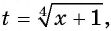
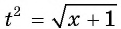
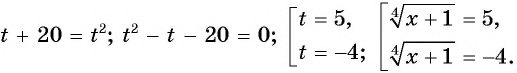
Тогда
Ответ: 624.
Пример №24
Решите уравнение
Решение:
Пусть 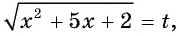
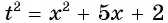
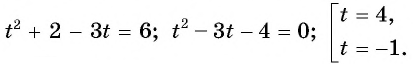
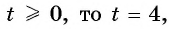
Ответ: -7; 2.
Примеры заданий и их решения
Пример №25
Решите уравнение:
Решение:
Ответ. 65.
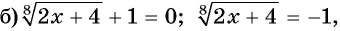
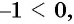
Ответ: нет корней.
Ответ:
Пример №26
Решите уравнение:
Решение:
Ответ: -5; 5.
Ответ:
Ответ. -2; 2.
Пример №27
Решите уравнение:
Решение:
Ответ: 3.
б) Возведем обе части уравнения в квадрат и получим:
Проверка: при 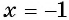
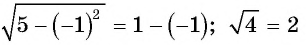
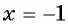
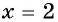
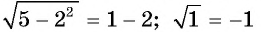
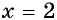
Ответ: -1.
Ответ: 0,5.
Пример №28
Решите уравнение:
Решение:
Ответ: -4.
б) Возведем обе части уравнения в квадрат и получим:
Проверка: при 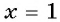
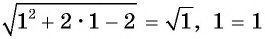
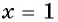
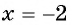
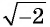
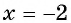
Ответ: 1.
Ответ: -1
Пример №29
Решите уравнение:
Решение:
а) Запишем уравнение в виде 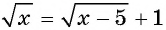
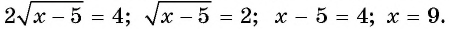
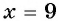
Ответ: 9.
б) Функция 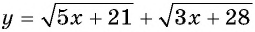
При 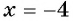
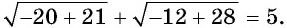
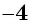
Ответ:
Пример №30
Решите уравнение
Решение:
Пусть 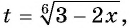
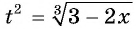
Второе уравнение совокупности не имеет корней. Тогда
Ответ.
При решении иррациональных уравнений используют прием возведения левой и правой частей уравнения в одну степень.
Теорема 9.
Возведение левой и правой частей уравнения в нечетную натуральную степень дает уравнение, равносильное данному, а возведение в четную степень — уравнение, являющееся следствием данного уравнения.
Доказательство:
Пусть 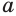
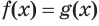
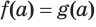
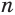
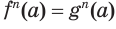
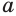
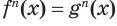
Поскольку каждый корень уравнения 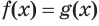
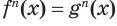
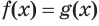
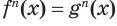
Пусть 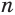
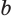
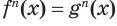
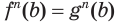
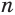
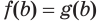
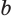
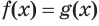
Поскольку при нечетном натуральном 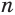
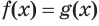
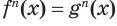
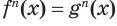
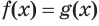
Пример №31
Решим уравнение
Данное уравнение равносильно уравнению 
Полученное квадратное уравнение имеет корнями числа -3 и 4. Сделаем проверку. Подставив числа -3 и 4 в данное уравнение, получим числовые равенства
из которых истинно только первое равенство.
Ответ. -3.
Этот пример иллюстрирует ту часть теоремы 9, в которой утверждается, что возведение в четную степень обеих частей уравнения дает уравнение, которое является следствием данного уравнения. Появление постороннего корня 4 связано с тем, что возведением в квадрат к уравнению 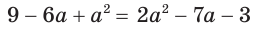
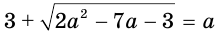
Вообще, при решении уравнений нужно быть внимательным к выполняемым преобразованиям. Полученные в результате решения числа включаются в ответ только в случае, когда все преобразования были преобразованиями равносильности.
Пример №32
Решим уравнение 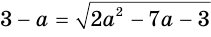
Некоторые иррациональные уравнения могут быть решены приемом введения вспомогательных переменных.
Пример №33
Решим уравнение 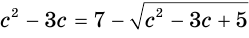
Обратим внимание на то, что данное уравнение равносильно уравнению 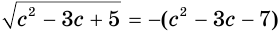
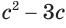
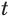
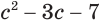
Тогда 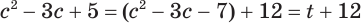
Это позволяет данное уравнение заменить уравнением 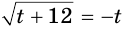
Вернемся к исходной переменной:
Полученное уравнение имеет корнями числа -1 и 4. Они и являются корнями исходного уравнения.
Ответ. -1; 4.
Иногда бывает удобно ввести две вспомогательные переменные.
Пример:
Решим уравнение 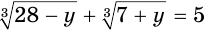
Обозначим 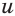
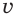
Тогда данное уравнение запишется как
Из системы (1) получим еще одно уравнение, связывающее переменные 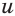
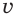
Таким образом, для нахождения значений переменных 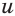
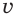
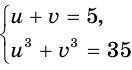
Теперь, чтобы найти значения исходной переменной, достаточно решить любое из уравнений системы (1).
Для 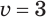
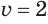
Анализ выполненных преобразований показывает, что все они являются преобразованиями равносильности. Поэтому оба полученных значения переменной 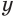
Ответ. 1; 20.
Пример №34
Решим систему уравнений
Обозначим 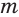
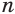
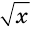
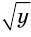
Выразим 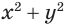
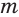
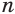
С учетом этого исходная система запишется так:
Поскольку 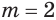
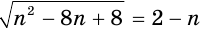
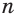
Учитывая, что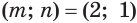
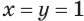
Ответ. (1; 1).
Иногда при решении системы бывает полезна тригонометрическая подстановка.
Пример №35
Решим систему уравнений 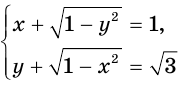
Обратим внимание на то, что модули переменных 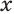
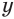
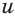
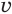
Выразим через них исходную систему и найдем ее решения:
При переходе (1) мы покомпонентно второе уравнение разделили на первое, при переходе (2) учли то, что поскольку 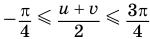
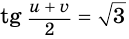
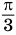
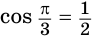
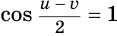
Вернувшись к исходным переменным, получим, что 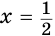
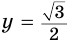
Ответ. 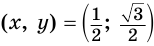
- Иррациональные неравенства
- Производная в математике
- Как найти производную функции
- Асимптоты графика функции
- Формулы двойного аргумента
- Формулы преобразования суммы и разности синусов (косинусов) в произведение
- Корень n-й степени из числа и его свойства
- Свойства и график функции y=ⁿ√x (n>1, n∈N)