Как найти все корни принадлежащие отрезку тригонометрия

В этой статье и постараюсь объяснить 2 способа отбора корней в тригонометрическом уравнение: с помощью неравенств и с помощью тригонометрической окружности. Перейдем сразу к наглядному примеру и походу дела будем разбираться.

а) Решить уравнение sqrt(2)cos^2x=sin(Pi/2+x)
б) Найдите все корни этого уравнения, принадлежащие промежутку [-7Pi/2; -2Pi]

Решим пункт а.

Воспользуемся формулой приведения для синуса sin(Pi/2+x) = cos(x)

sqrt(2)cos^2x = cosx

sqrt(2)cos^2x — cosx = 0

cosx(sqrt(2)cosx — 1) = 0

cosx = 0

x1 = Pi/2 + Pin, n ∈ Z

sqrt(2)cosx — 1 = 0

cosx = 1/sqrt(2)

cosx = sqrt(2)/2

x2 = arccos(sqrt(2)/2) + 2Pin, n ∈ Z
x3 = -arccos(sqrt(2)/2) + 2Pin, n ∈ Z

x2 = Pi/4 + 2Pin, n ∈ Z
x3 = -Pi/4 + 2Pin, n ∈ Z

Решим пункт б.

1) Отбор корней с помощью неравенств

Здесь все делается просто, полученные корни подставляем в заданный нам промежуток [-7Pi/2; -2Pi], находим целые значения для n.

-7Pi/2 меньше или равно Pi/2 + Pin меньше или равно -2Pi

Сразу делим все на Pi

-7/2 меньше или равно 1/2 + n меньше или равно -2

-7/2 — 1/2 меньше или равно n меньше или равно -2 — 1/2

-4 меньше или равно n меньше или равно -5/2

Целые n в этом промежутку это -4 и -3. Значит корни принадлежащие этому промежутку буду Pi/2 + Pi(-4) = -7Pi/2, Pi/2 + Pi(-3) = -5Pi/2

Аналогично делаем еще два неравенства

-7Pi/2 меньше или равно Pi/4 + 2Pin меньше или равно -2Pi
-15/8 меньше или равно n меньше или равно -9/8

Целых n в этом промежутке нет

-7Pi/2 меньше или равно -Pi/4 + 2Pin меньше или равно -2Pi
-13/8 меньше или равно n меньше или равно -7/8

Одно целое n в этом промежутку это -1. Значит отобранный корень на этом промежутку -Pi/4 + 2Pi*(-1) = -9Pi/4.

Значит ответ в пункте б: -7Pi/2, -5Pi/2, -9Pi/4

2) Отбор корней с помощью тригонометрической окружности

Чтобы пользоваться этим способом надо понимать как работает эта окружность. Постараюсь простым языком объяснить как это понимаю я. Думаю в школах на уроках алгебры эта тема объяснялась много раз умными словами учителя, в учебниках сложные формулировки. Лично я понимаю это как окружность, которую можно обходить бесконечное число раз, объясняется это тем, что функции синус и косинус периодичны.

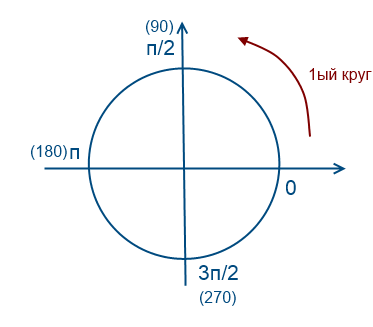
Обойдем раз против часовой стрелки

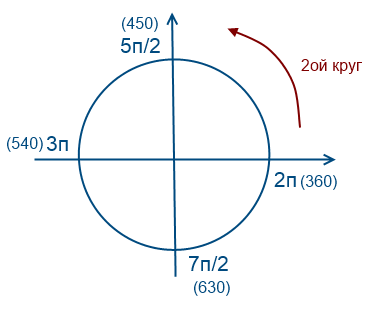
Обойдем 2 раза против часовой стрелки

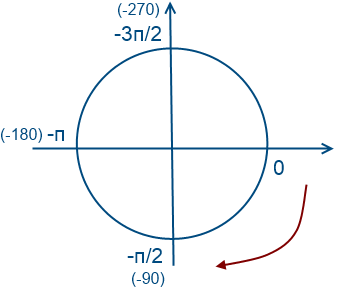
Обойдем 1 раз по часовой стрелки (значения будут отрицательные)

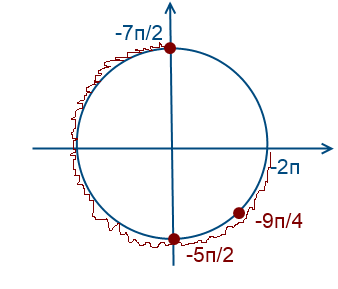
Вернемся к нашем вопросу, нам надо отобрать корни на промежутке [-7Pi/2; -2Pi]

Чтобы попасть к числам -7Pi/2 и -2Pi надо обойти окружность против часовой стрелки два раза. Для того, чтобы найти корни уравнения на этом промежутке надо прикидывать и подставлять.

Рассмотри x = Pi/2 + Pin. Какой приблизительно должен быть n, чтобы значение x было где-то в этом промежутке? Подставляем, допустим -2, получаем Pi/2 — 2Pi = -3Pi/2, очевидно это не входит в наш промежуток, значит берем меньше -3, Pi/2 — 3Pi = -5Pi/2, это подходит, попробуем еще -4, Pi/2 — 4Pi = -7Pi/2, также подходит.

Рассуждая аналогично для Pi/4 + 2Pin и -Pi/4 + 2Pin, находим еще один корень -9Pi/4.

Сравнение двух методов.

Первый способ (с помощью неравенств) гораздо надежнее и намного проще для пониманию, но если действительно серьезно разобраться с тригонометрической окружностью и со вторым методом отбора, то отбор корней будет гораздо быстрее, можно сэкономить около 15 минут на экзамене.

Просмотры: 158965 |
Статью добавил: slava191 |
Категория: математика

Тригонометрические уравнения

В данной статье мы расскажем об основных типах тригонометрических уравнений и методах их решения. Тригонометрические уравнения чаще всего встречаются в задаче 12 ЕГЭ.

В вариантах ЕГЭ задача, где нужно решить уравнение, состоит из двух пунктов. Первый пункт – решение самого уравнения. Второй – нахождение его корней на некотором отрезке.

Некоторые из методов (например, замена переменной или разложение на множители) являются универсальными, то есть применяются и в других разделах математики. Другие являются специфическими именно для тригонометрии.

Необходимых формул по тригонометрии не так уж и много. Учите наизусть!
Тригонометрические формулы.

Любой метод решения тригонометрических уравнений состоит в том, чтобы привести их к простейшим, то есть к уравнениям вида sin x = a, cos x = a, tg x = a, ctg x = a.

Если вы не помните, как решать простейшие тригонометрические уравнения, — читайте материал на нашем сайте: Простейшие тригонометрические уравнения, часть 1.

О том, что такое арксинус, арккосинус, арктангенс и арккотангенс, — еще одна статья на нашем сайте: Простейшие тригонометрические уравнения,часть 2.

Теперь — сами методы. Теория и примеры решения задач.

к оглавлению ▴

Замена переменной и сведение к квадратному уравнению

Это универсальный способ. Применяется в любых уравнениях — степенных, показательных, тригонометрических,  логарифмических, каких угодно. Замена не всегда видна сразу, и уравнение нужно сначала преобразовать.

1. а) Решите уравнение:
б) Найдите корни уравнения, принадлежащие отрезку

Решение:

а) Рассмотрим уравнение

Преобразуем его, применив основное тригонометрическое тождество:

Заменяя sin x на t, приходим к квадратному уравнению:

Решая его, получим:

Теперь вспоминаем, что мы обозначили за t. Первый корень приводит нас к уравнению 
Оно не имеет решений, поскольку

Второй корень даёт простейшее уравнение

Решаем его:

б) Найдем корни уравнения на отрезке с помощью двойного неравенства.

Разделим обе части неравенства на

Вычтем из обеих частей неравенства:

Разделим на 2 обе части неравенства:

Единственное целое решение – это n=0. Тогда — это единственный корень, который принадлежит отрезку

Ответ:

2. а) Решите уравнение:
б) Укажите корни этого уравнения, принадлежащие отрезку

Решение:

а)

Выразим косинус двойного угла по формуле

Получим:

Заменяя cos⁡x на t, приходим к квадратному уравнению:

1)

2) нет решений, т. к.

Получим:

б) Отметим отрезок и найденные серии решений на единичной окружности.

Видим, что данному отрезку принадлежит только точка

Ответ: а)
б)

3. а) Решите уравнение: 
б) Найдите все корни этого уравнения, принадлежащие отрезку 

Решение:

а)  Чтобы упростить уравнение  применяем формулу приведения.

Так как  получим:

Сделаем замену:    Получим квадратное уравнение:

Сделаем обратную замену.

1)  — нет решений, т. к.  

2) 

б) Найдем корни уравнения, принадлежащие отрезку , с помощью двойного неравенства.

Для серии решений получим:

Так как то

Для серии решений получим:

отсюда

У этого неравенства нет целых решенией, и значит, из второй серии ни одна точка в указанный отрезок не входит.

Ответ: а)
б)

к оглавлению ▴

Разложение на множители

Во многих случаях уравнение удаётся представить в таком виде, что в левой части стоит произведение двух или нескольких множителей, а в правой части — ноль. Произведение двух или нескольких множителей равно нулю тогда и только тогда, когда хотя бы один из них равен нулю. Сложное уравнение, таким образом, распадается в совокупность более простых.

4. а) Решите уравнение:
б) Найдите все корни уравнения на отрезке

Решение:

а) Применяем формулу синуса двойного угла:

Ни в коем случае не сокращайте на косинус! Ведь может случиться, что cos x обратится в нуль, и мы потеряем целую серию решений. Переносим всё в одну часть, и общий множитель выносим за скобки:

Полученное уравнение равносильно совокупности двух уравнений: cosx = 0 и 2sinx — 1 = 0.

Получим:

Все эти три серии решений являются ответом в части (а).

б) Отметим отрезок и найденные серии решений на единичной окружности.

Видим, что данному отрезку принадлежат точки

Ответ: а)
б)

5. а) Решите уравнение:
б) Найдите все корни уравнения на отрезке

Решение:

Применим формулу суммы синусов:

Дальше действуем так же, как и в предыдущей задаче:

Решаем уравнение :

(1)

Решаем уравнение :

(2)

Ну что, перечисляем обе серии (1) и (2) в ответе через запятую? Нет! Серия (2) является в данном случае частью серии (1). Действительно, если в формуле (1) число n кратно 5, то мы получаем все решения серии (2).

Поэтому ответ в пункте (а):

б) Найдем корни уравнения, принадлежащие отрезку с помощью двойного неравенства:

Этот промежуток содержит 8 целых чисел: -2; -1; 0; 1; 2; 3; 4; 5.

Для каждого из этих n найдем x. Получим 8 решений на данном промежутке:

Ответ: а)
б)

6. В следующей задаче также применяется метод разложения на множители. Но это заметно не сразу.

а) Решите уравнение:
б) Найдите все корни уравнения на отрезке

Решение:

Используем формулу понижения степени:

Получаем:

Применяем формулу суммы косинусов:

Получаем:

Произведение двух множителей равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю, а другой при этом имеет смысл. Уравнение равносильно совокупности:

б) Найдем корни уравнения, принадлежащие отрезку с помощью двойного неравенства:

1)

Решив неравенство, получим:

Так как n ∈ Z, получим для n целые значения: 0, 1, 2.

Им соответствуют решения:

2) Из серии решений на указанном отрезке лежит только корень Но он уже входит в первую серию решений.

Можно также заметить, что вся вторая серия решений является подмножеством первой.

Ответ: а)
б)

к оглавлению ▴

Однородные уравнения

7. а) Решите уравнение:
б) Найдите все корни уравнения на отрезке

Решение:

Такое уравнение называется однородным.

Степень каждого слагаемого в левой части равна двум. Точно так же, как в обычном многочлене степень каждого слагаемого равна двум. Мы помним, что степень одночлена — это сумма степеней входящих в него сомножителей.

Для однородных уравнений существует стандартный приём решения — деление обеих его частей на .

Возможность этого деления, однако, должна быть обоснована: а что, если косинус равен нулю?

Следующий абзац предлагаем выучить наизусть и всегда прописывать его при решении однородных уравнений.

Предположим, что cosx = 0. Тогда в силу уравнения и sinx = 0, что противоречит основному тригонометрическому тождеству. Следовательно, любое решение данного уравнения удовлетворяет условию cosx 0, и мы можем поделить обе его части на .

В результате деления приходим к равносильному квадратному уравнению относительно тангенса:

Сделаем замену: получим:

б) Отметим отрезок  и найденные серии решений на единичной окружности.

О том, как отметить на единичной окружности точки из первой серии решений, то есть арктангенс минус трех, читайте здесь: Простейшие тригонометрические уравнения, часть 2.

Видим, что данному отрезку принадлежат  точки:

Ответ: а) 
б) 

8. а) Решите уравнение:
б) Найдите все корни уравнения на отрезке

Если бы в правой части стоял нуль, уравнение было бы однородным. Мы поправим ситуацию изящным приёмом: заменим число 3 на выражение

Получили однородное уравнение второй степени.

Так как не существует такой точки на единичной окружности, в которой одновременно синус и косинус равнялись бы нулю, мы разделим обе части уравнения на .

Получим: 

Выполним замену: tgx = y, получим:

Обратная замена: 

Ответом в пункте (а) являются  две серии решений.

б) Найдем корни уравнения, принадлежащие отрезку  с помощью единичной окружности. Для этого отметим на ней данный отрезок и  найденные серии решений.

Видим, что данному отрезку принадлежит только точка 

Ответ: а)
б) 

к оглавлению ▴

Введение дополнительного угла

Этот метод применяется для уравнений вида acosx + bsinx=c. Он присутствует в школьных учебниках. Правда, в них рассматриваются только частные случаи — когда числа a и b являются значениями синуса и косинуса углов в 30°, 45° или 60°.

9. а) Решим уравнение: 
б) Найдите все корни уравнения на отрезке 

Решение:

Делим обе части на 2:

Замечаем, что

В левой части получили синус суммы:

отсюда 

б) Отметим на единичной окружности отрезок  и найденные серии решений.

Обратите внимание, что в этой задаче отрезок больше, чем полный круг. Как нам поступить? Один из способов – нарисовать рядом две окружности.

Видим, что данному отрезку принадлежат точки:

Ответ: а) 
б)

Другой пример.

10. а) Решите уравнение: 
б) Найдите все корни уравнения на отрезке 

Решение:

Делим обе части на 

Сделаем теперь для разнообразия в левой части косинус разности:

б) Найдем корни уравнения, принадлежащие отрезку  с помощью единичной окружности. Отметим на ней данный отрезок и найденные серии решений.

Видим, что данному отрезку принадлежат  точки 0 и 

Ответ: а) 
б)  

Покажем, как применяется метод введения дополнительного угла в общем случае.

Рассмотрим  уравнение 

Делим обе части на

(4)

Для чего мы выполнили это деление? Всё дело в получившихся коэффициентах при косинусе и синусе. Легко видеть, что сумма их квадратов равна единице:

Это означает, что данные коэффициенты сами являются косинусом и синусом некоторого угла :

Соотношение (4) тогда приобретает вид:

или

Исходное уравнение сведено к простейшему. Теперь понятно, почему рассматриваемый метод называется введением дополнительного угла. Этим дополнительным углом как раз и является угол

к оглавлению ▴

Универсальная подстановка

Запомним две важные формулы:

Их ценность в том, что они позволяют выразить синус и косинус через одну и ту же функцию — тангенс половинного угла. Именно поэтому они получили название универсальной тригонометрической подстановки. 

Единственная неприятность, о которой не надо забывать: правые части этих формул не определены при . Поэтому если применение универсальной подстановки приводит к сужению ОДЗ, то данную серию нужно проверить непосредственно.

11. а) Решите уравнение: 
б) Найдите все корни уравнения на отрезке 

Решение:

Выражаем , используя универсальную тригонометрическую подстановку:

Делаем замену  :

Получаем кубическое уравнение:

Оно имеет единственный корень .

Стало быть, , откуда .

Сужения ОДЗ в данном случае не было, так как уравнение с самого начала содержало .

б) Найдем корни уравнения, принадлежащие отрезку    с помощью двойного неравенства:

Получим, что

Ответ: а)
б) 

Универсальная тригонометрическая подстановка может также пригодиться при решении задач по планиметрии из второй части ЕГЭ. Поэтому формулы лучше выучить.

к оглавлению ▴

Учет ОДЗ уравнения

12. а) Рассмотрим уравнение: 
б) Найдите все корни уравнения на отрезке 

Решение:

Перепишем уравнение в виде, пригодном для возведения в квадрат:

Тогда наше уравнение равносильно системе:

Решаем уравнение системы:

,

,

Второе уравнение данной совокупности не имеет решений, а первое даёт две серии:

Теперь нужно произвести отбор решений в соответствии с неравенством . Серия  не удовлетворяет этому неравенству, а серия удовлетворяет ему. Следовательно, решением исходного уравнения служит только серия .

Ответ в пункте (а):  .

б) Найдем корни уравнения, принадлежащие отрезку  с помощью двойного неравенства:

Неравенство имеет единственное целое решение 

Тогда 

Ответ: а)
б) 

Мы рассмотрели основные методы решения тригонометрических уравнений, которые применяются в задаче 12 ЕГЭ.

Где же еще нам могут встретиться тригонометрические уравнения? Конечно, в задачах с параметрами. Или на олимпиадах по математике. Сейчас мы увидим еще несколько полезных приемов решения.

к оглавлению ▴

Метод оценки

В некоторых уравнениях на помощь приходят оценки .

13. Рассмотрим уравнение: 

Так как оба синуса не превосходят единицы, данное равенство может быть выполнено лишь в том случае, когда они равны единице одновременно:

Таким образом, должны одновременно выполняться следующие равенства:

Обратите внимание, что сейчас речь идёт о пересечении множества решений (а не об их объединении, как это было в случае разложения на множители). Нам ещё предстоит понять, какие значения x удовлетворяют обоим равенствам. Имеем:

Умножаем обе части на 90 и сокращаем на π:

;

;

Правая часть, как видим, должна делиться на 5. Число n при делении на 5 может давать остатки от 0 до 4; иначе говоря, число n может иметь один из следующих пяти видов: 5n, 5m + 1, 5m + 2, 5m + 3 и 5m + 4, где. Для того, чтобы 9n+ 1 делилось на 5, годится лишь n = 5m + 1.

Искать k, в принципе, уже не нужно. Сразу находим x:

Ответ:

14. Рассмотрим уравнение: 

Ясно, что данное равенство может выполняться лишь в двух случаях: когда оба синуса одновременно равны 1 или −1. Действуя так, мы должны были бы поочерёдно рассмотреть две системы уравнений.

Лучше поступить по-другому: умножим обе части на 2 и преобразуем левую часть в разность косинусов:

;

Тем самым мы сокращаем работу вдвое, получая лишь одну систему:

Имеем:

Ищем пересечение:

Умножаем на 21 и сокращаем на π:

Данное равенство невозможно, так как в левой части стоит чётное число, а в правой — нечётное.

Ответ: решений нет.

Это был тренировочный пример. А в задачах ЕГЭ решения есть всегда.

Посмотрите, как применяется метод оценки в задачах с параметрами.

15. Страшное с виду уравнение  также решается методом оценок.

В самом деле, из неравенства  следует, что .

Следовательно, , причём равенство возможно в том и только в том случае, когда

Остаётся решить полученную систему. Это не сложно.

Перенесем в левую часть и вынесем общий множитель за скобки ,  получим:

Произведение равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю, а другой при этом имеет смысл.

Каждое уравнение равносильно совокупности:

Это значит, что синус угла х равен нулю, а его косинус равен 0, 1 или -1.

Или синус угла х равен 1, а косинус этого угла равен 0, 1 или -1.

Такие углы легко найти на тригонометрическом круге. Найденные серии решений запишем в ответ.

Ответ: 

к оглавлению ▴

Тригонометрические уравнения повышенной сложности.
Приемы решения

16. Рассмотрим такое уравнение: 

Сделаем замену .

Как выразить  через t? Имеем:

,

откуда . Получаем:

Начнем со второго уравнения.

Так как  и   то их сумма может быть равна 2, только оба слагаемых равны 1. Но на единичной окружности не существует точки, в которой одновременно синус и косинус равен единице. Значит, второе уравнение корней не имеет.

Решим первое уравнение методом введения дополнительного угла.

Для этого разделим обе части уравнения на  и получим:

Ответ: 

17. Помним формулы косинуса и синуса тройного угла:

,

Вот, например, уравнение:

Оно сводится к уравнению относительно :

,

,

Произведение двух множителей равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю, а другой при этом имеет смысл. Уравнение равносильно совокупности:

Решим второе уравнение с помощью замены sinx = t.

Получим:  или 

Обратная замена:

А решением первого уравнения sinx = 0 являются числа вида 

Ответ: 

Интересно, что формулы синуса и косинуса тройного угла также могут пригодиться вам в решении задач по планиметрии из второй части ЕГЭ.

18. Как бороться с суммой четвёртых степеней синуса и косинуса?

Рассмотрим уравнение: 

Выделяем полный квадрат!

;

;

;

;

;

;

19. А как быть с суммой шестых степеней?

Рассмотрим такое уравнение: 

Раскладываем левую часть на множители как сумму кубов: .

Получим:

;

С суммой четвёртых степеней вы уже умеете обращаться.

Мы рассмотрели основные методы решения тригонометрических уравнений. Знать их нужно обязательно, это — необходимая база.

В более сложных и нестандартных задачах нужно ещё догадаться, как использовать те или иные методы. Это приходит только с опытом. Именно этому мы и учим на наших занятиях.

Одно из заданий второй части ЕГЭ по математике — решение тригонометрических уравнений с корнем. Основная его сложность в том, что нужно уметь не только упрощать выражения и находить ответ, но и проводить отбор корней. Как это сделать, мы разберем в статье. 

Что такое тригонометрическое уравнение

Тригонометрическое уравнение содержит в себе функцию синуса, косинуса, тангенса или котангенса. Решение без отбора корней происходит по следующим формулам: 

• sinx = a при |a| ≤ 1 → x = (-1)narcsina + πn;

• cosx = a при |a| ≤ 1 → x = ± arccosa + 2πn;

• tgx = b при b — любое число → x = arctgb + πn;

• сtgx = b при b — любое число → x = arcсtgb + πn.

Многие корни тригонометрических уравнений имеют конечные значения. Например, при sinx = -1 ответ следующий: x = π/2 + 2πn. Полная таблица достаточно большая, поэтому ее мы приводить тут не будем. 

Отбор 

Прежде чем изучить методы отбора корней, решим один несложный пример. 

Задание. 

а) Решите cos2x — 3cosx + 2 = 0

б) Найдите все ответы, принадлежащие отрезку -4; —52

Решение. 

Первое слагаемое распишем по формуле косинуса двойного угла: 

2cos2x — 1 — 3cosx + 2 = 0

Приведем однородные слагаемые: 

2cos2x — 3cosx + 1 = 0

Произведем замену: 

Пусть cosx = t, где |t| ≤ 1

Получаем: 

2t2 — 3t + 1 = 0

Находим дискриминант: 

D = (-3)2 — 4 • 2 • 1 = 9 — 8 = 1

Решаем:

x1=3+122=44=1

x2=3-122=24=12

Возвращаемся к исходной переменной и получаем: 

cosx = 1 → x = 2πn, n ∈ Z

cosx = ½ → x = ± π/3 + 2πk, k ∈ Z

Области допустимых значений нет, поэтому оба значения используем при решении пункта «б».

Теперь проведем отбор корней разными способами.

Арифметический

Для решения нужно перебирать все значения целочисленного параметра и считать корни. Разберем на примере cosx = 1.

Решение. x = 2πn

При n = -1 получаем x = 2 • (-1)π = -2π = -4π/2. Это больше, чем -5π/2, следовательно, ответ: не принадлежит отрезку.

При n = -2 получаем x = 2 • (-2)π = -4π. Число принадлежит отрезку.

При n = -3 получаем x = 2 • (-3)π = -6π. Это меньше, чем -4π, следовательно, значение не принадлежит отрезку. 

Далее то же самое нужно сделать с остальными корнями. Тогда вы получите ответ. 

Алгебраический

Чтобы отобрать корни, нужно решить неравенства относительно известного целочисленного параметра. Рассмотрим на примере первого значения. 

Решение. -4π ≤ 2πn ≤ -5π/2

Делим все части неравенства на «2π»: 

-2 ≤ n ≤ -5/4

Согласно условию, n ∈ Z. Рассматриваем только ответ n = -2. Получаем x = -4π.

Геометрический

Рисуем единичную окружность, наносим на нее числа из области и корни. После определяем, попадают ли они в промежуток. Отсчет промежутка происходит против часовой стрелки!

По рисунку видно, что в указанный промежуток попадает два корня. Первый: -4π. Второй нужно посчитать. Для этого к «-4π» мы прибавляем «π/3». Получаем: -11π/3. 

Функционально-графический

Для решения нарисуем функцию косинуса на области от y = -1 до y = 0,5. Зная значения промежутка, найдем абсциссы точек пересечения на заданном отрезке. 

Как видно по рисунку, у нас получаются те же корни, что и в предыдущем методе. 

Теперь вы знаете основные способы отбора корней в тригонометрических уравнениях. Это поможет вам правильно решать задания из второй части. Дома вам сложно практиковаться, не хватает помощи учителя? Тогда записывайтесь на курсы подготовки к ЕГЭ в центре «Уникум» при Российском университете дружбы народов. Центр предлагает не только полезные уроки с экспертами ЕГЭ, но и доступ к учебному порталу. На нем вы сможете делать домашние задания, решать пробные варианты экзамена и изучать полезные материалы. Форматы курсов разные  — очный и дистанционный. 

Содержание данной статьи носит ознакомительный характер. Для подготовки к сдаче ЕГЭ пользуйтесь дополнительными источниками информации!

Всероссийский конкурс для школьных педагогов на лучшую образовательную статью «Просто о сложном»

Автор Лисицына Елена Федоровна.

учитель математики

МБОУ «Гимназия№11»

г. Бийска Алтайского кр.

Методы отбора корней в тригонометрических уравнениях

или

Ох уж эта тригонометрия!

Решение тригонометрических уравнений и отбор корней, принадлежащих заданному промежутку — это одна из сложнейших тем математики, которая выносится на Единый Государственный Экзамен в течение уже более 10лет. По результатам анкетирования многие учащиеся затрудняются или вообще не умеют решать тригонометрические уравнения и особенно затрудняются в отборе корней, принадлежащих промежутку. Необходимо также знать тригонометрические формулы, табличные значения тригонометрических функций для решения еще целого ряда заданий Единого Государственного Экзамена по математике. Постоянно работая в 10-11 классах, я регулярно сталкивалась с определенными проблемами при работе с вышеуказанным разделом тригонометрии: долго не могла установить баланс между доступностью изложения материала и достаточностью обоснований развернутого решения этой категории заданий. В моей практике были случаи, когда вполне успевающие по математике учащиеся начинали испытывать неуверенность и просто страх при решении тригонометрических уравнений с отбором корней, будь то принадлежность корней области допустимых значений переменной или указанному в задании промежутку. В результате целенаправленной многолетней работы в этом направлении у меня сложилась определенная методика работы с данным разделом, которая оказалась довольно успешной, что подтверждает следующая таблица результатов выполнения учащимися задания №13 профильного ЕГЭ по математике с 2015 по 2021 г.г. ( в % от общего количества учеников 11-х классов гимназии, сдающих профильный ЕГЭ по математике)

В тригонометрическом уравнении отбор корней можно осуществлять следующими способами: арифметическим, алгебраическим, геометрическим и функционально-графическим.

Арифметический способ отбора корней состоит в непосредственной подстановке полученных корней в уравнение, учитывая имеющиеся ограничения, при переборе значений целочисленного параметра.

Алгебраический способ предполагает составление неравенств, соответствующих дополнительным условиям, и их решение относительно целочисленного параметра.

Геометрический способ предполагает использование при отборе корней двух вариантов: тригонометрического круга или числовой прямой. Тригонометрический круг более удобен, когда речь идет об отборе корней на промежутке или в случае, когда значение обратных тригонометрических функций, входящих в решения, не являются табличными. Числовую прямую удобно использовать при отборе корней на промежутке, длина которого превосходит полный оборот или требуется найти наибольший отрицательный или наименьший положительный корень уравнения.

Функционально-графический способ предполагает отбор корней осуществлять с использование графиков тригонометрических функций. Чтобы использовать данный способ отбора корней, требуется умение схематичного построения графиков тригонометрических функций.

Моя практика показала, что чаще всего можно обойтись применением тригонометрического круга при отборе корней , а в случае, если промежуток превышает по длине полный оборот- алгебраическим способом. При этом, безусловно, следует познакомить учащихся и с остальными способами. Таким образом, работа над данным разделом разделилась у меня на следующие этапы:

1)Знакомство с устройством тригонометрического круга и отработка умений находить числа и промежутки на нем в ходе выполнения следующих упражнений:

2)Отработка навыков работы с тригонометрическим кругом при решении простейших тригонометрических уравнений с отбором корней , которая предполагает выполнение большого количества упражнений по типу приведенных ниже:

3)Отбор корней в одном и том же уравнении разными способами, чтобы учащиеся имели возможность выбора в соответствии со своими предпочтениями, например

Например,
а) Решить уравнение cos2x=sin(π/2+x).
б) Найдите все корни этого уравнения, принадлежащие промежутку [–7π/2; –2π].

Решим пункт а)Воспользуемся формулой приведения для синуса sin(π/2+x) = cos(x);cos2x = cosx ;
cos2x – cosx = 0; cosx(cosx – 1) = 0, т.е.

Решим пункт б).

I . Отбор корней с помощью неравенств

Здесь все делается просто, полученные корни подставляем в заданный нам промежуток [–7π/2; –2π], находим целые значения для n.
–7π/2 ≤ π/2 + πn ≤ –2π;

Сразу делим все на π или умножаем на 1/ π
–7/2 ≤ 1/2 + n ≤ –2;
–7/2 – 1/2 ≤ n ≤ –2 – 1/2 ;
–4 ≤ n ≤ –5/2.
Целые n в этом промежутке это: n=–4 n= –3.

Значит, корни, принадлежащие этому промежутку, будут следующие:

х= π/2 + π(–4) = –7π/2; х=π/2 + π(–3) = –5π/2.
Аналогично решаем еще два неравенства:
–7π/2 ≤ π/4 + 2πk ≤ –2π;
–15/8 ≤ k ≤ –9/8.
Получили, что целых k в этом промежутке нет.
–7π/2 ≤ –π/4 + 2πm ≤ –2π;
–13/8 ≤ m ≤ –7/8.
Получили одно целое n в этом промежутке, m =–1. Значит, отобранный корень на этом промежутке имеет вид: х= –π/4 + 2π·(–1) = –9π/4.
Ответ: –7π/2, –5π/2, –9π/4.

II. Отбор корней с помощью тригонометрической окружности.

Чтобы использовать этот способ надо понимать, как работать с окружностью. Так как функции синус, косинус, тангенс и котангенс периодичны, то окружность, можно обходить бесконечное число раз.

«Обойдем» окружность один раз против часовой стрелки (положительное направление, т.е. значения будут положительные)

«Обойдем» окружность два раза против часовой стрелки (положительное направление т.е. значения будут положительные)

«Обойдем» 1 раз по часовой стрелки (отрицательное направление, т.е. значения будут отрицательные)

Вернемся к вопросу об отборе корней на промежутке

[–7π/2; –2π].
Чтобы попасть к числам –7π/2 и –2π надо «обойти» окружность против часовой стрелки два раза. Для того, чтобы найти корни уравнения на этом промежутке надо прикидывать и подставлять.

Рассмотри x = π/2 + πn. Какой приблизительно должен быть n, чтобы значение x было где–то в этом промежутке? Предположим n= –2, получаем х=π/2 – 2π = –3π/2, очевидно, это не входит в наш промежуток. Значит, берем меньше n=–3, то х= π/2 – 3π = –5π/2, это подходит. Попробуем еще n=–4, то х=π/2 – 4π = –7π/2, также подходит.
Рассуждая аналогично для х=π/4 + 2πk, k ∈ Z и х=–π/4 + 2πm, m ∈ Z находим еще один корень x=–9π/4.

После того, как отбор корней произвели разными способами, прошу проанализировать преимущества каждого из них, получились, в частности такие итоги: первый способ (с помощью неравенств) гораздо надежнее и намного проще для понимания, но нужно уметь решать простейшие неравенства. Если действительно серьезно разобраться с тригонометрической окружностью, то отбор корней по второму методу будет гораздо быстрее. Плюс экономия времени на экзамене.

4)Проведение смотра знаний по данной теме в форме математической игры «Своя игра»

(идея заимствована здесь https://kopilkaurokov.ru/matematika/uroki/okh-uzh-eta-trighonomietriia )

5)Рассмотрение реальных работ участников ЕГЭ прошлых лет, оцененных экспертами, с целью нахождения ошибок при выполнении отбора корней в тригонометрических уравнениях, например оценка эксперта-1 балл. Почему не засчитано решение п.б)?

Вывод: отбор корней нельзя назвать обоснованным, так как перебор остановлен на корне принадлежащем отрезку.

Вывод: при отборе корней отсутствует решение и ошибочно указано число, которое не является корнем тригонометрического уравнения.

В заключение отмечу, что поскольку задание № 13 (или №12 в модели профильного ЕГЭ 2022 года) является самым простым из заданий с развернутым решением, то целенаправленная работа над ним дает возможность большему числу выпускников успешно справиться с ним и получить высокий результат на экзамене.

Список используемых ресурсов:

1. Виленкин Н. Я. Алгебра и математический анализ 10 класс. Учебник для углубленного изучения математики в общеобразовательных учреждениях, Издательство Мнемозина, 13-е изд. стереотипное, 2006. — 336с.

2. Гельфанд И.М., Львовский С.М., Тоом А.Л. Тригонометрия, М. : МЦНМО, 2003.-7-16 с.

3. Захарова, И. Г. Информационные технологии в образовании: учебное пособие для студ. пед. учеб. заведений/ И. Г. Захарова,– М.: Издательский центр «Академия», 2003. – 192 с.

4. Звавич В.И., Пигарев Б.П. Тригонометрические уравнения (решение уравнений + варианты самостоятельных работ)//Математика в школе.№3, С.18-27.

5. А.Н. Колмагорова Алгебра и начала анализа. Учебник для 10-11 классов общеобразовательных учреждений, 17-е изд. – М. : Просвещение, 2008. — 384 с.

6. Королев С.В. Тригонометрия на экзамене по математике, изд. Экзамен, 2006. – 254 с.

7. Марасанов А.Н. О методологическом подходе в обучении тригонометрии/ Н.И. Попов, А.Н. Марасанов// Знание и понимание. Умение. -2008. — №4. — 139-141 с.

8. Марасанов А.Н. Тригонометрия: учебное пособие, 2-е изд., испр и доп. (Н.И. Попов, А.Н. Марасанов.-Йошкар-Ола; Мар. гос. Ун-т, 2009.-114с.)

9. Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б. Тригонометрия. 10 класс, М. : Просвещение, 2008. – 61 с.

10. Мордкович А.Г. Алгебра и начала анализа.10-11 классы. Часть 1.Учебник для учащихся общеобразовательных учреждений(базовый уровень). – 10-е изд., стер. – М. : Мнемозина, 2009. – 399 с.:ил.

11. Мордкович А.Г. Алгебра и начала анализа.10-11 классы. Часть 2. Задачник для учащихся общеобразовательных учреждений(базовый уровень), – 10-е изд., стер. – М. : Мнемозина, 2009. – 399 с.:ил. 69

12. Мирошин В. Отбор корней в тригонометрических уравнениях.//Математика. Приложение к газете «Первое сентября» №17, 2006г.

13. Просветов Г.И. Тригонометрия. Задачи и решения, Альфа-Пресс, 2010. – 72 с.

14. Решетников Н.Н. Тригонометрия в школе: М. Педагогический университет «Первое сентября», 2006, лк 1.

15. Смоляков А.Н., Севрюков П.Ф. Приемы решения тригонометрических уравнений//Математика в школе. 2004. №1. С.24-26.

16. Шабашова О.В. Приемы отбора корней в тригонометрических уравнениях//Математика в школе. 2004. №1. С.20-24.

17. https://ppt-online.org/491236

18. Методические материалы для председателей и членов предметных комиссий субъектов Российской Федерации по проверке выполнения заданий с развёрнутым ответом экзаменационных работ ЕГЭ 2022 года. МАТЕМАТИКА. Федеральный институт педагогических измерений, 2022

19. https://kopilkaurokov.ru/matematika/uroki/okh-uzh-eta-trighonomietriia