В принципе все уже изложено в предыдущих разделах. Однако описанная схема может быть достаточно трудоемкой из-за того, что некоторые вычисления будут несколько раз повторяться. Покажем, как этих повторений можно избежать.
Пусть задана СЛАУ Ax = b. Запишем ее расширенную матрицу (A | b). Каждому элементарному преобразованию строк расширенной матрицы соответствует аналогичное преобразование уравнений в исходной СЛАУ:
а) умножение i-й строки матрицы на число λ ≠ 0 означает умножение i-го уравнения СЛАУ на это же число;
б) перестановке i-й и k-й строк в матрице отвечает перестановка i-го и k-го уравнений СЛАУ;
в) добавление к i-й строке матрицы ее k-й строки равнозначно замене i-го уравнения его суммой с k-м уравнением СЛАУ.
Указанные преобразования СЛАУ не изменяют множество решений этой СЛАУ. Поэтому приведение расширенной матрицы системы к ступенчатому виду с помощью элементарных преобразований ее строк означает сведение самой СЛАУ к эквивалентной системе, имеющей ступенчатую матрицу.
Итак, сначала приводим расширенную матрицу (A | b) заданной СЛАУ с помощью элемен-тарных преобразований строк к ступенчатому виду (A’ | b’). При этих преобразованиях ранги матриц не меняются, поэтому Rg(A | b) = Rg(A’ | b’), а Rg A = Rg A’. Ранги матриц A’ и (A’ | b’) равны количеству их ненулевых строк. Если эти ранги равны, то по теореме 13.1 Кронекера — Капелли СЛАУ совместна, а в противоположном случае — несовместна.
Приведение расширенной матрицы СЛАУ к ступенчатому виду преследует две цели: во-первых, позволяет проверить, является ли система совместной; во-вторых, если СЛАУ совместна, мы ее сводим к более простому виду.
Предположим, что, решаемая система совместна. В матрице A’ ступенчатого вида выбираем базисный минор и фиксируем соответствующие ему базисные и свободные неизвестные (см. 12.3). В матрице (A’| b’) ступенчатого вида отбрасываем нулевые строки (им соответствуют тривиальные уравнения) и по получившейся матрице восстанавливаем СЛАУ. В уравнениях этой СЛАУ слагаемые со свободными неизвестными переносим в правые части и получаем систему, матрица которой является верхней треугольной и невырожденной, так как ее определитель совпадает с базисным минором матрицы A’. Последовательно исключая неизвестные, выражаем базисные неизвестные через свободные. Свободные неизвестные обозначаем как произвольные постоянные и записываем общее решение СЛАУ в виде линейной комбинации столбцов, выделяя в правых частях полученных выражений в отдельные столбцы: а) свободные члены; б) коэффициенты при каждой произвольной постоянной. В этой записи столбец свободных членов есть частное решение СЛАУ, а столбцы при произвольных постоянных образуют нормальную фундаментальную систему решений однородной СЛАУ, соответствующей заданной неоднородной системе.
Если исходная СЛАУ является однородной, то изложенный метод решения чуть упрощается, поскольку в расширенной матрице последний столбец является всегда нулевым и не меняется при элементарных преобразованиях строк. Имея это в виду, его опускают, т.е. все преобразования проводят с матрицей системы.
Пример 14.1. Решим однородную СЛАУ
Чтобы найти общее решение, запишем матрицу системы и преобразуем ее при помощи эле-ментарных преобразований строк к ступенчатому виду:
Базисный минор в преобразованной матрице стоит вверху слева и имеет второй порядок.
Это значит, что ранг r матрицы системы равен двум, фундаментальная система решений со
стоит из n — r = 4 — 2 = 2 решений, а сама СЛАУ эквивалентна следующей системе, которая соответствует преобразованной матрице:
Базисными неизвестными являются х1 и х2, а свободными — х3и х4. Выражаем базисные неизвестные через свободные:
Вводим обозначения x3 = c1, x4 = c2 и записываем общее решение СЛАУ:
Используя матричную форму записи, получаем
нормальная фундаментальная система решений, а c1, c2 — произвольные постоянные.
Пример 14.2. Решим неоднородную СЛАУ
Преобразуем расширенную матрицу этой СЛАУ при помощи элементарных преобразований строк к ступенчатому виду:
Теперь видно, что для преобразованной матрицы минор М1,21,2 является базисным. Поэтому Rg A = Rg(A | b) = 2 = r, и, согласно теореме 13.1 Кронекера — Капелли, СЛАУ совместна. Кроме того, СЛАУ свелась к эквивалентной системе
которая соответствует преобразованной матрице. Однако можно продолжить преобразования в матрице, упрощая базисные столбцы (1-й и 2-й) с помощью элементарных преобразований строк так, чтобы в каждом из них остался один ненулевой элемент, причем нулевые строки можно отбросить:
По этой матрице восстанавливаем систему
Перенося свободные неизвестные x3, x4 в правые части уравнений, получаем
Для свободных неизвестных положим x3 = c1, x4 = c2, и тогда
Полученное общее решение очень наглядно: 1-й столбец — частное решение неоднородной СЛАУ, а два последних — нормальная фундаментальная система решений соответствующей однородной СЛАУ (ср. пример 14.1).
Пример 14.3. Решим неоднородную СЛАУ
отличающуюся от системы из примера 14.2 лишь одним коэффициентом.
Преобразуем расширенную матрицу этой СЛАУ при помощи элементарных преобразований строк к ступенчатому виду:
Теперь видно, что в преобразованной матрице минор М1,21,2 является базисным для матрицы системы, а минор М1,2,51,2,5 — для расширенной матрицы. Поэтому Rg A = 2, Rg(A | b) = 3 и, согласно теореме 13.1 Кронекера — Капелли, СЛАУ несовместна. Впрочем, несовместность очевидна и так, потому что последней матрице соответствует СЛАУ, в которой третье уравнение имеет вид: 0x1 + 0x2 + 0x3 + 0x4 = 1.
Пример 14.4. Найдем все матрицы, перестановочные с матрицей
Обозначим искомые матрицы через X. Условие перестановочности означает выполнение ма-тричного равенства AX = XA. Чтобы существовало произведение в левой части этого равенства, матрица X должна иметь две строки, а чтобы существовало произведение в правой части — два столбца. Следовательно, X — квадратная матрица второго порядка, т.е.
и для ее нахождения требуется решить матричное уравнение
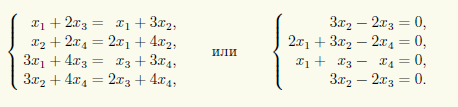
Перемножая матрицы в этом уравнении и приравнивая элементы, стоящие на одинаковых местах в получающихся матрицах, приходим к равносильной системе четырех уравнений
Эта система имеет простой вид, и мы можем отойти от общей схемы решения однородных СЛАУ, продемонстрированной в примере 14.1. Легко увидеть, что если из второго уравнения вычесть удвоенное третье, то получится такое же уравнение, как первое и последнее. Поэтому первые два уравнения в этой системе можно отбросить и тогда
Итак, x3, x4 — свободные, а x1, x2 — базисные неизвестные. Для свободных неизвестных положим x3 = c1, x4 = c2 и тогда получим ответ в виде
или в матричной форме
где c1, c2 ∈ R — произвольные постоянные. Если фиксировать для c1, c2 конкретные значения, то из множества всех перестановочных с A матриц будет выделена одна. Например, при c1 = 0 и с2 = 0 получается нулевая матрица, а при c1 = 0 и с2 = 1 — единичная.
to continue to Google Sites
Not your computer? Use Guest mode to sign in privately. Learn more
Определение 5. Две матрицы
,
,
,
и
,
,
,
будем называть равными, если
.
Краткая запись:
.
Таким образом, две матрицы считаются
равными, если они имеют одинаковые
порядки и их соответствующие элементы
равны.
Определение 6. Суммой двух матриц
,
,
,
и
,
,
,
называется такая матрица
,
,
,
что
.
Иначе говоря, складывать можно только
матрицы одних и тех же порядков, причем
сложение осуществляется поэлементно.
Пример 8.
Найти сумму матриц
и

В соответствии с определением 6 найдем

Правило сложения матриц распространяется
на сумму любого конечного числа слагаемых.
Определение 7. Произведением
матрицы
,
,
,
на вещественное число
называется такая матрица
,
,
,
для которой
.
Иными словами, чтобы умножить матрицу
на число, нужно умножить на это число
все ее элементы и оставить полученные
произведения на прежних местах.
Пример 9.
Найти линейную комбинацию
матриц
и
.
Пользуясь определением 7, получаем
,
,
далее привлекаем определение суммы
матриц (определение 6):
.
Свойства операций сложения матриц и умножения на число:
1. Сложение коммутативно:
.
2. Сложение ассоциативно:.
3. Существует нулевая матрица
,
удовлетворяющая условию
для всех А.
4. Для любой матрицы А существует
противоположная матрица В,
удовлетворяющая условию
.
Для любых матриц А и В и любых
действительных чисел
имеют место равенства:
5.
.
6.
.
7.
.
8.
.
Проверим свойство 1. Обозначим
,
.
Пусть
,
,
.
Имеем
,
и так как равенство доказано для
произвольного элемента, в соответствии
с определением 5
.
Свойство 1 доказано.
Аналогично доказывается свойство 2.
В качестве матрицы
возьмем матрицу порядка
,
все элементы которой равны нулю.
Сложив
с любой матрицей
по правилу, данному в определении 6, мы
матрицу
не изменим, и свойство 3 справедливо.
Проверим свойство 4. Пусть

Положим

Тогда
,
следовательно, свойство 4 справедливо.
Проверку свойств 5 — 8 опустим.
Определение 8. Произведением
матрицы
,
,
,
на матрицу
,
,
,
называется матрица
,
,
,
с элементами
.
Краткая запись:
.
Пример 10.
Найти произведение матриц
и
.
В соответствии с определением 8 найдем
.
Пример 11.
Перемножить матрицы
и

Имеем
.
Замечание 1.
Число элементов в строке матрицы
равно числу элементов в столбце матрицы
(число столбцов матрицы
равно числу строк матрицы
).
Замечание 2.
В матрице
строк столько же, сколько в матрице
,
а столбцов столько же, сколько в
.
Замечание 3.
Вообще говоря,
(умножение матриц некоммутативно).
Чтобы обосновать замечание 3, достаточно
привести хотя бы один пример.
Пример 12.
Перемножим в обратном порядке матрицы
и
из примера 10.
,
таким образом, в общем случае
.
Отметим, что в частном случае равенство
возможно.
Матрицы
и
,
для которых выполняется равенство
,
называются перестановочными, или
коммутирующими.
Упражнения.
1. Найти все матрицы, перестановочные с
данной:
а)
;
б)
.
2. Найти все матрицы второго порядка,
квадраты которых равны нулевой матрице.
3. Доказать, что
.
Соседние файлы в папке rzhavinskaya_lektsii
- #
- #
- #
- #
- #
- #
- #
- #
- #
Сообщения без ответов | Активные темы | Избранное
Правила форума
В этом разделе нельзя создавать новые темы.
Если Вы хотите задать новый вопрос, то не дописывайте
его в существующую тему, а создайте новую в корневом разделе «Помогите решить/разобраться (М)».
Если Вы зададите новый вопрос в существующей теме, то в случае нарушения оформления или других правил форума Ваше сообщение и все ответы на него могут быть удалены без предупреждения.
Не ищите на этом форуме халяву
, правила запрещают участникам публиковать готовые решения стандартных учебных задач. Автор вопроса обязан привести свои попытки решения
и указать конкретные затруднения.
Обязательно просмотрите тему
Правила данного раздела, иначе Ваша тема может быть удалена
или перемещена в Карантин, а Вы так и не узнаете, почему.
|
|
Матрицы, перестановочные с данной
|
|
19/01/13 |
Дана матрица И еще. Требуется найти все квадратные матрицы второго порядка, равные своим квадратам. Там получается нелинейная система. Нет ли способа легче?
|
|
|
|
|
ewert |
Re: Матрицы, перестановочные с данной
|
||
11/05/08 |
Верно ли я понимаю, что это решается через систему линейных уравнений? Да, наверное так проще всего. Там получается нелинейная система. Нет ли способа легче? Есть — подумайте, какими могут быть собственные числа такой матрицы. Там совсем немного вариантов.
|
||
|
|
|||
|
FMS |
Re: Матрицы, перестановочные с данной
|
|
19/01/13 |
Да, наверное так проще всего. Спасибо! Цитата: Там получается нелинейная система. Нет ли способа легче? Есть — подумайте, какими могут быть собственные числа такой матрицы. Там совсем немного вариантов.
|
|
|
|
|
ewert |
Re: Матрицы, перестановочные с данной
|
||
11/05/08 |
Нет. Какому уравнению должно отвечать любое собственное число?
|
||
|
|
|||
|
FMS |
Re: Матрицы, перестановочные с данной
|
|
19/01/13 |
|
|
|
|
|
ewert |
Re: Матрицы, перестановочные с данной
|
||
11/05/08 |
Тогда 0 и 1 Ну да. Теперь можете перебрать возможные жордановы формы, подходящие под эти условия — их и будет всего-то три штуки. Хотя с жордановостью и вообще собственными числами я, надо сказать, переборщил (постоянно забываю эту задачу). Поскольку матрица всего лишь второго порядка — всё гораздо проще. Если матрица невырожденна, то на неё уравнение
|
||
|
|
|||
|
FMS |
Re: Матрицы, перестановочные с данной
|
|
19/01/13 |
Да, действительно, очень просто. Спасибо за предложенный вариант.
|
|
|
|
Модераторы: Модераторы Математики, Супермодераторы
Кто сейчас на конференции |
|
Сейчас этот форум просматривают: нет зарегистрированных пользователей |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |

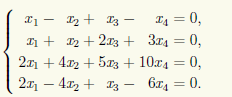
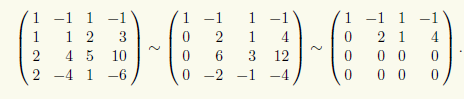
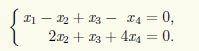
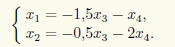
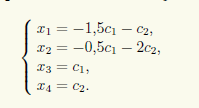
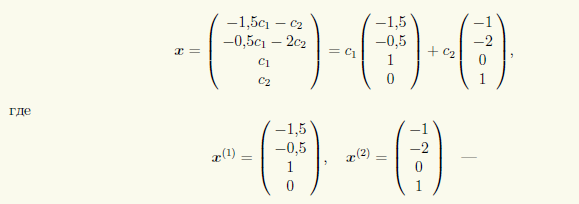
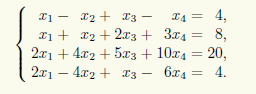
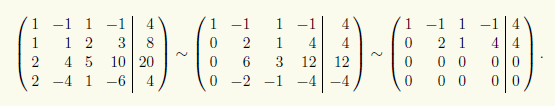
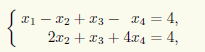

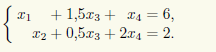
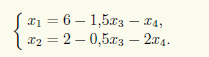
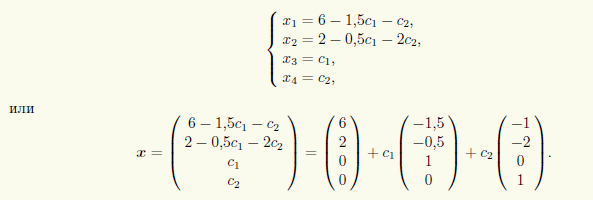
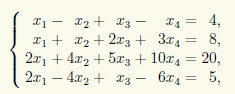
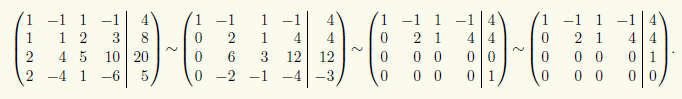
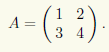
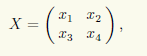
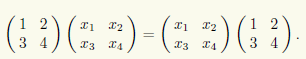
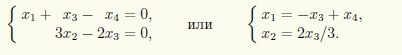
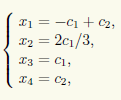
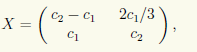


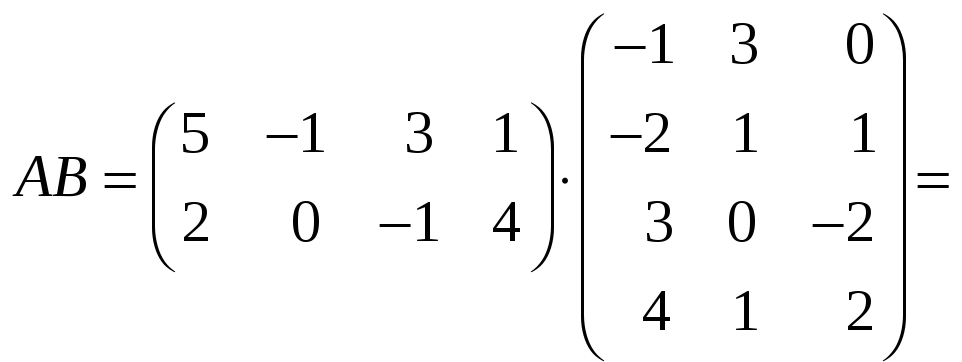
 Требуется найти все перестановочные с ней.
Требуется найти все перестановочные с ней. и
и  ?
? можно сократить. А если вырожденна, то такие матрицы в двумерном случае наперечёт — их ранг не выше одного, т.е. их строки/столбцы пропорциональны:
можно сократить. А если вырожденна, то такие матрицы в двумерном случае наперечёт — их ранг не выше одного, т.е. их строки/столбцы пропорциональны:  , и остаётся лишь отобрать среди них те, которые удовлетворяют тому уравнению.
, и остаётся лишь отобрать среди них те, которые удовлетворяют тому уравнению.