В данной статье мы рассмотрим определение и свойства медиан, проведенных к основанию и боковым сторонам равнобедренного треугольника, а также разберем пример решения задачи для закрепления теоретического материала.
- Определение медианы
-
Свойства медианы в равнобедренном треугольнике
- Свойство 1
- Свойство 2
- Свойство 3
- Свойство 4
- Свойство 5
- Свойство 6
- Пример задачи
Определение медианы
Медианой называется отрезок в треугольнике, который соединяет вершину и середину противоположной стороны.
- BD – медиана △ABC;
- AD = DC.
Треугольник является равнобедренным, если две его стороны равны (боковые), а третья сторона – это основание фигуры.
- AB = BC – боковые стороны;
- AC – основание.
Свойства медианы в равнобедренном треугольнике
Свойство 1
Медиана в равнобедренном треугольнике, проведенная к основанию, одновременно является высотой, опущенной на основание, и биссектрисой угла, из которого она проведена.
- BD – медиана и высота, опущенная на основание AC, а также биссектриса угла ABC.
- ∠ABD = ∠CBD
Свойство 2
В равнобедренном треугольнике медианы пресекаются в одной точке (центр тяжести) и делятся в этой точке в отношении 2:1.
- O – центр тяжести или центроид треугольника;
- AO = 2OF;
- BO = 2OD;
- CO = 2OE.
Свойство 3
Медиана делит равнобедренный треугольник на 2 равных по площади (равновеликих) треугольника. Следовательно, S1 = S2.
Свойство 4
Если провести три медианы в равнобедренном треугольнике, образуются 6 равновеликих треугольников (S1 = S2 = S3 = S4 = S5 = S6).
Свойство 5
Длину медианы в равнобедренном треугольнике, проведенную к основанию, можно найти по следующей формуле:
- a – основание;
- b – боковая сторона.
Свойство 6
Данной свойство, в отличие от перечисленных выше, не относится к медиане, опущенной на основание фигуры. Оно гласит:
Медианы, проведенные к боковым сторонам равнобедренного треугольника, равны между собой.
AF = CE, следовательно, AE = EB = BF = FC.
Пример задачи
Основание равнобедренного треугольника равняется 7 см, а боковая сторона – 12 см. Найдите длину медианы, проведенной к основанию фигуры.
Решение
Воспользуемся формулой, представленной в Свойстве 5, подставив в нее известные нам по условиям задачи значения:
Формулы для вычисления высоты, биссектрисы и медианы.
В равнобедренном треугольнике: высота, биссектриса и медиана, исходящие из угла образованного равными сторонами, один и тот же отрезок.
L — высота = биссектриса = медиана
a — одинаковые стороны треугольника
b — основание
α — равные углы при основании
β — угол образованный равными сторонами
Формулы высоты, биссектрисы и медианы, через сторону и угол, (L):
Формула высоты, биссектрисы и медианы, через стороны, (L):
- Подробности
-
Опубликовано: 07 октября 2011
-
Обновлено: 13 августа 2021
Определение и свойства медианы в равнобедренном треугольнике
В данной статье мы рассмотрим определение и свойства медиан, проведенных к основанию и боковым сторонам равнобедренного треугольника, а также разберем пример решения задачи для закрепления теоретического материала.
Определение медианы
Медианой называется отрезок в треугольнике, который соединяет вершину и середину противоположной стороны.
Треугольник является равнобедренным, если две его стороны равны (боковые), а третья сторона – это основание фигуры.
- AB = BC – боковые стороны;
- AC – основание.
Свойства медианы в равнобедренном треугольнике
Свойство 1
Медиана в равнобедренном треугольнике, проведенная к основанию, одновременно является высотой, опущенной на основание, и биссектрисой угла, из которого она проведена.
- BD – медиана и высота, опущенная на основание AC, а также биссектриса угла ABC.
- ∠ABD = ∠CBD
Свойство 2
В равнобедренном треугольнике медианы пресекаются в одной точке (центр тяжести) и делятся в этой точке в отношении 2:1.
Свойство 3
Медиана делит равнобедренный треугольник на 2 равных по площади (равновеликих) треугольника. Следовательно, S1 = S2.
Свойство 4
Если провести три медианы в равнобедренном треугольнике, образуются 6 равновеликих треугольников (S1 = S2 = S3 = S4 = S5 = S6).
Свойство 5
Длину медианы в равнобедренном треугольнике, проведенную к основанию, можно найти по следующей формуле:
Свойство 6
Данной свойство, в отличие от перечисленных выше, не относится к медиане, опущенной на основание фигуры. Оно гласит:
Медианы, проведенные к боковым сторонам равнобедренного треугольника, равны между собой.
AF = CE, следовательно, AE = EB = BF = FC.
Пример задачи
Основание равнобедренного треугольника равняется 7 см, а боковая сторона – 12 см. Найдите длину медианы, проведенной к основанию фигуры.
Решение
Воспользуемся формулой, представленной в Свойстве 5, подставив в нее известные нам по условиям задачи значения:
Равнобедренный треугольник: свойства, признаки и формулы
О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Определение равнобедренного треугольника
Какой треугольник называется равнобедренным?
Равнобедренным называется треугольник, у которого две стороны равны.
Давайте посмотрим на такой треугольник:
На рисунке хорошо видно, что боковые стороны равны. Это равенство и делает треугольник равнобедренным.
А вот как называются стороны равнобедренного треугольника:
AB и BC — боковые стороны,
AC — основание треугольника.
Для понимания материала нам придется вспомнить, что такое биссектриса, медиана и высота, если вы вдруг забыли.
Биссектриса — луч, который исходит из вершины угла и делит этот угол на два равных угла.
Даже если вы не знаете определения, то про крысу, бегающую по углам и делящую их пополам, наверняка слышали. Она не даст вам забыть, что такое биссектриса. А если вам не очень приятны крысы, то вместо нее бегать может кто угодно. Биссектриса — это киса. Биссектриса — это лИса. Никаких правил для воображения нет. Все правила — для геометрии.
Обратите внимание на рисунок. В представленном равнобедренном треугольнике биссектрисой будет отрезок BH.
Медиана — отрезок, который соединяет вершину треугольника с серединой противолежащей стороны.
Для медианы не придумали веселого правила, как с биссектрисой, но можно его придумать. Например, буддийская запоминалка: «Медиана — это Лама, бредущий из вершины треугольника к середине его основания и обратно».
В данном треугольнике медианой является отрезок BH.
Высота треугольника — перпендикуляр, опущенный из вершины треугольника на противоположную сторону или на прямую, содержащую сторону треугольника.
Высотой в представленном равнобедренном треугольнике является отрезок BH.
Признаки равнобедренного треугольника
Вот несколько нехитрых правил, по которым легко определить, что перед вами не что иное, как его величество равнобедренный треугольник.
- Если у треугольника два угла равны, то этот треугольник — равнобедренный.
- Если высота треугольника совпадает с его медианой, проведенной из того же угла, то такой треугольник — равнобедренный.
- Если высота треугольника совпадает с его биссектрисой, проведенной из того же угла, то такой треугольник — равнобедренный.
- Если биссектриса треугольника совпадает с его медианой, проведенной из того же угла, то такой треугольник снова равнобедренный!
Свойства равнобедренного треугольника
Чтобы понять суть равнобедренного треугольника, нужно думать как равнобедренный треугольник, стать равнобедренным треугольником — и выучить 4 теоремы о его свойствах.
Теорема 1. В равнобедренном треугольнике углы при основании равны.
Пусть AС — основание равнобедренного треугольника. Проведем биссектрису DK. Треугольник ADK равен треугольнику CDK по двум сторонам и углу между ними (AD = DC, DK — общая, а так как DK — биссектриса, то угол ADK равен углу CDK). Из равенства треугольников следует равенство всех соответствующих элементов, значит угол A равен углу C. Изи!
Теорема 2: В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.
Δ ABH = Δ CBH по двум сторонам и углу между ними (углы ABH и CBH равны, потому что BH биссектриса, AB = BC, потому что Δ ABC равнобедренный, BH — общая сторона).
Значит, во-первых, AH = HC и BH — медиана.
Во-вторых, углы BHA и BHC равны, а ещё они смежные, т. е. в сумме дают 180 градусов. Значит, они равны по 90 градусов и BH — высота.
Теорема 3: В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.
Δ ABH = Δ CBH по трём сторонам (AH = CH равны, потому что BH медиана, AB = BC, потому что Δ ABC равнобедренный, BH — общая сторона).
Значит, во-первых, углы ABH и CBH равны и BH — биссектриса.
Во-вторых, углы BHA и BHC равны, а ещё они смежные, т. е. в сумме дают 180 градусов. Значит они равны по 90 градусов и BH — высота.
Теорема 4: В равнобедренном треугольнике высота, проведенная к основанию, является биссектрисой и медианой.
Δ ABH = Δ CBH по признаку прямоугольных треугольников, равенство гипотенуз и соответствующих катетов (AB = BC, потому что Δ ABC равнобедренный, BH — общая сторона).
Значит, во-первых, углы ABH и CBH равны и BH — биссектриса.
Во-вторых, AH = HC и BH — медиана.
Примеры решения задач
Нет ничего приятнее, чем поупражняться и поискать углы и стороны в равнобедренном треугольнике. Ну… почти ничего.
Задачка раз. Дан ΔABC с основанием AC: ∠C = 80°, AB = BC. Найдите ∠B.
Поскольку вы уже знакомы с различными теоремами, то для вас не секрет, что углы при основании в равнобедренном треугольнике равны, а треугольник ABC — равнобедренный, так как AB = BC.
Значит, ∠A = ∠C = 80°.
Не должно вас удивить и то, что сумма углов треугольника равна 180°.
∠B = 180° − 80° − 80° = 20°.
Задачка два. В треугольнике ABC провели высоту BH, угол CAB равен 50°, угол HBC равен 40°. Найдите сторону BC, если BA = 5 см.
Сумма углов треугольника равна 180°, а значит в Δ ABH мы можем узнать угол ABH, который будет равен 180° − 50° − 90° = 40°.
А ведь получается, что углы ABH и HBC оба равны по 40° и BH — биссектриса.
Ну и раз уж BH является и биссектрисой, и высотой, то Δ ABC — равнобедренный, а значит BC = BA = 5 см.
Изучать свойства и признаки равнобедренного треугольника лучше всего на курсах по математике с опытными преподавателями в Skysmart.
Как найти медиану в равнобедренном треугольнике
Вчера ко мне подошла старшая дочь и спросила: «Мам, ты знаешь, как найти медиану в равнобедренном треугольнике?» Я в панике начала вспоминать, а что такое медиана? Многое из геометрии я помню, но тема медиан вылетела из головы. Почитав немного теории в учебнике, конечно, я сразу вспомнила и про медианы, и про треугольники. И скажу, что на практике все намного проще, чем в теории.
Вычисление медианы по двум сторонам треугольника
Вообще, медиана – это отрезок, проведенный из угла треугольника к противоположной ему стороне, при этом поделив эту сторону на две равные части.
В равнобедренном треугольнике две стороны и два угла у основания равны. А медиана, проведенная к основанию, не только делит его пополам, но еще и является высотой. Высота в свою очередь образует с основанием прямой угол.
Равнобедренный треугольник поделился на два одинаковых прямоугольных. Высота h в таком треугольнике – это один из катетов. По теореме Пифагора найдем этот катет:
Квадрат катета – это разность квадрата гипотенузы и квадрата второго катета.
Значит, катет – квадратный корень из разности квадрата гипотенузы и квадрата второго катета.
Предположим, в условии даны стороны равнобедренного треугольника: a и b. Из этого следует, что в прямоугольном треугольнике получилась гипотенуза a и катет b / 2.
Подставляем значения и получаем, что высота равна:

- a ^ 2 = 25
- (b ^ 2) / 4 = 9
- h ^ 2 = (a ^ 2) – (b ^ 2)
- h ^ 2 = 25 – 9
- h ^ 2 = 16
- h = 4
Вычисление медианы по основанию и площади треугольника
Если из условия задачи мы знаем площадь равнобедренного треугольника и его основание, то без труда найдем медиану.
- Площадь равнобедренного треугольника находится по формуле:
S = (b * h) / 2 - Выражаем h:
h = 2S / b - Например, дано: площадь S = 12, основание b = 6. Найти медиану h.
h = 2 * 12 / 6
h = 4
Пока я помогала дочери решать задачи, поняла, что их школьное детство намного проще нашего. Мало того, что все формулы есть в интернете, так еще есть и онлайн-калькуляторы, которые выдают правильный ответ и подробное решение за секунду! Однако это скорее минус. Нам приходилось запоминать все формулы и правила, а сегодняшние дети полагаются на мобильных помощников.

http://skysmart.ru/articles/mathematic/chto-takoe-ravnobedrennyj-treugolnik
http://dobriy-sovet.ru/kak-najti-medianu-v-ravnobedrennom-treugolnike/

Онлайн калькуляторы
На нашем сайте собрано более 100 бесплатных онлайн калькуляторов по математике, геометрии и физике.

Справочник
Основные формулы, таблицы и теоремы для учащихся. Все что нужно, чтобы сделать домашнее задание!

Заказать решение
Не можете решить контрольную?!
Мы поможем! Более 20 000 авторов выполнят вашу работу от 100 руб!
Медиана в равнобедренном треугольнике
Определение и формулы медианы равнобедренного треугольника
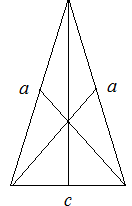
В равнобедренном треугольнике медиана, опущенная на основание, является высотой и биссектрисой.
Для медиан равнобедренного треугольника справедливы следующие утверждения:
- Медианы равнобедренного треугольника пересекаются в одной точке, которая делит каждую из них в отношении 2:1, считая от вершины. Эта точка называется центром тяжести треугольника.
- Медиана разбивает равнобедренный треугольник на два треугольника с одинаковой площадью.
- Весь равнобедренный треугольник делится своими медианами на шесть равновеликих (т.е. с одинаковой площадью) треугольников.
Медиана равнобедренного треугольника, проведенная к его основанию, вычисляется по формуле:
где – основание равнобедренного треугольника,
– боковые стороны треугольника.
Примеры решения задач
| Понравился сайт? Расскажи друзьям! | |
Как найти медиану равнобедренного треугольника
Треугольник называется равнобедренным, если у него есть две равных стороны. Они называются боковыми. Третья сторона называется основанием равнобедренного треугольника. Такой треугольник обладает рядом специфических свойств. Медианы, проведенные к боковым сторонам, равны. Таким образом в равнобедренном треугольнике две разные медианы, одна проведена к основанию треугольника, вторая — к боковой стороне.

Инструкция
Пусть дан треугольник ABC, являющийся равнобедренным. Известны длины его боковой стороны и основания. Надо найти медиану, опущенную на основание этого треугольника. В равнобедренном треугольнике эта медиана является одновременно медианой, биссектрисой и высотой. Благодаря этому свойству, найти медиану к основанию треугольника очень просто. Воспользуйтесь теоремой Пифагора для прямоугольного треугольника ABD: AB² = BD² + AD², где BD — искомая медиана, AB — боковая сторона (для удобства пусть она равна a), а AD — половина основания (для удобства возьмите основание равным b). Тогда BD² = a² — b²/4. Найдите корень из этого выражения и получите длину медианы.
Чуть более сложно обстоят дела с медианой, проведенной к боковой стороне. Для начала изобразите обе таких медианы на рисунке. Эти медианы равны. Обозначьте боковую сторону буквой a, а основание — b. Обозначьте равные углы при основании α. Каждая из медиан делит боковую сторону на две равные части a/2. Обозначьте длину искомой медианы x.
По теореме косинусов можно выразить любую сторону треугольника через две другие и косинус угла между ними. Запишем теорему косинусов для треугольника AEC: AE² = AC² + CE² — 2AC·CE·cos∠ACE. Или, что то же, (3x)² = (a/2)² + b² — 2·ab/2·cosα = a²/4 + b² — ab·cosα. По условиям задачи стороны известны, а вот угол при основании нет, поэтому вычисления продолжаются.
Теперь примените теорему косинусов к треугольнику ABC, чтобы найти угол при основании: AB² = AC² + BC² — 2AC·BC·cos∠ACB. Другими словами, a² = a² + b² — 2ab·cosα. Тогда cosα = b/(2a). Подставьте это выражение в предыдущее: x² = a²/4 + b² — ab·cosα = a²/4 + b² — ab·b/(2a) = a²/4 + b² — b²/2 = (a²+2b²)/4. Вычислив корень правой части выражения, вы найдете медиану, проведенную к боковой стороне.
Источники:
- Равнобедренные и равносторонние треугольники
- Медианы, биссектрисы и высоты треугольника
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.





















