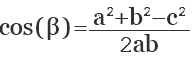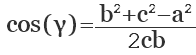Как найти все неизвестные углы треугольника

Ответ:

1. Дано в треугольнике NKM: ∠K=35°, ∠M=25°. Сумма всех внутренних углов треугольника равна 180°. Тогда ∠N+∠K+∠M=180° и поэтому  

∠N=180°–∠K–∠M=180°–35°–25°=120°.

2. Дано в треугольнике EPK: ∠P=40°, ∠K=60°. Сумма всех внутренних углов треугольника равна 180°. Тогда ∠E+∠P+∠K=180° и поэтому  

∠E=180°–∠P–∠K=180°–40°–60°=80°.

3. Дано в треугольнике STM: ∠T=90°, ∠M=30°. Сумма всех внутренних углов треугольника равна 180°. Тогда ∠S+∠T+∠M=180° и поэтому  

∠S=180°–∠T–∠M=180°–90°–30°=60°.

4. Дано в треугольнике BAC: ∠A=40°, AC=BC, то есть треугольник BAC равнобедренный. Углы при основании равнобедренного треугольника равны и сумма всех внутренних углов треугольника равна 180°. Значит, ∠B=∠A=70° и ∠A+∠B+∠C=180° и поэтому  

∠C=180°–∠A–∠B=180°–70°–70°=40°.

5. Дано в треугольнике QMN: QM=MN=QN, то есть треугольник QMN равносторонний. Известно, что все углы равностороннего треугольника равны и имеют градусную меру 60°. Значит, ∠Q=∠M=∠N=60°.

6. Дано в треугольнике KEP: ∠E=90°, ∠K=30°. Сумма всех внутренних углов треугольника равна 180°. Тогда ∠K+∠E+∠P=180° и поэтому  

∠P=180°–∠E–∠K=180°–90°–60°=30°.

9. Дано в треугольнике NMK: внешний угол при M равен 130°, NM=NK, то есть треугольник NMK равнобедренный. Известно, что  

а) углы при основании равнобедренного треугольника равны;

б) внешний угол треугольника равен сумме двух других внутренних не смежных с ним;

в) сумма смежных углов равна 180°.  

Тогда ∠M=∠K, ∠N+∠K=130° и ∠M=180°–130°=50°.  

Значит, ∠K=∠M=50° и ∠N=130°–∠K=130°–50°=80°.

10. Дано в треугольнике DCE: внешний угол при E равен 140°, ∠C=80°. Известно, что  

а) внешний угол треугольника равен сумме двух других внутренних не смежных с ним;

б) сумма смежных углов равна 180°;

в) сумма всех внутренних углов треугольника равна 180°.  

Тогда ∠C+∠D=140°, ∠E=180°–140°=40° и ∠D+∠C+∠E =180°.  

Отсюда ∠D=180°–∠C–∠E =180°–80°–40°=60°.

Решение треугольников онлайн

С помощю этого онлайн калькулятора можно решить треугольники, т.е. найти неизвестные элементы (стороны, углы) треугольника. Теоретическую часть и численные примеры смотрите ниже.

Решение треугольников − это нахождение всех его элементов (трех сторон и трех углов) по трем известным элементам (сторонам и углам). В статье Треугольники. Признаки равенства треугольников рассматриваются условия, при которых два треугольника оказываются равными друг друга. Как следует из статьи, треугольник однозначно определяется тремя элементами. Это:

1. Три стороны треугольника.
2. Две стороны треугольника и угол между ними.
3. Две стороны и угол противостоящий к одному из этих сторон треугольника.
4. Одна сторона и любые два угла.

Заметим, что если у треугольника известны два угла, то легко найти третий угол, т.к. сумма всех углов треугольника равна 180°.

Решение треугольника по трем сторонам

Пусть известны три стороны треугольника a, b, c (Рис.1). Найдем .

(1)

(2)

Из (1) и (2) находим cosA, cosB и углы A и B (используя калькулятор). Далее, угол C находим из выражения

.

Пример 1. Известны стороны треугольника ABC: Найти (Рис.1).

Решение. Из формул (1) и (2) находим:

И, наконец, находим угол C:

Решение треугольника по двум сторонам и углу между ними

Пусть известны стороны треугольника a и b и угол между ними C (Рис.2). Найдем сторону c и углы A и B.

Найдем сторону c используя теорему косинусов:

.

.

Далее, из формулы

.

.

(3)

Далее из (3) с помощью калькулятора находим угол A.

Поскольку уже нам известны два угла то находим третий:

.

Пример 2. Известны две стороны треугольника ABC: и (Рис.2). Найти сторону c и углы A и B.

Решение. Иcпользуя теорму косинусов найдем сторону c:

,

Из формулы (3) найдем cosA:

.

Поскольку уже нам известны два угла то находим третий:

Решение треугольника по стороне и любым двум углам

Пусть известна сторона треугольника a и углы A и B (Рис.4). Найдем стороны b и c и угол C.

Так как, уже известны два угла, то можно найти третий:

.

Далее, для находждения сторон b и c воспользуемся тероемой синусов:

Пример 3. Известна одна сторона треугольника ABC: и углы (Рис.3). Найти стороны b и c и угол С.

Решение. Поскольку известны два угла, то легко можно найти третий угол С:

Найдем сторону b. Из теоремы синусов имеем:

Найдем сторону с. Из теоремы синусов имеем:

Углы треугольника

Геометрическая фигура из трех отрезков, соединенных между собой тремя точками, не лежащими на одной прямой, называется треугольником. Это — многоугольник с тремя углами. Сумма всех углов треугольника равна 180°. Если известна величина двух из них, третий угол определяем вычитанием из 180° величины двух известных углов.

α = 180°-β-γ

Если известны стороны треугольника, можно рассчитать его углы, воспользовавшись теоремой косинусов. Здесь, квадрат одной стороны треугольника (а) равен сумме квадратов двух его других сторон (b,с), образующих искомый угол (α), плюс удвоенное произведение этих сторон (b,с) на косинус угла.

a 2 = b 2 + c 2 + 2abc cos (α)

Отсюда, косинус искомого угла равняется сумме квадратов смежных сторон (b, с) минус квадрат третей стороны треугольника (а), противолежащей искомому углу, и все это делится на удвоенное произведение смежных сторон:

cos (α) = (b 2 + c 2 — a 2 ) / 2bc

,
где а, b, с — стороны треугольника.
Используя теорему косинусов, определяем косинусы остальных углов. Величины углов в градусах находим по тригонометрической таблице.

Углы прямоугольного треугольника

Калькулятор расчёта углов прямоугольного треугольника

Прямоугольный треугольник — это геометрическая фигура, образованная тремя отрезками соединяющихся тремя точками, у которой все углы внутренние, при этом один из углов прямой (равен 90°).

Тангенс угла tg(α) — это тригонометрическая функция выражающая отношение противолежащего катета a к прилежащему катету b.

Формула тангенса

• tg α — тангенс угла α
• a — противолежащий катет
• b — прилежащий катет

Арктангенс — это обратная тригонометрическая функция. Арктангенсом числа x называется такое значение угла α, выраженное в радианах, для которого tg α = x . Вычислить арктангенс, означает найти угол α, тангенс которого равен числу x.

Углы треугольника

Сумма углов треугольника всегда равна 180 градусов:

Так как у прямоугольного треугольника один из углов равен 90°, то сумма двух других углов равна 90°.

Поэтому, если известен один из острых углов треугольника, второй угол можно посчитать по формуле:

Острый угол — угол, значение которого меньше 90°.

У прямоугольного треугольника один угол прямой, а два других угла — острые.

5)из рисунка видно, что треугольник QMN — равносторонний, значит все его углы (по св-ву равностороннего треугольника) равны по  60(град)

6)треугольник ЕКР- прямоугольный, значит угол Р=90-60=30(град)

7)треугольник DMN- равнобедренный, значит по св-ву равнобедренного треугольника углы при основании равны, значит угол M = углу N. По теореме о сумме углов треугольника имеем, что сумма всех углов 180(град), значит угол M=N=(180-100):2=40(град)

8)угол САМ и САВ — смежные углы и в сумме дают 180(град), значит угол САВ= 180-130=50(град). по теореме о сумме углов треугольника имеем, что угол С=180-(60+50)=70(град)

9) Аналогично угол М=180-130=50(град), треугольник MNK- равнобедренный, значит угол М = углу К=50(град), а угол N =180-(50+50)=80(град)

10)Угол СЕФ- внешний, по св-ву внешнего угла, он равен сумме двух других углов не смежных с ним, значит угол Д=140-80=60(град), а угол СЕД = 180-(80+60)=40(град)

11)Треугольник АВС — прямоугольный, значит угол С = 90(град), угол ВАД-внешний, значит равен сумме углов С и В, отсюда угол В=150-90=60(град), а угол А=90-60=30(град)-по теореме о сумме углов треугольника

12)Треугольники ДМА и ДВМ — прямоугольные,значит угол ДМВ и ДМА = 90(град), угол МАС — внешний, значит угол МДА=135-90=45(град) и угол МАД= 180-135=45(град). Треугольник АДВ — равнобедренный, значит угол В= углу А=45(град), следовательно угол MDB=90-45=45(град)

Калькулятор длин сторон треугольника онлайн умеет вычислять длину сторон 14 способами.
Калькулятор может:

1. Найти все стороны треугольника.
2. Найти все углы треугольника.
3. Найти площадь (S) и периметр (P) треугольника.
4. Найти радиус (r) вписанной окружности.
5. Найти радиус (R) описанной окружности.
6. Найти высоту (h) треугольника.

Просто введите любые имеюшиеся данные и, если их достаточно, то калькулятор сам подберет нужные формулы для вычислений и покажет подробный расчет с выводом формул.
 

Сторона треугольника (или длина сторон) может быть найдена различными методами. 
В большинстве случаев достаточно воспользоваться одной из ниже приведенных формул. Однако не редки случаи когда для нахождения искомой стороны понадобиться обратиться к дополнительным материалам или решения в два действия.

Как найти длину стороны треугольника?

Найти длину сторон треугольника очень просто на нашем онлайн калькуляторе. Так же длина может быть найдена самостоятельно по формулам. Выбор нужной формулы зависит от того какие данные известны.

Для прямоугольного треугольника:

1) Найти катет через гипотенузу и другой катет

где a и b — катеты, с — гипотенуза.

2) Найти гипотенузу по двум катетам

где a и b — катеты, с — гипотенуза.

3) Найти катет по гипотенузе и противолежащему углу

где a и b — катеты, с — гипотенуза,α° и β° — углы напротив катетов.

4) Найти гипотенузу через катет и противолежащий угол

где a и b — катеты, с — гипотенуза,α° и β°- углы напротив катетов.

Для равнобедренного треугольника:

1) Найти основание через боковые стороны и угол между ними

где a — искомое основание, b — известная боковая сторона,α° — угол между боковыми сторонами.

2) Найти основание через боковые стороны и угол при основании

где a — искомое основание,b — известная боковая сторона,β° — угол при осноавнии.

3) Найти боковые стороны по углу между ними

где b — искомая боковая сторона, a — основание,α° — угол между боковыми сторонами.

4) Найти боковые стороны по углу при основании

где b — искомая боковая сторона, a — основание,β° — угол при осноавнии.

​​​​​Для равностороннего треугольника:

1) Найти сторону через площадь

где a — искомая сторона, S — площадь треугольника.

2) Найти сторону через высоту

где a — искомая сторона,h — высота треугольника.

3) Найти сторону через радиус вписанной окружности

где a — искомая сторона,r — радиус вписанной окружности.

4) Найти сторону через радиус описанной окружности

где a — искомая сторона,R — радиус описанной окружности.

​​​​​Для произвольного треугольника:

1) Найти сторону через две известные стороны и один угол (теорема косинусов)

где a — искомая сторона, b и с — известные стороны, α° — угол напротив неизвестной стороны.

2) Найти сторону через одну известную сторону и два угла (теорема синусов)

где a — искомая сторона, b — известная сторона, α° и β° известные углы.

Скачать все формулы в формате Word