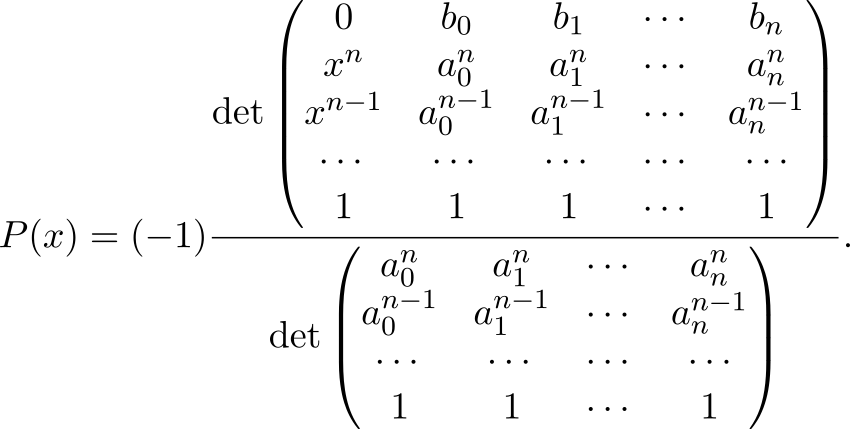
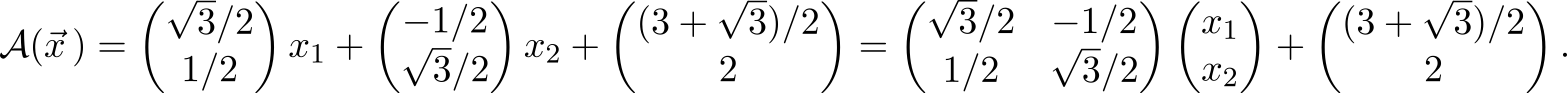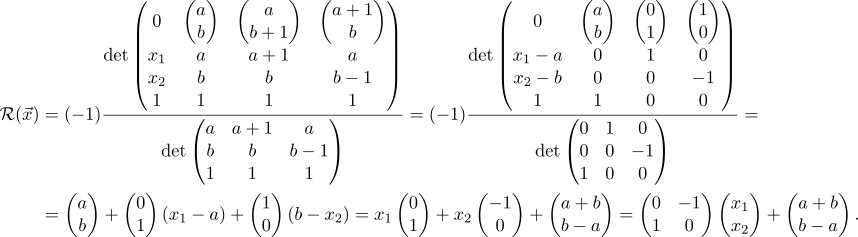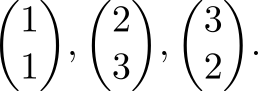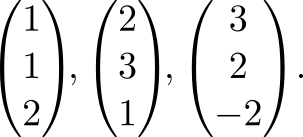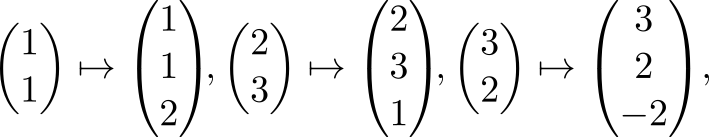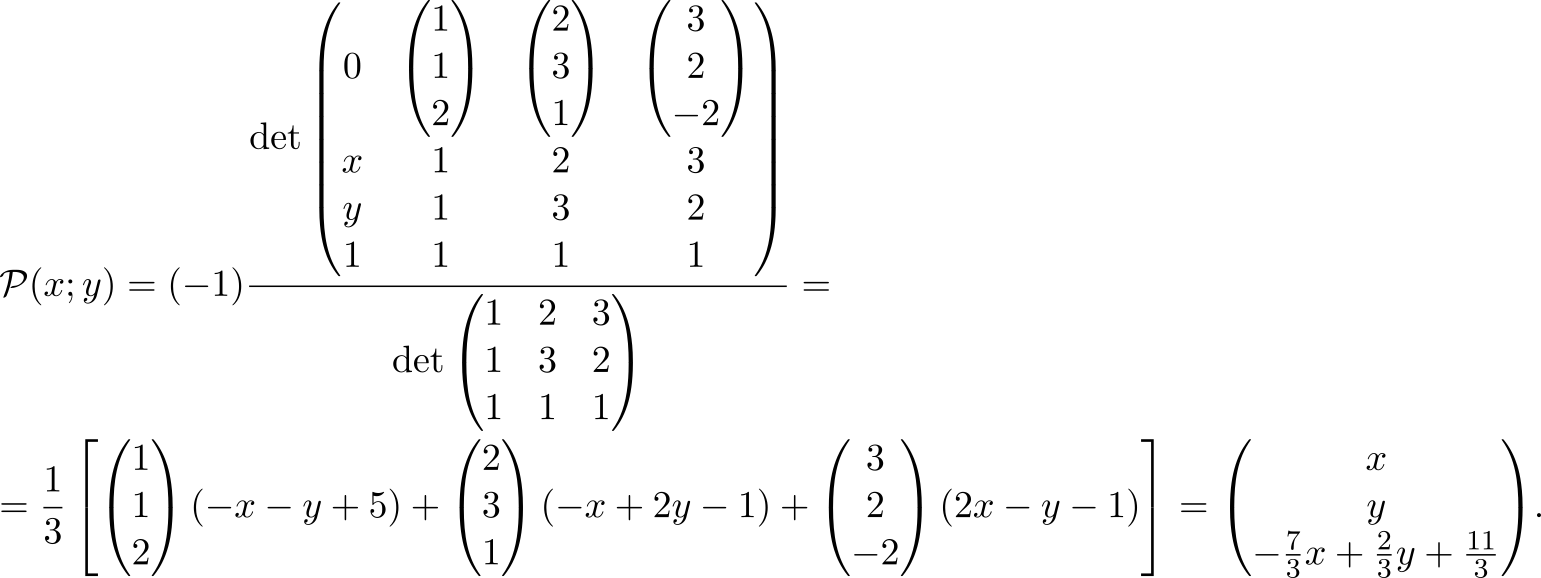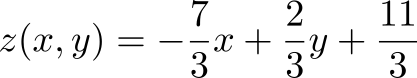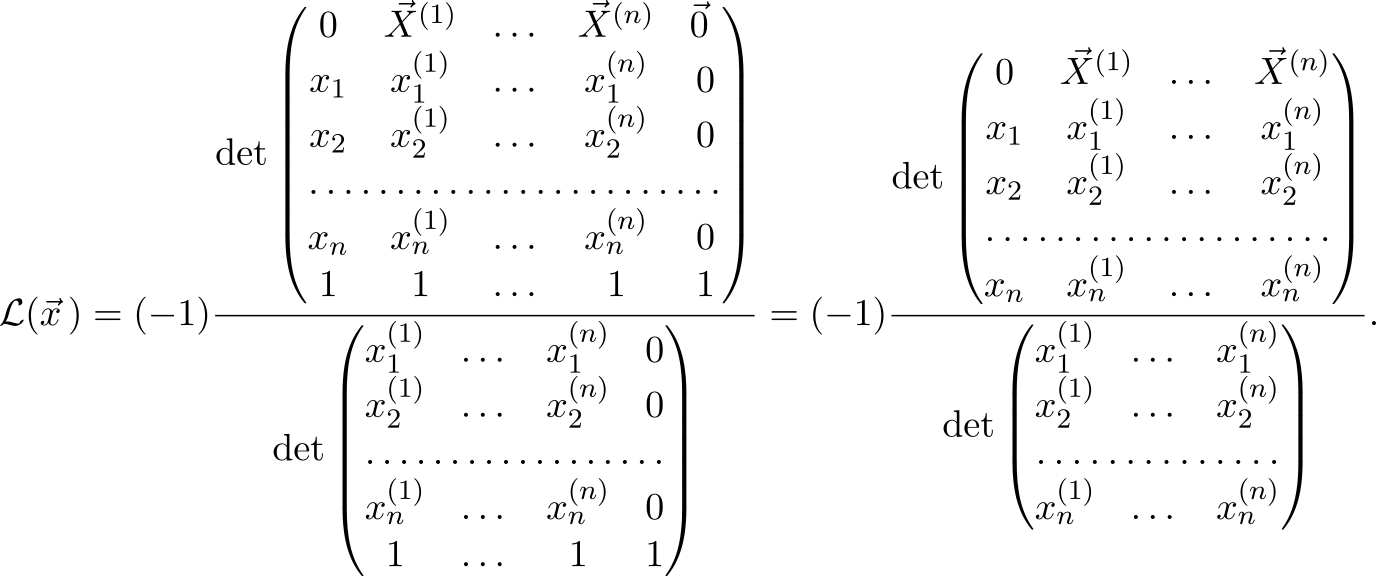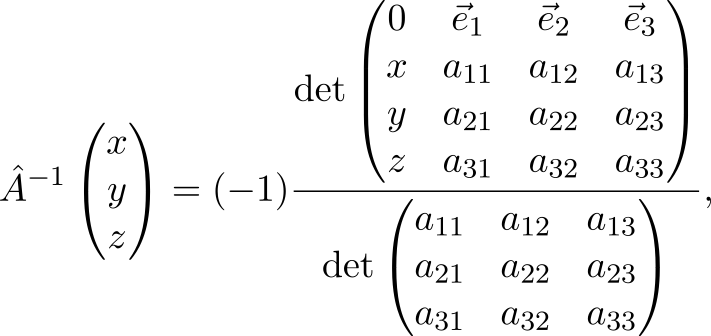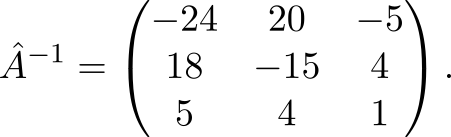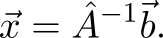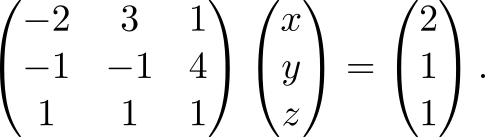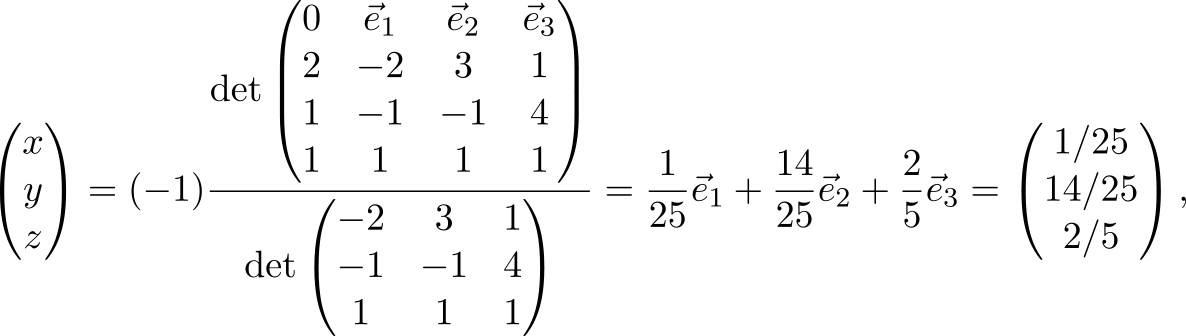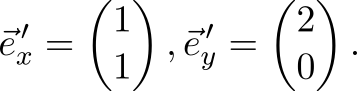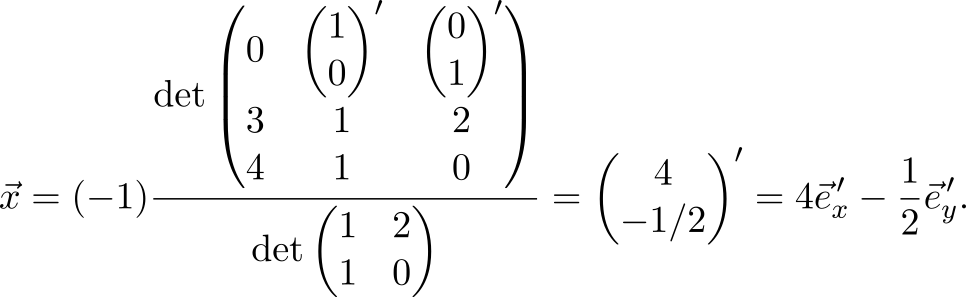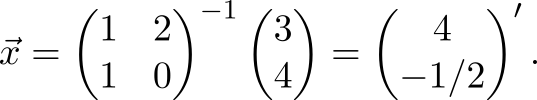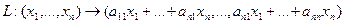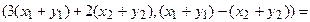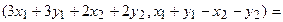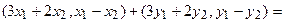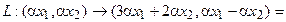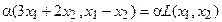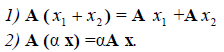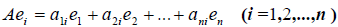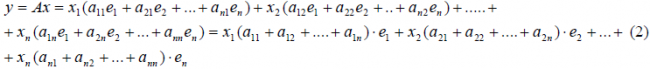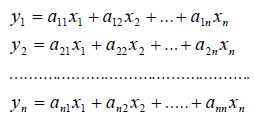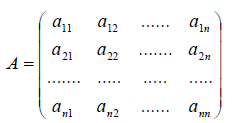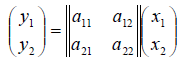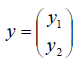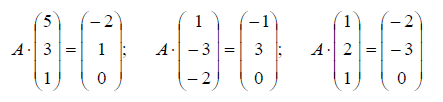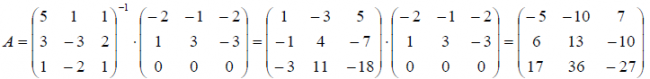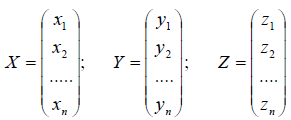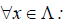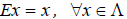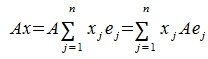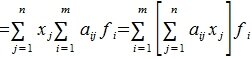Как найти все образы преобразования - Исправление недочетов и поиск решений вместе с Examum.ru

Ядром линейного
преобразования

называется совокупность всех векторов

для которых

.
Ядро линейного преобразования

будем обозначать символом

.
Итак,

□ Теорема 3.5.
Ядро

линейного преобразования

совпадает с множеством решений однородной
системы уравнений

.

Доказательство
теоремы
вытекает из следующей цепочки равносильных
утверждений:

решение системы уравнений

.
■

Следствие.
Множество

является подпространством.

Так как множество
решений однородной системы линейных
уравнений является подпространством,
то из теоремы 3.5 следует, что множество

является подпространством.

Пример

Найти ядро линейного
преобразования

,
где

Решение. Так
как ядро

совпадает с множеством решений системы
уравнений

,
то базисом подпространства

является фундаментальный набор решений
этой системы уравнений. Найдем этот
базис

Векторы

образуют базис системы векторов

.
Вектор

разлагается по векторам

:

.
Отсюда следует, что фундаментальный
набор решений системы линейных уравнений
состоит из одного вектора

,
который является базисом

.
Итак, ядро

Так как

является подпространством пространства

,
то вектор

принадлежит

.
Линейное преобразование

называется невырожденным,
если

содержит только нулевой вектор, т. е.

.

□ Теорема 3.6.
Дано линейное преобразование

.
Тогда равносильны следующие утверждения:

1. Линейное
преобразование

является невырожденным.

2. Линейное
преобразование f
переводит базис пространства

в
базис этого пространства, т.е. если

базис

,
то и

базис пространства

3. Линейное
преобразование

обратимо.

Доказательство

1)
2).
Дано, что ядро

.
Докажем, что если

базис

,
то

также базис пространства

.
Сначала докажем линейную независимость
системы векторов

.
Для этого рассмотрим произвольное
разложение вектора

по этой системе векторов

(1)

Равенство (1)
перепишем в виде

(2)

Теперь из равенства
(2) вытекает, что вектор

.
Отсюда, в виду

вытекает

=
.
(3)
Так как

линейно независимая система векторов,
то из соотношения (3) следуют равенства

.
Этим доказана линейная независимость
системы векторов

.
Она содержит n
векторов
и, значит, является базисом пространства

2)
3).
Диагональная система

является базисом пространства

Из условия 2) теоремы получаем, что

базис пространства

.
Так как

матрица
линейного преобразования

то

.
Следовательно,

− линейно независимая система векторов
и, значит, матрица

обратима, т. е.

− обратимое преобразование.

3)
1).
Дано, что линейное преобразование

обратимо. Докажем, что ядро

.
Пусть вектор

,
т. е.

Отсюда

.
Следовательно,

.
■

Множество всех
векторов

,
,
называется образом
линейного преобразования

и обозначается символом

.
Итак,

Теперь докажем
следующую теорему.

□ Теорема 3.7.
Множество

является подпространством пространства
.

Доказательство.
Пусть
,
−
произвольные векторы подпрост-ранства

.
Тогда найдутся такие векторы

,

в пространстве

что

.
Теперь имеем

Из этих равенств
вытекает, что векторы

принадлежат множеству

.
Следовательно,

является подпространством. ■

В следующей теореме
содержится задание подпространства

в виде линейной оболочки.

□ Теорема 3.8.
Если система
векторов

,
,…,

базис пространства

то

=

.

Доказательство
теоремы
вытекает из следующей цепочки равносильных
утверждений:

■

Пример

Найти образ
линейного преобразования

Решение.
Диагональная система

,
,

является базисом пространства

.
Так как

то из теоремы 3.8
следует, что

Задачи

1. Доказать, что
существует единственное линейное
преобразование

пространства

,
переводящее его базис

соответственно в векторы

.
Найти матрицу этого линейного
преобразования.

2. Найти ядро
линейного преобразования, которое
переводит базис пространства

соответственно в векторы

3. Доказать, что
линейное преобразование

обратимо тогда и только тогда, когда из
неравенства

следует, что

4. Доказать
равносильность следующих утверждений:

а)

;

б)

.

5. Доказать, что
для каждого линейного преобразования

справедливо равенство

6. Доказать, что
для каждого линейного преобразования

пространства

сумма размерностей ядра и образа равна
n,

т. е.

.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Обратные задачи аффинных преобразований или об одной красивой формуле

Время на прочтение
12 мин

Количество просмотров 21K

В этой статье я расскажу об одной необычной формуле, которая позволяет взглянуть под новым углом на аффинные преобразования, а особенно на обратные задачи, которые возникают в связи с этими преобразованиями. Обратными я буду называть задачи, требующие вычисления обратной матрицы: нахождение преобразования по точкам, решение системы линейных уравнений, преобразование координат при смене базиса и т.д. Сразу оговорюсь, что в статье не будет ни фундаментальных открытий, ни уменьшения алгоритмической сложности — я просто покажу симметричную и легко запоминающуюся формулу, с помощью которой можно решить неожиданно много ходовых задач. Для любителей математической строгости есть более формализованное изложение здесь [1] (ориентированно на студентов) и небольшой задачник вот здесь [2].

Аффинное преобразование обычно задается матрицей

$A$ и вектором трансляции и действует на вектор‑аргумент по формуле

Впрочем, можно обойтись и без

, если воспользоваться аугментированной матрицей и однородными координатами для аргумента (как хорошо известно пользователям OpenGL). Однако оказывается, кроме этих форм записи можно ещё использовать детерминант особой матрицы, в которой содержатся как координаты аргумента, так и параметры, задающие преобразование. Дело в том, что детерминант обладает свойством линейности по элементам любой своей строки или столбца и это позволяет использовать его для представления аффинных преобразований. Вот, собственно, как можно выразить действие аффинного преобразования на произвольный вектор

Не спешите убегать в ужасе — во‑первых, здесь записано преобразование, действующее на пространствах произвольной размерности (отсюда так много всего), а во‑вторых, хотя формула и выглядит громоздко, но просто запоминается и используется. Для начала, я выделю логически связанные элементы рамками и цветом

Итак, мы видим, что действие любого аффинного преобразования

на вектор можно представить как отношение двух детерминантов, при чем вектор‑аргумент входит только в верхний, а нижний — это просто константа, зависящая только от параметров.

Выделенный синим цветом вектор

— это аргумент, вектор на который действует аффинное преобразование

. Здесь и далее нижние индексы обозначают компоненту вектора. В верхней матрице компоненты

занимают почти весь первый столбец, кроме них в этом столбце только ноль (сверху) и единица (снизу). Все остальные элементы в матрице — это векторы‑параметры (нумеруются верхним индексом, взятым в скобки, чтобы не перепутать со степенью) и единицы в последней строке. Параметры выделяют среди множества всех аффинных преобразований то, которое нам нужно. Удобство и красота формулы в том, что смысл этих параметров очень прост: они задают аффинное преобразование, которое переводит векторы

$vec{x}^{,(i)}$ в

$vec{X}^{(i)}$ . Поэтому векторы

$vec{x}^{,(1)},dots,vec{x}^{,(n+1)}$ , мы будем называть «входными» (в матрице они обведены прямоугольниками) — каждый из них покомпонентно записан в своём столбце, снизу дописывается единица. Сверху же записываются «выходные» параметры (выделены красным цветом)

$vec{X}^{(1)}, dots, vec{X}^{(n+1)}$ , но теперь уже не покомпонентно, а как цельная сущность.

Если кого‑то удивляет такая запись, то вспомните о векторном произведении

$[vec{a} times vec{b}] = det begin{pmatrix} vec{e}_1 & vec{e}_2 & vec{e}_3\ a_1 & a_2 & a_3 \ b_1 & b_2 & b_3 \ end{pmatrix},$

где была очень похожая структура и первую строку точно так же занимали векторы. При этом необязательно, чтобы размерности векторов

$vec{X}^{(i)}$ и

$vec{x}^{(i)}$ совпадали. Все детерминанты считаются как обычно и допускают обычные «трюки», например, к любому столбцу можно прибавить другой столбец.

С нижней матрицей всё предельно просто — она получается из верхней вычёркиванием первой строки и первого столбца. Недостаток (1) в том, что приходится считать детерминанты, однако если эту рутинную задачу переложить на компьютер, то окажется, что человеку останется лишь правильно заполнить матрицы числами из его задачи. При этом с помощью одной формулы можно решить довольно много распространенных на практике задач:

нахождение аффинного преобразования по точкам;
расчёт барицентрических координат;
полилинейную интерполяцию;
задачи на линейные преобразования (без трансляции):
- обращение матрицы;
- правило Крамера в одну формулу (нет, то что вы видели, это не в одну формулу);
- пересчет координат вектора при изменении базиса;
- интерполяцию полиномами Лагранжа.

Аффинное преобразование по трем точкам на плоскости

Под действием неизвестного аффинного преобразования три точки на плоскости перешли в другие три точки. Найдем это аффинное преобразование.
Для определенности, пусть наши входные точки

а результатом действия преобразования стали точки

Найдем аффинное преобразование

На самом деле, решать эту задачу можно по‑разному: с помощью системы линейных уравнений, барицентрических координат… но мы пойдем своим путем. Думаю, по использованным обозначениям Вы догадываетесь к чему я клоню: берём уравнение (1) для размерности

$n=2$ и подставляем

$vec{x}^{,(i)}$ в качестве входных параметров, а

$vec{X}^{,(i)}$ — в качестве выходных

а дальше остается лишь посчитать детерминанты

Намётанный глаз легко обнаружит здесь поворот на

$30^{circ}$ и трансляцию на

$((3 + sqrt{3})/2, 2)^{mathsf{T}}$ .

Когда формула применима?

Входные и выходные векторы могут иметь разную размерность — формула применима для аффинных преобразований, действующих на пространствах любой размерности. Впрочем, входных точек должно быть достаточно и они не должны «слипаться»: если аффинное преобразование действует из

$n$ -мерного пространства — точки должны образовывать невырожденный симплекс из

$n+1$ точки. Если это условие не выполнено, то однозначно восстановить преобразование невозможно (никаким методом вообще, не только этим) — формула предупредит об этом нулём в знаменателе.

Зачем восстанавливать аффинные преобразования программисту?

Часто нужно найти преобразование между двумя картинками (для расчёта положения камеры, например). Если у нас найдётся несколько надёжных особых точек (фич) на этих изображениях, ну или просто не хочется начинать сразу с ранзаков и борьбы с аутлаерами, то вполне можно использовать эту формулу.

Еще один пример — текстурирование. Вырезать треугольник из текстуры и натянуть на треугольник где‑нибудь на плоскости или в пространстве — типичная задача на применение аффинного преобразования к точкам из пространства текстуры, переводящее их в пространство, где «живут модели». И довольно часто нам легко указать каким точкам на текстуре соответствуют вершины треугольника модели, но вот установить куда переходят неугловые точки может потребовать некоторых размышлений. С этой же формулой достаточно просто вставить числа в правильные ячейки и будет вот такая красота.

Из того, с чем приходилось лично сталкиваться: нейросеть выдаёт координаты углов маркера и мы хотим «дополнить реальность» виртуальным объектом, который располагается на маркере.
Очевидно, при перемещении маркера объект должен повторять все его движения. И тут формула (1) как нельзя кстати — она нам поможет передвинуть объект вслед за маркером.

Или вот еще пример: нужно запрограммировать вращение различных объектов на сцене с помощью инструмента «гизмо». Для этого мы должны уметь вращать выбранную модель вокруг трех осей параллельных осям координат и проходящих через центр объекта. На картинке показан случай вращения модели вокруг оси параллельной

$OZ$ .

В конечном итоге всё сводится к двумерной задаче о вращении вокруг произвольной точки. Давайте даже решим её для какого‑то простого случая, скажем, поворота на

против часовой стрелки вокруг

$(a;b)$ (общий случай решается так же, просто не хочется загромождать выкладки синусами‑косинусами). Конечно, можно пойти путём самурая и перемножить три матрицы (трансляция точки вращения в ноль, собственно вращение и трансляция назад), а можно и так — найти координаты любых трёх точек до и после вращения и воспользоваться формулой. Первая точка находится легко — мы и так знаем, что

$(a;b)$ переходит в себя. Давайте рассмотрим точку на единичку правее, для неё верно

. Ну и ещё одну на единичку ниже, тут очевидно, что

. Дальше всё просто

Барицентрические координаты

Разложим верхний детерминант (1) по первой строке согласно правилу Лапласа. Ясно, что в результате мы получим некоторую взвешенную сумму векторов

$vec{X}^{(i)}$ . Оказывается, что коэффициентами в этой сумме служат барицентрические координаты аргумента

по отношению к симплексу, заданному

$vec{x}^{,(i)}$ (за доказательствами смотреть в [1]). Если нас интересуют только барицентрические координаты точки, можно схитрить и заполнить первую строку единичными ортами — после вычисления детерминантов мы получим вектор, чьи компоненты совпадают с барицентрическими координатами

. Графически такое преобразование

, переводящее точку в пространство её барицентрических координат, будет выглядеть следующим образом

Давайте опробуем этот «рецепт» на практике. Задача: найти барицентрические координаты точки по отношению к заданному треугольнику. Пусть для определённости это будет точка

$(2,2)^mathsf{T}$ , а в качестве вершин треугольника возьмём

Дело за малым — взять (1) для

$n=2$ , правильно расположить там данные задачи и посчитать детерминанты

Вот и решение: барицентрическими координатами

$(2,2)^mathsf{T}$ по отношению к заданному треугольнику есть

$0.6$ ,

$0.3$ и

$0.1$ . В программировании расчёт барицентрических координат часто возникает в контексте проверки, находится ли точка внутри симплекса (тогда все барицентрические координаты больше ноля и меньше единицы), а также для различных интерполяций, о которых сейчас пойдёт речь.

Заметьте, формула (1) обладает приятной двойственностью: если разложить детерминант по первому столбцу — получим стандартную запись для аффинной функции, а если по первой строке — аффинную комбинацию выходных векторов.

Полилинейная интерполяция

Итак, мы обнаружили, что аффинное преобразование взвешивает выходные векторы с коэффициентами, равными барицентрическим координатам аргумента. Естественно воспользоваться этим свойством для полилинейной интерполяции.

Интерполяция цвета

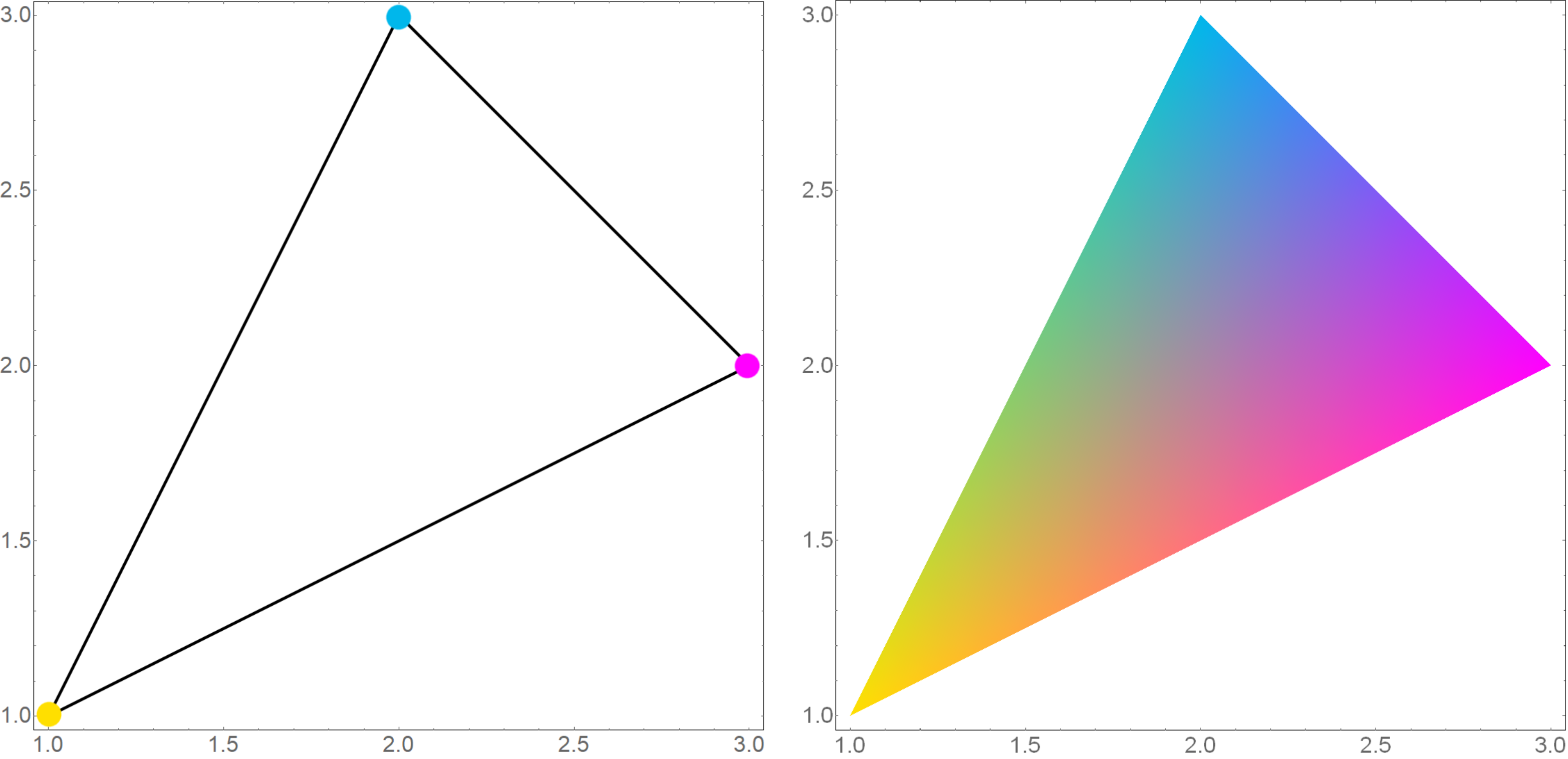
Для примера, давайте просчитаем стандартный GL‑ный «привет мир» — раскрашенный треугольник. Конечно, OpenGL прекрасно умеет интерполировать цвета и тоже делает это с помощью барицентрических координат, но сегодня мы это сделаем сами.

Задача: в вершинах треугольника заданы цвета, произвести интерполяцию цвета внутри треугольника. Для определённости, пусть вершины нашего треугольника имеют координаты

Припишем им цвета: жёлтый, циан и маджента

Тройки чисел — это RGB‑компоненты цвета. Возьмём (1) и правильно расставим входные данные

Здесь компоненты

указывают как закрасить точку

$(x,y)$ в терминах RGB. Давайте посмотрим, что вышло.

Можно сказать, мы только что произвели аффинное преобразование двумерного пространства картинки в трехмерное пространство цветов (RGB).

Интерполяция нормалей (шейдинг Фонга)

Мы можем вкладывать самый разный смысл в векторы, которые мы интерполируем, в том числе это могут быть векторы нормалей. Более того, именно так и делается шейдинг Фонга (Phong shading), только после интерполяции векторы нужно нормировать. Для чего нужна такая интерполяция хорошо иллюстрирует следующее изображение (взятое из Википедии commons.wikimedia.org/w/index.php?curid=1556366).

Приводить расчёты, я думаю, уже не стоит — все детали рассмотрены в [2], а вот картинку с результатом я покажу.

Векторы на ней не единичные и для использования в шейдинге Фонга должны быть сначала отнормированы, к тому же, для наглядности, они направлены в очень разные стороны, что редко бывает на практике.

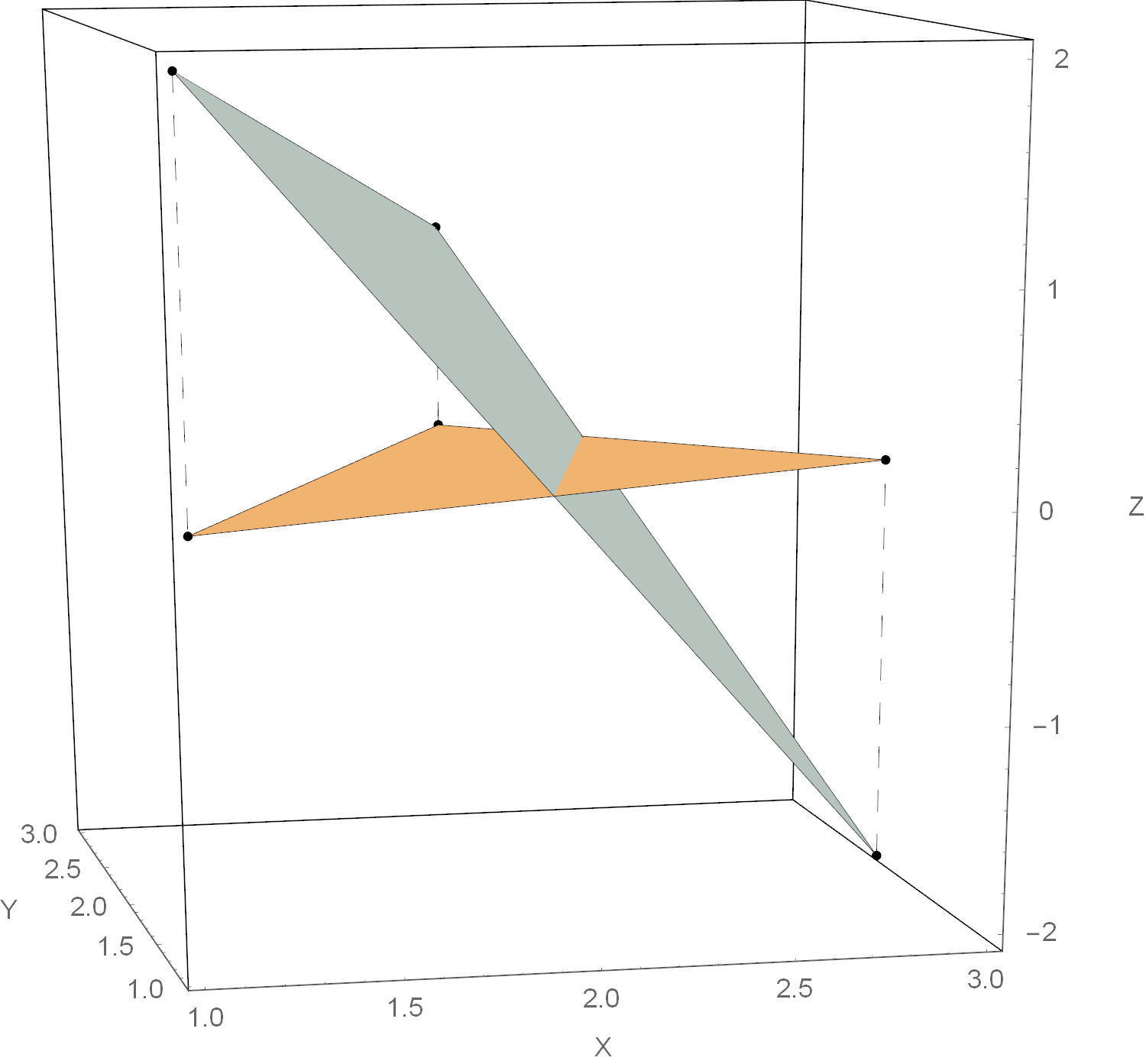
Найти плоскость по трем точкам

Рассмотрим еще один необычный пример применения аффинного преобразования.
Даны три точки

Найдём уравнение проходящей через них плоскости в виде

. И сделаем это с помощью аффинных преобразований: известно ведь, что они переводят плоскости в плоскости. Для начала спроектируем все точки на плоскость

$XY$ , что несложно. А теперь установим аффинное преобразование, которое переводит проекции точек в изначальные трехмерные точки

и которое «подхватит» вместе с точками и всю плоскость

$XY$ да так, что после преобразования она будет проходить через интересующие нас точки.

Как обычно, мы лишь должны распределить числа по элементам матриц

Перепишем последнее выражение в привычном виде

и нарисуем что вышло.

Линейные преобразования

Несмотря на всю практическую важность аффинных преобразований, чаще приходится иметь дело с линейными. Конечно, линейные преобразования — частный случай аффинных, оставляющие на месте точку

. Это позволяет немного упростить формулу (ведь один из столбцов будет состоять почти из одних нулей и по нему можно разложить детерминант)

Как видим, из формулы пропала последняя строчка с единицами и один столбец. Этот результат вполне согласуется с нашими представлениями, что для задания линейного преобразования достаточно указать его действие на

$n$ линейно независимых элементах.

Линейное преобразование по трем точкам

Давайте решим задачу, чтобы увидеть как всё работает. Задача: известно, что под действием некоторого линейного преобразования

Найдём это линейное преобразование.

Берём упрощённую формулу и ставим правильные числа на правильные места:

Готово!

Нахождение обратного преобразования

Напомню, что матрица линейного преобразования

содержит в своих столбцах образы единичных векторов:

Итак, действуя матрицей на орты, мы получаем её столбцы. А что можно сказать об обратном преобразовании (допустим, оно существует)? Оно все делает «наоборот»:

Постойте‑ка, ведь мы только что нашли образы трёх точек под действием линейного преобразования — достаточно, чтоб восстановить само преобразование!

где

$vec{e}_1 = (1; 0; 0)^mathsf{T}$ ,

$vec{e}_2 = (0; 1; 0)^mathsf{T}$ и

$vec{e}_3 = (0; 0; 1)^mathsf{T}$ .

Не будем себя ограничивать трехмерным пространством и перепишем предыдущую формулу в более общем виде

Как видим, надо приписать к матрице слева колонку с компонентами вектора‑аргумента, сверху — строчку с координатными векторами, а дальше дело только за умением брать детерминанты.

Задача на обратное преобразование

Давайте опробуем приведённый метод на практике. Задача: обратить матрицу

Воспользуемся (2) для

$n=3$

Сразу видно, что

Правило Крамера в одну формулу

Ещё со школы мы сталкиваемся с уравнениями вида

Если матрица

невырожденная, то решение можно записать в виде

Хм… не в предыдущем ли разделе я видел такое же выражение, только вместо

$b$ стояла другая буква? Воспользуемся им.

Это не что иное, как правило Крамера. В этом легко убедиться, разложив детерминант по первой строке: вычисление

$x_i$ как раз предполагает, что мы вычеркнем столбец с

$vec{e}_i$ , а с ним и

$i$ ‑й столбец матрицы

. Теперь если переставить столбец

$b$ на место удалённого, то мы как раз и получим правило «вставить столбец

$b$ на место

$i$ ‑го столбца и найти детерминант». И да, со знаками всё хорошо: одни

$pm$ мы генерируем при разложении по строке, а другие при перестановке — в результате они друг друга компенсируют.

Присмотревшись к полученному уравнению, можно заметить его схожесть с уравнением для нахождения барицентрических координат: решение системы линейных уравнений— это нахождение барицентрических координат точки

по отношению к симплексу, одна из вершин которого

, а остальные задаются столбцами матрицы

Решение системы линейных уравнений

Решим систему линейных уравнений

В матричной форме она выглядит так

Используем полученную формулу

откуда ответ

Преобразование координат вектора при смене базиса

Предположим, что мы выбрали новый базис (перешли к другой системе координат). Известно, что новые координаты векторов выражаются через старые линейно. Поэтому неудивительно, что мы можем использовать наш инструментарий для смены базиса. Как это сделать, я покажу на примере.

Итак, пускай мы перешли от стандартного базиса

${vec{e}_x, vec{e}_y}$ к базису, состоящему из векторов

В старом базисе задан вектор

$vec{x}=(3,4)^mathsf{T}$ . Найдём координаты этого вектора в новом базисе. В новой координатной системе векторы нового базиса станут ортами и будут иметь координаты

здесь и далее штрихи возле столбцов означают, что координаты в них относятся к новому базису. Несложно догадаться, что линейное преобразование, которое переводит

также нужным образом преобразует координаты нашего вектора. Осталось только применить формулу

Решение задачи привычным образом требует обращения матрицы (которое, впрочем, также в основном состоит из вычисления детерминантов) и умножения

Мы лишь упаковали эти шаги в одну формулу.

Почему формула работает для обратных задач?

Эффективность формулы в решении обратных задач объясняется тем, что выполняется следующее равенство (доказательство есть в [1])

Таким образом, формула прячет в себе обратную матрицу и умножение на еще одну матрицу в придачу. Это выражение и есть стандартное решение задачи нахождения линейного преобразования по точкам. Заметьте, что делая вторую матрицу в произведении единичной, мы получим просто обратную матрицу. С ее помощью решается система линейных уравнений и задачи, которые к ней сводятся: нахождение барицентрических координат, интерполяция полиномами Лагранжа, и т.д. Однако, представление в виде произведения двух матриц, не даёт нам получить те самые «два взгляда», связанные с разложением по первой строке и по первому столбцу.

Интерполяция Лагранжа и ее свойства

Напомню, что интерполяция Лагранжа — это нахождение полинома наименьшей степени проходящего через точки

$dots$ ,

. Не то чтобы это была распространённая в программистской практике задача, но всё равно давайте ее рассмотрим.

Как связаны полиномы и линейные преобразования?

Дело в том, что полином

можно рассматривать как линейное преобразование, которое отображает вектор

$(x^n; x^{n-1}; dots; 1)^T$ в

. Значит, задача интерполяции точек

$dots$ ,

сводится к нахождению такого линейного преобразования, что

а это мы делать умеем. Подставим правильные буквы в правильные ячейки и получим формулу

Доказательство, что это будет именно полином Лагранжа (а не чей‑то другой), можно посмотреть в [1]. Кстати, выражение в знаменателе — это определитель Вандермонда. Зная это и разложив детерминант в числителе по первой строке, придем к более привычной формуле для полинома Лагранжа.

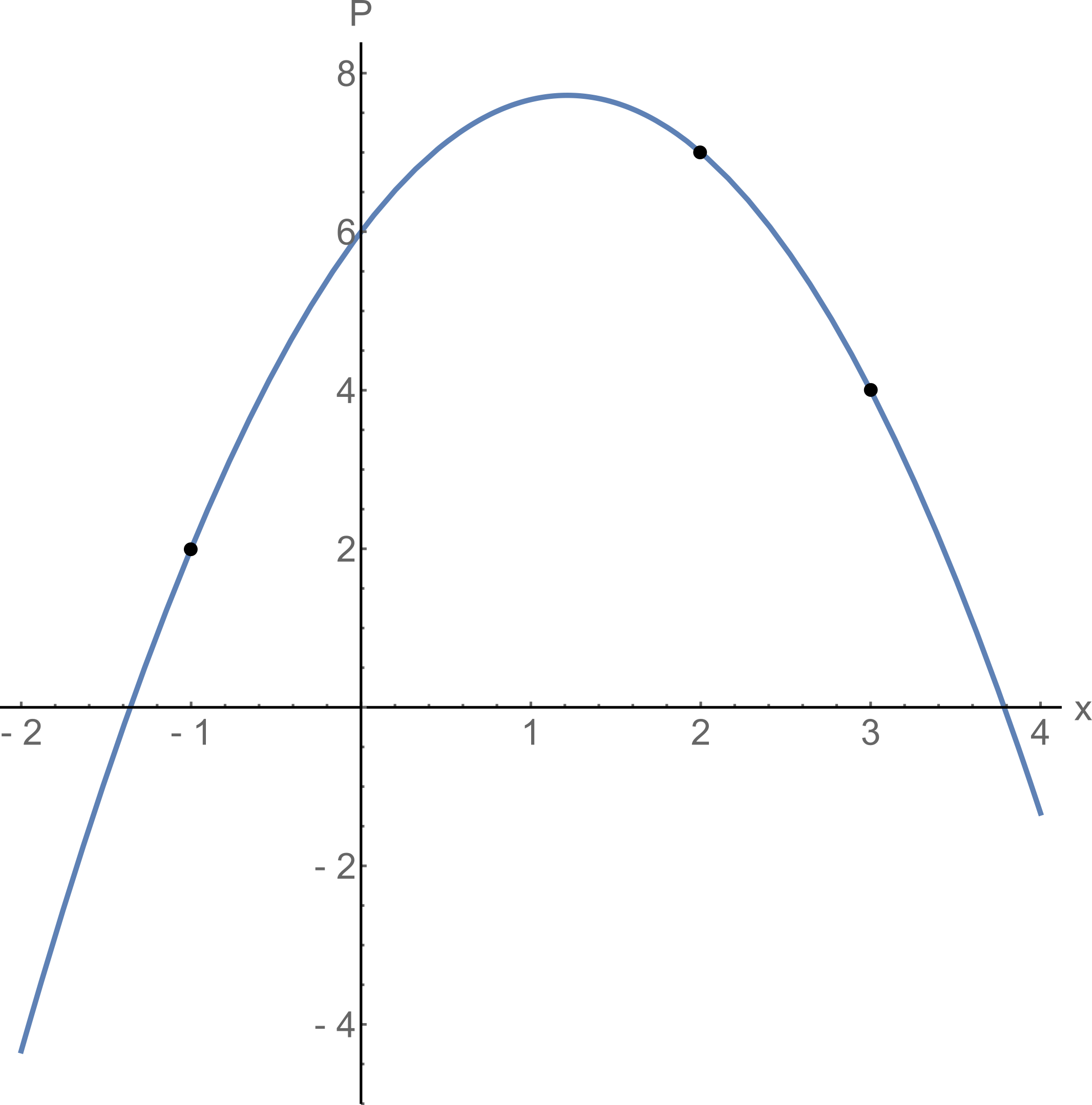
Задача на полином Лагранжа

Сложно ли этим пользоваться? Давайте попробуем силы на задаче: найти полином Лагранжа, проходящий через точки

Подставим эти точки в формулу

На графике всё будет выглядеть так.

Свойства полинома Лагранжа

Разложив верхний детерминант по первой строке и первому столбцу, мы взглянем на полином Лагранжа с двух разных сторон. В первом случае получим классическую формулу из Википедии, а во втором — запись полинома в виде суммы одночленов

, где

А ещё мы теперь можем сравнительно просто доказывать довольно замысловатые утверждения. Например, в [2] в одну строчку доказывается, что сумма базисных полиномов Лагранжа равна единице и что полином Лагранжа, интерполирующий

$(a_0;a_0^{n+1})$ ,

$dots$ ,

$(a_n;a_n^{n+1})$ , имеет в нуле значение

$(-1)^{n}a_0cdotcdotscdot a_n$ . Ну и не Лагранжем единым — подобный подход можно применить к интерполяции синусами‑косинусами или какими‑то другими функциями.

Заключение

Спасибо всем, кто дочитал до конца. В этой статье мы решали стандартные задачи с помощью одной нестандартной формулы. Мне она понравилась тем, что, во‑первых, показывает, что аффинные(линейные) преобразования, барицентрические координаты, интерполяция и даже полиномы Лагранжа тесно связаны. Ведь когда решения задач записываются единообразно, мысль об их сродстве возникает сама собой. Во‑вторых, большую часть времени мы просто расставляли входные данные в правильные ячейки без дополнительных преобразований.

Задачи, которые мы рассматривали, можно решить и вполне привычными методами. Однако, для задач небольшой размерности или учебных задач формула может быть полезной. Кроме того, мне она кажется красивой.

Список литературы

[1] Beginner’s guide to mapping simplexes affinely

[2] Workbook on mapping simplexes affinely

Источник

Матрица линейного оператора примеры

Построение матрицы по заданной формуле отображения.

Пусть отображение задано с помощью формулы:

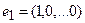
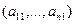
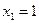
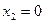
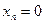
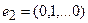
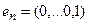
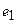
то есть для координат произвольного исходного вектора определены координаты его образа. Тогда, рассматривая вместо произвольного вектора x вектор , найдём его образ, это будет вектор . Для этого в формуле, задающей образ вектора, полагаем , ,…, . Аналогично находим образы для ,…, . Из координат образа вектора составляем 1-й столбец матрицы линейного оператора, аналогично из координат последующих векторов – остальные столбцы. Рассмотрим на примере.

Пример 1. Пусть оператор задан с помощью формулы:

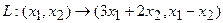
Прежде всего, докажем, что это отображение – действительно линейный оператор.

Отобразим сумму векторов:

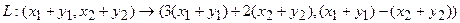
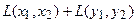
Теперь каждую координату получившегося вектора можем преобразовать:

Аналогично для умножения на константу:

Для того чтобы найти матрицу этого линейного оператора, нужно, как было сказано выше, подставить значения x₁ = 1, x₂ = 0, а затем x₁ = 0, x₂ = 1. В этом примере образы базисных векторов – соответственно (3, 1) и (2, -1).

Поэтому матрица линейного оператора будет иметь вид:

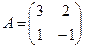
Аналогичным способом решается задача и для 3 и большего количества переменных.

Пример 2. .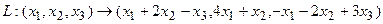

Построим матрицу оператора. Отображая вектор (1,0,0), получаем (1,4,-1), соответственно (0,1,0) переходит в (2,1,-2), а вектор (0,0,1) – в (-1,1,3).

Матрица линейного оператора:

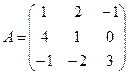
2.2. Построение матрицы оператора в случае, когда известен исходный базис и система векторов, в которую он отображается.

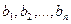
Если задана система из n векторов, образующих базис, и какая-нибудь произвольная система n векторов (возможно, линейно-зависимая), то однозначно определён линейный оператор, отображающий каждый вектор первой системы в соответствующий вектор второй системы.

Матрицу этого оператора можно найти двумя способами: с помощью обратной матрицы и с помощью системы уравнений.

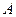
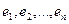
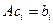
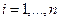
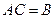
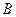
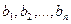
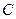
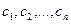
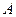
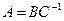
Пусть – матрица оператора в базисе . По условию, для всех индексов . Данные n равенств можно записать в виде одного матричного равенства: , при этом столбцы матрицы – это векторы , а столбцы матрицы – векторы . Тогда матрица может быть найдена в виде .

Пример. Найти матрицу линейного оператора, отображающего базис

в систему векторов .

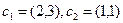
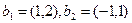
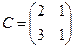
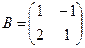
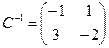
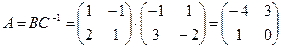
Здесь , , , и получаем:

Проверка осуществляется умножением получившейся матрицы на каждый вектор: .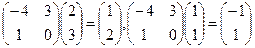

Аналогично решаются подобные задачи и для трёхмерного пространства. В приложении (§5) есть несколько вариантов таких задач.

2.3. Прочие способы нахождения матрицы оператора.

Существуют также примеры, где линейный оператор задаётся другими способами, отличными от рассмотренных в п. 2.1 и 2.2.

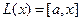
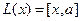
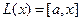
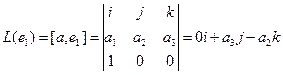
Пример. Линейными операторами являются как правое, так и левое векторное умножение на фиксированный вектор в трёхмерном пространстве, то есть отображения вида и . Построим матрицу одного из этих операторов, . Для этого найдём образы всех трёх базисных векторов линейного пространства.

Аналогично, ,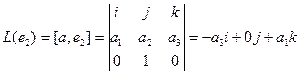

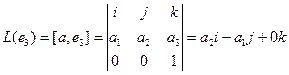
Координаты полученных векторов запишем в виде столбцов матрицы оператора.

Матрица оператора: .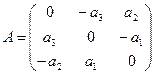

Аналогично можно построить матрицу линейного оператора :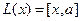

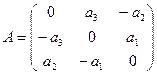
Пример. Линейный оператор дифференцирования в пространстве всех многочленов степени не более n. Это пространство размерности n + 1. Возьмём в качестве базиса элементы , , ,…, .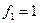

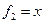
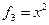
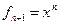
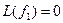
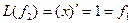
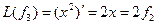
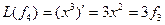
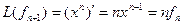
, , , аналогично получим ,…, .

Матрица этого линейного оператора:

Линейные операторы могут отображать не только пространства конечной размерности, но и бесконечномерные пространства. Так, оператор дифференцирования может рассматриваться также в пространстве всех непрерывных функций. (В этом пространстве нет конечного базиса). В этом случае, очевидно, оператор не может быть задан матрицей конечного порядка.

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Для студента самое главное не сдать экзамен, а вовремя вспомнить про него. 10219 – | 7588 – или читать все.

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно

Матрица линейного оператора

Определение 1. Если задан закон, который каждому вектору x?? ставит в соот ветствие вектор y . то говорят, что в линейном пространстве ? задан оператор A , при этом пишут:

Определение 2. Оператор A называется линейным, если для любых x 1 ?? и x 2 ?? и произвольного числа ? выполняются условия:

Рассмотрим теперь в евклидовом пространстве E n базис e 1 ,e 2 . e n и пусть в этом пространстве определён линейный оператор A : y = A x .

Разложим векторы x и y по базису e 1 ,e 2 . e n :

В силу линейности оператора A можно написать

Заметим, что каждый вектор 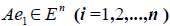, следовательно, его также можно разложить по базису e 1 ,e 2 . e n , т.е.

В силу единственности разложения по данному базису мы можем при равнять коэффициенты при базисных векторах в правых частях формул (1) и (2); тогда получим:

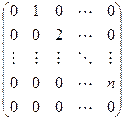
Получили, что линейному оператору A в данном базисе соответствует квадратная матрица

которая называется матрицей линейного оператора A , i -й столбец которой состоит из координат вектора Ae i (i = 1,2. n ) относительно данного базиса. Отметим, что матрица A оператора A зависит от выбора базиса e 1 ,e 2 . e n .

Итак, мы показали, что всякому линейному оператору A в евклидовом пространстве E n соответствует матрица A ; можно доказать и обратное утверждение: всякую квадратную матрицу A можно рассматривать как матрицу некоторого линейного оператора A в данном базисе e 1 ,e 2 . e n .

Представляют интерес невырожденные линейные операторы, т.е. такие операторы, матрицы которых имеют обратную A -1 , т.е. также являются невырожденными. В этом случае каждому вектору y (образу), определённому соотношением, отвечает единственный вектор x (прообраз) и при этом имеет место матричное равенство: X = A -1 ? Y .

Примеры линейных операторов

1. В пространстве 2-мерных векторов линейным оператором является правило

связывающее вектор-прообраз 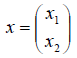с вектором-образом

2. В пространстве бесконечно дифференцируемых функций линейным оператором является операция дифференцирования, ставящая в соответствие каждому элементу этого простран ства его производную функцию.

3. В пространстве многочленов P n (t) линейным оператором является операция умножения многочлена на независимую переменную t .

Пример: Известны образы базисных векторов E 3 под действием оператора A :

Найти матрицу этого оператора в исходном базисе.

Решение: По определению y = A x, значит в матричном виде можно записать, что A = X -1 Y . Для нашего примера получаем

Действия над операторами

Сложение линейных операторов. Пусть x?E n , A и B – два линейных оператора в этом пространстве.

Определение 1. Суммой линейных операторов A и B в E n называется оператор C, определяемый равенством Cx = A x + Bx , где x – любой вектор из E n .

Сумма линейных операторов является линейным оператором, причём его матрица C = A + B, где A и B – матрицы линейных операторов A и B .

Умножение линейного оператора на число. Пусть x?E n , линейный оператор A определён в E n , ? – некоторое число.

Определение 2. Произведением линейного оператора A на число ? называется оператор ?A , определяемый равенством .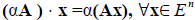

?A является линейным оператором, а матрица этого линейного оператора получается из матрицы A умножением её на число ? , т.е. она равна ? ? A.

Умножение линейных операторов. Пусть x? E n , y ? E n , z ? E n и кроме того в E n определены линейные операторы A и B таким образом, что y = Bx, z = A y .

Определение 3. Произведением A ? B линейных операторов A и B называется оператор C, определяемый соотношением Cx = A (Bx) .

Таким образом, перемножение линейных операторов состоит в последовательном их применении по отношению к вектору x .

Рассмотрим матрицы – столбцы:

и обозначим через A, B и C – соответственно матрицы линейных операторов A, B и C. Тогда Z = A ? (B ? X) = (A ? B) ? X = C ? X , таким образом, C = A ? B, т.е. матрица произведения линей ных операторов также является линейным оператором.

a) (A ? B)(x + y) = A (B(x + y)) = A (Bx + By) = A (Bx) + A (By) = = (A ? B) ? x + (A ? B) ? y

б) (A ? B)(? x) = A (B(? x)) = A (?Bx) =?A (Bx) =? (A ? B)x

Свойства умножения линейных операторов вытекают из свойств умножения матриц.

Определение 4. Линейные операторы A и В называются равными, если 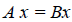. Равенство операторов обозначается как A = B .

Определение 5. Оператор E называется единичным (или тождественным) оператором, если каждому элементу x линейного пространства он ставит в соответствие тот же самый элемент, то есть

1. Понятие линейного оператора

Пусть R и S линейные пространства, которые имеют размерность n и m соответственно. Оператором A действующим из R в S называется отображение вида , сопоставляющее каждому элементу x пространства R некоторый элемент y пространства S. Для этого отображения будем использовать обозначение y= A(x) или y= Ax.

Определение 1. Оператор A действующий из R в S называется линейным, если для любых элементов x₁ и x₂ пространства R и любого λ из числового поля K выполняются соотношения

Если пространство S совпадает с пространством R, то линейный оператор, который действует из R в R называют линейным преобразованием пространства R.

Пусть заданы два векторных пространства n-мерный R и m-мерный S, и пусть в этих пространствах заданы базисы и соответственно. Пусть задано отображение

где A – m×n -матрица с коэффициентами из поля K. Тогда каждому элементу из R соответствует элемент y=Ax из S. Отображение (1) определяет оператор A. Покажем, что этот оператор обладает свойством линейности. Действительно, учитывая свойства умножения матриц, можно записать:

Покажем теперь обратное, т.е. что для любого линейного оператора A, отображающего пространство R в S и произвольных базисов и в R и S соответственно, существует такая матрица A с элементами из численного поля K, что определяемое этой матрицей линейное отображение (1) выражает координаты отображенного вектора y через координаты исходного вектора x.

Пусть x − произвольный элемент в R. Тогда

(3)

является разложением x в по базису .

Применим оператор A к базисным векторам :

(4)

где a_ij − координаты полученного вектора в базисе .

Тогда применяя оператор A к элементу x и учитывая (3) и (4), имеем

Сделаем следующее обозначение:

(6)

Тогда равенство (5) примет следующий вид:

(7)

Из равенства (7) следует, что любой элемент из пространства R при отображении оператором A, в пространстве S и в базисе имеет координаты y_i, i=1,2. m. В свою очередь, из (6) следует, что этим координатам соответствуют линейные комбинации координатов элемента x_j, j=1,2. n с коэффициентами a_ij i=1,2. m; j=1,2. n.

Построим матрицу A с элементами a_ij:

(8)

Тогда выражение (6) можно записать в матричном виде:

Матрица A называется матрицей линейного оператора в заданных базисах и .

2. Сложение линейных операторов

Пусть A и B два линейных оператора действующих из R в S и пусть A и B – mxn − матрицы соответствующие этим операторам.

Определение 2. Суммой линейных операторов A и B называется оператор C, определяемый равенством

где x∈R означает, что x принадлежит пространстве R.

Сумма линейных операторов обозначается так C=A+B. Легко убедится, что сумма линейных операторов также является линейным оператором.

Применим оператор C к базисному вектору e_j, тогда:

Ce_j= Ae_j+ Be_j=	n	(a_ij+b_ij) e_j
∑
j= 1

Следовательно оператору C отвечает матрица ,где i=1,2. m, j=1,2. n, т.е.

3. Умножение линейных операторов

Пусть заданы три линейных пространства R, S и T. Пусть линейный оператор B отображает R в S, а линейный оператор A отображает S в T.

Определение 3. Произведением операторов A и B называется оператор C, для которого выполняется следующее равенство при любом x из R:

Произведение линейных операторов обозначается C=AB. Легко убедится, что произведение линейных операторов также является линейным оператором.

Таким образом оператор C отображает пространство R в T. Выберем в пространствах R, S и T базисы и обозначим через A, B и C матрицы операторов A, B и C соответствующие этим базисам. Тогда отображения линейных операторов A, B, C

можно записать в виде матричных равенств

где x, y, z − векторы x, y, z − представленные в виде координатных столбцов. Тогда

Учитывая произвольность х, получим

Следовательно произведению операторов C=AB соответствует матричное произведение C=AB.

4. Умножение линейного оператора на число

Пусть задан линейный оператор A отображающий R в S и некоторое число λ из поля K.

Определение 4. Произведением оператора A на число λ называется оператор C, для которого выполняется следующее равенство при любом x из R:

Таким образом оператор C отображает пространство R в S. Выберем в пространствах R и S базисы и обозначим через A матрицу оператора A соответствующее этим базисам векторные равенства

можно записать в виде матричных равенств

где x, y, z − векторы x, y, z − представленные в виде координатных столбцов. Тогда

Учитывая произвольность х, получим

Следовательно произведению оператора C на число λ соответствует произведение матрицы A на число λ.

5. Нулевой оператор

Оператор, отображающий все элементы пространства R в нулевой элемент пространства S называется нулевым оператором и обозначается через O. Действие нулевого оператора можно записать так:

6. Противоположный оператор

Противоположным оператору A называется оператор −A удовлетворяющий равенству:

7. Ядро линейного оператора

Определение 5. Ядром линейного оператора A называется множество всех тех элементов x пространства R, для которых выполняется следующее равенство: Ax=0.

Ядро линейного оператора также называют дефектом оператора. Ядро линейного оператора обозначается символом ker A.

8. Образ линейного оператора

Определение 6. Образом линейного оператора A называется множество всех элементов y пространства R, для которых выполняется следующее равенство: y=Ax для всех x из R.

Образ линейного оператора обозначается символом im A.

9. Ранг линейного оператора

Определение 7. Рангом линейного оператора A обозначаемое символом rang A называется число равное размерности образа im A оператора A, т.е.: rang A=dim(im A).

Ядро и образ линейного отображения

Ядром линейного отображения называется множество таких векторов , что , т.е. множество векторов из , которые отображаются в нулевой вектор пространства . Ядро отображения обозначается:

Образом линейного отображения называется множество образов всех векторов из . Образ отображения обозначается или

Заметим, что символ следует отличать от — мнимой части комплексного числа.

Примеры ядер и образов линейных отображений

1. Ядром нулевого отображения является все пространство , а образом служит один нулевой вектор, т.е.

2. Рассмотрим отображение , которое ставит в соответствие каждому вектору n-мерного линейного пространства его координатный столбец относительно заданного базиса . Ядром этого отображения является нулевой вектор пространства , поскольку только этот вектор имеет нулевой координатный столбец . Образ преобразования совпадает со всем пространством , так как это преобразование сюръективно (любой столбец из является координатным столбцом некоторого вектора пространства ).

3. Рассмотрим отображение , которое каждому вектору n-мерного евклидова пространства ставит в соответствие алгебраическое значение его проекции на направление, задаваемое единичным вектором . Ядром этого преобразования является ортогональное дополнение — множество векторов, ортогональных . Образом является все множество действительных чисел .

4. Рассмотрим отображение , которое каждому многочлену степени не выше ставит в соответствие его производную. Ядром этого отображения является множество многочленов нулевой степени, а образом — все пространство .

Свойства ядра и образа линейного отображения

1. Ядро любого линейного отображения является подпространством: .

В соответствии с определением требуется доказать, что множество является непустым и замкнутым относительно операций сложения векторов и умножения вектора на число. В самом деле, из однородности отображения следует, что

т.е. нулевой вектор отображается в нулевой вектор . Следовательно, ядро любого линейного отображения не является пустым и содержит, по крайней мере, нулевой элемент: . Покажем, что множество замкнуто по отношению к операциям сложения векторов и умножения вектора на число. Действительно:

Следовательно, множество является линейным подпространством пространства .

2. Образ любого линейного отображения является подпространством: .

В самом деле, докажем, например, замкнутость множества по отношению к операции умножения вектора на число. Если , то существует вектор такой, что . Тогда , то есть .

Поскольку ядро и образ линейного отображения являются линейными подпространствами (свойства 1 и 2), можно говорить об их размерностях.

Дефектом линейного отображения называется размерность его ядра: , а рангом линейного отображения — размерность его образа: .

3. Ранг линейного отображения равен рангу его матрицы (определенной относительно любых базисов).

В самом деле, если любой базис пространства , то . Поэтому максимальное число линейно независимых векторов системы (ранг системы векторов) равно максимальному числу линейно независимых столбцов матрицы отображения, т.е. рангу матрицы: .

4. Линейное отображение инъективно тогда и только тогда, когда , другими словами, когда дефект отображения равен нулю: .

Действительно, образом нулевого вектора служит нулевой вектор . Поэтому, если отображение инъективно, то ядро содержит только нулевой вектор , иначе два разных вектора имели бы один и тот же образ . Обратно, при условии разные векторы не могут иметь одинаковые образы , так как в этом случае из равенств , следует, что ненулевой вектор (приходим к противоречию).

5. Линейное отображение сюръективно тогда и только тогда, когда , другими словами, когда ранг отображения равен размерности пространства образов: .

6. Линейное отображение биективно (значит, обратимо) тогда и только тогда, когда и одновременно.

Теорема (9.1) о размерностях ядра и образа. Сумма размерностей ядра и образа любого линейного отображения равна размерности пространства прообразов:

Действительно, пусть . Выберем в подпространстве базис и дополним его векторами до базиса всего пространства . Покажем, что векторы образуют базис подпространства .

Во-первых, , так как образ любого вектора линейно выражается через векторы

Во-вторых, образующие линейно независимы. Если их линейная комбинация равна нулевому вектору:

то вектор принадлежит ядру (его образ — нулевой вектор). Однако, по построению этот вектор принадлежит алгебраическому дополнению . Учитывая, что , заключаем: . Получили разложение нулевого вектора по линейно независимой системе векторов, значит, все коэффициенты . Поэтому равенство справедливо только для тривиальной линейной комбинации, т.е. система векторов линейно независимая.

Таким образом, векторы образуют базис подпространства , а его размерность определяется количеством базисных векторов, т.е. , что равносильно (9.3).

Следствие. Линейное отображение биективно (значит, обратимо) тогда и только тогда, когда обратима его матрица (определенная относительно любых базисов).

Действительно, для обратимости преобразования (см. свойство 6) его матрица (размеров ) должна удовлетворять условиям (см. свойства 3,4,5):

Тогда по теореме 9.1 заключаем, что , т.е. матрица — квадратная n-го порядка и невырожденная , что и требовалось доказать.

Обратимые линейные отображения называются также невырожденными (имея в виду невырожденность их матрицы).

Линейные операторы

1. Понятие линейного оператора

где A — m×n -матрица с коэффициентами из поля K. Тогда каждому элементу из R соответствует элемент y=Ax из S. Отображение (1) определяет оператор A. Покажем, что этот оператор обладает свойством линейности. Действительно, учитывая свойства умножения матриц, можно записать:

Пусть x − произвольный элемент в R. Тогда

(3)

является разложением x в по базису .

Применим оператор A к базисным векторам :

(4)

где a_ij − координаты полученного вектора в базисе .

Тогда применяя оператор A к элементу x и учитывая (3) и (4), имеем

Сделаем следующее обозначение:

(6)

Тогда равенство (5) примет следующий вид:

(7)

Построим матрицу A с элементами a_ij:

(8)

Тогда выражение (6) можно записать в матричном виде:

Матрица A называется матрицей линейного оператора в заданных базисах и .

2. Сложение линейных операторов

Пусть A и B два линейных оператора действующих из R в S и пусть A и B — mxn − матрицы соответствующие этим операторам.

Определение 2. Суммой линейных операторов A и B называется оператор C, определяемый равенством

где x∈R означает, что x принадлежит пространстве R.

Применим оператор C к базисному вектору e_j, тогда:

Ce_j= Ae_j+ Be_j=	n	(a_ij+b_ij) e_j
∑
j= 1

Следовательно оператору C отвечает матрица ,где i=1,2. m, j=1,2. n, т.е.

3. Умножение линейных операторов

можно записать в виде матричных равенств

где x, y, z − векторы x, y, z − представленные в виде координатных столбцов. Тогда

Учитывая произвольность х, получим

Следовательно произведению операторов C=AB соответствует матричное произведение C=AB.

4. Умножение линейного оператора на число

Пусть задан линейный оператор A отображающий R в S и некоторое число λ из поля K.

можно записать в виде матричных равенств

где x, y, z − векторы x, y, z − представленные в виде координатных столбцов. Тогда

Учитывая произвольность х, получим

Следовательно произведению оператора C на число λ соответствует произведение матрицы A на число λ.

5. Нулевой оператор

6. Противоположный оператор

Противоположным оператору A называется оператор −A удовлетворяющий равенству:

7. Ядро линейного оператора

8. Образ линейного оператора

Образ линейного оператора обозначается символом im A.

9. Ранг линейного оператора

источники:

http://mathhelpplanet.com/static.php?p=yadro-i-obraz-linyeinogo-otobrazheniya

http://matworld.ru/linear-algebra/linear-operator.php

Источник

Ортогональные преобразования.

Начать изучение
Определение линейных преобразований.

Начать изучение
Произведение линейных преобразований.

Начать изучение
Образ вектора при линейном преобразовании.

Начать изучение

Ортогональные преобразования.

Определение.

Ортогональными называются такие преобразования плоскости, которые не меняют расстояния между любыми двумя точками, то есть преобразования (f) ортогональное, если для любых точек (A) и (B) выполнено (|AB|=|f(A)f(B)|).

Основными примерами ортогональных преобразований служат параллельный перенос, поворот и осевая симметрия.

Получим координатную запись ортогонального преобразования в декартовой прямоугольной системе координат (O, boldsymbol{e}_{1}, boldsymbol{e}_{2}). Обозначим через (A) и (B) концы базисных векторов: (boldsymbol{e}_{1}=overrightarrow{OA}), (boldsymbol{e}_{2}=overrightarrow{OB}) (рис. 12.1). При ортогональном преобразовании равнобедренный прямоугольный треугольник (OAB) перейдет в равный ему треугольник (O^{*}A^{*}B^{*}). Рассмотрим произвольную точку (M(x, y)). Она перейдет в точку (M^{*}) с координатами ((x^{*}, y^{*})). Нам надо выразить ((x^{*}, y^{*})) через ((x, y)).

Рис. 12.1. Ортогональное преобразование.

По определению координат (overrightarrow{OM}=xoverrightarrow{OA}+yoverrightarrow{OB}). Отсюда следует, что (overrightarrow{O^{*}M^{*}}=xoverrightarrow{O^{*}A^{*}}+yoverrightarrow{O^{*}B^{*}}). Действительно, векторы (overrightarrow{O^{*}A^{*}}) и (overrightarrow{O^{*}B^{*}}) взаимно перпендикулярны и по длине равны 1, а потому компоненты (overrightarrow{O^{*}M^{*}}) по этим векторам равны его скалярным проекциям на них. Эти проекции равны проекциям (overrightarrow{OM}) на (boldsymbol{e}_{1}, boldsymbol{e}_{2}), что видно из равенства соответствующих треугольников. Теперь мы можем написать
$$
overrightarrow{OM^{*}}=overrightarrow{OO^{*}}+overrightarrow{O^{*}M^{*}}=overrightarrow{OO^{*}}+xoverrightarrow{O^{*}A^{*}}+yoverrightarrow{O^{*}B^{*}}.label{ref1}
$$

Обозначим через (varphi) угол между (overrightarrow{O^{*}A^{*}}) и (boldsymbol{e}_{1}). Поскольку (|overrightarrow{O^{*}A^{*}}|=1), координаты этого вектора в базисе (boldsymbol{e}_{1}, boldsymbol{e}_{2}) равны ((cos varphi, sin varphi)). Тогда перпендикулярный вектор единичной длины (overrightarrow{O^{*}B^{*}}) имеет координаты ((mp sin{y}, pm cos{y})), причем верхние знаки берутся в том случае, когда пара векторов (overrightarrow{O^{*}A^{*}}) и (overrightarrow{O^{*}B^{*}}) ориентирована так же, как (boldsymbol{e}_{1}, boldsymbol{e}_{2}). Координаты точки (O^{*}) обозначим через ((c_{1}, c_{2})).

Теперь мы можем разложить все члены равенства eqref{ref1} по базису:
$$
begin{array}{cc}
& x^{*}=x cos varphi mp y sin varphi+c_{1},\
& y^{*}=x sin varphi pm y cos varphi+c_{2}.
end{array}label{ref2}
$$

Итак, мы доказали следующее утверждение.

Утверждение 1.

Произвольное ортогональное преобразование в декартовой прямоугольной системе координат записывается формулами eqref{ref2}, где (varphi) — угол, на который поворачивается первый базисный вектор, a (c_{1}) и (c_{2}) — координаты образа начала координат. При этом выбираются верхние знаки, если образы базисных векторов ориентированы так же, как и сами эти векторы, и нижние знаки в противоположном случае.

Пример 1.

Параллельный перенос на вектор с сопоставляет точке (M) с координатами ((x, y)) в некоторой декартовой системе координат точку (M^{*}) с координатами
$$
x^{*}=x+c_{1}, y^{*}=y+c_{2},nonumber
$$
где (c_{1}) и (c_{2}) — координаты (c).

Пример 2.

Напишем уравнения поворота плоскости на угол (varphi) вокруг некоторой точки, приняв эту точку за начало декартовой прямоугольной системы координат. В этом случае (O=O^{*}) и, следовательно, (c_{1}=c_{2}=0). Должны быть выбраны верхние знаки. Итак
$$
x^{*}=x cos{varphi}-y sin{varphi}, y^{*}=x sin{varphi}+y cos{varphi},nonumber
$$

Пример 3.

Рассмотрим осевую симметрию относительно некоторой прямой. Примем ось симметрии за ось абсцисс декартовой прямоугольной системы координат. Тогда точка (M(x, y)) переходит в точку (M^{*}) с координатами
$$
x^{*}=x, y^{*}=-y.nonumber
$$
Здесь (c_{1}=c_{2}=0) и (varphi=0) при нижних знаках в формулах eqref{ref2}.

Определение линейных преобразований.

Основным объектом для нас будет более широкий класс преобразований, включающий в себя ортогональные преобразования.

Определение.

Преобразование (f) плоскости (P) называется линейным, если на (P) существует такая декартова система координат, в которой (f) может быть записано формулами
$$
begin{array}{cc}
& x^{*}=a_{1}x+b_{1}y+c_{1},\
& y^{*}=a_{2}x+b_{2}y+c_{2}.
end{array}label{ref3}
$$
Взаимно однозначное линейное преобразование называется аффинным преобразованием.

Подчеркнем, что в определении линейного преобразования, вовсе не требуется, чтобы коэффициенты в формулах eqref{ref3} не обращались в нуль одновременно. Они могут быть любыми. Докажем следующее утверждение.

Утверждение 2.

Для того чтобы преобразование, задаваемое формулами eqref{ref3}, было взаимно однозначным, необходимо и достаточно,
$$
begin{vmatrix}
a_{1}& b_{1}\
a_{2}& b_{2}
end{vmatrix} neq 0.label{ref4}
$$

Таким образом, аффинное преобразование определяется формулами eqref{ref3} при условии eqref{ref4}.

Доказательство.

Наше утверждение вытекает по существу из утверждения о существовании решения системы линейных уравнений. Нам нужно узнать, при каком условии каждая точка плоскости имеет единственный прообраз. Формулы eqref{ref3} связывают координаты ((x^{*}, y^{*})) точки (M^{*}) и координаты ((x, y)) ее прообраза. Их можно рассматривать как систему линейных уравнений для нахождения (x) и (y), и эта система имеет единственное решение при любых свободных членах (x^{*}-c_{1}) и (y^{*}-c_{2}) (а значит, при любых (x^{*}) и (y^{*})) тогда и только тогда, когда выполнено условие eqref{ref4}.

Как видно из доказанного утверждения, ортогональные преобразования являются линейными. Проверка условия eqref{ref4} показывает, что они аффинные. Рассмотрим другие примеры.

Пример 4.

Рассмотрим сжатие к прямой и примем эту прямую за ось абсцисс декартовой прямоугольной системы координат. Легко видеть, что в такой системе координат сжатие с коэффициентом (lambda) записывается формулами
$$
x^{*}=x, y^{*}=lambda y.nonumber
$$
Сжатие к прямой — аффинное преобразование.

Пример 5.

Проектирование на прямую в такой декартовой прямоугольной системе координат, для которой эта прямая — ось абсцисс, записывается формулами
$$
x^{*}=x, y^{*}=0.nonumber
$$
Это — линейное, но не аффинное преобразование.

Пример 6.

Для записи уравнений гомотетии не существенно, чтобы система координат была прямоугольной, но уравнения проще, если начало координат поместить в центр гомотетии. По определению гомотетии с коэффициентом (lambda) вектор (overrightarrow{OM}) переходит в вектор (overrightarrow{OM^{*}}=lambdaoverrightarrow{OM}). Если (O) — начало координат, координаты точек (M) и (M^{*}) будут связаны равенствами
$$
x^{*}=lambda x, y^{*}=lambda y.nonumber
$$
Гомотетия — аффинное преобразование.

Пример 7.

Преобразование, сопоставляющее каждой точке плоскости одну и ту же точку (C), записывается формулами (x^{*}=c_{1}), (y^{*}=c_{2}), где (c_{1}) и (c_{2}) — координаты точки (C). Оно линейное, но не аффинное.

Определение аффинного преобразования содержит упоминание о некоторой определенной системе координат, и заранее не известно, будет ли преобразование записываться формулами вида eqref{ref3} в какой-либо другой системе координат. Давайте докажем следующее утверждение.

Утверждение 3.

В любой декартовой системе координат, линейное преобразование задается формулами вида eqref{ref3}, то есть:
$$
begin{array}{cc}
& x^{*}=a_{1}x+b_{1}y+c_{1},\
& y^{*}=a_{2}x+b_{2}y+c_{2}.
end{array}nonumber
$$

Доказательство.

Пусть преобразование задано равенствами eqref{ref3} в системе координат (O, boldsymbol{e}_{1}, boldsymbol{e}_{2}). Перейдем к системе координат (O’, boldsymbol{e}’_{1}, boldsymbol{e}’_{2}). Как мы знаем, старые координаты точки (M(x, y)) выражаются через новые координаты ((x’, y’)) по следующим формулам:
$$
x=alpha_{1}x’+beta_{1}y’+gamma_{1}, y=alpha_{2}x’+beta_{2}y’+gamma_{2}.label{ref5}
$$
Для образа (M^{*}) точки (M) нам нужно будет, наоборот, выразить новые координаты ((x’^{*}, y’^{*})) через его старые координаты ((x^{*}, y^{*})). Они выражаются такими же формулами, разумеется, с другими коэффициентами:
$$
x’^{*}=lambda_{1}(x^{*})+mu_{1}y^{*}+nu_{1}, y’^{*}=lambda_{2}x^{*}+mu_{2}y^{*}+nu_{2}.label{ref6}
$$

Нам требуется найти выражение новых координат ((x’^{*}, y’^{*})) точки (M^{*}) через новые координаты ((x’, y’)) точки (M). С этой целью подставим в равенства eqref{ref6} значения (x^{*}) и (y^{*}) из формул eqref{ref3}:
$$
begin{array}{cc}
& x’^{*}=lambda_{1}(a_{1}x+b_{1}y+c_{1})+mu_{1}(a_{2}x+b_{2}y+c_{2})+nu_{1},\
& y’^{*}=lambda_{2}(a_{1}x+b_{1}y+c_{1})+mu_{2}(a_{2}x+b_{2}y+c_{2})+nu_{2}.
end{array}nonumber
$$

Для нас важно, что правые части этих равенств — многочлены степени не выше 1 относительно (x) и (y):
$$
x’^{*}=A_{1}x+B_{1}y+C_{1}, y’^{*}=A_{2}x+B_{2}y+C_{2}.label{ref7}
$$
Подставив сюда выражения (x) и (y) по формулам eqref{ref5}, мы найдем искомую зависимость:
$$
begin{array}{cc}
& x’^{*}=A_{1}(alpha_{1}x’+beta_{1}y’+gamma_{1})+B_{1}(alpha_{2}x’+beta_{2}y’+gamma_{2})+C_{1},\
& y’^{*}=A_{2}(alpha_{1}x’+beta_{1}y’+gamma_{1})+B_{2}(alpha_{2}x’+beta_{2}y’+gamma_{2})+C_{2}.
end{array}nonumber
$$
Мы видим, что правые части этих равенств — многочлены степени не выше 1 относительно (x’) и (y’). Это нам и требовалось доказать.

Заметим, что аффинные преобразования выделяются из линейных требованием взаимной однозначности, которое не зависит от системы координат. Поэтому без дополнительных проверок мы можем быть уверены, что формулы, задающие аффинное преобразование в новой системе координат, удовлетворяют условию eqref{ref4}.

Произведение линейных преобразований.

Доказательство последнего утверждения было основано на том, что результат подстановки многочленов степени не выше 1 в многочлен степени не выше 1 оказывается таким же многочленом. Это же обстоятельство лежит в основе следующего утверждения.

Утверждение 4.

Произведение линейных преобразований является линейным преобразованием. Произведение аффинных преобразований — аффинное преобразование.

Доказательство.

Пусть заданы линейные преобразования (f) и (g) и выбрана система координат. Тогда координаты точки (f(M)) выражаются через координаты точки (M) формулами
$$
x^{*}=a_{1}x+b_{1}y+c_{1}, y^{*}=a_{2}x+b_{2}y+c_{2}.label{ref8}
$$
а координаты точки (g(f(M))) через координаты точки (f(M)) формулами
$$
x^{**}=d_{1}x^{*}+e_{1}y^{*}+f_{1}, y^{**}=d_{2}x^{*}+e_{2}y^{*}+f_{2}.label{ref9}
$$
Подстановка равенств eqref{ref9} в eqref{ref8} выражает координаты g(f(M)) через координаты (M). В результате подстановки мы получаем многочлены степени не выше 1, что и доказывает первую часть предложения.

Для доказательства второй части достаточно вспомнить, что по согласно ранее доказанного утверждения произведение двух взаимно однозначных преобразований взаимно однозначно.

Утверждение 5.

Преобразование, обратное аффинному преобразованию, также является аффинным.

Если преобразование (f) записано уравнениями eqref{ref3}, то координатная запись его обратного преобразования получается решением уравнений eqref{ref3} относительно (x) и (y). Для того чтобы решить эти уравнения, умножим первое из них на (b_{2}), второе — на (b_{1}) и вычтем одно уравнение из другого. Мы получим ((a_{1}b_{2}-a_{2}b_{1})x=b_{2}(x^{*}-c_{1})-b_{1}(y^{*}-c_{2})). Из условия eqref{ref4} следует, что (x) — линейный многочлен от (x^{*}) и (y^{*}). Выражение для (y) получается аналогично.

Образ вектора при линейном преобразовании.

Рассмотрим вектор (overrightarrow{M_{1}M_{2}}). Если координаты точек (M_{1}) и (M_{2}) в системе координат (O, boldsymbol{e}_{1}, boldsymbol{e}_{2}) обозначить соответственно (x_{1}, y_{1}) и (x_{2}, y_{2}), то компоненты вектора будут равны (x_{2}-x_{1}) и (y_{2}-y_{1}). Пусть формулы eqref{ref3} задают преобразование (f) в выбранной системе координат. Тогда образы (M_{2}^{*}) и (M_{1}^{*}) точек (M_{2}) и (M_{1}) имеют абсциссы
$$
x_{2}^{*}=a_{1}x_{2}+b_{1}y_{2}+c_{1}, x_{1}^{*}=a_{1}x_{1}+b_{1}y_{1}+c_{1}.nonumber
$$
Следовательно, первая компонента вектора (overrightarrow{M_{1}^{*}M_{2}^{*}}) равна
$$
x_{2}^{*}-x_{1}^{*}=a_{2}(x_{2}-x_{1})+b_{1}(y_{2}-y_{1}).nonumber
$$
Аналогично находим вторую компоненту этого вектора
$$
y_{2}^{*}-y_{1}^{*}=a_{2}(x_{2}-x_{1})+b_{2}(y_{2}-y_{1}).nonumber
$$

Обратим внимание на то, что компоненты (overrightarrow{M_{1}^{*}M_{2}^{*}}) выражаются только через компоненты (overrightarrow{M_{1}M_{2}}), а не через координаты точек (M_{1}) и (M_{2}) по отдельности. Два равных вектора имеют одинаковые компоненты и, следовательно, при линейном преобразовании перейдут в векторы, компоненты которых также одинаковы. Итак, мы получаем ещё одно утверждение.

Утверждение 6.

При линейном преобразовании равные векторы переходят в равные векторы. Компоненты (alpha_{1}^{*}), (alpha_{2}^{*}) образа вектора выражаются через его компоненты (alpha_{1}), (alpha_{2}) формулами
$$
begin{array}{cc}
& alpha_{1}^{*}=a_{1}alpha_{1}+b_{1}alpha_{2},\
& alpha_{2}^{*}=a_{2}alpha_{1}+b_{2}alpha_{2}.
end{array}label{ref10}
$$

Если быть точным, говорить об образе вектора при преобразовании (f) неправильно: преобразование отображает точки, а не векторы. Точнее было бы сказать, что (f) порождает преобразование (tilde{f}) множества векторов. Но ниже мы, тем не менее, будем придерживаться не совсем точной, но более удобной и общепринятой терминологии — говорить, что преобразование (f) переводит вектор (boldsymbol{a}) в вектор (boldsymbol{a}^{*}) и обозначать последний через (f(boldsymbol{a})).

Из формул eqref{ref10} вытекает, что для линейного преобразования (f) при любых векторах (boldsymbol{a}) и (boldsymbol{b}) и любом числе (lambda)
$$
begin{array}{cc}
& f(boldsymbol{a}+boldsymbol{b})=f(boldsymbol{a})+f(boldsymbol{b}),\
& f(lambdaboldsymbol{a})=lambda f(boldsymbol{a}).
end{array}label{ref11}
$$

Докажем, например, первое из этих равенств. Пусть (gamma_{1}^{*}) и (gamma_{2}^{*}) — компоненты вектора (f(boldsymbol{a}+boldsymbol{b})). Тогда
$$
gamma_{1}^{*}=a_{1}(alpha_{1}+beta_{1})+b_{1}(alpha_{2}+beta_{2}), gamma_{2}^{*}=a_{2}(alpha_{1}+beta_{1})+b_{2}(alpha_{2}+beta_{2}),nonumber
$$
где (alpha_{1}, alpha_{2}) и (beta_{1}, beta_{2}) — компоненты векторов (boldsymbol{a}) и (boldsymbol{b}). Отсюда
$$
begin{array}{cc}
& gamma_{1}^{*}=(a_{1}alpha_{1}+b_{1}alpha_{2})+(a_{1}beta_{1}+b_{1}beta_{2})=alpha_{1}^{*}+beta_{1}^{*},\
& gamma_{2}^{*}=(a_{2}alpha_{1}+b_{2}alpha_{2})+(a_{2}beta_{1}+b_{2}beta_{2})=alpha_{2}^{*}+beta_{2}^{*}.
end{array}nonumber
$$
Это — координатная запись доказываемого равенства. Второе из равенств eqref{ref11} доказывается аналогично.

Из равенств eqref{ref11} следует, что при линейном преобразовании (f) линейно зависимые векторы переходят в линейно зависимые. Действительно, как легко видеть, (f(boldsymbol{0})=boldsymbol{0}). Тогда любое соотношение вида (lambda boldsymbol{a}+mu boldsymbol{b}=boldsymbol{0}) влечет за собой (lambda f(boldsymbol{a})+mu f(boldsymbol{b})=boldsymbol{0}).

Если преобразование аффинное, то линейно независимые векторы переходят в линейно независимые. В самом деле, в противном случае из равенства (lambda f(boldsymbol{a})+mu f(boldsymbol{b})=boldsymbol{0}), (lambda^{2}+mu^{2} neq 0), при обратном преобразовании мы получили бы (lambda boldsymbol{a}+mu boldsymbol{b}=boldsymbol{0}).

Следующее утверждение устанавливает геометрический смысл коэффициентов в формулах, задающих линейное преобразование.

Утверждение 7.

Пусть преобразование (f) записано в системе координат (O, boldsymbol{e}_{1}, boldsymbol{e}_{2}) формулами eqref{ref3}. Тогда (c_{1}) и (c_{2}) — координаты точки (f(O)), a (a_{1} a_{2}) и (b_{1}, b_{2}) — компоненты векторов (f(boldsymbol{e}_{1})) и (f(boldsymbol{e}_{2})) в системе координат (O, boldsymbol{e}_{1}, boldsymbol{e}_{2}).

Доказательство.

Для доказательства подставим в формулы eqref{ref3} значения (x=0) и (y=0) координат точки (O) и увидим, что координаты (f(O)) равны (c_{1}) и (c_{2}).

Подставим в формулы eqref{ref10} координаты вектора (boldsymbol{e}_{1}) (alpha_{1}=1), (alpha_{2}=0) и найдем (a_{1}^{*}=a_{1}), (a_{2}^{*}=a_{2}). Следовательно, (f(boldsymbol{e}_{1})) имеет компоненты (a_{1}) и (a_{2}). Так же доказывается, что компоненты (f(boldsymbol{e}_{2})) равны (b_{1}) и (b_{2}).

Утверждение 8.

Каковы бы ни были три точки (L), (M), (N), не лежащие на одной прямой, и три точки (L^{*}), (M^{*}) и (N^{*}), существует единственное линейное преобразование (f) такое, что (L^{*}=f(L)), (M^{*}=f(M)) и (N^{*}=f(N)). Это преобразование аффинное тогда и только тогда, когда точки (L^{*}), (M^{*}) и (N^{*}) также не лежат на одной прямой.

Доказательство.

Векторы (overrightarrow{LM}) и (overrightarrow{LN}) не коллинеарны. Следовательно, (L), (overrightarrow{LM}), (overrightarrow{LN}) — декартова система координат. Пусть (c_{1}, c_{2}) — координаты (L^{*}), а (a_{1}, a_{2}) и (b_{1}, b_{2}) — компоненты векторов (overrightarrow{L^{*}M^{*}}) и (overrightarrow{L^{*}N^{*}}) в этой системе координат. Формулы
$$
x^{*}=a_{1}x+b_{1}y+c_{1}, y^{*}=a_{2}x+b_{2}y+c_{2}nonumber
$$
определяют линейное преобразование (f), которое, как легко видеть, обладает требуемым свойством. При этом согласно предложению 7, коэффициенты в формулах однозначно определены.

Условие eqref{ref4}, равносильное аффинности преобразования, необходимо и достаточно для того, чтобы векторы (overrightarrow{L^{*}M^{*}}) и (overrightarrow{L^{*}N^{*}}) были не коллинеарны, то есть (L^{*}), (M^{*}) и (N^{*}) не лежали на одной прямой. Предложение доказано.

Заметим, что в том случае, когда преобразование (f) аффинное, точка (f(O)) и векторы (f(boldsymbol{e}_{1})) и (f(boldsymbol{e}_{2})) могут быть использованы как система координат. Для этой системы координат имеет место ещё одно утверждение.

Утверждение 9.

При аффинном преобразовании (f) образ (M^{*}) точки (M) в системе координат (f(O)), (f(boldsymbol{e}_{1})), (f(boldsymbol{e}_{2})) имеет те же координаты, что и точка (M) в системе координат (O, boldsymbol{e}_{1}, boldsymbol{e}_{2}).

Доказательство.

Равенство (overrightarrow{OM}=x boldsymbol{e}_{1}+y boldsymbol{e}_{2}) означает, что (x), (y) — координаты (M) в системе координат (O, boldsymbol{e}_{1}, boldsymbol{e}_{2}). Подействовав преобразованием (f) на обе части этого равенства, мы получаем (overrightarrow{f(O)f(M)}=x f(boldsymbol{e}_{1})+y f(boldsymbol{e}_{2})), которое означает, что (x) и (y) — координаты (M^{*}) в системе координат (f(O)), (f(boldsymbol{e}_{1})), (f(boldsymbol{e}_{2})).

Источник

Предложите, как улучшить StudyLib

(Для жалоб на нарушения авторских прав, используйте

другую форму
)

Ваш е-мэйл

Заполните, если хотите получить ответ

Оцените наш проект

Источник