math4school.ru
Уравнения в целых числах
Немного теории
Уравнения в целых числах – это алгебраические уравнения с двумя или более неизвестными переменными и целыми коэффициентами. Решениями такого уравнения являются все целочисленные (иногда натуральные или рациональные) наборы значений неизвестных переменных, удовлетворяющих этому уравнению. Такие уравнения ещё называют диофантовыми, в честь древнегреческого математика Диофанта Александрийского, который исследовал некоторые типы таких уравнений ещё до нашей эры.
Современной постановкой диофантовых задач мы обязаны французскому математику Ферма. Именно он поставил перед европейскими математиками вопрос о решении неопределённых уравнений только в целых числах. Наиболее известное уравнение в целых числах – великая теорема Ферма: уравнение
не имеет ненулевых рациональных решений для всех натуральных n > 2.
Теоретический интерес к уравнениям в целых числах достаточно велик, так как эти уравнения тесно связаны со многими проблемами теории чисел.
В 1970 году ленинградский математик Юрий Владимирович Матиясевич доказал, что общего способа, позволяющего за конечное число шагов решать в целых числах произвольные диофантовы уравнения, не существует и быть не может. Поэтому следует для разных типов уравнений выбирать собственные методы решения.
При решении уравнений в целых и натуральных числах можно условно выделить следующие методы:
способ перебора вариантов;
применение алгоритма Евклида;
представление чисел в виде непрерывных (цепных) дробей;
разложения на множители;
решение уравнений в целых числах как квадратных (или иных) относительно какой-либо переменной;
метод бесконечного спуска.
Задачи с решениями
1. Решить в целых числах уравнение x 2 – xy – 2y 2 = 7.
Запишем уравнение в виде (x – 2y)(x + y) = 7.
Так как х, у – целые числа, то находим решения исходного уравнения, как решения следующих четырёх систем:
1) x – 2y = 7, x + y = 1;
2) x – 2y = 1, x + y = 7;
3) x – 2y = –7, x + y = –1;
4) x – 2y = –1, x + y = –7.
Решив эти системы, получаем решения уравнения: (3; –2), (5; 2), (–3; 2) и (–5; –2).
Ответ: (3; –2), (5; 2), (–3; 2), (–5; –2).
2. Решить в целых числах уравнение:
а) 20х + 12у = 2013;
в) 201х – 1999у = 12.
а) Поскольку при любых целых значениях х и у левая часть уравнения делится на два, а правая является нечётным числом, то уравнение не имеет решений в целых числах.
Ответ: решений нет.
б) Подберём сначала некоторое конкретное решение. В данном случае, это просто, например,
Поскольку числа 5 и 7 взаимно простые, то
Значит, общее решение:
х = 1 + 7k, у = 2 – 5k,
где k – произвольное целое число.
Ответ: (1+7k; 2–5k), где k – целое число.
в) Найти некоторое конкретное решение подбором в данном случае достаточно сложно. Воспользуемся алгоритмом Евклида для чисел 1999 и 201:
НОД(1999, 201) = НОД(201, 190) = НОД(190, 11) = НОД(11, 3) = НОД(3 , 2) = НОД(2, 1) = 1.
Запишем этот процесс в обратном порядке:
1 = 2 – 1 = 2 – (3 – 2) = 2·2 – 3 = 2· (11 – 3·3) – 3 = 2·11 – 7·3 = 2·11 – 7(190 – 11·17) =
= 121·11 – 7·190 = 121(201 – 190) – 7·190 = 121·201 – 128·190 =
= 121·201 – 128(1999 – 9·201) = 1273·201 – 128·1999.
Значит, пара (1273, 128) является решением уравнения 201х – 1999у = 1. Тогда пара чисел
x0 = 1273·12 = 15276, y0 = 128·12 = 1536
является решением уравнения 201х – 1999у = 12.
Общее решение этого уравнения запишется в виде
х = 15276 + 1999k, у = 1536 + 201k, где k – целое число,
или, после переобозначения (используем, что 15276 = 1283 + 7·1999, 1536 = 129 + 7·201),
х = 1283 + 1999n, у = 129 + 201n, где n – целое число.
Ответ: (1283+1999n, 129+201n), где n – целое число.
3. Решить в целых числах уравнение:
а) x 3 + y 3 = 3333333;
б) x 3 + y 3 = 4(x 2 y + xy 2 + 1).
а) Так как x 3 и y 3 при делении на 9 могут давать только остатки 0, 1 и 8 (смотрите таблицу в разделе «Делимость целых чисел и остатки»), то x 3 + y 3 может давать только остатки 0, 1, 2, 7 и 8. Но число 3333333 при делении на 9 даёт остаток 3. Поэтому исходное уравнение не имеет решений в целых числах.
Ответ: целочисленных решений нет.
б) Перепишем исходное уравнение в виде (x + y) 3 = 7(x 2 y + xy 2 ) + 4. Так как кубы целых чисел при делении на 7 дают остатки 0, 1 и 6, но не 4, то уравнение не имеет решений в целых числах.
Ответ: целочисленных решений нет.
а) в простых числах уравнение х 2 – 7х – 144 = у 2 – 25у;
б) в целых числах уравнение x + y = x 2 – xy + y 2 .
а) Решим данное уравнение как квадратное относительно переменной у. Получим
у = х + 9 или у = 16 – х.
Поскольку при нечётном х число х + 9 является чётным, то единственной парой простых чисел, которая удовлетворяет первому равенству, является (2; 11).
Так как х, у – простые, то из равенства у = 16 – х имеем
С помощью перебора вариантов находим остальные решения: (3; 13), (5; 11), (11; 5), (13; 3).
Ответ: (2; 11), (3; 13), (5; 11), (11; 5), (13; 3).
б) Рассмотрим данное уравнение как квадратное уравнение относительно x:
x 2 – (y + 1)x + y 2 – y = 0.
Дискриминант этого уравнения равен –3y 2 + 6y + 1. Он положителен лишь для следующих значений у: 0, 1, 2. Для каждого из этих значений из исходного уравнения получаем квадратное уравнение относительно х, которое легко решается.
Ответ: (0; 0), (0; 1), (1; 0), (1; 2), (2; 1), (2; 2).
5. Существует ли бесконечное число троек целых чисел x, y, z таких, что x 2 + y 2 + z 2 = x 3 + y 3 + z 3 ?
Попробуем подбирать такие тройки, где у = –z. Тогда y 3 и z 3 будут всегда взаимно уничтожаться, и наше уравнение будет иметь вид
Чтобы пара целых чисел (x; y) удовлетворяла этому условию, достаточно, чтобы число x–1 было удвоенным квадратом целого числа. Таких чисел бесконечно много, а именно, это все числа вида 2n 2 +1. Подставляя в x 2 (x–1) = 2y 2 такое число, после несложных преобразований получаем:
y = xn = n(2n 2 +1) = 2n 3 +n.
Все тройки, полученные таким образом, имеют вид (2n 2 +1; 2n 3 +n; –2n 3 – n).
6. Найдите такие целые числа x, y, z, u, что x 2 + y 2 + z 2 + u 2 = 2xyzu.
Число x 2 + y 2 + z 2 + u 2 чётно, поэтому среди чисел x, y, z, u чётное число нечётных чисел.
Если все четыре числа x, y, z, u нечётны, то x 2 + y 2 + z 2 + u 2 делится на 4, но при этом 2xyzu не делится на 4 – несоответствие.
Если ровно два из чисел x, y, z, u нечётны, то x 2 + y 2 + z 2 + u 2 не делится на 4, а 2xyzu делится на 4 – опять несоответствие.
Поэтому все числа x, y, z, u чётны. Тогда можно записать, что
и исходное уравнение примет вид
Теперь заметим, что (2k + 1) 2 = 4k(k + 1) + 1 при делении на 8 даёт остаток 1. Поэтому если все числа x1, y1, z1, u1 нечётны, то x1 2 + y1 2 + z1 2 + u1 2 не делится на 8. А если ровно два из этих чисел нечётно, то x1 2 + y1 2 + z1 2 + u1 2 не делится даже на 4. Значит,
и мы получаем уравнение
Снова повторив те же самые рассуждения, получим, что x, y, z, u делятся на 2 n при всех натуральных n, что возможно лишь при x = y = z = u = 0.
7. Докажите, что уравнение
(х – у) 3 + (y – z) 3 + (z – x) 3 = 30
не имеет решений в целых числах.
Воспользуемся следующим тождеством:
(х – у) 3 + (y – z) 3 + (z – x) 3 = 3(х – у)(y – z)(z – x).
Тогда исходное уравнение можно записать в виде
(х – у)(y – z)(z – x) = 10.
Обозначим a = x – y, b = y – z, c = z – x и запишем полученное равенство в виде
Кроме того очевидно, a + b + c = 0. Легко убедиться, что с точностью до перестановки из равенства abc = 10 следует, что числа |a|, |b|, |c| равны либо 1, 2, 5, либо 1, 1, 10. Но во всех этих случаях при любом выборе знаков a, b, c сумма a + b + c отлична от нуля. Таким образом, исходное уравнение не имеет решений в целых числах.
8. Решить в целых числах уравнение 1! + 2! + . . . + х! = у 2 .
если х = 1, то у 2 = 1,
если х = 3, то у 2 = 9.
Этим случаям соответствуют следующие пары чисел:
Заметим, что при х = 2 имеем 1! + 2! = 3, при х = 4 имеем 1! + 2! + 3! + 4! = 33 и ни 3, ни 33 не являются квадратами целых чисел. Если же х > 5, то, так как
5! + 6! + . . . + х! = 10n,
можем записать, что
1! + 2! + 3! + 4! + 5! + . . . + х! = 33 + 10n.
Так как 33 + 10n – число, оканчивающееся цифрой 3, то оно не является квадратом целого числа.
Ответ: (1; 1), (1; –1), (3; 3), (3; –3).
9. Решите следующую систему уравнений в натуральных числах:
a 3 – b 3 – c 3 = 3abc, a 2 = 2(b + c).
3abc > 0, то a 3 > b 3 + c 3 ;
таким образом имеем
b 2 2 + х = у 4 + у 3 + у 2 + у.
Разложив на множители обе части данного уравнения, получим:
х(х + 1) = у(у + 1)(у 2 + 1),
х(х + 1) = (у 2 + у)(у 2 + 1)
Такое равенство возможно, если левая и правая части равны нулю, или представляют собой произведение двух последовательных целых чисел. Поэтому, приравнивая к нулю те или иные множители, получим 4 пары искомых значений переменных:
Произведение (у 2 + у)(у 2 + 1) можно рассматривать как произведение двух последовательных целых чисел, отличных от нуля, только при у = 2. Поэтому х(х + 1) = 30, откуда х5 = 5, х6 = –6. Значит, существуют ещё две пары целых чисел, удовлетворяющих исходному уравнению:
Ответ: (0; 0), (0; –1), (–1; 0), (–1; –1), (5; 2), (–6; 2.)
Задачи без решений
1. Решить в целых числах уравнение:
б) х 2 + у 2 = х + у + 2.
2. Решить в целых числах уравнение:
а) х 3 + 21у 2 + 5 = 0;
б) 15х 2 – 7у 2 = 9.
3. Решить в натуральных числах уравнение:
4. Доказать, что уравнение х 3 + 3у 3 + 9z 3 = 9xyz в рациональных числах имеет единственное решение
5. Доказать, что уравнение х 2 + 5 = у 3 в целых числах не имеет решений.
Объясните, пожалуйста, как решать такое задание :Найдите все пары целых чисел (x ; y), удовлетворяющих уравнению 7x + 4y = 123?
Алгебра | 5 — 9 классы
Объясните, пожалуйста, как решать такое задание :
Найдите все пары целых чисел (x ; y), удовлетворяющих уравнению 7x + 4y = 123.
Линейное диофантово уравнение 7х + 4у = 123.
Если коэффициенты перед х и упростые числа, то это уравнение имеет решение в целых числах.
НОД(7, 4) = 1 ⇒ 7 и 4 — простые числа.
Подберём частное решение $(x_0,y_0)$ .
В этом уравнении это сделать не совсем просто, поэтому воспользуемся теоремой :
чтобы найти решение уравнения ах + ву = с при взаимно — простых а и в, нужно найти решение$(x_0,y_0)$ уравнения ах + ву = 1.
Тогдачисла $(cx_0,cy_0)$ составляют решение
уравнения ах + ву = с .
7х + 4у = 1 ⇒ $x_0=-1; ,; ; y_0=2$ .
$7cdot (-1)+4cdot 2=-7+8=1$
$cx_0=123cdot (-1)=-123; ,; ; cy_0=2cdot 123=246; ; to \\7x+4y=123; ; (star)\\7cdot (-123)+4cdot 246=123; ; (star star )$
Из ( * ) вычтем ( * * ) , получим :
Чтобы (у — 246) было целым, надо чтобы (х + 123) нацело делилось на 4, то есть х + 123 = 4к ⇒ х = 4к — 123 , k∈Z .
Тогда $y-246= frac<-7cdot 4k> <4>=-7k; ; Rightarrow ; ; y=-7k+246$
Найдите все пары целых чисел, удовлетворяющих уравнениюа)ху = 17?
Найдите все пары целых чисел, удовлетворяющих уравнению
Найдите все пары натуральных чисел удовлетворяющих уравнению xy — 2x — y = 9?
Найдите все пары натуральных чисел удовлетворяющих уравнению xy — 2x — y = 9.
Найдите все пары натуральных чисел, удовлетворяющих уравнению ху — 2х — у = 11?
Найдите все пары натуральных чисел, удовлетворяющих уравнению ху — 2х — у = 11.
Найдите такую пару чисел, удовлетворяющую уравнению 3x + 5y = 19, сумма которых равна 5 ?
Найдите такую пару чисел, удовлетворяющую уравнению 3x + 5y = 19, сумма которых равна 5 .
Объясните пожалуйста, как решать такие уравнения?
Объясните пожалуйста, как решать такие уравнения?
Найдите все пары целых чисел (х ; у), удовлетворяющие уравнению 4у — х = 27?
Найдите все пары целых чисел (х ; у), удовлетворяющие уравнению 4у — х = 27.
Найдите все пары целых чисел, удовлетворяющие уравнению 4x ^ 2 — y ^ 2 = 3?
Найдите все пары целых чисел, удовлетворяющие уравнению 4x ^ 2 — y ^ 2 = 3.
Найдите все пары целых чисел , удовлетворяющие уравнению х ^ 2 — 4y ^ 2 = 5?
Найдите все пары целых чисел , удовлетворяющие уравнению х ^ 2 — 4y ^ 2 = 5.
Как РЕШАТЬ задания такого типа, объясните пожалуйста?
Как РЕШАТЬ задания такого типа, объясните пожалуйста.
Найдите пары целых чисел (x ; y) удовлетворяющих уравнению 2y + x = 15?
Найдите пары целых чисел (x ; y) удовлетворяющих уравнению 2y + x = 15.
На этой странице сайта, в категории Алгебра размещен ответ на вопрос Объясните, пожалуйста, как решать такое задание :Найдите все пары целых чисел (x ; y), удовлетворяющих уравнению 7x + 4y = 123?. По уровню сложности вопрос рассчитан на учащихся 5 — 9 классов. Чтобы получить дополнительную информацию по интересующей теме, воспользуйтесь автоматическим поиском в этой же категории, чтобы ознакомиться с ответами на похожие вопросы. В верхней части страницы расположена кнопка, с помощью которой можно сформулировать новый вопрос, который наиболее полно отвечает критериям поиска. Удобный интерфейс позволяет обсудить интересующую тему с посетителями в комментариях.
√((x — 2) / (1 — 2x))> — 1 ОДЗ : (x — 2) / (2x — 1)≥0 — ∞__ — __1 / 2__ + __2__ — __ + ∞ x∈[1 / 2 ; 2] 1 — 2x≠0 2x≠1 x≠1 / 2 ⇒ x∈(1 / 2 ; 2]. (√((x — 2) / (1 — 2x)))²>( — 1)² (x — 2) / (1 — 2x)>1 x — 2>1 — 2x 3x>3 |÷3 x>1⇒ Ответ : x∈(1 ; 2].
2 2 25b — 30ab + 9a Это ответ, думаю что правильно.
25b(2 кводрат) — 9а(кводрат).
Вот решения на все твои вопросы).
√113 ^ 2 — 112 ^ 2 = 113 — 112 ^ 2 = — 12431 √3 ^ 6 * 5 ^ 2 = 3 ^ 3 * 25 = 27 * 25 = 675 √6 ^ 4 * 2 ^ 6 = 6 ^ 2 * 2 ^ 6 = 36 * 64 = 2304.
2p — 3p + ( — 2b + c) = 2p — 3p — 2b + c = — p — 2b + c.
Пусть угол между боковыми сторонамиравен х, тогда угол при основанииравен 7х. В равнобедренном треугольнике углы при основании равны. И т. к. Сумма углов в треугольнике равна180°, то получим уравнение : 7х + 7х + х = 180 15х = 180 х = 12° — угол м..
В равнобедренном треугольнике углы при основании равны. Обозначим угол при вершине через x, тогда углы при основании каждый 7x. Cумма углов в треугольнике равна 180°, составим и решим уравнение. X + 7x + 7x = 180 15x = 180 x = 12° — угол при верши..
Системы линейных уравнений с примерами решений
Содержание:
Системы уравнений, как и отдельные уравнения, используют для решения сложных и необходимых задач. Системы уравнений бывают с двумя, тремя и более переменными. В этой главе вы ознакомитесь с простейшими системами двух уравнений с двумя переменными. Основные темы лекции:
- уравнения с двумя переменными;
- график линейного уравнения;
- системы уравнений;
- способ подстановки;
- способ сложения;
- решение задач составлением системы уравнений.
Уравнения с двумя переменными
До сих пор мы рассматривали уравнение с одной переменной. Однако существуют задачи, решение которых приводит к уравнениям с двумя переменными.
Пример:
На 22 руб. купили несколько книжек по 5 руб. и географических карт — по 3 руб. Сколько купили книжек и карт?
Решение:
Пусть купили х книжки у карт. За книжки заплатили 5х руб., а за карты — 3у руб. Всего заплатили 22 руб., то есть, 5х + Зу = 22.
Это уравнение с двумя переменными. Приведём и другие примеры таких уравнений с двумя переменными:
Уравнение вида ах + by = с, где а, b, с — данные числа, называется линейным уравнением с двумя переменными х и у. Если
Примеры линейных уравнений:
два первых из них — уравнение первой степени с двумя переменными.
Паре чисел х = -1 и у = 9 удовлетворяет уравнение 5х + Зу -= 22, так как А пара чисел х = 1 и у = 2 этому уравнению не удовлетворяет, поскольку
Каждая пара чисел, удовлетворяющая уравнение с двумя переменными, т. е. обращающая это уравнение в верное равенство, называется решением этого уравнения.
Обратите внимание: одно решение состоит из двух чисел, на первом месте записывают значение х, на втором — у. Корнями их не называют.
Чтобы найти решение уравнения с двумя переменными, следует подставить в уравнение произвольное значение первой неременной и, решив полученное уравнение, найти соответствующее значение второй переменной.
Для примера найдем несколько решений уравнения
Если х = 1, то отсюда у = -2. Пара чисел х = 1 и у = -2 — решение данного уравнения. Его записывают ещё и так: (1; -2). Придавая переменной х значения 2, 3, 4, . , так же можно найти сколько угодно решений уравнения: (2; 1), (3; 4), (4; 7), (5; 10), . Каждое уравнение первой степени с двумя переменными имеет бесконечно много решений.
Уравнение также имеет бесконечно много решений, но сформулированную выше задачу удовлетворяет только одно из них: (2; 4).
Два уравнения с двумя переменными называют равносильными, если каждое из них имеет те же решения, что и другое. Уравнения, не имеющие решений, также считаются равносильными.
Для уравнения с двумя переменными остаются справедливыми свойства, сформулированные для уравнений с одной переменной.
Обе части уравнения с двумя переменными можно умножить или разделить на одно и то же число, отличное от нуля. Любой член такого уравнения можно перенести из одной части уравнения в другую, изменив его знак на противоположный. В результате получается уравнение, равносильное данному.
Например, уравнение можно преобразовать так: . Каждое из этих уравнений равносильно друг другу.
Иногда возникает потребность решить уравнение с двумя переменными во множестве целых чисел, то есть определить решения, являющиеся парами целых чисел. Способы решения таких уравнений определил древнегреческий математик Диофант (III в.), поэтому их называют диофантовыми уравнениями. Например, задача о книжках и картах сводится к уравнению где х и у могут быть только целыми (иногда натуральными) числами.
Переменную у из этого уравнения выразим через х:
Будем подставлять в равенство вместо х первые натуральные числа до тех пор, пока не получим целое значение переменной у. Это можно делать устно. Если х = 2, то у = 4. Других натуральных решений уравнение не имеет. Поэтому задача имеет единственное решение: 2 книги и 4 карты.
Пример:
Решение:
а) При любых значениях х и у значения выражения не может быть отрицательным числом. Поэтому уравнение не имеет решений.
б) Значение выражения равно нулю только при условии, когда x -3 = 0 и y = 0. Значит, уравнение имеет только одно решение: х = 3, у = 0.
Пример:
Составьте уравнение с двумя переменными, решением которого будет пара чисел (1; -5).
Решение:
Пишем любой двучлен с переменными х и у, например Если х = 1, а у = -5, то значение даного двучлена равно 28. Следовательно, уравнение удовлетворяет условие задачи.
Есть много других линейных уравнений с двумя переменными, имеющих такое же решение (1; -5).
График линейного уравнения с двумя переменными
Рассмотрим уравнение Давая переменной х значения -2, -1,0,1,2, 3. найдём соответствующие значения переменной у. Будем иметь решение данного уравнения: (-2; -б), (-1; -4,5), (0; -3),
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
http://algebra.my-dict.ru/q/4813707_obasnite-pozalujsta-kak-resat-takoe-zadanie/
http://www.evkova.org/sistemyi-linejnyih-uravnenij
СПОСОБЫ РЕШЕНИЙ УРАВНЕНИЙ В ЦЕЛЫХ ЧИСЛАХ
- Авторы
- Руководители
- Файлы работы
- Наградные документы
Свиридова А.В. 1
1МБОУ СОШ «Аннинский Лицей»
Дрёмова О.Н. 1
1МБОУ СОШ «Аннинский Лицей»
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF
Введение.
Объект исследования.
Исследования касаются одного из наиболее интересных разделов теории чисел — решения уравнений в целых числах.
Предмет исследования.
Решение в целых числах алгебраических уравнений с целыми коэффициентами более чем с одним неизвестным представляет собой одну из труднейших и древнейших математических задач и не достаточно глубоко представлена в школьном курсе математики. В своей работе я представлю достаточно полный анализ уравнений в целых числах, классификацию данных уравнений по способам их решения, описание алгоритмов их решения, а также практические примеры применения каждого способа для решения уравнений в целых числах.
Цель.
Познакомиться со способами решения уравнений в целых числах.
Задачи:
Изучить учебную и справочную литературу;
Собрать теоретический материал по способам решения уравнений;
Разобрать алгоритмы решения уравнений данного вида;
Описать способы решения;
Рассмотреть примеры решения уравнений с применением данных способов.
Гипотеза:
Столкнувшись с уравнениями в целых числах в олимпиадных заданиях, я предположила, что трудности в их решении обусловлены тем, что далеко не все способы их решения мне известны.
Актуальность:
Решая примерные варианты заданий ЕГЭ, я заметила, что часто встречаются задания на решение уравнений первой и второй степени в целых числах. Кроме того олимпиадные задания различных уровней также содержат уравнения в целых числах или задачи, которые решаются с применением умений решать уравнения в целых числах. Важность знания способов решения уравнений в целых числах и определяет актуальность моих исследований.
Методы исследования
Теоретический анализ и обобщение сведений научной литературы об уравнениях в целых числах.
Классификация уравнений в целых числах по методам их решения.
Анализ и обобщение методов решения уравнений в целых числах.
Результаты исследования
В работе описаны способы решений уравнений, рассмотрен теоретический материал теоремы Ферма, теорема Пифагора, алгоритма Евклида, представлены примеры решений задач и уравнений различных уровней сложности.
2.История уравнений в целых числах
Диофант – ученый – алгебраист Древней Греции, по некоторым данным он жил до 364 года н. э. Он специализировался на решении задач в целых числах. Отсюда и пошло название Диофантовы уравнения. Наиболее известной, решенной Диофантом, является задача «о разложении на два квадрата». Ее эквивалентом является известная всем теорема Пифагора. Жизнь и деятельность Диофанта протекала в Александрии, он собирал и решал известные и придумывал новые задачи. Позднее он объединил их в большом труде под названием «Арифметика». Из тринадцати книг, входивших в состав «Арифметики», только шесть сохранились до Средних веков и стали источником вдохновения для математиков эпохи Возрождения.«Арифметика» Диофанта — это сборник задач, каждая включает в себя решение и необходимое пояснение. В собрание входят разнообразные задачи, а их решение часто в высшей степени остроумно. Диофанта интересуют только положительные целые и рациональные решения. Иррациональные решения он называет «невозможными» и тщательно подбирает коэффициенты так, чтобы получились искомые положительные, рациональные решения.
Для решения уравнений в целых числах применяется теорема Ферма. История доказательства которой достаточно интересная. Над полным доказательством Великой теоремы работало немало выдающихся математиков, и эти усилия привели к получению многих результатов современной теории чисел. Считается, что теорема стоит на первом месте по количеству неверных доказательств.
Замечательный французский математик Пьер Ферма высказал утверждение, что уравнение при целом n ≥ 3 не имеет решений в целых положительных числах x, y, z ( xyz = 0 исключается положительностью x, y, z.Для случая n = 3 эту теорему в X веке пытался доказать среднеазиатский математик ал-Ходжанди, но его доказательство не сохранилось. Несколько позже сам Ферма опубликовал доказательство частного случая для n = 4.
Эйлер в 1770 доказал теорему для случая n = 3, Дирихле и Лежандр в 1825 — для n = 5,Ламе — для n = 7. Куммер показал, что теорема верна для всех простых n, меньших 100, за возможным исключением 37, 59, 67.
В 1980-х годах появился новый подход к решению проблемы. Из гипотезы Морделла, доказанной Фальтингсом в 1983 году, следует, что уравнение
при n > 3 может иметь лишь конечное число взаимно простых решений.
Последний, но самый важный, шаг в доказательстве теоремы был сделан в сентябре 1994 года Уайлсом. Его 130-страничное доказательство было опубликовано в журнале «AnnalsofMathematics». Доказательство основано на предположении немецкого математика Герхарда Фрая о том, что Великая теорема Ферма является следствием гипотезы Таниямы — Симуры (это предположение было доказано Кеном Рибетом при участии Ж.‑П.Серра. ).Первый вариант своего доказательства Уайлс опубликовал в 1993 году (после 7 лет напряжённой работы), но в нём вскоре обнаружился серьёзный пробел; с помощью Ричарда Лоуренса Тейлора пробел удалось достаточно быстро ликвидировать. В 1995 году был опубликован завершающий вариант. 15 марта 2016 года Эндрю Уайлз получает премию Абеля. В настоящее время премия составляет 6 миллионов норвежских крон, то есть примерно 50 миллионов рублей. По словам Уайлса, присуждение премии стало для него «полной неожиданностью».
3.Линейные уравнения в целых числах
Линейные уравнения – самые простые из всех диофантовых уравнений .
Уравнение вида ах=b, где a и b – некоторые числа, а х- неизвестная переменная, называется линейным уравнением с одной неизвестной. Здесь требуется найти только целые решения уравнения. Можно заметить, что если а ≠ 0, то целочисленное решение уравнение будет иметь только в том случае, когда b нацело делится на а и это решение х= b/ф. Если же а=0, то целочисленное решение уравнение будет иметь тогда, когда b=0 и в этом случае х любое число.
Примеры:
4х=12
т.к. 12 нацело делится на 4, то
х=12/4
х=3
0х=0
Т.к. а=о и b=0, то х любое число
10х=7
Т.к. 7 нацело не делится на 10, то решений нет.
4. Способ перебора вариантов.
В способе перебора вариантов необходимо учитывать признаки делимости чисел, рассмотреть все возможные варианты равенства конечного перебора. Этот способ можно применить решая данные задачи:
№1 Найти множество всех пар натуральных чисел, которые являются решением уравнения 49x+69y=602
Решение:
49x+69y=602
Выражаем из уравнения х =,
Т.к. x и y натуральные числа, то х = ≥ 1, умножаем все уравнение на 49, чтобы избавиться от знаменателя:
602-51y ≥ 49,
Переносим 602 в левую сторону:
51y ≤ 553, выражаем y, y= 10
1 ≤ y ≤ 10
Полный перебор вариантов показывает, что натуральными решениями уравнения являются x=5, y=7.
Ответ:(5,7).-
№2 Решить задачу
Из цифр 2, 4, 7 следует составить трёхзначное число, в котором ни одна цифра не может повторяться более двух раз.
Решение.
Найдем количество всех трехзначных чисел, которые начинаются с цифры 2: (224, 242, 227, 272, 247, 274, 244, 277) – их 8.
Аналогично находим все трехзначные цифры начинающиеся с цифр 4 и 7: (442, 424, 422, 447, 474, 427, 472, 477).
(772, 774, 727, 747, 722, 744, 724, 742) – их тоже по 8 чисел. Следует всего 24 числа.
Ответ: 24 числа.
5. Цепная дробь и алгоритм Евклида
Цепной дробью называется выражение обыкновенной дроби в виде
где q1 – целое число, а q2, … ,qn – натуральные числа. Такое выражение называется цепной (конечной непрерывной) дробью. Различают конечные и бесконечные цепные дроби.
Для рациональных чисел цепная дробь имеет конечный вид. Кроме того, последовательность ai— это ровно та последовательность частных, которая получается при применении алгоритма Евклида к числителю и знаменателю дроби.
Решая уравнения цепной дробью, я составила общий алгоритм действий для данного способа решения уравнений в целых числах.
Алгоритм
1) Составить отношение коэффициентов при неизвестных в виде дроби
2) Преобразовать выражение в неправильную дробь
3) Выделить целую часть неправильной дроби
4) Правильную дробь заменить равной ей дробью
5) Проделать 3,4 с полученной в знаменателе неправильной дробью
6) Повторять 5 до конечного результата
7) У полученного выражения отбросить последнее звено цепной дроби, превратить получающуюся при этом новую цепную дробь в простую и вычесть ее из исходной дробь.
Пример №1 Решить в целых числах уравнение 127x- 52y+ 1 = 0
Решение:
Преобразуем отношение коэффициентов при неизвестных.
Прежде всего, выделим целую часть неправильной дроби ; = 2 +
Правильную дробь заменим равной ей дробью .
Откуда = 2+
Проделаем такие же преобразования с полученной в знаменателе неправильной дробью.
Теперь исходная дробь примет вид: .Повторяя те же рассуждения для дроби получим Выделяя целую часть неправильной дроби, придем к окончательному результату:
Мы получили выражение, которое называется конечной цепной или непрерывной дробью. Отбросив последнее звено этой цепной дроби — одну пятую, превратим получающуюся при этом новую цепную дробь в простую и вычтем ее из исходной дроби :
2+;
Приведем полученное выражение к общему знаменателю и отбросим его.
Откуда 127∙9–52∙22+1=0. Из сопоставления полученного равенства с уравнением 127x- 52y+1 = 0 следует, что тогда x= 9, y= 22 — решение исходного уравнения, и согласно теореме все его решения будут содержаться в прогрессиях x= 9+ 52t, y= 22+ 127t, где t=( 0; ±1; ±2…..).Полученный результат наводит на мысль о том, что и в общем случае для нахождения решения уравнения ax+by+c=0 надо разложить отношение коэффициентов при неизвестных в цепную дробь, отбросить ее последнее звено и проделать выкладки, подобные тем, которые были приведены выше.
Для доказательства этого предположения будут нужны некоторые свойства цепных дробей.
Рассмотрим несократимую дробь . Обозначим через q1 частное и через r2 остаток от деления a на b. Тогда получим:
Пусть, далее, q2 – частное и r3 – остаток от деления b на r2.
Тогда b=q2r2+r3,
Точно так же
r2=q3r3+r4, ;
r3=q4r4+r5,;
………………………………..
Величины q1, q2,… называются неполными частными. Приведенный выше процесс образования неполных частных называется алгоритмом Евклида. Остатки от деления r2, r3,…удовлетворяют неравенствам
т.е. образуют ряд убывающих неотрицательных чисел.
Пример№2 Решить уравнение170х+190у=3000 в целых числах
После сокращения на 10 уравнение выглядит так,
17х+19у=300.
Для нахождения частного решения воспользуемся разложением дроби в цепную дробь
Свернув предпоследнюю подходящую к ней дробь в обыкновенную
Частное решение данного уравнения имеет вид
Х0= (-1)4300∙9=2700, y0=(-1)5300∙8=-2400,
а общее задается формулой
х=2700-19k, y= -2400+17k.
откуда получаем условие на параметр k
Т.е. k=142, x=2, y=14. .
6. Метод разложения на множители
Метод перебора вариантов неудобный способ, так как бывают случаи когда найти перебором всецелые решения, невозможно, так как таких решений бесконечное множество. Метод разложения на множители очень интересный прием и встречается он как и в элементарной математике так и в высшей.
Суть состоит в тождественном преобразовании. Смысл любого тождественного преобразования — это запись выражения в другом виде с сохранением его сути. Рассмотрим примеры применения данного метода.
№1 Решить уравнение в целых числах y3 — x3 = 91.
Решение:
Используя формулы сокращенного умножения, разложим правую часть уравнения на множители:
(y — x)(y2 + xy + x2) = 91
Выписываем все делители числа 91: ± 1; ± 7; ± 13; ± 91
Замечаем, что для любых целых x и y число
y2 + yx + x2 ≥ y2 — 2|y||x| + x2 = (|y| — |x|)2 ≥ 0,
следовательно, оба сомножителя в левой части уравнения должны быть положительными. Тогда исходное уравнение равносильно совокупности систем уравнений:
; ; ;
Решив системы, отбираем те корни, которые являются целыми числами.
Получаем решения исходного уравнения: (5; 6), (-6; -5); (-3; 4),(-4;3).
Ответ: (5; 6); (-6; -5); (-3; 4); (-4;3).
№2 Найти все пары натуральных чисел, удовлетворяющих уравнению х2 –у2= 69
Решение:
Разложим левую часть уравнения на множители и запишем уравнение в виде
.
Т.к. делителями числа 69 являются числа 1, 3, 23 и 69, то 69 можно получить двумя способами: 69=1·69 и 69=3·23. Учитывая, что х-у > 0, получим две системы уравнений, решив которые мы сможем найти искомые числа:
или
Выразив одну переменную и подставив ее в второе уравнение находим корни уравнений.Первая система имеет решение x=35;y=34 , а вторая система имеет решение x=13, y=10.
Ответ: (35; 34), (13; 10).
№3 Решить уравнение х+у =ху в целых числах:
Решение:
Запишем уравнение в виде
Разложим левую часть уравнения на множители. Получим
Произведение двух целых чисел может равняться 1 только в двух случаях: если оба они равны 1 или -1. Получим две системы:
или
Первая система имеет решение х=2, у=2, а вторая система имеет решение х=0, у=0.Ответ: (2; 2), (0; 0).
№4 Доказать, что уравнение (x — y)3 + (y — z)3 + (z — x)3 = 30 не имеет решений в целых числах.
Решение:
Разложим левую часть уравнения на множители и обе части уравнения разделим на 3, в результате получим уравнение:
( x — y)(y — z)(z — x) = 10
Делителями 10 являются числа ±1, ±2, ±5, ±10. Заметим также, что сумма сомножителей левой части уравнения равна 0. Нетрудно проверить, что сумма любых трех чисел из множества делителей числа 10, дающих в произведении 10, не будет равняться 0. Следовательно, исходное уравнение не имеет решений в целых числах.
7. Метод остатков
Основная задача метода — находить остаток от деления обоих частей уравнения на целое число, на основе полученных результатов. Часто полученная информация уменьшает возможности множеств решений уравнения. Рассмотрим примеры:
№1 Доказать, что уравнение x2 = 3y + 2 не имеет решений в целых числах.
Доказательство.
Рассмотрим случай, когда x, y ∈ N. Рассмотрим остатки от деления обоих частей на 3. Правая часть уравнения дает остаток 2 при делении на 3 при любом значении y. Левая же часть, которая является квадратом натурального числа, при делении на 3 всегда дает остаток 0 или 1. Исходя из этого получаем, что решения данного уравнения в натуральных числах нет.
Рассмотрим случай, когда одно из чисел равно 0. Тогда очевидно, решений в целых числах нет.
Случай, когда y — целое отрицательное не имеет решений, т.к. правая часть будет отрицательна, а левая — положительна.
Случай, когда x — целое отрицательное, также не имеет решений, т.к. попадает под один из рассмотренных ранее случаев ввиду того, что (-x)2 = (x)2.
Получается, что указанное уравнение не имеет решений в целых числах, что и требовалось доказать.
№2 Решите в целых числах 3х= 1 + y2 .
Не сложно заметить, что (0; 0) — решение данного уравнения. Остаётся доказать, что других целых корней уравнение не имеет.
Рассмотрим случаи:
1) Если x∈N, y∈N, то З делится на три без остатка, а 1 + y2при делении на 3 дает
остаток либо 1, либо 2. Следовательно, равенство при натуральных
значениях х, у невозможно.
2) Если х— целое отрицательное число,y∈Z , тогда 0< 3х< 1, а 1 + y2 ≥ 0 и
равенство также невозможно. Следовательно, (0; 0) — единственное
решение.
Ответ: (0; 0).
№3 Решить уравнение 2х2 -2ху+9х+у=2 в целых числах:
Выразим из уравнения то неизвестное, которое входит в него только в первой степени, то есть переменную у:
2х2 +9х-2=2ху-у, откуда
У =
Выделим у дроби целую часть с помощью правила деления многочлена на многочлен «углом». Получим:
Очевидно, разность 2х-1 может принимать только значения -3, -1, 1 и 3.
Осталось перебрать эти четыре случая, в результате чего получаем решения: (1;9), (2;8), (0;2), (-1;3)
Ответ: (1;9), (2;8), (0;2), (-1;3)
8.Пример решения уравнений с двумя переменными в целых числах как квадратных относительно одной из переменных
№1 Решить в целых числах уравнение 5х2+5у2 + 8ху+2у-2х +2=0
Данное уравнение можно решить методом разложения на множители, однако этот способ применительно к данному уравнению достаточно трудоёмкий. Рассмотрим более рациональный способ.
Запишем уравнение в виде квадратного относительно переменной х:
5x2+(8y-2)x+5y2+2y+2=0
Находим его корни.
Х1,2=
Данное уравнение имеет решение тогда и только тогда, когда дискриминант
этого уравнения равен нулю, т.е. — 9(у+1)2 =0, отсюда у= — 1.
Если у= -1,то х= 1.
Ответ: (1; — 1).
9.Пример решения задач с помощью уравнений в целых числах.
№ 1. Решить в натуральных числах уравнение: где n>m
Решение:
Выразим переменную n через переменную m:
Найдем делители числа 625: это 1; 5; 25; 125; 625
1) если m-25 =1, то m=26, n=25+625=650
2) m-25 =5, то m=30, n=150
3) m-25 =25, то m=50, n=50
4) m-25 =125, то m=150, n=30
5) m-25 =625, то m=650, n=26
Ответ: m=150, n=30
m=650, n=26
№ 2. Решить уравнение в натуральных числах: mn +25 = 4m
Решение: mn +25 = 4m
1) выразим переменную 4m через n:
4m – mn =25
m(4-n) =25
m =
2) найдем натуральные делители числа 25: это 1; 5; 25
если 4-n =1, то n=3, m=25
4-n=5, то n=-1, m=5; 4-n =25, то n=-21, m=1 (посторонние корни)
Ответ: (25;3)
Помимо заданий решить уравнение в целых числах, встречаются задания на доказательство того факта, что уравнение не имеет целых корней.
При решении таких задач, необходимо помнить следующие свойства делимости:
1) Если n Z; n делится на 2, то n = 2k, k ∈ Z.
2) Если n ∈ Z; n не делится на 2, то n = 2k+1, k ∈ Z.
3) Если n ∈ Z; n делится на 3, то n = 3k, k ∈ Z.
4) Если n ∈ Z; n не делится на 3, то n = 3k±1, k ∈ Z.
5) Если n ∈ Z; n не делится на 4, то n = 4k+1; n = 4k+2; n = 4k+3. k ∈ Z.
6) Если n ∈ Z; n(n+1) делится на 2, то n (n+1)(n+2) делится на 2;3;6.
7) n; n+1 – взаимно простые.
№3 Доказать, что уравнение x2– 3у = 17 не имеет целых решений.
Решение:
Доказательство:
x2– 3у = 17
Пусть x; y – решения уравнения
x2= 3у – 17
x2 = 3(у+6)-1 Т.к. y ∈ Z то y+6 ∈ Z , значит 3(y+6) делится на 3, следовательно, 3(y+6)-1 не делится на 3, следовательно, x2 не делится на 3, следовательно, x не делится на 3, значит x = 3k±1, k ∈ Z.
Подставим это в исходное уравнение.
.
Получили противоречие. Значит у уравнения нет целых решений, что и требовалось доказать.
10.Формула Пика
Формула Пика была открыта австрийским математиком Георгом Пиком в 1899 году. Формула связанна с уравнениями в целых числах тем, что из многоугольников берут только целые узлы, как и целые числа в уравнениях.
При помощи этой формулы можно находить площадь фигуры построенной на листе в клетку (треугольник, квадрат, трапеция, прямоугольник, многоугольник).
В этой формуле будем находить целые точки внутри многоугольника и на его границе.
В задачах, которые будут на ЕГЭ есть целая группа заданий, в которых дан многоугольник построенный на листе в клетку и стоит вопрос о нахождении площади. Масштаб клетки это один квадратный сантиметр.
Пример№1
М – количество узлов на границе треугольника (на сторонах и вершинах)
N – количество узлов внутри треугольника.
*Под «узлами» имеется ввиду пересечение линий. Найдём площадь треугольника:
Отметим узлы:
M = 15 (обозначены красным)
N = 34 (обозначены синим)
Пример №2
Найдём площадь многоугольника: Отметим узлы:
M = 14 (обозначены красным)
N = 43 (обозначены синим)
12.Метод спуска
Один из методов решений уравнений в целых числах – метод спуска — опирается на теорему Ферма.
Методом спуска называется метод, который заключается в построении одного решения бесчисленной последовательности решений с неограниченно убывающим положительным z.
Алгоритм этого метода рассмотрим на примере решения конкретного уравнения.
Пример 1. Решить уравнение в целых числах 5x + 8y = 39.
1) Выберем неизвестное, имеющее наименьший коэффициент (в нашем случае это х), и выразим его через другое неизвестное:
2) Выделим целую часть: Очевидно, что х будет целым, если выражение окажется целым, что, в свою очередь, будет иметь место тогда, когда число 4 – 3y без остатка делится на 5.
3) Введем дополнительную целочисленную переменную z следующим образом: 4 –3y = 5z. В результате получим уравнение такого же типа, как и первоначальное, но уже с меньшими коэффициентами.
4) Решаем его уже относительно переменной y, рассуждая точно также как в п.1, 2: Выделяя целую часть, получим:
5) Рассуждая аналогично предыдущему, вводим новую переменную u: 3u = 1 – 2z.
6) Выразим неизвестную с наименьшим коэффициентом, в этом случае переменную z: . Требуя, чтобы было целым, получим: 1 – u = 2v, откуда u = 1 – 2v. Дробей больше нет, спуск закончен (процесс продолжаем до тез пор, пока в выражении для очередной переменной не останется дробей).
7) Теперь необходимо «подняться вверх». Выразим через переменную v сначала z, потом y и затем x:

Таким образом, метод спуска предполагает сначала последовательное выражение одной переменой чрез другую, пока в представлении переменной не останется дробей, а затем, последовательное «восхождение» по цепочке равенств для получения общего решения уравнения.
12.Заключение
В результате исследования подтвердилась гипотеза о том, что трудности при решении уравнений в целых числах обусловлены тем, что далеко не все способы их решения были мне известны. В ходе исследований мне удалось отыскать и описать малоизвестные способы решения уравнений в целых числах, проиллюстрировать их примерами. Результаты моих исследований могут быть полезны всем ученикам, интересующимся математикой.
13.Библиография
Книжные ресурсы:
1. Н. Я. Виленкин и др., Алгебра и математический анализ/10класс, 11 класс// М., «Просвещение», 1998 год;
2. А. Ф. Иванов и др., Математика. Учебно-тренировочные материалы для подготовки к экзамену// Воронеж, ГОУВПО ВГТУ, 2007 год
3. А. О. Гельфонд, Математика, теория чисел// Решение уравнений в целых числах// Книжный дом «ЛИБРОКОМ»
Ресурсы сети интернет:
4. Демонстрационные варианты контрольных измерительных материалов единого государственного экзамена по математике http://fipi.ru/
5. Примеры решений уравнений в целых числахhttp://reshuege.ru
6. Примеры решений уравнений в целых числахhttp://mat-ege.ru
7.История Диофантовых уравнений http://www.goldenmuseum.com/1612Hilbert_rus.html
8. История Диофанта http://nenuda.ru/%D1%83%D1%80%D0%B0%D0%B2%D0%BD%D0%B5%D0%BD%D0%B8%D1%8F-%D1%81-%D0%B4%D0%B2%D1%83%D0%BC%D1%8F-%D0%BD%D0%B5%D0%B8%D0%B7%D0%B2%D0%B5%D1%81%D1%82%D0%BD%D1%8B%D0%BC%D0%B8-%D0%B2-%D1%86%D0%B5%D0%BB%D1%8B%D1%85-%D1%87%D0%B8%D1%81%D0%BB%D0%B0%D1%85.htm
9.История Диофантовых уравненийhttp://dok.opredelim.com/docs/index-1732.html
10. История Диофанта http://www.studfiles.ru/preview/4518769/
11. http://pandia.ru/text/78/004/3180.php
Просмотров работы: 26485
МБОУ «Высокогорская средняя общеобразовательная школа №2
Высокогорского муниципального района Республики Татарстан»
Олимпиадные задания.
Решение уравнений в целых числах
Разработала:
Аксанова Ильсияр Исмагиловна
Учитель математики высшей категории
МБОУ ВСОШ № 2
С. Высокая Гора – 2015 г.
Введение
Работа посвящена решению уравнений в целых числах. Актуальность этой темы обусловлена тем, что задачи, основанные на решении уравнений в целых числах, часто встречаются на вступительных экзаменах в высшие учебные заведения и на олимпиадах по математике и на ЕГЭ в старших классах. В школьной программе эта тема рассматривается в ознакомительном порядке. В работе представлены различные способы решения уравнений в целых числах, разобраны конкретные примеры. Данная работа будет полезна учителям старших классов для подготовки к ЕГЭ и олимпиадам.
Уравнения в целых числах – это алгебраические уравнения с двумя или более неизвестными переменными и целыми коэффициентами. Решениями такого уравнения являются все целочисленные наборы значений неизвестных переменных, удовлетворяющих этому уравнению. Такие уравнения ещё называют диофантовыми, в честь древнегреческого математика Диофанта Аксандрийского, который исследовал некоторые типы таких уравнений ещё до нашей эры.
Наиболее известное уравнение в целых числах – великая теорема Ферма: уравнение
xn + yn = zn
не имеет ненулевых рациональных решений для всех натуральных n > 2.
При решении уравнений в целых и натуральных числах можно условно выделить следующие способы решения:
- способ перебора вариантов;
- применение алгоритма Евклида;
- применение цепных дробей;
- разложения на множители;
- решение уравнений в целых числах как квадратных относительно какой-либо переменной;
- метод остатков;
- метод бесконечного спуска;
- оценка выражений, входящих в уравнение.
В работе представлены два приложения: приложение 1. Таблица остатков при делении степеней (an:m); приложение 2. Задачи для самостоятельного решения
1. Способ перебора вариантов.
Пример 1.1. Найти множество всех пар натуральных чисел, которые являются решениями уравнения 49х + 51у = 602.
Решение. Выразим из уравнения переменную х через у х =, так как х и у – натуральные числа, то
х =
602 — 51у ≥ 49, 51у≤553, 1≤у≤10
.
Полный перебор вариантов показывает, что натуральными решениями уравнения являются х=5, у=7.
Ответ: (5;7).
2. Применение алгоритма Евклида. Теорема.
Дано уравнение ax+by=c, где a, b, c-целые числа, a и b не равны 0.
Теорема: Если c не делится нацело на НОД(a,b), то уравнение не разрешимо в целых числах. Если НОД(a,b)=1или c делится на НОД(a,b), то уравнение разрешимо в целых числах. Если (x0, y0 )- какое-нибудь решение уравнения, то все решения уравнения задаются формулами:
x=x0-bt
y=y0+at , где t— принадлежит множеству целых чисел.
Пример 2.1. Решить уравнение в целых числах 5х + 7у = 19
Подберём сначала некоторое конкретное решение. В данном случае, это просто, например,
x0 = 1, y0 = 2.
Тогда 5x0 + 7y0 = 19, откуда
5(х – x0) + 7(у – y0) = 0,
5(х – x0) = –7(у – y0).
Поскольку числа 5 и 7 взаимно простые, то
х – x0 = 7k, у – y0 = –5k.
Значит, общее решение:
х = 1 + 7k, у = 2 – 5k,
где k – произвольное целое число.
Ответ: (1+7k; 2–5k), где k – целое число.
Пример 2.2. Решить уравнение 201х – 1999у = 12.
Найти некоторое конкретное решение подбором в данном случае достаточно сложно. Воспользуемся алгоритмом Евклида для чисел 1999 и 201:
НОД(1999, 201) = НОД(201, 190) = НОД(190, 11) = НОД(11, 3) = НОД(3 , 2) = НОД(2, 1) = 1.
Запишем этот процесс в обратном порядке:
1 = 2 – 1 = 2 – (3 – 2) = 2·2 – 3 = 2· (11 – 3·3) – 3 = 2·11 – 7·3 = 2·11 – 7(190 – 11·17) =
= 121·11 – 7·190 = 121(201 – 190) – 7·190 = 121·201 – 128·190 =
= 121·201 – 128(1999 – 9·201) = 1273·201 – 128·1999.
Значит, пара (1273, 128) является решением уравнения 201х – 1999у = 1. Тогда пара чисел
x0 = 1273·12 = 15276, y0 = 128·12 = 1536
является решением уравнения 201х – 1999у = 12.
Общее решение этого уравнения запишется в виде
х = 15276 + 1999k, у = 1536 + 201k, где k – целое число,
или, используя, что 15276 = 1283 + 7·1999, 1536 = 129 + 7·201, имеем
х = 1283 + 1999n, у = 129 + 201n, где n – целое число.
Ответ: (1283+1999n, 129+201n), где n – целое число.
3. Метод остатков.
Этот метод основан на исследовании возможных остатков левой и правой частей уравнения от деления на некоторое фиксированное натуральное число.
Замечание. Говоря строго математическим языком, для решения уравнения в данном случае применяется теория сравнений.
Рассмотрим примеры, которые раскрывают сущность данного метода.
Пример 3.1. Решить уравнение в целых числах x3 + y3 = 3333333;
Так как x3 и y3 при делении на 9 могут давать только остатки 0, 1 и 8 (смотрите таблицу в приложении 1), то x3 + y3 может давать только остатки 0, 1, 2, 7 и 8. Но число 3333333 при делении на 9 даёт остаток 3. Поэтому исходное уравнение не имеет решений в целых числах.
Ответ: целочисленных решений нет.
Пример 3.2. Решить уравнение в целых числах x3 + y3 = 4(x2y + xy2 + 1).
Перепишем исходное уравнение в виде (x + y)3 = 7(x2y + xy2) + 4. Так как кубы целых чисел при делении на 7 дают остатки 0, 1 и 6, но не 4, то уравнение не имеет решений в целых числах.
Ответ: целочисленных решений нет.
Пример 3.3. Решить в целых числах уравнение x2 + 1 = 3y.
Решение. Заметим, что правая часть уравнения делится на 3 при любом целом y.
Исследуем какие остатки может иметь при делении на три левая часть этого уравнения.По теореме о делении с остатком целое число х либо делится на 3, либо при делении на три в остатке дает 1 или 2.
Если х = 3k, то правая часть уравнения на 3 не делится.
Если х = 3k+1, то x2 + 1= (3k+1)2+1=3m+2, следовательно, опять левая часть на 3 не делится.
Если х = 3k+2, то x2 + 1= (3k+2)2+1=3m+2, следовательно, и в этом случае левая часть уравнения на три не делится.
Таким образом, мы получили, что ни при каких целых х левая часть уравнения на 3 не делится, при том, что левая часть уравнения делится на три при любых значениях переменной y. Следовательно, уравнение в целых числах решений не имеет.
Ответ: целочисленных решений нет.
Пример 3.4. Решить в целых числах x³ — 3y³ — 9z³ = 0 (1)
Решение. Очевидно, что решением уравнения будет тройка чисел (0; 0; 0).
Выясним, имеет ли уравнение другие решения. Для этого преобразуем уравнение (1) к виду
x³ = 3y³ + 9z³ (2)
Так как правая часть полученного уравнения делится на 3, то и левая должна делиться на три, следовательно, так как 3 — число простое, х делится на 3, т.е. х = 3k, подставим это выражение в уравнение (2), получим:
27k3 = 3y³ + 9z³, откуда
9k3 = y³ + 3z³ (3)
следовательно, y³ делится на 3 и y = 3m. Подставим полученное выражение в уравнение (3): 9k3 = 27m³ + 3z³, откуда
3k3 = 9m³ + z³ (4)
В свою очередь, из этого уравнения следует, что z3 делится на 3, и z = 3n. Подставив это выражение в (4), получим, что k3 должно делиться на 3.
Итак, оказалось, что числа, удовлетворяющие первоначальному уравнению, кратны трём, и сколько раз мы не делили бы их на 3, опять должны получаться числа, кратные трём. Единственное целое число, удовлетворяющее этому условию, будет нуль, т. е. решение данного уравнения (0; 0; 0) является единственным.
Ответ: (0;0;0).
4. Решение уравнений в целых числах сведением их к квадратным.
Пример 4.1. Решить в простых числах уравнение
х2 – 7х – 144 = у2 – 25у.
Решим данное уравнение как квадратное относительно переменной у. Получим: у = х + 9 или у = 16 – х.
Поскольку при нечётном х число х + 9 является чётным, то единственной парой простых чисел, которая удовлетворяет первому равенству, является (2; 11).
Так как х, у – простые, то из равенства у = 16 – х, имеем
2 < х < 16, 2 < у < 16.
С помощью перебора вариантов находим остальные решения: (3; 13), (5; 11), (11; 5), (13; 3).
Ответ: (2; 11), (3; 13), (5; 11), (11; 5), (13; 3).
Пример 4.2. Решить в целых числах уравнение x + y = x2 – xy + y2.
Рассмотрим данное уравнение как квадратное уравнение относительно x:
x2 – (y + 1)x + y2 – y = 0.
Дискриминант этого уравнения равен –3y2 + 6y + 1. Он положителен лишь для следующих значений у: 0, 1, 2. Для каждого из этих значений из исходного уравнения получаем квадратное уравнение относительно х, которое легко решается.
Ответ: (0; 0), (0; 1), (1; 0), (1; 2), (2; 1), (2; 2).
Пример 4.3. Решить уравнение в целых числах: 5х2+5у2+8ху+2у-2х+2=0.
Решение:
Рассмотрим уравнение как квадратное относительно х:
5х2 + (8у — 2)х + 5у2 + 2у + 2 = 0
D = (8у — 2)2 — 4·5(5у2 + 2у + 2) = 64у2 — 32у + 4 = -100у2 — 40у – 40 = = -36(у2 + 2у + 1) = -36(у + 1)2
Для того, чтобы уравнение имело решения, необходимо, чтобы D = 0.
-36(у + 1)2 = 0. Это возможно при у = -1, тогда х = 1.
Ответ: (1;-1).
5. Разложение на множители.
Пример 5.1. Решить в целых числах уравнение x2 – xy – 2y2 = 7.
Разложим левую часть на множители (x – 2y)(x + y) = 7.
Так как х, у – целые числа, то находим решения исходного уравнения, как решения следующих четырёх систем:
1) x – 2y = 7, x + y = 1;
2) x – 2y = 1, x + y = 7;
3) x – 2y = –7, x + y = –1;
4) x – 2y = –1, x + y = –7.
Решив эти системы, получаем решения уравнения: (3; –2), (5; 2), (–3; 2) и (–5; –2).
Ответ: (3; –2), (5; 2), (–3; 2), (–5; –2).
Пример 5.2. Решить уравнение в целых числах: х2 + 23 = у2
Решение. Перепишем уравнение в виде:
у2 — х2 = 23, (у — х)(у + х) = 23
Так как х и у – целые числа и 23 – простое число, то возможны случаи:
Решая полученные системы, находим:
Ответ: (-11;12);(11;12);(11;-12);(-11;-12).
Пример 5.3. Решить уравнение в целых числах y3 — x3 = 91.
Решение. Используя формулы сокращенного умножения, разложим правую часть уравнения на множители:
(y — x)(y2 + xy + x2) = 91
Выпишем все делители числа 91: ± 1; ± 7; ± 13; ± 91
Проводим исследование. Заметим, что для любых целых x и y число
y2 + yx + x2 ≥ y2 — 2|y||x| + x2 = (|y| — |x|)2 ≥ 0,
следовательно, оба сомножителя в левой части уравнения должны быть положительными. Тогда уравнение равносильно совокупности систем уравнений:
;
;
;
Решив системы, получим: первая система имеет решения (5; 6), (-6; -5); третья (-3; 4),(-4;3); вторая и четвертая решений в целых числах не имеют.
Ответ: (5; 6); (-6; -5); (-3; 4); (-4;3).
Пример 5.4. Решить в целых числах уравнение x + y = xy.
Решение. Перенесем все члены уравнения влево и к обеим частям полученного уравнения прибавим (–1)
x + y – xy – 1 = – 1
Сгруппируем первое – четвертое и второе – третье слагаемые и вынесем общие множители, в результате получим уравнение: (x — 1)(y — 1) = 1
Произведение двух целых чисел может равняться 1 в том и только в том случае, когда оба этих числа равны или 1, или (–1). Записав соответствующие системы уравнений и, решив их, получим решение исходного уравнения.
Ответ: (0,0) и (2,2).
Пример 5.5. Доказать, что уравнение (x — y)3 + (y — z)3 + (z — x)3 = 30 не имеет решений в целых числах.
Решение. Разложим левую часть уравнения на множители и обе части уравнения разделим на 3, в результате получим уравнение:
(x — y)(y — z)(z — x) = 10
Делителями 10 являются числа ±1, ±2, ±5, ±10. Заметим также, что сумма сомножителей левой части уравнения равна 0. Нетрудно проверить, что сумма любых трех чисел из множества делителей числа 10, дающих в произведении 10, не будет равняться 0. Следовательно, исходное уравнение не имеет решений в целых числах.
Ответ: целочисленных решений нет.
6. Метод бесконечного спуска.
Метод спуска предполагает сначала последовательное выражение одной переменой чрез другую, пока в представлении переменной не останется дробей, а затем, последовательное «восхождение» по цепочке равенств для получения общего решения уравнения.
Пример 6.1. Решить уравнение в целых числах 5x + 8y = 39.
Выберем неизвестное, имеющее наименьший коэффициент , и выразим его через другое неизвестное: . Выделим целую часть:
Очевидно, что х будет целым, если выражение
окажется целым, что, в свою очередь, будет иметь место тогда, когда число 4 – 3y без остатка делится на 5.
Введем дополнительную целочисленную переменную z следующим образом: 4 –3y = 5z. В результате получим уравнение такого же типа, как и первоначальное, но уже с меньшими коэффициентами. Решать его будем уже относительно переменной y, рассуждая аналогично: . Выделяя целую часть, получим:
.
Рассуждая аналогично предыдущему, вводим новую переменную
u: 3u = 1 – 2z.
Выразим неизвестную с наименьшим коэффициентом, в этом случае переменную z: =
. Требуя, чтобы
было целым, получим: 1 – u = 2v, откуда u = 1 – 2v. Дробей больше нет, спуск закончен.
Теперь необходимо «подняться вверх». Выразим через переменную v сначала z, потом y и затем x:
z = =
= 3v – 1;
=
3 – 5v.
=
= 3+8v.
Формулы x = 3+8v и y = 3 – 5v, где v – произвольное целое число, представляют общее решение исходного уравнения в целых числах.
Ответ: x = 3+8v и y = 3 – 5v.
7. Оценка выражений, входящих в уравнение.
Пример 7.1. Решить в целых числах уравнение (х2 + 4)(у2 + 1) = 8ху
Решение. Заметим, что если (х;у
) – решение уравнения, то (-х
;-у
) – тоже решение.
И так как х = 0 и у = 0 не являются решением уравнения, то, разделив обе части уравнения на ху, получим:
∙
= 8, (х +
)(у +
) = 8.
Пусть х > 0, у > 0, тогда, согласно неравенству Коши,
х +
= 4, у +
= 2,
тогда их произведение (х + )(у +
) = 4·2 = 8, значит, х +
= 4 и у +
= 2.
Отсюда находим х = 2 и у = 1 – решение, тогда х = -2 и у = -1 – тоже решение.
Ответ: (2;1); (-2;-1)
Пример 7.2. Решить уравнение в целых числах
x2 + 13y2 – 6xy = 100
Решение. x2+13y2–6xy=100 ↔ (x-3y)2+4y2=100. Так как (x-3y)2≥0, то 4y2≤100, или │2y│≤10. Аналогично, в силу 4y2≥0 должно выполняться │x-3y│≤10.
Возможны 12 случаев:
|
1. |
|
↔ |
|
2. |
|
↔ |
|
|
|
3. |
|
↔ |
|
4. |
|
↔ |
|
|
|
5. |
|
↔ |
|
6. |
|
↔ |
|
|
|
7. |
|
↔ |
|
8. |
|
↔ |
|
|
|
9. |
|
↔ |
|
10. |
|
↔ |
|
|
|
11. |
|
↔ |
|
12. |
|
↔ |
|
Ответ: (±15; ±5); (±10; ±0); (±18; ±4);
(±6; ±4); (±17; ±3); (±1; ±3).
8. Применение цепных дробей.
Пример 8.1. Решите в целых числах уравнение 25x-18y+1=0.
Найдем наибольший общий делитель пары чисел 25 и 18 с помощью цепных дробей, то есть используем один из вариантов алгоритма Евклида.
Преобразуем неправильную дробь , последовательно выделяя целые части неправильных дробей:
= 1 +
= 1 +
= 1 +
= 1 +
= 1 +
= 1 +
= 1 +
,
где выражение 1+ называется целой дробью.
Числа 1, 2, 1, 1, выделенные в этом выражении, являются последовательными частными алгоритма Евклида для нахождения наибольшего общего делителя пары чисел 25 и18.
Отбросим дробь и преобразуем получившуюся цепную дробь в обыкновенную:
1 + – 1 +
–
.
Вычтем полученную дробь из исходной дроби :
–
=
=
.
Приведем ее к общему знаменателю: 25 ∙ 5 – 18 ∙ 7 + 1 = 0.
Получили частное решение исходного уравнения х = 5, у = 7.
Общее решение исходного уравнения: х = 5 + 18t; y = 7 + 25t, t Z.
Ответ: х = 5+18t; у = 7+25t.
Приложение 1. Таблица остатков при делении степеней (an:m)
|
an |
2 |
3 |
4 |
5 |
|
3 |
0;1 |
0;1;2 |
0;1 |
0;1;2 |
|
4 |
0;1 |
0;1;3 |
0;1 |
0;1;3 |
|
5 |
0;1;4 |
0;1;2;3;4 |
0;1 |
0;1;2;3;4 |
|
6 |
0;1;3;4 |
0;1;2;3;4;5 |
0;1;3;4 |
0;1;2;3;4;5 |
|
7 |
0;1;2;4 |
0;1;6 |
0;1;2;4 |
0;1;2;3;4;5;6 |
|
8 |
0;1;4 |
0;1;3;5;7 |
0;1 |
0;1;3;5;7 |
|
9 |
0;1;4;7 |
0;1;8 |
0;1;4;7 |
0;1;2;3;4;5;7;8 |
|
10 |
0;1;4;5;6;9 |
0;1;2;3;4;5;6;7;8;9 |
0;1;5;6 |
0;1;2;3;4;5;6;7;8;9 |
Приложение 2. Задачи для самостоятельного решения
- Решить в простых числах уравнение x2 — 2y2 = 1.
- Доказать, что уравнение x3 + x + 10y = 20004 неразрешимо в целых числах.
- Доказать, что уравнение x5 + 3x4y — 5x3y2 — 15x2y3 + 4xy4 + 12y5 = 33 неразрешимо в целых числах.
- Решить в целых числах уравнение 2x3 + xy — 7 = 0.
- Доказать, что уравнения не имеют целочисленных решений:
а) y2 = 5x2 + 6; б) x3 = 2 + 3y2
- Решить в целых числах уравнения: а) x2 + x = y4 + y3 + y2 + y;
б) x² — y² = 91; в) 2ху = х² + 2y; г) 3x2 +4ху – 7y2 =13
- Решите в натуральных числах уравнения:
а) 2х² + 5ху – 12у² = 28; б) х² — 4ху – 5у² = 1996.
- Докажите, что система уравнений не имеет решений в целых числах.
- Найти все пары целых чисел, удовлетворяющих уравнению
а) x2 = y2+ 2y +13; б) xy = 20 – 3x + y; в) xy + 1 = x + y; г) x2– 3xy + 2y2 = 3
- Существуют ли целые числа m и n, удовлетворяющие уравнению
m2 + 1994 = n2
- Найти все простые числа, которые одновременно являются суммой двух простых чисел и разностью двух простых чисел.
- Докажите, что уравнение x2 – y2 = 30 не имеет решений в целых числах.
- Решите уравнение x2 – 2х + y2 – 4y + 5 = 0.
- Если первую цифру трехзначного числа увеличить на n, то полученное число будет в n раз больше исходного. Найдите число n и исходное число.
- Решить в целых числах уравнение x2 + y2 + z2 = 2xyz.
- Решить в целых числах уравнение x2 — 2y2 + 8z = 3.
- Решите в натуральных числах систему уравнений:
а) б)
- Найдите два натуральных числа, разность квадратов которых равна 45.
- Найдите все пары натуральных чисел, удовлетворяющих уравнению:
а) x2 — y2 = 105; б) 2x2 + 5xy – 12y2 = 28
- Решите в целых числах уравнение:
а) xy + 3x – 5y = – 3; б) x – y =
- Докажите, что система не имеет целочисленных решений
Литература:
1. Бардушкин В.В., Кожухов И.Б., Прокофьев А.А., Фадеичева Т.П. Основы теории делимости чисел. Решение уравнений в целых числах. Факультативный курс. – М.: МГИЭТ(ТУ). 2003. – 224 с.
2. В. Серпинский. О решении уравнений в целых числах. 1961.
3. Карпова И.В. Решение уравнений в целых числах.
4. http://www.fmclass.ru/pic/48503321f105d/uravneniya-v-celyh-chislah.pdf
Образовательный портал «Физ/Мат класс» www.fmclass.ru.
5. http://diofant.na.by/
6. www.a-elita.net/userfiles/File/…/Integer%20solutions_2012_10.pdf
7. http://math4school.ru/uravnenija_v_celih_chislah.html
Муниципальное бюджетное общеобразовательное учреждение г.Стерлитамак
Республики Башкортостан МАОУ «Гимназия№6»
Исследовательская работа
«Решение уравнений в целых числах»
Выполнила:
Чигинцева Виктория, 10 класс
Научный руководитель:
Кузнецова Л.В. , учитель математики
высшей категории
г.Стерлитамак, 2017
Содержание
Введение…………………………………………………………………………….
Глава I. Историческая справка………………………………………………….
Глава II. Общие сведения о решении уравнений в целых числах…………
2.1 Применение теории делимости к решению неопределенных
уравнений в целых числах …………………………………………………….
2.2 Алгоритм решения уравнения в целых числах……………………
Глава III. Применение способов решения уравнений……………………
-
Алгоритм Евклида………………………………………………………
-
Способ перебора вариантов…………………………………………………
3.3. Метод разложения на множители…………………………………………
3.4 Метод остатков………………………………………………………………
3.5. Задачи экзаменационного уровня …………………………………………
Заключение…………………………………………………………………………
Литература………..……………………………………………………………….
Введение
Решение в целых числах алгебраических уравнений с целыми коэффициентами более чем с одним неизвестным представляет собой одну из труднейших и древнейших математических задач. Этими задачами много занимались самые выдающиеся математики древности, например, греческий математик Пифагор (VI век до н.э.), александрийский математик Диофант (III век н.э.), П.Ферма(XVII в.), Л.Эйлер(XVIII век), Ж.Л.Лагранж(XVIII век), П.Дирихле(XIX век), К.Гаусс(XIX век), П.Чебышев(XIX в.) и многие другие.
Решение уравнений в целых числах является важной задачей и для современной математики. Теоретический интерес уравнений в целых числах достаточно велик, так как эти уравнения тесно связаны со многими проблемами теории чисел, что и определило актуальность нашей работы «Решение уравнений в целых числах»
Мы обратились к этой теме, так как она недостаточно полно изложена в действующих учебниках математики, а задачи по этой теме предлагаются как на олимпиадах, так и на вступительных экзаменах в ВУЗы. Кроме того решение уравнений, неравенств, задач, сводящихся к решению уравнений в целых числах с помощью оценок для переменных, встречается в различных математических сборниках и сборниках ЕГЭ.
Безусловно, тема решения уравнений в целых числах была, есть и будет актуальна. Это и без слов понятно. Недаром ей занимались с самого зарождения математики.
Теория решения подобных уравнений является классическим разделом элементарной математики. В ней не приходится писать сложные и громоздкие формулы, а необходимо проводить аккуратные рассуждения, базирующиеся на определенных понятиях теории чисел и связанные в стройную логическую конструкцию. В рамках это теории можно дать исчерпывающее решение рассматриваемого класса задач с четко описанным алгоритмом получения ответа.
Проблема: Решая примерные варианты заданий ЕГЭ, мы заметили, что чаще всего встречаются в С6 задания на решение уравнений первой и второй степени в целых числах. Но мы не знаем способы решения таких уравнений. В связи с этим возникла необходимость изучить теорию таких уравнений и алгоритм их решения.
Цель: Освоить способ решения уравнений с двумя неизвестными первой и второй степени в целых числах.
Задачи:
-
Изучить учебную и справочную литературу;
-
Собрать теоретический материал по способам решения уравнений;
-
Разобрать алгоритм решения уравнений данного вид;
-
Описать способ решения.
-
Рассмотреть ряд примеров с применением данного приема.
-
Решить уравнения с двумя переменными в целых числах из материалов ЕГЭ С6.
Объект исследования: Решение уравнений
Предмет исследования: Уравнения с двумя переменными в целых числах.
Гипотеза: Данная тема имеет большое прикладное значение. В школьном курсе математики подробно изучаются уравнения с одной переменной и различные способы их решения. Потребности учебного процесса требуют, чтобы ученики знали и умели решать простейшие уравнения с двумя переменными. Поэтому повышенное внимание к этой теме не только оправдано, но и является актуальной в школьном курсе математики.
Данная работа может быть использована для изучения данной темы на факультативных занятиях учениками, при подготовке к выпускным и вступительным экзаменам. Мы надеемся, что наш материал поможет старшеклассникам научится решать уравнения такого вида.
Глава I. Историческая справка
Диофант Александрийский — древнегреческий математик, живший предположительно в III веке нашей эры.
О подробностях его жизни практически ничего неизвестно. С одной стороны, Диофант цитирует Гипсикла (II век до н. э.); с другой стороны, о Диофанте пишет Теон Александрийский (около 350 года н. э.), — откуда можно сделать вывод, что его жизнь протекала в границах этого периода. Возможное уточнение времени жизни Диофанта основано на том, что его «Арифметика» посвящена «достопочтеннейшему Дионисию». Полагают, что этот Дионисий — не кто иной, как епископ Дионисий Александрийский, живший в середине III в. н. э.
В Палатинской антологии содержится эпиграмма-задача, из которой можно сделать вывод, что Диофант прожил 84 года:
Прах Диофанта гробница покоит, дивись ей и камень
Мудрым искусством его скажет усопшего век.
Волей богов шестую часть жизни он прожил ребенком.
И половину шестой встретил с пушком на щеках.
Только минула седьмая, с подругой он обручился.
С нею, пять лет проведя, сына дождался мудрец;
Только полжизни отцовской возлюбленный сын его прожил.
Отнят он был у отца ранней могилой своей.
Дважды два года родитель оплакивал тяжкое горе,
Тут и увидел предел жизни печальной своей.
Используя современные методы решения уравнений, можно сосчитать, сколько лет прожил Диофант. Составим и решим уравнение:
Решением этого уравнения является число 84. Таким образом, Диофант прожил 84 года. Однако достоверность сведений не может быть подтверждена.
Основное произведение Диофанта — Арифметика в 13 книгах. К сожалению, сохранились только 6 первых книг из 13.
Первая книга предварена обширным введением, в котором описаны ис пользуемые Диофантом обозначения. Неизвестную Диофант называет «числом» (ápιθμός) и обозначает буквой ς, квадрат неизвестной символом 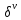
Большая часть труда — это сборник задач с решениями (в сохранившихся шести книгах их всего 189), умело подобранных для иллюстрации общих методов. Главная проблематика Арифметики нахождение положительных рациональных решений неопределённых уравнений. Рациональные числа трактуются Диофантом так же, как и натуральные, что не типично для античных математиков.
Сначала Диофант исследует системы уравнений 2-го порядка от 2 неизвестных; он указывает метод нахождения других решении, если одно уже известно. Затем аналогичные методы он применяет к уравнениям высших степеней.
В X веке Арифметика была переведена на арабский язык, после чего математики стран ислама (Абу Камил и др.) продолжили некоторые исследования Диофанта. В Европе интерес к Арифметике возрос после того, как Рафаэль Бомбелли обнаружил это сочинение в Ватиканской библиотеке и опубликовал 143 задачи из него в своей Алгебре (1572). В 1621 году появилася классический, подробно прокомментированный латинский перевод Арифметиуи, выполненный Баше де Мезириаком.
В XX веке под именем Диофанта обнаружен арабский текст еще 4 книг Арифметики. И. Г. Башмакова и Е. И. Славутин, проанализировав этот текст, выдвинули гипотезу, что их автором был не Диофант, а хорошо разбиравшийся в методах Диофанта комментатор, вероятнее всего — Гипатия.
Глава II. Общие сведения о решении уравнений в целых числах
2.1. Применение теории делимости к решению неопределенных уравнений в целых числах.
Неопределенные уравнения – уравнения, содержащие более одного неизвестного. Под одним решением неопределенного уравнения понимается совокупность значений неизвестных, которая обращает данное уравнение в верное равенство.
Для решения в целых числах уравнения вида ах + by = c, где а, b, c – целые числа, отличные от нуля, приведем ряд теоретических положений, которые позволят установить правило решения. Эти положения основаны также на уже известных фактах теории делимости.
Теорема 1. Если НОД(а, b) = d, то существуют такие целые числа х и у, что имеет место равенство ах + bу = d.
(Это равенство называется линейной комбинацией или линейным представлением наибольшего общего делителя двух чисел через сами эти числа.)
Доказательство теоремы основано на использовании равенства алгоритма Евклида для нахождения наибольшего общего делителя двух чисел (наибольший общий делитель выражается через неполные частные и остатки, начиная с последнего равенства в алгоритме Евклида).
Пример.
Найти линейное представление наибольшего общего делителя чисел 1232 и 1672.
Решение.
1. Составим равенства алгоритма Евклида:
1672 = 1232 ∙1 + 440,
1232 = 440 ∙ 2 + 352,
440 = 352 ∙ 1 + 88,
352 = 88 ∙ 4, т.е. (1672,352) = 88.
2) Выразим 88 последовательно через неполные частные и остатки, используя полученные выше равенства, начиная с конца:
88 = 440 — 352∙1 = (1672 — 1232) — (1232 — 1672∙2 + 1232∙2) = 1672∙3 — 1232∙4, т.е. 88 = 1672∙3 + 1232∙(-4).
Теорема 2. Если уравнение ах + bу = 1, если НОД(а, b) = 1, достаточно представить число 1 в виде линейной комбинации чисел а и b.
Справедливость этой теоремы следует из теоремы 1. Таким образом, чтобы найти одно целое решение уравнения ах + bу = 1, если НОД (а, в) = 1, достаточно представить число 1 в виде линейной комбинации чисел а и в.
Пример.
Найти целое решение уравнения 15х + 37у = 1.
Решение.
1. 37 = 15 ∙ 2 + 7,
15 = 7 ∙ 2 + 1.
2. 1 = 15 — 7∙2 = 15 — (37 — 15∙2) ∙2 = 15∙5 + 37∙(-2),
т.е. х

Теорема 3. Если в уравнении ах + bу = с НОД(а, b) = d1 и с не делится на d, то уравнение целых решений не имеет.
Для доказательства теоремы достаточно предположить противное.
Пример.
Найти целое решение уравнения 16х — 34у = 7.
Решение.
(16,34)=2; 7 не делится на 2, уравнение целых решений не имеет.
Теорема 4. Если в уравнении ах + bу = с НОД(а, b) = d1 и с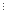





При доказательстве теоремы следует показать, что произвольное целое решение первого уравнения является также решением второго уравнения и обратно.
Теорема 5. Если в уравнении ах + bу = с НОД(а, b) = 1, то все целые решения этого уравнения заключены в формулах:
х = х



t – любое целое число.
При доказательстве теоремы следует показать, во-первых, что приведенные формулы действительно дают решения данного уравнения и, во-вторых, что произвольное целое решение этого уравнения заключено в приведенных формулах.
Приведенные теоремы позволяют установить следующее правило решения в целых числах уравнения ах+ bу = с НОД(а, b) = 1:
-
Находится целое решение уравнения ах + bу = 1 путем представления 1 как линейной комбинации чисел а и b (существуют и другие способы отыскания целых решений этого уравнения, например при использовании цепных дробей);
-
Составляется общая формула целых решений данного уравнения х = х
с + bt, у = y
c — at, где х
, y
— целое решение уравнения ах + bу = 1, t – любое целое число.
Придавая t определенные целые значения, можно получить частные решения данного уравнения: наименьшие по абсолютной величине, наименьшие положительные (если можно) и т.д.
При решении уравнений в целых и натуральных числах можно условно выделить следующие методы:
-
Алгоритм Евклида.
-
Способ перебора вариантов.
-
Метод разложения на множители
-
Цепные дроби.
-
Метод остатков.
-
Решение уравнений в целых числах как квадратных относительно какой-либо переменной.
-
Meтод бесконечного спуска.
2.2 Алгоритм решения уравнения в целых числах
Алгоритм решения в целых числах уравнения вида
-
Найти наибольший общий делитель чисел
и
, если
и с не делится на d, то уравнение целых решений не имеет;
если 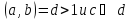
-
Разделить почленно уравнение
на d, получив при этом уравнение
, в котором
.
-
Найти целое решение
уравнения
путем представления 1 как линейной комбинации чисел
и
;
-
Составить общую формулу целых решений данного уравнения
где -целое решение уравнения
,
— любое целое число.
Глава III. Применение способов решения уравнений
3.1. Алгоритм Евклида
Задача 1.Решить уравнение в целых числах 407х -2816у 33.
Воспользуемся составленным алгоритмом.
-
Используя алгоритм Евклида, найдем наибольший общий делитель чисел 407 и 2816:
2816 = 407*6 + 374;
407 = 374*1 + 33;
374=33*11+11;
33 = 11*3
Следовательно (407,2816)=11, причем 33 делится на 11
-
Разделим обе части первоначального уравнения на 11, получим уравнение
, причем (37,256)=1
-
С помощью алгоритма Евклида найдем линейное представлена числа 1 через числа 37 и 256.
256=37*6+34;
37=34*1+3;
34=3*11+1
Выразим 1 из последнего равенства, затем последовательно поднимаясь по равенствам будем выражать 3; 34 и полученные выражения подставим в выражение для 1.
1=34-3*11=34-(37-34*1)*11=34*12-37*11=(256-37*6)*12-37*11=-83*37-256*(-12)
Таким образом, 37*(-83)-256*(-12)=1, следовательно пара чисел есть решение уравнения
-
Запишем общую формулу решений первоначального уравнения
Где -любое целое число.
3.2 Способ перебора вариантов
Задача 2. В клетке сидят кролики и фазаны, всего у них 18 ног. Узнать, сколько в клетке тех и других?
Решение: Составляется уравнение с двумя неизвестными переменными, в котором х — число кроликов, у — число фазанов:
4х + 2у = 18, или 2х + у = 9.
Выразим у через x:у = 9 — 2х.
Далее воспользуемся методом перебора:
|
x |
1 |
2 |
3 |
4 |
|
y |
7 |
5 |
3 |
1 |
Таким образом, задача имеет четыре решения.
Ответ: (1; 7), (2;5), (3;3), (4;1).
Задача. В загоне находятся одноглавые сороконожки и трехглавые змеи. Всего у них 298 ног и 26 голов. Сколько ног у трехглавых змей?
-
Обозначим за «х» сороконожек, а за «у» трехглавых змей, тогда голов 3у + х = 26.
-
Обозначим за «z» количество ног у одного змея, тогда ног уz + 40х = 298.
-
Имеем систему уравнений:
Ответ: у трехглавого змея 14 ног.
-
Метод разложения на множители
Перебор вариантов при нахождении натуральных решений уравнения с двумя переменными оказывается весьма трудоемким. Кроме того, если уравнение имеет целые решения, то перебрать их невозможно, так как таких решений бесконечное множество. Поэтому покажем еще один прием — метод разложения на множители
-
Вынесение множителя за скобку;
-
Использование формул сокращённого умножения;
-
Способ группировки;
-
Предварительное преобразование.
Задача 3.Найти все пары натуральных чисел, удовлетворяющих уравнению .
Решение. Разложим левую часть уравнения на множители и запишем уравнение в виде
Т.к. делителями числа 69 являются числа 1,3,23 и 69, то 69 можно получить двумя способами: 69=1*69 и 69=3*23. Учитывая, что , получим две системы уравнений, решив которые мы сможем найти искомые числа:
Первая система имеет решение = 35;
= 34, а вторая система имее решение
Ответ: (35;34),(13;10).
Задача 4. Решить уравнение в целых числах у3 — х3 = 91.
Решение:
1) Используя формулы сокращенного умножения, разложим правую часть уравнения на множители:
(1)
2) Выпишем все делители числа 91 :± 1; ± 7; ± 13; ± 91.
3) Проводим исследование. Заметим, что для любых целых х и у число
следовательно, оба сомножителя в левой части уравнения должны быть положительными. Тогда уравнение (1) равносильно совокупности систем уравнении:
4)Решив системы, получим: первая система имеет решения (5; 6), (-6;-5); третья(-3;4), (-4;3); вторая и четвертая решений в целых числах не имеют.
Ответ: уравнение (1) имеет четыре решения (5; 6); (-6;-5); (-3; 4);(-4;3).
Задача 5. Решить уравнение в целых числах:
Решение. Запишем уравнение в виде
Разложим левую часть уравнения на множители. Получим
Произведение двух целых чисел может равняться 1 только в двух случаях: если оба они равны 1 или -1. Получим две системы:
Первая система имеет решение х=2, у=2, а вторая система имеет решение х=0, у=0.
Ответ: (2,2), (0;0).
Задача 6. Решить в целых числах уравнение
Решение. Запишем данное уравнение в виде
Разложим левую часть уравнения на множители способом группировки, получим
Произведение двух целых чисел может равняться 7 в следующих случаях: 7=1*7=7*1=-1*(-7)=-7*(-1). Таким образом, получим четыре системы:
Решением первой системы является пара чисел х = -5, у = — 6. Решая вторую систему, получим х = 13, у = 6.Для третьей системы решением являются числа х =5, у = 6. Четвёртая система имеет решение х = -13, у =-6.
Ответ: (-5;-6), (13;6), (5;6), (-13;-6).
Задача 7. Доказать, что уравнение не имеет решений в целых числах.
Решение.
1) Разложим левую часть уравнения на множители и обе части уравнения разделим на 3, в результате получим уравнение:
(2)
-
Делителями 10 являются числа ±1, ±2, ±5, ±10. Заметим также, что сомножителей левой части уравнения (2) равна 0. Нетрудно проверить, что сумма любых трех чисел из множества делителей числа 10, дающих в произведении 10, не будет равняться 0. Следовательно, исходное уравнение не имеет решений в целых числах.
Задача 8. Решить уравнение: х2 — у2 =3 в целых числах.
Решение:
1. Применим формулу сокращенного умножения
2. Найдем делители числа
3.Данное уравнение равносильно совокупности 4 систем
Ответ: (2;1), (2;-1), (-2;1), (-2;-1).
3.4 Метод остатков
Задача 9. Решить уравнение: х2+ху=10
Решение:
Выразим переменную у через x:
-
Дробь
будет целой, если
-
Найдем 8 значений
.
Если
|
|
|
|
|
|
|
|
|
|
|
|
Задача 10. Решить уравнение в целых числах:
Решение: выразим из уравнения то неизвестное, которое входит в него только в первой степени — в данном случае у :
Выделим у дроби целую часть с помощью правила деления многочлена на многочлен «углом» Получим:
Следовательно, разность 2x-1 может принимать только значения -3, -1, 1, 3.
Осталось перебрать эти четыре случая.
Ответ: (1;9), (2;8), (0,2), (-1,3)
3.5. Задачи экзаменационного уровня
Рассмотрев несколько способов решения уравнений первой степени с
двумя переменными в целых числах, мы заметили, что чаще всего применяются метод разложения на множители и метод остатков.
Уравнения, которые даны в вариантах ЕГЭ, в основном решаются методом остатков.
1. Решить в натуральных числах уравнение: где
Решение:
Выразим переменную п через переменную т :
Найдем делитель числа 625:
-
если m-25=1, то m=26, n=25+625=650
-
m-25=5, то m=30, n=150
-
m-25=25, то m=50, n=150
-
m-25=125, то m=150, n=30
-
m-25=625, то m=650, n=26
Ответ: m=150 , n=30
m=650,n=26
2.Решите уравнение в натуральных числах: mn+25=4m
Решение: mn+25=4m
-
выразим переменную m через n:
-
найдем натуральные делители числа 25:
если 4-n=1, то n=3, m=25
4-n=5, то n=-1, m=5 (посторонние корни, т.к не натуральное число)
4-n=25, то n=-21, m=1 (посторонние корни, т.к не натуральное число)
Ответ: (25;3)
3.Найдите все пары (x;y) целых чисел, удовлетворяющие системе неравенств:
Решение: Выделяя полные квадраты, получим:
Из первого и второго неравенства системы:
Подставляем x=12 в систему, получим:
Ответ: (12;-8)
Заключение
В процессе работы над темой «Решение уравнений в целых числах» было замечено множество интереснейших фактов. Решение уравнений в целых числах — очень увлекательная задача. С древнейших времён накопилось множество способов решения конкретных диофантовых уравнений, однако, только в нашем веке предстали общие приёмы их исследования. Теорема Пифагора и теорема Ферма также являются диофантовым уравнением.
Решение уравнений в целых числах — один из самых красивых разделов математики. Ни один крупный математик не прошёл мимо теории диофантовых уравнений. Ферма и Эйлер, Лагранж и Дирихле, Гаусс и Чебышев оставили неизгладимый след в этой интереснейшей теории.
Решение различного вида уравнений является одной из содержательных линий школьного курса математики, но при этом методы решения уравнений с несколькими неизвестными практически не рассматриваются. Вместе с тем, решение уравнений от нескольких неизвестных в целых числах является одной из древнейших математических задач. Большинство методов решения таких уравнений основаны на теории делимости целых чисел, интерес к которой в настоящее время определяется бурным развитием информационных технологий. В связи с этим, учащимся старших классов будет небезинтересно познакомиться с методами решения некоторых уравнений в целых числах, тем более что на олимпиадах разного уровня очень часто предлагаются задания, предполагающие решение какого-либо уравнения в целых числах, а в этом году такие уравнения включены еще и в материалы ЕГЭ.
В своей работе мы рассматривали только неопределенные уравнения первой и второй степени. Уравнения первой степени, как мы увидели, решаются довольно просто. Мы выделили виды таких уравнений и алгоритмы их решений. Также было найдено общее решение таких уравнений.
Литература
1. Диофант Александрийский. Арифметика и книга о многоугольных числах (перевод с древнегреческого И. Н. Веселовского; редакция и комментарии И. Г. Башмаковой). Москва, «Наука», 1974.
2. Конкурсные задачи, основанные на теории чисел. В.Я. Галкин, Д.Ю. Сычугов. МГУ, ВМК, Москва, 2005.
3. Задачи повышенной трудности в курсе алгебры 7-9 классов. Н.П. Косрыкина. «Просвещение», Москва, 1991 г.
4. Ляпин С.Е. и др. Сборник задач по элементарной алгебре. Учебное пособие для студентов физико — математических факультетов педагогических институтов. Москва, «Просвещение», 1973 г.
5. Галкин Е.В. Нестандартные задачи по математике: Задачи логического характера: Книга для учащихся 5-11 классов. Москва, «Просвещение», 1996 г.
6. Панферов В.С., Сергеев И.Н. Отличник ЕГЭ. Математика. Решение сложных задач; ФИПИ – Москва: Интеллект – Центр, 2010 г.
ответы
ваш ответ
Можно ввести 4000 cимволов
отправить
дежурный
Нажимая кнопку «отправить», вы принимаете условия пользовательского соглашения
похожие темы
похожие вопросы 5

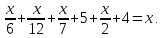
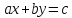
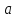 и
и 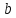 , если
, если 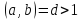 и с не делится на d, то уравнение целых решений не имеет;
и с не делится на d, то уравнение целых решений не имеет;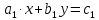 , в котором
, в котором