Как найти все периоды функции косинус

ВИДЕО УРОК

Периодические функции.

Функцию  у = f(х),  х ∈ Х, называют периодической,
если существует такое отличное от нуля число 
Т, что для любого  х  из области определения функции справедливо
равенство:

f(х + Т) = f(х) = f(х – Т).

Число  Т  называют периодом функции  у = f(х).

Из этого
определения сразу следует, что если  Т –
период функции 

у = f(х), то 

2Т, 3Т, 4Т, –Т, –2Т, –3Т,
–4Т

– также периоды
функций. Значит у периодической функции бесконечно много периодов.

Если  Т – период функции, то число вида  kТ,
где  k – любое целое
число, также является периодом функции.

Чаще всего (но не
всегда) среди множества положительных периодов функции можно найти наименьший.
Его называют основным периодом.

График периодической
функции состоит из неограниченно повторяющихся одинаковых фрагментов.

График каждой
периодической функции состоит из одинаковых линий повторяющихся и изолированных
друг от друга, как в рассматриваемом случае, или соединенных в одну общую линию
(синусоида и другие.)

Графики
периодических функций обладают следующей особенностью. Если  Т – основной период функции  у = f(х), то для построения её графика достаточно построить ветвь
графика на одном из промежутков оси  х  длиной 
Т, а затем осуществить параллельный перенос этой ветви по
оси  х  на

± Т, ±
2Т, ± 3Т, …

Чаще всего в
качестве такого промежутка длиной  Т  выбирают промежуток с концами в точках

(–^Т/₂; 0)  и  (^Т/₂; 0)  или

(0; 0)  и  (Т; 0).

ПРИМЕР:

Рассмотрим функцию

у = х – [х], где  [х] – целая часть числа. Если к
произвольному значение аргумента этой функции добавить 1, то значение функции от этого не изменится:

f(x + 1) = (x
+1) – [x + 1] = x + 1 – [x] – 1
= x – [x] = f (x).

Следовательно, при любом
значении  х

 f(x + 1) = f(x).  

А это значит, что рассматриваемая функция
периодическая, период которой равен 1. Любое целое число
также является периодом данной функции, но обычно рассматривают только
маленький положительный период функции.

График этой функции
приведен на рисунке. Он состоит из бесконечного множества равных отрезков, которые
повторяются.

Периодичность тригонометрических функций.

Возьмём произвольный угол  α  и построим
подвижной радиус  ОМ  единичной окружности такой, что угол,
составленный с осью  Ох  этим радиусом, равен  α.

Если мы к углу    прибавим 
2π  или  360° (то есть полный
оборот), то углу  α + 2π  или  α + 360°  будет соответствовать то же положение
подвижного радиуса  ОМ, что для угла  α.

Так как синус и косинус угла,
составленного с осью  Ох  подвижным радиусом  ОМ  единичной
окружности, по сути соответственно ордината 
у  и
абсцисса  х  точки  М, то

sin (α + 2π) = sin α  или 

sin (α + 360°) = sin α

и

cos (α + 2π)
= cos α  или 

cos (α + 360°) = cos α.

Таким образом, функции  sin α  и  cos α  от
прибавления к аргументу α   одного
полного оборота (2π  или  360°) не меняют своих значений.

Точно так же, прибавляя к
углу  α  любое целое
число полных оборотов, мы не изменим положения подвижного радиуса  ОМ, а потому:

sin (α + 2kπ) = sin α  или 

sin (α + 360°k) = sin α

и

cos (α + 2kπ) = cos α  или 

cos (α + 360°k) = cos α,

где  k – любое целое
число.

Функции, обладающие таким
свойством, что их значения не изменяются от прибавления к любому допустимому
значению аргумента определённого постоянного числа, называются периодическими.

Следовательно, функции  sin α  и  cos α – периодические.

Наименьшее положительное число,
от прибавления которого к любому допустимому значению аргумента не изменяется
значение функции, называется периодом функции.

Периодом функции  sin α  и  cos α 
является  2π  или  360°.

Функции  tg α  и  сtg α  также
периодические и их периодом является число 
π  или  180°.

В самом деле, пусть  α – произвольный угол, составленный с осью  Ох  подвижным
радиусом  ОМ  единичной окружности.

Построим точку  М‘,

симметричную точке  М  относительно
начала координат. Один из углов, образованных с осью  Ох  подвижным
радиусом  ОМ‘, будет равен  α + π.

Если  х  и  у – координаты точки 
М, то точки  М‘  будут  –х  и  –у. Поэтому

sin α = у, cos α = х,

sin (α + π) = –у,

cos (α + π) = –х.

Отсюда

и, следовательно,

tg (α + π) = tg α,

сtg (α + π)
= сtg α.

отсюда следует, что значения  tg α  и  сtg α  не
изменяются, если к углу  α  прибавить любое число полуоборотов:

tg (α + kπ) = tg α,

сtg (α + kπ) = сtg α.

где  k – любое целое
число.

Периоды функций

y = A sin (ωx + φ)  и

y = A cos (ωx + φ) 

вычисляются по формуле

T = ^2π/_ω,

а период функции

y = A tg (ωx + φ)

по формуле

T = ^π/_ω.

Если период функции  y = f(x)  равен  T₁, а период функции  y = g(x)  равен  T₂, то период функций

y = f(x) + g(x)  и

y = f(x) – g(x)

равен наименьшему числу, при делении которого
на  T₁  и  T₂  получаются целые числа.

ПРИМЕР:

Найти
период функции

y = 3 sin (x – 2) + 7 соs πx.

РЕШЕНИЕ:

Период
функции

y = 3 sin (x – 2)

равен

T₁ = ^2π/₁ = 2π.

Период
функции

y = 7 соs πx

равен

T₂ = ^2π/_π = 2.

Периода
у функции

y = 3 sin (x – 2) + 7 соs πx

не
существует, так как такого числа, при делении которого на  2π  и 
на  2  получались бы целые числа, нет.

ОТВЕТ:

Периода
не существует.

ПРИМЕР:

Доказать
следующее утверждение:

tg
3850° = tg 250°.

РЕШЕНИЕ:

Так как тангенс – периодическая функция с минимальным
периодом  20 ∙ 180°, то получим:

tg
3850° = tg (20 ∙ 180° + 250°) = tg 250°.

ПРИМЕР:

Доказать
следующее утверждение:

сos (–13π) = –1.

РЕШЕНИЕ:

Так как косинус – чётная и периодическая функция с
минимальным периодом  2π, то получим:

сos (–13π) = сos 13π = сos (π + 6 ∙ 2π) = сos π = –1.

ПРИМЕР:

Доказать
следующее утверждение:

sin (–7210°) = – sin 10°.

РЕШЕНИЕ:

Так как синус – нечётная и периодическая функция с
минимальным периодом  20 ∙ 360°, то получим:

sin (–7210°) = –sin 7210° = –sin (20 ∙ 360° + 10°) – sin 10°.

ПРИМЕР:

Найти основной период функции

sin 7х.

РЕШЕНИЕ:

Пусть  Т  основной период функции, тогда:

sin 7х = sin 7(х + t) = sin (7х + 7t)

так как   2πk   период синуса, то получим:

sin (7х + 7t) = sin (7х + 2πk),

ОТВЕТ:

ПРИМЕР:

Найти основной период функции

соs 0,3х.

РЕШЕНИЕ:

Пусть  Т  основной период функции, тогда:

соs 0,3х = соs 0,3(х + t)
= соs (0,3х + 0,3t)

так как   2πk   период косинуса, то получим:

соs (0,3х + 0,3t) = соs (0,3х + 2πk),

ОТВЕТ:

ПРИМЕР:

Найти период функции:

y = 5sin 2x + 2ctg 3х.

РЕШЕНИЕ:

Период функции

y = 5sin 2x

равен  Т₁ = ^2𝜋/₂ = π,

а период функции

y = 2ctg 3х

равен  Т₂ = ^𝜋/₃.

Наименьшее число, при делении которого на

Т₁ = π  и  Т₂ = ^𝜋/₃

– получаются целые числа будет число  π.
Следовательно, период заданной функции равен  Т = π.

ПРИМЕР:

Найти период функции:

y = 9sin (5x + ^π/₃) – 4cоs (7х + 2).

РЕШЕНИЕ:

Находим периоды слагаемых. Период функции

y = 9sin (5x + ^π/₃)

равен  Т₁ = ^2𝜋/₅,

а период функции

y = 4cоs (7х + 2)

равен   Т₂ = ^2𝜋/₇.

Очевидно, что период заданной функции равен

Т = 2π.

ПРИМЕР:

Найти период функции:

y = 3sin πx + 8tg (х + 5).

РЕШЕНИЕ:

Период функции

y = 3sin πx

равен  Т₁ = ^2π/_π = 2,

а период функции

y = 8tg (х + 5)

равен   Т₂ = ^𝜋/₁ = π.

Периода у заданной функции не существует, так как нет
такого числа, при делении которого на  2  и на  π  одновременно получались бы целые числа.

ПРИМЕР:

Найти период функции:

y = sin 3x + соs 5х.

РЕШЕНИЕ:

Период функции

y = sin 3x

равен  Т₁ = ^2π/₃,

а период функции

y = соs 5х

равен   Т₂ = ^2π/₅.

Приведём к общему знаменателю периоды:

Т₁ = ^10π/₁₅,  Т₂ = ^6π/₁₅.

Тогда наименьшее общее кратное (НОК) будет:

НОК (10π; 6π)
= 30π.

Теперь найдём период заданной функции:

Т = ^30π/₁₅ = 2π.

Как найти период функции вида y=Af(kx+b), где A, k и b — некоторые числа? Поможет формула периода функции

   

где T — период функции y=f(x). Эта формула позволяет быстро найти период тригонометрических функций такого вида. Для функций y=sin x и y=cos x наименьший положительный период T=2п, для y=tg x и y=ctg x T=п. Рассмотрим на конкретных примерах, как найти период функции, используя данную формулу.

Найти период функции:

1) y=5sin(3x-п/8).

Здесь А=5, k=3, b=-п/8. Для нахождения периода нам нужно только k — число, стоящее перед иксом. Поскольку период синуса T=2п, то период данной функции

   

   

А=2/7, k=-1/11, b=п/5. Поскольку период косинуса T=2п, то

   

   

А=0,3, k=5/9, b=п/7. Период тангенса равен п, поэтому период данной функции

   

   

А=9, k=0,4, b=-7. Период котангенса равен п, поэтому период данной функции есть

   

Видеоурок «Периодичность функций у = sin х, у = cos х» раскрывает понятие периодичности функции, рассматривает описание примеров решения задач, в которых используется понятие периодичности функции. Данный видеоурок является наглядным пособием для объяснения темы ученикам. Также данное пособие может стать самостоятельной частью урока, освобождая учителя для проведения индивидуальной работы с учениками.

Наглядность в представлении данной темы очень важна. Чтобы представить поведение функции, построение графика, ее необходимо визуализировать. Произвести построения с помощью классной доски и мела не всегда удается так, чтобы они были понятны всем ученикам. В видеоуроке есть возможность при построении выделять части рисунка цветом, производить преобразования с помощью анимации. Таким образом, построения становятся более понятными большинству учеников. Также возможности видеоурока способствуют лучшему запоминанию материала.

Демонстрация начинается с представления темы урока, а также напоминания ученикам материала, изученного на прошлых уроках. В частности, подытоживается перечень свойств, которые были выявлены в функциях у = sin х, а также у = cos х. Среди свойств рассматриваемых функций отмечены область определения, область значений, четность (нечетность), другие особенности — ограниченность, монотонность, непрерывность, точки наименьшего (наибольшего) значения. Ученикам сообщается, что на данном уроке изучается еще одно свойство функции – периодичность.

Представлено определение периодичной функции y=f(x), где xϵX, в которой выполняется условие f(x-Т)= f(x)= f(x+Т) для некоторого Т≠0. Иначе число Т называют периодом функции.

Для рассматриваемых функций синуса и косинуса выполнение условия проверяется, применяя формулы приведения. Очевидно, что вид тождества sin(x-2π)=sinx=sin(x+2π) соответствует виду выражения определяющего условие периодичности функции. Такое же равенство можно отметить для косинуса cos (x-2π)= cos x= cos (x+2π). Значит, данные тригонометрические функции являются периодическими.

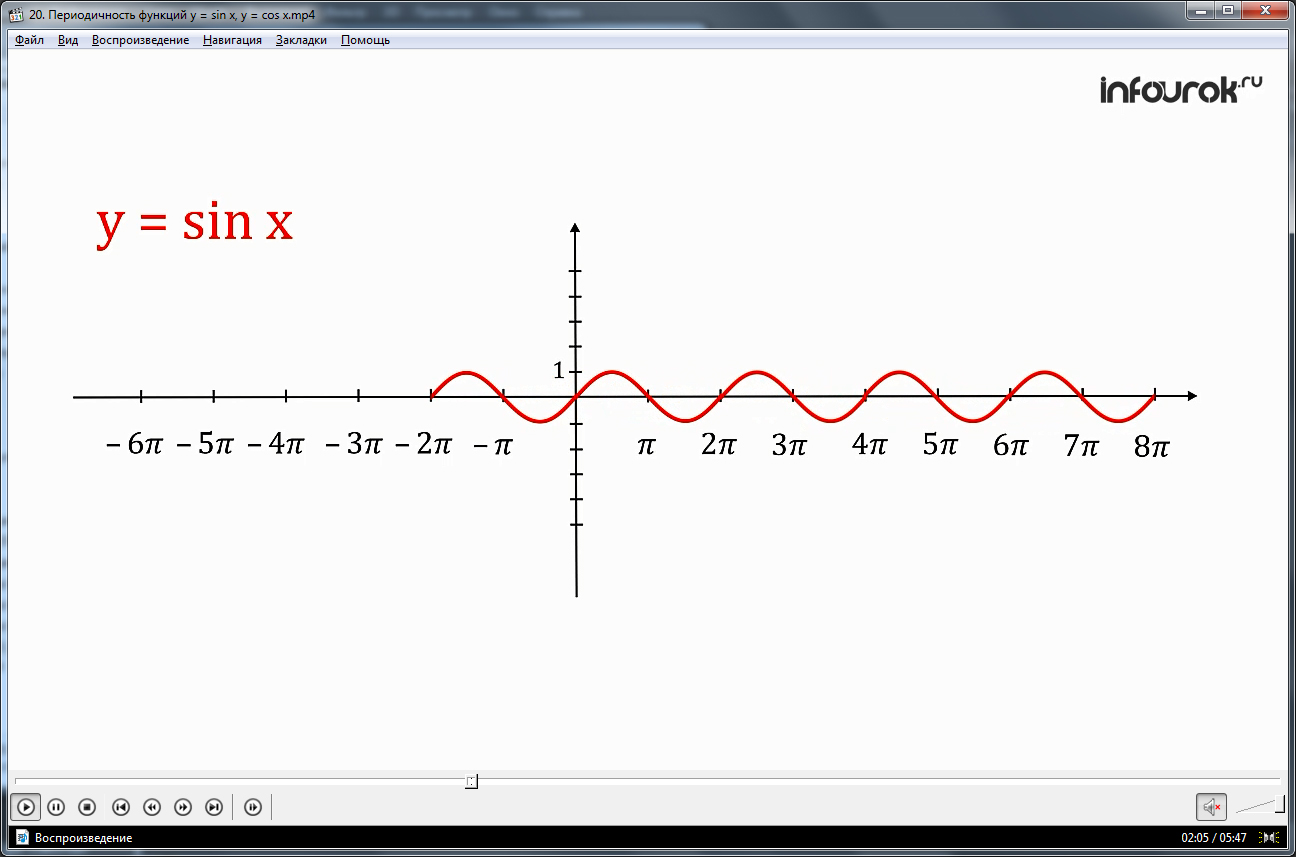
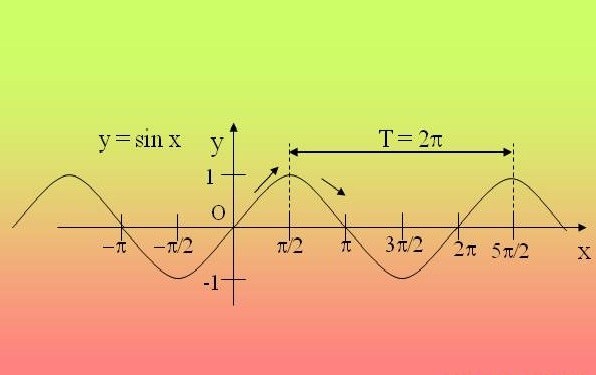
Далее отмечается, как свойство периодичности помогает строить графики периодичных функций. Рассматривается функция у = sin х. На экране строится координатная плоскость, на которой отмечены абсциссы от -6π до 8π с шагом π. На плоскости строится часть графика синуса, представленный одной волной на отрезке [0;2π]. На рисунке демонстрируется, как график функции формируется на всей области определения сдвигом построенного фрагмента, и получая длинную синусоиду.

Строится график функции у = cos х, используя свойство ее периодичности. Для этого на рисунке строится координатная плоскость, на которой изображается фрагмент графика. Отмечается, что обычно такой фрагмент строится на отрезке [-π/2;3π/2]. Аналогично графику функции синуса, построение графика косинуса выполняется сдвигом фрагмента. В результате построения образуется длинная синусоида.

Построение графика периодичной функции имеет особенности, которые можно использовать. Поэтому они даются в обобщенном виде. Отмечается, что для построения графика такой функции сначала строят ветвь графика на некотором промежутке длиной Т. затем необходимо сдвинуть построенную ветвь вправо и влево на Т, 2Т, 3Т и т.д. при этом указывается еще на одну особенность периода – для любого целого k≠0 число kТ также является периодом функции. Однако Т называется основным периодом, так как он наименьших из всех. Для тригонометрических функций синуса и косинуса основным периодом является 2π. Однако также являются периодами 4π, 6π и т.д.

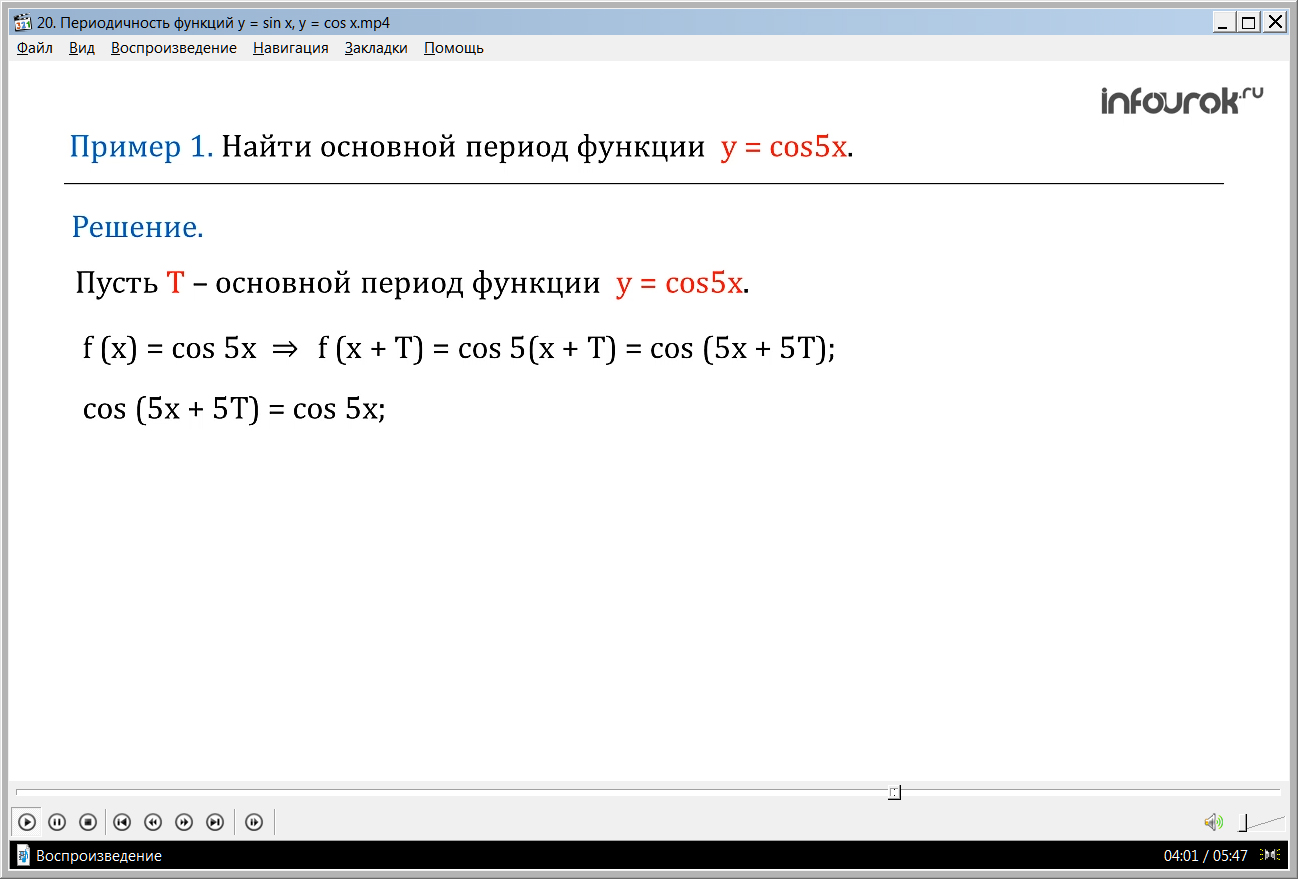
Далее предлагается рассмотреть нахождение основного периода функции у = cos 5х. Решение начинается с предположением, что Т – период функции. Значит, необходимо выполнение условия f(x-Т)= f(x)= f(x+Т). В данном тождестве f(x)= cos 5х, а f(x+Т)=cos 5(x+Т)= cos (5x+5Т). При этом cos (5x+5Т)= cos 5х, следовательно 5Т=2πn. Теперь можно найти Т=2π/5. Задача решена.

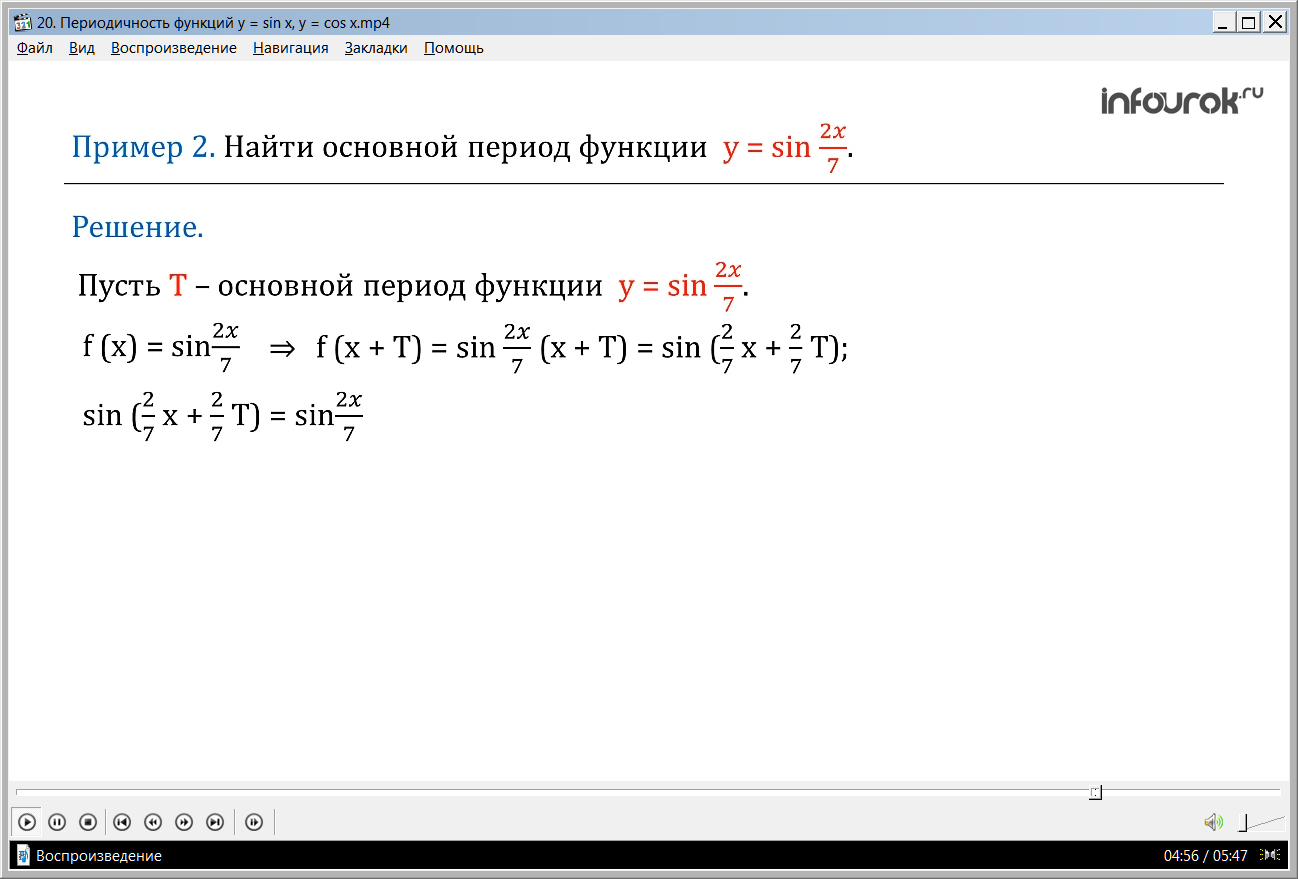
Во второй задаче необходимо найти основной период функции y=sin(2x/7). Предполагается, что основной период функции Т. для данной функции f(x)= sin(2x/7), а через период f(x+Т)=sin(2x/7)(х+Т)= sin(2x/7+(2/7)Т). после приведения получаем (2/7)Т=2πn. Однако нам необходимо найти основной период, поэтому берем наименьшее значение (2/7)Т=2π, из которого находим Т=7π. Задача решена.

В конце демонстрации результаты примеров обобщаются, сформировав правило для определения основного периода функции. Отмечается, что для функций у=sinkxи y=coskx основными периодами являются 2π/k.

Видеоурок «Периодичность функций у = sin х, у = cos х» может применяться на традиционном уроке математики для повышения эффективности урока. Также данный материал рекомендуется использовать учителю, осуществляющему дистанционное обучение для повышения наглядности объяснения. Видео может быть рекомендовано отстающему ученику для углубления понимания темы.

ТЕКСТОВАЯ РАСШИФРОВКА:

«Периодичность функций у = cos x,  y =sin x».

Для построения графиков функций y =sin x и у = cos x были использованы свойства функций:

1 область определения,

2 область значения,

3 четность или нечетность,

4 монотонность,

5 ограниченность,

6 непрерывность,

7 наибольшее и наименьшее значение.

Сегодня мы изучим еще одно свойство: периодичность функции.

ОПРЕДЕЛЕНИЕ. Функцию у = f ( x), где х ϵ Х( игрек равно эф от икс, где икс принадлежит множеству икс), называют периодической, если существует отличное от нуля число Т такое, что для любого х из множества Х выполняется двойное равенство: f ( x – Т)= f ( x) = f ( x + Т)( эф от икс минус тэ равно эф от икс и равно эф от икс плюс тэ). Число Т, которое удовлетворяет такому двойному равенству, называют периодом функции

у = f ( x).

А так как синус и косинус определены на всей числовой прямой и для любого х выполняются равенства  sin( x – 2π)= sin x= sin( x+ 2π) ( синус от икс минус два пи равен синусу икс и равен синусу от икс плюс два пи) и

cos ( x– 2π)= cos x = cos ( x+ 2π) ( косинус от икс минус два пи равен косинусу икс и равен косинусу от икс плюс два пи), то синус и косинус – это периодические функции с периодом 2π.

Периодичность позволяет  быстро построить график функции. Ведь для того, что бы построить график функции y = sin x , достаточно построить одну волну (чаще всего на отрезке [0; 2π] (от нуля до двух пи), а затем с помощью сдвига построенной части графика вдоль оси абсцисс  вправо и влево на 2π, затем на 4π и так далее получить синусоиду.

(показать сдвиг вправо и влево на 2π, 4π)

Аналогично  для графика функции

 у = cos x, только строим  одну волну чаще всего на отрезке [; ] (от  минус  пи на два до трех пи на два).

Обобщим выше сказанное и сделаем вывод: для построения графика периодической функции с периодом Т сначала нужно построить ветвь( или волну, или часть) графика на любом промежутке длины Т( чаще всего это промежуток с концами в точках 0 и Т или же  –  и (минус тэ на два и тэ на два), а затем сдвинуть эту ветвь вдоль оси х( икс) вправо и влево на Т, 2Т, 3Т и т. д.

Очевидно, что если функция периодическая с периодом Т, то при любом целом k0( ка не равном нулю) число вида kT( ка тэ) тоже период этой функции. Обычно стараются выделить наименьший положительный период, который называют основным периодом.

В качестве периода функций у = cos x,  y = sin x можно было бы взять  – 4π, 4π,– 6π, 6π и т.д.( минус четыре пи, четыре пи, минус шесть пи, шесть пи и так далее). Но число 2π является основным периодом и той, и другой функции.

Рассмотрим примеры.

ПРИМЕР 1.Найти основной период функции  у = сos5x (игрек равно косинус пяти икс).

Решение. Пусть Т – основной период функции  у = сos5x. Положим

 f (x) = сos5x, тогда f (x + Т)= сos5(x + Т)= сos (5x + 5Т) ( эф от икс плюс тэ равно косинусу   пяти, умноженного на сумму икса и тэ равно косинусу от суммы пяти икс и пяти тэ).

Чтобы число Т было периодом функции, должно выполнятся тождество

  сos (5x + 5Т)= сos5x. Отсюда 5Т= 2πn (пять тэ равно два пи эн), но по условию нужно найти основной период, значит, 5Т= 2π. Получаем Т= 

( период  данной функции равен  два пи, деленное на пять).

Ответ: Т=.

ПРИМЕР 2. Найти основной период функции  у = sin ( игрек равно синус частного двух икс на семь).

Решение. Пусть Т – основной период функции  у = sin . Положим

 f ( x) = sin , тогда f ( x + Т)= sin  ( x + Т) = sin ( x +  Т) ( эф от икс плюс тэ равно синусу произведения двух седьмых и суммы икса и тэ равно синусу от суммы двух седьмых икс и двух седьмых тэ).

Чтобы число Т было периодом функции, должно выполнятся тождество

  sin ( x +  Т) = sin . Отсюда  Т= 2πn (две седьмые тэ равно два пи эн), но по условию нужно найти основной период, значит,   Т= 2π. Получаем Т=7

( период  данной функции равен  семи пи).

Ответ: Т=7.

Обобщая результаты, полученные в примерах, можно сделать вывод: основной период функций  y =sin kx или у = cos kx (игрек равно синус ка икс или игрек равно косинус ка икс) равен  (два пи, деленное на ка).

Как найти период тригонометрической функции

Тригонометрические функции периодичны, то есть повторяются через определенный период. Благодаря этому достаточно исследовать функцию на этом промежутке и распространить найденные свойства на все остальные периоды.

Инструкция

Если вам дано простое выражение, в котором присутствует лишь одна тригонометрическая функция (sin, cos, tg, ctg, sec, cosec), причем угол внутри функции не умножен на какое-либо число, а она сама не возведена в какую-либо степень – воспользуйтесь определением. Для выражений, содержащих sin, cos, sec, cosec смело ставьте период 2П, а если в уравнении есть tg, ctg – то П. Например, для функции у=2 sinх+5 период будет равен 2П.

Если угол х под знаком тригонометрической функции умножен на какое-либо число, то, чтобы найти период данной функции, разделите стандартный период на это число. Например, вам дана функция у= sin 5х. Стандартный период для синуса – 2П, разделив его на 5, вы получите 2П/5 – это и есть искомый период данного выражения.

Чтобы найти период тригонометрической функции, возведенной в степень, оцените четность степени. Для четной степени уменьшите стандартный период в два раза. Например, если вам дана функция у=3 cos^2х, то стандартный период 2П уменьшится в 2 раза, таким образом, период будет равен П. Обратите внимание, функции tg, ctg в любой степени периодичны П.

Если вам дано уравнение, содержащее произведение или частное двух тригонометрических функций, сначала найдите период для каждой из них отдельно. Затем найдите минимальное число, которое умещало бы в себе целое количество обоих периодов. Например, дана функция у=tgx*cos5x. Для тангенса период П, для косинуса 5х – период 2П/5. Минимальное число, в которое можно уместить оба этих периода, это 2П, таким образом, искомый период – 2П.

Если вы затрудняетесь действовать предложенным образом или сомневаетесь в ответе, попытайтесь действовать по определению. Возьмите в качестве периода функции Т, он больше нуля. Подставьте в уравнение вместо х выражение (х+Т) и решите полученное равенство, как если бы Т было параметром или числом. В результате вы найдете значение тригонометрической функции и сможете подобрать минимальный период. Например, в результате упрощения у вас получилось тождество sin (Т/2)=0. Минимальное значение Т, при котором оно выполняется, равно 2П, это и будет ответ задачи.