Как найти все пути в дереве - Исправление недочетов и поиск решений вместе с Examum.ru

Для заданного бинарного дерева напишите эффективный алгоритм для вывода всех путей от корневого узла до каждого конечного узла в нем.

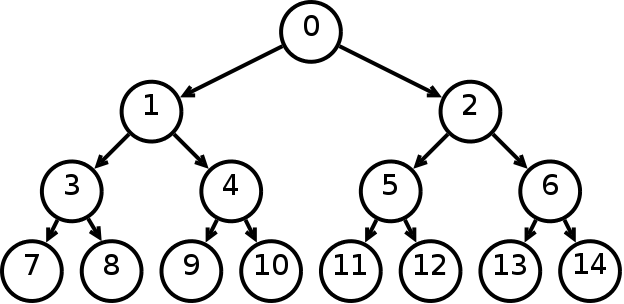
Например, рассмотрим следующее бинарное дерево:

The binary tree has four root-to-leaf paths:

1 —> 2 —> 4
1 —> 2 —> 5
1 —> 3 —> 6 —> 8
1 —> 3 —> 7 —> 9

Потренируйтесь в этой проблеме

Идея состоит в том, чтобы обойти дерево в предзаказ моды и сохранить каждый встреченный узел на текущем пути от корня к листу в векторе. Если мы встретим листовой узел, выведите все узлы, присутствующие в векторе. Ниже приведена реализация этой идеи на C++, Java и Python:

C++

#include <iostream>

#include <vector>

using namespace std;

// Структура данных для хранения узла бинарного дерева

struct Node

{

int data;

Node *left, *right;

Node(int data)

{

this->data = data;

this->left = this->right = nullptr;

}

};

// Функция для проверки, является ли данный узел листовым узлом или нет

bool isLeaf(Node* node) {

return (node->left == nullptr && node->right == nullptr);

}

// Рекурсивная функция для поиска путей от корневого узла к каждому конечному узлу

void printRootToLeafPaths(Node* node, vector<int> &path)

{

// базовый вариант

if (node == nullptr) {

return;

}

// включить текущий узел в путь

path.push_back(node->data);

// если конечный узел найден, вывести путь

if (isLeaf(node))

{

for (int data: path) {

cout << data << » «;

}

cout << endl;

}

// повторяется для левого и правого поддерева

printRootToLeafPaths(node->left, path);

printRootToLeafPaths(node->right, path);

// вернуться назад: удалить текущий узел после того, как левое и правое поддеревья завершены

path.pop_back();

}

// Основная функция для печати путей от корневого узла к каждому конечному узлу

void printRootToLeafPaths(Node* node)

{

// vector для хранения пути от корня к листу

vector<int> path;

printRootToLeafPaths(node, path);

}

int main()

{

/* Построим следующее дерево

2 3

/ /

4 5 6 7

8 9

Node* root = new Node(1);

root->left = new Node(2);

root->right = new Node(3);

root->left->left = new Node(4);

root->left->right = new Node(5);

root->right->left = new Node(6);

root->right->right = new Node(7);

root->right->left->left = new Node(8);

root->right->right->right = new Node(9);

// вывести все пути от корня к листу

printRootToLeafPaths(root);

return 0;

}

Скачать Выполнить код

результат:

1 2 4
1 2 5
1 3 6 8
1 3 7 9

Java

import java.util.ArrayDeque;

import java.util.Deque;

// Класс для хранения узла бинарного дерева

class Node

{

int data;

Node left = null, right = null;

Node(int data) {

this.data = data;

}

class Main

{

// Функция для проверки, является ли данный узел листовым узлом или нет

public static boolean isLeaf(Node node) {

return (node.left == null && node.right == null);

}

// Рекурсивная функция для поиска путей от корневого узла к каждому конечному узлу

public static void printRootToLeafPaths(Node node, Deque<Integer> path)

{

// базовый вариант

if (node == null) {

return;

}

// включить текущий узел в путь

path.addLast(node.data);

// если конечный узел найден, вывести путь

if (isLeaf(node)) {

System.out.println(path);

}

// повторяется для левого и правого поддерева

printRootToLeafPaths(node.left, path);

printRootToLeafPaths(node.right, path);

// вернуться назад: удалить текущий узел после того, как левое и правое поддеревья завершены

path.removeLast();

}

// Основная функция для печати путей от корневого узла к каждому конечному узлу

public static void printRootToLeafPaths(Node node)

{

// список для хранения пути от корня к листу

Deque<Integer> path = new ArrayDeque<>();

printRootToLeafPaths(node, path);

}

public static void main(String[] args)

{

/* Построим следующее дерево

2 3

/ /

4 5 6 7

8 9

Node root = new Node(1);

root.left = new Node(2);

root.right = new Node(3);

root.left.left = new Node(4);

root.left.right = new Node(5);

root.right.left = new Node(6);

root.right.right = new Node(7);

root.right.left.left = new Node(8);

root.right.right.right = new Node(9);

// вывести все пути от корня к листу

printRootToLeafPaths(root);

}

Скачать Выполнить код

результат:

[1, 2, 4]
[1, 2, 5]
[1, 3, 6, 8]
[1, 3, 7, 9]

Python

from collections import deque

# Класс для хранения узла бинарного дерева.

class Node:

def __init__(self, data, left=None, right=None):

self.data = data

self.left = left

self.right = right

# Функция для проверки, является ли данный узел листовым узлом или нет.

def isLeaf(node):

return node.left is None and node.right is None

# Рекурсивная функция для поиска путей от корневого узла к каждому конечному узлу

def printRootToLeafPaths(node, path):

# Базовый вариант

if node is None:

return

# включает текущий узел в путь

path.append(node.data)

#, если конечный узел найден, вывести путь

if isLeaf(node):

print(list(path))

# повторяется для левого и правого поддерева

printRootToLeafPaths(node.left, path)

printRootToLeafPaths(node.right, path)

# Возврат #: удалить текущий узел после завершения левого и правого поддеревьев.

path.pop()

# Основная функция для печати путей от корневого узла до каждого конечного узла.

def printRootToLeafPath(root):

# Список # для хранения корневого пути

path = deque()

printRootToLeafPaths(root, path)

if __name__ == ‘__main__’:

»’ Construct the following tree

2 3

/ /

4 5 6 7

8 9

»’

root = Node(1)

root.left = Node(2)

root.right = Node(3)

root.left.left = Node(4)

root.left.right = Node(5)

root.right.left = Node(6)

root.right.right = Node(7)

root.right.left.left = Node(8)

root.right.right.right = Node(9)

# распечатать все пути от корня к листу

printRootToLeafPath(root)

Скачать Выполнить код

результат:

[1, 2, 4]
[1, 2, 5]
[1, 3, 6, 8]
[1, 3, 7, 9]

Временная сложность приведенного выше решения равна O(n), куда n это общее количество узлов в бинарном дереве. Программа требует O(h) дополнительное место для стека вызовов, где h это высота дерева.

Проблема кажется немного сложной для решения без рекурсии. Существует один обходной путь, когда мы сохраняем путь от корня к листу в строке, когда мы итеративно проходим по дереву, и печатаем путь всякий раз, когда встречаем какой-либо конечный узел. Это показано ниже на C++, Java и Python:

C++

#include <iostream>

#include <stack>

#include <string>

using namespace std;

// Структура данных для хранения узла бинарного дерева

struct Node

{

int data;

Node *left, *right;

Node(int data)

{

this->data = data;

this->left = this->right = nullptr;

}

};

void printRootToleafPathIterative(Node* root)

{

// базовый вариант

if (root == nullptr) {

return;

}

// создаем пустой stack для хранения пары узлов дерева и

// его путь от корневого узла

stack<pair<Node*, string>> stack;

// нажимаем корневой узел

stack.push(make_pair(root, «»));

// цикл до тех пор, пока stack не станет пустым

while (!stack.empty())

{

// извлекаем узел из stack и помещаем данные в выходной стек

pair<Node*, string> p = stack.top();

stack.pop();

// получаем текущий узел

Node* curr = p.first;

string path = p.second;

// добавить текущий узел к существующему пути

string delim = (path == «») ? «n» : » —> «;

path += (delim + to_string(curr->data));

// печатаем путь, если узел является листом

if (curr->left == nullptr && curr->right == nullptr) {

cout << path;

}

// помещаем в stack левый и правый дочерние элементы извлеченного узла

if (curr->right) {

stack.push(make_pair(curr->right, path));

}

if (curr->left) {

stack.push(make_pair(curr->left, path));

}

int main()

{

/* Построим следующее дерево

2 3

/ /

4 5 6 7

8 9

Node* root = new Node(1);

root->left = new Node(2);

root->right = new Node(3);

root->left->left = new Node(4);

root->left->right = new Node(5);

root->right->left = new Node(6);

root->right->right = new Node(7);

root->right->left->left = new Node(8);

root->right->right->right = new Node(9);

printRootToleafPathIterative(root);

return 0;

}

Скачать Выполнить код

результат:

1 —> 2 —> 4
1 —> 2 —> 5
1 —> 3 —> 6 —> 8
1 —> 3 —> 7 —> 9

Java

100

101

102

103

104

105

106

107

import java.util.ArrayDeque;

import java.util.Deque;

// Класс для хранения узла бинарного дерева

class Node

{

int data;

Node left = null, right = null;

Node(int data) {

this.data = data;

}

// Pair class

class Pair<U, V>

{

public final U first; // первое поле пары

public final V second; // второе поле пары

// Создает новую пару с указанными значениями

private Pair(U first, V second)

{

this.first = first;

this.second = second;

}

// Фабричный метод для создания неизменяемого экземпляра Typed Pair

public static <U, V> Pair <U, V> of(U a, V b)

{

// вызывает приватный конструктор

return new Pair<>(a, b);

}

class Main

{

public static void printRootToleafPathIterative(Node root)

{

// базовый вариант

if (root == null) {

return;

}

// создаем пустой stack для хранения пары узлов дерева и

// его путь от корневого узла

Deque<Pair<Node, String>> stack = new ArrayDeque<>();

// нажимаем корневой узел

stack.add(Pair.of(root, «»));

// цикл до тех пор, пока stack не станет пустым

while (!stack.isEmpty())

{

// извлекаем узел из stack и помещаем данные в выходной стек

Pair<Node, String> pair = stack.pollLast();

// получаем текущий узел

Node curr = pair.first;

String path = pair.second;

// добавить текущий узел к существующему пути

String separator = (path.equals(«»)) ? «n» : » —> «;

path += (separator + curr.data);

// печатаем путь, если узел является листом

if (curr.left == null && curr.right == null) {

System.out.print(path);

}

// помещаем в stack левый и правый дочерние элементы извлеченного узла

if (curr.right != null) {

stack.add(Pair.of(curr.right, path));

}

if (curr.left != null) {

stack.add(Pair.of(curr.left, path));

}

public static void main(String[] args)

{

/* Построим следующее дерево

2 3

/ /

4 5 6 7

8 9

Node root = new Node(1);

root.left = new Node(2);

root.right = new Node(3);

root.left.left = new Node(4);

root.left.right = new Node(5);

root.right.left = new Node(6);

root.right.right = new Node(7);

root.right.left.left = new Node(8);

root.right.right.right = new Node(9);

printRootToleafPathIterative(root);

}

Скачать Выполнить код

результат:

1 —> 2 —> 5
1 —> 2 —> 4
1 —> 3 —> 7 —> 9
1 —> 3 —> 6 —> 8

Python

from collections import deque

# Класс для хранения узла бинарного дерева.

class Node:

def __init__(self, data, left=None, right=None):

self.data = data

self.left = left

self.right = right

def printRootToLeafPathIterative(root):

# Базовый вариант

if not root:

return

# создает пустой stack для хранения пары узлов дерева и

# его путь от корневого узла

stack = deque()

# нажимает корневой узел

stack.append((root, «»))

# Цикл # до тех пор, пока stack не станет пустым

while stack:

# извлекает узел из stack и помещает данные в выходной стек.

curr, path = stack.pop()

# добавить текущий узел к существующему пути

path += (» —> « if path else «n») + str(curr.data)

# напечатать путь, если узел является листом

if curr.left is None and curr.right is None:

print(path, end=»)

# помещает в stack левый и правый потомки извлеченного узла.

if curr.right:

stack.append((curr.right, path))

if curr.left:

stack.append((curr.left, path))

if __name__ == ‘__main__’:

»’ Construct the following tree

2 3

/ /

4 5 6 7

8 9

»’

root = Node(1)

root.left = Node(2)

root.right = Node(3)

root.left.left = Node(4)

root.left.right = Node(5)

root.right.left = Node(6)

root.right.right = Node(7)

root.right.left.left = Node(8)

root.right.right.right = Node(9)

printRootToLeafPathIterative(root)

Скачать Выполнить код

результат:

1 —> 2 —> 4
1 —> 2 —> 5
1 —> 3 —> 6 —> 8
1 —> 3 —> 7 —> 9

Упражнение:

1. Напишите итеративное решение вышеуказанной задачи.

2. Измените решение, чтобы печатать пути от корня к листу, имеющие сумму узлов, равную заданному числу.

Источник

Бинарные деревья поиска и рекурсия – это просто

Время на прочтение
8 мин

Количество просмотров 525K

Существует множество книг и статей по данной теме. В этой статье я попробую понятно рассказать самое основное.

Бинарное дерево — это иерархическая структура данных, в которой каждый узел имеет значение (оно же является в данном случае и ключом) и ссылки на левого и правого потомка. Узел, находящийся на самом верхнем уровне (не являющийся чьим либо потомком) называется корнем. Узлы, не имеющие потомков (оба потомка которых равны NULL) называются листьями.

Рис. 1 Бинарное дерево

Бинарное дерево поиска — это бинарное дерево, обладающее дополнительными свойствами: значение левого потомка меньше значения родителя, а значение правого потомка больше значения родителя для каждого узла дерева. То есть, данные в бинарном дереве поиска хранятся в отсортированном виде. При каждой операции вставки нового или удаления существующего узла отсортированный порядок дерева сохраняется. При поиске элемента сравнивается искомое значение с корнем. Если искомое больше корня, то поиск продолжается в правом потомке корня, если меньше, то в левом, если равно, то значение найдено и поиск прекращается.

Рис. 2 Бинарное дерево поиска
Сбалансированное бинарное дерево поиска — это бинарное дерево поиска с логарифмической высотой. Данное определение скорее идейное, чем строгое. Строгое определение оперирует разницей глубины самого глубокого и самого неглубокого листа (в AVL-деревьях) или отношением глубины самого глубокого и самого неглубокого листа (в красно-черных деревьях). В сбалансированном бинарном дереве поиска операции поиска, вставки и удаления выполняются за логарифмическое время (так как путь к любому листу от корня не более логарифма). В вырожденном случае несбалансированного бинарного дерева поиска, например, когда в пустое дерево вставлялась отсортированная последовательность, дерево превратится в линейный список, и операции поиска, вставки и удаления будут выполняться за линейное время. Поэтому балансировка дерева крайне важна. Технически балансировка осуществляется поворотами частей дерева при вставке нового элемента, если вставка данного элемента нарушила условие сбалансированности.

Рис. 3 Сбалансированное бинарное дерево поиска

Сбалансированное бинарное дерево поиска применяется, когда необходимо осуществлять быстрый поиск элементов, чередующийся со вставками новых элементов и удалениями существующих. В случае, если набор элементов, хранящийся в структуре данных фиксирован и нет новых вставок и удалений, то массив предпочтительнее. Потому что поиск можно осуществлять алгоритмом бинарного поиска за то же логарифмическое время, но отсутствуют дополнительные издержки по хранению и использованию указателей. Например, в С++ ассоциативные контейнеры set и map представляют собой сбалансированное бинарное дерево поиска.

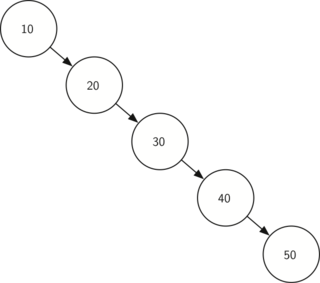
Рис. 4 Экстремально несбалансированное бинарное дерево поиска

Теперь кратко обсудим рекурсию. Рекурсия в программировании – это вызов функцией самой себя с другими аргументами. В принципе, рекурсивная функция может вызывать сама себя и с теми же самыми аргументами, но в этом случае будет бесконечный цикл рекурсии, который закончится переполнением стека. Внутри любой рекурсивной функции должен быть базовый случай, при котором происходит выход из функции, а также вызов или вызовы самой себя с другими аргументами. Аргументы не просто должны быть другими, а должны приближать вызов функции к базовому случаю. Например, вызов внутри рекурсивной функции расчета факториала должен идти с меньшим по значению аргументом, а вызовы внутри рекурсивной функции обхода дерева должны идти с узлами, находящимися дальше от корня, ближе к листьям. Рекурсия может быть не только прямой (вызов непосредственно себя), но и косвенной. Например А вызывает Б, а Б вызывает А. С помощью рекурсии можно эмулировать итеративный цикл, а также работу структуры данных стек (LIFO).

int factorial(int n)
{
    if(n <= 1)  // Базовый случай
    {
        return 1;
    }
    return n  * factorial(n - 1); //рекурсивеый вызов с другим аргументом
}
// factorial(1):     return 1
// factorial(2):     return 2 * factorial(1) (return 2 * 1)
// factorial(3):     return 3 * factorial(2) (return 3 * 2 * 1)
// factorial(4):     return 4 * factorial(3) (return 4 * 3 * 2 * 1)
// Вычисляет факториал числа n (n должно быть небольшим из-за типа int
// возвращаемого значения. На практике можно сделать long long  и вообще
// заменить рекурсию циклом. Если важна скорость рассчетов и не жалко память, то
// можно совсем избавиться от функции и использовать массив с предварительно
// посчитанными факториалами).

void reverseBinary(int n)
{
    if (n == 0)  // Базовый случай
    {
        return;
    }
    cout << n%2;
    reverseBinary(n/2); //рекурсивеый вызов с другим аргументом
}
// Печатает бинарное представление числа в обратном порядке

void forvardBinary(int n)
{
    if (n == 0)  // Базовый случай
    {
        return;
    }
    forvardBinary(n/2); //рекурсивеый вызов с другим аргументом
    cout << n%2;
}
// Поменяли местами две последние инструкции
// Печатает бинарное представление числа в прямом порядке
// Функция является примером эмуляции стека

void ReverseForvardBinary(int n)
{
    if (n == 0)  // Базовый случай
    {
        return;
    }
    cout << n%2; // печатает в обратном порядке
    ReverseForvardBinary(n/2); //рекурсивеый вызов с другим аргументом
    cout << n%2; // печатает в прямом порядке
}
// Функция печатает сначала бинарное представление в обратном порядке,
// а затем в прямом порядке


int product(int x, int y)
{
    if (y == 0)  // Базовый случай
    {
        return 0;
    }
    return (x + product(x, y-1)); //рекурсивеый вызов с другим аргументом
}
// Функция вычисляет произведение x * y ( складывает x y раз)
// Функция абсурдна с точки зрения практики,
// приведена для лучшего понимания рекурсии

Кратко обсудим деревья с точки зрения теории графов. Граф – это множество вершин и ребер. Ребро – это связь между двумя вершинами. Количество возможных ребер в графе квадратично зависит от количества вершин (для понимания можно представить турнирную таблицу сыгранных матчей). Дерево – это связный граф без циклов. Связность означает, что из любой вершины в любую другую существует путь по ребрам. Отсутствие циклов означает, что данный путь – единственный. Обход графа – это систематическое посещение всех его вершин по одному разу каждой. Существует два вида обхода графа: 1) поиск в глубину; 2) поиск в ширину.

Поиск в ширину (BFS) идет из начальной вершины, посещает сначала все вершины находящиеся на расстоянии одного ребра от начальной, потом посещает все вершины на расстоянии два ребра от начальной и так далее. Алгоритм поиска в ширину является по своей природе нерекурсивным (итеративным). Для его реализации применяется структура данных очередь (FIFO).

Поиск в глубину (DFS) идет из начальной вершины, посещая еще не посещенные вершины без оглядки на удаленность от начальной вершины. Алгоритм поиска в глубину по своей природе является рекурсивным. Для эмуляции рекурсии в итеративном варианте алгоритма применяется структура данных стек.

С формальной точки зрения можно сделать как рекурсивную, так и итеративную версию как поиска в ширину, так и поиска в глубину. Для обхода в ширину в обоих случаях необходима очередь. Рекурсия в рекурсивной реализации обхода в ширину всего лишь эмулирует цикл. Для обхода в глубину существует рекурсивная реализация без стека, рекурсивная реализация со стеком и итеративная реализация со стеком. Итеративная реализация обхода в глубину без стека невозможна.

Асимптотическая сложность обхода и в ширину и в глубину O(V + E), где V – количество вершин, E – количество ребер. То есть является линейной по количеству вершин и ребер. Записи O(V + E) с содержательной точки зрения эквивалентна запись O(max(V,E)), но последняя не принята. То есть, сложность будет определятся максимальным из двух значений. Несмотря на то, что количество ребер квадратично зависит от количества вершин, мы не можем записать сложность как O(E), так как если граф сильно разреженный, то это будет ошибкой.

DFS применяется в алгоритме нахождения компонентов сильной связности в ориентированном графе. BFS применяется для нахождения кратчайшего пути в графе, в алгоритмах рассылки сообщений по сети, в сборщиках мусора, в программе индексирования – пауке поискового движка. И DFS и BFS применяются в алгоритме поиска минимального покрывающего дерева, при проверке циклов в графе, для проверки двудольности.
Обходу в ширину в графе соответствует обход по уровням бинарного дерева. При данном обходе идет посещение узлов по принципу сверху вниз и слева направо. Обходу в глубину в графе соответствуют три вида обходов бинарного дерева: прямой (pre-order), симметричный (in-order) и обратный (post-order).

Прямой обход идет в следующем порядке: корень, левый потомок, правый потомок. Симметричный — левый потомок, корень, правый потомок. Обратный – левый потомок, правый потомок, корень. В коде рекурсивной функции соответствующего обхода сохраняется соответствующий порядок вызовов (порядок строк кода), где вместо корня идет вызов данной рекурсивной функции.

Если нам дано изображение дерева, и нужно найти его обходы, то может помочь следующая техника (см. рис. 5). Обводим дерево огибающей замкнутой кривой (начинаем идти слева вниз и замыкаем справа вверх). Прямому обходу будет соответствовать порядок, в котором огибающая, двигаясь от корня впервые проходит рядом с узлами слева. Для симметричного обхода порядок, в котором огибающая, двигаясь от корня впервые проходит рядом с узлами снизу. Для обратного обхода порядок, в котором огибающая, двигаясь от корня впервые проходит рядом с узлами справа. В коде рекурсивного вызова прямого обхода идет: вызов, левый, правый. Симметричного – левый, вызов, правый. Обратного – левый правый, вызов.

Рис. 5 Вспомогательный рисунок для обходов

Для бинарных деревьев поиска симметричный обход проходит все узлы в отсортированном порядке. Если мы хотим посетить узлы в обратно отсортированном порядке, то в коде рекурсивной функции симметричного обхода следует поменять местами правого и левого потомка.

struct  TreeNode
{
    double data; // ключ/данные
    TreeNode *left; // указатель на левого потомка
    TreeNode *right; // указатель на правого потомка
};

void levelOrderPrint(TreeNode *root) {
    if (root == NULL)
    {
       return;
    }
    queue<TreeNode *> q; // Создаем очередь
    q.push(root); // Вставляем корень в очередь

    while (!q.empty() ) // пока очередь не пуста
    {
        TreeNode* temp = q.front(); // Берем первый элемент в очереди
        q.pop();  // Удаляем первый элемент в очереди
        cout << temp->data << " "; // Печатаем значение первого элемента в очереди

        if ( temp->left != NULL )
            q.push(temp->left);  // Вставляем  в очередь левого потомка

        if ( temp->right != NULL )
            q.push(temp->right);  // Вставляем  в очередь правого потомка
   }
}


void preorderPrint(TreeNode *root)
{
    if (root == NULL)   // Базовый случай
    {
       return;
    }
    cout << root->data << " ";
    preorderPrint(root->left);   //рекурсивный вызов левого поддерева
    preorderPrint(root->right);  //рекурсивный вызов правого поддерева
}
// Функция печатает значения бинарного дерева поиска в прямом порядке.
// Вместо печати первой инструкцией функции может быть любое действие
// с данным узлом

void inorderPrint(TreeNode *root)
{
    if (root == NULL)   // Базовый случай
    {
       return;
    }
    preorderPrint(root->left);   //рекурсивный вызов левого поддерева
    cout << root->data << " ";
    preorderPrint(root->right);  //рекурсивный вызов правого поддерева
}
// Функция печатает значения бинарного дерева поиска в симметричном порядке.
// То есть в отсортированном порядке

void postorderPrint(TreeNode *root)
{
    if (root == NULL)   // Базовый случай
    {
       return;
    }
    preorderPrint(root->left);   //рекурсивный вызов левого поддерева
    preorderPrint(root->right);  //рекурсивный вызов правого поддерева
    cout << root->data << " ";
}
// Функция печатает значения бинарного дерева поиска в обратном порядке.
// Не путайте обратный и обратноотсортированный (обратный симметричный).

void reverseInorderPrint(TreeNode *root)
{
    if (root == NULL)   // Базовый случай
    {
       return;
    }
    preorderPrint(root->right);  //рекурсивный вызов правого поддерева
    cout << root->data << " ";
    preorderPrint(root->left);   //рекурсивный вызов левого поддерева

}
// Функция печатает значения бинарного дерева поиска в обратном симметричном порядке.
// То есть в обратном отсортированном порядке

void iterativePreorder(TreeNode *root)
{
    if (root == NULL)
    {
       return;
    }
    stack<TreeNode *> s;  // Создаем стек
    s.push(root);  // Вставляем корень в стек
    /* Извлекаем из стека один за другим все элементы.
       Для каждого извлеченного делаем следующее
       1) печатаем его
       2) вставляем в стек правого! потомка
          (Внимание! стек поменяет порядок выполнения на противоположный!)
       3) вставляем в стек левого! потомка */
    while (s.empty() == false)
    {
        // Извлекаем вершину стека и печатаем
        TreeNode *temp = s.top();
        s.pop();
        cout << temp->data << " ";

        if (temp->right)
            s.push(temp->right); // Вставляем в стек правого потомка
        if (temp->left)
            s.push(temp->left);  // Вставляем в стек левого потомка
    }
}
// В симметричном и обратном итеративном обходах просто меняем инструкции
// местами по аналогии с рекурсивными функциями.

Надеюсь Вы не уснули, и статья была полезна. Скоро надеюсь последует продолжение

~~банкета~~

статьи.

Источник

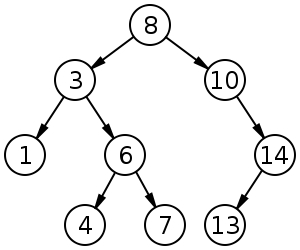
Бинарное дерево поиска из 9 элементов

Бинарное дерево поиска (англ. binary search tree, BST) — структура данных для работы с упорядоченными множествами.

Бинарное дерево поиска обладает следующим свойством: если — узел бинарного дерева с ключом , то все узлы в левом поддереве должны иметь ключи, меньшие , а в правом поддереве большие .

Содержание

1 Операции в бинарном дереве поиска
- 1.1 Обход дерева поиска
- 1.2 Поиск элемента
- 1.3 Поиск минимума и максимума
- 1.4 Поиск следующего и предыдущего элемента
  - 1.4.1 Реализация с использованием информации о родителе
  - 1.4.2 Реализация без использования информации о родителе
- 1.5 Вставка
  - 1.5.1 Реализация с использованием информации о родителе
  - 1.5.2 Реализация без использования информации о родителе
- 1.6 Удаление
  - 1.6.1 Нерекурсивная реализация
  - 1.6.2 Рекурсивная реализация
2 Задачи о бинарном дереве поиска
- 2.1 Проверка того, что заданное дерево является деревом поиска
- 2.2 Задачи на поиск максимального BST в заданном двоичном дереве
- 2.3 Восстановление дерева по результату обхода preorderTraversal
3 См. также
4 Источники информации

Операции в бинарном дереве поиска

Для представления бинарного дерева поиска в памяти будем использовать следующую структуру:

struct Node:
  T key                    // ключ узла
  Node left                // указатель на левого потомка
  Node right               // указатель на правого потомка
  Node parent              // указатель на предка

Обход дерева поиска

Есть три операции обхода узлов дерева, отличающиеся порядком обхода узлов:

— обход узлов в отсортированном порядке,
— обход узлов в порядке: вершина, левое поддерево, правое поддерево,
— обход узлов в порядке: левое поддерево, правое поддерево, вершина.

func inorderTraversal(x : Node):
   if x != null
      inorderTraversal(x.left)
      print x.key
      inorderTraversal(x.right)

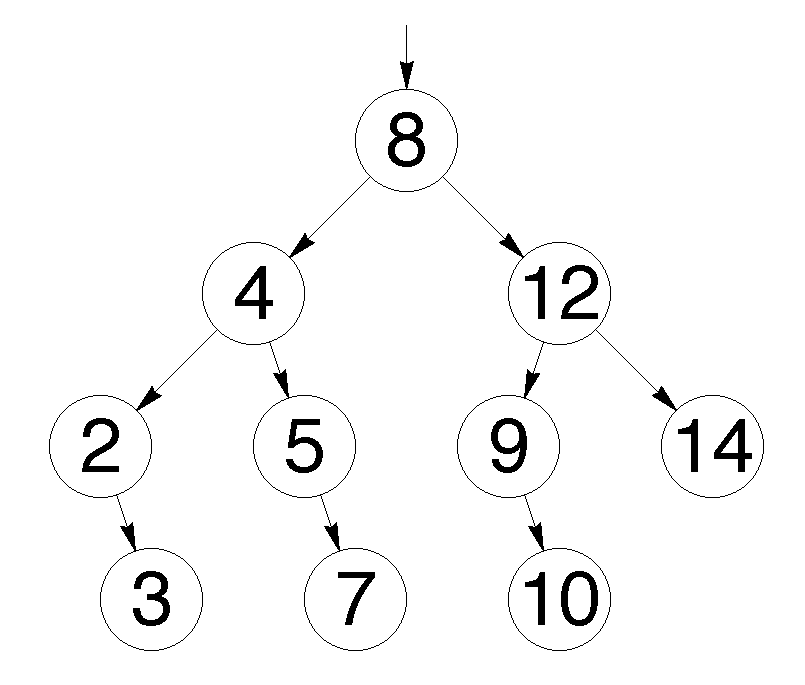
При выполнении данного обхода вершины будут выведены в следующем порядке: 1 3 4 6 7 8 10 13 14.

func preorderTraversal(x : Node)
   if x != null
      print x.key
      preorderTraversal(x.left)
      preorderTraversal(x.right)

При выполнении данного обхода вершины будут выведены в следующем порядке: 8 3 1 6 4 7 10 14 13.

func postorderTraversal(x : Node)
   if x != null
      postorderTraversal(x.left)
      postorderTraversal(x.right)
      print x.key

При выполнении данного обхода вершины будут выведены в следующем порядке: 1 4 7 6 3 13 14 10 8.

Данные алгоритмы выполняют обход за время , поскольку процедура вызывается ровно два раза для каждого узла дерева.

Поиск элемента

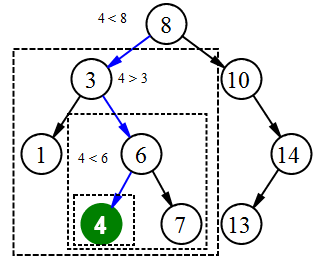
Поиск элемента 4

Для поиска элемента в бинарном дереве поиска можно воспользоваться следующей функцией, которая принимает в качестве параметров корень дерева и искомый ключ. Для каждого узла функция сравнивает значение его ключа с искомым ключом. Если ключи одинаковы, то функция возвращает текущий узел, в противном случае функция вызывается рекурсивно для левого или правого поддерева. Узлы, которые посещает функция образуют нисходящий путь от корня, так что время ее работы , где — высота дерева.

Node search(x : Node, k : T):
   if x == null or k == x.key
      return x
   if k < x.key
      return search(x.left, k)
   else
      return search(x.right, k)

Поиск минимума и максимума

Чтобы найти минимальный элемент в бинарном дереве поиска, необходимо просто следовать указателям от корня дерева, пока не встретится значение . Если у вершины есть левое поддерево, то по свойству бинарного дерева поиска в нем хранятся все элементы с меньшим ключом. Если его нет, значит эта вершина и есть минимальная. Аналогично ищется и максимальный элемент. Для этого нужно следовать правым указателям.

Node minimum(x : Node):
  if x.left == null
     return x
  return minimum(x.left)

Node maximum(x : Node):
  if x.right == null
     return x
  return maximum(x.right)

Данные функции принимают корень поддерева, и возвращают минимальный (максимальный) элемент в поддереве. Обе процедуры выполняются за время .

Поиск следующего и предыдущего элемента

Реализация с использованием информации о родителе

Если у узла есть правое поддерево, то следующий за ним элемент будет минимальным элементом в этом поддереве. Если у него нет правого поддерева, то нужно следовать вверх, пока не встретим узел, который является левым дочерним узлом своего родителя. Поиск предыдущего выполнятся аналогично. Если у узла есть левое поддерево, то предыдущий ему элемент будет максимальным элементом в этом поддереве. Если у него нет левого поддерева, то нужно следовать вверх, пока не встретим узел, который является правым дочерним узлом своего родителя.

Node next(x : Node):
   if x.right != null
      return minimum(x.right)
   y = x.parent
   while y != null and x == y.right
      x = y
      y = y.parent
   return y

Node prev(x : Node):
   if x.left != null
      return maximum(x.left)
   y = x.parent
   while y != null and x == y.left
      x = y
      y = y.parent
   return y

Обе операции выполняются за время .

Реализация без использования информации о родителе

Рассмотрим поиск следующего элемента для некоторого ключа . Поиск будем начинать с корня дерева, храня текущий узел и узел , последний посещенный узел, ключ которого больше .
Спускаемся вниз по дереву, как в алгоритме поиска узла. Рассмотрим ключ текущего узла . Если , значит следующий за узел находится в правом поддереве (в левом поддереве все ключи меньше ). Если же , то , поэтому может быть следующим для ключа , либо следующий узел содержится в левом поддереве . Перейдем к нужному поддереву и повторим те же самые действия.
Аналогично реализуется операция поиска предыдущего элемента.

Node next(x : T):
   Node current = root, successor = null                // root — корень дерева
   while current != null
      if current.key > x
         successor = current
         current = current.left
      else
         current = current.right
   return successor

Вставка

Операция вставки работает аналогично поиску элемента, только при обнаружении у элемента отсутствия ребенка нужно подвесить на него вставляемый элемент.

Реализация с использованием информации о родителе

func insert(x : Node, z : Node):            // x — корень поддерева, z — вставляемый элемент
   while x != null
     if z.key > x.key
        if x.right != null
           x = x.right
        else
           z.parent = x
           x.right = z
           break
     else if z.key < x.key
        if x.left != null
           x = x.left
        else
           z.parent = x
           x.left = z
           break

Реализация без использования информации о родителе

Node insert(x : Node, z : T):               // x — корень поддерева, z — вставляемый ключ
   if x == null 
      return Node(z)                        // подвесим Node с key = z
   else if z < x.key
      x.left = insert(x.left, z)
   else if z > x.key
      x.right = insert(x.right, z)
   return x

Время работы алгоритма для обеих реализаций — .

Удаление

Нерекурсивная реализация

Для удаления узла из бинарного дерева поиска нужно рассмотреть три возможные ситуации. Если у узла нет дочерних узлов, то у его родителя нужно просто заменить указатель на . Если у узла есть только один дочерний узел, то нужно создать новую связь между родителем удаляемого узла и его дочерним узлом. Наконец, если у узла два дочерних узла, то нужно найти следующий за ним элемент (у этого элемента не будет левого потомка), его правого потомка подвесить на место найденного элемента, а удаляемый узел заменить найденным узлом. Таким образом, свойство бинарного дерева поиска не будет нарушено. Данная реализация удаления не увеличивает высоту дерева. Время работы алгоритма — .

Случай	Иллюстрация
Удаление листа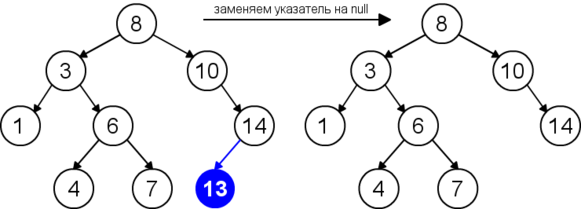
Удаление узла с одним дочерним узлом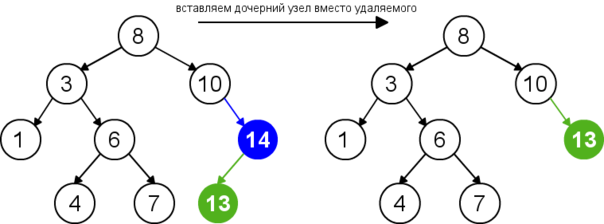
Удаление узла с двумя дочерними узлами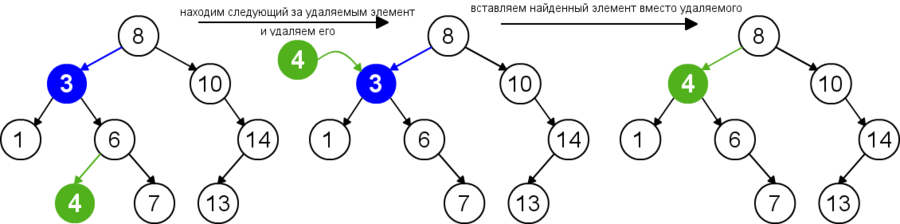

func delete(t : Node, v : Node):                 //  — дерево,  — удаляемый элемент
   p = v.parent                                  // предок удаляемого элемента
   if v.left == null and v.right == null         // первый случай: удаляемый элемент - лист
     if p.left == v
       p.left = null
     if p.right == v
       p.right = null
   else if v.left == null or v.right == null     // второй случай: удаляемый элемент имеет одного потомка
       if v.left == null                 
           if p.left == v
             p.left = v.right
           else
             p.right = v.right
           v.right.parent = p 
       else
           if p.left == v
               p.left = v.left
           else
               p.right = v.left
           v.left.parent = p
   else                                          // третий случай: удаляемый элемент имеет двух потомков
     successor = next(v, t)                   
     v.key = successor.key
     if successor.parent.left == successor
       successor.parent.left = successor.right
       if successor.right != null
         successor.right.parent = successor.parent
     else
       successor.parent.right = successor.right
       if successor.right != null
         successor.right.parent = successor.parent

Рекурсивная реализация

При рекурсивном удалении узла из бинарного дерева нужно рассмотреть три случая: удаляемый элемент находится в левом поддереве текущего поддерева, удаляемый элемент находится в правом поддереве или удаляемый элемент находится в корне. В двух первых случаях нужно рекурсивно удалить элемент из нужного поддерева. Если удаляемый элемент находится в корне текущего поддерева и имеет два дочерних узла, то нужно заменить его минимальным элементом из правого поддерева и рекурсивно удалить этот минимальный элемент из правого поддерева. Иначе, если удаляемый элемент имеет один дочерний узел, нужно заменить его потомком. Время работы алгоритма — .
Рекурсивная функция, возвращающая дерево с удаленным элементом :

Node delete(root : Node, z : T):               // корень поддерева, удаляемый ключ
  if root == null
    return root
  if z < root.key
    root.left = delete(root.left, z)
  else if z > root.key
    root.right = delete(root.right, z)
  else if root.left != null and root.right != null
    root.key = minimum(root.right).key
    root.right = delete(root.right, root.key)
  else
    if root.left != null
      root = root.left
    else if root.right != null
      root = root.right
    else
      root = null
  return root

Задачи о бинарном дереве поиска

Проверка того, что заданное дерево является деревом поиска

Задача:

Определить, является ли заданное двоичное дерево деревом поиска.

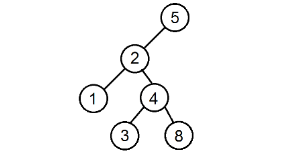
Пример дерева, для которого недостаточно проверки лишь его соседних вершин

Для того чтобы решить эту задачу, применим обход в глубину. Запустим от корня рекурсивную логическую функцию, которая выведет , если дерево является BST и в противном случае. Чтобы дерево не являлось BST, в нём должна быть хотя бы одна вершина, которая не попадает под определение дерева поиска. То есть достаточно найти всего одну такую вершину, чтобы выйти из рекурсии и вернуть значение . Если же, дойдя до листьев, функция не встретит на своём пути такие вершины, она вернёт значение .

Функция принимает на вход исследуемую вершину, а также два значения: и , которые до вызова функции равнялись и соответственно, где — очень большое число, т.е. ни один ключ дерева не превосходит его по модулю. Казалось бы, два последних параметра не нужны. Но без них программа может выдать неверный ответ, так как сравнения только вершины и её детей недостаточно. Необходимо также помнить, в каком поддереве для более старших предков мы находимся. Например, в этом дереве вершина с номером находится левее вершины, в которой лежит , чего не должно быть в дереве поиска, однако после проверки функция бы вернула .

bool isBinarySearchTree(root: Node):                    // Здесь root — корень заданного двоичного дерева.

  bool check(v : Node, min: T, max: T):                 // min и max — минимально и максимально допустимые значения в вершинах поддерева.
    if v == null                    return true
    if v.key <= min or max <= v.key return false
    return check(v.left, min, v.key) and check(v.right, v.key, max)

  return check(root, , )

Время работы алгоритма — , где — количество вершин в дереве.

Задачи на поиск максимального BST в заданном двоичном дереве

Задача:

Найти в данном дереве такую вершину, что она будет корнем поддерева поиска с наибольшим количеством вершин.

Если мы будем приведённым выше способом проверять каждую вершину, мы справимся с задачей за . Но её можно решить за , идя от корня и проверяя все вершины по одному разу, основываясь на следующих фактах:

Значение в вершине больше максимума в её левом поддереве;
Значение в вершине меньше минимума в её правом поддереве;
Левое и правое поддерево являются деревьями поиска.

Введём и , которые будут хранить минимум в левом поддереве вершины и максимум в правом. Тогда мы должны будем проверить, являются ли эти поддеревья деревьями поиска и, если да, лежит ли ключ вершины между этими значениями и . Если вершина является листом, она автоматически становится деревом поиска, а её ключ — минимумом или максимумом для её родителя (в зависимости от расположения вершины). Функция записывает в количество вершин в дереве, если оно является деревом поиска или в противном случае. После выполнения функции ищем за линейное время вершину с наибольшим значением .

int count(root: Node):                 // root — корень заданного двоичного дерева.

  int cnt(v: Node):
    if v == null
      v.kol = 0
      return = 0
    if cnt(v.left) != -1 and cnt(v.right) != -1
      if v.left == null and v.right == null
        v.min = v.key
        v.max = v.key
        v.kol = 1
        return 1
      if v.left == null
        if v.right.max > v.key
          v.min = v.key
          v.kol = cnt(v.right) + 1
          return v.kol
      if v.right == null
        if v.left.min < v.key
          v.max = v.key
          v.kol = cnt(v.left) + 1
          return v.kol
      if v.left.min < v.key and v.right.max > v.key 
        v.min = v.left.min
        v.max = v.right.max
        v.kol = v.left.kol + v.right.kol + 1
        v.kol = cnt(v.left) + cnt(v.right) + 1
        return v.kol
    return -1

  return cnt(root)

Алгоритм работает за , так как мы прошлись по дереву два раза за время, равное количеству вершин.

Восстановление дерева по результату обхода preorderTraversal

Задача:

Восстановить дерево по последовательности, выведенной после выполнения процедуры .

Восстановление дерева поиска по последовательности ключей

Как мы помним, процедура выводит значения в узлах поддерева следующим образом: сначала идёт до упора влево, затем на каком-то моменте делает шаг вправо и снова движется влево. Это продолжается до тех пор, пока не будут выведены все вершины. Полученная последовательность позволит нам однозначно определить расположение всех узлов поддерева. Первая вершина всегда будет в корне. Затем, пока не будут использованы все значения, будем последовательно подвешивать левых сыновей к последней добавленной вершине, пока не найдём номер, нарушающий убывающую последовательность, а для каждого такого номера будем искать вершину без правого потомка, хранящую наибольшее значение, не превосходящее того, которое хотим поставить, и подвешиваем к ней элемент с таким номером в качестве правого сына. Когда мы, желая найти такую вершину, встречаем какую-нибудь другую, уже имеющую правого сына, проходим по ветке вправо. Мы имеем на это право, так как если такая вершина стоит, то процедура обхода в ней уже побывала и поворачивала вправо, поэтому спускаться в другую сторону смысла не имеет. Вершину с максимальным ключом, с которой будем начинать поиск, будем запоминать. Она будет обновляться каждый раз, когда появится новый максимум.

Процедура восстановления дерева работает за .

Разберём алгоритм на примере последовательности .

Будем выделять красным цветом вершины, рассматриваемые на каждом шаге, чёрным жирным — их родителей, курсивом — убывающие подпоследовательности (в случаях, когда мы их рассматриваем) или претендентов на добавление к ним правого ребёнка (когда рассматривается вершина, нарушающая убывающую последовательность).

Состояние последовательности	Действие	Пояснение
8 2 1 4 3 5	Делаем вершину корнем.	Первая вершина всегда будет корнем, так как вывод начинался с него.
8 2 1 4 3 5	Находим убывающую подпоследовательность. Каждую вершину подвешиваем к последней из взятых ранее в качестве левого сына.	Каждая последующая вершина становится левым сыном предыдущей, так как выводя ключи, мы двигались по дереву поиска влево, пока есть вершины.
8 2 1 4 3 5
8 2 1 4 3 5	Для вершины, нарушившей убывающую последовательность, ищем максимальное значение, меньшее его. В данном случае оно равно . Затем добавляем вершину.	На моменте вывода следующего номера процедура обратилась уже к какому-то из правых поддеревьев, так как влево идти уже некуда. Значит, нам необходимо найти узел, для которого данная вершина являлась бы правым сыном. Очевидно, что в её родителе не может лежать значение, которое больше её ключа. Но эту вершину нельзя подвесить и к меньшим, иначе нашёлся бы более старший предок, также хранящий какое-то значение, которое меньше, чем в исследуемой. Для этого предка вершина бы попала в левое поддерево. И тогда возникает противоречие с определением дерева поиска. Отсюда следует, что родитель определяется единственным образом — он хранит максимум среди ключей, не превосходящих значения в подвешиваемой вершине, что и требовалось доказать.
8 2 1 4 3 5	Находим убывающую подпоследовательность. Каждую вершину подвешиваем к последней из взятых ранее в качестве левого сына.	Зайдя в правое поддерево, процедура обхода снова до упора начала двигаться влево, поэтому действуем аналогичным образом.
8 2 1 4 3 5	Для этой вершины ищем максимальное значение, меньшее его. Затем добавляем вершину.	Здесь процедура снова обратилась к правому поддереву. Рассуждения аналогичны. Ключ родителя этой вершины равен .

См. также

Поисковые структуры данных
Рандомизированное бинарное дерево поиска
Красно-черное дерево
АВЛ-дерево

Источники информации

Википедия — Двоичное дерево поиска
Wikipedia — Binary search tree
Кормен, Т., Лейзерсон, Ч., Ривест, Р., Штайн, К. Алгоритмы: построение и анализ = Introduction to Algorithms / Под ред. И. В. Красикова. — 2-е изд. — М.: Вильямс, 2005. — 1296 с. — ISBN 5-8459-0857-4

Источник

Бинарное (двоичное) дерево поиска, обходы и применение

Дерево — это один из абстрактных типов данных, а также любая структура данных, которая этот тип реализует. Деревья моделируют иерархичную древовидную структуру (ну например, семейное древо), в котором существует только один корень (корневой элемент) и узлы (другие элементы), связанные отношениями потомок — родитель, где любой отдельно взятый элемент имеет только одного родителя (кроме корня, у него-то родителей нет).

Ещё деревья можно определить рекурсивно: дерево может быть или пустым, или состоять из узла (корня), являющимся родительским узлом для некоторого количества деревьев. Количество дочерних узлов обозначает арность дерева; другими словами, n-арное дерево не может содержать более n дочерних элементов (далее дочерний узел, дочерний элемент и потомок будут иметь один и тот же смысл) для каждого узла. Арность дерева — это тоже самое, что и степень дерева. Если же для каждого узла дерева определяется индивидуальная степень, то говорят только про степень конкретных узлов.

Помимо этого необходимо знать ещё 2 понятия в разговоре о деревьях: путь до вершины (всегда начинаем от корня) и высота дерева (реже — глубина). Путь — это множество переходов в дереве, от корня к необходимому узлу. Число узлов в любом пути называется длиной пути, а максимальная длина пути из всех — высотой дерева. Поскольку дерево — частный случай графа, то такие переходы называют рёбрами, а узлы — вершинами.

Одной из форм записи деревьев «на бумаге» называется скобочной записью:

(8 (3 (1) (6 (4) (7))) (10 (14 (13))))

А для наглядности расставим пробелы и переносы:

А так оно выглядит на самом деле:

Бинарное дерево поиска

Деревья полезны, они используются во многих задачах, например:

парсеры и трансляторы используют синтаксическое дерево;
при работе со строками используются суффиксные деревья;
бинарные деревья используются в большом количестве задач: от сортировки и поиска, до создания на их базе других, более сложных структур данных.

Важно место в информатике занимают бинарные (или двоичные) деревья, у которых для каждого узла не более 2-х дочерних элементов, это левый и правый наследники. БНФ форма его определения выглядит так:

<дерево> ::= ( <данные> <дерево> <дерево> ) | nil

Существуют множество разных бинарных деревьев, например, двоичная куча (или сортирующее дерево). Оно используется в пирамидальной сортировке и при реализации приоритетных очередей. Для этого на обычное бинарное дерево нужно всего лишь наложить такие ограничения:

Значение в любой вершине не меньше, чем значения её потомков.
Глубина всех листьев (расстояние до корня) отличается не более чем на 1 слой.
Последний слой заполняется слева направо без «дырок».

А вот другое — бинарное дерево поиска. Используется для организации хранения данных таким образом, чтобы гарантировать поиск элемента за логарифмическое время:

Оба поддерева — левое и правое — являются двоичными деревьями поиска.
У всех узлов левого поддерева для произвольного узла значения ключей меньше значения ключа этого узла.
У всех узлов правого поддерева для произвольного узла значения ключей больше либо равны значения ключа этого узла.

Поиск элемента с заданным значением в таком дереве происходит очевидным образом: начиная с корня сравниваем текущее значение узла с заданным; если они равны, то значение найдено, иначе сравниваем значения и выбираем следующий узел для проверки: левый или правый.

Чтобы работать с деревьями, нужно уметь обходить его элементы. Существуют такие 3 варианта обхода:

Прямой обход (КЛП): корень → левое поддерево → правое поддерево.
Центрированный обход (ЛКП): левое поддерево → корень → правое поддерево.
Обратный обход (ЛПК): левое поддерево → правое поддерево → корень

Прямой обход

Центрированный обход

Обратный обход

Такие обходы называются поиском в глубину, поскольку на каждом шаге итератор пытается продвинуться вертикально вниз по дереву перед тем, как перейти к родственному узлу (узлу на том же уровне). Ещё существует поиск в ширину. Его суть в обходе узлов дерева по уровням, начиная с корня (нужно пройти всего лишь 1 узел) и далее (на втором 2 узла, на третьем 4 узла, ну и т.д.; сколько узлов надо пройти на k-м уровне?).

Обход в ширину

Реализация поиска в глубину может осуществляться или с использованием рекурсии или с использованием стека, а поиск в ширину реализуется за счёт использования очереди:

Рекурсивный:

preorder(node)
  if (node = null)
    return
  visit(node)
  preorder(node.left)
  preorder(node.right)

Через стек:

iterativePreorder(node)
  s ← empty stack
  s.push(node)
  while (not s.isEmpty())
    node ← s.pop()
    visit(node)
    if (node.right ≠ null)
      s.push(node.right)
    if (node.left ≠ null)
      s.push(node.left)

Правый потомок заносится первым, так что левый потомок обрабатывается первым

Через очередь:

levelorder(root)
  q ← empty queue
  q.enqueue(root)
  while (not q.isEmpty())
    node ← q.dequeue()
    visit(node)
    if (node.left ≠ null)
      q.enqueue(node.left)
    if (node.right ≠ null)
      q.enqueue(node.right)

Чтобы реализовать центрированный обход, не обязательно использовать рекурсии или стек. Для этого добавляют новые связи (полученное дерево будет называться прошитым бинарным деревом), где каждому левому потомку, у которого нет своего левого потомка, назначают указатель на предыдущий элемент в порядке центрированного обхода, а для правых по тем же причинам — следующий.

Прошитое бинарное дерево поиска

Типичная структура данных одного узла такого дерева выглядит так:

struct node {    
	data_type_t dat;    
	node *left, *right; //теперь left и right могут указывать как на дочерние элементы, так и содержать нитки, ведущие на другие уровни    
	bool left_is_thread, right_is_thread;
}

Другой способ обхода дерева заключается в способе хранения информации о связях в массиве. Такой способ позволяет быстро находить дочерние и родительские элементы, производя обычные арифметические операции (а именно — для левого потомка и для правого, где — индекс родительского узла, если считать с 1). Но эффективность заполнения такого массива напрямую зависит от полноты бинарного дерева. Самый худший вариант развития событий произойдёт тогда, когда у дерева есть только один дочерний элемент в каждом узле (не важно, левого или правого). Тогда для хранения узлов потребуется ячеек в массиве.

Использование обхода бинарных деревьев облегчает работу с алгебраическими выражениями. Так, обратная польская нотация для алгебраического выражения получается путём обратного обхода заранее построенного бинарного дерева. Такое дерево называется деревом синтаксического разбора выражения, в котором узлы хранят операнды (+, –, *, /), а листья — числовые значения.

Источник

В дереве путь между вершинами всегда единственный

Если задача всё-таки стоит для графа общего вида (судя по тому, что в C входят две дуги):

Для нахождения всех простых путей в заданную вершину нужно помечать пройденные вершины, чтобы не использовать их на дальнейших уровнях рекурсии, но эти пометки не должны быть глобальными.

Пример рекурсивной реализации на Delphi отсюда для небольшого числа вершин (до 32), для хранения текущих пометок используются биты целого числа.

Двумерный массив Adj работает как словарь со списками, shl — битовый сдвиг влево <<

Забит граф в виде шестиугольника с большим циклом 013652, и вершина 4 соединена с 0,3,5

var
  Adj: array of array of Byte;
  Src, Dest: Integer;

  procedure FindRoute(V: Integer; Used: Integer; Route: string);
  var
    i, W: Integer;
  begin
    if V = Dest then
      Memo1.Lines.Add(Route)
    else
      for i := 0 to High(Adj[V]) do begin
        W := Adj[V, i];
        if (Used and (1 shl W)) = 0 then
          FindRoute(W, Used or (1 shl W), Route + IntToStr(W) + ' ');
      end;
  end;

begin
  SetLength(Adj, 7);
  SetLength(Adj[0], 3);
  SetLength(Adj[1], 2);
  SetLength(Adj[2], 2);
  SetLength(Adj[3], 3);
  SetLength(Adj[4], 3);
  SetLength(Adj[5], 3);
  SetLength(Adj[6], 2);
  Adj[0, 0] := 1;
  Adj[1, 0] := 0;
  Adj[0, 1] := 2;
  Adj[2, 0] := 0;
  Adj[0, 2] := 4;
  Adj[4, 0] := 0;
  Adj[1, 1] := 3;
  Adj[3, 0] := 1;
  Adj[2, 1] := 5;
  Adj[5, 0] := 2;
  Adj[3, 1] := 4;
  Adj[4, 1] := 3;
  Adj[3, 2] := 6;
  Adj[6, 0] := 3;
  Adj[4, 2] := 5;
  Adj[5, 1] := 4;
  Adj[5, 2] := 6;
  Adj[6, 1] := 5;
  Src := 0;
  Dest := 3;
  FindRoute(Src, 1 shl Src, IntToStr(Src) + ' ');
end;

выдача
0 1 3 
0 2 5 4 3 
0 2 5 6 3 
0 4 3 
0 4 5 6 3

Источник