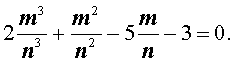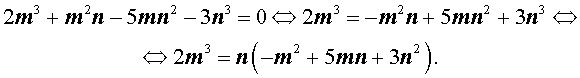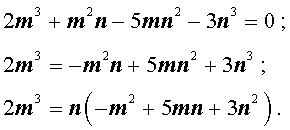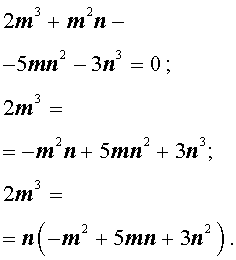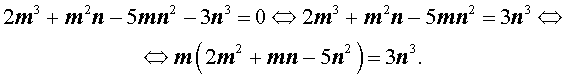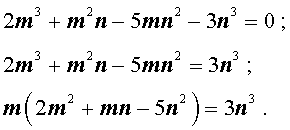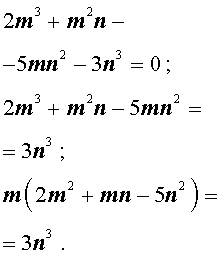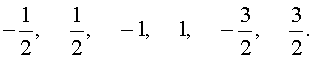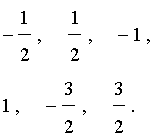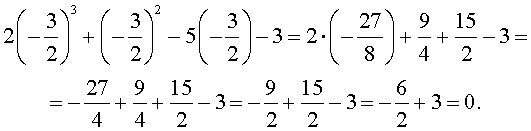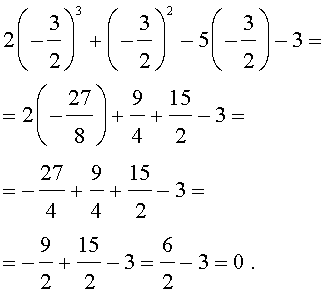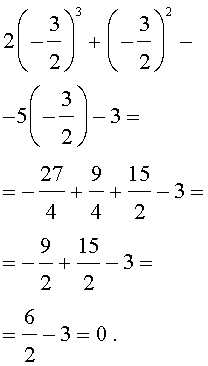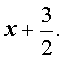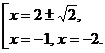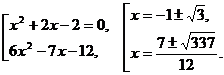Как найти все рациональные корни уравнения

10.5. НАХОЖДЕНИЕ РАЦИОНАЛЬНЫХ КОРНЕЙ МНОГОЧЛЕНА С ЦЕЛЫМИ КОЭФФИЦИЕНТАМИ

Теорема 4. Если многочлен с целыми коэффициентами f (x) = a_nxⁿ + a_n-1x^n-1 + … + a₁x+a₀  имеет рациональный корень x=p/q (q ≠ 0, дробь p/q  несократимая), то р является делителем свободного члена (a₀), а q — делителем коэффициента при стар­шем члене а_n.

     Если p/q является корнем многочлена f (х), то f(p/q) = 0. Подставляем p/q вместо х в f(x) и из последнего равенства имеем

an * pn/qn + an-1 * pn-1/qn-1 + … + a1 * p/q + a0 = 0.

(1)

            Умножим обе части равенства (1) на  (q ≠ 0). Получаем

аnрn + an-1pn-1q + … + a1pqn-1 + a0qn = 0.

(2)

В равенстве (2) все слагаемые, кроме последнего, делятся на р. Поэтому

a₀qⁿ = -(а_nрⁿ + a_n-1p^n-1q + … + a₁pq^n-1) делится на р.

Но когда мы записываем рациональное число в виде p/q, то эта дробь счи­тается несократимой, то есть р и q не имеют общих делителей. Произве­дение a₀qⁿ может делиться на р (если р и q — взаимно простые числа) только тогда, когда a₀ делится на р. Таким образом, р — делитель свобод­ного члена a₀.

Аналогично все слагаемые равенства (2), кроме первого, делятся на q. Тогда

a_npⁿ = -(a_n-1p^n-1q + … + a₁pq^-1 + a₀qⁿ) делится на q. Поскольку р и q — взаимно простые числа, то a_n делится на q, следовательно, q — де­литель коэффициента при старшем члене.

Отметим два следствия из этой теоремы. Если взять q = 1, то корнем многочлена будет целое число р — делитель a₀. Таким образом, имеет место:

Следствие 1. Любой целый корень многочлена с целыми коэффи­циентами является делителем его свободного члена.

Если в заданном многочлене f (х) коэффициент а_n = 1, то делителями а_n могут быть только числа ±1, то есть q =±1, и имеет место:

Следствие 2. Если коэффициент при старшем члене уравнения с целыми коэффициентами равен 1, то все рациональные корни этого уравнения (если они существуют) — целые числа.

Задача 1 Найдите рациональные корни многочлена 2х³ – х² + 12х – 6.

Пусть несократимая дробь p/q является корнем многочлена. Тогда р не­обходимо искать среди делителей свободного члена, то есть среди чисел ±1, ±2, ±3, ±6, а q — среди делителей старшего коэффициента: ±1, ±2.

Таким образом, рациональные корни многочлена необходимо искать сре­ди чисел ±1/2, ±1, +±3/2, ±2, ±3, ±6. Проверять, является ли данное число корнем многочлена, целесообразно с помощью схемы Горнера. При x = 1/2 имеем следующую таблицу.

Кроме того, по схеме Горнера мож­но записать, что

2х³ – х² + 12х – 6 = (x – 1/2) (2x² + 12).

Многочлен 2х² + 12 не имеет действительных корней (а тем более рацио­нальных), поэтому заданный многочлен имеет единственный рациональ­ный корень x =1/2.

Задача 2 Разложите многочлен Р (х) = 2х⁴ + 3х³ – 2х² – х – 2 на множители.

Ищем целые корни многочлена среди делителей свободного члена: ±1, ±2. Подходит 1. Делим Р (х) на х – 1 с помощью схемы Горнера.

Тогда Р (х) = (х – 1)(2х3 + 5х² + 3х + 2). Ищем целые корни кубического многочлена 2х³ + 5х² + 3х + 2 среди делителей его свободного члена: ±1, ±2. Подходит (–2). Делим на х + 2

Имеем  Р (х) = (х – 1)(х + 2)(2х² + х +1).

Квадратный трехчлен 2х² + х +1 не имеет действительных корней и на линейные множители не расклады­вается.

Ответ: Р (х) = (х – 1)(х + 2)(2х² + х +1).

Отметим, что во множестве действительных чисел не всегда можно найти все корни многочлена (например, квадратный трехчлен х² + х + 1 не имеет действительных корней). Таким образом, многочлен n-й степени не всегда можно разложить на линейные множители. В курсах высшей алгебры дока­зывается, что многочлен нечетной степени всегда можно разложить на ли­нейные и квадратные множители, а многочлен четной степени представить в виде произведения квадратных трехчленов.

Например, многочлен четвертой степени раскладывается в произведение двух квадратных трехчленов. Для нахождения коэффициентов этого раз­ложения иногда можно применить метод неопределенных коэффициентов.

Задача 3 Разложите на множители многочлен х⁴ + х³ + 3х² + х + 6.

Попытка найти рациональные корни ничего не дает: многочлен не имеет рациональных (целых) корней.

Попытаемся разложить этот многочлен в произведение двух квадратных трехчленов. Поскольку старший коэффициент многочлена равен 1, то и у квадратных трехчленов возьмем старшие коэффициенты равными 1. То есть будем искать разложение нашего многочлена в виде:

х4 + х3 + 3х2 + х + 6 = (х2 + ах + b)(х2 + сх + d),

(3)

где а, b, с и d — неопределенные (пока что) коэффициенты. Многочлены, стоящие в левой и правой частях этого равенства, тождественно равны, поэтому и коэффициенты при одинаковых степенях х у них равны. Рас­кроем скобки в правой части равенства и приравняем соответствующие коэффициенты. Это удобно записать так:

х⁴ + х³ + 3х² + х + 6 = x⁴ + cx³ + dx² +

                                                      + ax³ + acx² + adx +

                                                                    + bx² + bcx + bd.

Получаем систему

(4)

Попытка решить эту систему методом подстановки приводит к уравне­нию 4-й степени, поэтому попробуем решить систему (4) в целых числах. Из последнего равенства системы (4) получаем, что b и d могут быть толь­ко делителями числа 6. Все возможные варианты запишем в таблицу.

Коэффициенты b и d в равенстве (3) равноправны, поэтому мы не рас­сматриваем случаи b = 6 и d = 1 или b = –6 и d = –1 и т. д.

Для каждой пары значений b и d из третьего равенства системы (4) най­дем ас = 3 – (b + d), а из второго равенства имеем а + с = 1.

Зная а + с и ас, по теореме, обратной теореме Виета, находим а и с как корни квадратного уравнения. Найденные таким образом значения а, b, с, d подставим в четвертое равенство системы (4) bс + ad = 1, чтобы выбрать те числа, которые являются решениями системы (4). Удобно эти рассуждения оформить в виде таблицы:

Как видим, системе (4) удовлетворяет набор целых чисел а = –1, b = 2, с = 2, d = 3. Тогда равенство (3) имеет вид

x4 + х3 + 3х2 + х + 6 = (х2 – х + 2)(х2 + 2х + 3).

(5)

Поскольку квадратные трехчлены х² – х + 2 и х² + 2х + 3 не имеют не только рациональных, но и действительных корней, то равенство (5) дает окончательный ответ.

Упражнения

1. Найдите целые корни многочлена:

1) х³ – 5х + 4;

2) 2x³ + x² – 13x + 6;

3) 5х³ + 18х² – 10х – 8;

4) 4х⁴ – 11х² + 9х – 2.

1. Найдите рациональные корни уравнения:

1) х³ – 3х² + 2 = 0;

2) 2х³ – 5х² – х + 1 = 0;

3) 3х⁴ + 5х³ – х² – 5х – 2 = 0;

4) 3х⁴ – 8х³ – 2х² + 7х – 2 = 0.

1. Разложите многочлен на множители:

1) 2х³ – х² – 5х – 2;

2) х³ + 9х² + 23х +15;

3) х⁴ – 2х³ + 2х – 1;

4) х⁴ – 2х³ – 24х² + 50х – 25.

1. Найдите действительные корни уравнения:

1) х³ + х² – 4х + 2 = 0;

2) х³ – 7х – 6 = 0;

3) 2х⁴ – 5х³ + 5х² – 2 = 0;

4) 2х³ – 5х² + 1 = 0.

5*. Разложите многочлен на множители методом неопределенных коэффи­циентов:

1) х⁴ + х³ – 5х² + 13х – 6;

2) х⁴ – 4х³ – 20х² + 13х – 2.

6*. Разложите многочлен на множители, заранее записав его с помощью ме­тода неопределенных коэффициентов в виде (х² + bх + с)² – (mх + n)²: :

1) х⁴+ 4х – 1;

2) х⁴ – 4х³ – 1;

3) х⁴ + 4а³х – а⁴.

Содержание:

1. Теорема о рациональных корнях
2. Задача пример №8
3. Задача пример №9
4. Задача пример №10

Теорема о рациональных корнях

Если для многочлена с целыми коэффициентами существует рациональный корень, то этот корень имеет вид

Доказательство:

Пусть несократимая дробь является корнем многочлена с целыми коэффициентами:

Умножим обе части равенства на :

Так как в последнем равенстве каждый член, кроме члена , содержит множитель и каждый член, кроме члена , содержит множитель , то коэффициент должен делится на , а коэффициент должен делится на .

Задача пример №8

Найдите рациональные корни многочлена .

Решение:

свободный член 6, старший коэффициент 2.

Для , запишем все возможные числа вида

, т.е. одним из множителей является двучлен . Другие множители найдем, используя синтетическое деление:

Так как, , получим, что являются корнями многочлена.

Следствие 1. Если старший коэффициент ±1 и многочлен имеет рациональный корень, то он является целым числом.

Следствие 2. Целые корни многочлена с целыми коэффициентами (если они имеются) являются делителями свободного члена.

Задача пример №9

Найдите корни многочлена .

Решение:

по теореме о рациональных корнях многочлена, целый корень данного многочлена (если он существует) надо искать среди делителей числа 5. Это числа ±5; ±1.

Запишем это короче при помощи синтетического деления и проверим, являются ли эти числа корнями многочлена.

Так как , то, решив квадратное уравнение , получим другие корни: . Значит данный многочлен третьей степени имеет три корня: —.

Внимание! Если коэффициенты многочлена являются рациональными числами, то для нахождения рациональных корней уравнения сначала обе части уравнения надо умножить на такое число (отличное от нуля), чтобы коэффициенты стали целыми.

Например, для нахождения корней многочлена надо умножить все члены уравнения на 12, а затем решить полученное уравнение .

Для нахождения рациональных корней выполните следующие действия:

1. Записывается множество всех возможных дробей, числителями которых являются делители свободного члена, а знаменателями являются делители старшего коэффициента.

2. Из этих чисел выбирается число (обращающее значение многочлена в нуль), которое является корнем многочлена, т.е. определяется двучлен , на который многочлен делится без остатка.

3. Для данного многочлена при помощи синтетического деления на двучлен определяется другой множитель.

4. Если другой множитель является квадратным трехчленом или его можно разложить при помощи формул сокращенного умножения, находятся другие корни. Иначе все линейные множители находятся синтетическим делением.

5. Возможно, что ни одно число из списка не будет нулем многочлена. В этом случае многочлен не имеет рациональных корней. Например, рациональными корнями многочлена могут являться числа ±1.

Проверим: ; . Значит, многочленах не имеет рациональных корней.

Исследование:

1) Перепишите примеры в тетрадь и проведите обсуждение.

a) Многочлен первой степени имеет один корень:

b) Многочлен второй степени имеет два корня: , ;

c) Многочлен третьей степени имеет три корня:

d) Многочлен четвертой степени имеет четыре корня:

e) Принимая во внимание, что уравнение имеет кратные корни, получим 5 корней:

2) Укажите степень и найдите корни многочленов, разложение на множители которых имеет вид .

3) Равна ли степень произвольного многочлена количеству его корней?

Покажем на примере, что многочлен n-ой степени имеет n корней.

Задача пример №10

Найдите все корни многочлена .

Решение:

рациональными корнями данного многочлена (если они существуют), согласно правилу, могут являться числа ±1, ±5. Проверим:

.

Значит, является корнем данного многочлена . Другие корни найдем синтетическим делением.

В выражении для множителя вновь применим теорему о рациональных корнях и синтетическое деление. Тогда ; . Решим уравнение ; ; (корень кратности 2); ;

Корни:

Во всех рассмотренных нами примерах уравнение n-ой степени всегда имеет n корней, включая кратные корни (действительных или комплексных).

Эта лекция взята из раздела решения задач по математике, там вы найдёте другие лекци по всем темам математики:

Другие темы которые вам помогут понять математику:

Теорема об остатке

Теорема о разложении на множители

Основная теорема алгебры

Функция-многочлен

Рациональные корни многочлена с целыми коэффициентами

Вопрос о нахождении
рациональных корней многочлена f(x)Q[x]
(с рациональными коэффициентами) сводится
к вопросу об отыскании рациональных
корней многочленов k
∙ f(x)Z[x]
(с целыми коэффициентами). Здесь число
k
является наименьшим общим кратным
знаменателей коэффициентов данного
многочлена.

Необходимые, но
не достаточные условия существования
рациональных корней многочлена с целыми
коэффициентами дает следующая теорема.

Теорема 6.1 (о
рациональных корнях многочлена с целыми
коэффициентами).
Если
–рациональный
корень многочлена f(x)
= a_n

xⁿ+
+
…+ a₁

x
+ a₀
с
целыми
коэффициентами,
причем (p,
q)
= 1, то числитель
дроби p
является делителем свободного члена
а₀,
а знаменатель q
является делителем старшего коэффициента
а₀.

Теорема
6.2. Если
Q
(где
(p,
q)
= 1)
является
рациональным корнем многочлена
f(x)
с целыми
коэффициентами, то
–целые
числа.

Пример. Найти
все рациональные
корни
многочлена

f(x)
= 6
x⁴
+ x³
+ 2
x²
–
4 х+
1.

1. По теореме 6.1:
если
–рациональный
корень многочлена f(x),
(где
(p,
q)
= 1), то
a₀
= 1

p,
a_n
= 6
q.
Поэтому p
{
1}, q{1,
2, 3, 6}, значит,

.

2. Известно, что
(следствие 5.3) число а
является корнем многочлена f(x)
тогда и только тогда, когда f(x)
делится на (х
– а).

Следовательно,
для проверки того, являются ли числа 1
и –1 корнями многочлена f(x)
можно воспользоваться схемой Горнера:

	6	1	2	– 4	1
1	6	7	9	5	6
– 1	6	– 5	7	–11	12

f(1)
= 60,f(–1)
= 120,
поэтому 1 и –1 не являются корнями
многочленаf(x).

3. Чтобы отсеять
часть оставшихся чисел
,
воспользуемся теоремой 6.2. Если выраженияилипринимает целые значения для соответствующих
значений числителяp
и знаменателя q,
то в соответствующих клетках таблицы
(см. ниже) будем писать букву “ц”, в
противном случае – “др”.

=	ц	ц	ц	др	др	др
=	ц	ц	ц	ц	др	др

4. С помощью схемы
Горнера проверяем, будут ли оставшиеся
после отсеивания числа
корнямиf(x).
Вначале разделим f(x)
на (х
–
).

	6	1	2	– 4	1
	6	4	4	–2	0

В результате
имеем: f(x)
= (х
–
)(6
x³
+ 4
x²
+
4 х
– 2) и
– кореньf(x).
Частное q(x)
= 6 x³
+ 4
x²
+
4 х
– 2 разделим
на (х
+
).

	6	1	2	– 4	1
–	6	–2	3	–5	3

Так
как q
(–)
= 30, то (–) не является корнем многочленаq(x),
а значит и многочлена f(x).

Наконец,
разделим многочлен q(x)
= 6 x³
+ 4
x²
+
+ 4 х
– 2 на (х
–
).

	6	1	2	– 4	1
	6	3	3	–3	0

Получили:
q
()
= 0, т.е.– кореньq(x),
а значит,
– кореньf
(x).
Таким образом, многочлен f
(x)
имеет два рациональных корня:
и.

Освобождение от алгебраической иррациональности в знаменателе дроби

В школьном курсе
при решении некоторых типов задач на
освобождение от иррациональности в
знаменателе дроби достаточно домножить
числитель и знаменатель дроби на число
сопряженное знаменателю.

Примеры. 1.
t
=
.

Здесь в знаменателе
срабатывает формула сокращенного
умножения (разность квадратов), что
позволяет освободиться от иррациональности
в знаменателе.

2. Освободиться от
иррациональности в знаменателе дроби

t
=

. Выражение
– неполный квадрат разности чисела
=
иb
= 1. Воспользовавшись формулой сокращенного
умножения а³
– b³=
(а
+ b)
· (a²
– ab
+ b²),
можно определить множитель m
= (а + b)
=
+ 1, на который следует домножать числитель
и знаменатель дробиt,
чтобы избавиться от иррациональности
в знаменателе дроби t.
Таким образом,

t
=
.

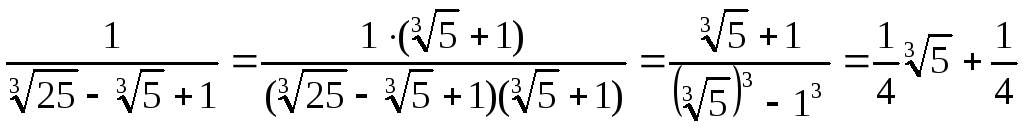
В ситуациях, где
формулы сокращенного умножения не
работают, можно использовать другие
приемы. Ниже будет сформулирована
теорема, доказательство которой, в
частности, позволяет найти алгоритм
освобождения от иррациональности в
знаменателе дроби в более сложных
ситуациях.

Определение 6.1.
Число z
называется алгебраическим
над полем
F,
если существует многочлен f(x)
F[x],
корнем которого является z,
в противном случае число z
называется трансцендентным
над полем F.

Определение 6.2.
Степенью
алгебраического над полем
F
числа
z
называется степень неприводимого над
полем F
многочлена p(x)F[x],
корнем которого является число z.

Пример. Покажем,
что число z
=
является алгебраическим над полемQ
и найдем его
степень.

Найдем неприводимый
над полем Q
многочлен p(х),
корнем которого является x
=
.
Возведем обе части равенстваx
=
в
четвертую степень, получимх⁴
= 2 или х⁴
– 2
= 0. Итак, p(х)
= х⁴
– 2, а степень
числа z
равна deg
p(х)
= 4.

Теорема 6.3
(об освобождении
от алгебраической иррациональности в
знаменателе дроби). Пусть
z
– алгебраическое число над полем F
степени n.
Выражение вида t
=
,где
f(x),
(x)F[x],
(z)0

единственным
образом может быть представлено в виде:

t
= с_n-1
z^n-1
+ c_n-2
z^n-2
+ … + c₁
z
+ c₀,
c_i

F.

Алгоритм освобождения
от иррациональности в знаменателе дроби
продемонстрируем на конкретном примере.

Пример.
Освободиться от иррациональности в
знаменателе дроби:

t
=

1. Знаменателем
дроби является значение многочлена
(х)
= х²
– х
+1 при х
=
.
В предыдущем примере показано, что– алгебраическое число над полемQ
степени 4, так как оно является корнем
неприводимого над Q
многочлена p(х)
= х⁴
– 2.

2. Найдем линейное
разложение НОД ((х),
p(x))
с помощью алгоритма Евклида.

_
x⁴

– 2 |
x²
– x
+ 1

x⁴–
x³+
x²


x²
+ x = q₁(x)

_
x³–
x²
–
2

x³–
x²+
x

x²
– x
+ 1 |
– x
–2 = r₁
(x)

x²
+ 2x

– x +
3
= q₂(x)

_–3x
+
1

–3x
– 6

_
– x
–2 |7
= r₂

– x
–2
—x
—
=q₃(x)

0

Итак, НОД ((х),
p(x))
= r₂
=
7. Найдем
его линейное разложение.

Запишем
последовательность Евклида, пользуясь
обозначениями многочленов.

p(x)
=
(x)
· q₁(x)
+ r₁(x)
r₁(x)
=
p(x)
–
(x)
· q₁(x)

(x)
= r₁(x)
· q₂(x)
+ r₂(x)
r₂(x)
=
(x)
– r₁(x)
· q₂(x)

r₁(x)
= r₂(x)
· q₂(x).

Подставим в
равенство 7= r₂(x)
=
(x)
– r₁(x)
· q₂(x)
значение остатка r₁(x)
= p(x)
–
(x)
· q₁(x),
после преобразований получим линейное
разложение НОД((х),
p(x)):
7 = p(x)
· (– q₂(x))
+
(x)
· [1 + q₁(x)
· q₂(x)].
Если подставить в последнее равенство
вместо обозначений соответствующие
многочлены и учесть, что p()
= 0, то имеем:

(1 –
+)
· (–+ 2+ 3+ 1)] = 7 (1)

3. Из равенства (1)
следует, что если знаменатель дроби t
умножить на число m
= [1 + (–
+ 2+ 3+ 1)], то получим 7. Таким образом,

t
=
=.

МЕТОДИКА 16.
Тема урока: Стандартный вид многочлена

Класс: 7

Тип урока: урок проверки и контроля
знаний и умений

Цели урока:

— проверить умения приводить многочлен
к стандартному виду

— развивать у учащихся логическое
мышление, внимание

— воспитывать самостоятельность

Структура урока:

1. Организационный момент

2. Инструктаж

3. Самостоятельная работа.

Задания:

1. Дополните предложения:

а) Выражение, содержащее сумму одночленов
называют …(многочленом).

б) Многочлен состоящий из стандартных
одночленов и не содержащий подобных
слагаемых называется … (стандартным
многочленом).

в) Наибольшую из степеней одночленов
входящих в многочлен стандартного вида
называют … (степенью многочлена).

г) Прежде чем определить степень
многочлена, нужно … (привести его к
стандартному виду).

д) Для нахождения значения многочлена
нужно сделать первое…(представить
многочлен в стандартном виде), второе
…(подставить значение переменной в
данное выражение).

2. Найти значение многочлена:

а) 2a⁴—ab+2b²приa=-1, b=-0,5

б) x²+2xy+y²приx=1,2, y=-1,2

3. Привести многочлен к стандартному
виду:

а) -5ах²
+ 7а²х + 2а²х +
9ах² – 4ах² –
8а²х;

б) (5х²
– 7х – 13) – (3х² – 8х + 17);

в) 2а
– (1,4ав + 2а² – 1) + (3а + 6,4ав);

г)
(2с² – 1,6с + 4) – ((10,6с²
+ 4,4с – 0,3) – (3,6с² – 7с –
0,7));

4.
Привести многочлен к стандартному виду
и выяснить при каких значениях хего значение равно 1:

а)
2x²-3x—x²-5+2x—x²+10;

б)
0,3x³—x²+x—x³+3x²+0,7x³-2x²+0,07

Билет
№ 17.
Делимость
целых чисел

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Нахождение рациональных корней

Содержание:

Теорема о рациональных корнях

Если для многочлена с целыми коэффициентами существует рациональный корень, то этот корень имеет вид

Доказательство:

Пусть несократимая дробь является корнем многочлена с целыми коэффициентами:

Умножим обе части равенства на :

Так как в последнем равенстве каждый член, кроме члена , содержит множитель и каждый член, кроме члена , содержит множитель , то коэффициент должен делится на , а коэффициент должен делится на .

Задача пример №8

Найдите рациональные корни многочлена .

Решение:

свободный член 6, старший коэффициент 2.

Для , запишем все возможные числа вида

, т.е. одним из множителей является двучлен . Другие множители найдем, используя синтетическое деление:

Так как, , получим, что являются корнями многочлена.

Следствие 1. Если старший коэффициент ±1 и многочлен имеет рациональный корень, то он является целым числом.

Следствие 2. Целые корни многочлена с целыми коэффициентами (если они имеются) являются делителями свободного члена.

Задача пример №9

Найдите корни многочлена .

Решение:

по теореме о рациональных корнях многочлена, целый корень данного многочлена (если он существует) надо искать среди делителей числа 5. Это числа ±5; ±1.

Запишем это короче при помощи синтетического деления и проверим, являются ли эти числа корнями многочлена.

Так как , то, решив квадратное уравнение , получим другие корни: . Значит данный многочлен третьей степени имеет три корня: —.

Внимание! Если коэффициенты многочлена являются рациональными числами, то для нахождения рациональных корней уравнения сначала обе части уравнения надо умножить на такое число (отличное от нуля), чтобы коэффициенты стали целыми.

Например, для нахождения корней многочлена надо умножить все члены уравнения на 12, а затем решить полученное уравнение .

Для нахождения рациональных корней выполните следующие действия:

1. Записывается множество всех возможных дробей, числителями которых являются делители свободного члена, а знаменателями являются делители старшего коэффициента.

2. Из этих чисел выбирается число (обращающее значение многочлена в нуль), которое является корнем многочлена, т.е. определяется двучлен , на который многочлен делится без остатка.

3. Для данного многочлена при помощи синтетического деления на двучлен определяется другой множитель.

4. Если другой множитель является квадратным трехчленом или его можно разложить при помощи формул сокращенного умножения, находятся другие корни. Иначе все линейные множители находятся синтетическим делением.

5. Возможно, что ни одно число из списка не будет нулем многочлена. В этом случае многочлен не имеет рациональных корней. Например, рациональными корнями многочлена могут являться числа ±1.

Проверим: ; . Значит, многочленах не имеет рациональных корней.

Исследование:

1) Перепишите примеры в тетрадь и проведите обсуждение.

a) Многочлен первой степени имеет один корень:

b) Многочлен второй степени имеет два корня: , ;

c) Многочлен третьей степени имеет три корня:

d) Многочлен четвертой степени имеет четыре корня:

e) Принимая во внимание, что уравнение имеет кратные корни, получим 5 корней:

2) Укажите степень и найдите корни многочленов, разложение на множители которых имеет вид .

3) Равна ли степень произвольного многочлена количеству его корней?

Покажем на примере, что многочлен n-ой степени имеет n корней.

Задача пример №10

Найдите все корни многочлена .

Решение:

рациональными корнями данного многочлена (если они существуют), согласно правилу, могут являться числа ±1, ±5. Проверим:

.

Значит, является корнем данного многочлена . Другие корни найдем синтетическим делением.

В выражении для множителя вновь применим теорему о рациональных корнях и синтетическое деление. Тогда ; . Решим уравнение ; ; (корень кратности 2); ;

Корни:

Во всех рассмотренных нами примерах уравнение n-ой степени всегда имеет n корней, включая кратные корни (действительных или комплексных).

Эта лекция взята из раздела решения задач по математике, там вы найдёте другие лекци по всем темам математики:

Математика: полный курс решений задач в виде лекций

Другие темы которые вам помогут понять математику:

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

Рациональные корни многочленов с целыми коэффициентами. Алгебраические и трансцендентные числа

Рациональные корни многочленов с целыми коэффициентами

Прежде, чем дать общую формулировку теоремы о рациональных корнях многочленов с целыми коэффициентами , решим следующую задачу.

Задача . Найти все корни уравнения

Решение . Предположим, что рассматриваемое уравнение имеет корень, являющийся рациональным числом. Тогда, поскольку каждое рациональное число можно представить в виде несократимой дроби

,

где m – число целое, а n – число натуральное, то выполняется равенство:

Умножая это равенство на n 3 , получаем равенство:

2m 3 + m 2 n – 5 m n 2 – – 3n 3 = 0.

(1)

Теперь преобразуем равенство (1):

Отсюда вытекает, что число 2m 3 нацело делится на число n . А из этого, в свою очередь, следует, что, поскольку числа m и n не имеют общих простых делителей, то число n является делителем числа 2 . Таким образом, число n равно 1 или 2 .

Теперь преобразуем равенство (1) по-другому:

Значит, число 3n 3 нацело делится на число m . А из этого, в свою очередь, следует, что, так как числа m и n не имеют общих простых делителей, то число m является делителем числа 3. Таким образом, число m может быть равно: – 1, 1, – 3 или 3 .

Далее, рассматривая все возможные комбинации чисел m и n , получаем, что дробь

может принимать только следующие значения:

Таким образом, если у исходного уравнения и есть рациональный корень, то искать его нужно среди полученных шести чисел. Других рациональных корней у исходного уравнения быть не может.

Подставляя поочередно каждое из этих чисел в исходное уравнение, получаем, что корнем уравнения является лишь число .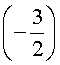

Оставляя читателю проверку того, что другие числа корнями исходного уравнения не являются, покажем, что число 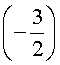действительно является его корнем:

Ответ . Число 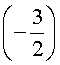является единственным рациональным корнем исходного уравнения.

Замечание . Для того, чтобы найти все остальные корни исходного уравнения, нужно, воспользовавшись теоремой Безу, разделить многочлен

В результате деления получится квадратный трехчлен

Теорема . Если рациональное число (несократимая дробь)

,

где m – число целое, а n – число натуральное, является корнем многочлена k -ой степени

которого являются целыми числами, то числитель дроби m является делителем коэффициента a_k , а знаменатель дроби n является делителем коэффициента a₀ .

Коэффициент a₀ называют старшим коэффициентом многочлена, а коэффициент a_k – свободным членом многочлена.

Алгебраические и трансцендентные числа

Определение . Действительное число называют действительным алгебраическим числом , если существует многочлен с целочисленными коэффициентами, корнем которого это число является. Если же такой многочлен не существует, то указанное число называют действительным трансцендентным числом .

Замечание . Числа π и e – наиболее известные примеры действительных трансцендентных чисел.

Утверждение . Каждое рациональное число является алгебраическим числом.

Доказательство . Каждое рациональное число представимо в виде несократимой дроби

,

где m – число целое, а n – число натуральное. Но указанная дробь является корнем уравнения первой степени

что и требовалось доказать.

Следствие . Каждое действительное трансцендентное число является иррациональным числом.

10.5. НАХОЖДЕНИЕ РАЦИОНАЛЬНЫХ КОРНЕЙ МНОГОЧЛЕНА С ЦЕЛЫМИ КОЭФФИЦИЕНТАМИ

Умножим обе части равенства (1) на (q ≠ 0). Получаем

В равенстве (2) все слагаемые, кроме последнего, делятся на р. Поэтому

Но когда мы записываем рациональное число в виде p/q, то эта дробь счи­тается несократимой, то есть р и q не имеют общих делителей. Произве­дение a₀q n может делиться на р (если р и q — взаимно простые числа) только тогда, когда a₀ делится на р. Таким образом, р — делитель свобод­ного члена a₀.

Аналогично все слагаемые равенства (2), кроме первого, делятся на q. Тогда

Отметим два следствия из этой теоремы. Если взять q = 1, то корнем многочлена будет целое число р — делитель a₀. Таким образом, имеет место:

Следствие 1. Любой целый корень многочлена с целыми коэффи­циентами является делителем его свободного члена.

Если в заданном многочлене f (х) коэффициент а_n = 1, то делителями а_n могут быть только числа ±1, то есть q =±1, и имеет место:

Следствие 2. Если коэффициент при старшем члене уравнения с целыми коэффициентами равен 1, то все рациональные корни этого уравнения (если они существуют) — целые числа.

Задача 1 Найдите рациональные корни многочлена 2х 3 – х 2 + 12х – 6.

Пусть несократимая дробь p/q является корнем многочлена. Тогда р не­обходимо искать среди делителей свободного члена, то есть среди чисел ±1, ±2, ±3, ±6, а q — среди делителей старшего коэффициента: ±1, ±2.

Таким образом, рациональные корни многочлена необходимо искать сре­ди чисел ±1/2, ±1, +±3/2, ±2, ±3, ±6. Проверять, является ли данное число корнем многочлена, целесообразно с помощью схемы Горнера. При x = 1/2 имеем следующую таблицу.

Кроме того, по схеме Горнера мож­но записать, что

Многочлен 2х 2 + 12 не имеет действительных корней (а тем более рацио­нальных), поэтому заданный многочлен имеет единственный рациональ­ный корень x =1/2.

Задача 2 Разложите многочлен Р (х) = 2х 4 + 3х 3 – 2х 2 – х – 2 на множители.

Ищем целые корни многочлена среди делителей свободного члена: ±1, ±2. Подходит 1. Делим Р (х) на х – 1 с помощью схемы Горнера.

Тогда Р (х) = (х – 1)(2х3 + 5х 2 + 3х + 2). Ищем целые корни кубического многочлена 2х 3 + 5х 2 + 3х + 2 среди делителей его свободного члена: ±1, ±2. Подходит (–2). Делим на х + 2

Квадратный трехчлен 2х 2 + х +1 не имеет действительных корней и на линейные множители не расклады­вается.

Ответ: Р (х) = (х – 1)(х + 2)(2х 2 + х +1).

Отметим, что во множестве действительных чисел не всегда можно найти все корни многочлена (например, квадратный трехчлен х 2 + х + 1 не имеет действительных корней). Таким образом, многочлен n-й степени не всегда можно разложить на линейные множители. В курсах высшей алгебры дока­зывается, что многочлен нечетной степени всегда можно разложить на ли­нейные и квадратные множители, а многочлен четной степени представить в виде произведения квадратных трехчленов.

Например, многочлен четвертой степени раскладывается в произведение двух квадратных трехчленов. Для нахождения коэффициентов этого раз­ложения иногда можно применить метод неопределенных коэффициентов.

Задача 3 Разложите на множители многочлен х 4 + х 3 + 3х 2 + х + 6.

Попытка найти рациональные корни ничего не дает: многочлен не имеет рациональных (целых) корней.

Попытаемся разложить этот многочлен в произведение двух квадратных трехчленов. Поскольку старший коэффициент многочлена равен 1, то и у квадратных трехчленов возьмем старшие коэффициенты равными 1. То есть будем искать разложение нашего многочлена в виде:

где а, b, с и d — неопределенные (пока что) коэффициенты. Многочлены, стоящие в левой и правой частях этого равенства, тождественно равны, поэтому и коэффициенты при одинаковых степенях х у них равны. Рас­кроем скобки в правой части равенства и приравняем соответствующие коэффициенты. Это удобно записать так:

Попытка решить эту систему методом подстановки приводит к уравне­нию 4-й степени, поэтому попробуем решить систему (4) в целых числах. Из последнего равенства системы (4) получаем, что b и d могут быть толь­ко делителями числа 6. Все возможные варианты запишем в таблицу.

Коэффициенты b и d в равенстве (3) равноправны, поэтому мы не рас­сматриваем случаи b = 6 и d = 1 или b = –6 и d = –1 и т. д.

Для каждой пары значений b и d из третьего равенства системы (4) най­дем ас = 3 – (b + d), а из второго равенства имеем а + с = 1.

Зная а + с и ас, по теореме, обратной теореме Виета, находим а и с как корни квадратного уравнения. Найденные таким образом значения а, b, с, d подставим в четвертое равенство системы (4) bс + ad = 1, чтобы выбрать те числа, которые являются решениями системы (4). Удобно эти рассуждения оформить в виде таблицы:

Как видим, системе (4) удовлетворяет набор целых чисел а = –1, b = 2, с = 2, d = 3. Тогда равенство (3) имеет вид

Поскольку квадратные трехчлены х 2 – х + 2 и х 2 + 2х + 3 не имеют не только рациональных, но и действительных корней, то равенство (5) дает окончательный ответ.

Упражнения

1. Найдите целые корни многочлена:

1. Найдите рациональные корни уравнения:

1. Разложите многочлен на множители:

1. Найдите действительные корни уравнения:

5*. Разложите многочлен на множители методом неопределенных коэффи­циентов:

6*. Разложите многочлен на множители, заранее записав его с помощью ме­тода неопределенных коэффициентов в виде (х 2 + bх + с) 2 – (mх + n) 2 : :

Многие уравнения с помощью различных приемов,
выполнив подходящие замены переменных, можно
свести к квадратным. Рассмотрим некоторые из них.

1) Такое
уравнение называется биквадратным.

Замена:
D = 1225 = ,

Ответ:

2)

Замена: тогда
получим

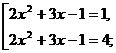
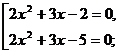
Ответ: –2,5, –2, 0,5, 1.

3) В уравнении , перемножая попарно скобки, получим Сделав замену сводим уравнение к
квадратному.

4)
О.Д.З.:

Замена: тогда получаем
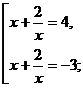
т.к. х0, то получаем

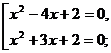
Ответ: –1, –2,

5) Симметрическим уравнением
называется уравнение вида где Заметим, что симметрическое уравнение
нечетной степени имеет корень х = –1,
симметрическое уравнение четной степени можно
решить, используя замену В школьном курсе математики часто
встречаются симметрические уравнения четвертой
степени, которые в общем виде можно записать так: где
Решим уравнение
О.Д.З.: R.
Заметим, что х = 0 не является корнем уравнения,
поэтому, разделив обе части уравнения на , получим уравнение
Пришли к уравнению, решение которого рассмотрено
в п.4.

6) Возвратным уравнением нечетной
степени называется уравнение вида где R.

Возвратное уравнение четной степени – это
уравнение вида
где R.

Заметим, что возвратное уравнение нечетной
степени имеет корень

Решим возвратное уравнение четверной степени
О.Д.З.: R. Заметим,
что Разделив
обе части уравнения на (,
получим
Замена : тогда

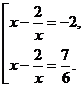
Ответ:

7) Однородным уравнением ой степени называется
уравнение вида
которое заменой
сводится к алгебраическому уравнению ой степени.

Решим уравнение, которое сводится к
однородному уравнению четвертой степени:

О.Д.З.:R.
Заметим, что , поэтому можем
разделить обе части уравнения на выражение , получим
, это уравнение
заменой
сводится к квадратному уравнению

Рассмотрим еще некоторые уравнения, сводящиеся
к квадратным.

О.Д.З.:
R.
Заметим, что х = 0 не является корнем уравнения,
поэтому можем разделить обе части его на получим

Замена:
Получаем квадратное уравнение

При решении последних уравнений мы
пользовались утверждением: при умножении
или делении обеих частей уравнения на число или
выражение, не равное нулю на области допустимых
значений переменной, получаем уравнение,
равносильное данному.

Можно использовать и другое утверждение: при
делении числителя и знаменателя дроби на число
или выражение, не равное нулю на области
допустимых значений переменной, получаем
уравнение, равносильное данному. Покажем,
как используется это утверждение.

9) О.Д.З.:
R

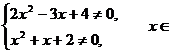
Заметим, что х = 0 не является корнем уравнения,
поэтому, разделив числитель и знаменатель каждой
дроби на х, получим 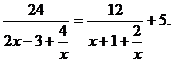Замена:
тогда

10) При решении уравнения вида можно воспользоваться
заменой

Решим уравнение: Сделаем замену:
получим

Ответ: –5, 1.

11) Рассмотрим метод выделения полного
квадрата при решении рационального уравнения.

12) Покажем, как при решении уравнений
может значительно упростить решение выделение
целой части дробного выражения.

О.Д.З.:

Выделять целую часть можно делением «уголком»
числителя на знаменатель или, например,
следующим образом:
Выполняя аналогичные преобразования каждой
дроби, получим
замена:

Ответ:

13) Уравнения вида иногда можно решить,
раскладывая левую часть уравнения на множители.
Раскладывать на множители можно разными
способами (вынесением общего множителя за
скобки, способом группировки и т.д.) .Рассмотрим
один из способов, основанный на подборе корней
уравнения по его коэффициентам.

Теорема. Пусть – многочлен с целыми коэффициентами.
Если – его
рациональный корень ( – несократимая дробь), то делится на
делится на .

Эту теорему можно применять для нахождения
корней уравнения с целыми коэффициентами. Если
коэффициенты в уравнении не являются целыми
числами, то предварительно необходимо умножить
обе части его на наименьший общий знаменатель и
получить уравнение с целыми коэффициентами.

Решим уравнение:

Если уравнение имеет рациональные корни, то все
они содержатся среди возможных значений дроби Проверить,
являются ли числа корнями данного уравнения можно по
следующему правилу: если х = 1 является корнем
уравнения, то сумма всех его коэффициентов равна
0, если х = –1 является корнем уравнения, то сумма
коэффициентов, стоящих на четных местах равна
сумме коэффициентов, стоящих на нечетных местах.
Нетрудно увидеть, что один из корней нашего
уравнения равен 1, а, следовательно, в разложении
левой части уравнения на множители будет
присутствовать множитель

Второй множитель можно найти либо, разделив
многочлен на «уголком», либо,
применяя схему Горнера.

Получаем,
Можно и дальше применять схему Горнера, а можно,
получив квадратный трехчлен, находить его корни
по известным формулам.
В итоге получим

Ответ: –3; –2; 0,5; 1.

Следующие задания можно предложить для
самостоятельной работы с целью закрепления
навыков решения уравнений рассмотренными
методами.

1)
2)
3)
4)
5)

6)
7)

9)
10)
11)
12)
13)
14)