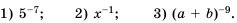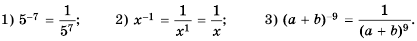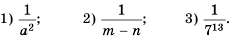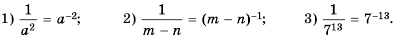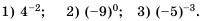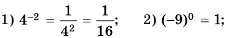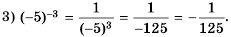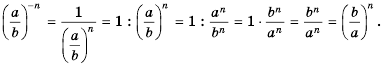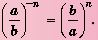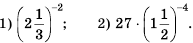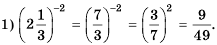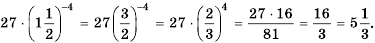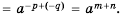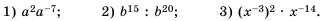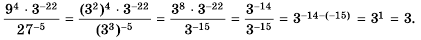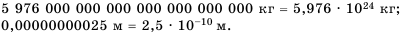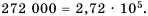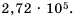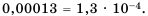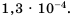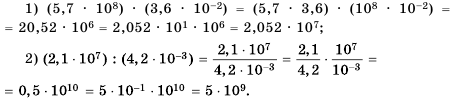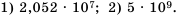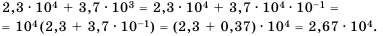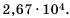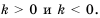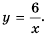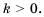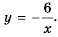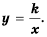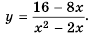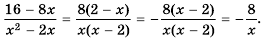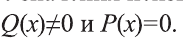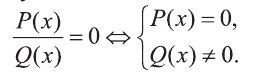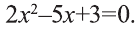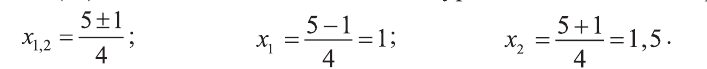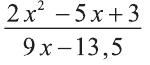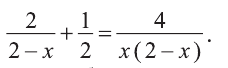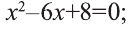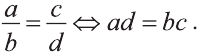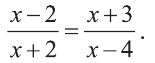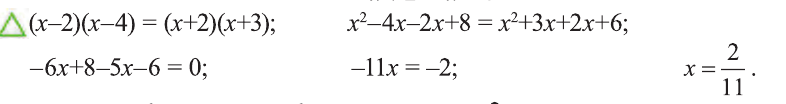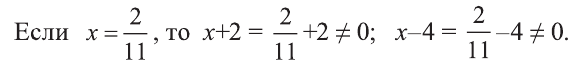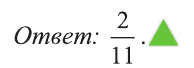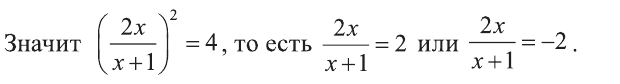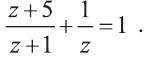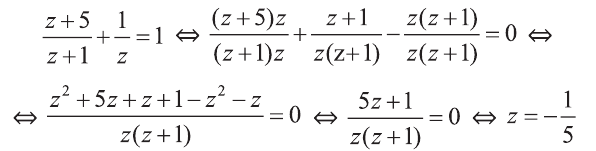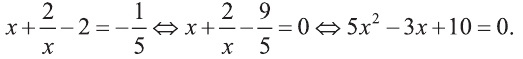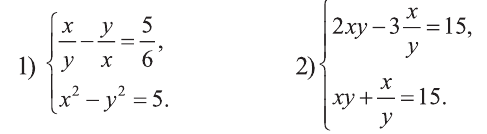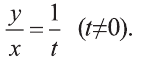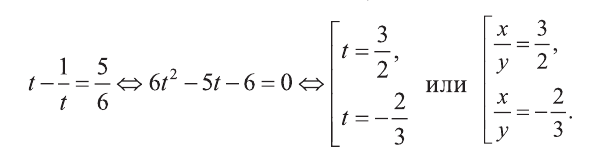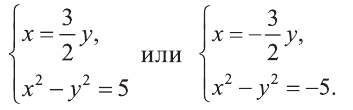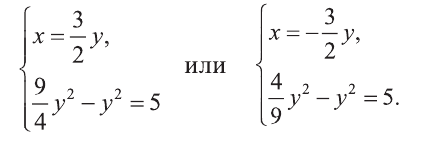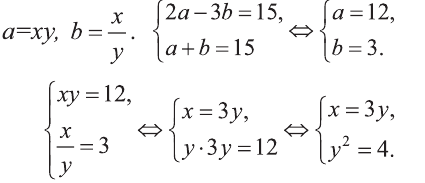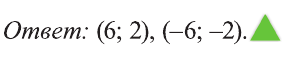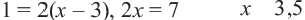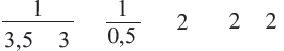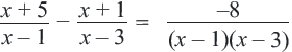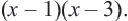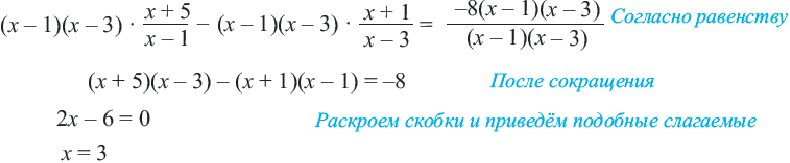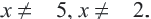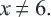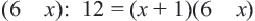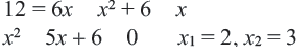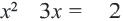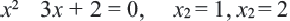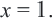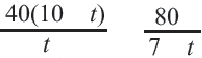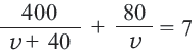Рациональные уравнения с примерами решения
Содержание:
Рациональные уравнения. Равносильные уравнения
два уравнения называют равносильными, если они имеют одни и те же корни. Равносильными считают и те уравнения, которые корней не имеют.
Так, например, равносильными будут уравнения
Уравнения 
Ранее, в 7 классе, вы знакомились со свойствами, которые преобразуют уравнения в равносильные им уравнения.
1) Если в любой части уравнения раскрыть скобки или привести подобные слагаемые, то получим уравнение, равносильное данному;
2) если в уравнении перенести слагаемое из одной части в другую, изменив его знак на противоположный, то получим уравнение, равносильное данному;
3) если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получим уравнение, равносильное данному.
Левая и правая части каждого из них являются рациональными выражениями.
Уравнении, левая и правая части которых являются рациональными выражениями, называют рациональными уравнениями.
В первых двух из записанных выше уравнений левая и правая части являются целыми выражениями. Такие уравнения называют целыми рациональными уравнениями. Если хотя бы одна часть уравнения — дробное выражение, то его называют дробным рациональным уравнением. Третье из записанных выше уравнений является дробным рациональным.
Как решать целые рациональные уравнения, мы рассмотрели при изучении математики в предыдущих классах. Рассмотрим теперь, как решать дробные рациональные уравнения, то есть уравнения с переменной в знаменателе.
Применение условия равенства дроби нулю
Напомним, что 
Пример №202
Решите уравнение
Решение:
С помощью тождественных преобразований и свойств уравнений приведем уравнение к виду 


Окончательно получим уравнение:
Чтобы дробь 


Тогда 




Решение последнего, равносильного данному, уравнения, учитывая условие равенства дроби нулю, удобно записывать так:
Значит, решая дробное рациональное уравнение, можно:
1) с помощью тождественных преобразований привести уравнение к виду
2) приравнять числитель 
3) исключить из его корней те, при которых знаменатель 
Использование основного свойства пропорции
Если 

Пример №203
Решите уравнение
Решение:
Найдем область допустимых значений (ОДЗ) переменной в уравнении. Так как знаменатели дробей не могут равняться нулю, то 


Сложив выражения в правой части уравнения, приведем его к виду: 
По основному свойству пропорции имеем:
Решим это уравнение:

Так как число 4 принадлежит ОДЗ переменной исходного уравнения, то 4 является его корнем.
Запись решения, чтобы не забыть учесть ОДЗ, удобно закончить так:
Таким образом, для решения дробного рационального уравнения можно:
1) найти область допустимых значений (ОДЗ) переменной в уравнении;
2) привести уравнение к виду
3) записать целое уравнение 
4) исключить из полученных корней те, которые не принадлежат ОДЗ, и записать ответ.
Метод умножения обеих частей уравнения на общий знаменатель дробей
Пример №204
Решите уравнение
Решение:
Найдем ОДЗ переменной и простейший общий знаменатель всех дробей уравнения, разложив знаменатели на множители:
Областью допустимых значений переменной будут те значения 



Умножим обе части уравнения на это выражение:
Получим: 



Число 0 не принадлежит ОДЗ переменной исходного уравнения, поэтому не является его корнем.
Следовательно, число 12 — единственный корень уравнения. Ответ. 12.
Решая дробное рациональное уравнение, можно:
3) умножить обе части уравнения на этот общий знаменатель;
4) решить полученное целое уравнение;
5) исключить из его корней те, которые не принадлежат ОДЗ переменной уравнения, и записать ответ.
Пример №205
Являются ли равносильными уравнения
Решение:
Поскольку уравнения являются равносильными в случае, когда они имеют одни и те же, или не имеют корней, найдем корни данных уравнений.
Первое уравнение имеет единственный корень 

Степень с целым показателем
Напомним, что в 7 классе мы изучали степень с натуральным показателем. По определению:
где 
В математике, а также при решении задач практического содержания, например в физике или химии, встречаются степени, показатель которых равен нулю или является целым отрицательным числом. Степень с отрицательным показателем можно встретить и в научной или справочной литературе. Например, массу атома гелия записывают так: 
Рассмотрим степени числа 3 с показателями 
В этой строке каждое следующее число втрое больше предыдущего. Продолжим строку в противоположном направлении, уменьшая каждый раз показатель степени на 1. Получим:
Число 




Нулевая степень отличного от нуля числа а равна единице, то есть 
Вернемся к строке со степенями числа 3, где слева от числа 




Приходим к следующему определению степени с целым отрицательным показателем:
если 
Дробно-рациональные уравнения
Что такое дробно-рациональные уравнения
Дробно-рациональными уравнениями называют такие выражения, которые представляется возможным записать, как:
при P ( x ) и Q ( x ) в виде выражений, содержащих переменную.
Таким образом, дробно-рациональные уравнения обязательно содержат как минимум одну дробь с переменной в знаменателе с любым модулем.
9 x 2 — 1 3 x = 0
1 2 x + x x + 1 = 1 2
6 x + 1 = x 2 — 5 x x + 1
Уравнения, которые не являются дробно-рациональными:
Как решаются дробно-рациональные уравнения
В процессе решения дробно-рациональных уравнений обязательным действием является определение области допустимых значений. Найденные корни следует проверить на допустимость, чтобы исключить посторонние решения.
Алгоритм действий при стандартном способе решения:
- Выписать и определить ОДЗ.
- Найти общий знаменатель для дробей.
- Умножить каждый из членов выражения на полученный общий параметр (знаменатель), сократить дроби, которые получились в результате, чтобы исключить знаменатели.
- Записать уравнение со скобками.
- Раскрыть скобки для приведения подобных слагаемых.
- Найти корни полученного уравнения.
- Выполним проверку корней в соответствии с ОДЗ.
- Записать ответ.
Пример 1
Разберем предложенный алгоритм на практическом примере. Предположим, что имеется дробно-рациональное уравнение, которое требуется решить:
x x — 2 — 7 x + 2 = 8 x 2 — 4
Начать следует с области допустимых значений:
x 2 — 4 ≠ 0 ⇔ x ≠ ± 2
Воспользуемся правилом сокращенного умножения:
x 2 — 4 = ( x — 2 ) ( x + 2 )
В результате общим знаменателем дробей является:
Выполним умножение каждого из членов выражения на общий знаменатель:
x x — 2 — 7 x + 2 = 8 x 2 — 4
x ( x — 2 ) ( x + 2 ) x — 2 — 7 ( x — 2 ) ( x + 2 ) x + 2 = 8 ( x — 2 ) ( x + 2 ) ( x — 2 ) ( x + 2 )
После сокращения избавимся от скобок и приведем подобные слагаемые:
x ( x + 2 ) — 7 ( x — 2 ) = 8
x 2 + 2 x — 7 x + 14 = 8
Осталось решить квадратное уравнение:
Согласно ОДЗ, первый корень является лишним, так как не удовлетворяет условию, по которому корень не равен 2. Тогда в ответе можно записать:
Примеры задач с ответами для 9 класса
Требуется решить дробно-рациональное уравнение:
x x + 2 + x + 1 x + 5 — 7 — x x 2 + 7 x + 10 = 0
x x + 2 + x + 1 x + 5 — 7 — x x 2 + 7 x + 10 = 0
Определим область допустимых значений:
О Д З : x + 2 ≠ 0 ⇔ x ≠ — 2
x 2 + 7 x + 10 ≠ 0
D = 49 — 4 · 10 = 9
x 1 ≠ — 7 + 3 2 = — 2
x 2 ≠ — 7 — 3 2 = — 5
Квадратный трехчлен x 2 + 7 x + 10 следует разложить на множители, руководствуясь формулой:
a x 2 + b x + c = a ( x — x 1 ) ( x — x 2 )
x x + 2 + x + 1 x + 5 — 7 — x ( x + 2 ) ( x + 5 ) = 0
Заметим, что общим знаменателем для дробей является: ( x + 2 ) ( x + 5 ) . Умножим на этот знаменатель уравнение:
x x + 2 + x + 1 x + 5 — 7 — x ( x + 2 ) ( x + 5 ) = 0
Сократим дроби, избавимся от скобок, приведем подобные слагаемые:
x ( x + 2 ) ( x + 5 ) x + 2 + ( x + 1 ) ( x + 2 ) ( x + 5 ) x + 5 —
— ( 7 — x ) ( x + 2 ) ( x + 5 ) ( x + 2 ) ( x + 5 ) = 0
x ( x + 5 ) + ( x + 1 ) ( x + 2 ) — 7 + x = 0
x 2 + 5 x + x 2 + 3 x + 2 — 7 + x = 0
2 x 2 + 9 x — 5 = 0
Потребуется решить квадратное уравнение:
2 x 2 + 9 x — 5 = 0
Первый корень не удовлетворяет условиям ОДЗ, поэтому в ответ нужно записать только второй корень.
Дано дробно-рациональное уравнение, корни которого требуется найти:
4 x — 2 — 3 x + 4 = 1
В первую очередь следует переместить все слагаемые влево и привести дроби к минимальному единому знаменателю:
4 ( x + 4 ) x — 2 — 3 ( x — 2 ) x + 4 — 1 ( x — 2 ) ( x + 4 ) = 0
4 ( x + 4 ) — 3 ( x — 2 ) — ( x — 2 ) ( x + 4 ) ( x — 2 ) ( x + 4 ) = 0
4 x + 16 — 3 x + 6 — ( x 2 + 4 x — 2 x — 8 ) ( x — 2 ) ( x + 4 ) = 0
x + 22 — x 2 — 4 x + 2 x + 8 ( x — 2 ) ( x + 4 ) = 0
Заметим, что получилось нулевое значение для дроби. Известно, что дробь может равняться нулю, если в числителе нуль, а знаменатель не равен нулю. На основании этого можно составить систему:
— x 2 — x + 30 ( x — 2 ) ( x + 4 ) = 0 ⇔ — x 2 — x + 30 = 0 ( x — 2 ) ( x + 4 ) ≠ 0
Следует определить такие значения для переменной, при которых в дроби знаменатель будет обращаться в нуль. Такие значения необходимо удалить из ОДЗ:
( x — 2 ) ( x + 4 ) ≠ 0
Далее можно определить значения для переменных, которые при подстановке в уравнение обращают числитель в нуль:
— x 2 — x + 30 = 0 _ _ _ · ( — 1 )
Получилось квадратное уравнение, которое можно решить:
Сравнив корни с условиями области допустимых значений, можно сделать вывод, что оба корня являются решениями данного уравнения.
Нужно решить дробно-рациональное уравнение:
x + 2 x 2 — 2 x — x x — 2 = 3 x
На первом шаге следует перенести все слагаемые в одну сторону и привести дроби к минимальному единому знаменателю:
x + 2 1 x ( x — 2 ) — x x x — 2 — 3 ( x — 2 ) x = 0
x + 2 — x 2 — 3 ( x — 2 ) x ( x — 2 ) = 0
x + 2 — x 2 — 3 x + 6 x ( x — 2 ) = 0
— x 2 — 2 x + 8 x ( x — 2 ) = 0 ⇔ — x 2 — 2 x + 8 = 0 x ( x — 2 ) ≠ 0
Перечисленные значения переменной обращают знаменатель в нуль. По этой причине их необходимо удалить из области допустимых значений.
— x 2 — 2 x + 8 = 0 _ _ _ · ( — 1 )
Корни квадратного уравнения:
x 1 = — 4 ; x 2 = 2
Заметим, что второй корень не соответствует ОДЗ. Таким образом, в ответе остается только первый корень.
Найти корни уравнения:
x 2 — x — 6 x — 3 = x + 2
Согласно стандартному алгоритму решения дробно-рациональных уравнений, выполним перенос всех слагаемых в одну сторону. Далее необходимо привести к дроби к наименьшему общему знаменателю:
x 2 — x — 6 1 x — 3 — x ( x — 3 ) — 2 ( x — 3 ) = 0
x 2 — x — 6 — x ( x — 3 ) — 2 ( x — 3 ) x — 3 = 0
x 2 — x — 6 — x 2 + 3 x — 2 x + 6 x — 3 = 0
0 x x — 3 = 0 ⇔ 0 x = 0 x — 3 ≠ 0
Такое значение переменной, при котором знаменатель становится равным нулю, нужно исключить из области допустимых значений:
Заметим, что это частный случай линейного уравнения, которое обладает бесконечным множеством корней. При подстановке какого-либо числа на место переменной х в любом случае числовое равенство будет справедливым. Единственным недопустимым значением для х в данном задании является число 3, которое не входит в ОДЗ.
Ответ: х — любое число, за исключением 3.
Требуется вычислить корни дробно-рационального уравнения:
5 x — 2 — 3 x + 2 = 20 x 2 — 4
На первом этапе необходимо выполнить перенос всех слагаемых влево, привести дроби к минимальному единому знаменателю:
5 ( x + 2 ) x — 2 — 3 ( x — 2 ) x + 2 — 20 1 ( x — 2 ) ( x + 2 ) = 0
5 ( x + 2 ) — 3 ( x — 2 ) — 20 ( x — 2 ) ( x + 2 ) = 0
5 x + 10 — 3 x + 6 — 20 ( x — 2 ) ( x + 2 ) = 0
2 x — 4 ( x — 2 ) ( x + 2 ) = 0 ⇔ 2 x — 4 = 0 ( x — 2 ) ( x + 2 ) ≠ 0
( x — 2 ) ( x + 2 ) ≠ 0
Данные значения переменной х являются недопустимыми, так как в этом случае теряется смысл дроби в связи с тем, что знаменатель принимает нулевое значение.
Заметим, что 2 не входит в область допустимых значений. В связи с этим, можно заключить, что у уравнения отсутствуют корни.
Ответ: корни отсутствуют
Нужно найти корни уравнения:
x — 3 x — 5 + 1 x = x + 5 x ( x — 5 )
Начнем с определения ОДЗ:
— 5 ≠ 0 x ≠ 0 x ( x — 5 ) ≠ 0 x ≠ 5 x ≠ 0
При умножении обеих частей уравнения на единый знаменатель всех дробей и сокращении аналогичных выражений, которые записаны в числителе и знаменателе, получим:
x — 3 x — 5 + 1 x = x + 5 x ( x — 5 ) · x ( x — 5 )
( x — 3 ) x ( x — 5 ) x — 5 + x ( x — 5 ) x = ( x + 5 ) x ( x — 5 ) x ( x — 5 )
( x — 3 ) x + x = x + 5
Прибегая к арифметическим преобразованиям, можно записать уравнение в упрощенной форме:
x 2 — 3 x + x — 5 = x + 5 → x 2 — 2 x — 5 — x — 5 = 0 → x 2 — 3 x — 10 = 0
Для дальнейших действий следует определить, к какому виду относится полученное уравнение. В нашем случае уравнение является квадратным с коэффициентом при x 2 , который равен 1. Таким образом, целесообразно воспользоваться теоремой Виета:
x 1 · x 2 = — 10 x 1 + x 2 = 3
В этом случае подходящими являются числа: -2 и 5.
Второе значение не соответствует области допустимых значений.
Решение целых и дробно рациональных уравнений
Давайте познакомимся с рациональными и дробными рациональными уравнениями, дадим их определение, приведем примеры, а также разберем наиболее распространенные типы задач.
Рациональное уравнение: определение и примеры
Знакомство с рациональными выражениями начинается в 8 классе школы. В это время на уроках алгебры учащиеся все чаще начинают встречать задания с уравнениями, которые содержат рациональные выражения в своих записях. Давайте освежим в памяти, что это такое.
Рациональное уравнение – это такое уравнение, в обеих частях которого содержатся рациональные выражения.
В различных пособиях можно встретить еще одну формулировку.
Рациональное уравнение – это такое уравнение, запись левой части которого содержит рациональное выражение, а правая – нуль.
Определения, которые мы привели для рациональных уравнений, являются равнозначными, так как говорят об одно и том же. Подтверждает правильность наших слов тот факт, что для любых рациональных выражений P и Q уравнения P = Q и P − Q = 0 будут равносильными выражениями.
А теперь обратимся к примерам.
x = 1 , 2 · x − 12 · x 2 · y · z 3 = 0 , x x 2 + 3 · x — 1 = 2 + 2 7 · x — a · ( x + 2 ) , 1 2 + 3 4 — 12 x — 1 = 3 .
Рациональные уравнения точно также, как и уравнения других видов, могут содержать любое количество переменных от 1 до нескольких. Для начала мы рассмотрим простые примеры, в которых уравнения будут содержать только одну переменную. А затем начнем постепенно усложнять задачу.
Рациональные уравнения делятся на две большие группы: целые и дробные. Посмотрим, какие уравнения будут относиться к каждой из групп.
Рациональное уравнение будет являться целым в том случае, если в записи левой и правой его частей содержатся целые рациональные выражения.
Рациональное уравнение будет являться дробным в том случае, если одна или обе его части содержат дробь.
Дробно рациональные уравнения в обязательном порядке содержат деление на переменную или же переменная имеется в знаменателе. В записи целых уравнений такого деления нет.
3 · x + 2 = 0 и ( x + y ) · ( 3 · x 2 − 1 ) + x = − y + 0 , 5 – целые рациональные уравнения. Здесь обе части уравнения представлены целыми выражениями.
1 x — 1 = x 3 и x : ( 5 · x 3 + y 2 ) = 3 : ( x − 1 ) : 5 – это дробно рациональные уравнения.
К числу целых рациональных уравнений можно отнести линейные и квадратные уравнения.
Решение целых уравнений
Решение таких уравнений обычно сводится к преобразованию их в равносильные алгебраические уравнения. Достичь этого можно путем проведения равносильных преобразований уравнений в соответствии со следующим алгоритмом:
- сначала получим ноль в правой части уравнения, для этого на необходимо перенести выражение, которое находится в правой части уравнения, в его левую часть и поменять знак;
- затем преобразуем выражение в левой части уравнения в многочлен стандартного вида.
Мы должны получить алгебраическое уравнение. Это уравнение будет равносильным по отношению к исходному уравнению. Легкие случаи позволяют нам для решения задачи свести целое уравнение с линейному или квадратному. В общем случае мы решаем алгебраическое уравнение степени n .
Необходимо найти корни целого уравнения 3 · ( x + 1 ) · ( x − 3 ) = x · ( 2 · x − 1 ) − 3 .
Решение
Проведем преобразование исходного выражения с целью получить равносильное ему алгебраическое уравнение. Для этого произведем перенос выражения, содержащегося в правой части уравнения, в левую часть и заменим знак на противоположный. В итоге получим: 3 · ( x + 1 ) · ( x − 3 ) − x · ( 2 · x − 1 ) + 3 = 0 .
Теперь проведем преобразование выражения, которое находится в левой части в многочлен стандартного вида и произведем необходимые действия с этим многочленом:
3 · ( x + 1 ) · ( x − 3 ) − x · ( 2 · x − 1 ) + 3 = ( 3 · x + 3 ) · ( x − 3 ) − 2 · x 2 + x + 3 = = 3 · x 2 − 9 · x + 3 · x − 9 − 2 · x 2 + x + 3 = x 2 − 5 · x − 6
У нас получилось свести решение исходного уравнения к решению квадратного уравнения вида x 2 − 5 · x − 6 = 0 . Дискриминант этого уравнения положительный: D = ( − 5 ) 2 − 4 · 1 · ( − 6 ) = 25 + 24 = 49 . Это значит, действительных корней будет два. Найдем их, воспользовавшись формулой корней квадратного уравнения:
x = — — 5 ± 49 2 · 1 ,
x 1 = 5 + 7 2 или x 2 = 5 — 7 2 ,
x 1 = 6 или x 2 = — 1
Проверим верность корней уравнения, которые мы нашли в ходе решения. Для этого числа, которые мы получили, подставим в исходное уравнение: 3 · ( 6 + 1 ) · ( 6 − 3 ) = 6 · ( 2 · 6 − 1 ) − 3 и 3 · ( − 1 + 1 ) · ( − 1 − 3 ) = ( − 1 ) · ( 2 · ( − 1 ) − 1 ) − 3 . В первом случае 63 = 63 , во втором 0 = 0 . Корни x = 6 и x = − 1 действительно являются корнями уравнения, данного в условии примера.
Ответ: 6 , − 1 .
Давайте разберем, что значит «степень целого уравнения». С этим термином мы будем часто встречаться в тех случаях, когда нам надо будет представить целое уравнение в виде алгебраического. Дадим определение понятию.
Степень целого уравнения – это степень алгебраического уравнения, равносильного исходному целому уравнению.
Если посмотреть на уравнения из примера, приведенного выше, можно установить: степень данного целого уравнения вторая.
Если бы наш курс ограничивался решением уравнений второй степени, то рассмотрение темы на этом можно было бы закончить. Но все не так просто. Решение уравнений третьей степени сопряжено с трудностями. А для уравнений выше четвертой степени и вовсе не существует общих формул корней. В связи с этим решение целых уравнений третьей, четвертой и других степеней требует от нас применения целого ряда других приемов и методов.
Чаще прочих используется подход к решению целых рациональных уравнений, который основан на методе разложения на множители. Алгоритм действий в этом случае следующий:
- переносим выражение из правой части в левую с тем, чтобы в правой части записи остался нуль;
- представляем выражение в левой части как произведение множителей, а затем переходим к совокупности нескольких более простых уравнений.
Пример 4
Найдите решение уравнения ( x 2 − 1 ) · ( x 2 − 10 · x + 13 ) = 2 · x · ( x 2 − 10 · x + 13 ) .
Решение
Переносим выражение из правой части записи в левую с противоположным знаком: ( x 2 − 1 ) · ( x 2 − 10 · x + 13 ) − 2 · x · ( x 2 − 10 · x + 13 ) = 0 . Преобразование левой части в многочлен стандартного вида нецелесообразно в связи с тем, что это даст нам алгебраическое уравнение четвертой степени: x 4 − 12 · x 3 + 32 · x 2 − 16 · x − 13 = 0 . Легкость преобразования не оправдывает всех сложностей с решением такого уравнения.
Намного проще пойти другим путем: вынесем за скобки общий множитель x 2 − 10 · x + 13 . Так мы придем к уравнению вида ( x 2 − 10 · x + 13 ) · ( x 2 − 2 · x − 1 ) = 0 . Теперь заменим полученное уравнение совокупностью двух квадратных уравнений x 2 − 10 · x + 13 = 0 и x 2 − 2 · x − 1 = 0 и найдем их корни через дискриминант: 5 + 2 · 3 , 5 — 2 · 3 , 1 + 2 , 1 — 2 .
Ответ: 5 + 2 · 3 , 5 — 2 · 3 , 1 + 2 , 1 — 2 .
Точно также мы можем использовать метод введения новой переменной. Этот метод позволяет нам переходить к равносильным уравнениям со степенями ниже, чем были степени в исходном целом уравнении.
Есть ли корни у уравнения ( x 2 + 3 · x + 1 ) 2 + 10 = − 2 · ( x 2 + 3 · x − 4 ) ?
Решение
Если мы сейчас попробуем свести целое рациональное уравнение к алгебраическому, то получим уравнение 4 степени, которое не имеет рациональных корней. Потому нам будет проще пойти другим путем: ввести новую переменную у, которая заменит в уравнении выражение x 2 + 3 · x .
Теперь мы будем работать с целым уравнением ( y + 1 ) 2 + 10 = − 2 · ( y − 4 ) . Перенесем правую часть уравнения в левую с противоположным знаком и проведем необходимые преобразования. Получим: y 2 + 4 · y + 3 = 0 . Найдем корни квадратного уравнения: y = − 1 и y = − 3 .
Теперь проведем обратную замену. Получим два уравнения x 2 + 3 · x = − 1 и x 2 + 3 · x = − 3 . Перепишем их как x 2 + 3 · x + 1 = 0 и x 2 + 3 · x + 3 = 0 . Используем формулу корней квадратного уравнения для того, чтобы найти корни первого уравнения из полученных: — 3 ± 5 2 . Дискриминант второго уравнения отрицательный. Это значит, что действительных корней у второго уравнения нет.
Ответ: — 3 ± 5 2
Целые уравнения высоких степеней попадаются в задачах достаточно часто. Пугаться их не нужно. Нужно быть готовым применить нестандартный метод их решения, в том числе и ряд искусственных преобразований.
Решение дробно рациональных уравнений
Начнем рассмотрение этой подтемы мы с алгоритма решения дробно рациональных уравнений вида p ( x ) q ( x ) = 0 , где p ( x ) и q ( x ) – целые рациональные выражения. Решение остальных дробно рациональных уравнений всегда можно свести к решению уравнений указанного вида.
В основу наиболее употребимого метода решения уравнений p ( x ) q ( x ) = 0 положено следующее утверждение: числовая дробь u v , где v – это число, которое отлично от нуля, равна нулю только в тех случаях, когда числитель дроби равен нулю. Следуя логике приведенного утверждения мы можем утверждать, что решение уравнения p ( x ) q ( x ) = 0 может быть сведено в выполнению двух условий: p ( x ) = 0 и q ( x ) ≠ 0 . На этом построен алгоритм решения дробных рациональных уравнений вида p ( x ) q ( x ) = 0 :
- находим решение целого рационального уравнения p ( x ) = 0 ;
- проверяем, выполняется ли для корней, найденных в ходе решения, условие q ( x ) ≠ 0 .
Если это условие выполняется, то найденный корень является корнем исходного уравнения. Если нет, то корень не является решением задачи.
Найдем корни уравнения 3 · x — 2 5 · x 2 — 2 = 0 .
Решение
Мы имеем дело с дробным рациональным уравнением вида p ( x ) q ( x ) = 0 , в котором p ( x ) = 3 · x − 2 , q ( x ) = 5 · x 2 − 2 = 0 . Приступим к решению линейного уравнения 3 · x − 2 = 0 . Корнем этого уравнения будет x = 2 3 .
Проведем проверку найденного корня, удовлетворяет ли он условию 5 · x 2 − 2 ≠ 0 . Для этого подставим числовое значение в выражение. Получим: 5 · 2 3 2 — 2 = 5 · 4 9 — 2 = 20 9 — 2 = 2 9 ≠ 0 .
Условие выполняется. Это значит, что x = 2 3 является корнем исходного уравнения.
Ответ: 2 3 .
Есть еще один вариант решения дробных рациональных уравнений p ( x ) q ( x ) = 0 . Вспомним, что это уравнение равносильно целому уравнению p ( x ) = 0 на области допустимых значений переменной x исходного уравнения. Это позволяет нам использовать следующий алгоритм в решении уравнений p ( x ) q ( x ) = 0 :
- решаем уравнение p ( x ) = 0 ;
- находим область допустимых значений переменной x ;
- берем корни, которые лежат в области допустимых значений переменной x , в качестве искомых корней исходного дробного рационального уравнения.
Пример 7
Решите уравнение x 2 — 2 · x — 11 x 2 + 3 · x = 0 .
Решение
Для начала решим квадратное уравнение x 2 − 2 · x − 11 = 0 . Для вычисления его корней мы используем формулу корней для четного второго коэффициента. Получаем D 1 = ( − 1 ) 2 − 1 · ( − 11 ) = 12 , и x = 1 ± 2 3 .
Теперь мы можем найти ОДЗ переменной x для исходного уравнения. Это все числа, для которых x 2 + 3 · x ≠ 0 . Это то же самое, что x · ( x + 3 ) ≠ 0 , откуда x ≠ 0 , x ≠ − 3 .
Теперь проверим, входят ли полученные на первом этапе решения корни x = 1 ± 2 3 в область допустимых значений переменной x . Мы видим, что входят. Это значит, что исходное дробное рациональное уравнение имеет два корня x = 1 ± 2 3 .
Ответ: x = 1 ± 2 3
Второй описанный метод решения проще первого в случаях, когда легко находится область допустимых значений переменной x , а корни уравнения p ( x ) = 0 иррациональные. Например, 7 ± 4 · 26 9 . Корни могут быть и рациональными, но с большим числителем или знаменателем. Например, 127 1101 и − 31 59 . Это позволяет сэкономить время на проведении проверки условия q ( x ) ≠ 0 : намного проще исключить корни, которые не подходят, по ОДЗ.
В тех случаях, когда корни уравнения p ( x ) = 0 целые, целесообразнее использовать первый из описанных алгоритмов решения уравнений вида p ( x ) q ( x ) = 0 . Быстрее сразу находить корни целого уравнения p ( x ) = 0 , после чего проверять, выполняется ли для них условие q ( x ) ≠ 0 , а не находить ОДЗ, после чего решать уравнение p ( x ) = 0 на этой ОДЗ. Это связано с тем, что в таких случаях сделать проверку обычно проще, чем найти ОДЗ.
Найдите корни уравнения ( 2 · x — 1 ) · ( x — 6 ) · ( x 2 — 5 · x + 14 ) · ( x + 1 ) x 5 — 15 · x 4 + 57 · x 3 — 13 · x 2 + 26 · x + 112 = 0 .
Решение
Начнем с рассмотрения целого уравнения ( 2 · x − 1 ) · ( x − 6 ) · ( x 2 − 5 · x + 14 ) · ( x + 1 ) = 0 и нахождения его корней. Для этого применим метод решения уравнений через разложение на множители. Получается, что исходное уравнение равносильно совокупности четырех уравнений 2 · x − 1 = 0 , x − 6 = 0 , x 2 − 5 · x + 14 = 0 , x + 1 = 0 , из которых три линейных и одно квадратное. Находим корни: из первого уравнения x = 1 2 , из второго – x = 6 , из третьего – x = 7 , x = − 2 , из четвертого – x = − 1 .
Проведем проверку полученных корней. Определить ОДЗ в данном случае нам сложно, так как для этого придется провести решение алгебраического уравнения пятой степени. Проще будет проверить условие, по которому знаменатель дроби, которая находится в левой части уравнения, не должен обращаться в нуль.
По очереди подставим корни на место переменной х в выражение x 5 − 15 · x 4 + 57 · x 3 − 13 · x 2 + 26 · x + 112 и вычислим его значение:
1 2 5 − 15 · 1 2 4 + 57 · 1 2 3 − 13 · 1 2 2 + 26 · 1 2 + 112 = = 1 32 − 15 16 + 57 8 − 13 4 + 13 + 112 = 122 + 1 32 ≠ 0 ;
6 5 − 15 · 6 4 + 57 · 6 3 − 13 · 6 2 + 26 · 6 + 112 = 448 ≠ 0 ;
7 5 − 15 · 7 4 + 57 · 7 3 − 13 · 7 2 + 26 · 7 + 112 = 0 ;
( − 2 ) 5 − 15 · ( − 2 ) 4 + 57 · ( − 2 ) 3 − 13 · ( − 2 ) 2 + 26 · ( − 2 ) + 112 = − 720 ≠ 0 ;
( − 1 ) 5 − 15 · ( − 1 ) 4 + 57 · ( − 1 ) 3 − 13 · ( − 1 ) 2 + 26 · ( − 1 ) + 112 = 0 .
Проведенная проверка позволяет нам установить, что корнями исходного дробного рацинального уравнения являются 1 2 , 6 и − 2 .
Ответ: 1 2 , 6 , — 2
Найдите корни дробного рационального уравнения 5 · x 2 — 7 · x — 1 · x — 2 x 2 + 5 · x — 14 = 0 .
Решение
Начнем работу с уравнением ( 5 · x 2 − 7 · x − 1 ) · ( x − 2 ) = 0 . Найдем его корни. Нам проще представить это уравнение как совокупность квадратного и линейного уравнений 5 · x 2 − 7 · x − 1 = 0 и x − 2 = 0 .
Используем формулу корней квадратного уравнения для поиска корней. Получаем из первого уравнения два корня x = 7 ± 69 10 , а из второго x = 2 .
Подставлять значение корней в исходное уравнение для проверки условий нам будет достаточно сложно. Проще будет определить ОДЗ переменной x . В данном случае ОДЗ переменной x – это все числа, кроме тех, для которых выполняется условие x 2 + 5 · x − 14 = 0 . Получаем: x ∈ — ∞ , — 7 ∪ — 7 , 2 ∪ 2 , + ∞ .
Теперь проверим, принадлежат ли найденные нами корни к области допустимых значений переменной x .
Корни x = 7 ± 69 10 — принадлежат, поэтому, они являются корнями исходного уравнения, а x = 2 – не принадлежит, поэтому, это посторонний корень.
Ответ: x = 7 ± 69 10 .
Разберем отдельно случаи, когда в числителе дробного рационального уравнения вида p ( x ) q ( x ) = 0 находится число. В таких случаях, если в числителе находится число, отличное от нуля, то уравнение не будет иметь корней. Если это число будет равно нулю, то корнем уравнения будет любое число из ОДЗ.
Решите дробное рациональное уравнение — 3 , 2 x 3 + 27 = 0 .
Решение
Данное уравнение не будет иметь корней, так как в числителе дроби из левой части уравнения находится отличное от нуля число. Это значит, что ни при каких значениях x значение приведенной в условии задачи дроби не будет равняться нулю.
Ответ: нет корней.
Решите уравнение 0 x 4 + 5 · x 3 = 0 .
Решение
Так как в числителе дроби находится нуль, решением уравнения будет любое значение x из ОДЗ переменной x .
Теперь определим ОДЗ. Оно будет включать все значения x , при которых x 4 + 5 · x 3 ≠ 0 . Решениями уравнения x 4 + 5 · x 3 = 0 являются 0 и − 5 , так как, это уравнение равносильно уравнению x 3 · ( x + 5 ) = 0 , а оно в свою очередь равносильно совокупности двух уравнений x 3 = 0 и x + 5 = 0 , откуда и видны эти корни. Мы приходим к тому, что искомой областью допустимых значений являются любые x , кроме x = 0 и x = − 5 .
Получается, что дробное рациональное уравнение 0 x 4 + 5 · x 3 = 0 имеет бесконечное множество решений, которыми являются любые числа кроме нуля и — 5 .
Ответ: — ∞ , — 5 ∪ ( — 5 , 0 ∪ 0 , + ∞
Теперь поговорим о дробных рациональных уравнениях произвольного вида и методах их решения. Их можно записать как r ( x ) = s ( x ) , где r ( x ) и s ( x ) – рациональные выражения, причем хотя бы одно из них дробное. Решение таких уравнений сводится к решению уравнений вида p ( x ) q ( x ) = 0 .
Мы уже знаем, что мы можем получить равносильное уравнение при переносе выражения из правой части уравнения в левое с противоположным знаком. Это значит, что уравнение r ( x ) = s ( x ) равносильно уравнение r ( x ) − s ( x ) = 0 . Также мы уже разобрали способы преобразования рационального выражения в рациональную дробь. Благодаря этому мы без труда можем преобразовать уравнение r ( x ) − s ( x ) = 0 в тождественную ему рациональную дробь вида p ( x ) q ( x ) .
Так мы переходим от исходного дробного рационального уравнения r ( x ) = s ( x ) к уравнению вида p ( x ) q ( x ) = 0 , решать которые мы уже научились.
Следует учитывать, что при проведении переходов от r ( x ) − s ( x ) = 0 к p ( x ) q ( x ) = 0 , а затем к p ( x ) = 0 мы можем не учесть расширения области допустимых значений переменной x .
Вполне реальна ситуация, когда исходное уравнение r ( x ) = s ( x ) и уравнение p ( x ) = 0 в результате преобразований перестанут быть равносильными. Тогда решение уравнения p ( x ) = 0 может дать нам корни, которые будут посторонними для r ( x ) = s ( x ) . В связи с этим в каждом случае необходимо проводить проверку любым из описанных выше способов.
Чтобы облегчить вам работу по изучению темы, мы обобщили всю информацию в алгритм решения дробного рационального уравнения вида r ( x ) = s ( x ) :
- переносим выражение из правой части с противоположным знаком и получаем справа нуль;
- преобразуем исходное выражение в рациональную дробь p ( x ) q ( x ) , последовательно выполняя действия с дробями и многочленами;
- решаем уравнение p ( x ) = 0 ;
- выявляем посторонние корни путем проверки их принадлежности ОДЗ или методом подстановки в исходное уравнение.
Визуально цепочка действий будет выглядеть следующим образом:
r ( x ) = s ( x ) → r ( x ) — s ( x ) = 0 → p ( x ) q ( x ) = 0 → p ( x ) = 0 → о т с е и в а н и е п о с т о р о н н и х к о р н е й
Решите дробное рациональное уравнение x x + 1 = 1 x + 1 .
Решение
Перейдем к уравнению x x + 1 — 1 x + 1 = 0 . Преобразуем дробное рациональное выражение в левой части уравнения к виду p ( x ) q ( x ) .
Для этого нам придется привести рациональные дроби к общему знаменателю и упростить выражение:
x x + 1 — 1 x — 1 = x · x — 1 · ( x + 1 ) — 1 · x · ( x + 1 ) x · ( x + 1 ) = = x 2 — x — 1 — x 2 — x x · ( x + 1 ) = — 2 · x — 1 x · ( x + 1 )
Для того, чтобы найти корни уравнения — 2 · x — 1 x · ( x + 1 ) = 0 , нам необходимо решить уравнение − 2 · x − 1 = 0 . Получаем один корень x = — 1 2 .
Нам осталось выполнить проверку любым из методов. Рассмотрим их оба.
Подставим полученное значение в исходное уравнение. Получим — 1 2 — 1 2 + 1 = 1 — 1 2 + 1 . Мы пришли к верному числовому равенству − 1 = − 1 . Это значит, что x = − 1 2 является корнем исходного уравнения.
Теперь проведем проверку через ОДЗ. Определим область допустимых значений переменной x . Это будет все множество чисел, за исключением − 1 и 0 (при x = − 1 и x = 0 обращаются в нуль знаменатели дробей). Полученный нами корень x = − 1 2 принадлежит ОДЗ. Это значит, что он является корнем исходного уравнения.
Ответ: − 1 2 .
Найдите корни уравнения x 1 x + 3 — 1 x = — 2 3 · x .
Решение
Мы имеем дело с дробным рациональным уравнением. Следовательно, будем действовать по алгоритму.
Перенесем выражение из правой части в левую с противоположным знаком: x 1 x + 3 — 1 x + 2 3 · x = 0
Проведем необходимые преобразования: x 1 x + 3 — 1 x + 2 3 · x = x 3 + 2 · x 3 = 3 · x 3 = x .
Приходим к уравнению x = 0 . Корень этого уравнения – нуль.
Проверим, не является ли этот корень посторонним для исходного уравнения. Подставим значение в исходное уравнение: 0 1 0 + 3 — 1 0 = — 2 3 · 0 . Как видите, полученное уравнение не имеет смысла. Это значит, что 0 – это посторонний корень, а исходное дробное рациональное уравнение корней не имеет.
Ответ: нет корней.
Если мы не включили в алгоритм другие равносильные преобразования, то это вовсе не значит, что ими нельзя пользоваться. Алгоритм универсален, но он создан для того, чтобы помогать, а не ограничивать.
Решите уравнение 7 + 1 3 + 1 2 + 1 5 — x 2 = 7 7 24
Решение
Проще всего будет решить приведенное дробное рациональное уравнение согласно алгоритму. Но есть и другой путь. Рассмотрим его.
Отнимем от правой и левой частей 7 , получаем: 1 3 + 1 2 + 1 5 — x 2 = 7 24 .
Отсюда можно заключить, что выражение в знаменателе левой части должно быть равно числу, обратному числу из правой части, то есть, 3 + 1 2 + 1 5 — x 2 = 24 7 .
Вычтем из обеих частей 3 : 1 2 + 1 5 — x 2 = 3 7 . По аналогии 2 + 1 5 — x 2 = 7 3 , откуда 1 5 — x 2 = 1 3 , и дальше 5 — x 2 = 3 , x 2 = 2 , x = ± 2
Проведем проверку для того, чтобы установить, являются ли найденные корни корнями исходного уравнения.
http://wika.tutoronline.ru/algebra/class/9/drobnoraczionalnye-uravneniya
http://zaochnik.com/spravochnik/matematika/systems/reshenie-tselyh-i-drobno-ratsionalnyh-uravnenij/
Содержание:
Рациональные уравнения. Равносильные уравнения
Напомним что:
два уравнения называют равносильными, если они имеют одни и те же корни. Равносильными считают и те уравнения, которые корней не имеют.
Так, например, равносильными будут уравнения
Уравнения 
Ранее, в 7 классе, вы знакомились со свойствами, которые преобразуют уравнения в равносильные им уравнения.
1) Если в любой части уравнения раскрыть скобки или привести подобные слагаемые, то получим уравнение, равносильное данному;
2) если в уравнении перенести слагаемое из одной части в другую, изменив его знак на противоположный, то получим уравнение, равносильное данному;
3) если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получим уравнение, равносильное данному.
Рассмотрим уравнения:
Левая и правая части каждого из них являются рациональными выражениями.
Уравнении, левая и правая части которых являются рациональными выражениями, называют рациональными уравнениями.
В первых двух из записанных выше уравнений левая и правая части являются целыми выражениями. Такие уравнения называют целыми рациональными уравнениями. Если хотя бы одна часть уравнения — дробное выражение, то его называют дробным рациональным уравнением. Третье из записанных выше уравнений является дробным рациональным.
Как решать целые рациональные уравнения, мы рассмотрели при изучении математики в предыдущих классах. Рассмотрим теперь, как решать дробные рациональные уравнения, то есть уравнения с переменной в знаменателе.
Применение условия равенства дроби нулю
Напомним, что 
Пример №202
Решите уравнение
Решение:
С помощью тождественных преобразований и свойств уравнений приведем уравнение к виду 


Окончательно получим уравнение:
Чтобы дробь 


Тогда 




Решение последнего, равносильного данному, уравнения, учитывая условие равенства дроби нулю, удобно записывать так:
Ответ. 3.
Значит, решая дробное рациональное уравнение, можно:
1) с помощью тождественных преобразований привести уравнение к виду
2) приравнять числитель 
3) исключить из его корней те, при которых знаменатель 
Использование основного свойства пропорции
Если 

Пример №203
Решите уравнение
х — 1 х — 2
Решение:
Найдем область допустимых значений (ОДЗ) переменной в уравнении. Так как знаменатели дробей не могут равняться нулю, то 


Сложив выражения в правой части уравнения, приведем его к виду: 
По основному свойству пропорции имеем:
Решим это уравнение:

Так как число 4 принадлежит ОДЗ переменной исходного уравнения, то 4 является его корнем.
Запись решения, чтобы не забыть учесть ОДЗ, удобно закончить так:
Ответ. 4.
Таким образом, для решения дробного рационального уравнения можно:
1) найти область допустимых значений (ОДЗ) переменной в уравнении;
2) привести уравнение к виду
3) записать целое уравнение 
4) исключить из полученных корней те, которые не принадлежат ОДЗ, и записать ответ.
Метод умножения обеих частей уравнения на общий знаменатель дробей
Пример №204
Решите уравнение
Решение:
Найдем ОДЗ переменной и простейший общий знаменатель всех дробей уравнения, разложив знаменатели на множители:
Областью допустимых значений переменной будут те значения 



Умножим обе части уравнения на это выражение:
Получим: 



Число 0 не принадлежит ОДЗ переменной исходного уравнения, поэтому не является его корнем.
Следовательно, число 12 — единственный корень уравнения. Ответ. 12.
Решая дробное рациональное уравнение, можно:
1) найти ОДЗ переменной в уравнении; & 2) найти простейший общий знаменатель дробей, входящий в уравнение;
3) умножить обе части уравнения на этот общий знаменатель;
4) решить полученное целое уравнение;
5) исключить из его корней те, которые не принадлежат ОДЗ переменной уравнения, и записать ответ.
Пример №205
Являются ли равносильными уравнения
Решение:
Поскольку уравнения являются равносильными в случае, когда они имеют одни и те же, или не имеют корней, найдем корни данных уравнений.
Первое уравнение имеет единственный корень 

Ответ. Нет.
Степень с целым показателем
Напомним, что в 7 классе мы изучали степень с натуральным показателем. По определению:
где 
В математике, а также при решении задач практического содержания, например в физике или химии, встречаются степени, показатель которых равен нулю или является целым отрицательным числом. Степень с отрицательным показателем можно встретить и в научной или справочной литературе. Например, массу атома гелия записывают так: 
Рассмотрим степени числа 3 с показателями 
В этой строке каждое следующее число втрое больше предыдущего. Продолжим строку в противоположном направлении, уменьшая каждый раз показатель степени на 1. Получим:
Число 




Нулевая степень отличного от нуля числа а равна единице, то есть 
Вернемся к строке со степенями числа 3, где слева от числа 




Приходим к следующему определению степени с целым отрицательным показателем:
если 
Пример №206
Замените степень дробью:
Решение:
По определению:
Пример №207
Замените дробь степенью с целым отрицательным показателем:
Решение:
Пример №208
Вычислите:
Решение:
Рассмотрим, как возвести дробь 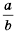
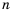
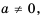
Следовательно,
Если 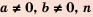
Пример №209
Найдите значение выражения:
Решение:
2) Учитывая порядок выполнения арифметических действий, сначала возведем дробь в степень, а затем выполним умножение:
Ответ.
Свойства степени с целым показателем
Свойства степени с натуральным показателем справедливы и для степени с ненулевым основанием и целым показателем. Следовательно,
Для любого 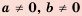
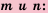
Эти свойства можно доказать на основании формулы 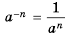
Докажем, например, формулу 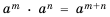
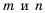
Пусть 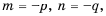
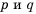
Следовательно, 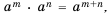
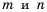
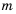
Пример №210
Выполните действие:
Решение:
Пример №211
Упростите выражение
Решение:
Пример №212
Вычислите
Решение:
Представим 9 и 27 в виде степени с основанием 3 и воспользуемся свойствами степени:
Ответ. 3.
Стандартный вид числа
В физике, химии, технике, астрономии часто имеют дело как с очень большими, так и с очень малыми значениями величин. Например, масса Земли равна 5 976 ООО ООО ООО ООО ООО ООО ООО кг, а диаметр молекулы водорода 0,00000000025 м.
Читать или записывать такие числа в виде десятичных дробей неудобно, неудобно и использовать десятичную их запись при вычислениях. В таких случаях имеет смысл записывать число в виде 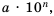
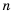
Например,
Говорят, что числа 5 976 000 000 000 000 000 000 000 и 0,00000000025 записаны в стандартном виде.
Стандартным видом числа называют его запись в виде произведении 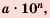
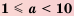
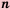
Если число записано в стандартном виде, то показатель степени 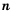
В стандартном виде можно записать любое положительное число. Порядок числа дает представление об этом числе.
Если порядок числа 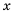
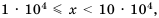
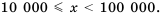
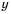
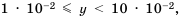
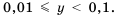
Следовательно, если говорят, что одно число на порядок больше второго, это означает, что оно в 10 раз больше второго, если на два порядка — в 100 раз больше и т. д.
Пример №213
Представьте число 272 000 в стандартном виде.
Решение:
В данном числе поставим занятую так, чтобы в целой части была одна цифра, отличная от нуля. В итоге будем иметь 2,72. Занятой отделили 5 цифр с конца числа, чем уменьшили данное число в 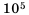
Ответ.
Пример №214
Представьте число 0,00013 в стандартном виде.
Решение:
В данном числе перенесем запятую на 4 знака вправо, будем иметь 1,3. При этом число увеличили в 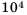
Ответ.
Пример №215
Выполните действия и представьте результат в стандартном виде:
Решение:
Ответ.
Пример №216
Найдите сумму 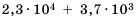
Решение:
Имеем два слагаемых разных порядков.
Ответ.
Функция Y=K/X ее график и свойства
Функция 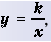
Пример №217
Пешеход должен преодолеть путь в 16 км. Если он будет двигаться со скоростью 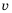
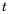
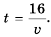
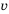
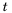
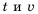
Пример №218
Площадь прямоугольника равна 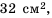
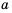
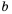
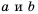
В примерах 1 и 2 переменные 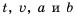
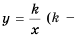
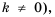
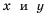
Функцию вида 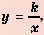
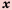
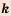
Область определения функции 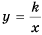
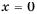

Построим график функции 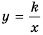
Пример №219
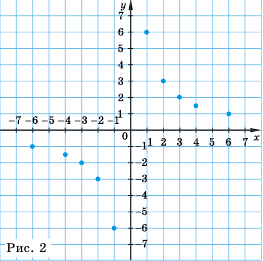
Постройте график функции
Решение:
Составим таблицу значений функции 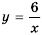
Отметим на координатной плоскости точки из составленной таблицы (рис. 2).
Если бы мы на этой плоскости обозначили больше точек, удовлетворяющих формуле 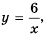
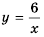
График обратной пропорциональности называют гиперболой.
Гипербола состоит из двух ветвей. Для функции 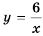
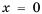
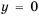
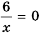
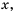
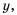
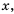
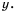
Так же выглядит график функции 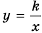
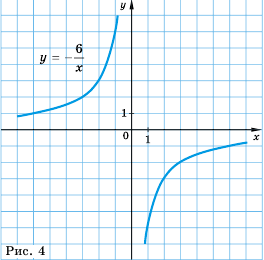
Пример №220
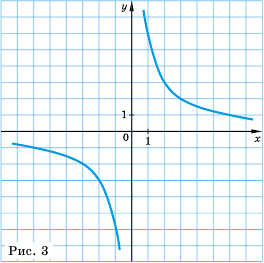
Постройте график функции
Решение:
Рассуждая как и в предыдущем примере, построим график функции 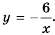
Это также гипербола, одна из ветвей которой лежит во второй координатной четверти, а другая — в четвертой.
Так же выглядит график функции 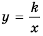
Обобщим свойства обратной пропорциональности
1. Область определения функции состоит из всех чисел за исключением нуля.
2. Область значений функции состоит из всех чисел за исключением нуля.
3. График функции — гипербола, ветви которой при 

4. Ветви гиперболы неограниченно приближаются к осям координат.
Пример №221
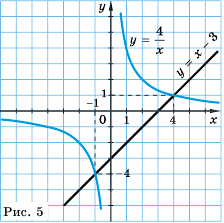
Постройте в одной системе координат графики функций 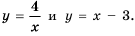
Решение:
График функции 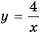
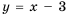
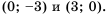
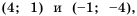
Действительно, при 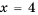
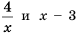
равные значения: 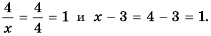
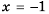
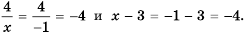
Ответ: 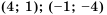
Предложенный в примере 5 метод решения уравнений называют графическим методом решения уравнений.
Если абсцисса точки пересечения графиков функций — целое число, надо выполнить проверку, т. к. часто корни уравнения этим методом можно найти только приблизительно.
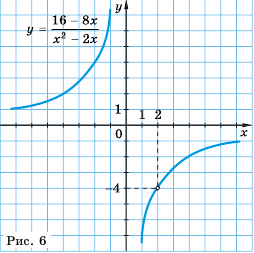
Пример №222
Постройте график функции
Решение:
Область определения функции — все числа за исключением чисел 0 и 2, которые обращают знаменатель 
Упростим дробь:
Значит при условии 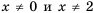
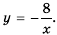
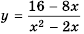
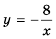
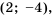
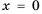
————
Если все решения одного уравнения также являются решениями второго, то второе уравнение называется следствием первого уравнения.
Если множества решений двух уравнений совпадают, то эти уравнения называются равносильными.
Пример 1.
Равносильны ли уравнения?
Решение:
1) Оба уравнения имеют общий корень: х=1. Так как они не имеют других корней, то они являются равносильными.
2) Первое уравнение имеет корень, равный 0. Второе же уравнение такого корня не имеет. Значит, данные уравнения не равносильны.
Пусть Р(х) и Q(x) — многочлены переменной х.
Выражение вида 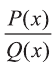
Пусть А(х) и В(х) — рациональные выражения. Уравнение вида А(х)=В(х) называется рациональным.
Рассмотрим сначала простейшее рациональное уравнение вида
Известно, что дробь 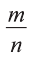
Для краткости, это мы будем записывать так:
- Заказать решение задач по высшей математике
Пример:
Решите уравнение:
Решение:
Уравнение 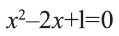
2) Квадратное уравнение 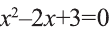
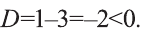
3) Для квадратного уравнения
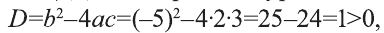
Однако число 1,5 обращает знаменатель выражения
в нуль, а число 1 — нет. Значит, данное уравнение имеет единственное решение х=1.
4) Уравнение 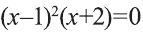
В случае, когда хотя бы одно из выражений А(х) и В(х) представимо в виде суммы нескольких рациональных выражений, рациональное уравнение А(х)=В(х) можно решить так:
- 1 шаг. Ищем общий знаменатель дробей, входящих в уравнение;
- 2 шаг. Обе части уравнения умножаем на этот общий знаменатель;
- 3 шаг. Ищем решения полученного уравнения;
- 4 шаг. Исключаем из множества найденных корней те, которые обращают общий знаменатель в нуль.
Пример:
Решите уравнение
Решение:
Умножаем обе части уравнения на общий знаменатель 2х(2-х). Упрощая полученное уравнение 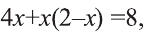
Так как D=9-8=l>0, то данное квадратное уравнение имеет два корня:
х=2; х=4.
Проверка.
При х=2 знаменатель обращается в нуль: х(2-х) = 2(2-2) = 0. Значит, х=2
не является решением исходного уравнения.
При х=4 знаменатель отличен от нуля х(2-х) = 4(2-4) Ф 0. Значит, х=4
является решением исходного уравнения.
Если 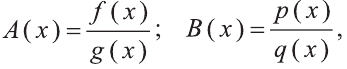
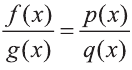
При этом получим следующий алгоритм решения:
- 1 шаг. Ищем решения уравнения f (х)q(х) = р(х)g(х)
- 2 шаг. Исключаем из множества найденных корней те, которые обращают общий знаменатель q(x)g(x) в нуль.
Пример:
Решите уравнение
Решение:
В некоторых случаях удачно выполненная замена позволяет привести заданное уравнение к более простому.
Пример:
Решите уравнение:
Решение:
1) Выполним замену 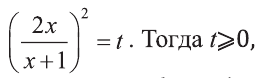
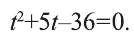
При 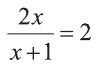
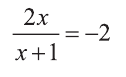
Ответ: х=-0,5.
2) Очевидно, что х=0 удовлетворяет уравнению. Пусть 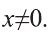
Тогда наше уравнение получит вид:
Решим последнее уравнение:
Теперь найдем x.
В силу того, что дискриминант квадратного уравнения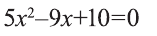
Системы рациональных уравнений
Решение систем, состоящих из рациональных уравнений, опирается на известные нам методы сложения, подстановки и т.д. При этом следует не забывать, что знаменатели, участвующих рациональных выражений, не могут обращаться в нуль.
Пример:
Решите систему:
Решение:
1) Сделаем в первом уравнении замену 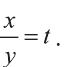
Отсюда или
Решим полученные системы:
Первая система имеет решения (3,2), (-3, -2), а вторая не имеет решений. Ответ: (3; 2), (-3; -2).
2). Обозначим
——
Рациональные уравнения
Рациональные уравнения широко применяются в приборостроении, космических исследованиях, финансовых операциях и т.д.
Подобие фигур широко применяется в измерительных, конструкторских и дизайнерских работах.
Это интересно!
На рисунке изображена модель орбитального космического корабля, предназначенная для полёта в космос туристов. Корабль рассчитан на 6 пассажиров и 2 членов экипажа.
Для того, чтобы рассчитать оптимальные размеры корабля конструкторам и инженерам пришлось решить много рациональных уравнений.
Рациональные уравнения
Уравнение, содержащее в левой и правой части рациональные выражения называется рациональным уравнением. Во многих задачах приходится решать рациональные уравнения, содержащие переменную в знаменателе. В этом случае необходимо указывать область допустимых значений переменных (ОДЗ).
Пример:
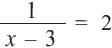
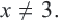
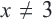
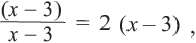
Подставим полученное значение в уравнение:
Таким образом, 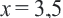
Пример:
Решим уравнение
ОДЗ данного уравнения 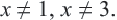
знаменатель
Пример:
В уравнении, 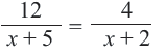
Используя свойство пропорции можно написать:
Пример:
Решим уравнение. 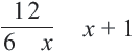
Умножим обе части уравнения на
Отсюда
Проверьте, являются ли оба этих числа корнями данного уравнения.
Пример:
Решим уравнение
Запишем уравнение в виде 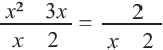
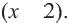
Отсюда
При проверке, убеждаемся что, 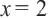
Внимание! После решения рационального уравнения, содержащего переменную в знаменателе, нужно обязательно выполнить проверку корней.
Решение задач с помощью рациональных уравнений
Задачи на работу
Задача. Двое рабочих могут выполнить некоторую работу за 12 дней. За сколько дней каждый рабочий выполнит эту работу в отдельности, если одному из них для выполнения этой работы потребуется на 10 дней больше ,чем другому? Решение: Пусть, 2-ой рабочий может выполнить работу за 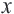
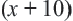
Первый рабочий за 1 день выполняет 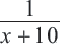
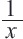
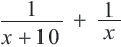
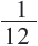
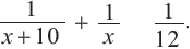
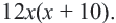
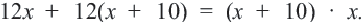


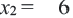

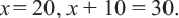
Задачи на движение
Задача. Путь длиной 480 км проходит по асфальтовой и по просёлочной дороге. Автомобиль расстояние 80 км по просёлочной дороге, прошёл со скоростью на 40 км/час меньше, чем по асфальтовой дороге. Зная, что на весь путь он затратил 7 часов, найдите время, которое потратил автомобиль при движении по просёлочной дороге.
1-й способ:
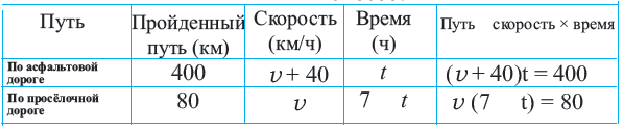
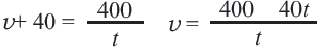
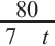
Разделим обе части уравнения на 40:
Получим 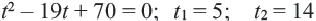
Ответ: по просёлочной дороге 2 часа
2-ой способ: Автомобиль ехал по дороге, покрытой асфальтом 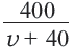
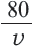
Зная, что на весь путь он потратил 7 часов, составим уравнение:
Решив данное уравнение, получим 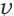
- Рациональные неравенства и их системы
- Геометрические задачи и методы их решения
- Прямые и плоскости в пространстве
- Интеграл и его применение
- Параллельность в пространстве
- Перпендикулярность в пространстве
- Векторы и координаты в пространстве
- Множества
Целые рациональные уравнения
Важно знать, что рациональные уравнения в свою очередь тоже разные бывают.
Если в дроби нет деления на переменную (то есть на ( displaystyle x), ( displaystyle y) и т.д.), тогда рациональное уравнение будет называться целым (или линейным) уравнением, вот примеры:
( displaystyle begin{array}{l}frac{2x}{3}=13-frac{3x}{2};\4(2y-3)=y-9.end{array})
Умеешь такие решать? – конечно, умеешь, упрощаешь и находишь неизвестное, тема-то 5-ого или 6-ого класса.
Ну, рассмотрим первый из примеров на всякий случай и по порядочку. Все неизвестные переносим влево, все известные вправо:
( displaystyle frac{2x}{3}+frac{3x}{2}=13);
Какой наименьший общий знаменатель будет?
Правильно ( displaystyle 6)!
Чтоб к нему привести домножаем и числитель и знаменатель первого слагаемое на ( displaystyle 2), а второго на ( displaystyle 3), этого делать не запрещено, если и числитель и знаменатель дроби умножить на одно и то же значение, то дробь от этого не изменится, т.к. ее можно будет сократить на то же число.
А ( displaystyle 13) не трогаем, оно нам не мешает, имеем:
( displaystyle frac{4x}{6}+frac{9x}{6}=13)
( displaystyle frac{13x}{6}=13),
А теперь делим обе части на ( displaystyle 13):
( displaystyle begin{array}{l}frac{x}{6}=1\x=6end{array})
Тут все просто?
Поскольку уравнение целое, что мы уже определили, то и ограничений никаких нет, ( displaystyle 6), так ( displaystyle 6), ну можно для верности подставить этот ответ в исходное уравнение, получим ( displaystyle 0=0), значит все верно и ответ подходит (ты можешь пересчитать, а вообще должно сойтись).
Дробно-рациональные уравнения
А вот еще одно уравнение ( displaystyle frac{5}{x+1}+frac{4{x}-6}{(x+1)cdot (x+3)}=3).
Это уравнение целое? НЕТ!!! Тут есть деление на переменную ( displaystyle x), а это говорит о том, что уравнение не целое. Тогда какое же оно? Это дробно рациональное уравнение.
Дробно-рациональное уравнение – рациональное (без знака корня) уравнение, в котором левая или правая части являются дробными выражениями.
На первый взгляд особой разницы не видно, ну давай попробуем решать его как мы решали целое (линейное) уравнение.
Для начала найдем наименьший общий знаменатель, это будет ( displaystyle (x+1)cdot (x+3)).
Важный момент!
В предыдущем примере, где было целое уравнение мы не стали свободный член ( displaystyle 13) приводить к знаменателю, т.к. умножали все на числа без переменных, но тут-то наименьший общий знаменатель ( displaystyle (x+1)cdot (x+3)).
А это тебе не шутки, переменная в знаменателе!
Решая дробно-рациональное уравнение, обе его части умножаем на наименьший общий знаменатель!
Это надеюсь, ты запомнишь, но давай посмотрим что вышло:
( displaystyle frac{5(x+1)cdot (x+3)}{x+1}+frac{(4{x}-6)cdot (x+1)cdot (x+3)}{(x+1)cdot (x+3)}=3cdot (x+1)cdot (x+3)).
Что-то оно огромное получилось, надо все посокращать:
( displaystyle 5(x+3)+(4{x}-6)=3cdot (x+1)cdot (x+3)).
Раскроем скобки и приведем подобные члены:
( displaystyle begin{array}{l}9x+9=3{{x}^{2}}+12x+9\3{{x}^{2}}+3x=0.end{array})
Ну как, это уже попроще выглядит, чем в начале было?
Выносим за скобку общий множитель: ( displaystyle 3xcdot (x+1)=0)
У этого уравнения два решения, его левая сторона принимает нулевое значение при ( displaystyle x=0) и ( displaystyle x=-1).
Вроде бы все, ну ладно давайте напоследок подставим корни ( displaystyle x=0) и ( displaystyle x=-1) в исходное уравнение, чтобы проверить, нет ли ошибок. Сначала подставим ( displaystyle 0), получается ( displaystyle 3=3) –нет претензий?
С ним все нормально. А теперь ( displaystyle -1), и тут же видим в знаменателе первого члена ( displaystyle -1+1)!
Но ведь это же будет ноль!
На ноль делить нельзя, это все знают, в чем же дело???
Дело в ОДЗ — Области Допустимых Значений!
(если забыл что это, повтори тему «ОДЗ — область допустимых значений»!)
Всякий раз когда ты видишь уравнение, где есть переменные (( displaystyle x,y) и т.д.) в знаменателе, прежде всего, нужно найти ОДЗ, найти какие значения может принимать икс.
Хотя удобнее в ОДЗ написать, чему икс НЕ может быть равен, ведь таких значений не так много, как правило.
Просто запомни, что на ноль делить нельзя! И перед тем как решать наше уравнение нам следовало сделать так:
ОДЗ: ( displaystyle x+1ne 0) и ( displaystyle x+3ne 0) ( displaystyle Rightarrow xne -1) и ( displaystyle xne -3).
Если бы мы сразу так написали, то заранее бы знали, что эти ответы стоит исключить и так, из полученных нами ( displaystyle x=0) и ( displaystyle x=-1) мы смело исключаем ( displaystyle x=-1), т.к. он противоречит ОДЗ.
Значит, какой ответ будет у решенного уравнения?
В ответ стоит написать только один корень, ( displaystyle x=0).
Стоит заметить, что ОДЗ не всегда сказывается на ответе, возможны случаи, когда корни, которые мы получили, не попадают под ограничения ОДЗ.
Но писать ОДЗ в дробно рациональных уравнениях стоит всегда – так просто спокойнее, что ты ничего не упустил и да,
ВСЕГДА по окончании решения сверяй свои корни и область допустимых значений!
Рациональные выражения, уравнения и дробно-рациональные уравнения
Повторим еще раз то, что прошил в предыдущих разделах, больше используя язык математики.
Рациональное выражение – это алгебраическое выражение, составленное из чисел и переменной ( displaystyle x) с помощью операций сложения, вычитания, умножения, деления и возведения в степень с натуральным показателем.
Ну а рациональное уравнение – это равенство двух рациональных выражений.
Дробно-рациональные уравнения – рациональные (без знака корня) уравнения, в которых левая или правая части являются дробными выражениями.
Например:
( displaystyle frac{{{x}^{2}}-2{x}-3}{{x}-1}-frac{x+1}{{x}-3}={{x}^{2}}-1) (чаще всего мы встречаем именно дробно рациональные уравнения).
В общем случае при решении рациональных уравнений мы стремимся преобразовать его к виду: Произведение = «( displaystyle 0)» или Дробь = «( displaystyle 0)«, например:
( displaystyle frac{left( {x}-2 right)left( x+3 right)left( {{x}^{2}}+1 right)}{xcdot left( {x}-3 right)}=0).
Тогда мы сможем сказать, что любой из множителей числителя может быть равен нулю, но знаменатель при этом нулю не равен.
Для этого нам нужно сначала всё перенести в левую часть уравнения (не забываем при этом поменять знаки между слагаемыми: «( displaystyle +)» на «( displaystyle —)» и наоборот).
Затем мы обычно приводим все к общему знаменателю, и пишем систему:
( displaystyle left{ begin{array}{l}Числитель=0,\Знаменательne 0.end{array} right.)
Например:
( displaystyle begin{array}{l}frac{{x}-2}{{{x}^{2}}+2{x}-3}-frac{x+1}{{{x}^{2}}+5x+6}=frac{3}{x+3}Leftrightarrow \Leftrightarrow frac{{x}-2}{left( {x}-1 right)left( x+3 right)}-frac{x+1}{left( x+2 right)left( x+3 right)}-frac{3}{x+3}=0Leftrightarrow end{array})
( displaystyle Leftrightarrow frac{{{x}^{2}}-4-left( {{x}^{2}}-1 right)-3left( {{x}^{2}}+{x}-2 right)}{left( {x}-1 right)left( x+2 right)left( x+3 right)}=0Leftrightarrow frac{-3{{x}^{2}}-3x+3}{left( {x}-1 right)left( x+2 right)left( x+3 right)}=0Leftrightarrow )
( displaystyle Leftrightarrow left{ begin{array}{l}{{x}^{2}}+{x}-1=0\left( {x}-1 right)left( x+2 right)left( x+3 right)ne 0end{array} right.Leftrightarrow left{ begin{array}{l}left[ begin{array}{l}x=frac{-1+sqrt{5}}{2}\x=frac{-1-sqrt{5}}{2}end{array} right.\xne 1\xne -2\xne -3end{array} right.Leftrightarrow left[ begin{array}{l}x=frac{-1+sqrt{5}}{2}\x=frac{-1-sqrt{5}}{2}.end{array} right.)
Если знаменателя нет, или он является числом, – тем лучше, не придется решать неравенство.
Как бы то ни было, в ЕГЭ все рациональные выражения степени больше ( displaystyle 2) легко преобразуются в произведение более простых выражений при помощи либо перегруппировки, либо замены переменных (см. раздел «Разложение многочлена на множители»).
Евгений Николаевич Беляев
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Рациональные уравнения — это уравнения, содержащие в себе рациональные выражения.
Определение 1
Рациональными выражениями при этом являются выражения, которые возможно записать в виде обыкновенной дроби вида $frac{m}{n}$, при этом $m$ и $n$ — целые числа и $n$ не может быть равно нулю. К рациональным выражениям относятся не только выражения, содержащие дроби вида $frac{2}{3}$, но и выражения, содержащие только целые числа, так как любое целое число можно представить в виде неправильной дроби.
Теперь рассмотрим более подробно, что же такое рациональные уравнения.
Как мы уже упомянули выше, рациональные уравнения — это уравнения, содержащие в себе рациональные выражения и переменные.
Соответственно тому, на каком именно месте стоит переменная в рациональном уравнении, оно может быть либо дробным рациональным уравнением, либо целым рациональным уравнением.
Дробные уравнения могут содержать дробь с переменной только в какой-то одной части уравнения, тогда как целые уравнения не содержат дробных выражений с переменной.
Целые рациональные уравнения примеры: $5x+2= 12$; $3y=-7(-4y + 5)$; $7a-14=256$.
Дробно-рациональные уравнения примеры: $frac{3x-2}{x+3}+frac{1}{2}=frac{5}{x}$; $frac{7}{2y-3}=5$;
Стоит отметить, что дробно-рациональными уравнениями называются только уравнения, содержащие дробь в знаменателе, так как уравнения, содержащие дробные выражения без переменных, легко сводятся к линейным целым уравнениям.
Как решать рациональные уравнения?
В зависимости от того, имеете ли вы дело с целым рациональным уравнением или с дробным, применяются несколько разные алгоритмы для решения.
Алгоритм решения целых рациональных уравнений
- В начале необходимо определить наименьший общий знаменатель для всего равенства.
- Затем нужно определить множители, на которые нужно домножить каждый член равенства.
- Следующий этап — приведение к общему знаменателю всего равенства.
- Наконец, осуществление поиска корней полученного целого рационального равенства.
«Решение рациональных уравнений» 👇
Пример 1
Решите уравнение: $frac{5x+9}{2}=frac{x}{4}$
Сначала найдём общий множитель — в данном случае это число $4$.
Для того чтобы избавиться от знаменателя, домножим левую часть на $frac{2}{2}$, получаем:
$10x+18=x$ — полученное уравнение является линейным, его корень $x=-2$.
Как решать дробно-рациональные уравнения?
В случае с дробными рациональными уравнениями порядок решения похож на алгоритм для решения целых рациональных, то есть сохраняются пункты 1-4, но после нахождения предполагаемых корней в случае использования неравносильных преобразований корни требуется проверить, подставив в уравнение.
Пример 2
Решите дробно-рациональное уравнение: $frac{x-3}{x-5}+frac{1}{x}=frac{x+5}{x cdot (x-5)}$
Для того чтобы привести дробь к общему знаменателю, здесь это $x cdot (x-5)$, домножим каждую дробь на единицу, представленную в виде необходимого для приведения к общему знаменателю множителя:
$frac{(x-3) cdot x}{(x-5)cdot x}+frac{1 cdot (x-5)}{x cdot (x-5)}=frac{x+5}{x cdot (x-5)}$
Теперь, когда вся дробь имеет общий знаменатель, от него можно избавиться:
$(x-3) cdot x+(x-5)=x+5$
$x^2 — 3x+x-5 = x+5$
$x^2-3x-10=0$
Воспользуемся теоремой Виета для решения получившегося квадратного уравнения:
$begin{cases} x_1 + x_2 = 3 \ x_1 cdot x_2 = -10 \ end{cases}$
$begin{cases} x_1=5 \ x_2=-2 \ end{cases}$
Так как преобразование, использовавшееся для упрощения уравнения, не является равносильным, полученные корни необходимо проверить в исходном уравнении, для этого подставим их:
$x_2=-2$:
$frac{-2-3}{-2-5} +frac{1}{-2}=frac{-2+5}{(-2) cdot (-2-5)}$
$frac{5}{7}-frac{1}{2}=frac{3}{14}$
$frac{3}{14}=frac{3}{14}$ — следовательно, корень $x_2=-2$ — верный.
$x_1=5$:
$frac{5-3}{5-5} +frac{1}{5}=frac{5+5}{(-2) cdot (5-5)}$
Здесь сразу видно, что в знаменателе образуется нуль, следовательно, корень $x_1=5$ — посторонний.
Необходимо помнить, что в случае, если уравнение, содержащее в левой или правой части выражение вида $frac{m}{n}$ равно нулю, равен нулю может быть только числитель дроби. Это происходит из-за того, что, если где-то в знаменателе образуется нуль, проверяемый корень не является корнем уравнения, так как всё равенство теряет смысл в этом случае. Корни, приводящие знаменатель к нулю, называются посторонними.
В случае если дробно-рациональное уравнение имеет довольно сложную форму, для его дальнейшего упрощения и решения возможно использовать замену части уравнения на новую переменную, наверняка вы уже видели примеры таких дробно-рациональных уравнений:
Пример 3
Решите уравнение:
$frac{1}{x^2+3x-3}+frac{2}{x^2+3x+1}=frac{7}{5}$
Для упрощения решения введём переменную $t= x^2+3x$:
$frac{1}{t-3}+frac{2}{t+1}=frac{7}{5}$
Общий знаменатель здесь $5 cdot (t-3)(t+1)$, домножим на необходимые множители все части уравнения чтобы избавиться от него:
$frac{5(t+1)}{5(t-3)(t+1)}+frac{2 cdot 5(t-3)}{5(t+1)(t-3)}=frac{7(t+1)(t-3)}{5(t-3)(t+1)}$
$5(t+1)+10(t-3)=7(t+1)(t-3)$
$5t+5+10t-30=7(t^2-3t+t-3)$
$15t-25=7t^2-14t-21$
$7t^2-29+4=0$
Через дискриминант вычислим корни:
$t_1=4;t_2=frac{1}{7}$
Так как мы использовали неравносильные преобразования, необходимо проверить полученные корни в знаменателе, они должны удовлетворять условию $5(t-3)(t+1)≠0$. Оба корня соответствуют этому условию.
Теперь подставим полученные корни вместо $t$ и получим два уравнения:
$x^2+3x=4$ и $x^2+3x=frac{1}{7}$.
По теореме Виета корни первого уравнения $x_1=-4; x_2=1$, корни второго же вычислим через дискриминант и имеем $x_{1,2}=frac{-3±sqrt{frac{67}{7}}}{2}$.
Все корни уравнения составят: $x_1=-4; x_2=1, x_{3,4}=frac{-3±sqrt{frac{67}{7}}}{2}$.
Преобразования для упрощения формы уравнения
Как вы уже могли увидеть выше, для решения рациональных уравнений используют различные преобразования.
Различают преобразования уравнений двух видов: равносильные (тождественные) и неравносильные.
Преобразования называются равносильными, если они приводят к уравнению нового вида, корни которого такие же, как у первоначального.
Тождественные преобразования, которые можно использовать для изменения вида первоначального уравнения без каких-либо проверок в дальнейшем, следующие:
- Умножение или деление всего уравнения на какое-либо число, отличное от нуля;
- Перенос частей уравнения из левой части в правую и наоборот.
Неравносильными преобразованиями называются преобразования, в ходе которых могут появиться посторонние корни. К неравносильным преобразованиям относят:
- Возведение обеих частей уравнения в квадрат;
- Избавление от знаменателей, содержащих переменную;
Корни рациональных уравнений, решённых с помощью неравносильных преобразований, необходимо проверять подстановкой в исходное уравнение, так как при неравносильных преобразованиях могут появиться посторонние корни. Не всегда неравносильные преобразования приводят к появлению посторонних корней, но всё же необходимо это учитывать.
Решение рациональных уравнений со степенями больше двух
Наиболее часто используемыми методами для решения уравнений со степенями больше двух являются метод замены переменной, рассмотренный нами выше на примере дробно-рационального уравнения, а также метод разложения на множители.
Рассмотрим более подробно метод разложения на множители.
Пусть дано уравнение вида $P(x)= 0$, при этом $P(x)$ — многочлен, степень которого больше двух. Если данное уравнение возможно разложить на множители так, что оно принимает вид $P_1(x)P_2(x)P_3(x)..cdot P_n(x)=0$, то решением данного уравнения будет множество решений уравнений $P_1(x)=0, P_2(x)=0, P_3(x)=0…P_n(x)=0$.
Пример 4
Решите уравнение: $x^3+2x^2+3x+6=0$
Вынесем общие множители:
$x^2(x+2)+3(x+2)=0$
$(x+2)(x^2+3)=0$
После разложения на множители нужно решить уравнения $x+2=0$ и $x^2+3=0$. Корень первого $x=-2$, второе уравнение корней не имеет, поэтому $x=-2$ — в данном случае окончательный ответ.
Определение 2
Уравнения, в которых коэффициент при переменной со старшей степенью равен единице, называются приведёнными.
Для приведённых уравнений справедливо следующее:
Если такое уравнение с целыми коэффициентами при переменных имеет рациональный корень, то этот корень непременно является целым числом.
Благодаря такому свойству этих уравнений их можно решать перебором целых делителей свободного члена.
Для тех, кто не помнит: свободный член уравнения — это член уравнений, не содержащий при себе в качестве множителя переменную. При этом найдя один из корней такого уравнения, его можно использовать для дальнейшего разложения уравнения на множители.
Пример 5
Решите уравнение:
$x^3+4x^2-24=0$
Делителями свободного члена будут числа $±1, ±2, ±3, ±4, ±6, ±8, ±12$ и $±24$. При их проверке подходящим корнем оказался $x=2$. Это значит, что данный многочлен можно разложить с использованием этого корня:
$(x-2)(x^2+6+12)=0$.
Многочлен во второй паре скобок корней не имеет корней, значит, единственным корнем данного уравнения будет $x=2$.
Другим типом уравнений со степенью больше двух являются биквадратные уравнения вида $ax^4+bx^2+ c=0$. Такие уравнения решаются путём замены $x^2$ на $y$, применив её, получаем уравнение вида $ay^2+y+c=0$, а после этого полученное значение новой переменной используют для вычисления исходной переменной.
Также существует ещё один тип уравнений, называемый возвратным. Такие уравнения выглядят так: $ax^4+bx^3+cx^2+bx+a=0$. Такое название они имеют из-за повторения коэффициентов при старших степенях и младших.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Целые рациональные уравнения
Если в уравнении нет переменной (x) в знаменателе, то такое уравнение называется целым. Или, другими словами, нигде в уравнении нет деления на переменную.
Метод решения целых рациональных уравнений сильно зависит от того, какой степени перед вами уравнения.
Степень уравнения — это максимальная степень у переменной (x).
Например, уравнение (x^2+5x-1=0) будет второй степени, так как есть (x^2).
Пример уравнения первой степени: (5x-1=17);
Уравнение третьей степени: (5x^3-3x^2=0);
Уравнение четвертой степени: (7x^4-5x^2+x-5=0);
И т.д.
Основной алгоритм решения целых уравнений:
- Если есть скобки, раскрываем их;
- Перекидываем все слагаемые в левую часть так, чтобы в правой части остался только (0). Не забываем при этом менять знак этих слагаемых;
- Приводим подобные слагаемые;
- Если получилось уравнение первой степени (в уравнении есть только (x)), то решаем его так (линейные уравнения);
- Если получилось уравнение второй степени (в уравнении есть (x^2)), то оно решается вот так (квадратные уравнения).
- А вот если в преобразованном уравнении получились члены (x^3) или большей степени, то придется применять нестандартные методы решения. Например, замена переменной, группировка, схема Горнера и т.д.
Чаще всего уравнения после преобразований будут сводиться к уравнениям первой (линейные уравнения) и второй (квадратные уравнения) степени.
Разберем примеры целых рациональных уравнений:
Пример 1
$$-4(-7+6x)=-9x-5;$$
Первым делом раскрываем скобки:
$$28-24x=-9x-5;$$
Перекидываем все слагаемые из правой части в левую:
$$28-24x+9x+5=0;$$
Поменяем слагаемые местами, чтобы удобнее было приводить подобные слагаемые:
$$-24x+9x+5+28=0;$$
$$-15x+33=0;$$
Получили линейное уравнение. Чтобы его решить, перекидываем свободный член (тот, что без (x)) в правую часть:
$$-15x=-33;$$
И поделим уравнение слева и справа на (-15):
$$x=frac{-33}{-15};$$
$$x=frac{11}{5}=2,2;$$
Ответ: (x=2,2.)
Важно отметить, то, что уравнение линейное, стало видно сразу после раскрытия скобок: у нас же не было степени у (x)-ов. Поэтому разумно было сразу решать его как линейное: перенести все слагаемые с (x) в левую часть, а все числа в правую. Так бы получилось немного короче.
Пример 2
$$4*(x+1)^2-2(x+3)=(2x-5)^2;$$
Тут сразу и не скажешь, какой степени уравнение. На первый взгляд кажется, что квадратное, но давайте раскроем скобки, воспользовавшись формулами сокращенного умножения:
$$4*(x^2+2x+1)-2x-6=4x^2-20x+25;$$
$$4*x^2+8x+4-2x-6=4x^2-20x+25;$$
Перекинем все в левую часть, не забывая поменять знак:
$$4*x^2+8x+4-2x-6-4x^2+20x-25=0;$$
Поменяем местами слагаемые, чтобы было проще приводить подобные:
$$4x^2-4x^2+8x-2x+20x+4-6-25=0;$$
$$26x-27=0;$$
Как видите, все квадраты сократились, и уравнение превратилось в линейное:
$$26x=27;$$
$$x=frac{27}{26};$$
Ответ: (x=frac{27}{26}.)
Пример 3
$$frac{x}{6}+frac{x}{12}+x=-frac{35}{4};$$
Домножим уравнение слева и справа на (12). Почему именно на (12)? Потому что в уравнении есть дроби с знаменателями (6), (12) и (4), на все эти числа (12) можно разделить:
$$12*(frac{x}{6}+frac{x}{12}+x)=12*(-frac{35}{4});$$
$$12*frac{x}{6}+12*frac{x}{12}+12*x=12*(-frac{35}{4});$$
$$2x+x+12x=-3*35;$$
$$15x=-105;$$
$$x=frac{-105}{15}=-7;$$
Ответ: (x=-7.)
Подробнее про линейные уравнения можно почитать в отдельной статье.
Пример 4
$$(x-1)^2=2x^2-6x-31;$$
Раскроем скобки:
$$x^2-2x+1=2x^2-6x-31;$$
$$x^2-2x+1-2x^2+6x+31=0;$$
$$x^2-2x^2-2x+6x+1+31=0;$$
$$-x^2+4x+32=0;$$
После приведения подобных слагаемых в уравнении остался (x^2), а значит перед нами квадратное уравнение, которое можно решить через дискриминант:
$$a=-1; quad b=4; quad c=32;$$
$$D=b^2-4ac=4^2-4*(-1)*32=16+128=144=12^2;$$
$$x_1=frac{-b+sqrt{D}}{2a}=frac{-4+12}{2*(-1)}=frac{8}{-2}=-4;$$
$$x_1=frac{-b-sqrt{D}}{2a}=frac{-4-12}{2*(-1)}=frac{-16}{-2}=8;$$
Ответ: (x=-4; qquad x=8.)
Подробнее про квадратные уравнения можно почитать здесь.
Методы решения уравнений третьей степени и старше
Не существует универсального удобного метода решения уравнений третьей степени или выше, как, например, квадратные уравнения, которые легко решаются через дискриминант, даже думать не надо.
Есть несколько методов, которые полезно знать: замена переменной, метод группировки, деление многочлена на многочлен, схема Горнера и т.д. Метод замены переменной заслуживает отдельного урока, поэтому про него мы подробно поговорим здесь. Сейчас мы обсудим метод группировки.
Метод группировки
Метод группировки слагаемых можно использовать и для решения квадратных уравнений, и, вообще говоря, для уравнений любой степени. Но проблема этого метода в том, что далеко не всегда удается его применить, и приходится использовать другие методы. Однако, если на экзамене вам не повезло, и попалось уравнение, которое сводится к уравнению 3й степени или старше, то в большинстве случаев оно будет решаться именно группировкой. Поэтому знать этот метод нужно обязательно.
Разберем метод группировки на примере кубического уравнения:
Пример 5
$$2x^3+4x^2-8x-16=0;$$
Посмотрите внимательно на уравнение, в нем 4 слагаемых, сгруппируем их попарно: первое слагаемое со вторым, а третье с четвертым:
$$(2x^3+4x^2)+(-8x-16)=0;$$
И вынесем общий множитель (2x^2) из первой пары, и (-8) из второй:
$$2x^2(x+2)-8(x+2)=0;$$
Теперь вместо 4-х слагаемых у нас всего два, но и у них есть общий множитель ((x+2)), который можно вынести за скобки:
$$(x+2)(2x^2-8)=0;$$
Произведение двух множителей (в нашем случае двух скобок) равно нулю, когда хотя бы один из множителей равен (0):
$$x+2-0 qquad Rightarrow qquad x_1=-2;$$
$$2x^2-8=0 qquad Rightarrow qquad 2x^2=8 qquad Rightarrow qquad x^2=frac{8}{2} qquadRightarrow $$
$$Rightarrow qquad x^2=4 qquad Rightarrow qquad x_{2,3}=pm 2;$$
Получилось три значения (x), но корень (x=-2) дублируется, поэтому исходное кубическое уравнение будет иметь 2 решения:
Ответ: (x=-2, quad x=2.)
Общий алгоритм разложения на множители:
- Объединяем слагаемые в группы, как правило, в пары, но иногда это могут быть и тройки;
- В каждой группе (паре) выносим общий множитель за скобки;
- Если в скобках в каждой паре получилось одинаковое выражение, то опять выносим общий множитель в виде одинакового выражения внутри этих скобок за «большие» скобки.
- Если в результате шагов (1) и (2) в каждой паре получились разные выражения в скобках, то нужно вернуться на шаг (1), поменять местами слагаемые и сгруппировать их в группы другим способом.
Попробуем решить уравнение четвертой степени:
Пример 6
$$4x^4+12x^3+6x^2+18x=0;$$
Опять сгруппируем слагаемые по парам: первое со вторым, а третье с четвертым:
$$(4x^4+12x^3)+(6x^2+18x)=0;$$
Вынесем общий множитель в каждой паре:
$$4x^3(x+3)+6x(x+3)=0;$$
Ура, в скобках получились одинаковые выражения ((x+3)), вынесем их за скобки:
$$(x+3)(4x^3+6x)=0;$$
Произведение равно нулю, когда хотя бы один из множителей равен нулю:
$$x+3=0 qquad qquad 4x^3+6x=0;$$
Первое уравнение имеет корень (x_1=-3), а второе выпишем отдельно и решим:
$$4x^3+6x=0;$$
Здесь тоже есть общий множитель (x), но это уже не группировка, а обычное вынесение общего множителя за скобки:
$$x(4x^2+6)=0;$$
$$x_2=0 qquad 4x^2+6=0;$$
Из уравнения (4x^2+6=0) выразим (x^2:)
$$4x^2=-6;$$
$$x^2=frac{-6}{4}=frac{-3}{2};$$
Но (x^2) никогда не может равняться отрицательному числу! Что бы вы не возвели в квадрат, всегда получите неотрицательное число. Поэтому последнее уравнение не будет иметь корней.
Осталось опять всего лишь два корня:
Ответ: (x_1=-3; qquad x_2=0.)
Дробно-рациональные уравнения
Если в уравнении есть деление на выражение, зависящее от переменной (x), то такое уравнение будет называться дробно-рациональным. Например, уравнения:
$$frac{1}{x}+3=x;$$
$$x+frac{20}{x+6}=6;$$
$$frac{x^2-3x-2}{x^2-3x+2}+frac{x^2-3x+16}{x^2-3x}=0;$$
все будут дробно-рациональными.
А уравнение
$$frac{x^2-3x}{5}+frac{x-7}{2}=1;$$
уже не будет дробно-рациональным, несмотря на то, что есть деление, но в знаменателе стоят обыкновенные числа, там нет переменной (x).
С тем, что такое дробно-рациональные уравнения, надеюсь, разобрались, теперь поговорим про алгоритм решения таких уравнений.
В общем виде дробно-рациональное уравнение выглядит так:
$$frac{P(x)}{Q(x)}=0;$$
где (P(x)) и (Q(x)) — целые рациональные выражения;
Схему решения можно записать в виде:
$$ begin{cases}
P(x)=0, \
Q(x) neq 0.
end{cases}$$
Простыми словами, решение дробно-рационального уравнения сводится к нахождению корней целого рационального уравнения (P(x)=0). И проверке того, чтобы найденные корни удовлетворяли неравенству (Q(x)neq0).
Пример 7
$$frac{x^2-5x+6}{x-3}=0;$$
Согласно приведенной выше схеме (P(x)=x^2-5x+6=0), а (Q(x)=x-3neq 0).
Или можно запомнить, что дробь равна нулю только тогда, когда числитель равен нулю. А делить на ноль в математике запрещено, поэтому еще и знаменатель не должен равняться нулю.
Приравниваем числитель к нулю:
$$x^2-5x+6=0;$$
$$D=(-5)^2-4*1*6=25-24=1;$$
$$x_1=frac{-(-5)+sqrt{1}}{2}=frac{5+1}{2}=3;$$
$$x_2=frac{-(-5)-sqrt{1}}{2}=frac{5-1}{2}=2;$$
И не забываем проверить, чтобы при найденных корнях знаменатель не был равен нулю:
$$x-3 neq 0;$$
При (x_1=3) знаменатель обращается в нуль, поэтому этот корень нам не подходит.
Ответ: (x_1=2.)
Рассмотрим более сложное уравнение:
Пример 8
$$frac{10}{x+6}=-frac{5}{3};$$
Чтобы решить такое уравнение, необходимо привести его к стандартному виду:
$$frac{P(x)}{Q(x)}=0;$$
Для этого переносим (-frac{5}{3}) в левую часть уравнения, не забываем, что (-frac{5}{3}) превращается в (+frac{5}{3}):
$$frac{10}{x+6}+frac{5}{3}=0;$$
Приводим дроби к общему знаменателю. Общим знаменателем здесь будет: (3*(x+6)). Поэтому домножаем числитель и знаменатель первой дроби на (3), а вторую дробь на ((x+6)):
$$frac{3*10}{3*(x+6)}+frac{5*(x+6)}{3*(x+6)}=0;$$
$$frac{30}{3*(x+6)}+frac{5*x+30}{3*(x+6)}=0;$$
Так как теперь знаменатели у дробей одинаковые, то можно сложить их числители и представить в виде одной большой дроби:
$$frac{30+5x+30}{3(x+6)}=0;$$
$$frac{60+5x}{3(x+6)}=0;$$
Получили стандартный вид дробно-рационального уравнения.
Дробь может быть равна нулю только в одном случае: если ее числитель равен нулю!
Иногда нулю еще пытаются приравнять знаменатель, но знаменатель не может быть равен нулю. Знак дроби — это то же самое, что и знак деления, а делить на ноль в математике категорически запрещено. Именно поэтому знаменатель дроби никак не может быть равен нулю.
Возвращаемся к нашему уравнению и приравниваем числитель к нулю:
$$60+5x=0;$$
$$5x=-60;$$
$$x=-12;$$
В качестве проверки подставим найденный корень в исходное уравнение:
$$frac{10}{x+6}=-frac{5}{3} quad Rightarrow quad frac{10}{-12+6}=-frac{5}{3} quad Rightarrow $$
$$Rightarrow quad frac{10}{-6}=-frac{5}{3} quad Rightarrow quad -frac{5}{3}=-frac{5}{3};$$
Получилось верное равенство, значит (x=-12) действительно будет корнем нашего уравнения.
Ответ: (x=-12.)
Алгоритм решения
- Переносим все слагаемые в левую часть, чтобы в правой части уравнения был 0, не забывая при этом менять знак;
- Приводим к общему знаменателю;
- Упрощаем получившееся выражение в числителе дроби: раскрываем скобки, приводим подобные слагаемые;
- Дробь равна нулю, когда числитель равен нулю. Поэтому избавляемся от знаменателя и приравниваем числитель к нулю;
- В результате вышеперечисленных действий дробно-рациональное уравнение сводится к целому рациональному уравнению;
- Решаем целое рациональное уравнение и проверяем найденные корни, чтобы при подстановке их в знаменатель, не получался ноль.
Посмотрим, как работает алгоритм на примерах:
Пример 9
$$frac{9}{x-11}+frac{11}{x-9}=2;$$
Перекидываем двойку в левую часть уравнения и приводим дроби к общему знаменателю ((x-11)(x-9)). Для этого в первой дроби домножаем числитель и знаменатель на ((x-9)), вторую дробь на ((x-11)), а (2-ку) мы всегда можем представить в виде дроби: (frac{2}{1}), и тоже приводим к знаменателю ((x-11)(x-9)):
$$frac{9*(x-9)}{(x-11)(x-9)}+frac{11*(x-11)}{(x-9)(x-11)}-frac{2(x-11)(x-9)}{(x-11)(x-9)}=0;$$
Получилось немного страшновато, но ничего: складываем дроби, раскрываем в числителе все скобки и приводим подобные слагаемые. Знаменатель при этом не трогаем.
$$frac{9(x-9)+11(x-11)-2(x-11)(x-9)}{(x-9)(x-11)}=0;$$
$$frac{9x-81+11x-121-2(x^2-9x-11x+99)}{(x-9)(x-11)}=0;$$
$$frac{9x-81+11x-121-2x^2+18x+22x-198}{(x-9)(x-11)}=0;$$
$$frac{-2x^2+60x-400}{(x-9)(x-11)}=0;$$
Дробь равна нулю, когда числитель равен нулю:
$$-2x^2+60x-400=0;$$
$$D=60^2-4*(-2)*(-400)=3600-3200=400;$$
$$x_1=frac{-60+sqrt{400}}{2*(-2)}=frac{-60+20}{-4}=10;$$
$$x_2=frac{-60-sqrt{400}}{2*(-2)}=frac{-60-20}{-4}=20;$$
Подставив оба корня в исходное уравнение, аналогично тому, как мы это делали в примере №7, можно убедиться в правильности найденных корней.
Ответ: (x_1=10 quad x_2=20.)
Пример 10
$$frac{x}{3x+2}+frac{5}{3x-2}=frac{3x^2+6x}{4-9x^2};$$
Когда вы видите в знаменателе формулы сокращенного умножения, общий множитель или группировку, то нужно обязательно ими воспользоваться, чтобы разложить многочлен в знаменателе на множители перед тем, как приводить к общему знаменателю.
Замечаем у дроби справа в знаменателе формулу разности квадратов (a^2-b^2=(a-b)(a+b):)
$$frac{x}{3x+2}+frac{5}{3x-2}=frac{3x^2+6x}{(2-3x)(2+3x)};$$
Перекидываем в левую часть уравнения:
$$frac{x}{3x+2}+frac{5}{3x-2}-frac{3x^2+6x}{(2-3x)(2+3x)}=0;$$
Приведем все дроби к общему знаменателю ((2-3x)(2+3x)):
- У первой дроби в знаменателе поменяем слагаемые местами (от перемены мест слагаемых сумма не меняется ((3x+2=2+3x)) и домножим ее числитель и знаменатель на ((2-3x)).
- У второй дроби в знаменателе стоит ((3x-2)), а нам надо ((2-3x)). Поэтому домножим числитель и знаменатель на (-1) и на ((2+3x)).
- С третьей дробью делать ничего не нужно. У нее и так нужный нам знаменатель.
$$frac{x(2-3x)}{(2+3x)(2-3x)}+frac{5*(-1)*(2+3x)}{(3x-2)*(-1)*(2+3x)}-frac{3x^2+6x}{(2-3x)(2+3x)}=0;$$
$$frac{x(2-3x)}{(2-3x)(2+3x)}+frac{-5*(2+3x)}{(2-3x)(2+3x)}-frac{3x^2+6x}{(2-3x)(2+3x)}=0;$$
Складываем дроби и раскрываем скобки:
$$frac{x(2-3x)-5*(2+3x)-(3x^2+6x)}{(2-3x)(2+3x)}=0;$$
Обратите внимание, что я всегда беру числитель в скобки, когда складываю дроби. Тем самым я показываю, что минус перед дробью действует на каждое слагаемое в числителе.
Это одна из самых распространенных ошибок. Будьте внимательны.
$$frac{2x-3x^2—10-15x—3x^2-6x}{(2-3x)(2+3x)}=0;$$
$$frac{-6x^2—19x-10}{(2-3x)(2+3x)}=0;$$
Дробь равна нулю, когда числитель равен нулю:
$$-6x^2-19x-10=0;$$
Для удобства умножим все уравнение на (-1):
$$6x^2+19x+10=0;$$
$$D=19^2-4*6*10=361-240=121;$$
$$x_1=frac{-19+sqrt{121}}{2*6}=frac{-19+11}{12}=frac{-8}{12}=-frac{2}{3};$$
$$x_2=frac{-19-sqrt{121}}{2*6}=frac{-19-11}{12}=frac{-30}{12}=-frac{5}{2};$$
Подставим корень (x_1=-frac{2}{3}) в исходное уравнение:
$$frac{x}{3x+2}+frac{5}{3x-2}=frac{3x^2+6x}{4-9x^2};$$
$$frac{-frac{2}{3}}{3*left(-frac{2}{3}right)+2}+frac{5}{3*left(-frac{2}{3}right)-2}=frac{3left(-frac{2}{3}right)^2+6left(-frac{2}{3}right)}{4-9left(-frac{2}{3}right)^2};$$
Оказывается, что мы не cможем это посчитать, так как в знаменателе получается ноль, а делить на ноль нельзя. В таком случае говорят, что найденный корень не подходит, и в ответ мы его не записываем. А если подставить (-frac{5}{2}), то все будет нормально.
Ответ:(x=-frac{5}{2}.)
Область допустимых значений. ОДЗ
Примеры выше показали нам, что не всегда найденные значения (x) будут корнями исходного уравнения.
Почему так происходит?
Когда мы решаем уравнение, мы преобразовываем его: переносим слагаемые из одной части уравнения в другую, приводим к общему знаменателю, считаем подобные слагаемые, избавляемся от знаменателя и т.д. Эти преобразования меняют вид нашего уравнения. В новом измененном уравнении «исчезает» информация, например, о том, что в нем раньше был знаменатель.
Поэтому мы подставляли найденные (x) в ИСХОДНОЕ уравнение, чтобы проверить, действительно ли они являются корнями, и не нарушаются ли правила математики, такие, как деление на ноль.
Но решений в уравнении может быть много, да и само уравнение может быть большим и сложным. Подставлять туда каждый найденный корень и проверять, действительно ли он является корнем исходного уравнения, может быть проблематично.
Чтобы не заниматься трудоемкой подстановкой, лучше всего находить область значений (x) (еще ее называют область определения), при которых не нарушаются правила математики для исходного уравнения. И уже на этой области (x) искать корни: если найденный корень лежит в разрешенной области, значит он может быть корнем, а если нет, то выкидываем его.
Разрешенная область значений (x) называется «областью допустимых значений», сокращенно ОДЗ. Чтобы найти ОДЗ в дробно-рациональных уравнениях, нужно приравнять к нулю все знаменатели исходного уравнения и решить получившееся уравнения. Другими словами, ищем такие (x), при которых возникает запрещенное деление на ноль в исходном уравнении. Все (x), не являющиеся корнями этих уравнений, и будут нашей областью допустимых значений.
Найдем ОДЗ уравнения из примера №9:
$$frac{x}{3x+2}+frac{5}{3x-2}=frac{3x^2+6x}{4-9x^2};$$
Выписываем все знаменатели и находим (x), при которых они не равны нулю:
$$ begin{cases}
3x+2 neq 0, \
3x-2 neq 0, \
(2-3x)(2+3x) neq 0.
end{cases}$$
Третье неравенство в системе сводится к первым двум, поэтому его можно исключить из рассмотрения.
$$ begin{cases}
x neq -frac{2}{3}, \
x neq frac{2}{3}.
end{cases}$$
Решив неравенства, мы получили, что (x) может принимать любые значения, кроме (frac{2}{3}) и (-frac{2}{3}). Это и есть ОДЗ.
Напомню, что в примере №9 у нас получились корни (x_1=-frac{2}{3}) и (x_2=-frac{5}{2}). Соотносим их с найденным ОДЗ и видим, что корень (x_1=-frac{2}{3}) не подходит. Для этого нам не понадобилось подставлять его в исходное уравнение, как мы делали при решении.
Алгоритм решения дробно-рациональных уравнений с использованием ОДЗ
- Находим ОДЗ. Для этого выписываем все знаменатели и приравниваем их к нулю;
- Решаем дробно-рациональное уравнение: перекидываем все в левую часть, приводим к общему знаменателю, приводим подобные слагаемые, избавляемся от знаменателя и решаем получившееся целое рациональное уравнение;
- Проверяем, чтобы найденные корни удовлетворяли ОДЗ. Если не удовлетворяют, то отбрасываем их.
Пример 11
$$frac{2x^2+7x+3}{x^2-9}=1;$$
Начинаем решение с ОДЗ:
$$x^2-9 neq 0;$$
Разность квадратов:
$$(x-3)(x+3) neq 0;$$
Произведение равно нулю, когда хотя бы один из множителей равен нулю:
$$x-3 neq 0 Rightarrow x neq 3;$$
$$x+3 neq 0 Rightarrow x neq -3;$$
ОДЗ нашли, приступаем к решению самого уравнения:
$$frac{2x^2+7x+3}{x^2-9}-1=0;$$
Приводим к общему знаменателю (x^2-9), для этого единицу представим в виде дроби ((1=frac{1}{1})) и домножим ее на (x^2-9):
$$frac{2x^2+7x+3}{x^2-9}-frac{1*(x^2-9)}{1*(x^2-9)}=0;$$
$$frac{2x^2+7x+3-(x^2-9)}{x^2-9}=0;$$
$$frac{2x^2+7x+3-x^2+9}{x^2-9}=0;$$
$$frac{x^2+7x+12}{x^2-9}=0;$$
$$x^2+7x+12=0;$$
$$D=7^2-4*1*12=49-48=1;$$
$$x_1=frac{-7+1}{2}=frac{-6}{2}=-3;$$
$$x_2=frac{-7-1}{2}=frac{-8}{2}=-4;$$
Сверяем найденные корни с ОДЗ ((x neq pm 3)) и видим, что корень (x_1=-3) не удовлетворяет ОДЗ.
Ответ: (x=-4.)
Пример 12
$$frac{x^2-6x+8}{x-1}-frac{x-4}{x^2-3x+2}=0;$$
Всегда начинаем решать с ОДЗ:
$$ begin{cases}
x-1 neq 0, \
x^2-3x+2 neq 0.
end{cases}$$
$$ begin{cases}
x neq 1, \
x neq 2.
end{cases}$$
Чтобы привести к общему знаменателю, разложим квадратный многочлен в знаменателе второй дроби на множители:
$$frac{x^2-6x+8}{x-1}-frac{x-4}{(x-1)(x-2)}=0;$$
Теперь видно, что общий знаменатель: ((x-1)(x-2)). Домножим первую дробь на ((x-2)):
$$frac{(x^2-6x+8)*(x-2)}{(x-1)*(x-2)}-frac{x-4}{(x-1)(x-2)}=0;$$
Если перемножить скобки в числителе, то получится многочлен третьей степени. Решать уравнение третьей степени не хочется, поэтому попробуем упростить нашу задачу: разложим на множители многочлен (x^2-6x+8=(x-2)(x-4)):
$$frac{(x-2)(x-4)*(x-2)}{(x-1)*(x-2)}-frac{x-4}{(x-1)(x-2)}=0;$$
$$frac{(x-2)^2(x-4)-(x-4)}{(x-1)(x-2)}=0;$$
Дробь равна нулю, когда числитель равен нулю:
$$(x-2)^2(x-4)-(x-4)=0;$$
Вынесем общий множитель: скобку ((x-4)):
$$(x-4)((x-2)^2-1)=0;$$
$$(x-4)(x^2-4x+4-1)=0;$$
$$(x-4)(x^2-4x+3)=0;$$
Произведение равно нулю, когда хотя бы один из множителей равен нулю:
$$x-4=0 Rightarrow x_1=4;$$
$$x^2-4x+3=0;$$
$$D=(-4)^2-4*1*3=16-12=4;$$
$$x_2=frac{-(-4)+sqrt{4}}{2}=frac{4+2}{2}=3;$$
$$x_3=frac{-(-4)-sqrt{4}}{2} =frac{4-2}{2}=1;$$
Проверяем, чтобы найденные корни удовлетворяли ОДЗ ((x neq 1; quad x neq 2)) и видим, что корень (x_3=1) не подходит.
Ответ: (x_1=4, qquad x_2=3.)
Чтобы научиться решать большинство уравнений из школьной программы необходимо также знать метод замены переменной. Это очень важный метод, который используется для решения некоторых рациональных и дробно-рациональных уравнений, и не только, поэтому он заслуживает того, чтобы поговорить о нем в отдельной статье, очень рекомендую.