Как найти все тела если известна масса - Исправление недочетов и поиск решений вместе с Examum.ru

Не уверен в ответе?

Найди верный ответ на вопрос ✅ «Как найти все тела если известна масса 0,1 кг и сила 1 н? …» по предмету 📙 Физика, а если ответа нет или никто не дал верного ответа, то воспользуйся поиском и попробуй найти ответ среди похожих вопросов.

Искать другие ответы

Источник

Загрузить PDF

Вес — сила, с которой тело действует на опору (или другой вид крепления), возникающая в поле силы тяжести. Масса связана с энергией и импульсом тела и эквивалентна энергии его покоя. Масса не зависит от силы тяжести (точнее от ускорения свободного падения). Поэтому тело, на Земле имеющее массу 20 кг, на Луне будет иметь массу 20 кг, но совсем другой вес (потому что ускорение свободного падения на Луне в 6 раз меньше, чем на Земле).

1

Для вычисления веса используйте формулу . Вес — это сила, с которой тело действует на опору, и его можно рассчитать, зная массу тела. В физике используется формула .^[1]
2

Определите массу тела. Так как ускорение свободного падения — это стандартная величина, то необходимо знать массу тела, чтобы найти его вес. Масса должна быть выражена в килограммах.
3
Узнайте величину ускорения свободного падения. На Земле, как уже было сказано выше, g = 9,8 м/с². В других местах Вселенной эта величина меняется.^[3]
- Ускорение свободного падения на поверхности Луны приблизительно равно 1,622 м/с² (примерно в 6 раз меньше, чем на поверхности Земли). Поэтому ваш вес на Луне будет в 6 раз меньше вашего земного веса.^[4]
- Ускорение свободного падения на Солнце приблизительно равно 274,0 м/с² (примерно в 28 раз больше, чем на Земле). Поэтому ваш вес на Солнце будет в 28 раз больше вашего земного веса (если, конечно, вы выживете на Солнце, что еще не факт!).^[5]
4

Подставьте значения в формулу . Теперь, когда вы знаете массу и ускорение свободного падения , подставьте их значения в формулу . Так вы найдете вес тела (измеряется в ньютонах, Н).

Реклама

1

Задача № 1. Найдите вес тела массой 100 кг на поверхности Земли.
2

Задача № 2. Найдите вес тела массой 40 кг на поверхности Луны.
3

Задача № 3. Найдите массу тела, которое на поверхности Земли весит 549 Н.

Реклама

1
Не путайте массу и вес. Самая распространенная ошибка — перепутать вес и массу (что немудрено, ведь в повседневной жизни мы обычно называем массу весом). Но в физике все не так. Запомните, масса — это постоянное свойство объекта, то, сколько в нем вещества (килограммов), где бы он ни находился. Вес — это сила, с которой объект всеми своими килограммами давит на поверхность, и эта сила на разных небесных телах будет различной.
- Масса измеряется в килограммах или граммах. Запомните, что в этих словах, как и в слове «масса», есть буква «м».
2

Используйте правильные единицы измерения. В задачах по физике вес или силу измеряют в ньютонах (Н), ускорение свободного падения — в метрах на секунду в квадрате (м/с²), а массу — в килограммах (кг). Если для какой-либо из этих величин вы возьмете не ту единицу измерения, воспользоваться формулой будет нельзя. Если масса в условиях задачи указана в граммах или тоннах, не забудьте перевести ее в килограммы.

Реклама

Приложение: вес, выраженный в кгс

Ньютон — это единица измерения силы в международной системе единиц СИ. Нередко сила выражается в килограмм-силах, или кгс (в системе единиц МКГСС). Эта единица очень удобна для сравнения весов на Земле и в космосе.
1 кгс = 9,8166 Н.
Разделите вес, выраженный в ньютонах, на 9,80665.
Вес космонавта, который «весит» 101 кг (то есть его масса равна 101 кг), составляет 101,3 кгс на Северном полюсе и 16,5 кгс на Луне.
Международная система единиц СИ — система единиц физических величин, которая является наиболее широко используемой системой единиц в мире.

Советы

Самая трудная задача — уяснить разницу между весом и массой, так как в повседневной жизни слова «вес» и «масса» используются как синонимы. Вес — это сила, измеряемая в ньютонах или килограмм-силах, а не в килограммах. Если вы обсуждаете ваш «вес» с врачом, то вы обсуждаете вашу массу.
Ускорение свободного падения также может быть выражено в Н/кг. 1 Н/кг = 1 м/с².
Плечевые весы измеряют массу (в кг), в то время как весы, работа которых основана на сжатии или расширении пружины, измеряют вес (в кгс).
Вес космонавта, который «весит» 101 кг (то есть его масса равна 101 кг), составляет 101,3 кгс на Северном полюсе и 16,5 кгс на Луне. На нейтронной звезде он будет весить еще больше, но он, вероятно, этого не заметит.
Единица измерения «Ньютон» применяется намного чаще (чем удобная «кгс»), так как можно найти множество других величин, если сила измеряется в ньютонах.

Предупреждения

Выражение «атомный вес» не имеет ничего общего с весом атома, это масса. В современной науке оно заменено на выражение «атомная масса».

Об этой статье

Эту страницу просматривали 113 770 раз.

Была ли эта статья полезной?

Источник

Для того чтобы определить плотность вещества, надо массу тела разделить на его объем:

(10.1)

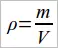
Массу тела можно определить с помощью весов. А как найти объем тела?

Если тело имеет форму прямоугольного параллелепипеда (рис. 24), то его объем находится по формуле

V = аbс.

Если же у него какая-то другая форма, то его объем можно найти методом, который был открыт древнегреческим ученым Архимедом в III в. до н. э.

Архимед родился в Сиракузах на острове Сицилия. Его отец, астроном Фидий, был родственником Гиерона, ставшего в 270 г. до н. э. царем города, в котором они жили.

До нас дошли не все сочинения Архимеда. О многих его открытиях стало известно благодаря более поздним авторам, в сохранившихся трудах которых описываются его изобретения. Так, например, римский архитектор Витрувий (I в. до н. э.) в одном из своих сочинений рассказал следующую историю:
«Что касается Архимеда, то изо всех его многочисленных и разнообразных открытий то открытие, о котором я расскажу, представляется мне сделанным с безграничным остроумием.

Во время своего царствования в Сиракузах Гиерон после благополучного окончания всех своих мероприятий дал обет пожертвовать в какой-то храм золотую корону бессмертным богам. Он условился с мастером о большой цене за работу и дал ему нужное по весу количество золота. В назначенный день мастер принес свою работу царю, который нашел ее отлично исполненной; после взвешивания вес короны оказался соответствующим выданному весу золота.

После этого был сделан донос, что из короны была взята часть золота и вместо него примешано такое же количество серебра. Гиерон разгневался на то, что его провели, и, не находя способа уличить это воровство, попросил Архимеда хорошенько подумать об этом. Тот, погруженный в думы по этому вопросу, как-то случайно пришел в баню и там, опустившись в ванну, заметил, что из нее вытекает такое количество воды, каков объем его тела, погруженного в ванну. Выяснив себе ценность этого факта, он, не долго думая, выскочил с радостью из ванны, пошел домой голым и громким голосом сообщал всем, что он нашел то, что искал. Он бежал и кричал одно и то же по-гречески: «Эврика, эврика! (Нашел, нашел!)».

Затем, пишет Витрувий, Архимед взял сосуд, доверху наполненный водой, и опустил в него золотой слиток, равный по весу короне. Измерив объем вытесненной воды, он снова наполнил сосуд водой и опустил в него корону. Объем воды, вытесненной короной, оказался больше объема воды, вытесненной золотым слитком. Больший объем короны означал, что в ней присутствует менее плотное, чем золото, вещество. Поэтому опыт, проделанный Архимедом, показал, что часть золота была похищена.

Итак, для определения объема тела, имеющего неправильную форму, достаточно измерить объем воды, вытесняемой данным телом. Располагая измерительным цилиндром (мензуркой), это сделать несложно.

В тех случаях, когда известны масса и плотность тела, его объем можно найти по формуле, вытекающей из формулы (10.1):

(10.2)

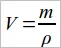
Отсюда видно, что для определения объема тела надо массу этого тела разделить на его плотность.

Если, наоборот, объем тела известен, то, зная, из какого вещества оно состоит, можно найти его массу:

m = ρV. (10.3)

Чтобы определить массу тела, надо плотность тела умножить на его объем.

1. Какие способы определения объема вы знаете? 2. Что вам известно об Архимеде? 3. Как можно найти массу тела по его плотности и объему?
Экспериментальное задание. Возьмите кусок мыла, имеющий форму прямоугольного параллелепипеда, на котором обозначена его масса. Проделав необходимые измерения, определите плотность мыла.

Источник

Содержание:

Масса
Второй закон Ньютона
Масса — мера инертности тела
Система единиц измерения механических величин
Примеры решения задач на второй закон Ньютона

Масса — это физическая величина, одна из основных характеристик материи, определяющая её инертные и гравитационные свойства, масса рассматривается как мера инертности тела по отношению к действующей на него силе и как источник поля тяготения равны (принцип эквивалентности), в международной системе единиц (си) обозначается в килограммах.

На странице -> решение задач по физике собраны решения задач и заданий с решёнными примерами по всем темам физики.

Масса

Всякое тело притягивается Землёй. Сила, с которой Земля притягивает тело, называется весом тела. С понятием веса тела тесно связано другое, более общее
понятие — масса тела.

Массой тела называется количество вещества, содержащегося в этом теле.

Масса литра воды в 1000 раз больше массы 1 см3 воды, масса бревна во много раз больше массы полена из такого же дерева. Словом, массы однородных тел тем больше, чем больше объёмы этих тел. При равенстве их объёмов равны и массы. Так, например, массы двух одинакового объёма кусков железа равны между собой. Если положить эти куски на чашки весов, то они окажутся в равновесии. Это даёт нам возможность измерять массы тел взвешиванием.

Рис. 98. Измерение массы тела.

Массы двух тел равны, если эти тела одинаково притягиваются Землёй в одном и том же месте,
т. е. если они уравновешивают друг друга на чашках рычажных весов. При этом совершенно безразлично, из каких веществ состоят эти тела. Если массу одного из этих тел принять за единицу массы, то и масса другого тела, которое уравновешивается первым, будет также равна единице массы.

За единицу массы принята масса платинового цилиндра, хранящегося в Сере (близ Парижа). Эта масса называется килограммом. В отличие от единицы силы, обозначаемой кГ, единица массы сокращённо обозначается кг.

В физике за единицу массы принимают 0,001 кг. Эта единица называется граммом (сокращённое обозначение—г).

В практике эталоны масс изготовляют в виде гирь различной величины.

Чтобы измерить массу тела, надо положить на одну чашку весов это тело, а на другую—гири. При равновесии весов масса тела равна массе гир,,. На рисунке 98 показано, что масса тела равна 0,5 кг.

Второй закон Ньютона

Во втором законе Ньютона устанавливается связь между силой, действующей на тело, массой тела и ускорением, с которым движется это тело.

Рис. 99. Прибор для установления зависимости ускорения от силы, действующей на тело.

Рассмотрим сначала, как зависит ускорение одного и того же тела от величины силы, действующей на тело. Проделаем следующий опыт (рис. 99). К тележке, которая может (с малым трением) двигаться по столу, прикреплён динамометр. К другому концу динамометра прикреплена нитка с грузом М, переброшенная через блок. По показаниям динамометра мы сможем определить силу, действующую на тележку. Пользуясь капельницей, отметим пути, пройденные тележкой при ускоренном движении за различные промежутки времени под действием постоянной силы. Измерения показывают, что пути эти пропорциональны квадратам времён. Таким образом, движение под действием постоянной силы есть равноускоренное движение.

Измерив длину пройденного тележкой пути за какой-нибудь промежуток времени t, по формуле определяем ускорение а.

Будем подвешивать к концам нити различные грузы, каждый раз измеряя динамометром силу и вычисляя соответствующее этой силе ускорение тележки.

Результаты таких измерений и вычислений отражены в таблице.

Из таблицы видно, что с увеличением силы в 1,5 раза ускорение увеличивается тоже в 1,5 раза; если сила увеличивается в 2 раза, в 2 раза увеличивается и ускорение, и т. д., т. е. ускорение тележки прямо пропорционально силе, действующей на тележку.

Математически это можно записать в виде формулы:

Чтобы установить, как зависит ускорение от массы тела, будем действовать на тележку какой-нибудь постоянной силой.

Нагружая тележку гирями, изменим массу движущихся тел.

Ускорение, получаемое тележкой, будем вычислять так же, как и в первом случае.

Результаты опытов снова занесём в таблицу.

Данные таблицы показывают, что при неизменной силе увеличение массы тела в два раза приводит к уменьшению ускорения в два раза, и наоборот, при уменьшении массы в два раза ускорение увеличивается в два раза, т. е. ускорение тележки с грузами обратно пропорционально их общей массе. Математически этот вывод можно
выразить формулой:

Итак, результаты опытов показывают, что ускорение, с которым движется тело, пропорционально действующей на тело силе и обратно пропорционально массе этого тела.

Кроме того, ускорение тела совпадает с этой силой по направлению.

Этот вывод, как показал Ньютон, имеет всеобщий характер; он носит название второго закона Ньютона.

Во втором законе Ньютона говорится о действии одной силы. Но практически на тело всегда действуют несколько сил. Нам уже известно, что в расчётных целях мы действие нескольких сил можем заменить действием одной силы — равнодействующей. Поэтому в случае, когда на тело действуют несколько сил, под силой, вызывающей ускорение тела, подразумевается их равнодействующая.

Второй закон Ньютона математически можно выразить в виде следующей формулы:

откуда

Величина силы равна произведению массы тела на ускорение.

Таким образом, второй закон Ньютона позволяет вычислить величину силы, если известна масса тела и ускорение, с которым оно движется.

В частности, на основании второго закона Ньютона вес тела Р можно выразить через массу этого тела т и ускорение свободного падения g:

Р = mg.

Из сопоставления формулы F=ma и P=mg видно, что

т. е. ускорение движения тела под действием некоторой силы во столько же раз больше или меньше ускорения свободного падения, во сколько раз действующая сила больше или меньше веса тела.

При решении задач с помощью указанного выше отношения однородные величины должны быть выражены в одних и тех же единицах.

Пример. Санки с седоком весят 70 кГ и скатываются с горы с ускорением Определить силу, движущую санки.

Р=70 кГ;

g=
а =
F = ?

Из формулы определим F:

Масса — мера инертности тела

Первый закон Ньютона утверждает, что всякое тело обладает свойством инерции, иначе говоря, всякое тело инертно. Какова мера инертности тела? Обратимся к следующему примеру.

Пусть по горизонтальному пути с одинаковой скоростью движутся два вагона, один пустой, другой гружёный. Пусть на каждый из них одновременно начали действовать одинаковые силы, тормозящие их движение. Какой из этих вагонов будет дольше сохранять своё движение? Опыт показывает, что гружёный вагон будет двигаться дольше, следовательно, можно сказать, что он обладает и большей инертностью. Но масса гружёного вагона больше массы пустого; отсюда следует, что чем больше масса тела, тем более оно инертно.

Рис. 100. Масса наковальни значительно больше массы молота.

Этот вывод непосредственно вытекает из второго закона Ньютона. Действительно, по второму закону Ньютона т. е. ускорение обратно пропорционально массе, а так как масса гружёного вагона больше массы пустого, то и ускорение его движения будет меньше (ускорение направлено против движения). Следовательно, гружёный вагон дольше будет сохранять своё движение.

Итак, масса тела является мерой его инертности.

Из второго закона Ньютона следует,что любая сколь угодно малая сила может вызвать ускоренное движение тела.

Не противоречит ли этому то, что мы иногда, толкая тяжёлый предмет, не можем сдвинуть его с места? Нисколько не противоречит. Дело в том, что между предметом и полом существует трение, и нам, чтобы привести его в движение,надо преодолеть это трение, а для этого сила, с которой мы толкаем предмет, должна быть больше силы трения, что не всегда бывает.

Изменение скорости тела зависит от массы тела и от времени действия силы на тело. Это видно хорошо на следующем опыте.

Положим на одну чашку весов тяжёлую плиту и уравновесим её гирями или каким-нибудь другим грузом. Если резко ударить небольшим молоточком по плите, то равновесие весов не нарушится.

Если же положить на чашки весов тела с малой массой, то уже при самом незначительном ударе равновесие весов нарушится.

Чем больше масса тела, тем меньшее изменение скорости вызывает действующая на него сила. Это учитывается в технике.

Рис. 101. Машина на массивном фундаменте.

Так, например, для уменьшения сотрясений от ударов делают массивными и прочно соединяют с землёй мостовые „быки“ и упоры; массивными делают наковальни: относительные размеры молота и наковальни видны на рисунке 100. По этой же причине станки и машины делают массивными и устанавливают их на массивные фундаменты. На рисунке 101 изображена машина, установленная на массивном основании.

Нам известен способ определения массы тела с помощью взвешивания тела на рычажных весах. Второй закон Ньютона даёт нам другой способ определения массы — как меры инертности тела по величине силы и ускорению:

Опытом проверено, что оба эти способа определения массы тела (по весу и по инертности) дают совершенно одинаковые результаты.

Система единиц измерения механических величин

Чтобы применять формулы для числовых расчётов, необходимо установить, в каких единицах измеряются физические величины.

Физические законы связывают физические величины определёнными зависимостями. Поэтому если произвольно выбрать единицы для измерения некоторых величин, то единицы для измерения других величин получатся на основе соответствующих законов. Например, в формуле s = vt дана зависимость между тремя величинами. Если мы произвольно выберем единицы каких-нибудь двух величин, то единица третьей величины определится из этого уравнения. Условившись, например, измерять путь в метрах, а время в секундах, мы должны будем измерять скорость в

Зависимости, существующие между физическими величинами, дают возможность составить такую совокупность единиц, в которой для измерения механических величин достаточно выбрать произвольно три единицы: единицу длины, единицу массы, или силы, и единицу времени; такая совокупность единиц называется системой единиц.

Выбранные произвольно единицы системы называются основными единицами, а все другие — производными единицами.

В физике принята система единиц, в которой основными единицами являются: единица длины—1 см (сотая часть международного метра), единица массы— 1 г (тысячная часть международного килограмма) и единица времени—1 сек ( средних солнечных суток, измеряемая весьма точными часами, которые систематически проверяются астрономическими наблюдениями) (Солнечные сутки—промежуток времени между двумя следующими друг за другом полуднями. Так как продолжительность солнечных суток в разные времена года несколько различна, то в практику введены средние солнечные сутки, продолжительность которых равна средней длительности суток за год).

Эта система называется системой единиц CGS (по первым буквам слов—сантиметр, грамм, секунда).

Единица скорости в этой системе единица ускорения

Полагая в формуле F=ma второго закона Ньютона m = 1 г, получим единицу силы в системе CGS:

За единицу силы в системе CGS принимается такая сила, под действием которой масса в 1 г движется с ускорением, равным Эта единица называется диной (сокращённо дн).

В системе единиц, применяемой в настоящее время в СССР при электрических и магнитных измерениях, за основные единицы принимаются:

единица длины — 1 м,

единица массы — 1 кг,

единица времени — 1 сек,

единица тока — 1 ампер.

Сокращённо мы эту систему единиц будем называть MKSA (по первым буквам слов—метр, килограмм, секунда, ампер).

Единицей силы в системе MKSA будет такая сила, под действием которой масса в 1 кг движется с ускорением Эта единица называется ньютон (сокращённо н). Таким образом,

Вычислим, сколько в одном ньютоне содержится дин. или
В практике довольно широко распространена так называемая техническая система единиц. В этой системе основными единицами являются:

единица длины —1 м,

единица силы —1 кГ,

единица времени—1 сек.

Единица массы в этой системе единиц является производной и может быть определена из равенства т. е. единицей массы в технической системе единиц является масса, которая под действием силы в 1 кГ движется с ускорением

Сокращённое обозначение этой единицы—т. е. м. Таким образом,

Между различными единицами массы и силы существуют следующие соотношения:

1 кГ есть сила, с которой Земля притягивает массу в 1 кг и сообщает ей ускорение Отсюда: или округлённо:

Так как то 1 кГ = 9,8 н.

Примеры решения задач на второй закон Ньютона

1. Постоянная сила, равная 2 кГ, действует на тело, вес которого 19,6 кГ. С какой скоростью будет двигаться тело в горизонтальном направлении по прошествии 5 сек., если начальная скорость движения равна нулю?

Расчёты ведём в системе CGS.

Дано: F = 2 кГ=2*980000 дн = 1960000 дн;

m=19600 г; t = 5 сек. Найти

Под действием постоянной силы тело будет двигаться равноускоренно. Скорость этого тела определим по формуле:

Время t дано по условиям задачи.

Ускорение найдем на основании второго закона:

Ответ:
2. Тело весом 98 кГ движется со скоростью, равной
Какую силу надо приложить, чтобы остановить это тело в течение 5 мин.? Расчёты провести в технической системе единиц.

Дано: Р = 98 кГ; t = 300 сек. Найти F.

Искомую силу найдём на основании второго закона:

F = mа.

Под действием этой силы тело будет двигаться равнозамедленно, отрицательное ускорение его а определим по формуле;

Так как то

По второму закону Ньютона Р = mg, откуда

Ответ.

3. На тело, движущееся с начальной скоростью в подействовали силой в 10 Г в направлении движения, после чего тело прошло за 5 сек. путь в 200 м. Определить вес тела. Расчёты провести в системе CGS.

Вес тела в системе CGS, выражаемый в динах, найдётся на основании второго закона Ньютона:

Надо найти массу в граммах. Для этого воспользуемся тем F же вторым законом, ускорение а по условиям задачи вычислим по формуле:

откуда

Масса тела

Ответ.

При решении физических задач мы производим математические действия не только с числовыми значениями величин, но и над их наименованиями. Если предварительно все величины, указанные в задаче, выразить в единицах одной системы единиц и правильно применить соотношения, существующие между физическими величинами, то ответ всегда получится в единицах этой системы. Это позволяет нам не загромождать вычисления наименованиями единиц; достаточно указать наименование величины только в окончательном результате.

Пример. Тело массой 0,01 кг, двигаясь равноускоренно без начальной скорости, за 1 мин. прошло в горизонтальном направлении путь, равный 18 м. Определить силу, действующую на тело.

Дано: m = 0,01 кг; t = 1 мин.; s = 18 м. Найти F.

Выражаем все данные в задаче величины в единицах одной системы, например в системе CGS.

m = 10 г; t = 60 сек.; s = 1800 см.

По второму закону Ньютона F = ma. (1)

Масса дана, ускорение а находим по формуле пути равноускоренного движения: откуда

Подставим значение а из равенства (2) в равенство (1), получим:

Подставляя численные значения величин в равенство (3), определим величину силы F:

Услуги по физике:

Заказать физику
Заказать контрольную работу по физике
Помощь по физике

Лекции по физике:

Физические величины и их измерение
Основные законы механики
Прямолинейное равномерное движение
Прямолинейное равнопеременное движение
Сила
Взаимодействия тел
Механическая энергия
Импульс
Вращение твердого тела
Криволинейное движение тел
Колебания
Колебания и волны
Механические колебания и волны
Бегущая волна
Стоячие волны
Акустика
Звук
Звук и ультразвук
Движение жидкости и газа
Молекулярно-кинетическая теория
Молекулярно-кинетическая теория строения вещества
Молекулярно — кинетическая теория газообразного состояния вещества
Теплота и работа
Температура и теплота
Термодинамические процессы
Идеальный газ
Уравнение состояния идеального газа
Изменение внутренней энергии
Переход вещества из жидкого состояния в газообразное и обратно
Кипение, свойства паров, критическое состояние вещества
Водяной пар в атмосфере
Плавление и кристаллизация
Тепловое расширение тел
Энтропия
Процессы перехода из одного агрегатного состояния в другое
Тепловое расширение твердых и жидких тел
Свойства газов
Свойства жидкостей
Свойства твёрдых тел
Изменение агрегатного состояния вещества
Тепловые двигатели
Электрическое поле
Постоянный ток
Переменный ток
Магнитное поле
Электромагнитное поле
Электромагнитное излучение
Электрический заряд (Закон Кулона)
Электрический ток в металлах
Электрический ток в электролитах
Электрический ток в газах и в вакууме
Электрический ток в полупроводниках
Электромагнитная индукция
Работа, мощность и тепловое действие электрического тока
Термоэлектрические явления
Распространение электромагнитных волн
Интерференционные явления
Рассеяние
Дифракция рентгеновских лучей на кристалле
Двойное лучепреломление
Магнитное поле и электромагнитная индукция
Электромагнитные колебания и волны
Природа света
Распространение света
Отражение и преломление света
Оптические приборы и зрение
Волновые свойства света
Действия света
Линзы и получение изображений с помощью линз
Оптические приборы и глаз
Фотометрия
Излучение и спектры
Квантовые свойства излучения
Специальная теория относительности в физике
Теория относительности
Квантовая теория и природа поля
Строение и свойства вещества
Физика атомного ядра
Строение атома

Источник

Масса сплошной детали

Это странное название статьи объясняется только тем, что детали одной и той же формы могут быть как сплошными, так и полыми (т.е. следующая статья будет называться «Масса полой детали»).

Тут самое время вспомнить, что масса тела — это его объем , умноженный на плотность его материала rho (см. таблицы плотностей):

Объем сплошной детали — это… ее объем и больше ничего.

Примечание. В приведенных ниже формулах все размеры измеряются в миллиметрах, а плотность — в граммах на кубический сантиметр.
Буквой обозначено отношение длины окружности к ее диаметру, составляющее примерно 3,14.

Рассмотрим несколько простых форм (более сложные, как вы помните, можно составить путем сложения или вычитания простых).

1. Масса параллелепипеда (бруска)

Объем параллелепипеда: , где — длина, — ширина, — высота.
Тогда масса:

2. Масса цилиндра

Объем цилиндра: $V~=~pi~*~{D^2/4}~*~H$ , где — диаметр основания, — высота цилиндра.
Тогда масса:

$m~=~{{pi~*~D^2~*~H}/4000}~*~rho$

3. Масса шара

шар Объем шара: $V~=~pi~*~{D^3/6}$ , где — диаметр шара.
Тогда масса:

$m~=~{{pi~*~D^3}/6000}~*~rho$

4. Масса сегмента шара

Объем сегмента шара: $V~=~{1/6}pi*H*(H^2+~{3/4}D^2)$ , где — диаметр основания сегмента, — высота сегмента.
Тогда масса:

$m~=~{{pi~*~H~*~(4H^2+~3D^2)}/24000}~*~rho$

5. Масса конуса

Объем любого конуса: , где — площадь основания, — высота конуса.
Для круглого конуса: $V~=~{1/12}pi*D^2*H$ , где — диаметр основания, — высота конуса.
Масса круглого конуса:

$m~=~{{pi~*~D^2~*~H}/12000}~*~rho$

6. Масса усеченного конуса

Поскольку невозможно объять необъятное, рассмотрим только круглый усеченный конус. Его объем — это разность объемов двух вложенных конусов: с основаниями и : $V~=~{1/12}pi*(D1^2*H1~-~D2^2*H2)$ , где , . После никому не интересных алгебраических преобразований получаем:
$V~=~{1/12}pi*H*(D1^2+D1*D2+D2^2)$ , где — диаметр большего основания, — диаметр меньшего основания, — высота усеченного конуса.
Отсюда масса:

$m~=~{{pi~*~H~*~(D1^2~+~D1*D2~+~D2^2)}/12000}~*~rho$

7. Масса пирамиды

Объем любой пирамиды равен одной трети произведения площади ее основания на высоту (то же самое, что и для конусов (часто мы не замечаем, насколько мироздание к нам благосклонно)): , где — площадь основания, — высота пирамиды.
Для пирамиды с прямоугольным основанием: , где — ширина, — длина, — высота пирамиды.
Тогда масса пирамиды:

8. Масса усеченной пирамиды

Рассмотрим усеченную пирамиду с прямоугольным основанием. Ее объем — это разность объемов двух подобных пирамид с основаниями W1*L1 и W2*L2 : , где , .
Исчеркав половину тетрадного листа, получаем: $V~=~{1/3}H*~{{W1^2L1~-~W2^2L2}/{W1~-~W2}}$ , где , — ширина и длина большего основания, , — ширина и длина меньшего основания, — высота пирамиды.
И, оставив в покое остальную половину листа, исходя из одних соображений симметрии, мы можем написать еще одну формулу, которая отличается от предыдущей только заменой W на L и наоборот. В чем разница между длиной и шириной? Только в том, что мы их так назвали. Назовем наоборот и получим: $V~=~{1/3}H*~{{L1^2W1~-~L2^2W2}/{L1~-~L2}}$ .
Тогда масса усеченной прямоугольной пирамиды: