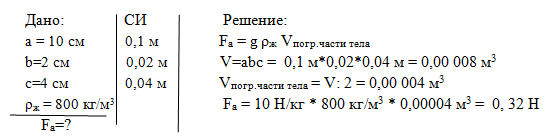План урока:
Сила Архимеда – выталкивающая сила
О жидкости, в которой нельзя утонуть
Почему не тонут корабли?
Воздухоплавание
Сила Архимеда – выталкивающая сила
Сидит на берегу рыбак с удочкой, внимательно смотрит на поплавок, ждет, когда рыбка клюнет. Вряд ли задумываются любители рыбной ловли над тем, какие законы физики используются для изготовления рыболовных снастей. Кроме лески и крючков берутся поплавок и грузило. Предназначение их совершенно противоположное. Поплавок должен плавать на поверхности воды, подергиваться при клеве. Грузило, наоборот, должно затонуть и опустить крючки на глубину, где плавает рыба.
Поплавок и грузило Источник
Простейшие явления, происходящие на воде, которые часто встречаются в жизни и взрослых, и детей, объясняются наличием внутри воды (да и любой жидкости тоже) выталкивающей силы.
Любой мяч, наполненный воздухом, будет плавать на поверхности. Не затонет и большой шар в зорбинге, даже если внутри него находится человек. Зорбинг – это современный экстремальный аттракцион на воде, иначе его называют «Водный шар». Сам шар – зорб. Однако, пройтись пешком по воде человек не сможет, хотя выталкивающая сила действует на человека тоже.
Зорбинг
Простой лабораторный опыт. Если взять динамометр, прикрепить к нему металлический цилиндр (пружина растянется под весом цилиндра), а затем опустить его в воду, показания динамометра уменьшатся. Это значит, что появилась сила, выталкивающая тело из воды, направленная вверх. Результирующая двух сил стала меньше.
Источник
Выталкивающая сила всегда направлена вверх. Какова же причина возникновения такой силы и ее происхождение?
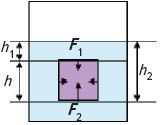
Пусть в стакане с водой находится правильное тело – параллелепипед. Пусть площадь его основания S и высота H.
Все грани параллелепипеда находятся под водой, верхняя — на глубине h1, нижняя – h2. Сверху давление p1 = ρ g h1, а снизу – p2 = ρ g h2.. Давление p2 больше p1, так как h2 больше h1. На вертикальные грани параллелепипеда действуют одинаковые давления, стремящиеся его сжать. Значит, сила давления снизу больше силы давления сверху. Разность этих сил и является силой, выталкивающей тело из жидкости. После алгебраических преобразований получается правило вычисления выталкивающей силы.
F = F2 – F1 = p2 S – p1 S = ρж g h2 S — ρж g h1 S = ρж g S (h2 – h1). Из рисунка видно, что разность h2 – h1 равна высоте параллелепипеда H, но произведение S∙H равно объему данной фигуры Vт. Тогда, F = ρж g S H = ρж g Vт. Результирующая сила, по которой вычисляют выталкивающую силу, запишется в следующем виде:
FA = ρж g Vт
ρж — плотность жидкости.
«Эврика!» — воскликнул Архимед, понимая, от чего зависит сила, выталкивающая тела из жидкости. Конечно, это легенда, но сила носит название архимедовой, потому что Архимед впервые определил эту силу.
Источник
Легенда такова: правитель города Сиракузы на острове Сицилия был родственником Архимеда. Однажды он приказал мастеру изготовить золотую корону. Когда корона была готова, Гирон засомневался в честности мастера, заподозрив, что мастер заменил частично золото серебром или другими примесями. Герон потребовал от Архимеда установить истину.
Чтобы решить эту проблему, надо знать объем короны и объем золота той же массы. Если они совпадут, то мастер – молодец, в противном случае он – лжец.
Объем тела неправильной формы находят с помощью мензурки. Корону в мензурку не поместить. Архимед придумал, как найти объем большого тела, когда сам погрузился в ванну с водой. Он увидел, что часть воды вытекла. Возглас Архимеда «Эврика!», что значит «Нашел!», вошел во все языки мира.
Определенные таким способом объемы куска золота и короны оказались различными. Изготовитель короны был нечестен.
Случай с Архимедом послужил толчком для его дальнейших исследований поведения тела в жидкости. В его сочинении «О плавающих телах» был сформулирован закон, позволяющий определить архимедову силу. Впоследствии закону дали имя: закон Архимеда. Этот закон устанавливает связь выталкивающей силы с весом вытесненной телом жидкости.
В формуле FA = ρж g Vт произведение ρж Vт = m – это масса вытесненной жидкости, объем ее равен объему тела, вытесняющему эту жидкость. Значит,
FA = Pт, т.е. тела выталкиваются из жидкости с силой, такой же, как и вес вытесненной жидкости.
Закон легко доказывается опытным путем:
Источник
Для опыта берется ведерко Архимеда, состоящее из двух частей: полое ведерко 2 и тяжелый цилиндр 3 такого же объема, что и ведерко. Ведерко и цилиндр вместе подвешиваются к динамометру 1, показания динамометра фиксируются (рис.а). Под цилиндр помещается сливной стакан 4 (стакан с носиком, направленным вниз для слива жидкости). Жидкость в стакан первоначально налита точно до сливного носика.
В тот момент, когда цилиндр помещается в воду, она вытесняется цилиндром и сливается в сосуд 5. На цилиндр вверх действует архимедова сила, показания динамометра уменьшаются (рис.б), т.е. вес цилиндра становится меньше.
Из сосуда 5 вытесненная жидкость выливается в пустое ведерко 2 (рис. в). Когда вся вода перелита в ведерко, динамометр фиксирует первоначальный вес (рис. г). Это означает, что при помещении в воду цилиндр потерял вес, равный весу жидкости, которая вытесняется из сливного стакана.
Итак,
- на все тела, помещенные в жидкость, оказывает действие направленная вверх архимедова сила;
- архимедова сила связана с давлением, а значит, с плотностью жидкости, и объемом тела, помещенного в жидкость;
- архимедова сила не зависит от плотности изучаемого тела и глубины погружения.
О жидкости, в которой нельзя утонуть
В воде одни тела сразу тонут, а другие плавают. Тот же поплавок у рыбака держится на поверхности, а грузило плавает. Не тонет сухая древесина, но, если она долго пробудет в воде, пропитается ею, то окажется на дне. Существуют древесные породы, например, бакаут[1] (железное дерево) и черное дерево[2], тонущие в воде в сухом виде. Почему одни тела свободно плавают, а другие тонут?
На тело, помещенное в жидкость, вниз действует сила тяжести и вверх — архимедова сила. Которая из двух сил преобладает, туда и направлена равнодействующая. Тело переместится в сторону равнодействующей силы:
Источник
Следует особо обратить внимание на разницу двух из приведенных случаев. Обычно говорят, что тело плавает, независимо, где оно плавает: внутри жидкости или на поверхности. Но, если Fтяж = FA, тело плавает внутри. Если Fтяж ˂ FA, тело плавает на поверхности (тело не может выпрыгнуть из жидкости и повиснуть над ней, сила тяжести вернет его).
При сравнении формул обеих сил просматривается объяснение, при каком условии силы различны или одинаковы.
FA = ρж g Vт Fтяж = mg = ρт Vт g.
В обеих формулах есть одинаковые множители: g и Vт. Отличие в плотностях. Видно, что, если ρт ˂ ρж, то сила тяжести меньше архимедовой – тело поднимается к поверхности жидкости. Если ρт ˃ ρж, то сила тяжести больше выталкивающей – тело идет на дно. Если ρт = ρж, силы тоже равны – тело плавает между дном и поверхностью (внутри) жидкости.
Именно поэтому поплавок, который обычно полый внутри (плотность воздуха 1,29 кг/м3), плавает на воде (плотность воды 1000 кг/м3). Свинцовое грузило (плотность свинца 11 300 кг/м3) тонет.
Конечно, условия такого плавания подходят для сплошных тел. Например, стекло с плотностью 2600 кг/м3 тонет в воде, а закупоренная стеклянная бутылка плавает, потому что весь объем закрытой бутылки занимает воздух с небольшой плотностью.
Способность бутылки плавать издавна использовали мореплаватели для передачи посланий о крушениях на землю. В пустую бутылку вкладывали свиток с текстом, бутылку закупоривали и бросали за борт. Долго бутылка путешествовала по морским просторам, но когда-то все равно волнами приливов прибивалась к суше.
Средняя плотность тела человека находится в пределах от 1030 до 1070 кг/м3. Значит, в чистой воде человек без умения плавать тонет.
Есть Мертвое море, где нельзя утонуть. В этом море, как и в воде залива Кара-Богаз-Гол (в Каспийском море) и озера Эльтон не утонуть, так как в них вода содержит около 27 % солей. Соли повышают плотность воды до 1180 кг/м3, что больше плотности человеческого тела. В обычной морской воде солей 2-3 % и плотность этой морской воды 1030 кг/м3.
Мертвое море
Некоторые домохозяйки используют для определения свежести купленных куриных яиц (плотность примерно 1090 кг/м3) простой способ. Через мелкие поры в тонкой скорлупе часть жидкости сырого яйца испаряется, замещаясь воздухом. Плотность такого яйца уменьшается. Свежее более плотное яйцо в чистой воде затонет, несвежее – всплывет.
Другой пример из жизни домохозяек. Они наливают в кастрюлю с водой, где отваривают макароны, растительное масло, чтобы макароны не слипались. Как бы ни размешивали смесь масла и воды, масло всплывает наверх. Объяснить просто. Плотность масла 930 кг/м3, меньше плотности воды. Стоит ли наливать масло? Не стоит. Масло будет плавать поверх воды. Большая часть макарон будет находиться в чистой воде. Поэтому масло никак не повлияет на макароны.
Нефть, мазут, бензин всегда находятся на поверхности воды, что представляет угрозу для окружающей среды при водных катастрофах, связанных с этими веществами.
Нефть на воде
Жидкости менее плотные плавают сверху, а более плотные опускаются вниз. В жидкой ртути плавает большинство металлов, только наиболее плотные (осмий, вольфрам, иридий, золото и некоторые другие) тонут.
Интересный пример плавания представляет подводная лодка. Она может плавать на поверхности воды, внутри ее и может залечь на дно. Можно схематически показать, как это происходит.
Источник
Конструкция лодки двухкорпусная: внутренний и внешний корпусы. Внутренний корпус предназначен для технических устройств, оборудования, людей. Между внешним и внутренним корпусами находятся балластные цистерны. Когда лодке требуется погружение, открываются кингстоны – отверстия, через которые забортная вода поступает между внутренним и внешним отсеками, заполняя балластные цистерны. Сила тяжести возрастает и становится больше архимедовой. Лодка погружается.
Чтобы прекратить погружение или всплыть, цистерны под большим давлением продуваются компрессорами, вода вытесняется в океан, ее место занимает воздух. Сила тяжести уменьшается. В момент равенства силы тяжести и архимедовой лодка будет плавать внутри воды. При дальнейшем заполнении цистерн воздухом лодка всплывает.
Почему не тонут корабли?
Теперь следует объяснить плавание судов. Понятно, что корабли, изготовленные из строительного деревянного материала, плавают по волнам, так как плотность дерева меньше плотности воды. Условие плавания здесь срабатывает безоговорочно. Современные корабли изготовлены преимущественно из металлов, у которых большая плотность. Почему металлический гвоздь тонет, а корабль нет?
Кораблю придают специальную форму, чтобы он как можно больше вытеснял воды, вес которой превосходит силу тяжести судна. Этот вес равен выталкивающей (архимедовой) силе, и значит, она больше силы тяжести. Из металла делают основной корпус судна, а остальной его объем заполнен воздухом. Корпусом корабль вытесняет значительное количество воды, достаточно глубоко погружаясь в нее.
Источник
Глубину погружения судна моряки называют осадкой. После загрузки корабля его осадка увеличивается. Перегружать корабль нельзя, иначе нарушится условие плавания, корабль может затонуть. Рассчитывается максимальная осадка, на судне проводится красная линия, которую называют ватерлинией, ниже ее корабль оседать не должен.
Вес корабля с максимально взятым грузом называется водоизмещением.
Мореплавание и судостроение неразрывно связаны с историей человечества. От плотов и лодок глубокой древности к каравеллам Колумба и Магеллана, Васко де Гамы и первому российскому военному кораблю «Орел» (1665г.), от первого парохода «Клермонт», построенного Р. Фультоном в США в 1807 году, до ледокола «Арктика», созданного в России в 1975 году.
Суда используются в различных целях: для пассажирских и грузовых перевозок, для научно-исследовательских работ, для охраны границ государства.
К сожалению, с кораблями происходят и неприятности. Во время шторма или других катастроф они могут затонуть. Опять приходит на помощь закон Архимеда.
Со спасательного судна[3] на прочных стропах опускают полые цилиндры большого объема. Чтобы они затонули, их заполняют водой. Водолазы закрепляют эти цилиндры на корпусе корабля. Сжатым воздухом под большим давлением, подаваемым по шлангам, вода из цилиндров вытесняется, заменяется воздухом. Вес цилиндров резко уменьшается. Они начинают выталкиваться из воды и вместе с кораблем всплывают на поверхность.
Спасение затонувшего корабля
В судоходстве, мореплавании, спасении судов помогает закон Архимеда, как один из самых важных законов природы.
Воздухоплавание
Красивое зрелище: цветные воздушные шары на разной высоте голубого неба. Какая сила поднимает их вверх?
5 июня 1783 года во Франции братья Монгольфьер наполнили дымом оболочку шара диаметром 10 м, и он стремительно полетел ввысь. Впервые официально было зарегистрировано изобретение, показавшее путь к воздухоплаванию. 27 августа 1783 года на Марсовом поле Парижа профессор Жак Шарль наполнил шар водородом, плотность которого 0,09 кг/м3. Около трехсот тысяч зрителей увидели, как шар стремительно поднялся вверх и стал вскоре невидимым. Началась история воздухоплавания.
Человек издавна мечтал освоить воздушный океан, как птица, поднявшись в небеса. Мечта стала явью благодаря открытой архимедом силе, действующей во всех жидкостях и газах. На все тела на Земле оказывает действие выталкивающая их из воздуха сила. Для твердых тел она значительно меньше силы тяжести, на практике ее не учитывают. Для газов эта сила имеет существенное значение.
Подъемная сила летящих воздушных шаров – это разность между весом воздуха, вытесненного шаром, и весом газа в оболочке. Что значит «вытесненного газом» и откуда вытесненного. Корабль вытесняет воду из моря. Это для моря как «комар для слона», но, тем не менее, это так. Человек вытесняет воду из ванны, что уже очень заметно. Так и воздушный шар вытесняет воздух из атмосферы.
А вот имеет ли воздух вес, проверяется очень легко, даже в домашних условиях: найти середину ровной палочки или линейки, вколотить туда маленький гвоздик так, чтобы палочка могла свободно вокруг него поворачиваться. Можно подвесить палочку на нитке за середину. На края палочки повесить два одинаково надутых шара. Палочка располагается горизонтально, т.е. наблюдается равновесие. Выпустить воздух из одного шарика. Равновесие нарушается. Шарик с воздухом перевешивает.
Источник
Опыт в лабораторных условиях проводится также легко и понятно. Находится масса открытого (значит, там есть воздух) стеклянного шара (рис. а). Затем насосом откачивается из шара воздух (рис.б) и шар плотно закрывается пробкой. Новое определение массы показывает, что масса шара без воздуха меньше (рис. в). Зная массу можно найти вес воздуха.
Источник
Газ в оболочке шара должен иметь плотность заметно меньшую плотности воздуха, как и плотность тела на поверхности какой-либо жидкости меньше плотности самой жидкости. Плотность гелия 0,18 кг/м3, водорода 0,09 кг/м3, а плотность воздуха 1,29 кг/м3. Поэтому для наполнения оболочек шаров используются подобные газы.
Создать подъемную силу для воздушного шара можно уменьшением плотности воздуха.
Из анализа таблицы зависимости плотности воздуха от температуры следует вывод: с ростом температуры снижается плотность воздуха. Соответственно с повышением температуры разница между архимедовой силой и силой тяжести возрастает. Эта разница сил и является подъемной силой шара.
При подъеме температура воздуха в оболочке шара снижается. Воздух приходится нагревать, что небезопасно.
Подогрев воздуха в шаре
Полет на таких шарах осуществляется недолго. Чтобы продлить его, используют балласт – дополнительный груз, который крепится на гондоле[4] (устройство, где находятся люди и приборы для работы). Сбрасывая балласт, можно подниматься выше. Спуская воздух из оболочки, можно опускаться вниз. Спускаясь или поднимаясь в разные слои атмосферы, можно уловить движение воздушных масс и двигаться в их направлении. Но подобрать нужное направление достаточно сложно. Таким способом можно лишь немного влиять на направление движения. Поэтому воздушные шары обычно движутся по направлению ветра.
Источник
На гигантских по своим размерам шарах (20 000 – 30 000 м3) удавалось достигать стратосферы. Такие шары называют стратостатами. Гондола стратостата должна иметь пригодный для жизни человека микроклимат. Воздух и температура в стратосфере не соответствуют условиям жизни человека. Приходится специально обустраивать гондолы стратостатов.
Другие, более простые, воздушные шары называют аэростатами. Если к гондоле шара пристроить двигатель, то получится управляемый человеком аэростат, называемый дирижаблем.
Дирижабль
К сожалению, полеты аэростатов зависят от капризов природы. Однако эти устройства обладают неоспоримыми преимуществами:
- огромная подъемная сила;
- экологически чистые аппараты;
- не нуждаются в больших количествах топлива;
- зрелищны.
Поэтому эти аппараты еще долго будут служить человеку.
Словарь
1. Бакаут (железное дерево) – вечнозеленое дерево тропиков с плотностью древесина близкой к плотности чугуна.
2. Черное эбеновое дерево – вечнозеленое тропическое дерево, в ядре которого не видны годичные кольца. Ядро твердое, тяжелое. Плотность дерева 1300 кг/м3.
3. Спасательное судно – судно специального (вспомогательного) назначения, служащее для подъема на поверхность затонувших объектов или для помощи кораблям, терпящим бедствие.
4. Гондола – устройство, крепящееся к воздушному шару для помещения туда людей, различных вещей и аппаратуры.
На прошлом уроке мы доказали с помощью опытов существование силы, действующей на тела, погруженные в жидкость или газ — выталкивающей силы. Также мы теперь знаем, что ее можно рассчитать по формуле: $F_{выт} = gm_ж = P_ж$. Но какое еще есть значение у этой силы? На этом уроке мы более подробно рассмотрим выталкивающую силу.
Выталкивающая сила и вес тела
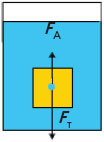
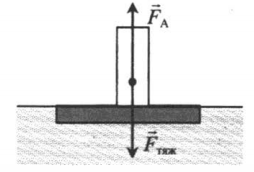
Как можно на опыте определить, с какой силой тело, погруженное целиком в жидкость, выталкивается из жидкости?
Давайте познакомимся с таким опытом. Он представлен на рисунке 1.
Подвесим на пружину небольшую емкость для жидкости и тело цилиндрической формы ниже. На конце пружины у нас расположена стрелка-указатель. Она отмечает растяжение пружины на штативе (рисунок 1, а). Таким образом, мы видим вес тела в воздухе.
Теперь опустим наше тело в большой сосуд. Сосуд имеет трубку для слива и наполнен жидкостью до уровня этой трубки (рисунок 1, б).
Когда мы полностью опустим тело в сосуд, часть жидкости из него выльется через трубку для слива в стакан. Объем этой жидкости будет равен объему тела. Мы уже знаем, что на тело действует выталкивающая сила: пружина сокращается, стрелка-указатель поднимается, вес тела в жидкости становится меньше.
А теперь возьмем жидкость, которая вылилась в стакан. Зальем ее в емкость, которая также подвешена к пружине (рисунок 1, в). Теперь стрелка-указатель вернулась к своему изначальному положению.
Так чему равна эта сила? Сделаем вывод из данного опыта.
Сила, выталкивающая целиком погруженное в жидкость тело, равна весу жидкости в объеме этого тела.
Если провести подобный опыт с газом, а не с жидкостью, то мы получим, что сила, выталкивающая тело из газа, равна весу газа, взятого в объеме тела.
Сила Архимеда
Как называют силу, которая выталкивает тела, погруженные в жидкости и газы?
Теперь мы добавим, что эту выталкивающую силу называют архимедовой силой. Архимед (рисунок 2) — древнегреческий ученый и инженер, сделавший множество открытий и в математике, и в физике. Именно он первый обнаружил наличие выталкивающей силы и рассчитал ее значение.
Как подсчитать архимедову силу?
В прошлом уроке мы получили формулу $F_{выт} = P_ж = g m_ж$. Теперь мы будем называть эту силу архимедовой $F_A$.
Из выше рассмотренных опытов мы можем выразить массу вытесненной жидкости через ее плотность и объем тела, который эту жидкость вытеснил (они одинаковы): $m_ж = rho_ж cdot V_т$. Получим формулу для архимедовой силы.
$F_A = g rho_ж V_т$.
От чего зависит архимедова сила?
Взгляните еще раз на формулу: $F_A = g rho_ж V_т$.
Ясно видно, что архимедова сила зависит только от плотности жидкости и от объема тела, которое мы погружаем в эту жидкость.
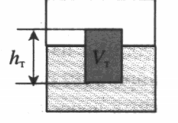
Если мы будем погружать в одну и ту же жидкость тела разной плотности и разной формы (рисунок 3), то значение силы меняться не будет (при условии, что эти тела будут обладать одинаковым объемом).
Определение веса тела, погруженного в жидкость или газ
На тело, погруженное в жидкость (или в газ), действуют две силы: сила тяжести и архимедова сила. Направлены они в противоположные стороны. Вес тела в жидкости $P_1$ будет меньше веса тела в вакууме $P$ на архимедову силу $F_A$. То есть:
$P_1 = P space − space F_A = gm space − space gm_ж$.
Если тело погружено в жидкость или газ, то его вес уменьшается на вес вытесненной им жидкости или газа.
Пример задачи
Определите выталкивающую силу, которая будет действовать на камень объемом $2.6 space м^3$, лежащий на морском дне.
Дано:
$V_т = 2.6 space м^3$
$rho_ж = 1030 frac{кг}{м^3}$
$g = 9.8 frac{Н}{кг}$
$F_A — ?$
Посмотреть решение и ответ
Скрыть
Решение:
Сила Архимеда рассчитывается по формуле:
$F_A = g rho_ж V_т$.
Подставим численные значения величин и рассчитаем эту силу:
$F_A = 9.8 frac {Н}{кг} cdot 1030 frac{кг}{ м^3} cdot 2.6 space м^3 approx 26 244 space Н approx 26.2 space кН$.
Ответ: $F_A approx 26,2 space кН$.
Забавное дополнение: легенда об Архимеде
Архимед, великий изобретатель, шокировал своих современников гениальными открытиями. Его имя упоминается во множестве легенд, но одна из них стала наиболее известной: легенда о том, как Архимед пришел к открытию выталкивающей силы.
Царь Гиерон поручил Архимеду проверить работу мастера, который изготовил для него золотую корону.
Долгое время ученый не мог найти ответ: как определить количество некачественных примесей? Проблема заключалась в том, что определить ее объем — сложная задача. По легенде озарение настигло Архимеда, когда он принимал ванну.
Ученый заметил, что из ванны вылилась вода, когда он залез в нее. И здесь его посетила гениальная мысль. Все вы слышали его известную цитату: «Эврика! Эврика!» (в переводе означает: «Нашел! Нашел!»).
Так Архимед победно выкрикивал свою фразу, потрясенный своим открытием, что она дошла в виде легенды и до наших времен.
Упражнения
Упражнение №1
К коромыслу весов подвешены два цилиндра одинаковой массы: свинцовый и алюминиевый (рисунок 4). Весы находятся в равновесии. Нарушится ли равновесие весов, если оба цилиндра одновременно погрузить в воду; в спирт? Ответ обоснуйте. Проверьте его на опыте. Как зависит выталкивающая сила от объема тела?
Посмотреть ответ
Скрыть
Ответ:
Когда мы погрузим цилиндры в жидкость, на каждый их них будет действовать сила Архимеда. Если эти силы будут равны, то весы останутся в равновесии.
Запишем формулы архимедовой силы для каждого цилиндра.
Для свинцового цилиндра:
$F_{A1} = g rho_ж V_1$.
Для алюминиевого цилиндра:
$F_{A2} = g rho_ж V_2$.
Мы видим, что равенство этих сил зависит от объемов цилиндров. Они равны? Нет, они имеют одинаковые массы, но разные плотности. Цилиндр из алюминия будет обладать большим объемом, чем свинцовый цилиндр ($V = frac{m}{rho}$). Значит, на алюминиевый цилиндр будет действовать большая выталкивающая сила, чем на свинцовый.
Если мы проверим это на опыте, то увидим подтверждение нашим выводам (рисунок 5).
При этом весы выйдут из равновесия в случае и с водой (рисунок 5, а), и со спиртом (рисунок 5, б). Так как мы опускаем цилиндры одновременно в один и тот же тип жидкости, значение архимедовой силы, действующей на цилиндры, будет различаться только в зависимости от объемов этих цилиндров — свинцовый перевесит алюминиевый в любой жидкости.
Заметим, что в случае погружения в воду, архимедова сила будет больше, чем в случае погружения в спирт. Это объясняется тем, что вода имеет большую плотность, чем спирт.
Упражнение №2
К коромыслу весов подвешены два алюминиевых цилиндра одинакового объема. Нарушится ли равновесие весов, если один цилиндр погрузить в воду, а другой — в спирт? Ответ обоснуйте. Зависит ли выталкивающая сила от плотности жидкости?
Посмотреть ответ
Скрыть
Ответ:
Если один цилиндр погрузить в воду, а другой — в спирт, то равновесие весов нарушится (рисунок 6). На цилиндр, находящийся в воде, будет действовать большая архимедова сила.
Так происходит, потому что архимедова сила зависит от объема погруженного тела (а они у нас одинаковые: $V_1 = V_2 = V$) и от плотности жидкости:
$F_А = g rho_ж V$.
Плотность спирта ($800 frac{кг}{м^3}$) меньше плотности воды ($1000 frac{кг}{м^3}$). Значит, на цилиндр, погруженный в воду, будет действовать большая архимедова сила, чем на тот, что погружен в спирт.
Упражнение №3
Объем куска железа равен $0.1 space дм^3$. Какая выталкивающая сила будет на него действовать при полном его погружении в воду; в керосин?
Дано:
$V = 0.1 space дм^3$
$g = 9.8 frac{Н}{кг}$
$rho_1 = 1000 frac{кг}{м^3}$
$rho_2 = 800 frac{кг}{м^3}$
СИ:
$V = 0.1 cdot 10^{-3} space м^3$
$F_{А1} — ?$
$F_{А2} — ?$
Посмотреть решение и ответ
Скрыть
Решение:
Рассчитаем архимедову силу, которая будет действовать на кусок железа в воде:
$F_{А1} = g rho_1 V$,
$F_{А1} = 9.8 frac{Н}{кг} cdot 1000 frac{кг}{м^3} cdot 0.1 cdot 10^{-3} space м^3 = 0.98 space Н approx 1 space Н$.
Теперь рассчитаем архимедову силу, которая будет действовать на кусок железа в керосине:
$F_{А2} = g rho_2 V$,
$F_{А2} = 9.8 frac{Н}{кг} cdot 800 frac{кг}{м^3} cdot 0.1 cdot 10^{-3} space м^3 = 0.784 space Н approx 0.8 space Н$.
Ответ: $F_{А1} approx 1 space Н$, $F_{А2} approx 0.8 space Н$.
Упражнение №4
Бетонная плита объемом $2 space м^3$ погружена в воду. Какую силу необходимо приложить, чтобы удержать ее в воде; в воздухе?
Дано:
$V = 2 space м^3$
$g = 9.8 frac{Н}{кг}$
$rho_1 = 1000 frac{кг}{м^3}$
$rho_2 = 1.29 frac{кг}{м^3}$
$rho_б = 2300 frac{кг}{м^3}$
$F_1 — ?$
$F_2 — ?$
Посмотреть решение и ответ
Скрыть
Решение:
Бетонная плита находится в воде. На нее действует сила тяжести и архимедова сила. Они направлены противоположно друг другу и будут иметь разные величины. Разность этих сил — и будет искомая сила $F_1$, которую нужно приложить, чтобы удержать бетонную плиту в воде (чтобы она не опускалась на дно и не всплывала):
$F_1 = F_{тяж} space − space F_{А1}$.
Сила тяжести рассчитывается по формуле:
$F_{тяж} = gm$.
Массу бетонной плиты мы можем выразить через ее плотность и объем:
$m = rho_б V$,
$F_{тяж} = g rho_б V$.
Архимедова сила, действующая на бетонную плиту в воде:
$F_{А1} = g rho_1 V$.
Подставим силу тяжести и архимедову силу в формулу и рассчитаем $F_1$:
$F_1 = F_{тяж} space − space F_{А1} = g rho_б V space − space g rho_1 V = gV cdot (rho_б space − space rho_1)$,
$F_1 = 9.8 frac {Н}{кг} cdot 2 space м^3 cdot (2300 frac{кг}{м^3} space − space 1000 frac{кг}{м^3}) = 25 space 480 space Н approx 25 space кН$.
Используем ту же формулу для того, чтобы рассчитать силу $F_2$, которую нужно приложить, чтобы удержать бетонную плиту в воздухе:
$F_2 = gV cdot (rho_б space − space rho_2)$,
$F_2 = 9.8 frac {Н}{кг} cdot 2 space м^3 cdot (2300 frac{кг}{м^3} space − space 1.29 frac{кг}{м^3}) approx 45 space 054 space Н approx 45 space кН$.
Ответ: $F_1 approx 25 space кН$, $F_2 approx 45 space Н$.
Упражнение №5
Предположив, что корона царя Гиерона в воздухе весит $20 space Н$, а в воде — $18.75 space Н$, вычислите плотность вещества короны. Полагая, что к золоту было подмешано только серебро, определите, сколько в короне было золота и сколько серебра. При решении задачи плотность золота считайте равной $20 space 000 frac{кг}{м^3}$, плотность серебра — $10 space 000 frac{кг}{м^3}$. Каков был бы объем короны из чистого золота?
Дано:
$P_1 = 20 space Н$
$P_2 = 18.75 space Н$
$rho_з = 20 space 000 frac{кг}{м^3}$
$rho_с = 10 space 000 frac{кг}{м^3}$
$g = 9.8 frac{Н}{кг}$
$rho_1 = 1.29 frac{кг}{м^3}$
$rho_2 = 1000 frac{кг}{м^3}$
$rho — ?$
$m_з — ?$
$m_с — ?$
$V_1 — ?$
Посмотреть решение и ответ
Скрыть
Решение:
Вес короны в воздухе $P_1$ будет меньше веса тела в вакууме $P$ на архимедову силу $F_{A1}$. То есть:
$P_1 = P space − space F_{A1}$.
Значит, вес короны в вакууме будет равен сумме ее веса в воздухе и архимедовой силы:
$P = P_1 space + space F_{А1}$,
$gm = P_1 space + space g rho_1 V$.
Теперь запишем такое же уравнение для веса короны в воде:
$gm = P_2 space + space g rho_2 V$.
Левые части уравнений у нас равны, поэтому мы можем приравнять правые части друг к другу:
$P_1 space + space g rho_1 V = P_2 space + space g rho_2 V$.
Перенесем элементы, содержащие неизвестный объем вправо:
$P_1 space − space P_2 = g rho_2 V space − space g rho_1 V$,
$P_1 space − space P_2 = gV (rho_2 space − space rho_1)$.
Выразим отсюда объем короны и рассчитаем его:
$V = frac{P_1 space − space P_2}{g (rho_2 space − space rho_1)}$,
$V = frac{20 space Н space − space 18.75 space Н}{9.8 frac{Н}{кг} (1000 frac{кг}{м^3} space − space 1.29 frac{кг}{м^3})} = frac{1.25}{9787} space м^3 = 12.8 cdot 10^{-5} space м^3$.
Используем одно из первых уравнений для веса короны в вакууме и в воздухе:
$gm = P_1 space + space g rho_1 V$.
Выразим отсюда массу короны и рассчитаем ее:
$m = frac{P_1 space + space g rho_1 V}{g}$,
$m = frac{20 space Н space + space 9.8 frac{Н}{кг} cdot 1.29 frac{кг}{м^3} cdot 12.8 cdot 10^{-5} space м^3}{9.8 frac{Н}{кг}} approx 2.04 space кг$.
Теперь мы знаем массу и объем короны. Рассчитаем ее плотность:
$rho = frac{m}{V}$,
$rho = frac{2.04 space кг}{12.8 cdot 10^{-5} space м^3} approx 16 space 000 frac{кг}{м^3}$.
Корона состоит из серебра и золота. Это означает, что ее общий объем мы можем записать в виде суммы объемов серебра и золота, ее составляющих:
$V = V_с space + space V_з$.
То же самое с общей массой короны:
$m = m_с space + space m_з$.
Запишем объемы через массы и плотности (а также выразим массу золота через общую массу короны и массу серебра):
$V_с = frac{m_с}{rho_с}$,
$V_з = frac{m_з}{rho_з} = frac{m space − space m_с}{rho_з}$.
Подставим эти объемы в формулу для общего объема короны и выразим из нее массу серебра:
$V = frac{m_с}{rho_с} space + space frac{m space − space m_с}{rho_з} = frac{m_с (rho_з space − space rho_с) space + space rho_с m}{rho_с rho_з} = m_с cdot frac{rho_з space − space rho_с}{rho_с rho_з} space + space frac{m}{rho_з}$,
$m_с = frac{V space − space frac{m}{rho_з}}{frac{rho_з space − space rho_с}{rho_с rho_з}} = frac{rho_с (V rho_з space − space m)}{rho_з space − space rho_с}$.
Рассчитаем массу серебра, содержащегося в короне:
$m_с = frac{10 space 000 frac{кг}{м^3} (12.8 cdot 10^{-5} space м^3 cdot 20 space 000 frac{кг}{м^3} space − space 2.04 space кг)}{20 space 000 frac{кг}{м^3} space − space 10 space 000 frac{кг}{м^3}} = frac{5200 frac{кг^2}{м^3}}{10 space 000 frac{кг}{м^3}} = 0.52 space кг$.
Теперь мы можем вычислить и количество золота в короне:
$m_з = m space − space m_с$,
$m_з = 2.04 space кг space − space 0.52 space кг = 1.52 space кг$.
Если бы вся корона была из золота, то ее объем был бы равен:
$V_1 = frac{m}{rho_з}$,
$V_1 = frac{2.04 space кг}{20 space 000 frac{кг}{м^3}} = 10.2 cdot 10^{-5} space м^3$.
Ответ: $rho approx 16 space 000 frac{кг}{м^3}$, $m_з = 1.52 space кг$, $m_с = 0.52 space кг$, $V_1 = 10.2 cdot 10^{-5} space м^3$.
Упражнение №6
По мелким камешкам ходить босыми ногами больно. Почему человек не испытывает боли, если ходит по таким же камням в воде?
Посмотреть ответ
Скрыть
Ответ:
Что означает фраза «ходить по камням»? Со стороны физики, когда мы наступаем на камни, мы давим на них своим весом: $p = frac{F}{S} = frac{P}{S}$.
Когда мы оказываемся в воде, наш вес уменьшается. Это следствие действия на нас архимедовой силы. Уменьшается вес — уменьшается и давление наших стоп на камни.
Спецвыпуск
Е. В.
Шерстобитова,
< russia74@yandex.ru >, лицей № 11, г. Челябинск
Сила Архимеда
- образовательная: обеспечить формирование понятия выталкивающая сила, используя задания исследовательского характера;
- развивающая: развитие познавательного интереса, самостоятельности, умения применять знания по физике, используя проблемные ситуации;
- воспитательная: содействовать профориентации учащихся и умению работать в коллективе.
Оборудование: компьютер, мультимедийная система, документ-камера, сосуды с водой, тела различной формы, массы и объёма, динамометры.
Ход урока
I. Организационно-ситуативный этап (определение задач урока)
Учитель (предъявляет слайд). «Ихтиандр протягивает руки вверх и хватает альбатроса за ноги. Испуганная птица раскрывает свои мощные крылья и поднимается, вытаскивая из воды Ихтиандра. Но на воздухе Ихтиандр и альбатрос грузно падают на волну…» (А.Р.Беляев. Человек-амфибия). Почему альбатрос упал в воду?
Учащиеся. В воде вес Ихтиандра был меньше, чем в воздухе.
Учитель. Почему вес тела в воде меньше веса тела в воздухе?
Учащиеся. Существует сила, действующая на тело в воде и направленная вертикально вверх.
Учитель. Давайте посмотрим, почему вес уменьшается. Рассмотрим силы, которые действуют со стороны жидкости на погружённое тело (слайд). Силы, действующие на боковые грани тела, попарно равны и уравновешивают друг друга. А вот силы, действующие на верхнюю и нижнюю грани тела, не одинаковы. На верхнюю грань с силой F1 давит столб жидкости высотой h1. На нижнюю грань тела снизу вверх с силой F2 давит столб жидкости высотой h2. Но h2 > h1, следовательно, и модуль силы F2 больше модуля силы F1. Поэтому тело выталкивается из жидкости с силой Fвыт = F2 – F1, так и называемой – выталкивающая сила. Если тело в воду бросить//Или просто опустить,//Будет сила Архимеда//Cнизу на него давить.
Итак: на тело, погружённое в жидкость, действует сила, выталкивающая это тело из жидкости.
Выталкивающая сила действует и в случае частичного погружения тела в жидкость. Эту силу называют силой Архимеда в честь древнегреческого учёного Архимеда, который впервые указал на её существование и рассчитал её значение.
Как найти величину выталкивающей силы? (Слайд.) Так как две силы, действующие на тело в этом случае, направлены в противоположные стороны (сила тяжести – вниз, архимедова сила – вверх), то вес тела в жидкости P1 будет меньше веса тела в вакууме Р = mg (m – масса тела) на архимедову силу FА = gmж (mж – масса жидкости, вытесненной телом), т.е. P1 = Р – FА, или
FА = Pв возд – Pв жидк ,
т.е. из веса тела в воздухе надо вычесть вес тела в воде.
Все тела в воде кажутся более лёгкими, чем в воздухе. Вода выталкивает и поддерживает их. Будучи вынутыми из воды, тела вновь обретают свой прежний вес, т.к. вода больше не держит их.
II. Объяснение новой темы (записи основных моментов в тетради)
Учитель. Давайте убедимся на опыте, что вес тела в воде уменьшается. (Учитель объясняет задание по слайду с планом действий. Ученики обсуждают план.)
- Определите вес данного вам тела в воздухе: Pв возд.
- Определите вес этого же тела в воде: Pв воде .
- Сравните результаты измерений и сделайте вывод: чему равна сила Архимеда.
Учитель (заслушав мнения). Есть сила одна, вот вам ответ, //Эту силу обнаружил Архимед.//Когда он опустился в воду,//То «Эврика!» – воскликнул он народу.//От чего зависит сила эта?//Нельзя вопрос оставить без ответа.
III. Практическое задание
Учитель. От чего же зависит сила Архимеда? Это вам придётся выяснить самостоятельно. Каждая группа получает своё задание. Пожалуйста, прочитайте задание и сформулируйте гипотезу исходя из условий. (Дети читают, высказывают гипотезы. Учитель записывает предложенные гипотезы в слайд презентации. Учащиеся приступают к выполнению заданий.)
Группа 1. Оборудование: сосуд с водой, динамометр, алюминиевый и медный цилиндры одинакового объёма, но разной массы из набора тел для калориметра, нить.
- Определите архимедовы силы, действующие па первое и второе тела.
- Сравните архимедовы силы, действующие на тела разной массы.
- Сделайте вывод о зависимости (независимости) архимедовой силы от массы тела.
Группа 2. Оборудование: сосуд с водой, тела разного объёма, но одинаковой массы, динамометр, нить.
- Определите архимедову силу, действующую на каждое из тел.
- Сравните эти силы.
- Сделайте вывод о зависимости (независимости) архимедовой силы от объёма тела.
Группа 3. Оборудование: динамометр, нить, сосуды с пресной водой, солёной водой и маслом, алюминиевый цилиндр.
- Определите архимедовы силы, действующие на тело в воде, пресной и солёной, и масле.
- Что можно сказать об архимедовых силах, действующих на тело в различных жидкостях?
- Установите зависимость архимедовой силы от рода жидкости.
Группа 4. Оборудование: мензурка с водой, алюминиевый цилиндр, нить, динамометр.
- Определите архимедовы силы, действующие на тело на глубине h1 и на глубине h2 >h1.
- Сделайте вывод о зависимости (независимости) архимедовой силы от глубины погружения тела.
Группа 5. Оборудование: кусочек пластилина, сосуд с водой, нить, динамометр.
- Кусочку пластилина придайте форму шара, куба, цилиндра.
- Поочерёдно опуская каждую фигурку в воду, с помощью динамометра определите архимедову силу, действующую на неё.
- Сравните эти силы и сделайте вывод о зависимости (независимости) архимедовой силы от формы тела.
(Выполнив задания, группы отчитываются о результатах своей работы и сообщают свои выводы. Результаты записываются в виде таблицы с помощью документ-камеры. Если сила зависит от величины, ставят «+», если нет, то «–». Один учащийся из группы подходит к камере и отмечает результат.)
|
Сила |
Масса |
Объём |
Форма |
Жидкость |
Глубина |
|
FА |
– |
+ |
– |
+ |
– |
Общий вывод: cила Архимеда зависит от объёма тела и рода жидкости (слайд).
(Проводится сравнение с предложенными в начале урока гипотезами.)
Учитель. Теперь вы сможете мне объяснить, почему собака-водолаз легко может тащить человека по воде, но только до берега.
Учащиеся. Вес человека на берегу увеличивается.
Учитель. А масса?
Учащиеся. Осталась прежней.
Учитель. В какой воде легче научиться плавать – в речной или морской?
Учащиеся. В морской, в ней больше выталкивающая сила.
Елена Васильевна Шерстобитова – учитель физики высшей квалификационной категории, окончила Челябинский ГПИ в 1992 г., педагогический стаж 17 лет. Основное направление: развитие творческих способностей учащихся. Занимается исследовательскими работами с учащимися 5–7-х классов. На российской конференции «Шаг в будущее. Юниор» её ученик удостоен диплома Общественной палаты РФ за исследовательскую работу «Модель и принцип действия гидротурбины». Замужем, дочке 6 лет. Хобби – гитара, вязание.
§ 1 Расчет архимедовой силы, условие плавания тел: формулы и определения
Рассмотрим решение задач на расчет архимедовой силы, условие плавания тел в жидкостях и газах.
Для решения задач нам нужно вспомнить следующие формулы и определения:
Архимедова силаравна произведению коэффициента силы тяжести на плотность жидкости и объем погруженной части тела: Fa = gρжVтела.
Тело плавает в жидкости, если вес вытесненной им жидкости равен весу этого тела в воздухе: P выт.жидкости = P тела.
Морские и речные суда могут перевозить грузы. Вес груза зависит от водоизмещения судна. Водоизмещение — это вес воды, вытесненной судном, равный его весу в воздухе.
Подъемная сила аэростатовравна разности между архимедовой силы и весом оболочки, гондолы и газа, которым наполнен аэростат.
При решении задач важно верно выразить величины в системе СИ.
Архимедова сила зависит от объема тела, поэтому вспомним размерности объема:
1 дм3 = 0,001 м3;
1 см3 = 0, 000 001 м3.
§ 2 Решение задач
Задача 1:Вычислите архимедову силу, действующую на брусок размером 2х10х4 см, если он наполовину погружен в спирт.
Решение:Запишем условие задачи. Нам известны размеры бруска: длина а = 10 см, ширина b=2 см, высота c=4 см. Плотность спирта ρж = 800 кг/м3. Выразим длину, ширину и высоту в системе СИ: 0,1 м, 0,02 м, 0,04 м.
Для решения запишем формулу вычисления архимедовой силы: Fa = gρжVпогр.части тела.
Объем всего бруска прямоугольной формы равен произведению длины на ширину и на высоту: V=abc = 0,1 м*0,02*0,04 м = 0,00 008 м3.
Объем погруженной части равен половине объема: Vпогр.части тела=0,00 004 м3.
Подставим числовые значения плотности спирта, коэффициента силы тяжести, объема погруженной части тела в формулу архимедовой силы и получим: Fa = 0,32 Н.
Ответ: на брусок в спирте действует архимедова сила 0,32 Н.
Задача 2:Какую силу нужно приложить к плите массой 4 т при ее подъеме со дна водоема, если объем плиты — 2 м3?
Решение:запишем условие задачи. Масса плиты m = 4 т, выразим в СИ: 4000 кг, объем плиты V = 2 м3, плотность воды ρж = 1000 кг/м3.
На тело, погруженное в жидкость или газ, действуют две силы: сила тяжести и архимедова сила, направленные противоположно. Поэтому вес плиты в воде уменьшается: Pв воде = Pв воздухе – Fа .
Вес тела в воздухе найдем по формуле P=mg, архимедову силу определим по формуле Fa = gρжVпогр. тела.
Тогда формула веса плиты в воде запишется так: Pв воде = mg — gρжVпогр. тела.
Подставим числовые значения величин, произведем вычисления и получим ответ: вес плиты в воде равен 20 000 Н, следовательно, для поднятия плиты в воде нужно приложить силу 20 кН.
Ответ: для поднятия плиты в воде нужно приложить силу 20 кН.
Задача 3: Какой по весу груз может удержать на поверхности воды пробковый пояс объемом 6,25 дм3 и массой 2 кг, если пояс будет погружен в воду полностью?
Решение: Запишем условие задачи. Нам известны объем пояса V = 6,25 дм3, его масса m = 2 кг, плотность воды ρж = 1000 кг/м3. Выразим объем в СИ, для этого 6, 25 поделим на 1000, равно 0,00 625 м3. Найти вес груза Pгр.
Известно, что вес груза, перевозимого судами, равен разности между водоизмещением судна и его весом. Водоизмещение — это вес воды, вытесненной судном с грузом. Тогда Pгруза = Pвытесненной воды — Pсудна.
Пробковый пояс при полном погружении вытесняет воду в объеме, равном объему пояса. Вычитая из веса вытесненной воды собственный вес пояса, можем найти вес груза:
Pгруза = Pвыт.воды – Pпояса.
Определим вес вытесненной воды. Для этого массу вытесненной воды умножим на коэффициент силы тяжести, а масса воды равна произведению плотности воды на ее объем. Объем вытесненной воды равен объему спасательного пояса. Тогда вес вытесненной воды равен произведению плотности воды на объем пояса и коэффициент тяжести:
Pвыт.воды = ρводы *Vводы *g
Определим вес пояса по формуле Pпояса =mпояса·g.
Подставим числовые значения величин и вычислим вес вытесненной поясом воды и вес пояса. Тогда вес груза равен их разности.
Ответ: пробковый пояс может удерживать в воде груз весом 42,5 Н.
Задача 4:Аэростат объемом 2000 м3 наполнен водородом. Вес оболочки и гондолы 16 000 Н. Определите подъемную силу аэростата.
Решение: Запишем условие задачи. Известны объем аэростата V = 2000 м3, вес оболочки и гондолы вместе Pоб =16 000 Н, плотность водорода, которым наполнен аэростат, ρгаза = 0,09 кг/м3, плотность воздуха при нормальном атмосферном давлении ρвозд. = 1,29 кг/м3. Все данные приведены в системе СИ. Требуется найти подъемную силу Fподъемн.
На аэростат действуют сила тяжести и архимедова сила, которая поднимает его вверх. Сила тяжести действует на оболочку, гондолу и газ, которым он наполнен. Вес оболочки и гондолы известен, нужно найти вес водорода, для этого массу водорода умножим на коэффициент тяжести. Массу водорода найдем по формуле плотности. Тогда вес газа равен произведению плотности газа на объем аэростата и коэффициент тяжести: Pгаза = ρгаза *Vаэростата *g.
Архимедову силу определим по формуле Fa = gρжVаэростата.
Подставим записанные формулы в формулу подъемной силы, вынесем одинаковые множители за скобки, вычислим.
Ответ: подъемная сила аэростата равна 8000 Н = 8 кН.
§ 3 Краткие итоги по теме урока
ВАЖНО ЗАПОМНИТЬ:
При решении задач нужно помнить основные формулы и определения.
Архимедова сила равна произведению коэффициента силы тяжести на плотность жидкости и объем погруженной части тела: Fa = gρжVтела.
Тело плавает в жидкости, если вес вытесненной им жидкости равен весу этого тела в воздухе.
Водоизмещение — это вес воды, вытесненной судном с грузом, равный весу судна вместе с грузом. Вес груза, перевозимого судами или выдерживаемого спасательным поясом, плотом, льдиной, равен разности между весом вытесненной жидкости и весом самого судна, пояса, плота, льдины.
Подъемная сила аэростатов равна разности между архимедовой силы и весом аэростата (т.е. весом оболочки, гондолы и газа, которым наполнен аэростат).
Архимедова сила (выталкивающая сила, подъемная сила) — сила, с которой жидкость или газ выталкивают погруженное в них тело.
Полезно знать и понимать!
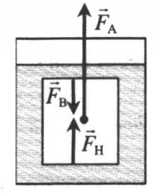
- Причина возникновения выталкивающей силы: нижняя грань тела находится на большей глубине, чем верхняя, поэтому давление жидкости снизу больше, чем сверху. Из-за разницы в давлениях возникает выталкивающая сила.
- Архимедова сила всегда направлена вертикально вверх.
- Архимедова сила равна разности сил давления на нижнюю и верхнюю грани:
FA = FH – FB
- Также выталкивающая сила равна разности веса тела в воздухе и веса тела в жидкости:
FA = Pвозд – Pж
- Модуль выталкивающей силы определяется с помощью закона Архимеда.
Закон Архимеда
Выталкивающая сила равна весу вытесненной жидкости.
FA = Pж
Частные случаи определения архимедовой силы
|
Полное погружение |
|
|
|
Архимедова сила равна произведению плотности жидкости, объема тела и ускорения свободного падения: FA = ρжVтg Vт — объем погруженного в жидкость тела. |
|
Неполное погружение |
|
|
|
Архимедова сила равна произведению плотности жидкости, объема погруженной части тела и ускорения свободного падения: FA = ρжVп.ч.g Vп.ч. — объем погруженной в жидкость части тела. |
Внимание! Если тело погружено в газ, то в формуле нужно использовать плотность этого газа.
Пример №1. При взвешивании груза в воздухе показание динамометра равно 1 Н. При опускании груза в воду показание динамометра уменьшается до 0,6 Н. Найдите значение выталкивающей силы.
Выталкивающая сила равна разности веса тела в воздухе и веса тело в воде. Следовательно:
FA = Pвозд – Pж = 1 – 0,6 = 0,4 (Н)
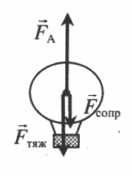
Воздухоплавание
Подъемной силой воздушного шара служит архимедова сила, равная:
FA = ρвоздVшg
Подъемной силе противостоят сила тяжести и сила сопротивления воздуха:
Fтяж = (Mшара + mгаза + mкорз + mгруза)g
Fсопр
Управление шаром:
- чтобы взлететь, шар заполняют нагретым воздухом или газом, плотность которого меньше плотности окружающего воздуха;
- чтобы увеличить высоту полета, с шара сбрасывают балласт;
- чтобы спуститься на землю, газ охлаждают.
Пример №2. Аэростат объемом 1000 м3 заполнен гелием. Плотность гелия 0,18 кг/м3, плотность воздуха 1,29 кг/м3. Какая выталкивающая сила действует на аэростат?
Выталкивающая сила зависит только от плотности окружающей среды и объема погруженного в него тела. Так как аэростат погружен в воздух полностью:
FA = ρвVтg = 1,29∙1000∙10 = 12,9 (кН)
Архимедова сила и законы Ньютона
Если тело полностью погружено в жидкость (или газ):
- Архимедова сила равна: FA = ρжVтg.
- Сила тяжести, действующая на тело: Fтяж = mg = ρтVтg.
Частный случай
Определить минимальную массу груза, который следует положить на плоскую однородную льдину площадью S, чтобы она полностью погрузилась в воду. Толщина льдины h, а плотность льда ρл, плотность воды ρв.
Второй закон Ньютона в векторной форме для льдины, полностью погруженной в воду (она не тонет и не всплывает):
→FA+→Fтяж=0
Так как эти силы направлены в противоположные стороны:
FA = Fтяж
Архимедова сила, действующая только на льдину, равна:
FA = ρвVлg
Сила тяжести равна сумме масс льдины и груза:
Fтяж = (mл + mгр)g
Массу льдины можно выразить через произведение ее плотности на объем, равные произведению ее площади на толщину:
mл = ρлSh
Пример №3. Какую силу надо приложить, чтобы поднять под водой камень, масса которого 30 кг, а объем 12 000 см3?
12 000 куб. см = 0,012 куб. м
Чтобы поднять под водой камень, потребуется сила, равная разности силе тяжести и архимедовой силы, действующей на этот камень:
F = Fтяж – FA = mg – ρвVтg = 30∙10 – 1000∙0,012∙10 = 180 (Н)
Условия плавания тел
На любое тело, погруженное в жидкость или газ, действуют две противоположно направленные силы: сила тяжести и архимедова сила. Направление движения тела зависит от того, какая из этих сил больше по модулю:
- Тело тонет, если: mg > FA; ρт > ρж.
- Тело плавает в толще среды, если: mg = FA; ρт = ρж.
- Тело всплывает, если: mg < FA; ρт < ρж.
Внимание! Тело, имеющее плотность меньшую, чем плотность жидкости, в которой оно плавает, будет находиться на поверхности, погрузившись в жидкость частично.
Если тело плавает на поверхности:
- Архимедова сила и сила тяжести, действующие на него, равны: FA= Fтяж.
- Сила тяжести равна: Fтяж = mg = ρтVтg.
- Архимедова сила равна: FA = ρжVп.ч.g.
- Взаимосвязь между объемом и высотой тела правильной формы: V = Sh.
Варианты условий задач на условия плавания тел
|
Сплошное тело объемом Vт плавает в воде. Причем под водой находится 3/4 его объема. Определите силу тяжести, действующую на тело. Плотность воды ρв. |
Второй закон Ньютона в векторной форме: →FA+→Fтяж=0 Отсюда (проекция на вертикальную ось): FA = Fтяж Fтяж = 3ρвVтg/4 |
|
Какая часть (в процентах) айсберга находится под водой? Плотность льда ρл, а воды ρв. |
Второй закон Ньютона в векторной форме: →FA+→Fтяж=0 Отсюда (проекция на вертикальную ось): FA = Fтяж Отсюда: ρлVлg = ρвVп.ч.g Ускорение свободного падения взаимоуничтожается. Чтобы найти погруженную часть айсберга в процентах, нужно: Vп.ч.Vл=ρлρв Найденное отношение остается умножить на 100%. |
|
Полое тело плотностью ρт плавает в воде, погрузившись на 1/5 своего объема. Найдите объем полости Vп, если объем тела Vт, а плотность воды ρв. |
Второй закон Ньютона в векторной форме: →FA+→Fтяж=0 Отсюда (проекция на вертикальную ось): FA = Fтяж Отсюда: ρвVп.ч.g = ρт(Vт – Vп)g Преобразовав выражение, получим: Vп=Vт(5ρт−ρв)5ρт |
Пример №4. Кубик массой 40 г и объемом 250 см3 плавает на поверхности воды. Найдите значение выталкивающей силы, действующей на кубик.
40 г = 0,04 кг
250 см3 = 250∙10–6 м3
Так как тело плавает, Архимедова сила будет равна по модулю силе тяжести, которая определяется формулой:
FA = Fтяж = 0,04∙10 = 0,4 (Н)
Задание EF18524

Для каждой величины определите соответствующий характер изменения:
- Увеличится.
- Уменьшиться.
- Не изменится.
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Алгоритм решения
- Записать условие плавания тел.
- На основании условия плавания тел сделать вывод о том, как изменятся указанные физические величины.
Решение
По условию задачи деревянный шарик плавает на поверхности воды. Но это возможно, лишь когда архимедова сила равна силе тяжести:
FAв = Fтяж
Если шарик будет плавать в подсолнечном масле, также можно применить условие плавания тел:
FAм = Fтяж
Сила тяжести зависит только от массы тела, которая остается неизменной. Поэтому сила тяжести тоже не меняется. Но из этого следует:
FAв = FAм
Это возможно благодаря тому, что объем погруженной части шарика в масло будет больше объема погруженной части шарика в воду. Этим компенсируется разница в плотностях жидкостей, но архимедова сила при этом остается неизменной.
Верный ответ: 33.
Ответ: 33
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18477
Ученик изучает силу Архимеда, действующую на тела, полностью погружённые в жидкость. В его распоряжении имеется установка, состоящая из ёмкости с водой и сплошного деревянного шарика объёмом 30 см3. Какая из следующих установок необходима ещё ученику для того, чтобы на опыте обнаружить зависимость силы Архимеда от объёма тела?
| № установки | Жидкость, налитая в ёмкость | Объём шарика | Материал, из которого сделан шарик |
| 1 | вода | 30 см3 | сталь |
| 2 | вода | 20 см3 | дерево |
| 3 | керосин | 20 см3 | дерево |
| 4 | подсолнечное масло | 30 см3 | сталь |
Ответ:
а) установка № 1
б) установка № 2
в) установка № 3
г) установка № 4
Алгоритм решения
- Сделать анализ задачи. Определить, какие величины в опыте остаются постоянными.
- Определить, какие величины должны быть в опыте переменными.
Решение
Ученик изучает силу Архимеда, действующую на тела, полностью погружённые в жидкость. В формулировке слово «жидкость» используется в единственном числе. Следовательно, жидкость во всех опытах будет одной и той же (плотность жидкости будет постоянной). У ученика уже есть установка, в которую входит емкость с водой. Поэтому во второй установке в качестве жидкости тоже должна использоваться вода. Варианты 3 и 4 исключаются.
В формулировки задачи также говорится о «телах». Они могут быть выполнены из разных материалов, и они могут иметь разный объем. Но известно, что архимедова сила зависит только от объема тела. Поэтому во второй установке нужно использовать тело другого объема. В вариантах 1 и 2 этому условию соответствует деревянный шарик объемом 20 куб. см (так как в первой установке используется шарик объемом 30 куб. см).
Отсюда верный ответ: б.
Ответ: б
pазбирался: Алиса Никитина | обсудить разбор
Задание EF22696
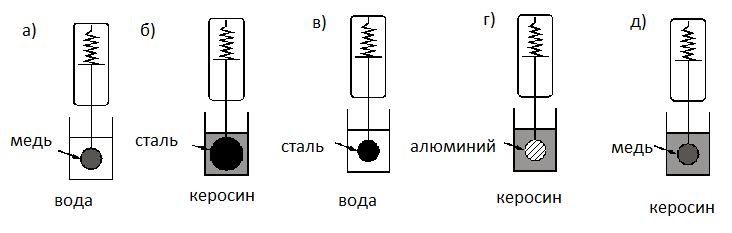
Необходимо экспериментально изучить зависимость силы Архимеда, действующей на тело, погружённое в жидкость, от плотности жидкости.
Какие две установки следует использовать для проведения такого исследования?
Алгоритм решения
- Установить цели опыта.
- Сделать вывод о том, какие величины в опыте должны быть постоянными, а какие — переменными.
- Выбрать установки, соответствующие выводу.
Решение
В опыте нужно изучить зависимость силы Архимеда, действующей на тело, погружённое в жидкость, от плотности жидкости. Это значит, что плотность жидкости — величина переменная. Все остальные величины при этом должны оставаться постоянным. Поэтому нам нужны установки с разными жидкостями, но одинаковыми телами. Этому условию соответствуют две установки: «а» и «д».
Ответ: ад
pазбирался: Алиса Никитина | обсудить разбор
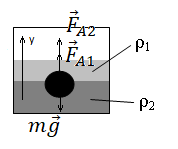
Задание EF18057
Алгоритм решения
1.Записать исходные данные.
3.Записать второй закон Ньютона в векторной форме.
4.Записать второй закон Ньютона в проекции на ось ординат.
5.Выполнить общее решение.
6.Вычислить искомую величину, подставив известные данные.
Решение
Запишем исходные данные:
• Плотность первой жидкости: ρ1 = 400 кг/м3.
• Плотность второй жидкости: ρ2 = 2ρ1.
• Объем шарика выше границы раздела двух жидкостей: V1 = V/4.
• Объем шарика выше границы раздела двух жидкостей: V2 = 3V/4.
Построим рисунок и укажем все силы, действующие на шарик:
Запишем второй закон Ньютона в векторном виде:
m→g+→FA1+→FA2=0
Запишем второй закон Ньютона в виде проекции на ось ординат:
mg=FA1+FA2
Выразим массу тела через его объем и плотность, выразим выталкивающие силы через закон Архимеда и получим:
ρVg=ρ1gV1+ρ2gV2
Преобразуем выражение, сократив ускорение свободного падения и подставив выражения для объемов погруженных в жидкости частей тела, а также выражение для плотности второй жидкости:
ρV=ρ1V4+2ρ13V4
Объемы сокращаются. Остается:
ρ=ρ14+2ρ134=7ρ14=7·4004=700 (кгм3)
Ответ: 700
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 9k