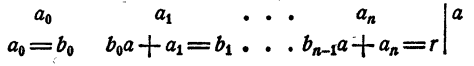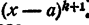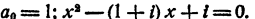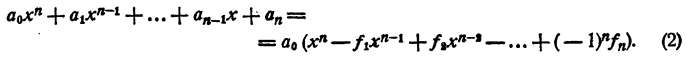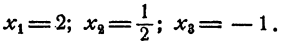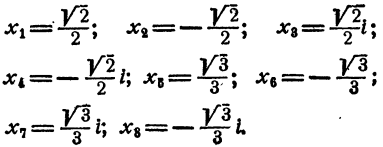Алгоритм расчёта вещественных корней полиномов
Основополагающая идея этого алгоритма очень проста и может быть изложена двумя предложениями. Вещественный корень полинома всегда находится на участке монотонного изменения полинома, т.е. между корнями производной полинома. Но производная полинома — это тоже полином, однако, меньшей степени и, найдя его вещественные корни, надо искать корни исходного полинома между корнями производной методом деления пополам.
А теперь по порядку.
Проблема нахождения корней алгебраических полиномов известна давно, по крайней мере со средневековья. В школе учат решать квадратные уравнения. В википедии можно найти формулы Кардано для решения кубических уравнений и описание метода Феррари для решения в радикалах уравнения четвёртой степени. Там же описан метод Лобачевского для решения алгебраических уравнений произвольной степени. Суть метода Лобачевского вкратце сводится к следующему.
Нетрудно, имея некоторый исходный полином, построить полином2, имеющий те же по модулю корни, что и исходный полином, но с противоположным знаком. Перемножая исходный полином и полином2, получаем полином, корни которого равны квадратам корней исходного полинома.
Это преобразование (квадрирование) полезно повторить несколько раз. В результате, если корни исходного полинома не были равны друг другу, их многократно квадрированные значения оказываются далеко разнесёнными по величине, а их приближенные значения очень просто выражаются через коэффициенты соответствующего квадрированного полинома.
В частности, если коэффициент при старшей степени аргумента полинома равен единице, то следующий по старшинству коэффициент равен (с обратным знаком) сумме корней уравнения, а поскольку значения этих корней сильно разнесены, то приближенно можно считать эту сумму равной наибольшему по модулю корню.
Для конкретности сообщим, что для полинома 4-й степени с корнями 1, 2, 3, 4 метод Лобачевского уже после четвёртого квадрирования даёт правильные до второго знака после запятой значения корней. При этом для представления коэффициентов полиномов достаточно формата long double.
Бесспорно, этот метод является ценным инструментом в руках исследователя, наделённого интеллектом. Однако, его программирование для современной вычислительной техники вызывает серьёзные затруднения при необходимости строгой гарантии достоверности результата при всевозможных особых случаях расположения корней.
Теперь я начну описывать иной метод. В общедоступной печати упоминание о нём начинается с работы [1]. Какие-либо независимые публикации о применении такого метода мне неизвестны. Этот алгоритм сводится к последовательному исследованию интервалов монотонного изменения исходного полинома. Если на границах этого интервала монотонности значения полинома имеют разные знаки, то запускается процедура деления отрезка пополам для расчёта точного значения очередного корня. Границами интервалов монотонности являются точки, в которых значение производной полинома обращается в нуль, т.е. это корни производного полинома. Производный полином имеет степень на единицу меньшую, чем исходный полином, и процесс расчёта коэффициентов производных полиномов следует продолжить до полинома первой степени, корень которого находится непосредственно, без привлечения процедуры деления отрезка пополам. В результате этого шага получим два интервала монотонного изменения для производного полинома второй степени.
Теперь можно найти два вещественных корня производного полинома второй степени (если они существуют) и далее по лестнице из производных полиномов подниматься до корней исходного полинома. Остаётся пояснить, как технически реализуются границы «плюс, минус бесконечность» интервалов монотонности исходного и производных полиномов.
Нормируем полином так, чтобы коэффициент при старшей степени аргумента стал равным единице. Пусть M — наибольшее по модулю значение среди его остальных коэффициентов. Тогда значение полинома больше единицы для всех значений аргумента, больших, чем M+1.
Для доказательства рассмотрим расчёт полинома p(x)=x^n+k[n-1]*x^(n-1)+. +k[1]*x+k[0] по схеме Горнера.
На первом шаге вычисляется p[1]=k[n-1]+x и очевидно, что p[1]>1.
На втором шаге вычисляется p[2]=k[n-2]+x*p[1] и вновь очевидно, что p[2]>1.
Аналогичное имеет место на последующих шагах.
На последнем шаге вычисляется p(x)=k[0]+x*p[n-1] и окончательно получим p(x)>1.
Таким образом, если нужно определить знак полинома при бесконечном значении аргумента, следует взять аргумент равным M+1.
Прилагаемый текст соответствующей программы вполне заменяет занудное изложение отдельных технических подробностей описанного тут алгоритма.
Прокомментирую, наконец, не вполне очевидную особенность реализации алгоритма деления отрезка пополам.
Пробная точка pt, расположенная посередине между текущими концами ng и vg отрезка, вычисляется оператором pt=0.5*(ng+vg); а цикл делений пополам прерывается оператором if(pt =vg)break;.
В силу конечной точности представления вещественных чисел в машине рано или поздно наступает состояние, при котором операция деления пополам вместо нового числа даёт значение одной из исходных границ. Именно в этом состоянии следует прекратить цикл делений пополам. Это состояние соответствует максимально достижимой точности результата.
Недавно мне удалось использовать этот алгоритм для решения задачи вычисления комплексного корня полинома, не имеющего вещественных корней. Но об этом я планирую рассказать на Хабре в следующей статье.
Ниже, как приложение, приведен полный текст файла polynomRealRoots.cpp, реализующего описанныйалгоритм.
Примите также текст заголовочного файла polynomRealRoots.h, позволяющего легко организовать ссылку на приведенный выше программный модуль.
Литература
1. Костин И.К. Семейство алгоритмов расчета интервалов прохождения космического аппарата над круговым наземным объектом с учетом продольной ошибки определения параметров орбиты
Вопросы радиоэлектроники, сер. РЛТ, 2004г., вып. 1
Эту ссылку можно найти в Яндексе поиском по закавыченной фразе «семейство алгоритмов расчета», но текст этой статьи в электронном виде, кажется, недоступен. Поэтому приведу здесь цитату из двух предложений этой статьи:
Вещественный корень полинома всегда находится на участке монотонного изменения полинома, т.е. между корнями производной полинома.
Но производная полинома — это тоже полином, однако, меньшей степени и, найдя его вещественные корни, надо искать корни исходного полинома между корнями производной методом деления пополам.
Решение квадратных уравнений: формула корней, примеры
В продолжение темы «Решение уравнений» материал данной статьи познакомит вас с квадратными уравнениями.
Рассмотрим все подробно: суть и запись квадратного уравнения, зададим сопутствующие термины, разберем схему решения неполных и полных уравнений, познакомимся с формулой корней и дискриминантом, установим связи между корнями и коэффициентами, ну и конечно приведем наглядное решение практических примеров.
Квадратное уравнение, его виды
Квадратное уравнение – это уравнение, записанное как a · x 2 + b · x + c = 0 , где x – переменная, a , b и c – некоторые числа, при этом a не есть нуль.
Зачастую квадратные уравнения также носят название уравнений второй степени, поскольку по сути квадратное уравнение есть алгебраическое уравнение второй степени.
Приведем пример для иллюстрации заданного определения: 9 · x 2 + 16 · x + 2 = 0 ; 7 , 5 · x 2 + 3 , 1 · x + 0 , 11 = 0 и т.п. – это квадратные уравнения.
Числа a , b и c – это коэффициенты квадратного уравнения a · x 2 + b · x + c = 0 , при этом коэффициент a носит название первого, или старшего, или коэффициента при x 2 , b – второго коэффициента, или коэффициента при x , а c называют свободным членом.
К примеру, в квадратном уравнении 6 · x 2 − 2 · x − 11 = 0 старший коэффициент равен 6 , второй коэффициент есть − 2 , а свободный член равен − 11 . Обратим внимание на тот факт, что, когда коэффициенты b и/или c являются отрицательными, то используется краткая форма записи вида 6 · x 2 − 2 · x − 11 = 0 , а не 6 · x 2 + ( − 2 ) · x + ( − 11 ) = 0 .
Уточним также такой аспект: если коэффициенты a и/или b равны 1 или − 1 , то явного участия в записи квадратного уравнения они могут не принимать, что объясняется особенностями записи указанных числовых коэффициентов. К примеру, в квадратном уравнении y 2 − y + 7 = 0 старший коэффициент равен 1 , а второй коэффициент есть − 1 .
Приведенные и неприведенные квадратные уравнения
По значению первого коэффициента квадратные уравнения подразделяют на приведенные и неприведенные.
Приведенное квадратное уравнение – это квадратное уравнение, где старший коэффициент равен 1 . При иных значениях старшего коэффициента квадратное уравнение является неприведенным.
Приведем примеры: квадратные уравнения x 2 − 4 · x + 3 = 0 , x 2 − x − 4 5 = 0 являются приведенными, в каждом из которых старший коэффициент равен 1 .
9 · x 2 − x − 2 = 0 — неприведенное квадратное уравнение, где первый коэффициент отличен от 1 .
Любое неприведенное квадратное уравнение возможно преобразовать в приведенное уравнение, если разделить обе его части на первый коэффициент (равносильное преобразование). Преобразованное уравнение будет иметь такие же корни, как и заданное неприведенное уравнение или так же не иметь корней вовсе.
Рассмотрение конкретного примера позволит нам наглядно продемонстрировать выполнение перехода от неприведенного квадратного уравнения к приведенному.
Задано уравнение 6 · x 2 + 18 · x − 7 = 0 . Необходимо преобразовать исходное уравнение в приведенную форму.
Решение
Cогласно указанной выше схеме разделим обе части исходного уравнения на старший коэффициент 6 . Тогда получим: ( 6 · x 2 + 18 · x − 7 ) : 3 = 0 : 3 , и это то же самое, что: ( 6 · x 2 ) : 3 + ( 18 · x ) : 3 − 7 : 3 = 0 и далее: ( 6 : 6 ) · x 2 + ( 18 : 6 ) · x − 7 : 6 = 0 . Отсюда: x 2 + 3 · x — 1 1 6 = 0 . Таким образом, получено уравнение, равносильное заданному.
Ответ: x 2 + 3 · x — 1 1 6 = 0 .
Полные и неполные квадратные уравнения
Обратимся к определению квадратного уравнения. В нем мы уточнили, что a ≠ 0 . Подобное условие необходимо, чтобы уравнение a · x 2 + b · x + c = 0 было именно квадратным, поскольку при a = 0 оно по сути преобразуется в линейное уравнение b · x + c = 0 .
В случае же, когда коэффициенты b и c равны нулю (что возможно, как по отдельности, так и совместно), квадратное уравнение носит название неполного.
Неполное квадратное уравнение – такое квадратное уравнение a · x 2 + b · x + c = 0 , где хотя бы один из коэффициентов b и c (или оба) равен нулю.
Полное квадратное уравнение – квадратное уравнение, в котором все числовые коэффициенты не равны нулю.
Порассуждаем, почему типам квадратных уравнений даны именно такие названия.
При b = 0 квадратное уравнение примет вид a · x 2 + 0 · x + c = 0 , что то же самое, что a · x 2 + c = 0 . При c = 0 квадратное уравнение записано как a · x 2 + b · x + 0 = 0 , что равносильно a · x 2 + b · x = 0 . При b = 0 и c = 0 уравнение примет вид a · x 2 = 0 . Уравнения, которые мы получили, отличны от полного квадратного уравнения тем, что в их левых частях не содержится либо слагаемого с переменной x , либо свободного члена, либо обоих сразу. Собственно, этот факт и задал название такому типу уравнений – неполное.
Например, x 2 + 3 · x + 4 = 0 и − 7 · x 2 − 2 · x + 1 , 3 = 0 – это полные квадратные уравнения; x 2 = 0 , − 5 · x 2 = 0 ; 11 · x 2 + 2 = 0 , − x 2 − 6 · x = 0 – неполные квадратные уравнения.
Решение неполных квадратных уравнений
Заданное выше определение дает возможность выделить следующие виды неполных квадратных уравнений:
- a · x 2 = 0 , такому уравнению соответствуют коэффициенты b = 0 и c = 0 ;
- a · x 2 + c = 0 при b = 0 ;
- a · x 2 + b · x = 0 при c = 0 .
Рассмотрим последовательно решение каждого вида неполного квадратного уравнения.
Решение уравнения a·x 2 =0
Как уже было указано выше, такому уравнению отвечают коэффициенты b и c , равные нулю. Уравнение a · x 2 = 0 возможно преобразовать в равносильное ему уравнение x 2 = 0 , которое мы получим, поделив обе части исходного уравнения на число a , не равное нулю. Очевидный факт, что корень уравнения x 2 = 0 это нуль, поскольку 0 2 = 0 . Иных корней это уравнение не имеет, что объяснимо свойствами степени: для любого числа p , не равного нулю, верно неравенство p 2 > 0 , из чего следует, что при p ≠ 0 равенство p 2 = 0 никогда не будет достигнуто.
Таким образом, для неполного квадратного уравнение a · x 2 = 0 существует единственный корень x = 0 .
Для примера решим неполное квадратное уравнение − 3 · x 2 = 0 . Ему равносильно уравнение x 2 = 0 , его единственным корнем является x = 0 , тогда и исходное уравнение имеет единственный корень — нуль.
Кратко решение оформляется так:
− 3 · x 2 = 0 , x 2 = 0 , x = 0 .
Решение уравнения a · x 2 + c = 0
На очереди — решение неполных квадратных уравнений, где b = 0 , c ≠ 0 , то есть уравнений вида a · x 2 + c = 0 . Преобразуем это уравнение, перенеся слагаемое из одной части уравнения в другую, сменив знак на противоположный и разделив обе части уравнения на число, не равное нулю:
- переносим c в правую часть, что дает уравнение a · x 2 = − c ;
- делим обе части уравнения на a , получаем в итоге x = — c a .
Наши преобразования являются равносильными, соответственно полученное уравнение также равносильно исходному, и этот факт дает возможность делать вывод о корнях уравнения. От того, каковы значения a и c зависит значение выражения — c a : оно может иметь знак минус (допустим, если a = 1 и c = 2 , тогда — c a = — 2 1 = — 2 ) или знак плюс (например, если a = − 2 и c = 6 , то — c a = — 6 — 2 = 3 ); оно не равно нулю, поскольку c ≠ 0 . Подробнее остановимся на ситуациях, когда — c a 0 и — c a > 0 .
В случае, когда — c a 0 , уравнение x 2 = — c a не будет иметь корней. Утверждая это, мы опираемся на то, что квадратом любого числа является число неотрицательное. Из сказанного следует, что при — c a 0 ни для какого числа p равенство p 2 = — c a не может быть верным.
Все иначе, когда — c a > 0 : вспомним о квадратном корне, и станет очевидно, что корнем уравнения x 2 = — c a будет число — c a , поскольку — c a 2 = — c a . Нетрудно понять, что число — — c a — также корень уравнения x 2 = — c a : действительно, — — c a 2 = — c a .
Прочих корней уравнение не будет иметь. Мы можем это продемонстрировать, используя метод от противного. Для начала зададим обозначения найденных выше корней как x 1 и − x 1 . Выскажем предположение, что уравнение x 2 = — c a имеет также корень x 2 , который отличается от корней x 1 и − x 1 . Мы знаем, что, подставив в уравнение вместо x его корни, преобразуем уравнение в справедливое числовое равенство.
Для x 1 и − x 1 запишем: x 1 2 = — c a , а для x 2 — x 2 2 = — c a . Опираясь на свойства числовых равенств, почленно вычтем одно верное равенство из другого, что даст нам: x 1 2 − x 2 2 = 0 . Используем свойства действий с числами, чтобы переписать последнее равенство как ( x 1 − x 2 ) · ( x 1 + x 2 ) = 0 . Известно, что произведение двух чисел есть нуль тогда и только тогда, когда хотя бы одно из чисел является нулем. Из сказанного следует, что x 1 − x 2 = 0 и/или x 1 + x 2 = 0 , что то же самое, x 2 = x 1 и/или x 2 = − x 1 . Возникло очевидное противоречие, ведь вначале было условлено, что корень уравнения x 2 отличается от x 1 и − x 1 . Так, мы доказали, что уравнение не имеет иных корней, кроме x = — c a и x = — — c a .
Резюмируем все рассуждения выше.
Неполное квадратное уравнение a · x 2 + c = 0 равносильно уравнению x 2 = — c a , которое:
- не будет иметь корней при — c a 0 ;
- будет иметь два корня x = — c a и x = — — c a при — c a > 0 .
Приведем примеры решения уравнений a · x 2 + c = 0 .
Задано квадратное уравнение 9 · x 2 + 7 = 0 . Необходимо найти его решение.
Решение
Перенесем свободный член в правую часть уравнения, тогда уравнение примет вид 9 · x 2 = − 7 .
Разделим обе части полученного уравнения на 9 , придем к x 2 = — 7 9 . В правой части мы видим число со знаком минус, что означает: у заданного уравнения нет корней. Тогда и исходное неполное квадратное уравнение 9 · x 2 + 7 = 0 не будет иметь корней.
Ответ: уравнение 9 · x 2 + 7 = 0 не имеет корней.
Необходимо решить уравнение − x 2 + 36 = 0 .
Решение
Перенесем 36 в правую часть: − x 2 = − 36 .
Разделим обе части на − 1 , получим x 2 = 36 . В правой части — положительное число, отсюда можно сделать вывод, что x = 36 или x = — 36 .
Извлечем корень и запишем окончательный итог: неполное квадратное уравнение − x 2 + 36 = 0 имеет два корня x = 6 или x = − 6 .
Ответ: x = 6 или x = − 6 .
Решение уравнения a·x 2 +b·x=0
Разберем третий вид неполных квадратных уравнений, когда c = 0 . Чтобы найти решение неполного квадратного уравнения a · x 2 + b · x = 0 , воспользуемся методом разложения на множители. Разложим на множители многочлен, который находится в левой части уравнения, вынеся за скобки общий множитель x . Этот шаг даст возможность преобразовать исходное неполное квадратное уравнение в равносильное ему x · ( a · x + b ) = 0 . А это уравнение, в свою очередь, равносильно совокупности уравнений x = 0 и a · x + b = 0 . Уравнение a · x + b = 0 линейное, и корень его: x = − b a .
Таким образом, неполное квадратное уравнение a · x 2 + b · x = 0 будет иметь два корня x = 0 и x = − b a .
Закрепим материал примером.
Необходимо найти решение уравнения 2 3 · x 2 — 2 2 7 · x = 0 .
Решение
Вынесем x за скобки и получим уравнение x · 2 3 · x — 2 2 7 = 0 . Это уравнение равносильно уравнениям x = 0 и 2 3 · x — 2 2 7 = 0 . Теперь следует решить полученное линейное уравнение: 2 3 · x = 2 2 7 , x = 2 2 7 2 3 .
Далее осуществим деление смешанного числа на обыкновенную дробь и определяем, что x = 3 3 7 . Таким образом, корни исходного уравнения это: x = 0 и x = 3 3 7 .
Кратко решение уравнения запишем так:
2 3 · x 2 — 2 2 7 · x = 0 x · 2 3 · x — 2 2 7 = 0
x = 0 или 2 3 · x — 2 2 7 = 0
x = 0 или x = 3 3 7
Ответ: x = 0 , x = 3 3 7 .
Дискриминант, формула корней квадратного уравнения
Для нахождения решения квадратных уравнений существует формула корней:
x = — b ± D 2 · a , где D = b 2 − 4 · a · c – так называемый дискриминант квадратного уравнения.
Запись x = — b ± D 2 · a по сути означает, что x 1 = — b + D 2 · a , x 2 = — b — D 2 · a .
Нелишним будет понимать, как была выведена указанная формула и каким образом ее применять.
Вывод формулы корней квадратного уравнения
Пускай перед нами стоит задача решить квадратное уравнение a · x 2 + b · x + c = 0 . Осуществим ряд равносильных преобразований:
- разделим обе части уравнения на число a, отличное от нуля, получим приведенное квадратное уравнение: x 2 + b a · x + c a = 0 ;
- выделим полный квадрат в левой части получившегося уравнения:
x 2 + b a · x + c a = x 2 + 2 · b 2 · a · x + b 2 · a 2 — b 2 · a 2 + c a = = x + b 2 · a 2 — b 2 · a 2 + c a
После этого уравнения примет вид: x + b 2 · a 2 — b 2 · a 2 + c a = 0 ; - теперь возможно сделать перенос двух последних слагаемых в правую часть, сменив знак на противоположный, после чего получаем: x + b 2 · a 2 = b 2 · a 2 — c a ;
- наконец, преобразуем выражение, записанное в правой части последнего равенства:
b 2 · a 2 — c a = b 2 4 · a 2 — c a = b 2 4 · a 2 — 4 · a · c 4 · a 2 = b 2 — 4 · a · c 4 · a 2 .
Таким образом, мы пришли к уравнению x + b 2 · a 2 = b 2 — 4 · a · c 4 · a 2 , равносильному исходному уравнению a · x 2 + b · x + c = 0 .
Решение подобных уравнений мы разбирали в предыдущих пунктах (решение неполных квадратных уравнений). Уже полученный опыт дает возможность сделать вывод касательно корней уравнения x + b 2 · a 2 = b 2 — 4 · a · c 4 · a 2 :
- при b 2 — 4 · a · c 4 · a 2 0 уравнение не имеет действительных решений;
- при b 2 — 4 · a · c 4 · a 2 = 0 уравнение имеет вид x + b 2 · a 2 = 0 , тогда x + b 2 · a = 0 .
Отсюда очевиден единственный корень x = — b 2 · a ;
- при b 2 — 4 · a · c 4 · a 2 > 0 верным будет: x + b 2 · a = b 2 — 4 · a · c 4 · a 2 или x = b 2 · a — b 2 — 4 · a · c 4 · a 2 , что то же самое, что x + — b 2 · a = b 2 — 4 · a · c 4 · a 2 или x = — b 2 · a — b 2 — 4 · a · c 4 · a 2 , т.е. уравнение имеет два корня.
Возможно сделать вывод, что наличие или отсутствие корней уравнения x + b 2 · a 2 = b 2 — 4 · a · c 4 · a 2 (а значит и исходного уравнения) зависит от знака выражения b 2 — 4 · a · c 4 · a 2 , записанного в правой части. А знак этого выражения задается знаком числителя, (знаменатель 4 · a 2 всегда будет положителен), то есть, знаком выражения b 2 − 4 · a · c . Этому выражению b 2 − 4 · a · c дано название — дискриминант квадратного уравнения и определена в качестве его обозначения буква D . Здесь можно записать суть дискриминанта – по его значению и знаку делают вывод, будет ли квадратное уравнение иметь действительные корни, и, если будет, то каково количество корней — один или два.
Вернемся к уравнению x + b 2 · a 2 = b 2 — 4 · a · c 4 · a 2 . Перепишем его, используя обозначение дискриминанта: x + b 2 · a 2 = D 4 · a 2 .
Вновь сформулируем выводы:
- при D 0 уравнение не имеет действительных корней;
- при D = 0 уравнение имеет единственный корень x = — b 2 · a ;
- при D > 0 уравнение имеет два корня: x = — b 2 · a + D 4 · a 2 или x = — b 2 · a — D 4 · a 2 . Эти корни на основе свойства радикалов возможно записать в виде: x = — b 2 · a + D 2 · a или — b 2 · a — D 2 · a . А, когда раскроем модули и приведем дроби к общему знаменателю, получим: x = — b + D 2 · a , x = — b — D 2 · a .
Так, результатом наших рассуждений стало выведение формулы корней квадратного уравнения:
x = — b + D 2 · a , x = — b — D 2 · a , дискриминант D вычисляется по формуле D = b 2 − 4 · a · c .
Данные формулы дают возможность при дискриминанте больше нуля определить оба действительных корня. Когда дискриминант равен нулю, применение обеих формул даст один и тот же корень, как единственное решение квадратного уравнения. В случае, когда дискриминант отрицателен, попытавшись использовать формулу корня квадратного уравнения, мы столкнемся с необходимостью извлечь квадратный корень из отрицательного числа, что выведет нас за рамки действительных чисел. При отрицательном дискриминанте у квадратного уравнения не будет действительных корней, но возможна пара комплексно сопряженных корней, определяемых теми же полученными нами формулами корней.
Алгоритм решения квадратных уравнений по формулам корней
Решить квадратное уравнение возможно, сразу задействуя формулу корней, но в основном так поступают при необходимости найти комплексные корни.
В основной же массе случаев обычно подразумевается поиск не комплексных, а действительных корней квадратного уравнения. Тогда оптимально перед тем, как использовать формулы корней квадратного уравнения, сначала определить дискриминант и удостовериться, что он не является отрицательным (в ином случае сделаем вывод, что у уравнения нет действительных корней), а после приступить к вычислению значения корней.
Рассуждения выше дают возможность сформулировать алгоритм решения квадратного уравнения.
Чтобы решить квадратное уравнение a · x 2 + b · x + c = 0 , необходимо:
- по формуле D = b 2 − 4 · a · c найти значение дискриминанта;
- при D 0 сделать вывод об отсутствии у квадратного уравнения действительных корней;
- при D = 0 найти единственный корень уравнения по формуле x = — b 2 · a ;
- при D > 0 определить два действительных корня квадратного уравнения по формуле x = — b ± D 2 · a .
Отметим, что, когда дискриминант есть нуль, можно использовать формулу x = — b ± D 2 · a , она даст тот же результат, что и формула x = — b 2 · a .
Примеры решения квадратных уравнений
Приведем решение примеров при различных значениях дискриминанта.
Необходимо найти корни уравнения x 2 + 2 · x − 6 = 0 .
Решение
Запишем числовые коэффициенты квадратного уравнения: a = 1 , b = 2 и c = − 6 . Далее действуем по алгоритму, т.е. приступим к вычислению дискриминанта, для чего подставим коэффициенты a , b и c в формулу дискриминанта: D = b 2 − 4 · a · c = 2 2 − 4 · 1 · ( − 6 ) = 4 + 24 = 28 .
Итак, мы получили D > 0 , а это означает, что исходное уравнение будет иметь два действительных корня.
Для их нахождения используем формулу корня x = — b ± D 2 · a и, подставив соответствующие значения, получим: x = — 2 ± 28 2 · 1 . Упростим полученное выражение, вынеся множитель за знак корня с последующим сокращением дроби:
x = — 2 + 2 · 7 2 или x = — 2 — 2 · 7 2
x = — 1 + 7 или x = — 1 — 7
Ответ: x = — 1 + 7 , x = — 1 — 7 .
Необходимо решить квадратное уравнение − 4 · x 2 + 28 · x − 49 = 0 .
Решение
Определим дискриминант: D = 28 2 − 4 · ( − 4 ) · ( − 49 ) = 784 − 784 = 0 . При таком значении дискриминанта исходное уравнение будет иметь лишь один корень, определяемый по формуле x = — b 2 · a .
x = — 28 2 · ( — 4 ) x = 3 , 5
Ответ: x = 3 , 5 .
Необходимо решить уравнение 5 · y 2 + 6 · y + 2 = 0
Решение
Числовые коэффициенты этого уравнения будут: a = 5 , b = 6 и c = 2 . Используем эти значения для нахождения дискриминанта: D = b 2 − 4 · a · c = 6 2 − 4 · 5 · 2 = 36 − 40 = − 4 . Вычисленный дискриминант отрицателен, таким образом, исходное квадратное уравнение не имеет действительных корней.
В случае, когда стоит задача указать комплексные корни, применим формулу корней, выполняя действия с комплексными числами:
x = — 6 + 2 · i 10 или x = — 6 — 2 · i 10 ,
x = — 3 5 + 1 5 · i или x = — 3 5 — 1 5 · i .
Ответ: действительные корни отсутствуют; комплексные корни следующие: — 3 5 + 1 5 · i , — 3 5 — 1 5 · i .
В школьной программе стандартно нет требования искать комплексные корни, поэтому, если в ходе решения дискриминант определен как отрицательный, сразу записывается ответ, что действительных корней нет.
Формула корней для четных вторых коэффициентов
Формула корней x = — b ± D 2 · a ( D = b 2 − 4 · a · c ) дает возможность получить еще одну формулу, более компактную, позволяющую находить решения квадратных уравнений с четным коэффициентом при x (либо с коэффициентом вида 2 · n , к примеру, 2 · 3 или 14 · ln 5 = 2 · 7 · ln 5 ). Покажем, как выводится эта формула.
Пусть перед нами стоит задача найти решение квадратного уравнения a · x 2 + 2 · n · x + c = 0 . Действуем по алгоритму: определяем дискриминант D = ( 2 · n ) 2 − 4 · a · c = 4 · n 2 − 4 · a · c = 4 · ( n 2 − a · c ) , а затем используем формулу корней:
x = — 2 · n ± D 2 · a , x = — 2 · n ± 4 · n 2 — a · c 2 · a , x = — 2 · n ± 2 n 2 — a · c 2 · a , x = — n ± n 2 — a · c a .
Пусть выражение n 2 − a · c будет обозначено как D 1 (иногда его обозначают D ‘ ). Тогда формула корней рассматриваемого квадратного уравнения со вторым коэффициентом 2 · n примет вид:
x = — n ± D 1 a , где D 1 = n 2 − a · c .
Легко увидеть, что что D = 4 · D 1 , или D 1 = D 4 . Иначе говоря, D 1 – это четверть дискриминанта. Очевидно, что знак D 1 такой же, как знак D , а значит знак D 1 также может служить индикатором наличия или отсутствия корней квадратного уравнения.
Таким образом, чтобы найти решение квадратного уравнения со вторым коэффициентом 2 · n , необходимо:
- найти D 1 = n 2 − a · c ;
- при D 1 0 сделать вывод, что действительных корней нет;
- при D 1 = 0 определить единственный корень уравнения по формуле x = — n a ;
- при D 1 > 0 определить два действительных корня по формуле x = — n ± D 1 a .
Необходимо решить квадратное уравнение 5 · x 2 − 6 · x − 32 = 0 .
Решение
Второй коэффициент заданного уравнения можем представить как 2 · ( − 3 ) . Тогда перепишем заданное квадратное уравнение как 5 · x 2 + 2 · ( − 3 ) · x − 32 = 0 , где a = 5 , n = − 3 и c = − 32 .
Вычислим четвертую часть дискриминанта: D 1 = n 2 − a · c = ( − 3 ) 2 − 5 · ( − 32 ) = 9 + 160 = 169 . Полученное значение положительно, это означает, что уравнение имеет два действительных корня. Определим их по соответствующей формуле корней:
x = — n ± D 1 a , x = — — 3 ± 169 5 , x = 3 ± 13 5 ,
x = 3 + 13 5 или x = 3 — 13 5
x = 3 1 5 или x = — 2
Возможно было бы произвести вычисления и по обычной формуле корней квадратного уравнения, но в таком случае решение было бы более громоздким.
Ответ: x = 3 1 5 или x = — 2 .
Упрощение вида квадратных уравнений
Иногда существует возможность оптимизировать вид исходного уравнения, что позволит упростить процесс вычисления корней.
К примеру, квадратное уравнение 12 · x 2 − 4 · x − 7 = 0 явно удобнее для решения, чем 1200 · x 2 − 400 · x − 700 = 0 .
Чаще упрощение вида квадратного уравнения производится действиями умножения или деления его обеих частей на некое число. К примеру, выше мы показали упрощенную запись уравнения 1200 · x 2 − 400 · x − 700 = 0 , полученную делением обеих его частей на 100 .
Такое преобразование возможно, когда коэффициенты квадратного уравнения не являются взаимно простыми числами. Тогда обычно осуществляют деление обеих частей уравнения на наибольший общий делитель абсолютных величин его коэффициентов.
Как пример используем квадратное уравнение 12 · x 2 − 42 · x + 48 = 0 . Определим НОД абсолютных величин его коэффициентов: НОД ( 12 , 42 , 48 ) = НОД(НОД ( 12 , 42 ) , 48 ) = НОД ( 6 , 48 ) = 6 . Произведем деление обеих частей исходного квадратного уравнения на 6 и получим равносильное ему квадратное уравнение 2 · x 2 − 7 · x + 8 = 0 .
Умножением обеих частей квадратного уравнения обычно избавляются от дробных коэффициентов. При этом умножают на наименьшее общее кратное знаменателей его коэффициентов. К примеру, если каждую часть квадратного уравнения 1 6 · x 2 + 2 3 · x — 3 = 0 перемножить с НОК ( 6 , 3 , 1 ) = 6 , то оно станет записано в более простом виде x 2 + 4 · x − 18 = 0 .
Напоследок отметим, что почти всегда избавляются от минуса при первом коэффициенте квадратного уравнения, изменяя знаки каждого члена уравнения, что достигается путем умножения (или деления) обеих частей на − 1 . К примеру, от квадратного уравнения − 2 · x 2 − 3 · x + 7 = 0 можно перейти к упрощенной его версии 2 · x 2 + 3 · x − 7 = 0 .
Связь между корнями и коэффициентами
Уже известная нам формула корней квадратных уравнений x = — b ± D 2 · a выражает корни уравнения через его числовые коэффициенты. Опираясь на данную формулу, мы имеем возможность задать другие зависимости между корнями и коэффициентами.
Самыми известными и применимыми являются формулы теоремы Виета:
x 1 + x 2 = — b a и x 2 = c a .
В частности, для приведенного квадратного уравнения сумма корней есть второй коэффициент с противоположным знаком, а произведение корней равно свободному члену. К примеру, по виду квадратного уравнения 3 · x 2 − 7 · x + 22 = 0 возможно сразу определить, что сумма его корней равна 7 3 , а произведение корней — 22 3 .
Также можно найти ряд прочих связей между корнями и коэффициентами квадратного уравнения. Например, сумма квадратов корней квадратного уравнения может быть выражена через коэффициенты:
x 1 2 + x 2 2 = ( x 1 + x 2 ) 2 — 2 · x 1 · x 2 = — b a 2 — 2 · c a = b 2 a 2 — 2 · c a = b 2 — 2 · a · c a 2 .
Решения кубических уравнений с вещественными коэффициентами. Универсальные методы. Дискриминант кубического уравнения. Формула Виета для кубического уравнения.
Решения кубических уравнений с вещественными коэффициентами. Универсальные методы. Дискриминант кубического уравнения. Формула Виета для кубического уравнения.
Кубическим уравнением называется уравнение вида
- ax 3 + bx 2 + cx +d = 0 , (1)
- где a, b,c ,d — постоянные коэффициенты, а х — переменная.
Мы рассмотрим случай, когда коэффициенты являются веществеными числами.
Корни кубического уравнения. Нахождение корней (решение) кубического уравнения.
Число х называется корнем кубического уравнения (1), если при его подстановке уравнение (1) обращается в верное равенство.
Кубическое уравнение имеет не более трех корней (над комплексным полем всегда три корня, с учетом кратности) . И всегда имеет хотя бы 1 (вещественный) корень. Все возможные случаи состава корней легко определить с помощью знака дискриминанта кубического уравнения, т.е.:
Δ= -4b 3 d + b 2 c 2 — 4ac 3 + 18abcd — 27a 2 d 2 (Да, это дискриминант кубического уравнения)
Итак, возможны только 3 следующих случая:
- Δ > 0 — тогда уравнение имеет 3 различных корня. (Для продвинутых — три различных вещественных корня)
- Δ 3 + py + q = 0 (2)
К такому виду можно привести любое кубическое уравнение вида (1) с помощью следующей замены:
- x= y — b/3a (3)
- p= — b 2 /3a 2 + c/a
- q= 2b 3 /27a 3 — bc/3a 2 + d/a
Итак, приступим к вычислению корней. Найдем следующие величины:
Дискриминант уравнения (2) в этом случае равен
Дискриминант исходного уравнения (1) будет иметь тот же знак , что и вышеуказанный дискриминант. Корни уравнения (2) выражаются следующим образом:
Соответственно, если Q>0, то уравнения (2) и (1) будут иметь лишь 1 (вещественный) корень, y1. Подставим его в (3) и найдем х для уравнения (1). (если вас интересуют также мнимые корни, то просто вычислите еще и y2, y3 и подставьте их в (3).
Если Q 3 + ax 2 + bx +c = 0 (4)
Очевидно, любое уравнение вида (1) можно привести к виду (4), просто поделив его на коэффициент а.
Итак, алгоритм применения этой формулы:
3. a) Если S>0, то вычисляем
И наше уравнение имеет 3 корня (вещественных):
Тогда единственный корень (вещественный): x1= -2sgn(R)*|Q| 1/2 *ch(φ) — a/3
Для тех, кого интересуют также и мнимые корни:
- ch(x)=(e x +e -x )/2
- Arch(x) = ln(x + (x 2 -1) 1/2 )
- sh(x)=(e x -e -x )/2
- sgn(x) — знак х
в) Если S=0,то уравнение имеет меньше трех различных решений:
Консультации и техническая
поддержка сайта: Zavarka Team
http://zaochnik.com/spravochnik/matematika/systems/reshenie-kvadratnyh-uravnenij/
http://dpva.ru/Guide/GuideMathematics/Equations/cubeEquationsUniversalMethods/
Алгоритм расчёта вещественных корней полиномов
Время на прочтение
8 мин
Количество просмотров 29K
Основополагающая идея этого алгоритма очень проста и может быть изложена двумя предложениями. Вещественный корень полинома всегда находится на участке монотонного изменения полинома, т.е. между корнями производной полинома. Но производная полинома — это тоже полином, однако, меньшей степени и, найдя его вещественные корни, надо искать корни исходного полинома между корнями производной методом деления пополам.
А теперь по порядку.
Проблема нахождения корней алгебраических полиномов известна давно, по крайней мере со средневековья. В школе учат решать квадратные уравнения. В википедии можно найти формулы Кардано для решения кубических уравнений и описание метода Феррари для решения в радикалах уравнения четвёртой степени. Там же описан метод Лобачевского для решения алгебраических уравнений произвольной степени. Суть метода Лобачевского вкратце сводится к следующему.
Нетрудно, имея некоторый исходный полином, построить полином2, имеющий те же по модулю корни, что и исходный полином, но с противоположным знаком. Перемножая исходный полином и полином2, получаем полином, корни которого равны квадратам корней исходного полинома.
Это преобразование (квадрирование) полезно повторить несколько раз. В результате, если корни исходного полинома не были равны друг другу, их многократно квадрированные значения оказываются далеко разнесёнными по величине, а их приближенные значения очень просто выражаются через коэффициенты соответствующего квадрированного полинома.
В частности, если коэффициент при старшей степени аргумента полинома равен единице, то следующий по старшинству коэффициент равен (с обратным знаком) сумме корней уравнения, а поскольку значения этих корней сильно разнесены, то приближенно можно считать эту сумму равной наибольшему по модулю корню.
Для конкретности сообщим, что для полинома 4-й степени с корнями 1, 2, 3, 4 метод Лобачевского уже после четвёртого квадрирования даёт правильные до второго знака после запятой значения корней. При этом для представления коэффициентов полиномов достаточно формата long double.
Бесспорно, этот метод является ценным инструментом в руках исследователя, наделённого интеллектом. Однако, его программирование для современной вычислительной техники вызывает серьёзные затруднения при необходимости строгой гарантии достоверности результата при всевозможных особых случаях расположения корней.
Теперь я начну описывать иной метод. В общедоступной печати упоминание о нём начинается с работы [1]. Какие-либо независимые публикации о применении такого метода мне неизвестны. Этот алгоритм сводится к последовательному исследованию интервалов монотонного изменения исходного полинома. Если на границах этого интервала монотонности значения полинома имеют разные знаки, то запускается процедура деления отрезка пополам для расчёта точного значения очередного корня. Границами интервалов монотонности являются точки, в которых значение производной полинома обращается в нуль, т.е. это корни производного полинома. Производный полином имеет степень на единицу меньшую, чем исходный полином, и процесс расчёта коэффициентов производных полиномов следует продолжить до полинома первой степени, корень которого находится непосредственно, без привлечения процедуры деления отрезка пополам. В результате этого шага получим два интервала монотонного изменения для производного полинома второй степени.
Теперь можно найти два вещественных корня производного полинома второй степени (если они существуют) и далее по лестнице из производных полиномов подниматься до корней исходного полинома. Остаётся пояснить, как технически реализуются границы «плюс, минус бесконечность» интервалов монотонности исходного и производных полиномов.
Нормируем полином так, чтобы коэффициент при старшей степени аргумента стал равным единице. Пусть M — наибольшее по модулю значение среди его остальных коэффициентов. Тогда значение полинома больше единицы для всех значений аргумента, больших, чем M+1.
Для доказательства рассмотрим расчёт полинома p(x)=x^n+k[n-1]*x^(n-1)+…+k[1]*x+k[0] по схеме Горнера.
На первом шаге вычисляется p[1]=k[n-1]+x и очевидно, что p[1]>1.
На втором шаге вычисляется p[2]=k[n-2]+x*p[1] и вновь очевидно, что p[2]>1.
Аналогичное имеет место на последующих шагах.
На последнем шаге вычисляется p(x)=k[0]+x*p[n-1] и окончательно получим p(x)>1.
Таким образом, если нужно определить знак полинома при бесконечном значении аргумента, следует взять аргумент равным M+1.
Прилагаемый текст соответствующей программы вполне заменяет занудное изложение отдельных технических подробностей описанного тут алгоритма.
Прокомментирую, наконец, не вполне очевидную особенность реализации алгоритма деления отрезка пополам.
Пробная точка pt, расположенная посередине между текущими концами ng и vg отрезка, вычисляется оператором pt=0.5*(ng+vg); а цикл делений пополам прерывается оператором if(pt<=ng||pt>=vg)break;.
В силу конечной точности представления вещественных чисел в машине рано или поздно наступает состояние, при котором операция деления пополам вместо нового числа даёт значение одной из исходных границ. Именно в этом состоянии следует прекратить цикл делений пополам. Это состояние соответствует максимально достижимой точности результата.
Недавно мне удалось использовать этот алгоритм для решения задачи вычисления комплексного корня полинома, не имеющего вещественных корней. Но об этом я планирую рассказать на Хабре в следующей статье.
Ниже, как приложение, приведен полный текст файла polynomRealRoots.cpp, реализующего описанныйалгоритм.
файл polynomRealRoots.cpp
//*************************************************************************
double polinom(int n,double x,double *k)
//полином вида x^n+k[n-1]*x^(n-1)+k[n-2]*x^(n-2)+...+k[1]*x+k[0]
//со старшим коэффициентом, равным единице
{
double s=1;
for(int i=n-1;i>=0;i--)
s=s*x+k[i];
return s;
}//polinom
//расчёт корня полинома методом деления пополам отрезка, содержащего этот корень
double dihot(int degree,double edgeNegativ,double edgePositiv,double *kf)
{
for(;;)
{//цикл деления отрезка пополам
double x=0.5*(edgeNegativ+edgePositiv);
if(x==edgeNegativ||x==edgePositiv)return x;
if(polinom(degree,x,kf)<0)edgeNegativ=x;
else edgePositiv=x;
}//цикл деления отрезка пополам
}//dihot
//один шаг подъёма по лестнице из производных полиномов
void stepUp(
int level, //индекс достигаемой ступеньки лестницы
double **A, //вспомогательные массивы
double **B, //параметров производных полиномов
int *currentRootsCount //сформированные в вызывающей процедуре
)
{
//аргумент полинома, равносильный его бесконечно большому значению
double major=0;
for(int i=0;i<level;i++)
{//формирование major
double s=fabs(A[level][i]);
if(s>major)major=s;
}//формирование major
major+=1.0;
currentRootsCount[level]=0; //рабочая инициализация
//основной цикл поиска корня уравнения
//A[level][0]+A[level][1]*x+...+A[level][level-1]*x^(level-1)+x^level=0
//на очередном интервале монотонности
for(int i=0;i<=currentRootsCount[level-1];i++)
{//очередной интервал монотонности
//signLeft signRight - знаки текущего A-полинома на левой и правой границе интервала монотонности
int signLeft,signRight;
//предварительная левая и правая границы интервала поиска
double edgeLeft,edgeRight;
//границы интервала монотонности, несущие информацию о знаке полинома на них
double edgeNegativ,edgePositiv;
//формирование левой границы поиска
if(i==0)edgeLeft=-major;
else edgeLeft=B[level-1][i-1];
//значение текущего A-полинома на левой границе
double rb=polinom(level,edgeLeft,A[level]);
if(rb==0)
{//маловероятный случай попадания в корень
B[level][currentRootsCount[level]]=edgeLeft;
currentRootsCount[level]++;
continue;
}//маловероятный случай попадания в корень
//запомнить знак текущего A-полинома на левой границе
if(rb>0)signLeft=1;else signLeft=-1;
//формирование правой границы поиска
if(i==currentRootsCount[level-1])edgeRight=major;
else edgeRight=B[level-1][i];
//значение текущего A-полинома на правой границе
rb=polinom(level,edgeRight,A[level]);
if(rb==0)
{//маловероятный случай попадания в корень
B[level][currentRootsCount[level]]=edgeRight;
currentRootsCount[level]++;
continue;
}//маловероятный случай попадания в корень
//запомнить знак текущего A-полинома на правой границе
if(rb>0)signRight=1;else signRight=-1;
//если знаки полинома на границах интервала монотонности совпадают,
//то корня нет
if(signLeft==signRight)continue;
//теперь можно определить плюс границу и минус границу поиска корня
if(signLeft<0){edgeNegativ=edgeLeft;edgePositiv=edgeRight;}
else {edgeNegativ=edgeRight;edgePositiv=edgeLeft;}
//всё готово для локализации корня методом деления пополам интервала поиска
B[level][currentRootsCount[level]]=dihot(level,edgeNegativ,edgePositiv,A[level]);
currentRootsCount[level]++;
}//очередной интервал монотонности
return;
}//stepUp
//процедура находит все вещественные корни полинома любой степени
void polynomRealRoots(
int n, //степень исходного полинома
double *kf, //массив коэффициентов исходного полинома
double *rootsArray, //выходной массив вычисленных корней
int &rootsCount //количество найденных корней
)
{
//используются вспомогательные массивы A и B, имеющие следующее содержание
//A это коэффициенты а B корни производных полиномов
//все A-полиномы нормируются так,
//чтобы коэффициент при старшей степени был равен единице
//A[n] - это массив нормированных коэффициентов исходного полинома
//B[n] - это массив корней исходного полинома
//A[n-1] - это массив нормированных коэффициентов производного полинома
//B[n-1] - это массив корней производного полинома
//аналогичным образом
//A[n-2] и B[n-2] - это коэффициенты и корни дважды производного полинома
//наконец A[1] - это массив коэффициентов последнего полинома
//в цепочке производных полиномов
//это линейный полином и B[1] - это массив его корней,
//представленный единственным значимым элементом
//выделение памяти для вспомогательных массивов
double **A=new double *[n+1];
double **B=new double *[n+1];
//количество вещественных корней для каждого из A-полиномов
int *currentRootsCount=new int[n+1];
for(int i=1;i<=n;i++)
{
A[i]=new double[i];
B[i]=new double[i];
}
//нормировка исходного полинома
for(int i=0;i<n;i++)A[n][i]=kf[i]/kf[n];
//расчёт производных A-полиномов
for(int i1=n,i=n-1;i>0;i1=i,i--)
{
for(int j1=i,j=i-1;j>=0;j1=j,j--)
{
A[i][j]=A[i1][j1]*j1/i1;
}
}
//формирование исходного корня последнего производного полинома
currentRootsCount[1]=1;
B[1][0]=-A[1][0];
//подъём по лестнице производных полиномов
for(int i=2;i<=n;i++)stepUp(i,A,B,currentRootsCount);
//формирование результата
rootsCount=currentRootsCount[n];
for(int i=0;i<rootsCount;i++)rootsArray[i]=B[n][i];
//очистка памяти
for(int i=1;i<=n;i++)
{
delete[]A[i];
delete[]B[i];
}
delete[]A;
delete[]B;
delete[]currentRootsCount;
return;
}//polynomRealRoots
//*************************************************************************
Примите также текст заголовочного файла polynomRealRoots.h, позволяющего легко организовать ссылку на приведенный выше программный модуль.
//*************************************************************************
//процедура вычисления вещественных корней полинома
void polynomRealRoots(int n,double *kf,double *rootsArray,int &rootsCount);
//**
***********************************************************************
Литература
1. Костин И.К. Семейство алгоритмов расчета интервалов прохождения космического аппарата над круговым наземным объектом с учетом продольной ошибки определения параметров орбиты
Вопросы радиоэлектроники, сер. РЛТ, 2004г., вып. 1
Эту ссылку можно найти в Яндексе поиском по закавыченной фразе «семейство алгоритмов расчета», но текст этой статьи в электронном виде, кажется, недоступен. Поэтому приведу здесь цитату из двух предложений этой статьи:
Вещественный корень полинома всегда находится на участке монотонного изменения полинома, т.е. между корнями производной полинома.
Но производная полинома — это тоже полином, однако, меньшей степени и, найдя его вещественные корни, надо искать корни исходного полинома между корнями производной методом деления пополам.
Пусть
многочлен (уравнение) с действительными
коэффициентами
не
имеет кратных корней и
Найдем
производную от этого многочлена
и обозначим остаток от деления f(x)
на
,
взятый с обратным знаком, через
;
остаток (с обратным знаком) от деления
на
обозначим через
и
так далее пока не получим в остатке
число, которое так же берем с обратным
знаком и обозначим через
.
В результате такой процедуры построена
так называемая последовательность
Штурма:
2)
,
,
,
,…,
.
Вычислим
значения членов последовательности 2)
на концах отрезка
:
3а)
,
,
,
,…,
;
3б)
,
,
,
,…,
.
Пусть
Ф(а) есть число перемен знака в
последовательности 3а), а Ф(b)
— число перемен знака в последовательности
3б). Тогда согласно теореме Штурма число
действительных корней многочлена на
отрезке
равно разности
4)
Ф(а)-Ф(b).
Замечание.
Выяснение вопроса – имеет ли данный
многочлен кратные корни? – происходит
во время построения последовательности
Штурма: если последний остаток этой
последовательности отличен от нуля, то
кратных корней нет.
Очень
просто ответить на вопрос – сколько
действительных корней вообще у данного
многочлена? Для этого необходимо
определить число перемен знака в
последовательности Штурма при
Тогда разность
4а)
Ф(- )-Ф(+
)
дает
точное число действительных корней
многочлена. Например, многочлен
имеет
последовательность Штурма:

Последний
остаток не равен нулю; стало быть,
исходный многочлен кратных корней не
имеет. Так как Ф(-)=2
(-,+,-,-), а Ф(+)=1 (+,+,+,-),
то многочлен имеет один действительный
корень (Ф(-)-Ф(+)=2-1=1),
причем корень этот положительный, ибо
Ф(0)=2 и Ф(0)-Ф(+)=2-1=1.
Пример
1. Определить число действительных
корней в уравнении
Решение.
Строим последовательность Штурма для
данного уравнения:
х+1
делим
на
,
умножив предварительно
на три:
—
-
-
-6х — 3
С
3х+1,5
тало быть,
=6х+3.
Делим
на
,
разделив предварительно
на
два:
х+1,5
—
—
-
=
=2,25.
Итак,
имеем последовательность Штурма:

Так
как
,
то исходное уравнение кратных корней
не имеет. Далее, f(-)=3
(-,+,-,+);
Ф(+)=0 (+,+,+,+);
Ф(-)-Ф(+)=3-0=3;
стало быть, уравнение имеет три
действительных корня, два их которых –
отрицательные (Ф(0)=1 (-,+,+);
Ф(-)-Ф(0)=3-1=2).
Ответ:
.
Построим
график многочлена, исследованного в
примере. Так как
то критическими точками будут
Так как
=6х+6,
то sgn
>0
min
f(x)=f(0)=-1, sgn
<0
max f(x)=
f(-2)=-8+12-1=3.
Подсчитаем дополнительные точки
f(-3)=-27+27-1=-1;
f(-1)=-1+3-1=1;
f(1)=1+3-1=3. Из рисунка хорошо видно
наличие трех корней: двух отрицательных
и одного положительного. Сами корни
согласно графику расположены в интервалах:
(-3;-2), (-1,0), (0,1).
Аналитическая
оценка расположения корней может быть
проведена следующим образом. Верхняя
граница положительных корней уравнения
(1) удовлетворяет соотношению Лагранжа
(см. формулу 3.3):
5)
0<x<1+
.
Для
уравнения из вышеприведенного
примера (
)
имеем: А=1, k=2,
=1;
и верхняя граница положительного корня
определяется числом, равным 2 (0<x<1+
).
Если
известна верхняя граница положительных
корней, то этого достаточно для определения
нижней границы положительных корней,
а так же нижней и верхней границ
отрицательных корней. Пусть
f(x) есть многочлен степени «n»
с верхней границей положительных корней,
равной
.
Рассмотрим многочлены:
где
суть соответственно верхние границы
положительных корней многочленов
Число
будет нижней границей положительных
корней исходного многочлена f(x):
если «» есть
положительный корень f(x), то
будет положительным корнем для
,
и из
<
следует >
.
Таким образом, все положительные корни
многочлена f(x) удовлетворяют
двойному неравенству :
-
<х<
.
Аналогично
нетрудно получить интервал, в котором
располагаются все отрицательные корни
многочлена f(x):

—
<x<
.
Определим
нижнюю границу положительного корня в
примере 1. Строим функцию
Для определения
используем многочлен
где А=3,
,
k=1. Тогда
<1+
=0,25.
Таким образом, имеем отделение
положительного корня в интервал (0,25;
2), в то время как раньше имели (0; 1); стало
быть, положительный корень уравнения
лежит в интервале (0,25; 1).
После
отделения действительного корня
приближенно можно просчитать его
значение с любой заданной точностью.
Существует много методов приближенного
вычисления корней уравнения, но в задачу
настоящего пособия это не входит.
Ограничимся оценкой положительного
корня в нашем примере, используя идею
так называемого метода половинного
деления. Так, в уравнении примера 1
(
=0)
имеем отделение положительного корня
в интервал (0,25; 1). f(1)=3;
просчитаем
;
получаем отрицательную величину
;
поэтому считаем
;
получаем опять отрицательную величину,
равную
;
далее имеем:
=1,125;
=0,45;
=-0,003;
стало быть, х0,56 с
точностью не менее 1%.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Решения кубических уравнений с вещественными коэффициентами. Универсальные методы. Дискриминант кубического уравнения. Формула Виета для кубического уравнения.
Кубическим уравнением называется уравнение вида
- ax3 + bx2 + cx +d = 0 , (1)
- где a, b,c ,d — постоянные коэффициенты, а х — переменная.
Мы рассмотрим случай, когда коэффициенты являются веществеными числами.
Корни кубического уравнения. Нахождение корней (решение) кубического уравнения.
Число х называется корнем кубического уравнения (1), если при его подстановке уравнение (1) обращается в верное равенство.
Кубическое уравнение имеет не более трех корней (над комплексным полем всегда три корня, с учетом кратности) . И всегда имеет хотя бы 1 (вещественный) корень. Все возможные случаи состава корней легко определить с помощью знака дискриминанта кубического уравнения, т.е.:
Δ= -4b3d + b2c2 — 4ac3 + 18abcd — 27a2d2 (Да, это дискриминант кубического уравнения)
Итак, возможны только 3 следующих случая:
- Δ > 0 — тогда уравнение имеет 3 различных корня. (Для продвинутых — три различных вещественных корня)
- Δ < 0 — уравнение имеет лишь 1 корень. (1 вещественный и пару комплексно сопряженных корней)
- Δ = 0 — хотя бы 2 корня уравнения совпадают. Т.е. мы имеем дело либо с уравнением с 2умя совпадающими корнями, и еще 1ним отличным от них, либо с уравнением с 3емя совпадающими корнями. (В любом случае все корни вещественные. И уравнение имеет 3 совпадающих корня, тогда и только тогда, когда результант его и его второй производной равен нулю)
На практике часто , решение кубических уравнений упирается в разложении их на множители. Т.е. алгоритм приблизительно следующий: угадываем один корень, пусть это будет корень α. Затем делим многочлен на (х- α), (если α корень, то он должен поделиться без остатка). Ну а дальше мы имеем дело с обычным квадратным уравнением. Но угадать можно только рациональный корень, и то, если коэффициенты подобраны удачным образом, так что этот корень просто угадывается. Мы же рассмотрим универсальные методы решения кубичесих уравнений.
Формула Кардано решения кубических уравнений (нахождения корней).
Это формула для нахождения корней канонической формы кубического уравнения. (Над полем комлексных чисел).
Канонической формой кубического уравнения называется уравнение вида
y3 + py + q = 0 (2)
К такому виду можно привести любое кубическое уравнение вида (1) с помощью следующей замены:
- x= y — b/3a (3)
- p= — b2/3a2 + c/a
- q= 2b3/27a3 — bc/3a2 + d/a
Итак, приступим к вычислению корней. Найдем следующие величины:
- Q=(p/3)3 + (q/2)2
- α = (-q/2 + Q1/2)1/3
- β = (-q/2 — Q1/2)1/3
Дискриминант уравнения (2) в этом случае равен
Δ = — 108Q
Дискриминант исходного уравнения (1) будет иметь тот же знак , что и вышеуказанный дискриминант. Корни уравнения (2) выражаются следующим образом:
- y1= α + β
- y2= — (α + β)/2 + (31/2(α — β)/2)i
- y3 =- (α + β)/2 — (31/2(α — β)/2)i
Соответственно, если Q>0, то уравнения (2) и (1) будут иметь лишь 1 (вещественный) корень, y1. Подставим его в (3) и найдем х для уравнения (1). (если вас интересуют также мнимые корни, то просто вычислите еще и y2, y3 и подставьте их в (3).
Если Q<0, то уравнение (2), как и уравнение (1) имеет три различных вещественных корня, но для их вычисления нужно уметь извлекать квадратный корень из отрицательного числа. Если вы это умеете, то проделайте расчеты, получите три корня y1, y2, y3 и подставьте их в (3).
Если же Q =0, то все корни уравнений (1) и (2) вещественные, причем как минимум 2 корня каждого из уравнений совпадают. При этом имеем
- α = β, и
- y1=2α,
- y2= y3 = — α.
Аналогично подставляем в (3) и получаем ответ.
Тригонометрическая формула Виета решения кубических уравнений (нахождения корней).
Эта формула находит решения приведенного кубического уравнения, то есть уравнения вида
x3 + ax2 + bx +c = 0 (4)
Очевидно, любое уравнение вида (1) можно привести к виду (4), просто поделив его на коэффициент а.
Итак, алгоритм применения этой формулы:
1. Вычисляем
- Q=(a2— 3b)/9
- R=(2a3 — 9ab + 27c)/54
2. Вычисляем
S = Q3 — R2
3. a) Если S>0, то вычисляем
φ=(arccos(R/Q3/2))/3
И наше уравнение имеет 3 корня (вещественных):
- x1= — 2(Q)1/2cos(φ) — a/3
- x2= — 2(Q)1/2cos(φ+2π/3) — a/3
- x3= — 2(Q)1/2cos(φ-2π/3) — a/3
б) Если S<0, то заменим тригонометрические функции гиперболическими.
Вычисляем
φ=(Arch( |R|/|Q|3/2)/3
Тогда единственный корень (вещественный): x1= -2sgn(R)*|Q|1/2*ch(φ) — a/3
Для тех, кого интересуют также и мнимые корни:
- x2= sgn(R)*|Q|1/2*ch(φ) — a/3 +(3|Q|)1/2 sh(φ)i
- x3= sgn(R)*|Q|1/2*ch(φ) — a/3 -(3|Q|)1/2sh(φ)i
ГДЕ:
- ch(x)=(ex+e-x)/2
- Arch(x) = ln(x + (x2-1)1/2)
- sh(x)=(ex-e-x)/2
- sgn(x) — знак х
в) Если S=0,то уравнение имеет меньше трех различных решений:
- x1= -2*R1/3 — a/3
- x2=x3=R1/3 — a/3
Уравнение n-й степени с одним неизвестным:
Определение:
Уравнением n-й степени с одним неизвестным х называется уравнение
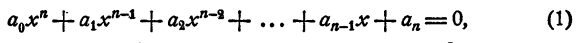
где 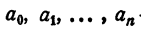
Изучение уравнения (1) в общем виде выходит за рамки школьного курса алгебры. В этой главе рассматриваются лишь некоторые свойства уравнения (1) и, кроме того, изучаются некоторые его частные виды.
Деление многочлена относительно х на х—а
Теорема:
Остаток от деления многочлена относительно х на двучлен х — а равен значению этого многочлена при х, равном а.
Доказательство:
Разделим многочлен n-й степени
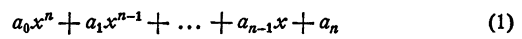
на двучлен х — а. Как известно, частным (неполным) в этом случае будет многочлен n— 1 степени
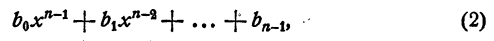
а остатком — некоторое число r. Так как делимое равно делителю, умноженному на частное, плюс остаток, то
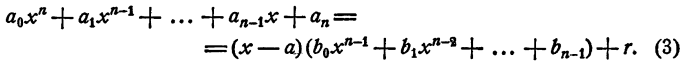
Равенство (3) есть тождество, оно справедливо при любых значениях х. В частности, оно справедливо и при х = а. При х = а. первое слагаемое правой части равенства (3) обращается в нуль, а потому
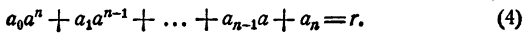
Следствие:
Для того чтобы многочлен относительно х делился на двучлен х — а, необходимо и достаточно, чтобы число а было корнем этого многочлена, т. е. чтобы при х = а многочлен обращался в нуль.
Доказательство:
Необходимость:
Пусть многочлен (1) делится на х — а, т. е. остаток r равен нулю. Тогда на основании равенства (4)
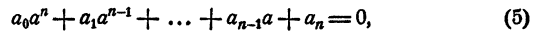
т. е. а — корень многочлена (1).
Достаточность:
Пусть а — корень многочлена (1), т. е. имеет место равенство (5). Тогда на основании равенства (4) r = 0, т. е. многочлен (1) делится на двучлен х — а.
Рассмотрим вновь тождество (3). Если в правой части его раскрыть скобки и сделать приведение подобных членов, в результате должен получиться тот же многочлен, что и в левой части. На этом основании, приравнивая коэффициенты при одинаковых степенях х, получаем
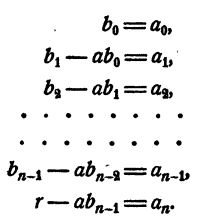
Перепишем эти равенства так:
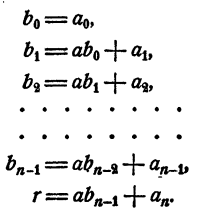
Полученные равенства показывают, что коэффициенты частного и остаток, т. е. 
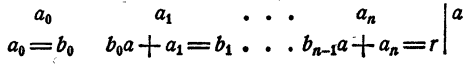
Пример:
Разделить многочлен
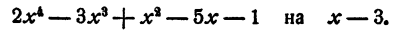
Решение:
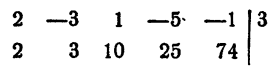
Первый коэффициент 2 второй строки просто сносится (b₀ = а₀). Второй коэффициент 3 получен так:
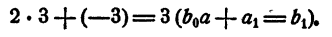
Третий коэффициент 10 получен так:
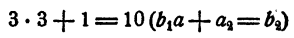
и т. д. Неполное частное равно
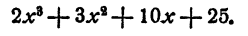
Остаток 74.
Пример:
Найти значение многочлена
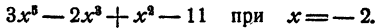
Решение:
Искомое значение многочлена равно остатку от деления многочлена на x + 2
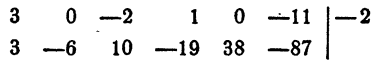
В двух местах первой строки потребовалось вписать 0. Объясняется это тем, что делимое имеет следующий вид:
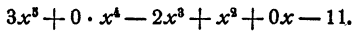
Обычно члены, коэффициенты которых равны нулю, пропускаются. Здесь их пропускать нельзя.
Ответ. —87.
Составление уравнения n-й степени по его корням
Теорема:
Каковы бы ни были числа 
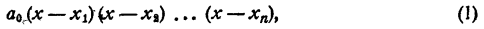
где a₀ — любое число, отличное от нуля. При x = x₁ двучлен x — x₁ обращается в нуль, значит, при этом значении х обращается в нуль и произведение (1). При х = х₂ обращается в нуль двучлен х — x₂, и опять произведение (1) обращается в нуль. То же самое происходит при х =x₃; х = хₙ.
Пусть теперь х = а, где a — число, отличное от x₁ x₂ , …., хₙ . Ни одна из разностей а— x₁ а— x₂ ,…..о— хₙ „ не равна нулю. Число а₀ тоже отлично от нуля. Значит, и произведение
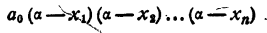
отлично от нуля.
Таким образом, уравнение
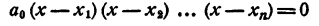
имеет корнями x₁ x₂ , …., хₙ и только эти числа.
Раскрыв скобки и выполнив приведение подобных членов, получим в левой части уравнения многочлен n-й степени относительно х, т. е.
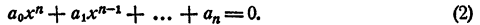
Корнями уравнения (2) являются числа x₁ x₂ , …., хₙ и только эти числа.
Возможно, что корни x₁ x₂ , …., хₙ уравнения (2) не все различны между собой. В этих случаях говорят, что уравнение (2) имеет кратные корни. Так, например, если x₁ = x₂ и отлично от других корней уравнения (2), число является корнем второй кратности уравнения (2). Левая часть уравнения (2) делится в этом случае на (x — x₁ )³ и не делится на (х — x₁)³. Если x₁ = x₂ = x₃ и отлично от других корней уравнения (2), число x₁ является корнем третьей кратности уравнения (2). Левая часть уравнения (2) делится в этом случае на (х — x₁ )³ и не делится на (х— x₁ )⁴.
Вообще корнем кратности k уравнения (2) называется такое число а, что левая часть уравнения (2) делится на (х — а)ᵏ и не делится на
Пример:
Составить уравнение второй степени, корни которого
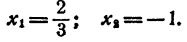
Решение:
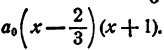
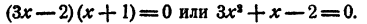
Пример:
Составить уравнение второй степени, корни которого x₁ = 1; х₂ =i.
Решение:
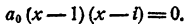
Пример:
Составить уравнение четвертой степени, корни которого i; —i; 1+i; 1-i
Решение:
Имеем
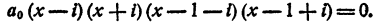
Положим а₀ = 1.
Пример:
Составить уравнение третьей степени, корни которого x₁ = 1; х₂ = 1; х₃ = — 1.
Решение:
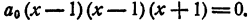
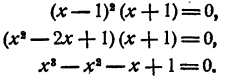
Число единица является здесь корнем второй кратности,
Основная теорема алгебры и некоторые следствия из нее
Мы видели, что, выбрав произвольные п комплексных чисел, можно составить уравнение п-й степени, корнями которого будут выбранные числа. Коэффициенты этого уравнения могут при -этом оказаться как вещественными, так и мнимыми. Возникает следующий весьма важный вопрос.
Дано уравнение n-й степени с комплексными коэффициентами
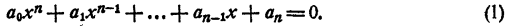
Можно ли утверждать, что среди комплексных чисел найдется хоть одно число, являющееся корнем этого уравнения?
В свое время мы видели, что среди целых чисел нет числа, являющегося корнем уравнения 2х— 3 = 0 с целыми коэффициентами. Среди положительных чисел нет числа, являющегося корнем уравнения x+ 1 = 0 с положительными коэффициентами.
Среди рациональных чисел нет числа, являющегося корнем уравнения x² — 2 = 0 с рациональными коэффициентами. Среди действительных чисел нет числа, являющегося корнем уравнения x²+ 1 = 0 с действительными коэффициентами.
Понятно поэтому, сколь важное значение имеет поставленный вопрос. Ответ на него дает основная теорема алгебры.
Всякое уравнение n-й степени с любыми комплексными коэффициентами имеет комплексный корень.
Доказательство этой теоремы выходит за рамки школьной программы.
Теорема:
Всякий многочлен n-й степени с любыми комплексными коэффициентами может быть представлен и притом единственным образом в виде произведения п двучленов первой степени, т. е.
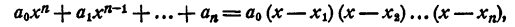
где a ≠ 0, n ≥ 1. (Два таких разложения, отличающиеся только порядком расположения множителей, не считаются различными.)
Доказательство:
Доказательство разбивается на две части. В первой части доказывается возможность представления многочлена n-й степени в виде произведения п двучленов первой степени, во второй—единственность такого представления.
Для n = 1 теорема верна, так как
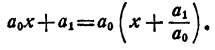
Предположим, что теорема справедлива для многочленов степени n—1.
Согласно основной теореме алгебры многочлен 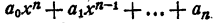
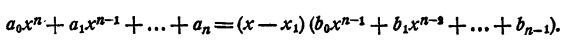
Здесь b₀ = a₀ (см. § 2).
Для многочлена 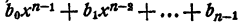
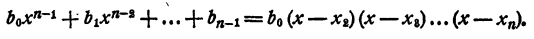
Следовательно,
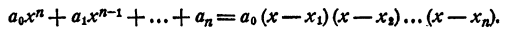
Допустим, что имеется два таких разложения:
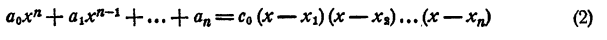
и
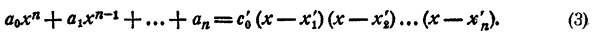
Так как коэффициенты при хⁿ в правой и левой частях равенств (2) и (3) должны быть равны, то
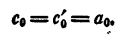
Приравниваем правые части равенств (2) и (3). После сокращения на а₀ имеем
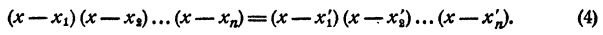
Методом математической индукции докажем, что правая и левая части равенства (4) состоят из соответственно равных множителей, но, быть может, записанных в другом порядке.
Для n= 1 утверждение, очевидно, справедливо.
Пусть утверждение справедливо для произведений, состоящих из n—1 множителей. Докажем, что утверждение справедливо и для произведений, состоящих из n множителей.
Левая часть равенства (4) при x = x₁ обращается в нуль. Значит, при x = x₁ обращается в нуль и правая часть этого равенства, т. е.
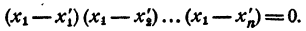
Произведение равно нулю. Значит, хоть один из сомножителей равен нулю. Допустим, что 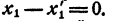
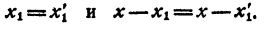
Сократим равенство (4) на х— x₁ получим
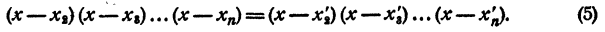
По допущению правая и левая части равенства (5) состоят из соответственно равных множителей, но, быть может, записанных в другом порядке. Приписав в каждую часть равенства (5) по одинаковому множителю х— x₁ получим, что правая и левая части равенства (4) состоят из соответственно равных сомножителей.
Теорема доказана полностью.
В разложении
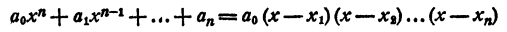
некоторые из сомножителей правой части могут быть одинаковы. Обозначив 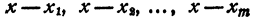
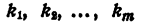
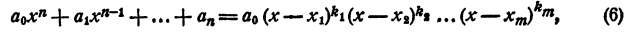
где 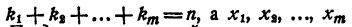
Представление левой части уравнения в виде (6) называется представлением левой части уравнения в канонической форме.
Теорема:
Всякое уравнение п-й степени с любыми комплексными коэффициентами имеет ровно п корней, среди которых могут быть и равные друг другу.
Доказательство:
Дано уравнение
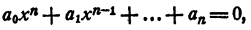
где a₀ ≠ 0, n ≥ 0 Как доказано, левая часть может быть представлена в виде произведения n множителей первой степени. Таким образом, имеем
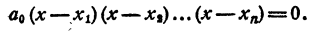
При x=x₁; х = х₂; х=хₙ левая часть уравнения превращается в нуль и, следовательно, х₁, х₂, …,xₙ— корни уравнения. Покажем, что никакое число а, отличное от х₁ х₂,…..хₙ, не может быть корнем этого уравнения.
Действительно, произведение а₀ (а — x₁) (а — х ₂ ,)… (а — x ₙ )не равно нулю, так как ни один из множителей его не равен нулю. Таким образом, корнями рассматриваемого уравнения являются числа x₁; х ₂ ;…; x ₙ и других корней нет.
Следствие:
Уравнение n-й степени имеет n корней, если каждый корень считать столько раз, какова его кратность.
Теорема:
Если уравнение n-й степени имеет действительные коэффициенты и мнимое число а + bi является корнем этого уравнения, то и сопряженное число а — bi является также корнем этого уравнения.
Доказательство:
Пусть мнимое число а + bi является корнем уравнения
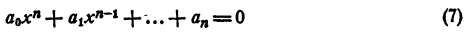
с действительными коэффициентами. Требуется доказать, что сопряженное число а — bi также является корнем уравнения (7). Составим многочлен
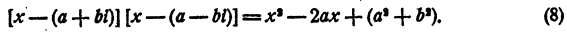
Этот многочлен имеет действительные коэффициенты. Разделим левую часть уравнения (7) на многочлен (8). В частном получим многочлен n— 2 степени с действительными коэффициентами, в остатке многочлен степени не выше первой и тоже с действительными коэффициентами.
Так как делимое равно делителю, умноженному на частное плюс остаток, то
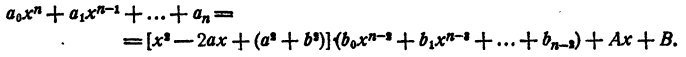
Положим в этом равенстве х = а + bi . Получим
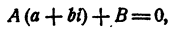
так как и левая часть равенства и трехчлен 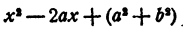
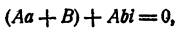
следовательно,

Так как b ≠ 0, то A = 0. Из первого уравнения системы (9) имеем В = 0. Выходит, что остаток Ах + В равен нулю, т. е.
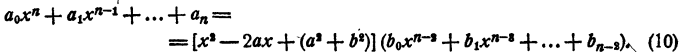
При х = а — bi первый сомножитель правой части равенства (10) превращается в нуль, значит, и левая часть равенства тоже обращается в нуль. Значит, число а — bi является корнем уравнения (7).
Теорема:
Всякий многочлен n-й степени с действительными коэффициентами может быть представлен в виде произведения многочленов первой или второй степени с действительными коэффициентами.
Доказательство этой теоремы проводится методом математической индукции. Теорема, очевидно, справедлива для многочленов первой и второй степени. При этом многочлен второй степени либо имеет действительные корни и тогда разлагается на множители первой степени с действительными коэффициентами, либо он имеет два мнимых сопряженных корня, и тогда он на множители с действительными коэффициентами не разлагается.
Допустим, что теорема справедлива для многочленов n— 2 степени и многочленов n—1 степени. Докажем, что тогда она справедлива и для многочленов n-й степени.
Пусть 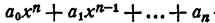
Если этот многочлен имеет действительный корень x₁ то он представляется в виде произведения многочлена первой степени на многочлен n—1 степени с действительными коэффициентами, т. е.
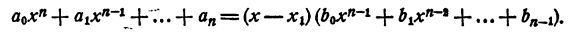
Если же многочлен действительных корней не имеет, то он имеет мнимый корень а + bi и сопряженный с ним корень а — bi. В этом случае многочлен представляется в виде произведения трехчлена второй степени на многочлен n— 2 степени с действительными коэффициентами, т. е.
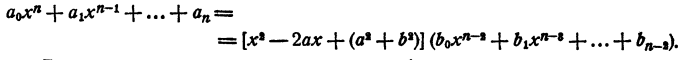
Так как теорема для многочленов п—1 степени и многочленов n— 2 степени справедлива, то она справедлива и для многочленов степени n.
Теорема Виета
Из равенства
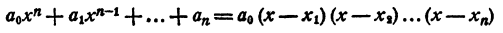
легко получить теорему Виета для уравнений любой степени. Перепишем это равенство так:
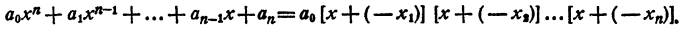
К правой части этого равенства применим правило умножения двучленов, первые члены которых одинаковы (см. гл. VIII, § 5). Получаем
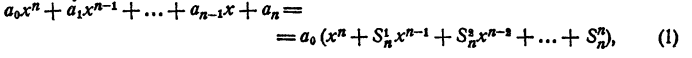
где 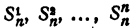
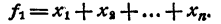
Знаком f₂ обозначим сумму всевозможных произведений корней, взятых по два. Подобный же смысл имеют знаки f₃, f₄, …, f ₙ . Тогда
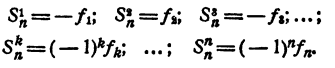
Равенство (1) теперь можно переписать так:
Приравнивая коэффициенты при одинаковых степенях х в правой и левой частях равенства (2), получим
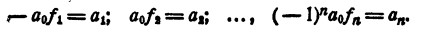
Теперь имеем
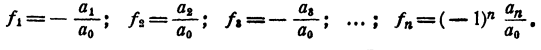
Последние равенства и выражают теорему Виета для уравнения любой степени. При n= 2, т. е. для уравнения 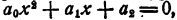
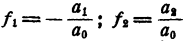
Пример:
Не решая уравнения 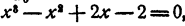
Решение:
Пусть х₁ x₂, х₃, — корни данного уравнения. Рассмотрим равенство
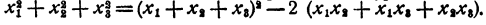
По теореме Виета
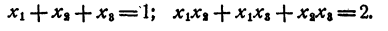
Значит,
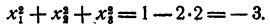
Полученный результат означает, что среди чисел х₁ x₂, х₃, имеются мнимые, иначе сумма квадратов их не могла бы быть отрицательной.
Предложенное уравнение нетрудно решить и подсчитать сумму квадратов корней непосредственно:
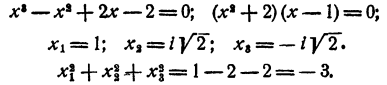
О решении уравнений высших степеней
Прежде всего возникает такой вопрос: можно ли для уравнений любой степени составить формулы для выражения корней уравнения через его коэффициенты, подобно известной формуле для квадратного уравнения? Оказывается, что это можно сделать для уравнений 3-й и 4-й степени, при этом формулы эти содержат столь сложные радикалы, что на практике ими предпочитают не пользоваться.
Что же касается уравнений выше 4-й степени, то доказано, что для них при помощи радикалов такие формулы составить нельзя.
В математике разработан ряд способов, дающих возможность вычислить любой корень любого уравнения с любой точностью. Один из таких способов разработан великим русским математиком, творцом неевклидовой геометрии Н. И. Лобачевским.
Ограничимся рассмотрением графического способа. Этот способ может применяться для вычисления действительных корней уравнений с действительными коэффициентами.
Пример:
Вычислить вещественные корни уравнения
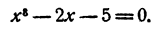
Решение:
Построим график функции у = х³ — 2х— 5 (рис. 107). Имеем
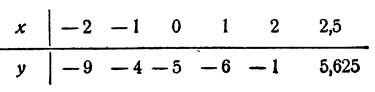
Нетрудно видеть, что при x > 2,5 первое слагаемое х³ будет столь большим сравнительно с остальными, что у будет положительным числом.
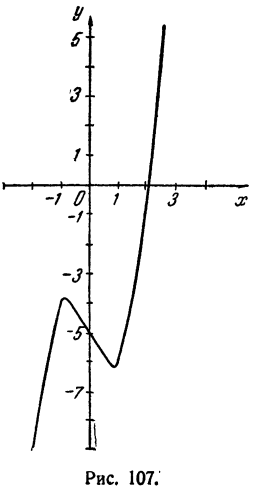
По мере продвижения направо от х = 2,5 график будет подниматься кверху и, следовательно, больше пересекать ось Ох не будет.
Точно так же при х < — 2 первое слагаемое х³ будет столь большим по абсолютной величине, что у будет отрицательным числом. По мере продвижения влево от х = — 2 график будет опускаться книзу и больше пересекать ось Ох не будет.
График пересекает ось Ох в одной точке, и это означает, что уравнение имеет один действительный корень два других корня уравнения — мнимые сопряженные).
Как видно из таблицы, действительный корень заключен между 2 и 2,5. По графику видно, что он ближе к 2, чем к 2,5. Определим знак у при x = 2,1. Имеем
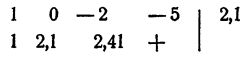
Это означает, что точка 2,1 лежит правее корня, так как соответствующая ордината положительна (см. график).
Таким образом, 2 < x < 2,1. Корень вычислен с точностью до 0,1. Для получения более точного результата можно воспользоваться приемом, указанным в гл. IV, § 7. Можно показать, что с точностью до 0,000001 x = 2,094551.
Вычисление рациональных корней уравнений с целыми коэффициентами
Теорема:
Для того чтобы несократимая дробь 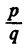
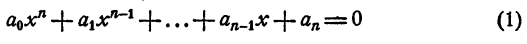
с целыми коэффициентами, необходимо, чтобы р было делителем свободного члена аₙ, a q было делителем старшего коэффициента а₀.
Доказательство:
Пусть 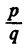
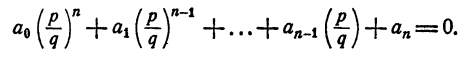
Умножим обе части тождества на qⁿ, получим
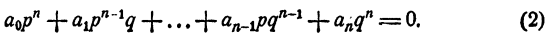
Из тождества (2) имеем
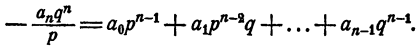
Правая часть равенства — целое число. Значит,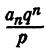
По условию, дробь 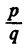
Из тождества (2) имеем
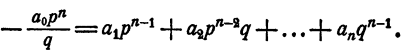
Так как ни одно простое число, входящее в q, не входит в р, число 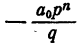
Следствие:
Если уравнение имеет целые коэффициенты и старший из них равен единице, то рациональными корнями такого уравнения могут быть только целые числа.
Действительно, а₀ = 1, a q — делитель а₀ . Значит, q = ± 1, а тогда 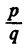
Следствие:
Целые корни уравнения с целыми коэффициент тами являются делителями свободного члена.
Пример:
Вычислить рациональные корни уравнения
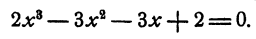
Решение:
Свободный член равен 2. Поэтому для р возможны только следующие значения: 1, —1, 2 и —2.
Старший коэффициент равен 2. Поэтому для q возможны только следующие значения: 1, —1, 2, —2.
Составляя всевозможными способами несократимые дроби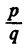
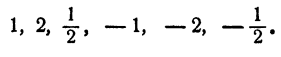
Подстановкой в уравнение легко выяснить, что из этих шести
чисел удовлетворяют уравнению 2, 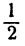
Таким образом, уравнение имеет три рациональных корня:
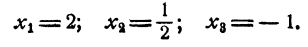
Для испытания, является ли данное число корнем уравнения, удобно пользоваться правилом сокращенного деления многочлена на двучлен х — а. Для данного примера эти испытания проводятся так:
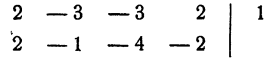
1 не является корнем уравнения, так как при делении левой части уравнения на х — 1 в остатке получилось — 2.
Испытываем число 2
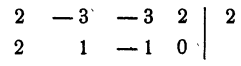
2 — корень уравнения. В результате деления оказалось, что
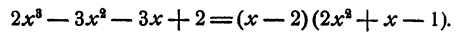
Поэтому для отыскания остальных корней данного уравнения достаточно решить уравнение
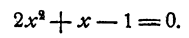
Ответ.
Пример:
Найти рациональные корни уравнения
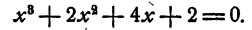
Решение:
Старший коэффициент уравнения равен единице, поэтому рациональными корнями уравнения могут быть только целые числа.
Делители свободного члена суть: 1,2, — 1, — 2. Сразу видно,-что никакое положительное число не может быть корнем данного уравнения, так как при любом положительном значении х левая часть уравнения положительна. Остается испытать — 1 и — 2:
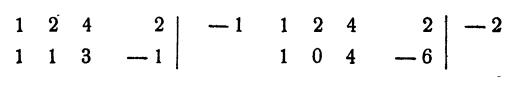
Ответ. Уравнение рациональных корней не имеет.
Полученный в последнем примере результат означает, что корни рассматриваемого уравнения иррациональные или мнимые.
Пример:
Решить уравнение
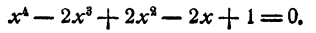
Решение:
Выясним прежде всего, не имеет ли уравнение рациональных корней. Испытанию подлежат два числа 1 и — 1:
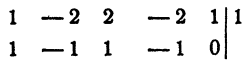
x₁² = 1. Остальные корни данного уравнения являются корнями уравнения третьей степени х³ — х² + х —1=0:
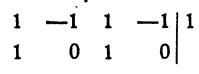
x₂ = 1. Остальные корни данного уравнения являются корнями квадратного уравнения х² + 1 = 0.
Ответ. x₁ = x₂ = 1; х₃ = i; x₄= — 1.
Решение двучленных уравнений 3-й, 4-й и 6-й степени
Определение. Двучленным уравнением n-й степени называется уравнение вида 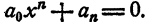
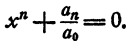
В этом параграфе излагается решение двучленных уравнений с действительными коэффициентами при n= 3, 4 и 6.
а) n = 3.
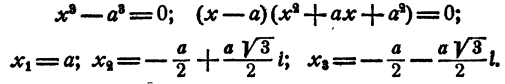
Уравнение имеет один действительный и два мнимых сопряженных корня.
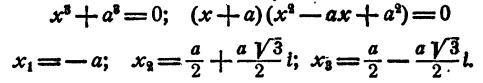
Уравнение имеет один действительный и два мнимых сопряженных корня.
б) n = 4.
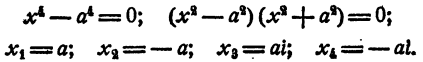
Уравнение имеет два действительных и два мнимых сопряженных корня.
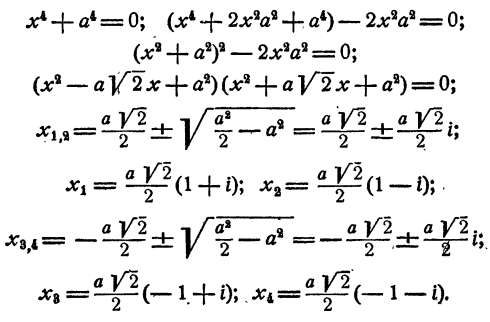
Уравнение имеет две пары мнимых сопряженных корней.
в) n = 6.
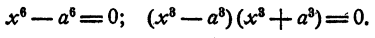
Уравнение распадается на два кубических двучленных уравнения. На основании рассмотренного в п. а)
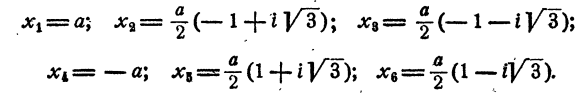
Уравнение имеет два действительных и две пары мнимых сопряженных корней
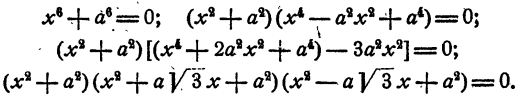
Уравнение распадается на три квадратных уравнения. Решая их, получаем
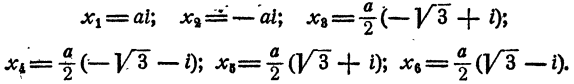
Уравнение имеет три пары мнимых сопряженных корней.
Замечание. Пользуясь извлечением корня n-й степени из комплексного числа, можно решить двучленное уравнение хⁿ = а любой степени n при любой правой части а.
Корнями уравнения хⁿ = а являются все значения корня n-й степени из а.
Пример:
Решить уравнение
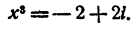
Решение:
Запишем правую часть уравнения в тригонометрической форме
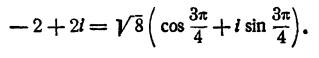
Пусть кубический корень из —2 + 2i равен р (cos 0 +isin 0). Тогда имеем
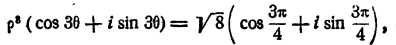
отсюда (§ 9 гл. IX) имеем
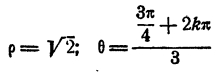
Для получения всех значений корня достаточно k положить равным 0, 1, 2. При k = 0 имеем
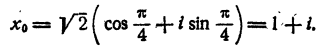
При k= 1 имеем
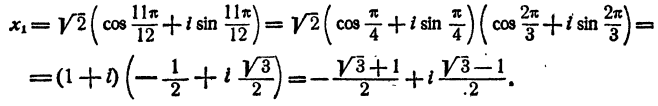
При к = 2 имеем
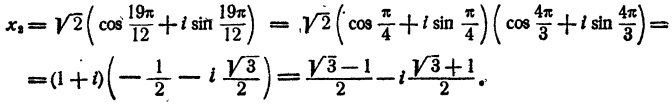
Ответ.
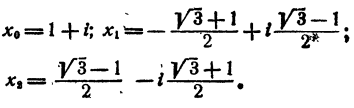
Решение трехчленных уравнений
Определение:
Трехчленным уравнением называется уравнение вида
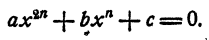
При n= 2 уравнение является биквадратным.
Решение трехчленного уравнения подстановкой хⁿ = у сводятся к квадратному уравнению ay² + by + с = 0 и двучленному уравнению n-й степени.
Пример:
Решить уравнение
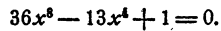
Решение:
Положим x⁴ = у. Имеем
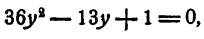
отсюда
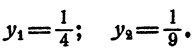
Теперь имеем
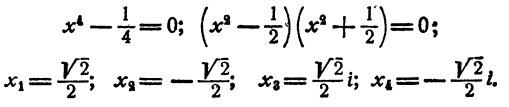
Далее,
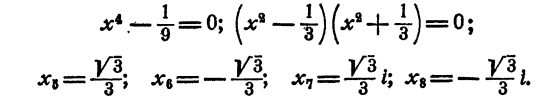
Ответ.
Решение заданий и задач по предметам:
- Математика
- Высшая математика
- Математический анализ
- Линейная алгебра
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат