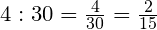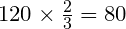Задачи на дроби
- Выражение части в долях целого
- Нахождение дроби от числа
- Нахождение числа по его дроби
Выражение части в долях целого
Чтобы выразить часть в долях целого, нужно часть разделить на целое.
Задача. В классе 30 учащихся, отсутствуют четверо. Какая часть учащихся отсутствует?
Решение:
Ответ: В классе отсутствует 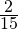
Нахождение дроби от числа
Для решения задач, в которых требуется найти часть целого справедливо следующее правило:
Если часть целого выражена дробью, то чтобы найти эту часть, можно целое разделить на знаменатель дроби и результат умножить на её числитель.
Задача 1. Было 600 рублей, 
Решение: Чтобы найти 
600 : 4 = 150 (р.).
Ответ: Истратили 150 рублей.
Задача 2. Было 1000 рублей, 
Решение: Из условия задачи мы знаем, что 1000 рублей состоит из пяти равных частей. Сначала найдём сколько рублей составляет одна пятая часть от 1000, а затем узнаем сколько рублей составляют две пятых:
1) 1000 : 5 = 200 (р.) — одна пятая часть.
2) 200 · 2 = 400 (р.) — две пятых части.
Эти два действия можно объединить:
1000 : 5 · 2 = 400 (р.).
Ответ: Было истрачено 400 рублей.
Второй способ нахождения части целого:
Чтобы найти часть целого, можно умножить целое на дробь, выражающую эту часть целого.
Задача 3. По уставу кооператива, для правомочности отчётного собрания на нём должно присутствовать не менее 
Решение:
Ответ: Отчётное собрание может состояться при наличии 80 членов организации.
Нахождение числа по его дроби
Для решения задач, в которых требуется найти целое по его части справедливо следующее правило:
Если часть искомого целого выражена дробью, то чтобы найти это целое, можно данную часть разделить на числитель дроби и результат умножить на её знаменатель.
Задача 1. Потратили 50 рублей, это составило 
Решение: Из описания задачи мы видим, что 50 рублей в 6 раз меньше первоначальной суммы, т. е. первоначальная сумма в 6 раз больше, чем 50 рублей. Чтобы найти эту сумму, надо 50 умножить на 6:
50 · 6 = 300 (р.).
Ответ: Первоначальная сумма — 300 рублей.
Задача 2. Потратили 600 рублей, это составило 
Решение: Будем считать, что искомое число состоит из трёх третьих долей. По условию две трети числа равны 600 рублей. Сначала найдём одну треть от первоначальной суммы, а затем сколько рублей составляют три третьих (первоначальная сумма):
600 : 2 · 3 = 900 (р.).
Ответ: Первоначальная сумма — 900 рублей.
Второй способ нахождения целого по его части:
Чтобы найти целое по величине выражающей его часть, можно разделить эту величину на дробь, выражающую данную часть.
Задача 3. Отрезок AB, равный 42 см, составляет 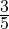
Решение:
Ответ: Длина отрезка CD 70 см.
Задача 4. В магазин привезли арбузы. До обеда магазин продал 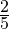
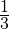
Решение: Сначала узнаем, какую часть от привезённых арбузов составляет число 80. Для этого примем за единицу общее количество привезённых арбузов и вычтем из неё то количество арбузов, которое получилось реализовать (продать):
Итак, мы узнали, что 80 арбузов составляет 

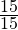
2) 80 : 4 · 15 = 300 (арбузов).
Ответ: Всего в магазин привезли 300 арбузов.
Решение задач на дроби
Ключевые слова конспекта: решение задач на дроби, решения задач в 5-6 классе, ответы на задачи, нахождение части целого, восстановление целого по известной его части, нахождение отношения величин, увеличение (уменьшение) на часть целого, часть от части целого, нахождение целого по его части, выражение остатка через часть целого, выражение величины частью целого, часть от части целого, оставшаяся часть целого.
Решение основных и типовых задач на дроби для учащихся 5-6 классов, включая углубленный уровень изучения математики.
Задача № 1.
Нахождение части целого.
Андрей вышел из дома к озеру, до которого 900 м. Пройдя 3/5 пути, он встретил друга. На каком расстоянии от дома Андрей встретил друга?
РЕШЕНИЕ:
Целое задано числом 900. Чтобы ответить на вопрос задачи, надо найти 3/5 от 900.
Способ 1.
Найдем 1/5 от 900 и результат умножим на 3; получим 900 : 5 • 3 = 180 • 3 = 540.
Способ 2.
Умножим число 900 на дробь 3/5 и получим 540.
Ответ: 540 м.
Задача № 2.
Восстановление целого по известной его части.
Андрей вышел из дома к озеру и, пройдя 3/5 расстояния до озера, он встретил друга. Расстояние от дома до встречи с другом составило 540 м. Каково расстояние от дома Андрея до озера?
РЕШЕНИЕ:
Известна часть целого – число 540. Этой части соответствует дробь 3/5. Чтобы ответить на вопрос задачи, надо найти по дроби – неизвестное целое.
Способ 1.
Так как 540 – это три пятых целого, то одна пятая – это 540 : 3 = 180. А все целое – это пять пятых и оно равно 180 • 5 = 900.
Способ 2.
Разделим число 540 на дробь 3/5, получим 900.
Ответ: 900 м.
Задача № 3.
Нахождение отношения величин.
В школе 630 учащихся. В спартакиаде приняло участие 345 учащихся школы. Какая часть всех учащихся школы приняла участие в спартакиаде?
РЕШЕНИЕ:
Один учащийся школы – это 1/630 часть всех учащихся школы. Поэтому 345 учащихся составляют 345/630 всех учащихся школы. Сократив полученную дробь, запишем 23/42 всех учащихся школы.
Ответ: 23/42 всех учащихся школы.
Задача № 4.
Увеличение (уменьшение) на часть целого.
Цена упаковки составляет 3/50 цены игрушки. Какова стоимость игрушки с упаковкой, если цена игрушки 650 р.?
РЕШЕНИЕ:
Способ 1.
Сначала найдем цену упаковки: 650 : 50 • 3 = 39 (р.). Теперь, увеличив цену, найдем стоимость игрушки е упаковкой: 650 + 39 = 689 (р.).
Способ 2.
Если целое 1 и его часть 3/50, то будем искать 13/50 от 650 р.
Имеем 650 • 53/50 = 689 (р.).
Ответ: 689 р.
Задача № 5.
Часть от части целого.
Из 550 учащихся школы в референдуме по вопросу о введении Ученического совета участвовали 22/25 числа всех учащихся. На вопрос референдума 3/4 числа учащихся, принявших участие в голосовании, ответили «да». Какую часть числа всех учащихся школы составили те учащиеся, которые ответили положительно?
РЕШЕНИЕ:
Вычислим число учащихся, утвердительно ответивших на вопрос референдума. Имеем 550 • 22/25 • 3/4 = 363 (уч.). Теперь найдем ответ на вопрос задачи: 363 : 550 = 33/50.
Ответ: 33/50 или 0,66.
Дополнительный вопрос: можно ли ответить на вопрос задачи, не зная числа учащихся школы?
Ответ: да, надо перемножить дроби, т.е найти 3/4 от 22/25.
Задача № 6.
Нахождение целого по его части.
В сборнике фантастики две повести. Первая занимает 35 страниц, а вторая – 2/7 книги. Сколько всего страниц в книге?
РЕШЕНИЕ:
Сначала найдем, какую часть рукописи занимает первая повесть: 1 – 2/7 = 5/7, а потом – целое по его части: 35 : 5/7 = 49.
Ответ: 49 страниц.
Задача № 7.
Выражение остатка через часть целого.
На пошив детской одежды ушел весь рулон ткани. Из 3/8 рулона сшили куртки, из четверти рулона – юбки, из оставшихся 24 м сшили несколько брюк. Сколько всего метров ткани было в рулоне?
РЕШЕНИЕ:
Найдем, из какой части всего рулона сшили куртки и юбки: 3/8 + 1/4 = 5/8. Теперь понятно, что на пошив брюк осталась часть, равная 1 – 5/8 = 3/8 рулона, которая составляет 24 м. Значит, во всем рулоне было 24 : 3/8 = 64 (м).
Ответ: 64 м.
Задача № 8.
Выражение величины частью целого.
Оля истратила треть имевшейся у нее суммы денег, а потом еще 100 р. В итоге она истратила половину суммы. Сколько денег было у Оли первоначально?
РЕШЕНИЕ:
Чтобы разобраться в условии задачи, обратимся к рисунку.
Сначала узнаем, какую часть всей суммы составляют 100 р.: 1/2 – 1/3 = 1/6. Теперь мы знаем, что 100 р. – это 1/6 всей суммы. Чтобы ответить на вопрос задачи, нужно найти целое по его части. В данном случае можно попросту 100 р. умножить на 6. Получим, что у Оли было 600 р.
Ответ: 600 р.
Задача № 9.
Часть от части целого.
Перед поездкой бак автомобиля был заполнен на 4/5. Во время поездки была истрачена четверть имевшегося запаса бензина. Какая часть бака заполнена бензином к концу поездки?
РЕШЕНИЕ:
Если истрачена четверть от 4/5 бака, то это значит, что осталось 3/4 от 4/5 бака, т.е. всего наполнено бензином 3/5 бака.
Ответ: 3/5 бака.
Задача № 10.
Оставшаяся часть целого.
Ученик закрасил 3/8 круга синим цветом и 3/10 оставшейся части – желтым цветом. Какая часть круга осталась незакрашенной?
РЕШЕНИЕ:
Способ 1.
После закрашивания синим цветом остались незакрашенными 1 – 3/8 = 5/8 круга. Найдем 3/10 от 5/8 – получим 3/16. Сложим закрашенные части и получим 9/16. Значит, незакрашенными остались – 7/16.
Способ 2.
После закрашивания синим цветом остались незакрашенными 5/8 круга. После закрашивания желтым цветом остались незакрашенными 1 – 3/10 = 7/10 оставшейся части. Найдем 7/10 от 5/8 – получим 7/16.
Ответ: 7/16. Проверьте ответ, сделав рисунок.
Это конспект по математике на тему «Решение задач на дроби». Выберите дальнейшие действия:
- Перейти к следующему конспекту:
- Вернуться к списку конспектов по Математике.
- Проверить знания по Математике.
В 5 классе на уроках математики ученики знакомятся с дробями и процентами. В 6 классе эта тема повторяется, но изучается более глубоко. А встречаться дроби и проценты продолжат вплоть до задач внешнего тестирования (ЗНО) для 11 класса.

Число под чертой (знаменатель), показывает, на сколько частей разделили целое.
Число над чертой (числитель) показывает, сколько этих частей выбрано.
То есть дробь $frac{3}{8}$ (три восьмых) означает, что целое было разделено на 8 частей, а взято из них три.
Существуют три класса задач на дроби: нахождение дроби от числа, нахождение числа по его дроби и выражение отношения чисел в виде дроби.
Как найти дробь от числа
В задачах на дробь от числа известно само число и дробь, которая от него взята. А найти требуется, какую величину составит эта дробь. Рассмотрим такую задачу
Пример 1.1.
В самолёте 120 пассажиров. $frac{2}{5}$ (две пятых) из них летят в самолёте в первый раз. Сколько пассажиров летит в первый раз?
Это задача на нахождение дроби от числа.
Есть число: 120.
Есть дробь: $frac{2}{5}$
Нужно найти, чему равны две пятых от 120.
Решаются задачи на нахождение дроби от числа так.
Решение
Задаём себе два вопроса:
1. Чему равна $frac{1}{5}$ (одна пятая) от 120?
Для этого 120 делим на 5, получаем 24.
2. Чему равны $frac{2}{5}$ (две пятых) от 120?
Результат 24, корый мы получили, нужно умножить на 2.
Получаем 48.
Значит, $frac{2}{5}$ от 120 составляет 48.
Ответ: 48 пассажиров летят впервые.
Попробуем решить ещё одну задачу на нахождение дроби от числа.
Пример 1.2.
В городе живут 1 500 000 человек. Из них $frac{3}{25}$ — школьники. Сколько в городе школьников?
Решение
1. Чему равна $frac{1}{25}$ от 1 500 000?
1 500 000:25 = 60 000
2. Чему равны $frac{2}{25}$ от 1 500 000?
60 000*3 = 180 000
Ответ: 180 000 школьников.
Когда вы набрались опыта решать такие задачи по вопросам, эти два вопроса можно свести в одно действие и использовать правило:
Чтобы найти дробь от числа, нужно это число умножить на дробь
Или, что то же самое:
Чтобы найти дробь от числа, нужно это число разделить на знаменатель дроби и умножить на её числитель
Пример 1.3.
В автосалон завезли 14 автомобилей. За месяц продали 2/7 этого количества. Сколько автомобилей продали?
Решение
Умножим 14 на $frac{2}{7}$:
$14cdot frac{2}{7} = frac{14cdot 2}{7} = 2cdot 2 = 4$
Ответ: 4 автомобиля.
Теперь рассмотрим задачи второго типа:
Как найти число по дроби
В задачах этого типа исходное число неизвестно. Зато известна величина некоторой части от этого числа и какую дробь составляет эта часть от исходного числа. Для удобства рассмотрим, как бы выглядели эти же три задачи, если бы в них требовалось найти число по дроби.
Пример 2.1.
В самолёте сидят пассажиры (сколько их неизвестно!). Известно, что 48 пассажиров или $frac{2}{5}$ (две пятых) от их количества летят впервые. Нужно найти: сколько всего пассажирова в самолёте?
Решение
Эти 48 пассажиров, которые летят впервые, составляют две пятых ($frac{2}{5}$) от общего количества пассажиров в салоне. Мы можем найти одну пятую?
Да, нужно 48 разделить на 2.
48:2 = 24.
Мы узнали, что одна пятая часть от всех пассажиров — это 24 человека. Сколько всего пассажиров? В пять раз больше, то есть 24х5 = 120.
Ответ: 120 пассажиров всегов самолёте
Понятно? Давайте разберём ещё одну задачу.
Пример 2.2.
Три двадцать пятых ($frac{3}{25}$) населения города составляют школьники. Школьников в городе 180 000. Каково общее население города?
Решение
Опять само число (то есть население города) на неизвестно, зато известно, чему равны $frac{3}{25}$ от него.Значит, можно сначала найти, чему равна $frac{1}{25}$ от населения города. Разделим 180 000 на 3:
180 000:3 = 60 000
Зная одну двадцать пятую, можно найти и целое, умножив 60 000 на 25.
60 000х25 = 1 500 000
Ответ: в городе 1 500 000 жителей
Когда будете уверенно решать задачи на нахождение числа по его дроби по вопросам, можно будет заменить эти вопросы одним действием и использовать правило:
Чтобы найти число по его дроби, известную величину нужно разделить на эту дробь
Или, что то же самое:
Чтобы найти число по его дроби, известную величину нужно разделить на числитель дроби и умножить на её знаменатель
Пример 2.3.
Из завезённых в автосалон автомобилей за месяц продали удалось продать всего 4, что составляет 2/7 всех автомобилей. Сколько автомобилей завезли в салон?
Решение
Разделим 4 на $frac{2}{7}$:
$4: frac{2}{7} = frac{4cdot 7}{2} = 2cdot 7 = 14$
Ответ: 14 автомобилей завезли в салон.
И перейдём теперь к третьему типу задач на дроби, которые изучаются в математике 5 класса:
Как найти отношение двух чисел и выразить его в виде дроби
В задачах на нахождение отношения оба числа известны, а нужно найти, какую дробь второе число составляет от первого. Решаются они проще всего
Пример 3.1.
В самолёте 120 пассажиров. Из них 48 человек летят в первый раз. Какая часть пассажиров летит в первый раз?
Решение
Чтобы найти, какую дробь 48 составляет от общего количества пассажиров (120), нужно 48 разлелить на 120 и затем скоратить, что возможно.
Доля летящих впервые пассажиров составляет $frac{48}{120}$.
И числитель, и знаменатель делятся на 2, значит, можно сократить на 2.
$frac{48}{120}=frac{24}{60}$
Сократим ещё раз на 2:
$frac{24}{60} = frac{12}{30}$
И ещё раз:
$frac{12}{30} = frac{6}{15}$
Теперь можно сократить на 3:
$frac{6}{15} = frac{2}{5}$
Больше сокращать не на что — это и можно записать как окончательный ответ задачи.
Ответ: $frac{2}{5}$ пассажиров летят впервые.
Так что правило для решения задач на нахождение отношения чисел самое простое:
Чтобы найти, в виде какой дроби выражается отноешние двух чисел, нужно сначала записать дробь, в которой числитель и знаменатель — эти числа, а затем сократить её.
Обратите внимание, что дробь $frac{A}{B}$ обозначает, какую долю величина А составляет от величины В и правильно записывайте величины в числитель и знаменатель.
Разберём ещё два примера.
Пример 3.2.
В городе с населением 1 500 000 жителей живут 180 000 школьников. Какую часть населения города составляют школьники?
Решение
Нужно найти, какую часть 180 000 составляет от 1 500 000?
Записываем дробь и сокращаем:
$frac{180000}{1500000}=frac{18}{150}=frac{9}{75}=frac{3}{25}$
Ответ: школьники составляют $frac{3}{25}$ от общего населения города
Пример 3.3.
Из завезённых в автосалон автомобилей за месяц продали удалось продать всего 4. Какую часть от всех автомобилей это составляет, если всегов автомалон завезли 14 машин?
Решение
Точно так же, берём дробь $frac{4}{14}$ и сокращаем:
$frac{4}{14}=frac{2}{7}$
Ответ: продали $frac{2}{7}$ от общего количества автомобилей.
Вот как решаются задачи на дроби. Вы найдёте справочники по формулам математики 5, 6 и других классов в разделе «Математика в школе».
Анализ методической литературы и личного опыта
при проведении уроков по теме “Обыкновенные
дроби” показывает необходимость обобщения и
систематизации материала, связанного с решением
задач на дроби.
Требования к математической подготовке
учащихся 5–6-х классов общеобразовательных
учреждений предполагают, что в результате
изучения курса математики учащиеся должны “решать
основные задачи на дроби”, уметь находить часть
числа и числа по его части [2;6]. С учетом
этого строится тематическое планирование
учебного материала, ориентированное на учебник
“Математика, 5” авторов Н.Я.Виленкина, В.И.Жохова,
А.С.Чеснокова, С.И.Шварцбурда, где говорится, что “с
пониманием смысла дроби связаны три основные
задачи на дроби, осознанного решения которых
важно добиться от учащихся”.
В задачах на дроби речь идет о некоторой
величине а, принятой за единицу (“целое”), и
некоторой ее части в, выраженной дробью :
Тип задачи определяется тем, что неизвестно – а,
в или .
Соответственно, выделяются три типа задач на
дроби:
1. Задачи на нахождение части от числа,
выраженной дробью:
1 – а
– ?
Чтобы найти часть числа, выраженную дробью,
можно это число разделить на знаменатель дроби и
умножить на ее числитель:
b = a : n • m
2. Задачи на нахождение числа по его части,
выраженной дробью:
1 – ?
– в
Чтобы найти число по его части, выраженной
дробью, можно эту часть разделить на числитель
дроби и умножить на ее знаменатель:
a = в : т • п
3. Задачи на нахождение дроби, которую одно
число составляет от другого.
1 – а
? – в
Чтобы найти дробь, которую одно число
составляет от другого, можно первое число
разделить на второе:
= а: в
При изучении темы важно научить учащихся
понимать, что принимается за единицу (целое) в
каждой конкретной задаче, на сколько долей она
разбивается, каково значение одной доли, сколько
долей берут, каково значение всех взятых долей,
каковы правила нахождения дроби от числа, числа
по дроби и дроби, которую одно число составляет
от другого.
Представленный ниже материал можно
использовать как в отдельных фрагментах уроков,
так и в специально выделенных уроках по решению
задач на дроби.
1. Задачи на нахождение части от числа,
выраженной дробью
| № | Текст задачи | Краткая запись | Схема | Решение |
| 889 | Купили кусок ткани длиной 2 м 50 см и из платье для куклы. Сколько сантиметров ткани ушло на это платье? |
250см -1
?см — |
 |
250:5·1=50(см)
Ответ: 50см |
| 890 | От дыни массой 2 кг 400 г Ване отрезали каждого отрезанного куска? Сколько граммов дыни осталось? |
2400г – 1
?г – ?г – ост.–?г |
 |
2400:5·1=480(г)
2400:6·1=400(г) 3) 2400––(480+400)= =1520(г)
Ответ: 480г, 400г, 1520г |
| 891 | Петя готовил уроки 1 ч 40 мин. На математику он потратил этого времени, а на историю – минут Петя готовил уроки по математике и сколько по истории? |
120мин-1
?мин- ост.- ?мин ?мин – |
120:5·1=24(мин) 120-24=96(мин) 96:4·1=24(мин)
Ответ: 24 мин, 24 мин |
|
| 902 | На базу в Антарктиду доставили 22 собаки. Из собак составили упряжку, на которой отправились в поход. Сколько собак не вошло в упряжку? |
22с. – 1
?с. – ост. –?с. |
 |
1) 22:11·5=10 (с.)
2) 22-10=12 (с.)
Ответ: 12 собак |
| К задачам №№900; 901; 903; 909; 928; 929; 960; 968; 1134(1,2); 1141; 1337; 1338; 1296(1,2); 1681(1,2); 980; 983; 1001; 1014; 1015; 1019;1043; 1044; 1733; 1343; 1344; 1345; 1377; 1494; 1595 можно |
2. Задачи на нахождение части от числа,
выраженной дробью
| № | Текст задачи | Краткая запись | Схема | Решение |
| 904 | Сколько молока в бидоне, если составляет 13 л? |
13 л – ? л – 1(все молоко) |
 |
13:1·5=65(л)
Ответ: 65 л |
| 905 | Дорога от Фабричного до Кратова равна 5 км, что составляет Найдите расстояние от Фабричного до Ильинского. |
5 км – ? км – 1(расстояние от Ф.до И.) |
 |
5:5·8=8(км)
Ответ: 8 км |
| 906 | Человек прошел дороги, если он прошел 4 км? |
4 км – ? км – 1(вся дорога) |
 |
4:2·3=6(км)
Ответ: 6 км |
| 907 | Велосипедист проехал дороги, если он проехал 40 км? |
40 км – ? км – 1(вся дорога) |
 |
40:2·9=180(км)
Ответ:180 км |
| 908 | Миша исписал 10 страниц тетради, что составляет всей тетради. Сколько страниц в тетради? |
10 стр. – ? стр. – 1(вся тетрадь) |
 |
10:5·6=12 (стр.)
Ответ: 10 страниц |
| К задачам №№930; 931; 962; 969; 981; 1046; 1824; 982; 1002; 1020; 1021; 1731; 1732; 1346; 1347; 1378; 1481(1,2); 1495; 1594 можно составить аналогично краткую |
3. Задачи на нахождение дроби, которую одно
число составляет от другого
| № | Текст задачи | Краткая запись | Схема | Решение |
| 896 | Дорога от Фабричного до Ильинского равна 8 км. Лена прошла по этой дороге 3 км. Какую |
8 км – 1
3 км – ? часть (от всей дороги) |
 |
3:8= Ответ: |
| 897 | В январе 31 день, а в году 365 дней. Какую часть года составляет январь? |
365 дней – 1
31 день (январь) – ? часть (от |
 |
31:365= Ответ: |
| 898 | В январе 1995 года с 1 января по 10 января были зимние каникулы. 15, 22 и 29 января были воскресными днями, а остальные – учебными. Какую часть января составили свободные от учебы дни? Какую |
31 день – 1
13 дней (свободные) – ? часть 18 дней (учебные) – ? часть (от января) |
 |
13:31= 18:31=
Ответ: |
| 899 | Площадь поля 16 км2. Пшеницей засеяли 11 км2, а рожью – 5 км2. Какая часть поля засеяна пшеницей и какая рожью? |
16 км2 – 1
11 км2 – ? часть (от 5 км2 – ? часть (от поля) |
 |
1) 11:16= 2) 5:16=
Ответ: |
| К задачам №№926; 956; 957; 958; 959; 961; 1037(1,2); 1045; 1069; 1070; 1727; 1822; 1823; 1245; 1013; 1729; 1730 можно |
Литература:
- Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд
С.И. Математика: учебник для 5 класса
общеобразовательных учреждений в двух частях.
Часть 2 (Дробные числа)/, – 18-е издание. – Москва:
Мнемозина, 2006. - Жохов В.И. Разработки уроков, нормативные и
контрольно-методические материалы: Математика,
5-6: Книга для учителя. – Москва: ИЛНКСА, 2007. - Шевкин А. В. Материалы курса “Текстовые задачи в
школьном курсе математики”: Лекции 1-4, 5-8. –
Москва: Педагогический университет “Первое
сентября”, 2006. - Петерсон Л.Г. Математика. 4 класс. Часть 1, 2. –
Москва: Издательство “Ювента”. 2005. - Дорофеев Г.В., Петерсон Л.Г. Математика. 5 класс.
Часть 2. – Москва: Издательство “Ювента”. 2006. - Программы для общеобразовательных учреждений.
Математика/ Сост. Г.М. Кузнецова, Н.Г. Миндюк, –
Москва, 2000.
Задачи на дроби
Задача 1. В классе 
Решение
Если 

Задача 2. В классе 


Задача 3. В классе 24 школьника. 


Решение
24 : 6 × 1 = 4 × 1 = 4 (отличника)
24 : 6 × 3 = 4 × 3 = 12 (хорошистов)
24 : 6 × 2 = 4 × 2 = 8 (троечников)
Проверка
4 + 12 + 8 = 24 (школьника)
24 = 24
Задача 4. В классе 

Решение
Школьники разделены на 6 частей. На одну из частей приходятся отличники, на три части — хорошисты. Нетрудно догадаться, что на остальные две части приходятся троечники. Значит 
Не приводя рисунков можно сложить дроби 


Задача 5. В классе 16 школьников. Из них 

Решение
16 : 4 × 1 = 4 × 1 = 4 (отличника)
16 : 16 × 12 = 1 × 12 = 12 (хорошистов)
Задача 6. В классе 16 школьников. Из них 


Решение
16 : 8 × 1 = 2 × 1 = 2 (отличника)
16 : 16 × 10 = 1 × 10 = 10 (хорошистов)
16 : 4 = 4 (троечника)
Задача 7. Из зерен пшеницы производят полтавскую крупу, масса которой составляет 
Решение
Найдем 
Теперь найдем массу кормовых отходов. Для этого вычтем из 500 ц массу полтавской крупы:
Значит из 500 центнеров зерен пшеницы можно получить 320 центнеров полтавской крупы и 180 центнеров кормовых отходов.
Задача 8. Килограмм сахара стоит 88 рублей. Сколько стоит 



Решение
1) 
88 : 2 = 44
44 × 1 = 44 рубля
2) 

88 : 4 = 22
22 × 1 = 22 рубля
3) Дробь 


4) Дробь 
Одиннадцать восьмых это один целый килограмм и 


Стоимость 

88 : 8 = 11
11 × 11 = 121
Но выделив целую часть можно хорошо понять, как сформировалась цена на 
Задача 9. Финики содержат 

Решение
Узнаем сколько граммов сахара содержится в одном килограмме фиников. Один килограмм это тысяча грамм. Найдем 
1000 : 25 = 40
40 × 18 = 720 г
В одном килограмме фиников содержится 720 грамм сахара. Чтобы узнать сколько грамм сахара содержится в четырех килограммах, нужно 720 умножить на 4
720 × 4 = 2880 г
Теперь узнаем сколько минеральных солей содержится в 4 килограммах фиников. Но сначала узнаем сколько минеральных солей содержится в одном килограмме. Один килограмм это тысяча грамм. Найдем 
1000 : 200 = 5
5 × 3 = 15 г
В одном килограмме фиников содержится 15 грамм минеральных солей. Чтобы узнать сколько грамм минеральных солей содержится в четырех килограммах, нужно 15 умножить на 4
15 × 4 = 60 г
Значит в 4 кг фиников содержится 2880 грамм сахара и 60 грамм минеральных солей.
Решение для данной задачи можно записать значительно короче, двумя выражениями:
Суть в том, что от 4 килограмм нашли 

Задача 10. Поезд прошел 840 км, что составляет 
Решение
В задаче говорится, что 840 км это 

840 : 4 = 210 км.
А поскольку весь путь состоит из семи частей, то расстояние всего пути можно найти, умножив 210 на 7:
210 × 7 = 1470 км.
Теперь ответим на второй вопрос задачи — какое расстояние осталось пройти поезду? Если длина пути 1470 км, а пройдено 840, то оставшийся путь равен 1470−840, то есть 630
1470 − 840 = 630
Задача 11. Одна из групп, покорившая горную вершину Эверест, состояла из спортсменов, проводников и носильщиков. Спортсменов в группе было 25, число проводников составляло 
Решение
Спортсменов группе 25. Проводников составляет 

25 : 5 × 4 = 20
Спортсменов и проводников вместе — 45 человек. Это число составляет 

45 : 9 × 140 = 5 × 140 = 700
Задача 12. В школу привезли 900 новых учебников, из них учебники по математике составляли 

Узнаем сколько составляют учебники по математике:
900 : 25 × 8 = 288 (книг по математике)
Узнаем сколько учебников по русскому языку:
900 : 100 × 33 = 297 (книг по русскому языку)
Узнаем сколько учебников по литературе. Для этого из общего числа книг вычтем учебники по математике и по русскому:
900 – (288+297) = 900 – 585 = 315
Проверка
288 + 297 + 315 = 900
900 = 900
Задача 13. В первый день продали 

Решение
За два дня продали 

Можно представить поступивший в магазин виноград в виде шести гроздей. Тогда 



Задача 14. Вера в первый день прочитала 

Решение
Определим часть книги, прочитанной во второй день. Сказано, что во второй день прочитано на 

Во второй день Вера прочитала 
За два дня Вера прочитала 

Сделаем проверку. Предположим что книга, которую читала Вера, имела 180 страниц. В первый день она прочла 

180 : 9 × 5 = 100 (страниц)
Во второй день Вера прочитала на 

180 : 6 × 1 = 30 × 1 = 30 (страниц)
100 − 30 = 70 (страниц во второй день)
Проверим, являются ли 70 страниц 
180 : 18 × 7 = 10 × 7 = 70 (страниц)
Теперь ответим на второй вопрос задачи — успела ли Вера прочитать все 180 страниц за два дня. Ответ — не успела, поскольку за два дня она прочла только 170 страниц
100 + 70 = 170 (страниц)
Осталось прочесть еще 10 страниц. В задаче в роли остатка у нас была дробь 

180 : 18 × 1 = 10 × 1 = 10 (страниц)
Задача 15. В одном пакете 

Решение
Определим массу второго пакета. Она на 
Масса второго пакета 
Масса обоих пакетов 



1000 : 2 × 1 = 500 × 1 = 500 г
1000 : 5 × 1 = 200 × 1 = 200 г
Во втором пакете на 200 граммов меньше, поэтому чтобы определить массу второго пакета, нужно из 500 г вычесть 200 г
500 − 200 = 300 г
Ну и напоследок сложить массы обоих пакетов:
500 + 300 = 800 г
Задача 16. Туристы прошли путь от турбазы до озера за 4 дня. В первый день они прошли 

Решение
В задаче сказано, что во второй день туристы прошли 



В третий и четвертый день туристы прошли 24 км и это составляет 

24 : 4 × 7 = 6 × 7 = 42 км
Во второй, третий и четвертый день туристы прошли 42 км. Теперь найдем 
42 : 7 × 3 = 6 × 3 = 18 км
Теперь возвращаемся к началу задачи. Сказано, что в первый день туристы прошли 
Зная, что 
42 : 3 × 4 = 56 км
Значит длина пути от турбазы до озера составляет 56 километров. Сделаем проверку. Для этого сложим все пути, пройденные туристами в каждый из четырех дней.
Сначала найдем путь пройденный в первый день:
56 : 4 × 1 = 14 (в первый день)
14 + 18 + 12 + 12 = 56
56 = 56
Задача из арифметики известного среднеазиатского математика Мухаммеда ибн-Мусы ал-Хорезми (IX век н. э.)
«Найти число, зная, что если отнять от него одну треть и одну четверть, то получится 10»
Изобразим число, которое мы хотим найти, в виде отрезка, разделенного на три части. В первой части отрезка отметим треть, во второй — четверть, оставшаяся третья часть будет изображать число 10.
Сложим треть и четверть:
Теперь изобразим отрезок, разделенный на 12 частей. Отметим на нем дробь 
Зная, что пять двенадцатых числа составляют число 10, мы можем найти всё число:
10 : 5 × 12 = 2 × 12 = 24
Мы нашли всё число — оно равно 24.
Эту задачу можно решить не приводя рисунков. Для этого, сначала нужно сложить треть и четверть. Затем из единицы, которая играет роль неизвестного числа, вычесть результат сложения трети и четверти. Затем по полученной дроби определить всё число:
Задача 17. Семья, состоящая из четырех человек, в месяц зарабатывает 80 тысяч рублей. Бюджет распланирован следующим образом: 






Решение
80 : 40 × 7 = 14 (тыс. на еду)
80 : 20 × 1 = 4 × 1 = 4 тыс. (на коммунальные услуги)
80 : 20 × 1 = 4 × 1 = 4 тыс. (на Интернет и ТВ)
80 : 20 × 3 = 4 × 3 = 12 тыс. (на лечение и походы по врачам)
80 : 10 × 1 = 8 × 1 = 8 тыс. (на пожертвование в детский дом)
80 : 20 × 3 = 4 × 3 = 12 тыс. (на проживание в съемной квартире)
80 : 40 × 13 = 2 × 13 = 26 тыс. (в копилку)
Проверка
14 + 4 + 4 + 12 + 8 + 12 + 26 = 80
80 = 80
Задача 18. Туристы во время похода за первый час прошли 

Решение
Найдем числа по дробям. 

Определим длину пути, пройденного туристами за второй час. Для этого к 3 км 700 м нужно прибавить 1 км 200 м
3 км 700 м + 1 км 200 м = 3700м + 1200м = 4900м = 4 км 900 м
Определим длину пути, пройденного туристами за два часа:
3 км 700 м + 4 км 900 = 3700м + 4900м = 8600м = 8 км 600 м
Значит за два часа туристы прошли 8 километров и еще 600 метров. Решим эту задачу с помощью дробей. Так её можно значительно укоротить
Получили ответ 
Задача 19. Геологи прошли долину, расположенную между горами, за три дня. В первый день они прошли 

Решение
Изобразим путь в виде отрезка, разделенного на три части. В первой части отметим 

Сложим части пути, пройденные в первый и во второй день:
За первый и второй дни геологи прошли 


28 : 4 × 9 = 7 × 9 = 63 км
Проверка
63 : 9 × 5 = 7 × 5 = 35
63 : 9 × 4 = 7 × 4 = 28
35 + 28 = 63
63 = 63
Задача 20. Для приготовления крема использовали сливки, сметану и сахарную пудру. Сметану и сливки составляют 844,76 кг, а сахарная пудра и сливки 739,1 кг. Сколько в отдельности сливок, сметаны и сахарной пудры содержится в 1020,85 кг крема?
Решение
сметана и сливки — 844,76 кг
сахарная пудра и сливки — 739,1 кг
Вытащим из 1020,85 кг крема сметану и сливки (844,76 кг). Так мы найдем массу сахарной пудры:
1020,85 кг — 844,76 кг = 176,09 (кг сахарной пудры)
Вытащим из сахарной пудры и сливок сахарную пудру (176,09 кг). Так мы найдем массу сливок:
739,1 кг — 176,09 кг = 563,01 (кг сливок)
Вытащим сливки из сметаны и сливок. Так мы найдем массу сметаны:
844,76 кг — 563,01 кг = 281,75 (кг сметаны)
176,09 (кг сахарная пудра)
563,01 (кг сливки)
281,75 (кг сметана)
Проверка
176,09 кг + 563,01 кг + 281,75 кг = 1020,85 кг
1020,85 кг = 1020,85 кг
Задача 21. Масса бидона, заполненного молоком равна 34 кг. Масса бидона, заполненного наполовину, равна 17,75 кг. Какова масса пустого бидона?
Решение
Вычтем из массы бидона, заполненного молоком, массу бидона заполненного наполовину. Так мы получим массу содержимого бидона, заполненного наполовину, но уже без учета массы бидона:
34 кг − 17,75 кг = 16,25 кг
16,25 это масса содержимого бидона заполненного наполовину. Умножим эту массу на 2, получим массу бидона заполненного полностью:
16,25 кг × 2 = 32,5 кг
32,5 кг это масса содержимого бидона. Чтобы вычислить массу пустого бидона, нужно из 34 кг вычесть массу его содержимого, то есть 32,5 кг
34 кг − 32,5 кг = 1,5 кг
Ответ: масса пустого бидона составляет 1,5 кг.
Задача 22. Сливки составляют 0,1 массы молока, а сливочное масло составляет 0,3 массы сливок. Сколько сливочного масла можно получить из суточного надоя коровы, равного 15 кг молока?
Решение
Определим сколько килограмм сливок можно получить с 15 кг молока. Для этого найдем 0,1 часть от 15 кг.
15 × 0,1 = 1,5 (кг сливок)
Теперь определим сколько сливочного масла можно получить с 1,5 кг сливок. Для этого найдем 0,3 часть от 1,5 кг
1,5 кг × 0,3 = 0,45 (кг сливочного масла)
Ответ: из 15 кг молока можно получить 0,45 кг сливочного масла.
Задача 23. 100 кг клея для линолеума содержат 55 кг асфальта, 15 кг канифоли, 5 кг олифы и 25 кг бензина. Какую часть этого клея образует каждая из его составляющих?
Решение
Представим, что 100 кг клея как 100 частей. Тогда на 55 частей приходится асфальт, на 15 частей — канифоль, на 5 частей — олифа, на 25 частей — бензин. Запишем эти части в виде дробей, и по возможности сократим получающиеся дроби:
Ответ: