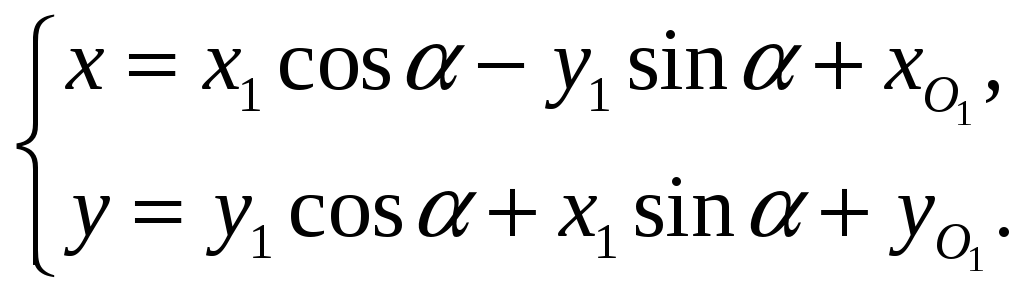Как найти вспомогательную систему координат

Перейти к содержанию

Параболой
называется геометрическое место точек
на плоскости, равноудалённых от заданной
точки, называемой фокусом,
и заданной прямой, называемой директрисой.
Пусть
–
фокус. Ось Ox
проведём через

перпендикулярно директрисе (рис. 26).

П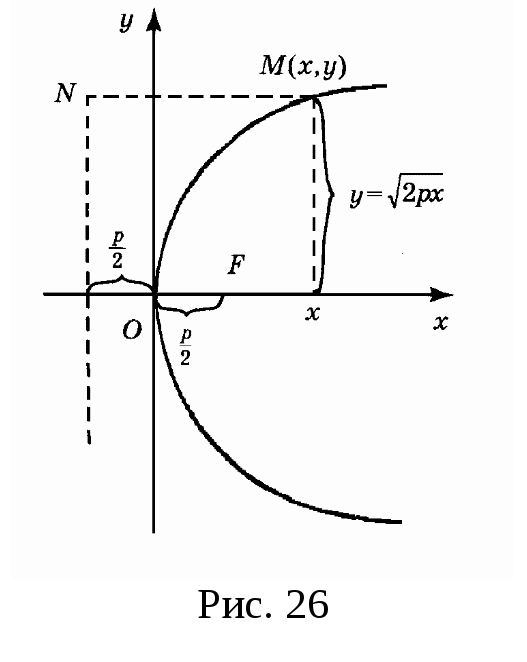усть
–
расстояние от фокуса

до директрисы. Это число задано и
называется параметром
параболы.
Начало координат возьмём в середине
перпендикуляра, опущенного из точки

на директрису. Тогда фокус будет иметь
координаты
.
Директриса имеет уравнение
.
Пусть

– произвольная точка параболы,

– основание перпендикуляра, опущенного
из точки

на директрису. Из рис. 26 видно, что
расстояние

. (45)

Запишем расстояние
от

до
:

(46)

Для любой точки

параболы имеем

(по определению). Подставим сюда выражения
(45), (46) и получим уравнение параболы

.

Упростим его,
избавляясь от корня. Получим
каноническое уравнение параболы

.
(47)

И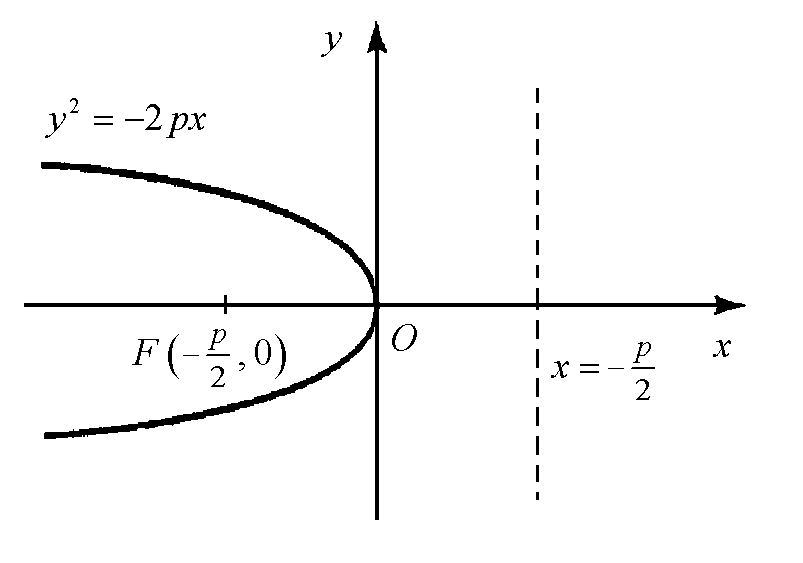сследуем
форму параболы по уравнению (47). Так как
это уравнение содержит

только во второй степени, то, как и в
случае эллипса, Ox
является осью симметрии параболы.
Следовательно, вид параболы достаточно
установить в верхней полуплоскости,
где
.
Для таких значений

уравнение (47) запишем в виде
.
Эта формула выражает ординату точки
,
абсцисса которой равна
.
Когда
,
согласно последней формуле
,
точка

совпадает с
.
С увеличением
–
абсциссы точки

– её ордината, равная
,
неограниченно растёт, и точка

уходит вверх и вправо. В силу симметрии
остальная часть параболы вычерчивается
сразу. Если Ox
провести от

к директрисе, то получим параболу,
изображенную на рис. 27. Легко проверить,
что уравнение параболы в этом случае
будет иметь вид

Пусть теперь ось Oy
направлена
п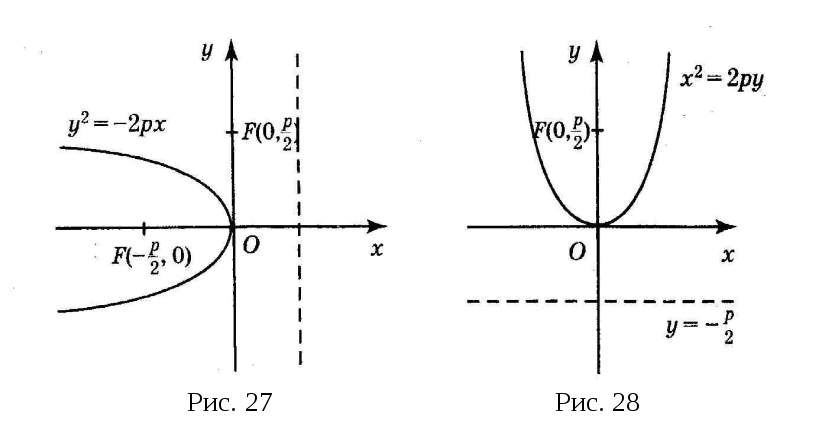ерпендикулярно
к директрисе и проходит через
.
При этом уравнение параболы будет иметь
вид

(см. рис. 28).

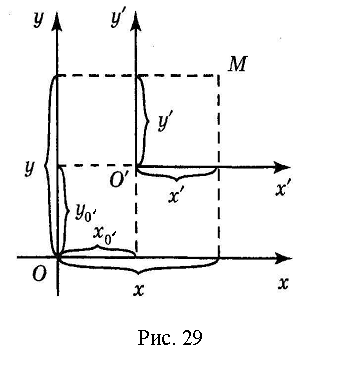
§16. Преобразование координат на плоскости

Параллельный
перенос осей координат. Пусть

– исходная система координат,

– новая система координат, полученная
параллельным переносом исходной
системы, как показано на рис. 29.
Положение новой системы по отношению
к старой определим, задав координаты

нового начала

в старой системе координат, где

– заданные числа. Пусть
,

– координаты точки

в новой системе,

– координаты точки

в исходной системе. Как видно из рис. 29,
,
.
Итак,

(48)

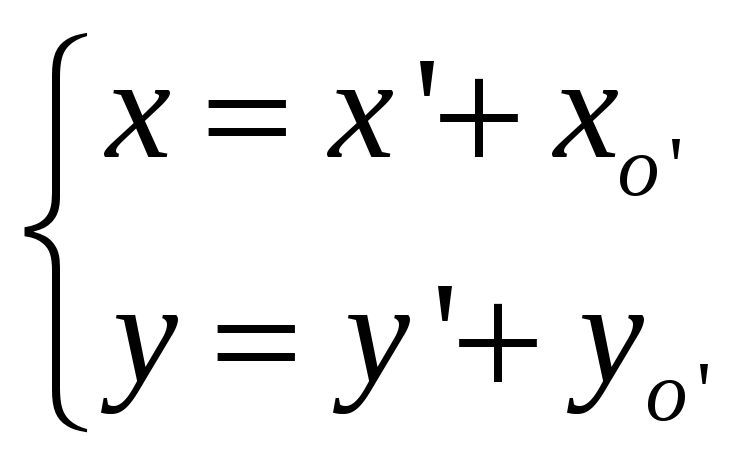
Эти формулы
выражают старые координаты

точки

через её новые координаты.

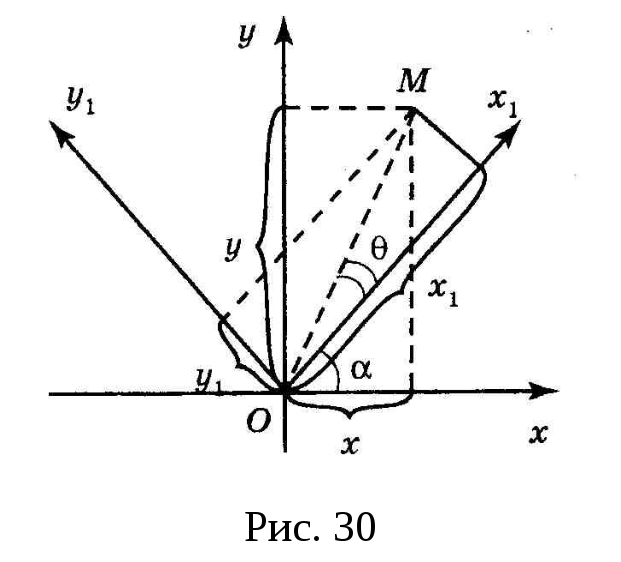
Поворот осей
координат. Пусть

– исходная система координат, а новая
система координат получена поворотом
исходной вокруг начала координат на
угол ,
где 
– заданное число (см. рис. 30). Угол

берётся со знаком «+», если отсчёт
ведётся против хода часовой стрелки
от оси Ox.
Пусть

– координаты точки

в системе
,


– координаты точки
в
системе
.
Пусть

и

– угол, образованный отрезком

с осью
,
причём, как и

этот угол берётся со знаком «+», если
отсчёт ведётся от оси

против хода часовой стрелки. Из рис. 30
видно, что

(49)

С другой стороны,

(50)

Формулы (50)
перепишем, использовав известные
формулы тригонометрии для косинуса и
синуса суммы:


С учётом (49) запишем

(51)

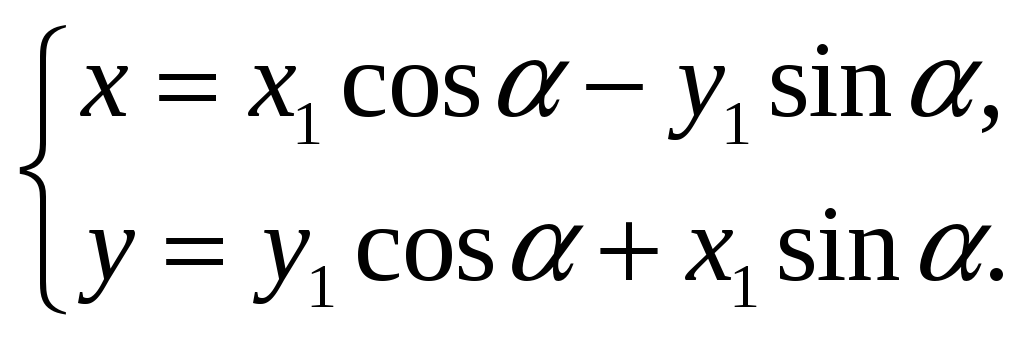
Эти формулы
выражают старые координаты точки

через её новые координаты в случае
поворота осей координат.

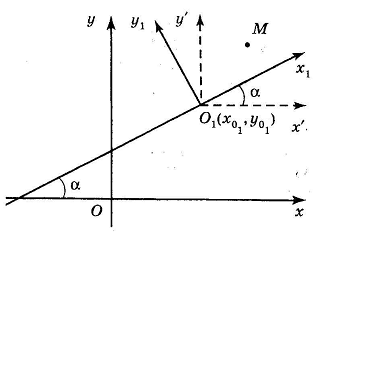
Общий случай.
Пусть

– исходная система координат,

– новая система координат (рис. 31).
Положение новой системы по отношению
к старой определим, задав:

• координаты
  
  нового начала
  
  в старой системе координат;

• угол
  
  который образует ось
  
  с Ox.

П

Рис. 31

усть

– координаты точки

в старой системе, а

– координаты точки

в новой системе. Нужно найти связь между
ними. С этой целью введём вспомогательную
систему координат
,
полученную параллельным переносом
старой системы

Пусть
,

– координаты точки
в
этой вспомогательной системе. Так как
новая система координат

получена поворотом вспомогательной
системы

на угол

то координаты
,

точки

через координаты

этой точки выражаются формулами (51), в
которых

нужно заменить на
,
:

(52)

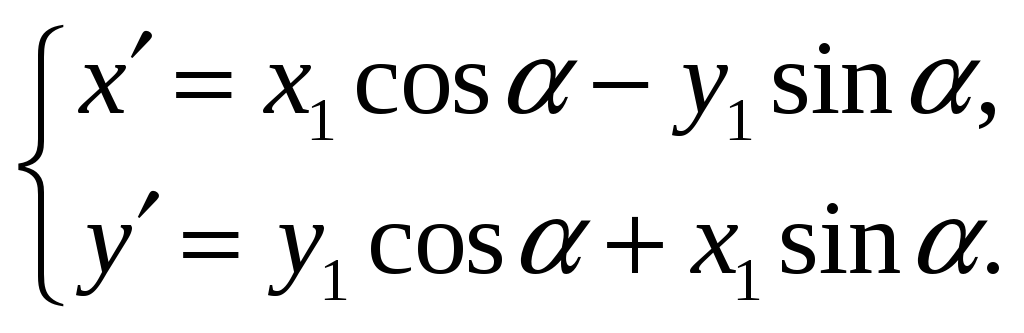
Так как система
координат

получена параллельным переносом
,
то координаты

точки

в исходной системе выражаются через
координаты
,

по формулам (48), в которых

нужно заменить на
:

В эти формулы вместо
,

подставим (52) и получим

(53)

Эти формулы
выражают старые координаты

точки

через её новые координаты

в новой системе.

Преобразования
координат на плоскости применяются, в
частности, для упрощения вида уравнений
кривых. В системе координат

возьмём, например, эллипс с каноническим
уравнением

(54)

Подставим вместо

их выражения (53) через
,
тем самым получим уравнение эллипса в
новой системе координат
.
Это будет уравнение общего вида (после
раскрытия скобок)

.

Таким образом,
перейдя к системе
,
от канонического уравнения (54) эллипса
мы перешли к более сложному уравнению
– уравнению второй степени общего
вида. Можно показать, что, наоборот, от
последнего уравнения в системе
,
подобрав другую систему координат

можно получить каноническое уравнение,
определяющее либо окружность, либо
эллипс, либо параболу, либо гиперболу,
либо пару прямых, как, например, уравнение

(,
),
если не имеет место случай, когда
уравнение определяет лишь точку или
ничего не определяет.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Вспомогательная система координат — это система координат, которая получается параллельным переносом. 
Параллельный перенос осуществляется относительно начала отсчёта, а координаты начала отсчёта вспомогательной системы координат определяются координатами вершины.
В данном случае O1(2; -1).

P.s: чтобы построить график функции y = (x — l)ⁿ, нужно перенести график функции y = xⁿ на l единиц вправо, если l > 0, или на l единиц влево, если l < 0.
Чтобы построить график функции y = xⁿ — m, нужно перенести график функции y = xⁿ на m единиц вниз, если m > 0, или на m единиц вверх, если m > 0.

Вспомогательная система — координата

Cтраница 1

Вспомогательная система координат — прямоугольная правая пространственная система координат, фиксированно связанная с одним из конструктивных элементов проектируемого приспособления пли обрабатываемой детали.
 [1]

Вспомогательная система координат зг ( xlt уг, z) проведена таким образом, что ее начало совпадает с центром С шарика ( рис. 12.12, а, б), а ось уг с касательной к винтовой линии на цилиндре радиуса R.
 [2]

Построим вспомогательную систему координат Сх у г, оси которой параллельны соответствующим осям системы Охуг.
 [3]

Воспользуемся вспомогательной системой координат х Ау, начало которой поместим в точку А, а ось абсцисс направим по линии, соединяющей центры А и С так, чтобы точка С всегда лежала на ее положительном направлении.
 [5]

Со стойкой связана еще вспомогательная система координат Ахьуьгь, ее ось гь совмещена с осью шарнира А, а ось уъ параллельна оси у и направлена в ту же сторону.
 [7]

Со стойкой связана еще вспомогательная система координат Ахьуьгь, ее ось Zft совмещена с осью шарнира А, а ось уь параллельна оси у и направлена в ту же сторону.
 [8]

Со стойкой связана еще вспомогательная система координат Ахъуьгъ, ее ось гь совмещена с осью шарнира А, а ось уъ параллельна оси у и направлена в ту же сторону.
 [10]

Отметим, что вспомогательную систему координат удобно выбирать так, чтобы ее оси были главными как можно для большего числа подобластей.
 [11]

Поставим задачу нахождения направляющих косинусов вспомогательной системы координат ОХ / j ZJ ( связанной с корпусом инклинометра, относительно основной системы координат OXYZ, связанной с направлением магнитного меридиана и вектора силы тяжести.
 [12]

Поместим в точке у е А вспомогательную систему координат 0г так, чтобы ось аз была направлена по отрицательной нормали к А, а оси ai, a2 были касательными к линиям кривизны в этой точке.
 [13]

В соответствии с этим мы можем ввести вспомогательную систему координат, которая, двигаясь поступательно, совершает такое же элементарное перемещение Дз, как и все точки тела.
 [14]

Для решения поставленной задачи целесообразно несколько преобразовать вспомогательную систему координат, принятую для решения обратной геодезической задачи, а именно: ось х располагают в плоскости меридиана первой точки в направлении оси вращения эллипсоида; ось у — под прямым углом к оси х, а ось z — по направлению нормали.
 [15]

Страницы:  

   1

   2

   3

Прямоугольная система координат

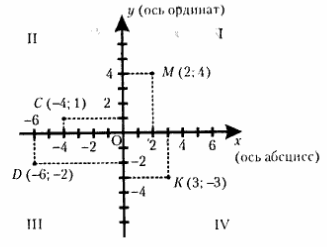
Прямоугольная (другие названия — плоская, двухмерная) система координат, названная по имени французского ученого Декарта (1596—1650) «декартовой системой координат на плоскости», образуется пересечением на плоскости под прямым углом (перпендикулярно) двух числовых осей так, что положительная полуось одной направлена вправо (ось x, или ось абсцисс), а второй — вверх (ось y, или ось ординат).

Точка пересечения осей совпадает с точкой 0 каждой из них и называется началом координат.

Для каждой из осей выбирается произвольный масштаб (единичный отрезок длины). Каждой точке плоскости соответствует одна пара чисел, названная координатами этой точки на плоскости. И наоборот, любой упорядоченной паре чисел соответствует одна точка плоскости, для которой эти числа являются координатами.

Первая координата точки называется абсциссой этой точки, а вторая координата — ординатой.

Вся плоскость координат делится на 4 квадранта (четверти). Квадранты расположены от первого до четвертого против часовой стрелки (см. рис.).

Чтобы определить координаты точки, нужно найти ее расстояние до оси абсцисс и оси ординат. Так как расстояние (кратчайшее) определяется по перпендикуляру, то из точки опускаются два перпендикуляра (вспомогательные линии на плоскости координат) на оси так, что точка их пересечения — это и есть место заданной точки в плоскости координат. Точки пересечения перпендикуляров с осями называются проекциями точки на оси координат.

Первый квадрант ограничен положительными полуосями абсцисс и ординат. Следовательно, координаты точек в этой четверти плоскости будут положительными
(знаки « + » и < + »).

Например, точка M (2; 4) на рисунке вверху.

Второй квадрант ограничен отрицательной полуосью абсцисс и положительной полуосью ординат. Следовательно, координаты точек по оси абсцисс будут отрицательными (знак «-»), а по оси ординат — положительными (знак « + »).

Например, точка C (-4; 1) на рисунке выше.

Третий квадрант ограничен отрицательной полуосью абсцисс и отрицательной полуосью ординат. Следовательно, координаты точек по оси абсцисс и оси ординат будут отрицательными (знаки «-» и «-»).

Например, точка D (-6; -2) на рисунке выше.

Четвертый квадрант ограничен положительной полуосью абсцисс и отрицательной полуосью ординат. Следовательно, координаты точек по оси абсцисс будут положительными (знак «+»). а по оси ординат — отрицательными (знак «-»).

Например, точка R (3; -3) на рисунке выше.

Построение точки по ее заданным координатам

1. первую координату точки найдем на оси абсцисс и проведем через нее вспомогательную линию — перпендикуляр;

2. вторую координату точки найдем на оси ординат и проведем через нее вспомогательную линию — перпендикуляр;

3. точка пересечения двух перпендикуляров (вспомогательных линий) и будет соответствовать точке с заданными координатами.

Запись опубликована в рубрике Математика с метками координаты, система. Добавьте в закладки постоянную ссылку.