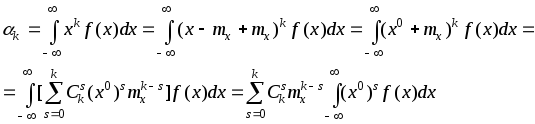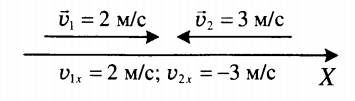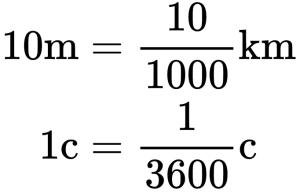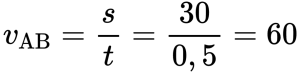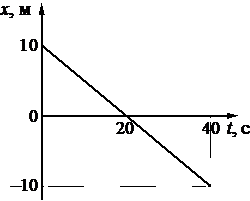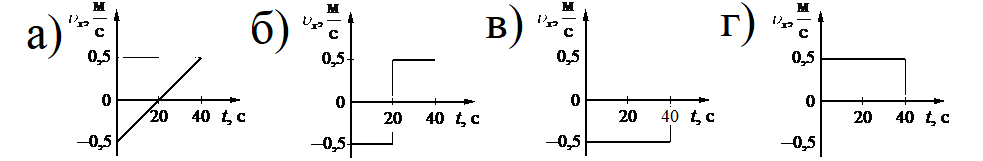Как найти второй начальный момент времени

Начальные и центральные моменты случайной величины

• Краткая теория
• Примеры решения задач

Краткая теория

---

Начальные моменты

Начальным моментом порядка

 случайной величины

 называют математическое ожидание величины

:

В
частности:

Пользуясь
этими моментами, формулу для вычисления дисперсии

 можно записать так:

Центральные моменты

Кроме
моментов случайной величины

 целесообразно рассматривать моменты отклонения

.

Центральным моментом порядка

 случайной величины

 называют математическое ожидание величины

:

В
частности,

Взаимосвязь центральных и начальных моментов

Легко
выводятся соотношения, связывающие начальные и центральные моменты:

Моменты
более высоких порядков применяются редко.

Формулы для вычисления моментов дискретных и непрерывных случайных величин

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Нетрудно
заметить, что при

 первый
начальный момент случайной величины

 есть ее
математическое ожидание, то есть

, при

 второй
центральный момент – дисперсия, то есть

.

Асимметрия и эксцесс случайной величины

Третий центральный момент

 служит для
характеристики асимметрии (скошенности) распределения. Он имеет размерность
куба случайной величины. Чтобы получить безразмерную величину, ее делят на

, где

 – среднее
квадратическое отклонение случайной величины

. Полученная величина

 называется
коэффициентом асимметрии случайной величины:

Если распределение симметрично относительно
математического ожидания, то коэффициент асимметрии

.

Четвертый центральный момент

 служит для
характеристики крутости (островершинности или плосковершинности) распределения.

Эксцессом (или коэффициентом
эксцесса) случайной величины называется число

Число 3 вычитается из отношения

 потому, что для
наиболее часто встречающегося нормального распределения отношение

. Кривые, более островершинные, чем нормальная,
обладают положительным эксцессом, более плосковершинные – отрицательным
эксцессом.

Смежные темы решебника:

• Асимметрия и эксцесс распределения
• Дискретная случайная величина
• Непрерывная случайная величина

Примеры решения задач

---

Пример 1

Дискретная
случайная величина X задана законом распределения:

	1	3	4	5
	0,2	0,3	0,1	0,4

Найти начальные моменты первого, второго и третьего
порядков.

Решение

Найдем
начальный момент 1-го порядка:

Начальный
момент 2-го порядка:

Начальный
момент 3-го порядка:

Ответ:

.

---

Пример 2

Дискретная
случайная величина X задана законом распределения:

	0	3	5	6
	0,3	0,2	0,3	0,2

Найти центральные моменты первого, второго,
третьего и четвертого порядков.

Решение

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Центральный
момент первого порядка равен нулю:

Для
вычисления центральных моментов удобно воспользоваться формулами, выражающими
центральные моменты через начальные, поэтому предварительно найдем начальные
моменты:

Начальный
момент 2-го порядка:

Начальный
момент 3-го порядка:

Начальный
момент 4-го порядка:

Найдем центральные моменты:

Ответ:
.

---

Пример 3

Непрерывная случайная
величина X задана плотностью распределения:

Найти
математическое ожидание, дисперсию, асимметрию и эксцесс.

Решение

Математическое
ожидание (начальный момент первого порядка):

Начальный
момент второго порядка:

Дисперсия
(центральный момент второго порядка):

Среднее
квадратическое отклонение:

Начальный
момент третьего порядка:

Начальный
момент четвертого порядка:

Вычисляем
центральные моменты третьего и четвертого порядков:

Коэффициент
асимметрии:

Эксцесс:

Ответ:

.

• Краткая теория
• Примеры решения задач

3.4. Моменты
случайной величины.

Выше мы познакомились
с исчерпывающими характеристиками СВ:
функцией распределения и рядом
распределения — для дискретной СВ,
функцией распределения и плотностью
вероятности — для непрерывной СВ. Эти
попарно эквивалентные по информационному
содержанию характеристики представляют
собой функции
и полностью описывают СВ с вероятностной
точки зрения. Однако, во многих практических
ситуациях или невозможно, или нет
необходимости характеризовать случайную
величину исчерпывающим образом. Зачастую
бывает достаточно указать один или
несколько числовых
параметров, до некоторой степени
описывающих основные черты распределения,
а иногда нахождение исчерпывающих
характеристик является хотя и желательным,
но слишком трудным математически, и
оперируя числовыми параметрами, мы
ограничиваемся хотя и приближенным, но
более простым описанием. Указанные
числовые параметры называются числовыми
характеристиками случайной
величины и играют большую роль в
применениях теории вероятности к
различным областям науки и техники,
облегчая решение задач и позволяя
представить результаты решения в простой
и наглядной форме.

Наиболее часто
применяемые числовые характеристики
можно условно разбить на два вида:
моменты и
характеристики положения.
Существует несколько видов моментов,
из них наиболее часто применяются два
вида: начальные
и центральные.
Другие виды моментов, например, абсолютные
моменты, факториальные моменты,
мы не рассматриваем. Чтобы избегнуть
применения обобщения интеграла — так
называемого интеграла Стильтьеса, дадим
определения моментов по отдельности
для непрерывных и дискретных СВ.

Определения. 1.
Начальным
моментом k-го
порядка дискретной СВ называется
величина

, k=0, 1, 2, …

(3.4.1)

где {x_i}
, i=1,
2, …, N
— значения
СВ, {p_i}
, i=1,
2, …, N
— вероятности
этих значений, N
— число
значений (при бесконечном числе значений
следует вместо N
писать
).

2. Начальным
моментом k-го
порядка непрерывной СВ называется
величина

, k=0, 1, 2, …

(3.4.2)

где f(x)
— плотность вероятности данной СВ.

3. Центральным
моментом k-го
порядка дискретной СВ
называется величина

, k=0, 1, 2, …

(3.4.3)

где m=
— начальный
момент первого порядка (об этой важной
величине см. ниже), остальные обозначения
в правой части — те же, что и в (3.4.1).

4. Центральным
моментом k-го
порядка непрерывной СВ
называется величина

, k=0, 1, 2, …

(3.4.4)

В случаях, когда
одновременно в рассмотрении находятся
несколько СВ, удобно, во избежание
недоразумений, указывать принадлежность
момента; мы будем это делать, указывая
обозначение соответствующей СВ в
скобках, например,
,
и т. д. Не следует путать это обозначение
с записью функции, а букву в скобках — с
аргументом функции. Суммы и интегралы
в правых частях равенств (3.4.1 — 3.4.4) могут
сходиться или расходиться в зависимости
от значения k
и конкретного распределения. В первом
случае говорят, что момент не
существует или расходится,
во втором — что момент
существует или сходится. Если
у дискретной СВ конечное число конечных
значений (N
конечно),
то все ее моменты конечного порядка k
существуют. При бесконечном N,
начиная с некоторого k
и для бо¢льших
порядков, моменты дискретной СВ
(одновременно начальные и центральные)
могут не существовать. Моменты непрерывной
СВ, как видно из определений, выражаются
несобственными интегралами, которые
могут расходится, начиная с некоторого
k
и для бо¢льших
порядков (одновременно начальные и
центральные). Моменты нулевого порядка
всегда сходятся.

Рассмотрим более
подробно сначала начальные, а затем
центральные моменты. С математической
точки зрения начальный момент k-го
порядка есть «взвешенное среднее» k-ых
степеней значений СВ; в случае дискретной
СВ весами являются вероятности значений,
в случае непрерывной СВ весовой функцией
является плотность вероятности. Такого
рода операции широко применяются в
механике для описания распределения
масс (статические моменты, моменты
инерции и т. д.); возникающие в связи с
этим аналогии рассмотрены ниже.

Для лучшего
понимания начальных моментов рассмотрим
их отдельно при заданных k.
В теории вероятностей наиболее важны
моменты низших порядков, т. е. при малых
k,
поэтому рассмотрение следует вести в
порядке возрастания
значений k.
Начальный момент нулевого порядка равен

=1
, для дискретной СВ;

=1
, для непрерывной СВ,

т.е. для любой СВ
он равен одному и тому же значению —
единице, и поэтому не несет никакой
информации о статистических свойствах
СВ.

Начальный момент
первого порядка (или первый начальный
момент) равен

,
для дискретной СВ;

,
для непрерывной СВ.

Этот момент —
важнейшая числовая характеристика
любой СВ, чему есть несколько взаимосвязанных
причин. Во-первых, согласно теореме
Чебышёва (см. п. 7.4), при неограниченном
числе испытаний над СВ среднее
арифметическое наблюденных значений
стремится (в некотором смысле) к
,
таким образом, для любой СВ

— это характерное число, вокруг которого
группируются ее значения на опыте.
Во-вторых, для непрерывной СВ

численно равен х-овой
координате центра тяжести криволинейной
трапеции, образуемой кривой f(x)
(аналогичное свойство имеет место и для
дискретной СВ), поэтому этот момент
можно было бы назвать «центром тяжести
распределения». В-третьих, этот момент
имеет замечательные математические
свойства, которые выяснятся в процессе
прохождения курса, в частности, поэтому
его величина входит в выражения для
центральных моментов (см. (3.4.3) и (3.4.4)).

Важность этого
момента для теоретических и практических
задач теории вероятностей и его
замечательные математические свойства
привели к тому, что кроме обозначения

и названия «первый начальный момент»
в литературе используются и другие
обозначения и названия, в большей или
меньшей мере удобные и отражающие
упомянутые свойства. Наиболее часто
встречаются названия: математическое
ожидание,
среднее
значение, и
обозначения: m,
M[X],
.
Мы будем чаще всего использовать термин
«математическое ожидание» и обозначение
m;
при наличии нескольких СВ будем
использовать нижний индекс, указывающий
принадлежность математического ожидания,
например, m_x
, m_y
и т. д.

Начальный момент
второго порядка (или второй начальный
момент) равен

,
для дискретной СВ;

,
для непрерывной СВ;

иногда он называется
средним
квадратом случайной величины
и обозначается M[].

Начальный момент
третьего порядка (или третий начальный
момент) равен

,
для дискретной СВ;

,
для непрерывной СВ

иногда он называется
средним кубом
случайной величины
и обозначается M[X³].

Нет смысла продолжать
дальше перечисление начальных моментов.
Остановимся на важной интерпретации
моментов порядка k>1.
Пусть, наряду со СВ X
имеется
также СВ Y,
причем Y=X^k
(k=2,
3, …). Это
равенство означает, что случайные
величины X
и Y
связаны
детерминировано в том смысле, что когда
СВ X
принимает
значение x,
СВ Y
принимает значение y=x^k
(в
дальнейшем такая связь СВ будет
рассмотрена более подробно). Тогда,
согласно (3.4.1) и (3.4.2)

=m_y
, k=2,
3, …,

т. е. k-ый
начальный момент СВ равен математическому
ожиданию k-ой
степени этой случайной величины.
Например, третий начальный момент длины
ребра случайного кубика равен
математическому ожиданию объема кубика.
Возможность понимания моментов как
неких математических ожиданий — еще
одна грань важности понятия математического
ожидания.

Перейдем к
рассмотрению центральных моментов.
Поскольку, как выяснится несколько
ниже, центральные моменты однозначно
выражаются через начальные и наоборот,
встает вопрос, зачем вообще нужны
центральные моменты и почему недостаточно
начальных моментов. Рассмотрим СВ X
(непрерывную или дискретную) и другую
СВ Y,
связанную с первой как Y=X+a
, где a0
— неслучайное вещественное число. Каждому
значению x
случайной
величины X
соответствует значение y=x+a
случайной
величины Y,
следовательно распределение СВ Y
будет иметь ту же форму
(выраженную
многоугольником распределения в
дискретном случае или плотностью
вероятности — в непрерывном случае), что
и распределение СВ X,
но сдвинуто по оси абсцисс на величину
a
. Следовательно, начальные моменты СВ
Y
будут
отличаться от соответствующих моментов
СВ X.
Например,
как нетрудно видеть, m_y=m_x+a
(моменты
более высокого порядка связаны более
сложными соотношениями). Итак, мы
установили, что начальные
моменты не инвариантны относительно
сдвига распределения в целом.
Тот же результат получится, если сдвигать
не распределение, а начало оси абсцисс
по горизонтали на величину —a,
т.е. справедлив и эквивалентный вывод:
начальные
моменты не инвариантны относительно
сдвига начала оси абсцисс по горизонтали.

От этого недостатка
свободны центральные моменты,
предназначенные для описания тех свойств
распределений, которые не зависят от
их сдвига в целом. Действительно, как
видно из (3.4.3) и (3.4.4), при сдвиге распределения
в целом на величину a,
или, что то же самое, сдвиге начала оси
абсцисс на величину —a,
все значения x,
при тех же вероятностях (в дискретном
случае) или той же плотности вероятности
(в непрерывном случае), изменятся на
величину a,
но настолько же изменится величина m,
так что значения скобок в правых частях
равенств не изменятся. Таким образом,
центральные
моменты инвариантны относительно сдвига
распределения в целом, или, что то же
самое, относительно сдвига начала оси
абсцисс по горизонтали.
Название
«центральные» эти моменты получили в
те времена, когда первый начальный
момент назывался «центром». Полезно
заметить, что центральный момент СВ X
можно
понимать как соответствующий начальный
момент СВ X⁰,
равной

X0=X-mx .

(3.4.5)

СВ X⁰
называется
центрированной
(по отношению к СВ X),
а приводящая к ней операция, т. е. вычитание
из случайной величины ее математического
ожидания, называется центрированием.
Как мы увидим в дальнейшем, это понятие
и эта операция будут полезны на протяжении
всего курса. Заметим, что центральный
момент порядка k>1
можно
рассматривать как математическое
ожидание (среднее) k-ой
степени центрированной СВ:
.

Рассмотрим по
отдельности центральные моменты низших
порядков. Центральный момент нулевого
порядка равен

,
для дискретных СВ;

,
для непрерывных СВ;

т. е. для любой СВ

и не несет никакой информации о
статистических свойствах этой СВ.

Центральный момент
первого порядка (или первый центральный
момент) равен

,

для дискретной
СВ;

,

для непрерывной
СВ; т. е. для любой СВ

и не несет никакой информации о
статистических свойствах этой СВ.

Центральный момент
второго порядка (или второй центральный
момент) равен

,
для дискретной СВ;

,
для непрерывной СВ.

Как выяснится
ниже, этот момент — один из важнейших в
теории вероятностей, т. к. используется
как характеристика меры разброса (или
рассеяния) значений СВ, поэтому часто
называется дисперсией
и обозначается D_х
.
Заметим, что

можно понимать как средний квадрат
центрированной СВ.

Центральный момент
третьего порядка (третий центральный
момент) равен

, для дискретной
СВ;

, для непрерывной
СВ;

и может пониматься
как математическое ожидание куба
центрированной СВ.

Центральный момент
четвертого порядка (четвертый центральный
момент) равен

, для дискретной
СВ;

, для непрерывной
СВ;

и может пониматься
как математическое ожидание четвертой
степени центрированной СВ.

Нет смысла продолжать
дальше перечисление центральных
моментов. Установим связь между начальными
и центральными моментами. Для непрерывной
СВ

;

разлагая степень
скобки в подынтегральном выражении в
бином Ньютона:

,

(—
число сочетаний из k
по s),
меняя порядок интегрирования и
суммирования:

,

и учитывая, что
интеграл в правой части равен

, находим

.

(3.4.6)

Полученное равенство
показывает, что центральный момент k-го
порядка выражается через начальные
моменты порядков до k-го
включительно. Аналогичным путем то же
самое равенство выводится и для дискретных
СВ. Из (3.4.6) находим:

,

,

,

(3.4.7)

,

,

……………………………………………

Первые два равенства
нам уже были известны, равенство (3.4.7)
исключительно важно и будет в дальнейшем
часто использоваться (его необходимо
помнить наизусть).

Мы выразили
центральные моменты через начальные,
теперь, наоборот, выразим начальные
моменты через центральные. Для непрерывной
СВ, обозначив x-m_x=x⁰
,
находим:

т. е.

.

(3.4.8)

Полученное равенство
показывает, что начальный момент k-го
порядка выражается через центральные
моменты порядков до k-го
включительно. Аналогичным путем то же
самое равенство выводится и для дискретных
СВ. Из (3.4.8) находим:

,

,

,

,

,

………………………………………..

Первые два равенства
нам уже были известны, третье повторяет
равенство (3.4.7).

Соседние файлы в папке Конспект лекций Глазова

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

---

Задание:

Случайная величина X задана рядом распределения: x_i -1 0 a; p_i b 0,5 0,25. Найти второй начальный момент случайной величины X, если M[X] = 0.

Решение:

Ответ: 0,500

Вспомним геометрический смысл определённого интеграла: определённый интеграл от некоторой неотрицательной функции f(x), заданной на отрезке [a; b] численно равен площади криволинейной трапеции (фигуры, ограниченной сверху графиком функции f(x), снизу осью OX, сбоку — прямыми x=a и x=b).

Нам дан график зависимости силы от времени F(t), следовательно величина площади, находящейся под графиком есть скалярное значение изменения импульса тела (ибо изменение импульса тела есть интеграл от силы по времени). То есть, если нужно найти на сколько изменился импульс тела, например, с 1 до 2 секунд, то достаточно узнать площадь трапеции.

Нам дано значение кинетической энергии тела. Что бы не возиться со скоростью и ускорением, узнаем какому значению импульса соответствует данная нам кинетическая энергия. Применяя известную формулу, имеем:

Eк=p^2/2*m.

Отсюда

p=sqrt(2*m*Eк).

Найдём значение импульса.

p=sqrt(2*0.5*81);

p=9(кг*м/с).

Итак, на оси t нам нужно найти такое значение, которое будет отсекать фигуру площади 9.

Найдём площадь всей фигуры. Она будет равна сумме площадей квадрата, прямоугольной трапеции и прямоугольника. Математически находим:

S=2*1+(2+4)*1/2+4*1=2+3+4=9.

Итак, площадь всей фигуры получилась 9, а это значит, прямая, отсекающая данную фигуру проходит через значение t=3. Отсюда вывод. При значении времени t=3(с) тело имело импульс p=9(кг*м/с) и энергию Eк=81(Дж).

Ответ: t=3(с).

Определение

Равномерное прямолинейное движение — это такое движение, при котором тело совершает за любые равные промежутки времени равные перемещения.

Скорость при прямолинейном равномерном движении

Если тело движется равномерно и прямолинейно, его скорость остается постоянной как по модулю, так и по направлению. Ускорение при этом равно нулю.

Векторный способ записи скорости при равномерном прямолинейном движении:

s — вектор перемещения, ΔR— изменение радиус-вектора, t — время, а ∆t — его изменение.

Проекция скорости на ось ОХ:

s_x — проекция перемещения на ось ОХ, ∆x — изменение координаты точки (ее абсциссы).

Знак модуля скорости зависит от направления вектора скорости и оси координат:

Основная единица измерения скорости — 1 метр в секунду. Сокращенно — 1 м/с.

Дополнительные единицы измерения

• 1 км/ч (километр в час) = 1000 м/3600 с.
• 1 км/мин (километр в минуту) = 1000 м/60 с.
• 1 км/с (километр в секунду) = 1000 м/с.
• 1 м/мин (метр в минуту) = 1 м/60 с.
• 1 см/с (сантиметр в секунду) = 0,01 м/с.

Спидометр — прибор для измерения модули скорости тела.

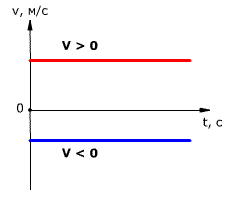
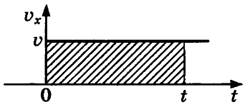
График зависимости скорости от времени представляет собой прямую линию, перпендикулярную оси скорости и параллельную оси времени. Выглядит он так:

Определение направления движения по графику скорости

• Если график скорости лежит выше оси времени, тело движется в направлении оси ОХ.
• Если график скорости лежит ниже оси времени, тело движется против оси ОХ.
• Если график скорости совпадает с осью времени, тело покоится.

Чтобы сравнить модули скоростей на графике, нужно оценить их удаленность от оси времени. Чем дальше график от оси, тем больше модуль.

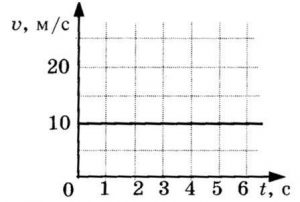
Пример №1. Найти модуль скорости и направление движения тела относительно оси ОХ. Выразить скорость в км/ч.

График скорости пересекает ось в точке со значением 10. Единица измерения — м/с. Поэтому модуль скорости равен 10 м/с. График лежит выше оси времени. Это значит, что тело движется по направлению оси ОХ. Чтобы выразить скорость в км/ч, нужно перевести 10 м в километры и 1 с в часы:

Теперь нужно разделить километры на часы:

Перемещение и координаты тела при равномерном прямолинейном движении

Геометрический смысл перемещения заключается в том, что его модуль равен площади фигуры, ограниченной графиком скорости, осями скорости и времени, а также линией, проведенной перпендикулярно оси времени.

При прямолинейном равномерном движении эта фигура представляет собой прямоугольник. Поэтому модуль перемещения вычисляется по следующей формуле:

Вектор перемещения равен произведению вектора скорости на время движения:

Внимание!

При равномерном прямолинейном движении путь и перемещение совпадают. Поэтому путь, пройденный телом, можно найти по этим же формулам.

Формула проекции перемещения:

График проекции перемещения

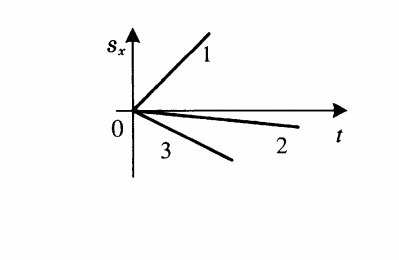
График проекции перемещения показывает зависимость этой проекции от времени. При прямолинейном равномерном движении он представляет собой луч, исходящий из начала координат. Выглядит он так:

Определение направления движения по графику проекции перемещения

• Если луч лежит выше оси времени, тело движется в направлении оси ОХ.
• Если луч лежит ниже оси времени, тело движется против оси ОХ.
• Если луч совпадает с этой осью, тело покоится.

Чтобы по графику проекции перемещения сравнить модули скоростей, нужно сравнить углы их наклона к оси s_x.Чем меньше угол, тем больше модуль. Согласно рисунку выше, модули скорости тел, которым соответствуют графики 1 и 3, равны. Они превосходят модуль скорости тела 2, так как их угол наклона к оси s_x меньше.

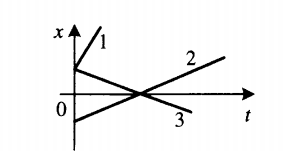
График координаты

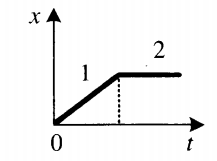
График координаты представляет собой график зависимости координаты от времени. Выглядит он так:

Так как график координаты представляет собой график линейной функции, уравнение координаты принимает вид:

Определение направления движения тела по графику координаты

• Если с течением времени координата увеличивается (график идет снизу вверх), тело движется в направлении оси ОХ. На картинке выше этому соответствуют графики тел 1 и 2.
• Если с течением времени координата уменьшается (график идет сверху вниз), тело движется противоположно направлению оси ОХ. На картинке выше этому соответствует график тела 3.
• Если координата не изменяется, тело покоится.

Чтобы сравнить модули скоростей тел по графику координат, нужно сравнить углы наклона графика к оси координат. Чем меньше угол, тем больше модуль скорости. На картинке выше наибольший модуль скорости соответствует графику 1. У графиков 2 и 3 модули равны.

Чтобы по графику координат найти время встречи двух тел, нужно из точки пересечения их графиков провести перпендикуляр к оси времени.

Пример №2. График зависимости координаты тела от времени имеет вид:

Изучите график и на его основании выберите два верных утверждения:

1. На участке 1 скорость тела постоянна, а на участке 2 равна нулю.
2. Проекция ускорения тела на участке 1 положительна, а на участке 2 — отрицательна.
3. На участке 1 тело движется равномерно, а на участке 2 оно покоится.
4. На участке 1 тело движется равноускорено, а на участке 2 оно движется равномерно.
5. Проекция ускорения тела на участке 1 отрицательна, а на участке 2 — положительна.

На участке 1 координата растет, и ее график представляет собой прямую. Это значит, что на этом участке тело движется равномерно (с постоянной скоростью). На участке 2 координата с течением времени не меняется, что говорит о том, что тело покоится. Исходя из этого, верными утверждениями являются номера 1 и 3.

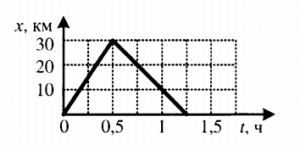
Пример №3. На рисунке изображен график движения автомобиля из пункта А (х=0 км) в пункт В (х=30 км). Чему равна минимальная скорость автомобиля на всем пути движения туда и обратно?

Согласно графику, с начала движения до прибытия автомобиля в пункт 2 прошло 0,5 часа. А с начала движения до возвращения в пункт А прошло 1,5 часа. Поэтому время, в течение которого тело возвращалось из пункта В в пункт А, равно:

1,5 – 0,5 = 1 (час).

Туда и обратно автомобиль проходил равные пути, каждый из которых равен 30 км. Поэтому скорость во время движения от А к В равна:

Скорость во время движения от В к А равна:

Минимальная скорость автомобиля на всем пути движения составляет 30 км/ч.

Алиса Никитина | Просмотров: 13.7k