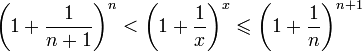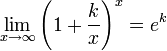Второй замечательный предел
Данная статья: «Второй замечательный предел» посвящена раскрытию в пределах неопределенностей вида:
$ bigg[frac{infty}{infty}bigg]^infty $ и $ [1]^infty $.
Так же такие неопределенности можно раскрывать с помощью логарифмирования показательно-степенной функции, но это уже другой метод решения, о котором будет освещено в другой статье.
Формула и следствия
Формула второго замечательного предела записывается следующим образом: $$ lim_{x to infty} bigg (1+frac{1}{x}bigg)^x = e, text{ где } e approx 2.718 $$
Из формулы вытекают следствия, которые очень удобно применять для решения примеров с пределами: $$ lim_{x to infty} bigg (1 + frac{k}{x} bigg)^x = e^k, text{ где } k in mathbb{R} $$ $$ lim_{x to infty} bigg (1 + frac{1}{f(x)} bigg)^{f(x)} = e $$ $$ lim_{x to 0} bigg (1 + x bigg)^frac{1}{x} = e $$
Стоить заметить, что второй замечательный предел можно применять не всегда к показательно-степенной функции, а только в случаях когда основание стремится к единице. Для этого сначала в уме вычисляют предел основания, а затем уже делают выводы. Всё это будет рассмотрено в примерах решений.
Примеры решений
Рассмотрим примеры решений с использованием прямой формулы и её следствий. Так же разберем случаи, при которых формула не нужна. Достаточно записать только готовый ответ.
| Пример 1 |
| Найти предел $ lim_{xtoinfty} bigg( frac{x+4}{x+3} bigg)^{x+3} $ |
| Решение |
|
Подставим бесконечность в предел и посмотрим на неопределенность: $$ lim_{xtoinfty} bigg( frac{x+4}{x+3} bigg)^{x+3} = bigg(frac{infty}{infty}bigg)^infty $$ Найдем предел основания: $$ lim_{xtoinfty} frac{x+4}{x+3}= lim_{xtoinfty} frac{x(1+frac{4}{x})}{x(1+frac{3}{x})} = 1 $$ Получили основание равное единице, а это значит уже можно применить второй замечательный предел. Для этого подгоним основание функции под формулу путем вычитания и прибавления единицы: $$ lim_{xtoinfty} bigg( 1 + frac{x+4}{x+3} — 1 bigg)^{x+3} = lim_{xtoinfty} bigg( 1 + frac{1}{x+3} bigg)^{x+3} = $$ Смотрим на второе следствие и записываем ответ: $$ lim_{xtoinfty} bigg( 1 + frac{1}{x+3} bigg)^{x+3} = e $$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$ lim_{xtoinfty} bigg( 1 + frac{1}{x+3} bigg)^{x+3} = e $$ |
| Пример 2 |
| Определить предел $ lim_{xtoinfty} bigg (1+frac{1}{x^3}bigg)^{x^2} $ |
| Решение |
|
Замечаем, что основание степени стремится к единице $ 1+frac{1}{x^3} to 1 $, при $ xtoinfty $, а показатель $ x^2 to infty $. Поэтому можно применить второе следствие. Но сперва, разберемся с показателем и приведем его в нужный вид — сделаем равным знаменателю основания. Для этого умножим его на $ x $ и разделим на него же. Получаем: $$ lim_{xtoinfty} bigg (1+frac{1}{x^3}bigg)^{x^2 cdot frac{x}{x}} = lim_{xtoinfty} bigg (1+frac{1}{x^3}bigg)^{frac{x^3}{x}} = $$ Уже теперь применяем формулу и получаем: $$ lim_{xtoinfty}e^ frac{1}{x} = e^{lim_{xtoinfty} frac{1}{x}} = e^0 = 1 $$ |
| Ответ |
| $$ lim_{xtoinfty} bigg (1+frac{1}{x^3}bigg)^{x^2} = 1 $$ |
| Пример 3 |
| Вычислить предел $ lim_{xto 1} (6-5x)^frac{x}{x-1} $ |
| Решение |
|
Получаем неопределенность $ 1^infty $. Для её раскрытия воспользуемся вторым замечательным пределом. Но у нас $ xto 1 $. Как быть? Выполняем замену $ y = x-1 $, тогда $ yto 0 $, при $ x to 1 $. Из замены следует, что $ x = y + 1 $. $$ lim_{xto 1} (6-5x)^frac{x}{x-1} = lim_{yto 0} (6-5(y+1))^frac{y+1}{y} = 1^infty = $$ $$ = lim_{yto 0} (1-5y)^frac{y+1}{y} = lim_{yto 0} (1+(-5y))^frac{(y+1)cdot (-5)}{-5cdot y} = $$ $$ = lim_{yto 0} e^{-5cdot (y+1)} = e^{-5} $$ |
| Ответ |
| $$ lim_{xto 1} (6-5x)^frac{x}{x-1} = e^{-5} $$ |
| Пример 4 |
| Решить предел $ lim_{xto infty} bigg (frac{3x^2+4}{3x^2-2} bigg) ^{3x} $ |
| Решение |
|
Находим предел основания и видим, что $ lim_{xtoinfty} frac{3x^2+4}{3x^2-2} = 1 $, значит можно применить второй замечательный предел. Стандартно по плану прибавляем и вычитаем единицу из основания степени: $$ lim_{xto infty} bigg (1+frac{3x^2+4}{3x^2-2}-1 bigg) ^{3x} = lim_{xto infty} bigg (1+frac{6}{3x^2-2} bigg) ^{3x} = $$ Подгоняем дробь под формулу 2-го замеч. предела: $$ = lim_{xto infty} bigg (1+frac{1}{frac{3x^2-2}{6}} bigg) ^{3x} = $$ Теперь подгоняем степень. В степени должна быть дробь равная знаменателю основания $ frac{3x^2-2}{6} $. Для этого умножим и разделим степень на неё, и продолжим решать: $$ = lim_{xto infty} bigg (1+frac{1}{frac{3x^2-2}{6}} bigg) ^{frac{3x^2-2}{6} cdot frac{6}{3x^2-2}cdot 3x} = lim_{xto infty} e^{frac{18x}{3x^2-2}} = $$ Предел, расположенный в степени при $ e $ равен: $ lim_{xto infty} frac{18x}{3x^2-2} = 0 $. Поэтому продолжая решение имеем: $$ = e^0 = 1 $$ |
| Ответ |
| $$ lim_{xto infty} bigg (frac{3x^2+4}{3x^2-2} bigg) ^{3x} = 1 $$ |
Разберем случаи, когда задача похожа на второй замечательный предел, но решается без него.
| Пример 5 |
| Найти $ lim_{xtoinfty} bigg ( frac{x+3}{3x+4} bigg )^{x+1} $ |
| Решение |
|
Начинаем с проверки равен ли предел основания единице. Имеем: $$ lim_{xtoinfty} frac{x+3}{3x+4} = frac{1}{3} $$ А это значит, что формулировка второго замечательного предела не соответствует данной задаче, так как $ frac{1}{3}ne 1 $ Продолжаем вычисление предела: $$ lim_{xtoinfty} bigg ( frac{x+3}{3x+4} bigg )^{x+1} = bigg (frac{1}{3} bigg ) ^infty = 0 $$ |
| Ответ |
| $$ lim_{xtoinfty} bigg ( frac{x+3}{3x+4} bigg )^{x+1} = 0 $$ |
| Пример 6 |
| Найти $ lim_{xtoinfty} bigg ( frac{3x+4}{x+3} bigg )^{x-5} $ |
| Решение |
|
Начинаем с проверки равен ли предел основания единице. Имеем: $$ lim_{xtoinfty} frac{3x+4}{x+3} = 3 $$ А это значит, что формулировка второго замечательного предела не соответствует данной задаче, так как $ 3 ne 1 $ Продолжаем вычисление предела: $$ lim_{xtoinfty} bigg ( frac{3x+4}{x+3} bigg )^{x-5} = 3^infty = infty $$ |
| Ответ |
| $$ lim_{xtoinfty} bigg ( frac{3x+4}{x+3} bigg )^{x-5} =infty $$ |
В статье: «Второй замечательный предел: примеры решений» была разобрана формула, её следствия и приведены частые типы задач по этой теме.
Второй замечательный предел
Обычно второй замечательный предел записывают в такой форме:
$$
begin{equation}
lim_{xtoinfty}left(1+frac{1}{x}right)^x=e
end{equation}
$$
Число $e$, указанное в правой части равенства (1), является иррациональным. Приближённое значение этого числа таково: $eapprox{2{,}718281828459045}$. Если сделать замену $t=frac{1}{x}$, то формулу (1) можно переписать в следующем виде:
$$
begin{equation}
lim_{tto{0}}biggl(1+tbiggr)^{frac{1}{t}}=e
end{equation}
$$
Как и для первого замечательного предела, неважно, какое выражение стоит вместо переменной $x$ в формуле (1) или вместо переменной $t$ в формуле (2). Главное – выполнение двух условий:
- Основание степени (т.е. выражение в скобках формул (1) и (2)) должно стремиться к единице;
- Показатель степени (т.е. $x$ в формуле (1) или $frac{1}{t}$ в формуле (2)) должен стремиться к бесконечности.
Говорят, что второй замечательный предел раскрывает неопределенность $1^infty$. Заметьте, что в формуле (1) мы не уточняем, о какой именно бесконечности ($+infty$ или $-infty$) идёт речь. В любом из этих случаев формула (1) верна. В формуле (2) переменная $t$ может стремиться к нулю как слева, так и справа.
Отмечу, что есть также несколько полезных следствий из второго замечательного предела. Примеры на использование второго замечательного предела, равно как и следствий из него, очень популярны у составителей стандартных типовых расчётов и контрольных работ.
Пример №1
Вычислить предел $lim_{xtoinfty}left(frac{3x+1}{3x-5}right )^{4x+7}$.
Решение
Сразу отметим, что основание степени (т.е. $frac{3x+1}{3x-5}$) стремится к единице:
$$
lim_{xtoinfty}frac{3x+1}{3x-5}=left|frac{infty}{infty}right|
=lim_{xtoinfty}frac{3+frac{1}{x}}{3-frac{5}{x}}
=frac{3+0}{3-0}
=1.
$$
При этом показатель степени (выражение $4x+7$) стремится к бесконечности, т.е. $lim_{xtoinfty}(4x+7)=infty$.
Основание степени стремится к единице, показатель степени – к бесконечности, т.е. мы имеем дело с неопределенностью $1^infty$. Применим формулу (1) для раскрытия этой неопределённости. В основании степени формулы (1) расположено выражение $1+frac{1}{x}$, а в рассматриваемом нами примере основание степени таково: $frac{3x+1}{3x-5}$. Посему первым действием станет формальная подгонка выражения $frac{3x+1}{3x-5}$ под вид $1+frac{1}{x}$. Для начала прибавим и вычтем единицу:
$$
lim_{xtoinfty}left(frac{3x+1}{3x-5}right )^{4x+7}
=|1^infty|
=lim_{xtoinfty}left(1+frac{3x+1}{3x-5}-1right)^{4x+7}
$$
Следует учесть, что просто так добавить единицу нельзя. Если мы вынуждены добавить единицу, то её же нужно и вычесть, дабы не изменять значения всего выражения. Для продолжения решения учтём, что
$$
frac{3x+1}{3x-5}-1
=frac{3x+1}{3x-5}-frac{3x-5}{3x-5}
=frac{3x+1-3x+5}{3x-5}
=frac{6}{3x-5}.
$$
Так как $frac{3x+1}{3x-5}-1=frac{6}{3x-5}$, то:
$$
lim_{xtoinfty}left(1+ frac{3x+1}{3x-5}-1right)^{4x+7}
=lim_{xtoinfty}left(1+frac{6}{3x-5}right )^{4x+7}
$$
Продолжим «подгонку». В выражении $1+frac{1}{x}$ формулы (1) в числителе дроби находится 1, а в нашем выражении $1+frac{6}{3x-5}$ в числителе находится $6$. Чтобы получить $1$ в числителе, опустим $6$ в знаменатель с помощью следующего преобразования:
$$
1+frac{6}{3x-5}
=1+frac{1}{frac{3x-5}{6}}
$$
Таким образом,
$$
lim_{xtoinfty}left(1+frac{6}{3x-5}right )^{4x+7}
=lim_{xtoinfty}left(1+frac{1}{frac{3x-5}{6}}right )^{4x+7}
$$
Итак, основание степени, т.е. $1+frac{1}{frac{3x-5}{6}}$, подогнано под вид $1+frac{1}{x}$, который требуется в формуле (1). Теперь начнём работать с показателем степени. Заметьте, что в формуле (1) выражения, стоящие в показатели степени и в знаменателе, одинаковы:
Значит, и в нашем примере показатель степени и знаменатель нужно привести к одинаковой форме. Чтобы получить в показателе степени выражение $frac{3x-5}{6}$, просто домножим показатель степени на эту дробь. Естественно, что для компенсации такого домножения, придется тут же домножить на обратную дробь, т.е. на $frac{6}{3x-5}$. Итак, имеем:
$$
lim_{xtoinfty}left(1+frac{1}{frac{3x-5}{6}}right )^{4x+7}
=lim_{xtoinfty}left(1+frac{1}{frac{3x-5}{6}}right )^{frac{3x-5}{6}cdotfrac{6}{3x-5}cdot(4x+7)}
=lim_{xtoinfty}left(left(1+frac{1}{frac{3x-5}{6}}right)^{frac{3x-5}{6}}right)^{frac{6cdot(4x+7)}{3x-5}}
$$
Отдельно рассмотрим предел дроби $frac{6cdot(4x+7)}{3x-5}$, расположенной в степени:
$$
lim_{xtoinfty}frac{6cdot(4x+7)}{3x-5}
=left|frac{infty}{infty}right|
=lim_{xtoinfty}frac{6cdotleft(4+frac{7}{x}right)}{3-frac{5}{x}}
=6cdotfrac{4}{3}
=8.
$$
Согласно формуле (1) имеем $lim_{xtoinfty}left(1+frac{1}{frac{3x-5}{6}}right )^{frac{3x-5}{6}}=e$. Кроме того, $lim_{xtoinfty}frac{6cdot(4x+7)}{3x-5}=8$, поэтому возвращаясь к исходному пределу, получим:
$$
lim_{xtoinfty}left(left(1+frac{1}{frac{3x-5}{6}}right )^{frac{3x-5}{6}}right)^{frac{6cdot(4x+7)}{3x-5}}
=e^8.
$$
Полное решение без промежуточных пояснений будет иметь такой вид:
$$
lim_{xtoinfty}left(frac{3x+1}{3x-5}right )^{4x+7}=left|1^inftyright|
=lim_{xtoinfty}left(1+frac{3x+1}{3x-5}-1right)^{4x+7}
=lim_{xtoinfty}left(1+frac{6}{3x-5}right)^{4x+7}=\
=lim_{xtoinfty}left(1+frac{1}{frac{3x-5}{6}}right)^{4x+7}
=lim_{xtoinfty}left(1+frac{1}{frac{3x-5}{6}}right )^{frac{3x-5}{6}cdotfrac{6}{3x-5}cdot(4x+7)}
=lim_{xtoinfty}left(left(1+frac{1}{frac{3x-5}{6}}right)^{frac{3x-5}{6}}right)^{frac{6cdot(4x+7)}{3x-5}}
=e^8.
$$
Кстати сказать, вовсе не обязательно использовать первую формулу. Если учесть, что $frac{6}{3x-5}to{0}$ при $xtoinfty$, то применяя формулу (2), получим:
$$
lim_{xtoinfty}left(frac{3x+1}{3x-5}right )^{4x+7}=left|1^inftyright|
=lim_{xtoinfty}left(1+frac{3x+1}{3x-5}-1right)^{4x+7}
=lim_{xtoinfty}left(1+frac{6}{3x-5}right)^{4x+7}=\
=lim_{xtoinfty}left(1+frac{6}{3x-5}right)^{frac{3x-5}{6}cdotfrac{6}{3x-5}cdot(4x+7)}
=lim_{xtoinfty}left(left(1+frac{6}{3x-5}right)^{frac{3x-5}{6}}right)^{frac{6cdot(4x+7)}{3x-5}}
=e^8.
$$
Ответ: $lim_{xtoinfty}left(frac{3x+1}{3x-5}right)^{4x+7}=e^8$.
Пример №2
Найти предел $lim_{xto{1}}biggl(7-6xbiggr)^{frac{x}{3x-3}}$.
Решение
Выражение, стоящее в основании степени, т.е. $7-6x$, стремится к единице при условии $xto{1}$, т.е. $lim_{xto{1}}(7-6x)=7-6cdot1=1$. Для показателя степени, т.е. $frac{x}{3x-3}$, получаем: $lim_{xto{1}}frac{x}{3x-3}=infty$. Итак, здесь мы имеем дело с неопределенностью вида $1^infty$, которую раскроем с помощью второго замечательного предела.
Для начала отметим, что в формуле (1) переменная $x$ стремится к бесконечности, в формуле (2) переменная $t$ стремится к нулю. В нашем случае $xto{1}$, поэтому имеет смысл ввести новую переменную, чтобы она стремилась или к нулю (тогда применим формулу (2)), или к бесконечности (тогда применим формулу (1)). Введение новой переменной, вообще говоря, не является обязательным, это будет сделано просто для удобства решения. Проще всего новую переменную $y$ ввести так: $y=x-1$. Так как $xto{1}$, то ${x-1}to{0}$, т.е. $yto{0}$. Подставляя $x=y+1$ в рассматриваемый пример, и учитывая $yto{0}$, получим:
$$
lim_{xto{1}}biggl(7-6xbiggr )^{frac{x}{3x-3}}
=left|begin{aligned}&y=x-1;;x=y+1\&yto{0}end{aligned}right|=\
=lim_{yto{0}}biggl(7-6cdot(y+1)biggr)^{frac{y+1}{3cdot(y+1)-3}}
=lim_{yto{0}}biggl(1-6ybiggr)^frac{y+1}{3y}
=lim_{yto 0}biggl(1+(-6y)biggr)^frac{y+1}{3y}
$$
Применим формулу (2). Выражение в основании степени в формуле (2), т.е. $1+t$, соответствует форме выражения в основании степени нашего примера, т.е. $1+(-6y)$ (выражение $-6y$ играет роль $t$). Формула (2) предполагает, что показатель степени будет иметь вид $frac{1}{t}$, т.е. в нашем случае в показателе степени следует получить $frac{1}{-6y}$. Домножим показатель степени на выражение $frac{1}{-6y}$. Для компенсации такого домножения нужно домножить показатель степени на обратную дробь, т.е. на выражение $frac{-6y}{1}=-6y$:
$$
lim_{yto{0}}biggl(1-6ybiggr)^frac{y+1}{3y}=lim_{yto{0}}biggl(1+(-6y)biggr)^{frac{1}{-6y}cdot(-6y)cdotfrac{y+1}{3y}}
=lim_{yto{0}}left(biggl(1+(-6y)biggr)^{frac{1}{-6y}}right)^{-2(y+1)}
$$
Так как $lim_{yto{0}}biggl(1+(-6y)biggr)^{frac{1}{-6y}}=e$ и $lim_{yto{0}}(-2(y+1))=-2$, то получим:
$$
lim_{yto{0}}left(biggl(1+(-6y)biggr)^{frac{1}{-6y}}right)^{-2(y+1)}
=e^{-2}
=frac{1}{e^2}.
$$
Полное решение без пояснений таково:
$$
lim_{xto{1}}biggl(7-6xbiggr)^{frac{x}{3x-3}}
=left|begin{aligned}&y=x-1;;x=y+1\&yto{0}end{aligned}right|
=lim_{yto{0}}biggl(7-6cdot(y+1)biggr)^{frac{y+1}{3cdot(y+1)-3}}=\
=lim_{yto{0}}biggl(1-6ybiggr)^frac{y+1}{3y}
=lim_{yto{0}}biggl(1+(-6y)biggr)^{frac{1}{-6y}cdot(-6y)cdotfrac{y+1}{3y}}
=lim_{yto{0}}left(biggl(1+(-6y)biggr)^{frac{1}{-6y}}right)^{-2(y+1)}
=e^{-2}
=frac{1}{e^2}.
$$
Ответ: $lim_{xto{1}}biggl(7-6xbiggr)^{frac{x}{3x-3}}=frac{1}{e^2}$.
Пример №3
Найти предел $lim_{xto{0}}biggl(cos{2x}biggr)^{frac{1}{sin^2{3x}}}$.
Решение
Так как $lim_{xto{0}}(cos{2x})=1$ и $lim_{xto{0}}frac{1}{sin^2{3x}}=infty$ (напомню, что $sin{u}to{0}$ при $uto{0}$), то мы имеем дело с неопределённостью вида $1^infty$. Преобразования, аналогичные рассмотренным в примерах №1 и №2, укажем без подробных пояснений, ибо они были даны ранее:
$$
lim_{xto{0}}biggl(cos{2x}biggr)^{frac{1}{sin^2{3x}}}
=|1^infty|
=lim_{xto{0}}biggl(1+cos{2x}-1biggr)^{frac{1}{sin^2{3x}}}
$$
Так как $sin^2x=frac{1-cos{2x}}{2}$, то $cos{2x}-1=-2sin^2x$, поэтому:
$$
lim_{xto{0}}biggl(1+cos{2x}-1biggr)^{frac{1}{sin^2{3x}}}
=lim_{xto{0}}biggl(1+left(-2sin^2xright)biggr)^{frac{1}{-2sin^2x}cdot(-2sin^2x)cdotfrac{1}{sin^2 3x}}=\
=lim_{xto{0}}left(biggl(1+left(-2sin^2xright)biggr)^{frac{1}{-2sin^2x}}right)^{frac{-2sin^2{x}}{sin^2{3x}}}
=e^{-frac{2}{9}}.
$$
Здесь мы учли, что $lim_{xto{0}}frac{sin^2{x}}{sin^2{3x}}=frac{1}{9}$. Подробное описание того, как находить этот предел, дано в соответствующей теме.
Ответ: $lim_{xto{0}}biggl(cos{2x}biggr)^{frac{1}{sin^2{3x}}}=e^{-frac{2}{9}}$.
Пример №4
Найти предел $lim_{xto+infty}xleft(ln(x+1)-ln{x}right)$.
Решение
Так как при $x>0$ имеем $ln(x+1)-ln{x}=lnleft(frac{x+1}{x}right)$, то:
$$
lim_{xto+infty}xleft(ln(x+1)-ln{x}right)
=lim_{xto+infty}left(xcdotlnleft(frac{x+1}{x}right)right)
$$
Раскладывая дробь $frac{x+1}{x}$ на сумму дробей $frac{x+1}{x}=1+frac{1}{x}$ получим:
$$
lim_{xto+infty}left(xcdotlnleft(frac{x+1}{x}right)right)
=lim_{xto+infty}left(xcdotlnleft(1+frac{1}{x}right)right)
=lim_{xto+infty}left(lnleft(frac{x+1}{x}right)^xright)
=ln{e}
=1.
$$
Ответ: $lim_{xto+infty}xleft(ln(x+1)-ln{x}right)=1$.
Пример №5
Найти предел $lim_{xto{2}}biggl(3x-5biggr)^{frac{2x}{x^2-4}}$.
Решение
Так как $lim_{xto{2}}(3x-5)=6-5=1$ и $lim_{xto{2}}frac{2x}{x^2-4}=infty$, то мы имеем дело с неопределенностью вида $1^infty$. Подробные пояснения даны в примере №2, здесь же ограничимся кратким решением. Сделав замену $t=x-2$, получим:
$$
lim_{xto{2}}biggl(3x-5biggr)^{frac{2x}{x^2-4}}
=left|begin{aligned}&t=x-2;;x=t+2\&tto{0}end{aligned}right|
=lim_{tto{0}}biggl(1+3tbiggr)^{frac{2t+4}{t^2+4t}}=\
=lim_{tto{0}}biggl(1+3tbiggr)^{frac{1}{3t}cdot 3tcdotfrac{2t+4}{t^2+4t}}
=lim_{tto{0}}left(biggl(1+3tbiggr)^{frac{1}{3t}}right)^{frac{6cdot(t+2)}{t+4}}
=e^3.
$$
Можно решить данный пример и по-иному, используя замену: $t=frac{1}{x-2}$. Разумеется, ответ будет тем же:
$$
lim_{xto{2}}biggl(3x-5biggr)^{frac{2x}{x^2-4}}
=left|begin{aligned}&t=frac{1}{x-2};;x=frac{2t+1}{t}\&ttoinftyend{aligned}right|
=lim_{ttoinfty}left(1+frac{3}{t}right)^{tcdotfrac{4t+2}{4t+1}}=\
=lim_{ttoinfty}left(1+frac{1}{frac{t}{3}}right)^{frac{t}{3}cdotfrac{3}{t}cdotfrac{tcdot(4t+2)}{4t+1}}
=lim_{ttoinfty}left(left(1+frac{1}{frac{t}{3}}right)^{frac{t}{3}}right)^{frac{6cdot(2t+1)}{4t+1}}
=e^3.
$$
Ответ: $lim_{xto{2}}biggl(3x-5biggr)^{frac{2x}{x^2-4}}=e^3$.
Пример №6
Найти предел $lim_{xtoinfty}left(frac{2x^2+3}{2x^2-4}right)^{3x} $.
Решение
Выясним, к чему стремится выражение $frac{2x^2+3}{2x^2-4}$ при условии $xtoinfty$:
$$
lim_{xtoinfty}frac{2x^2+3}{2x^2-4}
=left|frac{infty}{infty}right|
=lim_{xtoinfty}frac{2+frac{3}{x^2}}{2-frac{4}{x^2}}
=frac{2+0}{2-0}=1.
$$
Таким образом, в заданном пределе мы имеем дело с неопределенностью вида $1^infty$, которую раскроем с помощью второго замечательного предела:
$$
lim_{xtoinfty}left(frac{2x^2+3}{2x^2-4}right)^{3x}
=|1^infty|
=lim_{xtoinfty}left(1+frac{2x^2+3}{2x^2-4}-1right)^{3x}=\
=lim_{xtoinfty}left(1+frac{7}{2x^2-4}right)^{3x}
=lim_{xtoinfty}left(1+frac{1}{frac{2x^2-4}{7}}right)^{3x}=\
=lim_{xtoinfty}left(1+frac{1}{frac{2x^2-4}{7}}right)^{frac{2x^2-4}{7}cdotfrac{7}{2x^2-4}cdot 3x}
=lim_{xtoinfty}left(left(1+frac{1}{frac{2x^2-4}{7}}right)^{frac{2x^2-4}{7}}right)^{frac{21x}{2x^2-4}}
=e^0
=1.
$$
Ответ: $lim_{xtoinfty}left(frac{2x^2+3}{2x^2-4}right)^{3x}=1$.
Второй замечательный предел и его следствия
Предел последовательности 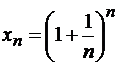
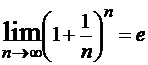
Число e является иррациональным и приблизительно равно 2.718. Это число принято за основание логарифмов, которые называют натуральными логарифмами и обозначают ln(x) (ln(x)=logex).
Формула (1) выполняется и для функций
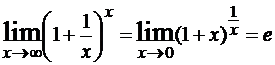
Предел (2) называется вторым замечательным пределом. Критерий для его распознавания включает в себя три требования:
1) должна быть неопределенность вида 1∞,
2) 1+бесконечно малая, или короче: 1+б.м.,
3) 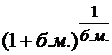
Так, среди пределов 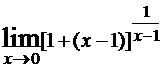
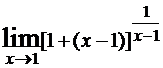
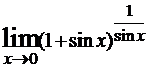
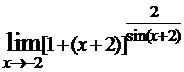
Примечание: число «пи» (π) записывается как pi, знак ∞ как infinity
Типовые замены в пределах
cos(π x) ≈ (-1)x, x → ∞sin(π x) ≈ (-1)x, x → ∞cos(x) ≈ [-1;1], x → ∞sin(x) ≈ [-1;1], x → ∞cos2(x) ≈ [0;1], x → ∞sin2(x) ≈ [0;1], x → ∞
Примеры решений
Пример 1. Используя свойства бесконечно малых и бесконечно больших функций, найти следующие пределы:

Пример 2.

Пример 3.

Пример 4.

Пример 5.

Пример 6.

Единицу можно было бы получить делением многочлена на многочлен: 

Следствиями второго замечательного предела являются следующие пределы (эквивалентные функции):





С их помощью легко решаются многие задачи на раскрытие неопределенностей.
Пример 7.


Пример 8. 
Пример 9.

Пример 10.

Пример 11. 
Пример 12.

Задать свои вопросы или оставить замечания можно внизу страницы в разделе Disqus.
Можно также оставить заявку на помощь в решении своих задач у наших проверенных партнеров (здесь или здесь).
Второй замечательный предел
17 декабря 2021
Второй замечательный предел: основная формула, доказательство, следствия и примеры.
1. Основная формула
Второй замечательный предел:
[limlimits_{nto +infty } {{left( 1+frac{1}{n} right)}^{n}}=text{e}]
Число $text{e}$ иррациональное:
[text{e}=2,718 281 828 459…]
Второй замечательный предел можно рассматривать и как предел последовательности для $nin mathbb{N}$, и как предел функции — в этом случае $nin mathbb{R}$.
2. Доказательство
Сначала докажем существование предела для $nin mathbb{N}$.
1. Рассмотрим последовательность
[{{y}_{n}}={{left( 1+frac{1}{n} right)}^{n}}]
Запишем несколько её первых членов:
[begin{array}{l|c|c|c|c} n & 1 & 2 & 3 & 4 \ hline {{y}_{n}} & 2,00 & 2,25 & approx 2,37 & approx 2,44 \ end{array}]
Видим, что последовательность монотонно возрастает. Но кто сказал, что так будет всегда?
2. Докажем, что последовательность ${{y}_{n}}$ возрастает всегда. Для этого вспомним формулу Бинома Ньютона:
[begin{align} {{left( a+b right)}^{n}} & =sumlimits_{k=0}^{n}{C_{n}^{k}{{a}^{n-k}}{{b}^{k}}}= \ & =1cdot {{a}^{n}}+ncdot {{a}^{n-1}}b+frac{nleft( n-1 right)}{1cdot 2}{{a}^{n-2}}{{b}^{2}}+ \ & +ldots +frac{nleft( n-1 right)cdot ldots cdot left( n-left( n-1 right) right)}{1cdot 2cdot 3cdot …cdot n}{{b}^{n}} end{align}]
Здесь мы переписали биноминальные коэффициенты $C_{n}^{k}$ в специальном виде:
[begin{align} C_{n}^{k} & =frac{n!}{k!left( n-k right)!}= \ & =frac{nleft( n-1 right)cdot ldots cdot left( n-k right)cdot ldots cdot 1}{1cdot 2cdot 3cdot ldots cdot kcdot left( n-k right)cdot ldots cdot 1}= \ & =frac{nleft( n-1 right)cdot ldots cdot left( n-left( k-1 right) right)}{1cdot 2cdot 3cdot ldots cdot k} end{align}]
Если вам не понятно, что такое формула Бинома Ньютона, биноминальные коэффициенты и какие у них свойства — обязательно повторите урок про Бином Ньютона.
Теперь положим $a=1$, $b={1}/{n};$:
[begin{align} {{left( 1+frac{1}{n} right)}^{n}} & =sumlimits_{k=0}^{n}{C_{n}^{k}cdot {{1}^{n-k}}cdot frac{1}{{{n}^{k}}}}= \ & =1+ncdot frac{1}{n}+frac{nleft( n-1 right)}{1cdot 2}cdot frac{1}{{{n}^{k}}}+ \ & +ldots +frac{nleft( n-1 right)cdot ldots cdot left( n-left( n-1 right) right)}{1cdot 2cdot 3cdot …cdot n}cdot frac{1}{{{n}^{n}}} end{align}]
Перепишем эту сумму так:
[{{left( 1+frac{1}{n} right)}^{n}}=1+1+{{S}_{2}}+ldots +{{S}_{n}}]
где слагаемые ${{S}_{k}}$ считаются по формуле
[begin{align} {{S}_{k}} & =frac{nleft( n-1 right)cdot ldots cdot left( n-left( k-1 right) right)}{1cdot 2cdot 3cdot ldots cdot k}cdot frac{1}{{{n}^{k}}}= \ & =frac{1}{k!}cdot frac{n-1}{n}cdot frac{n-2}{n}cdot ldots cdot frac{n-left( k-1 right)}{n}= \ & =frac{1}{k!}left( 1-frac{1}{n} right)left( 1-frac{2}{n} right)cdot ldots cdot left( 1-frac{k-1}{n} right) end{align}]
В последней строке мы видим дробь с факториалом и ровно $k-1$ множителей-скобок. С ростом $n$ каждая такая скобка растёт, поэтому растёт и ${{S}_{k}}$:
[begin{align} {{S}_{k}} & =frac{1}{k!}left( 1-frac{1}{n} right)left( 1-frac{2}{n} right)cdot ldots cdot left( 1-frac{k-1}{n} right) lt \ & lt frac{1}{k!}cdot left( 1-frac{1}{n+1} right)cdot left( 1-frac{2}{n+1} right)cdot ldots cdot left( 1-frac{k-1}{n+1} right) \ end{align}]
Кроме того, cростом $n$ в сумме появляются новые слагаемые: ${{S}_{n+1}}$, затем ${{S}_{n+2}}$ и т.д. Все они положительны, поэтому сумма тоже растёт:
[begin{align} {{left( 1+frac{1}{n} right)}^{n}} & =1+1+{{S}_{2}}+ldots +{{S}_{n}} lt \ & lt 1+1+{{S}_{2}}+ldots +{{S}_{n}}+{{S}_{n+1}}= \ & ={{left( 1+frac{1}{n+1} right)}^{n+1}} \ end{align}]
Итак, мы доказали, что последовательность $left{ {{y}_{n}} right}$ возрастает. Теперь докажем её ограниченность, чтобы применить теорему Вейерштрасса.
3. В самом деле, слагаемые ${{S}_{k}}$ составлены из множителей-скобок, каждая из которых меньше единицы:
[begin{align} {{S}_{k}} & =frac{1}{k!}left( 1-frac{1}{n} right)left( 1-frac{2}{n} right)cdot ldots cdot left( 1-frac{k-1}{n} right) lt \ & lt frac{1}{k!}cdot 1cdot 1cdot ldots cdot 1=frac{1}{k!} \ end{align}]
Кроме того, факториалы растут быстрее, чем степени двойки:
[begin{align} {{S}_{k}} & lt frac{1}{k!}=frac{1}{1cdot 2cdot 3cdot ldots cdot k} lt \ & lt frac{1}{1cdot 2cdot 2cdot ldots cdot 2}=frac{1}{{{2}^{k-1}}} \ end{align}]
Поэтому сумма таких слагаемых ${{S}_{k}}$ тоже ограничена:
[begin{align} {{left( 1+frac{1}{n} right)}^{n}} & =1+1+{{S}_{2}}+ldots +{{S}_{n}} lt \ & lt 1+1+frac{1}{2}+frac{1}{{{2}^{2}}}+ldots +frac{1}{{{2}^{n}}} \ end{align}]
Слагаемые, начиная со второго образуют убывающую геометрическую прогрессию $left{ {{b}_{n}} right}$, где ${{b}_{1}}=1$, $q={1}/{2};$. Её сумма ограничена:
[begin{align} & 1+frac{1}{2}+frac{1}{{{2}^{2}}}+ldots +frac{1}{{{2}^{n}}} lt \ lt & 1+frac{1}{2}+frac{1}{{{2}^{2}}}+ldots +frac{1}{{{2}^{n}}}+ldots = \ = & 1cdot frac{1-{{left( {1}/{2}; right)}^{n}}}{1-left( {1}/{2}; right)}=2 \ end{align}]
Поэтому и вся последовательность $left{ {{y}_{n}} right}$ тоже ограничена:
[begin{align} {{left( 1+frac{1}{n} right)}^{n}} & lt 1+1+frac{1}{2}+frac{1}{{{2}^{2}}}+ldots frac{1}{{{2}^{n}}} lt \ & lt 1+2=3 \ end{align}]
Мы доказали ограниченность. Теперь настало время теоремы Вейерштрасса.
4. Итак, последовательность $left{ {{y}_{n}} right}$ возрастает (доказано в п.2) и ограничена (доказано в п.3). Следовательно, по теореме Вейерштрасса у этой последовательности есть предел, который мы обозначим буквой $text{e}$:
[limlimits_{xto n} {{left( 1+frac{1}{n} right)}^{n}}=text{e}]
Формула второго замечательного предела доказана.
Обратите внимание. Число $text{e}$ равно второму замечательному пределу по определению.
Чтобы найти его приближённое значение и тем более доказать иррациональность, нужны совсем другие (и весьма объёмные) выкладки. Этому будет посвящён отдельный урок.
3. Следствия из второго замечательного предела
- $limlimits_{xto 0} {{left( 1+x right)}^{frac{1}{x}}}=text{e}$
- $limlimits_{nto +infty } {{left( 1+frac{k}{n} right)}^{frac{1}{n}}}={{text{e}}^{k}}$
- $limlimits_{xto 0} frac{ln left( 1+x right)}{x}=1$
- $limlimits_{xto 0} frac{{{e}^{x}}-1}{x}=1$
- $limlimits_{xto 0} frac{{{a}^{x}}-1}{xln a}=1$ ($a gt 0$, $ane 1$)
- $limlimits_{xto 0} frac{{{left( 1+x right)}^{alpha }}-1}{alpha x}=1$
Пункты 1—2 являются прямыми следствиями второго замечательного предела. Пункты 3—4 наверняка знакомы вам из лекции про эквивалентные бесконечно малые функции.
Смотрите также:
- Что такое бесконечно малая функция
- Первый замечательный предел
- Тест к уроку «Что такое числовая дробь» (легкий)
- Метод коэффициентов, часть 1
- Деление многочленов уголком
- Случай четырехугольной пирамиды
Второй замечательный предел
или
Доказательство
второго замечательного предела:
Доказательство
для натуральных значений x [показать]
Зная,
что второй замечательный предел верен
для натуральных значений x, докажем
второй замечательный предел для
вещественных x, то есть докажем, что
.
Рассмотрим два случая:
1.
Пусть
.
Каждое значение x заключено между двумя
положительными целыми числами:
,
где
—
это целая часть x.
Отсюда
следует:
,
поэтому
.
Если
,
то
.
Поэтому, согласно пределу
,
имеем:
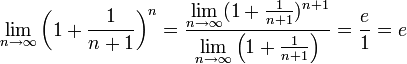
.
П
о
признаку (о пределе промежуточной
функции) существования пределов
.
2.
Пусть
.
Сделаем подстановку − x = t,
тогда
.
Из
двух этих случаев вытекает, что
для
вещественного x.
Следствия
-
-
-
-
-
для
, -
примеры

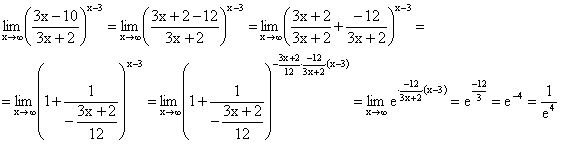

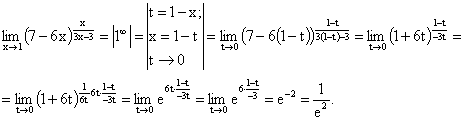
Билет
33 .
Бесконечно
малая (величина) —
числовая функция или последовательность,
которая стремится к нулю.
Бесконечно
большая (величина) —
числовая функция или последовательность,
которая стремится к бесконечности определённого
знака.
Исчисление бесконечно малых и больших
Исчисление
бесконечно малых —
вычисления, производимые с бесконечно
малыми величинами, при которых производный
результат рассматривается как
бесконечная суммабесконечно
малых. Исчисление бесконечно малых
величин является общим понятием
для дифференциальных и интегральных
исчислений,
составляющих основу современной высшей
математики.
Понятие бесконечно малой величины тесно
связано с понятием предела.
[Править]Бесконечно малая величина
Последовательность an называется бесконечно
малой,
если
.
Например, последовательность чисел
—
бесконечно малая.
Функция
называется бесконечно
малой в окрестности точки x0,
если
.
Функция
называется бесконечно
малой на бесконечности,
если
либо
.
Также
бесконечно малой является функция,
представляющая собой разность функции
и её предела, то есть если
,
то f(x)
− a =
α(x),
.
[Править]Бесконечно большая величина
Во
всех приведённых ниже формулах
бесконечность справа от равенства
подразумевается определённого знака
(либо «плюс», либо «минус»). То есть,
например, функцияxsin x,
неограниченная с обеих сторон, не
является бесконечно большой при
.
Последовательность an называется бесконечно
большой,
если
.
Функция
называется бесконечно
большой в окрестности точки x0,
если
.
Функция
называется бесконечно
большой на бесконечности,
если
либо
.
[Править]Свойства бесконечно малых
-
Сумма
конечного числа бесконечно малых —
бесконечно малая. -
Произведение
бесконечно малых — бесконечно малая. -
Произведение
бесконечно малой последовательности
на ограниченную — бесконечно малая.
Как следствие, произведение бесконечно
малой на константу — бесконечно
малая. -
Если an —
бесконечно малая последовательность,
сохраняющая знак, то
— бесконечно
большая последовательность.
[Править]Сравнение бесконечно малых
Отношение
бесконечно малых величин образует
так называемую неопределённость
.
[Править]Определения
Допустим,
у нас есть бесконечно малые при одном
и том же
величины α(x) и β(x) (либо,
что не важно для определения, бесконечно
малые последовательности).
-
Если
,
то β —
бесконечно малая высшего
порядка малости,
чем α.
Обозначают β
= o(α). -
Если
,
то β —
бесконечно малая низшего
порядка малости,
чем α.
Соответственно α
= o(β). -
Если
(предел
конечен и не равен 0), то α и β являются
бесконечно малыми величинами одного
порядка малости.
Это
обозначается как β
= O(α) или α
= O(β) (в
силу симметричности данного отношения).
-
Если
(предел
конечен и не равен 0), то бесконечно
малая величина β имеет m-й
порядок малости относительно
бесконечно малой α.
Для
вычисления подобных пределов удобно
использовать правило
Лопиталя.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #