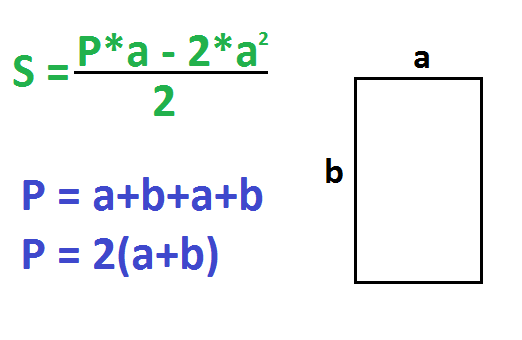Как найти вторую часть прямоугольника - Исправление недочетов и поиск решений вместе с Examum.ru

Самый простой способ – перемножить две стороны. Но иногда эти две стороны неизвестны.

11 448

Умножьте его ширину на высоту. Это самый простой способ найти площадь прямоугольника. Например, если ширина прямоугольника равна 4 см, а высота – 2 см, то площадь будет равна 4*2 = 8 см.

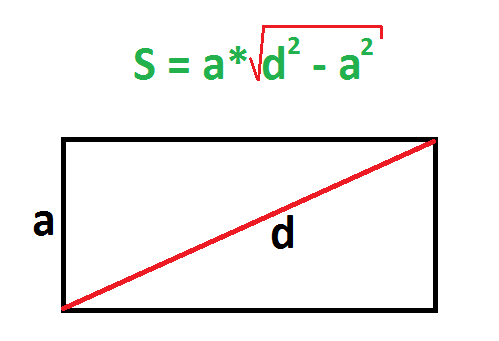
По диагонали и стороне

Должна быть известна диагональ и любая из сторон. Действия:

Найти квадрат диагонали, то есть умножить ее на саму себя.
Найти квадрат известной стороны.
Из квадрата диагонали вычесть квадрат стороны.
Найти квадратный корень получившейся разности.
Умножить его на известную сторону.

Пример. Сторона прямоугольника равна 3 см, а диагональ – 5 см. Найдите площадь.

Квадрат стороны = 3*3 = 9 см.
Квадрат диагонали = 5*5 = 25 см.
Вычитаю из квадрата диагонали квадрат стороны: 25-9 = 16 см.
Нахожу квадратный корень получившейся разности. Корень из 16 = 4 см.
Умножаю корень разности на известную сторону: 16*9 = 144 см.

Ответ: 144 см.

Обратите внимание

Диагональ в прямоугольнике – это гипотенуза, потому что она всегда находится напротив угла в 90 градусов. Найти диагональ можно по формуле нахождения гипотенузы, например, поделив катет угла A на синус угла A.

По стороне и диаметру описанной окружности

Вокруг любого прямоугольника можно описать окружность. Вам надо знать диаметр этой окружности и любую из сторон прямоугольника.

Действия:

Найдите квадрат диаметра – умножьте диаметр на диаметр.
Найдите квадрат известной стороны.
Отнимите от квадрата диаметра квадрат стороны.
Найдите квадратный корень разности.
Умножьте квадратный корень на известную сторону.

Пример. Найдите площадь прямоугольника, если диаметр описанной окружности равен 10 см, а одна из сторон равна 8 см.

Квадрат диаметра: 10*10 = 100 см.
Квадрат стороны: 8*8 = 64 см.
Отнимаю от квадрата диаметра квадрат стороны: 100-64 = 36 см.
Квадратный корень из 36 равен 6 см (потому что 6*6 = 36).
Умножаю сторону на корень из разности: 8*6 = 48 см.

Ответ: 48 см.

Лайфхак

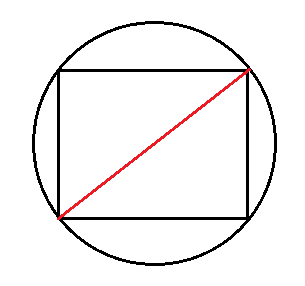
Диаметр описанной окружности всегда равен диагонали прямоугольника. Смотрите:

А найти диагональ можно по формуле гипотенузы прямоугольного треугольника.

Диаметр равен двум радиусам, потому что радиус – это половина диаметра.

Как найти площадь треугольника – все способы от самых простых до самых сложных

Зависит от того, какой треугольник.

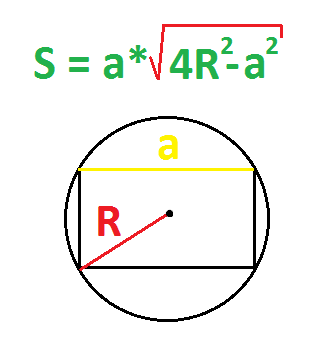
По радиусу описанной окружности и стороне

Можно просто найти диаметр (умножить радиус на два) и использовать формулу выше.

Другой способ:

Найти квадрат радиуса (умножьте радиус на радиус).
Умножить квадрат радиуса на 4.
Найти квадрат известной стороны.
Отнять от четырех радиусов в квадрате квадрат известной стороны (из второго отнять третье).
Найти квадратный корень разности.
Умножить корень на известную сторону.

Пример. Найдите площадь прямоугольника, если радиус описанной окружности равен 5 см, а одна из сторон равна 6 см.

Квадрат радиуса: 5*5=25 см.
Четыре квадрата радиуса: 4*25 = 100 см.
Квадрат стороны: 6*6 = 36 см.
Отнимаю от четырех радиусов в квадрате квадрат стороны: 100-36 = 64 см.
Нахожу квадратный корень разности. Корень из 64 равен 8 см.
Умножаю корень на сторону: 8*6 = 48 см.

Ответ: 48 см.

Помните

Радиус = половине диаметра.

Радиус = половине гипотенузы прямоугольного треугольника, вокруг которого описана окружность. Потому что эта гипотенуза = диагонали прямоугольника = диаметру.

По стороне и периметру – 1 способ

Периметр – это сумма всех сторон прямоугольника. P=a+b+a+b. Другая формула периметра: P=2(a+b).

Если известен периметр и одна сторона, надо найти вторую сторону и перемножить их.

Пример. Периметр прямоугольника равен 14 см, а одна из сторон равна 3 см. Найдите площадь.

Нахожу вторую сторону прямоугольника:
1. P=2(a+b).
2. P=2a+2b.
3. 14= 2*3+2b.
4. 14 = 6+2b.
5. 2b = 14-6 = 8.
6. b = 8/2.
7. b = 4.
Нахожу площадь по основной формуле. S = 3*4 = 12 см.

Ответ: 12 см.

По стороне и периметру – 2 способ

Действия такие:

Умножьте периметр на сторону.
Найдите квадрат стороны.
Умножьте квадрат стороны на 2.
Отнимите от произведения периметра и стороны два квадрата стороны (от первого отнимите третье).
Поделите на 2.

Пример. Сторона прямоугольника равна 8, а периметр равен 28. Найдите площадь.

Умножаю периметр на сторону: 8*28 = 224 см.
Нахожу квадрат стороны: 8*8 = 64 см.
Умножаю квадрат стороны на два: 64*2 = 84 см.
Отнимаю из первого третье: 224-84 = 140 см.
Делю разность на два: 140/2 = 70 см.

Ответ: 70 см.

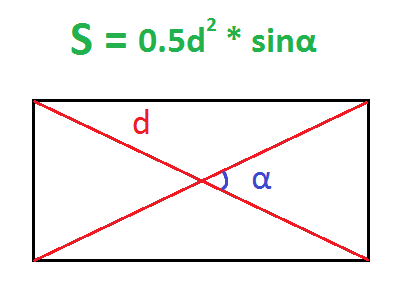
По диагонали и углу между диагоналями

Диагонали прямоугольника всегда равны.

Действия:

Найти квадрат диагонали (умножить диагональ на саму себя).
Найти половину этого квадрата – умножить его на 0,5.
Найти синус угла между диагоналями.
Умножить половину квадрата диагонали на синус угла между диагоналями.

Пример. Найдите площадь прямоугольника, диагональ которого равна 10 см, а угол между диагоналями – 30 градусов.

Квадрат диагонали: 10*10 = 100 см.
Половина этого квадрата: 0,5*100 = 50 см.
Синус угла между диагоналями: sin 30 градусов = 0,5.
Перемножаю половину квадрата и синус угла, чтобы найти площадь: 50*0,5 = 25 см.

Ответ: 25 см.

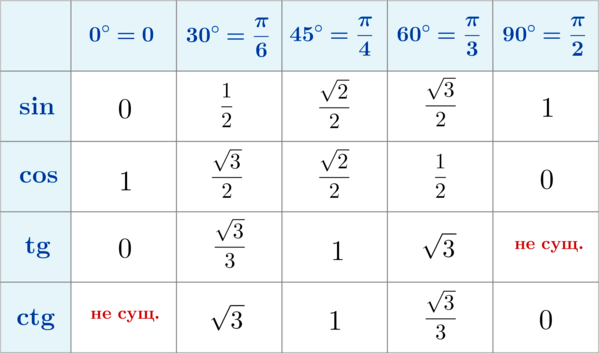
Вот еще вам таблица основных значений из тригонометрии. Там как раз отмечено, что синус 30 градусов всегда равен 0,5 (1/2).

По радиусу описанной окружности и углу между диагоналями – первый способ

Радиус описанной окружности равен половине ее диаметра, а диаметр равен диагонали прямоугольника. Надо найти диаметр и посчитать площадь по формуле выше.

Пример. Найдите площадь прямоугольника, если радиус описанной окружности равен 6 см, а угол между диагоналями – 30 градусов.

Находим длину диагонали: 6*2 =12 см.
Квадрат диагонали равен 144 см.
Половина квадрата: 72 см.
Синус 30 градусов равен 0,5.
Умножаем половину квадрата на синус: 72*0,5 = 36 см.

Ответ: 36 см.

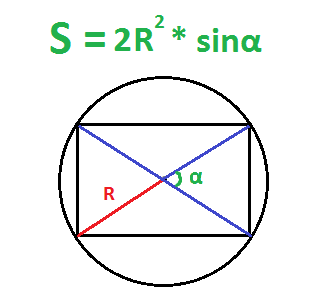
По радиусу описанной окружности и углу между диагоналями – второй способ

Действия:

Найти квадрат радиуса (умножить радиус на радиус).
Умножить квадрат радиуса на два.
Найти синус угла между диагоналями.
Умножить синус угла на два радиуса в квадрате.

Пример. Найдите площадь прямоугольника, если радиус описанной окружности равен 6, а угол между диагоналями – 30 градусов.

Квадрат радиуса: 6*6 = 36.
Два радиуса в квадрате: 36*2 = 72.
Синус 30 градусов равен 0,5.
Произведение синуса и двух радиусов в квадрате: 72*0,5 = 36 см.

Ответ: 36 см.

Покритикуйте статью и стиль подачи материала в комментариях, я внесу правки. Это моя вторая статья по математике, я хочу, чтобы они все были образцовыми.

( 1 оценка, среднее 5 из 5 )

Оцените статью

ЕЖЕНЕДЕЛЬНАЯ РАССЫЛКА

Получайте самые интересные статьи по почте и подписывайтесь на наши социальные сети

Источник

Зная в прямоугольнике площадь и сторону можно найти вторую сторону, и затем все остальные параметры по порядку. Вторая сторона прямоугольника будет равна отношению площади к известной стороне.
b=S/a

Для того чтобы найти периметр прямоугольника через площадь и сторону, необходимо подставить в формулу вместо второй стороны полученное отношение
P=2(a+b)=2(a+S/a)

Диагональ прямоугольника можно найти через теорему Пифагора в прямоугольном треугольнике, который она образует. Обе диагонали прямоугольника принимают одно и то же значение. Выразив b через площадь и известную сторону, получим следующее выражение. (рис. 56.1)
d_1=d_2=√(a^2+b^2 )=√(a^2+(S/a)^2 )=√(a^2+S^2/a^2 )

Используя тригонометрические отношения в полученном треугольнике можно найти углы при пересечении диагоналей со сторонами. Для этого проще всего будет использовать тангенс, как отношение катетов друг к другу. Точно также, как и в предыдущих формулах, заменяем неизвестную сторону на равное ей выражение.
α=arc tan⁡〖b/a〗=arc tan⁡〖S/a^2 〗
β=arc tan⁡〖a/b=arc tan⁡〖a^2/S〗〗

Угол, образованный при пересечении диагоналей, и дополнительный ему до 180° зависят только от углов при диагонали и стороне, и равны удвоенному их значению. (рис. 56.2)
γ=2α
δ=2β

Радиус описанной вокруг прямоугольника окружности равен половине диагонали, так как лежит на ней и исходит из точки пересечения диагоналей. (рис. 56.3)
R=d/2=√(a^2+S^2/a^2 )/2

Источник

S прямоугольника = a * b, где а,b — стороны прямоугольника.

————

4 * 8 = 32 см² — площадь первоначального прямоугольника.

Чтобы найти вторую часть этого прямоугольника, можно площадь первоначального поделить на 2, т.е.

32 : 2 = 16 см² — площадь второй части прямоугольника.

или

Чтобы отделить вторую часть, мы поделили длину на 2, т.е.

8 см : 2 = 4 см

и теперь найдем S

4 * 4 = 16 см²

Ответ: 16 см²

Источник

Участник Знаний
@Участник Знаний

April 2022
1
72
Report

найдите вторую часть площади прямоугольника если его стороны равны 12см и 6см

С УСЛОВИЯМИ

Please enter comments

Please enter your name.

Please enter the correct email address.

Agree to terms of service

You must agree before submitting.

Answers & Comments

inzhuka009

Ответ:

А-12см

В-6см

S-?см в квадрате

12*6=78 (см в квадрате)-S

Ответ: 78 см в квадрате

Пошаговое объяснение:

Надеюсь хоть как то помогла

5 votes
Thanks 9

inzhuka009

Незашто

Источник

Школьная математика » Блог » Как найти стороны прямоугольника при известных периметре и площади

В этой статье я хочу рассмотреть две математические задачи повышенной сложности для 4 класса.

Видеоурок по теме этой статьи можно посмотреть по ссылке.

Площадь прямоугольника 32 см², а периметр – 24 см. Найти стороны прямоугольника.

Площадь прямоугольника 126 см², а периметр – 46 см. Найти его длину и ширину.

С этими задачами, я уверен, без труда справится более старший школьник, знакомый с решением системы уравнений и квадратных уравнений. Кстати, подобная задача есть в учебнике по геометрии Атанасяна, глава VI № 454 пункт б за 8 класс.

Но почему же эти задачи указаны в математических сборниках как задачи для 4 класса, в котором еще не изучают алгебраические понятия и методы решения? Нет ли здесь ошибки?

Нет, никакой ошибки здесь нет. Эти, и аналогичные им задачи можно решить и без использования алгебраических знаний.

Первое, что приходит на ум – это по значению периметра прямоугольника (а периметр – это удвоенная сумма двух его сторон) найти сумму двух сторон, а после простым подбором определить два числа, произведение которых равно данной по условию площади прямоугольника, а сумма – половине периметра.

Я хочу показать вам математически точное решение, которое безо всяких подборов приводит к правильному результату.

Нахождение сторон прямоугольника при известных периметре и площади

Рассмотрим первую задачу:

Площадь прямоугольника 32 см², а периметр – 24 см. Найти стороны прямоугольника.

Как известно, периметр прямоугольника находится по формуле ({color{red} P=2cdot (a+b)}) , площадь – по формуле ({color{red} S=acdot b}) .

Так как периметр прямоугольника – это удвоенное произведение суммы двух сторон прямоугольника, то мы можем найти эту сумму, разделив значение периметра на 2:

({color{red} a + b = 24 : 2 = 12}) см.

А дальше мы рассуждаем так.

Найдем максимально возможную площадь прямоугольника при данном значении суммы двух его сторон, то есть, полупериметра. Так как полупериметр – четное число, то очевидно, что прямоугольник с максимально возможным значением площади при сумме его двух сторон, равной 12, – это квадрат со стороной ({color{red} 12 : 2 = 6}) см.

Тогда площадь этого квадрата равна

({color{red}S_{k}=6cdot 6=36}) см².

По условию нашей задачи площадь прямоугольника составляет 32 см². Находим разницу между полученной площадью квадрата и заданной площадью прямоугольника.

({color{red} S–S _{k}=36-32=4}) см².

Это значит, что нам нужно изменить стороны рассматриваемого квадрата со стороной 6 см так, чтобы уменьшилась его площадь, но не изменился периметр.

Так как квадрат имеет самую большую площадь среди прямоугольников с одинаковым периметром, то для уменьшения площади нам нужно увеличить разницу между его длиной и шириной. То есть, ширину уменьшить, а длину увеличить на одно и то же число.

Но на какое?

Площадь 4 см² – это квадрат со стороной 2 см. Это и есть нужное нам число.

Тогда, ширина искомого прямоугольника будет равна:

({color{red} a=6-2=4}) см

а длина:

({color{red} b=6+2=8}) см.

Проверим найденные длины сторон, определив периметр и площадь полученного прямоугольника:

({color{red} P=2cdot (4+8)=2cdot 12=24}) см

({color{red} S=4cdot 8=32}) см².

Задача решена верно.

Теперь рассмотрим вторую задачу.

Площадь прямоугольника 126 см², а периметр – 46 см. Найти его длину и ширину.

Находим полупериметр, то есть, сумму двух сторон прямоугольника.

({color{red} a+b=46:2=23}) см.

Найдем максимально возможную площадь прямоугольника при данном значении суммы двух его сторон, то есть, полупериметра. Так как полупериметр – нечетное число, значит, нам нужен такой прямоугольник, разница между значениями ширины и длины которого в натуральных числах минимальна, то есть, единица. Это прямоугольник со сторонами 11 и 12, т.к. ({color{red} 23=11+12}).

Площадь такого прямоугольника равна:

({color{red}S_{2}=11cdot 12=132}) см².

Разница между полученной площадью и заданной по условию задачи составляет:

({color{red}S_{2}-S=132-126=6}) см².

6 см² – это площадь прямоугольника со сторонами 2 и 3 см. Чтобы уменьшить площадь нашего прямоугольника со сторонами 11 см и 12 см, нужно увеличить разницу между значениями этих сторон, а именно, уменьшить его короткую сторону, то есть, ширину. При этом длину также нужно увеличить на это же число, чтобы сохранить значение периметра.

Для этого ширину 11 мы уменьшаем на одноименное значение, то есть, тоже на ширину прямоугольника с площадью 6 см², а именно, на 2.

Кстати, подумайте и напишите в комментарии к этой статье, почему мы рассматриваем разницу в площадях именно как прямоугольник с максимальной площадью (например, в этой задаче как прямоугольник 2 на 3, а не 1 на 6, а в первой – как квадрат 2 на 2, а не прямоугольник 1 на 4), и почему ширину уменьшаем именно на ширину (в этой задаче 11 – 2, а не 11 – 3).

Находим ширину искомого прямоугольника:

({color{red} a=11-2=9}) см.

Длину нужно увеличить также на это число, чтобы не изменился периметр прямоугольника:

({color{red} b=12+2=14}) см.

Проведем проверку:

({color{red} P=2cdot (9+14)=2cdot 23=46}) см.

({color{red}S=9cdot 14=126}) см².

И эта задача решена тоже верно.

На этом все. Не забудьте написать в комментарии ответы на вопросы, почему мы рассматриваем разницу в площадях именно как прямоугольник с максимальной площадью, и почему ширину уменьшаем именно на ширину.

Вам также пригодится:

Источник