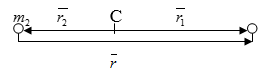При взаимодействии тел на оба тела действует одинаковая сила и тела приобретают скорости, обратно пропорциональные массам этих тел, при условии отсутствия начальных скоростей. Значит, чтобы определить массу тела с помощью второго тела известной массы, необходимо привести эти тела во взаимодействие, измерить пробег тел после взаимодействия, чтобы оценить их скорости. Величина, обратная отношению скоростей покажет во сколько раз масса одного тела больше массы другого.
Сергей Феликсович Савельев
Эксперт по предмету «Физика»
Задать вопрос автору статьи
Приведенная масса
Решение уравнений динамики системы материальных точек встречает непреодолимые математические трудности, т.к. точного решения этих уравнений для произвольных сил не найдено уже в случае трех материальных точек.
В связи с этим важна задача о замкнутой системе двух точек, называемая задачей двух тел. Она имеет простое и исчерпывающее решение — сводится к основной задаче динамики одной материальной точки. Решение задачи двух тел используется в небесной механике, описывающей движение планет и их спутников в Солнечной системе, в задачах на столкновение частиц, в статистической физике и других вопросах.
Определение 1
Рассмотрим замкнутую систему двух материальных точек, взаимодействующих между собой. Как известно центр масс такой системы движется равномерно и прямолинейно (или покоится). Задача просто решается в системе с началом в центре масс, движущейся поступательно (такая система называется Ц-системой).
Рисунок 1.
Обозначим массы частиц через $m_{1} $ и $m_{2} $ и их радиус-векторы, проведенные от центра масс, соответственно $overline{r_{1} }$ и $overline{r_{2} }$. Пусть $overline{r}$- вектор, проведенный от точки $m_{2} $ к $m_{1} $. Из определения радиус-вектора центра масс имеем:
Непосредственно из рисунка следует соотношение между радиус-векторами:
$overline{r}_{1} =overline{r}_{2} +overline{r}$. (1)
Два последних равенства позволяют выразить радиус-векторы $overline{r_{1} }$ и $overline{r_{2} }$ через вектор $overline{r}$, соединяющий точки $m_{2} $ и $m_{1} $. Имеем:
$overline{r}_{1} =frac{m_{2} }{m_{1} +m_{2} } overline{r}$, $overline{r}_{2} =frac{m_{1} }{m_{1} +m_{2} } overline{r}$. (2)
Запишем основные уравнения для движения обеих точек в Ц-системе:
$begin{array}{l} {m_{1} overline{ddot{r}_{1} }=overline{F}_{2,1} (r)} \ {m_{2} overline{ddot{r}_{2} }=overline{F}_{1,2} (r)} end{array}$ (3)
Силы в уравнениях (3) зависят от расстояния между точками, а не от расстояния до центра масс, т.е. решать уравнения (1) отдельно для каждой точки нельзя.
«Задача двух тел» 👇
Пользуясь выражениями для радиус-векторов (2), исключим из основных уравнений (3) $overline{r_{1} }$ и $overline{r_{2} }$. Тогда получаем уравнения движения:
Так как по третьему закону Ньютона $overline{F}_{2,1} (r)=-overline{F}_{1,2} (r)$, оба уравнения становятся тождественными, и движение системы двух точек, в результате их взаимодействия эквивалентно движению одной точки в соответствии с уравнением:
$frac{m_{1} B_{2} }{m_{1} +m_{2} } overline{ddot{r}}=overline{F}(r)$. (4)
Уравнение (4) отличается от известного уравнения движения материальной точки в поле заданной силы только тем, что вместо массы $m$здесь выступает комбинация масс двух точек:
$m’=frac{m_{1} B_{2} }{m_{1} +m_{2} } $ (5)
Величина $m’$ называется приведенной массой.
Итак, задача двух тел свелась к задаче о движении одной материальной точки с приведенной массой в Ц-системе под действием центральной силы; уравнение движения имеет обычный вид:
$m’overline{ddot{r}}=overline{F}(r)$ (6)
Но при использовании результатов решения уравнения (6) необходимо помнить, что точка $m’$, движущаяся на конце радиус-вектора $overline{r}$под действием силового центра в начале координат Ц-системы, является не реальной, а изображающей движение системы. От ее движения, после того как уравнение (6) проинтегрировано, следует переходить к реальному движению двух материальных точек $m_{2} $ и $m_{1} $.
Движение двух материальных точек в системе центра масс
Движение изображающей точки в соответствии с уравнением (6) будет плоским. Пусть кинематическое уравнение движения найдено: $overline{r}=overline{r}(t)$.
В таком случае с помощью формулы (2) находим кинематическое уравнение движения обеих материальных точек в Ц-системе:
$overline{r}_{1} =frac{m_{2} }{m_{1} +m_{2} } overline{r}(t),$ $overline{r}_{2} =frac{m_{1} }{m_{1} +m_{2} } overline{r}(t)$. (7)
Очевидно, что траектория движения изображающей точки и точек $m_{2} $ и $m_{1} $ будут подобными кривыми относительно центра масс, а отношение подобия есть обратное отношение масс, т.е.:
$frac{r_{1} }{r_{2} } =frac{m_{2} }{m_{1} } $ (8)
Нетрудно найти и скорости движения точек. Дифференцируя (7) по времени, имеем:
$overline{v}_{1} =frac{m_{2} }{m_{1} +m_{2} } overline{v},$ $overline{v}_{2} =frac{m_{1} }{m_{1} +m_{2} } overline{v}$. (9)
Задача двух тел решена.
Пример 1
Момент импульса для системы двух точек имеет вид: $overline{L}=m_{1} left|overline{r}_{1} overline{v}_{1} right|+m_{2} left|overline{r}_{2} overline{v}_{2} right|$. Необходимо записать выражение для собственного момента импульса системы через приведенную массу.
Дано:
Момент импульса системы двух точек: $overline{L}=m_{1} left|overline{r}_{1} overline{v}_{1} right|+m_{2} left|overline{r}_{2} overline{v}_{2} right|$.
Найти: собственный момент импульса системы — ?
Момент импульса системы двух точек:
[overline{L}=m_{1} left|overline{r}_{1} overline{v}_{1} right|+m_{2} left|overline{r}_{2} overline{v}_{2} right|.]
Внесем сюда выражения $overline{r_{1} }$ и $overline{r_{2} }$через вектор $overline{r}$, выражающийся формулой (7) и получим равенство:
[overline{L}=frac{m_{1} m_{2} }{m_{1} +m_{2} } left|overline{r}overline{v}_{1} right|-frac{m_{1} m_{2} }{m_{1} +m_{2} } left|overline{r}overline{v}_{2} right|=frac{m_{1} m_{2} }{m_{1} +m_{2} } (overline{r}left|overline{v}_{1} -overline{v}_{2} right|).]
Вектор $overline{v}_{1} -overline{v}_{2} $ есть скорость $overline{v’}$первой частицы относительно второй или скорость изображающей точки $overline{v}$ и окончательный результат выражается равенством:
[overline{L}=m'[overline{r}overline{cdot v}].]
Ответ: собственный момент импульса системы $overline{L}=m'[overline{r}overline{cdot v}]$
Замечание 1
Выводы:
-
задача о движении двух тел сводится к задаче о движении одной точки под действием заданной силы;
-
особую роль при этом играет приведенная масса системы, через нее выражаются основные динамические параметры системы — энергия, импульс, момент импульса.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
В статье обсуждаются несколько подходов и несколько примеров того, как рассчитать массу по силе и расстоянию.
Сэр Исаак Ньютон сформулировал многочисленные законы и теории которые дают нам различные подходы к вычислению массы тела с расстояния, пройденного под действием силы. Плюс кинематические уравнения движения и формула работы-энергии Помогите нам определить массу по силе и расстоянию.
Рассчитайте массу, используя закон всемирного тяготения Ньютона
Мы можем вычислить массу, используя закон всемирного тяготения Ньютона, следующим образом:
к вычислить массу через силу и расстояния, мы можем использовать законы тяготения Ньютона, которые гласят: «сила гравитации, действующая между двумя телами, прямо пропорциональна их массам и обратно пропорциональна квадрату расстояния между центрами масс».
Гравитация универсальна. Это означает, что все объекты во Вселенной притягиваются друг к другу гравитацией, и Закон всемирного тяготения Ньютона объясняет эту универсальность гравитации. По закону всемирного тяготения
Fg ∝м1m2/r2
Где, Fg = сила тяжести между двумя объектами
m1 масса объекта 1
m2 масса объекта 2
r — расстояние, разделяющее центры обоих объектов ..
(Кредит: Shutterstock)
Поскольку сила тяжести прямо пропорциональна массам обоих объектов, более крупные объекты будут притягивать друг друга с более значительной силой тяжести.
Переписывая формулу в терминах константы пропорциональности,
Fg=G*(м1m2/r2)………………(1)
Где, G есть универсальная гравитационная постоянная с постоянным значением 6.67 x 10-11 Nm2/ кг2.
В уравнении (1), как и постоянное значение G, у нас также есть постоянное значение массы объекта 2, которое является массой земли; как и в большинстве случаев, мы вычисляем силу тяжести любого объекта относительно земли. Следовательно, постоянное значение массы Земли равно m2 есть, 5.98 x 1024 кг.
Из уравнения (1),
Если мы определим расстояние d и силу тяжести на объекте Fg, мы можем вычислить его массу m1 используя закон всемирного тяготения Ньютона.
Сила тяжести между землей и мальчиком составляет 680 Н, когда он стоит на расстоянии 6.38 х 10.6м от центра Земли. Определите массу мальчика, стоящего на земле.
Данный:
Fg = 680 Н
г = 6.38 х 106 m
m2= 5.98 x 1024 kg
G = 6.67 х 10-11 Nm2/ кг2
Найти: m1 =?
Формула:
Fg=G*(м1m2/r2)
Решения:
Масса мальчика, стоящего на земле, рассчитывается по формуле закона всемирного тяготения:
Fg=G*(м1m2/r2)
Переставляем по м1,
m1=(43.384*108)/(39.904*1013)
m1 = 108.67 кг
Масса стоящего на земле мальчика 108.67 кг.
Расчет массы с использованием второго кинематического уравнения движения
Мы можем вычислить массу, используя второй закон движения Ньютона:
Чтобы вычислить массу объекта, мы можем использовать популярную формулу второго закона движения Ньютона, которая показывает связь между ускорением, силой и массой. Затем мы можем реализовать это во втором кинематическом уравнении движения, которое касается расстояния.
Второй закон движения объясняет, что объект ускоряется (а) с трудом, когда сила (F) применяется к объекту, имеющему массу m.
а=Ф/м………………… (2)
(Кредит: Shutterstock)
Второе кинематическое уравнение движения о расстоянии d есть;
d=ut+(1/2)в2…………………. (3)
Подставляя уравнение (3) в уравнение выше, получаем
d=ut+(Ft2/ 2м)
If мы определяем расстояние (d), пройденное объектом за время (t), когда на него действует сила (F), мы можем вычислить его массу, используя второе кинематическое уравнение движения.
Чистая сила 10 Н действует на объект, который преодолевает расстояние 40 м с начальной скоростью 1 м / с за 5 с. Рассчитайте массу объекта.
Данный:
F = 10 Н
d = 40 м
u = 1 м / с
t = 5 с
Найти: м =?
Формула:
d=ut+(1/2)в2
Решения:
Массу объекта можно рассчитать, используя второе кинематическое уравнение движения.
d=ut+(1/2)в2
Согласно второму закону Ньютона, a=F/m
Подставляя значение ‘a’ в уравнение кинематики, получаем
d=ut+(Ft2/ 2м)
Подставляя все значения,
Масса объекта 3.57 кг.
Расчет массы с использованием третьего кинематического уравнения движения
Мы можем рассчитать массу, используя третье кинематическое уравнение движения.
Чтобы вычислить массу объекта, мы можем реализовать формулу второго закона движения Ньютона в третьем кинематическом уравнении движения, которое касается скорости.
Третье кинематическое уравнение движения о скорости v есть,
v2=u2+2реклама………………….(4)
Реализуем второй закон движения Ньютона (2) в третье кинематическое уравнение движения (4),
v2=u2+(2fd/м)………….(5)
Предположим, мы определяем расстояние (d), которое проходит объект, когда его скорость v изменяется от начальной скорости u из-за силы F. В этом случае мы можем вычислить его массу, используя третье кинематическое уравнение движения.
Объект движется по прямой траектории в 5 м от исходного положения со скоростью 5 м / с, когда сила 50 Н приложена к тому же объекту в состоянии покоя. Рассчитайте массу объекта.
Данный:
d = 5м
v = 5 м / с
u = 0, поскольку объект изначально находится в состоянии покоя.
F = 50 Н
Найти: м =?
Формула:
v2=u2+2объявление
Решения:
Массу объекта можно рассчитать по третьему кинематическому уравнению движения,
v2=u2+2объявление
Подставляя значение ‘a’ в уравнение кинематики, получаем
v2=u2+(2fd/м)
Подставляя все значения,
Масса объекта 20 кг.
Рассчитайте массу с помощью формулы работы-энергии
Мы можем вычислить массу, используя следующую формулу работы-энергии:
Чтобы вычислить массу объекта, мы можем использовать формулу работы-энергии, которая показывает, что работа, выполняемая над объектом, равна его преобразованию кинетической энергии, когда он перемещается на определенное расстояние из-за приложенной силы.
(Кредит: Shutterstock)
Выполненная работа рассчитывается как побочный продукт приложенной силы и пройденного расстояния.
W = Fd ……………………. (6)
Проделанная работа — это преобразование кинетической энергии объекта. Следовательно, проделанная работа равна кинетической энергии,
W = KE
Вт=(1/2)мв2…………………. (7)
Подставляя значение W (6),
Fd==(1/2)мв2 …………… .. (8)
Если мы определим расстояние (d), которое проходит объект со скоростью v, когда к нему применяется сила (F), мы можем вычислить его массу, используя формулу работы-энергии.
Примечание: здесь мы считаем, что сила трения незначительна.
Коробка скользит примерно на 10 м по горизонтальной поверхности со скоростью 20 м / с, когда мы прикладываем силу толчка 50 Н. Рассчитайте массу ящика.
Данный:
d = 10 м
v = 20 м / с
F = 50 Н
Найти: m =?
Формула:
Вт=(1/2)мв2
Решения:
Массу ящика можно рассчитать по формуле работы-энергии:
Вт=(1/2)мв2
Подставляя стоимость проделанной работы W,
Fд=(1/2)мв2
Преобразуя уравнение для ‘m’,
m=2Fd/v2
Подставляя все значения,
Масса ящика 2.5 кг.
F = m * a — Сила равна произведению массы на ускорение. Масса — скалярная физическая величина, измеряющая количество вещества в теле, мера инерции тела по отношению к действующей на него силе. m = F / a — Масса равна отношению силы к ускорения.
Как вычислить массу в физике?
Масса тела выражается через плотность и объем следующей формулой: Масса тела — есть произведение плотности вещества из которого состоит тело на его объем.
Как найти массу через силу?
Для вычисления веса используйте формулу Р = mg.
Так как вес является силой, X Источник информации эту формулу можно записать и как F = mg. P или F — соответственно, вес или сила (измеряется в ньютонах, Н). m — масса тела (измеряется в килограммах, кг).
Как найти массу с помощью скорости?
Чтобы рассчитать массу или скорость, формулу преобразуют следующим образом: m = 2 ⋅ E кин v 2 и v = 2 ⋅ E кин m . С увеличением массы тела в линейной зависимости увеличивается также и его кинетическая энергия.
Как найти массу и силу тяжести?
Формула силы тяжести Fт=m*g, где m-масса тела, g-ускорение свободного падения. Для тела массой m=400 г =0.4 кг сила тяжести составит Fт=0.4*10=4 Н.
Чему равна масса в физике?
Масса тела равна его плотности умноженной на объём. – его объём. Единица измерения массы – килограмм (кг). Плотность вещества определяется свойствами молекул, из которых оно состоит и их взаимным расположением (молекулярной структурой вещества).
Как найти массу?
Решение: Чтобы найти массу тела, нужно плотность умножить на объем: m = ρ · V. Подставим числовые значения величин: 930 кг/м3 · 0,003 м3 = 2,79 кг.
Как найти массу тела по его весу?
Для расчета индекса массы тела требуется вес в килограммах, поделить на рост в метрах, взятый в квадрат, т. е. ИМТ = вес (кг)/рост (м)2.
Как по плотности и объему найти массу тела?
Вес можно рассчитать по формуле: m=V*p, где р – плотность, V – объем материала. Например, 10 м3 речного песка весят 13 тонн. Если известна масса материала, то объем можно узнать по формуле: V = m/ p.
Как найти массу тела имея силу и ускорение?
m = F / a — Масса равна отношению силы к ускорения.
Как найти массу тела в физике формула?
Чтобы найти массу тела нежно его плотность умножить на объем. Чтобы найти объем тела, нужно его массу разделить на плотность.
Как можно найти массу вещества?
И наоборот, массу вещества определяют как произведение молярной массы на количество вещества: m = n . M. Так, масса 0,1 моля Na составляет 0,1 моль×23 г/моль = 2,3 Молярная масса численно всегда совпадает с молекулярной массой (или атомной массой — если вещество состоит не из молекул, а из атомов).
Как вычислить силу тяжести своего тела?
Силу, с которой Земля притягивает тела, можно рассчитать по формуле F = m ⋅ g , где m — масса тела, а g — ускорение свободного падения.
Загрузить PDF
Загрузить PDF
Масса – это количество материи, содержащейся в данном теле. Материя – это все, что можно физически ощутить. В большинстве случаев масса зависит от размеров тела, но это не всегда так – например, размеры воздушного шара могут быть больше размеров определенного тела, но при этом масса шара будет меньше массы этого тела. Эта статья расскажет вам, как найти массу.
-
1
Используйте трехрычажные весы. Любые весы используются для нахождения массы тел. В рассматриваемых весах есть три рычага, на каждом из которых имеется передвижная гиря.[1]
Также каждый рычаг снабжен шкалой, вдоль которой двигается гиря определенной массы.[2]
- На показания трехрычажных весов не влияет сила тяжести, что позволяет произвести точные измерения массы. В таких весах неизвестная масса сравнивается с известной массой.
- Средняя шкала имеет шаг 100 г. Дальняя шкала имеет шаг 10 г. Ближняя шкала измеряет вес в диапазоне 0-10 г.
- При помощи трехрычажных весов можно произвести очень точные измерения массы тела. В случае использования таких весов ошибка измерения составит всего 0,06 г. Принцип работы таких весов похож на принцип работы детской карусели.[3]
-
2
Передвиньте гири в крайнее левое положений. Это нужно сделать тогда, когда чаша весов пустая. В этом случае весы будут показывать 0.
- Если индикатор, расположенный справа, не совпадает с фиксированной меткой, откалибруйте весы, поворачивая калибровочный винт (он находится слева под чашей весов).
- Калибруют весы для того, чтобы масса чаши не влияла на показания весов, то есть когда чаша пустая, весы должны показывать 0 г. Масса чаши называется весом тары.
- Для того чтобы с чашей весы показывали 0 г, покрутите калибровочный винт, расположенный под чашей. Затем положите на чашу предмет (тело), массу которого вы хотите найти (это делается при помощи передвижных гирь).
-
3
Двигайте гири по одной. Для начала передвиньте гирю по средней шкале (с шагом 100 г). Передвигайте гирю вправо до тех пор, пока индикатор не опустится ниже фиксированной метки. Деление, находящееся слева от гири, указывает на число сотен граммов. За один раз передвигайте гирю на одно деление.
- Затем передвиньте гирю по дальней шкале (с шагом 10 г). Передвигайте гирю вправо до тех пор, пока индикатор не опустится ниже фиксированной метки. Деление, находящееся слева от гири, указывает на число десятков граммов.
- Ближняя шкала делений не имеет. Вы можете перемещать гирю по ней в любом направлении. Числа на этой шкале обозначают граммы, а штриховые метки между числами – десятые грамма.
-
4
Найдите массу тела. Теперь вы можете определить массу тела, находящегося на чаше весов. Для этого сложите показания трех шкал.
- Показания каждой шкалы читаются аналогично показаниям линейки. При этом учитывают показания до ближайшей середины между делениями.
- Например, измерим массу банки с содовой. Если дальняя шкала показывает 70 г, средняя шкала показывает 300 г, а ближняя шкала показывает 3,34 г, то масса банки равна 373,34 г.
Реклама
-
1
Вычисление массы через объем и плотность. Формула для вычисления плотности: плотность = масса / объем. Для того чтобы воспользоваться этой формулой, вам нужно знать объем и плотность тела.[4]
- Согласно этой формуле масса тела равна произведению плотности на объем: масса = объем Х плотность. Например, объем алмаза равен 0,00500 кубическим метрам, а его плотность равна 3,520 кгм^3. Для вычисления массы алмаза перемножьте эти значения: 0,00500 Х 3,520.
- Для перемножения значений воспользуйтесь онлайн-калькулятором. Его можно найти на разных сайтах.[5]
[6]
- Вы можете воспользоваться специальным калькулятором для вычисления объема тела. Например, вы можете найти объем конуса, если вам известны радиус его основания и высота.[7]
-
2
Уясните разницу между массой и весом. Это разные величины. Масса – это количество материи, содержащейся в данном теле. Вес – это сила, с которой тело действует на опору и которая возникает в поле силы тяжести. Вес тела возрастает с увеличением его массы.
- Помните, что вес тела зависит от его местоположения, потому что при этом меняется сила тяжести. Масса тела не зависит от его местоположения.[8]
Не забудьте вычислить массу тела в соответствующих единицах измерения (килограммах и граммах), а для обозначения массы используйте специальный символ (букву латинского алфавита). - Вес тел одинаковой массы может быть различным (в зависимости от силы тяжести). Например вес тела на Земле будет отличаться от веса того же тела на Луне.[9]
- Не измеряйте массу тела в фунтах и унциях.[10]
- Помните, что вес тела зависит от его местоположения, потому что при этом меняется сила тяжести. Масса тела не зависит от его местоположения.[8]
-
3
Вычисление массы через силу и ускорение. Формула для вычисление силы: F = m Х a.
- Таким образом, формула для вычисления массы: m = F/a, то есть масса равна силе, деленной на ускорение. Масса тела присутствует в формулировке второго закона Ньютона, который гласит, что ускорение прямо пропорционально вызывающей его силе и обратно пропорционально массе тела.
- Масса измеряется в килограммах (кг). Сила измеряется в ньютонах (Н).[11]
Реклама
Советы
- Масса обозначается буквой m. Масса считается постоянной величиной.
Реклама
Об этой статье
Эту страницу просматривали 19 961 раз.