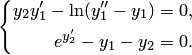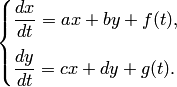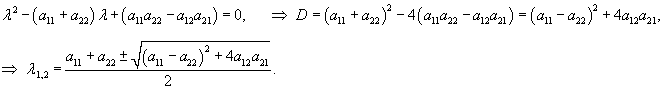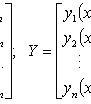Пошаговый калькулятор производных онлайн
Ввод распознает различные синонимы функций, как asin , arsin , arcsin
Знак умножения и скобки расставляются дополнительно — запись 2sinx сходна 2*sin(x)
Список математических функций и констант :
• ln(x) — натуральный логарифм
• sh(x) — гиперболический синус
• ch(x) — гиперболический косинус
• th(x) — гиперболический тангенс
• cth(x) — гиперболический котангенс
• sch(x) — гиперболический секанс
• csch(x) — гиперболический косеканс
• arsh(x) — обратный гиперболический синус
• arch(x) — обратный гиперболический косинус
• arth(x) — обратный гиперболический тангенс
• arcth(x) — обратный гиперболический котангенс
• arsch(x) — обратный гиперболический секанс
• arcsch(x) — обратный гиперболический косеканс
Производная функции заданной параметрически онлайн
Пусть функция задана в виде параметрических уравнений (т.н. параметрическое задание функции):
где x ( t ) , y ( t ) — дифференцируемые функции и x ‘ ( t ) ≠ 0 . Тогда производная
определяется по формуле:
где — производная от параметрического уравнения y ( t ) по параметру t и — производная от параметрического уравнения x ( t ) , по параметру t .
Наш онлайн сервис найдет производную от параметрической функции с подробным решением. Пример подробного решения, выдаваемого нашим сервисом, можно посмотреть здесь .
Найти производную: алгоритм и примеры решений
Операция отыскания производной называется дифференцированием.
В результате решения задач об отыскании производных у самых простых (и не очень простых) функций по определению производной как предела отношения приращения к приращению аргумента появились таблица производных и точно определённые правила дифференцирования. Первыми на ниве нахождения производных потрудились Исаак Ньютон (1643-1727) и Готфрид Вильгельм Лейбниц (1646-1716).
Поэтому в наше время, чтобы найти производную любой функции, не надо вычислять упомянутый выше предел отношения приращения функции к приращению аргумента, а нужно лишь воспользоваться таблицей производных и правилами дифференцирования. Для нахождения производной подходит следующий алгоритм.
Чтобы найти производную, надо выражение под знаком штриха разобрать на составляющие простые функции и определить, какими действиями (произведение, сумма, частное) связаны эти функции. Далее производные элементарных функций находим в таблице производных, а формулы производных произведения, суммы и частного — в правилах дифференцирования. Таблица производных и правила дифференцирования даны после первых двух примеров.
Пример 1. Найти производную функции

Решение. Из правил дифференцирования выясняем, что производная суммы функций есть сумма производных функций, т. е.

Из таблицы производных выясняем, что производная «икса» равна единице, а производная синуса — косинусу. Подставляем эти значения в сумму производных и находим требуемую условием задачи производную:

Пример 2. Найти производную функции

Решение. Дифференцируем как производную суммы, в которой второе слагаемое с постоянным множителем, его можно вынести за знак производной:
Если пока возникают вопросы, откуда что берётся, они, как правило, проясняются после ознакомления с таблицей производных и простейшими правилами дифференцирования. К ним мы и переходим прямо сейчас.
Таблица производных простых функций
| 1. Производная константы (числа). Любого числа (1, 2, 5, 200. ), которое есть в выражении функции. Всегда равна нулю. Это очень важно помнить, так как требуется очень часто |  |
| 2. Производная независимой переменной. Чаще всего «икса». Всегда равна единице. Это тоже важно запомнить надолго |  |
| 3. Производная степени. В степень при решении задач нужно преобразовывать неквадратные корни. |  |
| 4. Производная переменной в степени -1 |  |
| 5. Производная квадратного корня |  |
| 6. Производная синуса |  |
| 7. Производная косинуса |  |
| 8. Производная тангенса |  |
| 9. Производная котангенса |  |
| 10. Производная арксинуса |  |
| 11. Производная арккосинуса |  |
| 12. Производная арктангенса |  |
| 13. Производная арккотангенса |  |
| 14. Производная натурального логарифма |  |
| 15. Производная логарифмической функции |  |
| 16. Производная экспоненты |  |
| 17. Производная показательной функции |  |
Правила дифференцирования
| 1. Производная суммы или разности |  |
| 2. Производная произведения |  |
| 2a. Производная выражения, умноженного на постоянный множитель |  |
| 3. Производная частного |  |
| 4. Производная сложной функции |  |
Правило 1. Если функции
дифференцируемы в некоторой точке 
т.е. производная алгебраической суммы функций равна алгебраической сумме производных этих функций.
Следствие. Если две дифференцируемые функции отличаются на постоянное слагаемое, то их производные равны, т.е.
Правило 2. Если функции
дифференцируемы в некоторой точке 
т.е. производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой.
Следствие 1. Постоянный множитель можно выносить за знак производной:
Следствие 2. Производная произведения нескольких дифференцируемых функций равна сумме произведений производной каждого из сомножителей на все остальные.
Например, для трёх множителей:
Правило 3. Если функции
дифференцируемы в некоторой точке 

т.е. производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя.
Где что искать на других страницах
При нахождении производной произведения и частного в реальных задачах всегда требуется применять сразу несколько правил дифференцирования, поэтому больше примеров на эти производные — в статье «Производная произведения и частного функций».
Замечание. Следует не путать константу (то есть, число) как слагаемое в сумме и как постоянный множитель! В случае слагаемого её производная равна нулю, а в случае постоянного множителя она выносится за знак производных. Это типичная ошибка, которая встречается на начальном этапе изучения производных, но по мере решения уже нескольких одно- двухсоставных примеров средний студент этой ошибки уже не делает.
А если при дифференцировании произведения или частного у вас появилось слагаемое u‘v , в котором u — число, например, 2 или 5, то есть константа, то производная этого числа будет равна нулю и, следовательно, всё слагаемое будет равно нулю (такой случай разобран в примере 10).
Другая частая ошибка — механическое решение производной сложной функции как производной простой функции. Поэтому производной сложной функции посвящена отдельная статья. Но сначала будем учиться находить производные простых функций.
По ходу не обойтись без преобразований выражений. Для этого может потребоваться открыть в новых окнах пособия Действия со степенями и корнями и Действия с дробями.
Если Вы ищете решения производных дробей со степенями и корнями, то есть, когда функция имеет вид вроде 
Если же перед Вами задача вроде 
Пошаговые примеры — как найти производную
Пример 3. Найти производную функции

Решение. Определяем части выражения функции: всё выражение представляет произведение, а его сомножители — суммы, во второй из которых одно из слагаемых содержит постоянный множитель. Применяем правило дифференцирования произведения: производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой:
Далее применяем правило дифференцирования суммы: производная алгебраической суммы функций равна алгебраической сумме производных этих функций. В нашем случае в каждой сумме второе слагаемое со знаком минус. В каждой сумме видим и независимую переменную, производная которой равна единице, и константу (число), производная которой равна нулю. Итак, «икс» у нас превращается в единицу, а минус 5 — в ноль. Во втором выражении «икс» умножен на 2, так что двойку умножаем на ту же единицу как производную «икса». Получаем следующие значения производных:
Подставляем найденные производные в сумму произведений и получаем требуемую условием задачи производную всей функции:
А проверить решение задачи на производную можно на калькуляторе производных онлайн.
Пример 4. Найти производную функции
Решение. От нас требуется найти производную частного. Применяем формулу дифференцирования частного: производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя. Получаем:
Производную сомножителей в числителе мы уже нашли в примере 2. Не забудем также, что произведение, являющееся вторым сомножителем в числителе в текущем примере берётся со знаком минус:
Если Вы ищете решения таких задач, в которых надо найти производную функции, где сплошное нагромождение корней и степеней, как, например, 
Если же Вам нужно узнать больше о производных синусов, косинусов, тангенсов и других тригонометрических функций, то есть, когда функция имеет вид вроде 
Пример 5. Найти производную функции
Решение. В данной функции видим произведение, один из сомножителей которых — квадратный корень из независимой переменной, с производной которого мы ознакомились в таблице производных. По правилу дифференцирования произведения и табличному значению производной квадратного корня получаем:
Проверить решение задачи на производную можно на калькуляторе производных онлайн.
Пример 6. Найти производную функции
Решение. В данной функции видим частное, делимое которого — квадратный корень из независимой переменной. По правилу дифференцирования частного, которое мы повторили и применили в примере 4, и табличному значению производной квадратного корня получаем:
Чтобы избавиться от дроби в числителе, умножаем числитель и знаменатель на 
Проверить решение задачи на производную можно на калькуляторе производных онлайн.
Найти производные самостоятельно, а затем посмотреть решения
Пример 7. Найти производную функции

Пример 8. Найти производную функции

Пример 9. Найти производную функции

Пример 10. Найти производную функции

Пример 11. Найти производную функции

Ещё больше домашних заданий на нахождение производных
Продолжаем искать производные вместе
Пример 12. Найти производную функции

Решение. Применяя правила вычисления производной алгебраической суммы функций, вынесения постоянного множителя за знак производной и формулу производной степени (в таблице производных — под номером 3), получим

Пример 13. Найти производную функции
Решение. Применим правило дифференцирования произведения, а затем найдём производные сомножителей, так же, как в предыдущей задаче, пользуясь формулой 3 из таблицы производных. Тогда получим
Пример 14. Найти производную функции
Решение. Как и в примерах 4 и 6, применим правило дифференцирования частного:
Теперь вычислим производные в числителе и перед нами уже требуемый результат:
Пример 15.Найти производную функции
Шаг1. Применяем правило дифференцирования суммы:
Шаг2. Найдём производную первого слагаемого. Это табличная производная квадратного корня (в таблице производных — номер 5):
Шаг3. В частном знаменатель — также корень, только не квадратный. Поэтому преобразуем этот корень в степень:
и далее дифференцируем частное, не забывая, что число 2 в первом слагаемом числителя — это константа, производная которой равна нулю, и, следовательно всё первое слагаемое равно нулю:
Корень из константы, как не трудно догадаться, является также константой, а производная константы, как мы знаем из таблицы производных, равна нулю:

а производная, требуемая в условии задачи:
Ещё больше домашних заданий на нахождение производных
Напоминаем, что чуть более сложные примеры на производную произведения и частного — в статьях «Производная произведения и частного функций» и «Производная суммы дробей со степенями и корнями».
Также настоятельно рекомендуем изучить производную сложной функции.
источники:
http://mathforyou.net/online/calculus/derivative/parametric/
http://function-x.ru/derivative.html
Заказать задачи по любым предметам можно здесь от 10 минут
Найти решение системы дифференциальных уравнений
СОДЕРЖАНИЕ ТЕКУЩЕЙ СТАТЬИ
- Основные понятия
- Метод исключения
-
- Пример 1
- Пример 2
- Пример 3
- Метод Эйлера
-
- Пример 4
Основные понятия
В данной статье рассмотрим линейные системы дифференциальные уравнений, которые делятся на два вида: однородные и неоднородные. В общем виде они записываются следующим образом $$begin{cases} frac{dx}{dt} = a_1 x(t) + b_1 y(t) + f_1(t) \ frac{dy}{dt} = a_2 x(t) + b_2 y(t) + f_2(t) end{cases},$$где $a_1, b_1, c_1, a_2$ коэффициенты, функции $f_1(t)$ и $f_2(t)$ могут отсутствовать, либо быть константами, $x(t),y(t)$ неизвестные функции, которые требуется найти в качестве решения системы ДУ. Напоминаем, что аналогичная запись $frac{dx}{dt} = x'(t)$ и $frac{dy}{dt} = y'(t)$.
Если хотя бы один из коэффициентов $f_1(t)$ или $f_2(t)$ не равен нулю, то система называется неоднородной. Если $f_1(t) = f_2(t) = 0$, то система однородная.
Решением системы дифференциальных уравнений называется пара функций $y(t), x(t)$, подстановка которых в систему обращает её в тождество.
Разберём два основных способа решения линейных систем дифференциальных уравнений: метод исключения и метод Эйлера.
Метод исключения
Суть метода в том, что два уравнения сводятся к одному линейному дифференциальному уравнению. Для этого есть примерный алгоритм:
- Находим производную одного из уравнений системы, например, $y»_t$
- В получившейся производной исключаем всё что связано с $x$
- Решаем линейное дифференциальное уравнение относительно $y(t)$
- Подставляем получившийся $y(t)$ в одно из уравнений системы, чтобы найти $x(t)$
| Пример 1 |
| Решить систему дифференциальных уравнений методом исключения $$begin{cases} frac{dx}{dt} =y-7 \ frac{dy}{dt} = -2x — 3y end{cases}.$$ |
| Решение |
|
Применим метод исключения, чтобы из двух уравнений получить одно. Берем первое уравнение и дифференцируем его по $t$. $$frac{d^2 x}{dt^2} = frac{dy}{dt}$$ В получившееся уравнения вместо $frac{dy}{dt}$ подставим второе уравнение системы. $$frac{d^2 x}{dt^2} = -2x — 3y$$ Теперь нужно избавиться от $y$, чтобы остались только $x$, и тогда можно будет решить дифференциальное уравнение относительно $x(t)$. Для этого берём первое уравнение системы и получаем из него $$y = frac{dx}{dt}+7.$$ Продолжаем решение с учётом полученного $y$ $$frac{d^2 x}{dt^2} = -2x — 3 (frac{dx}{dt}+7).$$ После раскрытия скобок и преобразований получаем уравнение $$frac{d^2 x}{dt^2} + 3frac{dx}{dt} + 2x = 21.$$ Это линейное неоднородное дифференциальное уравнение второго порядка. Решение его будем искать в виде $x_text{о.н.} = x_text{о.о.} + x_text{ч.н.}$. Сначала находим общее решение однородного уравнения $x_text{о.о.}$. Для этого отбрасываем правую часть уравнения и составляем характеристический многочлен и находим его корни. $$lambda^2 + 3lambda + 2 = 0,$$ $$lambda_{1,2} = frac{-3pm sqrt{9-4cdot 1 cdot 2}}{2} = frac{-3pm 1}{2},$$ $$lambda_1 = -1, lambda_2 = -2.$$ Итак, записываем $$x_text{о.о.} = C_1 e^{-t} + C_2 e^{-2t}.$$ Искать частное решение $x_text{ч.н.}$ будем искать методом подбора правой части исходного неоднородного линейного дифференциального уравнения. В данном случае в правой части стоит константа, значит подбор будет в виде $x_text{ч.н.} = A$. Находим первую и вторую производную и подставляем в исходное решаемое уравнение. $$x’_text{ч.н.} = 0, x»_text{ч.н.} = 0$$ $$0 + 3 cdot 0 + 2 A = 21 Rightarrow A = frac{21}{2}.$$ Значит, $x_text{ч.н.} = frac{21}{2}$. Записываем окончательно, что $$x(t) = x_text{о.н.} = x_text{о.о.} + x_text{ч.н.} = C_1 e^{-t} + C_2 e^{-2t} + frac{21}{2}$$ Теперь зная $x(t)$ можно получить $y(t)$. Для этого нужно вернуться к началу решения и вспомнить, что мы выражали $y = frac{dx}{dt}+7$. Таким образом осталось в него подставить полученное решение $x(t)$ $$y(t) = (C_1 e^{-t} + C_2 e^{-2t} + frac{21}{2})’ + 7 = -C_1 e^{-t} — 2C_2 e^{-2t} + 7$$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$begin{cases} x(t) = C_1 e^{-t} + C_2 e^{-2t} + frac{21}{2} \ y(t) = -C_1 e^{-t} — 2C_2 e^{-2t} + 7 end{cases}$$ |
| Пример 2 |
| Найти решение системы дифференциальных уравнений $$begin{cases} x’ = -2y+3t \ y’ = 2x+4 end{cases},$$ где $x(t),y(t)$ — искомые функции, $t$ — независимая переменная. |
| Решение |
|
Решаем методом исключения, то есть два уравнения приводим к одному. Берем производную первого уравнения по $t$. $$x» = (-2y+3t)’_t = -2y’+3$$ Знаем чему равен $y’$ из второго уравнения системы и поэтому его подставляем в получившееся последнее уравнение. $$x» = -2(2x+4)+3 = -4x — 8 + 3 = -4x — 5$$ Переписываем последнее получившееся уравнение в форме линейного неоднородного дифференциального уравнения второго порядка. $$x» + 4x = -5$$ Общее решение этого уравнения найдем в качестве суммы общего решения однородного уравнения и частного решения неоднородного $x_text{о.н.} = x_text{о.о.} + x_text{ч.н.}$. Итак, составляем характеристический многочлен и находим его корни. $$lambda^2 + 4 = 0$$ $$lambda_1 = -2i, lambda_2 = 2i.$$ Так как получились комплексные корни, то общее решение записывается следующим образом $$x_text{о.о.} = C_1cos 2t + C_2 sin 2t.$$ Осталось найти $x_text{ч.н.}$. Для этого воспользуемся методом подбора правой части. Так как она представляет собой константу, то значит $x_text{ч.н.} = A$. Отсюда следует, что $x»_text{ч.н.} = 0$. Подставляя эти данные в дифференциальное уравнение получаем значение $A$. $$0 + 4A = -5,$$ $$A = -frac{5}{4}.$$ Таким образом можно записать, что $$x(t) = x_text{о.о.} + x_text{ч.н.} = C_1cos 2t + C_2 sin 2t -frac{5}{4}.$$ Осталось найти функцию $y(t)$. Для этого выразим её из первого уравнения и подставим ранее полученный $x(t)$. $$y = frac{3}{2}t — frac{x’}{2},$$ $$y = frac{3}{2}t — frac{1}{2}(C_1cos 2t + C_2 sin 2t -frac{5}{4})’ = $$ $$ = frac{3t}{2} + C_1 sin 2t — C_2 cos 2t.$$ |
| Ответ |
| $$begin{cases} x(t) = C_1cos 2t + C_2 sin 2t -frac{5}{4} \ y(t) = frac{3t}{2} + C_1 sin 2t — C_2 cos 2t end{cases}$$ |
| Пример 3 |
| Найти общее и частное решение системы дифференциальных уравнений $$begin{cases} frac{dx}{dt} = 2x+y \ frac{dy}{dt} = x+2y end{cases}, x(0)=1, y(0)=3$$ |
| Решение |
|
Берем второе уравнение и находим его производную по $t$. $$frac{dy^2}{dt^2} = frac{dx}{dt}+2frac{dy}{dt}$$ В полученное равенство вместо frac{dx}{dt} подставим первое уравнение системы. $$frac{dy^2}{dt^2} = 2x+y + 2frac{dy}{dt}$$ Осталось избавиться от $x$. Для этого выразим его из второго уравнения системы и подставим в последнее полученное уравнение. $$frac{dy^2}{dt^2} = 2(frac{dy}{dt} — 2y) + y + 2frac{dy}{dt}$$ Раскроем скобки и перенесем всё в левую сторону. Затем запишем для удобства $frac{dy}{dt} = y’$. $$y» — 4y’ + 3y = 0$$ Получившееся дифференциальное уравнение называется однородным линейным ду второго порядка. Для его решения составляем характеристический многочлен и находим его корни. $$lambda^2 — 4lambda + 3 = 0,$$ $$lambda_{1,2} = frac{4pm sqrt{16 — 4 cdot 1 cdot 3}}{2} = frac{4pm 2}{2},$$ $$lambda_1 = 1, lambda_2 = 3.$$ Общее решение такого уравнения записывается в виде $$y = C_1 e^{3t} + C_2e^{t}.$$ Так как мы нашли $y(t)$, то теперь можем найти $x(t)$. Для этого подставляем $y(t)$ во второе уравнение системы и выражаем $x(t)$. $$x(t) = frac{dy}{dt} — 2y = (C_1 e^{3t} + C_2e^{t})’ — 2(C_1 e^{3t} + C_2e^{t})$$ После раскрытия скобок и упрощения остаётся $$x(t) = 3C_1 e^{3t} + C_2 e^t — 2C_1 e^{3t} — 2C_2 e^t = C_1 e^{3t} — C_2 e^t.$$ Вот таким образом находится общее решение системы дифференциальных уравнений $$begin{cases} x(t) = C_1 e^{3t} — C_2 e^t \ y(t) = C_1 e^{3t} + C_2e^{t} end{cases}.$$ По условию задания необходимо кроме общего найти частное решение. Для этого берем дополнительные условия из задачи $x(0)=1, y(0)=3$ и подставляем в полученное общее решение, чтобы вычислить константы $C_1$ и $C_2$. $$begin{cases} x(0) = C_1e^{0}-C_2e^0 = 1 \ y(0) = C_1 e^0 + C_2 e^0 = 3 end{cases},$$ $$ begin{cases} C_1-C_2 = 1 \ C_1 + C_2 = 3 end{cases} Rightarrow begin{cases} C_1 = 2 \ C_2 = 1 end{cases}.$$ Теперь зная постоянные можно записать частное решение системы дифференциальных уравнений $$begin{cases} x(t) = 2e^{3t} — e^t \ y(t) = 2e^{3t} + e^t end{cases}.$$ |
| Ответ |
| $$begin{cases} x(t) = C_1 e^{3t} — C_2 e^t \ y(t) = C_1 e^{3t} + C_2e^{t} end{cases}, begin{cases} x(t) = 2e^{3t} — e^t \ y(t) = 2e^{3t} + e^t end{cases}$$ |
Метод Эйлера
Примерный алгоритм решения по данному методу следующий:
- Построить матрицу $A$ из коэффициентов дифференциальных уравнений
- Найти собственные значения $lambda$ и векторы матрицы $overline{x}$
- Записать общее решение системы дифференциальных уравнений по формуле $$begin{pmatrix} x(t) \ y(t) end{pmatrix} = C_1 e^{lambda_1 t} overline{x}_1 + C_2 e^{lambda_2 t} overline{x}_2 $$
Рассмотрим данный метод решения на конкретном примере, так как практика учит лучше, чем теория.
| Пример 4 |
| Решить систему дифференциальных уравнений методом эйлера $$begin{cases} x’ = 2x+y \ y’ = 3x+4y end{cases}.$$ |
| Решение |
|
Первым делом нужно составить матрицу, элементы которой равны коэффициентам из правой части системы дифференциальных уравнений. $$A = begin{pmatrix} 2&1 \ 3&4 end{pmatrix}$$ Далее нужно найти собственные значения матрицы. Для этого необходимо составить характеристический многочлен и вычислить его корни. $$|A-lambda E| = 0 Rightarrow begin{vmatrix} 2 — lambda & 1 \ 3 & 4-lambda end{vmatrix} = 0$$ Раскрываем определитель два на два и решаем квадратное уравнение. $$(2-lambda)(4-lambda)-3 = 0,$$ $$8-2lambda -4lambda+lambda^2 — 3 = 0,$$ $$lambda^2 — 6lambda + 5 = 0,$$ $$lambda_{1,2} = frac{6pm sqrt{36-4 cdot 5}}{2} = frac{6pm 4}{2},$$ $$lambda_1 = 1, lambda_2 = 5.$$ Зная собственные значения матрицы получим собственные векторы матрицы по формуле $(A-lambda E)overline{x} = 0$. 1) Для $lambda_1 = 1$ имеем $$(A-lambda_1 E)overline{x}_1 = 0 Rightarrow begin{cases} x_1 + x_2 = 0 \ 3x_1 + 3x_2 = 0 end{cases}$$ Видим, что после сокращения второго уравнения на 3 получится, что первое уравнение равно второму. $$x_1 + x_2 = 0 Rightarrow x_1 = -x_2$$ Так как $x_2$ свободный, то положим его $x_2 = 1$. Тогда $x_1 = -1$. Отсюда следует, что первый собственный вектор равен $$overline{x}_1 = begin{pmatrix} -1 \ 1 end{pmatrix}.$$ 2) Для $lambda_2 = 5$ имеем $$(A-lambda_2 E)overline{x}_2 = 0 Rightarrow begin{cases} -3x_1 + x_2 = 0 \ 3x_1 — x_2 = 0 end{cases}$$ Замечаем, что первое уравнение одно и тоже что второе, если домножить на (-1) одно из них. $$3x_1 — x_2 = 0 Rightarrow x_1 = frac{x_2}{3}$$ Так как $x_2$ свободный, то зададим его $x_2 = 3$. Таким образом $x_1 = 1$. Из этих значений получаем второй собственный вектор $$overline{x}_2 = begin{pmatrix} 1 \ 3 end{pmatrix}.$$ Находим общее решение системы дифференциальных уравнений по формуле $$begin{pmatrix} x(t) \ y(t) end{pmatrix} = C_1 e^{lambda_1 t} overline{x}_1 + C_2 e^{lambda_2 t} overline{x}_2 = $$ $$ = C_1 e^t begin{pmatrix} -1 \ 1 end{pmatrix} + C_2 e^{5t} begin{pmatrix} 1\3 end{pmatrix} = begin{pmatrix} -C_1 e^t \ C_1e^t end{pmatrix} + begin{pmatrix} C_2 e^{5t} \ 3C_2 e^{5t} end{pmatrix} = $$ $$ = begin{pmatrix} -C_1 e^t + C_2 e^{5t} \ C_1 e^t + 3C_2 e^{5t} end{pmatrix} Rightarrow begin{cases} x(t) = -C_1 e^t + C_2 e^{5t} \ y(t) = C_1 e^t + 3C_2 e^{5t} end{cases}$$ |
| Ответ |
| $$begin{cases} x(t) = -C_1 e^t + C_2 e^{5t} \ y(t) = C_1 e^t + 3C_2 e^{5t} end{cases}$$ |
Мы ограничимся здесь рассмотрением систем дифференциальных уравнений первого порядка с двумя и тремя неизвестными функциями. Переход к общему случаю не представляет каких-либо принципиальных затруднений.
Определение 1. Нормальная система двух дифференциальных уравнений называется линейной системой первого порядка, если она имеет вид

Определение 2. Линейная система дифференциальных уравнений (1) называется однородной, если
В дальнейшем обратимся лишь к частному случаю – однородной линейной системе с постоянными коэффициентами.
Решением системы (1) называется всякий набор из двух функций
, (2)
Обращающих оба уравнения системы (1) в тождество.
Задача Коши для системы (1) состоит в том, чтобы найти такое решение (2), которое при принимало бы заданные значения (начальные условия)
Общее решение системы содержит две произвольные постоянные и
, фиксируя которые, находят любое частное решение.
Геометрически решение (2) определяет некоторую линию ( интегральную кривую системы) на плоскости . Если считать, что аргумент
играет роль времени, то указанная кривая будет служить траекторией точки, движущейся на плоскости
.
Тат как в этом случае определяет вектор скорости, то с механической точки зрения система (1) означает задание поля скоростей в каждый момент времени
, а решение задачи Коши равносильно нахождению траектории точки, движущейся под воздействием этого поля и занимавшей в начальный момент времени
положение
. Плоскость
, на которой рассматривается движение называется Фазовой.
Нормальная система трех уравнений первого порядка имеет вид:
(3)
Все основные понятия и определения, сказанные выше для системы двух уравнений, повторяются и для системы (3) с той лишь разницей, что добавляется везде третья функция , а вместо фазовой плоскости надо рассматривать фазовое пространство
.
Для решения системы дифференциальных уравнений может быть использован обычный метод исключения неизвестных, сводящий систему (1) к одному дифференциальному уравнению от неизвестной функции второго порядка, а систему (3) – к дифференциальному уравнению третьего порядка. Если метод исключения применяется к линейной системе, то получается также линейное дифференциальное уравнение, к решению которого можно применять выше рассмотренные методы.
Пример. Решить задачу Коши для линейной системы
Решение. Запишем систему в виде
И, применяя метод исключения, выразим из первого уравнения через
и
:
После подстановки
во второе уравнение будем иметь ( при
):
Получили неоднородное дифференциальное уравнение с постоянными коэффициентами второго порядка. Используя метод решения такого вида уравнений, рассмотренный выше, получим его общее решение
А так как было выражено через
, то вычисляя производную
и подставив
выражение
Получим общее решение данной системы
.
Теперь обратимся к начальным условиям, используя которые, определим постоянные и
.
Так как , то при
имеем
И так как ,
, следовательно,
Получим систему
Таким образом, решением данной задачи Коши являются функции
Пример. Проинтегрировать систему уравнений
Или
Решение. Из первого уравнения данной системы находим и подставим его производную
во второе уравнение системы, тогда получим
.
Уравнение второго порядка неоднородное с постоянными коэффициентами. Для решения этого уравнения воспользуемся методом решения для этого вида уравнения, рассмотренным выше.
Общее решение уравнения будет функция
.
Так как , то, вычислив производную
, подставим ее выражение в это равенство
.
Общее решение системы
.
Пример. Найти общее решение системы

Где — неизвестные функции.
Решение. Исключим из этих уравнений; для этого из третьего уравнения найдем
.
Продифференцируем полученное равенство по :
, подставив значения
и
в первое уравнение, найдем из него
, следовательно,
.
Подставив значения во второе уравнение системы, будем иметь
или
.
Получили линейное однородное дифференциальное уравнение третьего порядка. Составим характеристическое уравнение и найдем его корни
Следовательно, — общее решение уравнения будет
.
Чтобы определить неизвестные функции и
, найдем
и
из последнего равенства:
,
Откуда
.
Общим решением данной системы будет система функций
.
Для интегрирования однородных линейных систем с постоянными коэффициентами применяется также Метод Эйлера.
Пусть дана однородная линейная система дифференциальных уравнений

Где .
Определение. Линейной комбинацией вектор-функций и
на интервале
называется вектор-функция
.
Теорема. Пусть вектор-функция
Решения на однородной системы (4). Тогда любая их комбинация
также есть решение на
этой системы.
Рассмотрим на конкретном примере метод Эйлера.
Пример. Решить систему

Решение. Искомыми функциями являются функции .
Составим характеристический многочлен для данной системы
.
Находим корни характеристического уравнения
Составим для вспомогательную алгебрагическую систему
:
Получили систему, имеющую бесчисленное множество решений. Выразим через
:
и пусть
, тогда
. Тогда вектор-функция
— это первое фундаментальное решение.
Составим вспомогательную алгебрагическую систему для
:
Получили систему с бесчисленным множеством решений; выразим через
:
и пусть
, тогда
.
Тогда вектор-функция — второе фундаментальное решение.
Итак, фундаментальная система решений состоит из двух вектор-функций
.
Следовательно, вся совокупность решений системы есть множество
| < Предыдущая |
|---|
Сообщения без ответов | Активные темы
Найти производную функции для системы уравнений
Модераторы: Prokop, mad_math
| Автор | Сообщение | ||
|---|---|---|---|
|
avg2010 |
Заголовок сообщения: Найти производную функции для системы уравнений
|
||
|
Прошу помочь с нахождением производной y'(x) для системы уравнений: [math]begin{cases}x=ln3t+t+3,\y=t^2+2t+3end{cases}[/math]
|
||
| Вернуться к началу |
|
||
|
avg2010 |
Заголовок сообщения: Re: Найти производную функции для системы уравнений
|
|
Т.е. речь о производной сложной функции, типа [math]frac{dy}{dx}=frac{dy}{dt}*frac{dt}{dx}[/math] или я что-то напутал и достаточно взять производную как в вашем примере (в обоих уравнениях по переменной t)
|
|
| Вернуться к началу |
|
|
avg2010 |
Заголовок сообщения: Re: Найти производную функции для системы уравнений
|
|
Всем огромное спасибо за подробные разъяснения, в частности Alexdemath за полное решение. Со времен ВУЗа полностью доверил все расчеты Mathсad, а ему подобные системки не по душе (видимо причина в вычислении ln), вот и вогнал меня в ступор) Теперь знаю куда можно обратиться с подобными вопросами.
|
|
| Вернуться к началу |
|
| Похожие темы | Автор | Ответы | Просмотры | Последнее сообщение |
|---|---|---|---|---|
|
Найти производную функции для системы уравнений
в форуме Дифференциальное исчисление |
celviano |
5 |
475 |
28 фев 2016, 22:42 |
|
Найти частную производную через матрицу Якоби для системы
в форуме Пределы числовых последовательностей и функций, Исследования функций |
ramil1999 |
0 |
133 |
25 окт 2018, 04:42 |
|
Найти ФСР однородной системы уравнений
в форуме Линейная и Абстрактная алгебра |
f0rt1q |
2 |
602 |
17 ноя 2013, 13:56 |
|
Найти векторы x и y из системы уравнений
в форуме Линейная и Абстрактная алгебра |
Vlad_ok |
9 |
525 |
04 фев 2021, 21:40 |
|
Найти вектор из системы уравнений
в форуме Векторный анализ и Теория поля |
slava_psk |
8 |
393 |
09 дек 2021, 13:40 |
|
Найти частные решения системы уравнений
в форуме Комплексный анализ и Операционное исчисление |
Nevermind_qqq |
1 |
463 |
13 июн 2013, 00:42 |
|
Найти частичные решения системы диф. уравнений
в форуме Комплексный анализ и Операционное исчисление |
offering |
2 |
387 |
18 ноя 2013, 18:28 |
|
Найти общее решение системы уравнений
в форуме Линейная и Абстрактная алгебра |
Pabel |
3 |
415 |
09 ноя 2013, 13:53 |
|
Найти другое решение системы уравнений
в форуме Алгебра |
Petja234 |
12 |
677 |
17 май 2021, 17:01 |
|
Найти общее решение системы уравнений
в форуме Дифференциальные и Интегральные уравнения |
maxyland |
3 |
430 |
30 ноя 2013, 15:07 |
Кто сейчас на конференции |
|
Сейчас этот форум просматривают: нет зарегистрированных пользователей и гости: 3 |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
Powered by phpBB © 2000, 2002, 2005, 2007 phpBB Group
Вы можете создать форум бесплатно PHPBB3 на Getbb.Ru, Также возможно сделать готовый форум PHPBB2 на Mybb2.ru
Русская поддержка phpBB
ЛЕКЦИЯ 7
Система
дифференциальных уравнений
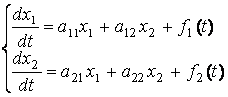
где — искомые
функции от t; — постоянные
числа; —
заданные
функции, называется системой
линейных дифференциальных уравнений
с постоянными коэффициентами второго
порядка.
Такую
систему методом исключения можно
привести к одному линейному урав-нению
не выше второго порядка. Решение этой
задачи рассмотрим на примерах.
Пример
1 
Дифференцируем
первое уравнение по t : 
Подставляем сюда из
системы уравнений производные :

первого уравне-ния системы , тогда

. Т
.о., 
линейное уравнение; решая его
известным способом, найдем ; далее,
находим
из со-отношения
. Общее
решение системы :

Решим
задачу Коши с начальными данными
: .
.

|
|
|
Нормальная записывается
где xi (t) − которые заданные Используя
где
В так имеет |
Привести
к каноническому виду систему
дифференциальных уравнений
Решение. Данная
система имеет третий порядок, так
как и,
значит, .
Разрешая первое уравнение относительно ,
а второе относительно ,
получим каноническую систему
Система
обыкновенных дифференциальных уравнений
первого порядка вида
|
(3) |
где —
независимая переменная; —
неизвестные функции от ,
называется нормальной
системой.
Число называется порядком
нормальной системы (3).
Две системы дифференциальных уравнений
называются эквивалентными,
если они обладают одними и теми же
решениями.
Любую
каноническую систему (2) можно привести
к эквивалентной ей нормальной системе
(3), причем порядок этих систем будет
одним и тем же.
Задачей
Коши для системы (3)
называется задача нахождения решения
этой
системы, удовлетворяющего начальным
условиям
|
(4) |
где —
заданные числа.
Теорема
существования и единственности решения
задачи Коши.
Пусть
имеем нормальную систему дифференциальных
уравнений (3) и пусть функции
,
определены в некоторой n+1-мерной
области изменения
переменных .
Если существует окрестность точки
,
в которой функции а)
непрерывны, 6) имеют ограниченные частные
производные по переменным ,
то найдется интервал изменения
,
в котором существует единственное
решение нормальной системы (3),
удовлетворяющее начальным условиям
(4).
Система дифференцируемых
функций
|
(5) |
независимой
переменной и
произвольных
постоянных называется
общим решением нормальной системы (3),
если: 1) при любых допустимых
значениях система
функций (5) обращает уравнения (3) в
тождества, 2) в области, где выполняются
условия теоремы Коши, функции (5) решают
любую задачу Коши.
Частным
случаем канонической системы
дифференциальных уравнений является
одно уравнение n-го порядка, разрешенное
относительно старшей производной.
Введением
новых функций
это
уравнение заменяется нормальной
системой уравнений
Можно
утверждать и обратное, что, вообще
говоря, нормальная система уравнений
первого порядка эквивалентна
одному уравнению порядка .
На этом основан один из методов
интегрирования систем дифференциальных
уравнений — метод
исключения.
Проиллюстрируем
этот метод на примере системы двух
уравнений:
|
(1) |
Здесь —
постоянные коэффициенты, а и
—
заданные функции; и
—
искомые функции. Из первого уравнения
системы (1) находим
|
(2) |
Подставляя
во второе уравнение системы вместо у
правую часть (2), а вместо производную
от правой части (2), получаем уравнение
at второго порядка относительно
где —
постоянные. Отсюда находим .
Подставив найденное выражение для и
в
(2), найдем .
Нормальная
линейная система дифференциальных
уравнений с постоянными коэффициентами
n-го порядказаписывается
в виде
где x1(t), x2(t),
…, xn(t) −
неизвестные функции переменной t,
которая часто имеет смысл времени,aij −
заданные постоянные
коэффициенты, которые могут быть как
действительными, так и комплексными,fi (t) −
заданные (в общем случае комплексные)
функции переменной t.
Будем
считать, что все указанные функции
являются непрерывными на некотором
интервале [a,
b]действительной
числовой оси t.
Полагая
систему
дифференциальных уравнений можно
переписать в матричной форме:
Если
вектор f(t) тождественно
равен нулю: ,
то система называется однородной:
Однородные
системы уравнений с постоянными
коэффициентами можно
решать различными способами. Чаще всего
используются следующие методы решений:
-
метод
исключения (метод сведения
системы n уравнений
к одному уравнению n-го
порядка);
-
метод
интегрируемых комбинаций;
-
метод
собственных значений и собственных
векторов (включая метод
неопределенных коэффициентов или использование
жордановой формы в
случае кратных корней характеристического
уравнения);
-
метод
матричной экспоненты.
Ниже
на данной странице мы обсудим детально метод
исключения.
Другие способы решения систем уравнений
рассматриваются отдельно на соответствующих
страницах.
Метод
исключения
Используя
метод исключения, нормальную линейную
систему n уравнений
можно привести к одному линейному
уравнению n-го
порядка. Этот метод удобно использовать
для решения простых систем − прежде
всего, для систем 2-го порядка.
Рассмотрим
однородную систему двух уравнений с
постоянными коэффициентами:
где
функции x1, x2 зависят
от переменной t.
Продифференцируем
первое уравнение и подставим
производную x2‘ из
второго уравнения:
Из
первого уравнения подставим a12x2.
Получаем линейное
однородное уравнение 2-го порядка:
Его
решение легко построить, если известны
корни характеристического уравнения:
В
случае действительных коэффициентов aij корни
могут быть как действительными (различными
или кратными), так и комплексными. В
частности, если коэффициенты a12 и a21 одного
знака, то дискриминант характеристического
уравнения всегда будет положительным
и, соответственно, корни будут
действительными и различными.
После
определения функции x1(t) другую
функцию x2(t) можно
найти из первого уравнения системы.
Метод
исключения можно применять не только
к однородным линейным системам. Его
можно использовать также для решения
неоднородных систем дифференциальных
уравнений или систем уравнений с
переменными коэффициентами.
Собственные
векторы и собственные значения
Пусть
A – матрица некоторого линейного
преобразования порядка
n.
Определение. Многочлен
n-ой степени
P()=det(A-Е) (1.1)
называется характеристическим
многочленом матрицы
А, а его корни, которые могут быть как
действительными, так и комплексными,
называются характеристическими
корнями этой
матрицы.
Определение. Ненулевой
вектор x линейного пространства V,
удовлетворяющий условию
А(х)=х, (1.2)
называется собственным
вектором преобразования A.
Число называется собственным
значением.
Замечание. Если
в пространстве V задан базис, то это
условие можно переписать следующим
образом:
Ах=х, (1.3)
где
A – матрица преобразования, x – координатный
столбец.
Определение. Алгебраической
кратностью собственного
значения jназывается
кратность корня j характеристического
многочлена.
Определение. Совокупность
всех собственных значений называетсяспектром
матрицы.
Алгоритм
нахождения собственных значений и
собственных векторов
-
Найти
собственные значения матрицы:
-
записать характеристическое
уравнение:
det(A-Е)=0; (1.4)
-
найти
его корни j,
j=1,…,n и их кратности.
Найти
собственные векторы матрицы:
-
для
каждого j решить
уравнение
(A- jE)x=0; (1.5)
-
найденный
вектор х и
будет собственным вектором, отвечающим
собственному значению j.
Линейная
однородная система дифференциальных
уравнений с постоянными коэффициентами
В
векторной форме:
dY/dx = AY,
где
Характеристическое
уравнение
или .
Соседние файлы в папке HaoZip RAR Архив_1
- #
- #
- #
- #
- #
- #
- #
- #