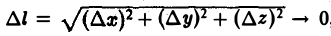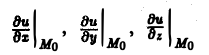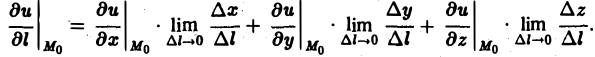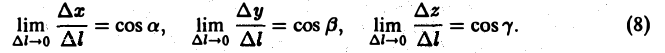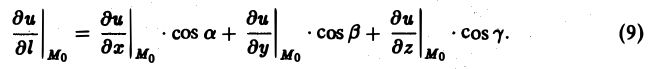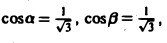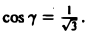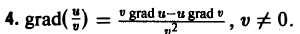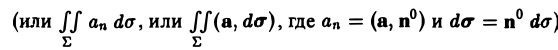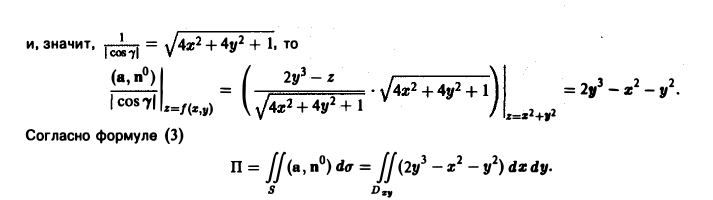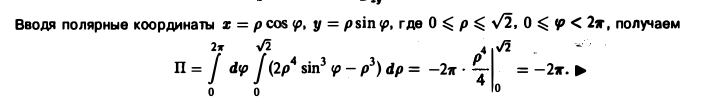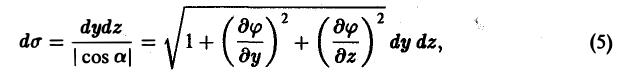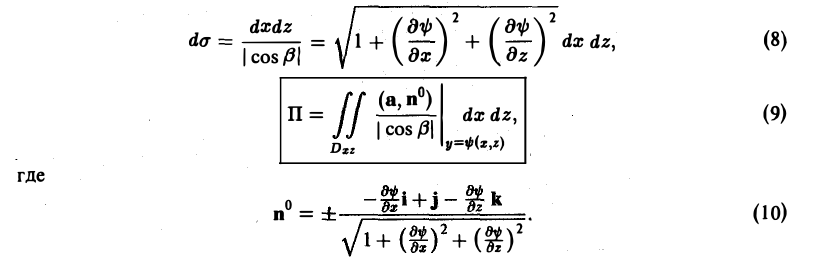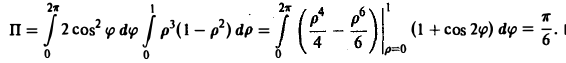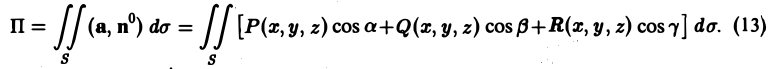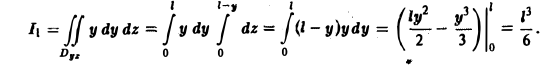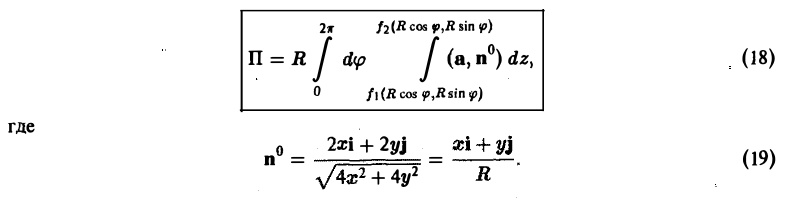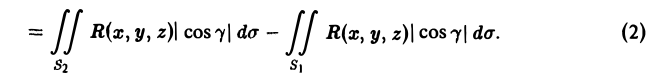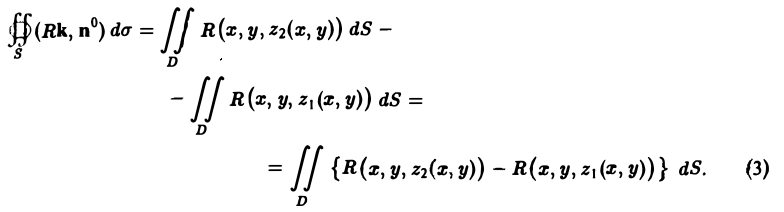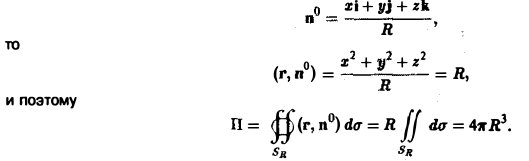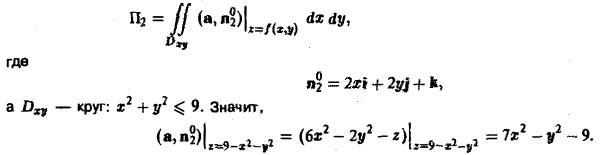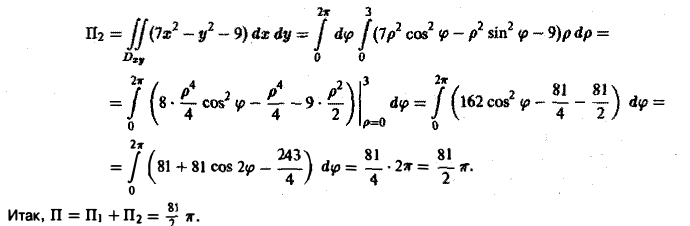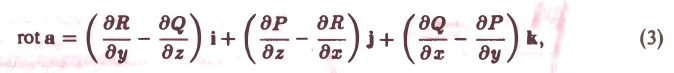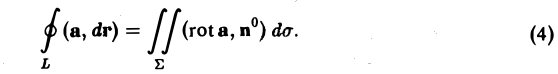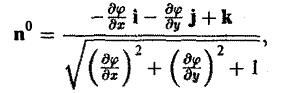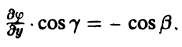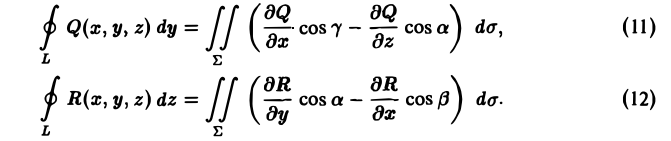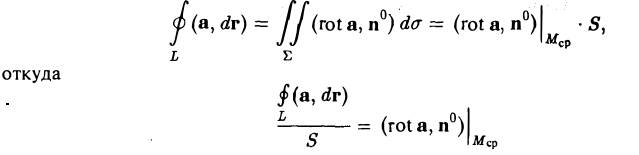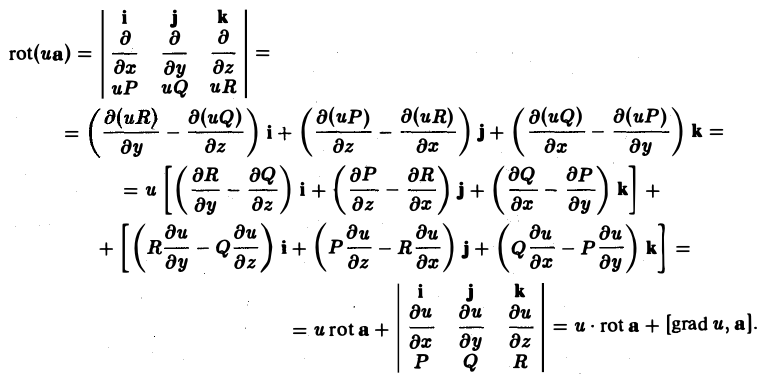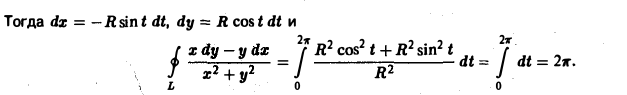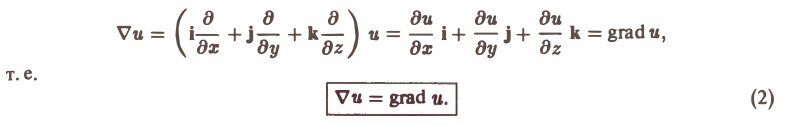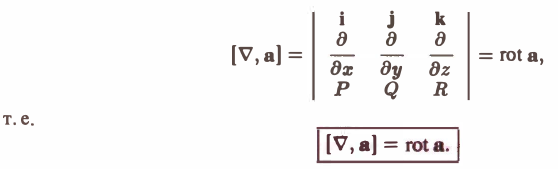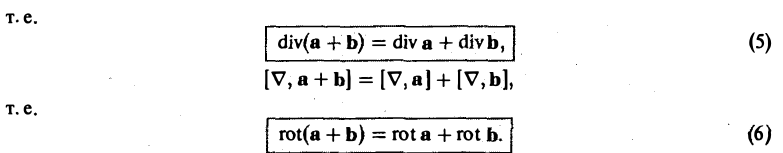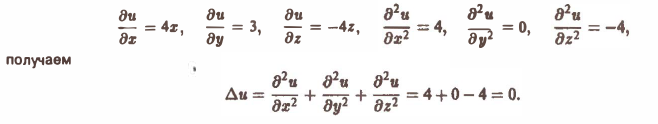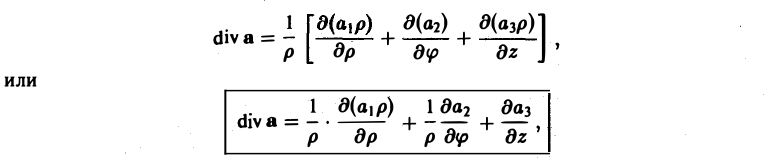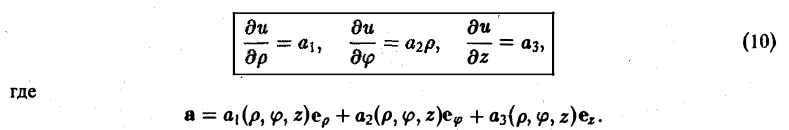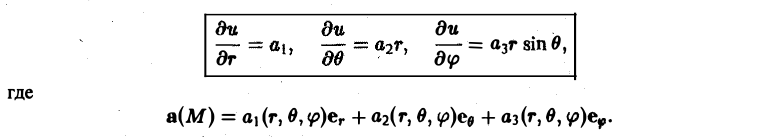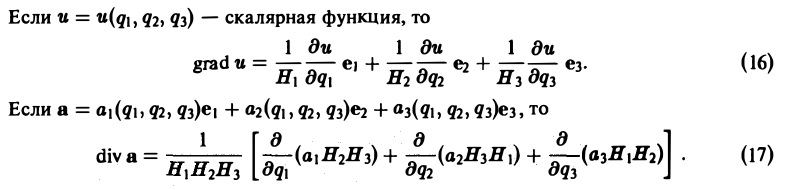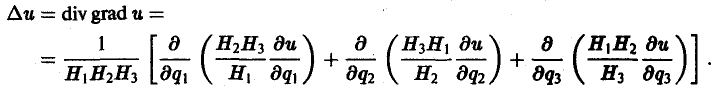1. Учимся искать производные#
Когда мы работаем с одномерными функциями, для поиска любых производных нам хватает небольшой таблицы со стандартными случаями и пары правил. Для случая матриц все эти правила можно обобщить, а таблицы дополнить специфическими функциями вроде определителя.
Удобнее всего оказывается работать в терминах «дифференциала» — с ним можно не задумываться о промежуточных размерностях, а просто применять стандартные правила.
Мы будем работать в этом конспекте со скалярами, векторами и матрицами. Нас будет интересовать, что именно мы дифференцируем, по чему мы дифференцируем и что получается в итоге.
Строчными буквами мы будем обозначать векторы-столбцы и константы. Заглавными буквами мы будем обозначать матрицы. Производная столбца — это столбец. Производная по столбцу — это столбец.
[begin{split}
x = begin{pmatrix}x_1 \ ldots \ x_n end{pmatrix} qquad X = begin{pmatrix}x_{11} & ldots & x_{1n} \ ldots & ddots & ldots \ x_{n1} & ldots & x_{nn} end{pmatrix}.
end{split}]
Мы рассмотрим постепенно много разных входов и выходов, и получим таблицу из канонических случаев. По строчкам будем откладывать то, откуда бьёт функция, то есть входы. По столбцам будем откладывать то, куда бьёт функция, то есть выходы. Для ситуаций обозначенных прочерками обобщения получить не выйдет.
|
скаляр |
вектор |
матрица |
|
|---|---|---|---|
|
скаляр |
(f'(x) dx) |
(mathfrak{J} dx) |
– |
|
вектор |
(nabla_x f(x)^T dx) |
(mathfrak{J} dx) |
– |
|
матрица |
(tr(nabla_X f(X)^T dX)) |
– |
– |
Символом (nabla_x f) обозначается градиент (вектор из производных). Символом (mathfrak{J}) обозначена матрица Якоби. Символом (H) мы будем обозначать матрицу Гессе из вторых производных.
Найдём производную и дифференциал функции (f(x) = x^2), где (x) скаляр. Функция бьёт из скаляров в скаляры
[
f(x) : mathbb{R} to mathbb{R}.
]
Примером такой функции может быть (f(x) = x^2). Мы знаем, что по таблице производных (f'(x) = 2x). Также мы знаем, что дифференциал – это линейная часть приращения функции, а производная – это предел отношения приращения функции к приращению аргумента при приращении аргумента стремящемся к нулю.
Грубо говоря, дифференциал помогает представить приращение функции в линейном виде
[
d{f(x)} = f'(x) dx.
]
Если мы находимся в какой-то точке (x_0) и делаем из неё небольшое приращение (dx,) то наша функция изменится примерно на (df(x)). Оказывается, что именно в терминах дифференциалов удобно работать с матричными производными.
Свойства матричных дифференциалов очень похожи на свойства обычных. Надо только не забыть, что мы работаем с матрицами.
[begin{equation*}
begin{aligned}
& d{(XY)} = d{X}Y + X cdot d{Y}, quad d{X} cdot Y ne Y cdot d{X} \
& d{(alpha X + beta Y)} = alpha d{X} + beta d{Y} \
& d{(X^T)} = (d{X})^T \
& d{A} = 0, quad A — text{матрица из констант}
end{aligned}
end{equation*}]
Чтобы доказать все эти свойства достаточно просто аккуратно расписать их. Кроме этих правил нам понадобится пара трюков по работе со скалярами. Если (s) — скаляр размера (1 times 1), тогда (s^T = s) и (tr(s) = s), где (tr) — операция взятия следа матрицы.
С помощью этих преобразований мы будем приводить дифференциалы к каноническому виду и вытаскивать из них производные.
а) Найдите производную (nabla_x f(x)), где (f(x) = a^T x), где (a) и (x) векторы размера (1 times n)
Рассмотрим вторую ситуацию из таблицы, функция бьёт из векторов в скаляры. Это обычная функция от нескольких аргументов
[
f(x) : mathbb{R}^n to mathbb{R}.
]
Мы уже умеем брать такие производные. Если мы хотим найти производную функции (f(x_1, x_2, ldots, x_n)), нам надо взять производную по каждому аргументу и записать их все в виде вектора. Такой вектор называют градиентом.
[begin{split}
nabla_x f(x) = begin{pmatrix} frac{partial f(x)}{partial x_1} \ frac{partial f(x)}{partial x_2} \ ldots \ frac{partial f(x)}{partial x_n} end{pmatrix}
end{split}]
Если умножить градиент на вектор приращений, у нас получится дифференциал
[begin{multline*}
d{f(x)} = nabla_x f(x)^T dx = begin{pmatrix} frac{partial f(x)}{partial x_1} & frac{partial f(x)}{partial x_2} & ldots & frac{partial f(x)}{partial x_n} end{pmatrix} begin{pmatrix} dx_1 \ dx_2 \ ldots \ dx_n end{pmatrix} = \ = frac{partial f(x)}{partial x_1} cdot dx_1 + frac{partial f(x)}{partial x_2} cdot dx_2 + ldots +frac{partial f(x)}{partial x_n} cdot dx_n.
end{multline*}]
При маленьком изменении (x_i) на (dx_i) функция будет при прочих равных меняться пропорционально соответствующей частной производной. Посмотрим на конкретный пример, скалярное произведение. Можно расписать умножение одного вектора на другой в виде привычной нам формулы
[begin{equation*}
underset{[1 times 1]}{f(x)} = underset{[1 times n]}{a^T} cdot underset{[n times 1]}{x} = begin{pmatrix} a_1 & a_2 & ldots &a_n end{pmatrix} cdot begin{pmatrix} x_1 \ x_2 \ ldots \ x_n end{pmatrix} = a_1 cdot x_1 + a_2 cdot x_2 + ldots + a_n cdot x_n.
end{equation*}]
Из неё чётко видно, что (frac{partial f(x)}{partial x_i} = a_i). Увидев это мы можем выписать градиент функции
[begin{split}
nabla_x f(x) = begin{pmatrix} frac{partial f(x)}{partial x_1} \ frac{partial f(x)}{partial x_2} \ ldots \ frac{partial f(x)}{partial x_n} end{pmatrix} = begin{pmatrix} a_1 \ a_2 \ ldots \ a_n end{pmatrix} = a,
end{split}]
теперь можно записать дифференциал
[begin{multline*}
df(x) = a^T dx = frac{partial f(x)}{partial x_1} cdot dx_1 + frac{partial f(x)}{partial x_2} cdot dx_2 + ldots +frac{partial f(x)}{partial x_n} cdot dx_n = \ = a_1 cdot dx_1 + a_2 cdot dx_2 + ldots + a_n cdot dx_n.
end{multline*}]
В то же самое время можно было бы просто воспользоваться правилами нахождения матричных дифференциалов
[
df(x) = dx{a^T x} = a^T dx = nabla f(x)^T dx,
]
откуда ( nabla_x f(x) = a). Производная найдена. При таком подходе нам не надо анализировать каждую частную производную по отдельности. Мы находим одним умелым движением руки сразу же все производные.
б) Найдите первую и вторую производные функции (f(x) = x^T A x), где (x) вектор размера (1 times n), (A) матрица размера (n times n)
Функция по-прежнему бьёт из векторов в скаляры. Попробуем перемножить все матрицы и расписать её в явном виде по аналогии со скалярным произведением
[begin{equation*}
underset{[1 times 1]}{f(x)} = underset{[1 times n]}{x^T} cdot underset{[n times n]}{A} cdot underset{[n times 1]}{x} = sum_{i = 1}^n sum_{j=1}^n a_{ij} cdot x_i cdot x_j.
end{equation*}]
Если продолжить в том же духе, мы сможем найти все частные производные, а потом назад вернём их в матрицу. Единственное, что смущает – мы делаем что-то неестественное. Всё было записано в красивом компактном матричном виде, а мы это испортили. А что, если множителей будет больше? Тогда суммы станут совсем громоздкими, и мы легко запутаемся.
При этом, если воспользоваться тут правилами работы с матричными дифференциалами, мы легко получим красивый результат
[
df(x) = d{x^T A x} = d(x^T) cdot A cdot x + x^T cdot d(Ax) = d(x^T) cdot A cdot x + x^T underset{d{A} = 0}{d{(A)}} x + x^T A dx(x).
]
Заметим, что (d(x^T) A x) это скаляр. Мы перемножаем матрицы с размерностями (1 times n), (n times n) и (n times 1). В результате получается размерность (1 times 1). Мы можем смело транспонировать скаляр, когда нам это надо. Эта операция никак не повлияет на результат
[
df(x) = d(x^T) A x + x^T A dx = x^T A^T dx + x^T A dx = x^T(A^T + A) dx.
]
Мы нашли матричный дифференциал и свели его к каноничной форме
[
df(x) = nabla^T_x f dx = x^T(A^T + A) dx
]
Получается, что искомая производная (nabla_x f(x) = (A + A^T) x). Обратите внимание, что размерности не нарушены и мы получили столбец из производных, то есть искомый градиент нашей функции (f(x)).
По аналогии мы легко можем найти вторую производную. Для этого надо взять производную производной. Функция (g(x) = (A + A^T) x) бьёт из векторов в вектора
[
f(x) : mathbb{R}^n to mathbb{R}^m.
]
На самом деле с такой ситуацией мы также знакомились на математическом анализе. Если (n=1) то у нас есть (m) функций, каждая из которых применяется к (x). На выходе получается вектор
[begin{split}
begin{pmatrix} f_1(x) \ f_2(x) \ ldots \ f_m(x). end{pmatrix}
end{split}]
Если мы хотим найти производную, нужно взять частную производную каждой функции по (x) и записать в виде вектора. Дифференциал также будет представлять из себя вектор, так как при приращении аргумента на какую-то величину изменяется каждая из функций
[begin{split}
df(x) = begin{pmatrix} frac{partial f_1}{partial x} \ frac{partial f_2}{partial x} \ ldots \ frac{partial f_m}{partial x} end{pmatrix} cdot begin{pmatrix} dx \ dx \ ldots \ dx end{pmatrix} = begin{pmatrix} frac{partial f_1}{partial x} dx \ frac{partial f_2}{partial x} dx \ ldots \ frac{partial f_m}{partial x} dx end{pmatrix}.
end{split}]
Если (n > 1), то аргументов на вход в такой вектор из функций идёт несколько, на выходе получается матрица
[begin{split}
begin{pmatrix} f_1(x_1) & f_1(x_2) & ldots & f_1(x_n) \ f_2(x_1) & f_2(x_2) & ldots & f_2(x_n) \ ldots & ldots & ddots & ldots \ f_m(x_1) & f_m(x_2) & ldots & f_m(x_n) end{pmatrix}
end{split}]
Производной такой многомерной функции будет матрица из частных производных каждой функции по каждому аргументу
[begin{split}
begin{pmatrix} frac{partial f_1}{partial x_1} & frac{partial f_1}{partial x_2} & ldots & frac{partial f_1}{partial x_n} \ frac{partial f_2}{partial x_1} & frac{partial f_2}{partial x_2} & ldots & frac{partial f_2}{partial x_n} \ ldots & ldots & ddots & ldots \ frac{partial f_m}{partial x_1} & frac{partial f_m}{partial x_2} & ldots & frac{partial f_m}{partial x_n} end{pmatrix}.
end{split}]
Дифференциал снова будет представлять из себя вектор
[begin{split}
df(x) = begin{pmatrix} frac{partial f_1}{partial x_1} & frac{partial f_1}{partial x_2} & ldots & frac{partial f_1}{partial x_n} \ frac{partial f_2}{partial x_1} & frac{partial f_2}{partial x_2} & ldots & frac{partial f_2}{partial x_n} \ ldots & ldots & ddots & ldots \ frac{partial f_m}{partial x_1} & frac{partial f_m}{partial x_2} & ldots & frac{partial f_m}{partial x_n} end{pmatrix} cdot begin{pmatrix} dx_1 \ dx_2 \ ldots \ dx_n end{pmatrix} = begin{pmatrix} frac{partial f_1}{partial x_1} dx_1 + frac{partial f_1}{partial x_2} dx_2 + ldots + frac{partial f_1}{partial x_n} dx_n \ frac{partial f_2}{partial x_1} dx_1 + frac{partial f_2}{partial x_2} dx_2 + ldots + frac{partial f_2}{partial x_n} dx_n \ ldots \ frac{partial f_m}{partial x_1} dx_1 + frac{partial f_m}{partial x_2} dx_2 + ldots + frac{partial f_m}{partial x_n} dx_n end{pmatrix}.
end{split}]
В обоих ситуациях мы можем записать дифференциал через матричное произведение. Вернёмся к поиску второй производной
[
dg(x) = (A + A^T) dx.
]
Выходит, что матрица из вторых производных для функции (f(x)) выглядит как (A + A^T.) Обратите внимание, что для этой ситуации в каноническом виде нет транспонирования. Когда мы вытаскиваем из записи дифференциала производную, нам не надо его применять.
в) Найдите производную (nabla_x f(x)), где (f(x) = ln(x^T A x)), где (x) вектор размера (1 times n), (A) матрица размера (n times n)
Когда мы хотим найти производную (f(x) = ln(x^T A x)), мы просто можем применить правила взятия производной от сложной функции (f(y) = ln(y).) К логарифму на вход идет скаляр, а значит его производная равна (frac{1}{y}). Выходит, что
[
df(x) = dln(y) = frac{1}{y} dy = frac{1}{y} d(x^T A x) = frac{1}{x^T A x} cdot x^T(A^T + A) dx.
]
Если отображение бьёт в матрицы или вектора, производная будет браться аналогичным образом. Надо будет чуть аккуратнее следить за размерностями. На такой кейс мы посмотрим немного позже.
г) Найдите производную (f(x) = a^TXAXa), где (x) вектор размера (1 times n), (A) матрица размера (n times n)
Движемся к следующей ситуации. Функция бьёт из матриц в скаляры
[
f(X) : mathbb{R}^{n times k} to mathbb{R}.
]
В таком случае нам надо найти производную функции по каждому элементу матрицы, то есть дифференциал будет выглядеть как
[
d{f(X)} = f’_{x_{11}} dx_{11} + f’_{x_{12}} dx_{12} + ldots + f’_{x_{nk}} dx_{nk}.
]
Его можно записать в компактном виде через след матрицы как
[
df(X) = tr(nabla f(X)^T dX),
]
где
[begin{split}
nabla_X f(X) = begin{pmatrix} f’_{x_{11}} & ldots & f’_{x_{1k}} \
ldots & ddots & ldots \
f’_{x_{n1}} & ldots & f’_{x_{nk}}
end{pmatrix}
end{split}]
Вполне естественен вопрос, почему это можно записать именно так? Давайте попробуем увидеть этот факт на каком-нибудь простом примере. Пусть у нас есть две матрицы
[begin{split}
A_{[2 times 3]} = begin{pmatrix} a_{11} & a_{12} & a_{13} \ a_{21} & a_{22} & a_{23} end{pmatrix} qquad X_{[2 times 3]} = begin{pmatrix} x_{11} & x_{12} & x_{13} \ x_{21} & x_{22} & x_{23} end{pmatrix}.
end{split}]
Посмотрим на то, как выглядит (tr(A^T dX)). Как это не странно, он совпадает с дифференциалом
[begin{split}
tr(A^T dX) = tr left( begin{pmatrix} a_{11} & a_{21} \ a_{12} & a_{22} \ a_{13} & a_{23} end{pmatrix} begin{pmatrix} dx_{11} & dx_{12} & dx_{13} \ dx_{21} & dx_{22} & dx_{23} end{pmatrix} right),
end{split}]
при произведении на выходе получаем матрицу размера (3 times 3)
[begin{split}
begin{pmatrix} a_{11} dx_{11} + a_{21} dx_{21} & a_{11} dx_{12} + a_{21} dx_{22} & a_{11} dx_{13} + a_{21} dx_{23} \ a_{12} dx_{11} + a_{22} dx_{21} & a_{12} dx_{12} + a_{22} dx_{22} & a_{12} dx_{13} + a_{22} dx_{23} \ a_{13} dx_{11} + a_{23} dx_{21} & a_{13} dx_{12} + a_{23} dx_{22} & a_{13} dx_{13} + a_{23} dx_{23} end{pmatrix}.
end{split}]
Когда мы берём её след, остаётся сумма элементов по диагонали. Это и есть требуемый дифференциал. Дальше мы периодически будем пользоваться таким приёмом. Например, норму Фробениуса
[
||X-A||_F^2 = sum_{i,j} (x_{ij} — a_{ij})^2
]
можно записать в матричном виде как
[
||X-A||_F^2 = tr((X-A)^T (X-A)).
]
Итак, найдём производную от (f(X) = a^TXAXa). Нам нужно выписать дифференциал и привести его к каноническому виду
Обратим внимание на то, что мы бьём из матриц в скаляры. Дифференциал будет по своей размерности совпадать со скаляром. Производная будет размера матрицы
[
df(X) = d(a^TXAXa) = underset{[1 times 1]}{a^Td(X)AXa} + underset{[1 times 1]}{a^TXA cdot d(X)a}.
]
Оба слагаемых, которые мы получаем после перехода к дифференциалу – скаляры. Мы хотим представить дифференциал в виде (tr(text{нечто} d{X})). След от скаляра это снова скаляр. Получается, что мы бесплатно можем навесить над правой частью наешго равенство знак следа и воспользоваться его свойствами
[begin{multline*}
df(X) = d(a^TXAXa) = tr(a^T cdot d(X) cdot AXa) + tr(a^TXA cdot d(X) cdot a) = \ = tr(AXaa^T cdot d(X)) + tr(aa^TXA cdot d(X)) = \ = tr(AXaa^T cdot d(X) + aa^TXA cdot dX) = tr((AXaa^T + aa^TXA)dX).
end{multline*}]
Производная найдена, оказалось что это
[
nabla_X f(X) = (AXaa^T + aa^TXA)^T = aa^TX^TA^T + A^TXaa^T.
]
Как бы мы нашли это, всё по-честному перемножив, даже боюсь себе представлять.
д) Найдите производную (f(x) = x x^T x), где (x) вектор размера (1 times n)
Ещё один пример на ситуацию, когда функция бьёт из векторов в вектора
[
underset{[n times 1]}{f(x)} = underset{[n times 1]}{x} underset{[1 times n]}{x^T} underset{[n times 1]}{x}.
]
В нём надо аккуратно вести себя со сложением матриц со скалярами. Берём дифференциал
[
df(x) = d{xx^Tx} = dx cdot x^Tx + x dx^T cdot x + xx^T cdot dx.
]
В первом слагаемом пользуемся тем, что (x^Tx) скаляр и его можно вынести перед дифференциалом. Этот скаляр умножается на каждый элемент вектора. Дальше мы захотим вынести дифференциал за скобку, чтобы не испортить матричное сложение, подчеркнём факт этого перемножения на каждый элемент единичной матрицей. Во втором слагаемом пользуемся тем, что (dx^T cdot x) скаляр и транспонируем его
[
df(x) = underset{[1 times 1]}{x^Tx} underset{[n times n]}{I_n} underset{[n times 1]}{dx} + x x^T dx + xx^T dx = (x^Tx I_n + 2 x x^T)dx.
]
Обратите внимание, что без единичной матрицы размерности у сложения поломаются. Получается, что наша производная выглядит как
[begin{split}
mathfrak{J} = x^Tx I_n + 2 x x^T = begin{pmatrix} sum x_i^2 + 2 x_1^2 & 2 x_1 x_2 & ldots & 2 x_1 x_n \
2 x_1 x_2 & sum x_i^2 + 2 x_2^2 & ldots & 2 x_2 x_n \
ldots & ldots & ddots &ldots \
2 x_1 x_n & 2 x_n x_2 & ldots & sum x_i^2 + 2 x_n^2 \
end{pmatrix}.
end{split}]
Как и ожидалось, на выходе получилась матрица.
В нашей таблице. осталось ещё несколько ситуаций, которые остались вне поля нашего зрения. Давайте их обсудим более подробно. Например, давайте посмотрим на ситуацию когда отображение бьёт из матриц в вектора
[
f(X) : mathbb{R}^{n times k} to mathbb{R}^m.
]
Тогда (X) матрица, а (f(X)) вектор. Нам надо найти производную каждого элемента из вектора (f(X)) по каждому элементу из матрицы (X). Получается, что (frac{partial f}{partial X}) – это трёхмерная структура. Обычно в таких ситуациях ограничиваются записью частных производных либо прибегают к более сложным, многомерным методикам. Мы такие ситуации опустим.
Вектор-функция
г = г
(t),
заданная на промежутке [t/,Z>],
называется дифференцируемой
в точке /о е [а,/?], если существует предел
lim
Этот
предел называется производной
вектор-функции г
= г (!)
в точке и обозначается г'(^о) • Итак,
r'(/0)
= lim
t—tо
Производная
от вектор-функции в точке представляет
собой вектор. Если же точку не фиксировать,
то производной от вектор-функции
является также вектор-функция. Производная
обо-
clr
значается
г
(!)
или —.
dt
Теорема
5.1. Для
того, чтобы вектор-функция r(t)
=
=
х(1)
/ + y(t)
j
+ z(t)
к
была дифференцируемой в точке t0,
необходимо и достаточно, чтобы в этой
точке были дифференцируемы ее
координаты x(t),
y(t),
z(t).
При этом
г
‘{t)=
х’ (!) I
+ у’
(!) j
+ z‘
(t)
к
R(t)
Не
координатами будут функции
*(0-*(‘0)
у(О-уОо)
z(t)-z(t0)
t
— tQ t — tQ t — /q
По
теореме 1 функция Rft)
будет иметь предел тогда и только тогда,
когда будут иметь пределы эти три
функции. А так как пределами указанных
функций служат их производные х’
(t),
у’ (I)
, z‘ft),
то г
(/)
дифференцируема, причем,
г
t)=
x‘(t)
I + у'(t)j
+ z‘(tj
к
.
Tеорема
доказана.
§6. Техника дифференцирования
Пусть
а
= a(t),
b
= b(t),
с = c(t)
— три вектор-функции, а Я = ?Л)
скалярная функция того же аргумента
на промежутке [а. р]. Если все они являются
непрерывными и дифференцируемыми
в точке е[а, Р], то:
(14.
) Сумма aft)
+ bft)
является дифференцируемой функцией в
точке tо
, причем
{aft)
+ b(t))
‘ = a'(t) + b’ft)
-
Произведение
Ml)-
aft)
является дифференцируемым в точке
/о,причем
(Л/t)-
aft))’ =
Я'(I)
• aft)
+ Aft)-
a’ft)
-
Скалярное
произведение aft)-
bft)
является дифференцируемой функцией
в точке I
о и
(ia(t)
b(t))’ = a’ ft)- bft)
+ aft)-
b’ ft)
-
Векторное
произведение [a(t)
■ b(t)]
является дифференцируемой функцией
в точке /о и
[a(t)-bft)Y =
[a'(t)-bft)]
+ [a(t)-b’ft)]
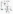
(u(t)
■ bit)- c(t))’ = a'(t)- b(t)- c(t)
+ a(t)
■ b’ (O’ c(0
+
a(t) ■
b(t) ■ c’ (t).
Докажем,
например, свойство 3. Пусть a(t)
= х
(t)
1
+ Vi
(t)
j
+ z
(t)
к
; b(t)
= x2
(t)
I
+ y2
(t)
j
+ z2
(t)
k.
Тогда
a(t)‘
b(t) = X (t) x2
(t)
+ y
(t) y2
(t)
+ z
(t) z2
(t). Продифференцируем,
используя
правила
дифференцирования
обычных
функций:
(a(t)-b(t))’
= x'(t)x2(t)
+x(t)x2‘(t)
+y'(t)y2(t)
+У
(t)yi'(t)
+ f z,'(t)
z2(t)
+ z(t)zi(t)
= a'(t)- b(t) + a(t)-b'(t).
Аналогично
доказываются остальные свойства.
§7. Производные высших порядков
Аналогично
тому, как это делается в учебниках по
математическому анализу для функций
одного аргумента, можно ввести понятие
производных высших порядков для вектор-
функций.
Производная
г
’(t)
от вектор-функции является также
вектор-функцией, поэтому ее можно
дифференцировать. Вектор-функция
г»{0
= (г
f(tjy
называегся
второй
производной
от
d2r
вектор-функции
г
(t)
и обозначается г»
(t)
или —— . Коорди-
dt
натами
второй производной служат вторые
производные от соответствующих
координат исходной вектор-функции:
r»(t)=x»(t)I
+ y»(t)j + z»(t)k .
Дальнейшее
дифференцирование приводит нас к
третьей, четвертой, …, /7-й производной.
Используются обозначения
‘»‘»■IF «m‘lF
Будем
говорить, что вектор-функция г
= г
(/), заданная на промежутке [a,b],
принадлежит классу Ск
, если она во всех точках промежутка
имеет непрерывные производные до к-того
‘
/*
—1—
аА)-
Ь’
Ct- c(t)
+ a(t)
• b(t)
• с’ (t).
Ллииллшчио
доказываются остл и : -s
-—
— к
V
R
<Л
—
Vt
/»
/У С
оражение
определяет в npocipaifcr-
в
е
некоторый путь
/. Вектор- функцию г
= г (!)
будем называть п араметрп чес к 11
м 11
ред ста в л ен и ем ну 1
и /.
Путь
/ называется регулярным,
если определяющая его вектор-функция
/*(/) е Су,, /ч
и всюду
на
промежутке [а.
b
j
г
t)
*0.
Если
к
—
1, то путь называется гладким. Пусть
путь / определяется вектор-функцией г
= г
(?), где t
е а,
& ], а путь т
вектор-функцией
g
= g(r),
те [a,
f3
]
порядка
включительно. Записывается: r(t)eC^b].
Очевидно,
что
вектор-функция г
(t)
принадлежит классу С тогда и только
тогда, когда все ее координаты принадлежат
классу Ск,
то есть, имеют на промежутке [a,b]
непрерывные производные до
A-того
порядка.
Мы
можем обычную скалярную функцию
разложить в ряд Тейлора. Если мы это
сделаем для каждой координаты
вектор-функции, то тем самым мы
разложим вектор-функцию в ряд Тейлора:
r (0= x(t) i + у (I)
j +z(t) к (1.1) 1
3
3 — з 2
lim a(t) = a0
, lim b(t) = b0 , lim A(/) = 17
lim (а(0 ± b(t)) =
а0 ± Ь0 17
lim X(t) a(t) = Я0
-а0 17
lim a{t) • b(t) = а0
■ b{) 17
t — tQ
t — tQ t
— /q 19
(Л/t)-
aft))’ = Я’(I) • aft) + Aft)- a’ft) 19
‘»‘»■IF
«m‘lF 21
оражение
определяет в npocipaifcr- 22
(12.1) 26
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Производные скалярной, векторной и матричной функций по векторному аргументу
Рассмотрим скалярную (числовую) функцию нескольких переменных . Упорядоченный набор переменных
будем называть векторным аргументом этой функции и обозначать
. Первый дифференциал функции
имеет вид:
(6.1)
Сумму в правой части можно представить как произведение строки на столбец
, либо как произведение строки
на столбец
.
Матрица-строка или матрица-столбец
определяют производную скалярной функции по векторному аргументу (градиент скалярной функции). Двойственность определения относится только к форме записи, поскольку векторный аргумент функции можно считать столбцом (в этом случае дифференциал
— столбец) или понимать как строку. В любом случае для первого дифференциала получаем одно и то же выражение (6.1).
Второй дифференциал функции имеет вид
(6.2)
Обозначим через матрицу частных производных второго порядка (матрицу Гессе). Тогда правую часть (6.2) можно записать в виде произведения
Замечания 6.1
1. Для записи производных можно использовать символические векторы (столбцы или строки):
При этом дифференцирование функции формально записывается как умножение функции на символический вектор производных. Например, градиент функции есть произведение вектора на функцию
, а матрица Гессе есть произведение символической матрицы
на функцию
.
2. Определитель матрицы Гессе называется гессианом.
3. Свойства градиента функции и матрицы Гессе используются в методах поиска экстремума функции.
Пример 6.2. Найти первую и вторую производные сложной функции , применяя матричные обозначения.
Решение. Находим производные функции , заменяя суммирование операциями умножения соответствующих матриц:
Сравним матричную форму записи этих производных с производными в случае скалярной функции
Выражения для первой производной совпадают, а для второй производной -отличаются незначительно, причем полное совпадение будет, если учесть, что для скалярной величины
.
Производные векторной функции по векторному аргументу
Пусть задан столбец функций нескольких переменных (говорят, что задана вектор-функция векторного аргумента). Первый дифференциал вектор-функции имеет вид:
Обозначим через матрицу частных производных первого порядка заданных функций (матрицу Якоби). Тогда выражение для первого дифференциала можно записать в виде
, т.е.
— производная вектор-функции векторного аргумента.
Как и в случае с аргументом , упорядоченный набор функций можно считать не матрицей-столбцом, а матрицей-строкой
. Этот случай сводится к предыдущему, учитывая, что операции дифференцирования и транспонирования можно выполнять в любом порядке, так как
(здесь и далее аргумент
для упрощения записи опущен). Поэтому из равенства
получаем
, где
— транспонированная матрица Якоби вектор-функции .
Заметим, что из равенства следует правило транспонирования производных вектор-функции:
.
Правила дифференцирования по векторному аргументу
Векторный аргумент , его приращение
считаем матрицами-столбцами размеров
.
1. Первый дифференциал скалярной функции имеет вид:
где — градиент функции, а
.
2. Второй дифференциал скалярной функции имеет вид
где
— матрица Гессе.
3. Первый дифференциал вектор-функции {матрицы-столбца) имеет вид:
, где
— матрица Якоби.
Первый дифференциал матрицы-строки: .
4. В частном случае, когда , получаем
, где
— единичная матрица n-го порядка.
5. Числовую матрицу (соответствующих размеров) можно выносить за знак производной:
Последняя формула следует из правила транспонирования производных:
6. Производные суммы, разности и произведения вектор-функций и
одинаковых размеров
Докажем, например, последнее равенство. Найдем частную производную скалярной функции по переменной
Тогда первый дифференциал функции имеет вид
Запишем это выражение, используя матричные обозначения
Сравнивая полученное выражение с , приходим к равенству
, что и требовалось доказать.
7. Производная сложной функции , где
и
вычисляется по формуле:
или, опуская аргументы,
.
Действительно, запишем первый дифференциал вектор-функции: . Заметим, что матрицы Якоби в правой части формулы согласованы: матрица
имеет размеры
, матрица
. Найдем, используя обычные правила дифференцирования, частную производную
. В правой части стоит произведение i-й строки матрицы
на j-й столбец матрицы
, что и требовалось показать.
Использование матричных обозначений позволяет записывать и применять правила дифференцирования по векторному аргументу аналогично правилам дифференцирования в скалярном случае. Например, правило 7 дифференцирования сложной вектор-функции формально совпадает с обычным «цепным» правилом дифференцирования скалярной сложной функции одной переменной. Разумеется, что формальное совпадение правил становится фактическим в скалярном случае, когда все матрицы имеют размеры
.
Пример 6.3. Применяя правила дифференцирования по векторному аргументу, найти производные следующих функций:
а) ; б)
; в)
; г)
; д)
,
где — квадратная числовая матрица n-го порядка;
— столбцы размеров
, причем столбец
числовой.
Решение. а) Вынося постоянный множитель (матрицу-строку) по правилу 5 и учитывая правило 4, получаем:
б) Учитывая, что величина скалярная, т.е.
, получаем
. Заметим, что
.
в) По правилам 4 и 5 находим: .
г) По правилам 4 и 5 находим: .
д) Представляя скалярное выражение как произведение строки
на столбец
, по правилу 6 (где
) получаем
с учетом правила транспонирования производных
Учитывая результат п. «б», имеем .
Замечания 6.2
1. В некоторых областях прикладной математики, например, в методах оптимизации и теории управления, часто используются другие соглашения, совпадающие с изложенными с точностью до операции транспонирования. Производная (градиент функции
) считается матрицей-столбцом, а производная
— матрицей-строкой:
Тогда соответствующие формулы дифференцирования, аналогичные полученным в примере 6.3, имеют вид:
2. Если матрица Якоби квадратная , то ее определитель называется якобианом.
3. След матрицы Якоби (при ) определяет
дивергенцию вектор-функции
векторного аргумента
.
Производные матричной функции по векторному аргументу
Рассмотрим функциональную матрицу , элементами которой служат функции
векторного аргумента
. Дифференциал этой функции имеет вид
где — частная производная матрицы по одной переменной. Совокупность частных производных (градиент функциональной матрицы) представляет объект, элементы которого
нумеруются тремя индексами: номер строки, номер столбца и номер переменной дифференцирования. Поэтому заменить операцию суммирования в правой части формулы операцией умножения матриц в данном случае не представляется возможным. Необходимо вводить другие объекты — тензоры и операции над ними. Поясним формальную сторону получения удобных формул дифференцирования на примере функциональных матриц. Примем следующие правила индексирования:
1) элементы матрицы обозначаются
, где
— номер строки, а
— номер столбца. В частности,
— матрица-столбец (или просто столбец), а
— матрица-строка (или просто строка);
2) частную производную функции (скалярной, векторной или матричной) по переменной
будем обозначать, приписывая нижний индекс
в скобках:
;
3) если в произведении одинаковые индексы встречаются сверху и снизу, то по ним производится суммирование (хотя знак суммы не указывается). Например, если — матрица размеров
,
— столбец размеров
,
— строка размеров
, то
т.е. — i-й элемент столбца
,
— j-й элемент строки
,
— число
.
Применяя эти соглашения, запишем дифференциалы:
— скалярной функции: ;
— вектор-функции (функции-столбца):
;
— функциональной матрицы , где
— частная производная первого порядка элемента
функциональной матрицы
по переменной
.
Одним из преимуществ принятых соглашений является получение простого вида формул. Другие преимущества раскрываются и используются в тензорном анализе.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Векторный анализ — раздел математики, распространяющий методы математического анализа на векторы, как правило в двух- или трёхмерном пространстве. Объектами приложения векторного анализа являются: Векторные поля — отображения одного векторного пространства в другое.
Скалярное поле. Поверхности и линии уровня. Производная по направлению
Если в каждой точке пространства или части пространства определено значение некоторой величины, то говорят, что задано иоде данной величины. Поле называется скалярным, если рассматриваемая величина скалярна, т.е. вполне характеризуется своим числовым значением. Например, поле температур.
Скалярное поле задается скалярной функцией точки и = f(М). Если в пространстве введена декартова система координат, то и есть функция трех переменных х, у, z — координат точки М:
u = f(x,y,z). (1)
Определение:
Поверхностью уровня скалярного поля называется множество точек, в которых функция f(М) принимает одно и то же значение. Уравнение поверхности уровня
f(x, y, z) = с = const. (2)
Пример:
Найти поверхности уровня скалярного поля
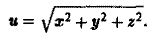
Согласно определению уравнением поверхности уровня будет
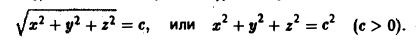
Это уравнение сферы (с ≠ 0) с центром в начале координат.
Скалярное поле называется плоским, если во всех плоскостях, параллельных некоторой плоскости, поле одно и то же. Если указанную плоскость принять за плоскость хОу, го функция поля не будет зависеть от координаты г, т. е. будетфункцией только аргументов х и у,
u=f(x, y). (3)
Плоское поле можно характеризовать с помощью линий уровня — множества точек плоскости, в которых функция f(x, у) имеет одно и то же значение. Уравнение линии уровня —
f(х, у) = с = const. (4)
Пример:
Найти линии уровня скалярного поля
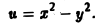
Линии уровня задаются уравнениями
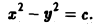
При с = О получаем пару прямых у = х, у = -х. При с ≠ 0 получаем семейство гипербол (рис. 1).
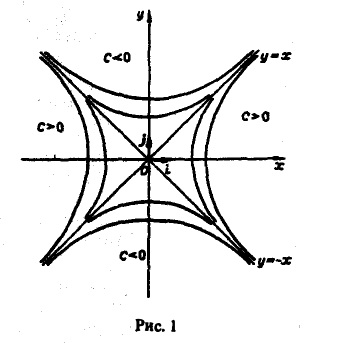
Производная по направлению
Пусть имеется скалярное поле, определяемое скалярной функцией и = f(M). Возьмем точку М0 и выберем направление, определяемое вектором I. Возьмем другую точку М так, чтобы вектор М0М был параллелен вектору 1 (рис.2). Обозначим длину вектора МоМ через ∆l, а приращение функции f(М) — f(Mo), соответствующее перемещению ∆l, через ∆и. Отношение
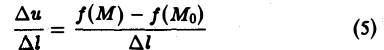
определяет среднюю скорость изменения скалярного поля на единицу длины поданному направлению I.
Пусть теперь ∆l стремится к нулю так, чтобы вектор М0М все время оставался параллельным вектору I.
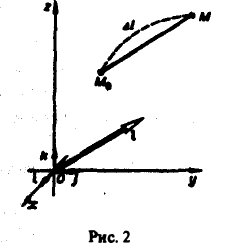
Определение:
Если при ∆l —> 0 существует конечный предел отношения (5), то его называют производной функции и = f(M) в данной точке М0 по данному направлению I и обозначают символом
Так что, по определению,
(6)
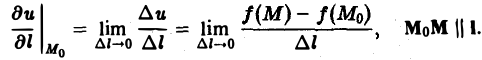
Это определение не связано с выбором системы координат, т. е. Hocит вариантный характер.
Найдем выражение для производной по направлению в декартовой системе координат. Пусть функция f(М) = f(х, у, z) дифференцируема в точке Мо(хо, yо, zо). Рассмотрим значение f(M) в точке М(х0 + ∆х,у0 + ∆y, zo + ∆z). Тогда полное приращение функции можно записать в следующем виде:
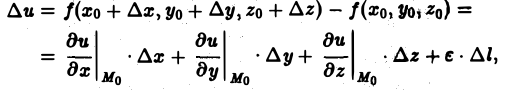
где ε = 0 при
а символы
означают, что частные производные вычислены в точке Мо. Отсюда (7)
Здесь величины 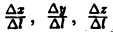
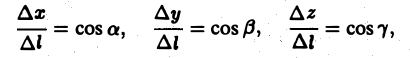
где
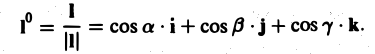
Так как M —» Mo, оставаясь все время на прямой, параллельной вектору I, то углы а, β, γ постоянны, а потому
Окончательно из равенств (7) и (8) получаем
Замечание:
Частные производные 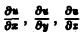
Пример:
Найти производную функции
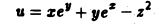
в точке Mo(3,0,2) по направлению к точке M1(4,1, 3).
Имеем
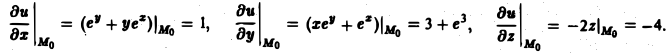
Вектор МoМ = {1, 1, 1} имеет длину |МоМ| = /3. Его направляющие косинусы:
По формуле (9) будем иметь
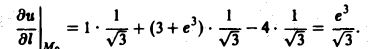
Тот факт, что 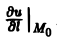
Для плоского поля U = f(x, у) производная по направлению 1 в точке Мо(х0, у0) вычисляется по формуле (10)
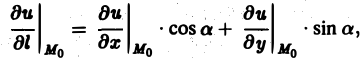
где а — угол, образованный вектором I с осью Ох.
Замечание:
Формула (9) для вычисления производной по направлению I в данной точке М0 остается в силе и тогда, когда точка М стремится к точке Мо по кривой, для которой вектор I является касательным в точке Мо.
Пример:
Вычислить производную скалярного поля
и = arctg(xy)
в точке Mo(1, 1), принадлежащей параболе у = х2, по направлению этой кривой (в направлении возрастания абсциссы).
Направлением I параболы у = х2 в точке Mo{1, 1) считается направление касательной к параболе в этой точке (рис.3).
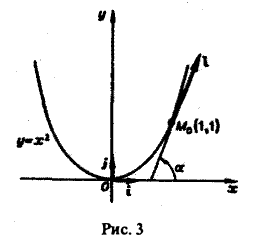
Пусть касательная к параболе в точке Мо образует с осью Ох угол a. Тогда tga =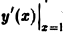
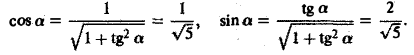
Вычислим значения 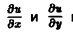
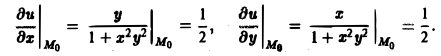
Теперь по формуле (10) получаем
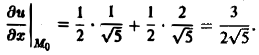
Пример:
Найти производную скалярного поля и = In(xy + yz + zx) в точке Mo(0, 1, 1) по направлению окружности
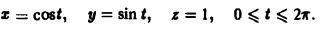
Векторное уравнение окружности имеет вид
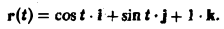
Находим единичный вектор т касательной к окружности
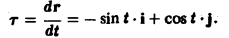
Точке Mo(0,1, 1) соответствует значение параметра t= π/2 Значение т в точке Мо будет равно
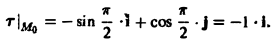
Отсюда получаем направляющие косинусы касательной к окружности в точке Mо: cos a = — 1, cos β = 0, cos γ = 0.
Вычислим значения частных производных данного скалярного поля в точке Mo(0, 1, 1)
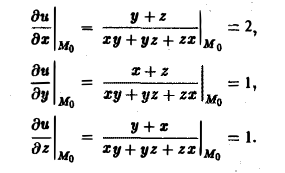
Значит, искомая производная
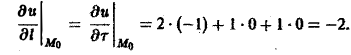
Градиент скалярного поля
Пусть скалярное поле определяется скалярной функцией
u = f(x, y. z),
которая предполагается дифференцируемой.
Определение:
Градиентом скалярного поля u в данной точке М называется вектор, обозначаемый символом grad и и определяемый равенством
(1)
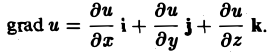
Ясно, что этот вектор зависит от функции f, так и от точки М, в которой вычисляется ее производная.
Пусть I° — единичный вектор в направлении I, т. е.
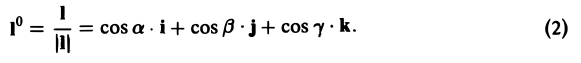
Тогда формулу для производной по направлению можно записать в следующем виде:
(3)
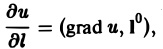
тем самым производная от функции и по направлению I равна скалярному произведению градиента функции u(M) на орт I° направления I.
Основные свойства градиента
Теорема:
Градиент скалярного поля перпендикулярен к поверхности уровня (или к линии уровня, если поле плоское).
Проведем через произвольную точку М поверхность уровня и = const и выберем на этой поверхности гладкую кривую L, проходящую через точку М (рис. 4). Пусть 1 — вектор, касательный к кривой L в точке М.
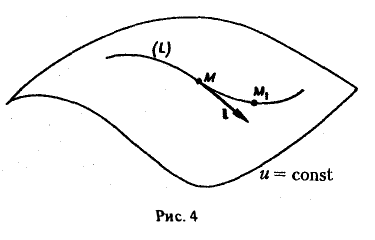
Так как на поверхности уровня и(М) = и(М1) для любой точки М1 ∈ L, то
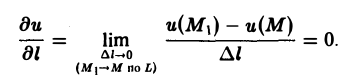
С другой стороны, 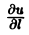
Итак, вектор grad и ортогонален к любой касательной к поверхности уровня в точке М. Тем самым он ортогонален к самой поверхности уровня в точке М.
Теорема:
Градиент направлен в сторону возрастания функции поля.
Ранее мы доказали, что градиент скалярного поля направлен по нормали к поверхности уровня, которая может быть ориентирована либо в сторону возрастания функции и(М), либо в сторону ее убывания.
Обозначим через п нормаль к поверхности уровня, ориентированную в сторону возрастания функции и(М), и найдем производную функции и в направлении этой нормали (рис. 5). Имеем
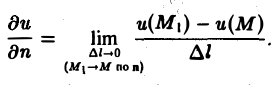
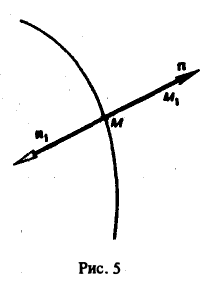
Так как по условию и(М1) > и(М), то и(М1) — и(М) > 0, и поэтому
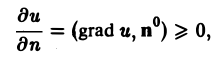
т.е. (grad и, п°) ≥ 0.
Отсюда следует, что grad и направлен в ту же сторону, что и выбранная нами нормаль п, т.е. в сторону возрастания функции и(М).
Теорема:
Длина градиента равна наибольшей производной по направлению в данной точке поля,
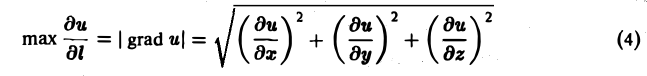
(здесь mах 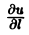
Имеем
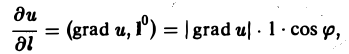
где φ — угол между векторами I и grad n. Так как наибольшее значение cos φ равно 1, то наибольшим значением производной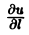
Пример:
Найти направление наибольшего изменения скалярного поля
и = ху + yz + zx
в точке Mо(1, 1, 1), а также величину этого наибольшего изменения в указанной точке.
Направление наибольшего изменения скалярного поля указывается вектором grad u(M). Имеем grad u(М) = (у + z)i + (х + г)j + (у + х)к, так что
grad и{Мo) = 2i + 2j + 2k.
Этот вектор определяет направление наибольшего возрастания поля в точке Мо(1,1,1). Величина наибольшего изменения поля в этой точке равна
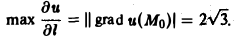
Инвариантное определение градиента
Величины, характеризующие свойства изучаемого объекта и не зависящие от выбора системы координат, называются инвариантами данного объекта. Например, длина кривой — инвариант этой кривой, а угол касательной к кривой с осью Ох — не инвариант.
Основываясь на доказанных выше трех свойствах градиента скалярного поля, можно дать следующее инвариантное определение градиента.
Определение:
Градиент скалярного поля есть вектор, направленный по нормали к поверхности уровня в сторону возрастания функции поля и имеющий длину, равную наибольшей производной по направлению (в данной точке).
Пусть п° — единичный вектор нормали, направленный в сторону возрастания поля. Тогда

Пример:
Найти градиент расстояния
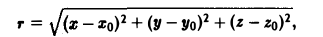
где Мo(хo,уo,zo) — некоторая фиксированная точка, а М(х,у,z) — текущая.
Имеем
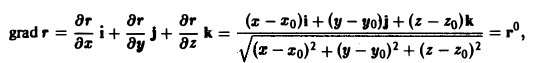
где r° — единичный вектор направления MoM.
Правила вычисления градиента
- grad си(М) = с grad и{М), где с — постоянное число.
- grad(u + v) = grad и + grad v.
Приведенные формулы получаются непосредственно из определения градиента и свойств производных.
3. grad(u v) = v grad и+ и grad v.
По правилу дифференцирования произведения
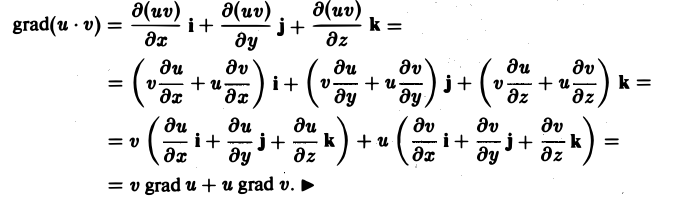
Доказательство аналогично доказательству свойства 3.
Пусть F(u) — дифференцируемая скалярная функция. Тогда
grad F(u) = F'(u) grad и.
По определению градиента имеем
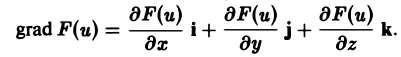
Применим ко всем слагаемым правой части правило дифференцирования сложной функции. Получим
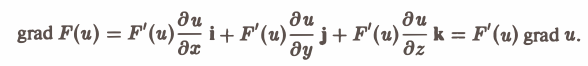
В частности,
grad F(r) = F'(r) • p°. (6)
Формула (6) следует из формулы grad r = r°.
Пример:
Найти производную по направлению радиус-вектора r от функции u = sin r, где r = |r|. По формуле (3)

а по формуле (6) grad sin r = cos r • r° . В результате получим, что
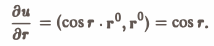
Пример:
Пусть дано плоское скалярное поле

где r1, r2 — расстояния от некоторой точки Р(х,у) плоскости до двух фиксированных точек F1 и F2 этой плоскости, F1 ≠ F2.
Рассмотрим произвольный эллипс с фокусами F1 и F2 и докажем, что всякий луч света, вышедший из одного фокуса эллипса, после отражения от эллипса попадает в другой его фокус.
Линии уровня функции (7) суть
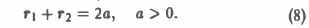
Уравнения (8) описывают семейство эллипсов с фокусами в точках F1 и F2.
Согласно результату примера 2 имеем
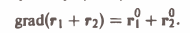
Тем самым градиент заданного поля равен вектору PQ диагонали ромба, построенного на ортах 
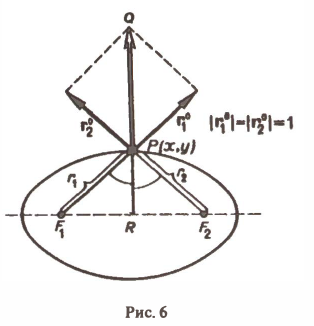
По теореме 1 градиент PQ перпендикулярен к эллипсу (8) в точке Р(х,у). Следовательно, нормаль к эллипсу (8) в любой его точке делит пополам угол между радиус-векторами, проведенными в эту точку. Отсюда и из того, что угол падения равен углу отражения, получаем: луч света, вышедший из одного фокуса эллипса, отразившись от него, непременно попадает в другой фокус этого эллипса.
Векторное поле. Векторные линии и их дифференциальные уравнения
Определение:
Если в каждой точке M(x,y,z) пространства или части пространства определена векторная величина
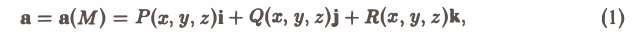
то говорят, что там задано векторное поле а.
Задание векторного поля равносильно заданию трех скалярных функций от трех переменных Р(х, у, z), Q(x, у, z), R(x, у, z).
Примерами векторных полей могут служить: силовое поле — поле некоторой силы F, поле скоростей v течения некоторой жидкости и др.
Для геометрической характеристики векторного поля служат векторные линии. Векторной линией векторного поля а называется кривая, касательная к которой в любой точке М имеет то же направление, что и вектор поля а в этой точке (рис. 7).
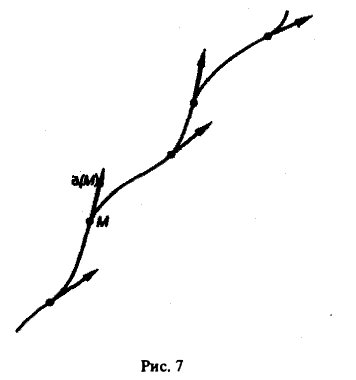
В силовом поле векторные линии называются силовыми линиями‘, в поле скоростей движения жидкости векторные линии называются линиями тока.
Дифференциальные уравнения векторных линий
Пусть векторное поле определяется вектор-функцией
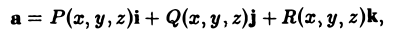
где P(x,y,z), Q(x, у, z), R(x,y,z) — непрерывные функции переменных х, у, z, имеющие ограниченные частные производные первого порядка. Пусть
r(t) = x(t)i + y(t)j + z(t)k
— есть радиус-вектор текущей точки векторной линии векторного поля a (t — параметр). Из определения векторной линии следует, что вектор
а = Р(х, у, z)i + Q{x, у, z)j + R(x, у, z)k
и вектор касательной к этой кривой
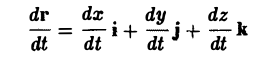
должны быть коллинеарны в каждой точке векторной линии. Условием коллинеарности векторов является пропорциональность их координат:
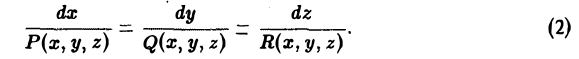
Таким образом, мы получили для векторных линий систему дифференциальных уравнений в симметричной форме.
Допустим, что нам удалось найти два независимых интеграла системы (2): (3)
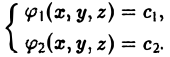
Система уравнений (3) определяет векторную линию как линию пересечения двух поверхностей. Произвольно меняя параметры c1 и c2 мы получаем семейство векторных линий как семейство с двумя степенями свободы.
Пример:
Hайти векторные линии векторного поля
а = хi + уj + 2zk.
Выписываем дифференциальные уравнения векторных линий, dx dy dz
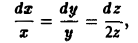
или
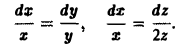
Интегрируя эту систему, получим два уравнения
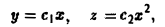
где c1, c2 — произвольные постоянные. Пересечение плоскостей у = c1х с параболическими цилиндрами z = c2x2 дает двухпараметрическое семейство векторных линий поля (рис. 8).
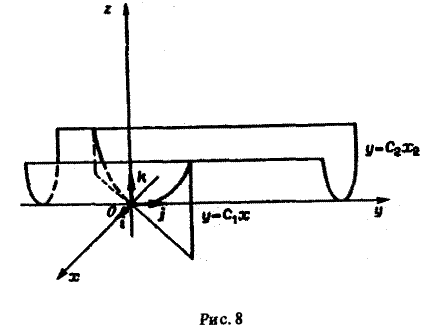
Определение:
Векторное поле называется плоским, если все векторы а параллельны одной и той же плоскости и в каждой плоскости, параллельной указанной, векторное поле одно и то же.
Посмотрим, как плоское векторное поле описывается в координатах. Если указанную в определении плоскость (или любую ей параллельную) принять за плоскость хОу, то векторы плоского поля не будут содержать компоненты по оси Oz и координаты векторов не будут зависеть от z:
Дифференциальные уравнения векторныхлиний плоского поля можно записать в следующем виде
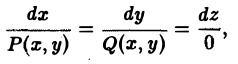
или
(5)
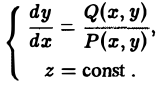
Отсюда видно, что векторные линии плоского поля являются плоскими кривыми, лежащими в плоскостях, параллельных плоскости хОу.
Пример:
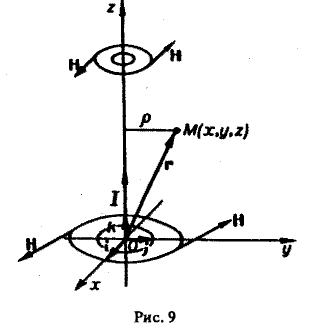
Найти векторные линии магнитного поля бесконечно длинного прямого провода.
Предположим, что проводник направлен вдоль оси Oz и по нему течет ток силы J, т. е. вектор тока
J = J • k.
Тогда вектор напряженности Н магнитного поля определяется по формуле

где
р = xi + yj + zk
— радиус-вектор точки М, р — расстояние от оси провода до точки М. Раскрывая векторное произведение (6), получим
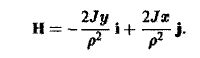
Дифференциальные уравнения векторных линий:
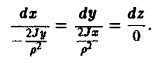
Отсюда x = const, 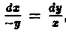
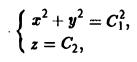
т.е. векторные линии являются окружностями с центрами на оси Oz (рис.9).
Пример:
Найти векторные линии поля сил тяготения, образованного притягивающей материальной точкой массы т, расположенной в начале координат.
В данном случае сила F определяется так:
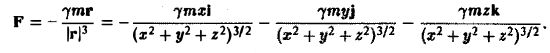
Дифференциальные уравнения векторных линий:
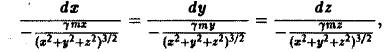
откуда, умножая каждую из дробей на 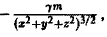
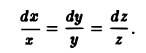
Чтобы получить уравнения векторных линий в параметрической форме, приравняем каждую из дробей величине 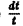
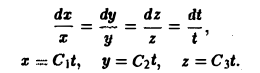
Это — полупрямые, выходящие из начала координат.
Чтобы из семейства векторных линий выделить одну, надо задать точку М0(хо, yo, zо). через которую эта векторная линия должна проходить, и по координатам заданной точки определить величины С1, C2, C3.
Пусть, например, точка Мо имеет координаты хо = 3, yо = 5, zо = 7. Уравнение векторной линии, проходящей через точку Mo(3, 5, 7), можно записать так:
x = 3t, у — 5t, z = 7t.
Сама точка Мо получается при значении параметра t = 1.
Поток вектора через поверхность и его свойства
Рассмотрим сначала частный случай поля скоростей v течения жидкости. Выделим в поле некоторую поверхность Σ. Потоком жидкости через поверхность Σ называется количество жидкости, протекающее через поверхность Σ за единицу времени.
Этот поток легко вычислить, если скорость течения постоянна (v = const), а поверхность Σ —плоская. В этом случае поток жидкости равен объему цилиндрического тела с параллельными основаниями и образующими длины |v|, так как за единицу времени каждая частица перемещается на величину v (рис. 10),
П =Sh,
где S — площадь основания, h = npnv = (v, n°) — высота цилиндра и n — нормаль к его основанию, |п°| = 1.
Итак, при постоянной скорости v поток жидкости через плоскую поверхность Σ равен
(1)
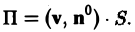
Если скорость v изменяется непрерывно, а поверхность Σ — гладкая, то можно разбить поверхность Σ на столь малые части Σk (k = 1, 2,…, п), чтобы каждую часть Σk можно было приближенно считать плоской и вектор v на ней постоянным.
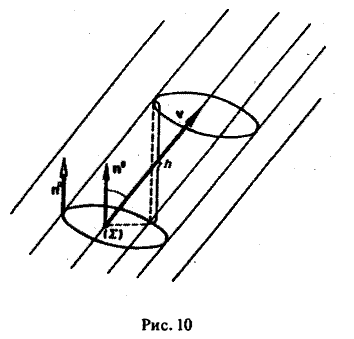
Так как поток жидкости через поверхность Σ равен сумме потоков жидкости через все ее части Σk, то мы получаем для вычисления потока приближенную формулу (2)
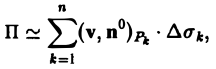
где п — общее число частей Σk, на которые разбита поверхность Σ, Рк — точка, лежащая на k-ой части, ∆σk — площадь части Σk поверхности, ( v, n°)pk означает скалярное произведение векторов v и п° в точке Pk ∈ Σk (рис. 11).
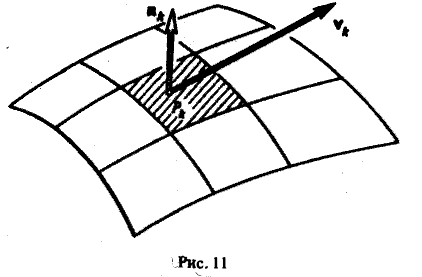
Назовем потоком жидкости через поверхность Σ предел суммы (2) при стремлении к нулю наибольшего из диаметров площадок Σk,
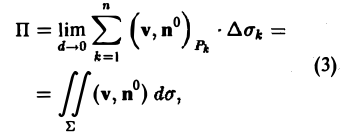
где d — наибольший из диаметров частей Σk (k= 1,2,…,п). Интеграл (3), определяющий поток жидкости, берется от скалярной функции (v, п°) по площади поверхности Σ.
Понятие потока произвольного вектора а через поверхность Σ вводится п о аналогии с введенным выше понятием потока жидкости через поверхность.
Определение:
Потоком вектора (векторного поля) а через поверхность Σ называется интеграл по поверхности Σ от проекции вектора а на нормаль к поверхности

Ясно, что интеграл (4) существует, если вектор а = Pi+Qj+Rk непрерывен, т. е. непрерывны его координаты Р(x, у, z), Q(x, у, z), R(x, y,z), и поверхность Σ — гладкая, т. е. имеет непрерывно меняющуюся касательную плоскость
Пример:
Поле создается точечным зарядом (электричесkое поле) или точечной маcсой (поле тяготения), помещенными в начале координат. Тогда вектор напряженности поля в любой точке Р будет равен
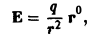
где q — величина заряда (массы), r = ОР — радиус-вектор точки Р. Требуется найти поток вектора напряженности Е через SR — сферу радиуса R с центром в начале координат.
Так как направление нормали к сфере совпадает с направлением радиус-вектора r, то п° = r° и поэтому
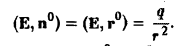
На сфере SR радиуса R имеем r = R, так что (Е, n°) = 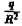
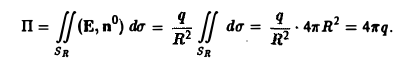
Свойства потока вектора через поверхность
1. Линейность.
(5)
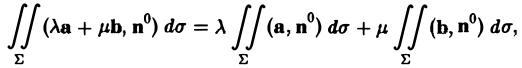
где λ и μ — постоянные числа.
2. Аддитивность. Если поверхность Σ разбита кусочно-гладкой кривой на две части Σ1 и Σ2, то поток через поверхность Σ равен сумме потоков через поверхности Σ1 и Σ2,
(6)
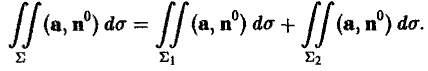
Это свойство позволяет распространить понятие потока на кусочно-гладкие поверхности Σ.
Понятие ориентации поверхности
Взяв, к примеру, цилиндрическую поверхность, замечаем, что если в некоторой ее точке М выбрать определенный (один из двух) единичный вектор нормали и непрерывно перемещаться затем по поверхности вместе с соответствующим вектором нормали по любому пути, не переходящему через край повержюсти, то при возвращении в точку М единичный вектор нормали совпадает с исходным (рис. 12).
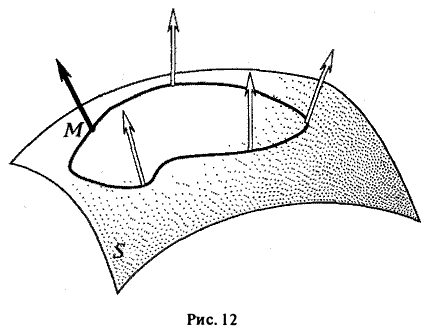
Вместе с тем, существуют поверхности, для которых это не так. Примером такой поверхности может служить лист Мёбиуса (рис. 13). Существует путь (отмеченная на рисунке пунктиром средняя линия листа), перемещаясь по которому, мы возвратимся в начальную точку с единичным вектором нормали, противоположным исходному.
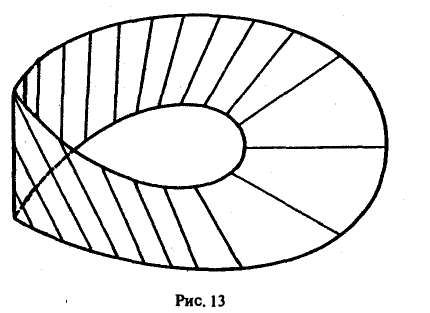
Описанное свойство разбивает все поверхности на два класса — двусторонние, или ориентируемые (плоскость, сфера, поверхность куба и т.п.), и односторонние, или неориентируемые (лист Мёбиуса).
3. Зависимость потока от ориентации поверхности (от ориентации вектора нормали к поверхности). Понятие потока вводится только для двусторонних поверхностей. Будем считать, что если в одной точке такой поверхности направление вектора нормали уже выбрано, то в любой другой ее точке берется тот вектор нормали, который получается из выбранного при непрерывном перемещении точки по поверхности (без перехода через границу). В частности, на замкнутой поверхности во всех точках берется либо внешняя нормаль, либо внутренняя (внутренняя нормаль направлена внутрь тела, ограниченного замкнутой поверхностью).
Обозначим через Σ+ ту сторону поверхности Σ, на которой выбран вектор нормали п+ = п, а через Σ- — сторону поверхности Σ, на которой берется вектор нормали (п_ = -п). Тогда получим
(7)
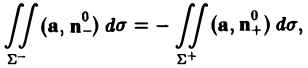
где п°_ = -п°+. Таким образом, при изменении ориентации поверхности (при изменении направления вектора нормали п° к поверхности Σ) поток вектора меняет знак на противоположный.
Пример:
Вычислить поток радиус-вектора r = хi + yj + zk через поверхность прямого кругового цилиндра высоты Н с радиусом основания R и осью Oz.
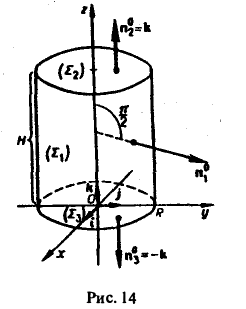
Поверхность Σ состоит из трех частей: боковой поверхности Σ1, верхнего основания Σ2 и нижнего основания Σ3 цилиндра. Искомый поток П в силу свойства аддитивности равен
П = П1 +П2 + П3,
где П1, П2, П3 — потоки данного поля через Σ1, Σ2 и Σ3 соответственно.
На боковой поверхности цилиндра вектор внешней нормали п°1 параллелен плоскости хОу, и поэтому
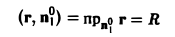
(см. рис. 14). Следовательно,
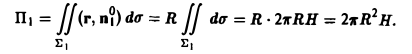
На верхнем основании Σ2 вектор нормали п°2 параллелен оси Оz, и поэтому можно положить п°2 = k. Тогда имеем
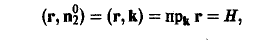
так что
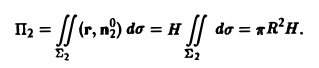
На нижнем основании Σ3 вектор г перпендикулярен к вектору нормали п°3 = -k. Поэтому (r, п°3) = (r, -k) = 0 и
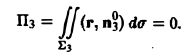
Значит, искомый поток
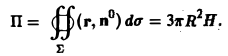
Здесь символ 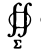
Поток вектора через незамкнутую поверхность
Укажем некоторые способы вычисления потока вектора через незамкнутые поверхности.
Метод проектирования на одну из координатных плоскостей
Пусть поверхность S однозначно проектируется на область Dxy плоскости хОу. В этом случае поверхность S можно задать уравнением вида
z = f(x, у).
Орт п° нормали к поверхности S находится по формуле
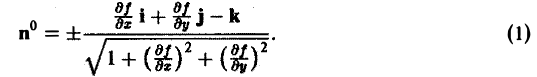
Если в формуле (1) берется знак « -», то угол γ между осью Oz и нормалью п° —острый; если же знак «+», то угол γ — тупой.
Так как элемент площади dσ этой поверхности равен
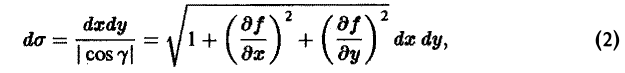
то вычисление потока П через выбранную сторону поверхности S сводится к вычислению двойного интеграла по формуле
(3)
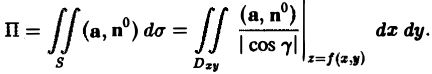
Символ
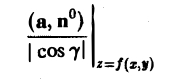
означает, что при вычислении в подынтегральной функции надо вместо z всюду поставить f(i, у).
Пример:
Найти поток вектора
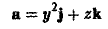
через часть поверхности параболоида
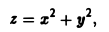
отсеченной плоскостью z = 2. По отношению к области, ограниченной параболоидом, берется внешняя нормаль (рис. 15).
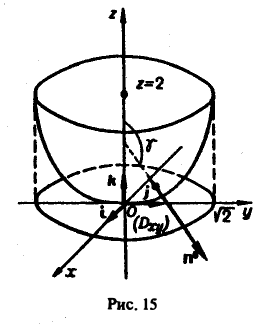
Данная поверхность проектируется на круг Dxy плоскости хОу с центром в начале координат радиуса R =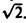
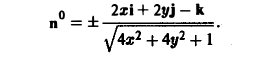
Согласно условию задачи вектор п° образует с осью Oz тупой угол γ, поэтому перед дробью следует взять знак минус. Таким образом,
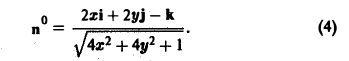
Находим скалярное произведение
Если поверхность S проектируется однозначно на область Dyz плоскости yOz, то ее можно задать уравнением х = φ{у, z). В этом случае имеем
(6)
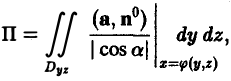
где
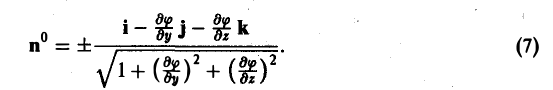
Знак «+» в последней формуле соответствует тому, что угол а между осью Ох и вектором нормали п° острый, и знак «-», если указанный угол тупой.
Наконец, если поверхность S проектируется однозначно на область Dxz плоскости xOz, то ее можно задать уравнением у = ψ(x, z) и тогда
Знак «+» перед дробью в формуле (10) означает, что угол β между осью Оу и вектором нормали п° — острый, а знак «—», что угол β — тупой.
Замечание:
Для нахождения потока вектора
а = Р(х, у, z)i + Q(z, у, z)j + R(х, у, k)
к через поверхность S, заданную уравнением z = f(x, у), методом проектирования на координатную плоскость хОу, не обязательно находить орт п° нормали, а можно брать вектор
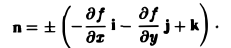
Тогда формула (2) для вычисления потока П примет вид:
(11)
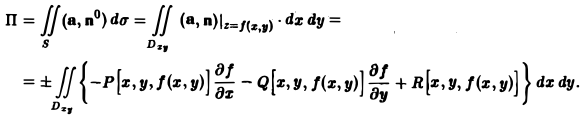
Аналогичные формулы получаются для потоков через поверхности, заданные уравнениями х = φ(у, z) или у = ψ(х, z).
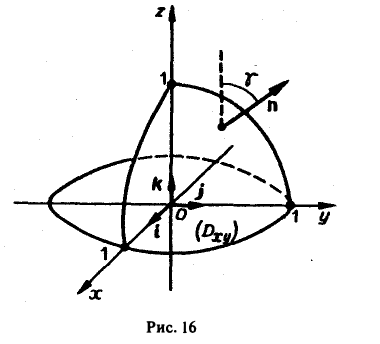
Пример:
Вычислить поток вектора
а = хzi
через внешнюю сторону параболоида
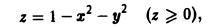
ограниченного плоскостью z = 0 (рис. 16).
Имеем
n = ±(2ri + 2yj+k).
Так как угол γ — острый, следует выбрать знак «+». Отсюда
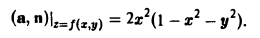
Искомый поток вычисляется так:
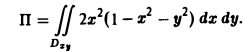
Переходя к полярным координатам х = р cos φ, y = p sin φ, 0 ≤ р ≤ 1. 0 ≤ φ < 2π, получим
Метод проектирования на все координатные плоскости
Пусть поверхность S однозначно проектируется на все три координатные плоскости. Обозначим через Dxy, Dxz, Dyz проекции S на плоскости хОу, xOz, yOz соответственно. В этом случае уравнение F(x, y, z) = 0 поверхности S однозначно разрешимо относительно каждого из аргументов, т. е.
x = x(y,z), y = y(x,z), z = z(x,y). (12)
Тогда поток вектора
а = Р(х, у, z)i + Q(x, у, z)j + R(x, у, z)k
через поверхность S, единичный вектор нормали к которой равен
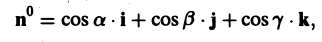
можно записать так:
Известно, что
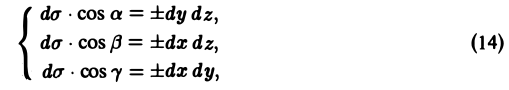
причем знак в каждой из формул (14) выбирается таким, каков знак cos a, cos β, cos γ на поверхности S. Подставляя соотношения (12) и (14) в формулу (13), получаем, что (15)
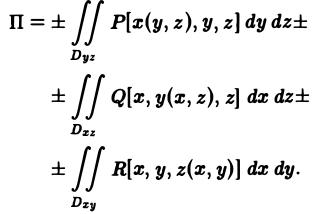
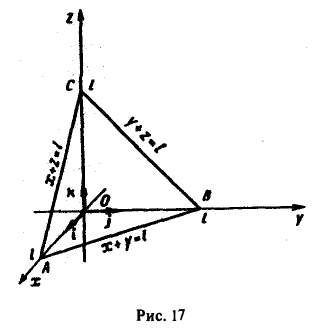
Пример:
Вычислить поток векторного поля
а = yi + zj + zk
через треугольник, ограниченный плоскостями z + y+ z = l (l>0), x=0, у — 0, z = 0 (угол γ — острый) (рис. 17).
Имеем
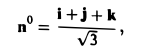
так что
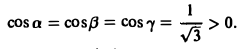
Значит, перед всеми интегралами в формуле (15) следует взять знак « + ». Полагая Р = у, Q = z, R = х, получим
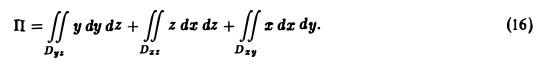
Вычислим первый интеграл в правой части формулы (16). Область Dyz — треугольник ВОС в плоскости yOz, уравнение стороны ВС: y+z = l, 0 ≤ у ≤ I. Имеем
Аналогично получим
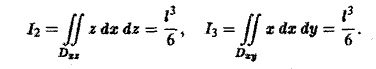
Значит, искомый лоток равен
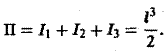
Метод введения криволинейных координат на поверхности
Если поверхность S является частью кругового цилиндра или сферы, при вычислении потока удобно, не применяя проектирования на координатные плоскости, ввести на поверхности криволинейные координаты.
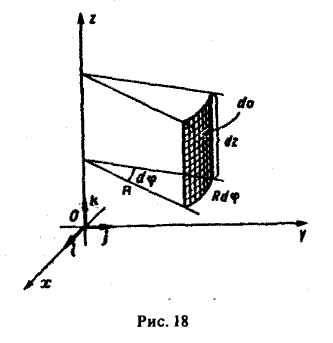
А. Поверхность S является частью кругового цилиндра
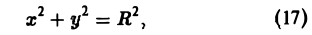
ограниченного поверхностями z = f1(x,y) и z = f2(х. у), где f1(x. y) ≤ f2(x, y) (рис. 18). Полагая х = R cos φ, у = R sin φ, z = z, будем иметь
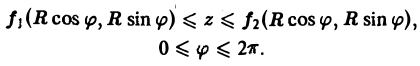
Элемент площади поверхности выражается так:
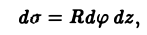
и поток вектора а через внешнюю сторону поверхности S вычисляется по формуле:
Пример:
Найти поток вектора
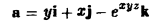
через внешнюю сторону поверхности цилиндра
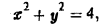
ограниченной плоскостями
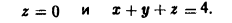
Имеем
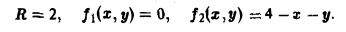
Так как
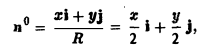
то скалярное произведение (а, п°) на цилиндре (х = 2 cos φ, у = 2 sin φ, z = z) равно:
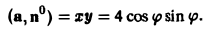
Тогда по формуле (18) получим
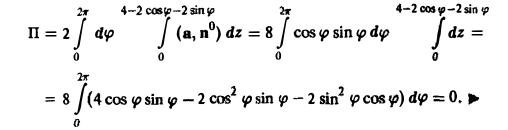
В. Поверхность S является частью сферы

ограниченной коническими поверхностями, уравнения которых в сферических координатах имеют вид 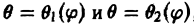
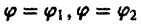
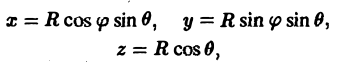
где 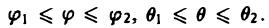
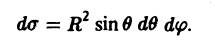
В этом случае поток векторного поля а через внешнюю часть поверхности S вычисляется по формуле
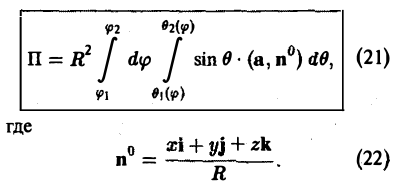
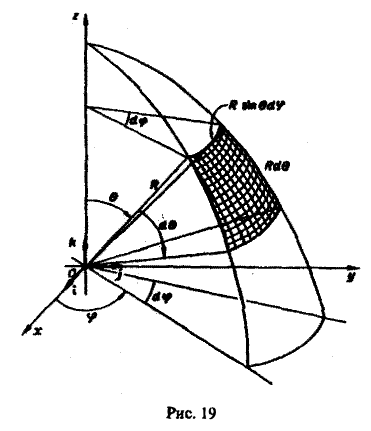
Пример:
Найти поток вектора
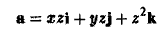
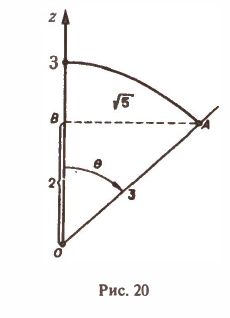
через внешнюю часть сферы
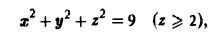
отсеченную плоcкостью z = 2 (рис. 20).
В данном случае имеем
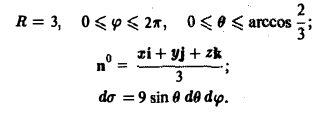
Положим
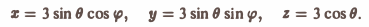
Тогда скалярное произведение (а, п°) выразится так:
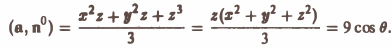
По формуле (21) получим
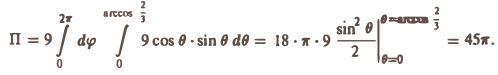
Замечание:
Здесь мы воспользовались формулой
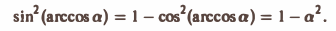
Поток вектора через замкнутую поверхность. Теорема Гаусса—Остроградского
Теорема:
Если в некоторой области G пространства R3 координаты вектора
а = Р(х, у, z)i + Q(x, у, z)j + R(x, у, z)k
непрерывны и имеют непрерывные частные производные 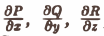
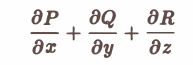
по области V, ограниченной поверхностью S:
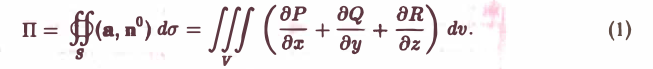
Здесь п0 — орт внешней нормали к поверхности, а символ 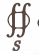
Рассмотрим сначала вектор а, имеющий только одну компоненту а = R(x, у, z)k, и предположим, что гладкая поверхность S пересекается каждой прямой, параллельной оси Oz, не более чем в двух точках. Тогда поверхность S разбивается на две части S1 и S2, однозначно проектирующиеся на некоторую область D плоскости хОу (рис.21).
Внешняя нормаль к поверхности S2 образует острый угол γ с осью Oz, а внешняя нормаль к поверхности S1 образует тупой угол с осью Oz. Поэтому cos γ = (п°, к) > 0 на S2 и cos γ < 0 на S1, так что на S2 имеем cos γ = |cos γ|, а на S1 cos γ = —| cos γ|. В силу аддитивности потока имеем
Пусть dσ — элемент площади на поверхности S. Тогда
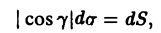
где dS — элемент площади области D. Сведем интегралы по поверхности к двойным интеграл ам по области D плоскости хОу, на которую проектируются поверхности S1 и S2. Пусть S2 описывается уравнением z = z2(x, у), а S, — уравнением z = z1(x, у). Тогда
Так как приращение непрерывно дифференцируемой функции можно представить как интеграл от ее производной
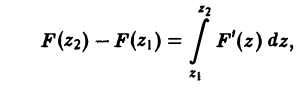
то для функции R(x, у, z) будем иметь
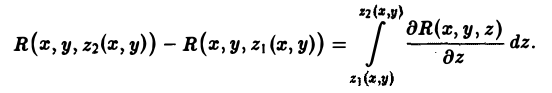
Пользуясь этим, получаем из формулы (3)
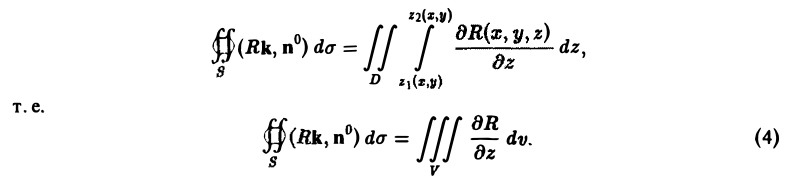
Если поверхность S содержит часть цилиндрической поверхности с образующими, параллельными оси Oz (рис. 22), то на этой части поверхности (Rk, п°) = 0 и интеграл ∫∫ (Rk, n°) dσ по ней равен нулю. Поэтому формула (4) остается справедливой и для поверхностей, содержащих указанные цилиндрические части.
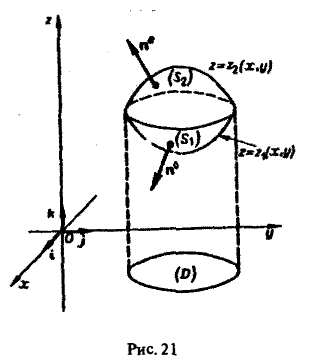
Формула (4) переносится и на случай, когда поверхность 5 пересекается вертикальной прямой более, чем в двух точках (рис. 23).
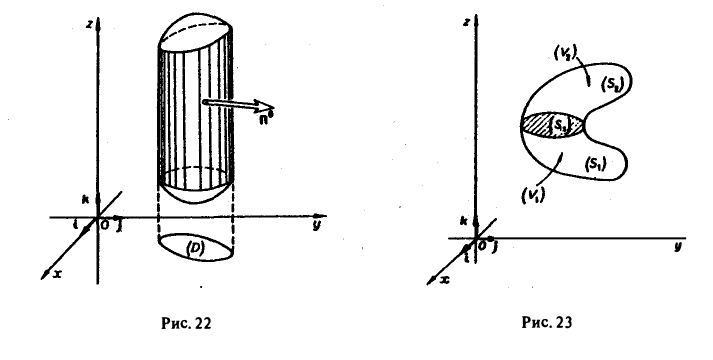
Разрежем область V на части, поверхность каждой из которых пересекается вертикальной прямой не более чем в двух точках, и обозначим через Sp поверхность разреза. Пусть S1 и S2 — те части поверхности S, на которые она разбивается разрезом Sp,a V1 и V2 — соответствующие части области V, ограниченные поверхностями
Здесь Sp+ означает, что вектор нормали к разрезу Sp направлен вверх (образует с осью Oz острый угол), a Sp— — что этот вектор нормали направлен вниз (образует с осью Oz тупой угол). Имеем:
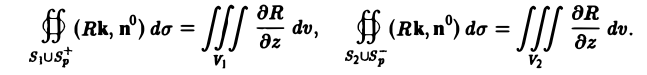
Складывая полученные равенства и пользуясь аддитивностью потока и тройного интеграла, получим
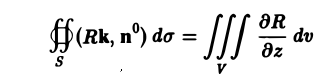
(интегралы по разрезу Sp взаимно уничтожаются). Рассмотрим, наконец, вектор
а = Р{х, у, z)i + Q(x, у, z)j + R(x, у, z)k.
Для каждой компоненты Pi, Qj, Rк мы можем написать формулу, аналогичную формуле (4) (все компоненты равноправны). Получим
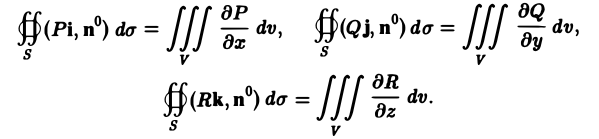
Складывая эти равенства и пользуясь линейностью потока и тройного интеграла, получаем формулу Гаусса—Остроградского
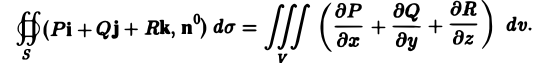
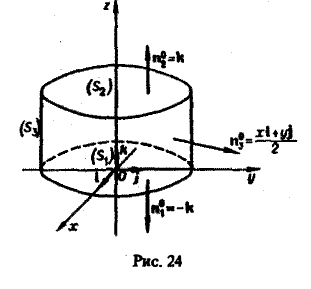
Пример:
Вычислить поток вектора
а = 2xi — (z — 1)k
через замкнутую поверхность
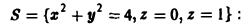
1) по определению, 2) по формуле Остроградского.
1) Поток вектора а равен сумме
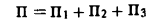
(рис. 24), где
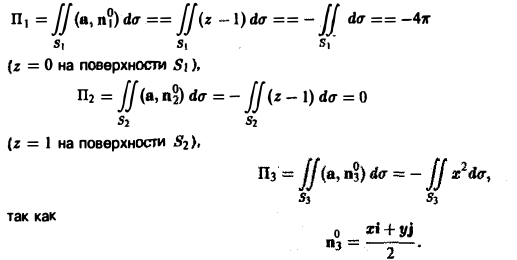
Перейдем на цилиндре к криволинейным координатам
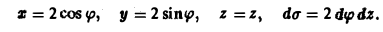
Тогда
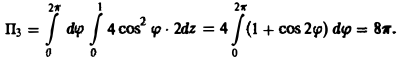
Следовательно, П = -4π + 0 + 8π = 4π.
2) По формуле Гаусса—Остроградского имеем
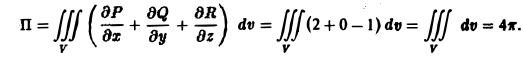
Пример:
Вычислить поток радиус-вектора
r = xi + yj + zk
через сферу радиуса R с центром в начале координат:
1) по определению; 2) по формуле Остроградского.
1) Так как для сферы
2) Сначала находим
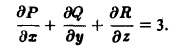
Отсюда
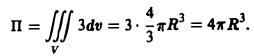
Пример:
Вычислить поток вектора
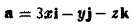
через замкнутую поверхность S, заданную условиями:
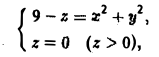
1) по определению; 2) по формуле Остроградстого (рис.25).
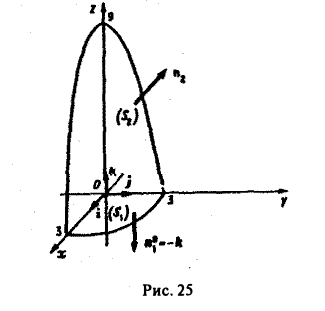
1} Имеем
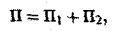
где
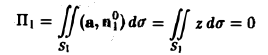
(на S1 имеем z = 0),
Поэтому
Имеем
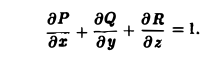
Поэтому
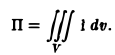
Переходя к цилиндрическим координатам
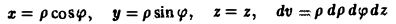
и замечая, что z = 9 — р на поверхности S, имеем
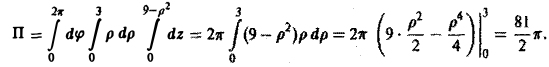
Замечание:
При вычислении потока через незамкнутую поверхность часто бывает удобно подходящим образом дополнить ее до замкнутой и воспользоваться формулой Гаусса—Оcтроградского.
Пример:
Вычислить поток вектора
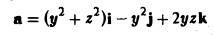
через поверхность S:
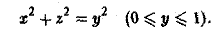
Заданная поверхность S есть конус с осью Оу (рис. 26).
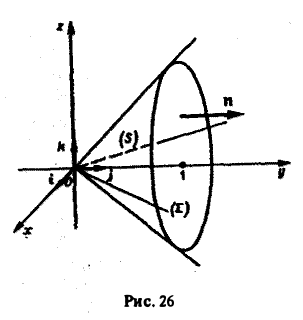
Замкнем этот конус куском Σ плоскости у = I. Тогда, обозначая через П1 искомый поток, а через П2 поток по поверхности Σ, будем иметь
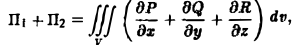
где V — объем конуса, ограниченного поверхностями S и Σ.
Так как
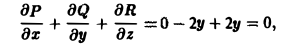
т.к. на поверхности Σ выполняется равенство у = 1. Следовательно, П1 = π.
Дивергенция векторного поля. Соленоидальные (трубчатые) поля
Пусть S — замкнутая поверхность. Рассмотрим поле скоростей v течения жидкости и вычислим поток жидкости через поверхность 5. Если он положителен, то это означает, что из той части пространства, которая ограничена поверхностью S, вытекает больше жидкости, чем втекает в нее. В этом случае говорят, что внутри S имеются источники (выделяющие жидкость). Напротив, если поток отрицателен, то внутрь S втекает больше жидкости, чем вытекает из нее. В этом случае говорят, что внутри S имеются стоки (поглощающие жидкость).
Тем самым, величина
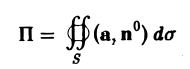
позволяет судить о природе части векторного поля, заключенного внутри поверхности S, а именно, о наличии источников или стоков внутри нее и их производительности (мощности).
Понятие о потоке вектора через замкнутую поверхность приводит к понятию дивергенции, или расходимости поля, которое дает некоторую количественную характеристику поля в каждой его точке.
Пусть М — изучаемая точка поля. Окружим ее поверхностью S произвольной формы, например, сферой достаточно малого радиуса. Область, ограниченную поверхностью 5, обозначим через (V), а ее объем через V.
Вычислим поток вектора а через поверхность S. Имеем
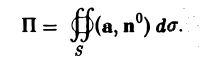
Составим отношение этого потока П к величине объема V,

Так как числитель представляет собой производительность источников (стоков) внутри области (V), то отношение (1) дает среднюю производительность единицы объема.
Определение:
Если отношение (1) имеет конечный предел, когда область (V) стягивается в точку М, то этот предел называют дивергенцией векторного поля (дивергенцией вектора а) в точке М и обозначают div а(М). То есть по определению
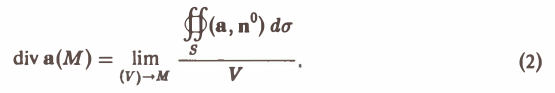
Дивергенция векторного поля есть скалярная величина (числитель и знаменатель дроби (2) суть скалярные величины).
Если diva(M) > 0, то в точке М расположен источник, если diva(M) < 0, то в точке М — сток.
Формула (2) позволяет сделать следующее заключение: дивергенция поля а в точке М есть объемная плотность потока вектора а в этой точке. Эта формула дает инвариантное определение дивергенции, не связанное с выбором систем координат — все величины, входящие в формулу (2), определяются непосредственно самим полем и от координатной системы не зависят.
Покажем, как вычисляется дивергенция в декартовых координатах при условии, что координаты вектора
а = Р(х, у, z)i + Q(x, у, z)j + R(x, y, z)k
непрерывны и имеют непрерывные частные производные 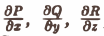
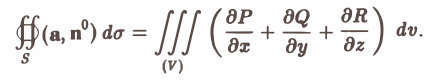
Пользуясь теоремой о среднем для тройного интеграла, получим
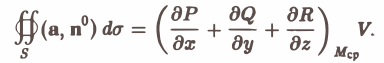
Подставляя это выражение в формулу (2), определяющую дивергенцию, найдем
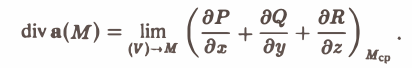
Когда область (V) стягивается в точку М, то и точка Мcp стремится к точке М и, в силу предположенной непрерывности частных производных, получаем
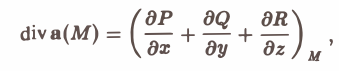
или, короче,
(3)
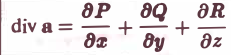
(все величины в формуле (3) вычисляются водной и той же точке).
Формула (3) дает выражение дивергенции в декартовых координатах. Попутно доказано само существование дивергенции вектора а при условии, что производные 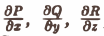
Используя формулу (3) для дивергенции, запишем формулу Гаусса—Остроградского в векторной форме. Имеем
(4)
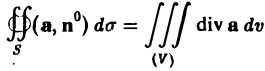
— поток вектора а через замкнутую поверхность S равен тройному интегралу от дивергенции вектора а по области (V), ограниченной поверхностью S.
Правила вычисления дивергенции
1, Дивергенция обладает свойством линейности
(5)
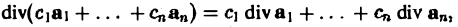
где С1,…, Сп — постоянные числа.
Пусть
а = Р(х, у, z)i + Q(x, у, z)j + R(x, у, z)k
и С — постоянное число. Тогда
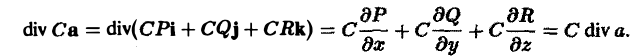
Если
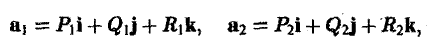
то
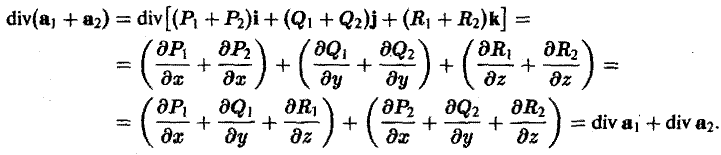
2. Дивергенция постоянного вектора с равна нулю
div e = 0. (6)
3. Дивергенция произведения скалярной функции и(М) на вектор а(М) вычисляется по формуле
div(ua) = u diva + (gprad u,a). (7)
В самом деле,
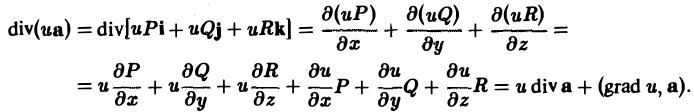
Пример:
Найти дивергенцию вектора
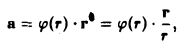
где r = |r| — расстояние от начала координат до переменной точки М(х,у,z),
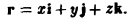
По формуле (7) имеем
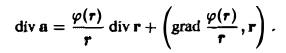
Так как r = xi + уj + zk. то
Трубчатое (соленоидальное) поле
Если во всех точках некоторой области G дивергенция векторного поля, заданного в этой области, равна нулю
div а ≡ 0, (8)
то говорят, что в этой области поле соленоидальное (или трубчатое).
Из формулы Гаусса—Остроградского вытекает, что в трубчатом поле поток вектора через любую замкнутую поверхность S, лежащую в этом поле, равен нулю
(9)
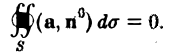
Свойства трубчатого поля
Рассмотрим в области, где задано поле вектора а, какую-нибудь площадку Σ (рис.27). Назовем векторной трубкой совокупность векторных линий, проходящих через границу γ = θΣ этой площадки. Пусть Σ1 — некоторое сечение векторной трубки. Выберем вектор нормали щ к сечению Σ1 так, чтобы он был направлен в ту же сторону, что и вектор а поля.
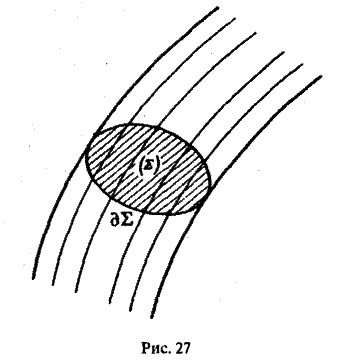
Теорема:
В трубчатом поле поток вектора а через любое сечение векторной трубки один и тот же.
Пусть Σ1 и Σ2 —непересекающиеся сечения одной и той же векторной трубки. Надо доказать, что
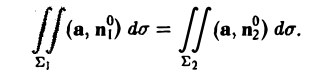
Обозначим через Σ3 часть поверхности векторной трубки, заключенную между сечениями Σ1 и Σ2. Поверхности Σ1, Σ2, Σ3 вместе образуют замкнутую поверхность Σ (рис.28).
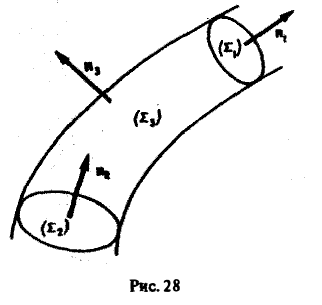
Так как по условию поле вектора а — трубчатое, то
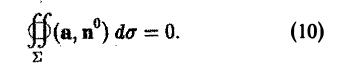
В силу аддитивности потока соотношение (10) можно переписать так:
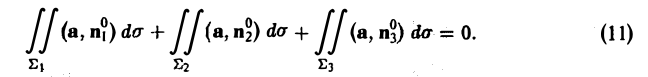
В точках поверхности Σ3, составленной из векторных линий, имеем 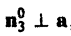
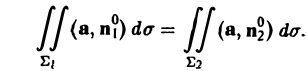
Пусть поверхность Σ имеет ориентированный замкнутый контур L своей границей. Будем говорить, что поверхность Σ натянута на контур L. Вектор нормали п к поверхности Σ будем ориентировать так, чтобы из конца нормали обход контура L был виден против часовой стрелки (рис. 29).
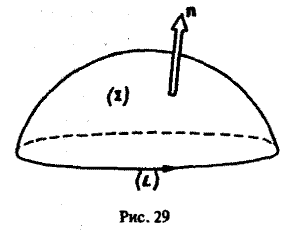
Теорема:
В трубчатом поле поток вектора а через любую поверхность, натянутую на данный контур, один и тот же:
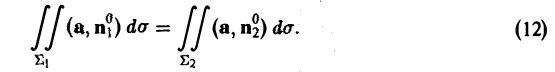
Замечание:
В трубчатом поле векторные линии могут быть либо замкнутыми кривыми, либо иметь концы на границе области, где поле задано.
Пример:
Рассмотрим силовое поле, создаваемое точечным зарядом q, помешенным в начале координат. Вычислим дивергенцию вектора Е напряженности

Имеем
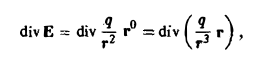
где
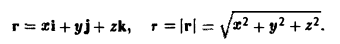
Пользуясь формулой (7), получим
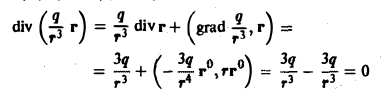
для r ≠ 0. Таким образом, поле вектора Σ, заданного формулой (13), будет трубчатым в любой области G, не содержащей точки O(0,0,0).
Вычислим поток вектора Σ через сферу Sr радиуса R с центром в начале координат O(0,0,0) (рис.30).
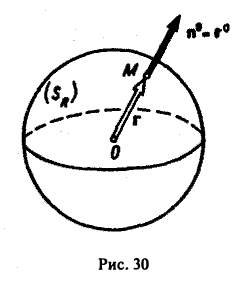
Имеем
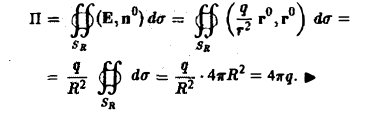
Замечание:
Можно показать, что поток вектора (13) через любую замкнутую поверхность Σ, охватывающую точку O(0,0,0), всегда равен 4 πg.
Циркуляция векторного поля. Ротор вектора. Теорема Стокса
Пусть в некоторой области G задано непрерывное векторное поле
а(М) = Р(х, у, х)i + Q(x, у, z)j + R(х, у, z)k
и замкнутый ориентированный контур L.
Определение:
Циркуляцией вектора а по замкнутому контуру L называется криволинейный интеграл 2-го рода от вектора а по контуру L
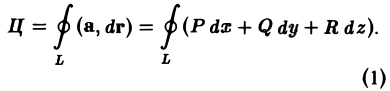
Здесь dr — вектор, длина которого равна дифференциалу дуги L, а направление совпадаете направлением касательной к L, определяемым ориентацией контура (рис. 31) символ 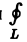
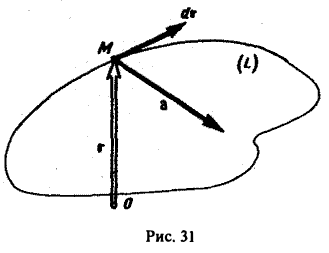
Пример:
Вычислить циркуляцию векторного поля
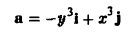
вдоль эллипса L:
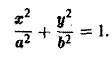
По определению циркуляции имеем
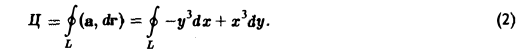
Параметрические уравнения данного эллипса имеют вид:
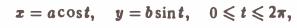
и, значит, dx = -a sin tdt, dy = b cos tdt. Подставляя эти выражения в формулу (2), найдем
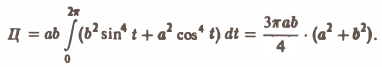
Ротор (вихрь) векторного поля
Рассмотрим поле вектора
а(М) = Р(х, у, z)i + Q(x, у, z)j + R(х, у, z)k,
Р, Q, R которого непрерывны и имеют непрерывные частные производные первого порядка по всем своим аргументам.
Определение:
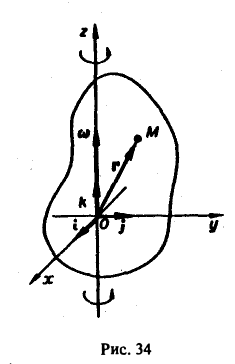
Ротором вектора а(M) называется вектор, обозначаемый символом rot а и определяемый равенством
или, в символической, удобной для запоминания форме,
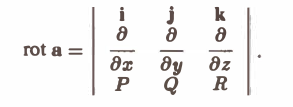
Этот определитель раскрывают по элементам первой строки, при этом операции умножения элементов второй строки на элементы третьей строки понимаются как операции дифференцирования, например,
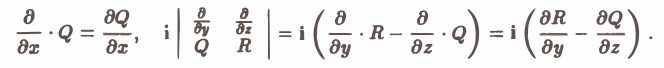
Определение:
Если в некоторой области G имеем rot а = 0, то поле вектора а в области G называется безвихревым.
Пример:
Найти ротор вектора
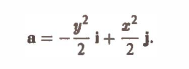
Согласно формуле (3) имеем
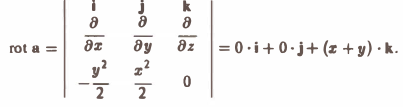
Так как rot а — вектор, то мы можем рассматривать векторное поле — поле ротора вектора а. Предполагая, что координаты вектора а имеют непрерывные частные производные второго порядка, вычислим дивергенцию вектора rot а. Получим
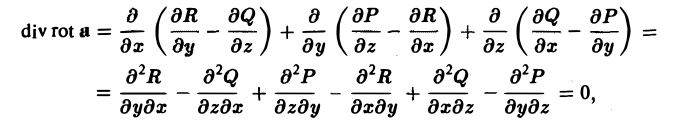
т. е.
div rot a = 0. (3′)
Таким образом, поле вектора rot а соленоидально.
Теорема Стокса:
Циркуляция вектора а вдоль ориентированного замкнутого контура L равна потоку ротора этого вектора через любую поверхность Е, натянутую на контур L,
При этом предполагается, что координаты вектора а имеют непрерывные частные производные в некоторой области G пространства, содержащей поверхность Σ, и что ориентация орта нормали п° к поверхности Σ С G согласована с ориентацией контура L так, что из конца нормали обход контура в заданном направлении виден совершающимся против часовой стрелки.
Учитывая, что а = Pi + Qj + Rk, n° = cos ai + cos βj + cos γk, и пользуясь определением ротора (3), перепишем формулу (4) в следующем виде:
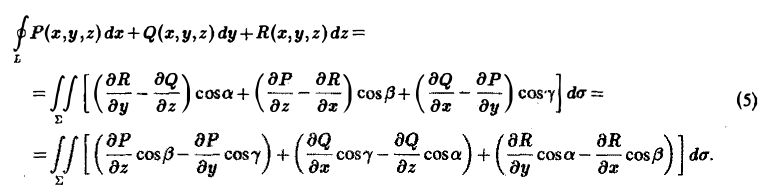
Рассмотрим сначала случай, когда гладкая поверхность Σ и ее контур L однозначно проектируются на область D плоскости хОу и ее границу — контур λ соответственно (рис. 32). Ориентация контура L порождает определенную ориентацию контура λ. Для определенности будем считать, что контур L ориентирован так, что поверхность Σ остается слева, так что веkтор нормали п к поверхности Σ составляет с осью Oz острый угол γ (cos γ > 0).
Пусть z = φ{х,у) — уравнение поверхности Σ и функция ф(х,у) непрерывна и имеет непрерывные частные производные 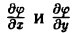
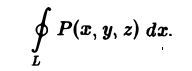
Линия L лежит на поверхности Σ. Поэтому, пользуясь уравнением этой поверхности z = φ(х, у),мы можем заменить z под знаком интеграла на φ(x, у). Координаты (х, у)
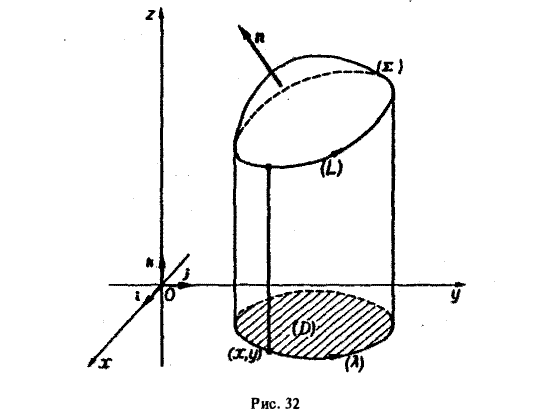
переменной точки кривой λ равны координатам соответствующей точки на кривой L, а потому интегрирование по L можно заменить интегрированием по λ,
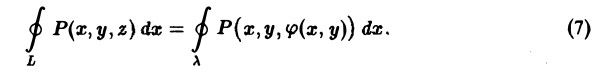
Применим к интегралу, стоящему справа, формулу Грина. Имеем
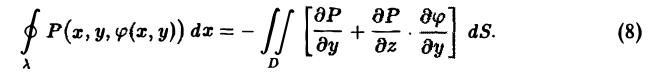
Перейдем теперь от интеграла по области D к интегралу по поверхности Σ. Так как dS = cos γ • dσ,то из формулы (8) получим, что
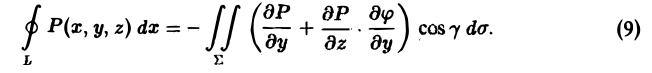
Вектор нормали n° к поверхности Σ определяется выражением
или n° = cos a • i + cos β • j + cos γ • k. Отсюда видно, что
Поэтому равенство (9) можно переписать так:
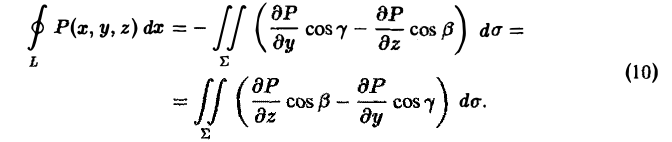
Считая Σ гладкой поверхностью, однозначно проектирующейся на все три координатные плоскости, аналогично убеждаемся в справедливости формул
Складывая равенства (10), (11) и (12) почленно, получим формулу Стокса (5), или, короче,
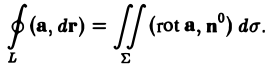
Замечание:
Мы показали, что поле вектора rota — соленоидальное, и потому поток вектора rota не зависит от вида поверхности Σ, натянутой на контур L.
Замечание:
Формула (4) выведена в предположении, что поверхность Σ однозначно проектируется на все три координатные плоскости. Ecли это условие не выполнено, то разбиваем Σ на части так, чтобы каждая часть указан ному условию удовлетворяла, а затем пользуемся аддитивностью интегралов.
Пример:
Вычислить циркуляцию вектора
а = yi — xj + k
по линии L:
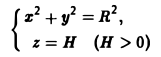
1) пользуясь определением; 2) по теореме Стокса.
1) Зададим линию L параметрически:
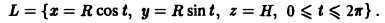
Тогда dx = -R sin t dt, dy = R cos t dt, H dz = 0, так что
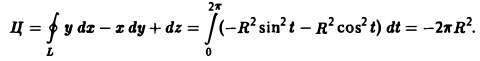
2) Найдем rot a:
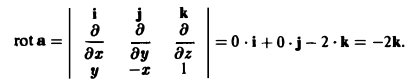
Натянем на контур L кусок плоскости z = H, так что п° = k. Тогда
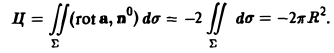
Инвариантное определение ротора поля
Из теоремы Стокса можно получить инвариантное определение ротора поля, не связанное с выбором системы координат.
Теорема:
Проекция ротора а на любое направление не зависит от выбора системы координат и равна поверхностной плотности циркуляции вектора а по контуру площадки, перпендикулярной этому направлению,
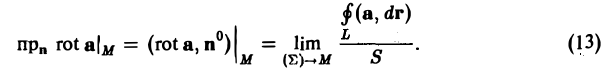
Здесь ( Σ ) — плоская площадка, перпендикулярная вектору п; S — площадь этой площадки; L — контур площадки, ориентированный так, чтобы обход контура был виден из конца вектора п против хода часовой стрелки; ( Σ ) → М означает, что площадка ( Σ ) стягиваетcя к точке М, в которой рассматривается вектор rot а, причем вектор нормали п к этой площадке остается все время одним и тем же (рис. 33).
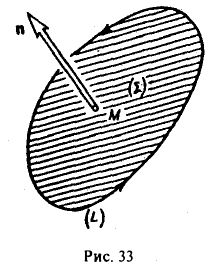
Применим сначала к циркуляции
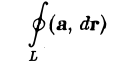
вектора а теорему Стокса, а затем к полученному двойному интегралу — теорему о среднем значении:
(скалярное произведение (rot a, n°) берется в некоторой средней точке Mср площадки ( Σ )).
При стягивании площадки ( Σ ) к точке М средняя точка Мср тоже стремится к точке М и, в силу предполагаемой непрерывности частных производных от координат вектора а (а значит, и непрерывности rot а), мы получаем
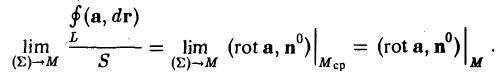
Поскольку проекция вектора rot а на произвольное направление не зависит от выбора системы координат, то сам вектор rota инвариантен относительно этого выбора. Отсюда получаем следующее инвариантное определение ротора поля: ротор поля есть вектор, длина которого равна наибольшей поверхностной плотности циркуляции в данной точке, направленный перпендикулярно той площадке, на которой эта наибольшая плотность циркуляции достигается; при этом ориентация вектора rot a согласуется с ориентацией контура, при которой циркуляция положительна, по правилу правого винта.
Физический смысл ротора поля
Пусть твердое тело вращается вокруг неподвижной оси l с угловой скоростью w. Не нарушая общности, можно считать, что ось l совпадает с осью Oz (рис. 34). Пусть М(г) — изучаемая точка тела, где
r = xi + уj + zk.
Вектор угловой скорости в нашем случае равен w ≡ wk, вычислим вектор v линейной скорости точки М,
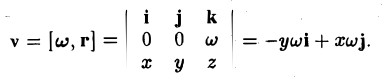
Отсюда
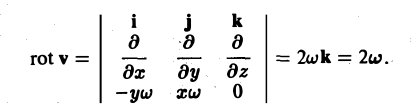
Итак, вихрь поля скоростей вращающегося твердого тела одинаков во всех точках поля, параллелен оси вращения и равен удвоенной угловой скорости вращения.
Правила вычисления ротора
1, Ротор постоянного вектора с равен нулевому вектору,
rot e = 0.
2. Ротор обладает свойством линейности
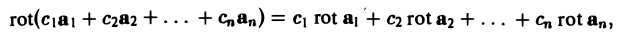
где c1, c2,…, cn — постоянные числа.
3. Ротор произведения скалярной функции и(М) на векторную а(М) вычисляется по формуле
rot(wa) = и rot а + [grad и, а].
В самом деле,
Независимость криволинейного интеграла от пути интегрирования
Определение:
Область G трехмерного пространства называется поверхностно односвязной, если на любой замкнутый контур, лежащий в этой области, можно натянуть поверхность, целиком лежащую в области G.
Например, внутренность сферы или все трехмерное пространство являются поверхностно односвязными областями; внутренность тора или трехмерное пространство, из которого исключена прямая, поверхностно односвязными областями не являются.
Пусть в поверхностно односвязной области G задано непрерывное векторное поле
а (М) = Р(М)i + Q(M)j + R(M) k.
Тогда имеет место следующая теорема.
Теорема:
Для того чтобы криволинейный интеграл
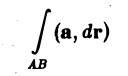
в поле вектора а не зависел от пути интегрирования, а зависел только от начальной и конечной точек пути (А и В), необходимо и достаточно, чтобы циркуляция вектора a вдаль любого замкнутого контура L, расположенного в области G, была равна нулю.
Необходимость. Пусть интеграл
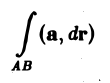
не зависит от пути интегрирования. Покажем, что тогда
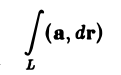
по любому замкнутому контуру L равен нулю.
Рассмотрим произвольный замкнутый контур L в поле вектора а и возьмем на нем произвольно точки A и В (рис.35).
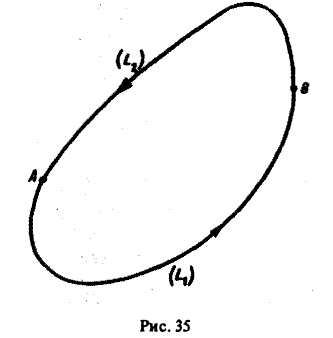
По условию имеем
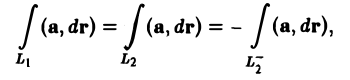
где L1 и L2 — различные пути, соединяющие точки А и В; откуда

Но L1 U L2 как раз и есть выбранный замкнутый контур L. Достаточность. Пусть
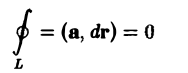
для любого замкнутого контура L. Покажем, что в этом случае интеграл
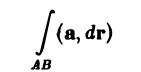
не зависит от пути интегрирования.
Возьмем в поле вектора а две точки А и В, соединим их произвольными линиями L1 и L2 к покажем, что

Для простоты ограничимся случаем, когда линии L1 и L2 не пересекаются. В этом случае объединение L1 ∪ L2 образует простой замкнутый контур L (рис. 36).
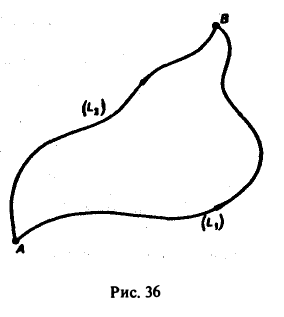
По условию
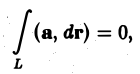
а по свойству аддитивности
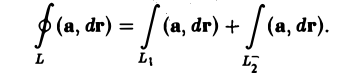
Следовательно,
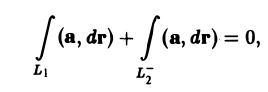
откуда справедливость равенства (2) и вытекает.
Теорема 9 выражает необходимое и достаточное условия независимости криволинейного интеграла от формы пути, однако эти условия трудно проверяемы. Приведем более эффективный критерий.
Теорема:
Для того, чтобы криволинейный интеграл
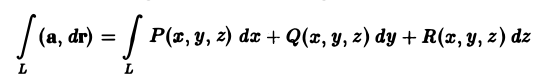
не зависел от пути интегрирования L, необходимо и достаточно, чтобы векторное поле а(М) = Р(X, у, z)i + Q(x, у, z)j + R(x, у, z)k было безвихревым,
rot a(M) = 0. (3)
Здесь предполагается, что координаты Р(х, у, z), Q(x, у, z), R(x, у, z) вектора а(М) имеют непрерывные частные производные первого порядка и область определения вектора а(М) поверхностно односвязна.
Замечание:
В силу теоремы 9 независимость криволинейного интеграла от пути интегрирования равносильна равенству нулю циркуляции вектора а вдоль любого замкнутого контура. Это обстоятельство мы используем при доказательстве теоремы.
Необходимость. Пусть криволинейный интеграл не зависит от формы пути, или, что то же, циркуляция вектора а по любому замкнутому контуру L равна нулю. Тогда
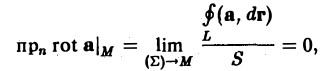
т. е. в каждой точке поля проекция вектора rot а на любое направление равна нулю. Это означает, что сам вектор rot а равен нулю во всех точках поля,
rot а ≡ 0.
Достаточность. Достаточность условия (3) вытекает из формулы Стокса, так как если rot а ≡ 0, то и циркуляция вектора по любому замкнутому контуру L равна нулю:
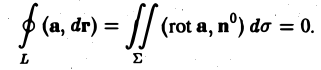
Ротор плоского поля a = P(x, y)i + Q(x, y)j равен
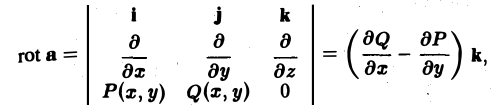
что позволяет сформулировать для плоского поля следующую теорему.
Теорема:
Для того, чтобы криволинейный интеграл
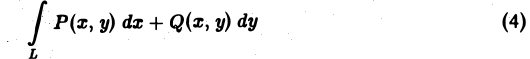
в односвязном плоском поле не зависел от формы линии L, необходимо и достаточно, чтобы соотношение

выполнялось тождественно во всей рассматриваемой области.
Если область неодносвязна, то выполнение условия
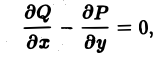
вообще говоря, не обеспечивает независимости криволинейного интеграла от формы линии.
Пример:
Пусть
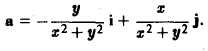
Рассмотрим интеграл
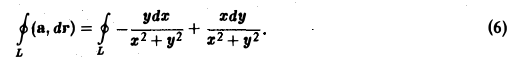
Ясно, что подынтегральное выражение не имеет смысла в точке 0(0,0). Поэтому исключим эту точку. В остальной части плоскости (это будет уже не сщносвязная область!) координаты вектора а непрерывны, имеют непрерывные частные производные и
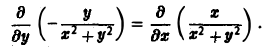
Рассмотрим интеграл (6) вдоль замкнутой кривой L — окружности радиуса R с центром в начале координат
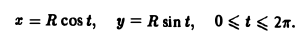
Отличие циркуляции от нуля показывает, что интеграл (6) зависит от формы пути интегрирования.
Потенциальное поле
Определение:
Поле вектора а(М) называется потенциальным, если существует скалярная функция и{М) такая, что
grad и = a. (1)
При этом функция и{М) называется потенциалом поля ее поверхности уровня называются эквипотенциальными поверхностями.
Пусть
а = Р(х, у, z)i + Q(x, у, z)j + R(x, у, z)k.
Так как
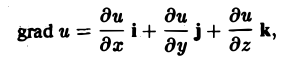
то соотношение (1) равносильно следующим трем скалярным равенствам:
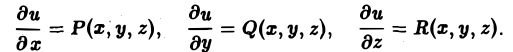
Заметим, что потенциал поля определяется с точностью до постоянного слагаемого: если grad и = а и grad v = а, то
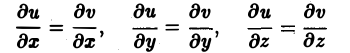
и, следовательно, и = v + с, где с — постоянное число.
Пример:
Поле радиус-вектора г является потенциальным, так как
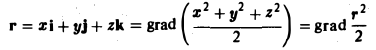
(напомним, что 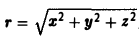
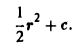
Пример:
Поле вектора
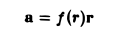
является потенциальным.
Пусть функция φ(r) такая, что
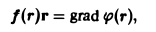
найдена. Тогда
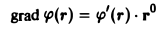
и
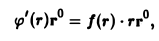
откуда
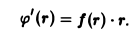
Значит,
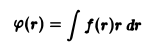
— потенциал поля.
Теорема:
Для того чтобы поле вектора а было потенциальным, необходимо и достаточно, чтобы оно было безвихревым,
rot а ≡ 0, (2)
т. е. чтобы его ротор равнялся нулю во всех точках поля. При этом предполагается непрерывность всех частных производных от координат вектора а и поверхностная односвязность области, в которой задан вектор а.
Необходимость. Необходимость условия (2) устанавливается непосредственным подсчетом: если поле потенциально, т. е. а = grad и, то
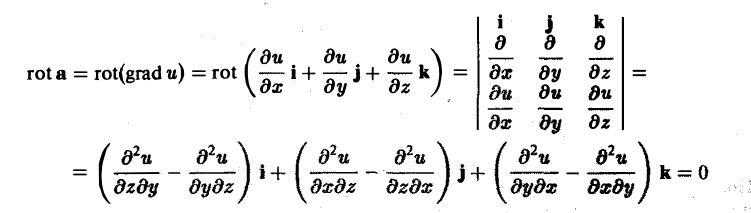
в силу независимости смешанных производных от порядка дифференцирования.
Достаточность. Пусть поле вектора безвихревое (2). Для того чтобы доказать потенциальность этого поля, построим его потенциал и(М). Из условия (2) следует, что криволинейный интеграл

не зависит от формы линии L, а зависит только от ее начальной и конечной точек. Зафиксируем начальную точку Мо(xo, yо, zo), а конечную точку М(х, y, z) будем менять. Тогда интеграл (3) будет функцией точки М(х, у, z). Обозначим эту функцию через и(М) и докажем, что
grad u = а.
В дальнейшем будем записывать интеграл (3), указывая лишь начальную и конечную точку пути интегрирования,
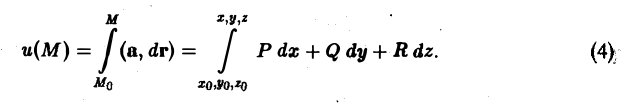
Равенство grad и = а равносильно трем скалярны м равенства м
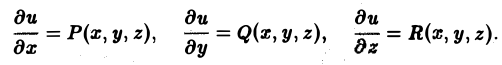
Докажем первое из них,
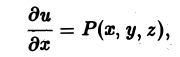
второе и третье равенства доказываются аналогично.
По определению частной производной имеем
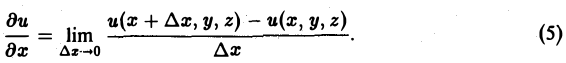
Рассмотрим точку М1(х + ∆х, у, z), близкую к точке M(x,y,z). Так как функция и(М) определяется соотношением (4), в котором криволинейный интеграл не зависит от пути интегрирования, то выберем путь интегрирования так, как указано на рис.37.
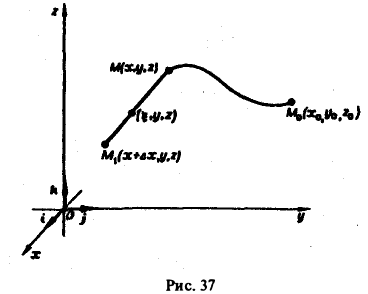
Тогда
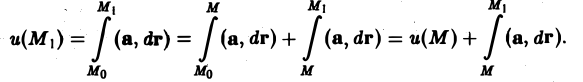
Отсюда
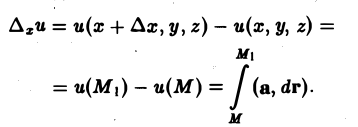
Последний интеграл берется вдоль отрезка прямой ММ1, параллельной оси Ох. На этом отрезке в качестве параметра можно принять координату х:
x = х, у = const, z = const.
Тогда dx = dx,dy = 0, dz = 0, так что
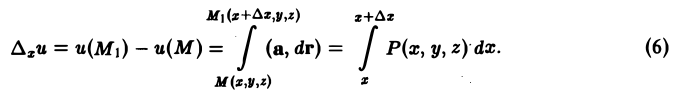
Применяя к интегралу в правой части (6) теорему о среднем, получаем

где величина ξ заключена между х и х + ∆х. Из формулы (7) вытекает, что
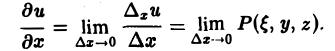
Так как ξ —► x при ∆x —» 0, то в силу непрерывности функции Р(х, у, z) получаем
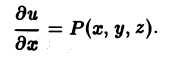
Аналогично доказывается, что
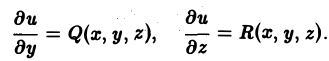
Следствие:
Векторное поле является потенциальным тогда и только тогда, когда криволинейный интеграл в нем не зависит от пути.
Вычисление криволинейного интеграла в потенциальном поле
Теорема:
Интеграл 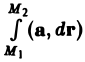
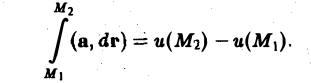
Ранее былодоказано, что функция

является потенциалом поля.
В потенциальном поле криволинейный интеграл
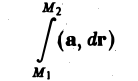
не зависит от пути интегрирования. Поэтому, выбирая путь отточки М1 к точке М2 так, чтобы он прошел через точку Mo (рис. 38), получаем
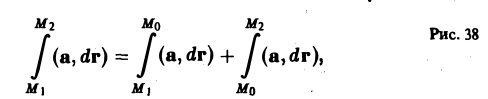
или, меняя ориентацию пути в первом интеграле справа,
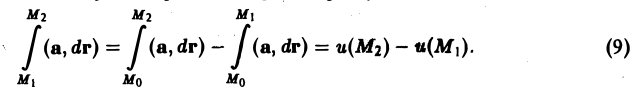
Так как потенциал поля определяется с точностью до постоянного слагаемого, то любой потенциал рассматриваемого поля можетбыть записан в виде
v(M) = u(M) + c, (10)
где с — постоянная.
Делая в формуле (10) замену u(M2) = v(M2) — с, и(М1) = v(M1) — с, получим для произвольного потенциала v(M) требуемую формулу
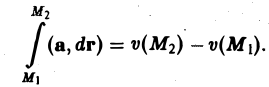
Пример:
В примере 1 было показано, что потенциалом поля радиус-вектора г является функция
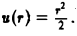
Поэтому
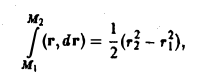
где ri (i = 1,2) — расстояние от точки Mi(i = 1,2) до начала координат.
Вычисление потенциала в декартовых координатах
Пусть задано потенциальное поле
а(М) = Р(х, у, г)i + Q(x, у, z)j + R(x, у, z)k.
Ранее было показано, что потенциальная функция и(М) может быть найдена по формуле
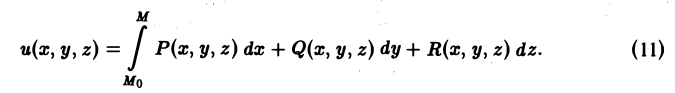
Интеграл (11) удобнее всего вычислять так: зафиксируем начальную точку Мо(хо, yо, zо) и соединим ее с достаточно близкой текущей точкой M(x,y,z) ломаной М0М1М2М, звенья которой параллельны координатным осям, М0М1,||Ох, M1М2||Оу, М2М|| Oz (рис.39).
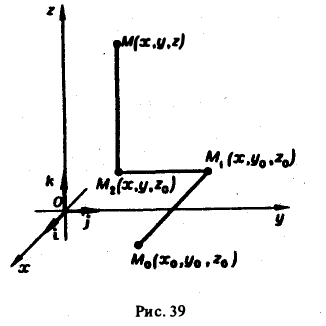
При этом на каждом звене ломаной изменяется только одна координата, что позволяет существенно упростить вычисления. В самом деле, на отрезке М0М1 имеем:
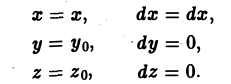
На отрезке М1М2:
х = const, dx = 0, у = у, dy = dy, z = z0 и dz = 0.
На отрезке M1M:
x = const, dx = 0, у = const, dy = 0, z = z и dz = dz.
Следовательно, потенциал u(M) равен
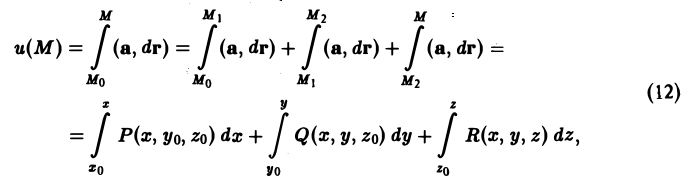
где x, у, z — координаты текущей точки на звеньях ломаной, вдоль которых ведется интегрирование.
Пример:
Доказать, что векторное поле
а = {у + z)i + (х + z)j + (х + y)k
является потенциальным, и найти его потенциал.
Проверим, будет ли поле вектора а(М) потенциально. С этой целью вычислим ротор поля. Имеем
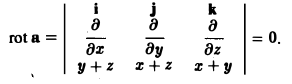
Поле является потенциальным. Потенциал этого поля найдем с помощью формулы (12). Возьмем за начальную точку Mо начало координат О (так обычно поступают, если поле а(М) определено в начале координат). Тогда получим
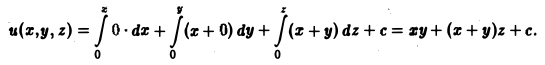
Итак,
u(z, у, z) = ху + xz + yz + с,
где с — произвольная постоянная.
Потенциал этого поля можно найти и по-иному. По определению потенциал и(х, у, г) есть скалярная функция, для которой grad и = а. Это векторное равенство равносильно трем скалярным равенствам:

Интегрируя (13) по х, получим
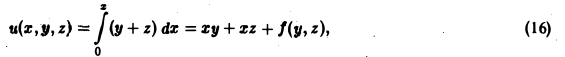
где f(y,z) — произвольная дифференцируемая функция от у и z. Продифференцируем (16) по у:
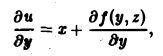
откуда, учитывая (14), будем иметь
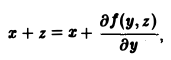
или

Проинтегрировав (17) по у, найдем
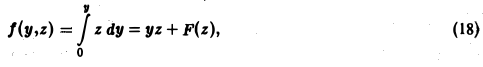
где F(z) — некоторая функция х. Подставив (18) в (16), получим
и(х, у, z) = ху + xz + у z + F(z).
Дифференцируя последнее равенство по z и учитывая соотношение (15), получим уравнение для F(z),
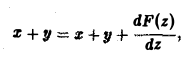
откуда 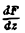
u(x,y,z) = ху +yz + zx +с.
Оператор Гамильтона
Мы рассмотрели три основные операции векторного анализа: вычисление grad и для скалярного поля и = и(х, у, z) и div а и rot а для векторного поля а = а(x, у, z). Эти операции могут быть записаны в более простом виде с помощью символического оператора ∇ («набла»): (1)
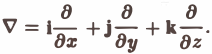
Оператор ∇ (оператор Гамильтона) обладает как дифференциальными, так и векторными свойствами. Формальное умножение, например, умножение 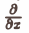
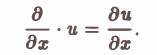
В рамках векторной алгебры формальные операции над оператором ∇ будем проводить так, как если бы он был вектором. Используя этот формализм, получим следующие основные формулы:
1, Если и = и(х, у, z) — скалярная дифференцируемая функция, то по правилу умножения вектора на скаляр получим
2. Если
a = P(x, y, z)i + Q(x, y, z)j + (x, y, z)k,
где P, Q, R — дифференцируемые функции, то по формуле для нахождения скалярного произведения получим
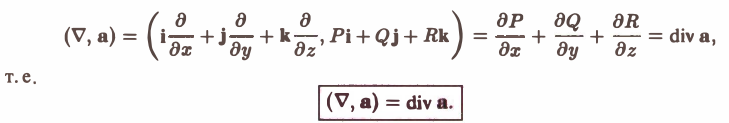
3. Вычисляя векторное произведение [ ∇, а], получим
Для постоянной функции и = с получим
∇c = 0,
а для постоянного вектора с будем иметь
( ∇, с) = 0 и [ ∇, с] = 0.
Из распределительного свойства для скалярного и векторного произведений получаем
( ∇, a + b) = ( ∇, а) + ( ∇, b),
Замечание:
Формулы (5) и (6) можно трактовать так же как проявление дифференциальных свойств оператора «набла»( ∇ — линейный дифференциальный оператор). Условились считать, что оператор ∇ действует на все величины, написанные за ним. В этом смысле, например,
( ∇, а) ≠ (а, ∇ ),
ибо ( ∇, а) = div а есть функция 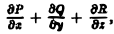
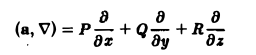
— скалярный дифференциальный оператор.
Применяя оператор ∇ к произведению каких-либо величин, надо иметь в виду обычное правило дифференцирования произведения.
Пример:
Доказать, что
grad(u v) = v Brad и + u grad v. (7)
По формуле (2) с учетом замечания 1 получаем
∇(uv) = v∇u + u ∇v,
или
grad(uv) = v grad u + u grad v.
Чтобы отметить тот факт, что «набла» не действует на какую-либо величину, входящую в состав сложной формулы, эту величину отмечают индексом с («const»), который в окончательном результате опускается.
Пример:
Пусть и(x,y,z) — скалярная дифференцируемая функция, a(x,y,z) — векторная дифференцируемая функция. Доказать, что
div(ua) =u diva + (a, grad u). (8)
Перепишем левую часть (8) в символическом виде
div(ua) = ( ∇, ua).
Учитывая дифференциальный характер оператора ∇, получаем
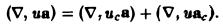
Так как ис — постоянный скаляр, то его можно вынести за знак скалярного произведения, так что
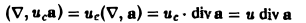
(на последнем шаге мы опустили индекс с).
В выражении ( ∇, иас) оператор ∇ действует только на скалярную функцию и, поэтому
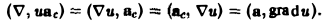
В итоге получаем
div(ua) = u div а + (a, grad и).
Замечание:
Используя формализм действий с оператором ∇ как с вектором, надо помнить, что ∇ не является обычным вектором — он не имеет ни длины, ни направления, так что, например, вектор ( ∇, а} не будет, вообще говоря, перпендикулярным вектору а (впрочем, для плоского поля а = Р(х, y)i + Q(x, y)j вектор
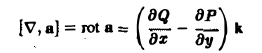
перпендикулярен плоскости хОу, а значит, и вектору а).
Не имеет смысла и понятие коллинеарности по отношению к символическому вектору ∇. Например, выражение [∇ φ, ∇ ψ] где φ и ψ — скалярные функции, формально напоминает векторное произведение двух кoллинеарных векторов, которое всегда равно нулю. Однако в общем случае это не имеет места. В самом деле, вектор ∇ φ = grad φ направлен по нормали к поверхности уровня φ = const, а вектор ∇ ψ = grad ψ определяет нормаль к поверхности уровня ψ = const. В общем случае эти нормали не обязаны быть коллинеарными (рис. 40). С другой стороны, в любом дифференцируемом скалярном поле φ (х, у, z) имеем [∇ φ, ∇ ψ] = 0.
Эта примеры показывают, что с оператором «набла» нужно обращаться с большой осторожностью и при отсутствии уверенности в полученном результате его следует проверить аналитическими методами.
Дифференциальные операции второго порядка. Оператор Лапласа
Дифференциальные операции второго порядка получаются в результате двукратного применения оператора ∇.
1, Пусть имеем скалярное поле и = и(x,y,z). В этом поле оператор ∇ порождает векторное поле
∇u = grad и.
В векторном поле grad и можно определить две операции:
( ∇, ∇u) = div grad u, (1)
что приводит к скалярному полю, и
[ ∇, ∇m] = rot grad u, (2)
что приводит к векторному полю.
2. Пусть задано векторное поле а = Pi + Qj + Rk. Тогда оператор (2) порождает в нем скалярное поле
(∇, а) = div a.
В скалярном поле div а оператор ∇ порождает векторное поле
∇ (∇,a) = grad div а. (3)
3. В векторном поле а = Pi + Qj + Rк оператор ∇ порождает также векторное поле
[∇, а] = rot a.
Применяя к этому полю снова оператор ∇, получим:
а) скалярное поле
(∇, [∇, а]) = div rot а, (4).
б) векторное поле
(∇, [∇, а]) = rot rot а. (5)
Формулы (1)-(5) определяют так называемые дифференциальные операции второго порядка.
Выберем в пространстве прямоугольную декартову систему координат Oxyz и рассмотрим каждую из формул (1)-(5) более подробно.
1, Предполагая, что функция и(х, у, z) имеет непрерывные вторые частные производные по х, у и z, получим
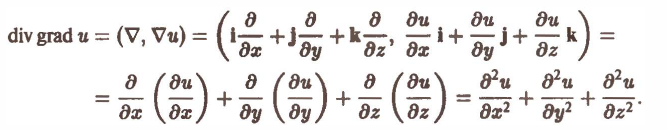
Символ
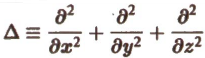
называется оператором Лапласа, или лапласианом. Его можно представить как скалярное произведение оператора Гамильтона ∇ на самого себя, т.е.
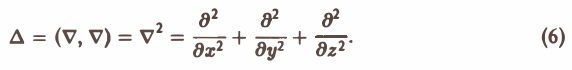
Оператор ∆ (дельта) играет важную роль в математической физике. Уравнение (6)
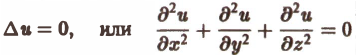
называется уравнением Лапласа. С его помощью описывается, например, стационарное распределение тепла.
Скалярное поле и(х, у, z), удовлетворяющее условию ∆и = 0, называется лапла-совым или гармоническим полем.
Например, скалярное поле и = 2х2 + Зу — 2x2 является гармоническим во всем трехмерном пространстве: из того, что
2. Пусть функция u(z, у, z) имеет непрерывные частные производные второго порядка включительно. Тогда
rot grad u ≡ 0. (7)
В самом деле, действуя формально, получим
rot grad и = [∇, ∇u] = [ ∇, ∇ ] u = 0,
ибо [∇, ∇] = 0 как векторное произведение двух одинаковых «векторов».
Тот же результат можно получить, используя выражения градиента и ротора в декартовых координатах
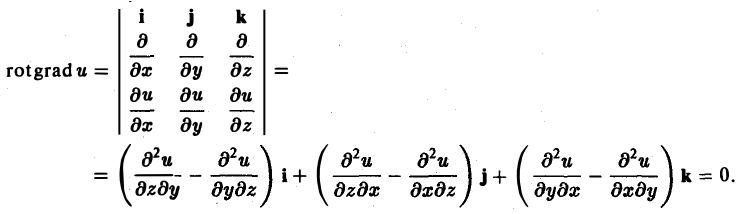
3. Пусть задано векторное поле
а = Р(х, у, z)i + Q(x, у, z)j + R(x, у, z)k,
координаты которого P, Q, R имеют непрерывные частные производные второго порядка. Тогда получим
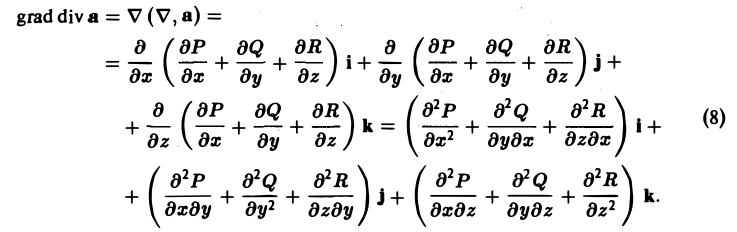
4. При тех же условиях, что и в пункте 3, имеем (9)
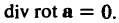
Это соотношение уже было доказано ранее путем непосредственных вычислений. Здесь мы приведем его формальное доказательство, используя известную формулу из векторной алгебры
(А, [В, С]) = (С,[А,В])= (В, [С, А]).
Имеем
div rot а = (∇, [∇, а]) = (а, [∇, ∇]) = О,
так как [∇, ∇] = 0 как векторное произведение двух одинаковых «векторов».
5. Покажем, наконец, что при тех же условиях, что и ранее,
rot rot а = grad div а — ∆а. (10)
Так как
rot rot а = [ ∇, [∇,a]),
то, полагая в формуле для двойного векторного произведения [А, [В, С]] = В(А, С) — (А, В)С,
А = ∇, B = ∇, С = а,
получим
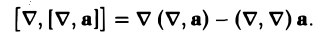
Но ( ∇, а) = div а и ( ∇, ∇) = ∆. Поэтому окончательно будем иметь
rot rot а = grad div а — ∆а,
где grad div а выражается по формуле (8), а ∆а для вектора а = Pi + Qj + Rk надо понимать так:
∆а = ∆Р • i + ∆Q • j + ∆R • k.
В заключение приведем таблицу дифференциальных операций второго порядка.
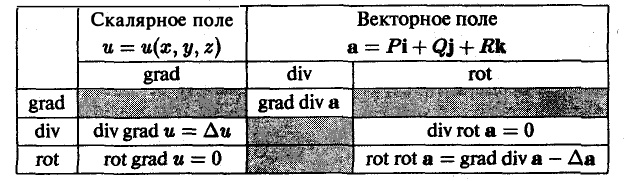
Заштрихованные прямоугольники означают, что соответствующая операция не имеет смысла (например, градиент от rot а).
Понятие о криволинейных координатах
Во многих задачах бывает удобно определять положение точки простр анства не декартовыми координатами (х, у, z), а тремя другими числами (q1, q2, q3), более естественно связанными с рассматриваемой частной задачей.
Если задано правило, согласно которому каждой точке М пространства отвечает определенная тройка чисел (q1, q2, q3) и, обратно, каждой такой тройке чисел отвечает единственная точка М, то говорят, что в пространстве задана криволинейная координатная система. В этом случае величины q1, q2, q3 называют криволинейными координатами точки М.
Координатными поверхностями в системе криволинейных координат q1, q2, q3 называются поверхности
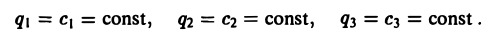
На координатных поверхностях одна из координат сохраняет постоянное значение. Линии пересечения двух координатных поверхностей называются координатными линиями.
В качестве примеров криволинейных координат рассмотрим цилиндрические и сферические координаты.
Цилиндрические координаты
В цилиндрических координатах положение точки М в пространстве определяется тремя координатами:
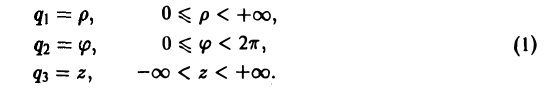
Координатные поверхности:
р = const — круговые цилиндры с осью Оz;
φ = const — полуплоскости, примыкающие к оси Oz;
z = const — плоскости, перпендикулярные оси Oz (рис. 41).
Координатные линии:
1) линии (р) — лучи, перпендикулярные оси Oz и имеющие начало на этой оси, т. е. линии пересечения координатных поверхностей φ = const, z = const;
2) линии (φ) — окружности с центрами на оси Oz, лежащие в плоскостях, перпендикулярных оси Oz;
3) линии (z) — прямые, параллельные оси Oz.
Связь декартовых координат точки (х, у, z) с цилиндрическими координатами (р, φ, z) задается формулами
x = p cos φ, y = p sin φ, z = z. (2)
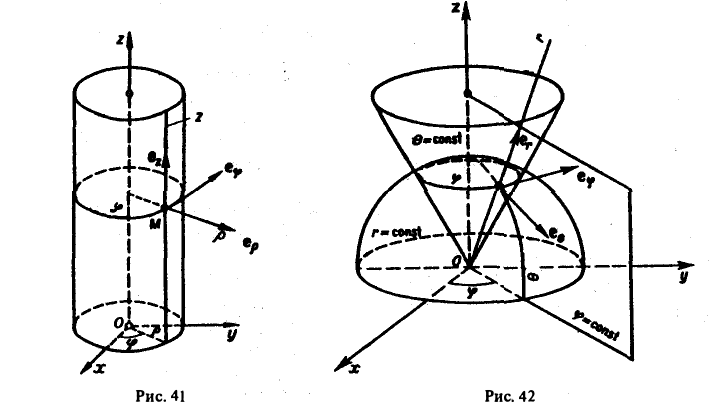
Сферические координаты
В сферических координатах положение точки М в пространстве определяется следующими координатами:
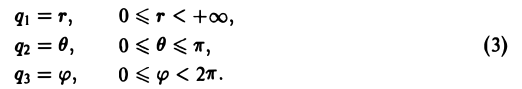
Координатные поверхности (рис. 42):
r = const — сферы с центром в точке О;
θ = const — круговые полуконусы с осью Oz;
φ = const — полуплоскости, примыкающие к оси Oz.
Координатные линии:
1) линии (г) — лучи, выходящие из точки О;
2) линии (θ) — меридианы на сфере;
3) линии (φ) — параллели на сфере.
Связь декартовых координат (х, у, z) точки М с ее сферическими координатами (r, θ, φ) задается формулами
х = r cos φ sin θ,
у = r sin φ sin θ, (4)
z = r cos θ.
Введем единичные векторы e1, е2, е3 (орты), направленные по касательным к координатным линиям(q1),(q2),(q3)в тoчке М в сторону возрастания переменных q1,q2,q3 соответственно.
Определение:
Система криволинейных координат называется ортогональной, если в каждой точке М орты e1, е2, е3 попарно ортогональны.
В такой системе ортогональны и координатные линии, и координатные поверхности.
Примерами ортогональных криволинейных координат служат системы цилиндрических и сферических координат. Мы ограничимся рассмотрением только ортогональных систем координат.
Пусть r = r(q1, q2, q3) — радиус-вектор точки М. Тогда можно показать, что
(5)
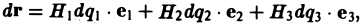
где
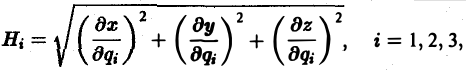
— коэффициенты Ламэ данной криволинейной системы координат. Вычислим коэффициенты Ламэ для цилиндрических координат
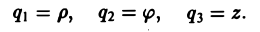
Так как х = р cos φ, у = р sin φ, z = z, то
(6)
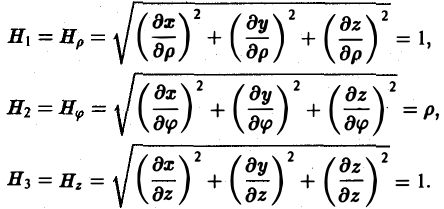
Аналогично для сферических координат имеем
(7)
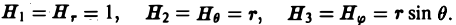
Величины
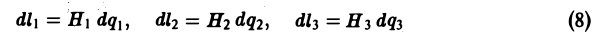
являются дифференциалами длин дуг соответствующих координатных линий.
Основные операции векторного анализа в криволинейных координатах
Дифференциальные уравнения векторных линий
Рассмотрим поле вектора
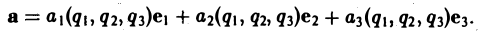
Уравнения векторных линий в криволинейных координатах q1,q2, q3 имеют вид
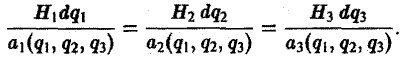
В цилиндрических координатах (q1 = р, q2= φ, q3 = z)
(1)
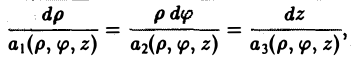
в сферических координатах (q1 = r, q2 = θ, q3 = φ)
(2)
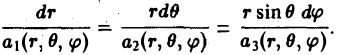
Градиент в ортогональных координатах
Пусть и = u(q1, q2, q3) — скалярное пoле. Тогда
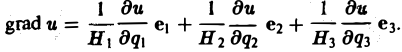
В цилиндрических координатах (q1 = р, q2 = φ, q3 = z)
(3)
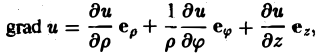
в сферических координатах (q1 = r, q2 = θ, q3 = φ) (4)
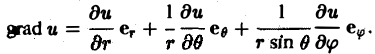
Ротор в ортогональных координатах
Рассмотрим векторное поле
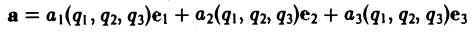
и вычислим rot а. Имеем
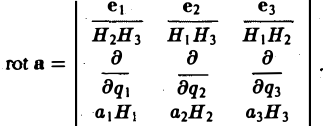
В цилиндрических координатах
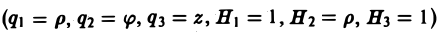
(5)
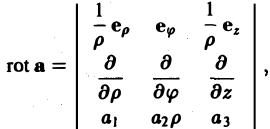
в сферических координатах
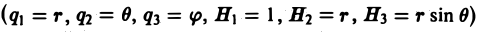
(6)
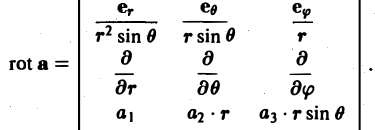
Дивергенция в ортогональных координатах
Дивергенция div а векторного поля
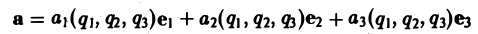
вычисляется по формуле
(7)
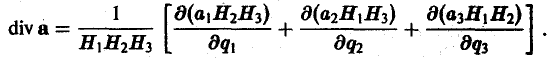
В цилиндрических координатах
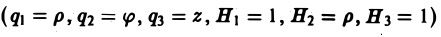
в цилиндрических координатах
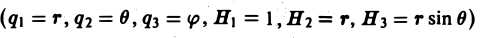
в сферических координатах
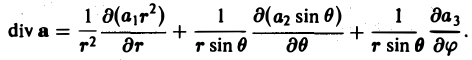
Применяя формулу (7) к единичным векторам е1, е2, е3, получим
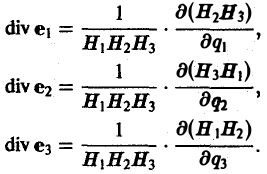
Вычисление потока в криволинейных координатах
Пусть S — часть координатной поверхности q1 = с = const, ограниченная координатными линиями
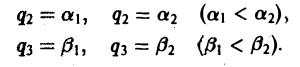
Тогда поток вектора
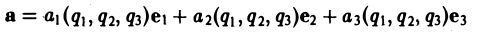
через поверхность S в направлении вектора e1 вычисляется по формуле
(8)
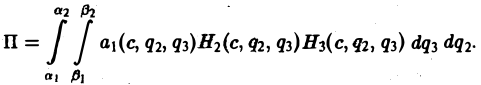
Аналогично вычисляется поток через часть поверхности q2 = с, а также через часть поверхности д3 = с, где с = const.
Пример:
Найти поток П векторного поля
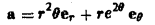
через внешнюю сторону верхней полусферы S радиуса R с центром в начале координат.
Полусфера S есть часть координатной поверхности r = const, а именно r = R. На полусфере S имеем
Учитывая, что в сферических координатах
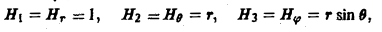
по формуле (8) найдем
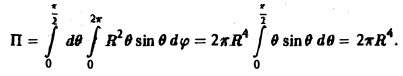
Вычисление потенциала в криволинейных координатах
Пусть в некоторой области Ω задано потенциальное векторное поле
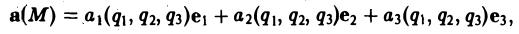
т. e. rot а = 0 в области Ω.
Для нахождения потенциала и = и(q1, q2, q3) этого векторного поля запишем равенство а(М) = grad u(M) в следующем виде:
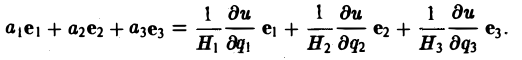
Отсюда следует, что
(9)
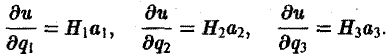
Интегрируя систему дифференциальных уравнений с частными производными (9), найдем искомый потенциал
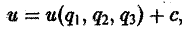
где с — произвольная постоянная.
В цилиндрических координатах
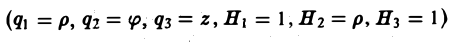
система (9) принимает вид
В сферических координатах
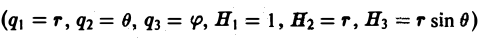
система (9) имеет вид
Пример:
Найти потенциал векторного поля, заданного в цилиндрических координатаx
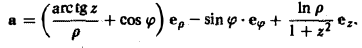
Убедимся, что rot a = 0. По формуле (S) получим
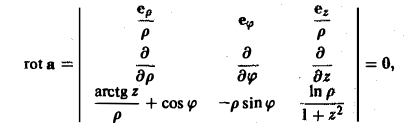
т.е. данное поле потенциально.
Искомый потенциал u = и(р, φ, z) является решением следующей системы дифференциальных уравнений с частными производными (см. формулу (10)):
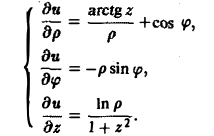
Интегрированием по р из первого уравнения находим
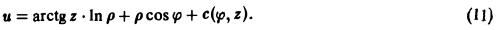
Дифференцируя соотношение (11) no φ и используя второе уравнение, получим
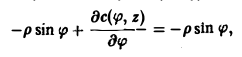
или 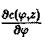
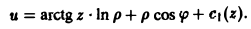
Дифференцируя это соотношение по z и используя третье уравнение, получим
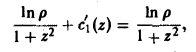
или c1`(z) =0, откуда c1(z) = с. Итак, потенциал данного поля
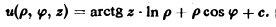
Линейный интеграл и циркуляция в ортогональных криволинейных координатах
Пусть векторное поле
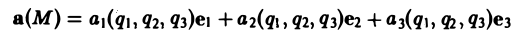
определено и непрерывно в области Ω изменения ортогональных криволинейных координат q1, q2, q3. Так как дифференциал радиус-вектора r любой точки M(q1, q2, q3) ∈ Ω выражается формулой
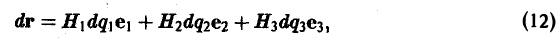
то криволинейный интеграл вектора а(М) по ориентированной гладкой или кусочно-гладкой кривой L ⊂ Ω будет равен
(13)
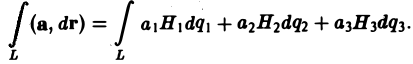
В частности, для цилиндрических координат (q1 = р, q2 = φ, q3 = z, Н1 = 1, Н2 = р, Н3=1) будем иметь
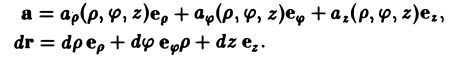
Отсюда по формуле (13) получим
(14)
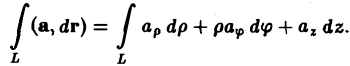
Аналогично для сферических координат (q1 = r, q2 = θ, q3 = φ, Н1 = 1, Н2 = r, H3 = r sin θ будем иметь
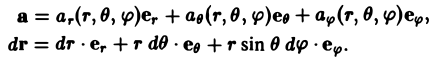
Отсюда по формуле (13) получим
(15)
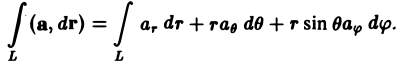
Если кривая L замкнута (начальная и конечная точки кривой L совпадают), то циркуляция Ц векторного поля а (М) в криволинейных координатах q1, q2, q3 вычисляется по формуле (13), а в случае цилиндрических или сферических координат — по формулам (14) или (15) соответственно.
Пример:
Вычислить циркуляцию векторного поля, заданного в цилиндрических координатах
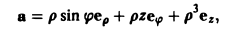
по замкнутой кривой L,
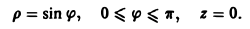
Координаты данного вектора равны соответственно
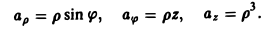
Контур L представляет собой замкнутую кривую, расположенную в плоскости z = 0 (рис. 43).
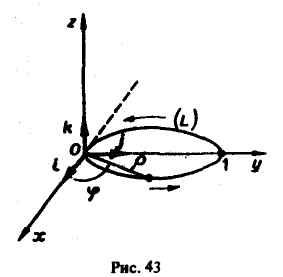
Подставляя координаты данного вектора в формулу .(14), получим
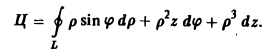
На кривой L имеем
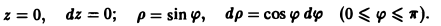
Искомая циркуляция будет равна
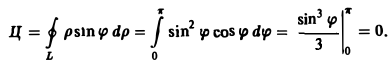
Оператор Лапласа в ортогональных координатах
Используя формулы (16) и (17), для оператора Лапласа ∆ получим следующее выражение:
В цилиндрических координатах
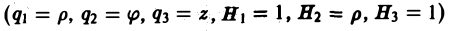
1) получим
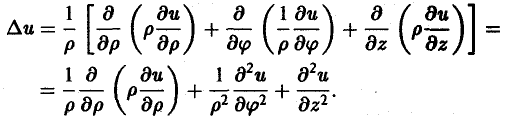
В сферических координатах
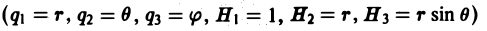
будем иметь
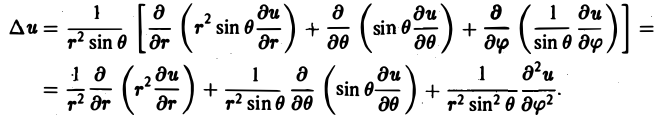
Пример:
Найти все решения уравнения Лапласа ∆и = 0, зависящие только от расстояния r.
Так как искомое решение и должно зависеть только от расстояния точки М от начала координат г, т. е. и = и (r), то уравнение Лапласа ∆и = 0 в сферических координатах будет иметь вид
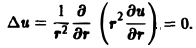
Отсюда 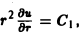
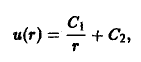
где С1 и С2 — постоянные.
Решение заданий и задач по предметам:
- Математика
- Высшая математика
- Математический анализ
- Линейная алгебра
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат
Вектор-функции
разделов
от теории до практики
примеров
Примеры решения задач
видео
Примеры решения задач
-
Предел и непрерывность вектор-функции.
Начать изучение
-
Понятие вектор-функции.
Начать изучение
-
Предел вектор-функции.
Начать изучение
-
Свойства пределов вектор-функций.
Начать изучение
-
Непрерывность вектор-функции.
Начать изучение
-
Производная и дифференциал вектор-функции.
Начать изучение
-
Производная вектор-функции.
Начать изучение
-
Дифференциал вектор-функции.
Начать изучение
-
Замена переменного.
Начать изучение
-
Теорема Лагранжа и локальная формула Тейлора для вектор-функции.
Начать изучение
Предел и непрерывность вектор-функции.
Понятие вектор-функции.
Если каждому значению (tin E), где (Esubsetmathbb{R}), поставлен в соответствие вектор (r(t)) трехмерного пространства, то говорят, что на множестве (E) задана векторная функция (r(t)) скалярного аргумента (t).
Пусть в пространстве фиксирована прямоугольная система координат (Oxyz). Тогда задание вектор-функции (r(t), tin E), означает задание координат (x(t), y(t), z(t)) вектора (r(t), tin E). Если (i,j,k) — единичные векторы координатных осей, то
$$
r(t)=x(t)i+y(t)j+z(t)k,qquad tin E,nonumber
$$
или
$$
r(t)=(x(t),y(t),z(t)).nonumber
$$
Если (z(t)=0) при всех (tin E), то вектор-функцию (r(t)) называют двумерной.
В случае, когда начало каждого из векторов (r(t)) совпадает с началом координат (рис. 21.1), эти векторы называют радиус-векторами, а множество их концов — годографом вектор-функции (r(t)), (tin E), который можно рассматривать как траекторию точки (M(t)) конца вектора (r(t)), если считать, что (t) — время.
Предел вектор-функции.
Вектор (a) называют пределом вектор-функции (r(t)) в точке (t_0) и пишут (displaystyle lim_{trightarrow t_{0}}r(t)=a) или (r(t)rightarrow a) при (trightarrow t_0), если
$$
lim_{trightarrow t_{0}} |r(t)-a|=0,label{ref1}
$$
то есть длина вектора (r(t)-a) стремится к нулю при (trightarrow t_0).
Утверждение 1.
Если заданы (r(t)=(x(t),y(t),z(t))) и (a=(a_{1},a_{2},a_{3})), то
$$
lim_{trightarrow t_{0}}r(t)=alabel{ref2}
$$
тогда и только тогда, когда
$$
x(t)rightarrow a_1, y(t)rightarrow a_2, z(t)rightarrow a_3quad при trightarrow t_0.label{ref3}
$$
Доказательство.
В самом деле, из неравенства
$$
|r(t)-a|=sqrt{(x(t)-a_1)^2+(y(t)-a_{2})^{2}+(z(t)-a_{3})^{2}}label{ref4}
$$
следует, что
$$
|x(t)-a_1| leq |r(t)-a|,quad|y(t)-a_2| leq |r(t)-a|,quad |z(t)-a_{3}| leq |r(t)-a|.nonumber
$$
Поэтому, если (r(t)rightarrow a) при (trightarrow t_0), то есть выполняется условие eqref{ref1}, то выполняется условие eqref{ref3}.
Обратно: если выполняются условия eqref{ref3}, то из равенства eqref{ref4} следует, что выполнено условие eqref{ref1}. (bullet)
При доказательстве свойств предела вектор-функции удобно использовать следующее очевидное утверждение: условие eqref{ref2} выполняется в том и только том случае, когда
$$
r(t)=a+alpha(t),nonumber
$$
где (alpha(t)) — бесконечно малая вектор-функция, то есть
$$
alpha(t)rightarrow 0quad mbox{при} trightarrow t_{0}.nonumber
$$
Свойства пределов вектор-функций.
Свойство 1.
Если (displaystyle lim_{trightarrow t_{0}}=a), то (displaystyle lim_{trightarrow t_{0}}|r(t)|=|a|).
Доказательство.
(circ) Это свойство следует из неравенства
$$
||r(t)|-|a|| leq |r(t)-a|.qquad bulletnonumber
$$
Свойство 2.
Если (r(t)rightarrow a) при (trightarrow t_{0}), а скалярная функция (f(t)) такова, что (f(t)rightarrow A) при (trightarrow t_{0}), то (f(t)r(t)rightarrow Aa) при (trightarrow t_{0}), то есть
$$
lim_{trightarrow t_0}f(t)r(t)=lim_{trightarrow t_{0}}f(t)lim_{trightarrow t_0}r(t).label{ref5}
$$
Доказательство.
(circ) Из определений пределов скалярной функции и вектор-функции следует, что (r(t)=a+alpha(t), f(t)=A+beta(t)), где (alpha(t)) — бесконечно малая вектор-функция, (beta(t)) — бесконечно малая функция при (trightarrow t_0). Поэтому (f(t)r(t)=Aa+gamma(t)), где (gamma(t)=Aalpha(t)+beta(t)a+beta(t)alpha(t)) — бесконечно малая вектор-функция при (trightarrow t_0), откуда получаем равенство eqref{ref5}. (bullet)
Свойство 3.
Если (r_1(t)rightarrow a_1, r_2(t)rightarrow a_2) при (trightarrow t_{0}), то (r_1+r_2rightarrow a_1+a_2, (r_1,r_2)rightarrow (a_1,a_2), [r_{1},r_2]rightarrow [a_1,a_2]) при (trightarrow t_{0}), то есть
$$
lim_{trightarrow t_{0}}(r_1(t)+r_2(t))=lim_{trightarrow t_{0}}r_1(t)+lim_{trightarrow t_{0}}r_2(t),label{ref6}
$$
$$
lim_{trightarrow t_{0}}(r_1(t),r_2(t))=left(lim_{trightarrow t_{0}}r_1(t),lim_{trightarrow t_{0}}r_2(t)right),label{ref7}
$$
$$
lim_{trightarrow t_{0}}[r_1(t),r_2(t)]=left[lim_{trightarrow t_{0}}r_1(t),lim_{trightarrow t_{0}}r_2(t)right].label{ref8}
$$
Доказательство.
(circ) По условию (r_{i}(t)=a_{i}+alpha_{i}), где (a_i(t)rightarrow 0) при (trightarrow t_{0} (i=1,2)). Поэтому (r_1(t)+r_2(t)=a_1+a_2+beta(t)), где (beta(t)=alpha_{1}(t)+alpha_2(t)rightarrow 0) при (trightarrow t_{0}), откуда следует eqref{ref6}. Докажем формулу eqref{ref7}. В силу свойств скалярного произведения
$$
(r_{1}(t),r_2(t))-(a_1,a_2)=(alpha_{1}(t),a_{2})+(alpha_{2}(t),a_1)+(alpha_1(t),alpha_2(t)),nonumber
$$
причем в правой части этого равенства — бесконечно малая функция, так как (alpha_{1}(t),alpha_{2}(t)) — бесконечно малые вектор-функции и (|(p,q)| leq |p|cdot|q|) для любых векторов (p) и (q).
Аналогично доказывается формула eqref{ref8}, в этом случае следует воспользоваться неравенством (|[p,q]| leq |p|cdot|q|). (bullet)
Непрерывность вектор-функции.
Вектор-функцию (r(t)) называют непрерывной при (t=t_{0}), если
$$
lim_{trightarrow t_{0}}r(t)=r(t_0).label{ref9}
$$
Непрерывность вектор-функции (r(t)=(x(t),y(t),z(t))) при (t=t_{0}) в силу эквивалентности условий eqref{ref2} и eqref{ref3} означает, что ее координаты (x(t),y(t),z(t)) непрерывны в точке (t_{0}).
Назовем вектор-функцию (Delta r=r((t_0+Delta t)-r(t_0)) приращением вектор-функции (r(t)) в точке (t_{0}). Тогда условие eqref{ref9} означает, что
$$
Delta rrightarrow 0quad приquad Delta trightarrow 0.label{ref10}
$$
Из определения непрерывности вектор-функции и свойств пределов векторных функций следует, что сумма, векторное и скалярное произведения вектор-функций (r_1(t)) и (r_2(t)) являются непрерывными функциями при (t=t_{0}), если вектор-функции (r_1(t)) и (r_2(t)) непрерывны в точке (t_{0}).
Производная и дифференциал вектор-функции.
Производная вектор-функции.
Если существует (displaystyle lim_{Delta trightarrow 0}frac{Delta r}{Delta t}) где (Delta r=r(t_0+Delta t)-r(t_0)), то этот предел называют производной вектор-функции (r(t)) в точке (t_0) и обозначают (r'(t_0)) или (dot{r}(t_0)).
Таким образом,
$$
r'(t_{0})=lim_{Delta trightarrow 0}frac{r(t_{0}+Delta t)-r(t_{0})}{Delta t}.label{ref11}
$$
Аналогично вводится понятие второй производной
$$
r″(t_{0})=lim_{Delta trightarrow 0}frac{r'(t_{0}+Delta t)-r'(t_{0})}{Delta t}nonumber
$$
и производной порядка (n > 2) вектор-функции. Заметим, что если (r(t)=(x(t),y(t),z(t))), то
$$
r'(t_{0})=(x'(t_0),y'(t_0),z'(t_0))label{ref12}
$$
Утверждение eqref{ref12} следует из определения eqref{ref11} и свойств пределов вектор-функций.
Аналогично, если существует (r″(t_{0})), то
$$
r″(t_{0})=(x″(t_0),y″(t_0),z″(t_0)).nonumber
$$
Из определения производной следует, что (Delta r=r'(t_0)Delta t+alpha(Delta t)Delta t), где (alpha(Delta t)rightarrow 0) при (Delta trightarrow 0), и потому (Delta rrightarrow 0) при (Delta trightarrow 0). Таким образом, выполняется условие eqref{ref10}, то есть вектор-функция (r(t)), имеющая производную в точке (t_{0}), непрерывна при (t=t_{0}).
Утверждение 2.
Справедливы следующие правила дифференцирования вектор-функций:
$$
(r_{1}+r_{2})’=r_{1}’+r_{2}’,label{ref13}
$$
$$
(fr)=f’r+fr’,label{ref14}
$$
$$
(r_1,r_2)’=(r_1′,r_2)+(r_1,r_2′),label{ref15}
$$
$$
[r_1,r_2]’=[r_1′,r_2]+[r_1,r_2′].label{ref16}
$$
Доказательство
(circ) Формулы eqref{ref13}-eqref{ref16} справедливы в точке (t), если в этой точке соответствующие функции имеют производные. Ограничимся доказательством формулы eqref{ref15}. Пусть (Delta r_{k}) — приращение вектор-функции (r_k(t)), соответствующее приращению аргумента (Delta t), то есть (Delta r_k=r_k(t+Delta t)-r_k(t), k=1,2). Тогда, используя свойства скалярного произведения и свойства пределов вектор-функций, получаем
$$
begin{array}{l}
(r_{1},r_{2})’=displaystylelim_{Delta trightarrow 0}frac{(r_{1}(t+Delta t),r_{2}(t+Delta t))-(r_{1}(t),r_{2}(t))}{Delta t}=\
=lim_{Delta trightarrow 0}left[left(r_{1}(t),frac{Delta r_{2}(t)}{Delta t}right)+left(frac{Delta r_{1}(t)}{Delta t},r_2(t)right)+left(frac{Delta r_{1}(t)}{Delta t},Delta r_2(t)right)right]=\
=(r_1,r_2′)+(r_1′,r_2),
end{array}nonumber
$$
так как (displaystyle frac{triangle mathrm{r}_{i}}{triangle t}rightarrow r_{i}'(t)) при (Delta trightarrow 0 (i=1,2)) и (Delta r_2rightarrow 0) при (Delta trightarrow 0). (bullet)
Пример 1.
Пусть существует (r'(t)) для всех (tin(alpha,beta)) и пусть (|r(t)|=C=const) для всех (tin(alpha,beta)).
Доказать, что ((r(t),r'(t))=0), то есть векторы (r(t)) и (r'(t)) ортогональны.
Решение.
(triangle) Используя формулу (|r(t)|^2=(r(t),r(t))), правило дифференцирования скалярного произведения (формула eqref{ref15}) и условие (|r(t)|=C), получаем ((r(t),r(t))’=2(r'(t),r(t))=0), так как (|r(t)|^{2})’=(C^{2})’=0). Итак,
$$
|r(t)|=CRightarrow (r(t),r'(t))=0.quadblacktrianglenonumber
$$
Дифференциал вектор-функции.
Вектор-функцию (r(t)), определенную в некоторой окрестности точки (t_{0}), называют дифференцируемой при (t=t_{0}), если ее приращение (Delta r=r(t_{0}+Delta t)-r(t_{0})) в точке (t_{0}) представляется в виде
$$
Delta r=aDelta t+Delta talpha(Delta t),label{ref17}
$$
где вектор (a) не зависит от (Delta t), (alpha(Delta t)rightarrow 0) при (Delta trightarrow 0).
В этом случае вектор (aDelta t) называют дифференциалом вектор-функции (r(t)) в точке (t_{0}) и обозначают (dr). Таким образом,
$$
dtextbf{r}=textbf{a}Delta t.nonumber
$$
Как и в случае скалярной функции, дифференцируемость вектор-функции (r(t)) в точке (t_{0}) равносильна существованию ее производной в точке (t_0), причем
$$
textbf{r}'(t_0)=textbf{a}.label{ref18}
$$
Следовательно,
$$
dr=r'(t_{0})Delta t.label{ref19}
$$
Если функция (r(t)) дифференцируема при (t=t_{0}), то, используя равенства eqref{ref17} и eqref{ref18}, получаем
$$
Delta r=r'(t_{0})Delta t+Delta t alpha(Delta t),label{ref20}
$$
где (alpha(Delta t)rightarrow 0) при (Delta trightarrow 0).
Полагая (dt=Delta t), запишем равенство eqref{ref19} в виде
$$
dr=r’dt,nonumber
$$
где опущено обозначение аргумента функции (r’). Отсюда получаем
$$
r’=frac{dr}{dt}.label{ref21} (21)
$$
Замена переменного.
Утверждение 3.
Если функция (t=t(s)) дифференцируема при (s=s_{0}, t(s_{0})=t_{0}), а вектор-функция (r(t)) дифференцируема в точке (t_{0}), то вектор-функция (rho(s)=r(t(s))) дифференцируема в точке (s_{0}), а производная этой функции выражается формулой
$$
rho’ (s_0)=r_s'(t(s_0))=r_{t}'(t_{0})t_{s}'(s_{0}),label{ref22}
$$
где индекс указывает, по какому переменному производится дифференцирование.
Доказательство.
(circ) Функция (alpha(Delta(t))) в формуле eqref{ref20} не определена при (Delta t=0). Доопределим ее при (Delta t=0), полагая (alpha(0)=0).
Так как (t=t(s)) — функция, дифференцируемая при (s=s_0), то (Delta t=t(s_{0}+Delta s)-t(s_{0})rightarrow 0) при (Delta srightarrow 0). Разделив обе части равенства eqref{ref20} на (Delta sneq 0), получим
$$
frac{Delta r}{Delta s}=r'(t_0)frac{Delta t}{Delta s}+alpha(Delta t)frac{Delta t}{Delta s}.label{ref23}
$$
Правая часть eqref{ref23} имеет при (Delta srightarrow 0) предел, равный (r'(t_0)t'(s_0)), так как (Delta trightarrow 0) при (Delta srightarrow 0) и (alpha(Delta t)rightarrow 0) при (Delta trightarrow 0). Следовательно, существует предел в левом части eqref{ref23}, и справедливо равенство eqref{ref22}. Формулу eqref{ref22} запишем кратко в виде равенства
$$
r_{s}’=r_{t}’t_{s}’,label{ref24}
$$
выражающего правило дифференцирования вектор-функции при замене переменного. (bullet)
Теорема Лагранжа и локальная формула Тейлора для вектор-функции.
Замечание 1.
Формула Лагранжа, то есть формула
$$
r(beta)-r(alpha)=r'(xi)(beta-alpha),quad xiin(alpha,beta),label{ref25}
$$
для вектор-функции, вообще говоря, неверна.
(circ) В самом деле, пусть формула eqref{ref25} верна, и пусть (r(t)=(cos t,sin t)), тогда (r'(t)=(-sin t,cos t), |r'(t)|=1). Полагая (alpha=0,beta=2pi), получим из равенства eqref{ref25} (0=r(2pi)-r(0)=r'(xi)2pi), что невозможно, так как (|r'(xi)|=1). (bullet)
Теорема Лагранжа.
(Для вектор-функций).
Если вектор-функция (r(t)) непрерывна на отрезке ([alpha,beta]) и дифференцируема на интервале ((alpha,beta)), то
$$
existsxiin(alpha,beta): |r(beta)-r(alpha)|leq|r'(xi)|(beta-alpha).label{ref26}
$$
Доказательство.
(circ) Рассмотрим скалярную функцию
$$
varphi(t)=(r(beta)-r(alpha),r(t)).nonumber
$$
эта функция непрерывна на отрезке ([alpha,beta]), так как вектор-функция (r(t)) непрерывна на этом отрезке. Кроме этого, функция (varphi(t)) дифференцируема на интервале ((alpha,beta)), так как функция (r(t)) дифференцируема этом интервале, причем в силу правила дифференцирования скалярного произведения
$$
varphi'(t)=(r(beta)-r(alpha),r'(t)).nonumber
$$
По теореме Лагранжа
$$
existsxiin(alpha,beta): varphi(beta)-varphi(alpha)=varphi'(xi)(beta-alpha)label{ref27}
$$
Преобразуем левую часть неравенства eqref{ref27}:
$$
begin{array}{l}
varphi(beta)-varphi(alpha)=(r(beta)-r(alpha),r(beta))-(r(beta)-r(alpha),r(alpha))=\
=(r(beta)-r(alpha),r(beta)-r(alpha))=|r(beta)-r(alpha)|^2
end{array}nonumber
$$
Тогда равенство eqref{ref27} примет вид
$$
|r(beta)-r(alpha)|^{2}=(r(beta)-r(alpha),r'(xi))(beta-alpha).label{ref28}
$$
Если (r(beta)=r(alpha)), то неравенство eqref{ref26} справедливо при любом (xiin in(alpha,beta)). Если (r(beta)neq r(alpha)), то (|r(beta)-r(alpha)| > 0). Тогда, используя неравенство (|(a,b)|leq|a|cdot|b|), из формулы eqref{ref28} получим
$$
|r(beta)-r(alpha)|^{2}leq|r(beta)-r(alpha)|cdot |r'(xi)|(beta-alpha),nonumber
$$
откуда, разделив обе части неравенства на (|r(beta)-r(alpha)| > 0), получим неравенство eqref{ref26}. (bullet)
Замечание 2.
Для вектор-функции (r(t)) справедлива локальная формула Тейлора
$$
r(t)=sum_{k=0}^{n}frac{r^{(k)}(t_{0})}{k!}(t-t_{0})^{k}+varepsilon(t-t_{0}),label{ref29}
$$
где (varepsilon(t-t_0)=o((t-t_{0})^{n})) — вектор-функция такая, что (varepsilon(t-t_0)=(t-t_{0})^{n}varepsilon_{1}(t-t_{0})), где (varepsilon_{1}(t-t_{0})rightarrow 0) при (trightarrow t_{0}).Эта формула справедлива в предположении, что существует (r^{(n)}(t_0)). Для доказательства формулы eqref{ref29} достаточно воспользоваться локальной формулой Тейлора для компонент вектор-функции (r(t)).