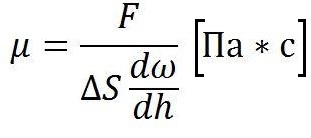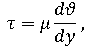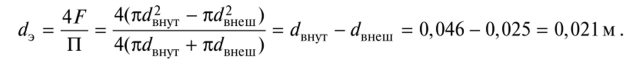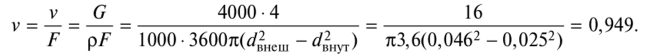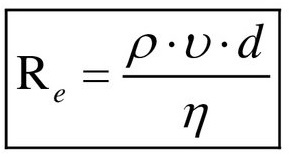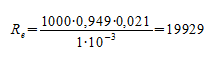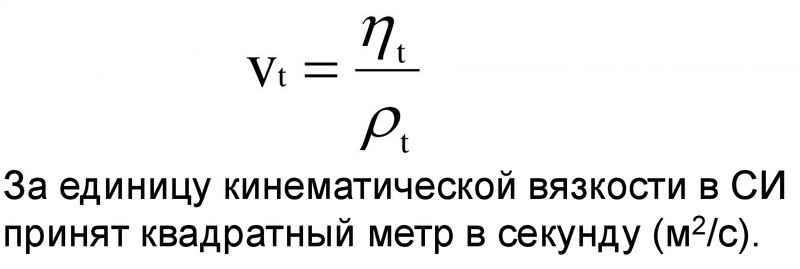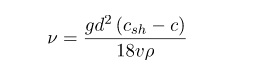Introduction
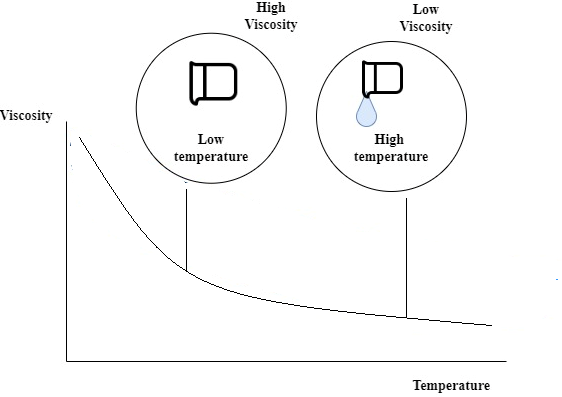
Viscosity is used for the measurement of the thinness and thickness of the fluid. On the other hand, density measures the space between two particles of a fluid. Generally, with the increase in temperature, the particles of the fluid fall apart. Thereby, resulting in a decrease in fluid density. Decreases in fluid density affect the viscosity of the liquid. The low density of fluid results in a lowering of the viscosity of the fluid and thereby transforming fluid into a less viscous fluid. The viscosity and density is an essential factor as they help to compare different fluids. The fluids that are more viscous will flow slower than the less viscous fluids.
Viscosity and Density: Difference
Temperature plays an important role in the viscosity and density of particle fluid. The density of the fluid decreases when the temperature increases and thereby resulting in less viscosity of the fluid.
Viscosity and dentistry are one of the two most important phenomena in physics. There are some differences between density and viscosity.
| Viscosity | Density |
|---|---|
| Viscosity is generally defined by the measurement of the resistance of a fluid that is deformed by either tensile stress or shear stress | Density generally refers to the mass per unit volume |
| Viscosity is the measurement of molecule shapes and inter-molecular forces | Density measures the molecular weight of a composition. |
| Viscosity generally changes quickly | Density changes slightly with the temperature. |
Dynamic Viscosity Measurement
Viscosity is one of the important factors of the fluid. Viscosity is used as an indicator of the quality by the consumers. The thicker liquid is considered as more superior to the thinner product. The rotational viscometer is one of the popular types of instruments that are used for the measurement of the dynamic viscosity. Viscosity is usually evaluated by the measurement of the torque or force which is essential for the rotation of the probe. The rotational viscometer is very useful to measure non-Newtonian liquids (Kassem Çamur & Bennur, 2018).
For example, if applied force can be increased, the viscosity of the non-Newtonian liquids also increases. If a probe moves within the liquid, the rotational viscometer synthesizes the tuning speed of it. According to da Silva et al. (2022), on the other hand, it is also found that in some other non-Newtonian liquids with the enhancement of the applied force, the reduction of viscosity happens.
Dynamic viscosity of the fluid generally refers to the measurement of the resistance to flow while an external force has been applied. The SI physical unit of dynamic viscosity ($mathrm{mu}$) is Pascal-second (Pa s) that is identical to 1 kg $mathrm{m^{-1}s^{-1}}$. Physical unit of dynamic viscosity in the centimeter gram second system of units (cgs) is poise (P). It is commonly expressed generally in ASTM standards.
Kinematic Viscosity Measurement
The kinematic viscosity is the atmospheric variable. Area and time are two important factors on which the units of the kinematic viscosity are generally established. As opined by Pham et al. (2018), there are a few methods that are generally used to measure the Kinematic Viscosity of a particular fluid. The most popular method that is used in the measurement of Kinematic Viscosity is by ascertaining the time that it takes for the fluid which flows through the capillary tube. The time generally converted directly to the kinematic viscosity Centistokes (cSt) is the unit to measure the kinematic viscosity (Pham et al. 2018). The SI unit of the Kinematic viscosity is m$mathrm{^{2}}$ s-1. Stokes (St) is the physical unit of kinematic viscosity.
The Equation of the Kinematic Viscosity
Physic not only depends on the mere theoretical description but it also includes the mathematical equations for a better understanding. The equation is mentioned below
v = n/p
Here,
-
V = Kinematic viscosity
-
n = Absolute viscosity/ Dynamic viscosity
-
P = Density
There are three types of units that are used to measure Kinematic Viscosity.
| Unit | Types of unit |
|---|---|
| SI unit | Kg/ms or N.s/m$mathrm{^{2}}$ |
| CGS Unit | gm/cm.sec or Poise |
| FPS unit | Pound or Reyan.s/inchm$mathrm{^{2}}$ |
Relation between Viscosity and Density
There is n such direct relation between viscosity and density. However, these two factors are affected by the changing in the temperature. In liquids with increasing temperatures, the viscosity of the liquid reduces. In liquids velocity generally increases with the increase of the density (Bae & Halloran, 2019). According to the kinetic theory gases must be proportional to the square root of absolute temperature.
For instance, we can take the example of honey. During the winter season, honey consists of high density as it solidifies and forms a solid-state. The particles are attached to this particular condition. When the same honey is kept under the sun, it melts. So, here is one thing that should be noted carefully.
According to Balla et al. (2020), under the high temperature, the inter-atomic particles form some distance and the friction between the layers of honey reduces while pouring it into the other vessel. These scenarios clearly describe the two parameters that are mentioned below.
-
The difference between Viscosity and density
-
The relation between Viscosity and density.
Conclusion
The viscosity and density are the two important factors that determine the characteristics of the fluid. These two factors help to measure the type and nature of the fluid. These two factors are dependent on the changing the temperatures.
FAQs
Q.1. What is viscosity?
Ans. Viscosity is one of the important characteristic properties of liquids. Viscosity is the measurement of the resistance to the foe that arises due to internal friction between the layers of fluid.
Q.2. How does temperature affect Viscosity?
Ans. The viscosity of the liquid generally decreases when the temperature increases. The molecules hold high kinetic energy and can surpass intermolecular forces to slip past each other between the layers.
Q.3. Which has a lower density than liquids and solids?
Ans. Gases have a lower density than liquids and solids. This happens because the particles of gases are compactly packed in the both states.
Q.4. How pressure is related to density?
Ans. Pressure is straightly proportional to the density in a constant temperature. When the pressure increases, the density also increases.
Загрузить PDF
Загрузить PDF
Вязкость можно определить как меру сопротивления жидкости течению, которое называют также внутренним трением жидкости. Возьмем, к примеру, воду и мед. Вода течет относительно легко, в то время как мед намного менее текуч. Поскольку мед менее подвержен течению, он обладает большей вязкостью, чем вода. Существует множество способов измерить вязкость, и в наиболее простом испольуется падение шарика в прозрачной емкости с жидкостью, вязкость которой нужно определить.
-
1
Узнайте, что такое вязкость. Вязкость определяет сопротивление жидкости течению.[1]
Жидкости с высокой вязкостью, например мед, текут очень медленно. В то же время жидкости с низкой вязкостью, такие как вода, перетекают быстро. Вязкость измеряется в паскалях на секунду (Па·с).[2]
-
2
Запишите уравнение вязкости. В описанном ниже эксперименте для определения вязкости измеряется скорость прохождения шарика через жидкость. Формула для определения вязкости записывается как [2(pш-pж)ga2]/9v, где pш — плотность шарика, pж — плотность жидкости, g — ускорение свободного падения, a — радиус шарика, v — скорость шарика.[3]
-
3
Рассмотрим входящие в формулу величины. Плотность предмета определяется как масса на единицу объема и обозначается буквой p. В нашей формуле необходимо определить плотность шарика pш и плотность жидкости pж, через которую он проходит. Чтобы определить радиус шарика a, можно измерить длину его окружности и поделить ее на 2π. Вызванное силой тяжестью ускорение свободного падения g является константой, которая зависит от планеты. Для Земли ускорение свободного падения составляет 9,8 м/с2.[4]
Скорость шарика v, которая измеряется в ходе эксперимента, представляет собой пройденное расстояние в метрах, поделенное на количество секунд (м/с).Реклама
-
1
Подготовьте все, что вам понадобится для проведения эксперимента. Чтобы определить вязкость жидкости, вам потребуются шарик, градуированная мензурка, линейка, секундомер, исследуемая жидкость, весы и калькулятор.[5]
Данный эксперимент состоит из нескольких шагов, и если выполнить все правильно, то можно определить вязкость жидкости.- Для эксперимента подойдет небольшой мраморный или стальной шарик. Его диаметр не должен превышать диаметра мензурки, чтобы он мог свободно падать в ней.
- Можно взять достаточно большую пластиковую мензурку с делениями на боковой поверхности, которые позволяют определить объем.
- Вместо секундомера можно использовать обычные часы, однако в этом случае вы получите менее точные результаты.
- Жидкость должна быть достаточно прозрачной, чтобы вы видели, как в ней опускается шарик. Попробуйте использовать различные жидкости с разной скоростью течения, чтобы посмотреть, как различается их вязкость. Например, можно взять воду, мед, сироп, растительное масло и молоко.
-
2
Рассчитайте плотность шарика. Чтобы определить вязкость, необходимо знать плотность как материала шарика, так и жидкости. Плотность d вычисляется по формуле
, где m — масса предмета, а V — его объем.
- Положите шарик на весы и измерьте его массу. Запишите полученную величину в граммах (g).
- Найдите объем шара V с помощью формулы V= (4/3) x π x r3, где π — константа, равная 3,14, а r — радиус шара. Радиус шара можно найти следующим образом: измерьте длину его окружности, а затем поделите ее на 2π.
- Можно также найти объем шара по количеству воды, которую он вытесняет из мензурки. Запишите первоначальную высоту уровня воды, затем опустите шарик в воду и отметьте новый уровень воды. Вычтите из нового первоначальный уровень. В результате вы получите объем шарика в миллилитрах (мл).
- Вычислите плотность по формуле
. В результате у вас получится плотность в граммах на миллилитры (г/мл).
-
3
Определите плотность исследуемой жидкости. Сделайте это с помощью той же формулы.
- Сначала измерьте массу пустой мензурки. Затем налейте в мензурку жидкость и взвесьте ее еще раз. Вычтите из массы мензурки с жидкостью массу пустой мензурки — в результате у вас получится масса жидкости в граммах (г).
- Чтобы найти объем жидкости, просто определите высоту ее уровня в мензурке с помощью делений на ее боковой поверхности. Запишите полученный результат в миллилитрах (мл).
- Подставьте результаты в формулу
, и у вас получится плотность жидкости в граммах на миллилитры (г/мл).
-
4
Залейте в мензурку жидкость и сделайте на ней метки. Заполните мензурку исследуемой жидкостью и поставьте на боковой поверхности метки. Медленно залейте в мензурку жидкость, так чтобы заполнить ее примерно на ½–¾.
- Нарисуйте метку в верхней части мензурки примерно на 2,5 сантиметра ниже уровня жидкости.
- Поставьте вторую метку примерно на 2,5 сантиметра выше дна мензурки.
- Измерьте расстояние между верхней и нижней меткой. Приложите к нижней метке начало линейки и измерьте расстояние до верхней метки.
-
5
Измерьте время, за которое шарик преодолевает расстояние между метками. Опустите шарик в жидкость и запустите секундомер, когда нижний край шарика сравняется с верхней меткой. Остановите секундомер, когда шарик достигнет нижней метки.
- Данные измерения сложнее проводить на жидкостях с низкой вязкостью, поскольку в них шарик падает быстрее и засечь точное время бывает непросто.
- Повторите данный шаг по меньшей мере три раза (чем больше измерений вы сделаете, тем точнее получится результат) и определите по трем величинам среднее значение. Чтобы найти среднее значение, сложите все полученные результаты и поделите их на число измерений.
- Для данного метода лучше всего использовать достаточно маленький шарик — в этом случае поток жидкости вокруг шарика будет действительно вязким и далеким от турбулентного. Кроме того, шарик должен быть достаточно мал по сравнению с мензуркой, чтобы во время падения расстояние между ним и ее стенками составляло хотя бы 10 радиусов шарика.
-
6
Вычислите скорость шарика. Скорость соответствует расстоянию, поделенному на время, затраченное для того, чтобы преодолеть это расстояние. Скорость v выражается формулой
, где d — пройденное расстояние, t — затраченное время.
- Подставьте измеренные значения в формулу
и определите скорость шарика.
- Подставьте измеренные значения в формулу
-
7
Вычислите вязкость жидкости. Подставьте найденные величины в формулу вязкость = [2(pш-pж)ga2]/9v, где pш — плотность шарика, pж — плотность жидкости, g — ускорение свободного падения (постоянная величина, равная 9,8 м/с2), a — радиус шарика, v — скорость шарика.[6]
- Предположим, плотность жидкости составляет 1,4 г/мл, плотность шарика равна 5 г/мл, его радиус равен 0,002 м, а скорость шарика составляет 0,05 м/с.
- Подставим эти значения в формулу и получим: вязкость = [2(5 – 1,4)(9,8)(0,002)^2]/(9 x 0,05) = 0,00062784 Па·с.
Реклама
Советы
- Записывайте все значения в таблицу, чтобы не запутаться в результатах измерений.
- Все измерения следует выполнять в метрической системе.
- Не забудьте в конечном результате указать единицы измерения.
Реклама
Предупреждения
- Для данного метода плотность шарика должна превышать плотность жидкости.
- Не наливайте в мензурку слишком много жидкости, чтобы ее верхний уровень не подходил слишком близко к краю мензурки. Если вы не оставите достаточно места, при опускании шарика в мензурку из нее может выплеснуться часть жидкости, что исказит результаты измерений.
- Вылейте из мензурки предыдущую жидкость и полностью высушите ее, прежде чем проводить измерения на новой жидкости.
- Перед началом экспериментов проверьте, чтобы в мензурке не было остатков воды или другой жидкости. Посторонняя жидкость отрицательно повлияет на точность полученных результатов.
Реклама
Что вам понадобится
- Небольшой твердый шарик или другой сферический предмет, который тонет в исследуемой жидкости
- Исследуемая жидкость
- Мерная мензурка с диаметром бо́льшим, чем у шарика
- Калькулятор
- Секундомер
- Измерительная рулетка или линейка
- Маркер
- Весы
Об этой статье
Эту страницу просматривали 16 919 раз.
Была ли эта статья полезной?
2.1. Плотность жидкости.Вязкость жидкостей. Капиллярные явления.Аномальные жидкости. Идеальная жидкость
Жидкости
с точки зрения механических свойств
разделяются на два класса – малосжимаемые
(капельные) и сжимаемые (газообразные).
С позиций физики капельные жидкости
значительно отличаются от газообразных.
А в механике жидкости часто законы,
которые справедливы для капельных
жидкостей, справедливы и для газообразных,
и наоборот.
Для
большинства случаев рассматриваемых
в данном пособии не будет иметь
принципиального значения, о какой
жидкости будет идти речь – капельной
или газообразной. Если же возникнет
необходимость – это будет оговариваться
отдельно.
Капельные
жидкости обладают вполне определенным
объемом, величина которого практически
не изменяется под действием внешних
сил. Газы занимают весь предоставляемый
им объем и могут значительно изменять
свой объем в зависимости от прилагаемых
внешних сил.
Основные
свойства жидкости, которые существенно
влияют на многие законы их движения –
это плотность и вязкость. В некоторых
ситуациях также большое значение может
иметь сила поверхностного натяжения.
Плотность
жидкостей– плотностью жидкостиназывается
ее масса, заключенная в единице объема:
(1)
где М– масса
жидкости в объемеW.
Плотность воды при
4° С ρ=1000
кг/м3
(102 кгсс2/м4).
Если жидкость неоднородна, то формула
(1) определяет лишь среднюю плотность
жидкости. Для определения плотности в
данной точке следует пользоваться
формулой:
(2)
В практических приложениях
о массе жидкости судят по ее весу. Вес
жидкости, приходящийся на единицу
объема, называется удельным весом:
=G/W, (3)
где G
— вес жидкости в
объеме W.
Удельный вес воды при 4° С =
9810 Н/м3(1000 кгс/м3).
Если жидкость неоднородна, то формула
(3) определяет лишь средний удельный вес
жидкости. Для определения удельного
веса жидкости в данной точке следует
пользоваться формулой
(4)
где G— вес жидкости в объемеW.
Плотность и удельный вес
связаны между собой известным соотношением
(5)
где g
— ускорение свободного
падения.
Относительным удельным
весом жидкости (или относительным весом)
называется отношение удельного веса
данной жидкости к удельному весу воды
при 4°С
(6)
В отличие от удельного относительный
удельный вес представляет собой
отвлеченную (безразмерную) величину,
численное значение которой не зависит
от выбранной системы единиц измерения.
Так, для пресной воды при 4°С имеем
(7)
В таблице 1 в качестве примера приведены
значения удельного веса и плотности
некоторых капельных, а в таблице 2 –
сжимаемых жидкостей (газов).
Плотность,
а, следовательно, удельный и относительный
удельный
вес жидкостей меняются с изменением
давления и температуры.
Эта зависимость различна для капельных
жидкостей и газов.
Сжимаемость
капельных жидкостей под действием
давления характеризуется
коэффициентом объемного сжатия β,
который
представляет собой относительное
изменение объема жидкости
на единицу изменения давления
(8)
где W0
— первоначальный объем жидкости;
∆W
— изменение этого объема при увеличении
давления на величину ∆р.
Коэффициент объемного
сжатия в системе СИ имеет размерность
Па—1.
Знак минус в формуле (8)
обусловлен тем, что положительному
приращению давления p соответствует
отрицательное приращение (т. е. уменьшение)
объема жидкости.
Таблица 1 – Плотность ρ
и удельный вес γ
капельных жидкостей
при 20°С
|
Жидкость |
γ |
ρ, |
|
Анилин |
9270 |
1040 |
|
Бензол |
8590—8630 |
876—880 |
|
Бензин авиационный |
7250—7370 |
739—751 |
|
Вода пресная |
9790 |
998,2 |
|
» морская |
10010—10090 |
1002—1029 |
|
Глицерин безводный |
12260 |
1250 |
|
Керосин |
7770—8450 |
792—840 |
|
Масло касторовое |
9520 |
970 |
|
» минеральное |
8000—8750 |
877—892 |
|
Нефть |
8340—9320 |
850—950 |
|
Ртуть |
132900 |
13547 |
|
Спирт этиловый |
7440 |
789,3 |
|
Хлористый натрий |
10690 |
1200 |
|
Эфир этиловый |
7010—7050 |
715—719 |
Таблица 2 – Приближенные
значения плотности ρ
и удельного веса γ
газов при давлении
740 мм рт. ст. и t
= 15°С
|
Газ |
γ, |
ρ, |
|
Водород |
0,81 |
0,08 |
|
Водяной пар |
7,25 |
0,74 |
|
Окись углерода |
11,3 |
1,15 |
|
Азот |
11,3 |
1,15 |
|
Воздух |
11,6 |
1,2 |
|
Кислород |
12,8 |
1,3 |
|
Углекислота |
17,6 |
1,8 |
Величина, обратная коэффициенту
объемного сжатия, называется модулем
упругости жидкости
(9)
Коэффициент
объемного сжатия капельных жидкостей
мало меняется
при изменении температуры и давления
(таблица 4).
Таблица
3 – Значения
коэффициента объемного сжатия воды при
разных температурах и давлениях
|
t 0С |
|
||||
|
500000 |
1000000 |
2000000 |
3900000 |
7800000 |
|
|
0 |
0,054 |
0,0537 |
0,0531 |
0,0523 |
0,0515 |
|
5 |
0,0529 |
0,0523 |
0,0518 |
0,0508 |
0,0493 |
|
10 |
0,0523 |
0,0518 |
0,0508 |
0,0498 |
0,0481 |
|
15 |
0,0518 |
0,051 |
0,0503 |
0,0488 |
0,047 |
|
20 |
0,0515 |
0,0505 |
0,0495 |
0,0481 |
0,046 |
Таким
образом, при повышении давления на
9,8·104
Па (1
ат) объем воды уменьшается на 1/20000 часть
первоначальной
величины. Коэффициент объемного сжатия
для других капельных
жидкостей имеет примерно тот же порядок.
В подавляющем
большинстве случаев, встречающихся в
практической деятельности
инженера-сантехника, изменения давления
не
достигают
больших величин, и поэтому сжимаемостью
воды можно
пренебрегать, считая удельный вес и ее
плотность не зависящими
от давления.
Прочность
жидкости на разрыв при решении практических
задач
не учитывается.
Температурное
расширение капельных жидкостей
характеризуется
коэффициентом температурного расширения
t,
выражающим относительное увеличение
объема жидкости при увеличении
температуры на 10С,
т. е.
(10)
где W0
— первоначальный объем жидкости;
∆W
— изменение этого объема при повышении
температуры
на величину ∆T.
Коэффициент температурного
расширения капельных жидкостей,
как это видно из таблицы 4, незначителен.
Так, для воды при
температуре от 10 до 20°С и давлении 105Па
– t=
0,00015
1/град.
Таблица 4 — Коэффициент
температурного расширения воды
|
Давление, |
t, |
||||
|
1-10 |
10-20 |
40-50 |
60-70 |
90-100 |
|
|
100000 |
0,000014 |
0,00015 |
0,000422 |
0,000556 |
0,000719 |
|
9800000 |
0,000043 |
0,000165 |
0,000422 |
0,000548 |
0,000714 |
|
19600000 |
0,000072 |
0,000183 |
0,000426 |
0,000539 |
— |
|
49000000 |
0,000149 |
0,000236 |
0,000429 |
0,000523 |
0,000661 |
|
88300000 |
0,000229 |
0,000294 |
0,000437 |
0,000514 |
0,000621 |
Однако
влияние температуры на удельный вес в
ряде случаев (при
значительных разностях температур)
приходится учитывать.
Плотность
и удельный вес капельных жидкостей, как
это следует из предыдущих рассуждений,
мало изменяются с изменением давления
и температуры. Можно приближенно считать,
что плотность не зависит от давления,
а определяется только температурой. Из
выражений (1) и (10) можно найти приближенное
соотношение для расчета изменения
плотности капельных жидкостей с
изменением температуры:
(11)
Значения
коэффициента βt
в (11) находятся из таблиц в пределах
заданного интервала температур (таблица
4).
Способность
жидкостей менять плотность (удельный
вес) при изменении температуры широко
используется для создания естественной
циркуляции в котлах, отопительных
системах, для удаления продуктов сгорания
и т. д.
В таблице
5 приведены значения плотности воды при
разных температурах.
В отличие
от капельных жидкостей газы характеризуются
значительной сжимаемостью и высокими
значениями коэффициента температурного
расширения. Зависимость плотности газов
от давления и температуры устанавливается
уравнением состояния.
Наиболее
простыми свойствами обладает газ,
разреженный настолько, что взаимодействие
между его молекулами может не
учитываться – так называемый идеальный
газ.
Таблица
5 – Зависимость
плотности ρ, кинематической υ
и динамической μ вязкости воды от
температуры
|
Температура, |
ρ, |
υ, |
μ, |
|
0 |
999,9 |
0,00000179 |
0,00179 |
|
4 |
1000 |
0,00000152 |
0,00157 |
|
20 |
998 |
0,00000101 |
0,00101 |
|
40 |
992 |
0,00000066 |
0,00065 |
|
60 |
983 |
0,00000048 |
0,00048 |
|
80 |
972 |
0,00000037 |
0,00036 |
|
90 |
965 |
0,00000033 |
0,00031 |
|
99 |
959 |
0,00000028 |
0,00027 |
Для
идеальных газов справедливо уравнение
Клапейрона, позволяющее
определять плотность газа при известных
давлении и температуре, т.е.
(12)
где р
—
абсолютное давление; R
—
удельная газовая постоянная, различная
для разных газов,
но не зависящая от температуры и давления
(для воздуха R=
287 Дж/(кг·К)); T
— абсолютная
температура.
Поведение
реальных газов в условиях, далеких от
сжижения,
лишь незначительно отличается от
поведения идеальных газов,
и для них в широких пределах можно
пользоваться уравнениями
состояния идеальных
газов.
В
технических расчетах плотность газа
обычно приводят к нормальным физическим
условиям (t=0°; р= 101 325 Па) или к стандартным
условиям (t=20°С; р=101325 Па), иногда к
нормальным техническим условиям (t=15°;
р= 98000 Па).
Плотность
воздуха при R
=
287
Дж/(кг·К)
в стандартных условиях по формуле (12)
будет равна =1,2
кг/м3.
Плотность
воздуха при других условиях определяется
по формуле
(13)
Так как
объем газа в большой мере зависит от
температуры и
давления, выводы, полученные при изучении
капельных жидкостей,
можно распространять на газы лишь в том
случае, если в
пределах рассматриваемого явления
изменения давления и температуры
незначительны. Значительные разности
давлений, вызывающие
существенное изменение плотности газов,
могут возникнуть при их движении с
большими скоростями. Соотношение
между скоростью движения жидкости и
скоростью звука в ней
позволяет судить о необходимости учета
сжимаемости в каждом
конкретном случае. Практически газ
можно принимать несжимаемым при скоростях
движения, не превышающих 100 м/с.
Вязкость
жидкостей.
Вязкостью называется свойство жидкостей
оказывать сопротивление сдвигу. Все
реальные жидкости обладают
определенной вязкостью, которая
проявляется в виде внутреннего
трения при относительном перемещении
смежных частиц
жидкости. Наряду с легко подвижными
жидкостями (например,
водой, воздухом) существуют очень вязкие
жидкости, сопротивление которых сдвигу
весьма значительно (глицерин, тяжелые
масла и др.). Таким образом, вязкость
характеризует степень текучести жидкости
или подвижности ее частиц.
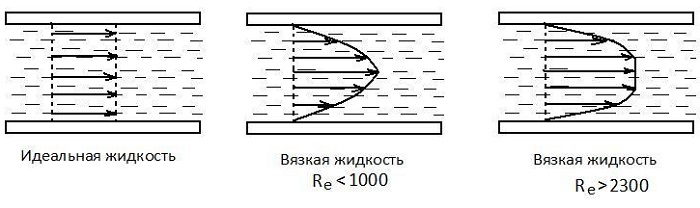
Пусть
жидкость течет вдоль плоской стенки
параллельными ей
слоями (рис. 1), как это наблюдается при
ламинарном движении. Вследствие
тормозящего влияния стенки слои жидкости
будут двигаться с разными скоростями,
значения которых возрастают
по мере отдаления от стенки.
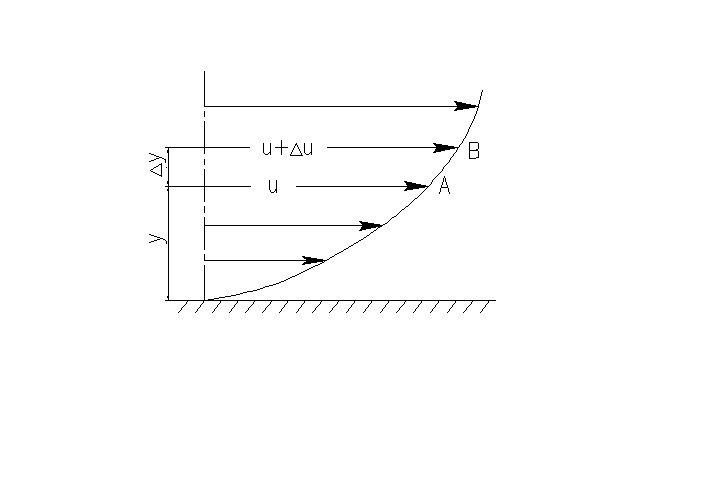
Рассмотрим
два слоя жидкости, двигающиеся на
расстоянии ∆y друг
от друга. Слой А движется со скоростью
и, а
слой В —
со
скоростью u+∆u. Вследствие разности
скоростей слой В
сдвигается
относительно слоя А
на
Рис. 1
— Распределение скоростей при течении
жидкости вдоль твердой стенки
величину
∆u (за единицу времени).
Величина ∆u
является абсолютным сдвигом слоя В
по
слою А,
а
∆u/∆у
есть градиент скорости (относительный
сдвиг).
Появляющееся при этом движении касательное
напряжение
(силу трения на единицу площади) обозначим
через τ. Тогда
аналогично явлению сдвига в твердых
телах мы получим следующую
зависимость между напряжением и
деформацией:
(14)
или, если слои будут находиться
бесконечно близко друг к другу,
(15)
Величина
μ, аналогичная коэффициенту сдвига в
твердых телах
и характеризующая сопротивляемость
жидкости сдвигу, называется
динамической или абсолютной вязкостью.
На существование
соотношения (15) первое указание имеется
у Ньютона,
и потому оно называется
законом трения Ньютона.
Сила
внутреннего трения в жидкости
(16)
т. е.
прямо пропорциональна градиенту
скорости, площади трущихся
слоев ω и динамической вязкости (тем
самым трение в
жидкости отличается от трения в твердых
телах, где сила трения
зависит от нормального давления и не
зависит от площади трущихся
поверхностей) [1,4].
В
международной системе единиц динамическая
вязкость выражается
в Н∙с/м2
или Па∙с.
В
технической системе единиц динамическая
вязкость имеет размерность
кгс∙с∙м-2.
В системе CGS
за единицу динамической вязкости
принимается пуаз (П) в память французского
врача Пуазейля,
исследовавшего законы движения крови
в сосудах человеческого
тела, равный 1 г∙см—1
∙с—1:
1 Па·с=0,102 кгс·с/м2.
Вязкость
жидкостей в сильной степени зависит от
температуры; при
этом вязкость капельных жидкостей при
увеличении температуры
уменьшается, а вязкость газов возрастает.
Таблица 6
— Кинематическая и динамическая вязкость
капельных жидкостей (при
t=20°С)
|
Жидкость |
μ, Па∙с |
υ, |
|
Вода |
0,00101 |
0,000001012 |
|
Глицерин безводный |
0,512 |
0,00041 |
|
Керосин (при |
0,0016-0,0025 |
0,000002-0,000003 |
|
Бензин (при |
0,0006-0,00065 |
0,00000083-0,00000093 |
|
Масло |
0,972 |
0,01002 |
|
» |
0,0275-1,29 |
0,0000313-0,0145 |
|
Нефть |
0,007-0,008 |
0,0000081-0,0000093 |
|
Ртуть |
0,0015 |
0,001000011 |
|
Спирт этиловый |
0,00119 |
0,00000151 |
Наряду
с понятием абсолютной или динамической
вязкости в
гидравлике находит применение понятие
кинематической вязкости,
представляющей собой отношение абсолютной
вязкости к
плотности жидкости:
(17)
В
международной системе единиц кинематическая
вязкость измеряется
в м2/с;
единицей для измерения кинематической
вязкости
в системе CGS
служит стокс (в честь английского физика
Стокса):
1 Ст=1 см2/с=10—4
м2/с.
Кинематическая
вязкость газов зависит как от температуры,
так и от давления, возрастая с увеличением
температуры и уменьшаясь
с увеличением давления (таблица 7).
Таблица 7 – Значения
кинематической вязкости
и удельной газовой
постоянной
R
для
некоторых газов
|
Газ |
, |
R, |
|||
|
0 |
20 |
50 |
100 |
||
|
Воздух Метан Этилен |
0,0000133 0,0000145 0,0000075 |
0,0000151 0,0000165 0,0000086 |
0,0000178 0,0000197 0,0000104 |
0,0000232 0,0000256 0,00000138 |
287 520 296 |
Экспериментально вязкость
жидкостей определяют вискозиметрами.
Капиллярные явления.
Молекулы жидкости, расположенные у
поверхности контакта с другой жидкостью,
газом или твердым
телом, находятся в условиях, отличных
от условий внутри некоторого
объема жидкости. Внутри объема жидкости
молекулы
окружены со всех сторон такими же
молекулами, вблизи поверхности
— лишь с одной стороны. Поэтому энергия
поверхностных
молекул отличается от энергии молекул
в объеме на некоторую
величину, называемую поверхностной
энергией. Эта энергия
пропорциональна площади поверхности
раздела s:
Эn
= s (18)
Коэффициент
пропорциональности ,
называемый коэффициентом
поверхностного натяжения, зависит от
природы соприкасающихся
сред. Этот коэффициент можно представить
в виде
σ=-F/l (19)
где F
–
сила поверхностного натяжения;
l
– длина линии, ограничивающей поверхность
раздела.
Исходя
из определения,
имеет
размерность энергии на единицу
площади или силы на единицу длины. Для
границы раздела
вода – воздух при t=20°С
коэффициент
поверхностного натяжения
σ=0,073 Дж/м2,
для границы раздела ртуть – воздух
коэффициент σ=0,48 Дж/м2.
Поверхностное
натяжение жидкости чувствительно к ее
чистоте
и температуре. Вещества, способные в
значительной степени
снизить силы поверхностного натяжения,
называются поверхностно-активными
веществами (ПАВ). При повышении температуры
величина поверхностного натяжения
уменьшается, а
в критической точке перехода жидкости
в пар обращается в нуль.
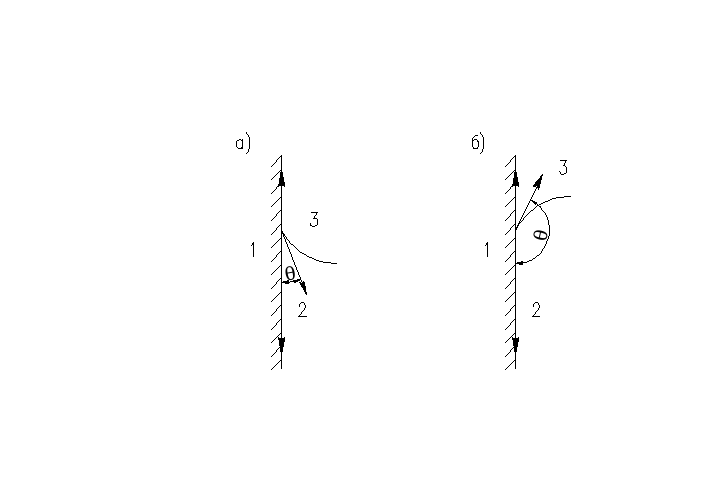
На
поверхности раздела трех фаз, например,
твердой стенки
1,
жидкости
2
и
газа 3
между
поверхностью жидкости и твердой
стенкой образуется так называемый
краевой угол θ (рис. 2).
Величина краевого угла зависит от
природы соприкасающихся
сред (от поверхностных натяжений на их
границах) и не зависит
ни от формы сосуда, ни от действия силы
тяжести. Если
край жидкости приподнят, ее поверхность
имеет вогнутую форму
(рис. 2 а) – краевой угол острый. В этом
случае жидкость
смачивает твердую поверхность. Чем хуже
смачивающая способность жидкости, тем
больше краевой угол. При θ>90°
жидкость
считается несмачивающей, при полном
несмачивании θ=180°.
Капли такой жидкости как бы поджимаются,
стараясь уменьшить
площадь контакта с твердой поверхностью.
От
явления смачивания зависит поведение
жидкости в тонких (капиллярных)
трубках, погруженных в эту жидкость. В
случае
смачивания жидкость в трубке поднимается
над уровнем свободной
поверхности, в случае несмачивания —
опускается. Высота
капиллярного поднятия (опускания)
жидкости находится
по формуле
(20)
где γ—
удельный вес жидкости;
r —
радиус трубки.
Во всех
явлениях, происходящих при совместном
действии сил поверхностного
натяжения и сил тяжести, значительную
роль играет
капиллярная постоянная
,
входящая в выражение(20)
и имеющая линейную размерность; для
воды при 20° С капиллярная
постоянная равна 0,0039 м.
Рис. 2
– Определение краевого угла
Аномальные
жидкости. К
жидкостям, не подчиняющимся закону
вязкости Ньютона (15), так называемым
«неньютоновским»
(или аномальным) жидкостям, можно отнести,
например, литой
бетон, глинистый раствор, употребляемый
при бурении
скважин, нефтепродукты при температуре,
близкой к температуре
застывания, коллоиды и др.
Опытами
установлено, что движение неньютоновских
жидкостей
начинается только после того, как
касательные напряжения
достигнут некоторого предельного
минимального значения (так называемое
начальное напряжение сдвига); при меньших
напряжениях
эти жидкости не текут, а испытывают
только упругие
деформации.
В
аномальных жидкостях касательное
напряжение определяется по формуле
Бингема
(21)
где τ0
— начальное напряжение сдвига.
Таким
образом, в аномальных жидкостях сила
трения возникает
еще в покоящихся жидкостях, но при
стремлении этих жидкостей прийти в
движение. На рис. 3 показана зависимость
между
касательным напряжением и градиентом
скорости для нормальных
1 и аномальных 2
жидкостей.
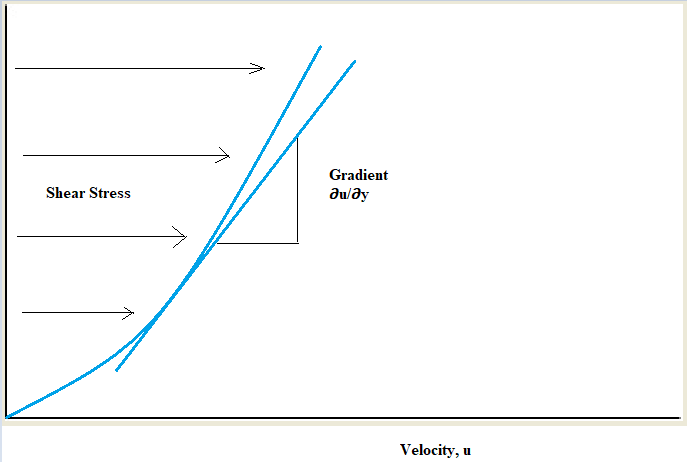
Рис. 3
– Зависимость касательного напряжения
от градиента скорости
Вязкость
аномальных жидкостей (так называемая
структурная
вязкость) в отличие от вязкости
ньютоновских жидкостей при
заданной температуре и давлении
непостоянна и изменяется
в функции от градиента скорости
.
Поведение различных
аномальных жидкостей под нагрузкой и
их динамические свойства излагаются в
реологии, выводы которой
имеют одинаковое значение, как для
механики жидкости,
так и для теории пластичности.
Идеальная жидкость. В
механике жидкости для облегчения решения
некоторых задач используется понятие
об идеальной жидкости.
Под
идеальной жидкостью понимают воображаемую
жидкость, лишенную вязкости, абсолютно
несжимаемую, не расширяющуюся с изменением
температуры, абсолютно неспособную
сопротивляться разрыву. Таким образом,
идеальная жидкость представляет собой
некоторую модель реальной жидкости.
Выводы, полученные исходя из свойств
идеальной жидкости, приходится, как
правило, корректировать, вводя поправочные
коэффициенты.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Коэффициент вязкости – это величина, используемая для обозначения силы внутреннего трения текучих веществ. Вязкость – разновидность явлений переноса. Жидкости и газы оказывают сопротивление перемещению двух слоев относительно друг друга. Эта особенность характерна для текучих веществ, связана с движением частиц, из которых и состоят вещества.
Вязкость называют внутренним трением. В его основе находится хаотическое движение молекул, передающих импульс между слоями. Такие импульсные обмены выравнивают скорости перемещения слоев.
Коэффициент динамической вязкости
Численное обозначение абсолютной вязкости является индексом сопротивляемости испытуемых веществ взаимному перемещению или скольжению их слоев.
Единицей измерения коэффициента в системе СИ приняты паскаль-секунды:
Физическая основа динамического показателя заключается в его соответствии касательному напряжению, которое происходит между слоями вещества, перемещающимися относительно друг друга, при условии расстояния между ними, равного единице длины, и на скорости, равной единице.
Вязкость жидкости
Вязкость жидкости определяется формулой, в которой динамический коэффициент определяет пропорциональность скорости движения слоев и расстояния между ними:
-
τ – касательное напряжение;
-
µ — показатель пропорциональности, который является динамическим индексом вещества.
Закон вязкости жидкости был установлен Ньютоном в конце 17 века. Абсолютный показатель зависит от типа газа или жидкости, температуры веществ.
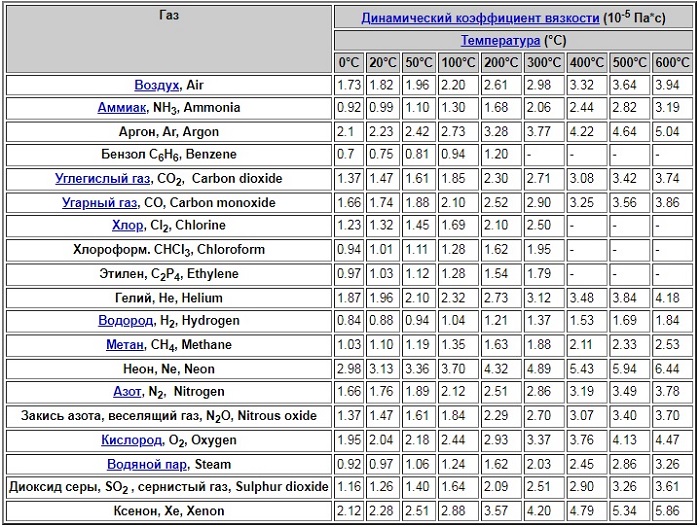
Коэффициент динамической вязкости газа
Для основных газов величины коэффициента при температуре 0 — 600 градусов Цельсия представлены в таблице:
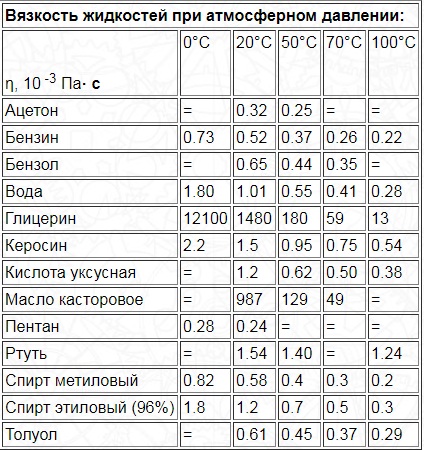
Коэффициент вязкости жидкостей
Для органических жидкостей показания напрямую зависят от температуры. Ниже приведена таблица со значениями абсолютного индекса для веществ при температурах от 0 до 100 градусов Цельсия.
Единица измерения – миллипаскаль-секунды, что соответствует сантипуазам.
Коэффициент динамической вязкости жидкостей уменьшается при условии нагревания вещества. Другими словами, чем выше температура жидкости, тем менее вязкой она становится.
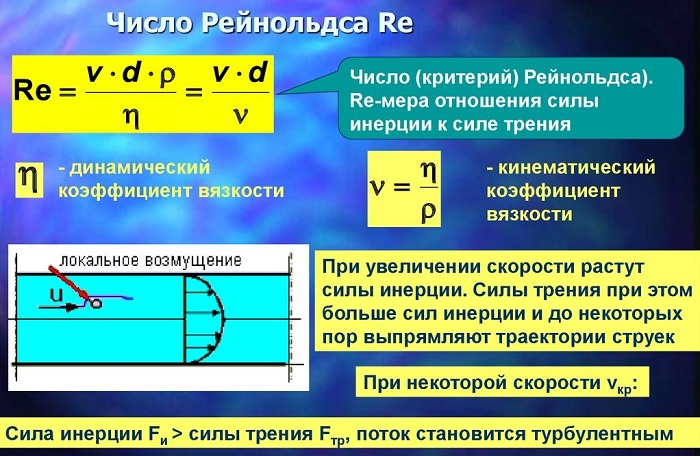
Связь коэффициента вязкости с числами Рейнольдса и силой трения
Английский механик, физик и инженер Оскар Рейнольдс установил (1876 — 1883 гг.), что характер течения зависит от величины, не имеющей размерностью, и называемой числом Re.
Число Рейнольдса используют для отображения соотношения кинематической энергии вещества к энергопотерям на установленной длине в условиях внутреннего трения.
Примеры решения задач
Попробуем решить следующую задачу.
Установить тип движения жидкого вещества по трубам теплообменника, имеющего структуру «труба в трубе». Параметры внутренней трубы – 25*2 мм, внешней – 50*2,5 мм. Массовый расход воды составляет 4000 кг/ч (обозначение G). Плотность жидкости – 1000 кг/м3. Абсолютный индекс составляет 1•10-3 Па*с.
Действие 1.
Следует узнать эквивалентный диаметр сечения межтрубного пространства:
Действие 2.
Определение скорости воды на основе уравнения расхода:
Действие 3.
По формуле Рейнольдса найти число Re:
Подставляя значения, получаем:
Ответ: режим перемещения воды в межтрубном пространстве является турбулентным.
Коэффициент кинематической вязкости
Кинематическая вязкость – это индекс, который отображает отношение абсолютного показателя вещества к его плотности при установленной температуре.
Физическая формула соотношения выглядит и единицы измерения можно увидеть на картинке:
Действие 4. Вычисление кинематического показателя, исходя из формулы:
Подставив в уравнение полученные и имеющиеся расчетные данные, получим кинематический индекс вещества.
Заключение
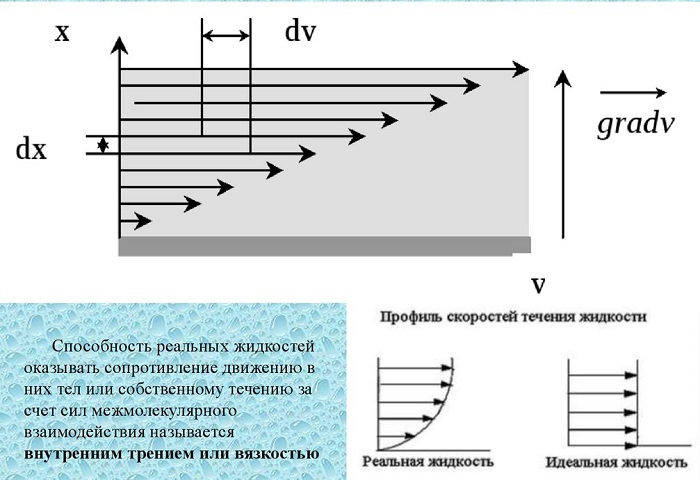
Физический смысл коэффициента вязкости заключается в том, что он демонстрирует, чему равна величина F внутреннего трения, действующая на 1 ед. площади поверхности соприкасающихся слоев при единичном градиенте скорости.
Размерность данной величины и перевод из одних единиц измерения в другие показаны на картинке:
Вязкость жидкости

Вязкость жидкости – это свойство реальных жидкостей оказывать сопротивление касательным усилиям (внутреннему трению) в потоке. Вязкость жидкости не может быть обнаружена при покое жидкости, так как она проявляется только при её движении. Для правильной оценки таких гидравлических сопротивлений, возникающих при движении жидкости, необходимо прежде всего установить законы внутреннего трения жидкости и составить ясное представление о механизме самого движения.
Содержание
- Физический смысл вязкости
- Вязкость кинематическая, динамическая и абсолютная
- Коэффициент вязкости жидкости
- Методы измерения вязкости. Метод Стокса.
- Видео по теме вязкости
Физический смысл вязкости
Для понятия физической сущности такого понятия как вязкость жидкости рассмотрим пример. Пусть есть две параллельные пластинки А и В. В пространство между ними заключена жидкость: нижняя пластинка неподвижна, а верхняя пластинка движется с некоторой постоянной скоростью υ1
Как при этом показывает опыт, слои жидкости, непосредственно прилегающие к пластинкам (так называемые прилипшие слои), будут иметь одинаковые с ним скорости, т.е. слой, прилегающий к нижней пластинке А, будет находиться в покое, а слой, примыкающий к верхней пластинке В, будет двигаться со скоростью υ1.
Промежуточные слои жидкости будут скользить друг по другу, причем их скорости будут пропорциональны расстояниям от нижней пластинки.
Ещё Ньютоном было высказано предположение, которое вскоре подтвердилось опытом, что силы сопротивления, возникающие при таком скольжении слоев, пропорциональны площади соприкосновения слоев и скорости скольжения. Если взять площадь соприкосновения равной единице, это положение можно записать в виде
где τ – сила сопротивления, отнесенная к единице площади, или напряжение трения
μ – коэффициент пропорциональности, зависящий от рода жидкости и называемый коэффициентом абсолютной вязкости или просто абсолютной вязкостью жидкости.
Величину dυ/dy – изменение скорости в направлении, нормальном к направлению самой скорости, называют скоростью скольжения.
Таким образом вязкость жидкости – это физическое свойство жидкости, характеризующее их сопротивление скольжению или сдвигу
Вязкость кинематическая, динамическая и абсолютная
Теперь определимся с различными понятиям вязкости:
Динамическая вязкость. Единицей измерения этой вязкости является паскаль в секунду (Па·с). Физический смысл состоит в снижении давления в единицу времени. Динамическая вязкость характеризует сопротивление жидкости (или газа) смещению одного слоя относительно другого.
Динамическая вязкость зависит от температуры. Она уменьшается при повышении температуры и увеличивается при повышении давления.
Кинематическая вязкость. Единицей измерения является Стокс. Кинематическая вязкость получается как отношение динамической вязкости к плотности конкретного вещества.
Определение кинематической вязкости производится в классическом случае измерением времени вытекания определенного объема жидкости через калиброванное отверстие при воздействии силы тяжести
Абсолютная вязкость получается при умножении кинематической вязкости на плотность. В международной системе единиц абсолютная вязкость измеряется в Н*с/м2 – эту единицу называют Пуазейлем.
Коэффициент вязкости жидкости
В гидравлике часто используют величину, получаемую в результате деления абсолютной вязкости на плотность. Эту величину называют коэффициентом кинематической вязкости жидкости или просто кинематической вязкостью и обозначают буквой ν. Таким образом кинематическая вязкость жидкости
ν = μ / ρ
где ρ – плотность жидкости.
Единицей измерения кинематической вязкости жидкости в международной и технической системах единиц служит величина м2/с.
В физической системе единиц кинематическая вязкость имеет единицу измерения см2/с и называется Стоксом(Ст).
Вязкость некоторых жидкостей
| Жидкость | t, °С | ν, Ст |
| Вода | 0 | 0,0178 |
| Вода | 20 | 0,0101 |
| Вода | 100 | 0,0028 |
| Бензин | 18 | 0,0065 |
| Спирт винный | 18 | 0,0133 |
| Керосин | 18 | 0,0250 |
| Глицерин | 20 | 8,7 |
| Ртуть | 0 | 0,00125 |
Величину, обратную коэффициенту абсолютной вязкости жидкости, называют текучестью
ξ = 1/μ
Как показывают многочисленные эксперименты и наблюдения, вязкость жидкости уменьшается с увеличением температуры. Для различных жидкостей зависимость вязкости от температуры получается различной.
Поэтому, при практических расчетах к выбору значения коэффициента вязкости следует подходить очень осторожно. В каждом отдельном случае целесообразно брать за основу специальные лабораторные исследования.
Вязкость жидкостей, как установлено из опытов, зависит так же и от давления. Вязкость возрастает при увеличении давления. Исключение в этом случае является вода, для которой при температуре до 32 градусов Цельсия с увеличением давления вязкость уменьшается.
Что касается газов, то зависимость вязкости от давления, так же как и от температуры, очень существенна. С увеличением давления кинематическая вязкость газов уменьшается, а с увеличением температуры, наоборот, увеличивается.
Методы измерения вязкости. Метод Стокса.

Область, посвященная измерению вязкости жидкости, называется вискозиметрия, а прибор для измерения вязкости называется вискозиметр.
Современные вискозиметры изготавливаются из прочных материалов, а при их производстве используются самые современные технологии, для обеспечение работы с высокой температурой и давлением без вреда для оборудования.
Существует следующие методы определения вязкости жидкости.
Капиллярный метод.
Сущность этого метода заключается в использовании сообщающихся сосудов. Два сосуда соединяются стеклянной трубкой известного диаметра и длины. Жидкость помещается в стеклянный канал и за определенный промежуток времени перетекает из одного сосуда в другой. Далее зная давление в первом сосуде и воспользовавшись для расчетов формулой Пуазейля определяется коэффициент вязкости.
Метод по Гессе.
Этот метод несколько сложнее предыдущего. Для его выполнения необходимо иметь две идентичные капиллярные установки. В первую помещают среду с заранее известным значением внутреннего трения, а во вторую – исследуемую жидкость. Затем замеряют время по первому методу на каждой из установок и составляя пропорцию между опытами находят интересующую вязкость.
Ротационный метод.
Для выполнения этого метода необходимо иметь конструкцию из двух цилиндров, причем один из них должен быть расположен внутри другого. В промежуток между сосудами помещают исследуемую жидкость, а затем придают скорость внутреннему цилиндру.
Жидкость вращается вместе с цилиндром со своей угловой скоростью. Разница в силе момента цилиндра и жидкости позволяет определить вязкость последней.
Метод Стокса

Для выполнения этого опыта потребуется вискозиметр Гепплера, который представляет из себя цилиндр, заполненный жидкостью.
Вначале делаются две пометки по высоте цилиндра и замеряют расстояние между ними. Затем шарик определенного радиуса помещается в жидкость. Шарик начинает погружаться в жидкость и проходит расстояние от одной метки до другой. Это время фиксируется. Определив скорость движения шарика затем вычисляют вязкость жидкости.
Видео по теме вязкости
Определение вязкости играет большую роль в промышленности, поскольку определяет конструкцию оборудования для различных сред. Например, оборудование для добычи, переработки и транспортировки нефти.
Вместе со статьей «Вязкость жидкости» смотрят:

Кавитация в насосах

Турбулентный режим движения жидкости

Уравнение неразрывности струи и потока жидкости.