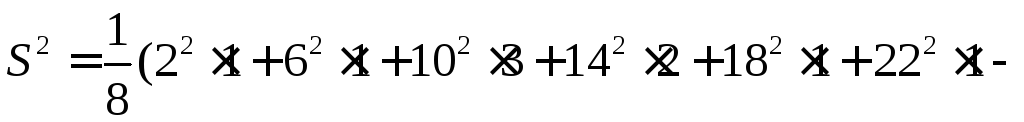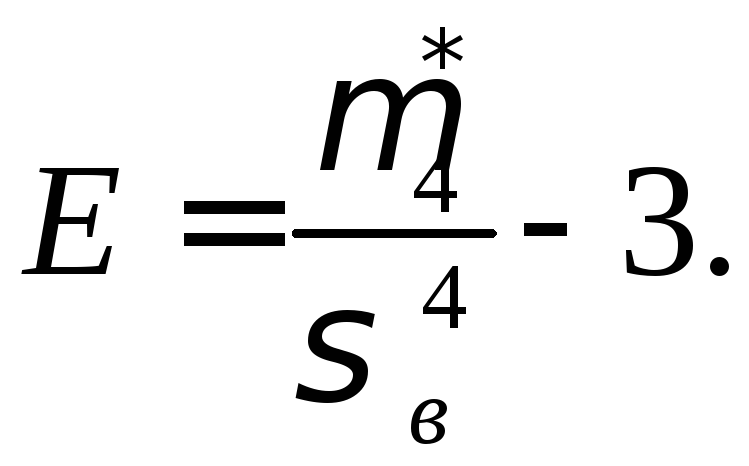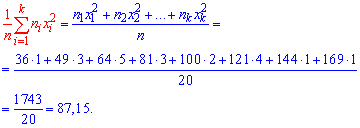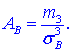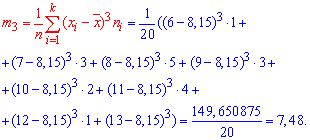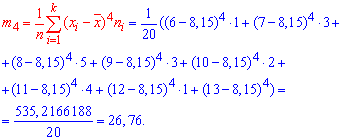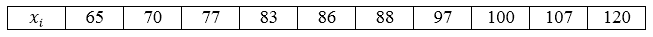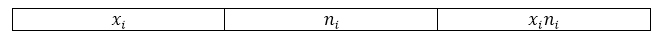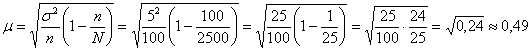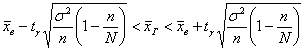Как найти выборочное среднее задачи

Образцы решения типовых задач

Пример 1.
Найти
выборочное среднее, несмещенную
выборочную дисперсию и несмещенное
выборочное среднее квадратическое
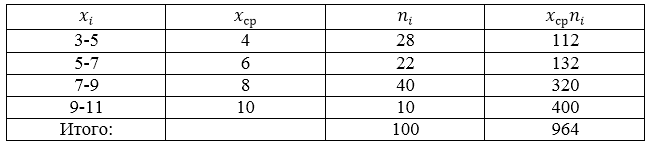
отклонение для статистического ряда

	2	7	9	10
	8	14	10	18

Решение.
Объем выборки
.
Находим выборочное среднее по формуле
(2.1):

Для
вычисления несмещенной выборочной
дисперсии используем формулу (2.4):

Несмещенное
выборочное среднее квадратичное
отклонение рассчитывается по формуле
(2.6):

Пример
2.
Найти выборочное среднее, исправленную
выборочную дисперсию и
исправленное
выборочное среднее квадратическое
отклонение для интервального
статистического ряда:

Границы интервалов
	1	1	3	2	1	1

Решение.
Объем
выборки
Выборка разбита на шесть интервалов
().
Найдем середины интервалов и добавим
их в исходную
таблицу:

Границы интервалов
Середины интервалов	2	6	10	14	18	22
	1	1	3	2	1	1

Выборочное
среднее, находим по формуле (2.3):

Несмещенная
выборочная дисперсия, определяется по
формуле (2.5):

Несмещенное
выборочное среднее квадратическое
отклонение рассчитывается по формуле
(2.6):

Пример
3.
Найти
выборочное среднее по выборке объема

	2560	2600	2620	2650	2700
	2	3	10	4	1

Решение.
Для
упрощения расчетов перейдем к условным
вариантам

и_i
= х_i
– 2620:

иi	– 60	– 20	0	30	80
mi	2	3	10	4	1

Тогда

и

Замечание.
В качестве числа, которое вычитается
при пе­реходе
к условным вариантам (условный нуль),
обычно выбирается варианта,
стоящая в середине ряда, либо та, для
которой частота максимальна
(выборочная мода). В данном примере они
совпа­дают.

Пример
4.
Найти
неисправленную выборочную дисперсию
по выборке объема :

	18,4	18,9	19,3	19,6
	5	10	20	15

Решение.
Перейдем
к условным вариантам и_i
= 10(х_i
– 19,3).
Тогда

Dи_i
= D(10

— 193)
= 100
Dх_i

и

иi	– 9	– 4	0	3
mi	5	10	20	15

Найдем
выборочную дисперсию для новой варианты

и_i
:

Переходя
к первоначальной варианте х_i,
получаем

Пример
5. По
выборке объема
найдена смещенная оцен­ка
теоретической дисперсии. Найти
исправленную оцен­ку
дисперсии генеральной совокупности.

Решение.
Несмещенная
оценка дисперсии связана со сме­щенной
следующей формулой:

Пример 6.
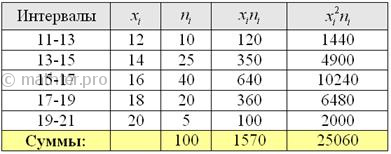
Вычислите
коэффициенты асимметрии и эксцесса
распределения числа проданных цветных
телевизоров по данным примера 5 подмодуля
1.1 (табл. 1.1).

Решение.  и интервального
вариационного ряда, приведенного в
таблице 1.1 подмодуля 1.1, найдем по формулам

и

По
аналогии, с приведенными выше примерами,
найдем и

Для
нахождения μ₃
и μ₄
составим вспомогательную расчетную
таблицу 2.1.

Таблица
2.1

xi	mi	ximi	xi –	(xi –)mi	(xi –)2mi	(xi –)3mi	(xi –)4mi
9	1	9	–6,5	–6,5	42,25	–274,625	1785,0625
12	2	24	–3,5	–7	24,5	–85,75	300,125
13	3	39	–2,5	–7,5	18,75	–46,875	117,1875
14	6	84	–1,5	–9	13,5	–20,25	30,375
15	5	75	–0,5	–2,5	1,25	–0,625	0,3125
16	3	48	0,5	1,5	0,75	0,375	0,1875
17	2	34	1,5	3	4,5	6,75	10,125
19	1	19	3,5	3,5	12,25	42,875	150,0525
21	1	21	5,5	5,5	30,25	166,375	915,0625
23	1	23	7,5	7,5	56,25	421,875	3164,0625
27	1	27	11,5	11,5	132,25	1520,875	17490,0625
Σ	26	403	–	0	336,5	1731	23962,63

=
=
=
=

=
1,4299.

=
–
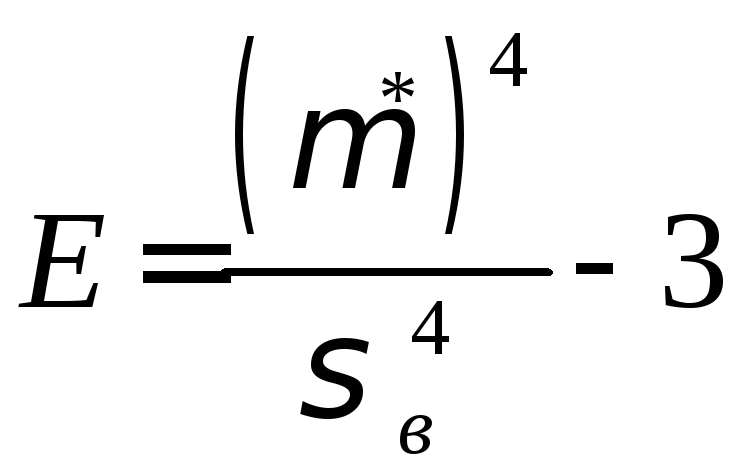
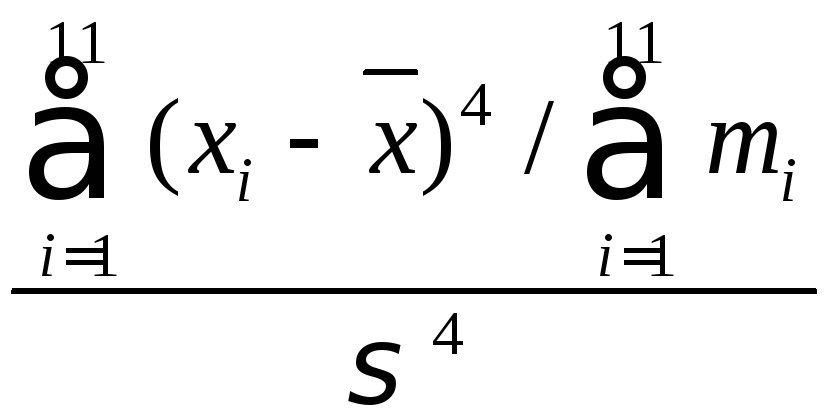
3 =
= 5,5022 – 3= = 2,5022.

Таким
образом, рассматриваемое распределение
числа проданных цветных телевизоров
обнаруживает не только некоторую
правосторон­нюю асимметрию, но и
положительный эксцесс.

Пример
7. В течение
недели регистрировались пропуски
занятий сту­дентами одной группы. В
результате регистрации получили
статистиче­ские данные:

2,
1, 3, 1, 2, 1, 2, 4, 3, 5, 3, 2, 2, 2, 1, 2, 3, 1, 0, 0, 0, 2, 3, 1,
4.

Вычислите
числовые характеристики выборки:
выборочное
среднее, выборочную дисперсию, моду,
медиану, коэффициенты асиммет­рии и
эксцесса, коэффициент вариации.

Решение.
Воспользуемся средствами MS
Excel.

1. Сформируем
   таблицу исходных данных:

1. Для
   подсчета выборочного среднего выберем
   ячейку А5
   и перейдем на вкладку Формулы
   – Другие функции – Статистические
   и выберем из раскрывающегося списка
   СРЗНАЧ.
   В появившемся окне в поле Число1
   вводим диапазон исходных данных (А1:J3).
   После нажатия кнопки ОК, в ячейке А5
   появится результат вычисления: 2.

2. Для
   подсчета выборочной дисперсии выберем
   ячейку А6
   и перейдем на вкладку Формулы
   – Другие функции – Статистические
   и выберем из раскрывающегося списка
   ДИСП.В.
   В появившемся окне в поле Число1
   вводим диапазон исходных данных (А1:J3).
   После нажатия кнопки ОК, в ячейке А6
   появится результат вычисления: ≈1,67

3. Для
   подсчета моды выберем ячейку А7
   и перейдем на вкладку Формулы
   – Другие функции – Статистические
   и выберем из раскрывающегося списка
   МОДА.ОДН.
   В появившемся окне в поле Число1
   вводим диапазон исходных данных (А1:J3).
   После нажатия кнопки ОК, в ячейке А7
   появится
   результат вычисления: 2.

4. Для
   подсчета медианы выберем ячейку А8
   и перейдем на вкладку Формулы
   – Другие функции – Статистические
   и выберем из раскрывающегося списка
   МЕДИАНА.
   В появившемся окне в поле Число1
   вводим диапазон исходных данных (А1:J3).
   После нажатия кнопки ОК, в ячейке А8
   появится результат вычисления: 2.

5. Для
   подсчета коэффициента асимметрии
   выберем ячейку А9
   и перейдем на вкладку Формулы
   – Другие функции – Статистические
   и выберем из раскрывающегося списка
   СКОС.
   В появившемся окне в поле Число1
   вводим диапазон исходных данных (А1:J3).
   После нажатия кнопки ОК, в ячейке А9
   появится результат вычисления: ≈0,38.

6. Для
   подсчета коэффициента эксцесса выберем
   ячейку А10
   и перейдем на вкладку Формулы
   – Другие функции – Статистические
   и выберем из раскрывающегося списка
   ЭКСЦЕСС.
   В появившемся окне в поле Число1
   вводим диапазон исходных данных (А1:J3).
   После нажатия кнопки ОК, в ячейке А10
   появится результат вычисления: ≈-0,1.

7. Для
   подсчета коэффициента вариации сначала
   найдем значение среднего квадратического
   отклонения для выборки, так как
   коэффициент вариации представляет
   собой отношение среднего квадратического
   отклонения к среднему арифметическому.
   Для этого выберем ячейку А11
   и перейдем на вкладку Формулы
   – Другие функции – Статистические
   и выберем из раскрывающегося списка
   СТАНДОТКЛОН.В.
   В появившемся окне в поле Число1
   вводим диапазон исходных данных (А1:J3).
   После нажатия кнопки ОК, в ячейке А11
   появится результат вычисления: ≈1,3.

8. Теперь
   для вычисления коэффициента вариации
   есть все необходимые величины. Выберем
   ячейку А12
   и введем в неё формулу: =(A11/A5)*100
   (Коэффициент вариации обычно выражается
   в процентах). После нажатия кнопки Enter
   в ячейке А12
   появится результат вычисления: ≈ 64,55.

Пример
8.  По
данным выборки

1,
5, 2, 4, 3, 4, 6, 4, 5,1,2, 2, 3, 4, 5, 3, 4, 5, 2, 1,

4,
5, 5, 4, 3, 4, 6, 1, 2, 4,4, 3, 5, 6, 4, 3, 3, 1, 3, 4,

3,
4, 3, 1, 2, 4, 4, 5, 6, 1,3, 4, 5, 4, 4, 3, 2, 6, 1, 2,

4,
5, 3, 3, 2, 3, 6, 4, 3, 4,5, 4, 3, 3, 2, 6, 3, 3, 5, 4,

4,
3, 3, 2, 1, 2, 1, 6, 5, 4,3, 2, 3, 4, 4, 3, 5, 6, 1, 5.

Определить
средний разряд рабочего, выборочную
дисперсию и выборочное среднее
квадратическое отклонение.

Решение.
1. Для начала сформируем таблицу исходных
данных в программе MS Excel:

2. Для
нахождения среднего разряда воспользуемся
функцией МОДА.ОДН:

а)
Необходимо выбрать ячейку, в которую
будет помещен результат (А11)

б)
Перейти на вкладку ФОРМУЛЫ – Другие
функции – Статистические и из выпадающего
списка выбрать МОДА.ОДН

в)
В поле Число1 указать диапазон исходных
данных (А1:К10)

г)
Нажать кнопку ОК. В ячейке А11
появится результат вычисления = 4.

3.
Для нахождения выборочной дисперсии
воспользуемся функцией ДИСП.В:

а)
Необходимо выбрать ячейку, в которую
будет помещен результат (А12)

б)
Перейти на вкладку ФОРМУЛЫ – Другие
функции – Статистические и из выпадающего
списка выбрать ДИСП.В

в)
В поле Число1 указать диапазон исходных
данных (А1:К10).

г)
Нажать кнопку ОК. В ячейке А12
появится результат вычисления ≈ 2,03.

4. Чтобы
найти выборочное среднее квадратическое
отклонение будем использовать функцию
СТАНДОТКЛОН.В:

а)
Необходимо выбрать ячейку, в которую
будет помещен результат (А13)

б)
Перейти на вкладку ФОРМУЛЫ – Другие
функции – Статистические и из выпадающего
списка выбрать СТАНДОТКЛОН.В

в)
В поле Число1 указать диапазон исходных
данных (А1:К10)

г)
Нажать кнопку ОК. В ячейке А13
появится результат вычисления ≈ 1,42.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Исследование выборки: числовые характеристики, графики

Исследование выборки — базовая тема при изучении математической статистики, с нее начинаются любые курсы МС. Нужно научиться находить объем выборки, числовые характеристики (выборочное среднее, дисперсию, исправленную дисперсию, среднее квадратическое отклонение, коэффициент вариации и т.п.). При этом для выборок большого объема часто требуется перейти к интервальному представлению (правильно рассчитав число интервалов и их длину, обычно по формуле Стерджеса). Это все относится к первичной обработке статистической выборки.

Помимо проведения вычислений (чаще всего с помощью Excel) нужно уметь графически представлять выборку: строить полигон, гистограмму, кумуляту, огиву и другие графики и диаграммы.

В этом разделе мы рассмотрим решения задач на исследование выборки, нахождение ее характеристик и построение соответствующих графиков. Изучайте!

Примеры решений онлайн

Простой вариационный ряд

Задача 1. Дан следующий вариационный ряд

1 2 3 4 5 6 7 8 9 10

1 1 2 2 4 4 4 5 5 5
Требуется
1) Построить полигон распределения
2) Вычислить выборочную среднюю, дисперсию, моду, медиану.
3) Построить выборочную функцию распределения
4) Найти несмещенные оценки математического ожидания и дисперсии.

Задача 2. Из изучаемой налоговыми органами обширной группы населения было случайным образом было отобрано 10 человек и собраны сведения об их доходах за истёкший год в тысячах рублей: х1, х2,….х10, найти выборочное среднее, выборочную дисперсию, исправленную выборочную дисперсию. Считая распределения доходов в группе нормальным и используя в качестве его параметров выборочное среднее и исправленную выборочную дисперсию, определить какой процент группы имеет годовой доход, превышающий а тысяч рублей

Задача 3. Из генеральной совокупности извлечена выборка объема n. Найти выборочную среднюю, выборочную дисперсию, выборочное среднее квадратическое отклонение, исправленную выборочную дисперсию, коэффициент вариации, моду и медиану.

10,5 11 11,5 12 12,5 13 13,5

2 18 40 25 6 5 4

Задача 4. Дана выборка. Требуется:
а) Построить статистический ряд распределения частот и полигон частот;
б) Вариационный ряд;
в) Найти оценки математического ожидания и дисперсии;
г) Найти выборочные моду, медиану, коэффициент вариации, коэффициент асимметрии.
10,20,20,5,15,20,5,10,20,5.

Задача 5. Найти методом произведений: 1) выборочную дисперсию, 2) выборочное среднее квадратическое отклонение по данному статистическому распределению выборки (в первой строке указаны выборочные варианты $x_i$, а во второй строке – соответствующие частоты $n_i$).

Задача 6. При определении удельного расхода корундового шлифовального круга при шлифовке стальных деталей (отношение изношенного объема круга в мм3 к объему сошлифованного металла в мм3) были получены следующие результаты:
Провести статистическую обработку результатов испытаний.

Интервальный ряд

Задача 7. Проведено выборочное обследование магазинов города. Имеются следующие данные о величине товарооборота для 50 магазинов города (xi – товарооборот, млн. руб.; ni – число магазинов).
xi 25-75 75-125 125-175 175-225 225-275 275-325
ni 12 15 9 7 4 3
Найти
а) среднее, среднее квадратическое отклонение S и коэффициент V;
б) построить гистограмму и полигон частот.

Задача 8. Ряд распределения заработной платы рабочих механического цеха приведен в таблице. Требуется вычислить коэффициент вариации $V$, приняв $i=1$.
Заработная плата (руб.) 212-214 214-216 216-218 218-220 220-222
Число рабочих 7 12 12 9 5

Задача 9. Требуется для решения:
— Построить интервальный ряд распределения, для каждого интервала подсчитать локальные, а также накопленные частоты, построить вариационный ряд.
— Построить полигон и гистограмму.
— определить выборочную среднюю, а также низшую и высшую частные средние ,моду и медиану, дисперсию и среднее квадратическое отклонение, коэффициент вариации.
— проверить при уровне значимости 0,05 гипотезу о нормальном законе распределения соответствующего признака с помощью критериев согласия Пирсона, и Смирнова.
-найти точечные и интервальные оценки генеральной средней и среднего квадратичного отклонения (при доверительной вероятности Р=0,95.
— найти ошибки выборочных оценок.
— произвести анализ всех вычисленных статистических параметров.
Задание: произвести обработку данных по среднегодовому удою молока по 11-70 хозяйствам, 80 хозяйств.

Задача 10. Для исследования доходов населения города, составляющего 20000 чел. по схеме бесповторной выборки было отобрано некоторое количество жителей. Получено следующее распределение жителей по месячному доходу (см. таблицу вариантов).
Построить гистограмму, полигон и кумуляту относительных частот.
Найти вероятность того, что истинный средний доход отличается от среднего дохода по выборке не более, чем на 45 у.е. (по абсолютной величине).
Определить границы, в которых заключен доход с вероятностью 0,99.
Найти объем выборки, при котором, гарантируется вероятность тех же границ, равная 0,9973.

Другие задания

Задача 11. Как изменится выборочное среднее, мода, медиана и выборочная дисперсия, если каждый член выборки уменьшить в 5 раз?

Полезные ссылки

• Статистические таблицы и формулы
• Решение задач по математической статистике на заказ
• Ссылки на учебники по математической статистике
• Решенные контрольные по математической статистике

1. выборочное среднее;
2. выборочную дисперсию;;
3. подправленную дисперсию;
4. выборочное среднее квадратичное отклонение;
5. подправленное среднее квадратичное отклонение;
6. размах выборки;
7. медиану;
8. моду;
9. квантильное отклонение;
10. коэффициент вариации;
11. коэффициент асимметрии;
12. эксцесс для выборки:

Выборка задана рядом 11, 9, 8, 7, 8, 11, 10, 9, 12, 7, 6, 11, 8, 7, 10, 9, 11, 8, 13, 8.

Решение:
Запишем выборку в виде вариационного ряда (в порядке возрастания):
6; 7; 7; 7; 8; 8; 8; 8; 8; 9; 9; 9; 10; 10; 11; 11; 11; 11; 12; 13.
Далее записываем статистическое распределение выборки в виде дискретного статистического распределения частот:

Эмпирическую функцию распределения определим по формуле

Здесь n_x – количество элементов выборки которые меньше х. Используя таблицу и учитывая что объем выборки равен n = 20, запишем эмпирическую функцию распределения:

Далее вычислим числовые характеристики статистического распределения выборки.
Выборочное среднее вычисляем по формуле

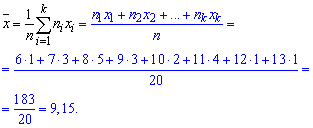
Выборочную дисперсию находим по формуле


Выборочное среднее, что фигурирует в формуле дисперсии в квадрате найдено выше. Остается все подставить в формулу

Подправленную дисперсию вычисляем согласно формулы

Выборочное среднее квадратичное отклонение вычисляем по формуле

Подправленное среднее квадратичное отклонение вычисляем как корень из подправленной дисперсии

Размах выборки вычисляем как разность между наибольшим и наименьшим значениями вариант, то есть:

Медиану находим по 2 формулам:
если число n — четное;
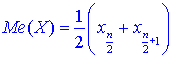
если число n — нечетное.
Здесь берем индексы в x_i согласно нумерации варианта в вариационном ряду.
В нашем случае n = 20, поэтому

Мода – это варианта которая в вариационном ряду случается чаще всего, то есть

Квантильное отклонение находят по формуле

где – первый квантиль, – третий квантиль.
Квантили получаем при разбивке вариационного ряда на 4 равные части.
Для заданного статистического распределения квантильное отклонения примет значение

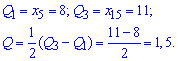
Коэффициент вариации равный процентному отношению подправленного среднего квадратичного к выборочному среднему

Коэффициент асимметрии находим по формуле

Здесь 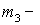центральный эмпирический момент 3-го порядка,

Подставляем в формулу коэффициента асимметрии

Эксцессом статистического распределения выборки называется число, которое вычисляют по формуле:

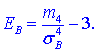
Здесь m₄ центральный эмпирический момент 4-го порядка. Находим момент

а далее эксцесс
Теперь Вы имеете все необходимые формулы чтобы найти числовые характеристики статистического распределения. Как найти моду, медиану и дисперсию должен знать каждый студент, который изучает теорию вероятностей.

Готовые решения по теории вероятностей

• Следующая статья — Построение уравнения прямой регрессии Y на X

Генеральная средняя

Пусть нам дана генеральная совокупность относительно случайной величины $X$. Для начала напомним следующее определение:

Пусть значения вариант $x_1, x_2,dots ,x_k$ имеют, соответственно, частоты $n_1, n_2,dots ,n_k$. Тогда генеральная средняя вычисляется по формуле:

Рассмотрим частный случай. Пусть все варианты $x_1, x_2,dots ,x_k$ различны. В этом случае $n_1, n_2,dots ,n_k=1$. Получаем, что в этом случае генеральная средняя вычисляется по формуле:

Выборочная средняя

Пусть нам дана выборочная совокупность относительно случайной величины $X$. Для начала напомним следующее определение:

Пусть значения вариант $x_1, x_2,dots ,x_k$ имеют, соответственно, частоты $n_1, n_2,dots ,n_k$. Тогда выборочная средняя вычисляется по формуле:

Рассмотрим частный случай. Пусть все варианты $x_1, x_2,dots ,x_k$ различны. В этом случае $n_1, n_2,dots ,n_k=1$. Получаем, что в этом случае выборочная средняя вычисляется по формуле:

«Средняя выборки: генеральная, выборочная» 👇

!!! В случае, когда значение вариант не являются дискретными, а представляют из себя интервалы, то в формулах для вычисления генеральной или выборочной средних значений за значение $x_i$ принимается значение середины интервала, которому принадлежит $x_i.$

Примеры задач на нахождение средней выборки



4.6. Оценка генеральной средней по повторной и бесповторной выборкам

Итак, вникаем: пусть из нормально распределенной (или около того) генеральной совокупности

объёма  проведена выборка объёма  и по её результатам найдена выборочная средняя . Тогда доверительный интервал для оценки

генеральной средней  имеет вид:
,  где  («дельта» большая) – точность

оценки, которую также называют предельной ошибкойвыборки.

Точность оценки рассчитывается как произведение  – коэффициента доверия  на среднюю ошибкувыборки («мю»).

Если известна дисперсия генеральной совокупности , то коэффициент доверия  отыскивается из лапласовского соотношения , а средняя ошибка рассчитывается по формуле:
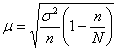
 – для бесповторной выборки или  – для повторной.

Если же генеральная дисперсия не известна, то в качестве её приближения используют исправленную выборочную дисперсию . В этом случае коэффициент доверия  определяют с помощью распределения Стьюдента, а при  можно использовать  соотношение . Средняя же ошибка рассчитывается по аналогичным формулам:
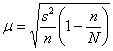
 – для бесповторной или  – для повторной выборки.

Напоминаю, что доверительная вероятность (надёжность)  задаётся наперёд и показывает, с какой вероятностью построенный

доверительный интервал  накрывает истинное

значение .

С конспектом отмучились, теперь задачи

Модифицируем задание Примера 19, а именно уточним способ отбора попугаев:

Пример 25

Известно, что генеральная совокупность распределена нормально со средним квадратическим отклонением . По результатам 4%-ной бесповторной выборки объёма , найдена выборочная средняя  (условно средний рост птицы).

1) Найти доверительный интервал для оценки генеральной средней   с надежностью .

2) Выборку какого объёма нужно организовать, чтобы уменьшить данный интервал в два раза?

Не решение даже, а целое исследование впереди, начинаем. Прежде всего, найдём объём генеральной

совокупности:
 попугаев, и на самом деле нам предстоит

ответить на следующий вопрос: а достаточно ли выборки объёма ? Или для качественного исследования роста попугаев нужно выбрать побольше

птиц?

1) Доверительный интервал для оценки генеральной средней составим по формуле:

, где  – точность оценки. В задачах данного типа у коэффициента доверия часто

опускают подстрочный индекс и пишут просто ,

однако я не буду следовать мейнстриму, т. к. эта «кастрация» ухудшает понимание.

По условию, нам известна генеральная дисперсия, поэтому коэффициент доверия найдём из

соотношения  . По таблице значений функции Лапласа либо на макете (пункт 1*) определяем, что этому значению функции соответствует аргумент .

Поскольку выборка бесповторная, то среднюю ошибку рассчитаем по

формуле:

Таким образом, точность оценки  и

соответствующий доверительный интервал:

 – с вероятностью  данный интервал накроет истинное значение генерального среднего

роста  попугая.

Теперь предположим, что нас не устраивает точность полученного результата. Хотелось бы уменьшить интервал. Или оставить

его таким же, но повысить доверительную вероятность. Этим вопросам и посвящён следующий пункт решения:

2) Выясним, сколько попугаев нужно взять, чтобы уменьшить полученный интервал в два раза. Иными словами, была точность

0,96, а мы хотим . При условии сохранения

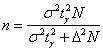
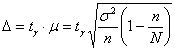
доверительной вероятности необходимый объём выборки можно рассчитать по формуле , которая выводится из .
А нашей задаче:
 и обязательно проверочка:
, ч.т.п.

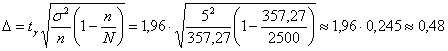
Таким образом, чтобы обеспечить точность  при

надёжности  нужно провести выборку объёмом

не менее 358 попугаев  (округлили в бОльшую сторону). В этом случае получится доверительный

интервал в два раза короче:

И внимание! Здесь нельзя использовать значение  предыдущего пункта! Почему? Потому что в новой выборке мы почти

наверняка получим НОВУЮ выборочную среднюю. Вот её-то и нужно будет подставить.

Осталось прикинуть, а не много ли это – 358 попугаев? Объём выборки составит:  от генеральной совокупности – ну, в принципе, сносно, хотя и многовато. Поэтому здесь

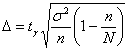
можно использовать другой подход: оставить точность оценки  прежней, но повысить доверительную вероятность до . В этом случае нужно найти новый коэффициент доверия  (из соотношения ) и решить уравнение , получив в качестве корня необходимый объём выборки . Желающие могут выполнить этот пункт самостоятельно, в результате

получается выборка в  попугаев или  генеральной совокупности. Что лучше, конечно, ведь измерить

линейкой 358 попугаев – задача хлопотная, они явно будут сопротивляться, а некоторые ещё и говорить нехорошие слова J.

Теперь распишем доверительный интервал  подробно:

и ответим вот на какой вопрос: а что будет, если генеральная совокупность великА или даже бесконечна? В

этом случае дробь  близкА к нулю, и мы получаем

интервал:
, который фигурировал в Примере 19. То есть по

умолчанию (когда не сказано, бесповторная выборка или нет), считают именно так.
Следует отметить, что полученный выше интервал соответствует повторной выборке со

средней ошибкой , таким образом, при слишком

большом объёме  генеральной совокупности

математическое различие между бесповторной и повторной выборкой стирается.

Пришло время запланировать собственное статистическое исследование:

Пример 26

В результате многократных независимых измерений некоторой физической величины  в прошлом достаточно точно определена генеральная дисперсия  ед.; при этом средняя величина склонна изменениям (от исследования к

исследованию). Сколько измерений нужно осуществить, чтобы с вероятностью  заключить текущее истинное значение генеральной средней  в интервале длиной 0,5 ед. 

И это как раз только что описанный случай: данную выборку можно считать бесповторной, при этом ген. совокупность

теоретически бесконечна; либо повторной, так как округлённые результаты измерений могут повторяться.

Краткое решение в конце книги, числа можете выбрать по своему вкусу J. Но здесь есть одно «странное» значение . Оно не случайно и соответствует

правилу «трёх сигм», т. е.,

практически достоверным является тот факт, что построенный интервал накроет истинное значение .

Разумеется, на практике генеральная дисперсия чаще не известна, и поэтому за неимением лучшего, используют исправленную

выборочную дисперсию:

Пример 27

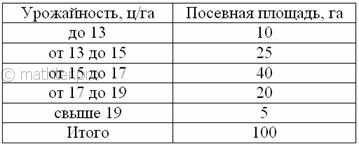
С целью изучения урожайности подсолнечника в колхозах области проведено 5%-ное выборочное обследование 100 га посевов,

отобранных в случайном порядке, в результате которого получены следующие данные:

С вероятностью 0,9974 определить предельную ошибку выборки и возможные границы, в которых ожидается средняя

урожайность подсолнечника в области.

Решение: в условии не указан тип отбора, но исходя из логики исследования, положим, что он

бесповторный. Поскольку выборка 5%-ная, то объем генеральной совокупности (общая посевная площадь области)

составляет:
 гектаров – не знаю, насколько это

реалистично, оставим этот вопрос на совести автора задачи.

По условию, требуется найти предельную ошибку выборки (точность оценки) , где  –

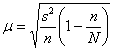
коэффициент доверия, соответствующий доверительной вероятности , и коль скоро выборка бесповторна и генеральной дисперсии мы не знаем, то средняя ошибка рассчитывается по формуле . Далее нужно составить интервал , который с вероятностью 99,74% (практически достоверно) накроет генеральную среднюю  урожайность

подсолнечника по области.

И если с коэффициентом «тэ гаммовое» трудностей никаких, то коэффициент «мю» здесь трудовой – по той причине, что нам не

известна исправленная выборочная дисперсия. Ну что же, хороший повод освежить пройденный материал. Смотрим на таблицу

выше и приходим к выводу, что нам предложен интервальный вариационный ряд с

открытыми крайними интервалами. Поскольку длина частичного интервала составляет  га, то вопрос закрываем так: 11-13 и 19-21 га.

Находим середины  интервалов (переходим к

дискретному ряду), произведения  и их суммы:

Вычислим выборочную среднюю:  центнеров с гектара.

Выборочную дисперсию вычислим по формуле:
 и этим частенько пренебрегают, но я

призываю поправлять дисперсию:
 – мелочь, а приятно.

Теперь составляем доверительный интервал ,

 где .

Найдём коэффициент доверия .

Поскольку нам известна лишь исправленная выборочная дисперсия (а не генеральная), то правильнее использовать распределение

Стьюдента. Но, к сожалению, в таблице нет значений для , но зато есть расчётный макет (пункт 2б). Для заданной надёжности и количества степеней свободы  получаем .

Поскольку объём выборки , то можно использовать

нормальное распределение, и тут получается конфетка:
, какой способ выбрать – зависит от вашей

методички, и я так подозреваю, второй :). Но сейчас выберем первый.

Вычислим среднюю ошибку бесповторной выборки:
 ц/га, таким образом, предельная ошибка

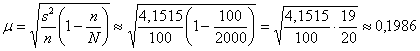
составляет  ц/га, и искомый доверительный

интервал:

 (ц/га) – границы, в которых ожидается

средняя урожайность подсолнечника в области с вероятностью  (практически достоверно).

Ответ:  ц/га,        (ц/га)

В рассмотренной задаче можно поставить вопросы, аналогичные Примеру 25, а именно попытаться улучшить исследование, в

частности, уменьшить точность оценки . В этом

случае для определения необходимого объема выборки используется та же формула 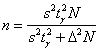, но она менее достоверна, поскольку в разных выборках мы будем получать разные значения

. Такие задачи, однако, встречаются, будьте

готовы. Да, и аналогичная формула для повторной выборки: .

Пример 28

По результатам 10%-ной бесповторной выборки объёма , найдены выборочная средняя  и дисперсия .

а) Найти пределы, за которые с доверительной вероятностью 0,954 не выйдет среднее значение генеральной совокупности.
б) Найти эти пределы, если выборка повторная. Какой способ точнее?

Значение 0,954 обусловлено тем, что автор задачи пощадил студентов, в методичке используется функция Лапласа и получается целое значение .

Решаем самостоятельно!

4.7. Оценка генеральной доли

4.5. Повторная и бесповторная выборка

| Оглавление |