Как найти выборочную дисперсию интервального ряда - Исправление недочетов и поиск решений вместе с Examum.ru

Интервальный вариационный ряд и его характеристики

Построение интервального вариационного ряда по данным эксперимента
Гистограмма и полигон относительных частот, кумулята и эмпирическая функция распределения
Выборочная средняя, мода и медиана. Симметрия ряда
Выборочная дисперсия и СКО
Исправленная выборочная дисперсия, стандартное отклонение выборки и коэффициент вариации
Алгоритм исследования интервального вариационного ряда
Примеры

п.1. Построение интервального вариационного ряда по данным эксперимента

Интервальный вариационный ряд – это ряд распределения, в котором однородные группы составлены по признаку, меняющемуся непрерывно или принимающему слишком много значений.

Общий вид интервального вариационного ряда

Интервалы, (left.left[a_{i-1},a_iright.right))	(left.left[a_{0},a_1right.right))	(left.left[a_{1},a_2right.right))	…	(left.left[a_{k-1},a_kright.right))
Частоты, (f_i)	(f_1)	(f_2)	…	(f_k)

Здесь k — число интервалов, на которые разбивается ряд.

Размах вариации – это длина интервала, в пределах которой изменяется исследуемый признак: $$ F=x_{max}-x_{min} $$

Правило Стерджеса
Эмпирическое правило определения оптимального количества интервалов k, на которые следует разбить ряд из N чисел: $$ k=1+lfloorlog_2 Nrfloor $$ или, через десятичный логарифм: $$ k=1+lfloor 3,322cdotlg Nrfloor $$

Скобка (lfloor rfloor) означает целую часть (округление вниз до целого числа).

Шаг интервального ряда – это отношение размаха вариации к количеству интервалов, округленное вверх до определенной точности: $$ h=leftlceilfrac Rkrightrceil $$

Скобка (lceil rceil) означает округление вверх, в данном случае не обязательно до целого числа.

Алгоритм построения интервального ряда
На входе: все значения признака (left{x_jright}, j=overline{1,N})
Шаг 1. Найти размах вариации (R=x_{max}-x_{min})
Шаг 2. Найти оптимальное количество интервалов (k=1+lfloorlog_2 Nrfloor)
Шаг 3. Найти шаг интервального ряда (h=leftlceilfrac{R}{k}rightrceil)
Шаг 4. Найти узлы ряда: $$ a_0=x_{min}, a_i=1_0+ih, i=overline{1,k} $$ Шаг 5. Найти частоты (f_i) – число попаданий значений признака в каждый из интервалов (left.left[a_{i-1},a_iright.right)).
На выходе: интервальный ряд с интервалами (left.left[a_{i-1},a_iright.right)) и частотами (f_i, i=overline{1,k})

Заметим, что поскольку шаг h находится с округлением вверх, последний узел (a_kgeq x_{max}).

Например:
Проведено 100 измерений роста учеников старших классов.
Минимальный рост составляет 142 см, максимальный – 197 см.
Найдем узлы для построения соответствующего интервального ряда.
По условию: (N=100, x_{min}=142 см, x_{max}=197 см).
Размах вариации: (R=197-142=55) (см)
Оптимальное число интервалов: (k=1+lfloor 3,322cdotlg ⁡100rfloor=1+lfloor 6,644rfloor=1+6=7)
Шаг интервального ряда: (h=lceilfrac{55}{5}rceil=lceil 7,85rceil=8) (см)
Получаем узлы ряда: $$ a_0=x_{min}=142, a_i=142+icdot 8, i=overline{1,7} $$

(left.left[a_{i-1},a_iright.right)) cм

(left.left[142;150right.right))

(left.left[150;158right.right))

(left.left[158;166right.right))

(left.left[166;174right.right))

(left.left[174;182right.right))

(left.left[182;190right.right))

(left[190;198right])

п.2. Гистограмма и полигон относительных частот, кумулята и эмпирическая функция распределения

Относительная частота интервала (left.left[a_{i-1},a_iright.right)) — это отношение частоты (f_i) к общему количеству исходов: $$ w_i=frac{f_i}{N}, i=overline{1,k} $$

Гистограмма относительных частот интервального ряда – это фигура, состоящая из прямоугольников, ширина которых равна шагу ряда, а высота – относительным частотам каждого из интервалов.
Площадь гистограммы равна 1 (с точностью до округлений), и она является эмпирическим законом распределения исследуемого признака.

Полигон относительных частот интервального ряда – это ломаная, соединяющая точки ((x_i,w_i)), где (x_i) — середины интервалов: (x_i=frac{a_{i-1}+a_i}{2}, i=overline{1,k}).

Накопленные относительные частоты – это суммы: $$ S_1=w_1, S_i=S_{i-1}+w_i, i=overline{2,k} $$ Ступенчатая кривая (F(x)), состоящая из прямоугольников, ширина которых равна шагу ряда, а высота – накопленным относительным частотам, является эмпирической функцией распределения исследуемого признака.
Кумулята – это ломаная, которая соединяет точки ((x_i,S_i)), где (x_i) — середины интервалов.

Например:
Продолжим анализ распределения учеников по росту.
Выше мы уже нашли узлы интервалов. Пусть, после распределения всех 100 измерений по этим интервалам, мы получили следующий интервальный ряд:

i	1	2	3	4	5	6	7
(left.left[a_{i-1},a_iright.right)) cм	(left.left[142;150right.right))	(left.left[150;158right.right))	(left.left[158;166right.right))	(left.left[166;174right.right))	(left.left[174;182right.right))	(left.left[182;190right.right))	(left[190;198right])
(f_i)	4	7	11	34	33	8	3

Найдем середины интервалов, относительные частоты и накопленные относительные частоты:

(x_i)	146	154	162	170	178	186	194
(w_i)	0,04	0,07	0,11	0,34	0,33	0,08	0,03
(S_i)	0,04	0,11	0,22	0,56	0,89	0,97	1

Построим гистограмму и полигон:

Построим кумуляту и эмпирическую функцию распределения:

Эмпирическая функция распределения (относительно середин интервалов): $$ F(x)= begin{cases} 0, xleq 146\ 0,04, 146lt xleq 154\ 0,11, 154lt xleq 162\ 0,22, 162lt xleq 170\ 0,56, 170lt xleq 178\ 0,89, 178lt xleq 186\ 0,97, 186lt xleq 194\ 1, xgt 194 end{cases} $$

п.3. Выборочная средняя, мода и медиана. Симметрия ряда

Выборочная средняя интервального вариационного ряда определяется как средняя взвешенная по частотам: $$ X_{cp}=frac{x_1f_1+x_2f_2+…+x_kf_k}{N}=frac1Nsum_{i=1}^k x_if_i $$ где (x_i) — середины интервалов: (x_i=frac{a_{i-1}+a_i}{2}, i=overline{1,k}).
Или, через относительные частоты: $$ X_{cp}=sum_{i=1}^k x_iw_i $$

Модальным интервалом называют интервал с максимальной частотой: $$ f_m=max f_i $$ Мода интервального вариационного ряда определяется по формуле: $$ M_o=x_o+frac{f_m-f_{m-1}}{(f_m-f_{m-1})+(f_m+f_{m+1})}h $$ где
(h) – шаг интервального ряда;
(x_o) — нижняя граница модального интервала;
(f_m,f_{m-1},f_{m+1}) — соответственно, частоты модального интервала, интервала слева от модального и интервала справа.

Медианным интервалом называют первый интервал слева, на котором кумулята превысила значение 0,5. Медиана интервального вариационного ряда определяется по формуле: $$ M_e=x_o+frac{0,5-S_{me-1}}{w_{me}}h $$ где
(h) – шаг интервального ряда;
(x_o) — нижняя граница медианного интервала;
(S_{me-1}) накопленная относительная частота для интервала слева от медианного;
(w_{me}) относительная частота медианного интервала.

Расположение выборочной средней, моды и медианы в зависимости от симметрии ряда аналогично их расположению в дискретном ряду (см. §65 данного справочника).

Например:
Для распределения учеников по росту получаем:

(x_i)	146	154	162	170	178	186	194	∑
(w_i)	0,04	0,07	0,11	0,34	0,33	0,08	0,03	1
(x_iw_i)	5,84	10,78	17,82	57,80	58,74	14,88	5,82	171,68

$$ X_{cp}=sum_{i=1}^k x_iw_i=171,68approx 171,7 text{(см)} $$ На гистограмме (или полигоне) относительных частот максимальная частота приходится на 4й интервал [166;174). Это модальный интервал.
Данные для расчета моды: begin{gather*} x_o=166, f_m=34, f_{m-1}=11, f_{m+1}=33, h=8\ M_o=x_o+frac{f_m-f_{m-1}}{(f_m-f_{m-1})+(f_m+f_{m+1})}h=\ =166+frac{34-11}{(34-11)+(34-33)}cdot 8approx 173,7 text{(см)} end{gather*} На кумуляте значение 0,5 пересекается на 4м интервале. Это – медианный интервал.
Данные для расчета медианы: begin{gather*} x_o=166, w_m=0,34, S_{me-1}=0,22, h=8\ \ M_e=x_o+frac{0,5-S_{me-1}}{w_me}h=166+frac{0,5-0,22}{0,34}cdot 8approx 172,6 text{(см)} end{gather*} begin{gather*} \ X_{cp}=171,7; M_o=173,7; M_e=172,6\ X_{cp}lt M_elt M_o end{gather*} Ряд асимметричный с левосторонней асимметрией.
При этом (frac{|M_o-X_{cp}|}{|M_e-X_{cp}|}=frac{2,0}{0,9}approx 2,2lt 3), т.е. распределение умеренно асимметрично.

п.4. Выборочная дисперсия и СКО

Выборочная дисперсия интервального вариационного ряда определяется как средняя взвешенная для квадрата отклонения от средней: begin{gather*} D=frac1Nsum_{i=1}^k(x_i-X_{cp})^2 f_i=frac1Nsum_{i=1}^k x_i^2 f_i-X_{cp}^2 end{gather*} где (x_i) — середины интервалов: (x_i=frac{a_{i-1}+a_i}{2}, i=overline{1,k}).
Или, через относительные частоты: $$ D=sum_{i=1}^k(x_i-X_{cp})^2 w_i=sum_{i=1}^k x_i^2 w_i-X_{cp}^2 $$

Выборочное среднее квадратичное отклонение (СКО) определяется как корень квадратный из выборочной дисперсии: $$ sigma=sqrt{D} $$

Например:
Для распределения учеников по росту получаем:

$x_i$	146	154	162	170	178	186	194	∑
(w_i)	0,04	0,07	0,11	0,34	0,33	0,08	0,03	1
(x_iw_i)	5,84	10,78	17,82	57,80	58,74	14,88	5,82	171,68
(x_i^2w_i) — результат	852,64	1660,12	2886,84	9826	10455,72	2767,68	1129,08	29578,08

$$ D=sum_{i=1}^k x_i^2 w_i-X_{cp}^2=29578,08-171,7^2approx 104,1 $$ $$ sigma=sqrt{D}approx 10,2 $$

п.5. Исправленная выборочная дисперсия, стандартное отклонение выборки и коэффициент вариации

Исправленная выборочная дисперсия интервального вариационного ряда определяется как: begin{gather*} S^2=frac{N}{N-1}D end{gather*}

Стандартное отклонение выборки определяется как корень квадратный из исправленной выборочной дисперсии: $$ s=sqrt{S^2} $$

Коэффициент вариации это отношение стандартного отклонения выборки к выборочной средней, выраженное в процентах: $$ V=frac{s}{X_{cp}}cdot 100text{%} $$

Подробней о том, почему и когда нужно «исправлять» дисперсию, и для чего использовать коэффициент вариации – см. §65 данного справочника.

Например:
Для распределения учеников по росту получаем: begin{gather*} S^2=frac{100}{99}cdot 104,1approx 105,1\ sapprox 10,3 end{gather*} Коэффициент вариации: $$ V=frac{10,3}{171,7}cdot 100text{%}approx 6,0text{%}lt 33text{%} $$ Выборка однородна. Найденное значение среднего роста (X_{cp})=171,7 см можно распространить на всю генеральную совокупность (старшеклассников из других школ).

п.6. Алгоритм исследования интервального вариационного ряда

На входе: все значения признака (left{x_jright}, j=overline{1,N})
Шаг 1. Построить интервальный ряд с интервалами (left.right[a_{i-1}, a_ileft.right)) и частотами (f_i, i=overline{1,k}) (см. алгоритм выше).
Шаг 2. Составить расчетную таблицу. Найти (x_i,w_i,S_i,x_iw_i,x_i^2w_i)
Шаг 3. Построить гистограмму (и/или полигон) относительных частот, эмпирическую функцию распределения (и/или кумуляту). Записать эмпирическую функцию распределения.
Шаг 4. Найти выборочную среднюю, моду и медиану. Проанализировать симметрию распределения.
Шаг 5. Найти выборочную дисперсию и СКО.
Шаг 6. Найти исправленную выборочную дисперсию, стандартное отклонение и коэффициент вариации. Сделать вывод об однородности выборки.

п.7. Примеры

Пример 1. При изучении возраста пользователей коворкинга выбрали 30 человек.
Получили следующий набор данных:
18,38,28,29,26,38,34,22,28,30,22,23,35,33,27,24,30,32,28,25,29,26,31,24,29,27,32,24,29,29
Постройте интервальный ряд и исследуйте его.

1) Построим интервальный ряд. В наборе данных: $$ x_{min}=18, x_{max}=38, N=30 $$ Размах вариации: (R=38-18=20)
Оптимальное число интервалов: (k=1+lfloorlog_2⁡ 30rfloor=1+4=5)
Шаг интервального ряда: (h=lceilfrac{20}{5}rceil=4)
Получаем узлы ряда: $$ a_0=x_{min}=18, a_i=18+icdot 4, i=overline{1,5} $$

(left.left[a_{i-1},a_iright.right)) лет

(left.left[18;22right.right))

(left.left[22;26right.right))

(left.left[26;30right.right))

(left.left[30;34right.right))

(left.left[34;38right.right))

Считаем частоты для каждого интервала. Получаем интервальный ряд:

(left.left[a_{i-1},a_iright.right)) лет	(left.left[18;22right.right))	(left.left[22;26right.right))	(left.left[26;30right.right))	(left.left[30;34right.right))	(left.left[34;38right.right))
(f_i)	1	7	12	6	4

2) Составляем расчетную таблицу:

(x_i)	20	24	28	32	36	∑
(f_i)	1	7	12	6	4	30
(w_i)	0,033	0,233	0,4	0,2	0,133	1
(S_i)	0,033	0,267	0,667	0,867	1	—
(x_iw_i)	0,667	5,6	11,2	6,4	4,8	28,67
(x_i^2w_i)	13,333	134,4	313,6	204,8	172,8	838,93

3) Строим полигон и кумуляту

Эмпирическая функция распределения: $$ F(x)= begin{cases} 0, xleq 20\ 0,033, 20lt xleq 24\ 0,267, 24lt xleq 28\ 0,667, 28lt xleq 32\ 0,867, 32lt xleq 36\ 1, xgt 36 end{cases} $$ 4) Находим выборочную среднюю, моду и медиану $$ X_{cp}=sum_{i=1}^k x_iw_iapprox 28,7 text{(лет)} $$ На полигоне модальным является 3й интервал (самая высокая точка).
Данные для расчета моды: begin{gather*} x_0=26, f_m=12, f_{m-1}=7, f_{m+1}=6, h=4\ M_o=x_o+frac{f_m-f_{m-1}}{(f_m-f_{m-1})+(f_m+f_{m+1})}h=\ =26+frac{12-7}{(12-7)+(12-6)}cdot 4approx 27,8 text{(лет)} end{gather*}
На кумуляте медианным является 3й интервал (преодолевает уровень 0,5).
Данные для расчета медианы: begin{gather*} x_0=26, w_m=0,4, S_{me-1}=0,267, h=4\ M_e=x_o+frac{0,5-S_{me-1}}{w_{me}}h=26+frac{0,5-0,4}{0,267}cdot 4approx 28,3 text{(лет)} end{gather*} Получаем: begin{gather*} X_{cp}=28,7; M_o=27,8; M_e=28,6\ X_{cp}gt M_egt M_0 end{gather*} Ряд асимметричный с правосторонней асимметрией.
При этом (frac{|M_o-X_{cp}|}{|M_e-X_{cp}|} =frac{0,9}{0,1}=9gt 3), т.е. распределение сильно асимметрично.

5) Находим выборочную дисперсию и СКО: begin{gather*} D=sum_{i=1}^k x_i^2w_i-X_{cp}^2=838,93-28,7^2approx 17,2\ sigma=sqrt{D}approx 4,1 end{gather*}
6) Исправленная выборочная дисперсия: $$ S^2=frac{N}{N-1}D=frac{30}{29}cdot 17,2approx 17,7 $$ Стандартное отклонение (s=sqrt{S^2}approx 4,2)
Коэффициент вариации: (V=frac{4,2}{28,7}cdot 100text{%}approx 14,7text{%}lt 33text{%})
Выборка однородна. Найденное значение среднего возраста (X_{cp}=28,7) лет можно распространить на всю генеральную совокупность (пользователей коворкинга).

Источник

Выборочная дисперсия, описание

Выборочная дисперсия является сводной характеристикой для наблюдения рассеяния количественного признака выборки вокруг среднего значения.

Определение

Выборочная дисперсия – это среднее арифметическое значений вариантов части отобранных объектов генеральной совокупности (выборки).

Связь выборочной и генеральной дисперсии

Генеральная дисперсия представляет собой среднее арифметическое квадратов отступлений значений признаков генеральной совокупности от их среднего значения.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Определение

Генеральная совокупность – это комплекс всех возможных объектов, относительно которых планируется вести наблюдение и формулировать выводы.

Выборочная совокупность или выборка является частью генеральной совокупности, выбранной для изучения и составления заключения касательной всей генеральной совокупности.

Как вычислить выборочную дисперсию

Выборочная дисперсия при различии всех значений варианта выборки находится по формуле:

({widehat D}_В=frac{displaystylesum_{i-1}^n{(x_i-{overline x}_В)}^2}n)

Для значений признаков выборочной совокупности с частотами n₁, n₂,…,n_kформула выглядит следующим образом:

({widehat D}_В=frac{displaystylesum_{i-1}^kn_i{(x_i-{overline x}_В)}^2}n)

Квадратный корень из выборочной дисперсии характеризует рассеивание значений вариантов выборки вокруг своего среднего значения. Данная характеристика называется выборочным средним квадратическим отклонением и имеет вид:

({widehatsigma}_В=sqrt{{widehat D}_В})

Упрощенный способ вычисления выборочной или генеральной дисперсии производят по формуле:

(D=overline{x^2}-left[overline xright]^2)

Если вариационный ряд выборочной совокупности интервальный, то за x_i принимается центр частичных интервалов.

Пример

Найти выборочную дисперсию выборки со значениями:

x_i: 1, 2, 3, 4;
n_i: 20, 15, 10, 5.

Решение

Для начала необходимо определить выборочную среднюю:

({overline x}_В=frac1{50}(1cdot20+2cdot15+3cdot10+4cdot5)=frac1{50}cdot100=2)

Затем найдем выборочную дисперсию:

(D_В=frac1{50}({(1-2)}^2cdot20+{(2-2)}^2cdot15+{(3-2)}^2cdot10+{(4-2)}^2cdot5)=1)

Исправленная дисперсия

Математически выборочная дисперсия не соответствует генеральной, поскольку выборочная используется для смещенного оценивания генеральной дисперсии. По этой причине математическое ожидание выборочной дисперсии вычисляется так:

(Mleft[D_Bright]=frac{n-1}nD_Г)

В данной формуле D_Г – это истинное значение дисперсии генеральной совокупности.

Исправить выборочную дисперсию можно путем умножения ее на дробь:

(frac n{n-1})

Получим формулу следующего вида:

(S^2=frac n{n-1}cdot D_В=frac{displaystylesum_{i=1}^kn_i{(x_i-{overline x}_В)}^2}{n-1})

Исправленная дисперсия используется для несмещенной оценки генеральной дисперсии и обозначается S².

Среднеквадратическая генеральная совокупность оценивается при помощи исправленного среднеквадратического отклонения, которое вычисляется по формуле:

(S=sqrt{S^2})

При нахождении выборочной и исправленной дисперсии разнятся лишь знаменатели в формулах. Различия в этих характеристиках при больших n незначительны. Применение исправленной дисперсии целесообразно при объеме выборки меньше 30.

Для чего применяют исправленную выборочную дисперсию

Исправленную выборочную используют для точечной оценки генеральной дисперсии.

Пример

Длину стержня измерили одним и тем же прибором пять раз. В результате получили следующие величины: 92 мм, 94 мм, 103 мм, 105 мм, 106 мм. Задача найти выборочную среднюю длину предмета и выборочную исправленную дисперсию ошибок измерительного прибора.

Решение

Сначала вычислим выборочную среднюю:

({overline x}_В=frac{92+94+103+105+106}5=100)

Затем найдем выборочную дисперсию:

(D_В=frac{displaystylesum_{i=1}^k{(x_i-{overline x}_В)}^2}n=frac{{(92-100)}^2+{(94-100)}^2+{(103-100)}^2+{(105-100)}^2+{(106-100)}^2}5=34)

Теперь рассчитаем исправленную дисперсию:

(S^2=frac5{5-1}cdot34=42,5)

Источник

Для того чтобы охарактеризовать
рассеяние наблюдаемых значений
количественного признака выборки вокруг
своего среднего значения ,
вводят сводную
характеристику — выборочную дисперсию.

Выборочной дисперсией

называют среднее
арифметическое квадратов отклонения
наблюдаемых значений признака от их
среднего значения .

Если все значения x₁,
х₂,
…, x_n
признака выборки объема п
различны, то

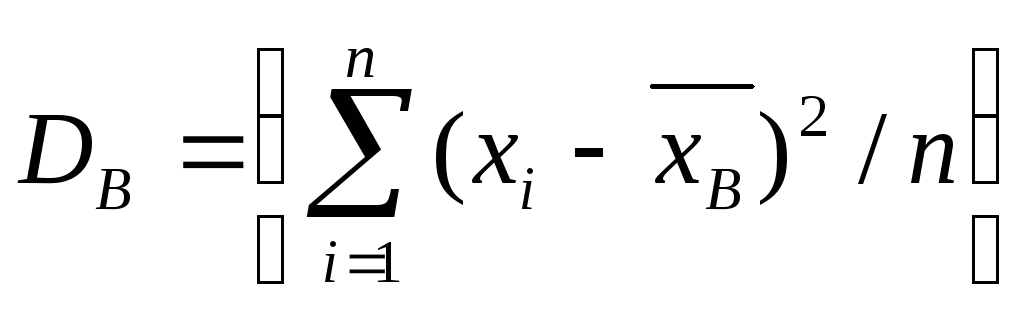
Если же значения признака
x₁,
х₂,
…, x_kимеют соответственно
частоты п₁,
n₂,…,
n_k,
причем n₁
+ n₂+…+n_k
= n, то

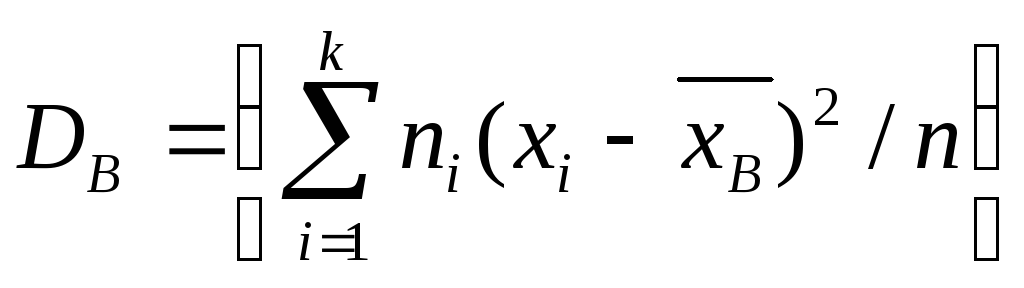
т.е. выборочная дисперсия есть средняя
взвешенная квадратов отклонений с
весами, равными соответствующим частотам.

Пример.
Выборочная
совокупность задана таблицей распределения

x_i

1
2 3 4

n_i
20 15
10
5

Найти выборочную
дисперсию.

Решение.
Найдем выборочную среднюю (см. § 4):

Найдем выборочную
дисперсию:

Кроме дисперсии для характеристики
рассеяния значений признака выборочной
совокупности вокруг своего среднего
значения пользуются сводной
характеристикой-средним квадратическим
отклонением.

Выборочным средним
квадратическим отклонением (стандартом)
называют квадратный
корень из выборочной дисперсии:

§ 10. Формула для вычисления дисперсии

Вычисление дисперсии, безразлично-выборочной
или генеральной, можно упростить,
используя следующую теорему.

Теорема. Дисперсия
равна среднему квадратов значений
признака минус квадрат общей средней:

Доказательство. Справедливость теоремы
вытекает из преобразований:

Итак,

где
,.

Пример.
Найти
дисперсию по данному распределению

x_i
1
2 3 4

n_i
20
15
10
5

Решение.
Найдем
общую среднюю:

Найдем
среднюю квадратов
значений признака:

Искомая дисперсия

=5-2²=1.

§11. Групповая, внутригрупповая, межгрупповая и общая дисперсии

Допустим, что все значения
количественного признака X
совокупности,
безразлично-генеральной или выборочной,
разбиты на k
групп. Рассматривая
каждую группу как самостоятельную
совокупность, можно найти групповую
среднюю (см. § 6) и дисперсию значений
признака, принадлежащих группе,
относительно групповой средней.

Групповой дисперсией называют
дисперсию значений признака, принадлежащих
группе, относительно групповой средней

где n_i—
частота значения
x_i;
j —
номер группы;

— групповая средняя
группы j;
—
объем группыj.

Пример
1. Найти
групповые дисперсии совокупности,
состоящей из следующих двух групп:

первая группа		вторая группа
	x_i	n_i		x_i	n_i
2	1	3	2
4	7	8	3
5	2

Решение.
Найдем
групповые средние:

;

Найдем
искомые
групповые дисперсии:

;

Зная дисперсию каждой группы, можно
найти их среднюю арифметическую.

Внутригрупповой дисперсией называют
среднюю арифметическую дисперсий,
взвешенную по объемам групп:

где N_j
— объем группы
j;
п =—
объем всей совокупности.

Пример
2.
Найти
внутригрупповую дисперсию по данным
примера 1.

Решение.
Искомая внутригрупповая дисперсия
равна

Зная групповые средние и общую среднюю,
можно найти дисперсию групповых средних
относительно общей средней.

Межгрупповой дисперсией называют
дисперсию групповых средних относительно
общей средней:

где
—
групповая средняя группыj;
N_j
— объем группы j;

— общая средняя;
n
=—
объем всей совокупности.

Пример
3. Найти
межгрупповую дисперсию по

данным
примера 1.

Решение.
Найдем общую среднюю:

Используя
вычисленные выше величины
=
4,=
6, найдем искомую межгрупповую дисперсию:

Теперь целесообразно ввести специальный
термин для дисперсии всей совокупности.

Общей дисперсией называют дисперсию
значений признака всей совокупности
относительно общей средней:

где n_i
— частота значения
x_i
;
—
общая средняя; n
— объем всей совокупности.

Пример
4. Найти
общую дисперсию по данным примера 1.

Решение.
Найдем искомую общую дисперсию, учитывая,
что общая средняя равна 14/3:

Замечание.
Найденная общая дисперсия равна сумме
внутригрупповой и межгрупповой дисперсий:

D_общ=
148/45;

D_внгр
+ D_межгр=
12/5 + 8/9= 148/45.

В следующем
параграфе будет доказано, что такая
закономерность справедлива для любой
совокупности.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Генеральная и выборочная дисперсия

Для анализа полученных данных в математической статистике используют различные виды показателей вариации, среди которых:

размах вариации;
среднее абсолютное отклонение;
дисперсия.

Разберем понятие дисперсии, ее виды и свойства.

Дисперсия — величина, являющаяся мерой разброса полученных в ходе наблюдений данных относительно истинного значения.

Дисперсия является точечной оценкой параметра, так как имеет одно конкретное числовое значение.

Статистический анализ при исследовании некоторого объекта может быть сплошным или выборочным в зависимости от охватываемого объема данных.

В обоих вариантах результаты анализа распространяют на генеральную совокупность, однако при сплошном анализе наблюдению подвергают абсолютно все имеющиеся данные. Выборочный анализ, напротив, предполагает наблюдение только за некоторой выбранной частью данных. При этом выбранная совокупность должна сохранять структуру и закономерности генеральной.

Дисперсию также делят на два вида в зависимости от используемых данных:

генеральная дисперсия;
выборочная дисперсия.

Как видно из названия, дисперсии отличаются объемом выборки, на основе которой происходит расчет и анализ.

Выборочная дисперсия, определение, формулы для вычисления

Пусть имеется некоторая выборка Y из генеральной совокупности объемом n. Среднее значение выборки обозначим как ({overline y}_в).

Выборочная дисперсия (D_в) — величина, равная среднему арифметическому отклонению квадратов разности признаков выборки (y_1,;y_2,;…y_n) от ее среднего значения ({overline y}_в).

Данные в выборке могут располагаться хаотично, то есть быть несгруппированными, или же сформированы в вариационный ряд.

Выборочную дисперсию для несгруппированной выборки можно посчитать по формуле:

Формула 1

(D_в=frac{{displaystylesum_{i=1}^n}(y_i-{overline y}_в)}n)

В случае вариационного ряда используют кратные значения и частоты для дискретного представления; середины частичных интервалов и частоты для интервального представления.

Формула 2

(D_в=frac{{displaystylesum_{i=1}^k}(y’_i-{overline y}_в)cdot n_i}n)

где (y’_i )— кратное (одинаковое) значение в выборке или значение, соответствующее середине интервала;

(n_i )— частота.

Выборочная дисперсия, рассчитанная по приведенным выше формулам, дает недостоверное (заниженное) значение. Это значит, что при большом количестве экспериментов выборочная дисперсия будет давать смещенное относительно истинного значения генеральной совокупности значение.

Чтобы получить несмещенную выборочную дисперсию, используют следующую формулу:

Формула 3

(D_в=frac{{displaystylesum_{i=1}^n}{(y_i-{overline y}_в)}^2}{n-1})

Примечание 1

Как правило при использовании термина «выборочная дисперсия» имеют в виду именно несмещенную выборочную дисперсию.

Генеральная дисперсия, определение, что является оценкой, формулы для вычисления

Пусть имеется некоторая генеральная совокупность X объемом N и среднее значение признаков совокупности (X — {overline x}_г.)

Генеральная дисперсия (D_г) есть среднее арифметическое отклонение квадратов разности признаков (x_1,;x_2,;…x_n) генеральной совокупности X от их среднего значения ({overline x}_г).

Примечание 2

Иногда генеральную дисперсию называют теоретической.

Аналогично выборочной, генеральная дисперсия может быть рассчитана для несгруппированных данных генеральной совокупности:

Формула 4

(D_г=frac{{displaystylesum_{i=1}^N}{(x_i-{overline x}_г)}^2}N)

и для сформированного вариационного ряда:

Формула 5

(D_г=frac{{displaystylesum_{i=1}^K}{(x’_i-{overline x}_г)}^2cdot n_i}N)

Значение теоретической дисперсии бывает сложно вычислить из-за большого объема данных или их недостатка. Тогда для оценки используют выборочную дисперсию. Но если для оценки генеральной дисперсии применить выборочную, это приведет к возникновению ряда систематических ошибок. В результате оценка будет произведена неверно, а значение генеральной дисперсии занижено.

Чтобы устранить возникающую погрешность в качестве оценки генеральной дисперсии используют исправленную или несмещенную выборочную дисперсию, формула которой представлена выше.

Оценки параметров распределения

Оценкой параметра в статистике считают численное значение какого-либо параметра данной выборки.

Приведем оценки параметров распределения случайной величины, которые связаны с дисперсией.

Среднеквадратическое отклонение (δ) — характеристика рассеивания случайной величины относительно ее математического ожидания. Определяется как корень квадратный из дисперсии.

Формула 6

(delta=sqrt D)

Математическое ожидание случайной величины X — среднее (по весу вероятностей возможных значений) значение случайной величины. Обозначается как M(X).

Математическое ожидание и дисперсия для дискретной случайной величины связаны соотношением:

Формула 7

(D=Mleft[X-M(X)right]^2)

для непрерывной:

Формула 8

(D=int_{-infty}^infty(x-M{(x))}^2cdot f(x)dx)

где f(x) — функция распределения случайной величины.

Отметим, что указанные выше параметры могут быть определены как для генеральной совокупности, так и для некоторой выборки.

Примеры решения задач

Пример 1

Напряжение в цепи измеряют 6 раз с помощью одного и того же вольтметра. Получены следующие значения: 210 В, 200 В, 195 В, 205 В, 190 В, 200 В. Найти выборочную смещенную дисперсию и дать оценку генеральной дисперсии.

Решение.

Сначала вычислим выборочное среднее значение:

({overline x}_в=frac{210+200+195+205+190+200}6=200;B.)

Теперь найдем выборочную дисперсию:

(D_в=frac{{(210-200)}^2+{(200-200)}^2+{(195-200)}^2+{(205-200)}^2+{(190-200)}^2+{(200-200)}^2}6=frac{250}6approx42.)

Оценкой генеральной дисперсии является исправленная или выборочная несмещенная дисперсия. Чтобы вычислить исправленную дисперсию, умножим полученную ранее выборочную дисперсию на множитель (frac n{n-1} (n=6):)

(D_и=frac n{n-1}cdot D_в=frac65cdotfrac{250}6=50.)

Примечание 3

Данный пример показывает, что значение выборочной смещенной дисперсии занижено относительно генеральной.

Пример 2

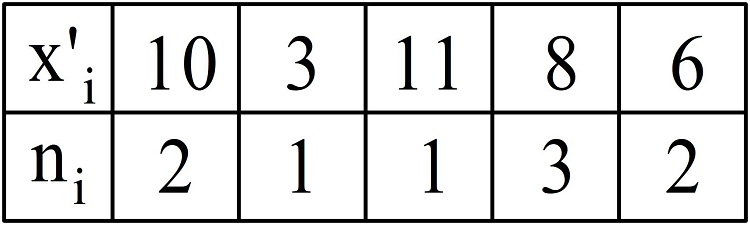
Случайная величина задана следующей таблицей распределения, среднее значение выборки равно 14. Найти выборочную несмещенную дисперсию и среднеквадратическое отклонение.

Решение.

Вычислим выборочную несмещенную дисперсию:

(D_в=frac{2{(10-14)}^2+1{(3-14)}^2+1{(11-14)}^2+3{(8-14)}^2+2{(6-14)}^2}9cdotfrac98=frac{398}8approx50.)

Теперь найдем среднеквадратическое отклонение:

(delta=sqrt{D_в}=sqrt{frac{398}8}=frac{sqrt{199}}2approx7.)

Источник

Евгений Николаевич Беляев

Эксперт по предмету «Математика»

Задать вопрос автору статьи

Генеральная дисперсия

Пусть нам дана генеральная совокупность относительно случайной величины $X$. Для начала напомним следующее определение:

Определение 1

Генеральная совокупность — совокупность случайно отобранных объектов данного вида, над которыми проводят наблюдения с целью получения конкретных значений случайной величины, проводимых в неизменных условиях при изучении одной случайной величины данного вида.

Определение 2

Генеральная дисперсия — среднее арифметическое квадратов отклонений значений вариант генеральной совокупности от их среднего значения.

Пусть значения вариант $x_1, x_2,dots ,x_k$ имеют, соответственно, частоты $n_1, n_2,dots ,n_k$. Тогда генеральная дисперсия вычисляется по формуле:

Сдай на права пока
учишься в ВУЗе

Вся теория в удобном приложении. Выбери инструктора и начни заниматься!

Получить скидку 3 000 ₽

Рассмотрим частный случай. Пусть все варианты $x_1, x_2,dots ,x_k$ различны. В этом случае $n_1, n_2,dots ,n_k=1$. Получаем, что в этом случае генеральная дисперсия вычисляется по формуле:

С этим понятием также связано понятие генерального среднего квадратического отклонения.

Определение 3

Генеральное среднее квадратическое отклонение — квадратный корень из генеральной дисперсии:

[{sigma }_г=sqrt{D_г}]

Выборочная дисперсия

Пусть нам дана выборочная совокупность относительно случайной величины $X$. Для начала напомним следующее определение:

Определение 4

Выборочная совокупность — часть отобранных объектов из генеральной совокупности.

Определение 5

Выборочная дисперсия — среднее арифметическое значений вариант выборочной совокупности.

«Дисперсия: генеральная, выборочная, исправленная» 👇

Пусть значения вариант $x_1, x_2,dots ,x_k$ имеют, соответственно, частоты $n_1, n_2,dots ,n_k$. Тогда выборочная дисперсия вычисляется по формуле:

Рассмотрим частный случай. Пусть все варианты $x_1, x_2,dots ,x_k$ различны. В этом случае $n_1, n_2,dots ,n_k=1$. Получаем, что в этом случае выборочная дисперсия вычисляется по формуле:

С этим понятием также связано понятие выборочного среднего квадратического отклонения.

Определение 6

Выборочное среднее квадратическое отклонение — квадратный корень из генеральной дисперсии:

[{sigma }_в=sqrt{D_в}]

Исправленная дисперсия

Для нахождения исправленной дисперсии $S^2$ необходимо умножить выборочную дисперсию на дробь $frac{n}{n-1}$, то есть

С этим понятием также связано понятие исправленного среднего квадратического отклонения, которое находится по формуле:

!!! В случае, когда значение вариант не являются дискретными, а представляют из себя интервалы, то в формулах для вычисления генеральной или выборочной дисперсий за значение $x_i$ принимается значение середины интервала, которому принадлежит $x_i.$

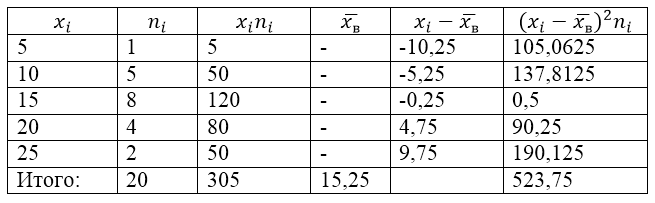
Пример задачи на нахождение дисперсии и среднего квадратического отклонения

Пример 1

Выборочная совокупность задана следующей таблицей распределения:

Рисунок 1.

Найдем для нее выборочную дисперсию, выборочное среднее квадратическое отклонение, исправленную дисперсию и исправленное среднее квадратическое отклонение.

Решение:

Для решения этой задачи для начала сделаем расчетную таблицу:

Рисунок 2.

Величина $overline{x_в}$ (среднее выборочное) в таблице находится по формуле:

[overline{x_в}=frac{sumlimits^k_{i=1}{x_in_i}}{n}]

То есть

[overline{x_в}=frac{sumlimits^k_{i=1}{x_in_i}}{n}=frac{305}{20}=15,25]

Найдем выборочную дисперсию по формуле:

[D_в=frac{sumlimits^k_{i=1}{{{(x}_i-overline{x_в})}^2n_i}}{n}=frac{523,75}{20}=26,1875]

Выборочное среднее квадратическое отклонение:

[{sigma }_в=sqrt{D_в}approx 5,12]

Исправленная дисперсия:

[{S^2=frac{n}{n-1}D}_в=frac{20}{19}cdot 26,1875approx 27,57]

Исправленное среднее квадратическое отклонение:

[S=sqrt{S^2}approx 5,25]

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Источник