Как найти выборочный коэффициент асимметрии - Исправление недочетов и поиск решений вместе с Examum.ru

Коэффициент асимметрии. Эксцесс распределения

Краткая теория

При изучении распределений, отличных от нормального,
возникает необходимость количественно оценить это различие. С этой целью вводят
специальные характеристики, в частности асимметрию и эксцесс. Для нормального
распределения эти характеристики равны нулю. Поэтому если для изучаемого
распределения асимметрия и эксцесс имеют небольшие значения, то можно
предположить близость этого распределения к нормальному.
Наоборот, большие значения асимметрии и эксцесса указывают на значительное
отклонение от нормального.

Асимметрией теоретического распределения называют отношение
центрального момента третьего порядка к кубу среднего квадратического
отклонения:

Коэффициент асимметрии характеризует скошенность
распределения по отношению к математическому ожиданию. Асимметрия положительна,
если «длинная часть» кривой распределения расположена справа от математического
ожидания; асимметрия отрицательна, если «длинная часть» кривой расположена слева
от математического ожидания.

На рисунке показаны две кривые распределения: I и II. Кривая I имеет
положительную (правостороннюю) асимметрию

,
а кривая II – отрицательную (левостороннюю)

Кроме вышеописанного коэффициента, для характеристики асимметрии
рассчитывают также показатель асимметрии Пирсона:

Коэффициент асимметрии Пирсона характеризует асимметрию только в
центральной части распределения, поэтому более распространенным и более точным
является коэффициент асимметрии, рассчитанный на основе центрального момента третьего
порядка.

Для оценки «крутости», т. е. большего или меньшего подъема кривой
теоретического распределения по сравнению с нормальной кривой, пользуются
характеристикой — эксцессом.

Эксцессом (или коэффициентом эксцесса) случайной величины
называется число:

Число 3 вычитается из отношения

потому, что для наиболее часто встречающегося
нормального распределения отношение

Кривые, более островершинные, чем нормальная,
обладают положительным эксцессом, более плосковершинные — отрицательным
эксцессом.

Примеры решения задач

Задача 1

Для заданного
вариационного ряда вычислить коэффициенты асимметрии и эксцесса.

Решение

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Составим расчетную
таблицу

Средняя:

Найдем моду — варианту, которой соответствует наибольшая частота.

Дисперсия:

Среднее квадратическое
отклонение:

Коэффициент асимметрии Пирсона:

Коэффициент асимметрии можно найти по формуле:

Центральный момент
3-го порядка:

Получаем:

Эксцесс можно найти по формуле:

Центральный момент
4-го порядка:

Получаем:

Задача 2

Для заданного
вариационного ряда (см. условие задачи 1) вычислить коэффициенты асимметрии и
эксцесса методом произведений, используя условные моменты.

Решение

Составим расчетную таблицу

Перейдем к условным вариантам

В качестве ложного нуля возьмем
3-ю варианту

Условные варианты вычислим по
формуле:

где

4
(разность между соседними вариантами)

Условный момент 1-го порядка:

Средняя:

Условный момент 2-го порядка:

Дисперсия:

Среднее квадратическое
отклонение:

Коэффициент асимметрии можно найти
по формуле:

Условный момент 3-го порядка:

Центральный момент 3-го порядка:

Получаем:

Эксцесс можно найти по формуле:

Условный момент 4-го порядка:

Центральный момент 4-го порядка:

Получаем:

Источник

Центральный
выборочный момент второго порядка
обозначается S²
и находится по следующей формуле:

.

10.Как вычисляется и что характеризует коэффициент асимметрии выборки? Коэффициент эксцесса?

Выборочный
коэффициент асимметрии:

Определяется
по формуле :

,

где
– центральный момент -го порядка()

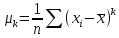
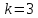
Выборочный
коэффициент эксцесса:

Определяется
по формуле :

Выборочный
коэффициент асимметрии
служит для характеристики смещения
вариационного ряда относительно среднего
значения по величине и направлению.
Если полигон асимметричен, то одна из
его ветвей, начиная с вершины, имеет
более пологий «спуск», чем другая. В
случае отрицательного коэффициента
асимметрии более пологий «спуск» полигон
наблюдается слева. В противном случае
– справа. В первом случае асимметрию
называют левосторонней, а во втором –
правосторонней. Асимметрия менее 0,5
считается малой.

Выборочный
эксцесс
служит для сравнения на «крутость»
выборочного распределения с нормальным
распределением. Эксцесс нормального
распределения равен нулю. Если выборочному
распределению соответствует отрицательный
эксцесс, то полигон имеет более пологую
вершину по сравнению с нормальной
кривой. В случае положительного эксцесса
– более крутой. Отрицательным пределом
величины эксцесса является число –2,
положительный предел – не существует.

11.Какие
оценки параметров называют точечными?
Перечислите основные свойства точечных
оценок.

Точечной
оценкой
неизвестного
параметра распределения θ
называется
приближенное значение этого параметра,
полученное по данным выборки
.

Основные
свойства точечных оценок: состоятельность,
несмещенность, эффективность.

12.Каковы точечные оценки математического ожидания и дисперсии?

Точечная
оценка математического ожидания
определяется по формуле

Точечная
оценка дисперсии
определяется по формуле

13.В чем состоит метод максимального правдоподобия?

Пусть
Х
– дискретная случайная величина, которая
в результате п
испытаний приняла значения х₁,
х₂,
…, х_п.
Предположим, что нам известен закон
распределения этой величины, определяемый
параметром Θ, но неизвестно численное
значение этого параметра. Найдем его
точечную оценку.

Пусть
р(х_i,
Θ)
– вероятность того, что в результате
испытания величина Х
примет значение х_i.
Назовем функцией правдоподобия дискретной
случайной величины Х
функцию аргумента Θ, определяемую по
формуле:

L
(х₁,
х₂,
…, х_п;
Θ)
= p(x₁,Θ)p(x₂,Θ)…p(x_n,Θ).

Тогда
в качестве точечной оценки параметра
Θ принимают такое его значение Θ* = Θ(х₁,
х₂,
…, х_п),
при котором функция правдоподобия
достигает максимума. Оценку Θ* называют
оценкой наибольшего правдоподобия.

Поскольку
функции L
и lnL
достигают максимума при одном и том же
значении Θ, удобнее искать максимум ln
L
– логарифмической функции правдоподобия.
Для этого нужно:

найти
производную
;
приравнять
ее нулю (получим так называемое уравнение
правдоподобия)
и найти критическую точку;
найти
вторую производную
;
если она отрицательна в критической
точке, то это – точка максимума.

Достоинства
метода наибольшего правдоподобия:
полученные оценки состоятельны (хотя
могут быть смещенными), распределены
асимптотически нормально при больших
значениях п
и имеют наименьшую дисперсию по сравнению
с другими асимптотически нормальными
оценками; если для оцениваемого параметра
Θ существует эффективная оценка Θ*, то
уравнение правдоподобия имеет единственное
решение Θ*; метод наиболее полно использует
данные выборки и поэтому особенно
полезен в случае малых выборок.

Недостаток
метода наибольшего правдоподобия:
сложность вычислений.

Для
непрерывной случайной величины с
известным видом плотности распределения
f(x)
и неизвестным параметром Θ функция
правдоподобия имеет вид:

L
(х₁,
х₂,
…, х_п;
Θ)
= f(x₁,Θ)f(x₂,Θ)…f(x_n,Θ).

Оценка
наибольшего правдоподобия неизвестного
параметра проводится так же, как для
дискретной случайной величины.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

См. начало:

CFA — Статистические концепции и рыночная доходность
CFA — Обобщение финансовых данных с использованием частотных распределений
CFA — Графическое представление финансовых данных
CFA — Среднее арифметическое и меры центральной тенденции
CFA — Медиана и меры центральной тенденции
CFA — Мода и меры центральной тенденции
CFA — Взвешенное среднее и меры центральной тенденции
CFA — Среднее геометрическое и меры центральной тенденции
CFA — Среднее гармоническое и меры центральной тенденции
CFA — Квартили, квинтили, децили и процентили
CFA — Квантили в инвестиционной практике
CFA — Размах, среднее абсолютное отклонение и меры дисперсии
CFA — Дисперсия и стандартное отклонение
CFA – Полудисперсия, полуотклонение и связанные с ними концепции
CFA — Неравенство Чебышева
CFA — Коэффициент вариации
CFA — Коэффициент Шарпа

Среднее значение и дисперсия могут неадекватно описывать распределение доходности инвестиций. Например, при расчете дисперсии, отклонения от среднего значения возводятся в квадрат, и поэтому мы не знаем, являются ли большие отклонения положительными или отрицательными.

Нам необходимо выйти за рамки мер центральной тенденции и дисперсии, чтобы выявить другие важные характеристики распределения. Одной из важных характеристик, представляющих интерес для аналитиков, является степень симметрии в распределениях доходности.

Если распределение доходности симметрично относительно его среднего значения, то каждая сторона распределения является зеркальным отражением другой. Таким образом, равные интервалы убытков и доходов показывают одинаковые частоты. Например, убытки от -5% до -3% происходят примерно с той же частотой, что и доходы от 3% до 5%.

Одним из наиболее важных распределений является нормальное распределение, изображенное на рисунке ниже. Это симметричное распределение в форме колокола играет центральную роль в модели среднего отклонения (англ. ‘mean-variance model’), которая используется для выбора портфеля. Оно также широко используется в управлении финансовыми рисками.

Нормальное распределение (англ. ‘normal distribution’) имеет следующие характеристики:

Его среднее значение и медиана равны.
Оно полностью описывается двумя параметрами — его средним значением и дисперсией.
Примерно 68% его наблюдений лежат между плюс и минус 1-м стандартным отклонением от среднего. 95% лежат между плюс и минус 2-мя стандартными отклонениями; и 99% лежат между плюс и минус 3 стандартными отклонениями.

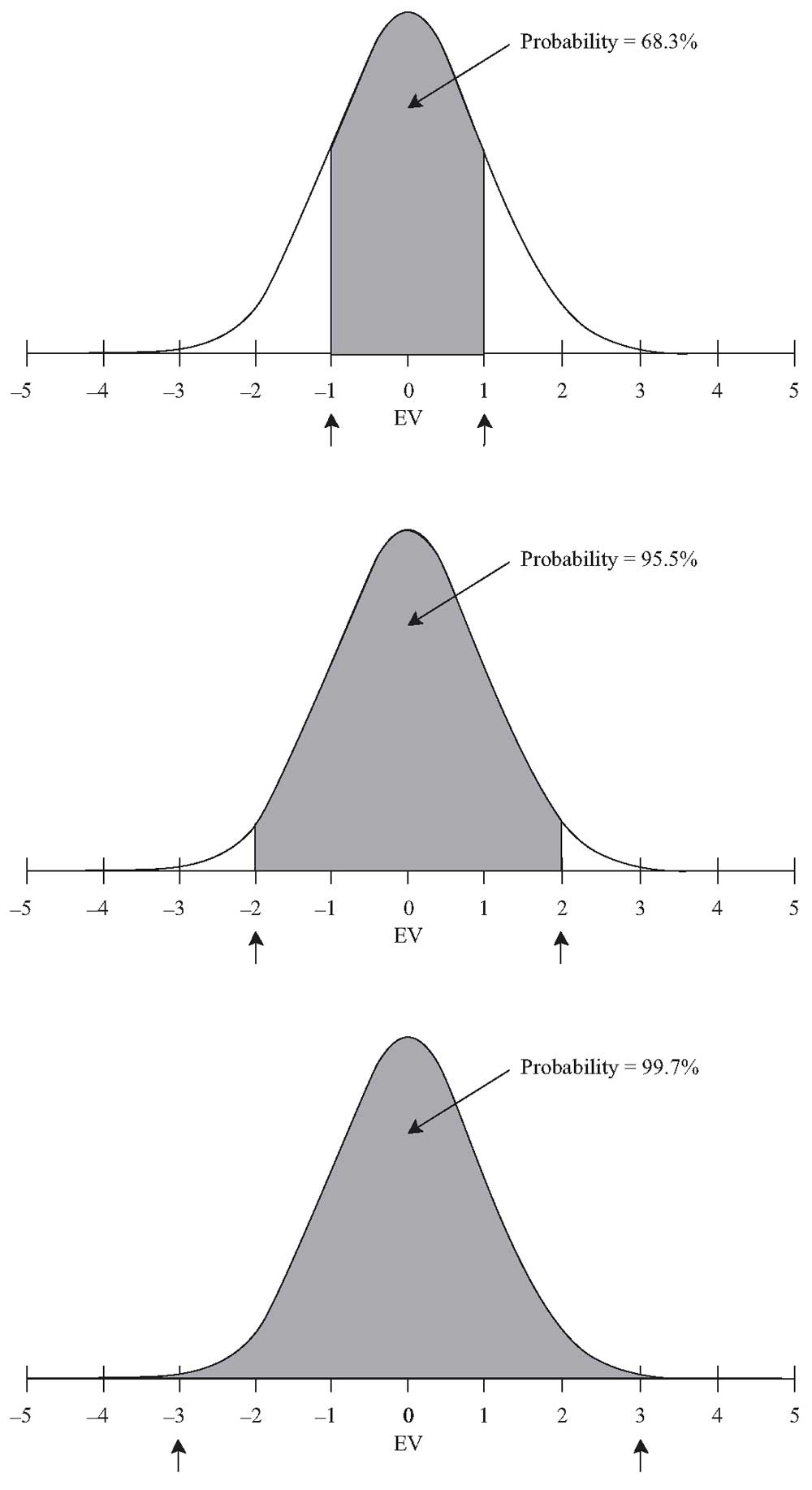
Свойства нормального распределения.

Распределение, которое не является симметричным, называется скошенным или ассиметричным.

Распределение доходности с положительной скошенностью (положительно ассиметричное) часто приносит небольшие убытки и несколько экстремальных доходов.

Распределение доходности с отрицательной скошенностью (отрицательно ассиметричное) часто приносит небольшие доходы и несколько экстремальных убытков. На графиках ниже показаны положительно и отрицательно скошенные распределения.

Свойства асимметричных распределений.

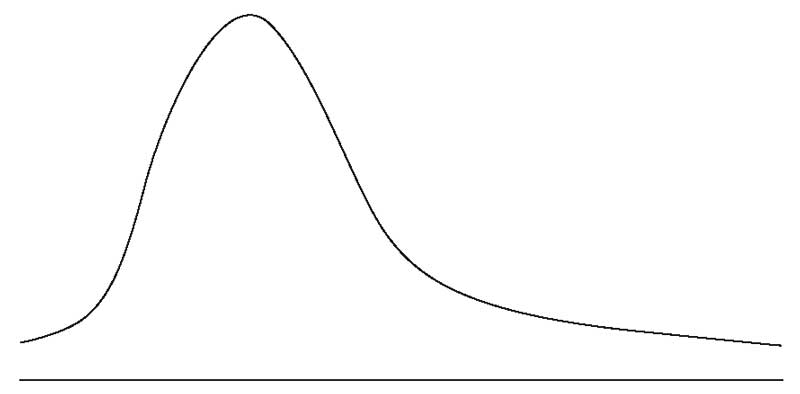
Распределение скошено вправо (положительно ассиметричное).

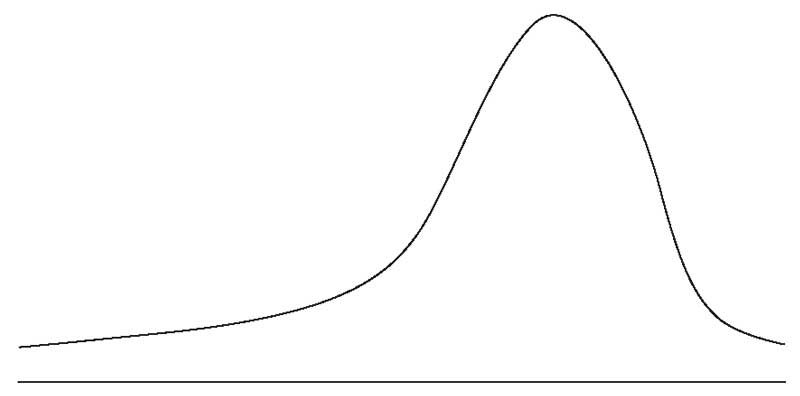
Распределение скошено влево (отрицательно ассиметричное).

Показанное на графике положительно скошенное распределение имеет длинный хвост с правой стороны. Отрицательно скошенное распределение имеет длинный хвост на левой стороне.

Для положительно скошенного унимодального распределения мода меньше медианы, а медиана меньше среднего. Для унимодального распределения с отрицательной скошенностью среднее значение меньше медианы, а медиана что меньше моды.

Инвесторов привлекает положительная ассиметричность, поскольку средняя доходность находится выше медианы. Вместе с тем, положительная ассиметричность (относительно среднего значения) означает небольшие, хотя и частые, убытки при крупных, но менее частых доходах.

Ассиметрия или скошенность (англ. ‘skewness’ или ‘skew’) — это термин, означающий статистическую меру ассиметрии. Как и дисперсия, асимметрия вычисляется с использованием отклонения каждого наблюдения от его среднего значения.

Асимметрия (иногда упоминаемая как относительная асимметрия) вычисляется как среднее кубическое отклонение от среднего, деленное на стандартное отклонение в кубе, что делает меру независимой от шкалы.

Здесь мы обсуждаем обычный коэффициент асимметрии. В некоторых учебниках представлен коэффициент асимметрии Пирсона, равный

3 (times) (Среднее — Медиана) / Стандартное отклонение

который имеет недостаток, заключающийся в необходимости вычисления медианы.

Симметричное распределение имеет асимметрию равную 0, положительно асимметричное распределение имеет положительную асимметрию, а отрицательно асимметричное распределение имеет отрицательную асимметрию.

Мы можем проиллюстрировать принцип, лежащий в основе этой меры, сосредоточившись на числителе. Куб, в отличие от квадрата, сохраняет знак отклонения от среднего. Если распределение положительно ассиметрично при среднем значении, превышающем его медиану, то более половины отклонений от среднего значения являются отрицательными, а менее половины — положительными.

Чтобы сумма была положительной, убытки должны быть небольшими и вероятными, а доходы менее вероятными, но более экстремальными. Следовательно, если асимметрия положительна, средняя величина положительных отклонений больше, чем средняя величина отрицательных отклонений.

Простой пример показывает, что симметричное распределение имеет показатель асимметрии, равный 0.

Предположим, у нас есть следующий ряд значений: 1, 2, 3, 4, 5, 6, 7, 8 и 9. Среднее равно 5, а отклонения составляют -4, -3, -2, -1, 0, 1, 2, 3 и 4. Возведение отклонений в куб дает -64, -27, -8, -1, 0, 1, 8, 27 и 64, что в сумме равно 0.

Числитель асимметрии (и, следовательно, сама асимметрия), таким образом, равен 0, что подтверждает наше утверждение. Ниже приведена формула для вычисления асимметрии по выборке.

Формула выборочного коэффициента асимметрии.

Выборочный коэффициент ассиметрии (англ. ‘sample skewness’, ‘sample relative skewness’), (S_K), рассчитывается по формуле:

( dst
S_K = left [ {n over (n-1)(n-2)} right ] {dsum_{i=1}^n (X_i — overline X)^3 over s^3} ) (Формула 17)

где

(n) — количество наблюдений в выборке, а
(s) — стандартное отклонение выборки.

Выражение ( n / [(n — 1) (n — 2)] ) в Формуле 17 корректирует смещение вниз в небольших выборках.

Алгебраический знак коэффициента указывает направление ассиметриии (скошенности), при этом отрицательный (S_K ) указывает на отрицательно скошенное распределение, а положительный (S_K ) указывает на положительную ассиметрию. Обратите внимание, что когда n становится большим, формула сводится к среднему кубическому отклонению:

( dst
S_K approx left( {1 over n} right) {dsum_{i=1}^n (X_i — overline X)^3 over s^3} )

Для выборки размером 100 или более наблюдений, с нормальным распределение, коэффициент асимметрии ( pm ) 0,5 будет считаться необычно большим.

Таблица 27 показывает несколько сводных статистических показателей для годовой и месячной доходности S&P 500.

Ранее мы обсуждали среднеарифметическую доходность и стандартное отклонение доходности, и а в следующей теме мы кратко обсудим эксцесс.

Таблица 27. Годовая и месячная совокупная доходность S&P 500
за 1926-2012 гг .: Сводная статистика.

Доходность	Кол-во периодов	Среднее арифметическое (%)	Стандартное отклонение (%)	Коэффициент ассиметрии	Коэффициент эксцесса
S&P 500 (Годовая)	87	11.82	20.18	-0.3768	0.0100
S&P 500 (Месячная)	1,044	0.94	5.50	0.3456	9.4288

Источник: Ibbotson Associates.

Таблица 27 показывает, что годовая доходность S&P 500 в течение этого периода была отрицательно ассиметрична, в то время как ежемесячная доходность была положительно ассиметрична, и размер асимметрии был больше для годовой доходности.

При аналогичном анализе других рыночных рядов мы обнаружили бы, что форма распределения доходности часто зависит от исследуемого периода владения активом.

Некоторые исследователи считают, что инвесторам следует отдавать предпочтение положительной асимметрии, при прочих равных условиях, то есть им следует отдавать предпочтение портфелям с распределениями, предлагающими относительно большую частоту необычно больших выплат.

О роли асимметрии при выборе портфеля — см. Reilly and Brown (2012) и Elton et al. (2013).

Для различных инвестиционных стратегий характерны различные типы и значения коэффициента асимметрии. Пример, приведенный ниже, иллюстрирует расчет асимметрии для управляемого портфеля.

Пример расчета асимметрии для взаимного фонда.

В Таблице 28 представлена 10-летняя годовая доходность фонда T. Rowe Price Equity Income (PRFDX).

Таблица 28. Годовая доходность T. Rowe Price Equity Income, 2003-2012 гг.

Год	Доходность (%)
2003	25.78
2004	15.05
2005	4.26
2006	19.14
2007	3.30
2008	-35.75
2009	25.62
2010	15.15
2011	-0.72
2012	17.25

Источник: performance.morningstar.com.

Используя информацию из Таблицы 28, сделайте следующее:

Рассчитайте асимметрию PRFDX, с точностью до двух десятичных знаков.
Охарактеризуйте форму распределения доходности PRFDX, основываясь на результате для части 1.

Решение для части 1:

Чтобы вычислить коэффициент асимметрии, мы находим сумму кубических отклонений от среднего значения, делим на кубическое стандартное отклонение и затем умножаем полученный результат на ( n / [(n — 1) (n — 2)]).

В Таблице 29 приведены соответствующие расчеты.

Таблица 29. Расчет асимметрии для PRFDX.

Год	( R_t )	( R_t — overline R )	( (R_t — overline R)^3 )
2003	25.78	16.87	4,801.150
2004	15.05	6.14	231.476
2005	4.26	-4.65	-100.545
2006	19.14	10.23	1,070.599
2007	3.30	-5.61	-176.558
2008	-35.75	-44.66	-89,075.067
2009	25.62	16.71	4,665.835
2010	15.15	6.24	242.971
2011	-0.72	-9.63	-893.056
2012	17.25	8.34	580.094
n =	10
R =	8.91%
Сумма =	-78,653.103
s =	18.12%	s³ =	5,949.419
Сумма / s3 =	-13.2203
n / [(n — 1) (n — 2)] =	0.1389
Ассиметрия =	-1.84

Источник: performance.morningstar.com.

Используя Формулу 17, вычисляем:

( S_K = dst left( {10 over (9)(8)} right) {-78,653.103 over 18.12^3} = -1.84 )

Решение для части 2:

Для этой небольшой выборки, распределение годовой доходности фонда представляется отрицательно ассиметричным.

В этом Примере 4 отклонения отрицательны, а 6 — положительны. Хотя в распределении больше положительных отклонений, они более чем компенсируются огромным отрицательным отклонением в 2008 году, когда фондовые рынки резко обвалились в результате мирового финансового кризиса.

Итоговый коэффициент асимметрии является отрицательным числом. Это подразумевает, что распределение скошено влево.

Источник

Материал из MachineLearning.

(Перенаправлено с Асимметрия)

Перейти к: навигация, поиск

Содержание

1 Определение
2 Выборочный коэффициент асимметрии
3 Проверка гипотезы симметричности
4 Литература
5 Ссылки

Коэффицие́нт асимметри́и (skewness) — числовая характеризующая степени несимметричности распределения данной случайной величины.

Определение

Пусть задана случайная величина , такая что $mathbb{E} |x|^3 < infty$ .

Коэффициент асимметрии распределения случайной величины определяется формулой:

$gamma_1 = frac{mu_3}{sigma^3},$

где

$mu_3 = mathbb{E}left[(x - mathbb{E}x)^3right]$

— третий центральный момент случайной величины

;

— стандартное отклонение случайной величины

;

$mathbb{D}[x] = mathbb{E}left[(x - mathbb{E}x)^2right]$

— дисперсия или второй центральный момент случайной величины

;

Если плотность распределения симметрична, то .

Если левый хвост распределения тяжелее, то .

Если правый хвост распределения тяжелее, то .

Иногда вместо gamma_1 используется обозначение alpha_3 .

Выборочный коэффициент асимметрии

Пусть задана случайная выборка наблюдений .

Выборочный коэффициент асимметрии определяется формулой:

$gamma_1 = frac{overset{bullet}M_3}{overset{bullet}M_2^{3/2}} = frac{sqrt{m(m-1)}}{m-2} left( frac{overset{circ}M_3}{overset{circ}M_2^{3/2}} right),$

где

$overset{circ}M_k = frac1m sum_{i=1}^m left( x_i - bar x right)^k$

— выборочный центральный момент k-го порядка;

$overset{bullet}M_2 = frac{m}{m-1} overset{circ}M_2$

— несмещённая оценка центрального момента второго порядка;

$overset{bullet}M_3 = frac{m^2}{(m-1)(m-2)} overset{circ}M_3$

— несмещённая оценка центрального момента третьего порядка.

Проверка гипотезы симметричности

Выборочный коэффициент асимметрии используется для проверки распределения на симметричность, а также для грубой предварительной проверки на нормальность.
Он позволяет отвергнуть, но не позволяет принять гипотезу нормальности.

Проверка основана на формуле для дисперсии выборочного коэффициента асимметрии:

$mathbb{D}left( frac{overset{circ}M_3}{overset{circ}M_2^{3/2}} right) = frac{6(m-2)}{(m+1)(m+3)}.$

Распределение gamma_1 довольно быстро стремится к нормальному.

Литература

Вероятность и математическая статистика: Энциклопедия / Под ред. Ю.В.Прохорова. — М.: Большая российская энциклопедия, 2003. — 912 с.
Кобзарь А. И. Прикладная математическая статистика. — М.: Физматлит, 2006.

Ссылки

Моменты случайной величины.
Статистика (функция выборки).
Коэффициент эксцесса.
Коэффициент асимметрии (Википедия).
Skewness (Wikipedia).

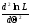Источник