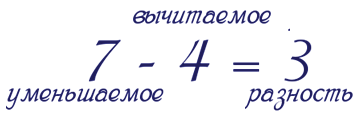Существуют четыре основных арифметических действия: сложение, вычитание, умножение и деление. Они – основа математики, с их помощью производятся все остальные, более сложные вычисления. Сложение и вычитание – простейшие из них и взаимно противоположны. Но с терминами, используемыми при сложении, мы чаще сталкиваемся в жизни.
Говорим о «сложении усилий» при старании совместно получить нужный результат, о «слагаемых достигнутого успеха» и т.п. Названия же, связанные с вычитанием, остаются в пределах математики, редко появляясь в повседневной речи. Поэтому менее привычны слова вычитаемое, уменьшаемое, разность. Правило нахождения каждого из данных компонентов возможно применить лишь при понимании значения этих названий.
Значение терминов
В отличие от многих научных терминов, имеющих греческое, латинское или арабское происхождение, в данном случае используются слова с русскими корнями. Так что понять их значение несложно, а значит легко и запомнить, что каким термином обозначается.
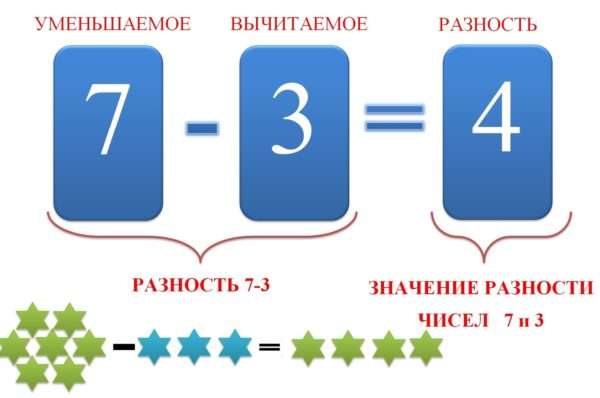
Что такое разность чисел в математике
Если присмотреться к самому названию, становится заметно, что оно имеет отношение к словам «разный», «разница». Из этого можно заключить, что имеется в виду установленная разница между количествами.
Это интересно! Как раскрыть модуль действительного числа и что это такое
Данное понятие в математике означает:
- разницу между двумя числами,
- это показатель того, насколько одно количество больше или меньше другого,
- это результат, полученный при выполнении вычитания такое определение предлагает школьная программа.
Обратите внимание! Если количества равны друг другу, то между ними нет разницы. Значит разность их равняется нулю.
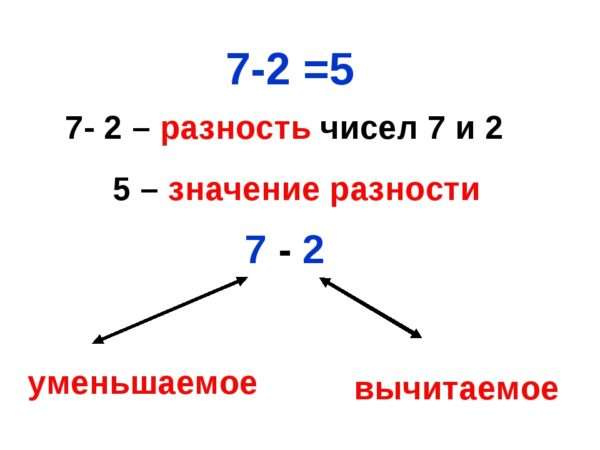
Что такое уменьшаемое и вычитаемое
Как следует из названия, уменьшаемое – это то, что делают меньше. А сделать количество меньшим можно, отняв от него часть. Таким образом, уменьшаемым называется число, от которого отнимают часть.
Вычитаемым, соответственно, называется то число, которое от него отнимают.
| Уменьшаемое | Вычитаемое | Разность | ||
| 18 | 11 | = | 7 | |
| 14 | 5 | = | 9 | |
| 26 | 22 | = | 4 |
Полезное видео: уменьшаемое, вычитаемое, разность
Правила нахождения неизвестного элемента
Разобравшись в терминах, несложно установить, по какому правилу находится каждый из элементов вычитания.
Поскольку разность – результат данного арифметического действия, то ее и находят с помощью этого действия, никаких других правил тут не требуется. Но они есть на случай, если неизвестен другой член математического выражения.
Это интересно! Уроки математики: умножение на ноль главное правило
Как найти уменьшаемое
Данным термином, как было выяснено, называют количество, из которого вычли часть. Но если одну вычли, а другая осталась в итоге, следовательно, из этих двух частей число и состоит. Получается, что найти неизвестное уменьшаемое можно, сложив два известных элемента.
Итак, в данном случае, чтобы найти неизвестное, следует выполнить сложение вычитаемого и разности:
| ? | – | 11 | = | 7 |
Искомое находится путем сложения известных элементов:
| 7 | + | 11 | = | 18 |
Так же и во всех подобных случаях:
| ? | – | 5 | = | 9 |
| 9 | + | 5 | = | 14 |
| ? | – | 22 | = | 4 |
| 4 | + | 22 | = | 26 |
Как найти вычитаемое
Если целое состоит из двух частей (в данном случае количеств), то при вычитании одной из них в результате получится вторая. Таким образом, чтобы найти неизвестное вычитаемое, достаточно вместо него вычесть из целого разность.
| 18 | – | ? | = | 7 |
Из примера видно, что от 18 отняли некоторую величину, и осталось 7. Чтобы найти эту величину, надо от 18 отнять 7.
| 18 | – | 7 | = | 11 |
По тому же правилу решаются и другие подобные примеры.
| 14 | – | ? | = | 9 |
| 14 | – | 9 | = | 5 |
| 26 | – | ? | = | 4 |
| 26 | – | 4 | = | 22 |
Таким образом, зная точное значение названий, можно легко догадаться, по какому правилу следует искать каждый неизвестный элемент.
Это интересно! Как разложить на множители квадратный трехчлен: формула
Полезное видео: как найти неизвестное уменьшаемое
Вывод
Четыре основных арифметических действия – та база, на которой основываются все математические вычисления, от простых до самых сложных. Конечно, в наше время, когда люди стремятся перепоручить технике все вплоть до мыслительного процесса, привычнее и быстрее производить вычисления с помощью калькулятора. Но любое умение увеличивает независимость человека – от технических средств, от окружающих. Не обязательно делать математику своей специальностью, но обладать хотя бы минимальными знаниями и умениями – значит иметь дополнительную опору для собственной уверенности.
Памятка по нахождению неизвестных компонентов действий.
Скачать:
Предварительный просмотр:
Выучи названия компонентов действий и правила нахождения неизвестных компонентов:
- Сложение: слагаемое, слагаемое, сумма. Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое.
- Вычитание: уменьшаемое, вычитаемое, разность. Чтобы найти уменьшаемое, нужно к вычитаемому прибавить разность. Чтобы найти вычитаемое, нужно из уменьшаемого вычесть разность.
- Умножение: множитель, множитель, произведение. Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель.
- Деление: делимое, делитель, частное. Чтобы найти делимое, нужно делитель умножить на частное. Чтобы найти делитель, нужно делимое разделить на частное.
Выучи названия компонентов действий и правила нахождения неизвестных компонентов:
- Сложение: слагаемое, слагаемое, сумма. Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое.
- Вычитание: уменьшаемое, вычитаемое, разность. Чтобы найти уменьшаемое, нужно к вычитаемому прибавить разность. Чтобы найти вычитаемое, нужно из уменьшаемого вычесть разность.
- Умножение: множитель, множитель, произведение. Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель.
- Деление: делимое, делитель, частное. Чтобы найти делимое, нужно делитель умножить на частное. Чтобы найти делитель, нужно делимое разделить на частное.
По теме: методические разработки, презентации и конспекты
- Мне нравится
- Главная
- Справочники
- Справочник по математике для начальной школы
- Вычитание
Познакомимся с вычитанием.
Рассмотрим числовой ряд и вспомним, в каком порядке идут числа.
Числа идут слева направо, по порядку, как при счёте.
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
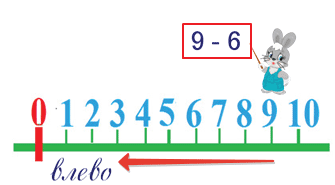
Посмотри на числовой ряд, по которому идёт заяц.
Какое действие выполняет заяц?
Вычитает число 6.
Из какого числа он вычитает число 6?
Из числа 9. Мы поставили зайчика на число 9.
В какую сторону он пойдёт?
Влево, потому что у него на табличке знак минус.
Сколько шагов влево сделает зайчик? 6.
На каком делении он остановится? На числе 3.
Когда вычитаем, становится меньше.
Чем левее, тем числа меньше.
9 — 6 = 3
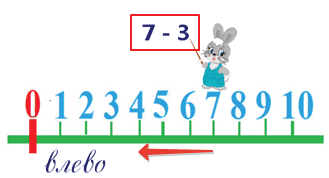
Рассмотрим еще один пример.
Какое действие выполняет заяц?
Вычитает число 3.
Из какого числа он вычитает число 3?
Из числа 7. Мы поставили зайчика на число 7.
В какую сторону он пойдёт?
Влево, потому что у него на табличке знак минус.
Сколько шагов влево сделает зайчик? 3.
На каком делении он остановится? На числе 4.
Когда вычитаем, становится меньше.
Чем левее, тем числа меньше.
7 — 3 = 4
Как называются числа при вычитании?
Число, из которого вычитают, становится МЕНЬШЕ, уменьшается, поэтому его называют «уменьшаемое».
Число, которое вычитают, называют «вычитаемое».
Число, которое получается в результате вычитания, называют «разность».
Рассмотри рисунок.
У жонглёра было 9 шариков.
Когда несколько шариков упало, осталось ещё 5 шариков.
Сколько шариков упало?
Каким действием будем находить? Вычитанием.
9 — 4 = 5
Как называются числа при вычитании?
9 — уменьшаемое
4 — вычитаемое
5 — разность
Как найти неизвестное вычитаемое
Рассмотри рисунок.
У жонглера было 9 шариков. Когда несколько шариков упало, осталось 5. Упали, значит, убрали.
Решаем вычитанием. Что нужно найти?
Нужно найти вычитаемое.
Чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть разность.
9 — 5 = 4
Вычитаемое равно 4.
Упало 4 шарика.
Как найти неизвестное уменьшаемое
Что известно?
Вычитаемое — 4.
Разность — 5.
Нужно найти уменьшаемое.
Чтобы найти уменьшаемое, нужно к разности прибавить вычитаемое.
5 + 4 = 9
Проверка вычитания
Если к разности прибавить вычитаемое, получится уменьшаемое.
Именно эта связь между разностью, уменьшаемым и вычитаемым используют для проверки вычитания.
Например, 35 — 15 = 20.
Правильно ли произведено вычисление? Можно проверить так:
20 + 15 = 35, мы к разности прибавили вычитаемое и получили уменьшаемое. Значит, вычисление произведено верно и пример решен правильно.
Советуем посмотреть:
Табличное вычитание
Письменное вычитание в столбик
Правило встречается в следующих упражнениях:
1 класс
Страница 40. Тест. Вариант 1,
Волкова, Проверочные работы
Страница 51,
Моро, Волкова, Степанова, Учебник, часть 2
Страница 69,
Моро, Волкова, Степанова, Учебник, часть 2
Страница 3,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 7,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 24,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 33. Урок 22,
Петерсон, Учебник, часть 1
Страница 35. Урок 23,
Петерсон, Учебник, часть 1
Страница 42. Урок 27,
Петерсон, Учебник, часть 1
Страница 56. Урок 29,
Петерсон, Учебник, часть 2
2 класс
Страница 17,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 15. Тест 2. Вариант 2,
Моро, Волкова, Проверочные работы
Страница 50. Тест. Вариант 1,
Моро, Волкова, Проверочные работы
Страница 66,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 70,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 11,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 42,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 61,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 74,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 5. Урок 2,
Петерсон, Учебник, часть 1
3 класс
Страница 4,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 22,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 78,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 97,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 99,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 78,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 98,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 104,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 7,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 29. Урок 13,
Петерсон, Учебник, часть 3
4 класс
Страница 19,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 73,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 90,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 93,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 83. Тест 2. Вариант 2,
Моро, Волкова, Проверочные работы
Страница 13,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 51,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 85,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 94,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 95,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Содержание материала
- Предварительный просмотр:
- Видео
- Нахождение неизвестного множителя
- Поиск вычитаемого
- Правила нахождения уменьшаемого
- Свойства сложения
- Общие правила
- Другие методы
- Сложение в столбик многозначных чисел
Предварительный просмотр:
Выучи названия компонентов действий и правила нахождения неизвестных компонентов:
- Сложение: слагаемое, слагаемое, сумма. Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое.
- Вычитание: уменьшаемое, вычитаемое, разность. Чтобы найти уменьшаемое, нужно к вычитаемому прибавить разность. Чтобы найти вычитаемое, нужно из уменьшаемого вычесть разность.
- Умножение: множитель, множитель, произведение. Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель.
- Деление: делимое, делитель, частное. Чтобы найти делимое, нужно делитель умножить на частное. Чтобы найти делитель, нужно делимое разделить на частное.
Выучи названия компонентов действий и правила нахождения неизвестных компонентов:
- Сложение: слагаемое, слагаемое, сумма. Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое.
- Вычитание: уменьшаемое, вычитаемое, разность. Чтобы найти уменьшаемое, нужно к вычитаемому прибавить разность. Чтобы найти вычитаемое, нужно из уменьшаемого вычесть разность.
- Умножение: множитель, множитель, произведение. Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель.
- Деление: делимое, делитель, частное. Чтобы найти делимое, нужно делитель умножить на частное. Чтобы найти делитель, нужно делимое разделить на частное.
Видео
Нахождение неизвестного множителя
Посмотрим на два уравнения: x·2=20 и 3·x=12. В обоих нам известно значение произведения и один из множителей, необходимо найти второй. Для этого нам надо воспользоваться другим правилом.
Для нахождения неизвестного множителя нужно выполнить деление произведения на известный множитель.
Данное правило базируется на смысле, который является обратным смыслу умножения. Между умножением и делением есть следующая связь: a·b=c при a и b, не равных , c: a=b, c: b=c и наоборот.
Вычислим неизвестный множитель в первом уравнении, разделив известное частное 20 на известный множитель 2. Проводим деление натуральных чисел и получаем 10. Запишем последовательность равенств:
x·2=20x=20:2x=10.
Подставляем десятку в исходное равенство и получаем, что 2·10=20. Значение неизвестного множителя было выполнено правильно.
Уточним, что в случае, если один из множителей нулевой, данное правило применять нельзя. Так, уравнение x·=11 с его помощью решить мы не можем. Эта запись не имеет смысла, поскольку для решения надо разделить 11 на , а деление на нуль не определено. Подробнее о подобных случаях мы рассказали в статье, посвященной линейным уравнениям.
Когда мы применяем это правило, мы, по сути, делим обе части уравнения на другой множитель, отличный от . Существует отдельное правило, согласно которому можно проводить такое деление, и оно не повлияет на корни уравнения, и то, о чем мы писали в этом пункте, с ним полностью согласовано.
Поиск вычитаемого
Нахождение вычитаемого — это такой же простой процесс, как и поиск уменьшаемого. Уравнение может иметь следующий вид: 7-x=3. Мы имеем разность — результат вычитания, и уменьшаемое число. Формулировка правила: чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность.
Так, если мы вычитаем из одного числа неизвестное число и получаем определённый результат (разность), значит, для поиска неизвестного вычитаемого вычтем из известного числа разность. В нашем примере x=7−3, результат равен 4. Для проверки вычтем 4 из 7, и получим 3 — решение верное. Ещё один вариант проверки — сложить 3 и 4. Так как сумма равна 7, решение правильное.
Правила нахождения уменьшаемого

При поиске уменьшаемого уравнение может выглядеть следующим образом: x-2=4. Мы имеем разность — результат вычитания и число, которое вычитаем. Необходимо найти уменьшаемое — самое большое число в примере. Формулировка правила: чтобы найти неизвестное уменьшаемое, необходимо к разности прибавить вычитаемое.
Так, если мы вычитаем из неизвестного числа другое число и получаем результат, известный нам, то для поиска уменьшаемого необходимо сложить разность и вычитаемое. Простейший пример: дома были конфеты. Их количество мы не знаем. После того как Дима съел 2 конфеты, их осталось 4. Вопрос: сколько их всего было изначально? Для того чтобы узнать, прибавим 2 к 4 и получим результат — было 6 конфет. Для проверки вычтем 2 из 6. Получим результат 4 — решение верное.
Свойства сложения
Сложение — это арифметическое действие, в котором единицы двух чисел объединяются в одно новое число
Для записи сложения используют знак «+» (плюс), который ставят между слагаемыми.
Слагаемые — это числа, единицы которых складываются.
Сумма — это число, которое получается в результате сложения.
Рассмотрим пример 2 + 5 = 7, в котором:
При этом саму запись (2 + 5) можно тоже назвать суммой.

Сложение двух чисел можно проверить вычитанием. Для этого вычитаем из суммы одно из слагаемых. Если разность окажется равной другому слагаемому — сложение выполнено верно.
Впервые мы сталкиваемся со свойствами сложения во 2 классе. С каждым годом задания усложняются, и появляются новые правила и законы. Рассмотрим свойства сложения для 4 класса.
Общие правила
Для того чтобы гораздо быстрее решать элементарные уравнения, необходимо знать некоторые правила математики и логики. Здесь даже навыки арифметики не имеют такого решающего значения, как понимание того, что именно необходимо находить.
В случае с неизвестным слагаемым оно находится очень просто. От перестановки слагаемых сумма не меняется. То есть совершенно неважно, какой вид имеет уравнение x+2=6, или 2+x=6. В любом случае компонент x будет равен 4.

Дело в том, что уравнения с одним неизвестным предусмотрены школьной программой третьего класса. А ученики могут путаться и испытывать трудности в их решении, не зная этого правила.
Первое, с чего стоит начинать развитие навыка решения — это многократное повторение. Достаточно решать 5—10 уравнений в день с одним неизвестным компонентом, и уже через несколько дней ученик будет справляться с подобными заданиями гораздо быстрее. И только потом можно переходить к более сложным заданиям.

А также для улучшения понимания необходимо решать обратные уравнения. Что это значит? Вычитание — процесс, обратный сложению. То есть при сложении 3 и 4 сумма равна 7. А при вычитании 4 из 7 разность равна 3. В первом уравнении можно искать неизвестные слагаемые. При этом решать его с теми же числами, но на поиск уменьшаемого или вычитаемого.
Решение подобных уравнений точно не навредит ученику, это лишь ускорит процесс формирования навыка. При проверке и решении обратных уравнений в голове откладывается взаимосвязь между всеми компонентами примеров, а их решение практически доводит до автоматизма. Главное — постоянно тренировать этот навык.
Другие методы
Правило, которое позволяет быстро найти неизвестное слагаемое, довольно простое. Однако для того, чтобы облегчить его понимание, из него можно вывести правила, связанные с вычитанием.
Так, в примерах со сложением мы имеем два слагаемых и сумму: 3+5=8. Здесь 3 и 5 — слагаемые, а 8 — сумма. А в примерах с вычитанием мы имеем:
- Уменьшаемое.
- Вычитаемое.
- Разность.
Например, 7 — 4=3. В этом случае уменьшаемое — 7, вычитаемое — 3, а разность — 4. Уменьшаемое и вычитаемое также могут быть неизвестными. И крайне важно знать, как их вычислять.
Сложение в столбик многозначных чисел
Сложение в столбик – это способ нахождения суммы чисел путем их записи друг под другом таким образом, чтобы соответствующие разряды разных чисел находились на одной вертикали (один под другим).
Итак, допустим, что нам нужно найти сумму : 5728+803
Теги
Содержание:
Действие вычитание и компоненты вычитания
Связь вычитания и сложения
Свойства разности
Как вычесть сумму из числа и число из суммы
Изменение разности при изменении вычитаемого и/или уменьшаемого
Правила вычитания разности
Вычитание однозначного числа
Вычитание в столбик многозначных чисел
Проверка действий сложение и вычитание
Пройти тест по теме «Сложение и вычитание натуральных чисел» можно по ссылке. Проверьте свои знания!
Мы можем не только собирать в группы различные предметы, то есть, складывать их, но и забирать из существующей группы определенное их количество.
Например, в кошельке было 1850 рублей. В магазине было потрачено 780 рублей. Чтобы узнать, сколько осталось денег, можно вытащить кошелек и пересчитать их. Но можно поступить по-другому: из той суммы, которая была в кошельке, отнять ту сумму, что была потрачена в магазине. Разница этих чисел, то есть, на сколько единиц изначальная сумма денег больше той суммы, которую потратили, и будет остатком денег.
Разность (или остаток) – это такое число, которое получится, если от одного числа отнять другое, то есть, от всех единиц одного числа отнять все единицы, которые содержатся в другом числе.
Уменьшаемое – это то число, от которого мы отнимаем единицы другого числа.
Вычитаемое – это число, которое мы вычитаем из другого числа. То есть, то число, на количество единиц которого мы уменьшаем другое число.
Вычитание – это арифметическое действие, которое выполняется для получения разности двух или нескольких чисел.
то есть, совершить действие вычитания – это найти такое число, которое получится, если от данного числа отнять определенное количество единиц другого числа.
Компоненты вычитания:
Про действие вычитание также говорят, что нужно из одного числа вычесть другое, или одно число уменьшить на другое.
Совершая вычитание натуральных чисел, вы должны помнить, что из одного натурального числа можно вычесть только равное ему или меньшее натуральное число. Действительно, мы никак не можем отобрать единиц предметов больше, чем их есть в наличии.
Поэтому, уменьшаемое натуральное число всегда больше или равное вычитаемому. Другими словами, мы всегда вычитаем из большего меньшее или из равного равное.
Связь вычитания и сложения
Действие вычитание непосредственно связано с действием сложение.
Действительно, когда мы ищем сумму, мы складываем все единицы, из которых состоят числа, вместе. То есть, получаем число, которое складывается из разных чисел.
А когда мы ищем разность, мы из одного числа (уменьшаемое) отнимаем некоторое количество единиц (вычитаемое), которые входят в его состав, и получаем другое количество единиц. То есть, получаем число (разность), которое также составляло уменьшаемое, пока от него не отняли вычитаемое. Поэтому разность и имеет второе название – остаток – то, что осталось от числа, после вычитания его части.
Из этого мы можем сделать вывод, что, если сложить обратно обе части одного числа (разность и вычитаемое), то мы получим уменьшаемое.
Поэтому, вычитание и сложение – это взаимно обратные действия. Если нам известна сумма двух слагаемых, мы можем превратить ее в разность двух чисел, и наоборот, разность можно перевести в сумму.
Уменьшаемое – это сумма вычитаемого и разности. То есть, разность и вычитаемое – это слагаемые.
Когда мы складываем числа, слагаемые нам известны, и нужно вычислить их сумму. А когда мы вычитаем, нам даются сумма (уменьшаемое) и одно из слагаемых (вычитаемое) этой суммы, а второе слагаемое (разность) нам нужно вычислить.
Рассмотрим это на примере. Мы нашли разность 8-5=3. Это означает, что мы разложили одно данное нам число 8 на два: 5 (данное нам уменьшаемое) и 3 (найденная нами разность). Но мы знаем, что состав числа – это слагаемые, которые в сумме дают нам это самое число. Поэтому, найденную нами разность чисел мы можем превратить в сумму чисел, сложив остаток с вычитаемым: 3+5=8.
Свойства разности натуральных чисел
Свойства разности натуральных чисел состоят из:
- Правила вычитания суммы из числа и числа из суммы;
- Зависимость разности от изменения уменьшаемого или вычитаемого.
- Правило вычитания разности из числа;
Рассмотрим каждый пункт подробнее.
Правила вычитания суммы из числа и числа из суммы
Как вычесть сумму из числа
Чтобы найти разность числа и суммы чисел нужно из данного числа вычесть последовательно каждое слагаемое суммы.
То есть, сначала мы находим разность между данным числом и первым слагаемым, потом от этой полученной разности отнимаем второе слагаемое, третье, и так далее до последнего слагаемого суммы.
Действительно, так как сумма – это объединение всех слагаемых, то очевидно, что, отнимая последовательно каждое слагаемое, каждое ее составляющее число, мы в конце концов отнимем всю сумму.
Рассмотрим это на примере из урока сложение чисел.
325+(12+64+5) = 325+81 = 406
Я запишу это в виде разности:
406-(12+64+5) = 325
и покажу, что результат будет равен первому слагаемому:
406—12 = 394;
394-64 = 330;
330-5 = 325.
Как видите, все верно.
Как вычесть число из суммы
Чтобы найти разность суммы чисел и некоторого числа, нужно отнять это число от какого-нибудь подходящего слагаемого этой суммы.
То есть, мы сначала находим разность одного из слагаемых и данного числа, а потом складываем получившийся результат последовательно с остальными слагаемыми.
Действительно, вы знаете, что, если уменьшить одно из слагаемых на какое-то число, то и сумма уменьшится на это же самое число. Следовательно, если нам нужно сумму чисел уменьшить на какое-то число, то для этого достаточно уменьшить на это число одно из слагаемых суммы.
Для рассмотрения я возьму тот же пример, только сумму расчленю на слагаемые, а слагаемое в скобках заменю суммой:
325+81 = (191+65+150)
Превращаю выражение в разность:
(191+65+150)-81 = 325
и покажу, что результат также будет равен первому слагаемому:
191-81 = 110;
110+65 = 175;
175+150 = 325
или
150-81 = 69;
69+191 = 260;
260+65 = 325.
Я недаром написал в правиле, что нужно отнимать от подходящего слагаемого суммы, потому что, если оно будет меньше вычитаемого, то оно нам не подходит. Так, в нашем примере 65<81.
Отсюда следует, что это правило применимо не к любой сумме натуральных чисел, а только к той, в которой хотя бы одно из слагаемых больше, чем вычитаемое.
Как меняется разность при изменении вычитаемого или уменьшаемого
Изменение разности при изменении вычитаемого и уменьшаемого является следствием описанных в уроке изменений суммы чисел с изменением ее слагаемых.
Если уменьшаемое увеличить на некоторое количество единиц, то и разность увеличится на такое же количество единиц.
Если уменьшаемое уменьшить на некоторое количество единиц, то и разность уменьшится на такое же количество единиц.
Если вычитаемое увеличить на некоторое количество единиц, то разность уменьшится на такое же количество единиц.
Если вычитаемое уменьшить на некоторое количество единиц, то разность увеличится на такое же количество единиц.
Если сразу оба числа, и уменьшаемое, и вычитаемое, увеличить или уменьшить на одно и то же количество единиц, то разность не изменится.
Правила вычитания разности
Если нужно вычесть из числа разность других чисел, можно воспользоваться одним из двух способов:
1. Прибавить к данному числу вычитаемое, и из получившейся суммы вычесть уменьшаемое;
2. Вычесть из данного числа уменьшаемое, а потом результат этого действия сложить с вычитаемым.
Это свойство выводится из предыдущих, рассмотренных нами.
Рассмотрим на примере 22-(17—3).
Для начала вычислим обычным способом: сперва узнаем разность в скобках (это будет 17-3=14), а потом вычтем 14 из 22. Получится 22-14=8.
22-(17—3) = 8
Теперь вернемся к исходному примеру и отнимем от 22 не разность 17-3, то есть, не 17 без 3 единиц, а все число 17.
22—17 = 5
Но мы ведь отняли больше, чем нужно было, поэтому нам нужно вернуть лишне взятые 3 единицы обратно, а именно, прибавить их к полученному результату.
5+3 = 8
Попробуем решить другим путем: увеличим и уменьшаемое (данное число), и вычитаемое (разность в скобках) на одно и то же число 3. Получим:
22+3-(17+3-3)
Так как 22+3=25, а 3-3=0, то в итоге получается:
25-17+0 = 8
Как видите, оба способа показали верный результат.
Вычитание однозначного числа
Вы сможете без каких-либо трудностей совершать вычитание любых чисел, если сперва хорошо натренируете себя вычитать однозначные числа в уме из однозначных и двухзначных.
А поскольку вычитание – это действие обратное сложению, тогда необходимо просто выучить на память все суммы однозначных чисел. Пользуясь ими, мы легко сможем получить необходимые вам разности.
Например, нам нужно найти разность чисел 17 и 8. Для этого нам необходимо вспомнить, какое число при сложении с числом 8 дает сумму 17? Это число 9, потому что 8+9=17. Значит, если от 17 отнять 8, мы получим: 17-8=9.
Хорошо натренировавшись в нахождении разности чисел из суммы однозначных чисел, можно переходить к более сложным случаям вычитания. Подробно эти приемы рассмотрены в разделе рубрики «Устный счет».
Вычитание в столбик многозначных чисел
Так же, как и сложение, разность многозначных чисел удобно находить, используя вычитание в столбик.
Вычитание в столбик – это способ нахождения разности чисел при помощи их записи друг под другом таким образом, чтобы соответствующие разряды разных чисел находились на одной вертикали (один под другим), и последующего вычисления.
Давайте найдем разность чисел 52063-4825.
Запишем их друг под другом таким образом, чтобы совпадали соответствующие разряды обоих чисел, т.е. единицы под единицами, десятки под десятками и т.д. После этого, под вторым слагаемым проводим горизонтальную черту, а между слагаемыми ставим знак действия, т.е. минус. У нас получилась такая запись:

Вычитание в столбик выполняется подобным способом, как и при сложении, только теперь мы отнимаем единицы от единиц, десятки от десятков и так далее.
От 3 единиц в уменьшаемом мы не можем отнять 5 единиц вычитаемого, поскольку 3<5. Поэтому, мы раскладываем соседние 6 десятков на 5 десятков и 1 десяток. Этот десяток содержит 10 единиц, которые мы складываем с 3 имеющимися в уменьшаемом единицами. Теперь у нас есть 13 единиц, и мы можем отнять от них 5, получим 8 единиц. Записываем их под чертой в разряде простых единиц, а над цифрой разряда десятков в уменьшаемом ставим одну точку, чтобы не забыть, что 1 десяток единиц мы оттуда уже забрали.
Переходим к десяткам. У уменьшаемого в разряде десятков мы уже забрали 1 десяток, о чем нам напоминает поставленная точка. Поэтому, мы отнимаем 2 десятка вычитаемого не от 6, а от 5 десятков, потому что 6-1=5.
5>2, значит, действие вычитания возможно: 5-2=3. Пишем цифру 3 под чертой в разряде десятков, и переходим к сотням.
Сотен в уменьшаемом у нас нет, поэтому мы смотрим, сколько в числе содержится тысяч? Их тоже 0. Смотрим следующий разряд. Здесь у нас 5 десятков тысяч. Из них мы берем 1 десяток тысяч (ставим точку над цифрой 5 в уменьшаемом), что составляет 10 тысяч единиц. Из них (из взятых в десятках тысячах) мы занимаем 1 тысячу для того, чтобы закончить вычитание в разряде сотен (ставим точку над цифрой 0 в разряде тысяч уменьшаемого).
1 тысяча единиц – это 10 сотен. Кроме этих занятых, больше в уменьшаемом сотен нет. В вычитаемом 8 сотен, поэтому находим разность сотен уменьшаемого и вычитаемого: 10-8=2. Пишем результат под чертой в разряде сотен.
В разряде тысяч уменьшаемого у нас осталось 9 тысяч единиц (потому что 1 тысячу мы отдали для разряда сотен в качестве 10 сотен). Отнимаем от нее 4 тысячи вычитаемого, получаем: 9-4=5, которые записываем под чертой в разряде тысяч.
Десятков тысяч в уменьшаемом осталось 5-1=4 (помните, мы для разряда сотен занимали?), в вычитаемом их нет совсем, то есть, 0. Поэтому мы просто сносим цифру 4 в результат под черту в разряд десятков тысяч.
После нахождения разности чисел способом вычитания в столбик записываем ответ в строчном примере:
50063-4825 = 45238.
Как проверить действия сложение и вычитание?
После того, как вы закончили арифметическое действие, нужно проверить правильность ответа, то есть, удостовериться, что вычисление было сделано без ошибок.
Проверить сложение можно двумя способами: обратным сложением и вычитанием.
Обратное сложение означает, что мы меняем слагаемые местами, и складываем их еще раз. Если результат будет такой же, как и после первого сложения, значит, вычисление было верным.
Например, в уроке сложение чисел мы находили сумму: 5728+803 = 6531. Проверим правильность результата способом обратного сложения:
Как видите, сложив слагаемые в другом порядке, мы получили тот же самый результат, а значит, вычисление было правильным.
Проверка сложения вычитанием – это способ, при котором нужно из суммы, которую получили после выполнения действия сложение, отнять одно из слагаемых. Если результат этого вычитания будет равен второму слагаемому (или сумме остальных слагаемых, если их больше двух), значит сложение было выполнено верно.
Проверим эту же сумму вычитанием: отнимем от результата 6531 слагаемое 5728.
И этот способ проверки показал правильность нашего решения.
Проверить вычитание также возможно и сложением, и другим вычитанием.
Проверка вычитания сложением основана на взаимосвязи вычитания и сложения. Зная, что уменьшаемое – это сумма, а остаток и вычитаемое – это слагаемые, мы можем сложить между собой вычитаемое и остаток, и, если получим в результате уменьшаемое, значит, мы правильно сделали действие.
Вот так выглядит проверка вычитания сложением на примере вычисленной на этом уроке разницы 50063-4825 = 45238:
Проверка вычитания вычитанием также основывается на взаимосвязи вычитания и сложения, а также на переместительном законе сложения. Так как уменьшаемое – это сумма двух слагаемых: вычитаемого и остатка, и сумма не зависит от порядка сложения слагаемых, то очевидно, что мы можем отнять от уменьшаемого остаток. Если результат этого действия будет равен вычитаемому, значит наша первая разность вычислена верно.
Проверка той же самой разницы вычитанием: