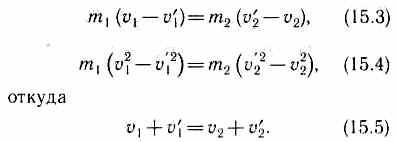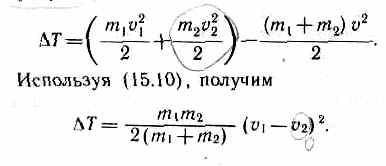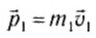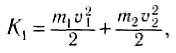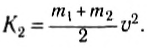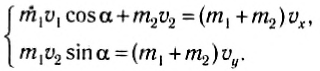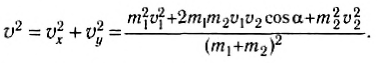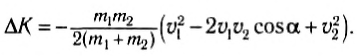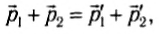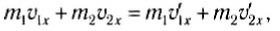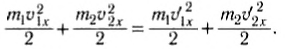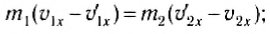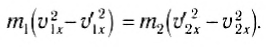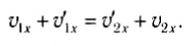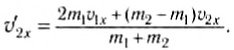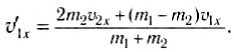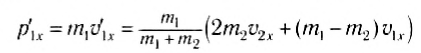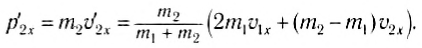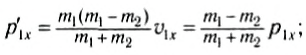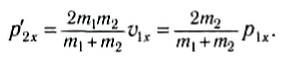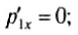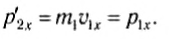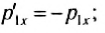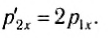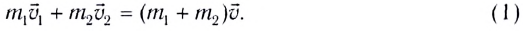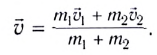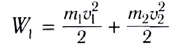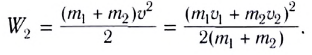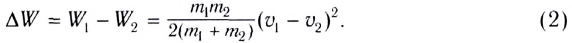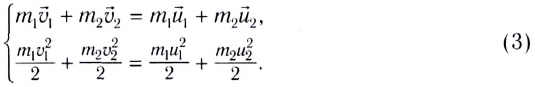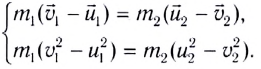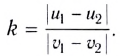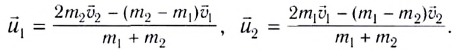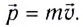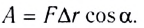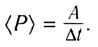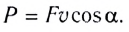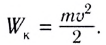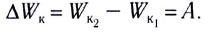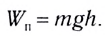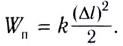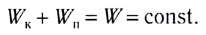Начиная с определений импульса и объяснения законов сохранения, в статье показывается способ решения ряда задач, в которых важно только начальное и конечное состояние (но, например, ничего нельзя сказать про время движения), в частности, задач на столкновение тел.
Введение
С помощью законов сохранения многие механические задачи решаются намного проще, чем при использовании динамических уравнений движений. С другой стороны, законами сохранения можно пользоваться только в тех случаях, когда необходимо, зная начальное состояние тела, найти конечное. При данном описании системы невозможно узнать время движения тела и все промежуточные состояния.
Для лучшего понимания темы различных соударений давайте еще раз повторим теорию по законам сохранения в механике.
Самыми распространенными законами сохранения является закон сохранения импульса и энергии.
Импульс
Определение. Импульсом p тела (материальной точки) называется векторная физическая величина, равная произведению массы m на скорость (здесь и далее жирным шрифтом выделены векторные величины).
p = mv.
Изменение импульса можно представить через второй закон Ньютона:
Δp = mΔv = FΔt
Если рассмотреть систему материальных точек, которые движутся с разными скоростями, то импульс задается следующим выражением:
p = m₁v₁+ m₂v₂ + …
Закон сохранения импульса
При отсутствии внешних сил импульс системы материальных точек сохраняется.
Замечание 1. Отсутствие внешних сил означает, что система замкнута.
Замечание 2. Часто в задачах есть внешние силы, но при этом законом сохранения импульса в каком-то виде пользоваться можно.
- Внешние силы есть, но они взаимно скомпенсированы (например сила тяжести и сила нормальной реакции опоры при движении по гладкой поверхности).
- Внешние силы не имеют проекции на какую-то заданную ось (например, ось ОX), тогда импульс может сохраняться вдоль этого направления.
- Если в некоторый момент времени внутренние силы много больше внешних, тогда импульс системы сохраняется (например, разрыв снаряда)
Так как задачи только на закон сохранения достаточно однообразные, то рассмотрим и закон сохранения энергии.
Работа и энергия
Любая механическая система характеризуется скалярной величиной E — энергией, которая однозначно определяет состояние системы. Зная энергию системы в двух состояниях, можно найти работу внешних сил, совершенную над системой:
ΔE = E₂ – E₁ = A.
Механическая работа
Определение. Если на тело, движущееся по прямой, действует постоянная сила F, то механической работой A этой силы на перемещение s называется скалярное произведение
A = (F, s) = |F||s| · cos(α) = Fs · cos(α),
где α — угол между векторами F и s.
Определение. Средняя мощность <P> силы F — это отношение работы А, совершенной силой F за время t, к интервалу времени t.
<P> = A / t.
Мощность также можно переписать так: <P> = Fv · cos(α).
Консервативные и диссипативные силы
Определение.Консервативные силы (потенциальные силы) —это силы, работа которых при перемещении из состояния 1 в состояние 2 не зависит от траектории, а зависит только от начального и конечного положения точек 1 и 2.
Примеры.Работа силы тяжести или электростатических сил не зависит от траектории, следовательно, это консервативные силы.
К диссипативным силам относятся различные виды силы трения.
Замечание. Работа диссипативных сил всегда отрицательна. Следовательно, они уменьшают механическую энергию тела, переводя ее в тепло.
Кинетическая и потенциальная энергия
Определение. Кинетическая энергия тела равна произведению массы тела на квадрат скорости, деленное на два:
Eкин = mv² / 2.
Так как работа консервативных сил зависит только от начального и конечного положения, то для нее можно определить потенциальную энергию.
Потенциальная энергия для силы тяжести определяется следующим выражением:
Eпот = mgh.
Замечание. Для силы тяжести можно легко вывести потенциальную энергию, зная работу силы притяжения.
Другие примеры.Зная силу растяжения или сжатия пружины, легко посчитать потенциальную энергию сжатой (растянутой) пружины:
Eпот = k(x₂ – x₁)² / 2.
Закон сохранения и изменения энергии
Формулировка. Механическая энергия в замкнутой системе сохраняется при отсутствии диссипативных сил:
ΔE = 0
Замечание 1. Механической энергией называется сумма потенциальной и кинетической энергии.
E = Eкин + Епот.
Замечание 2.При наличии консервативных сил может меняться скорость тела (системы тел) и их общая кинетическая энергия, но это будет происходить за счет перехода кинетической энергии в потенциальную.
Формулировка. Изменение механической энергии под действием внешних и внутренних неконсервативных сил равно суммарной работе этих сил А:
ΔE = A.
Теорема об изменении кинетической энергии
Формулировка. Работа всех сил (консервативных и диссипативных) равна изменению кинетической энергии системы.
∑A = ΔEкин.
Замечание. С помощью этой теоремы легко решать многие задачи. Например, рассмотрим задачу о нахождении тормозного пути автомобиля, движущегося со скоростью v = 60 км/ч по дороге с коэффициетом трения μ = 0,5.
Работа силы трения:
A = –μN = –μmgS,
где N — сила нормальной реакции, S — тормозной путь автомобиля.
Изменение кинетической энергии:
ΔE = –mv² / 2.
По теореме о изменении кинетической энергии:
–mv² / 2 = –μmgS.
S = v² / 2gμ = 29 м
Замечание.Скорость необходимо перевести в СИ.
Соударения
Определение. Центральный удар — это соударение 2 тел , при котором скорости каждого из тел направлены вдоль линии, соединяющей центры обоих тел.
Замечание. Если один из шаров покоится, то скорость второго тела должна быть направлена вдоль линии, соединяющей центры тел.
При решении задач на столкновение двух и более тел надо привыкнуть к следующим формулировкам:
- Абсолютно упругий удар (упругий удар) — это тип соударения, при котором выполняется закон сохранения энергии и закон сохранения импульса. Часто этот тип соударения применим к железным шарикам.
- Неупругий удар — это удар, при котором выполняется закон сохранения импульса и закон изменения механической энергии (так как теряется часть энергии при ударе).
- Абсолютно неупругий удар — это удар, при котором два тела продолжают двигаться как единое целое. При этом столкновении выполняется закон сохранения импульса и закон изменения механической энергии.
Замечание. Как мы видим, для решения задач нужно сначала записать соответствующие законы сохранения энергии и импульса или изменения энергии. Далее необходимо решить получившуюся систему уравнений.
Задача 1
Железный шар массы m = 500 г движется по гладкой горизонтальной поверхности со скоростью 10 м/с и сталкивается с неподвижным восковым шаром, имеющим массу М = 200 г, после чего оба шара движутся вместе. Найдите количество теплоты, выделившееся при ударе.
Решение. В этой задаче удар абсолютно неупругий, поэтому выполняется закон сохранения импульса (ЗСИ) и изменения энергии.
Запишем ЗСИ на ось OX:
mv = (m + M)V. (1)

Для того, чтобы найти выделившуюся энергию при соударении, необходимо записать закон изменения энергии (ЗИЭ)
ΔE = mv² / 2 — (m + M)V² / 2. (2)
Далее остается только математическая часть задачи — решить систему уравнений (1) и (2). Из (1) найдем V:
V = mv / (M + m).
Подставив в (2), получим:

Замечание. Такую задачу невозможно решить для неупругого удара, при котором тела не слипаются друг с другом, так как нам будет неизвестны скорости двух разлетевшихся тел.
Список литературы
- Белолипецкий С. Н., Еркович О. С., Казаковцева В. А., Цвецинская Т. С. Задачник по физике. М., 2005.
- Черноуцан А. Учебно-справочное пособие для старшеклассников и абитуриентов. М., 2000.
§6. Задачи на столкновения и законы сохранения импульса и энергии
В физике под столкновениями понимают процессы взаимодействия между телами (частицами) в широком смысле слова, а не только в буквальном — как соприкосновение тел. Сталкивающиеся тела на большом расстоянии являются свободными. Проходя друг мимо друга, тела взаимодействуют между собой, в результате могут происходить различные процессы — тела могут соединиться в одно тело (абсолютно неупругий удар), могут возникать новые тела и, наконец, может иметь место упругое столкновение, при котором тела после некоторого сближения вновь расходятся без изменения своего внутреннего состояния. Столкновения, сопровождающиеся изменением внутреннего состояния тел, называются неупругими. Тела (частицы), участвующие в столкновении, характеризуются (до и после столкновения) импульсами и энергиями. Процесс столкновения сводится к изменению этих величин в результате взаимодействия. Законы сохранения энергии и импульса позволяют достаточно просто устанавливать соотношения между различными физическими величинами при столкновении тел. Особенно ценным здесь является то обстоятельство, что зачастую законы сохранения могут быть использованы даже в тех случаях, когда действующие силы неизвестны. Так обстоит дело, например, в физике элементарных частиц.
Происходящие в обычных условиях столкновения макроскопических тел почти всегда бывают в той или иной степени неупругими – уже хотя бы потому, что они сопровождаются некоторым нагреванием тел, т. е. переходом части их кинетической энергии в тепло. Тем не менее, в физике понятие об упругих столкновениях играет важную роль. С такими столкновениями часто приходится иметь дело в физическом эксперименте в области атомных явлений, да и обычные столкновения можно часто с достаточной степенью точности считать упругими.
Сохранение импульса тел (частиц) при столкновении обусловлено тем, что совокупность тел, участвующих в столкновении, составляет либо изолированную систему, т. е. на тела, входящие в систему, не действуют внешние силы, либо замкнутую: внешние силы отличны от нуля, а сумма внешних сил равна нулю. Несколько сложнее обстоит дело с применением закона сохранения энергии при столкновениях. Обращение к сохранению энергии требует порой учёта различных форм внутренней энергии.
Можно сказать, что действие законов сохранения импульса и энергии в процессах столкновения подтверждено широким спектром опытных данных.
Неупругие столкновения
Два куска пластилина массами `m_1` и `m_2`, летящие со скоростями `vecv_1` и `vecv_2` слипаются. Найдите наибольшее `Q_max` и наименьшее количество `Q_min` теплоты, которое может выделиться в результате абсолютно неупругого соударения.
Рассмотрим абсолютно неупругое соударение («слипание») тел, движущихся в ЛСО скоростями `vecv_1` и `vecv_2` соответственно. В процессе абсолютно неупругого соударения импульс системы сохраняется.
`m_1vecv_1+m_2vecv_2=(m_1+m_2)vecv`.
Отсюда находим скорость составного тела
`vecv=(m_1vecv_1+m_2vecv_2)/(m_1+m_2)`.
Закон сохранения энергии принимает вид
`(m_1vecv_1^2)/2+(m_2vecv_2^2)/2=((m_1+m_2)*vecv)/2+Q`.
Из приведенных соотношений находим убыль кинетической энергии
`Q=(m_1*m_2*(vecv_2-vecv_1)^2)/(2(m_1+m_2))=1/2 mu(vecv_2-vecv_1)^2`,
здесь `mu=(m_1m_2)/(m_1+m_2)` — приведенная масса системы тел.
Итак, при абсолютно неупругом соударении во внутреннюю энергию переходит кинетическая энергия тела приведенной массы, движущегося с относительной скоростью.
Убыль механической энергии достигает наибольшей величины
`Q_max=(m_1*m_2*(vecv_2-vecv_1)^2)/(2(m_1+m_2))=1/2 mu(v_1+v_2)^2`
при `vecv_1 uarr darr vecv_2`.
Убыль механической энергии будет наименьшей
`Q_min=(m_1*m_2*(vecv_2-vecv_1)^2)/(2(m_1+m_2))=1/2 mu(v_2-v_1)^2`
при `vecv_1 uarr uarr vecv_2`.
Упругие столкновения
На гладкой горизонтальной поверхности лежит гладкая шайба массой `M`. На него налетает гладкая шайба массой `m`, движущийся со скоростью `vec v`. Происходит упругий центральный удар шайб. Найдите скорости `vecv_1` и `vecv_2` шайб после соударения. При каком условии налетающая шайба будет двигаться после соударения в прежнем направлении?
Задачу рассмотрим в ЛСО, ось `Ox` которой направим по линии центров шайб в момент соударения. Внешние силы, действующие на шайбы в процессе соударения, это силы тяжести и силы нормальной реакции опоры. Их сумма равна нулю. Следовательно, импульс системы шайб в процессе взаимодействия не изменяется. По закону сохранения импульса `m vec v = m vecv_1 + M vecv_2`.
Переходя к проекциям на ось `Ox`, получаем `mv = mv_(1x) + Mv_2`, здесь учтено, что направление скорости `vecv_1` налетающей шайбы после соударения не известно. По закону сохранения энергии
`(mv^2)/2 = (mv_(1x)^2)/2 + (Mv_2^2)/2`.
Полученные соотношения перепишем в виде
`m(v — v_(1x)) = Mv_2`,
`m(v^2 — v_(1x)^2) = Mv_2^2`.
Разделив второе равенство на первое `(v != v_(1x))`, приходим к линейной системе `v_2 = v + v_(1x)`, `m(v — v_(1x)) = Mv_2`, решение которой имеет вид
`v_(1x) = (m — M)/(m + M) v`, `v_2 = (2m)/(m + M) v`.
Налетающая шайба будет двигаться после соударения в прежнем направлении `(v_(1x) > 0)` при `m > M`, т. е. если масса налетающей шайбы больше массы покоящейся шайбы.
Две гладкие упругие круглые шайбы движутся поступательно по гладкой горизонтальной поверхности со скоростями `vecv_1` и `vecv_2`. Найдите скорости `vecv_1^’` и `vecv_2^’` шайб после абсолютно упругого нецентрального соударения. Массы шайб `m_1` и `m_2`.
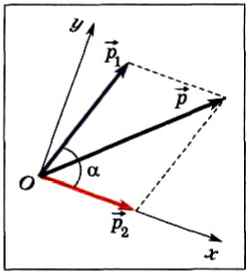
Задачу рассмотрим в ИСО, оси координат `Ox` и `Oy` которой лежат в горизонтальной плоскости, при этом ось `Ox` направлена по линии центров шайб в момент соударения (рис. 16).
В течение времени соударения на систему шайб действуют только вертикальные внешние силы: это силы тяжести и силы нормальной реакции. Их сумма равна нулю. Тогда импульс системы шайб в процессе взаимодействия сохраняется
`vecp_1 + vecp_2 = vecp_1^’ + vecp_2^’`,
здесь `vecp_1 = m_1 vecv_1`, `vecp_2 = m_2 vecv_2`, `vecp_1^’ = m_1 vecv_1^’`, `vecp_2^’ = m_2 vecv_2^’` — импульсы шайб до и после соударения.
Так как шайбы идеально гладкие, то в процессе соударения внутренние силы -силы упругого взаимодействия — направлены только по оси `Ox`. Эти силы не изменяют `y`-составляющие импульсов шайб. Тогда из `p_(1y) = p_(1y)^’`, `p_(2y) = p_(2y)^’` находим `y`-составляющие скоростей шайб после соударения
`vecv_(1y)^’ = v_(1y)`, `v_(2y)^’ = v_(2y)`,
т. е. в проекции на ось `Oy` скорости шайб в результате соударения не изменились.
Найдём `x`-составляющие скоростей шайб после упругого соударения. При таком соударении сохраняется кинетическая энергия
`(m_1 (v_(1x)^2 + v_(1y)^2))/2 + (m_2 (v_(2x)^2 + v_(2y)^2))/2 = (m_1 ((v_(1x)^’)^2 + (v_(1y)^’)^2))/2 + (m_2 ((v_(2x)^’)^2 + (v_(2y)^’)^2))/2`.
С учётом равенства `y`-составляющих скоростей шайб до и после соударения последнее равенство принимает вид
`(m_1 v_(1x)^2)/2 + (m_2 v_(2x)^2)/2 = (m_1 (v_(1x)^’)^2)/2 + (m_2 (v_(2x)^’)^2)/2`.
Обратимся к закону сохранения импульса и перейдём к проекциям импульсов шайб на ось `Ox`
`m_1 v_(1x) + m_2 v_(2x) = m_1 v_(1x)^’ + m_2 v_(2x)^’`.
Таким образом, исходная задача сведена к задаче об абсолютно упругом центральном ударе: именно такой вид приняли бы законы сохранения энергии и импульса, если бы скорости шайб были направлены по линии центров. Полученную нелинейную систему уравнений можно свести к линейной. Для этого следует (как и в предыдущей задаче) в обоих уравнениях по одну сторону знака равенства объединить слагаемые, относящиеся к первой шайбе, а по другую — ко второй, и разделить `(v_(1x) != v_(1x)^’)` полученные соотношения. Это приводит к линейному уравнению
`v_(1x) + v_(1x)^’ = v_(2x) + v_(2x)^’`.
Решая систему из двух последних уравнений, находим
`v_(1x)^’ = ((m_1 — m_2) v_(1x) + 2m_2 v_(2x))/(m_1 + m_2)`,
`v_(2x)^’ = (2m_1 v_(1x) + (m_2 — m_1) v_(2x))/(m_1 + m_2)`.
Полученные соотношения для `v_(1x)^’`, `v_(1y)^’` и `v_(2x)^’`, `v_(2y)^’` решают вопрос о проекциях и величинах скоростей шайб после соударения
`v_1^’ = sqrt((v_(1x)^’)^2 + (v_(1y)^’)^2)`, `v_2^’ = sqrt((v_(2x)^’)^2 + (v_(2y)^’)^2)`,
а также об углах `alpha_1` и `alpha_2`, которые векторы скорости `vecv_1^’` и `vecv_2^’` образуют с положительным направлением оси `Ox`:
`bbb»tg» alpha_1 = (v_(1y)^’)/(v_(1x)^’)`, `bbb»tg» alpha_2 = (v_(2y)^’)/(v_(2x)^’)`.
Построенное в общем виде решение задач упругого центрального и нецентрального соударений открывает дорогу к анализу целого ряда задач, для которых рассмотренная модель соответствует характеру взаимодействия тел (частиц).
Примером применения
законов сохранения импульса и энергии
при решении реальной физической
задачи является удар абсолютно упругих
и неупругих тел.
Удар
(или соударение)
—
это столкновение двух или более тел,
при котором взаимодействие длится очень
короткое время. Исходя из данного
определения, кроме явлений, которые
можно отнести к ударам в прямом смысле
этого слова
28
(столкновения
атомов или биллиардных шаров), сюда
можно отнести и такие, как удар человека
о землю при прыжке с трамвая и т. д. При
ударе в телах возникают столь
значительные внутренние силы, что
внешними силами, действующими на
них, можно пренебречь. Это позволяет
рассматривать соударяющиеся тела
как замкнутую систему и применять к ней
законы сохранения.
Тела
во время удара претерпевают деформацию.
Сущность удара заключается в том,
что кинетическая энергия относительного
движения соударяющихся тел на короткое
время преобразуется в энергию упругой
деформации. Во время удара имеет
место перераспределение энергии между
соударяющимися телами. Наблюдения
показывают, что относительная скорость
тел после удара не достигает своего
прежнего значения. Это объясняется
тем, что нет идеально упругих тел и
идеально гладких поверхностей.
Отношение нормальных составляющих
относительной скорости тел после и до
удара называется коэффициентом
восстановления :
=
v’n/vn.
Если
для сталкивающихся тел =0,
то такие тела называются абсолютно
неупругими, если
=1—абсолютно
упругими.
На
практике для всех тел 0<<1
(например, для стальных шаров 0,56,
для шаров из слоновой кости 0,89,
для свинца 0).
Однако в некоторых случаях тела можно
с большой точностью рассматривать либо
как абсолютно упругие, либо как
абсолютно неупругие.
Прямая,
проходящая через точку соприкосновения
тел и нормальная к поверхности их
соприкосновения, называется линией
удара. Удар
называется центральным,
если
тела до удара движутся вдоль прямой,
проходящей через их центры масс. Мы
будем рассматривать только центральные
абсолютно упругие и абсолютно
неупругие удары.
Абсолютно
упругий удар — столкновение
двух тел, в результате которого в обоих
взаимодействующих телах не остается
никаких деформаций и вся кинетическая
энергия, которой обладали тела до удара,
после удара снова превращается в
кинетическую энергию
.
Для абсолютно
упругого удара выполняются закон
сохранения импульса и закон сохранения
кинетической энергии.
Обозначим
скорости шаров массами m1
и
m2
до удара через v1
и
v2,
после
удара — через v’1
и
v’2
(рис.
18). При прямом центральном ударе
векторы скоростей шаров до и после удара
лежат на прямой линии, соединяющей их
центры. Проекции векторов скорости на
эту линию равны модулям скоростей. Их
направления учтем знаками: положительное
значение припишем движению вправо,
отрицательное — движению влево.
При указанных
допущениях законы сохранения имеют вид
Произведя
соответствующие преобразования в
выражениях (15.1) и (15.2), получим
Решая уравнения
(15.3) и (15.5), находим
Разберем несколько
примеров.
29
Проанализируем
выражения (15.8) и (15.9) для двух шаров
различных масс:
а) m1
=m2.
Если
второй шар до удара висел неподвижно
(v2=0)
(рис.
19), то после удара остановится первый
шар (v’1=0),
а второй будет двигаться с той же
скоростью и в том же направлении, в
котором двигался первый шар до удара
(v’2
= v1);
б)
m1>m2.
Первый
шар продолжает двигаться в том же
направлении, как и до удара, но с меньшей
скоростью (v’1<v1).
Скорость
второго шара после удара больше, чем
скорость первого после удара (v’2>v’1)
(рис.20);
в)
m1<m2.
Направление
движения первого шара при ударе изменяется
— шар отскакивает обратно. Второй шар
движется в ту же сторону, в которую
двигался первый шар до удара, но с меньшей
скоростью, т.е. v’2<v1
(рис.
21);
г)
m2>>m1
(например,
столкновение шара со стеной). Из уравнений
(15.8) и (15.9) следует, что v’1=-v1,
v’22m1v1/m20.
2) При
m1=m2
выражения
(15.6) и (15.7) будут иметь вид
v’1=v2,
v’2=v1,
т. е. шары равной
массы «обмениваются» скоростями.
Абсолютно
неупругий удар — столкновение
двух тел, в результате которого тела
объединяются, двигаясь дальше как единое
целое.
Продемонстрировать
абсолютно неупругий удар можно с
помощью шаров из пластилина (глины),
движущихся навстречу друг другу (рис.
22).
Если
массы шаров m1
и
m2,
их скорости до удара v1
и
v2,
то,
используя закон сохранения импульса,
можно записать
Если
шары движутся навстречу друг другу, то
они вместе будут продолжать двигаться
в ту сторону, в которую двигался шар,
обладающий большим импульсом. В частном
случае если массы шаров равны (m1=m2),
то
v
= (v1+v2)/2.
Выясним, как
изменяется кинетическая энергия
шаров при центральном абсолютно
неупругом ударе. Так как в процессе
соударения шаров между ними дей-
30
ствуют силы,
зависящие не от самих деформаций, а от
их скоростей, то мы имеем дело с силами,
подобными силам трения, поэтому закон
сохранения механической энергии не
должен соблюдаться. Вследствие деформации
происходит «потеря» кинетической
энергии, перешедшей в тепловую или
другие формы энергии. Эту «потерю» можно
определить по разности кинетической
энергии тел до и после удара:
Если
ударяемое тело было первоначально
неподвижно (v2=0),
то
Когда
m2>>m1
(масса
неподвижного тела очень большая), то
v<<v1
и
почти
вся кинетическая энергия тела при ударе
переходит в другие формы энергии.
Поэтому, например, для получения
значительной деформации наковальня
должна быть массивнее молотка.
Наоборот, при забивании гвоздей в стену
масса молотка должна быть гораздо
большей (m1>>m2),
тогда
vv1
и
практически вся энергия затрачивается
на возможно большее перемещение гвоздя,
а не на остаточную деформацию стены.
Абсолютно неупругий
удар — пример того, как происходит
«потеря» механической энергии под
действием диссипативных сил.
Контрольные
вопросы
• В чем различие
между понятиями энергии и работы?
• Как найти
работу переменной силы?
• Какую работу
совершает равнодействующая всех сил,
приложенных к телу, равномерно движущемуся
по окружности?
• Что такое
мощность? Вывести ее формулу.
• Дайте определения
и выведите формулы для известных вам
видов механической энергии. • Какова
связь между силой и потенциальной
энергией?
• Почему изменение
потенциальной энергии обусловлено
только работой консервативных сил?
• В чем заключается
закон сохранения механической энергии?
Для каких систем он выполняется?
• Необходимо
ли условие замкнутости системы для
выполнения закона сохранения механической
энергии?
• В чем физическая
сущность закона сохранения и превращения
энергии? Почему он является фундаментальным
законом природы?
• Каким свойством
времени обусловливается справедливость
закона сохранения механической энергии?
• Что такое
потенциальная яма? потенциальный барьер?
• Какие заключения
о характере движения тел можно сделать
из анализа потенциальных кривых?
• Как
охарактеризовать положения устойчивого
и неустойчивого равновесия? В чем их
различие?
• Чем отличается
абсолютно упругий удар от абсолютно
неупругого?
• Как определить
скорости тел после центрального абсолютно
упругого удара? Следствием каких законов
являются эти выражения?
31
Задачи
3.1. Определить:
1) работу поднятия груза по наклонной
плоскости; 2) среднюю и 3) максимальную
мощности подъемного устройства, если
масса груза 10 кг, длина наклонной
плоскости 2 м, угол ее наклона к горизонту
45°, коэффициент трения 0,1 и время подъема
2 с. [1) 170 Дж; 2) 85 Вт; 3) 173 Вт |
3.2. С башни высотой
35 м горизонтально брошен камень массой
0,3 кг. Пренебрегая сопротивлением
воздуха, определить: 1) скорость, с которой
брошен камень, если через 1 с после начала
движения его кинетическая энергия 60
Дж; 2) потенциальную энергию камня через
1 с после начала движения. [1) 17,4 м/с; 2)
88,6 Дж ]
3.3. Пренебрегая
трением, определить наименьшую высоту,
с которой должна скатываться тележка
с человеком по желобу, переходящему в
петлю радиусом 10 м, чтобы она сделала
полную петлю и не выпала из желоба. [25
м]
3.4.
Пуля массой m=
10 г, летевшая горизонтально со скоростью
v
= 500 м/с, попадает в баллистический
маятник длиной l=
1 м и массой М = 5 кг и застревает в нем.
Определить угол отклонения маятника.
[ 18°30′ ]
3.5.
Зависимость потенциальной энергии
частицы в центральном силовом поле от
расстояния r
до
центра
поля задается выражением П(r)
=A/r2
-B/r,
где А
и
В —
положительные постоянные.
Определить
значение r0,
соответствующее
равновесному положению частицы. Является
ли это положение положением устойчивого
равновесия? [r0
= 2А/В]
3.6.
При центральном абсолютно упругом ударе
движущееся тело массой m1
ударяется
в покоящееся тело массой m2,
в результате чего скорость первого тела
уменьшается в n=
1,5 раза. Определить: 1) отношение m1/m2;
2)
кинетическую энергию T’2,
с
которой начнет двигаться второе
тело, если первоначальная кинетическая
энергия первого тела T1
=
1000 Дж. [ 1) 5; 2) 555 Дж ]
3.7.
Тело массой m1=4
кг движется со скоростью v1=3
м/с
и ударяется о неподвижное тело такой
же массы. Считая удар центральным и
неупругим, определить количество
теплоты, выделившееся при ударе. [9 Дж ]
* У. Гамильтон
(1805—1865) — ирландский математик и
физик.
Соседние файлы в папке Трофимова
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Условие задачи:
Найти количество теплоты, выделившееся при лобовом абсолютно неупругом ударе двух свинцовых шаров массой 1 кг каждый, скользящих без вращения по абсолютно гладкой поверхности. До удара шары двигались по одной прямой в одном направлении. Скорость первого шара равна 10 см/с, скорость второго – 20 см/с.
Задача №2.10.3 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
(m=1) кг, (upsilon_1=10) см/с, (upsilon_2=20) см/с, (Q-?)
Решение задачи:
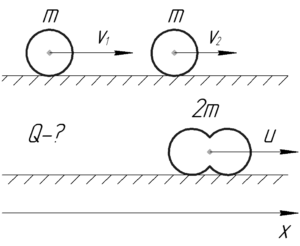
- закон сохранения импульса (ЗСИ) в проекции на ось (x), поскольку система, состоящая из двух шаров замкнута в этом направлении;
- закон сохранения энергии (ЗСЭ), но учтем, что часть начальной кинетической энергии шаров при абсолютно неупругом ударе переходит в теплоту (Q).
[left{ begin{gathered}
m{upsilon _1} + m{upsilon _2} = 2mu hfill \
frac{{mupsilon _1^2}}{2} + frac{{mupsilon _2^2}}{2} = frac{{2m{u^2}}}{2} + Q hfill \
end{gathered} right.]
Из ЗСИ выразим скорость шаров после удара:
[u = frac{{{upsilon _1} + {upsilon _2}}}{2}]
Полученное выражение подставим в ЗСЭ:
[frac{{mupsilon _1^2}}{2} + frac{{mupsilon _2^2}}{2} = frac{{2m}}{2}{left( {frac{{{upsilon _1} + {upsilon _2}}}{2}} right)^2} + Q]
Раскроем квадрат суммы в правой части уравнения:
[frac{{mupsilon _1^2}}{2} + frac{{mupsilon _2^2}}{2} = frac{{2m}}{2}left( {frac{{upsilon _1^2 + 2{upsilon _1}{upsilon _2} + upsilon _2^2}}{4}} right) + Q]
Откроем скобки:
[frac{{mupsilon _1^2}}{2} + frac{{mupsilon _2^2}}{2} = frac{{mupsilon _1^2}}{4} + frac{{m{upsilon _1}{upsilon _2}}}{2} + frac{{mupsilon _2^2}}{4} + Q]
[Q = frac{{mupsilon _1^2}}{4} – frac{{m{upsilon _1}{upsilon _2}}}{2} + frac{{mupsilon _2^2}}{4} = frac{m}{4}left( {upsilon _1^2 – 2{upsilon _1}{upsilon _2} + upsilon _2^2} right)]
[Q = frac{m}{4}{left( {{upsilon _1} – {upsilon _2}} right)^2}]
Получилась “красивая” формула для расчета ответа. Переведем скорости в единицы системы СИ.
[10; см/с = frac{{10}}{{100}}; м/с = 0,1; м/с]
[20; см/с = frac{{20}}{{100}}; м/с = 0,2; м/с]
Считаем ответ:
[Q = frac{1}{4}{left( {0,1 – 0,2} right)^2} = 2,5 cdot 10^{-3}; Дж = 2,5; мДж]
Ответ: 2,5 мДж.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.10.2 Тележка массой 100 кг движется со скоростью 2 м/с. Когда она проезжает мимо
2.10.4 Охотник стреляет из ружья. Определить силу отдачи, если масса дроби 35 г
2.10.5 Шары массами 1 и 2 кг движутся навстречу друг другу. Скорость первого шара 5 м/с
Содержание:
Столкновения:
Наиболее общим явлением, наблюдаемым в природе, является взаимодействие материальных тел. Бильярдные шары, сближаясь, в момент соприкосновения взаимодействуют друг с другом. В результате этого меняются скорости шаров, их кинетические энергии. О таком взаимодействии шаров говорят как об их столкновениях.
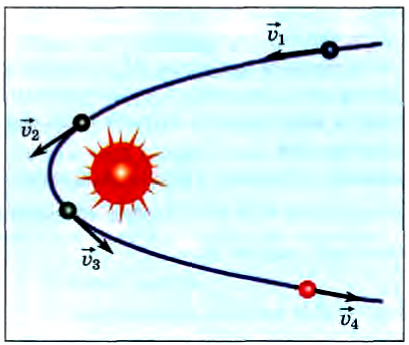
Но понятие «столкновение» относится не только к взаимодействиям, происходящим в результате соприкосновения материальных тел. Комета, прилетевшая из отдаленных областей пространства и прошедшая в окрестности Солнца, меняет свою скорость и удаляется. Этот процесс также является столкновением. хотя непосредственного соприкосновения между кометой и Солнцем не произошло, а осуществлено оно было посредством сил тяготения.
Характерная особенность этого взаимодействия, дающая нам возможность рассматривать его как столкновение, заключается в том, что область пространства, в котором оно произошло, относительно мала. Заметное изменение скорости кометы происходит вблизи Солнца (рис. 129).
Приведенные примеры позволяют нам дать следующее определение столкновения.
Что такое столкновение
Столкновением называется взаимодействие двух и большего числа тел, которое происходит в относительно малой области пространства в течение относительно малого промежутка времени. Вне этого промежутка времени можно говорить о начальных и конечных импульсах тел, когда тела можно считать невзаимодействующими.
Столкновение материальных тел часто называется ударом. Удар определяется как процесс, при котором изменяются импульсы соударяющихся тел без существенного изменения их положений. Это частный случай столкновения, например столкновение шаров, шайб, автомобилей и т. п.
Процессы столкновения являются чрезвычайно сложными. Например, при столкновении двух шаров в момент их соприкосновения начинается деформация шаров. В результате часть кинетической энергии переходит в потенциальную энергию деформации. Затем энергия деформации снова превращается в кинетическую, однако не полностью — часть энергии превращается во внутреннюю. Кроме того, после столкновения шары будут вращаться по иному, чем до столкновения.
Главный интерес при рассмотрении столкновений заключается в знании не самого процесса, а результата. Ситуация до столкновения называется начальным состоянием, а после — конечным. Между величинами, характеризующими начальное и конечное состояния, соблюдаются определенные соотношения. независящие от детального характера взаимодействия. Такими величинами. в частности, являются импульс и энергия системы тел.
В зависимости от характера изменения кинетической энергии тел все столкновения делятся на упругие и неупругие.
Если при столкновении кинетическая энергия тел сохраняется, то столкновение называется упругим, если же не сохраняется — неупругим.
Рассмотрим вначале абсолютно неупругое столкновение (абсолютно неупругий удар). Это частный случай неупругого столкновения, при котором после столкновения тела «слипаются» и движутся вместе.
Пусть в некоторой инерциальной системе отсчета первое тело массой m1 движется до столкновения со скоростью υ1, а второе тело массой m2 — со скоростью υ2. Следовательно, импульсы тел до столкновения равны соответственно:
Процесс столкновения обычно наглядно представляют с помощью векторной диаграммы импульсов (рис. 130). Нетрудно убедиться, что кинетическая энергия системы не сохраняется. До столкновения она составляет:
после столкновения —
Изменение кинетической энергии:
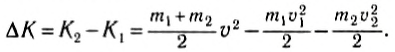
Для расчета выберем оси координат так, как показано на рисунке 130, и спроектируем на них равенство (1). B результате получим:
Рис. 130
Отсюда легко находится квадрат скорости тел после столкновения:
Подставив полученное выражение в (2), получим после несложных преобразований:
Как видно, кинетическая энергия системы уменьшилась. Часть кинетической энергии превратилась в теплоту.
Если тела при столкновении не «слипаются», то скорости тел после столкновения можно найти из закона сохранения импульса:
где штрихом отмечены импульсы тел после столкновения.
При этом кинетическая энергия может как уменьшаться, так и увеличиваться. Последнее происходит, например, при различных взрывах. В этом случае часть внутренней энергии превращается в кинетическую энергию осколков.
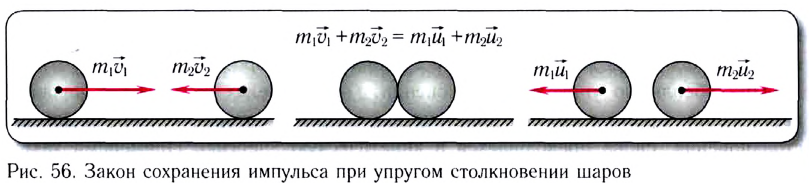
Как уже отмечалось, при упругом столкновении выполняется закон сохранения импульса и механической энергии.
Рассмотрим вначале лобовое столкновение, т. е. такое столкновение, при котором импульсы тел до и после столкновения параллельны некоторой прямой. Эту прямую мы примем за ось Ox (рис. 131). Закон сохранения импульса в этом случае примет вид:
а закон сохранения кинетической энергии —
Из этих уравнений найдем скорости тел после удара. Для этого перепишем (3) и (4) следующим образом:
Воспользовавшись тем, что a2 — b2 = (a-b)(a + b), из выражений (5) и (6) легко получить:
Выразив отсюда, например, 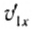
Аналогично:
Проекции импульсов тел после столкновения равны соответственно:
и
Проанализируем полученные выражения для некоторых частных случаев.
Предположим, что тело 2 до столкновения покоилось, т. е. 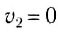
Тогда
При равных массах тел m1 = m2 получим:
Значит, первое тело остановится, а второе придет в движение с таким же импульсом.
Теперь предположим, что масса второго тела намного больше массы первого. Тогда, пренебрегая m1 по сравнению с m2 , получим:
Значит, первое тело отскочит назад с таким же по модулю импульсом, а тело 2 получит импульс, равный удвоенному значению импульса первого тела.
Найдем кинетическую энергию тел после столкновения для случая, когда 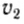
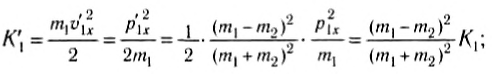
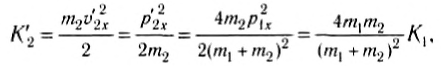
где K1 — кинетическая энергия первого тела до столкновения.
Из полученных выражений следует, что при m1 = m2 первое тело останавливается, а второе приобретает ту же энергию. Если масса второго тела m2 намного больше массы первого m1 то из (10) и (11) следует, что 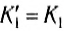
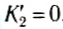
- Заказать решение задач по физике
Главные выводы:
- Столкновением называется взаимодействие двух и большего числа тел, которое происходит в относительно малой области пространства в течение относительно малого промежутка времени.
- Удар определяется как процесс, при котором изменяются импульсы соударяющихся тел без существенного изменения их положений.
- Столкновение тел называется упругим, если кинетическая энергия тел сохраняется. При неупругом столкновении кинетическая энергия тел не сохраняется.
- При столкновениях тел выполняется закон сохранения импульса.
Определение столкновения
Законы сохранения энергии и импульса позволяют провести теоретическое исследование процессов столкновения тел без описания сил, действующих между ними.
Под столкновениями понимают механические процессы взаимодействия между телами, происходящие за очень короткий промежуток времени. При этом силы взаимодействия между сталкивающимися телами настолько велики, что внешними силами, действующими на систему, можно пренебречь.
Вследствие того, что длительность столкновения мала по сравнению со временем наблюдения, различают механические состояния до и после столкновения, причем тела, находящиеся на большом расстоянии друг от друга, считают свободными.
Длительность столкновения бильярдных шаров 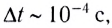
Различают упругие (абсолютно упругие) и неупругие столкновения. В первом случае не происходит выделения теплоты, и механическая энергия сохраняется. Во втором случае выделяется некоторое количество теплоты, поэтому механическая энергия после столкновения уменьшается.
Примером упругих столкновений служат столкновения металлических шаров, а примером неупругих — столкновения пластилиновых шаров, которые при этом слипаются и продолжают движение как одно целое.
Для макроскопических тел в большей степени характерными являются неупругие столкновения, в то время как для физики элементарных частиц, ядер атомов, молекул определяющую роль играет упругое взаимодействие.
Если в процессе столкновения тел на них не действуют внешние силы, то к телам применим закон сохранения импульса, а во многих случаях — и закон сохранения механической энергии. Именно эти законы позволяют, зная скорости тел до столкновения, определить их скорости после столкновения, совершенно не интересуясь тем, что происходило во время него.
При абсолютно неупругом столкновении скорости обоих взаимодействующих тел оказываются одинаковыми. Примером таких тел являются тела из различных пластичных веществ. Такое столкновение можно наблюдать, если подвесить тары из пластилина, развести их в разные стороны и отпустить. После столкновения они оба будут двигаться вместе с одинаковой скоростью.
При абсолютно упругом столкновении в обоих телах не остается никаких деформаций. Кроме того, вся кинетическая энергия, которой тела обладали до столкновения, снова превращается в кинетическую энергию. Примерами таких тел являются шары из стали или слоновой кости.
Рассмотрим простейшее столкновение — центральное, когда скорости тел находятся на линии, соединяющей их центры. Очень часто такое столкновение называют лобовым.
Скорость движения 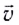
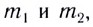
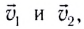
Откуда находим
Определим «потери» механической энергии, найдя кинетическую энергию
тел до столкновения:
и после столкновения:
Тогда часть механической энергии, перешедшая во внутреннюю, определяется выражением:
Следовательно, она зависит от масс сталкивающихся тел и относительной скорости 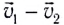
Задача о центральном абсолютно неупругом столкновении впервые была решена Дж. Валлисом в 1669 г.
При абсолютно упругом столкновении двух тел массами 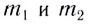
Здесь 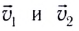
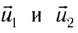
Преобразуем систему уравнений (3), перенеся в правую часть все величины, относящиеся к первому телу, а в левую — ко второму:
Разделив второе уравнение на первое, получим
Перепишем это уравнение в виде 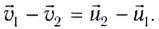
Из него следует, что при центральном абсолютно упругом столкновении тел любой массы их относительная скорость до и после столкновения не изменяется.
Теперь можно дать еще одно определение неупругого столкновения: если относительная скорость тел при центральном столкновении изменяется, то такое столкновение называется неупругим.
Меру неупругости k можно определить как отношение относительных скоростей сталкивающихся тел после и до столкновения:
Она называется коэффициентом восстановления и впервые была измерена Ньютоном в 1687 г. В частности, Ньютон получил значения коэффициента для стали k = 0,55 и стекла k = 0,94, которые приводят и современные справочники.
Абсолютно неупругим является столкновение, при котором скорости тел после столкновения равны 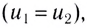
Решая уравнение (4) совместно с первым уравнением системы (3), находим скорости тел после столкновения:
На самом деле при столкновении всегда происходят «потери» механической энергии, т. е. переход части ее в теплоту. Но при малых «потерях» действительный процесс достаточно хорошо описывается абсолютно упругим столкновением.
Задача о центральном абсолютно упругом столкновении впервые была решена X. Гюйгенсом и К. Реном в 1669 г.
Отметим, что осуществить центральное, или лобовое, столкновение на практике очень трудно. Подавляющее число столкновений являются нецентральными.
Основные формулы
Импульс тела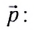
Закон изменения импульса системы тел:
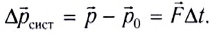
Закон сохранения импульса системы тел:
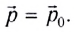
Работа:
Средняя мощность:
Мгновенная мощность:
Кинетическая энергия:
Теорема о кинетической энергии:
Потенциальная энергия:
Потенциальная энергия упруго деформированного тела:
Закон сохранения механической энергии:
- Рычаг в физике
- Блоки в физике
- Движение тела под действием нескольких сил
- Наклонная плоскость в физике
- Свободное падение тела
- Равнодействующая сила и движение тела под действием нескольких сил
- Сила давления в физике и единицы давления
- Механическое давление в физике