Как найти выходной резистор

Входное и выходное сопротивление является очень важным в электронике.

Предисловие

Ладно, начнем издалека… Как вы знаете, все электронные устройства состоят из блоков. Их еще часто называют каскады, модули, узлы и тд. В нашей статье будем использовать понятие «блок». Например, источник питания, собранный по этой схеме:

состоит из двух блоков. Я их пометил в красном и зеленом прямоугольниках.

В красном блоке мы получаем постоянное напряжение, а в зеленом блоке мы его стабилизируем. То есть блочная схема будет такой:

Блочная схема — это условное деление. В этом примере мы могли бы даже взять трансформатор, как отдельный блок, который понижает переменное напряжение одного номинала к другому. Как нам удобнее, так и делим на блоки нашу электронную безделушку. Метод «от простого к сложному» полностью работает в нашем мире. На низшем уровне находятся радиоэлементы, на высшем — готовое устройство, например, телевизор.

Ладно, что-то отвлеклись. Как вы поняли, любое устройство состоит из блоков, которые выполняют определенную функцию.

— Ага! Так что же получается? Я могу просто тупо взять готовые блоки и изобрести любое электронное устройство, которое мне придет в голову?

Да! Именно на это нацелена сейчас современная электроника Микроконтроллеры  и конструкторы, типа Arduino, добавляют еще больше гибкости в творческие начинания молодых изобретателей.

На словах все выходит прекрасно, но всегда есть подводные камни, которые следует изучить, чтобы начать проектировать электронные устройства. Некоторые из этих камушков называются входным и выходным сопротивлением.

Думаю, все помнят, что такое сопротивление и что такое резистор. Резистор хоть и обладает сопротивлением, но это активное сопротивление. Катушка индуктивности и конденсатор будут уже обладать, так называемым, реактивным сопротивлением. Но что такое входное и выходное сопротивление? Это уже что-то новенькое. Если прислушаться к этим фразам, то входное сопротивление — это сопротивление какого-то входа, а выходное — сопротивление какого-либо выхода. Ну да, все почти так и есть. И где же нам найти в схеме эти входные и выходные сопротивления?  А вот «прячутся» они в самих блоках радиоэлектронных устройств.

Входное сопротивление

Итак, имеем какой-либо блок. Как принято во всем мире, слева — это вход блока, справа — выход.

Как и полагается, этот блок используется в каком-нибудь радиоэлектронном устройстве и выполняет какую-либо функцию. Значит, на его вход будет подаваться какое-то входное напряжение U_вх от другого блока или от источника питания, а на его выходе появится напряжение U_вых (или не появится, если блок является конечным).

Но раз уж мы подаем напряжение на вход (входное напряжение U_вх), следовательно, у нас этот блок будет кушать какую-то силу тока I_вх.

Теперь самое интересное… От чего зависит I_вх ? Вообще, от чего зависит сила тока в цепи? Вспоминаем закон Ома для участка цепи :

Значит, сила тока у нас зависит от напряжения и от сопротивления. Предположим, что напряжение у нас не меняется, следовательно, сила тока в цепи будет зависеть от… СОПРОТИВЛЕНИЯ. Но где нам его найти?  А прячется оно в самом каскаде и называется входным сопротивлением.

То есть, разобрав такой блок, внутри него мы можем найти этот резистор? Конечно же нет). Он является своего рода сопротивлением радиоэлементов, соединенных по схеме этого блока. Скажем так, совокупное сопротивление.

Как измерить входное сопротивление

Как мы знаем, на каждый блок подается какой-либо сигнал от предыдущего блока или это может быть даже питание от сети или батареи. Что нам остается сделать?

1)Замерить напряжение U_вх, подаваемое на этот блок

2)Замерить силу тока I_вх, которую потребляет наш блок

3) По закону Ома найти входное сопротивление R_вх.

Если у вас входное сопротивление получается очень большое, чтобы замерить его как можно точнее, используют вот такую схему.

Мы  с вами знаем, что если входное сопротивление у нас большое, то входная сила тока в цепи у нас будет очень маленькая (из закона Ома).

Падение напряжения на резисторе R обозначим, как U_R

Из всего этого получаем…

Когда мы проводим эти измерения, имейте ввиду, что напряжение на выходе генератора не должно меняться!

Итак, давайте посчитаем, какой же резистор нам необходимо подобрать, чтобы как можно точнее замерять это входное сопротивление. Допустим, что у нас входное сопротивление R_вх=1 МегаОм, а резистор взяли  R=1 КилоОм. Пусть генератор выдает постоянное напряжение U=10 Вольт. В результате, у нас получается цепь с двумя сопротивлениями. Правило делителя напряжения гласит: сумма падений напряжений на всех сопротивлениях в цепи равняется ЭДС генератора.

В результате получается цепь:

 Высчитываем силу тока в цепи в Амперах

Получается, что падение напряжения на сопротивлении R в Вольтах будет:

Грубо говоря 0,01 Вольт. Вряд ли вы сможете точно замерить такое маленькое напряжение на своем китайском мультиметре.

Какой отсюда вывод? Для более точного измерения высокого входного сопротивления надо брать добавочное сопротивление также  очень большого номинала.  В этом случае работает правило шунта: на бОльшем сопротивлении падает бОльшее напряжение, и наоборот, на меньшем сопротивлении падает меньшее напряжение.

Измерение входного сопротивления на практике

Ну все, запарка прошла ;-). Давайте теперь на практике попробуем замерить входное сопротивление какого-либо устройства. Мой взгляд сразу упал на Транзистор-метр. Итак, выставляем на блоке питания рабочее напряжение этого транзистор-метра, то есть 9 Вольт, и во включенном состоянии замеряем потребляемую силу тока. Как замерить силу тока в цепи, читаем в этой статье. По схеме все это будет выглядеть вот так:

А на деле вот так:

Итак, у нас получилось 22,5 миллиАмпер.

Теперь, зная значение потребляемого тока, можно найти по этой формуле входное сопротивление:

Получаем:

Выходное сопротивление

Яркий пример выходного сопротивления — это закон Ома для полной цепи, в котором есть так называемое «внутреннее сопротивление». Кому лень читать про этот закон, вкратце рассмотрим его здесь.

Что мы имели? У нас был автомобильный аккумулятор, с помощью которого мы поджигали галогенную лампочку. Перед тем, как цеплять лампочку, мы замеряли напряжение на клеммах аккумулятора:

И как только  подсоединяли лампочку, у нас напряжение на аккумуляторе становилось меньше.

Разница напряжения,  то есть 0,3 Вольта (12,09-11,79) у нас падало на так называемом внутреннем сопротивлении r Оно же и есть ВЫХОДНОЕ СОПРОТИВЛЕНИЕ. Его также называют еще сопротивлением источника или эквивалентным сопротивлением.

У всех аккумуляторов есть это внутреннее сопротивление r, и «цепляется» оно последовательно с источником ЭДС (Е).

Но только ли аккумуляторы и различные батарейки обладают выходным сопротивлением? Не только. Выходным сопротивлением обладают все источники питания. Это может быть блок питания, генератор частоты, либо вообще какой-нибудь усилитель.

В теореме Тевенина (короче, умный мужик такой был)  говорилось, что любую цепь, которая имеет две клеммы и содержит в себе туеву кучу различных источников ЭДС и резисторов разного номинала можно привести тупо к источнику ЭДС с каким-то значением напряжения (E_{эквивалентное}) и с каким-то внутренним сопротивлением (R_{эквивалентное}).

E_экв  — эквивалентный источник ЭДС

R_экв  — эквивалентное сопротивление

То есть получается, если какой-либо источник напряжения питает нагрузку, значит, в источнике напряжения есть ЭДС и эквивалентное сопротивление, оно же выходное сопротивление.

В режиме холостого хода (то есть, когда к выходным клеммам не подцеплена нагрузка) с помощью мультиметра мы можем замерить ЭДС (E). С замером ЭДС вроде бы понятно, но вот как замерить R_вых ?

В принципе, можно устроить короткое замыкание. То есть замкнуть выходные клеммы толстым медным проводом, по которому у нас будет течь ток короткого замыкания I_кз.

В результате у нас получается замкнутая цепь с одним резистором. Из закона Ома получаем, что

Но есть небольшая загвоздка. Теоретически  — формула верна. Но на практике я бы не рекомендовал использовать этот способ. В этом случае сила тока достигает бешеного значения, да вообще, вся схема ведет себя неадекватно.

Измерение выходного сопротивления на практике

Есть другой, более безопасный способ. Не буду повторяться, просто скопирую со статьи закон Ома для полной цепи, где мы находили внутреннее сопротивление аккумулятора. В той статье, мы к акуму цепляли галогенную лампочку, которая была нагрузкой R. В результате по цепи шел электрический ток. На лампочке и на внутреннем сопротивлении у нас падало напряжение, сумма которых равнялась ЭДС.

Итак, для начала замеряем напряжение на аккумуляторе без лампочки.

Так как у нас в этом случае цепь разомкнута (нет внешней нагрузки), следовательно сила тока в цепи I равняется нулю. Значит, и падение напряжение на внутреннем резисторе U_r тоже будет равняться нулю. В итоге, у нас остается только источник ЭДС, у которого мы и замеряем напряжение. В нашем случае E=12,09 Вольт.

Как только мы подсоединили нагрузку, то у нас сразу же упало напряжение на внутреннем резисторе и на нагрузке, в данном случае на лампочке:

Сейчас на нагрузке (на галогенке) у нас упало напряжение U_R=11,79 Вольт, следовательно, на внутреннем резисторе падение напряжения составило U_r=E-U_R=12,09-11,79=0,3 Вольта. Сила тока в цепи равняется I=4,35 Ампер. Как я уже сказал, ЭДС у нас равняется E=12,09 Вольт. Следовательно, из закона Ома для полной цепи высчитываем, чему у нас будет равняться внутреннее сопротивление r:

Заключение

Входное и выходное сопротивление каскадов (блоков) в электронике играют очень важную роль. В этом мы убедимся, когда начнем рассматривать статью по согласованию узлов радиоэлектронных схем. Все качественные вольтметры и осциллографы также стараются делать с очень высоким входным сопротивлением, чтобы оно меньше сказывалось на замеряемый сигнал и не гасило его амплитуду.

С выходным сопротивлением все намного интереснее. Когда мы подключаем низкоомную нагрузку, то чем больше внутреннее сопротивление, тем больше напряжение падает на внутреннем сопротивлении. То есть в нагрузку будет отдаваться меньшее напряжение, так как разница осядет на внутреннем резисторе. Поэтому, качественные источники питания, типа блока питания либо генератора частоты, пытаются делать как можно с меньшим выходным сопротивлением, чтобы напряжение на выходе «не проседало» при подключении низкоомной нагрузки. Даже если сильно просядет, то мы можем вручную подкорректировать с помощью регулировки выходного напряжения, которые есть в каждом нормальном источнике питания. В некоторых источниках это делается автоматически.

Понятно, что просто подключив омметр к усилителю, измерить выходное или входное сопротивление УНЧ или другого радиоустройства не получится. А как тогда это правильно сделать? Сейчас узнаете…

Метод измерения входного сопротивления

Из треугольника сопротивления переменного тока можно определить входное или выходное сопротивление двухконтактной сети путем измерения переменного тока и напряжения слабого сигнала.

Для входа напряжение измеряется на входных клеммах, а ток измеряется путем включения измерителя последовательно с генератором сигналов. Используйте фиксированную частоту, например 1 кГц, и установите уровень генератора примерно на 20 мВ RMS. Тогда если среднеквадратичное значение 20 мВ и ток 10 мкА, то сопротивление равно 2 кОм. В цепях с высоким сопротивлением ток становится очень маленьким и его трудно измерить, поэтому требуется альтернативный метод.

Простой способ измерения небольших входных токов — использование постоянного резистора как показано на схеме. Измерьте переменное напряжение в точках V1 и V2, тогда входной ток Iin станет:

Iin = (V2 – V1) / R1

Затем входное сопротивление тестируемой цепи находится по формуле:

Z = V1 / Iin

Пример. Если используем резистор 10 кОм для R1 и измеряем V2 = 10,1 мВ и V1 = 10 мВ, тогда:

Ток 10 нА было бы очень трудно измерить, так как разрешение цифрового вольтметра очень низкое, но возможно измерение значений 10 мВ и 10,1 мВ, что позволяет найти входное сопротивление: оно будет 10 мВ / 10 нА = 1 МОм.

Использование программы моделирования

Для измерения входного сопротивления в полном спектре частот используйте следующую схему:

Вход представляет собой источник постоянного тока, его значение установлено на 1 ампер. Поскольку источники тока в большинстве программ моделирования являются идеальными и имеют бесконечное выходное сопротивление, придется использовать параллельно резистор с большим сопротивлением, как показано, чтобы избежать ошибок моделирования. Поскольку V = I х Z и используется 1 ампер, как показано для источника тока, то V = 1 х Z или V = Z. Следовательно, измерение входного напряжения возвращает входное сопротивление. Ось Y на выходном графике может быть помечена соответствующим образом.

Измерение выходного сопротивления

Выходное сопротивление также может быть определено с использованием аналогичной методики. Используется резистор с фиксированной нагрузкой, и выходное напряжение измеряется сначала при полной нагрузке, а затем без нагрузки.

На приведенной выше схеме Zo — это внутреннее выходное сопротивление измеряемой сети. Термин «сеть» является общим термином, так как схема может быть чем угодно: усилителем, фильтром, генератором и так далее.

Чтобы найти выходное сопротивление, сначала измеряется выходное напряжение без нагрузочного резистора, а затем с фиксированной нагрузкой (чисто резистивной).

Сначала снимается нагрузочный резистор Rl, измеряется и записывается выходное напряжение (В). Затем Rl снова включается в цепь и напряжение на выходе под нагрузкой (Vl). Выходное сопротивление Zo теперь находится по закону Ома для цепей переменного тока. Поскольку нагрузка является чисто резистивной, Z = V / I, где «V» — падение напряжения на выходном сопротивлении: (V — Vl), а «I» — выходной ток, Vl / Rl. Таким образом:

Делаем перестановку:

Использование программы моделирования

Для измерения входного сопротивления по полному спектру частот используйте следующую схему:

Вход представляет собой источник постоянного тока, его значение установлено на 1 ампер. Поскольку источники тока в большинстве программ моделирования являются идеальными и имеют бесконечное выходное сопротивление, придется использовать параллельно резистор с большим сопротивлением, чтобы избежать ошибок моделирования. Поскольку V = I х Z и используется 1 ампер, как показано для источника тока, то V = 1 х Z или V = Z. Следовательно измерение выходного напряжения возвращает выходное сопротивление.

Параметр «выходное
сопротивление»
определяет коэффициент усиления
усилительного каскада и частоту полюса
и поэтому является одним из важнейших
параметром для любых усилителей.
Поскольку он является малосигнальным
параметром, то все эквивалентные схемы
для его расчета являются линейными.
По умолчанию подразумевается, что
выходное сопротивление является активным
и НЕ включает в себя реактивных
компонентов.

По определению
выходное сопротивление активных схем
рассчитывается при условии протекания
в них стационарных
режимных токов и поддержании в узлах
стационарных
потенциалов. В этих условиях наиболее
приемлемый метод определения выходного
сопротивления
вi-м
узле схемы подразумевает:

(D)
удаление из схемного узла реактивных
компонентов;

(E)
удаление всех переменных входных
сигналов, т.е. подключение всех входов
схемы к источникам напряжения с
номиналами, равными режимным потенциалами
в этих узлах;

(F)
подключение к этому узлу малого пробного
источника тока
,
много меньшего режимного тока, протекающего
в этом узле (условиененарушения
стационарного состояния, бывшего ДО
подключения этого источника тока);

(G)
измерения величины изменения
потенциала
в узле;

(H)
вычисления отношения
,
которое определяется как:

(3.34)

При осуществлении
пункта (Б) предполагается, что наличие
входных переменных сигналов как минимум
усложняет (в большинстве случаев –
чрезмерно) расчет изменения
потенциала в узле. В экспериментальных
условиях наличие входных переменных
сигналов просто мешает как обнаружению
факта измененияпотенциала в узле, так и измерению его
с необходимой точностью.

Эквивалентная
малосигнальная схема для расчета
выходного сопротивления в простейшем
усилителе получается из схемы на рис.
3.7b
после выполнения условий (D)
и (E),
т.е. удалении источника переменного
тока
и конденсатора.
В результате вся эквивалентная схема
состоит из одного резистора,
и выходное сопротивление тождественно
равно ему, подтверждая правильность
названия «»
эквивалентного сопротивления в выражении
(3.12).

3.1.7. Элементарный анализ величины входной емкости. Емкость Миллера

Выше МДП транзистор
рассматривался только как совокупность
двух источников тока (источника
постоянного режимного тока и источника
переменного тока) и активного резистора
между стоком и истоком в пологой области.
С целью упрощения первоначального
анализа рассматриваемых вопросов, не
рассматривались присущие транзистору
внутренние емкости. Дальнейший анализ
требует их учета.

Рассмотрим влияние
на входную емкость простейшего
инвертирующего усилителя двух емкостей
входного транзистора, а, именно, его
емкости затвор-исток
и емкости затвор-сток(см. рис. 3.10).

Рис. 3.10. Иллюстрация
к анализу величины входной емкости
инвертирующего усилительного каскада.

Мерой любой емкости
по определению является заряд,
поступивший в конденсатор при приложении
к нему напряжения,
т.е..
Для установившегося синусоидального
напряженияможно записать упрощенное выражение:.

Конденсаторы
ивходят в состав входной емкости усилителя.
Особенности процесса перезарядки
конденсаторов влияют на заряды в
обкладках. У конденсатораодна из обкладок по переменному току
заземлена, поэтому зарядна этом конденсаторе выражается просто
как

(3.35а)

Следует отметить,
что емкостью затвор-исток
считается не только емкость непосредственного
перекрытия истока затвором на расстояниеLD.
В состав
в пологом режиме входит болееемкости активного канала относительно
затвора (см. главуII).
В оценочных расчетах целесообразно в
состав
вводитьвсю
емкость активного канала относительно
затвора и даже всю
емкость затвора,
поскольку в подавляющем большинстве
случаев это является наихудшим
случаем. Согласно этим замечаниям,
выражение для
запишем в виде:

(3.35b)

У конденсатора
,
находящегося в цепи обратной связиинвертирующего
усилителя, обе обкладки соединены с
узлами, имеющими переменные потенциалы.
Учитывая, что
,
где– коэффициент усиления, имеем:

(3.36)

Выражение (3.36)
указывает на эффективное увеличение
емкости затвор – сток как элемента
обратной связи в составе инвертирующего
усилителя в режиме малого сигнала. Этот
эффект называют эффектом Миллера, а
емкость обратной связи между входом и
инвертирующим выходом усилителя называют
емкостью Миллера.

В большинстве
случаев с достаточной точностью под
емкостью затвор-сток
можно принимать только емкость
непосредственного перекрытия стока
затвором на расстояниеLD,
т.е

(3.37)

Суммарная входная
емкость
инвертирующего усилителя с емкостьюобратной связи определяется выражением:

(3.38)

Как видно из (3.38),
для достижения наибольшей скорости
перезарядки входной емкости инвертирующего
усилителя необходимо (1) уменьшать
емкость обратной связи и (2) уменьшать
коэффициент передачи
от входа усилителя, к которому подключена
первая обкладка емкости обратной связи,
к узлу подключения второй обкладки.

Соседние файлы в папке Лекции

• #
• #
• #

1. Радиоэлектроника
2. Схемотехника
3. Основы электроники и схемотехники
4. Том 3 – Полупроводниковые приборы

1. Книги / руководства / серии статей
2. Основы электроники и схемотехники. Том 3. Полупроводниковые приборы

Добавлено 26 января 2018 в 06:04

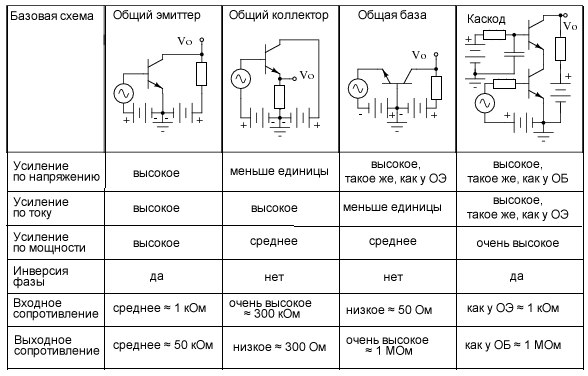
Входное сопротивление усилителя значительно варьируется в зависимости от конфигурации схемы, как показано на рисунке ниже. Оно также зависит от смещения. Здесь не учитывается, что входной импеданс является комплексной величиной и зависит от частоты. Для схем с общим эмиттером и общим коллектором он равен сопротивлению базы, умноженному на коэффициент β. Сопротивление базы по отношению к транзистору может быть как внутренним, так и внешним. Для схемы с общим коллектором:

(R_{вх} = beta R_Э)

Для схемы с общим эмиттером немного сложнее. Нам необходимо знать внутреннее сопротивление эмиттера r_Э. Оно вычисляется по формуле:

(r_Э = KT/I_Э m)

где

• K=1.38×10-23 Дж·К−1 – постоянная Больцмана;
• T – температура в Кельвинах, берем ≅300;
• IЭ – ток эмиттера;
• m – для кремния изменяется от 1 до 2.

(r_Э = 0,026 В/I_Э = 26 мВ/I_Э)

Таким образом, R_вх для схемы с общим эмиттером равно:

(R_{вх} = beta r_{Э})

Например, входное сопротивление усилителя на транзисторе с β = 100, на схеме с общим эмиттером и смещением 1 мА равно:

(r_Э = 26 мВ/ 1 мА = 26 ;Ом)

(R_{вх} = beta r_Э = 100 cdot 26 = 2600 ;Ом)

Для более точного определения R_вх для схемы с общим коллектором необходимо учитывать R_Э:

(R_{вх} = beta (R_Э + r_Э))

Формула выше также применима и для схемы с общим эмиттером с резистором эмиттера.

Входной импеданс схемы с общей базой равен R_вх = r_Э.

Высокий входной импеданс схемы с общим коллектором согласовывается с источниками с высоким выходным сопротивлением. Одним из таких источников с высоким импедансом является керамический микрофон. Схема с общей базой иногда используется в RF (радиочастотных) схемах для согласования с источником с низким импедансом, например, с коаксиальным кабелем 50 Ом. С источниками со средним импедансом хорошо согласуется схема с общим эмиттером. Примером может служить динамический микрофон.

Выходные сопротивления трех основных типов схем приведены на рисунке ниже. Средний выходной импеданс схемы с общим эмиттером сделал ее самой популярной в использовании. Низкое выходное сопротивление схемы с общим коллектором хорошо подходит для согласования, например, для бестрансформаторного соединения с 4-омным динамиком.

Подведем итоги

Смотрите рисунок выше.

Теги

Биполярный транзисторВходной импедансВыходной импедансКаскад с общей базойКаскад с общим коллекторомКаскад с общим эмиттеромКаскодный усилительКоэффициент усиления по напряжениюКоэффициент усиления по токуОбучениеЭлектроника