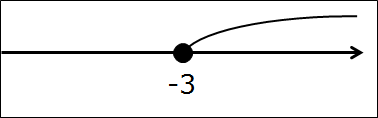
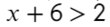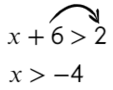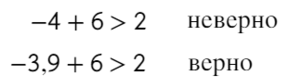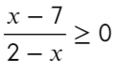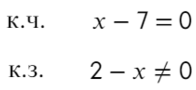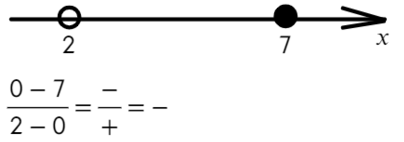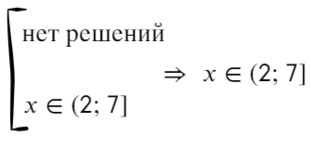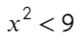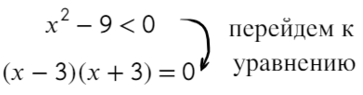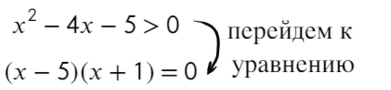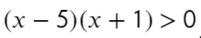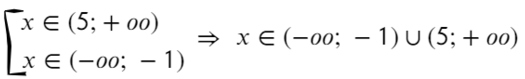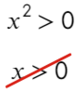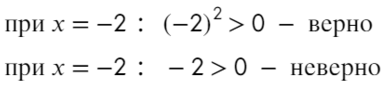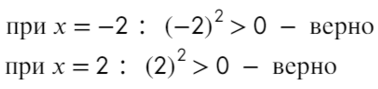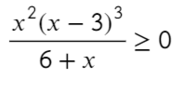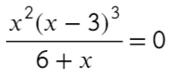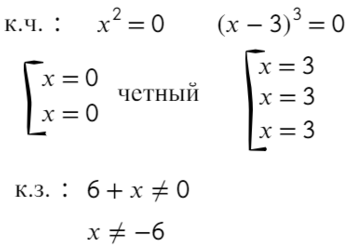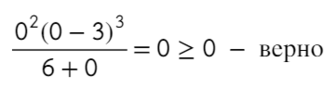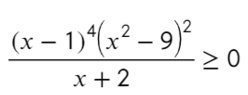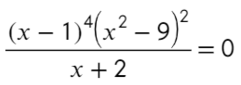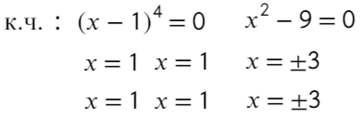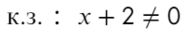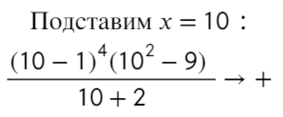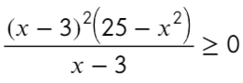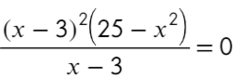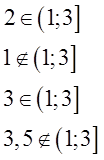Как найти выколотую точку на прямой - Исправление недочетов и поиск решений вместе с Examum.ru

Закрашенная и незакрашенная точка

Эта ассоциация поможет легко запомнить, выколотая точка или закрашенная на числовой прямой.

Сравните неравенства, при которых точка заштрихована: x≥a или x≤b и неравенства, в которых точка выколотая: x>a, x или Светлана Иванова, 27 Сен 2012

Сегодня мы узнаем, как использовать метод интервалов для решения нестрогих неравенств. Во многих учебниках нестрогие неравенства определяются следующим образом:

— это неравенство вида которое равносильно совокупности строгого неравенства и уравнения:

В переводе на русский язык это значит, что нестрогое неравенство это объединение классического уравнения и строгого неравенства Другими словами, теперь нас интересуют не только положительные и отрицательные области на прямой, но и точки, где функция равна нулю.

Отрезки и интервалы: в чем разница?

Прежде чем решать нестрогие неравенства, давайте вспомним, чем интервал отличается от отрезка:

— это часть прямой, ограниченная двумя точками. Но эти точки не принадлежат интервалу. Интервал обозначается круглыми скобками: и т.д.;
— это тоже часть прямой, ограниченная двумя точками. Однако эти точки тоже являются частью отрезка. Отрезки обозначаются квадратными скобками: и т.д.

Чтобы не путать интервалы с отрезками, для них разработаны специальные обозначения: интервал всегда обозначается выколотыми точками, а отрезок — закрашенными. Например:

На этом рисунке отмечен отрезок и интервал Обратите внимание: концы отрезка отмечены закрашенными точками, а сам отрезок обозначается квадратными скобками. С интервалом все иначе: его концы выколоты, а скобки — круглые.

Метод интервалов для нестрогих неравенств

К чему была вся эта лирика про отрезки и интервалы? Очень просто: для решения нестрогих неравенств все интервалы заменяются отрезками — и получится ответ. По существу, мы просто добавляем к ответу, полученному методом интервалов, границы этих самых интервалов. Сравните два неравенства:

Задача. Решите строгое неравенство:

Решаем методом интервалов. Приравниваем левую часть неравенства к нулю:

( x − 5)( x + 3) = 0;
x − 5 = 0 ⇒ x = 5;
x + 3 = 0 ⇒ x = −3;

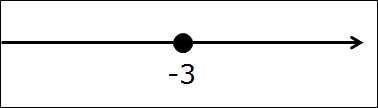
Отмечаем полученные корни на координатной оси:

Справа стоит знак плюс. В этом легко в этом убедиться, подставив миллиард в функцию:

f ( x ) = ( x − 5)( x + 3)

Осталось выписать ответ. Поскольку нас интересуют положительные интервалы, имеем:

Задача. Решите нестрогое неравенство:

Начало такое же, как и для строгих неравенств: работает метод интервалов. Приравниваем левую часть неравенства к нулю:

( x − 5)( x + 3) = 0;
x − 5 = 0 ⇒ x = 5;
x + 3 = 0 ⇒ x = −3;

Отмечаем полученные корни на координатной оси:

В предыдущей задаче мы уже выяснили, что справа стоит знак плюс. Напомню, в этом легко убедиться, подставив миллиард в функцию:

f ( x ) = ( x − 5)( x + 3)

Осталось записать ответ. Поскольку неравенство нестрогое, а нас интересуют положительные значения, имеем:

Итак, основное отличие строгих и нестрогих неравенств:

В строгих неравенствах нас не интересуют концы отрезка, поэтому они отмечаются выколотыми точками. Такие точки никогда не входят в ответ, о чем говорят круглые скобки на первом ответе: x ∈ (−∞; −3) ∪ (5; +∞);
И наоборот, в нестрогих неравенствах концы отрезка входят в ответ. На графике они отмечаются закрашенными точками, а в ответе указываются квадратными скобками: x ∈ (−∞; −3] ∪ [5; +∞).

Вот и вся разница! Просто запомните: в строгих неравенствах точки выколоты, а в нестрогих — закрашены.

Почему бесконечности всегда стоят в круглых скобках

У внимательного читателя наверняка возник вопрос: почему бесконечности отмечаются круглыми скобками даже в нестрогих неравенствах? Например, почему в последней задаче мы пишем

Что ж, это не опечатка. Бесконечность действительно обозначается круглой скобкой, даже если неравенство — нестрогое. Чтобы понять, почему так происходит, достаточно вспомнить определение бесконечности.

— это гипотетическое число, которое больше любого другого числа, участвующего в решении.

Трудность заключается в том, что нельзя работать с бесконечностью напрямую. Мы можем лишь приблизиться к ней, подставляя такие зверские числа, как 1 000 000 и даже 1 000 000 000. Но добраться до самой бесконечности все равно нельзя.

Именно поэтому бесконечность обозначают круглыми скобками. Ведь хотя бесконечность и ограничивает всю числовую прямую, сама она не принадлежит этой прямой.

Ситуация такая же, как с границами интервалов. Рассмотрим все числа из интервала:

Эта запись означает, что число не принадлежит интервалу, однако любое число, которое больше нуля и меньше единицы — принадлежит. В частности, этому интервалу принадлежат следующие числа:

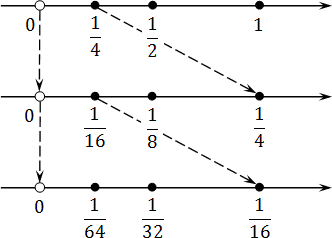
Попробуем отметить эти числа на координатной прямой. Поскольку каждое следующее число вдвое меньше предыдущего, нам придется несколько раз менять масштаб. Получим вроде этого:

Что дает нам этот график? Оказывается, при достаточно крупном масштабе можно отметить любое число, сколь угодно близкое к нулю. При этом сам ноль никуда не денется — он остается недостижимой границей. Именно это и подразумевается, когда речь заходит о концах интервала.

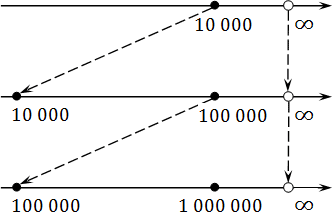
То же самое происходит и с бесконечностью. Разница лишь в том, что масштаб надо не увеличивать, а уменьшать:

Мы можем сколь угодно долго идти к бесконечности, но так и не достигнем ее. Вот почему бесконечности обозначают круглыми скобками, подобно границам интервала.

Примеры решения неравенств

В заключение кратко разберем два нестрогих неравенства. И если в первой задаче еще есть пояснения, то вторая задача будет оформлена именно так, как и надо оформлять настоящее решение.

Как обычно, приравниваем все к нулю:

( x + 8)( x − 3) = 0;
x + 8 = 0 ⇒ x = −8;
x − 3 = 0 ⇒ x = 3.

Теперь рассматриваем функцию, которая находится в левой части неравенства:

f ( x ) = ( x + 8)( x − 3)

Подставим в эту функцию бесконечность — получим выражение вида:

Чертим координатную ось, отмечаем корни и расставляем знаки:

Поскольку мы решаем неравенство или, что то же самое, осталось записать ответ:

x (12 − 2 x )(3 x + 9) ≥ 0

x (12 − 2 x )(3 x + 9) = 0;
x = 0;
12 − 2 x = 0 ⇒ 2 x = 12 ⇒ x = 6;
3 x + 9 = 0 ⇒ 3 x = −9 ⇒ x = −3.

x ≥ 6 ⇒ f ( x ) = x (12 − 2 x )(3 x + 9) → (+) · (−) · (+) = (−) x ∈ (−∞ −3] ∪ [0; 6].

Решение неравенств

Метод интервалов

Перенос знаков

Выбор точек

Система и совокупность

Точка знакопостоянства

Что нельзя делать в неравенстве, даже под пытками:

1) Домножать на знаменатель.

2) Умножать/делить на отрицательное число, не меняя знак.

3) Убирать бездумно логарифм или основание.

Начнем с простого:

Линейные уравнения решаются обычным переносом. Икс в одной части оставим, а числа перенесем в другую:

А само значение −4 нам подходит?

Нет, поэтому ставим круглые скобочки ()

Разберемся со скобками:

Когда мы включаем точку (корень числителя), или стоят знаки нестрогие ( ≥, ≤ ), ставим «[ ]» — квадратные скобки. Если не включаем (корень знаменателя), или знак строгий (>,

Если же возьмем пример, где придется делить или умножать на отрицательное число, то знак поменяется:

Ответ: x ∈ ( 0; +oo).

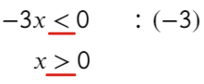
Следующий пример уже с дробью:

Приравняем числитель к нулю и скажем, что знаменатель не равен нулю:

к.ч. (корни числителя)

к.з. (корни знаменателя)

Расставляем корни числителя и знаменателя на одной прямой (сколько решаем неравенств, столько же чертим прямых). Попробуем подставить х = 0, чтобы определить знаки:

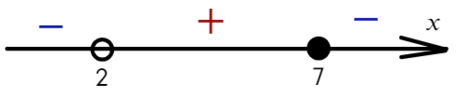
Там, где «0» (перед двойкой), ставим знак «−», а дальше знаки чередуем:

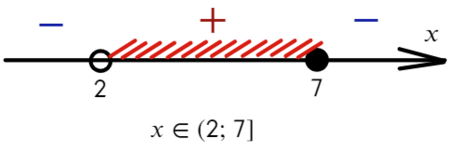
Из-за того, что знаком неравенства был «≥», нам подходят промежутки со знаком «+» и закрашенная точка:

Когда мы включаем точку (корень числителя), или стоят знаки (≥, ≤), ставим «[ ]» — квадратные скобки. Если не включаем (корень знаменателя), или знак строгий (>,

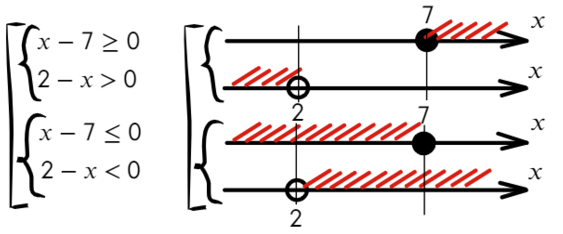
Данный пример можно решить по-другому. Подумаем, когда дробь больше нуля? Конечно, когда числитель и знаменатель — положительные значения или когда оба отрицательные. Поэтому данное неравенство можно разбить на две системы в совокупности:

Отметим на прямой решение каждого неравенства.

Решением совокупности «[» является тот участок, который включен хотя бы в одно неравенство.

Мой любимый пример:

Покажу мастер-класс, как делать не надо. Дома не повторять!

А теперь через метод интервалов разберемся, как сделать правильно:

Там, где ноль, ставим знак «−», рисуем прямую и отмечаем корни каждой скобки. А дальше чередуем:

В данном неравенстве знак меньше, поэтому записываем в ответ промежуток, где знак «−».

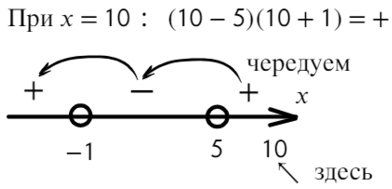
Перейдем к квадратному уравнению:

Разложим на множители и подставим x = 10, чтобы определить знак:

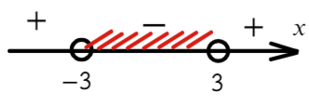
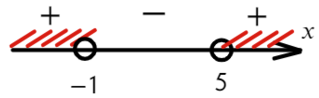
Нам требуются положительные значения:

Второй способ разложить на множители:

Ответ: x ∈ (−oo; −1) ∪ (5; +oo).

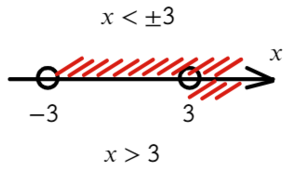
А теперь простой, но крайне показательный пример:

Убирать квадрат ни в коем случае нельзя. Простенький контрпример:

Надеюсь, убедил. Вместо знака больше поставим знак равно и попробуем решить методом интервалов:

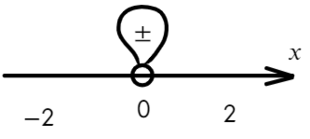
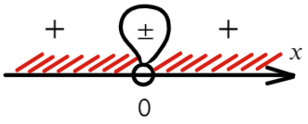
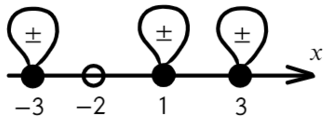
Если корень повторяется четное количество раз, то в этой точке знак меняться не будет. Отмечать будем такую точку восклицательным знаком (а внутри него ±, чуть ниже объясню, зачем это).

В данном неравенстве знак больше, тогда отметим те промежутки, где стоит знак «+».

Только точка «0» не подходит, 0 > 0 — неверно!

Ответ: x ∈ R <0>или x ∈ ( − oo; 0) ∪ (0; +oo).

Переходим на новый уровень:

Все говорят, что домножать на знаменатель нельзя, а я говорю, что буду! (joke)

По методу координат найдем корни числителя и знаменателя:

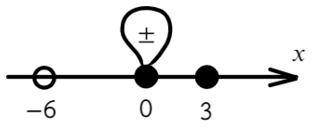
Отметим все корни на одной прямой (сколько неравенств, столько же и прямых). Ноль — корень четной кратности, над ним рисуем восклицательный знак! Если это корень числителя, то точка будет закрашена, если знаменателя — выколота (на ноль делить нельзя).

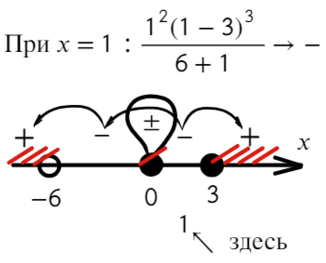
Требуется найти промежутки, где выражение больше или равно нулю. Нам подойдут все «промежутки», где знак плюс. Для этого подставим значение x = 1 и с промежутка [0; 3] начнем расставлять знаки. Там же находится единица.

Вот для чего ставят в восклицательном знаке ±: чтобы не потерять отдельные точки, в данном случае 0.

Ответ: (−oo; − 6) ∪ <0>∪ [ 3; +oo).

По той же схеме корни числителя и знаменателя:

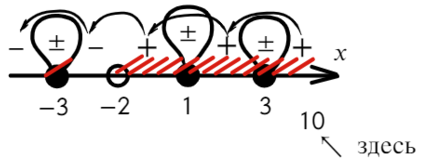
Определим знак при x = 10 и расставим знаки с промежутка, где присутствует 10:

Все точки от − 2 закрашены, значит эти промежутки можно объединить в один.

Точка x = 3 встречается 3 раза (2 раза в числителе и 1 раз в знаменателе), знак через нее меняться будет! А также эта точка будет выколота, проверь это, подставив в уравнение x = 3. На ноль же делить нельзя?

Узнать ещё

Эта ассоциация поможет легко запомнить, выколотая точка или закрашенная на числовой прямой.

Сравните неравенства, при которых точка заштрихована: x≥a или x≤b и неравенства, в которых точка выколотая: x>a, x<b. В первом случае в самом знаке неравенства есть прямая подсказка, что точку надо заштриховать, уже и штриховать начали, первый штрих сделали: ≥ или ≤. Поэтому и на чертеже на числовой прямой в таких неравенствах — заштрихованная точка:

А в знаках > или < штриха дополнительного нет, значит, и закрашивать точку не надо. Получилась выколотая точка.

С3 ГИА – построение графиков функций.

Для того, чтобы хорошо решать это задание, нужно быть знакомым с построением различных графиков функций, в том числе содержащих модуль. Предлагаю тем, кто неуверенно себя чувствует при решении таких заданий, перейти по ссылкам и изучить (или повторить) данные разделы. Задание С3 связано как с исследованием расположения корней квадратного трехчлена, так и с определением области определения функции, и области ее значений. На конкретных примерах мы попробуем научиться решать различные типы таких заданий.

Задача 1. Построить график функции y=x^2+4 и определить, при каких значениях график функции y=kx имеет с графиком 1 общую точку. Построить все такие прямые.

Задача о касательных к параболе

Графиком предложенной функции является парабола, ветви которой направлены вверх и вершина, которую подняли вверх на 4 единицы, лежит на оси ординат. Ее координаты (0;4). Второй график – это прямая, проходящая через начало координат, причем ее наклон может меняться (его определяет коэффициент ). Такая прямая только в одном случае имеет с параболой одну общую точку – если является касательной. Причем, поскольку данная парабола симметрична относительно оси ординат, то к ней можно провести две касательных – с точками касания в первом и третьем квадрантах: Чтобы определить, в какой точке прямая коснется параболы, нужно приравнять обе функции:

Поскольку точка касания – единственная общая точка данных графиков, то дискриминант данного уравнения равен нулю: Откуда k^2=16 и и решить это уравнение: Тогда касание произойдет в точке x=2 и симметричной ей точке x=-2 .

Задача 2. Построить график функции график функции y=a имеет с графиком три или более общие точки.

График, который подвергнется преобразованиям

Строить этот график будем поэтапно: сначала построим график , затем – график функции

“Опрокидываем” преобразованный график

Осталось выяснить, в каком же случае прямая y=a – а это прямая, параллельная оси абсцисс – будет иметь три (или же более) общие точки с графиком построенной нами функции. Прямая показана на рисунке зеленым цветом. Видно, что ниже указанного положения прямая будет иметь только две общие точки с графиком. Если y=-1 , то прямая имеет три точки с графиком – пересекает две его ветви и касается вершины. Выше прямая будет иметь четыре точки пересечения с графиком, однако при y=0 точек пересечения уже снова две. Значит, ответ надо записать так: a in [-1;0)

Задача 3. Построить график функции график функции y=a имеет с ним три и более общие точки.

Также построим график в два этапа: саму параболу (координаты ее вершины (-1;-9)), затем отразим всю часть, лежащую ниже оси х, вверх: Тогда три и более (а именно – четыре) общих точки графики будут иметь при a in (0;9]

Задача 4. Построить график функции и определить, при каких значениях график функции y=a имеет с ним 2 общие точки.

Из условия ясно, что такой график состоит из двух кусочков. Один из них – прямая, второй – парабола. Первый существует в точке 1 и левее ее, второй – правее этой точки. Нарисуем эти графики:

Координаты вершины параболы:

Красным показаны прямые y=1 и y=5 – именно они, и только они, имеют две общие точки с построенным графиком. Ответ: a=1 , a=5 .

Задача 5. Построить график функции график функции y=kx не имеет с графиком общих точек.

Давайте сначала попробуем упростить данное выражение, кроме того, нужно, безусловно, определить область допустимых значений данной функции. ОДЗ: . Теперь попробуем упростить данное выражение:

Определение коэффициента наклона касательной

Полученная функция – квадратичная, ее графиком является парабола. Данная парабола симметрична относительно оси y, ее вершина имеет координаты (0; 25). Необходимо заметить, что точка с координатами (1; 26) – выколотая точка (по ОДЗ). Тогда прямая, проходящая через начало координат – а именно таким будет график функции y=kx , не будет иметь с параболой общих точек в трех случаях: если коэффициент меньше, чем у касательной, расположенной справа, или он больше, чем у касательной, расположенной слева, или искомая прямая проходит прямо через выколотую точку. Наверное, проще найти каков этот коэффициент именно в третьем случае: так как прямая проходит через начало координат, достаточно подставить координаты нашей выколотой точки в уравнение прямой и найти : 26=k*1 , откуда k=26 . Проверим, не будет ли такая прямая иметь общих точек с параболой. Приравняем . По сумме коэффициентов это уравнение имеет корень 1, но и второй корень – 25, поэтому такая прямая будет иметь еще одну точку пересечения с параболой. В ответ эту прямую мы не включим. Теперь определим коэффициент наклона касательных, для этого приравняем оба уравнения: , и найдем дискриминант, который должен быть равен нулю при наличии единственной общей точки у двух этих графиков функций: Откуда k^2=100 и и решить это уравнение: Тогда касание произойдет в точке x=5 и симметричной ей точке x=-5 . Ответ: , .

Задача 6. Построить график функции он не имеет общих точек с графиком функции y=a .

Гипербола с выколотой точкой

Определим ОДЗ функции: , . (Для того, чтобы определить ОДЗ, приравняли знаменатель к нулю и решили данное уравнение). Теперь упростим выражение: – выколотая точка. В точке x=0 гипербола не существует, оси координат – ее асимптоты (одна из них войдет в ответ). Тогда, если прямая y=a пройдет через выколотую точку, графики не будут иметь общих точек. Найдем : для этого определим ординату выколотой точки: : Ответ: a=1/3 и a=0 .

Задача 7. Построить график функции график функции y=kx имеет с графиком 1 общую точку.

Подбор коэффициента наклона прямой

Определим ОДЗ функции: , . (Для того, чтобы определить ОДЗ, приравняли знаменатель к нулю и решили данное уравнение). Теперь упростим выражение: – выколота. В точке x=0 гипербола не существует, оси координат – ее асимптоты. Тогда, если прямая y=kx пройдет через выколотую точку, графики будут иметь одну общую точку. Найдем : для этого подставим в уравнение прямой абсциссу и ординату выколотой точки: 1=k/1 , k=1 : Ответ: k=1

Задача 8. Построить график функции график функции y=a имеет с ним 2 общие точки.

Построение функции с модулем

Эта функция – функция типа , то график y=-1 коснется обеих вершинок нашей “дублированной” параболы, то есть a=-1 – один из ответов. Также, если y=a пересечет обе ветви параболы, то есть все нас устраивают. Ответ: a=-1 ,.

Задача 9. Построить график функции график функции y=c не имеет с ним общих точек.

Кубическая парабола с выколотой точкой

Определим ОДЗ исходной функции: . Теперь можно упростить выражение: пройдет именно через эту точку, она не будет иметь общих точек с полученным нами графиком. Ответ: с=4.

Задача 10. Построить график функции график функции y=kx имеет с ним одну общую точку.

Для того, чтобы построить данный график, необходимо раскрыть модули. С этой целью приравняем подмодульное выражение к нулю, чтобы узнать, в какой точке оно меняет знак: x-1=0 x=1 и x+1=0 x=-1 Нанесем эти точки на числовую прямую и расставим знаки:

У нас получились три интервала, на каждом из которых можно теперь раскрыть модули: 1. 2. 3. Тогда наша функция – кусочно-линейная: .

Она выглядит так:

Зеленым цветом показано одно из возможных положений прямой y=kx . При таком расположении прямой , и может расти бесконечно. Заметим, что крайнее положение прямой – при k=1. При таком коэффициенте наклона она параллельна правой и левой частям графика, и имеет с ним одну точку пересечения – точку (0;0). Точно так же коэффициент наклона может быть и отрицательным. При этом коэффициент k=-1 – не войдет в ответ, так как в этом случае функция y=kx будет иметь общий отрезок с кусочно-линейной функцией, что не соответствует требованиям задачи. Таким образом,

Ответ: вершины парабол и расположены по одну сторону от оси х?

Обратим внимание на то, что у двух данных парабол ветви направлены в разные стороны: у первой старший коэффициент отрицателен, а у второй – положителен. Поэтому вершины будут лежать по одну сторону от оси, если одна из них будет иметь точки пересечения с осью х, а другая – нет. Иными словами, дискриминант одного квадратного уравнения должен быть положителен, а другого – отрицателен. Это приводит нас к двум системам неравенств:

Дискриминант и наличие пересечений параболы с осью х

Или же наоборот: . Эти два случая изображены на рисунке:

Определим дискриминанты обоих квадратных уравнений:

Тогда имеем систему неравенств:

– решений нет, так как квадрат числа – неотрицателен, и сумма квадрата числа с положительным числом не может быть меньше ноля.

– в этой системе второе неравенство всегда соблюдается, решение первого – , ,

Мы рассмотрели один способ решения – с использованием дискриминанта. Есть еще один способ решения такого задания – с помощью координат вершины параболы. Решим последнюю задачу вторым способом.

Нам потребуется определить координаты вершин обеих парабол:

– вторая система решений не имеет, а именно, нет решений у второго неравенства, поэтому решим первую. Второе неравенство первой системы справедливо всегда, осталось решить неравенство:

Решение этого неравенства и есть ответ задачи:

Источник

Информация

Если дробь (displaystyle frac{(x^2+4)(x-1)}{1-x}) просто сократить, то получим

(displaystyle frac{(x^2+4)(x-1)}{1-x}=-x^2-4)

При этом левая и правая части выражений имеют разные области допустимых значений:

дробь (displaystyle frac{(x^2+4)(x-1)}{1-x})не определена при (displaystyle x=1{small ; } )
многочлен (displaystyle -x^2-4) определен для всех (displaystyle xsmall.)

Равенство выражений имеет место только для тех (displaystyle xsmall,) для которых определены оба выражения.

Поэтому нужно обязательно записать область определения исходной функции.

Область определения функции

(displaystyle y=frac{(x^2+4)(x-1)}{1-x}small.)

Знаменатель не равен нулю:

(displaystyle x,cancel{=},1small.)

В области определения исходного выражения получаем:

(displaystyle frac{(x^2+4)(x-1)}{1-x}=frac{(x^2+4)cancel{(x-1)}}{-cancel{(x-1)}}=-(x^2+4)=-x^2-4small.)

Значит, с учетом области определения исходного выражения, необходимо построить параболу с выколотой точкой при(displaystyle x=1{small : } )

(displaystyle begin{cases}y=-x^2-4,\x,cancel{=},1.end{cases})

И определить, при каких значениях параметра (displaystyle k) прямая (displaystyle y=kx) имеет с построенной параболой ровно одну общую точку.

Построим график функции (displaystyle y=-x^2-4) для (displaystyle x,cancel{=},1small.)

1. Строим параболу (displaystyle y=-x^2-4small.)

Это парабола (displaystyle y=-x^2{ small ,}) сдвинутая на (displaystyle 4) единицы вниз.

2. Так как (displaystyle x,cancel{=},1small,) выкалываем на графике точку с абсциссой (displaystyle x=1small.)

Отметим, что выколотая точка имеет координаты (displaystyle (1;,-5)small.)

Прямая (displaystyle y=kx) – это прямая, которая

проходит через начало координат вне зависимости от значения (displaystyle k{small ; } )
при изменении (displaystyle k) поворачивается вокруг начала координат и принимает все положения кроме вертикального.

Тогда прямая (displaystyle y=kx) имеет с построенным графиком ровно одну общую точку, если

прямая проходит через выколотую точку параболы (красная прямая),
прямая касается параболы (displaystyle y=-x^2-4) (зеленые прямые).

Найдем, чему равно (displaystyle k) в каждом из этих случаев.

Если прямая (displaystyle y=kx) проходит через выколотую точку параболы, то (displaystyle k=-5)

Рассмотрим случай, когда прямая проходит через выколотую точку.

Прямая пересекает параболу (displaystyle y=-x^2-4) в двух точках (одна из точек не видна на рисунке).

Но точка (displaystyle (1;-5)) является выколотой точкой графика. Поэтому прямая и парабола имеют одну общую точку.

Прямая проходит через точку (displaystyle (1;-5){ small ,}) если при (displaystyle x=1) значение (displaystyle y=-5small.)

При подстановке в (displaystyle y=kx) получаем:

(displaystyle -5=kcdot 1small,)

(displaystyle k=-5small.)

Если прямая (displaystyle y=kx) касается параболы, то

(displaystyle k=4) или (displaystyle k=-4)

Рассмотрим случай, когда прямая касается параболы.

В общей точке прямой (displaystyle y=kx) и параболы (displaystyle y=-x^2-4) значения (displaystyle y) совпадают. Поэтому приравняем их:

(displaystyle kx=-x^2-4small,)

(displaystyle x^2+kx+4=0small.)

Поскольку прямая и парабола имеют только одну общую точку, то у данного уравнения должно быть одно решение.

Квадратное уравнение (displaystyle x^2+kx+4=0) имеет ровно один корень, если его дискриминант равен (displaystyle 0small.)

Приравняем дискриминант к нулю:

(displaystyle k^2-4cdot4=0small,)

Тогда

(displaystyle k^2=4^2small,)

(displaystyle k=4) или (displaystyle k=-4small.)

Таким образом, прямая (displaystyle y=kx) и график функции (displaystyle y=frac{(x^2+4)(x-1)}{1-x}) имеют одну общую точку при

(displaystyle k=-5) или (displaystyle k=4) или (displaystyle k=-4small.)

Ответ: (displaystyle kin{-5}cup{-4}cup{4}small.)

Источник

На этой странице вы узнаете

Как мы ежедневно расставляем знаки неравенства в жизни?
Как быстро определить верное обозначение точки на прямой?
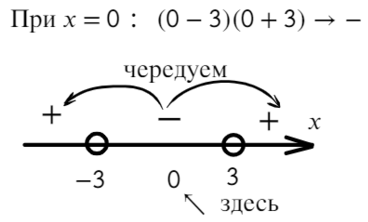
Как правильно чередовать знаки на числовой прямой?

Решая уравнение, мы стремимся к тому, чтобы обе части были равны. Но существуют такие примеры, где мы заведомо знаем, что два выражения не могут быть равны между собой. Они называются неравенствами.

Метод интервалов

Неравенство — это алгебраическое выражение, в котором одна сторона имеет отличное от другой значение. В неравенствах обычно одна сторона больше другой.

Для записи неравенств используют знаки > , < , ≥ , ≤ .

При этом “>” и “<” — это строгие знаки неравенства, а “≥” и “≤” — нестрогие знаки неравенства.

Их отличие в том, что нестрогие знаки неравенства включают граничные точки в итоговый промежуток, а строгие — нет.

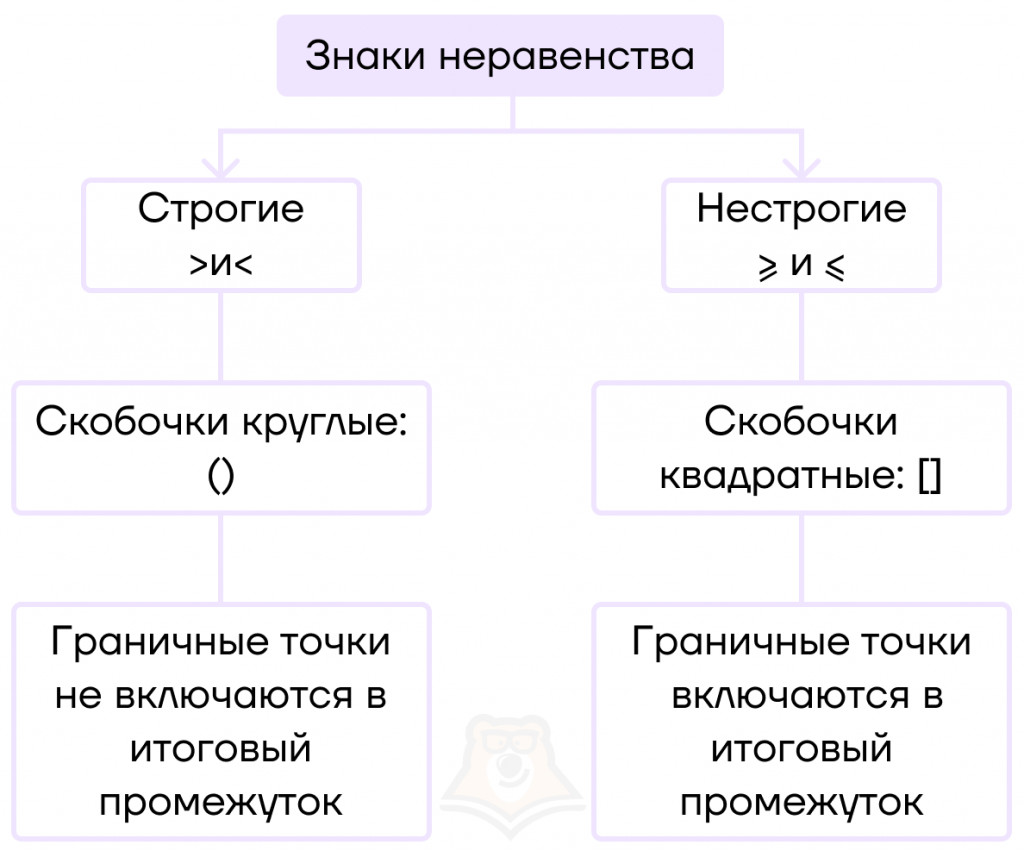
Как мы ежедневно расставляем знаки неравенства в жизни?

Посмотрим на привычные ситуации с точки зрения строгости знаков неравенства.

Например, возьмем известную игру “Камень, ножницы, бумага”.
Правила игры говорят нам, что камень всегда побеждает ножницы, а бумага побеждает камень. Если перенести это на язык неравенства, то получится:

Теперь зайдем в магазин цифровой техники и попробуем выбрать себе новый мобильный телефон. Задачка непростая, не так ли? Две разные модели могут настолько незначительно отличаться друг от друга своими характеристиками, что будут казаться почти одинаковыми. Тогда мы можем сказать, что они практически равны между собой, то есть неравенство нестрогое. Но один из них всё-таки понравился нам больше.

И каждый наш выбор, каждый шаг – это расстановка знака неравенства в настоящей жизни. Просто по бокам от него не цифры и переменные, а существующие ситуации и вещи.

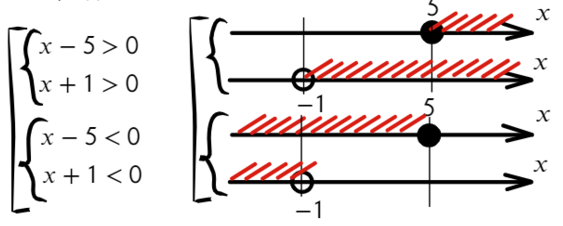
Рассмотрим пример неравенства (х — 10)(х + 21) > 0.

Его можно решить несколькими способами. Например, вспомним, что положительным будет произведение двух положительных или двух отрицательных множителей, тогда получается совокупность из двух систем.

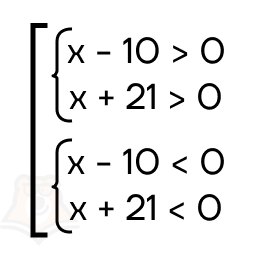
Однако этот способ решения очень трудоемкий и требует много времени. А если множителей будет больше, например, три или четыре, то время на решение в разы увеличивается.

Небольшой секрет тайм-менеджмента: как сократить время при решении неравенств? В таких случаях на помощь приходит метод интервалов.

Метод интервалов — специальный алгоритм решения для сложных неравенств вида f(x) > 0. При этом знак неравенства может быть любым.

Интервал — это промежуток на числовой прямой, ограниченный двумя различными числами.

Алгоритм решения неравенств методом интервалов

1 шаг. Перенести все части неравенства в одну сторону так, чтобы с другой остался только 0.

2 шаг. Найти нули функции, для этого необходимо решить уравнение f(x) = 0.

3 шаг. Начертить числовую прямую и отметить на ней все полученные корни. Таким образом, числовая прямая разобьется на интервалы.

4 шаг. Определить знаки на каждом интервале. Для этого необходимо подставить любое удобное значение в f(x) и определить, какой знак будет иметь функция на данном интервале.

Расставляя полученные корни на прямой, необходимо отмечать их точками. При этом от того, какая отмечена точка (выколотая или закрашенная), будет зависеть ответ.

Если в неравенстве стоит строгий знак неравенства, то все точки на прямой должны быть выколотыми.

Таким образом, граничные точки не будут включены в итоговый промежуток. Для записи таких точек используют круглые скобочки. Например, в промежуток (2;3) включаются все значения от 2 до 3, но не включаются граничные точки.

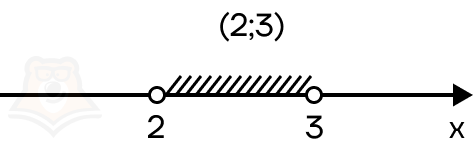
Если в неравенстве стоит нестрогий знак неравенства, то найденные корни должны быть отмечены закрашенными точками.

Это означает, что мы включаем их в итоговый промежуток. Для записи таких точек используют квадратные скобочки. Например, в промежуток [2;3] включаются все значения от 2 до 3, в том числе и граничные точки.

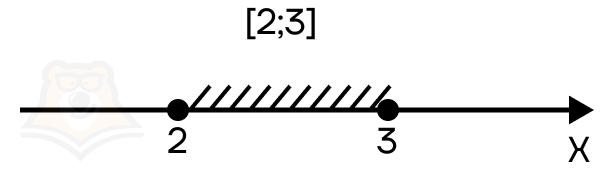
Если в неравенстве появляются ограничения и некоторые точки нельзя взять в ответ, то такие точки должны быть выколотыми на числовой прямой, при этом знак самого неравенства может быть как строгим, так и нестрогим.

Например, если необходимо решить неравенство с дробью, то нули знаменателя на числовой прямой обязательно должны быть обозначены выколотыми точками.

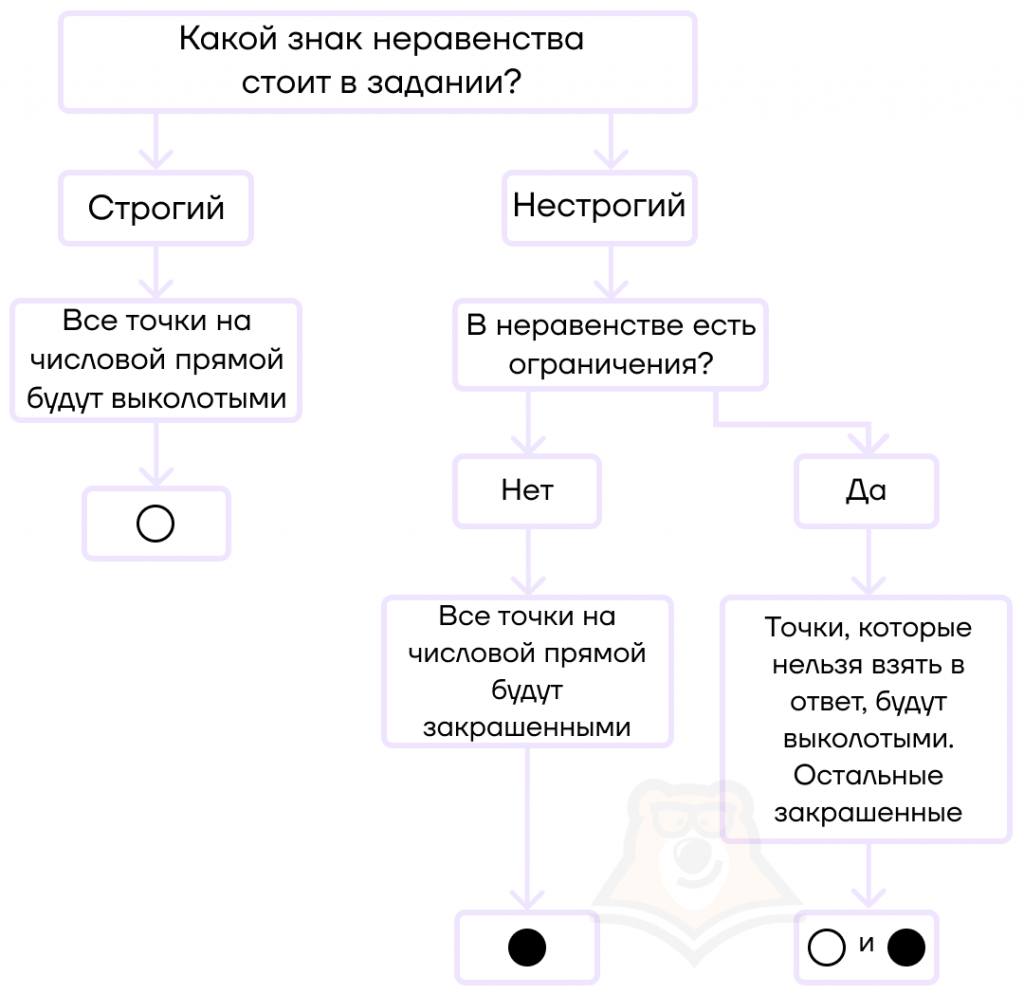
Как быстро определить верное обозначение точки на прямой?

В случае сомнений мы всегда можем проверить себя по простой схеме.

Вывод:
— если знак неравенства строгий, то все точки будут выколотыми;
— если знак неравенства нестрогий, то точки будут закрашенными, кроме тех точек, которые нельзя взять в ответ (например, они не удовлетворяют ОДЗ).

Стоит отметить, что непрерывная функция будет менять знак только в точках, в которых она равна 0. Подробнее узнать про смену знака функции можно в статье «Определение и график функции». Именно поэтому в методе интервалов мы ищем и отмечаем нули функции на прямой — только при переходе через них будет меняться знак функции.

При этом существует способ, с помощью которого можно быстро расставить знаки на прямой. Достаточно определить знак на одном из интервалов, а дальше чередовать знаки при переходе через каждую точку на прямой.

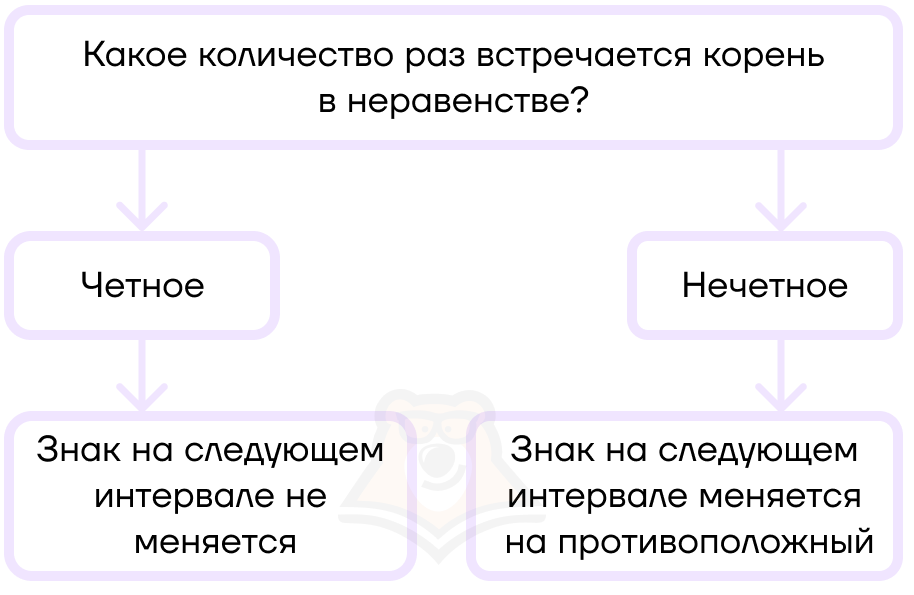
Правила чередования знаков:

Если корень повторяется нечетное количество раз (то есть его степень нечетная), то знак при переходе на следующий интервал меняется.

Если корень повторяется четное количество раз (его степень четная), то знак при переходе на следующий интервал не меняется.

Как правильно чередовать знаки на числовой прямой?

Всегда будет нелишним перепроверить знак на каждом интервале, подставив значения в функцию, и убедиться в правильности расстановки знаков на прямой.

Но при расстановке можно пользоваться следующим алгоритмом, что значительно сократит время расстановки знаков.

Методом интервалов можно решить практически любое неравенство в задании 14 из ЕГЭ по профильной математике, также он может понадобиться в заданиях 8, 11 и 17 «профиля» или в задании 17 ЕГЭ по базовой математике.

На ОГЭ данным методом можно воспользоваться при решении неравенств из первой и второй частей — №13 и №20.
Так что осваивайте метод и 2 балла ЕГЭ или 3 балла ОГЭ будут у вас в кармане. Обязательно следуйте алгоритму решения неравенств методом интервалов, тогда вы точно решите неравенство верно.

Практика

Рассмотрим несколько примеров, чтобы на практике разобрать применение метода интервалов для решения неравенств.

Пример 1. Решить неравенство x²+ 8x — 33 > 0.

Шаг 1. Первым шагом необходимо найти нули функции, для этого приравниваем выражение слева к 0: x²+ 8x — 33 = 0.

Шаг 2. Находим корни уравнения, получаем х = 3 и х = -11.

Шаг 3. Расставляем полученные корни на числовой прямой. Поскольку знак неравенства строгий, то точки должны быть выколотыми:

Шаг 4. Дальше необходимо определить знаки на каждом интервале. Для этого подставим х = -12 в x²+ 8x — 33. Получаем:

(-12)²+ 8*(-12) — 33 = 144 — 96 — 33 = 15.

Получается положительное число, следовательно, интервал от минус бесконечности до -11 положительный. Поскольку все корни в неравенстве повторяются нечетное количество раз (по одному разу), то знаки чередуются.

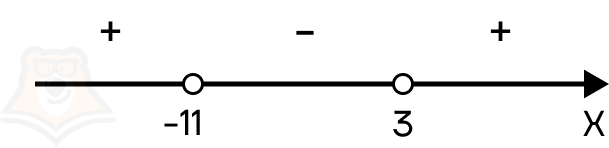
В ответ необходимо записать промежутки с положительным знаком, следовательно, ответом будет х ∈ (-∞; -11) U (3; +∞).

Пример 2. Решить неравенство (frac{2х^2 + 22х — 204}{(х-3)(х+5)} ≤ 0).

1. Находим нули функции.

Нули числителя: 2х²+ 22х — 204 = 0. Решая уравнение, получаем х = 6 и х = -17.

Нули знаменателя: (х — 3)(х + 5) = 0, следовательно, х = 3 и х = -5.

2. Расставляем полученные корни на числовой прямой. Нули числителя будут обозначены закрашенными точками, поскольку знак неравенства нестрогий. А вот нули знаменателя — выколотыми, поскольку знаменатель не может равняться 0, следовательно, и нули знаменателя не должны входить в итоговый промежуток.

3. Определяем знак на крайнем левом промежутке, подставляя х=-20 в дробь:

(frac{2(-20)^2 + 22(-20) — 204}{(-20 -3)(-20 +5)} = frac{2 * 400 — 440 — 204}{(-23) * (-15)} = 156345. )

Следовательно, промежуток положительный.

4. Поскольку каждый корень встречается один раз, то есть нечетное количество раз, то знаки будут чередоваться.

В ответ необходимо включить отрицательные промежутки. Следовательно, ответом будет х ∈ [-17; -5) U (3; 6].

Пример 3. Решить неравенство (frac{1}{х^2} ≥ frac{1}{х+2})

1. Первым делом следует отметить, что знаменатели не могут быть равны 0, следовательно, х²≠ 0 и х + 2 ≠ 0, отсюда получаем х ≠ 0 и х ≠ -2.

2. Теперь перенесем все части неравенства влево:

(frac{1}{х^2} — frac{1}{х+2} ≥ 0).

Приведем к общему знаменателю:

(frac{х + 2 — х^2}{х^2 (х + 2)} ≥ 0).

Для решения неравенства будет удобнее, если перед х² в числителе будет стоять положительный знак, для этого умножим неравенство на -1.

При умножении неравенства на отрицательное число знак неравенства меняется на противоположный.

Получаем:

(frac{х^2 — х — 2}{х^2 (х + 2)} ≤ 0).

Теперь найдем нули функции.

Нули числителя: х²— х — 2 = 0. Тогда х = -1 и х = 2.

Нули знаменателя: х = 0 и х = -2.

2. Расставим корни на числовой прямой, при этом нули числителя будут обозначены закрашенными точками, а нули знаменателя — выколотыми.

3. Определим знак на крайнем левом промежутке, подставив для этого х = -3 в дробь:

(frac{(-3)^2 — (-3) — 2}{(-3)^2 ((-3) + 2)} = frac{9 + 3 — 2}{9 * (-1)} = frac{10}{-9})

Промежуток отрицательный.

4. Дальше расставляем знаки, чередуя их. При этом следует заметить, что х = 0 — корень, повторяющийся четное количество раз (поскольку у х² четная степень). Следовательно, при переходе через эту точку знак функции меняться не будет.

В ответ необходимо включить отрицательные промежутки, следовательно: х ∈ (-∞; -2) U [-1; 0) U (0; 2].

Давайте подведем итог. Для чего мы это изучили?

Конечно же, эти знания пригодятся на экзаменах, а также в решении школьных примеров с 8 класса по 11 класс.

Советуем после прочтения этой статьи попрактиковаться в рубрике «Проверь себя», чтобы закрепить полученные знания. После чего можете приступить к решению заданий посложнее, чтобы на экзамене у вас точно получилось решить подобные задания и набрать за них максимум баллов.

Фактчек

Метод интервалов позволяет упростить решение любого неравенства, а также экономит время, которое ограничено на экзамене.
Чтобы решить неравенство с помощью метода интервалов необходимо найти нули функции, расставить их на числовой прямой, а после определить знак каждого полученного интервала.
Нули функции на прямой обозначаются точками, при этом закрашенные точки включают граничные значения в итоговый промежуток, а незакрашенные, напротив, исключают их из промежутка.
Для определения знака на каждом интервале необходимо подставить любое значение из этого интервала в функцию.
Для упрощения расстановки знаков можно пользоваться правилами чередования, определив знак только на одном интервале, а дальше менять знаки на каждом следующем. При этом если корень встречается в функции нечетное количество раз, то знак при переходе через эту точку на следующий интервал меняется, а если корень встречается четное количество раз, то знак на следующем интервале не меняется.

Проверь себя

Задание 1.
Какие знаки неравенства существуют?

Строгие
Нестрогие
Строгие и нестрогие
Больше и меньше

Задание 2.
Какой знак неравенства может встретиться в методе интервалов?

Только больше или меньше.
Только “больше или равно” или “меньше или равно”.
Только “больше” и “больше или равно” или только “меньше” и “меньше или равно”.
Любой.

Задание 3.
Какое утверждение верное?

Если в неравенстве строгий знак неравенства, то точки на числовой прямой закрашены.
Если в неравенстве строгий знак неравенства, то точки на числовой прямой выколоты.
Если в неравенстве нестрогий знак неравенства, то все точки на числовой прямой закрашены, даже если в неравенстве есть ограничения.
Если в неравенстве нестрогий знак неравенства, то все точки на числовой прямой выколоты.

Задание 4.
Какое утверждение верное?

При переходе на числовой прямой на следующий интервал, знак на интервале всегда будет меняться.
Если корень встречается в неравенстве четное количество раз, то при переходе через него на следующий интервал знак не меняется.
Если корень встречается в неравенстве нечетное количество раз, то при переходе через него на следующий интервал знак не меняется.
Невозможно определить правильное чередование знаков на прямой, не подставляя значение из каждого интервала в функцию.

Задание 5.
Если в неравенстве строгий знак неравенства, то какие скобочки могут встретиться в ответе?

Круглые
Квадратные
И круглые, и квадратные
Ни один из перечисленных вариантов

Ответы: 1. — 3 2. — 4 3. — 2 4. — 2 5. — 1

Источник

Числовая прямая (или, что то же самое, числовая ось) — понятие нехитрое. Более того, числовая прямая — главный помощник в решении любых заданий с неравенствами! Любых. От примитивных линейных неравенств до сложных показательных или логарифмических неравенств, систем неравенств и метода интервалов. Освоим темку, пока всё просто?)

Что такое числовая прямая? Что такое координатная прямая?

С понятием числовой прямой вы все уже сталкивались, когда изучали такие темы как координаты точек (5-й класс), страшное понятие модуля числа (6-й класс), и особенно когда рисовали графики функций (7-й класс). Вспомним ещё разок?)

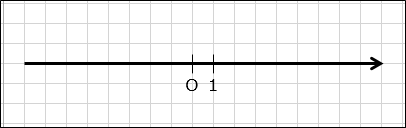
Всё то же самое, ничего нового! Первым делом возьмём и нарисуем в тетрадке самую обычную прямую и дополнительно укажем на ней:

1) Начало отсчёта или начало координат (точку О);

2) Положительное направление (стрелочкой);

3) Масштаб или единицу измерения длины (например, одна тетрадная клетка).

Вот и всё. Про устройство числовой прямой вы тоже давно в курсе (надеюсь). Но на всякий случай напоминаю. Начало координат всегда соответствует числу 0. Все положительные числа изображаются на положительной полуоси справа от нуля, в направлении стрелочки. А все отрицательные — слева от нуля, на отрицательной полуоси. Большее число всегда располагается правее меньшего, а меньшее — левее большего. Элементарно, Ватсон!)

Ну хорошо, прямая и прямая. Но почему — числовая? Ответ очевиден. Каждой точке на прямой соответствует какое-то число. Положительное, отрицательное, целое, дробное, иррациональное — какое угодно. Но — число! Поэтому и прямая — числовая. Это число имеет специальное и вполне научное название — координата точки. Отсюда следует, что числовая прямая — и координатная прямая тоже. Вот так. Два термина в одном флаконе.)

А вот теперь мы с вами колоссально расширяем наши возможности. Начинаем работать с числовой прямой на полную катушку! Готовы?)

Что такое числовой промежуток? Виды числовых промежутков.

В уравнениях было всё просто. Нашли икс, да и записали в ответ. Например, х=2. В неравенствах же ответом обычно служит не одно-два числа, а промежуток. Числовой промежуток. Или даже несколько числовых промежутков. Это и смущает поначалу…) Что это за зверь такой — числовой промежуток?

Всё элементарно.

Числовой промежуток — это просто какой-то кусочек числовой прямой. И всё!

Сейчас начинается самое весёлое. Сейчас мы нашу числовую прямую будем пилить.) Пилить не на дрова, а на… числовые промежутки.)

Вот прям берём числовую прямую и вырезаем из неё какой-то кусочек какими-то точками. Которые, напоминаю, соответствуют каким-то числам. Вот и получаем — числовой промежуток. Разумеется, вырезать конкретный кусочек числовой прямой можно по-разному, да…)

Соответственно, и числовые промежутки в математике бывают разных видов.

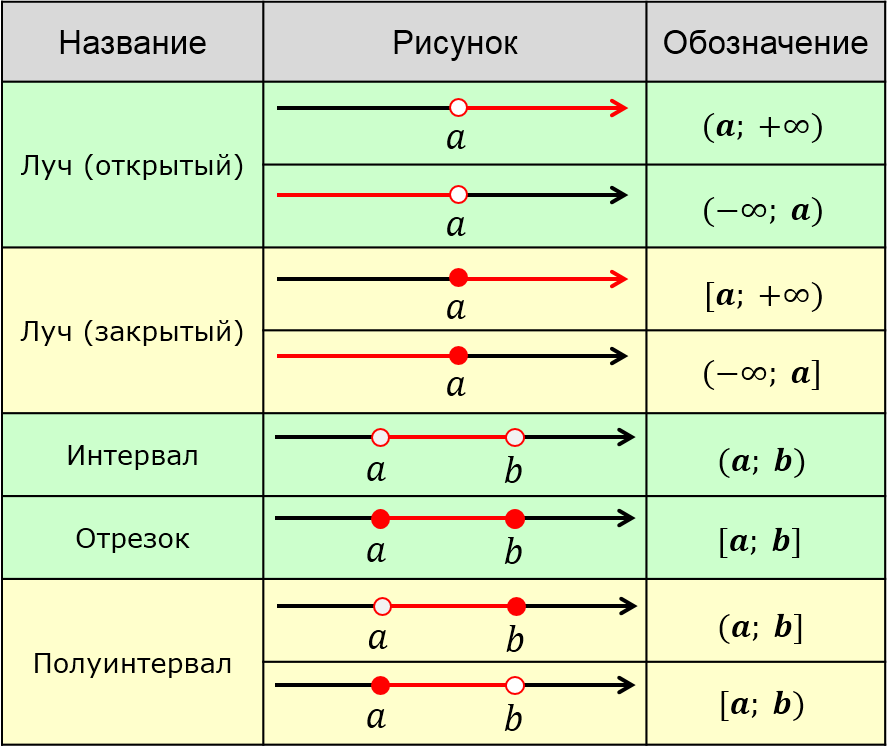
Вот они, эти виды (подкрашены красным цветом):

Смотрим на табличку и… мама родная! Какие-то непонятные кружочки (пустые внутри и закрашенные), какой-то странный иероглиф «∞», да ещё и со знаками плюс/минус, круглые и квадратные скобочки.

Вам и вправду страшно? Возможно… Но сейчас вы увидите, насколько всё просто! Читаем дальше.)

Граничные точки

Я разгадала знак бесконечность… (Земфира)

Те точки, которые нам указывают, в каких местах мы выпиливаем кусочек прямой, так и называются — граничные точки. В таблице эти самые граничные точки обозначены буковками a и b. Точка a — левая граница (меньшее число), точка b — правая граница (большее число).

А может ли числовой промежуток в каком-то направлении быть неограниченным?

А почему — нет? Запросто! Можно распилить числовую прямую не в двух точках, а в какой-то одной точке. И забрать себе одну часть — левую или правую. Бесконечную… Или — луч. Только для обозначения этой бесконечной границы буквы или числа не годятся. Зато есть специальный значок «∞«. Значок этот так и называется — «бесконечность». Очевидно, бесконечность бывает двух видов (точнее, двух знаков) — плюс (+∞) или минус (-∞). В зависимости от того, какой именно луч, какая часть прямой, правая или левая, берётся на дальнейшее рассмотрение.

Кружочки и скобочки…

Граничная точка — это, как и намекает название, точка, задающая границу числового промежутка. Слева или справа. Естественно, у думающих тут же возникает вполне логичный и важный вопрос: А куда относить саму граничную точку? Включать её в состав промежутка или нет?

Именно для ответа на этот вопрос нам и служат всякие кружочки и скобочки в обозначениях и на рисунках!

Запоминаем:

Если граничная точка в числовой промежуток НЕ ВХОДИТ, то на числовой прямой она рисуется НЕЗАКРАШЕННОЙ. Т.е. пустой внутри. В математике такие точки называются выколотыми точками. В обозначениях выколотые точки всегда соседствуют с круглыми скобками «(» или «)».

Если же граничная точка в числовой промежуток ВХОДИТ, то на числовой прямой она рисуется ЗАКРАШЕННОЙ, а в записи обозначается квадратной скобкой «[» или «]».

Вот и вся расшифровка.) Кстати говоря, специальные названия промежутков (луч, отрезок, интервал, полуинтервал) запоминать пока не обязательно. Всё равно поначалу будете путаться. Это для общей эрудиции сделано.) На практике обычно не заморачиваются и говорят «числовой промежуток такой-то…», без уточнения вида — луч, отрезок и т.д. А иногда и совсем кратко — просто «промежуток». Если и вы путаетесь — говорите так же. Не ошибётесь! А спецназвания оставим для старших классов. Но если запомнили (и поняли!) названия промежутков — что ж, только респект!)

Теперь можно потренироваться в записи и чтении числовых промежутков. Чтобы не мычать… Ну что, потренируемся?

Читаем числовые промежутки и рисуем их на оси!

С чтением и рисованием числовых промежутков обычно никаких проблем нет. Нужно только чётко понимать, что означают все эти скобочки и кружочки, что разбирались в предыдущем параграфе.

Например, задан числовой промежуток (0; 5].

Словами эта запись звучит так: числовой промежуток от нуля до пяти, не включая ноль и включая пять.

Читаем (и пишем) именно в таком порядке — от левой границы до правой.

Левая граница (т.е. число 0) соседствует с круглой скобкой «(«, о чём нам и говорят слова «не включая». Этот факт означает, что число 0 в наш промежуток не входит. Например, число 0,1 входит, и даже 0,000001 — ещё входит. Хоть чуть-чуть, да больше нуля. А вот ровно ноль — уже нет…

Пятёрка же — напротив, соседствует с квадратной скобкой «]», что говорит нам о том, что сама она также входит в наш промежуток. И отражено словом «включая» в словесной расшифровке.

А теперь нарисуем наш промежуток на оси. Для этого рисуем числовую прямую и отмечаем на ней граничные точки 0 и 5.

Вот так:

Заметили разницу между нулём и пятёркой? Ну да, трудно не заметить! Точка 0 изображена белой, т.е. незакрашенной. Пустой внутри. Или, по-математически, выколотой точкой. Это, как мы с вами уже выяснили, означает, что ноль — не входит в наш промежуток. В отличие от пятёрки, которая входит в промежуток. И на рисунке, соответственно, нарисованной чёрной. Закрашенной.) Я специально точки такими здоровыми изобразил. Чтобы хорошенько врезались в память…

Итак, мы отметили на оси границы промежутка. Осталось лишь отметить все остальные числа, которые входят в этот промежуток. Вы спросите: Как? Ведь между нулём и пятёркой находится бесконечно много чисел! Это и 1, и 2,5, и 3,14, и 4,9999 и так далее… И что? Все-все отмечать)?

Нет, конечно. Всё гораздо проще!) Сейчас мы с вами отметим на прямой все интересующие нас числа одним махом! Тут есть два варианта. Вариант первый — штриховка. Просто берём и подштриховываем весь кусочек прямой между 0 и 5.

Вот так:

Вариант второй рассмотрим на следующем примере.

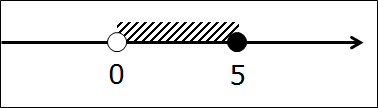
В этот раз дан промежуток такой: [-3; +∞).

Для начала читаем словами название промежутка с гордо поднятой головой: Числовой промежуток от минус трёх до плюс бесконечности, включая минус три!

Вот так. А теперь вопрос на засыпку: почему я оборвал чтение на словах «включая минус три…» и не продолжил мысль гениальными словами «…и не включая плюс бесконечность»?

Всё очень просто. Бесконечность (что плюс, что минус) не может включаться никогда. Это не число, это — символ. Поэтому в подобных записях бесконечность всегда соседствует с круглой скобкой, а в расшифровке говорится просто: «до плюс бесконечности». Или «до минус бесконечности». И всё.

А теперь всё как обычно, рисуем прямую, отмечаем на ней одну единственную точку минус три. Закрашенную, естественно, раз уж скобочка перед минус тройкой — квадратная. Вот так:

И отмечаем все остальные числа, входящие в промежуток от минус тройки до плюс бесконечности. На этот раз я отмечу нужный кусок оси дужкой (от слова дуга) вместо штриховки. Вот так:

Особой разницы между штриховкой и дужками нет. Рисуйте как удобнее. Но в сложных заданиях с неравенствами, где надо постоянно пересекать и объединять много промежутков, дужки предпочтительнее, ибо штриховка куда менее наглядна. Запутаться можно.

Я предпочитаю совмещать оба способа. Получается красиво и наглядно! В следующем уроке, на примерах, сами увидите.)

Вот так рисуются числовые промежутки на оси.

Входит и выходит… ))

А какая нам разница, входит число в указанный промежуток или не входит?

Вопрос смешной. Огромная! Ответ на этот вопрос (входит/не входит) — это ключевой этап в работе с промежутками и с неравенствами вообще! Даже значки специальные придуманы для этого. Вот такие:

∈

∉

За этими странными значками скрываются безобидные слова «принадлежит» и «не принадлежит».

Возьмём, к примеру, промежуток (1; 3].

Входит в этот промежуток, допустим, двойка? Конечно! Раз уж она посерёдке между единичкой и тройкой… А единичка? Э-э-э… Скобка перед ней — круглая! Не входит единичка в наш промежуток. Тройка входит? Попадает на границу, но скобочка — квадратная. Значит, входит! А вот три с половиной — снова не входит. 3,5 строго больше, чем тройка. Выпадает 3,5 из нашего промежутка…

Математически, с помощью значков принадлежности, эти факты можно записать вот так:

Кратко и точно!)

А словами можно прочитать вот так:

Два принадлежит промежутку от одного (не включая) до трёх (включая).

Или:

Один не принадлежит промежутку от одного (не включая) до трёх (включая).

И так далее…

В этом уроке было простое чтение и рисование промежутков на оси. Пока — цветочки. Переходим к ягодкам. К операциям над числовыми промежутками. Те ещё грабли, да…) Об этом — в следующем уроке.

Источник

Метод интервалов

Метод интервалов – простой способ решения дробно-рациональных неравенств. Так называются неравенства, содержащие рациональные (или дробно-рациональные) выражения, зависящие от переменной.

1. Рассмотрим неравенство: $genfrac{}{}{}{0}{displaystyle x^2+2x-3}{displaystyle left( x-7 right)left( x+5 right)} geqslant 0.$

Метод интервалов позволяет решить его за пару минут.

В левой части этого неравенства – дробно-рациональная функция. Рациональная, потому что не содержит ни корней, ни синусов, ни логарифмов – только рациональные выражения. В правой – нуль.

Метод интервалов основан на следующем свойстве дробно-рациональной функции.

Дробно-рациональная функция может менять знак только в тех точках, в которых она равна нулю или не существует.

Найдем нули функции в левой части нашего неравенства. Для этого разложим числитель на множители. (Если вы не помните, что такое нули функции и знак функции на промежутке – смотрите статью «Исследование графика функции»).

Напомним, как раскладывается на множители квадратный трехчлен, то есть выражение вида .

, где x_1 и x_2 — корни квадратного уравнения .

Получим:

$genfrac{}{}{}{0}{displaystyle left( x-1 right)left( x+3 right)}{displaystyle left( x-7 right)left( x+5 right)} geqslant 0.$

Рисуем ось X и расставляем точки, в которых числитель и знаменатель обращаются в нуль.

Нули знаменателя и — выколотые точки, так как в этих точках функция в левой части неравенства не определена (на нуль делить нельзя).

Напомним, что мы изображаем точку на числовой прямой выколотой (пустой), если соответствующее значение переменной никак не может быть решением неравенства. В нашем примере точки и выколотые, потому что в них знаменатель обращается в ноль.

Нули числителя и — закрашены, так как неравенство нестрогое. При x=-3 и x=1 наше неравенство выполняется, так как обе его части равны нулю.

Эти точки разбивают ось X на 5 промежутков.

Определим знак дробно-рациональной функции в левой части нашего неравенства на каждом из этих промежутков. Мы помним, что дробно-рациональная функция может менять знак только в тех точках, в которых она равна нулю или не существует. Это значит, что на каждом из промежутков между точками, где числитель или знаменатель обращаются в нуль, знак выражения в левой части неравенства будет постоянным — либо «плюс», либо «минус».

И поэтому для определения знака функции на каждом таком промежутке мы берем любую точку, принадлежащую этому промежутку. Ту, которая нам удобна.
x<-5 . Возьмем, например, x=-10 и проверим знак выражения $genfrac{}{}{}{0}{displaystyle left( x-1 right)left( x+3 right)}{displaystyle left( x-7 right)left( x+5 right)}$ в левой части неравенства. Каждая из «скобок» отрицательная. Левая часть имеет знак .

Следующий промежуток: -5<x<-3 . Проверим знак при x=-4 . Получаем, что левая часть поменяла знак на .

-3<x<1 . Возьмем x=0 . При x=0 выражение положительно — следовательно, оно положительно на всем промежутке от до .

При 1<x<7 левая часть неравенства отрицательна.

И, наконец, x>7 . Подставим x=10 и проверим знак выражения в левой части неравенства. Каждая «скобочка» положительна. Следовательно, левая часть имеет знак .

Мы нашли, на каких промежутках выражение $genfrac{}{}{}{0}{displaystyle left( x-1 right)left( x+3 right)}{displaystyle left( x-7 right)left( x+5 right)}$ положительно. Осталось записать ответ:

Ответ: .

Обратите внимание: знаки на промежутках чередуются. Это произошло потому, что при переходе через каждую точку ровно один из линейных множителей поменял знак, а остальные сохранили его неизменным.

Мы видим, что метод интервалов очень прост. Чтобы решить дробно-рациональное неравенство методом интервалов, приводим его к виду:

$genfrac{}{}{}{0}{displaystyle Pleft( x right)}{displaystyle Qleft( x right)} geqslant 0$ , или $genfrac{}{}{}{0}{displaystyle Pleft( x right)}{displaystyle Qleft( x right)} > 0$ , или $genfrac{}{}{}{0}{displaystyle Pleft( x right)}{displaystyle Qleft( x right)} leqslant 0$ , или $genfrac{}{}{}{0}{displaystyle Pleft( x right)}{displaystyle Qleft( x right)} < 0$

(в левой части — дробно-рациональная функция, в правой — нуль).

Затем — отмечаем на числовой прямой точки, в которых числитель или знаменатель обращаются в нуль.
Эти точки разбивают всю числовую прямую на промежутки, на каждом из которых дробно-рациональная функция сохраняет свой знак.
Остается только выяснить ее знак на каждом промежутке.
Мы делаем это, проверяя знак выражения $genfrac{}{}{}{0}{displaystyle Pleft( x right)}{displaystyle Qleft( x right)}$ в любой точке, принадлежащей данному промежутку. После этого — записываем ответ. Вот и всё.

Но возникает вопрос: всегда ли знаки чередуются? Нет, не всегда! Надо быть внимательным и не расставлять знаки механически и бездумно.

2. Рассмотрим еще одно неравенство: $genfrac{}{}{}{0}{displaystyle left( x-2 right)^2}{displaystyle left( x-1 right)left( x-3 right)}>0.$

Решение:

Снова расставляем точки на оси X. Точки и — выколотые, поскольку это нули знаменателя. Точка — тоже выколота, поскольку неравенство строгое, и значение переменной x=2 не может быть решением неравенства.

При x<1 числитель положителен, оба множителя в знаменателе отрицательны. Это легко проверить, взяв любое число с данного промежутка, например, x=0 . Левая часть имеет знак :

При 1<x<2 числитель положителен; первый множитель в знаменателе положителен, второй множитель отрицателен. Левая часть имеет знак :

При 2<x<3 ситуация та же! Числитель положителен, первый множитель в знаменателе положителен, второй отрицателен. Левая часть имеет знак :

Наконец, при x>3 все множители положительны, и левая часть имеет знак :

Ответ: .

Почему нарушилось чередование знаков? Потому что при переходе через точку 2 «ответственный» за неё множитель не изменил знак. Следовательно, не изменила знак и вся левая часть нашего неравенства.

Вывод: если линейный множитель стоит в чётной степени (например, в квадрате), то при переходе через точку знак выражения в левой части не меняется. В случае нечётной степени знак, разумеется, меняется.

3. Рассмотрим более сложный случай. От предыдущего отличается тем, что неравенство нестрогое:

$genfrac{}{}{}{0}{displaystyle left( x-2 right)^2}{displaystyle left( x-1 right)left( x-3 right)} geqslant 0.$

Решение:

Левая часть та же, что и в предыдущем примере. Та же будет и картина знаков:

Может, и ответ будет тем же? Нет! Добавляется решение x=2. Это происходит потому, что при x=2 и левая, и правая части неравенства равны нулю — следовательно, эта точка является решением.

Ответ: .

В задачах на ЕГЭ по математике такая ситуация встречается часто. Здесь абитуриенты попадают в ловушку и теряют баллы. Будьте внимательны!

4. Что делать, если числитель или знаменатель не удается разложить на линейные множители? Рассмотрим такое неравенство:

$genfrac{}{}{}{0}{displaystyle left( x+2 right)left( x^2-4x+7 right)}{displaystyle x-5}<0.$

Решение:

Квадратный трехчлен на множители разложить нельзя: дискриминант отрицателен, корней нет. Но ведь это и хорошо! Это значит, что знак выражения при всех одинаков, а конкретно — положителен. Подробнее об этом можно прочитать в статье о свойствах квадратичной функции.

И теперь мы можем поделить обе части нашего неравенства на величину , положительную при всех .

Придём к равносильному неравенству: $genfrac{}{}{}{0}{displaystyle x+2}{displaystyle x-5}<0.$

Решим неравенство методом интервалов. Действуем по алгоритму: числитель левой части равен нулю при x=-2, а знаменатель обращается в ноль при x=5 . Отметим эти точки на координатной прямой. Точки выколоты, потому что неравенство строгое. Эти точки разбивают числовую ось на три интервала. Найдем знаки на каждом из интервалов. На крайнем правом знак положителен, а дальше знаки чередуются.

Нам нужен «интервал со знаком минус», то есть такой, где $genfrac{}{}{}{0}{displaystyle x+2}{displaystyle x-5}<0.$ Выпишем ответ.

Ответ:

Обратите внимание — мы поделили обе части неравенства на величину, о которой точно знали, что она положительна. Конечно, в общем случае не стоит умножать или делить неравенство на переменную величину, знак которой неизвестен.

5. Рассмотрим еще одно неравенство, на вид совсем простое: $genfrac{}{}{}{0}{displaystyle 2}{displaystyle x}<1.$

Решение:

Так и хочется умножить его на . Но мы уже умные, и не будем этого делать. Ведь может быть как положительным, так и отрицательным. А мы знаем, что если обе части неравенства умножить на отрицательную величину — знак неравенства меняется.

Мы поступим по-другому — соберём всё в одной части и приведём к общему знаменателю. В правой части останется нуль:

$genfrac{}{}{}{0}{displaystyle 2}{displaystyle x}-1<0;$

$genfrac{}{}{}{0}{displaystyle 2-x}{displaystyle x}<0;$

$genfrac{}{}{}{0}{displaystyle x-2}{displaystyle x}>0.$

Применим метод интервалов.

Действуем по алгоритму. Отметим на координатной прямой точки x=2 и x=0 . Они выколотые, потому что неравенство строгое. Эти точки разбивают ось Х на три интервала. Расставим знаки на каждом из них.

Ответ:

6. Решите неравенство: $genfrac{}{}{}{0}{displaystyle 5}{displaystyle x}-genfrac{}{}{}{0}{displaystyle 3}{displaystyle 3-x}<0.$

Решение:

Приведем левую часть неравенства к общему знаменателю и преобразуем числитель:

$genfrac{}{}{}{0}{displaystyle 5}{displaystyle x}-genfrac{}{}{}{0}{displaystyle 3}{displaystyle 3-x}<0;$

$genfrac{}{}{}{0}{displaystyle 5}{displaystyle x}+genfrac{}{}{}{0}{displaystyle 3}{displaystyle x-3}<0;$

$genfrac{}{}{}{0}{displaystyle 5x-15+3x}{displaystyle x(x-3)}<0;$

$genfrac{}{}{}{0}{displaystyle 8x-15}{displaystyle x(x-3)}<0.$

Применим метод интервалов:

Числитель равен нулю при $displaystyle x=1frac{7}{8}.$ Знаменатель обращается в ноль при x=0 или x=3 . Неравенство строгое, поэтому все эти точки на числовой оси отмечаем как пустые.

Если x>3 , то $displaystyle frac{8x-15}{x(x-3)}>0$ . Далее знаки чередуются.

Нам нужны «интервалы со знаком минус». Выпишем их и получим ответ.

Ответ: $displaystyle xin(-infty;0)cup(1frac{7}{8};3).$

7. Решите неравенство $genfrac{}{}{}{0}{displaystyle 2x-7}{displaystyle x^2+2x-8}>1.$

Решение:

Приведем неравенство к виду: $genfrac{}{}{}{0}{displaystyle P(x)}{displaystyle Q(x)}>0.$

Для этого все перенесем в левую часть, приведем к общему знаменателю и разложим числитель и знаменатель на множители. Применяем формулу разности квадратов и формулу разложения квадратного трехчлена на множители

Получим:

$genfrac{}{}{}{0}{displaystyle 2x-7}{displaystyle x^2+2x-8}-1>0;$

$genfrac{}{}{}{0}{displaystyle 2x-7-x^2-2x+8}{displaystyle x^2+2x-8}>0;$

$genfrac{}{}{}{0}{displaystyle -x^2+1}{displaystyle x^2+2x-8}>0;$

$genfrac{}{}{}{0}{displaystyle x^2-1}{displaystyle x^2+2x-8}<0;$

$genfrac{}{}{}{0}{displaystyle (x-1)(x+1)}{displaystyle (x+4)(x-2)}<0.$

Найдем нули числителя и знаменателя и отметим их на числовой оси:

Выпишем интервалы, где неравенство выполняется, и получим ответ.

Ответ:

8. Решите неравенство:

Решение:

Разложим левую часть неравенства на множители.

Для этого вынесем общий множитель за скобки, а затем воспользуемся формулой:

Получим:

Применим метод интервалов.

Левая часть неравенства обращается в ноль, если x=-7 , x=-2 или x=0 . Нанесем эти точки на координатную прямую. Все точки закрашенные, так как неравенство нестрогое, в нем присутствует знак «меньше или равно».

Ответ:

9. Решите неравенство: $genfrac{}{}{}{0}{displaystyle x^3-3x^2-x+3}{displaystyle x^2+3x+2}geqslant 0.$

Решение:

Разложим числитель на множители с помощью группировки:

Знаменатель тоже разложим на множители:

Неравенство примет вид:

$genfrac{}{}{}{0}{displaystyle (x-3)(x-1)(x+1)}{displaystyle (x+1)(x+2)}geqslant 0.$

Мы видим, что числитель равен нулю при

Знаменатель равен нулю при . Множитель (x+1) стоит в числителе и в знаменателе, и он не может равняться нулю.

Отметим полученные точки на координатной прямой. Две из них закрашены (это 3 и 1), а две нет (это -1 и -2). Найдем знаки на каждом промежутке.

При переходе через точку x=-1 знак не меняется, так как множитель (x+1) присутствует и в числителе, и в знаменателе.

Выпишем ответ.

Ответ:

10. Решите неравенство: $genfrac{}{}{}{0}{displaystyle x^4-3x^3+2x^2}{displaystyle x^2-x-30}< 0.$

Решение:

Разложим числитель и знаменатель на множители:

Напомним, что выражение мы разложили на множители, решив квадратное уравнение:

$x^2-x-30=0 Leftrightarrow left[ begin{gathered} x = -5, \ x = 6; \ end{gathered} right.$

Неравенство примет вид:

$genfrac{}{}{}{0}{displaystyle x^2(x-1)(x-2)}{displaystyle (x+5)(x-6)}< 0.$

Воспользуемся методом интервалов.

Числитель дроби в левой части неравенства равен нулю, если Знаменатель обращается в ноль, если x=-5 или x=6 . Отметим эти точки на координатной прямой и определим знаки на интервалах.

Ответ:

11. Решите неравенство: $genfrac{}{}{}{0}{displaystyle (x-1)(x+2)^2}{displaystyle -1-x}geqslant 0.$

Решение:

Можно сразу применить метод интервалов.

Но лучше, чтобы не запутаться со знаками, умножить обе части неравенства на (-1) и не забыть поменять знак неравенства на противоположный.

$genfrac{}{}{}{0}{displaystyle (x-1)(x+2)^2}{displaystyle -1-x}geqslant 0 Leftrightarrow genfrac{}{}{}{0}{displaystyle (x-1)(x+2)^2}{displaystyle x+1}leqslant 0.$

Теперь применим метод интервалов.

Отметим на координатной прямой нули числителя и знаменателя и определим знаки на интервалах.

Обратите внимание, что знак не меняется при переходе через точку x=-2 , так как множитель x+2 входит в выражение в левой части неравенства в четной степени.

Ответ:

12. Решите неравенство: $genfrac{}{}{}{0}{displaystyle x^2-1}{displaystyle x^2-6x-7}< 0.$

Решение:

Разложим числитель и знаменатель на множители:

$genfrac{}{}{}{0}{displaystyle x^2-1}{displaystyle x^2-6x-7}< 0 Leftrightarrow genfrac{}{}{}{0}{displaystyle (x-1)(x+1)}{displaystyle (x-7)(x+1)}< 0.$

Сократим на множитель (x+1) при условии, что xneq-1 .

Здесь мы действуем чуть иначе, чем в задаче 9.

Неравенство равносильно системе:

$genfrac{}{}{}{0}{displaystyle (x-1)(x+1)}{displaystyle (x-7)(x+1)}< 0 Leftrightarrow$ $begin{cases} x neq -1, \ displaystyle frac{x-1}{x-7} <0. \ end{cases}$

Решаем второе неравенство системы методом интервалов:

Второму неравенству удовлетворяют точки 1<x<7 .

Точка x=-1 в этот промежуток не входит.

Ответ:

13. Решите неравенство: $genfrac{}{}{}{0}{displaystyle x^2-4x-5}{displaystyle (x-2)^4(x-4)^5} geqslant 0.$

Решение:

Разложив числитель на множители, получим:

$genfrac{}{}{}{0}{displaystyle x^2-4x-5}{displaystyle (x-2)^4(x-4)^5} geqslant 0 Leftrightarrow genfrac{}{}{}{0}{displaystyle (x-5)(x+1)}{displaystyle (x-2)^4(x-4)^5} geqslant 0.$

Применим метод интервалов.

Отметим на числовой оси точки, в которых числитель и знаменатель обращаются в ноль. Обратите внимание, что точки -1 и 5 закрашены, а точки 2 и 4 пустые.

Определим знаки на интервалах.

Знак не меняется при переходе через точку x=2 , так как множитель x-2 входит в выражение в левой части неравенства в четной степени. При переходе через точку 4 знак меняется, степень соответствующего множителя нечетная.

В ответе запишем интервалы, на которых неравенство выполняется.

Ответ:

14. Решите неравенство: $genfrac{}{}{}{0}{displaystyle (x^3-64)(x^2-1)}{displaystyle x^3+1} leqslant 0.$

Разложим числитель и знаменатель на множители, используя формулы сокращенного умножения: суммы и разности кубов, разности квадратов.

$genfrac{}{}{}{0}{displaystyle (x^3-64)(x^2-1)}{displaystyle x^3+1} leqslant 0 Leftrightarrow genfrac{}{}{}{0}{displaystyle (x-4)(x^2+4x+16)(x-1)(x+1)}{displaystyle (x+1)(x^2-x+1)}leqslant 0.$

Кажется, что неравенство сложное. Попробуем разложить на множители выражения и

Оказывается, что дискриминанты соответствующих квадратных уравнений отрицательны, поэтому и при всех х.

Разделим обе части неравенства на эти положительные выражения.

Получим: $genfrac{}{}{}{0}{displaystyle (x-4)(x-1)(x+1)}{displaystyle (x+1)} leqslant 0.$

Неравенство равносильно системе:

$begin{cases} (x-4)(x-1) leqslant 0\ x neq -1 \ end{cases} .$

Решим первое неравенство системы методом интервалов:

Его решением является промежуток [1;4], причем точка x=-1 в этот промежуток не входит.

Ответ:

Мы показали на различных примерах, как применяется метод интервалов.

Сделаем вывод:
Метод интервалов помогает решать дробно-рациональные неравенства по алгоритму. Правила просты: приводим неравенство к такому виду, что в его левой части – произведение множителей или дробь, а в правой – ноль. Находим точки, в которых левая часть обращается в ноль или не определена. Отмечаем на числовой оси эти точки. Они разбивают числовую ось (или координатную прямую) на интервалы, на каждом из которых функция в левой части неравенства сохраняет свой знак. Определяем знаки на интервалах, помня о правилах чередования знаков. И записываем ответ.

Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Метод интервалов» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена:
08.05.2023

Источник

Закрашенная и незакрашенная точка

Отрезки и интервалы: в чем разница?

Почему бесконечности всегда стоят в круглых скобках

Примеры решения неравенств

<img decoding="async" onError="javascript: wp_broken_images = window.wp_broken_images || function(){}; wp_broken_images(this);" src="https://ik-study.ru/uploads/s/v/d/w/vdwu9qwztel6/img/hgsT8tKi.jpg" />Решение неравенств

Метод интервалов

Перенос знаков

Выбор точек

Система и совокупность

Точка знакопостоянства

Узнать ещё

С3 ГИА – построение графиков функций.

На этой странице вы узнаете

Метод интервалов

Практика

Фактчек

Проверь себя

Метод интервалов

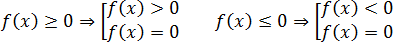
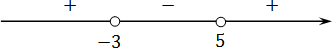
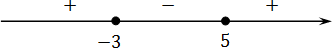
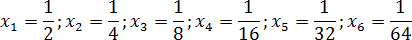
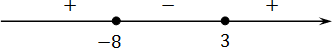
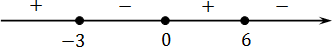
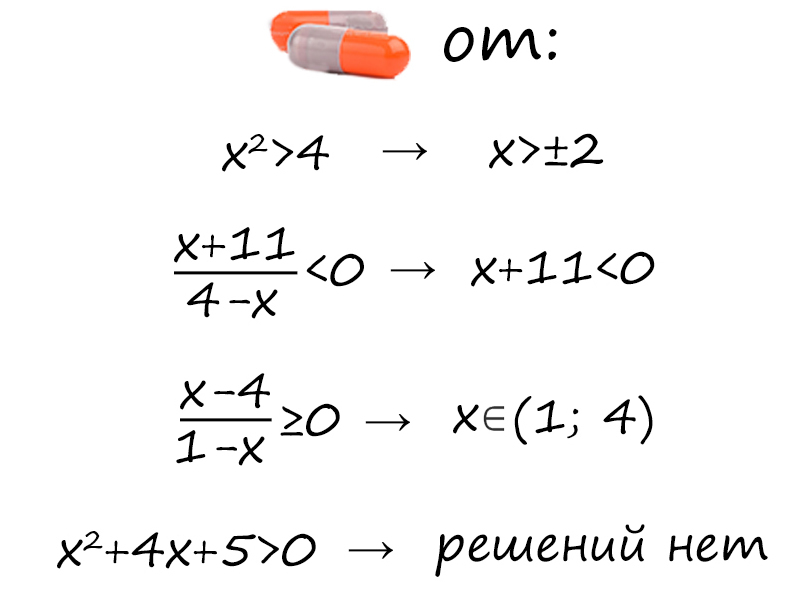Решение неравенств