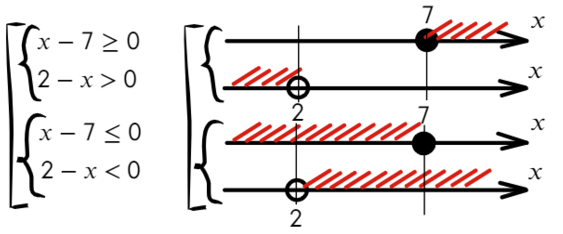
Закрашенная и незакрашенная точка
Эта ассоциация поможет легко запомнить, выколотая точка или закрашенная на числовой прямой.
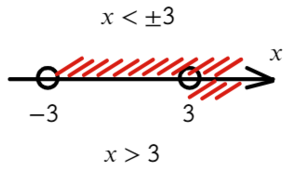
Сравните неравенства, при которых точка заштрихована: x≥a или x≤b и неравенства, в которых точка выколотая: x>a, x или Светлана Иванова, 27 Сен 2012
Сегодня мы узнаем, как использовать метод интервалов для решения нестрогих неравенств. Во многих учебниках нестрогие неравенства определяются следующим образом:
— это неравенство вида которое равносильно совокупности строгого неравенства и уравнения:
В переводе на русский язык это значит, что нестрогое неравенство это объединение классического уравнения и строгого неравенства Другими словами, теперь нас интересуют не только положительные и отрицательные области на прямой, но и точки, где функция равна нулю.
Отрезки и интервалы: в чем разница?
Прежде чем решать нестрогие неравенства, давайте вспомним, чем интервал отличается от отрезка:
- — это часть прямой, ограниченная двумя точками. Но эти точки не принадлежат интервалу. Интервал обозначается круглыми скобками: и т.д.;
- — это тоже часть прямой, ограниченная двумя точками. Однако эти точки тоже являются частью отрезка. Отрезки обозначаются квадратными скобками: и т.д.
Чтобы не путать интервалы с отрезками, для них разработаны специальные обозначения: интервал всегда обозначается выколотыми точками, а отрезок — закрашенными. Например:
На этом рисунке отмечен отрезок и интервал Обратите внимание: концы отрезка отмечены закрашенными точками, а сам отрезок обозначается квадратными скобками. С интервалом все иначе: его концы выколоты, а скобки — круглые.
Метод интервалов для нестрогих неравенств
К чему была вся эта лирика про отрезки и интервалы? Очень просто: для решения нестрогих неравенств все интервалы заменяются отрезками — и получится ответ. По существу, мы просто добавляем к ответу, полученному методом интервалов, границы этих самых интервалов. Сравните два неравенства:
Задача. Решите строгое неравенство:
Решаем методом интервалов. Приравниваем левую часть неравенства к нулю:
( x − 5)( x + 3) = 0;
x − 5 = 0 ⇒ x = 5;
x + 3 = 0 ⇒ x = −3;
Отмечаем полученные корни на координатной оси:
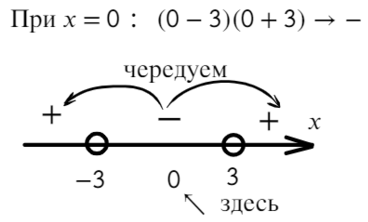
Справа стоит знак плюс. В этом легко в этом убедиться, подставив миллиард в функцию:
f ( x ) = ( x − 5)( x + 3)
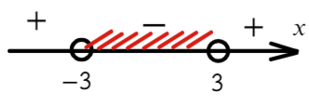
Осталось выписать ответ. Поскольку нас интересуют положительные интервалы, имеем:
Задача. Решите нестрогое неравенство:
Начало такое же, как и для строгих неравенств: работает метод интервалов. Приравниваем левую часть неравенства к нулю:
( x − 5)( x + 3) = 0;
x − 5 = 0 ⇒ x = 5;
x + 3 = 0 ⇒ x = −3;
Отмечаем полученные корни на координатной оси:
В предыдущей задаче мы уже выяснили, что справа стоит знак плюс. Напомню, в этом легко убедиться, подставив миллиард в функцию:
f ( x ) = ( x − 5)( x + 3)
Осталось записать ответ. Поскольку неравенство нестрогое, а нас интересуют положительные значения, имеем:
Итак, основное отличие строгих и нестрогих неравенств:
- В строгих неравенствах нас не интересуют концы отрезка, поэтому они отмечаются выколотыми точками. Такие точки никогда не входят в ответ, о чем говорят круглые скобки на первом ответе: x ∈ (−∞; −3) ∪ (5; +∞);
- И наоборот, в нестрогих неравенствах концы отрезка входят в ответ. На графике они отмечаются закрашенными точками, а в ответе указываются квадратными скобками: x ∈ (−∞; −3] ∪ [5; +∞).
Вот и вся разница! Просто запомните: в строгих неравенствах точки выколоты, а в нестрогих — закрашены.
Почему бесконечности всегда стоят в круглых скобках
У внимательного читателя наверняка возник вопрос: почему бесконечности отмечаются круглыми скобками даже в нестрогих неравенствах? Например, почему в последней задаче мы пишем
Что ж, это не опечатка. Бесконечность действительно обозначается круглой скобкой, даже если неравенство — нестрогое. Чтобы понять, почему так происходит, достаточно вспомнить определение бесконечности.
— это гипотетическое число, которое больше любого другого числа, участвующего в решении.
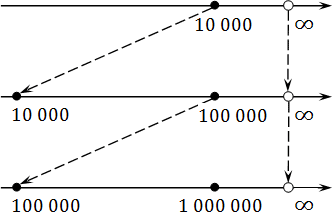
Трудность заключается в том, что нельзя работать с бесконечностью напрямую. Мы можем лишь приблизиться к ней, подставляя такие зверские числа, как 1 000 000 и даже 1 000 000 000. Но добраться до самой бесконечности все равно нельзя.
Именно поэтому бесконечность обозначают круглыми скобками. Ведь хотя бесконечность и ограничивает всю числовую прямую, сама она не принадлежит этой прямой.
Ситуация такая же, как с границами интервалов. Рассмотрим все числа из интервала:
Эта запись означает, что число не принадлежит интервалу, однако любое число, которое больше нуля и меньше единицы — принадлежит. В частности, этому интервалу принадлежат следующие числа:
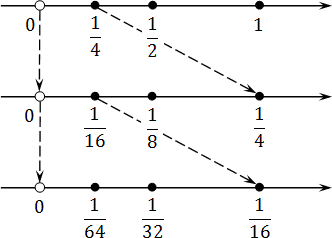
Попробуем отметить эти числа на координатной прямой. Поскольку каждое следующее число вдвое меньше предыдущего, нам придется несколько раз менять масштаб. Получим вроде этого:
Что дает нам этот график? Оказывается, при достаточно крупном масштабе можно отметить любое число, сколь угодно близкое к нулю. При этом сам ноль никуда не денется — он остается недостижимой границей. Именно это и подразумевается, когда речь заходит о концах интервала.
То же самое происходит и с бесконечностью. Разница лишь в том, что масштаб надо не увеличивать, а уменьшать:
Мы можем сколь угодно долго идти к бесконечности, но так и не достигнем ее. Вот почему бесконечности обозначают круглыми скобками, подобно границам интервала.
Примеры решения неравенств
В заключение кратко разберем два нестрогих неравенства. И если в первой задаче еще есть пояснения, то вторая задача будет оформлена именно так, как и надо оформлять настоящее решение.
Как обычно, приравниваем все к нулю:
( x + 8)( x − 3) = 0;
x + 8 = 0 ⇒ x = −8;
x − 3 = 0 ⇒ x = 3.
Теперь рассматриваем функцию, которая находится в левой части неравенства:
f ( x ) = ( x + 8)( x − 3)
Подставим в эту функцию бесконечность — получим выражение вида:
Чертим координатную ось, отмечаем корни и расставляем знаки:
Поскольку мы решаем неравенство или, что то же самое, осталось записать ответ:
x (12 − 2 x )(3 x + 9) ≥ 0
x (12 − 2 x )(3 x + 9) = 0;
x = 0;
12 − 2 x = 0 ⇒ 2 x = 12 ⇒ x = 6;
3 x + 9 = 0 ⇒ 3 x = −9 ⇒ x = −3.
x ≥ 6 ⇒ f ( x ) = x (12 − 2 x )(3 x + 9) → (+) · (−) · (+) = (−) x ∈ (−∞ −3] ∪ [0; 6].
 Решение неравенств
Решение неравенств
Метод интервалов
Перенос знаков
Выбор точек
Система и совокупность
Точка знакопостоянства
Что нельзя делать в неравенстве, даже под пытками:
1) Домножать на знаменатель.
2) Умножать/делить на отрицательное число, не меняя знак.
3) Убирать бездумно логарифм или основание.
Начнем с простого:
Линейные уравнения решаются обычным переносом. Икс в одной части оставим, а числа перенесем в другую:
А само значение −4 нам подходит?
Нет, поэтому ставим круглые скобочки ()
Разберемся со скобками:
Когда мы включаем точку (корень числителя), или стоят знаки нестрогие ( ≥, ≤ ), ставим «[ ]» — квадратные скобки. Если не включаем (корень знаменателя), или знак строгий (>,
Если же возьмем пример, где придется делить или умножать на отрицательное число, то знак поменяется:
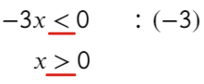
Следующий пример уже с дробью:
Приравняем числитель к нулю и скажем, что знаменатель не равен нулю:
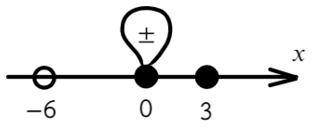
к.ч. (корни числителя)
к.з. (корни знаменателя)
Расставляем корни числителя и знаменателя на одной прямой (сколько решаем неравенств, столько же чертим прямых). Попробуем подставить х = 0, чтобы определить знаки:
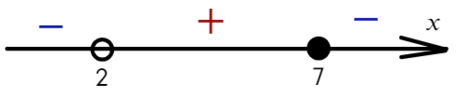
Там, где «0» (перед двойкой), ставим знак «−», а дальше знаки чередуем:
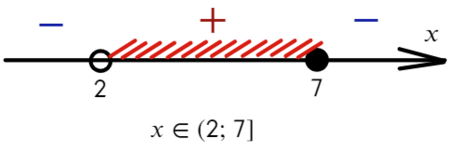
Из-за того, что знаком неравенства был «≥», нам подходят промежутки со знаком «+» и закрашенная точка:
Когда мы включаем точку (корень числителя), или стоят знаки (≥, ≤), ставим «[ ]» — квадратные скобки. Если не включаем (корень знаменателя), или знак строгий (>,
Данный пример можно решить по-другому. Подумаем, когда дробь больше нуля? Конечно, когда числитель и знаменатель — положительные значения или когда оба отрицательные. Поэтому данное неравенство можно разбить на две системы в совокупности:
Отметим на прямой решение каждого неравенства.
Решением совокупности «[» является тот участок, который включен хотя бы в одно неравенство.
Мой любимый пример:
Покажу мастер-класс, как делать не надо. Дома не повторять!
А теперь через метод интервалов разберемся, как сделать правильно:
Там, где ноль, ставим знак «−», рисуем прямую и отмечаем корни каждой скобки. А дальше чередуем:
В данном неравенстве знак меньше, поэтому записываем в ответ промежуток, где знак «−».
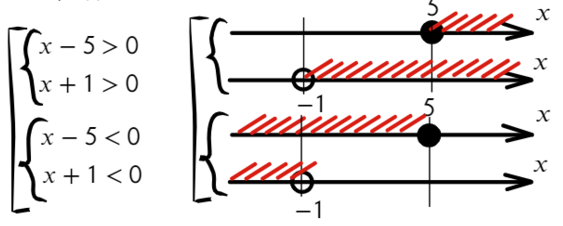
Перейдем к квадратному уравнению:
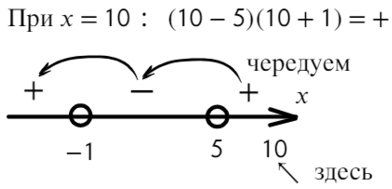
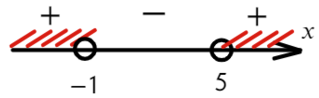
Разложим на множители и подставим x = 10, чтобы определить знак:
Нам требуются положительные значения:
Второй способ разложить на множители:
Ответ: x ∈ (−oo; −1) ∪ (5; +oo).
А теперь простой, но крайне показательный пример:
Убирать квадрат ни в коем случае нельзя. Простенький контрпример:
Надеюсь, убедил. Вместо знака больше поставим знак равно и попробуем решить методом интервалов:
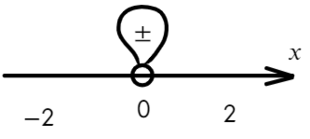
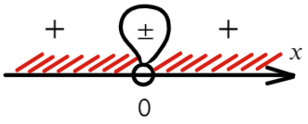
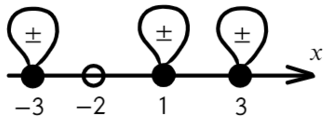
Если корень повторяется четное количество раз, то в этой точке знак меняться не будет. Отмечать будем такую точку восклицательным знаком (а внутри него ±, чуть ниже объясню, зачем это).
В данном неравенстве знак больше, тогда отметим те промежутки, где стоит знак «+».
Только точка «0» не подходит, 0 > 0 — неверно!
Ответ: x ∈ R <0>или x ∈ ( − oo; 0) ∪ (0; +oo).
Переходим на новый уровень:
Все говорят, что домножать на знаменатель нельзя, а я говорю, что буду! (joke)
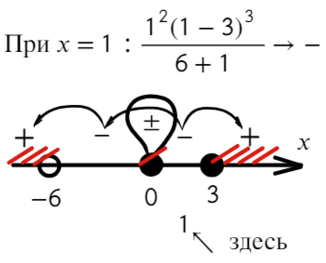
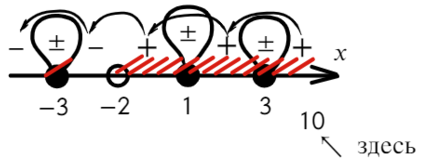
По методу координат найдем корни числителя и знаменателя:
Отметим все корни на одной прямой (сколько неравенств, столько же и прямых). Ноль — корень четной кратности, над ним рисуем восклицательный знак! Если это корень числителя, то точка будет закрашена, если знаменателя — выколота (на ноль делить нельзя).
Требуется найти промежутки, где выражение больше или равно нулю. Нам подойдут все «промежутки», где знак плюс. Для этого подставим значение x = 1 и с промежутка [0; 3] начнем расставлять знаки. Там же находится единица.
Вот для чего ставят в восклицательном знаке ±: чтобы не потерять отдельные точки, в данном случае 0.
Ответ: (−oo; − 6) ∪ <0>∪ [ 3; +oo).
По той же схеме корни числителя и знаменателя:
Определим знак при x = 10 и расставим знаки с промежутка, где присутствует 10:
Все точки от − 2 закрашены, значит эти промежутки можно объединить в один.
Точка x = 3 встречается 3 раза (2 раза в числителе и 1 раз в знаменателе), знак через нее меняться будет! А также эта точка будет выколота, проверь это, подставив в уравнение x = 3. На ноль же делить нельзя?
Узнать ещё
Эта ассоциация поможет легко запомнить, выколотая точка или закрашенная на числовой прямой.
Сравните неравенства, при которых точка заштрихована: x≥a или x≤b и неравенства, в которых точка выколотая: x>a, x<b. В первом случае в самом знаке неравенства есть прямая подсказка, что точку надо заштриховать, уже и штриховать начали, первый штрих сделали: ≥ или ≤. Поэтому и на чертеже на числовой прямой в таких неравенствах — заштрихованная точка:
А в знаках > или < штриха дополнительного нет, значит, и закрашивать точку не надо. Получилась выколотая точка.
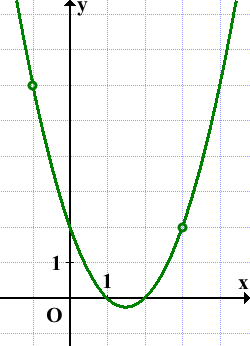
С3 ГИА – построение графиков функций.
Для того, чтобы хорошо решать это задание, нужно быть знакомым с построением различных графиков функций, в том числе содержащих модуль. Предлагаю тем, кто неуверенно себя чувствует при решении таких заданий, перейти по ссылкам и изучить (или повторить) данные разделы. Задание С3 связано как с исследованием расположения корней квадратного трехчлена, так и с определением области определения функции, и области ее значений. На конкретных примерах мы попробуем научиться решать различные типы таких заданий.
Задача 1. Построить график функции 


Задача о касательных к параболе
Графиком предложенной функции является парабола, ветви которой направлены вверх и вершина, которую подняли вверх на 4 единицы, лежит на оси ординат. Ее координаты (0;4). Второй график – это прямая, проходящая через начало координат, причем ее наклон может меняться (его определяет коэффициент 
Поскольку точка касания – единственная общая точка данных графиков, то дискриминант данного уравнения равен нулю: 





Задача 2. Построить график функции 

График, который подвергнется преобразованиям
Строить этот график будем поэтапно: сначала построим график 
“Опрокидываем” преобразованный график
Осталось выяснить, в каком же случае прямая 



Задача 3. Построить график функции 

Также построим график в два этапа: саму параболу (координаты ее вершины (-1;-9)), затем отразим всю часть, лежащую ниже оси х, вверх: Тогда три и более (а именно – четыре) общих точки графики 

Задача 4. Построить график функции 


Из условия ясно, что такой график состоит из двух кусочков. Один из них – прямая, второй – парабола. Первый существует в точке 1 и левее ее, второй – правее этой точки. Нарисуем эти графики:
Координаты вершины параболы:
Красным показаны прямые 



Задача 5. Построить график функции 

Давайте сначала попробуем упростить данное выражение, кроме того, нужно, безусловно, определить область допустимых значений данной функции. ОДЗ: 
Определение коэффициента наклона касательной
Полученная функция – квадратичная, ее графиком является парабола. Данная парабола симметрична относительно оси y, ее вершина имеет координаты (0; 25). Необходимо заметить, что точка с координатами (1; 26) – выколотая точка (по ОДЗ). Тогда прямая, проходящая через начало координат – а именно таким будет график функции 














Задача 6. Построить график функции 

Гипербола с выколотой точкой
Определим ОДЗ функции: 








Задача 7. Построить график функции 

Подбор коэффициента наклона прямой
Определим ОДЗ функции: 







Задача 8. Построить график функции 

Построение функции с модулем
Эта функция – функция типа 






Задача 9. Построить график функции 

Кубическая парабола с выколотой точкой
Определим ОДЗ исходной функции: 

Задача 10. Построить график функции 

Для того, чтобы построить данный график, необходимо раскрыть модули. С этой целью приравняем подмодульное выражение к нулю, чтобы узнать, в какой точке оно меняет знак: 

У нас получились три интервала, на каждом из которых можно теперь раскрыть модули: 1. 



Она выглядит так:
Зеленым цветом показано одно из возможных положений прямой 


Ответ: 


Обратим внимание на то, что у двух данных парабол ветви направлены в разные стороны: у первой старший коэффициент отрицателен, а у второй – положителен. Поэтому вершины будут лежать по одну сторону от оси, если одна из них будет иметь точки пересечения с осью х, а другая – нет. Иными словами, дискриминант одного квадратного уравнения должен быть положителен, а другого – отрицателен. Это приводит нас к двум системам неравенств:
Дискриминант и наличие пересечений параболы с осью х

Или же наоборот: 
Определим дискриминанты обоих квадратных уравнений:
Тогда имеем систему неравенств:




Мы рассмотрели один способ решения – с использованием дискриминанта. Есть еще один способ решения такого задания – с помощью координат вершины параболы. Решим последнюю задачу вторым способом.
Нам потребуется определить координаты вершин обеих парабол:
1.

Решение этого неравенства и есть ответ задачи:
Информация
Если дробь (displaystyle frac{(x^2+4)(x-1)}{1-x}) просто сократить, то получим
(displaystyle frac{(x^2+4)(x-1)}{1-x}=-x^2-4)
При этом левая и правая части выражений имеют разные области допустимых значений:
- дробь (displaystyle frac{(x^2+4)(x-1)}{1-x})не определена при (displaystyle x=1{small ; } )
- многочлен (displaystyle -x^2-4) определен для всех (displaystyle xsmall.)
Равенство выражений имеет место только для тех (displaystyle xsmall,) для которых определены оба выражения.
Поэтому нужно обязательно записать область определения исходной функции.
Область определения функции
(displaystyle y=frac{(x^2+4)(x-1)}{1-x}small.)
Знаменатель не равен нулю:
(displaystyle x,cancel{=},1small.)
В области определения исходного выражения получаем:
(displaystyle frac{(x^2+4)(x-1)}{1-x}=frac{(x^2+4)cancel{(x-1)}}{-cancel{(x-1)}}=-(x^2+4)=-x^2-4small.)
Значит, с учетом области определения исходного выражения, необходимо построить параболу с выколотой точкой при(displaystyle x=1{small : } )
(displaystyle begin{cases}y=-x^2-4,\x,cancel{=},1.end{cases})
И определить, при каких значениях параметра (displaystyle k) прямая (displaystyle y=kx) имеет с построенной параболой ровно одну общую точку.
Построим график функции (displaystyle y=-x^2-4) для (displaystyle x,cancel{=},1small.)
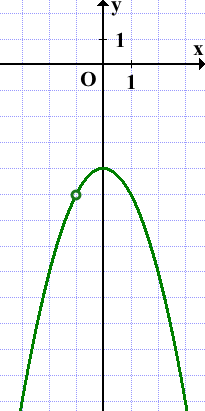
1. Строим параболу (displaystyle y=-x^2-4small.)
Это парабола (displaystyle y=-x^2{ small ,}) сдвинутая на (displaystyle 4) единицы вниз.
2. Так как (displaystyle x,cancel{=},1small,) выкалываем на графике точку с абсциссой (displaystyle x=1small.)
Отметим, что выколотая точка имеет координаты (displaystyle (1;,-5)small.)
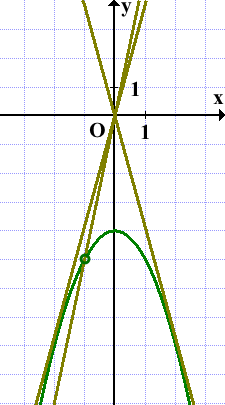
Прямая (displaystyle y=kx) – это прямая, которая
- проходит через начало координат вне зависимости от значения (displaystyle k{small ; } )
- при изменении (displaystyle k) поворачивается вокруг начала координат и принимает все положения кроме вертикального.
Тогда прямая (displaystyle y=kx) имеет с построенным графиком ровно одну общую точку, если
- прямая проходит через выколотую точку параболы (красная прямая),
-
прямая касается параболы (displaystyle y=-x^2-4) (зеленые прямые).
Найдем, чему равно (displaystyle k) в каждом из этих случаев.
Если прямая (displaystyle y=kx) проходит через выколотую точку параболы, то (displaystyle k=-5)
Рассмотрим случай, когда прямая проходит через выколотую точку.
Прямая пересекает параболу (displaystyle y=-x^2-4) в двух точках (одна из точек не видна на рисунке).
Но точка (displaystyle (1;-5)) является выколотой точкой графика. Поэтому прямая и парабола имеют одну общую точку.
Прямая проходит через точку (displaystyle (1;-5){ small ,}) если при (displaystyle x=1) значение (displaystyle y=-5small.)
При подстановке в (displaystyle y=kx) получаем:
(displaystyle -5=kcdot 1small,)
(displaystyle k=-5small.)
Если прямая (displaystyle y=kx) касается параболы, то
(displaystyle k=4) или (displaystyle k=-4)
Рассмотрим случай, когда прямая касается параболы.
В общей точке прямой (displaystyle y=kx) и параболы (displaystyle y=-x^2-4) значения (displaystyle y) совпадают. Поэтому приравняем их:
(displaystyle kx=-x^2-4small,)
(displaystyle x^2+kx+4=0small.)
Поскольку прямая и парабола имеют только одну общую точку, то у данного уравнения должно быть одно решение.
Квадратное уравнение (displaystyle x^2+kx+4=0) имеет ровно один корень, если его дискриминант равен (displaystyle 0small.)
Приравняем дискриминант к нулю:
(displaystyle k^2-4cdot4=0small,)
Тогда
(displaystyle k^2=4^2small,)
(displaystyle k=4) или (displaystyle k=-4small.)
Таким образом, прямая (displaystyle y=kx) и график функции (displaystyle y=frac{(x^2+4)(x-1)}{1-x}) имеют одну общую точку при
(displaystyle k=-5) или (displaystyle k=4) или (displaystyle k=-4small.)
Ответ: (displaystyle kin{-5}cup{-4}cup{4}small.)
Вопрос от
1489 дней назад
Зачем мы находим выколотые точки в этом задании? Что они дают, для чего нужны, и почему конкретно в этом примере х не должно равняться 0, но функция проходит через 0
Ответ от Оксана
выколотые точки — это те значения Х, подставляя которые в функцию переменная У не будет иметь значение.
В основном — их находим когда есть деление (дробь).
Так как на 0 делить нельзя, значит надо «выколоть» точки в которых знаменатель дроби равен 0.
В данном случае:
если посмотрим сразу на ф-цию, то скажем — знаменатель дроби равен 0 при Х=0.
Поэтому х=0 выкалываем.
Но с другой стороны, можно дробь сократить. Получим у=-х.
Мы строим график у=-х. Это прямая из 2 в 4 коорд.углы, проходящая через точки (1;-1) и (4;-4).
!!!!!! НО при этом помним, что Х не равен 0. Поэтому точку выкалываем (пустой кружок).
График функции с переменной в знаменателе
График функции с переменной в знаменателе — следующая группа заданий из номера 23 ОГЭ по математике.
Исследование любой функции начинается с нахождения её области определения.
Дробь имеет смысл, если знаменатель отличен от нуля. Следовательно, те значения переменной, при которых знаменатель обращается в нуль, не входят в область определения функции.
В этом случае возможно появление на графике выколотых точек.
Рассмотрим примеры построения графиков функций, содержащих переменную в знаменателе дроби.
1) Постройте график функции
и определите, при каких значениях k прямая y=kx имеет с графиком ровно одну общую точку.
Решение:
В знаменателе вынесем за скобки общий множитель x:
ВАЖНО: прежде чем сократить дробь, следует найти область определения функции!
Дробь имеет смысл, если знаменатель отличен от нуля:
x(5x-8)≠0,
x≠0, x≠8/5.
Область определения функции D(y): x∈(-∞;0)∪(0;8/5)∪(8/5;∞)
(или D(y): x∈R, кроме x=0 и x=8/5).
Теперь сократим дробь на 5x-8:
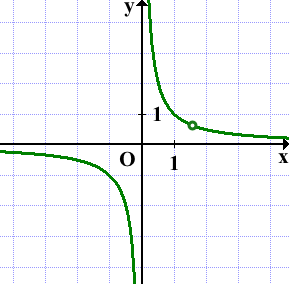
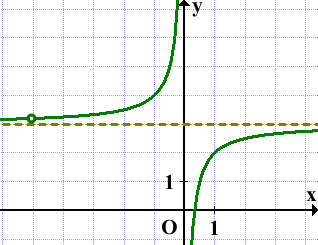
y=1/x — функция обратной пропорциональности. Её график — гипербола. Не забываем про выколотую точку: x≠8/5 (0 не входит в область определения функции y=1/x).
Для построения гиперболы возьмём несколько точек (в том числе, выколотую):
Отмечаем эти точки на координатной плоскости.
Строим гиперболу с выколотой точкой (8/5; 5/8):
Прямая y=kx имеет с графиком ровно одну общую точку, если она проходит через выколотую точку:
Чтобы найти k, подставляем координаты выколотой точки
(8/5; 5/8)
в формулу y=kx и находим k:
Ответ : 25/64.
2) Постройте график функции
и определите, при каких значениях m прямая y=m не имеет с графиком общих точек.
Решение:
В знаменателе вынесем за скобки общий множитель
(Не забываем: сначала следует найти область определения функции, и лишь после этого упрощать выражение!)
Ищем область определения функции.
x(x+5)≠0
x≠0; x≠-5;
D(y): x∈(-∞;-5)∪(-5;0)∪(0;∞).
Сокращаем дробь на x+5:
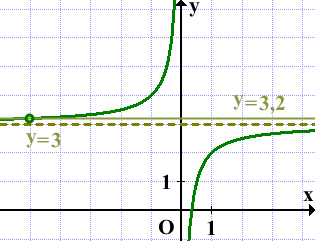
— функция обратной пропорциональности. График — гипербола, полученная из гиперболы
параллельным переносом на 3 единицы вверх вдоль оси Oy.
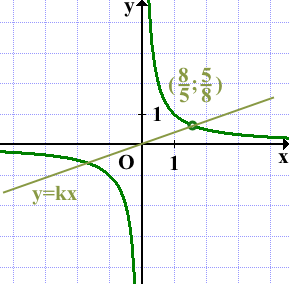
Сначала найдём несколько точек для построения графика y=-1/x:
Отметим эти точки на координатной плоскости. Затем каждую из них перенесем на 3 единицы вверх вдоль оси ординат.
Прямая y=0 (ось абсцисс) для гиперболы y=-1/x является асимптотой (то есть прямой, к которой график стремится, но никогда её не достигнет). Асимптоты принято изображать пунктирными линиями. Так как y=0 совпадает с осью Ox, то она изображена сплошной линией. При параллельном переносе на 3 единицы вверх прямая y=0 переходит в прямую y=3. Прямая y=3 — асимптота, поэтому изображаем её пунктиром.
Через полученные точки проведём гиперболу y=3-1/x:
Прямая y=m не имеет с графиком ни одной общей точки, если она проходит через выколотую точку либо совпадает с асимптотой y=3, то есть при m=3,2 и m=3:
Ответ: 3; 3,2.
3) Постройте график функции
и определите, при каких значениях k прямая y=kx имеет с графиком ровно одну общую точку.
Решение:
Найдём область определения функции.
-1-x≠0
x≠-1.
D(y):x∈(-∞;-1)∪(-1;∞).
Преобразуем дробь:
и сократим её на (x+1):
y=-x²-4 — квадратичная функция. График — парабола ветвями вниз (так как a=-1<0).
График может быть получен из графика функции y=-x² параллельным переносом на 4 единицы вниз вдоль оси Oy (не забываем про выколотую точку! x≠-1):
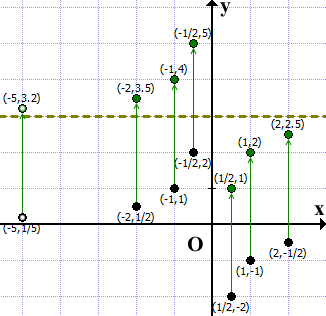
Прямая y=kx имеет с графиком ровно одну общую точку, если она проходит через выколотую точку либо если она является касательной к параболе:
Значения k в данном случае удобнее искать аналитически, а не с помощью графика.
Прямая y=kx имеет с графиком функции y=-x²-4, где x≠-1 ровно одну общую точку, если система
имеет одно решение.
Приравниваем правые части равенств:
-x²-4=kx
x²+kx+4=0.
Это квадратное уравнение имеет один корень в двух случаях: либо дискриминант равен нулю, либо дискриминант положителен, но один из корней равен -1.
D=b²-4ac=k²-4·1·4=k²-16.
k²-16=0 при k=4 или k=-4.
Если x=-1, подставив это значение в уравнение, найдём k:
(-1)²+k·(-1)+4=0
k=5.
Ответ: -4; 4; 5.
4) Постройте график функции
и определите, при каких значениях m прямая y=m имеет с графиком ровно одну общую точку.
Решение:
Формула функции содержит три квадратных трёхчлена. Чтобы разложить каждый из них на множители, решим три квадратных уравнения и воспользуемся теоремой о разложении квадратного трёхчлена на множители.
1)x²-4x+3=0
x1=1; x2=3
x²-4x+3=(x-1)(x-3).
2)x²-x-2=0
x1=-1; x2=2
x²-x-2=(x+1)(x-2).
3)x²-2x-3=0
x1=-1; x2=3
x²-2x-3=(x+1)(x-3).
Ищем область определения функции.
(x+1)(x-3)≠0
x≠-1, x≠3.
D(y): x∈(-∞;-1)∪(-1;3)∪(3;∞).
Сокращаем дробь на (x+1)(x+3):
-квадратичная функция. График — парабола ветвями вверх (так как a=1>0).
Координаты вершины параболы
От вершины — точки (1,5; -0,25) — строим параболу y=x². Поскольку координаты вершины — не целые числа, для построения графика удобно найти дополнительные точки с целыми координатами.
При y=0 (x — 1)(x — 2)=0,
x=1; x=2.
При x=0 y=0²-3·0+2=2.
Находим координаты выколотых точек
При x=-1 y=(-1)²-3·(-1)+2=6,
при x=3 y=3²-3·3+2=2.
Прямая y=m имеет с графиком ровно одну общую точку, если она проходит через одну из выколотых точек либо через вершину, то есть при m=2, m=6 и m=-0,25.
Ответ: -0,25; 2; 6.
Для того, чтобы хорошо решать это задание, нужно быть знакомым с построением различных графиков функций, в том числе содержащих модуль. Предлагаю тем, кто неуверенно себя чувствует при решении таких заданий, перейти по ссылкам и изучить (или повторить) данные разделы. Задание С3 связано как с исследованием расположения корней квадратного трехчлена, так и с определением области определения функции, и области ее значений. На конкретных примерах мы попробуем научиться решать различные типы таких заданий.
Задача 1. Построить график функции 


Задача о касательных к параболе
Графиком предложенной функции является парабола, ветви которой направлены вверх и вершина, которую подняли вверх на 4 единицы, лежит на оси ординат. Ее координаты (0;4). Второй график — это прямая, проходящая через начало координат, причем ее наклон может меняться (его определяет коэффициент 
Поскольку точка касания — единственная общая точка данных графиков, то дискриминант данного уравнения равен нулю: 







Задача 2. Построить график функции 


График, который подвергнется преобразованиям
Преобразованный график
Строить этот график будем поэтапно: сначала построим график 



«Опрокидываем» преобразованный график
Осталось выяснить, в каком же случае прямая 



Задача 3. Построить график функции 


Исходный график
Окончательный вид
Также построим график в два этапа: саму параболу (координаты ее вершины (-1;-9)), затем отразим всю часть, лежащую ниже оси х, вверх: Тогда три и более (а именно — четыре) общих точки графики 


Задача 4. Построить график функции 


Из условия ясно, что такой график состоит из двух кусочков. Один из них — прямая, второй — парабола. Первый существует в точке 1 и левее ее, второй — правее этой точки. Нарисуем эти графики:
Кусочная функция
Координаты вершины параболы: 
Красным показаны прямые 



Задача 5. Построить график функции 


Давайте сначала попробуем упростить данное выражение, кроме того, нужно, безусловно, определить область допустимых значений данной функции. ОДЗ: 
Определение коэффициента наклона касательной
Полученная функция — квадратичная, ее графиком является парабола. Данная парабола симметрична относительно оси y, ее вершина имеет координаты (0; 25). Необходимо заметить, что точка с координатами (1; 26) — выколотая точка (по ОДЗ). Тогда прямая, проходящая через начало координат — а именно таким будет график функции 

















Задача 6. Построить график функции 


Гипербола с выколотой точкой
Определим ОДЗ функции: 









Задача 7. Построить график функции 


Подбор коэффициента наклона прямой
Определим ОДЗ функции: 








Задача 8. Построить график функции 


Построение функции с модулем
Эта функция — функция типа 








Задача 9. Построить график функции 


Кубическая парабола с выколотой точкой
Определим ОДЗ исходной функции: 

График представлен на рисунке. Не забудем про выколотую точку — это точка с координатами (2;4). Поэтому, если прямая 
Задача 10. Построить график функции 


Для того, чтобы построить данный график, необходимо раскрыть модули. С этой целью приравняем подмодульное выражение к нулю, чтобы узнать, в какой точке оно меняет знак: 



У нас получились три интервала, на каждом из которых можно теперь раскрыть модули: 1. 



Она выглядит так:
Кусочно-линейная функция
Зеленым цветом показано одно из возможных положений прямой 


Ответ: 
Задача 11. При каких 


Обратим внимание на то, что у двух данных парабол ветви направлены в разные стороны: у первой старший коэффициент отрицателен, а у второй — положителен. Поэтому вершины будут лежать по одну сторону от оси, если одна из них будет иметь точки пересечения с осью х, а другая — нет. Иными словами, дискриминант одного квадратного уравнения должен быть положителен, а другого — отрицателен. Это приводит нас к двум системам неравенств:
Дискриминант и наличие пересечений параболы с осью х

Или же наоборот: 
Определим дискриминанты обоих квадратных уравнений:
Тогда имеем систему неравенств:




Мы рассмотрели один способ решения — с использованием дискриминанта. Есть еще один способ решения такого задания — с помощью координат вершины параболы. Решим последнюю задачу вторым способом.
Нам потребуется определить координаты вершин обеих парабол:
1.
2.
Ординаты вершин должны иметь один знак по условию, тогда имеем систему неравенств:

Решение этого неравенства и есть ответ задачи:
До встречи в новых постах, удачи на экзаменах!

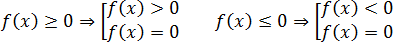

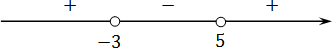
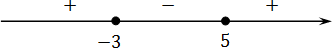
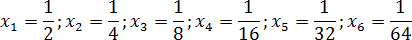
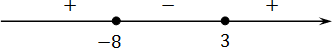
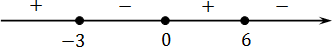
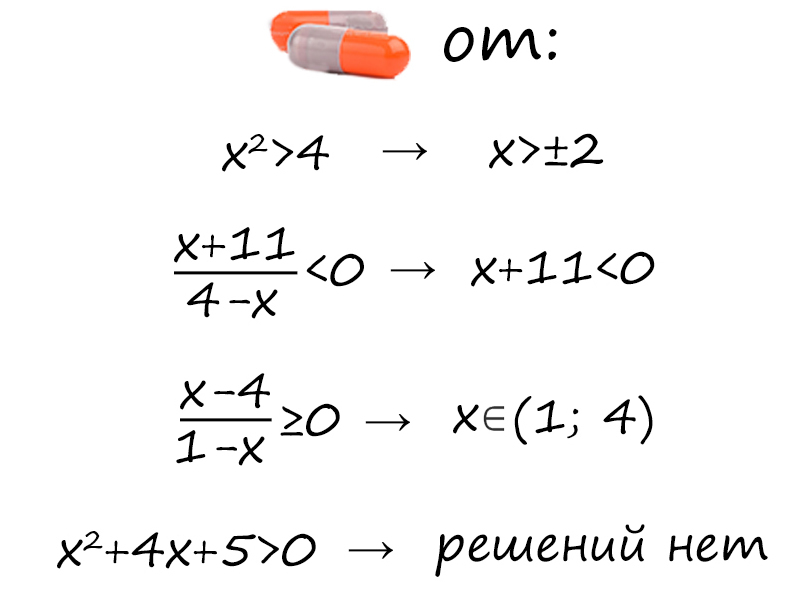 Решение неравенств
Решение неравенств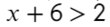
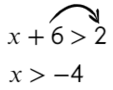
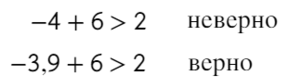
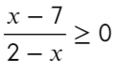
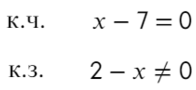
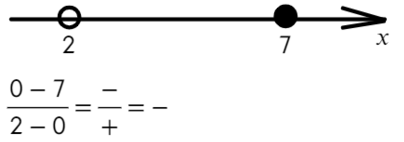
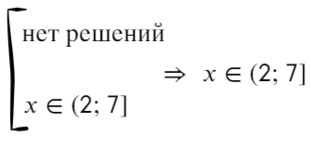
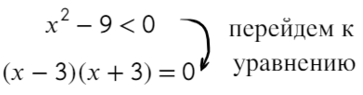
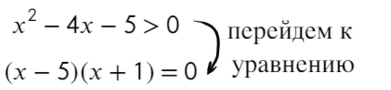
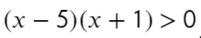
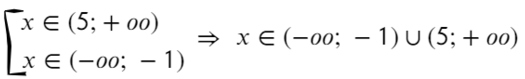
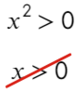
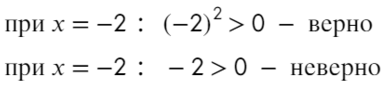

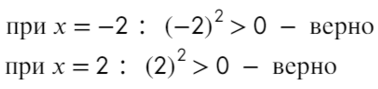
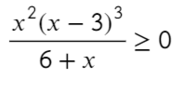
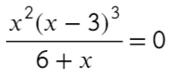
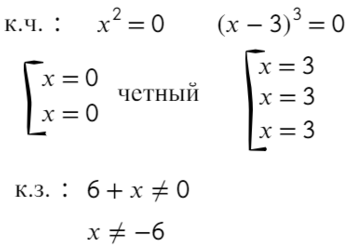
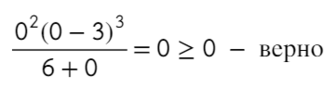
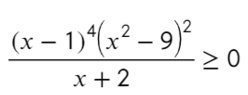
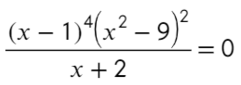
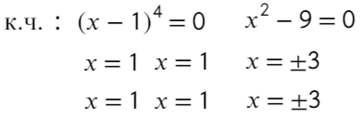
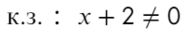
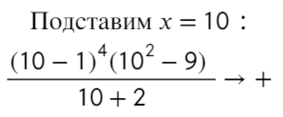
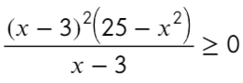
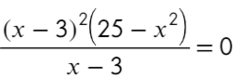





































![Rendered by QuickLaTeX.com [ frac{x}{y}left| {frac{{ - 2}}{{ - frac{1}{2}}}} right.left| {frac{{ - 1}}{{ - 1}}} right.left| {frac{{ - frac{1}{2}}}{{ - 2}}} right.left| {frac{{frac{1}{2}}}{2}} right.left| {frac{1}{1}} right.left| {frac{{frac{8}{5}}}{{frac{5}{8}}}} right.left| {frac{2}{{frac{1}{2}}}} right. ]](https://www.algebraclass.ru/wp-content/ql-cache/quicklatex.com-6b01205fceeb7f3128d1e7f3e964e8c5_l3.png)
![Rendered by QuickLaTeX.com [ frac{x}{y}left| {frac{{ - 5}}{{frac{1}{5}}}} right.left| {frac{{ - 2}}{{frac{1}{2}}}} right.left| {frac{{ - 1}}{1}} right.left| {frac{{ - frac{1}{2}}}{2}} right.left| {frac{{frac{1}{2}}}{{ - 2}}} right.left| {frac{1}{{ - 1}}} right.left| {frac{2}{{ - frac{1}{2}}}} right. ]](https://www.algebraclass.ru/wp-content/ql-cache/quicklatex.com-f0cd4ba35e486534ca4ff13d0cb17fe5_l3.png)
![Rendered by QuickLaTeX.com [ left{ begin{array}{l} y = - x^2 - 4, \ x ne - 1, \ y = kx \ end{array} right. ]](https://www.algebraclass.ru/wp-content/ql-cache/quicklatex.com-908c51743e7d36c9c27e60f6fea674ff_l3.png)