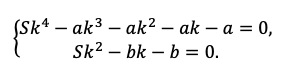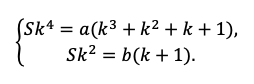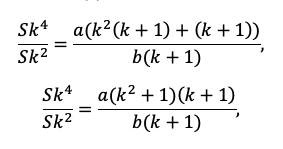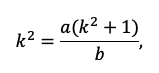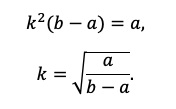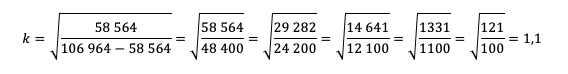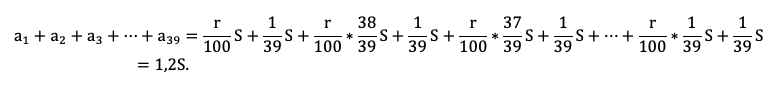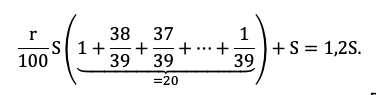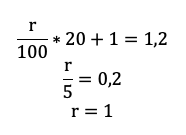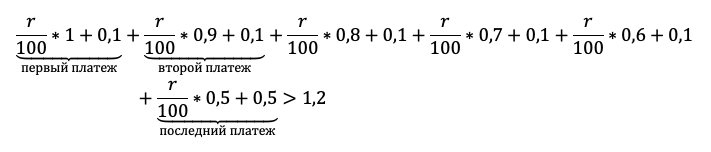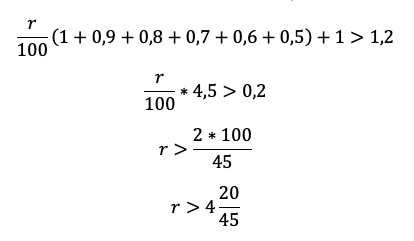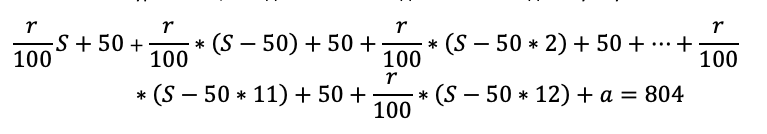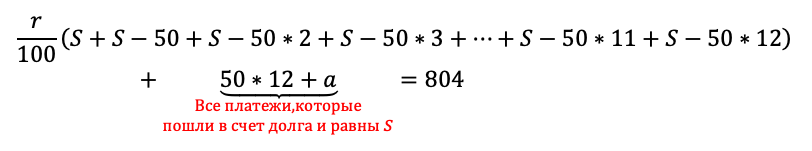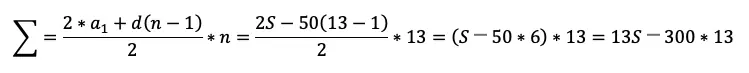Как найти выплаты в экономической задаче

В части с развернутым ответом в ЕГЭ по профильной математике есть уникальный номер, к которому школьник почти готов сразу после освоения материала для первых 12-ти заданий. Речь об экономической задаче под номером 17 в ЕГЭ по математике. Конечно, поготовиться придется, но, если повезет с прототипом, баллы можно урвать почти даром!

Прототипы для 17-го номера делятся на три большие группы: 

• банковские задачи, 
• на ценные бумаги,
• задачи на оптимальный выбор. 

В этой статье мы расскажем, как научить ученика структурировать условие любой банковской задачи, как составить по этим данным математическую модель и найти решение. Расскажем, на что обратить внимание ученика, чтобы школьник не потерял баллы из-за неверного оформления.

Главная трудность — школьник плохо понимает условие, ведь с кредитами и вкладами он пока не сталкивался.

• Как работает процент по кредиту?
• На какую сумму начисляется?
• Из каких частей состоит платеж?
• Как уменьшается долг?

На все эти вопросы вам придется ответить. Это отличная возможность показать пользу уроков математики, ведь 17-ый номер — едва ли не самая прикладная задача за весь школьный курс! 

Например, можно рассказать о том, какие бывают образовательные кредиты. Вы в курсе, что их дают с 14 лет, а платеж первые годы может быть ничтожным? Школьник об этом точно не знает.

С чего начать разбор экономической (банковской) задачи в ЕГЭ по математике

Экзамен немного утрирует реальную ситуацию, в жизни кредит работает сложнее. Однако грустно упускать возможность рассказать школьнику что-то из реальности! Если у вас есть опыт с кредитованием, самое время им поделиться. Если нет, то воспользуйтесь нашим:

• Например, расскажите, что клиенту придется сверх купить страховку на случай потери работоспособности, ведь банк не хочет терять прибыль даже если на заемщика кирпич упадет. Ваши ученики знают, как работает страховка?
• Расскажите о механизме аннуитетного платежа: как часть денег банк забирает себе в качестве дохода, то есть на погашение процентов за пользование кредитом; а на вторую часть уменьшает ваш долг. В реальности это разделение считается по специальной формуле, и совсем не в пользу заемщика.
• Например, по нашему опыту, в ипотеке на 10 лет из 20 тысяч ежемесячного платежа на первых порах всего 5 000 рублей идет в счет уменьшения долга, а 15 000 — забирает себе банк! Но каждый раз платеж чуть ребалансируется, и в счет долга идет чуть больше. Так в последних платежах через 10 лет в счет процентов идет буквально пара сотен, а все остальное гасит долг. 

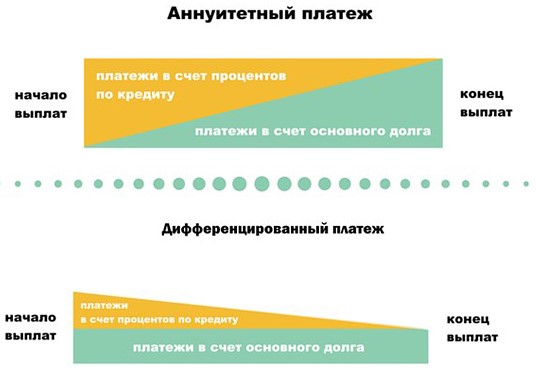
Хорошая новость в том, что в экзаменационных задачах подобной вакханалии не бывает. Долг и проценты или гасятся равномерно, или по заранее известному алгоритму, достаточно просто внимательно прочитать условие.

Еще одно частое упрощение в ЕГЭ — процент там обычно не годовой, а ежемесячный! То есть своим платежом заемщик гасит набежавший за этот месяц процент и уменьшает долг на заданную величину. Удобно.

Мы предлагаем научить школьника упорядочивать данные банковской задачи в ЕГЭ по математике с помощью таблицы. Табличка — не единственный способ решить 17-ый номер, кто-то использует последовательности, кто-то — считает прикладным методом как заправский бухгалтер. Однако наш метод универсален, а значит вы дадите школьнику один алгоритм на все типы банковских задач. Согласитесь, работать с одним алгоритмом проще, чем подбирать разные по ситуации.

Тип 1. Равные платежи

Особенность этого типа заданий в том, что заемщик всегда вносит одинаковые суммы.

В июле 2020 года планируется взять кредит в банке на некоторую сумму. Условия его возврата таковы:
— каждый январь долг увеличивается на r % по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить одним платежом часть долга.
Если ежегодно выплачивать по 58 564 рубля, то кредит будет полностью погашен за 4 года, а если ежегодно выплачивать по 106 964 рубля, то кредит будет полностью погашен за 2 года. Найдите r.

Очевидно, что эта схема должна оказаться у школьника в тетради. Ведь вы же знаете: того, чего нет в тетради, и на уроке-то не было!

Заполняем всю табличку. Учитываем обе ситуации из условия. Для наглядности каждую выделим жирной рамкой.

Теперь остался еще один непростой шаг — перейти от структурированных данных к математической модели. Дайте ученику возможность увидеть, что уже почти составил ее.

Мы получили два уравнения, которые подсветили в табличке оранжевым. Объединим их в систему и решим!

Напомните выпускнику о культуре вычислений! Порой эти задачи составлены так, что неудачная последовательность действий сделает их нерешаемыми без калькулятора. Потому не надо спешить делать первое попавшееся действие, пусть школьник тренируется думать на пару ходов вперед.

Например, разделим одно уравнение на другое, ведь так мы избавимся от одной неизвестной S:

Наше решение не зависит от суммы кредита, S сокращается. 

По сути, мы получили уравнение с одной неизвестной, ведь платежи a и b знаем из условия. Выразим k:

Пожалуй, все, проще уже некуда. Подставляем значения!   

Тут можно обратить внимание ученика на то, как составители экзамена на самом деле заботятся о нем! Ведь будь задачка хоть чуть-чуть другой, посчитать без калькулятора было бы невозможно.

Вспоминаем, что k=1+r/100, а найти нам надо r.

Ответ: 10%.

Не забудьте после решения расставить акценты в задаче:

Чтобы решить задачу и получить 3 балла, мы:
— Воспользовались простым алгоритмом упорядочивания данных,
— Составили математическую модель,
— Нашли удобный способ решить ее, ВСЕ!
Это и есть алгоритм решения банковской задачи.

Тип 2. Равномерно убывающий долг

В прошлой задаче заемщик платил одинаковую сумму каждый месяц. Тут ему нужно уменьшать долг на одну и ту же величину. То есть за месяц пользования деньгами банк начислил на них процент, клиент теперь должен чуть больше. Своим платежом он оплатит банку проценты, чтобы заем стал таким, как ДО их начисления. А сверху внесет сумму, которая как раз и пойдет на то самое РАВНОМЕРНОЕ уменьшение долга.  

15-го января планируется взять кредит в банке на 39 месяцев. Условия его возврата таковы:
— 1-го числа каждого месяца долг возрастает на r % по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца.
Известно, что общая сумма выплат после полного погашения кредита на 20% больше суммы, взятой в кредит. Найдите r.
(Считайте, что округления при вычислении платежей не производятся.)

Тут главный элемент в задаче — равномерно убывающий долг. Если мы взяли сумму S на 39 месяцев, и каждый месяц долг должен быть меньше на одинаковую величину, то что это за величина? Пусть правильный ответ 1/39 S даст ученик.

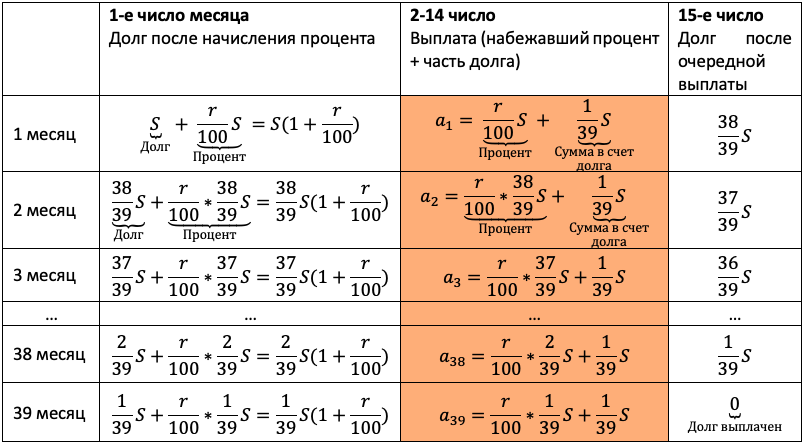
Проиллюстрируйте школьнику, как здорово работает наш алгоритм. Пусть выпускник проговаривает пункты вслух, а вы их выполняйте. Следите, чтобы каждый шаг подопечный фиксировал в тетради:

Продолжаем заполнять табличку. Пусть дальше пробует выпускник, ведь пока сам не попробуешь, не научишься:

Осталось увязать добытую информацию в уравнение или неравенство. Обратите внимание подопечного на то, что ненужных подробностей в задачах ЕГЭ не бывает! Единственная информация в задаче, которую мы до сих пор не использовали — общая сумма выплат. По условию она на 20% больше суммы кредита, то есть равна 1,2S:

Приведем подобные, вынесем общий множитель за скобку:

Решение в итоге снова не зависит от того, какую сумму взяли в долг. Разделим обе части на S и упростим выражение:

Ответ: 1%.

И снова все по нашему алгоритму, ничего нового, кроме него, мы не используем! Не забудьте излучать восторг, иначе школьник не проникнется мощью вашего метода решения.

Тип 3. Долг, убывающий согласно табличке

Задача похожа на прошлую. Разница лишь в том, что кроме процентов нам каждый месяц придется гасить не равную долю долга, а долю согласно таблице.

15-го января планируется взять кредит в банке на шесть месяцев в размере 1 млн рублей. Условия его возврата таковы:
— 1-го числа каждого месяца долг увеличивается на r процентов по сравнению с концом предыдущего месяца, где r — целое число;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен составлять некоторую сумму в соответствии со следующей таблицей.

Дата	15.01	15.02	15.03	15.04	15.05	15.06	15.07
Долг(в млн рублей)	1	0,9	0,8	0,7	0,6	0,5	0

Найдите наименьшее значение r, при котором общая сумма выплат будет больше 1,2 млн рублей.

Протестируем нашу универсальную табличку в третий раз, доверьте это непростое занятие школьнику. Пусть процессом командует он! По ответам будет ясно, ловит ли он суть.

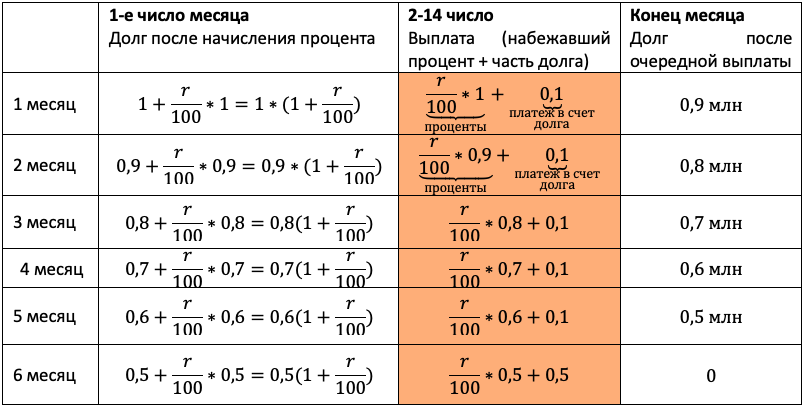
Отличие от прошлого типа будет лишь в том, что в третий столбец мы будем записывать не равномерно убывающий долг, а перенесем остаток долга из таблицы условия. Чтобы не таскать по решению нули, считать будем в миллионах:

Чтобы долг убывал согласно табличке, нам снова каждый раз придется гасить набежавшие проценты и первые 5 месяцев добавлять сверху 0,1 млн. После останется погасить весь остаток.

Акцентируйте внимание на механизме погашения, для школьника он не всегда очевиден.

«По условию нам снова дана общая сумма выплат, значит достаточно просуммировать оранжевый столбец, и уравнение готово», — вероятно, подумает школьник. Подловите его! Уравнение в этой задаче — прямой путь потерять балл! Сумма выплат должна быть БОЛЬШЕ 1,2 млн. Отразим это в модели с помощью неравенства:

Подопечный должен быть уверен в каждом символе в бланке ответа. Даже не пригодившиеся промежуточные вычисления с ошибкой приведут к катастрофе.

Приведем подобные и вынесем общие множители за скобку:

Последний шаг – не забыть, что по условию процент должен быть целым и округлить в верную сторону.

Ответ: 5%.

Правильная математическая модель — это суперважно! К ней проверяющие обязательно придерутся.

Тип 4. Погашение кредита в два этапа.

По сути, это та же прошлая задача, но месяцев больше

В 2017-2018 учебном году составителей экзамена посетило вдохновение, на свет родился вот этот тип банковских задач. Школьники были в шоке, и от страха завалили 17-ый номер. Хотя всего-то нужно было догадаться воспользоваться знаниями об арифметической прогрессии и достать из условия одно немного неочевидное дано!

15-го декабря планируется взять кредит в банке на 13 месяцев. Условия возврата таковы:
— 1-го числа каждого месяца долг возрастает на 2% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца с 1-го по 12-й долг должен быть на 50 тысяч рублей меньше долга на 15-е число предыдущего месяца;
— к 15-му числу 13-го месяца кредит должен быть полностью погашен.
Какую сумму планируется взять в кредит, если общая сумма выплат после полного его погашения составит 804 тысячи рублей?

И снова пусть по возможности командует школьник. По крайней мере он уже точно в курсе, что происходит первые 13 месяцев.

Последовательно начисляем процент на остаток долга – считаем выплату – фиксируем остаток долга после выплаты. Сумму кредита возьмем за S.

Научите школьника не спешить с вычислениями. Например, вместо того чтобы написать S-600, мы пишем S-50*12, потому что так удобнее: нам сразу ясно, что речь идет о двенадцатом месяце. Да и потом вычисления будут проще, если мы оставим маленькие числа.

Осталось составить уравнение, и модель готова. В задаче нам снова дали сумму всех выплат:

Как обычно, сгруппируем отдельно слагаемые с r/100, отдельно слагаемые без них:

Вот именно последняя группировка всех платежей в счет долга и оказалась неочевидной. Без нее в задаче остается одна лишняя неизвестная величина, которая рушит все решение.

Осталось привести уравнение к решаемому виду. Для этого надо просуммировать то, что получилось в скобках. Если внимательно приглядеться, то видно, что это сумма арифметической прогрессии:

Посчитаем эту сумму:

Подставляем выражение для суммы в уравнение, заметим, что по условию r=2:

Мы сокращали дробь, пока это было возможно, и в итоге довольно просто получили ответ даже без калькулятора. Ваш подопечный должен научиться также!

Ответ: 700 тысяч.

Зачем использовать формулу суммы прогрессии, если можно посчитать вручную? Все верно, можно. Но это только в данном случае кредит взяли всего на 13 месяцев. А бывают прототипы, когда срок – 21 и больше месяцев. В какой-то момент считать вручную станет совсем долго и неудобно, потому воспользоваться формулой суммы – более универсальный метод.

Чем закончить разбор экономической (банковской) задачи № 17 в ЕГЭ по математике

Чтобы у ученика окончательно сложилась картинка занятия, пробегитесь еще раз по основным выводам:

• Повторите алгоритм заполнения таблицы и решения задачи (да, пятый раз);
• Повторите типы задач и механизм распределения платежа на проценты и долг;
• Напомните, как важно считать культурно и быть уверенным в каждой циферке в бланке;
• Проговорите, что математическая модель должна точно отражать условие задачи.

Как показывает практика, чем больше повторяешь, тем больше шансов, что в голове выпускника останется хоть что-то.

За что дают баллы?

Знание критериев оценивания экономической (банковской) задачи № 17 в ЕГЭ по математике поможетученику чувствовать себя увереннее, ведь выставление баллов — это не какая-то магия и не вредность экспертов. Все правила игры прописаны в нормативных документах.

17-ый номер стоит 3 балла. Чтобы узнать, как их присуждают, мы залезли в методические рекомендации для членов предметных комиссий.

Согласно пояснениям из документа, для получения одного балла мало просто обоснованно составить математическую модель по задаче, надо предложить правильный метод ее анализа. 

Два балла получит школьник, который ошибся в вычислениях или не обосновал появление математической модели в решении. Например, согласно методическим рекомендациям, решение на 2 балла выглядит так:

А вот отсутствие промежуточных вычислений хоть и усложняет проверку, но баллы не снимает.

Идеально выполненная первая часть ЕГЭ по профильной математике принесет школьнику всего 62 тестовых балла. Добавим сюда пару ошибок по невнимательности, и останутся совсем крохи — баллов 50, не больше. Для поступления на бюджет мало, а значит необходимо планировать делать вторую часть! Чем раньше школьник это осознает, тем проще будет с ним работать. А банковская задача поможет получить дополнительные баллы с минимальными усилиями.

Однако кредиты – не единственный прототип 17-го номера, и в следующий раз мы расскажем, как научить школьника решать задачи на оптимальный выбор и ценные бумаги. 

Задание 15 Профильного ЕГЭ по математике — «экономическая» задача. Как вы уже поняли, речь пойдет о деньгах. О кредитах и вкладах. О ситуациях, где нужно узнать, при каких значениях переменной будет максимальна прибыль или минимальны издержки. С 2022 года задание 15 оценивается на ЕГЭ в 2 первичных балла.

В этой статье:

Как научиться решать «экономические» задачи. С чего начать.

Две схемы решения задач на кредиты и как их распознать.

Комбинированные задачи.

В чем основная сложность «экономической» задачи.

Задания на оптимальный выбор. В том числе — с применением производной.

Если материал покажется вам сложным — вернитесь к теме «Задачи на проценты» из первой части ЕГЭ по математике.

Надеемся, что вы уже сейчас сможете ответить на такие вопросы:

1. Что принимается за 100%?
2. Величина х увеличилась на p%. Как это записать?
3. Величина y дважды уменьшилась на р%. Как это записать?

Ответы на вопросы, а также подготовительные задачи — в статье «Задача 17 Профильного ЕГЭ по математике. Кредиты и вклады. Начисление процентов». Повторите эту тему.

Запомним, что есть всего две схемы решения задач на кредиты

Первая схема: кредит погашается равными платежами. Или известна информация о платежах. Подробно здесь.

Вторая схема: равномерно уменьшается сумма долга. Или дана информация об изменении суммы долга. Подробно здесь.

В задачах первого типа обычно применяется формула для суммы геометрической прогрессии. В задачах второго типа — формула суммы арифметической прогрессии.

Посмотрите, чем эти схемы отличаются друг от друга. На какие ключевые слова в условии надо обратить внимание.

Потому что первое, что надо сделать, когда решаете «экономическую» задачу на кредиты или вклады, — определить, к какому типу она относится.

Давайте потренируемся.

1. 31 декабря 2014 года Аристарх взял в банке 6 902 000 рублей в кредит под 12,5% годовых. Схема выплаты кредита следующая — 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 12,5%), затем Аристарх переводит в банк X рублей. Какой должна быть сумма X, чтобы Аристарх выплатил долг четырьмя равными платежами (то есть за четыре года)?

Конечно, это задача первого типа. Есть информация о платежах. В условии сказано, что Аристарх выплатит долг четырьмя равными платежами.

Введем обозначения:

тыс. рублей — сумма долга. Расчеты будем вести в тысячах рублей.

— процент банка,

— коэффициент, показывающий, во сколько раз увеличилась сумма долга после начисления процентов,

— сумма ежегодного платежа.

Составим схему погашения кредита. Заметим, что здесь 4 раза (то есть в течение 4 лет) повторяются одни и те же действия:

— сумма долга увеличивается в раз;

— Аристарх вносит на счет сумму в счет погашения кредита, и сумма долга уменьшается на .

Вот что получается:

Раскроем скобки:

Что у нас в скобках? Да, это геометрическая прогрессия, и ее проще записать как

. В этой прогрессии первый член равен 1, а каждый следующий в k раз больше предыдущего, то есть знаменатель прогрессии равен k.

Применим формулу суммы геометрической прогрессии:

И выразим из этой формулы .

Что же, можно подставить численные данные. Стараемся, чтобы наши вычисления были максимально простыми. Поменьше столбиков! Например, коэффициент k лучше записать не в виде десятичной дроби 1,125 — а в виде обыкновенной дроби , Иначе у вас будет 12 знаков после запятой!

И конечно, не спешить возводить эту дробь в четвертую степень или умножать на S = 6902000 рублей.

тыс.руб.

Ответ: 2296350 рублей.

Вот следующая задача.

2. Жанна взяла в банке в кредит 1,8 млн рублей на срок 24 месяца. По договору Жанна должна возвращать банку часть денег в конце каждого месяца. Каждый месяц общая сумма долга возрастает на 1 %, а затем уменьшается на сумму, уплаченную Жанной банку в конце месяца. Суммы, выплачиваемые Жанной, подбираются так, чтобы сумма долга уменьшалась равномерно, то есть на одну и ту же величину каждый месяц. Какую сумму Жанна вернёт банку в течение первого года кредитования?

В этой задаче сумма долга уменьшается равномерно — задача второго типа.

Пусть S — первоначальная сумма долга, S = 1800 тысяч рублей.

Нарисуем схему начисления процентов и выплат. И заметим некоторые закономерности.

Как обычно,

Сумма долга уменьшается равномерно. Можно сказать — равными ступеньками. И каждая ступенька равна После первой выплаты сумма долга равна после второй

Тогда первая выплата вторая выплата,

Последняя в году выплата

Сумма всех выплат в течение первого года:

В первой «скобке» — сумма 12 членов арифметической прогрессии, в которой   Обозначим эту сумму

Во второй скобке — также сумма 12 членов арифметической прогрессии, в которой Эту сумму обозначим

Общая сумма выплат за год:

тыс. рублей.

Ответ: 1066500 рублей.

Еще одна задача — комбинированная. Здесь мы рисуем такую же схему выплаты кредита, как в задачах второго типа.

3. В июле 2016 года планируется взять кредит в банке на пять лет в размере S тыс. рублей. Условия его возврата таковы:

− каждый январь долг возрастает на 25% по сравнению с концом предыдущего года;

− с февраля по июнь каждого года необходимо выплатить часть долга;

− в июле 2017, 2018 и 2019 долг остаётся равным S тыс. рублей;

− выплаты в 2020 и 2021 годах равны по 625 тыс. рублей;

− к июлю 2021 долг будет выплачен полностью.

Найдите общую сумму выплат за пять лет.

Введем переменные: тысяч рублей. Рисуем схему погашения кредита:

Общая сумма выплат: Кроме того, долг был полностью погашен последней выплатой .

Это значит, что и тогда

тысяч рублей.

Ответ: 1925 тыс. рублей.

Но не только задачи на кредиты и вклады могут встретиться в задании 15 Профильного ЕГЭ по математике. Есть еще задачи на оптимальный выбор. Например, нужно найти максимальную прибыль (при соблюдении каких-либо дополнительных условий), или минимальные затраты. Сначала в такой задаче нужно понять, как одна из величин зависит от другой (или других). Другими словами, нужна та функция, наибольшее или наименьшее значение которой мы ищем. А затем — найти это наибольшее или наименьшее значение. Иногда — с помощью производной. А если повезет и функция получится линейная или квадратичная — можно просто воспользоваться свойствами этих функций.

4. Консервный завод выпускает фруктовые компоты в двух видах тары—стеклянной и жестяной. Производственные мощности завода позволяют выпускать в день 90 центнеров компотов в стеклянной таре или 80 центнеров в жестяной таре. Для выполнения условий ассортиментности, которые предъявляются торговыми сетями, продукции в каждом из видов тары должно быть выпущено не менее 20 центнеров. В таблице приведены себестоимость и отпускная цена завода за 1 центнер продукции для обоих видов тары.

Вид тары	Себестоимость, 1 центнера	Отпускная цена, 1 центнера
стеклянная	1500 руб	2100 руб
жестяная	1100 руб	1750 руб

Предполагая, что вся продукция завода находит спрос (реализуется без остатка), найдите максимально возможную прибыль завода за один день (прибылью называется разница между отпускной стоимостью всей продукции и её себестоимостью).

По условию, завод не может выпускать компот только в стеклянных банках или только в жестяных — должны быть и те, и другие.

Пусть x — доля мощностей завода, занятых под поизводство компотов в стеклянных банках, а y — доля мощностей, занятых под производство компотов в жестяных банках, Тогда x+y=1. (Например, х=0,3 и у = 0,7 — то есть 30% производства — это компот в стеклянных банках, а 70% — компот в жестяных банках).

Если бы завод выпускал только компот в стеклянных банках, их бы получилось 90 центнеров в сутки. Однако выпускаются и те, и другие, и компотов в стеклянных банках производится 90x центнеров, а в жестяных банках — 80y центнеров в сутки.

Составим таблицу.

Вид тары	Доля в общем количестве	Производится в сутки	Прибыль за 1 центнер
стеклянная			2100 — 1500 = 600 руб
жестяная			1750 — 1100 = 650 руб

Общая прибыль завода за сутки равна

По условию, и , то есть и

Нужно найти наибольшее значение выражения при выполнении следующих условий:

Подставим в выражение для прибыли завода за сутки. Получим, что она равна Это линейная функция от x. Она монотонно возрастает и свое наибольшее значение принимает при Тогда и максимально возможная прибыль завода за день равна

руб.

Ответ: 53500 руб.

Больше задач по финансовой математике на нахождение наибольших и наименьших значений функций и применение производной — здесь:

Задача 15 Профильного ЕГЭ по математике. Исследование функций и производная

Вот такая она, задача с экономическим содержанием. Мы рассказали о ней самое главное. Если готов осваивать ее самостоятельно — желаем удачи. А если не все будет сразу получаться — приходи к нам в ЕГЭ-Студию на интенсивы, курсы или Онлайн-курс.

Если вам понравился наш материал — записывайтесь на курсы подготовки к ЕГЭ по математике онлайн

На этой странице вы узнаете

• С помощью какого инструмента можно решить любую экономическую задачу?
• Как сделать “буп” котику и быстро заполнить таблицу?
• Чек-лист: как правильно решать экономические задачи?

Мы ежедневно сталкиваемся с денежными операциями. Покупка вкусняшек, оплата проезда, или приобретение что-то для души — это все финансовые операции. И про кредиты слышали многие из нас. Давайте разберемся, как подходить ко всем этим вопросам математически грамотно. 

Финансовые задачи на каждый день

Кредиты берут и на покупку обычных бытовых вещей и на что-то более внушительное, как машина или квартира. В любом случае при обращении в банк за выдачей кредита каждый должен быть готов столкнуться с разными схемами платежей и понятиями процентов.

Про проценты, в том числе сложные проценты или увеличение и уменьшение числа на процент, можно подробнее прочитать в статье «Финансовые задачи. Проценты». 

Сейчас мы углубимся в основные схемы погашения кредита. На самом деле, их не так много, а если быть точнее, то всего две. Главное их различие в платежах.

Начнем разбираться в кредитах с аннуитетных платежей. 

Аннуитетные платежи

Аннуитетные платежи встречаются достаточно часто. В чем заключается их основная роль? Каждый месяц (или год) сумма выплат одинаковая. 

Например, если мы заключим договор с банком, в котором пропишут, что каждый месяц необходимо выплачивать 10 тысяч рублей — это и будет пример аннуитетных платежей. 

Аннуитетные платежи — такая система выплат, при которых кредит выплачивается раз в год (или в другой период времени в зависимости от договора) равными платежами. 

Главное словосочетание будет “равными платежами”. Вне зависимости от остатка долга, платеж менять не будет. 

Разберемся чуть подробнее. Мы знаем, что каждый расчетный период на кредит начисляются установленные проценты. Следовательно, выплачивая кредит по аннуитетным платежам, мы будем одновременно гасить и долг, и процент. Наш платеж будет складываться из процентов, начисленных на долг и самого тела долга. 

Также вспомним, что чем больше долг, тем больше начисленный на него процент. Поскольку сама выплата не меняется с течением времени, то в начале основная часть выплаты идет на погашение начисленных процентов, а остаток — на погашение самого долга. Со временем их отношение выравнивается и меняется в обратную сторону. 

Схему выплат аннуитетных платежей можно представить следующим образом. На ней видно, что с каждой выплатой уменьшается как сам долг, так и начисленный на него процент. 

Как определить, что перед нами задача на аннуитетные платежи? 

Нужно посмотреть на некоторые ключевые слова:

• выплаты равны между собой;
• выплаты фиксированные;
• сам долг уменьшается неравномерно. 

Рассмотрим задачу на аннуитетные платежи. 

Пример 1. Игорь хочет в мае взять кредит в банке на некоторую сумму. Условия его возврата таковы:

— Каждый январь долг возрастает на 10% по сравнению с концом предыдущего года. 

— С февраля по май каждого года нужно выплатить часть долга, равную 665,5 тыс. рублей. 

На какую сумму хочет взять кредит Игорь, если он был погашен тремя равными платежами?

Решение. Каждый год кредит будет увеличиваться на 10%, поэтому для удобства решения введем коэффициент (k = 1 + frac{10}{100} = 1,1). Обозначим взятый кредит за S, а ежегодную выплату за x=665,5 тыс. 

Что обычно включается в таблицу:

• остаток на начало периода,
• начисленный процент,
• выплата,
• остаток после выплаты. 

Таблица — очень гибкий инструмент. В зависимости от условия задачи она может меняться. Например, выплату можно разбить на два столбика: процентную часть и часть от основного долга. 

Чуть подробнее разберем составление таблицы. 

Поскольку выплаты фиксированные и равны между собой, мы можем сразу заполнить четвертый столбик:

Год	Долг без %	Долг с %	Выплата	Остаток
1			x
2			x
3			x

Что еще нам известно? То , что долг в начале был равен S, а в самом конце полностью выплачен. Значит на конец периода долг будет равен 0. Заполним соответствующие ячейки:

Год	Долг без %	Долг с %	Выплата	Остаток
1	S		x
2			x
3			x	0

Дальше мы можем найти долг с начисленными процентами в первый год. Для этого нужно долг умножить на коэффициент.

Год	Долг без %	Долг с %	Выплата	Остаток
1	S	1,1S	x
2			x
3			x	0

А теперь решим небольшую задачку: у Маши было 5 яблок. Она отдала два из них подруге. Сколько яблок осталось у Маши?

Без раздумий мы можем сразу сказать, что у Маши осталось 3 яблока. Внимательно посмотрим на таблицу: долг перед банком был 1,1S (5 яблок), после чего погасили его часть, равную х (2 яблока). Какой остаток останется? 1,1S — х. 

Было	Убрали	Получили
5 яблок	2 яблока	3 яблока
1,1S	x	1,1S-x

Таким образом, с помощью долга, выплаты и остатка можно составить уравнение: 

• “Долг с процентами” — “выплата” = “остаток”. 

Это же уравнение можно немного варьировать, например:

• “Долг с процентами” — “остаток” = “выплата”. 
  Этот случай можно использовать, когда нам неизвестна выплата, но известны остальные две величины. 
• “Остаток” + “выплата” = “долг с процентами”. 
  Этот случай используется в ситуациях, когда неизвестен первоначальный долг. 

В зависимости от условий задачи можно с помощью таблицы всегда выразить неизвестную величину. 

Заполним нужные ячейки. Сразу заметим, что долг без процентов в начале года будет равен остатку на конец предыдущего года.

Год	Долг без %	Долг с %	Выплата	Остаток
1	S	1,1S	x	1,1S-x
2	1,1S-x		x
3			x	0

Выполняем такой же алгоритм со вторым годом: начисляем проценты и ищем остаток. Важно заметить, что проценты начисляются на весь остаток, в том числе на переменную “х”. 

Год	Долг без %	Долг с %	Выплата	Остаток
1	S	1,1S	x	1,1S-x
2	1,1S-x	1,1(1,1S-x)	x	1,12S-1,1x-x
3			x	0

И по такой же схеме осталось заполнить только последние две ячейки.

Год	Долг без %	Долг с %	Выплата	Остаток
1	S	1,1S	x	1,1S-x
2	1,1S-x	1,1(1,1S-x)	x	1,12S-1,1x-x
3	1,12S-2,1x	1,1(1,12S-2,1x)	x	0

Вот и все заполнение таблицы, совсем ничего сложного. Нужно немного рассуждений и операций с числами. 

Составим итоговое уравнение. Посмотрим на последнюю строчку и вспомним уже выведенную формулу БУП. 

Было: 1,1 * (1,1² * S — 2,1x) = 1,1³ * S — 2,31 x. 
Убрали: “х”. 
Получили: 0. 

Тем самым мы получаем уравнение: 1,1³ * S — 2,31x — x = 0. Осталось только решить его.

1,1³ * S — 3,31 x = 0
(S = frac{3,31x}{1,1^{3}})

Тут уже можно заменить переменные на числа, вспомним, что x=665,5.

(S = frac{3,31 * 665,5}{1,331})
S = 1655 тыс.

Ответ: 1655 тысяч рублей. 

Пример 2. В сентябре 2023 года планируется взять кредит. Условия его возврата таковы: 

— В январе каждого года долг увеличивается на 20% по сравнению с концом предыдущего года.

— С февраля по сентябрь нужно выплатить  часть долга одним платежом. 

Известно, что кредит был погашен двумя равными платежами. Найдите, на какую сумму был взят кредит, если сумма его выплат на  136 тыс. больше суммы взятого кредита. 

Решение. 

1. Для начала введем переменные. S — кредит, х — выплаты в 1 и 2 год, (k = 1 + frac{20}{100} = 1,2) — коэффициент увеличения. 

2. Составим таблицу:

Год	Долг до %	Долг после %	Выплата	Остаток
1	S	1,2S	х	1,2S-x
2	1,2S-x	1,2(1,2S-x)	х	0

3. Теперь составим уравнение: 

1,2 * (1,2S — x) — x = 0
1,2² * S — 1,2x — x = 0
1,44 * S — 2,2x = 0. 

4. Внимательно прочитаем условие и отметим, что сумма выплат на 136 тысяч больше суммы кредита. Как найти сумму выплат? Нужно посмотреть на таблицу. В ней расписаны все наши выплаты, а значит их просто нужно сложить. Получается, что сумма выплат равна 2х.

Год	Долг до %	Долг после %	Выплата	Остаток
1	S	1,2S	х	1,2S-x
2	1,2S-x	1,2(1,2S-x)	х	0

Составим еще одно уравнение, опираясь на условие задачи: 2х = S + 136.

5. Мы получили два уравнения. Поскольку нам необходимо найти S, достаточно выразить “х” в одном из них и подставить в другое. 

2x = S + 136
x = 0,5 * S + 68

Тогда в уравнении 1,44 * S — 2,2 x = 0 получаем

1,44 * S — 2,2 * (0,5 * S + 68) = 0.
1,44 * S — 1,1 * S — 68 = 0
0,34 * S = 68
S = (frac{68}{0,34})
S = 200 тыс. 

Ответ: 200 тыс. рублей.

Пример 3. Юля хочет взять в кредит 150 тысяч рублей под 10% годовых. Погашение кредита происходит раз в год равными платежами (кроме последней выплаты). На какое минимальное количество лет Юля должна взять кредит, чтобы ежегодные выплаты были не более 50 тысяч рублей? 

Решение. Нет так быстро. Сначала рассмотрим еще одну логическую задачу, которая поможет в решении. 

Маша решила раздать шарики прохожим. Всего у нее 10 шариков. В каком случае большее количество людей получит шарики: если Маша будет раздавать по два или по одному шарику? 

Если Маша раздает по одному шарику, то их получит 10 человек. А если по 2, то их получит 5 человек. Чем больше шариков Маша отдает одному человеку, тем меньше людей получит шарики. 

В нашей задаче приводятся такие же рассуждения: чем больше выплату будет делать Юля, тем меньше лет она будет выплачивать кредит. То есть ее ежегодная выплата должна иметь максимальное значение, а по условию задачи это 50 тысяч рублей. 

1. Составим таблицу. Коэффициент увеличения будет равен (1 + frac{10}{100} = 1,1). 

В этой задаче в таблице удобнее сразу считать величины, а не подставлять переменные. 

Заполним первую строчку. Долг без процентов равен 150 тысяч, после начисления процентов он будет равняться 150 * 1,1 = 165 тысяч. 

Как мы определили выше, выплата должна равняться 50 тысяч. Тогда остаток: 165 — 50 = 115 тысяч.

Год	Долг без %	Долг после %	Выплата	Остаток
1	150	165	50	115

2. Аналогично считаем и заполняем все следующие строчки до тех пор, пока долг после начисления процентов не станет меньше 50:

Год	Долг без %	Долг после %	Выплата	Остаток
1	150	165	50	115
2	115	126,5	50	76,5
3	76,5	84,15	50	34,15
4	34,15	37,565

3. Заметим, что после этой выплаты есть возможность полностью погасить кредит. Следовательно, остаток будет равен 0. 

Тогда выплата равна 37,565 — 0 = 37,565. 

Год	Долг без %	Долг после %	Выплата	Остаток
1	150	165	50	115
2	115	126,5	50	76,5
3	76,5	84,15	50	34,15
4	34,15	37,565	37,565	0

Таким образом, с помощью только таблицы мы решили задачу. Минимальное число лет, на которое Юля может взять кредит — 4 года, что видно из таблицы. 

Год	Долг без %	Долг после %	Выплата	Остаток
1	150	165	50	115
2	115	126,5	50	76,5
3	76,5	84,15	50	34,15
4	34,15	37,565	37,565	0

Ответ: 4. 

Дифференцированные платежи

Разобравшись в аннуитетных платежах, следует перейти к дифференцированным. В них также нет ничего сложного. 

Главное отличие их от аннуитетных в том, что долг будет уменьшаться на одну и ту же величину.

Дифференцированные платежи — такая система выплат, при которой сумма долга уменьшается равномерно. 

В этом случае сумма кредита делится на несколько равных частей, которые выплачиваются банку вместе с начисленными на остаток процентами. Из этих двух частей будет складываться платеж: причем с каждым месяцем (годом) платеж будет уменьшаться, поскольку будет уменьшаться и процент, который начисляется на остаток. 

В отличие от аннуитетных платежей, выплаты в дифференцированных платежах не фиксированные. Со временем выплаты будут уменьшаться. 

Представим схему выплат дифференцированных платежей. Например, кредит S взяли на 4 года. Следовательно, каждый год он будет уменьшаться на (frac{1}{4})S часть, а проценты будут начисляться уже на остаток. 

Ключевые слова, чтобы определить, что перед нами схема с дифференцированными платежами:

• платежи разные;
• каждый платеж меньше предыдущего;
• долг уменьшается на одну и ту же величину. 

Рассмотрим примеры задач на дифференцированные платежи. 

Пример 1.  Вася взял кредит в банке на сумму 1 млн. рублей под 10% годовых. Условия его возврата таковы:

— После начисления процентов необходимо выплатить часть долга.

— После каждой выплаты долг должен быть на одну и ту же сумму меньше долга до выплаты.

— Кредит должен быть выплачен за 5 лет. 

Найдите общую сумму выплат по кредиту. 

Решение. Составим таблицу. Для этого введем коэффициент увеличения (k = 1 + frac{10}{100} = 1 + 0,1 = 1,1). 

Заметим, что кредит взят на 5 лет, а сумма долга уменьшается равномерно. Следовательно, каждый год долг должен уменьшаться на (frac{1}{5}) = 0,2 млн. рублей.

Таким образом мы можем заполнить последний столбик таблицы: достаточно просто вычитать каждый год из долга 0,2 млн рублей. Также мы сразу можем заполнить второй столбик таблицы, для этого достаточно переносить данные из последнего столбика. 

Год	Долг до %	Долг после %	Выплата	Остаток
1	1			1-0,2=0,8
2	0,8			0,6
3	0,6			0,4
4	0,4			0,2
5	0,2			0

Теперь, зная долг до процентов, мы можем узнать долг после процентов:

Год	Долг до %	Долг после %	Выплата	Остаток
1	1	1,1		1-0,2=0,8
2	0,8	0,88		0,6
3	0,6	0,66		0,4
4	0,4	0,44		0,2
5	0,2	0,22		0

Осталось найти выплату. А для этого мы можем использовать все тот же БУП. 

Год	Долг до %	Долг после %	Выплата	Остаток
1	1	1,1	1,1-0,8 = 0,3	1-0,2=0,8
2	0,8	0,88	0,88-0,6 = 0,28	0,6
3	0,6	0,66	0,66-0,4 = 0,26	0,4
4	0,4	0,44	0,44-0,2 = 0,24	0,2
5	0,2	0,22	0,22-0 = 0,22	0

Осталось найти сумму выплат, для этого нужно сложить все выплаты, которые были произведены по кредиту:

0,3 + 0,28 + 0,26 + 0,24 + 0,22 = 1,3 млн. рублей. 

Ответ: 1,3 млн. рублей. 

На примере этой задачи составим схему того, как выплачивался кредит. Она поможет нагляднее понять, как работает схема выплат при дифференцированных платежах. 

Пример 2. Лиза взяла кредит в банке на 12 месяцев. Условия его возврата таковы:

— 1 числа каждого месяца долг возрастает на 5% по сравнению с концом предыдущего месяца;

— со 2 по 14 число каждого месяца необходимо выплатить часть долга;

— 15 числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15 число предыдущего месяца. 

Какая сумма была взята в кредит, если известно, что 11 платеж составил 165 тысяч рублей?

Решение. Пусть S — кредит. Отметим, что кредит каждый месяц будет уменьшаться на (frac{S}{12}).

В этот раз составим немного другую таблицу, а именно разобьем выплату на проценты и основную часть от долга. Также таблица на 12 месяцев слишком большая (а в задачах могут встретиться таблицы еще больше), поэтому мы будем рассматривать только первые два и последние три месяца. 

Сразу заполним все данные, которые нам известны. 

Месяц	Долг до %	Долг после %	Выплата	Остаток
Процентная часть	Основная часть
1	S			S12	11S12
2	11S12			S12	10S12
…
10	3S12			S12	2S12
11	2S12			S12	S12
12	S12			S12	0

Теперь будем начислять процент. Введем переменную (k = frac{5}{100}). Заметим, что это не коэффициент увеличения, а значит долг после начисления процентов будет состоять из основной части и процентной. Заполним третий столбик: 

Месяц	Долг до %	Долг после %	Выплата	Остаток
Процентная часть	Основная часть
1	S	S+kS		S12	11S12
2	11S12	11S12+k*11S12		S12	10S12
…
10	3S12	3S12+k*3S12		S12	2S12
11	2S12	2S12+k*2S12		S12	S12
12	S12	S12+k*S12		S12	0

Чтобы закончить заполнение таблицы, вспомним БУП и найдем, чему будет равна процентная часть выплаты. 

Было: S + k * S 
Убрали: (x + frac{S}{12})
Осталось: (frac{11S}{12})

Тогда получаем: (S + k * S — (x + frac{S}{12}) = frac{11S}{12})
(S + k * S — x — frac{S}{12} = frac{11S}{12})
(frac{11S}{12} + k * S — x = frac{11S}{12})

x = k * S — это данные для четвертого столбика. Найти остальные ячейки можно таким же способом, но проще будет переносить процентную часть из третьего столбика. 

Месяц	Долг до %	Долг после %	Выплата	Остаток
Процентная часть	Основная часть
1	S	S+kS	kS	S12	11S12
2	11S12	11S12+k*11S12	k*11S12	S12	10S12
…
10	3S12	3S12+k*3S12	k*3S12	S12	2S12
11	2S12	2S12+k*2S12	k*2S12	S12	S12
12	S12	S12+k*S12	k*S12	S12	0

Таблица составлена. Осталось найти, чему равен 11 платеж. Для этого нужно найти выплату в 11 месяц, а значит сложить эти ячейки:

Месяц	Долг до %	Долг после %	Выплата	Остаток
Процентная часть	Основная часть
1	S	S+kS	kS	S12	11S12
2	11S12	11S12+k*11S12	k*11S12	S12	10S12
…
10	3S12	3S12+k*3S12	k*3S12	S12	2S12
11	2S12	2S12+k*2S12	k*2S12	S12	S12
12	S12	S12+k*S12	k*S12	S12	0

Получаем (k * frac{2S}{12} + frac{S}{12} = 165)

Подставляем вместо коэффициентов известные величины и решаем уравнение. 

(frac{S}{12} * (2k + 1) = 165)
(frac{S}{12} * (2 * 0,05 + 1) = 165)
S * (0,1 + 1) = 1980
1,1 * S = 1980
S = 1800 тыс.

Ответ: 1800 тысяч рублей. 

Пример 3. В октябре планируется взять кредит на сумму 15 млн рублей на целое число лет. Условия его возврата таковы:

— Каждый март долг возрастает на 10% по сравнению с концом предыдущего месяца.

— С марта по октябрь необходимо выплатить часть долга.

— В октябре каждого года долг будет на одну и ту же сумму меньше долга на октябрь предыдущего года. 

На сколько лет планируется взять кредит, если сумма выплат после его полного погашения составила 22,5 млн рублей? 

Решение. Пусть k = (frac{10}{100}), S = 15 млн — кредит, n — количество лет, на которое взят кредит. 

Заметим, что каждый год долг будет уменьшаться на (frac{S}{n}) лет. 

1. Составим таблицу. Поскольку нам неизвестно количество лет, рассматриваться будут только первые два и последние два года. 

Месяц	Долг до %	Долг после %	Выплата	Остаток
Процентная часть	Основная часть
1	S	S+ks	kS	Sn	S-Sn=n-1nS
2	n-1nS	n-1nS+k*n-1nS	k*n-1nS	Sn	n-2nS
…
n-1	2nS	2nS+k*2nS	k*2nS	Sn	1nS
n	1nS	1nS+k*1nS	k*1nS	Sn	0

Сумма выплат — это сумма всех платежей, которые были внесены за кредит. 

В таблице это будет сумма этих ячеек. Отметим, что между 2 и n-1 месяцем есть еще все оставшиеся выплаты, которые просто не прописаны в таблицы. Эти выплаты также обязательно учесть в уравнении. 

Месяц	Долг до %	Долг после %	Выплата	Остаток
Процентная часть	Основная часть
1	S	S+ks	kS	Sn	S-Sn=n-1nS
2	n-1nS	n-1nS+k*n-1nS	k*n-1nS	Sn	n-2nS
…
n-1	2nS	2nS+k*2nS	k*2nS	Sn	1nS
n	1nS	1nS+k*1nS	k*1nS	Sn	0

2. Составим уравнение: 

(kS + frac{S}{n} + k * frac{n — 1}{n}S + frac{S}{n} + … + k * frac{2}{n}S + frac{S}{n} + k * frac{1}{n}S + frac{S}{n} = 22,5)

Немного по-другому сгруппируем слагаемые и вынесем общие множители за скобку:

(kS * (1 + frac{n-1}{n}+ … + frac{2}{n} + frac{1}{n}) + n * frac{S}{n} = 22,5)
(kS * (frac{n}{n} + frac{n-1}{n} + … + frac{2}{n} + frac{1}{n}) + S = 22,5)

3. Заметим, что в скобках осталась арифметическая прогрессия, а нам необходимо найти ее сумму. Подробнее про арифметические прогрессии можно прочитать в статье «Арифметическая прогрессия». 

Сейчас сразу применим формулу суммы арифметической прогрессии:

(kS * (frac{frac{n}{n} + frac{1}{n}}{2}*n) + S = 22,5)
(kS * ((frac{n + 1}{n} * frac{1}{2}) * n) + S = 22,5)
(kS* frac{n + 1}{2}+ S = 22,5)

4. Заменим переменные на известные величины:

(0,1 * 15 * frac{n + 1}{2} + 15 = 22,5)
(1,5 * frac{n + 1}{2} = 7,5)
1,5 * (n + 1) = 15
n + 1 = 10
n = 9

Ответ: 9 лет. 

Мы рассмотрели задачи на аннуитетные и дифференцированные платежи. Подведем небольшой итог и сравним эти платежи. 

	Аннуитетные платежи	Дифференцированные платежи
Выплаты	Выплаты равны между собой	Выплаты со временем уменьшаются
Как уменьшается долг	Неравномерно	Равномерно
Из чего складывается выплата	Начисленные на остаток проценты и часть от долга.  В первое время выплачиваются в основном проценты, а долг лишь малой частью. Со временем в основном будет выплачиваться долг.	Начисленные на остаток проценты и часть от долга. Долг выплачивается равными частями.
График выплат

Если придерживаться приведенного выше чек-листа, можно решить экономическую задачу на любую схему выплат. 

Фактчек

• С кредитами мы встречаемся не только в математике, но и в реальной жизни. Для их выплат существуют две основные схемы: аннуитетная и дифференцированная. 
• Аннуитетные платежи — такая система выплат, при которых кредит выплачивается раз в год (или в другой период времени в зависимости от договора) равными платежами. Аннуитетные платежи фиксированные и равны между собой. А долг уменьшается неравномерно. 
• Дифференцированные платежи — такая система выплат, при которой сумма долга уменьшается равномерно. В этом случае долг будет уменьшаться равномерно, а вот платежи будут различными. Каждый новый платеж будет меньше предыдущего. 
• Для решения задач необходимо научиться составлять таблицы и уравнения на основе данных в условии. Также для решения можно пользоваться чек-листом, чтобы точно ничего не упустить.

Проверь себя

Задание 1. 
Как уменьшается долг при аннуитетных платежах?

1. равномерно;
2. неравномерно;
3. на одинаковую величину каждый расчетный период;
4. долг не уменьшается. 

Задание 2.
Как уменьшается долг при дифференцированных платежах? 

1. равномерно;
2. неравномерно;
3. на различную величину каждый расчетный период;
4. долг не уменьшается. 

Задание 3.
Из чего складывается выплата?

1. Выплачивается только долг.
2. Выплачиваются только проценты.
3. Выплата складывается из части долга и процентов, начисленных на остаток.
4. Выплата всегда складывается из части долга и процентов, начисленных на весь долг. 

Задание 4.
Что такое сумма выплат?

1. Это сумма всех процентов, начисленных на кредит.
2. Это сумма долга.
3. Это последний платеж, который был внесен за кредит.
4. Это сумма всех платежей, внесенных за кредит. 

Задание 5.
Для какой системы выплат характерны равные платежи?

1. дифференцированная;
2. аннуитетная;
3. и дифференцированная, и аннуитетная;
4. ничего из перечисленного выше. 

Ответы: 1. — 2 2. — 1 3. — 3 4. — 4 5. — 2

Размещённые в настоящем разделе сайта публикации носят исключительно ознакомительный характер, представленная в них информация не является гарантией и/или обещанием эффективности деятельности (доходности вложений) в будущем. Информация в статьях выражает лишь мнение автора (коллектива авторов) по тому или иному вопросу и не может рассматриваться как прямое руководство к действию или как официальная позиция/рекомендация АО «Открытие Брокер». АО «Открытие Брокер» не несёт ответственности за использование информации, содержащейся в публикациях, а также за возможные убытки от любых сделок с активами, совершённых на основании данных, содержащихся в публикациях. 18+

АО «Открытие Брокер» (бренд «Открытие Инвестиции»), лицензия профессионального участника рынка ценных бумаг на осуществление брокерской деятельности № 045-06097-100000, выдана ФКЦБ России 28.06.2002 (без ограничения срока действия).

ООО УК «ОТКРЫТИЕ». Лицензия № 21-000-1-00048 от 11 апреля 2001 г. на осуществление деятельности по управлению инвестиционными фондами, паевыми инвестиционными фондами и негосударственными пенсионными фондами, выданная ФКЦБ России, без ограничения срока действия. Лицензия профессионального участника рынка ценных бумаг №045-07524-001000 от 23 марта 2004 г. на осуществление деятельности по управлению ценными бумагами, выданная ФКЦБ России, без ограничения срока действия.

Задачи про кредиты, в которых неизвестно время

12 октября 2015

В этом уроке мы разберём, как решаются самые сложные задачи про кредиты из ЕГЭ по математике — в них неизвестно время. В первую очередь запомните формулу, связывающую общую сумму кредита, процент, срок и ежемесячные платежи:

$Ccdot {{x}^{n}}=Pcdot frac{{{x}^{n}}-1}{x-1}$.

Где $C$ — общая сумма кредита, $x$ — процент, $P$ — ежемесячный платёж, а число $n$ — это срок, на который берётся кредит. Именно его мы сегодня и будем искать, для чего нам потребуется выполнить два шага:

1. Примерно оценить срок. Для этого достаточно разделить кредит на платёж, а полученное число округлить в большую сторону. Если при делении получилось целое число, просто увеличиваем его на единицу.
2. Убедиться, что это число и есть ответ. Для этого придётся посчитать несколько степеней от довольно некрасивых чисел: 1,1; 1,03 и т.д.

Решая эту задачу, всегда помните связь между сроком и размером ежемесячного платежа:

Чем больше срок, тем меньше ежемесячный платёж. И наоборот: чем меньше срок, тем больше платёж.

Кроме того, есть важное правило, которое позволит существенно сократить объём выкладок. Вместо того, чтобы искать значение, скажем${{1,03}^{7}}$, можно найти какую-нибудь промежуточную степень (всё, что больше куба, для этого числа уже считается проблематично), а затем продолжить работу с верхними и нижними оценками этого числа. Что это за оценки и как с помощью них решить задачу 17 вдвое быстрее — смотрите в видеоуроке.:)

Самая сложная задача про кредиты из ЕГЭ

Сегодня мы разберем то, о чем я обещал поговорить еще в прошлом учебном году, когда мы впервые познакомились с задачами с экономическим содержанием из ЕГЭ по математике. Вообще, с момента появления этой задачи в Едином государственном экзамене прошло довольно много времени, и с тех пор такие задачи стали более разнообразными, чем изначально, однако самая сложная и часто встречающаяся задача осталась неизменной. Именно о ней мы сегодня и поговорим. А точнее, речь пойдет о самом сложном варианте этой задачи — о задаче на выплаты и кредиты, когда работает универсальная формула сложных процентов, выведенная в предыдущем видеоуроке, однако неизвестно в этот раз не кредит и не платеж, а именно время, на который взят этот самый кредит.

Формула сложных процентов в математике

Откуда берется эта формула расчета сложных процентов и как вообще все это работает, я подробно объяснял на предыдущем видеоуроке, поэтому если вы его не смотрели, очень рекомендую посмотреть. Однако из того же самого видеоурока возникла куча вопросов и, в частности, разбор самой сложной задачи мы оставили на потом. Именно этим мы сегодня и займемся.

Прежде чем решать эту задачу, давайте запишем нашу классическую формулу расчета сложных процентов, а именно:

[Ccdot {{x}^{n}}=Pcdot frac{{{x}^{n}}-1}{x-1}]

Где $C$ — общая сумма кредита, $x$ — процент, $P$ — ежемесячный платеж, $n$ — срок, на который берется кредит.

Эту формулу мы выводили на одном из предыдущих видеоуроков, ее можно без всяких сомнений использовать на настоящем экзамене, при этом предварительно обосновав примерно так же, как это сделано в предыдущем видеоуроке.

Задача № 1

Итак, экономическая задача, в которой неизвестной искомой величиной является время:

1 января 2015 года пенсионерка взяла в банке 1,5 млн. рублей в кредит. Схема выплаты кредита следующая: 1 числа каждого следующего месяца банк начисляет 10 процентов на оставшуюся сумму долга (то есть увеличивает долг на 10%), а затем пенсионерка переводит в банк платеж. На какое минимальное количество месяцев пенсионерка может взять кредит, чтобы ежемесячные платежи составили не более 350 тыс. рублей?

Шаг первый: выписываем известные данные

Итак, начинаем решать нашу задачу. Во-первых, выпишем все, что нам известно. Прежде всего, нам дан общий объем кредита:

Кредит = 1 500 000

Известно, что ежемесячный платеж не должен превышать 350 тыс. рублей. Давайте так и запишем:

Платеж = 350 000

Кроме того, известен процент. Мы знаем, что если 10% записать в виде коэффициента, то это будет:

% = 1,1

Шаг второй: составляем уравнение, используя формулу вычисления сложных процентов

А то, что нам неизвестно, так это число $n$ в данном уравнении. Давайте подставим все, что мы знаем в формулу сложных процентов и посмотрим, что получится:

[1500000cdot {{1,1}^{n}}=350000cdot frac{{{1,1}^{n}}-1}{1,1-1}]

[150cdot {{1,1}^{n}}=35cdot left( {{1,1}^{n}}-1 right)cdot 10left| :5 right.]

Давайте введем замену:

[{{1,1}^{n}}=t]

[]

В этом случае получим:

[3t=7left( t-1 right)]

[3t=7t-7]

[-4t=-7]

[t=frac{7}{4}=1,75]

Вспоминаем, что такое $t$. Нам предстоит решить следующее уравнение:

[{{1,1}^{n}}=1,75]

Шаг третий: находим наименьшее значение

Если вы попытаетесь решить данное уравнение с помощью калькулятора, то у вас ничего не получится — числа будут либо больше, либо меньше, но точного значения вы не получите. Поэтому давайте еще раз вернемся к условию задачи и прочитаем, что ежемесячные платежи должны составить не более 350 тыс. рублей. Давайте задумаемся: чем на больший срок берется один и тот же кредит, тем меньшими являются ежемесячные платежи. А поскольку нам требуется, чтобы ежемесячные платежи были не более 350 тысяч рублей, то это значит, что срок должен быть не менее чем указанный. На самом деле, с учетом того, что точно этому сроку наше значение не может быть равно, мы получаем, что нам нужно решить не уравнение, а неравенство вида

[{{1,1}^{n}} gt 1,75]

Еще раз внимательно посмотрите на этот переход — это принципиально важный момент во всей задачи. Мы не можем подобрать точное натуральное значение $n$ такое, чтобы $1,1$ в этой степени давала $1,75$, поэтому теперь наша задача — найти минимальное натуральное $n$ такое, чтобы выполнялось это неравенство. Спрашивается: а почему минимальное? Ведь можно взять кредит на 100 лет и тогда уж точно все получится, т.е. ${{1,1}^{n}}$ будет больше, чем $1,75$. Однако нам в задаче требуется найти именно минимальное количество. Поэтому из всех таких $n$, которые удовлетворяют этому неравенству, мы выберем наименьшее, а, по сути, мы сейчас сами найдем это самое наименьшее.

Составим небольшую таблицу.

месяц $left( n right)$	${{1,1}^{n}}$
1	1,1
2	1,21
3	1,331
4	1,4641
5	1,61051
6	1,771561

И вот мы впервые превзошли искомые ограничения — $1,75$. Обратите внимание: пяти месяцев нам еще недостаточно, потому что коэффициент не достигнет желаемой величины, а шести месяцев уже достаточно, потому что он не только достигнет, но и превзойдет желаемую величину. Поэтому окончательный ответ — шесть месяцев.

Нюансы решения

Как видите, в этом нет ничего сложного, даже если от нас требуется найти именно срок. Единственное, что нас могло смутить — довольно большой объем вычислений в самом конце, когда мы считали степени $1,1$. Однако неудивительно, так как это одна из самых последних и самых сложных задач из ЕГЭ по математике, поэтому если бы здесь было совсем все просто, то за нее не давали бы три первичных балла.

Кроме того, хотел бы обратить ваше внимание на окончательное обоснование ответа. Напоминаю, что мы решаем задачу из второй части: здесь недостаточно написать ответ, а нужно предоставить полное и грамотное обоснование. Итак, возводя в степени, мы в определенный момент получаем такие значения: $1,61051$ и $1,771561$. Возникает вопрос: а почему мы выбрали второе число? Мы решаем данное неравенство, которое было обосновано ранее, и второе значение под наше неравенство уже подходит, потому что

[{{1,1}^{6}}=1,771561]

А в $1,75$во втором знаке стоит «пять», т.е. цифра меньше и, следовательно, это число меньше. А вот если мы попытаемся выбрать в качестве ответа пять месяцев и связанный с этим значением коэффициент $1,61051$, то нас этот вариант точно не устроит. Почему? Потому что если мы подставим его в исходную формулу сложных процентов и попытаемся по этим данным посчитать итоговый ежемесячный платеж, то он окажется больше, чем требуемые 350 тыс. рублей.

Для того, чтобы успешно решить эту задачу, в том числе, когда требуется найти срок необходимо учесть два момента:

1. Помнить формулу решения сложных процентов и желательно уметь выводить ее на экзамене.
2. Помнить зависимость между сроками и размерами платежей. Зависимость обратно пропорциональная: чем больше срок, тем меньше ежемесячный платеж и наоборот — чем больше ежемесячный платеж, тем меньше срок, в течение которого придется выплачивать один и тот же кредит.

Задача № 2

1 января 2015 года пенсионерка взяла в банке 1,1 млн. рублей в кредит. Схема выплаты кредита следующая: 1 числа каждого следующего месяца банк начисляет 3 процента на оставшуюся сумму долга (то есть увеличивает долг на 3%), а затем пенсионерка переводит в банк платеж. На какое минимальное количество месяцев пенсионерка может взять кредит, чтобы ежемесячные платежи составили не более 220 тыс. рублей?

На первый взгляд задача ничем не отличается от предыдущей. Разве что пенсионерка стала более разумной, поэтому взяла лишь 1,1 млн. и, кроме того, процент в месяц составляет лишь 3%, а не 10%, и ежемесячные платежи должны составлять не более 220 тыс. рублей.

Шаг первый: выписываем известные данные

Вновь запишем нашу формулу сложных процентов:

[Ccdot {{x}^{n}}=Pcdot frac{{{x}^{n}}-1}{x-1}]

Где $C$ — общая сумма кредита, $x$ — процент, $P$ — ежемесячный платеж, $n$ — срок, на который берется кредит.

Давайте запишем известные данные:

Кредит = 1100000

Платеж = 220000

% = 1,3

Шаг второй: составляем уравнение, используя формулу расчета сложных процентов

Подставляем все эти данные в формулу. Вновь нам неизвестен срок, т.е. $n$:

[1100000cdot {{1,03}^{n}}=220000cdot frac{{{1,03}^{n}}-1}{1,03-1}left| :11 right.]

[{{1,3}^{n}}=2cdot left( 1,03-1 right)cdot frac{10}{3}left| 3 right.]

Введем замену:

[{{1,03}^{n}}=t]

[3t=20left( t-1 right)]

[3t=20t-20]

[3t=20t-20]

[-17t=-20]

[t=frac{20}{17}]

И вот тут мы натыкаемся на первую проблему, которой в предыдущей задачи не было: $frac{20}{17}$ не переводится в «красивую» десятичную дробь, а нам нужна именно десятичная дробь, потому что когда мы сделаем таблицу, то будем возводить $1,03$ в разные степени, а она, будучи десятичной дробью в разных степенях, тоже будет давать десятичные дроби. На самом деле выход просто: просто разделим и оставим первые четыре знака:

[frac{20}{17}=1,17647…]

Возвращаясь к нашей задаче, мы получим следующее:

[t=1,17647…]

Приравняем обе части:

[{{1,03}^{n}}=1,17647…]

По аналогии с предыдущей задачей несложно заметить, что нет такого натурального $n$, чтобы $1,03$ в этой степени давало нам $1,17647…$, поэтому мы спокойно заменяем наше равенство знаком неравенства:

[{{1,03}^{n}} gt 1,17647…]

При этом при решении данного неравенства в ответ пойдет наименьшее $n$. Давайте снова составим таблицу, где слева мы снова будем писать месяцы, а справа — коэффициент:

месяц $left( n right)$	${{1,03}^{n}}$
1	1,03
2	1,0609
3	1,092727
4
5
6

Шаг четвертый: находим верхнюю и нижнюю оценку, используя «метод оценок»

Мы столкнулись с еще одной проблемой: по мере роста номера месяца объем вычислений становится просто катастрофическим, поэтому дальнейшие вычисления нужно выполнять с помощью какого-то другого инструмента, иначе мы просто утонем в объеме выкладок. Эта проблема характерна для всех задач, в которых процент меньше десяти. Поэтому как только вы видите маленькие проценты, не думайте, что вам попалась легкая задача, наоборот — будут проблемы. Однако все эти проблемы легко решаются при помощи замечательного инструмента под названием «метод оценок». Сейчас я вам расскажу, что это такое и как его применять на примере данной задачи.

Итак, нам необходимо найти четвертую, пятую и шестую степень числа $1,03$. Мы находили при помощи предыдущей, умножая ее на $1,03$. Однако уже на третьем шаге объем вычислений оказался достаточно большим. Поэтому чтобы не утонуть в вычислениях, выполним следующую манипуляцию: давайте посмотрим на числа, которые у нас получились при возведении в квадрат и в третью степень. Сначала рассмотрим, что получилось в квадрате:

[{{1,03}^{2}}=1,0609]

Давайте отсечем два знака после запятой и запишем просто $1,06$. То же самое сделаем с третьей степенью, в которой мы получили такое выражение:

[{{1,03}^{3}}=1,092727]

Отсечем два знака после запятой и получим $1,09$. В обоих случаях мы берем лишь первые два знака. Что нам это даст? Дело в том, что в любом случае $1,0609$, т.е. истинное значение второй степени будет больше, чем только что найденное значение:

[1,06 lt 1,0609]

Аналогично можно сказать и про третью степень:

[1,09 lt 1,092727]

А теперь возьмем и к этим числам в последнем разряде прибавим «единицу». Получим:

[1,06+1=1,07]

[1,09+1=1,10]

Замечательное свойство этих чисел состоит в том, что в первом случае

[1,07 gt 1,0609]

А вот втором случае будет следующее неравенство:

[1,1 gt 1,092727]

Давайте запишем вот так:

[1,06 lt 1,0609 lt 1,07]

[1,09 lt 1,092727 lt 1,1]

Полученные значения называются верхней и нижней оценкой или округлением с недостатком и округлением с избытком. И вместо того, чтобы мучится с огромным объемом вычислений, мы будем просто перемножать эти числа. Каким образом и на каком основании? Давайте заметим следующее:

[{{1,03}^{4}}={{1,03}^{2}}cdot {{1,03}^{2}}]

[{{1,03}^{5}}={{1,03}^{3}}cdot {{1,03}^{2}}]

[{{1,03}^{6}}={{1,03}^{3}}cdot {{1,03}^{3}}]

Шаг пятый: находим наименьшее значение

Давайте заполним таблицу до конца:

месяц $left( n right)$	${{1,03}^{n}}$
1	1,03
2	1,0609
3	1,092727
4	$1,06cdot 1,06 lt * lt 1,07cdot 1,07$
5	$1,06cdot 1,09 lt * lt 1,07cdot 1,1$
6	${{1,09}^{2}} lt * lt {{1,1}^{2}}$

Что дают нам все эти верхние и нижние оценки? Во-первых, существенно сокращается объем вычислений, а, во-вторых, давайте посмотрим на последние значения:[{{1,1}^{2}}=1,21]

[{{1,09}^{2}}=1,1881]

Итого

[1,1881 lt {{1,03}^{6}} lt 1,21]

Что это значит? А то, что для $n=6$ мы уже точно превзойдем искомую величину. Мы уже знаем, что

[{{1,03}^{n}}=1,17647 lt 1,1881 lt {{1,03}^{6}} lt 1,21]

В принципе, «шесть» нас уже устраивает — это кандидат в ответ. Но проблема в том, что в задаче от нас требуется найти минимальное количество месяцев. А что, если минимальное количество месяцев будет «пять»? Давайте посчитаем и повторим все те же вычисления для «пяти»:

[1,1554 lt {{1,03}^{5}} lt 1,177]

Но такие оценки нам ничего не дадут. Почему? Потому что если мы начертим числовую прямую и отметим на ней нижнюю и верхнюю оценки, то получим следующее: между $1,1554$ и $1,177$ находится ${{1,03}^{5}}$. Но также между ними есть и $1,17647$, которое мы должны превзойти. Если это число лежит правее $1,17647$, то нас все устраивает, и ответом будет «пять». Однако если оно будет левее, то «пять» нас не устраивает и ответом будет «шесть». Как же проверить, какое из чисел нас устраивает? К сожалению, в рамках верхних и нижних оценок, которые мы записали, ответить на этот вопрос невозможно – нам просто не хватает точности. Поэтому давайте еще раз выпишем значения для $n=2$ и $n=3$.

месяц $left( n right)$	${{1,03}^{n}}$
2	1,0609
3	1,092727

До сих пор мы брали оценку с точностью до двух знаков после запятой. Но как только что мы убедились, такой точности недостаточно. Поэтому давайте возьмем оценку с точностью до трех знаков после запятой. В таком случае мы получим следующее:

месяц $left( n right)$	${{1,03}^{n}}$
2	$1,060 lt 1,0609 lt 1,061$
3	$1,092 lt 1,092727 lt 1,093$

Таким образом, какой бы не было $n$ в выражение ${{1,03}^{n}}$, оно в любом случае будет больше, чем $1,06cdot 1,092$, но в любом случае меньше, чем $1,061cdot 1,093$.

Запишем вычисления:

[1,06cdot 1,092 lt * lt 1,59673]

Это значит, что наши предположения верны. Искомое значение, если вновь попытаться начертить его на числовой прямой, будет снизу ограничено $1,1554$, а сверху —$1,159673$. Т.е. ${{1,03}^{5}}$ будет заведомо меньше, чем $1,159673$ и уж тем более меньше, чем $1,17647…$А это значит, что наше исходное предположение о том, что при $n=5$ мы уже превзойдем величину $1,17647…$ неверно. А это значит, что пятый месяц нас все еще не устроит. А вот шестой месяц, о котором мы сначала и подумали, действительно является таковым. Итого, окончательный ответ — шесть. Задача решена и полностью обоснована.

Полезные советы при решении задач с использованием формулы сложных процентов

Самое главное в это задаче — это понять, чем оценки отличаются от округления. Мы берем две цифры после запятой, отсекаем все, что идет после них, и записываем эти числа слева. Очевидно, что поскольку дальше идут какие-то цифры в настоящем числе, это число будет то, что мы получили слева (см. таблицу). Эти числа, которые находятся слева, и называются меньшими оценками. Затем к ним мы в самом последнем разряде (к последней цифре) прибавляем «единицу», и получаем число, на единицу большее в конце, например, было $1,06$ стало $1,07$ и т.д. Это будут верхние оценки. И далее, что бы мы не делали, какую бы степень и номер месяца не считали, все равно истинное значение нашей величины будет заключено между степенями верхней и нижней оценок.

Но есть одна проблема: в определенный момент мы получаем, что и число, и искомая величина лежат в одних и тех же пределах. Пределы получены, разумеется, при вычислении степеней оценок. В нашей ситуации такая проблема возникла в вычислениях значения для пятого месяца: левая оценка дала нам $1,1554$, а правая — $1,177$. Между этими двумя числами лежит как искомая величина, которую мы не знаем, так и наше искомое значение, т.е. ${{1,03}^{n}}$. Выход из такой ситуации напрашивается сам собой: если нам не хватает точности, то необходимо просто увеличить точность исходных оценок, т.е. после запятой мы берем не две, а три цифры. Но поскольку нас интересуют, прежде всего, верхние оценки, мы увеличим каждое из этих чисел на единицу в разряде, запишем и перемножим. В результате мы получим следующее: новая верхняя оценка для нашего числа, для пятого месяца, будет лежать между $1,1554$ и $1,159673$.

На самом деле, пятый месяц даст коэффициент, который будет находиться в вышеуказанном диапазоне, что явно меньше, чем искомая величина $1,174647…$ На первый взгляд может показаться, что сложность и объем всех этих вычислений будет существенно больше, чем если бы мы просто возвели числа в степень квадрат, куб и т.д. На самом деле это не так. Уже на третьей и четвертой степенях возникают большие числа, а до пятого и шестого месяца вы просто не дойдете.

Как определить кандидата в ответ, исходя из условия задачи

В качестве заключительного аккорда сегодняшнего видеоурока я хотел бы вам рассказать еще один довольно хитрый инструмент, который позволит еще с первого взгляда на задачу уже примерно оценить, какой месяц предстоит считать и какой месяц, скорее всего, является кандидатом в ответ.

Давайте посмотрим на исходную формулу. Всего объем кредит, который предстоит выплатить, составляет 1,1 млн. при этом ежемесячно нужно выплачивать по 220 тыс. рублей. Давайте разделим общий размер задолженности на ежемесячный платеж. В этом случае мы получим количество месяцев, которые необходимо будет потратить на выплату кредита, если бы на нас не начислялись проценты. Однако сами по себе проценты невелики — в нашем случае всего 3% в месяц. Это значит, что вряд ли накопится задолженность еще больше, чем на один месяц и, следовательно, нужно прибавить к полученной величине еще единицу, и мы получим наиболее вероятный кандидат на ответ.

В нашем случае, если 1,1млн. разделить на 220 тыс., то мы получим пять месяцев, но без учета начисленных процентов. Соответственно, еще один месяц потребуется на то, чтобы погасить проценты. И мы получим тот же самый ответ.

Однако хочу вас предупредить, что ни в коем случае нельзя использовать этот прием как единственно возможное обоснование того ответа, который у вас получается в задаче! Потому что мы решаем одну из самых сложных задач ЕГЭ: там требуется привести не только ответ, но и все подробные выкладки и обоснования. Такой прием — это лишь подсказка для нас самих, для того, чтобы понимать, какие именно месяцы, какие именно степени считать. Дальнейшим шагом нужно доказать, что, например, число, равное пяти месяцам, нас не устраивает, а шести месяцев точно устраивает. Каким образом можно это сделать. Например, с помощью числовой прямой, более точных вычислений, метода оценок или как вам будет удобнее. В любом случае, мы с учениками недавно убедились, что эта подсказка существенно облегчает выкладки и хотя бы дает представление о том, каким должен быть ответ.

Тренируйтесь, решайте задачи, оттачивайте навык с вычислением верхних и нижних оценок. Это далеко не последний урок на решение задач с экономическим содержанием, поскольку самих задач стало довольно много, и их условия стали более разнообразные. Поэтому оставайтесь с нами!

Смотрите также:

1. Задачи на кредит с плавающим платежом
2. Производительность труда в задаче 17 из ЕГЭ по математике: сложные случаи. Нет, это не текстовые задачи.:)
3. Тест к уроку «Что такое логарифм» (средний)
4. Комментарий к пробному ЕГЭ от 7 декабря
5. Опасные ошибки в задачах на площади
6. Задача B4: экономика