Одной из задач, возникающих при анализе рядов
динамики, является установление закономерности изменения уровней изучаемого
показателя во времени. В некоторых случаях эта закономерность, общая тенденция
развития объекта вполне ясно отображается уровнями динамического ряда. Но часто
приходится встречаться с такими рядами динамики, когда уровни ряда претерпевают
самые различные изменения (то возрастают, то убывают) и можно говорить лишь об
общей тенденции развития явления, либо о тенденции к росту, либо к снижению. В
этих случаях для определения основной тенденции развития явления, достаточно
устойчивой на протяжении данного периода, используют особые приемы обработки
рядов динамики.
Уровни ряда динамики формируются под совокупным
влиянием множества длительно и кратковременно действующих факторов и в том
числе различного рода случайных обстоятельств.
Выявление основной закономерности изменения уровней
ряда предполагает ее количественное выражение, в некоторой мере свободное от случайных
воздействий. Выявление основной тенденции развития (тренда) называется в
статистике также выравниванием временного ряда, а методы выявления основной
тенденции — методами выравнивания. Выравнивание позволяет характеризовать
особенность изменения во времени данного динамического ряда в наиболее общем
виде как функцию времени, предполагая, что через время можно выразить влияние
всех основных факторов.
Приемы сглаживания динамических рядов (укрупнение
интервала и метод скользящей средней) могут рассматриваться как важное
вспомогательное средство, облегчающее применение других методов и, в частности,
более строгих методов выявления тенденции. Для того чтобы представить
количественную модель, выражающую общую тенденцию изменений уровней
динамического ряда во времени, используется аналитическое выравнивание ряда
динамики.
В этом случае фактические уровни заменяются
уровнями, вычисленными на основе определенной кривой.
Предполагается, что она отражает общую тенденцию изменения во времени
изучаемого показателя.
При аналитическом выравнивании ряда динамики
закономерно изменяющийся уровень изучаемого показателя оценивается как функция
времени
,
Где
—
уровни динамического ряда, вычисленные по соответствующему аналитическому
уравнению на момент времени t.
При выборе формы уравнения следует исходить и из
объема имеющейся информации. Чем больше параметров содержит уравнение тренда,
тем больше должно быть наблюдений при одной и той же степени надежности
оценивания. Выбор формы кривой может осуществляться: и на основе принятого
критерия, в качестве которого может служить сумма квадратов отклонений
фактических значений от значений, рассчитанных по уравнению тренда. Из
совокупности кривых выбирается та, которой соответствует минимальное значение
критерия. Рассмотрим аналитическое выравнивание ряда динамики
по прямой, т.е. аналитическое уравнение вида:
где
-порядковый номер
периодов или моментов времени.
Параметры
и
прямой рассчитываются
по методу наименьших квадратов (МНК).
Система нормальных уравнений в данном
случае имеет вид:
Поиск параметров уравнения можно упростить, если
отсчет времени производить так, чтобы сумма показателей времени изучаемого ряда
динамики была равна нулю
.
При нечетном числе уровней ряда динамики уровень, находящийся в середине ряда, принимается за условное начало отчета времени
(этому периоду или моменту времени придается нулевое значение). Даты времени,
стоящие выше этого уровня, обозначаются натуральными числами со знаками минус,
а ниже -натуральными числами со знаками плюс.
При условии
получим:
Правильность расчета уровней выравниваемого ряда
динамики может быть проверена следующим образом: сумма значений эмпирического
ряда должна совпадать с суммой вычисленных уровней выровненного ряда, т.е.
Аналитическое уравнение представляет собой математическую
модель развития явления и дает выражение статистической закономерности,
проявляющейся в рядах динамики. Следует помнить, что прием аналитического
выравнивания содержит в себе ряд условностей, связанных
прежде всего с тем, что уровни, характеризующие тот или иной динамический ряд,
рассматриваются как функция времени. В действительности же развитие явлений
обусловлено не тем, сколько времени прошло с отправного момента, а тем, какие
факторы влияли на развитие, в каком направлении и с какой интенсивностью. Развитие явлений во времени выступает
как внешнее выражение этих факторов, как их суммарное действие; оказывающее
влияние на изменение уровня в отдельно взятые промежутки или моменты времени.
Выявить основную тенденцию развития явления методом наименьших квадратов можно
лишь тогда, когда выяснено, что изменяющиеся во времени процессы протекают на
всем рассматриваемом промежутке времени одинаково, что их количественное и
качественное изменение происходит под действием одного и того же комплекса основных
факторов, определяющих движение данного ряда динамики.
Модели, учитывающие общие закономерности изменения
экономического явления в изучаемый интервал времени и изменения во времени
влияния комплекса факторов, называют многофакторными динамическими моделями.
Выделим особенности моделей аналитического
выравнивания уровней динамического ряда, накладывающие ограничения на их
использование. Во-первых, динамические ряды, к которым применяется
аппроксимация, должны быть достаточно длинными. Во-вторых, применение
аппроксимации наиболее целесообразно в случае медленно и плавно меняющегося
уровня. В-третьих, аппроксимация как метод моделирования практически не
адаптируется к изменяющимся условиям формирования уровней ряда; при появлении
новых данных построение модели должно быть проведено заново. В-четвертых, при
использовании для расчета параметров уравнения метода наименьших квадратов
(МНК) считается, что значимость информации в пределах отрезка аппроксимации
одинакова независимо от давности полученных данных, в то время как более
поздние данные имеют большую ценность.
Помимо этого, динамические ряды экономических
показателей часто имеют небольшую длину и подвержены значительным колебаниям,
которые аппроксимация предвидеть не может.
Задача
В таблице приведены готовые данные о
трудоемкости производства:
| Год | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
|
Трудоемкость производства, человек-часов |
8 | 8.4 | 7.6 | 7 | 7.3 | 6.6 | 5.9 | 5 | 5.2 |
-
Провести аналитическое выравнивание ряда динамики по прямой.
Построить точечный и интервальный
прогноз на 2018 год.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Решение
1) Произведем аналитическое выравнивание ряда по прямой.
Составим расчетную таблицу:
Расчетная вспомогательная таблица 1
| Годы |
|
|
|
|
| 2009 | -4 | 8 | 16 | -32 |
| 2010 | -3 | 8,4 | 9 | -25,2 |
| 2011 | -2 | 7,6 | 4 | -15,2 |
| 2012 | -1 | 7 | 1 | -7 |
| 2013 | 0 | 7,3 | 0 | 0,0 |
| 2014 | 1 | 6,6 | 1 | 6,6 |
| 2015 | 2 | 5,9 | 4 | 11,8 |
| 2016 | 3 | 5 | 9 | 15 |
| 2017 | 4 | 5,2 | 16 | 20,8 |
| Итого | 0 | 61,0 | 60 | -25,2 |
Коэффициенты уравнения линейного тренда найдем по формулам:
Уравнение линейного тренда имеет вид:
2) Составим расчетную таблицу:
Расчетная вспомогательная таблица 2
| Годы |
|
|
Теоретические значения |
|
| 2009 | -4 | 8 | 8,48 | 0,2304 |
| 2010 | -3 | 8,4 | 8,06 | 0,1156 |
| 2011 | -2 | 7,6 | 7,64 | 0,0016 |
| 2012 | -1 | 7 | 7,22 | 0,0484 |
| 2013 | 0 | 7,3 | 6,8 | 0,25 |
| 2014 | 1 | 6,6 | 6,38 | 0,0484 |
| 2015 | 2 | 5,9 | 5,96 | 0,0036 |
| 2016 | 3 | 5 | 5,54 | 0,2916 |
| 2017 | 4 | 5,2 | 5,12 | 0,0064 |
| Итого | — | — | — | 0,996 |
Среднеквадратическая ошибка:
Точечный прогноз на 2018 год (t=5):
Ошибка
прогноза составит:
По таблице критерия Стьюдента,
для доверительной вероятности
(уровня значимости
) находим:
Вывод к задаче
Таким образом
тренд для трудоемкости производства выражается линейным уравнением
.
Согласно прогнозу, в 2018 году трудоемкость производства с вероятностью 0,95
будет лежать в пределах от 3,6 до 5,8 человеко-часов.
Наиболее точным и эффективным способом
выявления основной тенденции развития
является аналитическое выравнивание.
При этом фактические уровни ряда динамики
заменяются теоретическими уровнями,
вычисленными на основе определенной
кривой, описываемой аналитическим
выражением. Предполагается, что
теоретическая кривая свободна от
всевозможных колебаний и поэтому
наиболее точно отображает общую тенденцию
изменения во времени изучаемого
показателя.
При аналитическом выравнивании ряда
динамики, его уровни выражаются в виде
функции времени.
(12.1)
где
– теоретический уровень ряда динамики,
вычисленный по определенному
аналитическом выражению на момент
времени
.
Чаще всего при аналитическом выравнивании
используются следующие математические
зависимости:
-
линейная (уравнение прямой):
(12.2)
-
параболическая (уравнение параболы):
(12.3)
-
экспоненциальная (уравнение экспоненты):
(12.4)
-
гиперболическая (уравнение гиперболы):
(12.5)
Выбор формы кривой во многом определяет
результаты выявления тренда. Основанием
для выбора формы кривой может использоваться
содержательный анализ сущности развития
данного явления. Можно опираться на
результаты предыдущих исследований в
данной области.
На практике для этих целей прибегают к
анализу графического изображения
уровней ряда динамики (линейной
диаграммы). Однако из графического
представления эмпирических данных не
всегда удается произвести однозначный
выбор формы кривой (вида уравнения).
Поэтому целесообразно воспользоваться
графическим изображением сглаженных
уровней, в которых случайные и периодические
колебания в некоторой степени оказываются
сглаженными.
При выборе вида аналитической кривойдля выравнивания ряда динамики можно
воспользоваться следующими рекомендациями.
-
Линейная зависимостьиспользуется
в том случае, когда в исходном ряде
динамики наблюдается более или менее
постоянные абсолютные цепные приросты,
не проявляющие тенденции ни к увеличению,
ни к снижению. -
Параболическаязависимостьвыбирается в тех случаях, когда абсолютные
цепные приросты сами по себе обнаруживают
некоторую тенденцию развития, но
абсолютные цепные приросты абсолютных
приростов (разности второго порядка)
никакой тенденции развития не проявляют. -
Экспоненциальные зависимости, если
в исходном динамическом ряде наблюдается
либо более или менее постоянный
относительный рост (устойчивость цепных
темпов роста, темпов прироста,
коэффициентов роста), либо, при отсутствии
точного постоянства, – устойчивость
в изменении показателей относительного
роста (цепных темпов роста цепных же
темпов роста).
Для решения уравнений аналитических
кривых (формулы 12.2 – 12.5) в большинстве
случаев используют метод наименьших
квадратов, который обеспечивает
наименьшую сумму квадратов отклонений
фактических уровней от выровненных
(теоретических).
(12.6)
Рассмотрим технику аналитического
выравнивания ряда динамики с использованием
уравнения прямой, имеющей наиболее
простое выражение, на следующем примере.
Пример. Имеются данные за последние
10 лет по заводу, где производятся запасные
части для тракторов. Эти данные приведены
в табл. 12.3.
-
Для того, чтобы выдвинуть гипотезу о
предполагаемом законе распределения
уровней ряда динамики, построим график
зависимости выпуска продукции от
времени. Такой график для нашего примера
представлен на рис. 12.1.
Таблица 12.3
Выпуск продукции на заводе (тыс. шт.)
|
Годы |
Выпуск продукции, ( |
|
|
|
|
|
1991 |
39,4 |
-9 |
81 |
-354,60 |
39,43 |
|
1992 |
39,8 |
-7 |
49 |
-278,60 |
39,84 |
|
1993 |
40,0 |
-5 |
25 |
-200,00 |
40,25 |
|
1994 |
40,6 |
-3 |
9 |
-121,80 |
40,66 |
|
1995 |
41,4 |
-1 |
1 |
-41,40 |
41,07 |
|
1996 |
41,9 |
+1 |
1 |
41,90 |
41,47 |
|
1997 |
41,9 |
+3 |
9 |
125,70 |
41,88 |
|
1998 |
42,0 |
+5 |
25 |
210,00 |
42,29 |
|
1999 |
42,6 |
+7 |
49 |
298,20 |
42,70 |
|
2000 |
43,1 |
+9 |
81 |
387,90 |
43,11 |
|
Итого: |
412,7 |
0 |
330 |
67,30 |
412,70 |
Рис. 12.1. Динамика выпуска продукции по
годам
(ряд 1 – фактические данные ();
ряд 2 – выровненные данные ()).
-
По характеру фактических уровней,
принимаем гипотезу о существовании
прямолинейного тренда (динамика выпуска
характеризуется прямой линией). -
Запишем уравнение прямой
.
-
Решить это уравнение – значит найти
параметры
и
искомой прямой. Наиболее просто найти
значение этих параметров можно,
воспользовавшисьметодом наименьших
квадратов. Для этого необходимо
решить систему нормальных уравнений:
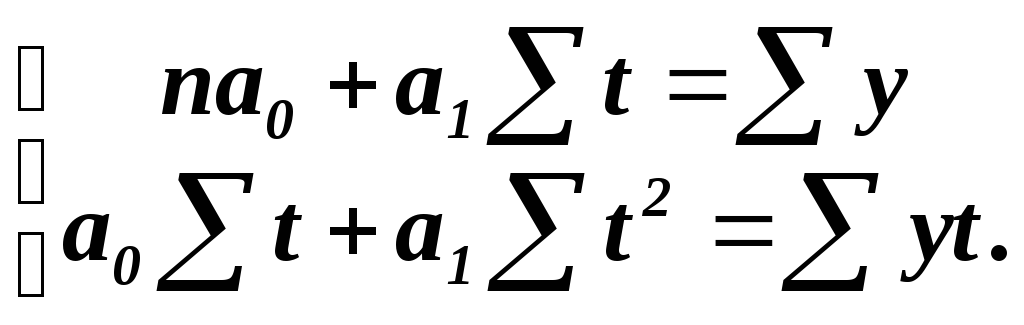
где – число членов ряда динамики;
– фактические уровни ряда динамики.
Система уравнений упрощается, если
подобрать так, чтобы их сумма равнялась
нулю, т.е. начало отсчета времени перенести
в середину рассматриваемого периода.
Тогда:
и
(12.8,
12.9)
В табл. 12.3 производим необходимые расчеты
и тогда:
и
Подставим найденные параметры
и
в уравнение прямой. Искомое уравнение
будет иметь вид:
По уравнению найдем расчетные значения
выровненных уровней ряда динамики,
подставляя в него значения
из табл. 12.3.
Полученное уравнение, описывающее
исследуемый ряд динамики, показывает,
что средний уровень производства деталей
составляет 41,27 тыс. шт.в год и ежегодно
увеличивается в среднем на0,20 тыс.
штукв год. Сумма уравнений эмпирического
ряда полностью совпадает с суммой
расчетных значений выровненного ряда.
Аналогичным способом производится
аналитическое выравнивание рядов
динамики с использованием других
уравнений кривых. Однако каждой кривой
соответствует своя система нормальных
уравнений. Так, например, для решения
уравнения параболы система уравнений
имеет вид:
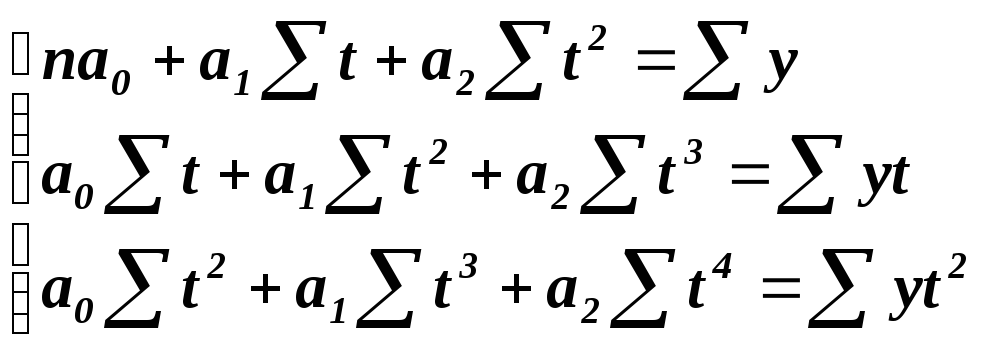
Для решения экспоненциального уравнения,
система нормальных уравнений имеет
вид:
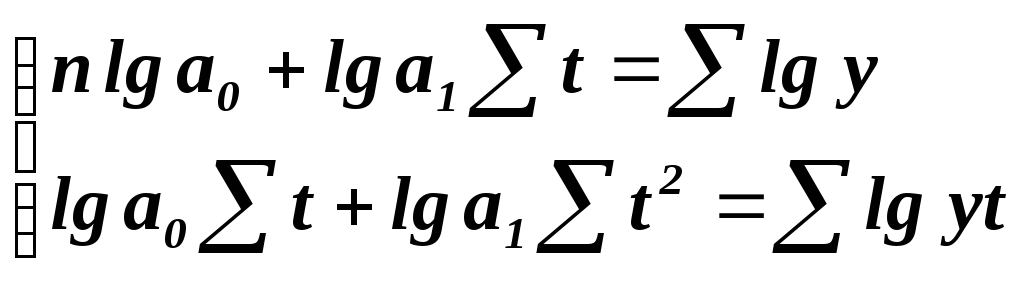
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Аналитическое выравнивание рядов динамики
Более совершенным приемом выявления основной тенденции развития в рядах динамики является аналитическое выравнивание. При изучении общей тенденции методом аналитического выравнивания исходят из того, что изменения уровней ряда динамики могут быть с той или иной степенью точности приближения выражены определенными математическими функциями. Вид уравнения определяется характером динамики развития конкретного явления. На практике по имеющемуся временному ряду задают вид и находят параметры функции y=f(t), а затем анализируют поведение отклонений от тенденции. Чаще всего при выравнивании используются следующие зависимости: линейная, параболическая и экспоненциальная. Во многих случаях моделирование рядов динамики с помощью полиномов или экспоненциальной функции не дает удовлетворительных результатов, так как в рядах динамики содержатся заметные периодические колебания вокруг общей тенденции. В таких случаях следует использовать гармонический анализ (гармоники ряда Фурье). Применение, именно, этого метода предпочтительно, поскольку он определяет закон, по которому можно достаточно точно спрогнозировать значения уровней ряда.
Целью же аналитического выравнивания динамического ряда является определение аналитической или графической зависимости y=f(t). Функцию y=f(t) выбирают таким образом, чтобы она давала содержательное объяснение изучаемого процесса. Это могут быть различные функции.
Системы уравнений вида y=f(t) для оценки параметров полиномов по МНК
(кликабельно)
Графическое представление полиномов n-порядка
1. Если изменение уровней ряда характеризуется равномерным увеличением (уменьшением) уровней, когда абсолютные цепные приросты близки по величине, тенденцию развития характеризует уравнение прямой линии.
2. Если в результате анализа типа тенденции динамики установлена криволинейная зависимость
, примерно с постоянным ускорением, то форма тенденции выражается уравнением параболы второго порядка.
3. Если рост уровней ряда динамики происходит в геометрической прогрессии, т.е. цепные коэффициенты роста более или менее постоянны, выравнивание ряда динамики ведется по показательной функции.
После выбора вида уравнения необходимо определить параметры уравнения. Самый распространенный способ определения параметров уравнения — это метод наименьших квадратов, в котором в качестве решения принимается точка минимума суммы квадратов отклонений между теоретическими (выравненными по выбранному уравнению) и эмпирическими уровнями.
Выравнивание по прямой (определение линии тренда) имеет выражение: yt=a0+a
1t
- t—условное обозначение времени;
- а0и a1—параметры искомой прямой.
Параметры прямой находятся из решения системы уравнений:
Система уравнений упрощается, если значения t подобрать так, чтобы их сумма равнялась Σt = 0, т. е. начало отсчета времени перенести в середину рассматриваемого периода. Если до переноса точки отсчета t = 1, 2, 3, 4…, то после переноса:
- если число уровней ряда нечетное t = -4 -3 -2 -1 0 +1 +2 +3 +4
- если число уровней ряда четное t = -7 -5 -3 -1 +1 +3 +5 +7
Таким образом, ∑t в нечетной степени всегда будет равна нулю.
Аналогично находятся параметры параболы 2-го порядка из решения системы уравнений:
Выравнивание по среднему абсолютному приросту или среднему коэффициенту роста:
- Δ-средний абсолютный прирост;
- К-средний коэффициент роста;
- У0-начальный уровень ряда;
- Уn-конечный уровень ряда;
- t-порядковый номер уровня, начиная с нуля.
Построив уравнение регрессии, проводят оценку его надежности. Значимость выбранного уравнения регрессии, параметров уравнения и коэффициента корреляции следует оценить, применив критические методы оценки:
F-критерий Фишера, t–критерий Стьюдента, при этом, расчетные значения критериев сравниваются с табличными (критическими) при заданном уровне значимости и числе степеней свободы. Fфакт > Fтеор — уравнение регрессии адекватно.
n — число наблюдений (уровней ряда), m — число параметров уравнения (модели) регрессии.
Проверка адекватности уравнения регрессии ( качества модели в целом) осуществляется с помощью средней ошибки аппроксимации, величина которой не должна превышать 10-12% (рекомендовано).
Рассмотрим на примере аналитическое выравнивание ряда динамики по прямой с переносом точки отсчета в середину ряда:
|
Годы |
Объем валовой продукции |
Условное обозн. года |
Расчетные значения |
Выровненный ряд |
|
|
Yi |
t |
t2 |
Y*t |
Ỹ=209,06+3,91t |
|
|
1990 |
187,8 |
-5 |
25 |
-939,00 |
189,51 |
|
1991 |
185,7 |
-4 |
16 |
-742,94 |
193,42 |
|
1992 |
195,8 |
-3 |
9 |
-587,29 |
197,33 |
|
1993 |
207,9 |
-2 |
4 |
-415,80 |
201,24 |
|
1994 |
208,3 |
-1 |
1 |
-208,32 |
205,15 |
|
1995 |
208,6 |
0 |
0 |
0,00 |
209,06 |
|
1996 |
219,7 |
1 |
1 |
219,70 |
212,97 |
|
1997 |
218,5 |
2 |
4 |
437,00 |
216,88 |
|
1998 |
222,2 |
3 |
9 |
666,60 |
220,79 |
|
1999 |
225,1 |
4 |
16 |
900,40 |
224,7 |
|
2000 |
220,0 |
5 |
25 |
1100,00 |
228,61 |
|
Итого |
2299,62 |
0 |
110 |
430,35 |
2299,62 |
|
ΣYi |
Σt |
Σt2 |
ΣY*t |
ΣỸ |
Решение системы линейных уравнений:
Σt в нечетной степени всегда равна нулю, поэтому система уравнений упрощается и принимает следующий вид:
Сумма уровней выровненного ряда должна равняться сумме уровней исходного ряда, что, в свою очередь, подтверждает правильность расчетов. Выровненный ряд динамики по прямой вида (линейный тренд): Ỹ=209,06+3,91t
Смотри аналитическое выравнивание на примере:
helpstat.ru
8.6 Аналитическое выравнивание ряда динамики
Использование
методов этой группы позволяет преодолеть
недостатки приемов механического
сглаживания. Они дают возможность
учитывать все уровни динамического
ряда, моделировать динамические процессы,
строить прогноз и интерполировать
отдельные значения анализируемого
показателя.
Основополагающей
в теории аналитического выравнивания
является идея о возможности геометрического
представления зависимости уровней
динамического ряда от фактора времени
(t).
Всегда можно найти плавную линию (прямую
или кривую), которая бы проходила через
центр распределения и минимизировала
сумму квадратов отклонений от нее до
каждой точки, представляющей отдельные
фактические значения у.
Чем лучше теоретическая кривая описывает
распределение значений анализируемого
показателя в динамике и меньше сумма
квадратов отклонений (ошибка функции
тренда), тем, следовательно, лучше сделан
выбор теоретической функции и надежнее
статистические выводы о закономерностях
в динамике для у
(рисунок 8.1).
Объём
реализации
yt
t
(годы)
y=f(t)
Рисунок
8.1 – Динамика объемов реализации
продукции предприятия
Составляется
модель зависимости значений показателя
от фактора времени t
. Эта модель называется уравнением
тренда.
Параметры
модели для ŷt
находят с использованием метода
наименьших квадратов, т.е. при условии,
что сумма квадратов ошибки модели
минимальна, близка к нулю:
Рассмотрим
аналитическое выравнивание по прямой.
Уравнение прямой имеет вид
yt=a0+a1t,
где
t
– время,
a0,
a1
–
параметры.
Величина
a0
характеризует
среднее значение признака в динамическом
ряду, , a1
– ежегодный
прирост значений признака, обусловленный
фактором времени.
Если
а1>0,
– имеется тенденция к росту, если а1<0,
имеется тенденция к снижению.
Параметры
a0
и
a1
можно найти из следующей системы
уравнений:
Поскольку
t
– время, можем перейти к условным годам,
выбрав начало отсчета таким образом,
чтобы сумма времени ∑t
была равна
0.
При
этом индексация временных периодов
производится по следующему правилу:
– если
во временном ряду четное число лет, то
обозначения t
принимаются с разницей в одну единицу
(таблица 8.3):
Таблица
8.3 – Выбор t-значений
при четном числе лет во временном ряду
|
Год |
2004 |
2005 |
2006 |
2007 |
2008 |
2009 |
2010 |
2011 |
|
Обозначение |
-7 |
-5 |
-3 |
-1 |
1 |
3 |
5 |
7 |
– если
в анализируемом периоде число лет
нечетно, то в центре динамического ряда
ставится ноль, а вправо и влево от него
годы нумеруются по порядку (таблица
8.4):
Таблица8.4 – Выбор t-значений при
нечетном числе лет во временном ряду
|
Год |
2005 |
2006 |
2007 |
2008 |
2009 |
2010 |
2011 |
|
Обозначение |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
При четном числе уровней динамического ряда
При
нечетном
Тогда,
подставив значение ∑t=0
в систему уравнений , получим следующую
систему уравнений:
.
Следовательно,
значения параметров a0
и
a1имеют вид:
Воспользуемся упрощенным алгоритмом
расчета и расчеты исходных сумм покажем
в таблице 8.5.
Таблица
8.5 – Расчет параметров уравнения линейной
функции по данным о реализации грузовых
автомобилей на рынке
|
Год |
Реализовано |
t |
t2 |
tyt |
Теоретическое
уt |
|
1 |
2 |
3 |
4 |
5 |
6 |
|
2004 |
15 |
-7 |
49 |
-105 |
14.33 |
|
2005 |
14 |
-5 |
25 |
-70 |
15,45 |
|
2006 |
16 |
-3 |
9 |
-48 |
16,57 |
|
2007 |
19 |
-1 |
1 |
-19 |
17,69 |
|
2008 |
20 |
1 |
1 |
20 |
18,81 |
|
2009 |
19 |
3 |
9 |
57 |
19,93 |
|
2010 |
21 |
5 |
25 |
105 |
21,05 |
|
2011 |
22 |
7 |
49 |
154 |
22,17 |
|
Итого |
146 |
— |
168 |
94 |
146 |
По
данным таблицы 8.5 находим
Уравнение
тренда запишем в следующем виде:
yt=18,25+0,56t.
В
этом уравнении
– среднее значение признака в динамическом
ряду,–
ежегодный прирост значений признака,
обусловленный фактором времениt.
В нашем примере средний годовой объем
реализации грузовых автомобилей на
рынке в течение 8-летнего периода составил
18,25 тыс. шт., ежегодный прирост объема
реализации – 0,56 тыс. шт.
Подставляя
в уравнение тренда условные значения
фактора времени t,
легко вычислить теоретические
(выровненные) значения показателя объема
реализации автомобилей (таблица 8.5).
Линейная
функция часто используется в анализе
динамики, и она наиболее проста. Однако
когда значения динамического показателя
изменяются неравномерно, линейная
функция может давать грубые ошибки и
следует искать функцию другого вида,
наиболее точно отвечающую эмпирическому
распределению значений изучаемого
показателя. Подбор функции при этом
осуществляется графически или
статистическим путем.
Статистика
располагает достаточно большим набором
теоретических функций, например уравнение
параболы второго порядка:
yt=а0+а1t+а2t2.
Такая
модель успешно используется при изменении
значений показателя в динамике с
ускорением (замедлением), система
нормальных уравнений в этом случае
будет иметь вид:
,
где
a0
– средний уровень динамического ряда,
а1
– средний годовой прирост уровня
динамического ряда,
а2
– скорость развития явления (ускорение),
т.е. дополнительный средний прирост уt
за счет более
высоких темпов развития явления в каждый
последующий год.
Кроме
того, могут использоваться наиболее
употребляемые виды функций:
– экспоненциальная:
yt=a0ea1
– явления имеют этапы замедленного и
(простая) ускоренного развития;
– степенная:
yt=a0ta1–
явления с
преобладающим ускоренным развитием;
– гиперболическая
I
типа: yt=a0+а1/t
–явления с
преобладающими этапами замедленного
развития;
Всплески
в развитии являются результатом
постепенного накопления количественных
изменений;
– гиперболическая
II типа: yt=1/(a0+a1t).
studfiles.net
Выделение тренда динамического ряда
После того как
динамический ряд был исследован на
предмет наличия в нем тренда, и данный
тренд был обнаружен, приступают к
непосредственному выделению тренда с
экстраполяцией полученных результатов.
Выравнивание динамического ряда
производят с помощью механических и
аналитических методов выравнивания.
Метод скользящей
средней заключается
в замене исходного динамического ряда
новым, расчетным рядом, состоящим из
средних уровней за определенный период,
со сдвигом на одну дату. Если исходный
динамический ряд обозначить как
,
то ряд, выровненный методом скользящей
средней (за трехлетний период), будет
выглядеть как:

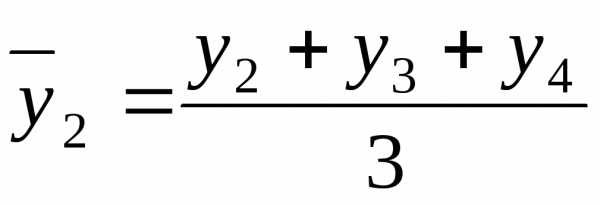
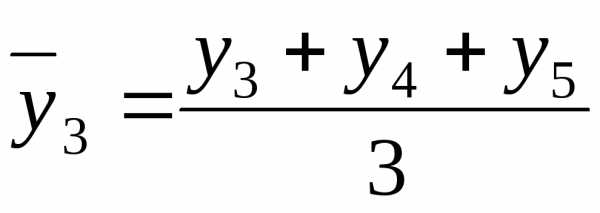
и т.д. (7.16)
Аналитическое
выравнивание
позволяет определить основную тенденцию
развития явления во времени, т.е.
обобщенный (суммарный), проявляющийся
во времени результат действия всех
факторов, влияющий на развития изучаемого
явления во времени. При этом уровни ряда
динамики выражаются как функции времени:
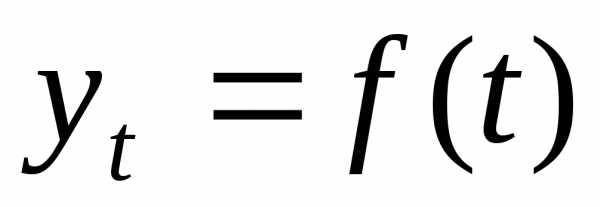
,
(7.17)
где
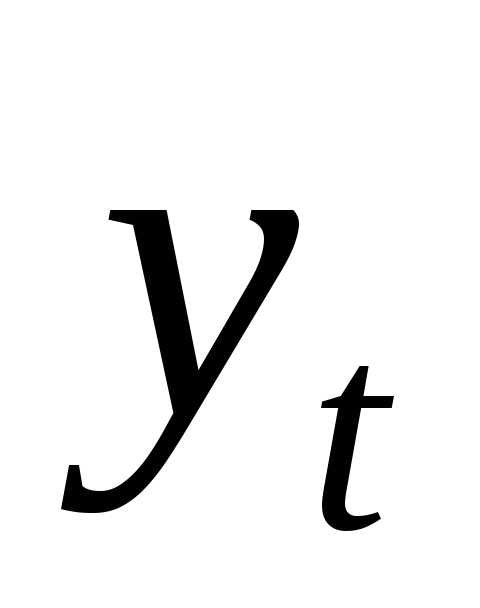
ряда;
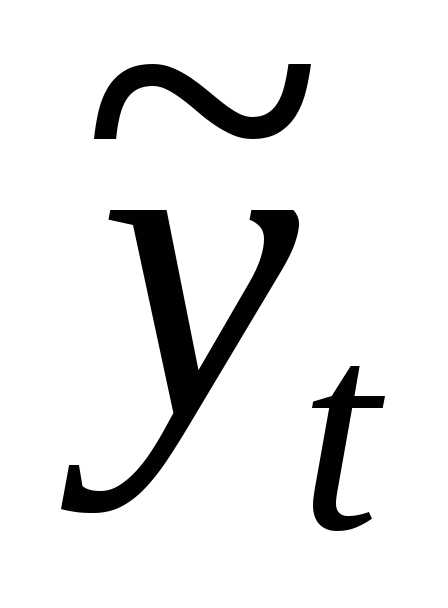
ряда, вычисленные по соответствующему
аналитическому уравнению на момент
времени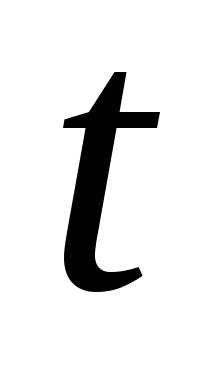
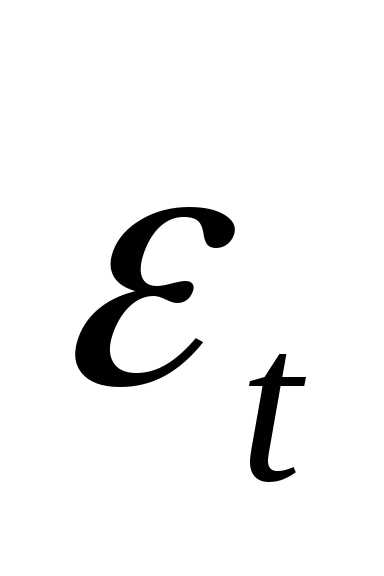
тенденции (случайное и циклическое).
При аналитическом
выравнивании чаще всего применяют
следующие трендовые модели:
-
Линейная
,
(7.18)
-
Парабола второго
порядка
,
(7.19)
-
Кубическая парабола
,
(7.20)
-
Показательная
,
(7.21)
-
Экспоненциальная
,
(7.23)
-
Модифицированная
экспонента
,
(7.24)
-
Кривая Гомперца
,
(7.25)
-
Логистическая
кривая
,
(7.26)
-
Логарифмическая
парабола
,
(7.27)
-
Гиперболическая
,
(7.28)
Выбор вида модели
проводят при помощи графического или
экспериментального методов.
Статистическую
оценку уравнения проводят при помощи
критерия
Фишера
.
Для чего рассчитывается фактический
уровень данного критерия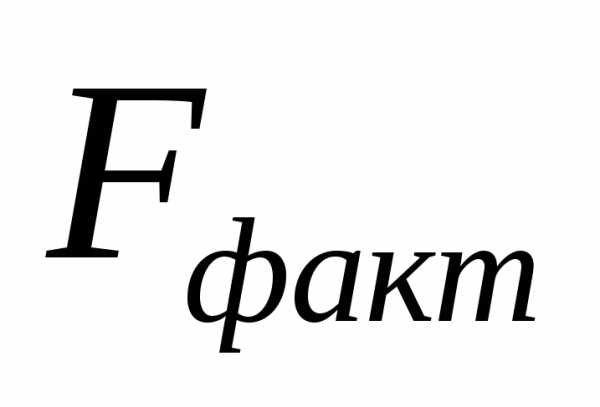
который сравнивается с теоретическим
(табличным) значением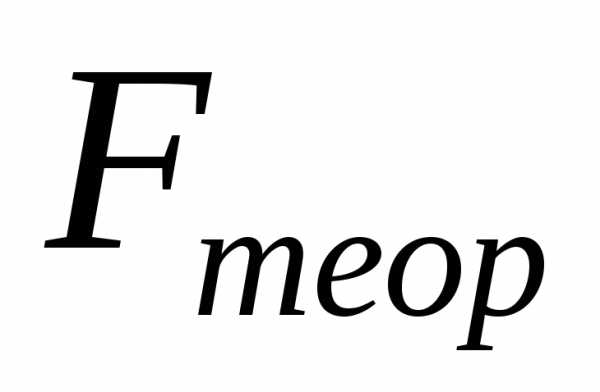

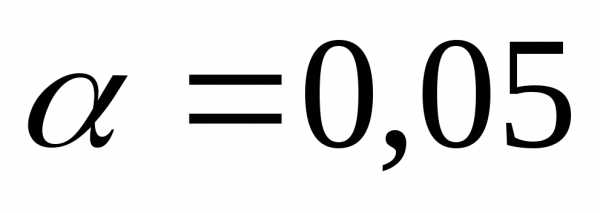
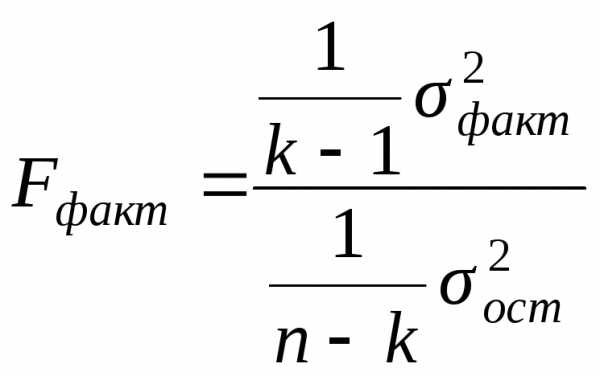
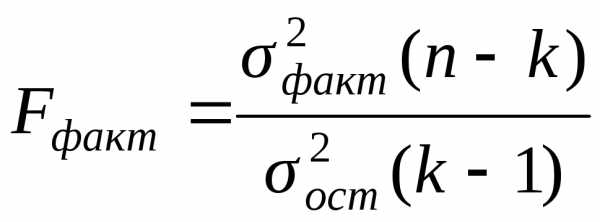
(7.29)
где
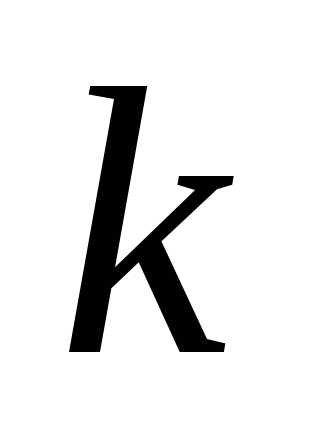
число параметров функции;
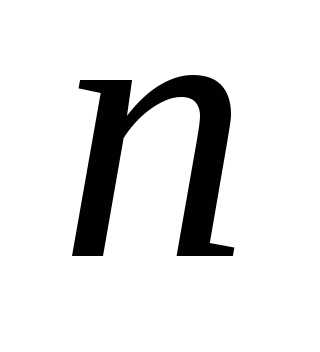
ряда;
,
(7.30)
,
(7.31)
,
(7.32)
Если
(приложение 3), то уравнение регрессии
значимо.
Аналитическое выравнивание по прямой
Аналитическое
уравнение прямой имеет вид:
,
(7.33)
Для того чтобы
рассчитать
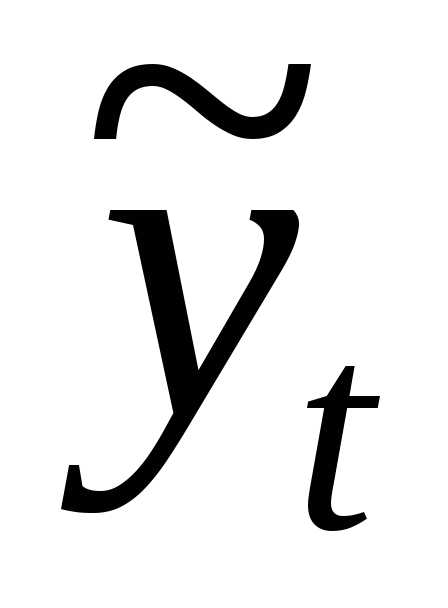
надо найти неизвестные параметры
уравнения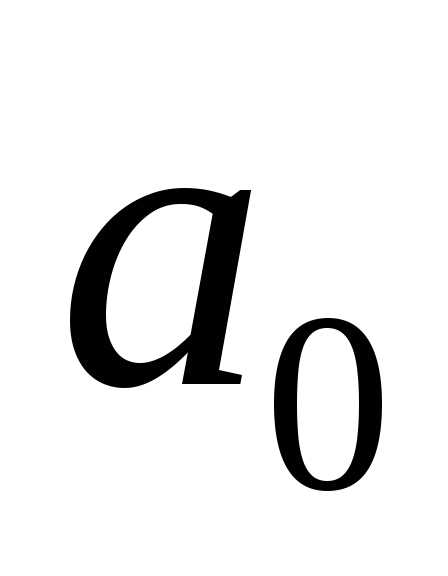

для чего воспользуемся методом наименьших
квадратов, который в данном случае даст
систему из двух нормальных уравнений:
,
(7.34)
Так как время
понятие относительное и зависит только
от точки отсчета, можно назначить такую
точку отсчета, что сумма показателей
времени исследуемого динамического
ряда будет равна нулю(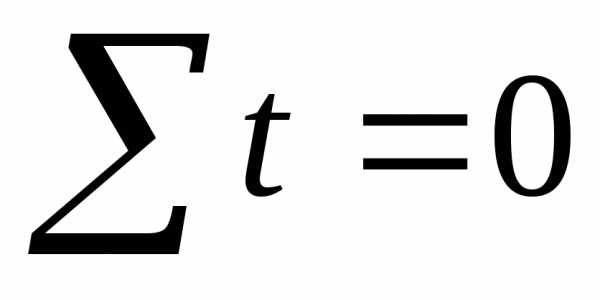
При нечетном
числе уровней изучаемого
динамического ряда за точку отсчета
принимают серединный уровень ряда,
который обозначают как

Периоды, стоящие выше данного уровня,
обозначают отрицательными натуральными
числамии т.д. Уровни, стоящие ниже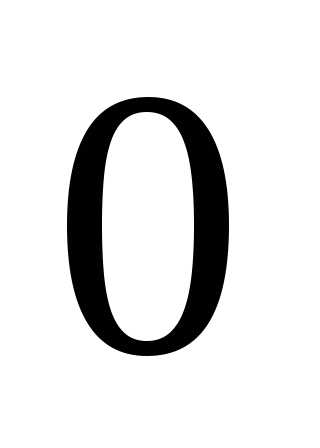
обозначают положительными числами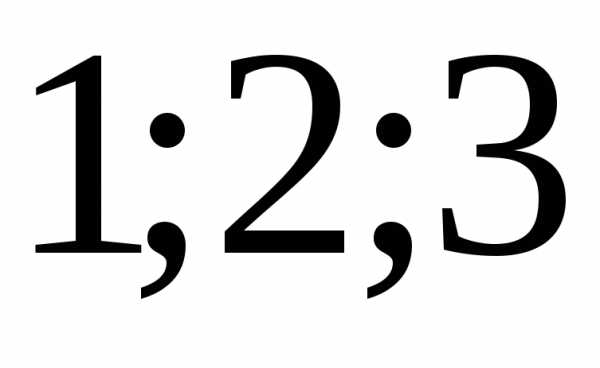
т.д. Например, ряд из семи уровней будет
обозначен как
Если число уровней
изучаемого динамического ряда четное,
то точку отсчета берут между двумя
серединами уровней, она не обозначается.
Периоды, стоящие выше, обозначают
отрицательными натуральными числами

положительными числами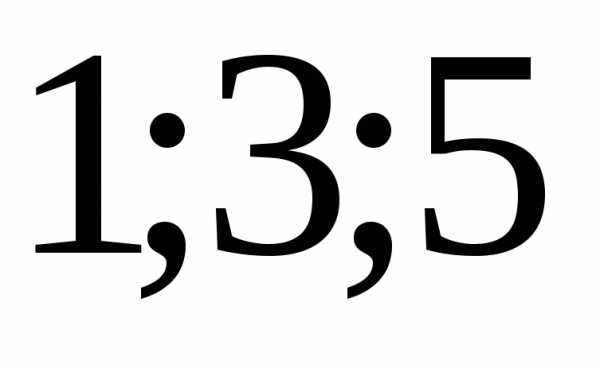
будет обозначен как.
Подставив
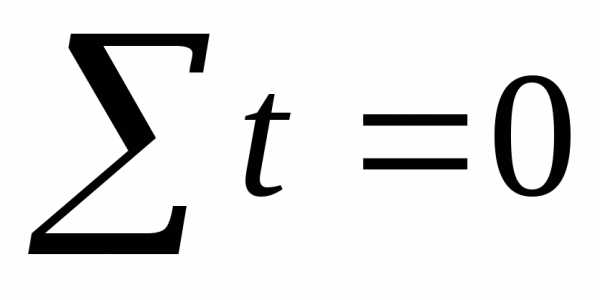
упростим:
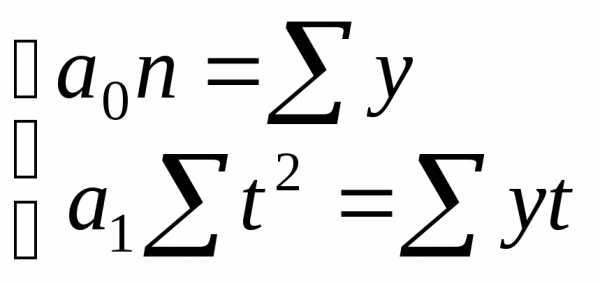
(7.35)
отсюда
и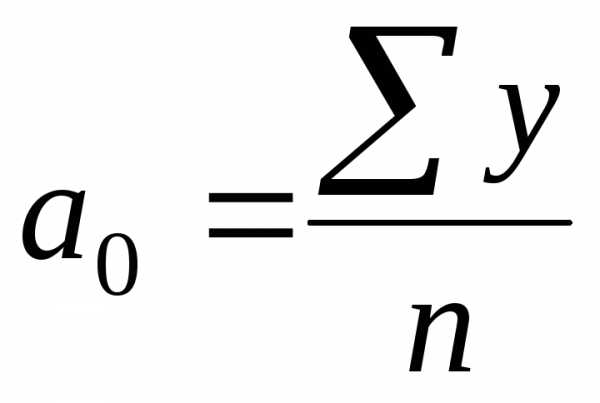
(7.36)
Для линейной
зависимости параметр
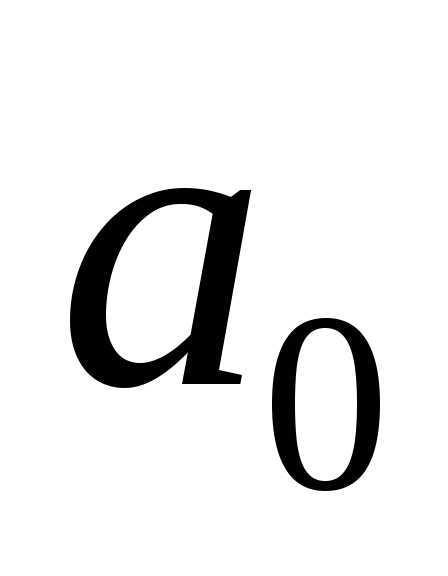
уровень ряда,
среднее изменение изучаемого явления
за один период времени.
Подставив значение
рассчитанных параметров уравнения
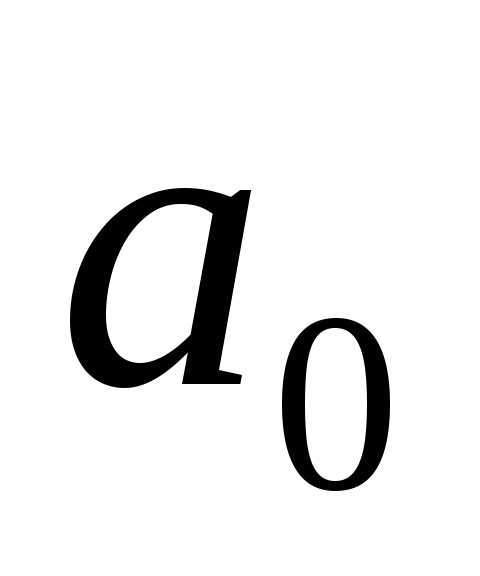
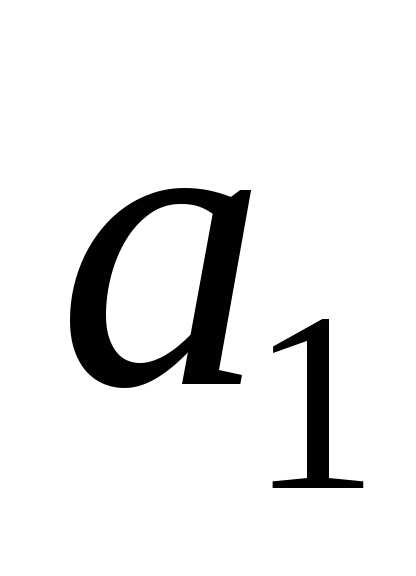

рассчитаем выровненные теоретические
значения уровней динамического ряда,
которые образуют теоретическую прямую
линию (линейный тренд). Далее проводят
оценку надежности полученного уравнения
с помощью критерия Фишера (см. выше).
studfiles.net
2. Выравнивание динамических рядов
Расчет показателей
динамики не дает в полной мере
характеристики тенденций развития.
Причем, средние показатели динамики
могут дать искаженную картину характера
динамики, поскольку они рассчитываются
на основе конечного и начального
уровней динамики и не учитывают колебания
внутри ряда.
Для анализа
тенденций развития применяют выравнивание
рядов динамики.
Наиболее простым
способом является сглаживание рядов
динамики с помощью средней скользящей.
При этом способе вычисляют средний
уровень за периоды, сдвигаемые на одну
дату. Величина интервала скольжения
определяется в зависимости от
конкретных особенностей динамики. Он
должен быть достаточным для погашения
случайных колебаний. Если в колебаниях
есть какая-то периодичность, то
целесообразно принять его равным периоду
этих колебаний. Если нет периодичности
в колебаниях, то следует последовательно
укрупнять интервал скольжения, пока
не выявится тенденция развития.
Скользящую среднюю
определяют по формулам:
;
;
………………………………….
,
где

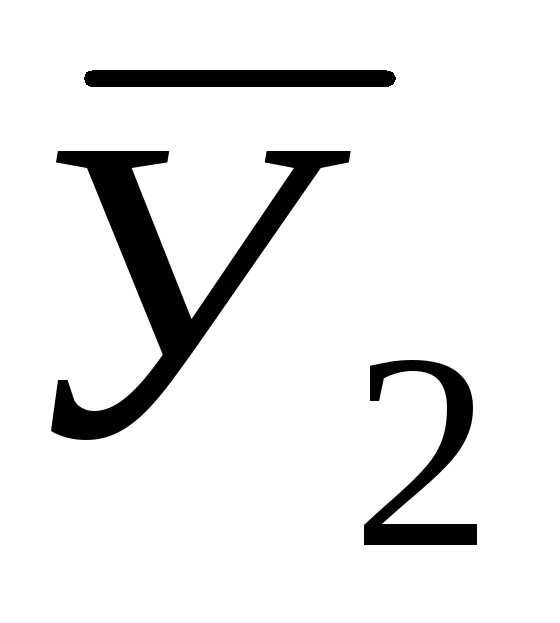
…,
скользящие средние;
У0,
У1,
…, Уn
уровни ряда;
k
– интервал
скольжения.
Сглаживание рядов
динамики не всегда четко показывает
закономерную тенденцию развития. Для
более четкого выявления тенденции
развития применяют аналитическое
выравнивание рядов динамики, которое
позволяет получить уравнение развития
(тренда). Аналитическое выравнивание
может производиться несколькими
способами: по среднему абсолютному
приросту, с помощью коэффициента роста,
способом наименьших квадратов.
Выравнивание рядов
динамики по среднему абсолютному
приросту проводят в случае, если цепные
абсолютные приросты примерно
одинаковы. Уравнение тенденции в этом
случае имеет вид:
,
где
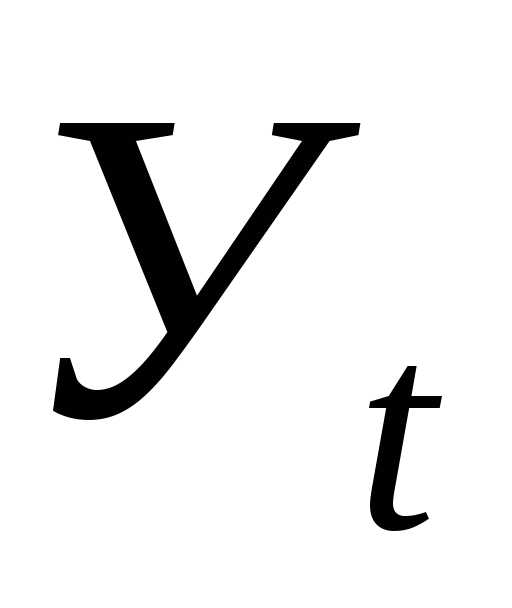
выровненные уровни;
У0
– начальный уровень;

прирост;
t
– порядковый номер даты (t
= 1, …,
n+1).
На графике
выровненный ряд имеет форму прямой,
соединяющей начальный и конечный
уровни ряда.
В случае если
стабильными являются коэффициенты
роста или темпы прироста, то выравнивание
ряда динамики осуществляют по среднему
коэффициенту роста:
,
где

средний коэффициент роста.
Выровненный ряд
имеет форму показательной кривой,
соединяющей начальный и конечный уровни
ряда.
Недостатком
выравнивания динамических рядов по
среднему абсолютному приросту и
среднему коэффициенту роста является
то, что они не учитывают колебаний внутри
ряда. Более эффективным способом
выравнивания динамических рядов является
применение метода наименьших квадратов.
Суть его заключается в подборе уравнения,
которое наиболее точно отражало бы
тенденцию развития. Подробно метод
наименьших квадратов рассмотрен в теме
«Корреляционный анализ».
При выравнивании
динамического ряда методом наименьших
квадратов находят уравнение зависимости
уровней ряда от времени. Выравнивание
может производиться с помощью различных
функций: линейной, параболической,
гиперболической, показательной и
других. Выбор функций чаще всего
осуществляют по графику исходного
ряда. В случае сильных колебаний
целесообразно использовать график
скользящей средней. Существенную
помощь оказывает также анализ цепных
абсолютных приростов и коэффициентов
роста. Например, если цепные абсолютные
приросты относительно стабильны, то в
качестве уравнения тренда может быть
принято уравнение прямой линии
.
Если имеют
тенденцию к замедленному снижению, то
выравнивание производят с помощью
уравнения гиперболы
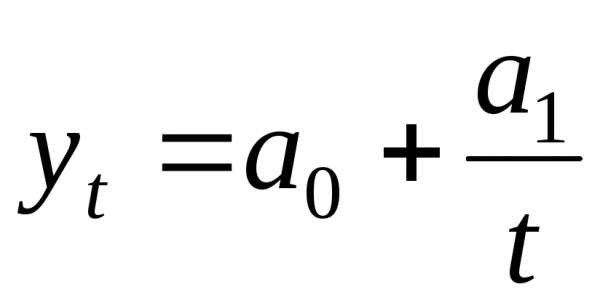
Оценку полученного
уравнения также как и при парной
корреляции производят с помощью
коэффициента или индекса корреляции,
который показывает тесноту связи между
исходными и выровненными уровнями
динамического ряда. Чем ближе коэффициент
или индекс корреляции к 1, тем в большей
степени уравнение тренда отражает
тенденцию развития.
Пример 1.
Имеются
данные по хозяйству о среднем настриге
шерсти от овцы в динамике за 13 лет (табл.
8.2).
Т а б л и ц а 8.2
studfiles.net
Аналитическое выравнивание ряда динамики.
Поиск Лекций
Министерство Образования и Науки Российской Федерации
РОССИЙСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ НЕФТИ И ГАЗА
Им. И.М. Губкина
Кафедра финансового менеджмента
Самостоятельная работа №2:
«Анализ временных рядов в нефтяной и газовой промышленности»
Вариант №7
Выполнил: Проверил:
студент 2 курса доцент кафедры
факультета Экономики и управления финансового менеджмента
группы ЭМ-10-08 Бережная Л.И.
Иплевич Екатерина
Москва
Цель данной работы – научиться анализировать динамику показателя, характеризующего рассматриваемое общественное явление и прогнозировать это явление, т.е. предсказывать будущие значения временного ряда по настоящим и прошлым значениям.
Актуальность работы:с помощью анализа временных рядов можно определить природу ряда и прогнозировать данное явление при определенных условиях. Обе эти цели требуют, чтобы модель ряда была идентифицирована и, более или менее, формально описана. Как только модель определена, можно с ее помощью интерпретировать рассматриваемые данные. Чтобы построить модель источника временного ряда, нам необходимо выявить структуру временного ряда. Источником для возникновения временных рядов служат изменения некоторых показателей. На практике этот метод используется для прогнозирования спроса и предложения на какие-либо товары, объемов добычи или затрат, а так же изменение цен.
Часть 1:
Расчет показателей, характеризующих ряд динамики.
Ряды последовательно расположенных показателей, характеризующих развитие общественного явления, образуют ряды динамики, которые определяются двумя показателями:
1.показателем времени (t),
2.уровнем ряда (y).
В зависимости от вида обобщающих показателей различают ряды динамики абсолютных, относительных и средних величин. Исходными являются ряды динамики абсолютных величин. Ряды динамики средних и относительных величин являются производными.
Таблица 1. Исходная информация
(Среднегодовая стоимость ОПФ, млн.руб)
| Год (ti) | ||||||||||
| Уровень ряда (yi) |
Ряды динамики абсолютных величин характеризуют уровни развития общественного явления либо на определенные моменты времени (моментные ряды) либо за определенные периоды времени (интервальные ряды).
Чтобы проанализировать динамику общественных явлений или процессов, рассчитывают следующие показатели:
1) абсолютный прирост
2) темп роста
3) темп прироста
4) абсолютный размер одного процента прироста
Исходной информацией для расчета показателей анализа являются уровни ряда.
Различают:
1.начальный уровень у1,
2.промежуточный уровень уi,
3.конечный уровень уn.
Таблица 2. Абсолютные и относительные показатели, характеризующие среднегодовую стоимость ОПФ.
| Периоды времени (ti) | Уровни ряда (yi) | Абсолютные приросты, Δy | Темпы роста, % | Темпы прироста, % | Абсолютный размер 1% прироста | |||
| Цепные | Базис. | Цепные | Базис. | Цепные | Базисные | |||
| 100,00% | 100,00% | — | — | — | ||||
| 114,85% | 114,85% | 14,85% | 14,85% | 98,09 | ||||
| 111,32% | 127,85% | 11,32% | 27,85% | 112,66 | ||||
| 113,48% | 145,09% | 13,48% | 45,09% | 125,41 | ||||
| 123,46% | 179,13% | 23,46% | 79,13% | 142,32 | ||||
| 114,47% | 205,06% | 14,47% | 105,06% | 175,71 | ||||
| 113,71% | 233,16% | 13,71% | 133,16% | 201,14 | ||||
| 112,68% | 262,73% | 12,68% | 162,73% | 228,71 | ||||
| 116,25% | 305,41% | 16,25% | 205,41% | 257,71 | ||||
| 117,60% | 359,18% | 17,60% | 259,18% | 299,58 | ||||
| Итого |
Для расчета среднего уровня моментного ряда применяем следующую формулу: yср= (0,5*y1+y2+…+yn-1+0,5*yn)/(n-1), где n – число уровней ряда.
yср=(0,5*9809+11266+12541+14232+17571+20114+22871+25771+29958+0,5*
*35232) / 9 = 176844,50 / 9 = 19649,39.
Абсолютный прирост (Δy) показывает, на сколько единиц данный уровень больше или меньше уровня, который принят за базу сравнения. Он выражается в единицах измерения уровня ряда.
а) Абсолютный цепной (ежегодный) прирост рассчитывается как разность между каждым уровнем ряда (yi) и его предыдущим уровнем (yi-1): Δyi/i-1 = yi-yi-1
б)Абсолютный базисный прирост рассчитывается как разность между каждым уровнем ряда (yi) и его начальным уровнем (y1): Δyi/1 = yi-y1
В данном случае уровни, характеризующие явление, возрастают, значит, абсолютные приросты будут выражены положительными числами.
Средний абсолютный прирост будем рассчитывать по следующей формуле:
Δyср= (yn-y1)/(n-1), где n-1 – число абсолютных ежегодных приростов.
Δyср = (35232-9809)/9 = 2824,78.
Темпы динамики (t) – это отношение уровня ряда одного периода к уровню ряда другого периода. Они показывают, во сколько раз сравниваемый уровень больше принятого за базу сравнения, или какую долю в нем занимает.
Темпы динамики могут быть рассчитаны:
— как базисные (если все уровни ряда относятся к первоначальному уровню):
ti/1 = (yi/y1)*100%,
— как цепные (ежегодные) (если уровни каждого периода относятся к уровню предыдущего периода): ti/i-1 = (yi/yi-1)*100%.
Средний темп динамики рассчитывается по формуле средней геометрической:
tср = (Пti/i-1)^(1/(n-1)).
tср = (100*114,85*111,32*113,48*123,46*114,47*113,71*112,68*116,25*117,6)^(1/9)
=359159419471858000000,00^(1/9) = 192,27
Темпы роста (Δt) показывают, на сколько процентов или долей сравниваемый уровень отличается от уровня, принятого за базу сравнения, и вычисляются как отношение абсолютного прироста к уровню ряда, принятого за базу сравнения.
а) Базисный темп прироста показывает, на сколько процентов (долей) каждый уровень ряда больше или меньше первоначального: Δti/1 = ((yi-y1)/y1)*100%
б)Цепной (ежегодный) темп прироста показывает, на сколько процентов (долей) каждый уровень ряда больше или меньше предыдущего:Δti/i-1 = ((yi-yi-1)/yi-1)*100%
Средний темп прироста рассчитывается исходя из среднего темпа роста:
Δtср= tср-100,т.к. в данном случае темп роста выражен в процентах.
Δtср = 192,27 — 100 = 92,27.
Абсолютный размер одного процента прироста рассчитывается как отношение абсолютного цепного (ежегодного) прироста к цепному (ежегодному) темпу прироста за тот же период, выраженному в процентах: Р = Δyi-1/( Δti/i-1*100)
В данной части работы это последний показатель, который необходимо рассчитать по каждому периоду времени.
Вывод:
В данном примере уровни ряда, характеризующие явление, возрастают, поэтому абсолютные приросты являются положительными и постоянно возрастающими (базисные). В ситуации с темпом прироста так же можно говорить об увеличении, потому что его значения постоянно возрастают (базисные). То же происходит в абсолютном размере одного процента прироста (базисные).
В цепных тенденциях мы не наблюдаем такой зависимости, потому что эти значения изменяются скачками.
Часть 2:
Аналитическое выравнивание ряда динамики.
Одна из задач анализа ряда динамика – установление закономерностей развития явления, для чего и определяется общая тенденция и характер динамики. Под общей тенденцией понимается тенденция либо к увеличению, либо к уменьшению, либо к стабильности уровня явления, а под характером динамики – своеобразие изменения абсолютного прироста, коэффициентов и темпов роста (прироста и др.)
Аналитическое выравнивание – один из методов определения тенденции в виде плавного уровня. Выравнивание уровней ряда динамики может производится по уравнению прямой линии, когда для всех уровней определяется средняя скорость их изменения, или по уравнению кривой линии, когда определяется и средняя скорость, и среднее ускорение изменения уровней ряда динамики.
Простейшим видом зависимости является прямая линия: yt = a + b*t,
гдеa — начальная ордината,b — средняя скорость изменения уровней, t — время.
Задача выравнивания сводится к определению параметров уравнения. Для этого используется способ наименьших квадратов: S = ∑(y-a-bt)2
Рассмотрим эту сумму как сумму двух параметровa и b.
Необходимое условие: равенство нулю частных производных функций по переменным.
Частная производная от S по а при условии, что b является постоянной величиной, имеет вид: ∑2(у – a – b*t )*(-1), по b: ∑2(у – a – b*t )*(-t).
После преобразования и приравнивая этих производных нулю, получаем:
n*a+b*∑t = ∑y
a*∑t+b*∑t2 = ∑y*t
Таким образом, для определения двух параметров «а» и «b» имеем систему нормальных отношений:
n*a+b*∑t = ∑y
a*∑t+b*∑t2 = ∑y*t
Значение «а»: a = (∑y- b∑t)/ n
Значение «b»: b = (n∑t*y — ∑y*∑t)/(n∑t2-(∑t)2)
Из полученных формул видно, что для нахождения двух параметров необходимо получить значения четырех следующих сумм: ∑y, ∑yt, ∑t, ∑t2.
Сравнение выравненных и фактических значений «y» производится, исходя из следующих свойств:
∑yt = ∑yi
∑( yi -yt)2 = 0
Если оказывается, что оба критерия соблюдаются, то уравнение тренда правильно выбрано для данной информации.
Чтобы сравнить фактические и расчетные значения, составим вспомогательную таблицу.
Таблица 3. Вспомогательные расчеты при выравнивании по прямой.
| ti | Условные обозначения t | yi | yi*ti | ti2 |
| -5 | -49045 | |||
| -4 | -45064 | |||
| -3 | -37623 | |||
| -2 | -28464 | |||
| -1 | -17571 | |||
| Итого: |
Теперь можем составить таблицу, с помощью которой можно сопоставить фактические и расчетные значения и выявить зависимость между ними.
Таблица 4. Сопоставление фактических и расчетных значений.
| ti | yi | yt | t | yi-yt | (yi-yt)2 | a | b |
| -5 | 1754,05 | 3076675,46 | 19936,50 | 2376,31 | |||
| -4 | 834,74 | 696784,80 | |||||
| -3 | -266,57 | 71061,02 | |||||
| -2 | -951,88 | 906079,00 | |||||
| -1 | 10,81 | 116,84 | |||||
| -2198,80 | 4834761,42 | ||||||
| -1818,10 | 3305553,72 | ||||||
| -1294,40 | 1675541,96 | ||||||
| 516,26 | 266528,14 | ||||||
| 3413,95 | 11655085,64 | ||||||
| Итого: | 26128995,98 |
Рассчитаем необходимые два параметра a и b, а также значения yt:
b = (n∑yi*ti — ∑yi*∑ti) / ( n∑ti2-(∑ti)2),
b = (10*261394-199365*0)/(10*110-0) = 2613940/1100 = 2376,31;
a = (∑yi— b∑ti) / n,
a = (199365-2376,31*0)/10 = 199365/10 = 19936,50;
yt = a + b*ti;
Теперь можем с помощью графика изобразить динамику теоретических и фактических уровней для того, чтобы сделать вывод о правильном выборе уравнения и найденных параметрах а и b.
Рис.1. График динамики теоретических и фактических уровней
Вывод:
Для сравнения теоретических и фактических значений y мы выбрали следующие критерии: ∑yt = ∑yi и ∑(yi -yt)2 = 0. В нашем примере эти два условия выполняются, значит, уравнение тренда выбрано правильно. По графику видим, что yt, как и уi, имеет возрастающую тенденцию и столбы гистограммы возрастают почти одинаково.
Вывод по проведенной работе:
Благодаря данной работе я научилась анализировать динамику показателя, характеризующего рассматриваемое общественное явление, определять природу уровней и предсказывать будущие значения временного ряда по настоящим и прошлым значениям, а так же сравнивать фактические и расчетные значения и выбирать уравнение тренда.
Рекомендуемые страницы:
Поиск по сайту
poisk-ru.ru
Динамический ряд, виды, методы выравнивания. Показатели динамического ряда, методика вычисления.
В
медицине, практике здравоохранения
нередко возникает необходимость
определить сдвиги в состоянии здоровья
в динамике, оценить эффективность
профилактических мероприятий за ряд
лет и т. д.
При
изучении динамики какого-либо явления
используют динамические
ряды.
Динамический
ряд
—
это ряд однородных статистических
величин, показывающих изменение
какого-либо явления во времени и
расположенных в хронологическом порядке
через определенные промежутки времени.
Величины,
из которых построен динамический ряд,
называются уровнями.
Уровень
ряда
—
размер (величина) того или иного явления,
достигнутый в определенный период или
к определенному моменту времени.
Уровни
ряда могут быть представлены абсолютными,
относительными (показатели интенсивности,
соотношения) и средними величинами.
Динамические
ряды делятся на простые,
состоящие
из абсолютных величин и сложные
(производные),
состоящие из относительных или средних
величин.
Простые
динамические
ряды могут быть моментными
и
интервальными.
Моментный
динамический ряд
состоит
из величин, характеризующих явление на
определенный момент (дату). Примером
могут служить статистические сведения,
обычно регистрируемые на начало или
конец месяца, квартала, года (численность
населения на начало года, число врачей,
средних медицинских работников на
конец года, число лечебных учреждений,
коек на конец года и т. д.).
Интервальный
динамический ряд
построен
из чисел, характеризующих явление за
определенный промежуток времени
(интервал) — за неделю, месяц, квартал,
год и т. д. Примером такого ряда могут
служить данные о числе родившихся,
умерших за год, число инфекционных
заболеваний за месяц и т. д. Особенностью
интервального ряда является то, что его
члены можно суммировать (при этом
укрупняется интервал), или дробить.
Например, имея данные о количестве
заболевших дизентерией, зарегистрированных
за каждый день, можно построить
динамический ряд с интервалом в неделю,
месяц, год.
Динамические
ряды могут подвергаться преобразованиям,
цель которых
– выявление
особенностей изменения изучаемого
процесса, а также достижение
наглядности.
Показатели
динамического ряда:
Абсолютный
прирост (убыль)
—
разность между последующим и предыдущим
уровнями; прирост выражается числами
с положительным знаком, убыль — с
отрицательным. Значение прироста или
убыли отражают изменения уровней
динамического ряда за определенный
промежуток времени.
Темп
роста (снижения) —
отношение каждого последующего уровня
к предыдущему, выраженное в %.
Темп
прироста (убыли)
—
отношение абсолютного прироста или
убыли каждого последующего элемента
ряда к уровню предыдущего, выраженное
в %.
Темп
прироста может
быть вычислен также по формуле:
Темп
роста — 100 %.
Абсолютное
значение одного процента прироста
(убыли)
—
отношение абсолютной величины
прироста (убыли) к показателю темпа
прироста (убыли) за тот же период.
Для
более наглядного выражения нарастания
или убывания ряда можно преобразовать
его путем вычисления показателей
наглядности,
показывающих отношение каждого члена
ряда к одному из них, принятому за 100 %.
Показатели,
характеризующие динамический ряд,
следует анализировать не раздельно, а
связанно: темп роста и темп прироста —
с учетом абсолютного уровня и абсолютного
прироста. При одном и том же темпе роста
и прироста может быть различный абсолютный
прирост. При одинаковом абсолютном
приросте — различные темпы роста и
прироста.
Выравнивание
динамического ряда
Изменение
явления во времени происходит под
влиянием многих факторов. Длительно
действующие факторы определяют основное
направление развития явления в
динамике — его тенденцию. Временно
действующие факторы обуславливают
случайные подъемы и спады величины
явления относительно тенденции.
Динамика
изучаемого явления обычно представлена
не в виде непрерывно меняющегося
уровня, а отдельными скачкообразными
изменениями. В этом случае для выявления
основной тенденции в развитии изучаемого
явления прибегают к выравниванию
динамического ряда.
При
этом могут быть использованы следующие
методы
выравнивания: графический, укрупнение
интервала, вычисление групповой средней,
вычисление
скользящей средней, наименьших квадратов.
Графический
метод
предполагает
выравнивание от руки или с помощью
линейки, циркуля графического изображения
динамики изучаемого явления.
Укрупнение
интервала
производят
путем суммирования данных за ряд смежных
периодов. В результате получаются итоги
за более продолжительные промежутки
времени. Этим сглаживаются случайные
колебания, и более четко определяется
характер динамики явления.
Вычисление
групповой средней
заключается
в определении средней величины
каждого укрупненного периода. Для этого
необходимо суммировать смежные уровни
соседних периодов, а затем сумму разделить
на число слагаемых. Этим достигается
большая ясность изменений во времени.
Вычисление
скользящей средней
в
некоторой степени устраняет влияние
случайных колебаний на уровни динамического
ряда, и более заметно отражает
тенденцию явления. При ее вычислении
каждый уровень ряда заменяется на
среднюю величину из данного уровня и
двух соседних с ним (предыдущего и
последующего). Чаше всего суммируются
последовательно три члена ряда, но можно
брать и больше.
Для
первого и последнего уровней скользящая
средняя не рассчитывается.
Метод
наименьших квадратов
—
один из наиболее точных способов
выравнивания динамического ряда. Этот
метод преследует цель устранить влияние
временно действующих причин, случайных
факторов и выявить основную тенденцию
в динамике явления, вызванную воздействием
только длительно действующих факторов.
Чтобы применить этот метод, динамический
ряд должен иметь не менее 5 хронологических
дат и интервалы между ними должны быть
равными.
Выравнивание
производится по линии, наиболее
соответствующей характеру динамики
изучаемого явления. Вначале определяют
характер изменения изучаемого явления
и подбирают уравнение зависимости между
явлением и временем. Существует много
уравнений, описывающих зависимость
между изучаемыми явлениями. Линейная
зависимость описывается параболой
первого порядка, квадратическая
зависимость — параболой второго порядка,
кубическая зависимость — параболой
третьего порядка и т. д. Чаще всего в
практике здравоохранения используют
выравнивание
по уравнению линейной зависимости,
т. е. параболе первого порядка (у
= а
+ bх).
Этот
метод позволяет определить направление
тенденции (снижение, рост), дать
количественную оценку выявленной
тенденции (стабилизация, умеренная,
выраженная тенденция), оценить средние
темпы ее развития и рассчитать
прогнозируемые уровни на следующий
год.
studfiles.net
30. Аналитическое сглаживание (выравнивание) рядов динамики.
Основы метода аналитического выравнивания
рядов динамики
Более совершенным приемом выявления
основной тенденции развития в рядах
динамики является аналитическое
выравнивание. При изучении общей
тенденции методом аналитического
выравнивания исходят из того, что
изменения уровней ряда динамики могут
быть с той или иной степенью точности
приближения выражены определенными
математическими функциями. Вид уравнения
определяется характером динамики
развития конкретного явления. На практике
по имеющемуся временному ряду задают
вид и находят параметры функции y=f(t), а
затем анализируют поведение отклонений
от тенденции. Чаще всего при выравнивании
используются следующие зависимости:
линейная, параболическая и экспоненциальная.
Во многих случаях моделирование рядов
динамики с помощью полиномов или
экспоненциальной функции не дает
удовлетворительных результатов, так
как в рядах динамики содержатся заметные
периодические колебания вокруг общей
тенденции. В таких случаях следует
использовать гармонический анализ
(гармоники ряда Фурье). Применение,
именно, этого метода предпочтительно,
поскольку он определяет закон, по
которому можно достаточно точно
спрогнозировать значения уровней ряда.
Целью же аналитического выравнивания
динамического ряда является определение
аналитической или графической зависимости
y=f(t). Функцию y=f(t) выбирают таким образом,
чтобы она давала содержательное
объяснение изучаемого процесса. Это
могут быть различные функции.
31. Измерение
периодических колебаний динамического
ряда.
Уровни ряда динамики формируются под
влиянием различных взаимодействующих
факторов, одни из которых определяют
тенденцию развития, а другие —колеблемость
(вариацию)
Колебания уровней ряда носят различный
характер. Наряду с трендом выделяют
циклические (долгопериодические),
сезонные (обнаруживаемые в рядах, где
данные приведены за кварталы или месяцы)
и случайные колебания.
— линия тренда
— средний уровень
уi — фактические уровни
Колебания фактических уровней yi
относительно среднего уровня и линии
тренда
Периодические колебания являются
результатом влияния природно-климатических
условий, общих экономических факторов,
а также многочисленных и разнообразных
факторов, которые часто являются
регулируемыми.
В широком понимании к сезонным относят
все явления, которые обнаруживают в
своем развитии четко выраженную
закономерность периодических изменений,
т.е. более или менее устойчиво повторяющиеся
колебания уровней.
Динамический ряд в этом случае называют
сезонным рядом динамики.
Метод изучения и измерения сезонности
заключается в построении специальных
показателей, которые называются индексами
сезонности.
Индексами сезонности являются процентные
отношения фактических внутригрупповых
уровней к теоретическим уровням,
выступающим в качестве базы сравнения.
Порядок определения индекс сезонности:
1) Для каждого месяца рассчитывается
средняя величина уровня
2) Затем вычисляется среднемесячный
уровень для всего ряда
3) Определяется показатель сезонной
волны — индекс сезонности Is:
, (6.24)
где — средний уровень для каждого
месяца;
— среднемесячный уровень для всего
ряда.
Когда уровень проявляет тенденцию к
росту или к снижению, то отклонения от
постоянного среднего уровня могут
исказить сезонные колебания.
-
Особенности
прогнозирования при исследовании
динамических рядов.
При сиил дин рядов стоит задача прогн
их послед знач. Экстаполяцией наз-ся
прогноз финанс и эконом явл и проц на
сонове выявл закономерн их развития в
прошлом и наст периодах, представл дин
рядом. Экстрапол всегда проводится за
пределы исслед времен. Ряда: в будущее
или прошлое
Различ перспективную экстраполяцию,
ретроспективную, интерполяцию(прогноз
неизвестн уровней внутри дин ряда)
Точность и надженость прогнозов,
полученных при экстраполяции зависит
от того, насколько инерционно то или
иное явление, насколько точно выявлена
тенденция развития явления и выбранного
метода дальнейшего прогноза
Важен период экстраполяции
Правила: период, на кот проводится
прогноз должен быть не длинее 1/3 исходного
ряда. Это связано с инерционностью
явления.
-
Прогнозирование
на основе: среднего уровня ряда динамики,
среднего абсолютного прироста.
Средний уровень рядаопределяет
обобщенную величину абсолютных уровней.
Он определяется по средней, исчисленной
из значений, меняющихся во времени.
Методы расчета среднего уровня
интервального и моментного рядов
динамики разные.
Средний уровень из абсолютных уровней
для интервальных рядов динамики
рассчитывается по формуле средней
арифметической:
-
При равных интервалах используют
среднюю арифметическую простую:
где у — абсолютные уровни ряда;
n — число уровней ряда.
-
При неравных интервалах используют
среднюю арифметическую взвешенную:
где у1,…,уn — уровни ряда динамики;
t1,… tn — веса, длительность интервалов
времени.
Средний уровень моментного ряда динамики
рассчитывается по формуле:
-
С равностоящими уровнями рассчитывается
по формуле средней хронологической
моментного ряда:
где у1,…,уn — уровни периода, за который
делается расчет;
n — число уровней;
n-1 — длительность периода времени.
-
С неравностоящими уровнями рассчитывается
по формуле средней хронологической
взвешенной:
где у1,…,уn — уровни рядов динамики;
t — интервал времени между смежными
уровнями
Средний абсолютный приростопределяется как среднее из абсолютных
приростов за равные промежутки времени
одного периода. Он рассчитывается по
формулам:
-
По цепным данным об абсолютных приростах
за ряд лет рассчитывают средний
абсолютный прирост как среднюю
арифметическую простую:
где n — число степенных абсолютных
приростов в исследуемом периоде.
-
Средний абсолютный прирост рассчитывают
через базисный абсолютный прирост в
случае равных интервалов
где m — число уровней ряда динамики в
исследуемом периоде, включая базисный.
-
Прогнозирование
на основе: среднего темпа роста,
аналитического выравнивания.
Средний темп ростаесть свободная
обобщающая характеристика интенсивности
изменения уровней ряда динамики и
показывает, во сколько раз в среднем за
единицу времени изменяется уровень
ряда динамики.
В качестве основы и критерия правильности
вычисления среднего темпа роста
(снижения) применяется обобщающий
показатель, который рассчитывается как
произведение цепных темпов роста, равное
темпу роста за весь рассматриваемый
период. Если значение признака образуется
как произведение отдельных вариантов,
то используют среднюю геометрическую.
Так как средний темп роста представляет
собой средний коэффициент роста, выражен
в процентах, то для равностоящих рядов
динамики расчеты по средней геометрической
сводятся к вычислению средних коэффициентов
роста из цепных по «цепному способу»:
где n — число цепных коэффициентов
роста;
Кц — цепные коэффициенты роста;
Кб — базисный коэффициент роста за
весь период.
Определение среднего коэффициента
роста может быть упрощено, если будут
ясны уровни динамического ряда. Так как
произведение цепных коэффициентов
роста равно базисному, то в подкоренное
выражение подставляют базисный
коэффициент роста.
Формула для определения среднего
коэффициента роста для равностоящих
рядов динамики по «базисному способу»
будет такая:
Более совершенным приемом выявления
основной тенденции развития в рядах
динамики является аналитическое
выравнивание. При изучении общей
тенденции методом аналитического
выравнивания исходят из того, что
изменения уровней ряда динамики могут
быть с той или иной степенью точности
приближения выражены определенными
математическими функциями. Вид уравнения
определяется характером динамики
развития конкретного явления. На практике
по имеющемуся временному ряду задают
вид и находят параметры функции y=f(t), а
затем анализируют поведение отклонений
от тенденции. Чаще всего при выравнивании
используются следующие зависимости:
линейная, параболическая и экспоненциальная.
Во многих случаях моделирование рядов
динамики с помощью полиномов или
экспоненциальной функции не дает
удовлетворительных результатов, так
как в рядах динамики содержатся заметные
периодические колебания вокруг общей
тенденции. В таких случаях следует
использовать гармонический анализ
(гармоники ряда Фурье). Применение,
именно, этого метода предпочтительно,
поскольку он определяет закон, по
которому можно достаточно точно
спрогнозировать значения уровней ряда.
Целью же аналитического выравнивания
динамического ряда является определение
аналитической или графической зависимости
y=f(t). Функцию y=f(t) выбирают таким образом,
чтобы она давала содержательное
объяснение изучаемого процесса. Это
могут быть различные функции.
Системы уравнений вида y=f(t) для оценки
параметров полиномов по МНК
Графическое представление полиномов
n-порядка
Если изменение уровней ряда характеризуется
равномерным увеличением (уменьшением)
уровней, когда абсолютные цепные приросты
близки по величине, тенденцию развития
характеризует уравнение прямой линии.
2. Если в результате анализа типа тенденции
динамики установлена криволинейная
зависимость, примерно с постоянным
ускорением, то форма тенденции выражается
уравнением параболы второго порядка.
3. Если рост уровней ряда динамики
происходит в геометрической прогрессии,
т.е. цепные коэффициенты роста более
или менее постоянны, выравнивание ряда
динамики ведется по показательной
функции.
После выбора вида уравнения необходимо
определить параметры уравнения. Самый
распространенный способ определения
параметров уравнения — это метод
наименьших квадратов, в котором в
качестве решения принимается точка
минимума суммы квадратов отклонений
между теоретическими (выравненными по
выбранному уравнению) и эмпирическими
уровнями.
Выравнивание по прямой (определение
линии тренда) имеет выражение: yt=a0+a1t
t—условное обозначение времени;
а0 и a1—параметры искомой прямой.
Параметры прямой находятся из решения
системы уравнений:
Система уравнений упрощается, если
значения t подобрать так, чтобы их сумма
равнялась Σt = 0, т. е. начало отсчета
времени перенести в середину
рассматриваемого периода. Если до
переноса точки отсчета t = 1, 2, 3, 4…, то
после переноса:
если число уровней ряда нечетное t = -4
-3 -2 -1 0 +1 +2 +3 +4
если число уровней ряда четное t =
-7 -5 -3 -1 +1 +3 +5 +7
Таким образом, ∑t в нечетной степени
всегда будет равна нулю.
Аналогично находятся параметры параболы
2-го порядка из решения системы уравнений:
Выравнивание по среднему абсолютному
приросту или среднему коэффициенту
роста:
-
Δ-средний абсолютный прирост;
-
К-средний коэффициент роста;
-
У0-начальный уровень ряда;
-
Уn-конечный уровень ряда;
-
t-порядковый номер уровня, начиная с
нуля.
Построив уравнение регрессии, проводят
оценку его надежности. Значимость
выбранного уравнения регрессии,
параметров уравнения и коэффициента
корреляции следует оценить, применив
критические методы оценки:
F-критерий Фишера, t–критерий Стьюдента,
при этом, расчетные значения критериев
сравниваются с табличными (критическими)
при заданном уровне значимости и числе
степеней свободы. Fфакт > Fтеор — уравнение
регрессии адекватно.
n — число наблюдений (уровней ряда), m —
число параметров уравнения (модели)
регрессии.
Проверка адекватности уравнения
регрессии ( качества модели в целом)
осуществляется с помощью средней ошибки
аппроксимации, величина которой не
должна превышать 10-12% (рекомендовано).
studfiles.net
Содержание:
Понятие о динамических рядах:
Динамическим рядом называют ряд показателей, характеризующих величину какого-либо явления по состоянию в определенные моменты или периоды (интервалы) времени. Существует три разновидности динамических рядов:
а) Моментные ряды, образованные показателями, измеряющими явление на определенные моменты времени.
Пример 1. Списочная численность рабочих предприятия.
б) Интервальные ряды, образованные показателями, измеряющими явления за какой-нибудь промежуток времени или интервал.
Пример 2. Фонд заработной платы рабочих предприятия.
в) Ряды производные (средних или относительных величин), образованные показателями, характеризующими моменты или интервалы времени с помощью средних или относительных величин.
Пример 3. Среднемесячная заработная плата рабочих предприятия.
Приемы обработки динамических рядов
Очень часто уровни динамических рядов колеблются; при этом тенденция (основное направление) развития явления во времени скрыта случайными отклонениями уровней в ту или иную сторону. Поэтому возникает необходимость преобразования рядов для выявления закономерностей его развития.
Разберем некоторые приемы преобразования рядов.
1. Использование среднего абсолютного прироста. Приростами динамического ряда называются разности между последующими уровнями ряда и предыдущими (обозначаются 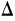

Число приростов на единицу меньше числа уровней ряда, т. е. составляет n—1. Найдем средний прирост ряда:
Таким образом:
Найденный средний абсолютный прирост позволяет путем последовательного прибавления его к первому фактическому уровню найти последующие уровни, отличающиеся от фактических тем, что они вычислены в предположении их плавного возрастания (или убывания), без скачков.
Рассмотрим такое преобразование динамического ряда на. примере.
Пример 4. Преобразуем ряд динамики месячного фонда заработной платы рабочих, приведенный в табл. 2, способом среднего прироста.
1) Находим средний прирост по формуле
где
2) Находим плавные уровни:
Располагаем фактические и исчисленные данные в одну таблицу.
При таком преобразовании первый и последний уровни остаются без изменения.
2. Использование среднего коэффициента или темпа роста. Коэффициентом роста называют отношение последующего уровня ряда динамики к предыдущему уровню того же ряда. Если выразить коэффициент роста в процентах, то получим темп роста.
Имеется динамический ряд:
Коэффициенты роста (обозначаются 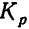
Следует обратить внимание на то обстоятельство, что число коэффициентов роста (так же, как и приростов) меньше числа уровней на единицу.
Вычисление среднего коэффициента роста производят по формуле средней геометрической.
где n — число коэффициентов роста.
Учитывая, что произведение всех коэффициентов роста равно
отношению последнего уровня (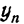
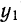
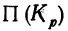
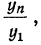
где n — число уровней.
Найденный средний коэффициент роста используется аналогично использованию среднего абсолютного прироста (см. предыдущий пример) с той разницей, что первый фактический уровень умножается на средний коэффициент роста в соответствующей степени.
Пример 5. Используя данные табл. 2, преобразовать ряд динамики месячного фонда заработной платы рабочих способом среднего коэффициента роста.
Решение: 1) Находим средний коэффициент роста:
откуда
2) Находим плавные уровни:
а) второй плавный уровень:
б) третий плавный уровень:
в) четвертый уровень: 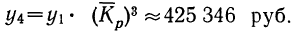
Механическое сглаживание
Кроме рассмотренных приемов преобразования динамических рядов, для нахождения плавных уровней путем использования среднего прироста или среднего коэффициента роста применяется метод механического сглаживания ряда скользящей средней.
Существует две разновидности сглаживания: методом невзвешенной и взвешенной скользящей средней.
Невзвешенная скользящая средняя. Применение метода сглаживания невзвешенной скользящей средней состоит в замене абсолютных данных средними арифметическими за определенные периоды. При выборе этих периодов мы производим скольжение, постепенно исключая из периода первые уровни и включая последующие.
Различают два случая: 1) когда период сглаживания состоит из нечетного числа членов; 2) когда период сглаживания состоит из четного числа членов.
Разберем 1-й случай.
Пример 6.
Требуется сгладить ряд методом незвешенной скользящей средней с трехдневным периодом (взято нечетное число дней).
Решение. Для сглаживания ряда методом скользящей средней (с трехчленным периодом) строим следующую таблицу:
При использовании этого способа найденные скользящие средние (колонка 4) располагаются в середине (центре) периода (первая скользящая средняя относится ко второму дню, вторая— к третьему дню и т. д.), т. е. являются центрированными.
После вычисления скользящих средних их вместе с фактическими данными наносят на график (см. график 1).
Разберем второй случай (с четным числом членов периода).
Пример 7. По данным примера 6 сгладить ряд методом невзвешенной скользящей средней с четырехдневным периодом (взято четное число дней).
Решение. Для сглаживания ряда методом скользящей средней (с четырехчленным периодом) строим следующую таблицу:
При использовании этого способа следовало найденные скользящие средние с четырехчленным периодом (колонка 4), как и в первом случае — с трехчленным периодом, — отнести к центру периода. Но этот центр не совпадает с определенной датой. Поэтому прибегают к приему, называемому центрированием и состоящему в нахождении средних (центра) между каждой парой уже найденных скользящих средних. Полученные средние называются центрированными средними (колонка 5).
После вычисления центрированных скользящих средних их вместе с фактическими данными наносят на график.
Взвешенная скользящая средняя. Вторая разновидность этого метода сглаживания состоит в применении взвешенной скользящей средней. Для определения весов можно представить себе многократно повторенное сглаживание скользящей средней с двучленным периодом.
Первые скользящие средние:
и т.д.
Используя найденные скользящие средние, получаем вторые скользящие средние (для трехчленного периода):
Еще одно применение скольжения (для четырехчленного периода) дает:
и далее для пятичленной средней:
Веса уровней ряда при сглаживании образуют коэффициенты бинома:
Ограничиваясь пятичленной взвешенной скользящей средней, рассмотрим ее практическое использование. Этот метод можно применять путем использования трафарета, имеющего следующий вид:
Этот трафарет прикладывается (слева) к фактическим данным, подлежащим сглаживанию.
Умножая фактические данные на веса (коэффициент трафарета), находим сумму произведений. Первую сумму записываем против коэффициента 6, затем передвигаем трафарет на одну строку вниз и умножением фактических данных на коэффициенты трафарета находим вторую сумму и т. д. Все найденные суммы делятся на 16 (сумму всех весов).
Пример:
По данным примера 6 сгладить ряд методом взвешенной скользящей средней с пятичленным периодом.
Решение. Располагаем все данные в таблицу и производим соответствующие расчеты передвижением трафарета на одну строку вниз.
Аналитическое выравнивание
Очень часто для преобразования динамического ряда применяют аналитическое выравнивание. Имеются следующие фактические уровни ряда:
Характер изменения этих уровней, т. е. движения динамического ряда, может быть различным. Нашей задачей является нахождение такой простой математической формулы, которая давала бы возможность вычислить теоретические уровни. Основное требование, предъявляемое к этой формуле, состоит в том, что уровни, исчисленные по ней, должны воспроизводить общую тенденцию фактических уровней. Нахождение этой формулы называется аналитическим выравниванием, представляющим собой не что иное, как удобный способ описания эмпирических данных. При этом обычно употребляют ограниченное число типов таких формул: прямой линии, параболы второго или третьего порядка, гиперболы и показательной функции. Общие соображения при выборе типа линии, по которой производится аналитическое выравнивание, могут быть сведены к следующим:
1) Если абсолютные приросты уровней ряда по своей величине колеблются около постоянной величины, то математической функцией, уравнение которой можно принять за основу аналитического выравнивания, следует считать прямую линию: 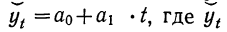
Если приросты приростов уровней, т. е. ускорения, колеблются около постоянной величины, то за основу аналитического выравнивания следует принять параболу второго порядка:
Показатели 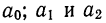
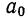
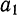
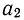
3) Если уровни изменяются с приблизительно постоянным относительным приростом, то выравнивание производится по показательной (экспонентной) функции:
Для нахождения аналитического уравнения, по которому производится выравнивание уровней динамического ряда, применяют различные способы. Один из способов состоит в расчленении динамического ряда на две примерно^ равные части; при этом сумма выравненных значений в каждой части должна совпадать с суммой фактических значений, или, иными словами, сумма отклонений фактических данных от выравненных равняется нулю, т. е.
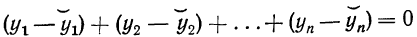
Это требование может быть записано в таком виде:
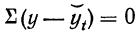
откуда
Если применить это требование к каждой из двух частей ряда, то, вычисляя для каждой части динамического ряда все необходимые данные, т. е. 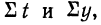
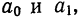
Недостатком указанного метода является то, что при произвольном расчленении ряда на две части (группы) мы получаем различные результаты. Несмотря на это, данный способ может найти широкое применение.
Пример 9.
Рассмотрим применение описанного способа на конкретных данных. Возьмем из примера 6 данные о добыче угля и произведем выравнивание уровней по прямой:
Решение. Так как имеются данные за 15 дней, то расчленение периода на примерно равные части дает в первой 7, во второй 8 дней.
Имеем: для первой части
для второй части
Составляем систему уравнений:
Уравниваем коэффициенты при ао путем умножения первого уравнения на —8, а второго на + 7.
откуда
Следовательно, аналитическое уравнение прямой примет следующий вид:
Подставляя значения t в найденное уравнение, получаем:
и т. д. (см. табл. 11).
Как видно из разобранного примера, выравненные данные довольно хорошо воспроизводят фактические. Сумма их отклонений от фактических уровней равна нулю. При выравнивании по параболе второго порядка 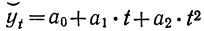
Второй способ — наименьших квадратов — основан на требовании о том, чтобы сумма квадратов отклонений фактических данных от выравненных (см. график 2) была наименьшей:
,S должно быть наименьшим (минимальным).
Принцип, положенный в основу метода наименьших квадратов, может быть записан в сжатом математическом виде следующим образом:
Из курса высшей математики известно, что при нахождении минимума функции нужно найти частные производные и приравнять их нулю. Найдем минимум данной функции, используя уравнение прямой линии.
имеем:
заменяем:
и получаем:
Находим частные производные функции S сначала по параметру 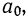
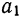
Преобразовывая, получаем:
На основании свойства сумм (см. стр. 11) выносим 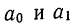
Полученная система называется системой нормальных уравнений для нахождения параметров 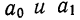
Аналогично получаем систему нормальных уравнений при выравнивании по параболе второго порядка:
Выравнивание по прямой линии
Покажем выравнивание по прямой линии на следующем примере.
Пример 10.
Поданным примера б произвести выравнивание по прямой линии методом наименьших квадратов.
Решение. Аналитическое уравнение прямой линии имеет вид:
Для нахождения параметров 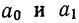
Для вычисления всех необходимых исходных данных построим расчетную таблицу (см. табл. 12).
Составляем систему нормальных уравнений:
Уравниваем коэффициенты при
Значит,
Из первого уравнения находим
После определения 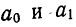
Подставляя значения t, получаем:
и т. д. (см. колонку 6, табл. 12).
При заполнении колонки 3 со значениями t производим нумерацию дат. Так, если бы в примере были годы или дни (понедельник, вторник и т. д.), мы, прибегая к нумерации, вели бы счет с первой даты, принимая t равным единице, двум и т. д.
Итог колонки 3 может быть найден без суммирования по формуле:
Проверим наш пример:
Итог колонки 4 можно определить по формуле и без предварительно, го возведения в квадрат всех значений t:
После вычислений всех значений 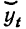
Упрощенный метод выравнивания по прямой линии
Выравнивание по прямой линии методом наименьших квадратов можно значительно упростить соответствующим подбором способа отсчета t так, чтобы 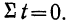
- Когда число членов динамического ряда нечетное, то следует отсчитывать t от середины ряда. При таком отсчете значение серединной даты (или периода) динамического ряда принимается равным 0, ранние даты имеют отрицательные значения (—1; —2; —3 и т. д.), а поздние даты — положительные значения (1; 2; 3 и т. д.).
- Когда число членов ряда четное, то в этом случае для соблюдения требований о равных интервалах между всеми значениями t и о том, чтобы сумма всех значений t равнялась нулю, подбор t производится так: находится серединная пара дат (или периодов), и значения t для нее принимают —1 и +1, а далее вверх идут —3; —5; —7 и т. д., и вниз +3; +7; +9 и т. д.
При таком способе отсчета t система нормальных уравнений упрощается и принимает вид:
Тогда:
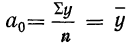
Пример 11.
Для практического использования данного метода рассмотрим предыдущий пример.
Выравнивание по прямой линии (упрощенным методом) (см. табл. 13).
Тогда аналитическое уравнение примет вид:
При различных значениях t получаем:
и т. д. (см. колонку б табл. 13).
Фактические данные и выравненная прямая изображены на графике 3.
Следует заметить, что в случае выравнивания по прямой линии упрощенным методом параметр 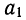
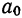
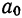
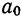
Выравнивание по параболе второго порядка
Аналитическое уравнение параболы имеет вид:
Что касается системы нормальных уравнений, то подбором способа отсчета t упростим нахождение параметров, так как
Получим:
Пример 12.
В табл. 14 приведены данные о производстве изделия А по годам.
Выровнять эти данные по параболе второго порядка и изобразить графически.
Решение. Для получения сумм, входящих в систему нормальных уравнений, построим расчетную таблицу.
Составляем систему нормальных уравнений:
откуда
Делим первое уравнение на 9, а второе на 60:
Таким образом,
Производим проверку найденных параметров:
Аналитическое уравнение параболы примет следующий вид:
После решения системы нормальных уравнений всегда следует проверить найденные параметры. Однако в дальнейшем производить проверку на страницах пособия мы не будем, предоставляя возможность читателю сделать это самостоятельно, путем подстановки в нормальные уравнения.
Подставляя значения t (от —4 до +4), получим выравнен ные значения производства изделия А (см. колонку 8 табл.15)
Теперь можно построить график, изобразив фактические данные и выравненные по параболе второго порядка аналогично тому, как это было показано при сглаживании методом скользящей средней и выравнивании по прямой линии.
Выравнивание по показательной (экспонентной) функции производится в том случае, если уровни изменяются с более или менее постоянным относительным приростом (по правилу сложных процентов). Выравнивание производится по следующей формуле: 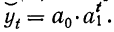
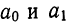
При способе отсчета t таким образом, чтобы 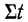
откуда
и
откуда
Пример 13.
Для иллюстрации произведем выравнивание по показательной функции динамического ряда, рассмотренного в примере 12 (см. табл. 14). Для получения исходных данных построим расчетную табл. 16.
Получаем:
откуда
Аналитическое уравнение показательной кривой примет вид:
Подставляем значения t и получаем (см. колонку 7 табл. 16):
Полученные выравненные уровни, а также фактические данные можно нанести на график.
В некоторых случаях более сложного изменения уровней динамического ряда можно применять выравнивание по параболе второго порядка с логарифмированием уровней по формуле:
Это будет означать выравнивание уровней по показательной функции следующего вида:
В этом случае параметры 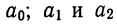
При условии 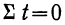
Пример 14.
Проиллюстрируем ход действий при выравнивании динамического ряда по. показательной функции 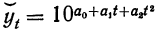
Получаем:
откуда
Следовательно,
Подставляя значения t, равные —4, —3, —2 и т. д., получаем значения 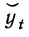
Интерполяция уровней
Интерполяцией называется нахождение промежуточных неизвестных уровней динамического ряда при наличии известных соседних уровней.
Интерполяция может производиться различными способами:
1) путем использования только двух уровней и 2) путем использования нескольких уровней.
Различные предположения о динамике развития явления при интерполяции приводят, естественно, к различным результатам. Поэтому практически при выборе того или иного предположения о тенденции развития изучаемого явления обычно просматривают динамический ряд до или после (можно и одновременно) интерполируемого периода и приходят к тому или иному заключению.
Рассмотрим применение интерполяции на конкретных примерах.
1. Имеются данные о выпуске продукции за 1956 и 1958 гг. Требуется произвести интерполяцию и вычислить предполагаемый уровень 1957 г.
а) Предполагая, что выпуск продукции увеличивался с постоянным приростом, равным
и, прибавляя его к начальному уровню, получим уровень 1957 г.
Это равносильно определению уровня 1957 г. как полусуммы продукции 1956 и 1958 гг.
б) Предположим, что уровни .выпуска продукции за эти годы менялись с постоянным (средним) коэффициентом роста. Найдем его:
Тогда
2. а) Пусть наряду с двумя известными уровнями выпуска продукции за 1956 и 1958 гг. известен еще один уровень, за 1955 г., равный 3 тыс. руб. Тогда, предполагая, что изменение выпуска продукции происходило по параболе второго порядка, получим:
Составляем систему трех уравнений с тремя неизвестными:
Вычитая из второго уравнения первое, получим новое уравнение уже не с тремя, а с двумя неизвестными:
Вычитаем из третьего уравнения второе:
Получилась система двух уравнений с двумя неизвестными:
Решим ее:
Тогда
Подставляя значения 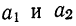
Следовательно, 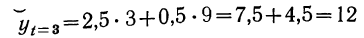
Этот же результат можно получить, пользуясь методом конечных разностей. Зная уровни, найдем первые и вторые разности.
Если исходить из предположения об изменении выпуска продукции по параболе второго порядка, то вторые разности (т. е. ускорения) должны быть постоянными.
Тогда
Отсюда
б) Интерполяция путем использования нескольких уровней, предшествующих неизвестным и последующих за ними, может быть произведена при помощи выравнивания способом наименьших квадратов.
Например, имеются уровни за 1954, 1955, 1956, 1959, 1960 и 1961 гг. Методом интерполяции рассчитать уровни 1957 и 1958 гг.
Предполагая, что уровни 1957 и 1958 гг. укладываются в общую тенденцию изменения уровней, произведем выравнивание по прямой линии способом наименьших квадратов, используя следующую таблицу:
Значит,
Следовательно, для 1957 г. при ( t=— 1)
а для 1958 г. (при t= + l).
Данным методом пользуются в тех случаях, когда уровни определенных периодов известны, но искажены действием каких-либо факторов, влияние которых необходимо оценить. Достигается это нахождением разностей между фактическими и выравненными уровнями.
Пусть нам известны уровни 1957 г.— 13. и 1958 г. — 16 единиц, искаженные действием определенного фактора (изменение, например, технологического процесса в эти годы или др.). Тогда можно оценить суммарное воздействие данного фактора на величину уровней (см. табл. 23).
Интерполяция в демографической статистике
Имеется ряд способов интерполяции, разработанных применительно к статистике населения. Они применяются при использовании надежных данных о численности населения по пятилетним интервалам для сглаживания возрастного распределения (т. е. интерполяции) и нахождения численности населения по каждому годичному интервалу внутри пятилетних интервалов, для сглаживания таблиц смертности и т. п.
Идея этих способов состоит в использовании скользящих, парабол различных порядков. Из числа этих способов рассмотрим два.
1) Способ С. А. Новосельского основан на применении для каждого пятилетнего интервала своей параболы второго порядка: 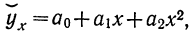
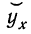
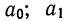
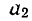
Получив систему трех уравнений:
и решая ее относительно параметров 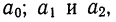
Теперь можно получить сглаженные значения численности каждого годичного интервала:
Если нужно произвести интерполяцию и получить сглаженные численности населения каждого годичного интервала из следующего пятилетнего интервала, обозначения соответственно меняются.
Этот метод впервые был применен для устранения аккумуляции возрастного распределения населения по переписи 1897 г.
при построении таблиц смертности 1896—1897 гг. Недостатком данного метода является плохое смыкание парабол соседних пятилетних интервалов.
Пример 15.
Используя данные переписи населения 1897 г. по Европейской России о численности мужчин, произведем интерполяцию возрастного интервала 45—49 лет и найдем сглаженные численности возрастов 45, 46, 47, 48 и 49 лет.
Решение:
а далее, используя вышеприведенные формулы, получаем:
Если сопоставить непосредственные данные, взятые из результатов переписи 1897 г. и искаженные аккумуляцией, со сглаженными, то увидим, что сумма фактических сглаженных данных по пятилетнему интервалу совпадает.
2) Способ Б. С. Ястремского, основанный на применении парабол третьего порядка, позволяет лучше смыкать соседние интервалы.
Имеем:
Для нахождения четырех параметров 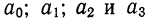
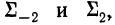
Пример 16.
Используя данные предыдущего примера о численности мужского населения по переписи 1897 г. для трех пятилетних интервалов и привлекая дополнительно данные о численности населения в пятилетних интервалах 35—39 и 55—59 лет, произведем интерполяцию пятилетнего интервала 45—49 лет.
Подставляем и получаем:
и далее аналогично для всех последующих возрастов.
Метод Б. С. Ястремского применялся при разработке материалов переписи 1920 г.
Экстраполяцией называется нахождение последующих уровней динамического ряда, когда предыдущие уровни известны, Для этой цели может быть использовано выравнивание уровней динамического ряда по способу наименьших квадратов и подстановка в полученное аналитическое уравнение соответствующих значений t.
Так, например, если мы, выравнивая уровни какого-нибудь ряда по параболе второго порядка, с 1956 по 1962 г., получили аналитическое уравнение 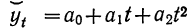
- Корреляция — определение и вычисление
- Элементы теории ошибок
- Методы математической статистики
- Комбинаторика — правила, формулы и примеры
- Линейный регрессионный анализ
- Вариационный ряд
- Законы распределения случайных величин
- Дисперсионный анализ
Более совершенным приемом выявления основной тенденции развития в рядах динамики является аналитическое выравнивание. При изучении общей тенденции методом аналитического выравнивания исходят из того, что изменения уровней ряда динамики могут быть с той или иной степенью точности приближения выражены определенными математическими функциями. Вид уравнения определяется характером динамики развития конкретного явления. На практике по имеющемуся временному ряду задают вид и находят параметры функции y=f(t), а затем анализируют поведение отклонений от тенденции. Чаще всего при выравнивании используются следующие зависимости: линейная, параболическая и экспоненциальная. Во многих случаях моделирование рядов динамики с помощью полиномов или экспоненциальной функции не дает удовлетворительных результатов, так как в рядах динамики содержатся заметные периодические колебания вокруг общей тенденции. В таких случаях следует использовать гармонический анализ (гармоники ряда Фурье). Применение, именно, этого метода предпочтительно, поскольку он определяет закон, по которому можно достаточно точно спрогнозировать значения уровней ряда.
Целью же аналитического выравнивания динамического ряда является определение аналитической или графической зависимости y=f(t). Функцию y=f(t) выбирают таким образом, чтобы она давала содержательное объяснение изучаемого процесса. Это могут быть различные функции.
Системы уравнений вида y=f(t) для оценки параметров полиномов по МНК
(кликабельно)
Графическое представление полиномов n-порядка
1. Если изменение уровней ряда характеризуется равномерным увеличением (уменьшением) уровней, когда абсолютные цепные приросты близки по величине, тенденцию развития характеризует уравнение прямой линии.
2. Если в результате анализа типа тенденции динамики установлена криволинейная зависимость, примерно с постоянным ускорением, то форма тенденции выражается уравнением параболы второго порядка.
3. Если рост уровней ряда динамики происходит в геометрической прогрессии, т.е. цепные коэффициенты роста более или менее постоянны, выравнивание ряда динамики ведется по показательной функции.
После выбора вида уравнения необходимо определить параметры уравнения. Самый распространенный способ определения параметров уравнения — это метод наименьших квадратов, в котором в качестве решения принимается точка минимума суммы квадратов отклонений между теоретическими (выравненными по выбранному уравнению) и эмпирическими уровнями.
Выравнивание по прямой (определение линии тренда) имеет выражение: yt=a0+a1t
- t—условное обозначение времени;
- а0 и a1—параметры искомой прямой.
Параметры прямой находятся из решения системы уравнений:
Система уравнений упрощается, если значения t подобрать так, чтобы их сумма равнялась Σt = 0, т. е. начало отсчета времени перенести в середину рассматриваемого периода. Если до переноса точки отсчета t = 1, 2, 3, 4…, то после переноса:
- если число уровней ряда нечетное t = -4 -3 -2 -1 0 +1 +2 +3 +4
- если число уровней ряда четное t = -7 -5 -3 -1 +1 +3 +5 +7
Таким образом, ∑t в нечетной степени всегда будет равна нулю.
Аналогично находятся параметры параболы 2-го порядка из решения системы уравнений:
Выравнивание по среднему абсолютному приросту или среднему коэффициенту роста:
- Δ-средний абсолютный прирост;
- К-средний коэффициент роста;
- У0-начальный уровень ряда;
- Уn-конечный уровень ряда;
- t-порядковый номер уровня, начиная с нуля.
Построив уравнение регрессии, проводят оценку его надежности. Значимость выбранного уравнения регрессии, параметров уравнения и коэффициента корреляции следует оценить, применив критические методы оценки:
F-критерий Фишера, t–критерий Стьюдента, при этом, расчетные значения критериев сравниваются с табличными (критическими) при заданном уровне значимости и числе степеней свободы. Fфакт > Fтеор – уравнение регрессии адекватно.
n — число наблюдений (уровней ряда), m — число параметров уравнения (модели) регрессии.
Проверка адекватности уравнения регрессии ( качества модели в целом) осуществляется с помощью средней ошибки аппроксимации, величина которой не должна превышать 10-12% (рекомендовано).
Рассмотрим на примере аналитическое выравнивание ряда динамики по прямой с переносом точки отсчета в середину ряда:
|
Годы |
Объем валовой продукции |
Условное обозн. года |
Расчетные значения |
Выровненный ряд |
|
|
Yi |
t |
t2 |
Y*t |
Ỹ=209,06+3,91t |
|
|
1990 |
187,8 |
-5 |
25 |
-939,00 |
189,51 |
|
1991 |
185,7 |
-4 |
16 |
-742,94 |
193,42 |
|
1992 |
195,8 |
-3 |
9 |
-587,29 |
197,33 |
|
1993 |
207,9 |
-2 |
4 |
-415,80 |
201,24 |
|
1994 |
208,3 |
-1 |
1 |
-208,32 |
205,15 |
|
1995 |
208,6 |
0 |
0 |
0,00 |
209,06 |
|
1996 |
219,7 |
1 |
1 |
219,70 |
212,97 |
|
1997 |
218,5 |
2 |
4 |
437,00 |
216,88 |
|
1998 |
222,2 |
3 |
9 |
666,60 |
220,79 |
|
1999 |
225,1 |
4 |
16 |
900,40 |
224,7 |
|
2000 |
220,0 |
5 |
25 |
1100,00 |
228,61 |
|
Итого |
2299,62 |
0 |
110 |
430,35 |
2299,62 |
|
ΣYi |
Σt |
Σt2 |
ΣY*t |
ΣỸ |
Решение системы линейных уравнений:
Σt в нечетной степени всегда равна нулю, поэтому система уравнений упрощается и принимает следующий вид:
Сумма уровней выровненного ряда должна равняться сумме уровней исходного ряда, что, в свою очередь, подтверждает правильность расчетов. Выровненный ряд динамики по прямой вида (линейный тренд): Ỹ=209,06+3,91t
Смотри аналитическое выравнивание на примере:
- п.V: Сезонная корректировка временного ряда
- Аналитическое выравнивание себестоимости зерновых культур

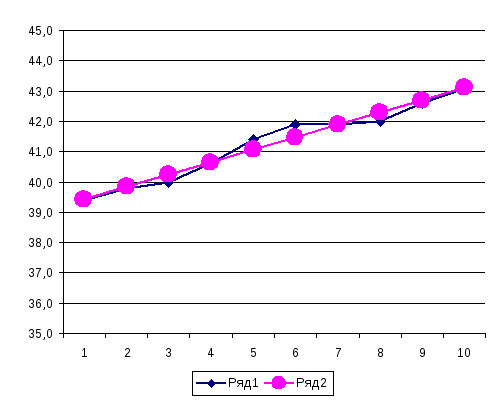
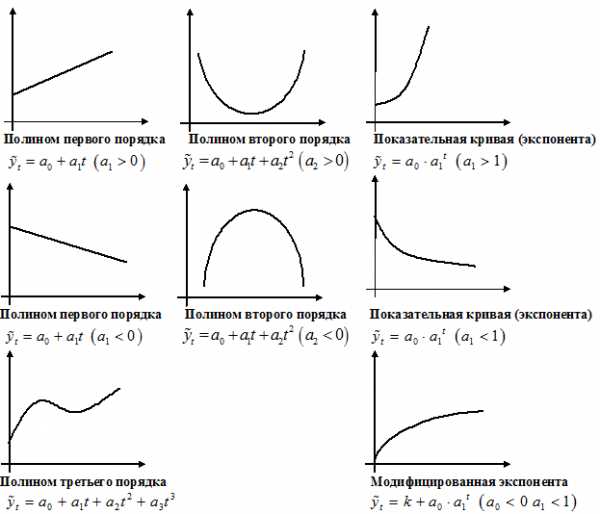
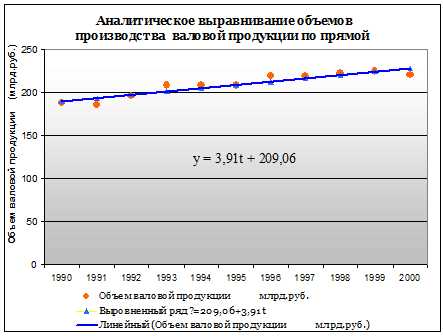
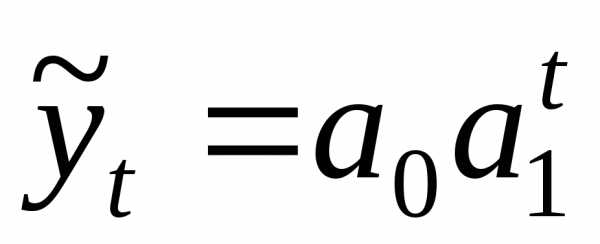 ,
,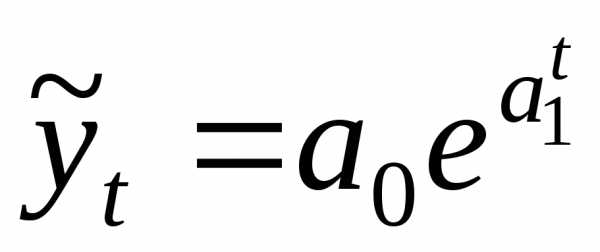 ,
,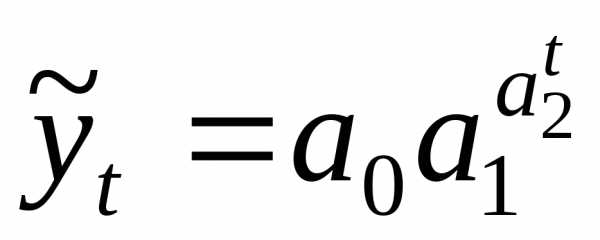 ,
,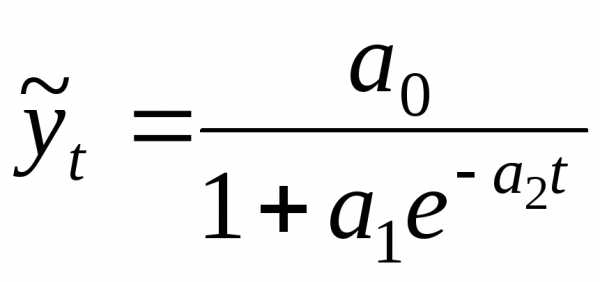 ,
,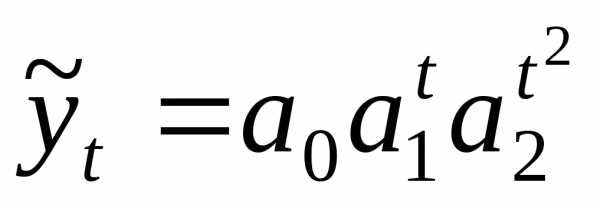 ,
,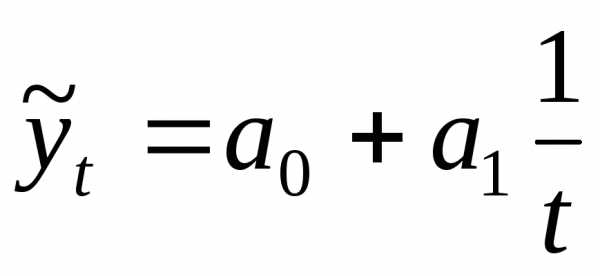 ,
,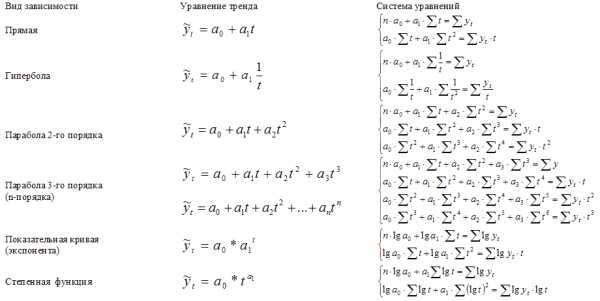
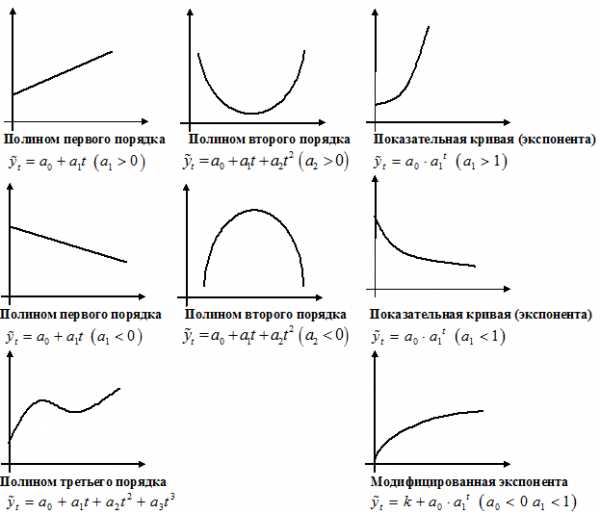
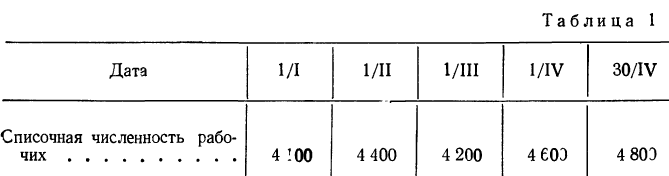



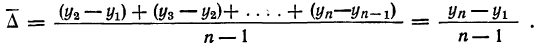
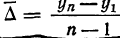
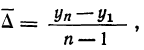
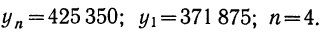
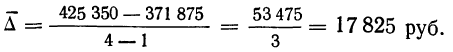
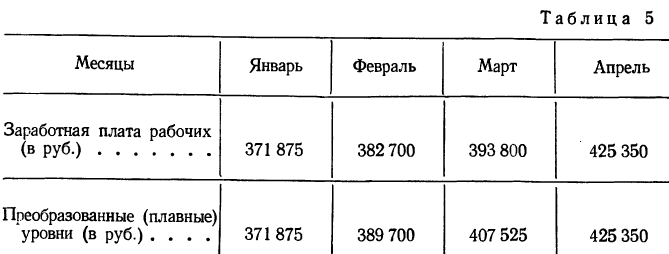
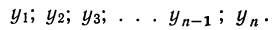
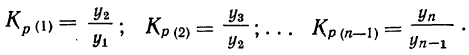
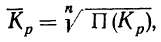
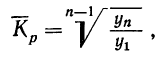
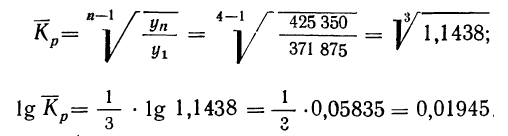
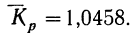
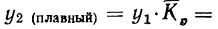
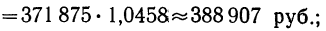
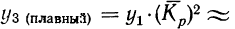
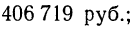
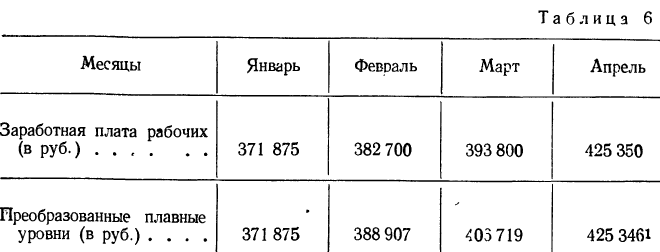
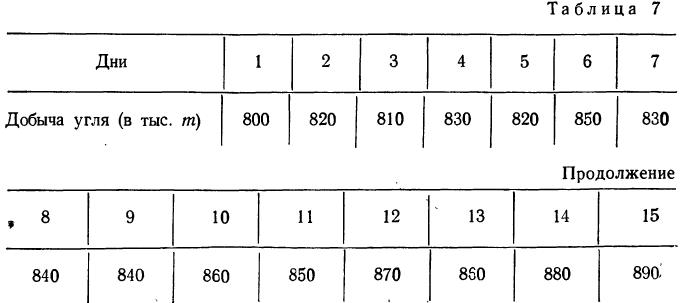
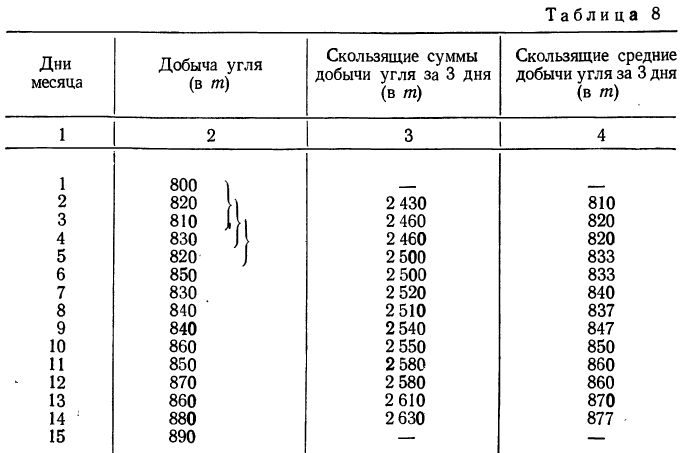
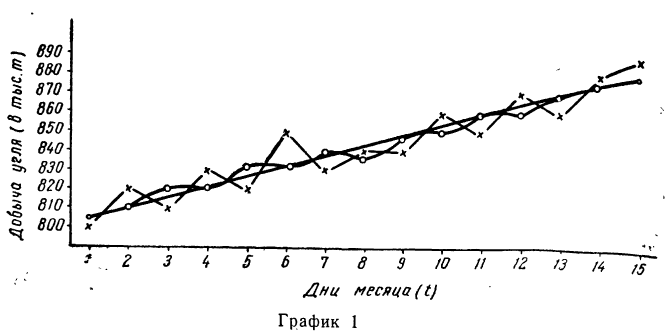
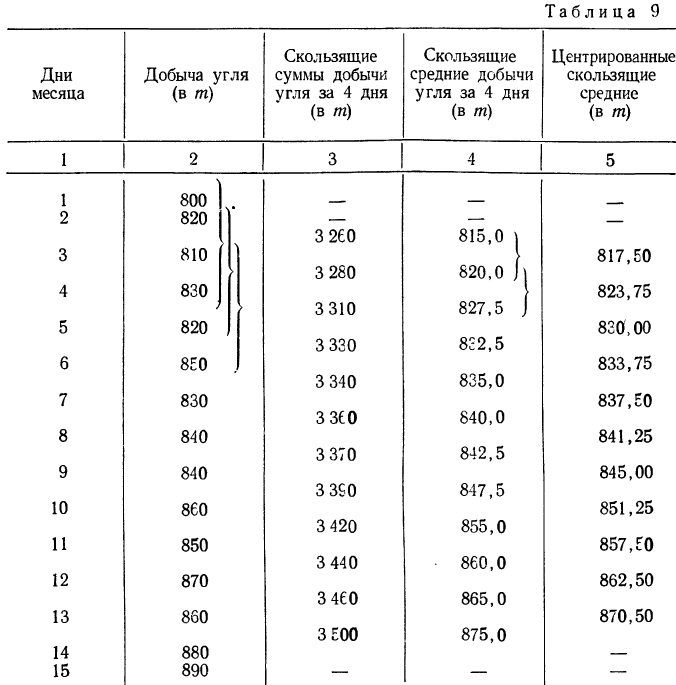
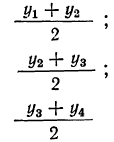
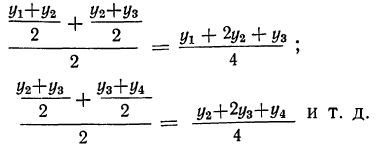
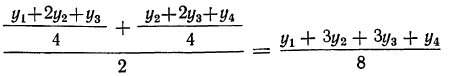
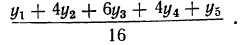
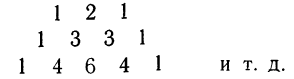
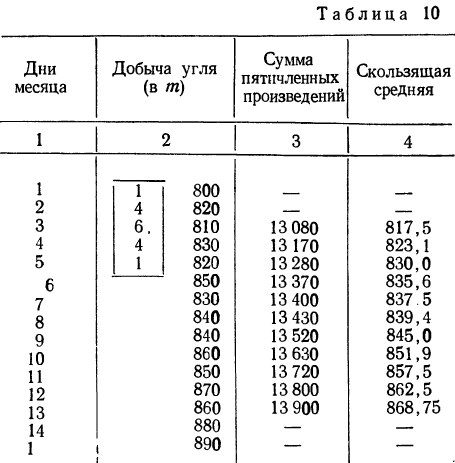
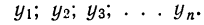
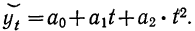
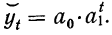
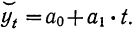
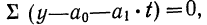
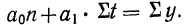
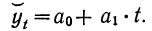
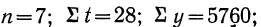
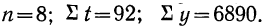
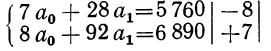
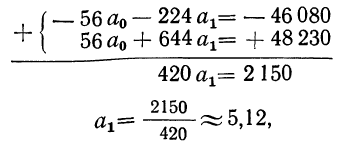
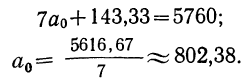
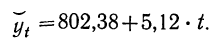
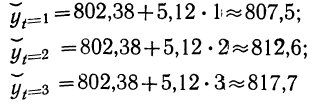
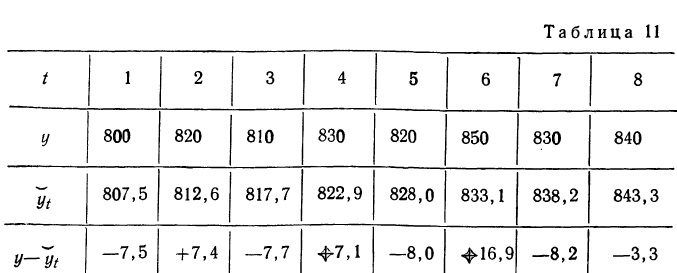
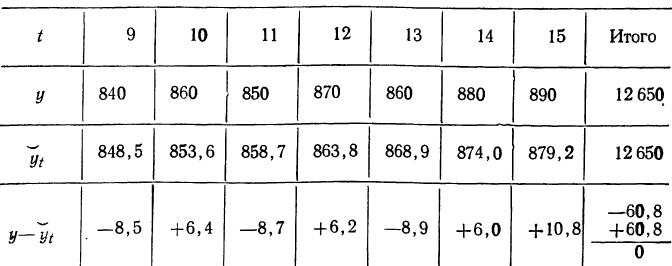
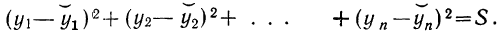
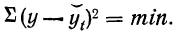
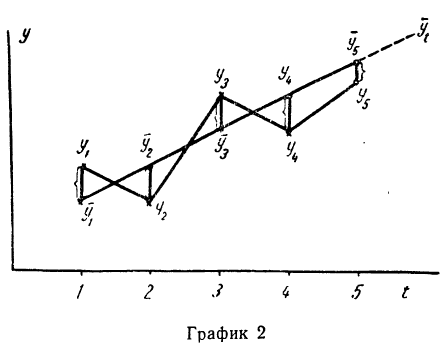
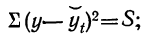
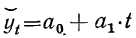
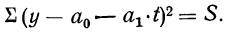
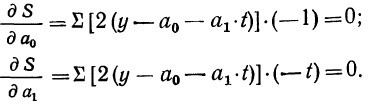
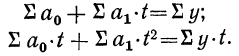
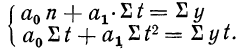
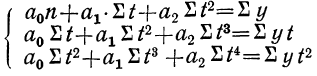
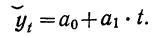
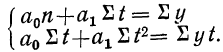
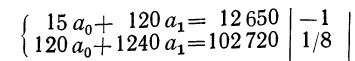
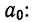
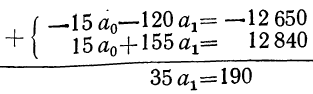
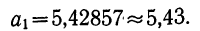
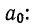
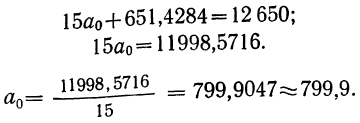
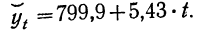
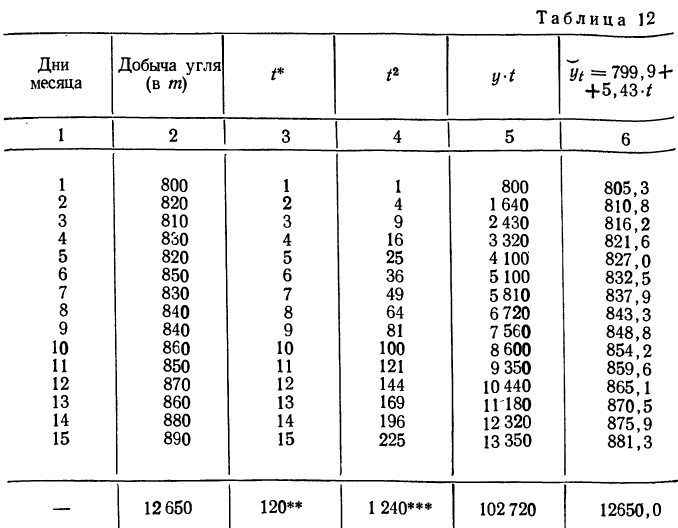
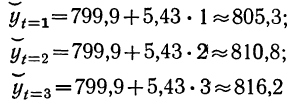
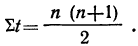
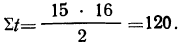
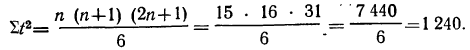
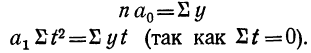
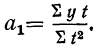
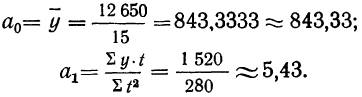
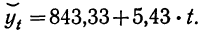
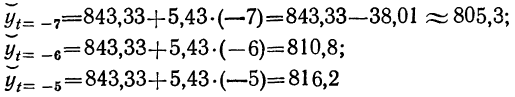
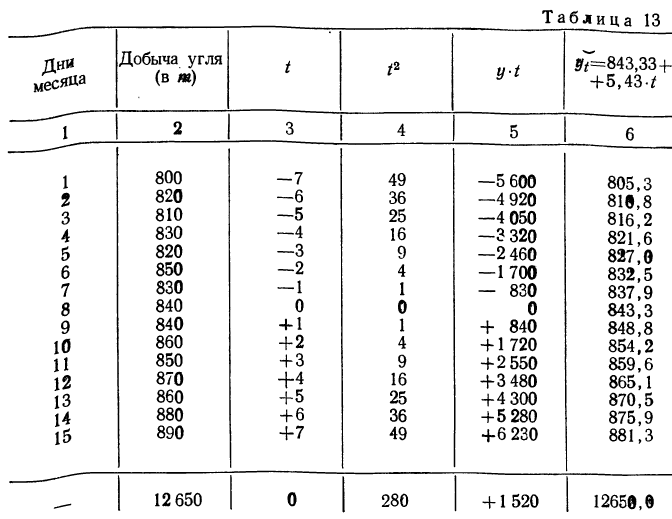
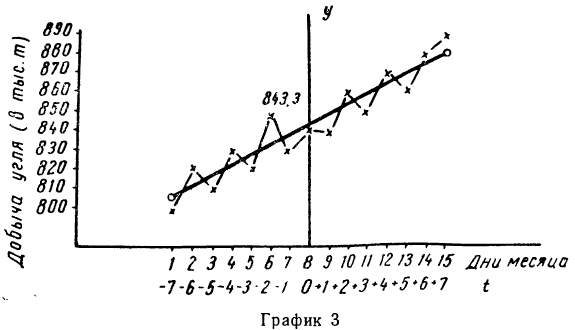
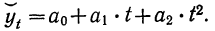
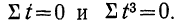
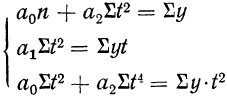
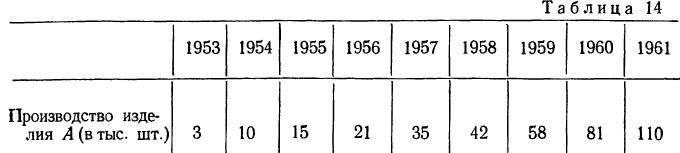
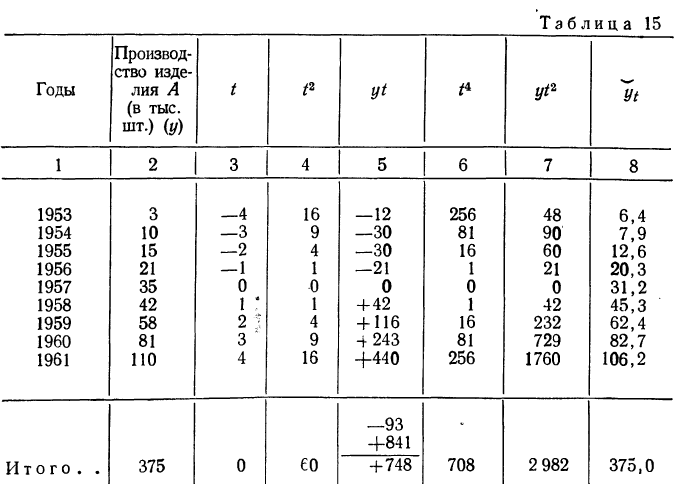
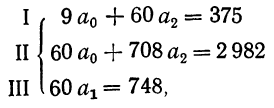
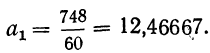
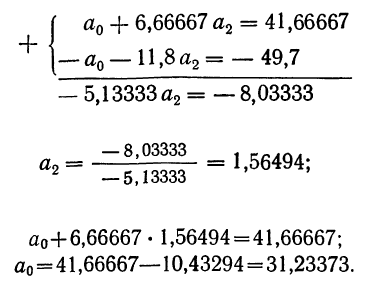
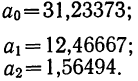
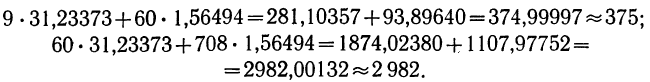
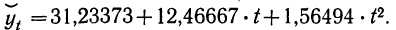

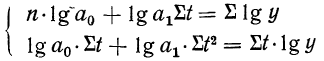
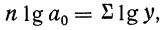
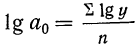
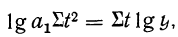
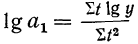
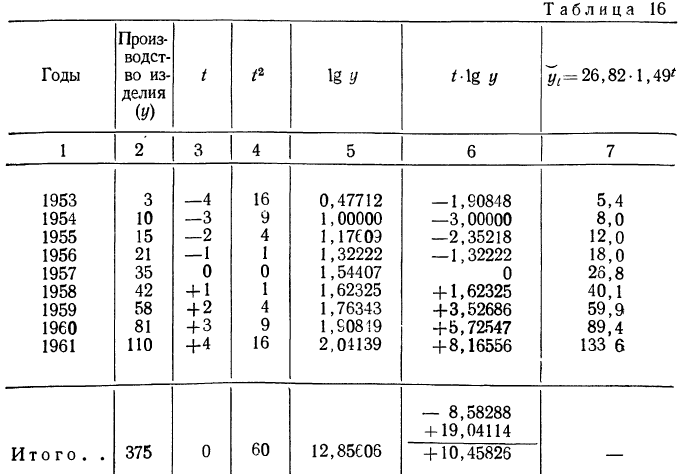
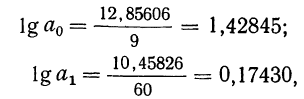
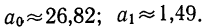
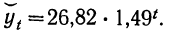
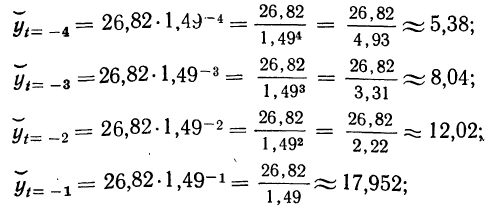
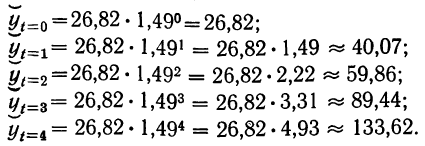
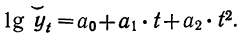
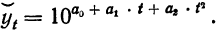
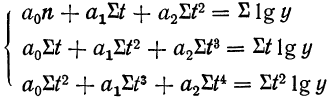
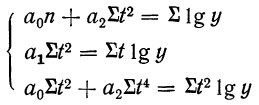
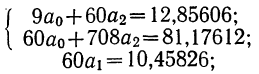
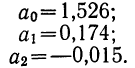
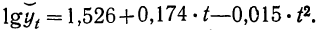
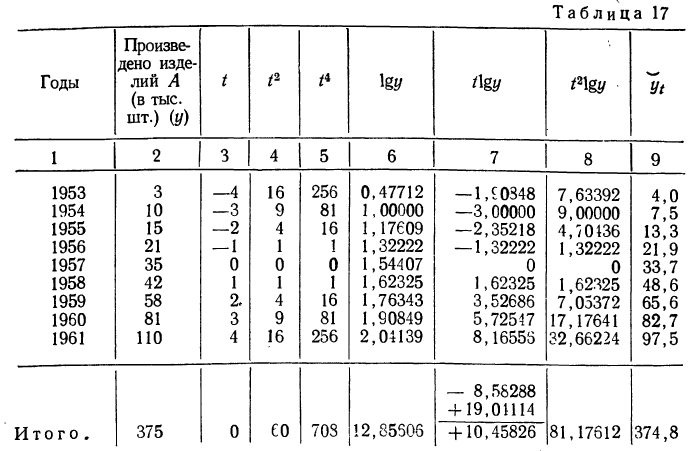
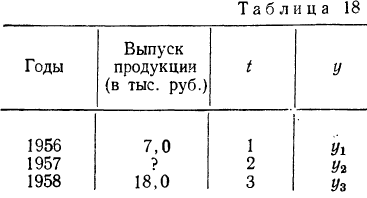
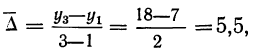
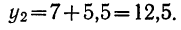
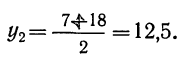
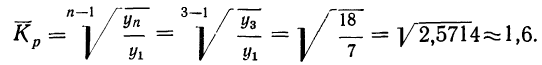
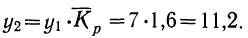

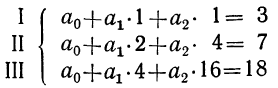
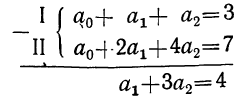
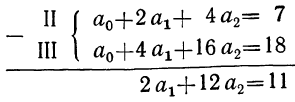
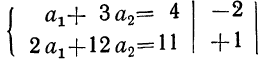
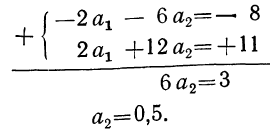
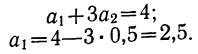
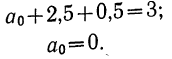
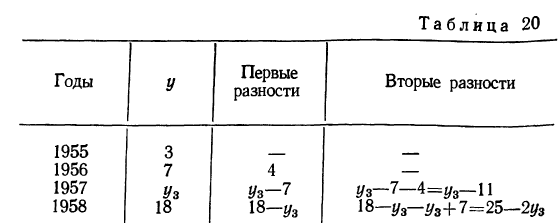
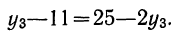
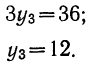
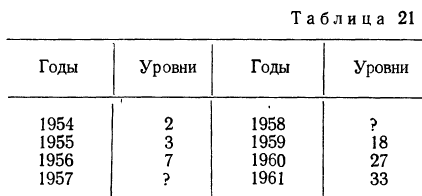
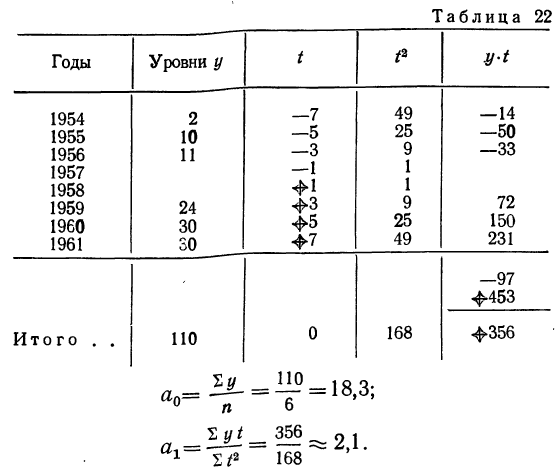
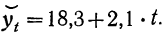
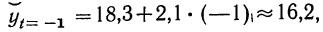
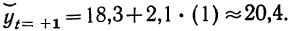

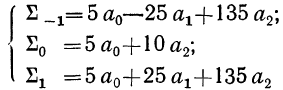
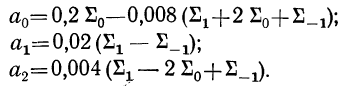
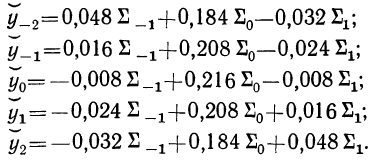
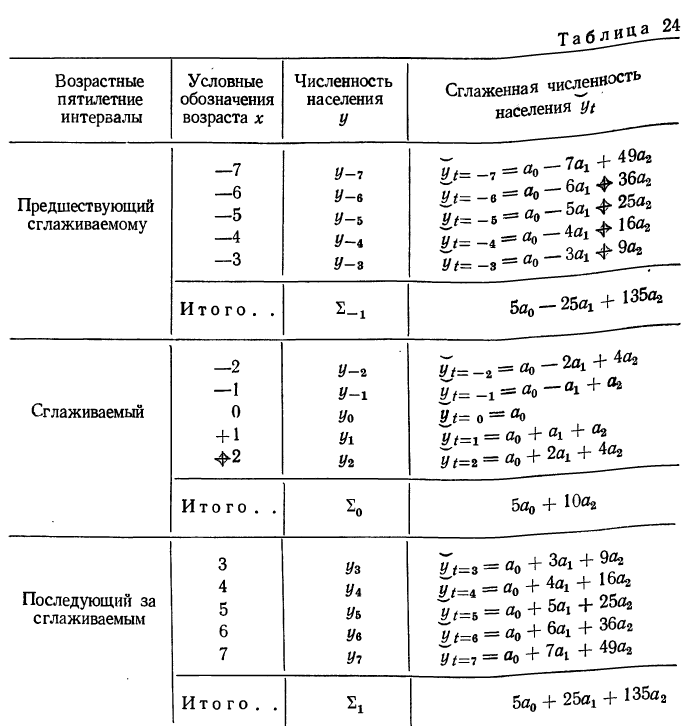

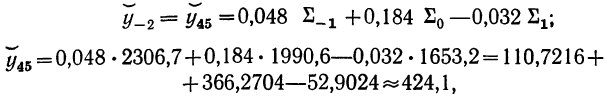
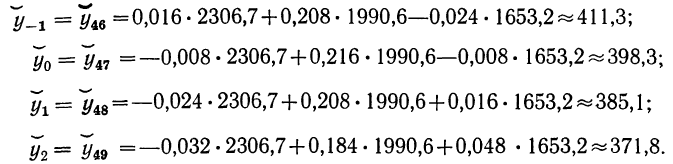
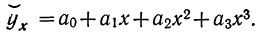
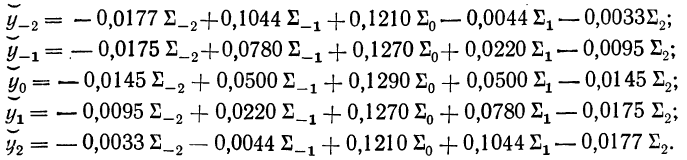

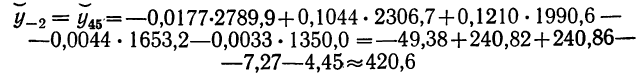



![Rendered by QuickLaTeX.com [left{ begin{gathered} sum {{y_i} = n{a_0} + {a_1}sum {{t_i}} } hfill sum {{y_i}{t_i} = {a_0}sum {{t_i} + {a_1}sum {t_i^2} } } hfill end{gathered} right.]](https://helpstat.ru/wp-content/ql-cache/quicklatex.com-8eefa365ccc5999df86b01ec72109949_l3.png)



