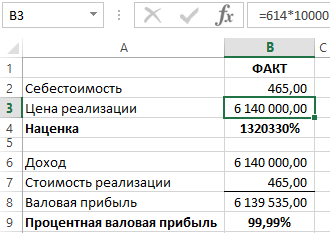
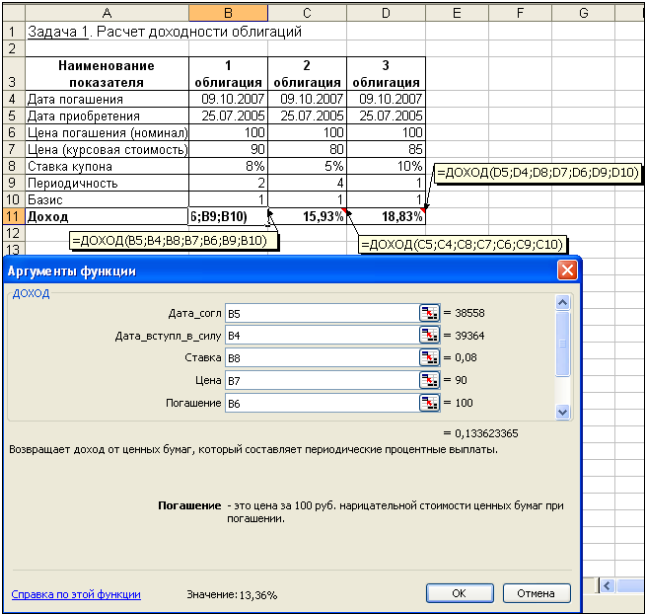
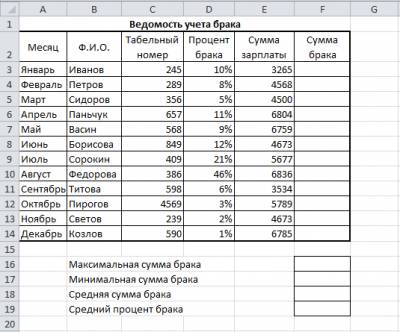
№1. В ячейке D3 электронной таблицы записана
формула =B$2+$B3. Какой вид приобретет формула, после того как ячейку
D3 скопируют в ячейку E4?
Примечание: знак $ используется для обозначения
абсолютной адресации.
1) =C$2+$B4
2) =A$2+$B1
3) =B$3+$C3
4) =B$1+$A3
Пояснение.
B$2: меняется столбец и не меняется номер строки.
$B3: столбец не меняется, меняется номер строки.
Номер столбца Е больше номера столбца D на 1. Значит
столбец B станет столбцом С.
Номер строки 4 на 1 больше номера строки 3, значит,
строка 3 станет строкой 4.
Окончательный вид =С$2+$B4.
Правильный ответ указан под номером 1.
№2 была скопирована формула. При копировании
адреса ячеек в формуле автоматически изменились, и значение формулы
стало равным 8. В какую ячейку была скопирована формула? В ответе укажите
только одно число – номер строки, в которой расположена ячейка.
|
A |
B |
C |
D |
E |
|
|
1 |
1 |
2 |
3 |
4 |
|
|
2 |
2 |
3 |
4 |
= B$3 + $C2 |
|
|
3 |
3 |
4 |
5 |
6 |
|
|
4 |
4 |
5 |
6 |
7 |
Примечание.
Знак $ обозначает абсолютную адресацию.
Пояснение.
При копировании формулы из ячейки D2 у первого слагаемого
может изменяться только номер столбца, а у второго — только номер строки.
Таким образом формулы в ячейках E1—E4:
E1 = C$3+$C1 = 8 E2 = C$3+$C2 = 9 E3 = C$3+$C3 =
10 E4 = C$3+$C4 = 11.
Таким образом, формула была скопирована в ячейку
E1.
Ответ: 1.
№3. Саше нужно с помощью электронных таблиц
построить таблицу значений выражения a2 + b2,
где a и b — целые числа, a меняется от 1 до 10, а b — от 6 до 15. Для этого
сначала в диапазоне В1:К1 он записал числа от 1 до 10, и в диапазоне
А2:А11 он записал числа от 6 до 15. Затем в ячейку С3 записал формулу
суммы квадратов чисел (А3 — значение b; С1 — значение a), после чего скопировал
её во все ячейки диапазона B2:К11. В итоге получил таблицу сумм квадратов
двузначных чисел. На рисунке ниже представлен фрагмент этой таблицы.
|
A |
B |
C |
D |
E |
|
|
1 |
1 |
2 |
3 |
4 |
|
|
2 |
6 |
37 |
40 |
45 |
52 |
|
3 |
7 |
50 |
53 |
58 |
65 |
|
4 |
8 |
65 |
68 |
73 |
80 |
|
5 |
9 |
82 |
85 |
90 |
97 |
В ячейке С3 была записана одна из следующих формул:
1) =С1^2+A3^2
2) =$С$1^2+$A$3^2
3) =С$1^2+$A3^2
4) =$С1^2+A$3^2
Укажите в ответе номер формулы, которая была записана
в ячейке С3.
Пояснение.
Формула, записанная в ячейку С3, должна иметь знак абсолютной
адресации перед буквой А, поскольку в противном случае, при копировании
формулы в ячейку B2, номер столбца будет автоматически уменьшаться,
появится неверная ссылка, произойдёт ошибка. Кроме того, формула должна
иметь знак абсолютной адресации перед цифрой 1, поскольку в противном
случае, при копировании формулы, например, в ячейку С2, номер строки
будет автоматически уменьшаться, появится неверная ссылка.
Правильный ответ указан под номером 3.
№4. Дан фрагмент электронной таблицы:
|
A |
B |
C |
|
|
1 |
3 |
4 |
|
|
2 |
=(A1 + B1+2)/(C1 – B1) |
=( 2*C1 – 2)/ A1 |
=B1*C1/(B1 – A1) |
Какое целое число должно быть записано в ячейке A1,
чтобы построенная после выполнения вычислений диаграмма по значениям
диапазона ячеек A2:С2 соответствовала рисунку?
Пояснение.
По рисунку видно, что значения всех трёх ячеек диапазона
A2:С2 равны. Приравняем значения в ячейках B2 и C2:
( 2*C1 – 2)/ A1 = B1*C1/(B1 – A1) ⇔ 6/ A1 =
12/(3 – A1) ⇔ A1 = 1 и A1
= 4.
Приравняв выражение в ячейке A2 и ячейке B2, находим
что A1 = 1.
Ответ: 1.
№5. Дан фрагмент электронной таблицы. Из
ячейки B2 в одну из ячеек диапазона A1:A4 была скопирована формула.
При копировании адреса ячеек в формуле автоматически изменились,
и числовое значение в этой ячейке стало равным 8. В какую ячейку была
скопирована формула? В ответе укажите только одно число — номер строки,
в которой расположена ячейка.
|
A |
B |
C |
D |
E |
|
|
1 |
4 |
3 |
2 |
1 |
|
|
2 |
= D$3 + $C2 |
4 |
3 |
2 |
|
|
3 |
6 |
5 |
4 |
3 |
|
|
4 |
7 |
6 |
5 |
4 |
Примечание. Знак $ обозначает абсолютную адресацию.
Пояснение.
При копировании формулы в в одну из ячеек диапазона
A1:A4 формула примет вид = C$3 + $Cn, где n — номер строки той ячейки в которую
скопировали формулу. Числовое значение в этой ячейке стало равно 8,
следовательно, для того, чтобы выполнялось равенство 5 + Cn = 8, n
должно быть равным 1.
Ответ: 1.
№6. В ячейке F7 электронной таблицы записана
формула =D$12+$D13. Какой вид приобретет формула, после того как ячейку
F7 скопируют в ячейку G8?
Примечание: знак $ используется для обозначения
абсолютной адресации.
1) =C$12+$D11
2) =D$11+$C13
3) =D$13+$E13
4) =E$12+$D14
Пояснение.
D$12: меняется столбец и не меняется номер строки.
$D13: столбец не меняется, меняется номер строки.
Номер столбца G больше номера столбца F на 1. Значит
столбец D станет столбцом Е.
Номер строки 8 на 1 больше номера строки 7, значит,
строка 13 станет строкой 14.
Окончательный вид =Е$12+$D14.
Правильный ответ указан под номером 4.
№7. В ячейке D3 электронной таблицы записана
формула =B$2-$B3. Какой вид приобретет формула, после того как ячейку
D3 скопируют в ячейку С4?
Примечание: знак $ используется для обозначения
абсолютной адресации.
1) =C$2-$B4
2) =A$2-$B4
3) =B$1-$C4
4) =B$1-$B4
Пояснение.
B$2: меняется столбец и не меняется номер строки.
$B3: столбец не меняется, меняется номер строки.
Номер столбца C меньше номера столбца D на 1. Значит
столбец B станет столбцом A.
Номер строки 4 на 1 больше номера строки 3, значит,
строка 3 станет строкой 4.
Окончательный вид =A$2-$B4.
Правильный ответ указан под номером 2.
№8. В ячейке F7 электронной таблицы записана
формула =D$12-$D13. Какой вид приобретет формула, после того как ячейку
F7 скопируют в ячейку E8?
Примечание: знак $ используется для обозначения
абсолютной адресации.
1) =C$12-$C14
2) =D$12-$D13
3) =D$13-$D14
4) =C$12-$D14
Пояснение.
D$12: меняется столбец и не меняется номер строки.
$D13: столбец не меняется, меняется номер строки.
Номер столбца Е меньше номера столбца F на 1. Значит
столбец D станет столбцом С.
Номер строки Е8 на 1 больше номера строки F7, значит,
строка 13 станет строкой 14.
Окончательный вид =С$12-$D14.
Правильный ответ указан под номером 4.
№9. В ячейке B1 записана формула =2*$A1.
Какой вид приобретет формула, после того как ячейку B1 скопируют в
ячейку C2?
1) =2*$B1
2) =2*$A2
3) =3*$A2
4) =3*$B2Н
Пояснение.
Запись $A1 означает , что столбец не меняется, меняется
номер строки.
Номер строки 2 на 1 больше номера строки 1, значит,
при копировании в ячейку C2 строка 1 станет строкой 2.
Окончательный вид =2*$A2.
Правильный ответ указан под номером 2.
№10. В ячейке C2 записана формула
=$E$3+D2. Какой вид приобретет формула, после того как ячейку C2 скопируют
в ячейку B1?
1) =$E$3+C1
2) =$D$3+D2
3) =$E$3+E
4) =$F$4+D2
Пояснение.
Запись $E$3 означает, что столбец не меняется и номер
строки не меняется.
Номер строки 2 уменьшился на 1, значит, при копировании
в ячейку B1 из C2 строка 2 станет строкой 1.
Номер столбца С уменьшился на 1, значит, при копировании
в ячейку B1 из C2 столбец D станет столбцом С.
Окончательный вид =$E$3+С1.
Правильный ответ указан под номером 1.
Определения значения формулы
№1. В электронной таблице значение формулы
=CP3HAЧ(A3:D3) равно 5. Чему равно значение формулы =СУММ(АЗ:СЗ), если значение
ячейки D3 равно 6?
1) 1
2) -1
3) 14
4) 4
Пояснение.
Функция СРЗНАЧ(A3:D3) считает среднее арифметическое
диапазона A3:D3, т. е. сумму значений четырёх ячеек A3, B3, C3, D3,
делённую на 4. Умножим среднее значение на число ячеек и получим сумму
значений ячеек A3 + B3 + C3 + D3 = 5 * 4 = 20.
Теперь вычтем значение ячейки D3 и найдём искомую
сумму: A3 + B3 + C3 = 20 — 6 = 14.
Правильный ответ указан под номером 3.
№2. В электронной таблице значение формулы
=СРЗНАЧ(С2:С5) равно 3. Чему равно значение формулы =СУММ(С2:С4), если значение
ячейки С5 равно 5?
1) 1
2) 7
3) -4
4) 4
Пояснение.
*Для лучшего понимания рекомендуется нарисовать
таблицу.
Функция СРЗНАЧ(С2:С5) считает среднее арифметическое
диапазона С2:С5, т. е. сумму значений четырёх ячеек С2, С3, C4, С5,
делённую на 4. Умножим среднее значение на число ячеек и получим сумму
значений ячеек С2 + С3 + C4 + С5 = 3 * 4 = 12
Теперь, вычтем значение ячейки С5 и найдём искомую
сумму: С2 + С3 + C4 = 12 — 5 = 7
Правильный ответ указан под номером 2.
№3. В электронной таблице значение формулы
=СУММ(А5:D5) равно 6. Чему равно значение формулы =СРЗНАЧ(А5:С5), если значение
ячейки D5 равно 9?
1) 1
2) -3
3) 3
4) -1
Пояснение.
*Для лучшего понимания рекомендуется нарисовать
таблицу.
Функция СУММ(А5:D5) считает сумму значений ячеек диапазона
A5:D5, т. е. A5 + B5 + C5 + D5 = 6
Функция СРЗНАЧ(А5:С5) считает среднее арифметическое
диапазона А5:С5, т. е. сумму значений трёх ячеек A5, B5, C5, делённую на
3.
Вычтем значение ячейки D5 из первой суммы и найдём
сумму: A5 + B5 + C5 = 6 — 9 = -3.
Теперь разделим ответ на 3 и найдём искомое среднее
значение: СРЗНАЧ(А5:С5) = -3 / 3 = -1.
Правильный ответ указан под номером 4.
№4. В электронной таблице значение формулы
=CУMM(D2:D5) равно 10. Чему равно значение формулы =CP3HAЧ(D2:D4), если значение
ячейки D5 равно −2?
1) 6
2) 2
3) 8
4) 4
Пояснение.
*Для лучшего понимания рекомендуется нарисовать
таблицу.
Функция СУММ(D2:D5) считает сумму значений ячеек диапазона
D2:D5, т. е. D2 + D3 + D4 + D5 = 10
Функция СРЗНАЧ(D2:D4) считает среднее арифметическое
диапазона D2:D4, т. е. сумму значений трёх ячеек D2, D3, D4, делённую на
3.
Вычтем значение ячейки D5 из первой суммы и найдём
сумму: D2 + D3 + D4 = 10 — (-2) = 12.
Теперь разделим ответ на 3 и найдём искомое среднее
значение: СРЗНАЧ(D2:D4) = 12 / 3 = 4.
Правильный ответ указан под номером 4.
№5. В электронной таблице значение формулы
=СРЗНАЧ(А4:С4) равно 5. Чему равно значение формулы СУММ(А4:D4), если значение
ячейки D4 равно 6?
1) 1
2) 11
3) 16
4) 21
Пояснение.
*Для лучшего понимания рекомендуется нарисовать
таблицу.
Функция СРЗНАЧ(A4:C4) считает среднее арифметическое
диапазона A4:C4, т. е. сумму значений трёх ячеек A4, B4, C4, делённую на
3. Умножим среднее значение на количество ячеек данного диапазона и
найдём: A4 + B4 + C4 = 5 * 3 = 15
Теперь прибавим к полученному резльтату значение
ячейки D4 и найдём искомую сумму:
A4 + B4 + C4 +
D4 = 15 + 6 = 21
Правильный ответ указан под номером 4.
№6. В электронной таблице значение формулы
=СРЗНАЧ(Е2:Е4) равно 3,
чему равно значение формулы =СУММ(Е2:Е5), если значение
ячейки Е5 равно 5?
1) 11
2) 2
3) 8
4) 14
Пояснение.
*Для лучшего понимания рекомендуется нарисовать
таблицу.
Функция СРЗНАЧ(Е2:Е4) считает среднее арифметическое
диапазона Е2:Е4, т. е. сумму значений трёх ячеек E2, E3, E4, делённую на
3. Умножим среднее значение на количество ячеек данного диапазона и
найдём: E2 + E3 + E4 = 3 * 3 = 9
Теперь прибавим к полученному резльтату значение
ячейки E5 и найдём искомую сумму:
E2 + E3 + E4 + E5 = 9 + 5 = 14
Правильный ответ указан под номером 4.
№7. В электронной таблице значение формулы
=СУММ(А7:С7) равно 9. Чему равно значение формулы =CPЗHAЧ(A7:D7). если значение
ячейки D7 равно 3?
1) -6
2) 6
3) 3
4) 4
Пояснение.
*Для лучшего понимания рекомендуется нарисовать
таблицу.
Функция СУММ(А7:С7) считает сумму значений ячеек А7, B7
и С7, поэтому А7 + B7 + С7 = 9.
Функция СРЗНАЧ(A7:D7) считает среднее арифметическое
диапазона A7:D7, т. е. сумму значений четырёх ячеек А7, B7, С7, D7,
делённую на 4. Поэтому прибавим к первой сумме значение ячейки D7 и
найдём:
А7 + B7 + С7 + D7 = 9 + 3 = 12.
Теперь разделим полученный резльтат на число ячеек и
найдём искомую величину:
СРЗНАЧ(A7:D7) = 12 / 4 = 3.
Правильный ответ указан под номером 3.
№8. В электронной таблице значение формулы
=СУММ(В2:В4) равно 6. Чему равно значение формулы =СРЗНАЧ(В2:В5), если значение
ячейки В5 равно 14?
1) 5
2) 8
3) 10
4) 20
Пояснение.
*Для лучшего понимания рекомендуется нарисовать
таблицу.
Функция СУММ(В2:В4) считает сумму значений ячеек B2, B3
и B4, поэтому B2 + B3 + B4 = 6.
Функция СРЗНАЧ(В2:В5) считает среднее арифметическое
диапазона В2:В5, т. е. сумму значений четырёх ячеек B2, B3, B4, B5,
делённую на их количество. Поэтому прибавим к первой сумме значение
ячейки В5 и найдём: B2 + B3 + B4 + В5 = 6 + 14 = 20.
Теперь разделим полученный резльтат на 4 и найдём искомую
величину: СРЗНАЧ(В2:В5) = 20 / 4 = 5.
Правильный ответ указан под номером 1.
№9. В электронной таблице значение формулы
=CPЗHAЧ(A3:D4) равно 5. Чему равно значение формулы =СРЗНАЧ(АЗ:С4), если
значение формулы =CУMM(D3:D4) равно 4?
1) 1
2) 6
3) 3
4) 4
Пояснение.
*Для лучшего понимания рекомендуется нарисовать
таблицу.
Функция СУММ(D3:D4) считает сумму значений ячеек D3 и
D4: D3 + D4 = 4.
Функция СРЗНАЧ(A3:D4) считает среднее арифметическое
диапазона A3:D4, т. е. сумму значений восьми ячеек A3, B3, C3, D3, A4,
B4, C4, D4, делённую на их количество. Умножим среднее значение на 8 и
найдём суммму значений этих ячеек: СУММ(A3:D4) = 5 * 8 = 40.
Вычтем из полученной суммы СУММ(A3:D4) значение суммы
D3 + D4 и найдём значение суммы СУММ(A3:C4): оно равно 40 — 4 = 36.
Теперь разделим полученный резльтат на количество
ячеек данной суммы (их здесь 6) и найдём искомую величину: СРЗНАЧ(АЗ:С4)
= 36 / 6 = 6.
Правильный ответ указан под номером 2.
№10. В электронной таблице значение формулы
=CPЗHAЧ(C2:D5) равно 4. Чему равно значение формулы =CУMM(C5:D5), если значение
формулы =CPЗHAЧ(C2:D4) равно 5
1) -6
2) 2
3) -4
4) 4
Пояснение.
*Для лучшего понимания рекомендуется нарисовать
таблицу.
Функция СРЗНАЧ(C2:D5) считает среднее арифметическое
диапазона C2:D5, т. е. сумму значений восьми ячеек С2, D2, C3, D3, C4,
D4, C5, D5, делённую на их количество. Умножим среднее значение на 8 и
найдём суммму значений этих ячеек: СУММ(C2:D5) = 4 * 8 = 32.
Аналогично для CPЗHAЧ(C2:D4), количество ячеек 6:
СУММ(C2:D4) = 5 * 6 = 30.
Вычтем из СУММ(C2:D5) значение СУММ(C2:D4) и найдём значение
суммы С5 + D5: оно равно
32 — 30 = 2.
Правильный ответ указан под номером 2.
Работа с таблицами
№1. В электронной таблице Excel отражены
данные о деятельности страховой компании за 4 месяца. Страховая
компания осуществляет страхование жизни, недвижимости, автомобилей
и финансовых рисков своих клиентов. Суммы полученных по каждому виду
деятельности за эти месяцы страховых взносов (в тысячах рублей)
также вычислены в таблице.
|
Страхование |
Страхование |
Страхование |
Страхование |
|
|
жизни |
автомобилей |
фин. рисков |
недвижимости |
|
|
тыс. р. |
тыс. р. |
тыс. р. |
тыс. р. |
|
|
Май |
10 |
3 |
20 |
11 |
|
Июнь |
2 |
4 |
8 |
10 |
|
Июль |
4 |
6 |
8 |
5 |
|
Август |
6 |
12 |
7 |
4 |
|
Сумма |
22 |
25 |
43 |
30 |
Известно, что за эти 4 месяца компании пришлось выплатить
двум клиентам по 20 000 рублей каждому.
Каков общий доход страховой компании в рублях за прошедшие
4 месяца?
1) 120 000
2) 100 000
3) 80 000
4) 60 000
Пояснение.
Найдём сумму значений из строки Сумма: 22 + 25 + 43 + 30
= 120(тыс. р.).
Двум клиентам компания выплатила 2 * 20000 = 40000.
Соответственно общий доход составит:
120000 — 40000 = 80000 руб.
Правильный ответ указан под номером 3.
№2. В электронной таблице Excel приведен
фрагмент банковских расчетов по вкладам населения. Таблица отражает
фамилии вкладчиков, процентные ставки по вкладам за два фиксированных
одногодичных промежутка времени и суммы вкладов с начисленными
процентами за соответствующие истекшие периоды времени. Также
приведены общие суммы всех вкладов в банке после начисления процентов
и доход вкладчиков за истекший двухгодичный период.
|
Вклад, р. |
4 % |
5 % |
Сумма начислений за два периода |
|
|
Осин |
2100000 |
2184000 |
2293200 |
193200 |
|
Пнев |
200000 |
208000 |
248400 |
18400 |
|
Чуйкин |
50000 |
52000 |
54600 |
4600 |
|
Шаталов |
2400000 |
2496000 |
2620800 |
220800 |
|
Общая сумма |
4750000 |
4940000 |
5187000 |
437000 |
Определите, кто из вкладчиков за истекшее с момента
открытия вклада время получил средний ежемесячный доход от вклада
более 9 000 рублей.
1) Осин
2) Пнев
3) Чуйкин
4) Шаталов
Пояснение.
Для определения среднемесячного дохода необходимо
разделить доход каждого на количество месяцев вклада, т. е. на
24 месяца.
Осин: 193200 / 24 = 8 050,
Пнев: 18400 / 24 = 766,7,
Чуйкин: сам доход меньше 9 000, поэтому он не подходит,
Шаталов: 220800 / 24 = 9 200.
Более 9 000 рублей имеет Шаталов.
Правильный ответ указан под номером 4.
№3. В электронной таблице Excel приведен
фрагмент банковских расчетов по вкладам населения. Таблица отражает
фамилии вкладчиков, процентные ставки по вкладам за фиксированные
промежутки времени и суммы вкладов с начисленными процентами за соответствующие
истекшие периоды времени. Также приведены общие суммы всех вкладов в
банке после начисления процентов.
|
Вклад, р. |
4 % |
3 % |
|
|
Агеев |
2100000 |
2184000 |
2249520 |
|
Агнесян |
200000 |
208000 |
214240 |
|
Сестров |
50000 |
52000 |
53560 |
|
Кучкин |
2300000 |
2392000 |
2463760 |
|
Общая сумма |
4650000 |
4836000 |
4981080 |
Определите общую сумму вкладов населения в банке в
рублях после очередного начисления процентов, если процентная ставка
будет составлять 10%.
1) 5 000 000
2) 5 134 567
3) 5 345 678
4) 5 479 188
Пояснение.
Общая сумма вкладов после начисления процентов составила
4 981 080. Увеличение на 10% можно заменить операцией умножения
на 1,1. Тогда общая сумма составит: 4 981 080 · 1,1 = 5 479 188.
Правильный ответ указан под номером 4.
№4. В электронной таблице Excel отражены
данные по продаже некоторого штучного товара в торговых центрах города
за четыре месяца. За каждый месяц в таблице вычислены суммарные продажи
и средняя по городу цена на товар, которая на 2 рубля больше цены поставщика
данного товара.
|
ТЦ |
Январь |
Февраль |
Март |
Апрель |
||||
|
Продано, шт. |
Цена, р. |
Продано, шт. |
Цена, р. |
Продано, шт. |
Цена, р. |
Продано, шт. |
Цена, р. |
|
|
Эдельвейс |
5 |
14 |
1 |
17 |
5 |
15 |
4 |
15 |
|
Покупочка |
6 |
13 |
2 |
16 |
6 |
11 |
4 |
14 |
|
Кошелек |
2 |
17 |
5 |
14 |
4 |
15 |
1 |
18 |
|
Солнечный |
8 |
12 |
7 |
13 |
7 |
11 |
7 |
13 |
|
Продано всего |
21 |
15 |
22 |
16 |
||||
|
Средняя цена |
14 |
15 |
13 |
15 |
Известно, что весь поступивший от поставщика в текущем
месяце товар реализуется в этом же месяце.
В каком месяце выручка поставщика данного товара
была максимальна?
1) Январь
2) Февраль
3) Март
4) Апрель
Пояснение.
Найдём выручку за продажи в торговых центрах на каждый
месяц. В том месяце, где она максимальна, поставщик также получил наибольшую
прибыль.
Январь: 21 * 14 = 294,
Февраль: 15 * 15 = 225,
Март: 22 * 13 = 286,
Апрель: 16 * 15 = 240.
Наибольшая прибыль в январе.
Правильный ответ указан под номером 1.
№5. В электронной таблице Excel отражены
данные о деятельности страховой компании за 4 месяца. Страховая
компания осуществляет страхование жизни, недвижимости,/автомобилей
и финансовых рисков своих клиентов. Суммы полученных по каждому виду
деятельности за эти месяцы страховых взносов (в тысячах рублей)
также вычислены в таблице.
|
Страхование жизни, тыс. р. |
Страхование автомобилей, тыс. р. |
Страхование фин. рисков, тыс. р. |
Страхование недвижимости, тыс, р. |
|
|
январь |
10 |
4 |
20 |
11 |
|
февраль |
8 |
4 |
80 |
14 |
|
март |
43 |
3 |
8 |
5 |
|
апрель |
6 |
12 |
7 |
65 |
|
сумма |
67 |
23 |
115 |
95 |
Известно, что за эти 4 месяца компании пришлось выдать
трем клиентам страховые выплаты по 30 000 рублей каждому. Каков общий
доход страховой компании в рублях за прошедшие 4 месяца?
1) 310 000
2) 200 000
3) 210 000
4) 300 000
Пояснение.
Найдём общую сумму: 67 + 23 + 115 + 95 = 300 (тыс. р).
Выплаты клиентам: 30 000 * 3 = 90 000 (р).
Общий доход: 300 000 — 90 000 = 210 000 рублей.
Правильный ответ указан под номером 3.
№6. В электронной таблице Excel приведен
фрагмент банковских расчетов по вкладам населения. Таблица отражает
фамилии вкладчиков, процентные ставки по вкладам за два фиксированных
одногодичных промежутка времени и суммы вкладов с начисленными
процентами за соответствующие истекшие периоды времени. Также
приведены общие суммы всех вкладов в банке после начисления процентов
и доход вкладчиков за истекший двухгодичный период.
|
Вклад р. |
4 % |
5 % |
Сумма начислений за два периода |
|
|
Столков |
3200000 |
3328000 |
3494400 |
294400 |
|
Чин |
3212000 |
3340480 |
3507504 |
295504 |
|
Прокопчин |
400000 |
416000 |
436800 |
36800 |
|
Щеглов |
1000000 |
1040000 |
1092000 |
92000 |
|
Общая сумма: |
7812000 |
8124480 |
8530704 |
718704 |
Определите, кто из вкладчиков за истекшее с момента
открытия вклада время получил средний ежемесячный доход от вклада
менее 2 000 рублей.
1) Столков
2) Чин
3) Прокопчин
4) Щеглов
Пояснение.
Сумма начислений указана за 2 года, т. е. за 24 месяца.
Чем меньше сумма, тем меньше средний доход. Самая маленькая сумма у Прокопчина.
Проверим 36800 / 24 = 1533,33.
Правильный ответ указан под номером 3.
№7. В 2000 году в РФ создано 7 федеральных
округов. Используя представленную таблицу укажите номер региона с
наименьшей плотностью населения.
|
Название |
Состав |
Площадь |
Население |
|
1. Северо-Западный |
11 регионов − |
1677,9 |
14158 |
|
2. Центральный |
18 регионов − |
650,7 |
36482 |
|
3. Приволжский |
15 регионов − |
1038 |
31642 |
|
4. Южный |
13 регионов − |
589,2 |
21471 |
|
5. Уральский |
6 регионов − |
1788,9 |
12520 |
|
6. Сибирский |
16 регионов − |
5114,8 |
20542 |
|
7. Дальневосточный |
10 регионов − |
6515,9 |
7038 |
1) 4
2) 5
3) 6
4) 7
Пояснение.
Проверим все варианты. Для этого найдём плотность населения
в округах 4—7, поделив население на площадь.
Увидим, что седьмой округ имеет наименьшую плотность населения.
Правильный ответ указан под номером 4.
№8. В 2000 году в РФ создано 7 федеральных
округов. Используя представленную таблицу укажите номер региона с
наибольшей плотностью населения.
|
Название |
Состав |
Площадь |
Население |
|
1. Северо-Западный |
11 регионов − |
1677,9 |
14158 |
|
2. Центральный |
18 регионов − |
650,7 |
36482 |
|
3. Приволжский |
15 регионов − |
1038 |
31642 |
|
4. Южный |
13 регионов − |
589,2 |
21471 |
|
5. Уральский |
6 регионов − |
1788,9 |
12520 |
|
6. Сибирский |
16 регионов − |
5114,8 |
20542 |
|
7. Дальневосточный |
10 регионов − |
6515,9 |
7038 |
1) 1
2) 2
3) 3
4) 4
Пояснение.
Проверим все варианты. Для этого найдём плотность населения
в округах 1—4, поделив население на площадь.
Увидим, что второй окурга имеет наибольшую плотность
населения.
Правильный ответ указан под номером 2.
№9. Коле нужно с помощью электронных таблиц
построить таблицу умножения чисел от 3 до 6.
Для этого сначала в диапазонах В1:Е1 и А2:А5 он записал
числа от 3 до 6. Затем в ячейку Е2 записал формулу умножения, после чего
скопировал её во все ячейки диапазона В2:Е5. В итоге на экране получился
фрагмент таблицы умножения (см. рисунок).
|
A |
B |
C |
D |
E |
|
|
1 |
3 |
4 |
5 |
6 |
|
|
2 |
3 |
9 |
12 |
15 |
18 |
|
3 |
4 |
12 |
16 |
20 |
24 |
|
4 |
5 |
15 |
20 |
25 |
30 |
|
5 |
6 |
18 |
24 |
30 |
36 |
Какая формула была записана в ячейке Е2?
1) =А$2*$Е1
2) =А2*Е1
3) =$А2*$Е1
4) =$А2*Е$1
Пояснение.
Формула, записанная в ячейку Е2, должна иметь знак абсолютной
адресации перед буквой А, поскольку в противном случае, при копировании
формулы в диапазон B2:D2, номер столбца будет автоматически уменьшаться,
появится неверная ссылка. произойдёт ошибка. Кроме того, формула должна
иметь знак абсолютной адресации перед цифрой 1, поскольку в противном
случае, при копировании формулы в диапазон E3:E5, номер строки будет
автоматически увеличиваться, появится неверная ссылка.
Следовательно, ответ 4.
№10. Коле нужно с помощью электронных таблиц
построить таблицу двузначных чисел от 50 до 89.
Для этого сначала в диапазоне В1:К1 он записал числа
от 0 до 9, и в диапазоне А2:А5 он записал числа от 5 до 8. Затем в ячейку
В2 записал формулу двузначного числа (А2 — число десятков;
В1 — число единиц), после чего скопировал её во все ячейки диапазона
В2:К5. В итоге получил таблицу двузначных чисел. На рисунке ниже представлен
фрагмент этой таблицы.
|
A |
B |
C |
D |
E |
|
|
1 |
0 |
1 |
2 |
3 |
|
|
2 |
5 |
50 |
51 |
52 |
53 |
|
3 |
6 |
60 |
61 |
62 |
63 |
|
4 |
7 |
70 |
71 |
72 |
73 |
|
5 |
8 |
80 |
81 |
82 |
83 |
Какая формула была записана в ячейке В2?
1) =А$2*10+$В1
2) =$А2*10+$В1
3) =А2*10+В1
4) =$А2*10+В$1
Пояснение.
Формула, записанная в ячейку В2, должна иметь знак абсолютной
адресации перед буквой А, поскольку в противном случае,при копировании
формулы в диапазон B5:E5, номер столбца будет автоматически увеличиваться,
появится неверная ссылка. Кроме того, формула должна иметь знак абсолютной
адресации перед цифрой 1, поскольку в противном случае, при копировании
формулы в диапазон B3:B5, номер строки будет автоматически увеличиваться,
появится неверная ссылка.
Следовательно, ответ 4.
Составление диаграмм по данным
№1. Сплавляются два вещества, состоящие
из серы, железа, водорода и меди. Массовые доли серы (S), железа (Fe),
водорода (Н) и меди (Си) в каждом веществе приведены на диаграммах.
Определите, какая из диаграмм правильно отражает соотношение
элементов в сплаве.
Пояснение.
Отталкиваемся от железа: в каждом веществе железа
было больше половины, следовательно, и в смеси его будет половина
или более, такой вариант изображён на диаграмме 3.
Правильный ответ: 3.
№2. На диаграмме представлен уровень зарплат
трех членов семьи за два месяца.
Какая из диаграмм правильно отражает суммарный за
два месяца доход каждого члена семьи?
Пояснение.
Визуально видно, что за два месяца папа набирает наибольшую
из всех сумму,
дочка на втором месте (стабильно за оба месяца), и на
третьем месте — мама.
Сразу отсеиваем диаграмму 2 и 3, а вот для 4ой скажем,
что заработок отца во много больше дочери, следовательно остается
диаграмма 1.
Правильный ответ: 1.
№3. Диаграмма отражает количество (в килограммах)
собранного за четыре месяца урожая двух сортов огурцов в парниковом
хозяйстве.
Какая из диаграмм правильно отражает объемы суммарного
за четыре месяца собранного урожая по каждому из сортов?
Пояснение.
1 сорт: 10+20+30+30=90 кг.
2 сорт: 20+40+30+30=120 кг.
2го сорта больше, чем 1го на 120 — 90 = 30 кг или на
30*100/120=25%, что соответствует графику 4.
Правильный ответ: 4.
№4. На диаграмме показано количество
участников тестирования по предметам в разных регионах России.
Какая из диаграмм правильно отражает соотношение
общего количества участников (из всех трех регионов) по каждому из
предметов тестирования?
Пояснение.
При помощи столбчатых диаграмм можно найти общее количество
учеников:
400+100+200+400+200+200+400+300+200=2400
Круговые диаграммы дают нам представление о долях отдельных
составляющих в общей сумме. Соответственно подсчитаем, какую долю тестируемых
составляют учащиеся, тестируемые по различным предметам:
Биология: 12002400=0,5=50%
История: 6002400=0,25=25%
Химия: 6002400,25=25%
Этим данным соответствует первая диаграмма
№5. На диаграмме показано количество
участников тестирования по предметам в разных регионах России.
Какая из диаграмм правильно отражает соотношение
общего количества участников тестирования по регионам?
Пояснение.
При помощи столбчатых диаграмм можно найти общее количество
учеников:
200+100+200+200+200+200+400+300+200=2000
Круговые диаграммы дают нам представление о долях отдельных
составляющих в общей сумме. Соответственно подсчитаем, какую долю тестируемых
составляют учащиеся из различных регионов:
Татарстан: 5002000=0,25=25%
Чувашия: 6002000=0,30=30%
Якутия: 9002000=0,45=45%
Этим данным соответствует третья диаграмма
№6. На диаграмме показано количество
участников тестирования по предметам в разных регионах России.
Какая из диаграмм правильно отражает соотношение
количества участников тестирования по химии в регионах?
Пояснение.
Из условия видно, что соотношение для всех регионов
по участникам тестирования по химии одинаково.
Правильный ответ соответствует четвертой диаграмме
№7. На диаграмме показано количество
участников тестирования по предметам в разных регионах России.
Какая из диаграмм правильно отражает соотношение
количества участников тестирования по истории в регионах?
Пояснение.
При помощи столбчатых диаграмм можно найти общее количество
учеников, принимавших участие в тестировании по истории:
100+200+300=600
Круговые диаграммы дают нам представление о долях отдельных
составляющих в общей сумме. Соответственно подсчитаем, какую долю тестируемых
составляют учащиеся из различных регионов:
Татарстан: 100600=0,17=17%
Чувашия: 200600=0,33=33%
Якутия: 300600=0,5=50%
Этим данным соответствует вторая диаграмма
№8. На диаграмме показано количество
участников тестирования по предметам в разных регионах России.
Какая из диаграмм правильно отражает соотношение
количества участников тестирования по русскому языку в регионах?
Пояснение.
При помощи столбчатых диаграмм можно найти общее количество
учеников, принимавших участие в тестировании по русскому языку:
200+200+200=600
Круговые диаграммы дают нам представление о долях отдельных
составляющих в общей сумме. Соответственно подсчитаем, какую долю тестируемых
составляют учащиеся из различных регионов:
Башкирия: 200600=0,33=33%
Калмыкия: 200600=0,33=33%
Удмуртия: 200600=0,33=33%
Этим данным соответствует четвёртая диаграмма.
Второй вариант рассуждения
Проанализировав диаграмму, увидим, что тестирование
по русскому языку проходило равное количество учеников во всех трех
регионах. Таким образом, диаграмма под номером 4 правильно отражает
соотношение количества участников тестирования по русскому
языку.
Правильный ответ указан под номером 4.
№9. В таблице представлены средние рыночные
цены для 4–х типов товаров на начало и конец года. Какая из диаграмм наиболее
верно отражает рост цен этих товаров в процентах относительно начала
года?
Пояснение.
Найдем на сколько процентов изменилась цена, для
этого нужно найти изменение цены каждого товара, а затем отнести его к
цене товара в начале года:
1-ый товар:
2-ой товар:
3-ий товар:
4-ый товар:
Анализируя столбчатые диаграммы, приходим к выводу,
что таким данным наиболее точно соответствует 2-ая диаграмма.
№10. На протяжении 3–х минут центральный
процессор компьютера был загружен следующим образом: 1–ю минуту
был загружен на 30%, 2–ю – на 10% и 3–ю – на 60%. Какая из диаграмм соответствует
загруженности процессора на протяжении 3–х минут?
Пояснение.
Для анализа круговых диаграмм необходимо выяснить,
какая доля памяти выделялась программе в течение каждого промежутка
времени. Анализируя круговые диаграммы, видим, что 1-я соответствует
условию задачи.
На второй диаграмме все части равные, что неверно.
На диаграмме 3 третья минута не занимает 60 %. На
четвёртой третья минута также меньше 60 %.
Ответ: 1.
Столбчатая и круговая диаграммы
№1. Все ученики старших классов (с 9-го по
11-й) участвовали в школьной спартакиаде. По результатам соревнований
каждый из них получил от 0 до 3-х баллов. На диаграмме I отражено распределение
учеников по классам, а на диаграмме II — количество учеников, набравших
баллы от 0 до 3-х. На обеих диаграммах каждый ученик учтён только один
раз.
Имеются четыре утверждения:
1 ) Среди учеников 9-го класса есть хотя бы один, набравший
2 или 3 балла.
2 ) Все ученики, набравшие 0 баллов, могут быть 9-классниками.
3 ) Все 10-классники могли набрать ровно по 2 балла.
4 ) Среди набравших 3 балла нет ни одного 10-классника.
Какое из этих утверждений следует из анализа обеих диаграмм?
Пояснение.
Столбчатая диаграмма дает нам представление о численных
данных. Из нее мы выясняем, что всего учеников 45 + 30 + 20 + 15 = 110.
Круговая диаграмма дает нам представление о долях отдельных
составляющих в общей сумме. Из нее мы выясняем, что
«9 класс»,=50%=55
«11 класс»,
«10 класс» .
Теперь рассмотрим утверждения:
1. Однозначно не следует из анализа обеих диаграмм,
поскольку суммарное количество учеников, набравших 2 или 3 балла
равно 20 + 15 = 35, а учеников девятого класса 55.
2. Могут, так как 0 баллов набрало 45, а 9-классников
55.
3. Не могли, так как 10-классников 37, а ровно по 2 балла
набрало всего 20.
4. Однозначно не следует из анализа обеих диаграмм.
№2. В магазине продаются мячи четырёх цветов
(синие, зелёные, красные и жёлтые) и трёх размеров (большие, средние и маленькие).
На диаграмме I отражено количество мячей разного размера, а на диаграмме
II — распределение мячей по цветам.
Имеются четыре утверждения:
1 ) Среди больших мячей должен быть хотя бы один синий.
2 ) Ни один мяч среднего размера не может быть красным.
3 ) Все маленькие мячи могут быть зелёными.
4 ) Все зелёные мячи могут быть маленькими.
Какое из этих утверждений следует из анализа обеих диаграмм?
Пояснение.
Столбчатая диаграмма дает нам представление о численных
данных. Из нее мы выясняем, что всего мячей 30+40+35+15=120.
Круговая диаграмма дает нам представление о долях отдельных
составляющих в общей сумме. Из нее мы выясняем, что М=50%=60, Ср=25%=30,
Б=25%=30.
Теперь рассмотрим утверждения:
1. Может, но не обязательно.
2. Может, так как Ср=30, а красных 35.
3. Не могут, так как М=60, а зеленых всего 40.
4. Могут так как зеленых всего 40, а М=60.
№3. В магазине продаются мячи четырёх цветов
(синие, зелёные, красные и жёлтые) и трёх размеров (большие, средние и маленькие).
На диаграмме I отражено количество мячей разного размера, а на диаграмме
II — распределение мячей по цветам.
Имеются четыре утверждения:
1 ) Все маленькие мячи могут быть синими или жёлтыми.
2 ) Среди больших мячей найдётся хотя бы один красный.
3 ) Среди маленьких мячей найдётся хотя бы один зелёный
или красный.
4 ) Все красные мячи могут быть среднего размера.
Какое из этих утверждений следует из анализа обеих диаграмм?
Пояснение.
Столбчатая диаграмма дает нам представление о численных
данных. Из нее мы выясняем, что всего мячей 30+40+35+15=120.
Круговая диаграмма дает нам представление о долях отдельных
составляющих в общей сумме. Из нее мы выясняем, что М=50%=60, Ср=25%=30,
Б=25%=30.
Теперь рассмотрим утверждения:
1. Не могут, так как М=60, а синих 30, жёлтых 15.
2. Может, но не обязательно.
3. Найдется, так как неверно «1.»
4. Не могут так как красных 35, а Ср=30.
№4. Заведующая детским садом обнаружила,
что в её саду все дети называются только четырьмя разными именами;
Саша, Валя, Миша и Ира. По цвету волос каждого из них можно чётко отнести
к блондинам, шатенам или брюнетам. На диаграмме I отражено количество
детей каждого имени, а на диаграмме II — распределение детей по цвету
волос.
Имеются четыре утверждения:
1 ) Всех брюнетов могут звать Саша.
2 ) Все Иры могут быть шатенками.
3 ) Среди Миш найдётся хотя бы один блондин.
4 ) Среди Саш нет ни одного шатена.
Какое из этих утверждений следует из анализа обеих диаграмм?
Пояснение.
Столбчатая диаграмма дает нам представление о численных
данных. Из нее мы выясняем, что всего детей
40+20+35+25=120
Круговая диаграмма дает нам представление о долях отдельных
составляющих в общей сумме. Из нее мы выясняем, что
«Бр»,=50%=60
«Бл»,
«Ш» .
Теперь рассмотрим утверждения:
1. Не могут, так «Бр»=60, а Саш 40.
2. Могут, так как «Ш»=45, а Ир 25.
3. Однозначно не следует из анализа обеих диаграмм.
4. Однозначно не следует из анализа обеих диаграмм.
№5. Заведующая детского сада обнаружила,
что в сад ходят дети только четырёх имен: Саши, Вали, Миши и Иры. По цвету
волос каждого из них можно чётко отнести к блондинам, шатенам и брюнетам.
На диаграмме I отражено количество детей каждого имени, а на диаграмме
II — распределение детей по цвету волос.
Имеются четыре утверждения:
1) Всех блондинов зовут Саша.
2) Все Миши могут быть блондинами.
3) Среди Саш может не быть ни одного шатена.
4) Среди брюнетов есть хотя бы один ребёнок по имени Валя
или Ира.
Какое из этих утверждений следует из анализа обеих диаграмм?
Пояснение.
Столбчатая диаграмма дает нам представление о численных
данных. Из нее мы выясняем, что всего детей
40+20+35+25=120
Круговая диаграмма дает нам представление о долях отдельных
составляющих в общей сумме. Из нее мы выясняем, что
«Бр»,=50%=60
«Бл»,
«Ш» .
Теперь рассмотрим утверждения:
1. Однозначно не следует из анализа обеих диаграмм.
2. Не могут, так как «Бл»=20, а Миш 35.
3. Может не быть.
4. Однозначно не следует из анализа обеих диаграмм.
№6. В магазине продаются головные уборы
трёх видов (панамки, шляпы и бейсболки) и четырёх материалов (брезент,
хлопок, шёлк и соломка).На диаграмме 1 отражено количество головных
уборов каждого вида, а на диаграмме II — распределение головных уборов
по материалам.
Имеются четыре утверждения:
A) Все шляпы могут быть из шёлка.
Б) Все панамы могут быть из соломки.
B) Среди головных уборов из соломки найдётся хотя бы
одна панама.
Г) Все бейсболки должны быть из хлопка.
Какое из этих утверждений следует из анализа обеих диаграмм?
Пояснение.
Столбчатая диаграмма дает нам представление о численных
данных. Из нее мы выясняем, что всего головных уборов
45+35+20=100
Круговая диаграмма дает нам представление о долях отдельных
составляющих в общей сумме. Из нее мы выясняем, что
«Х»
«Б»,
«С»,
«Ш» .
Теперь рассмотрим утверждения:
1. Могут, так как шляп 45, а «Ш»=50.
2. Не могут, так как «С»=25, а панам 35.
3. Однозначно не следует из анализа обеих диаграмм.
4. Однозначно не следует из анализа обеих диаграмм.
№7. В магазине продаются головные уборы
трёх видов (панамки, шляпы и бейсболки) и четырёх материалов (брезент,
хлопок, шёлк и соломка).На диаграмме I отражено количество головных
уборов каждого вида, а на диаграмме II — распределение головных уборов
по материалам.
Имеются четыре утверждения:
A) Все соломенные изделия могут быть бейсболками.
Б) Все панамки могут быть из хлопка или брезентовыми.
B) Среди изделий из шёлка может не быть ни одной шляпы.
Г) Среди изделий, сделанных не из соломки, может не
быть ни одной панамы.
Какое из этих утверждений следует из анализа обеих диаграмм?
Пояснение.
Столбчатая диаграмма дает нам представление о численных
данных. Из нее мы выясняем, что всего головных уборов
45+35+20=100
Круговая диаграмма дает нам представление о долях отдельных
составляющих в общей сумме. Из нее мы выясняем, что
«Х»
«Б»,
«С»,
«Ш» .
Теперь рассмотрим утверждения:
1. Не могут, так как «С»=25 а бейсболок 20.
2. Не могут, так как панам 35, а «Б» и
«Х» меньше 20.
3. Может, так как «Ш»=50, а шляп всего 45.
4. Не может.
№8. Молодой человек решил сделать подарок
своей невесте и пришёл в ювелирный магазин. Там он обнаружил кольца
из золота, серебра и платины, каждое из которых было украшено одним
драгоценным камнем (топазом, изумрудом, алмазом или рубином). Он исследовал
соотношение количества колец с разными камнями (результаты отражены
на диаграмме I) и количество колец разных материалов (результаты отражены
на диаграмме II).
Молодой человек сделал четыре предположения:
A) Все кольца с изумрудами могут быть из золота.
Б) Среди серебряных колец найдётся хотя бы одно с изумрудом.
B) Все кольца с рубинами и алмазами могут быть платиновыми.
Г) Все золотые кольца могут быть с алмазами.
Какое из этих предположений следует из анализа обеих
диаграмм?
Пояснение.
Столбчатая диаграмма дает нам представление о численных
данных. Из нее мы выясняем, что количество колец разных материалов
45+35+20=100
Круговая диаграмма дает нам представление о долях отдельных
составляющих в общей сумме. Из нее мы выясняем, что
«P» ,=25%*100=25
«A» ,=25%*100=25
«И» .
«Т» .
Теперь рассмотрим утверждения:
1. Могут, так как «И»=33, а золотых 45.
2. Однозначно не следует из анализа обеих диаграмм.
3. Не могут, так как платиновых всего 20, а
«P»+»A»=50.
4. Не могут, так как золотых 45, а «A»=25.
№9. Молодой человек решил сделать подарок
своей невесте и пришёл в ювелирный магазин. Там он обнаружил кольца
из золота, серебра и платины, каждое из которых было украшено одним
драгоценным камнем (топазом, изумрудом, алмазом или рубином). Он исследовал
соотношение количества колец с разными камнями (результаты отражены
на диаграмме I) и количество колец разных материалов (результаты отражены
на диаграмме И).
Молодой человек сделал четыре предположения:
A) Все кольца с изумрудами не могут быть серебряными.
Б) Среди золотых и серебряных колец найдётся хотя бы
одно с рубином.
B) Все золотые кольца могут быть с топазами.
Г) Все рубины находятся в серебряных кольцах.
Какое из этих предположений следует из анализа обеих
диаграмм?
Пояснение.
Столбчатая диаграмма дает нам представление о численных
данных. Из нее мы выясняем, что количество колец разных материалов
45+35+20=100
Круговая диаграмма дает нам представление о долях отдельных
составляющих в общей сумме. Из нее мы выясняем, что
«P» ,=25%*100=25
«A» ,=25%*100=25
«И» .
«Т» .
Теперь рассмотрим утверждения:
1. Могут, так как «И»=33, а серебряных 35.
2. Найдется, так как платиновых всего 20, а
«Р»=25, следовательно, 5 колец либо золотые, либо серебрянные.
3. Не могут, так как золотых 45, а «Т»=17.
4. Однозначно не следует из анализа обеих диаграмм.
№10. Все ученики старших классов (с 9–го по
11–й) участвовали в школьной спартакиаде. По результатам соревнований
каждый из них получил от 0 до 3–х баллов. На диаграмме I отражено распределение
учеников по классам, а на диаграмме II – количество учеников, набравших
баллы от 0 до 3–х. На обеих диаграммах каждый ученик учтён только один
раз.
Имеются четыре утверждения:
А) Среди учеников 9–го класса есть хотя бы один, кто набрал
0 баллов.
Б) Все 11–классники набрали больше 0 баллов.
В) Все ученики 11–го класса могли набрать ровно один
балл.
Г) Среди учеников 10–го класса есть хотя бы один, кто набрал
2 балла.
Какое из этих утверждений следует из анализа обеих диаграмм?
Пояснение.
Столбчатая диаграмма дает нам представление о численных
данных. Из нее мы выясняем, что всего учеников
45+30+20+110
Круговая диаграмма дает нам представление о долях отдельных
составляющих в общей сумме. Из нее мы выясняем, что
«9 класс»,=50%=55
«11 класс»,
«10 класс» .
Теперь рассмотрим утверждения:
A)Нельзя однозначно утверждать из анализа обеих диаграмм
Б)Нельзя однозначно утверждать из анализа обеих диаграмм
В)Да, могли, т.к. 11-классников 18, а учеников, набравших
один балл 30.
Г)Нельзя однозначно утверждать из анализа обеих диаграмм
Электронные таблицы и диаграммы
№1. Дан фрагмент электронной таблицы:
|
A |
B |
C |
|
|
1 |
4 |
2 |
|
|
2 |
=2*(A1–C1) |
=(2*B1+A1)/4 |
=C1-1 |
Какое целое число должно быть записано в ячейке C1,
чтобы построенная после выполнения вычислений диаграмма по значениям
диапазона ячеек A2:С2 соответствовала рисунку?
Пояснение.
По рисунку видно, что значения всех трёх ячеек диапазона
A2:С2 равны. По данным таблицы найдём значение B2: B2 = (2 * 2 + 4) / 4 =
2.
Выразим С1 из значения С2: С1 = С2 + 1 = B2 + 1 = 2 + 1
= 3.
Ответ: 3.
Источник: Яндекс: Тренировочная работа ЕГЭ по информатике. Вариант 1.
№2. Дан фрагмент электронной таблицы:
|
A |
B |
C |
|
|
1 |
4 |
2 |
|
|
2 |
=A1+C1 |
=B1+A1 |
=3*C1 |
Какое целое число должно быть записано в ячейке C1,
чтобы построенная после выполнения вычислений диаграмма по значениям
диапазона ячеек A2:С2 соответствовала рисунку?
Пояснение.
В ячейке В2 будет значение 6. Из диаграммы следует,
что значения в ячейках равны между собой. Следовательно, из того, что
6=3*C1 => C1= 2.
№3.
Дан фрагмент электронной таблицы.
|
A |
B |
C |
|
|
1 |
2 |
4 |
|
|
2 |
= (B1 – A1)/2 |
= 2 – A1/2 |
= (C1 – A1)*2 – 4 |
Какое целое число должно быть записано в ячейке C1,
чтобы построенная после выполнения вычислений диаграмма по значениям
диапазона ячеек A2 : С2 соответствовала рисунку? Известно, что все
значения диапазона, по которым построена диаграмма, имеют один и
тот же знак.
Пояснение.
В ячейке А2 будет значение 1. В ячейке В2 будет
значение 1. Из диаграммы следует, что значения в ячейке С2 в
2 раза больше. Следовательно, из того, что 2 = (C1 – A1)*2 – 4, следует,
что ответ 5.
№4. Дан фрагмент электронной таблицы:
|
A |
B |
C |
|
|
1 |
2 |
=A1+1 |
|
|
2 |
=C1-B1 |
=(3*B1+C1)/3 |
=B2+A1 |
Какое число должно быть записано в ячейке B1, чтобы построенная
после выполнения вычислений диаграмма по значениям диапазона ячеек
A2:С2 соответствовала рисунку? Известно, что все значения диапазона,
по которым построена диаграмма, имеют один и тот же знак.
Пояснение.
В ячейке С1 будет значение 3. С1 =
3, А1 = 2, следовательно В2 = В1 +
1, С2 = В2 + 2 = В1 + 3. Следовательно,
B2не равно С2, то есть, одно из них (судя по диаграмме)
больше другого в 2 раза. Решим эти уравнения последовательно для В2 =
2С2 и С2 = 2В2. В первом случае В1 =
-5, А2 = 8, В2 = −4, C2 = −2.
Это не соответствует диаграмме. Во втором случае В1 =
1, А2 = В2 = 2, C2 = 4. Этот вариант
соответствует диаграмме, следовательно, правильный ответ — 1.
№5. Дан фрагмент электронной таблицы:
|
A |
B |
C |
|
|
1 |
2 |
1 |
|
|
2 |
=C1-B1*5 |
=(B1+C1)/A1 |
=C1-5 |
Какое число должно быть записано в ячейке С1, чтобы построенная
после выполнения вычислений диаграмма по значениям диапазона
ячеек А2:С2 соответствовала рисунку?
Известно, что все значения диапазона, по которым построена
диаграмма, имеют один и тот же знак.
Пояснение.
По рисунку видно, что значения всех трёх ячеек диапазона
A2:С2 равны. Приравняем значения ячеек А2 и В2, решим уравнение: C1 − B1
* 5 = (B1 + C1) / A1, из него C1 = 11 при А1 равном 2, В1 равном 1.
Ответ: 11.
№6. Дан фрагмент электронной таблицы:
|
A |
B |
C |
|
|
1 |
2 |
1 |
|
|
2 |
=C1-B1*3 |
=(B1+C1)/A1 |
=C1-3 |
Какое число должно быть записано в ячейке С1, чтобы построенная
после выполнения вычислений диаграмма по значениям диапазона
ячеек А2:С2 соответствовала рисунку?
Известно, что все значения диапазона, по которым построена
диаграмма, имеют один и тот же знак.
Пояснение.
По рисунку видно, что значения всех трёх ячеек диапазона
A2:С2 равны. Приравняем значения ячеек А2 и В2, решим уравнение: C1 − B1
* 3 = (B1 + C1) / A1, из него C1 = 7 при А1 равном 2, В1 равном 1.
Ответ: 7.
№7.
Дан фрагмент электронной таблицы.
|
A |
B |
C |
|
|
1 |
5 |
=A1*2 |
|
|
2 |
=(B1-A1)/2 |
=B1-C1 |
=B2+A1 |
Какое число должно быть записано в ячейке В1, чтобы построенная
после выполнения вычислений диаграмма по значениям диапазона
ячеек А2:С2 соответствовала рисунку?
Известно, что все значения диапазона, по которым построена
диаграмма, имеют один и тот же знак.
Пояснение.
В ячейке С1 будет значение 10. С1 =
10, А1 = 5, следовательно, В2 = В1 −
10, С2 = В2 + 5 = В1 − 5. Поэтому
B2 не равно С2, одно из них, судя по диаграмме,
больше другого в 2 раза.
Решим эти уравнения последовательно для В2 =
2С2 и С2 = 2В2. В первом случае: В1 =
−5, А2 = 8, В2 = −4, C2 = 5.
Это не соответствует диаграмме. Во втором случае: В1 =
15, А2 = В2 = 5, C2 = 10. Этот
вариант соответствует диаграмме, следовательно, правильный ответ
— 15.
№8. Дан фрагмент электронной таблицы
|
A |
B |
C |
|
|
1 |
2 |
=A1*4 |
|
|
2 |
=b1/A1 |
=C1/B1 |
=B2+A1 |
Какое число должно быть записано в ячейке B1, чтобы построенная
после выполнения вычислений диаграмма по значениям диапазона
ячеек A2:C2 соответствовала рисунку?
Известно, что все значения диапазона, по которым построена
диаграмма, имеют один и тот же знак.
Пояснение.
Посчитаем значения в тех клетках, в которых это возможно.
|
A |
B |
C |
|
|
1 |
2 |
8 |
|
|
2 |
=B1/2 |
=8/B1 |
=8/B1+2 |
Из диаграммы видно, что две ячейки должны быть равны
друг другу. B2 не равно C2 значит, A2 = B2, а значение в ячейке C2 в два
раза больше.
Таким образом: B1/2 = 8/B1, B1 = 4.
№9. Дан фрагмент электронной таблицы:
|
A |
B |
C |
|
|
1 |
5 |
=A1*2 |
|
|
2 |
=B1/5 |
=A1/B1 |
=B2+C1/10 |
Какое число должно быть записано в ячейке B1, чтобы построенная
после выполнения вычислений диаграмма по значениям диапазона
ячеек A2:C2 соответствовала рисунку?
Известно, что все значения диапазона, по которым построена
диаграмма, имеют один и тот же знак.
Пояснение.
Вычислим значения в тех клетках, в которых это возможно.
|
A |
B |
C |
|
|
1 |
5 |
10 |
|
|
2 |
=B1/5 |
=5/B1 |
=5/B1+1 |
Из диаграммы видно, что две ячейки должны быть равны
друг другу, а значение в ячейке C2 в два раза больше. Поскольку B2 не
равно C2, имеем B1/5 = 5/B1, B1 = 5 и B1 = −5. Поскольку по условию все значения
диапазона, по которым построена диаграмма, имеют один и тот же знак,
ответ 5.
№10.
Дан фрагмент электронной таблицы:
|
A |
B |
C |
|
|
1 |
2 |
44 |
|
|
2 |
=С1 − В1*В1*5 |
=(В1*В1+С1)/А1 |
=C1−20 |
Какое целое число должно быть записано в ячейке B1,
чтобы построенная после выполнения вычислений диаграмма по значениям
диапазона ячеек A2:С2 соответствовала рисунку? Известно, что все
значения диапазона А1 :С2 имеют один и тот же знак.
Пояснение.
Преобразуем таблицу:
|
A |
B |
C |
|
|
1 |
2 |
44 |
|
|
2 |
=44 − В1·В1·5 |
=В1·В1/2+22 |
44−20 |
Из диаграммы следует, что значения в ячейках равны
между собой. Следовательно, из того, что
В1·В1/2 + 22 = 24, В1 = 2, либо
В1 = −2. Все значения диапазона А1 :С2 имеют один и тот же знак,
следовательно, ответ 2.
Светило науки — 768 ответов — 0 раз оказано помощи
Ответ:
На фото и в прикреплённом файле.
Объяснение:
1. Создаём таблицу строго как на фото. Форматирование и формат данных также как на фото (для данных в виде цифр используем «формат с разделениями», а также убираем лишние нули после запятой).
2. В ячейке A2 вписываем сегодняшнюю дату с помощью формулы: =СЕГОДНЯ().
3. В ячейке F7 вписываем формулу: =СУММ(B7:E7) для расчёта всей выручки всего. Протягиваем её вниз до F10.
4. В ячейке B12 вписываем формулу: =СУММ(B7:B10) для расчёта суммы по одному направлению (РАО-ЕС, Лукойл и т.д.), протягиваем формулу до F12.
5. В ячейке B13 вписываем формулу: =СРЗНАЧ(B7:B10) для расчёта среднего значения по одному направлению (РАО-ЕС, Лукойл и т.д.), протягиваем формулу до F13.
6. В ячейке B14 вписываем формулу: =МАКС(B7:B10) для расчёта максимального значения по одному направлению (РАО-ЕС, Лукойл и т.д.), протягиваем формулу до F14.
7. В ячейке B15 вписываем формулу: =МИН(B7:B10) для расчёта минимального значения по одному направлению (РАО-ЕС, Лукойл и т.д.), протягиваем формулу до F15.
8. В ячейке G7 вписываем формулу: =F7/$F$12 для расчёта процента от общей выручки, протягиваем формулу до G10.
9. Выставляем процентный формат для диапазона G7:G10.
10. Так как по условию не сказано, в каком формате должна быть представлена диаграмма, делаем всё самостоятельно. Выделяем диапазон A5:F10, вставляем линейчатую диаграмму на основе этих данных. Готово!

Урок посвящен тому, как решать 3 задание ЕГЭ по информатике про базы данных
Содержание:
- Объяснение заданий 3 ЕГЭ по информатике
- Базы данных
- Файловая система
- Сравнение строковых данных
- Решение заданий 3 ЕГЭ по информатике
- Задания с базами данных
- Задания прошлых лет для тренировки
- Задания для тренировки
- Задания со сравнением строковых данных
- Задания с файлами и масками файлов
3-е задание: «Реляционные базы данных»
Уровень сложности
— базовый,
Требуется использование специализированного программного обеспечения
— нет,
Максимальный балл
— 1,
Примерное время выполнения
— 3 минуты.
Проверяемые элементы содержания: Знание о технологии хранения, поиска и сортировки информации в реляционных базах данных
До ЕГЭ 2021 года — это было задание № 4 ЕГЭ
* Некоторые изображения страницы взяты из материалов презентации К. Полякова
Для решения задания 3 ЕГЭ необходимо рассмотреть тему предыдущего урока — структуризация данных (деревья).
Иногда также попадаются задания, которые требуют знаний основ алгебры логики.
Базы данных
База данных – это хранилище больших объемов данных некоторой предметной области, организованное в определенную структуру, т.е. хранящихся в упорядоченном виде.
Задания ЕГЭ в основном связаны с табличными базами данных, поэтому мы их кратко и рассмотрим.
Данные в табличных БД представлены, соответственно, в виде таблицы.
Строки таблицы носят название записи, а столбцы — поля:
- Абсолютно все поля должны быть снабжены уникальными именами. В примере: Фамилия, Имя, Адрес, Телефон.
- Поля имеют различные типы данных, в зависимости от их содержимого (например, символьный, целочисленный, денежный и т.п.).
- Поля могут быть обязательными для заполнения или нет.
- Таблица может иметь безграничное количество записей.
Ключевое поле – это поле, которое однозначно определяет запись.
В таблице не может быть двух и более записей с одинаковым значением ключевого поля (ключа).
- Для выбора ключевого поля берутся какие-либо уникальные данные об объекте: например, номер паспорта человека (второго такого номера ни у кого нет).
- Если в таблице не предусмотрены такие уникальные поля, то создается так называемый суррогатный ключ — поле (обычно ID или Код) с уникальными номерами — счетчик — для каждой записи в таблице.
Реляционная база данных – это совокупность таблиц, которые связываются между собой (между которыми устанавливаются отношения). Связь создается с помощью числовых кодов (ключевых полей).
Реляционная БД «Магазин»
Положительное в реляционных БД:
- исключено дублирование информации;
- если изменяются какие-либо данные, к примеру, адрес фирмы, то достаточно изменить его только в одной таблице — Продавцы;
- защита от неправильного ввода (или ввода с ошибками): можно выбрать (как бы ввести) только фирму, которая есть в таблице Продавцы;
- Для удобства осуществления поиска в базе данных часто создается специальная таблица Индексы.
- Индекс – это специальная таблица, предназначенная для осуществления быстрого поиска в основной таблице по выбранному столбцу.
Последовательность выполнения логических операций в сложных запросах:
- сначала выполняются отношения, затем – «И», потом – «ИЛИ». Чтобы изменить порядок выполнения используются скобки.
Индексы
Файловая система
* тема с масками скорее всего не будет представлена на ЕГЭ 2021 года
- файлы на диске хранятся в так называемых каталогах или папках;
- каталоги организованы в иерархическую структуру — дерево каталогов;
- главный каталог диска называется корневым каталогом и обозначается буквой логического диска, за которой следует двоеточие и знак «» (обратный слэш); например, A: – это обозначение корневого каталога диска А.
- каждый каталог (кроме корневого) имеет один единственный «родительский» каталог – это тот каталог, внутри которого и располагается данный каталог
- полный адрес каталога – это перечисление всех каталогов, в которые нужно войти, чтобы попасть в данный каталог (начиная с корневого каталога диска); например
- полный адрес файла состоит из адреса каталога, в котором он находится, символа
и имени файла, например - маска — выделение группы файлов по их именам; имена этих файлов имеют общие свойства, например, одинаковое расширение
- в масках, кроме стандартных символов используются два специальных символа: звездочка «*» и знак вопроса «?»;
- звездочка «*» обозначает любое количество любых символов, в том числе, может обозначать 0 символов;
- знак вопроса «?» обозначает ровно один любой символ.
Дерево каталогов
С:USERBINSCHOOL — полный путь каталога SCHOOL
Полный путь файла
Примеры масок файлов
Сравнение строковых данных
В задачах 3-го типа часто приходится сравнивать строковые значения. Посмотрим, как правильно это делать:
Любой символ всегда больше пустого:
Егифка ©:
Решение заданий 3 ЕГЭ по информатике
Плейлист видеоразборов задания на YouTube:
Задание демонстрационного варианта 2022 года ФИПИ
Задания с базами данных
3_1 new:
Задание выполняется с использованием прилагаемых файлов
В файле 3-2.xls приведён фрагмент базы данных «Рейсы» о рейсах самолетов. База данных состоит из одной таблицы. Таблица «Рейсы» содержит записи о городах отправления и прибытия, и также номер борта, совершающего рейс. На рисунке приведена схема данных.
Используя информацию из приведённой базы данных, определите сколько рейсов совершил борт 128 таких, что Москва была одним из концов маршрута — городом отправления или городом прибытия. В ответе запишите только число.
✍ Решение:
- Задание можно выполнить использую опцию Фильтр в Excel.
- Выделим полностью первую строку и применим к ней фильтр (меню Данные — Фильтр).
- В фильтре для столбца
Dвыбираем сначала Выделить всё (чтобы отменить все выделения), а затем — только значение128: - Для столбца
Bаналогичным образом выбираемМосква: - Получаем в результате 3 записи:
- Отменяем фильтр для столбца
Bи применяем его для столбцаС(Москва): - Получаем также 3 записи:
3 + 3 = 6
Ответ: 6
3_2 new:
Задание выполняется с использованием прилагаемых файлов
В файле 3-1.xls приведён фрагмент базы данных «Рейсы» о движении грузов на базе. База данных состоит из одной таблицы. Таблица «Рейсы» содержит записи о водителе, объеме перевезенного груза в килограммах и характере перевозки («привоз» на базу или «вывоз» с базы). На рисунке приведена схема данных.
Используя информацию из приведённой базы данных, определите на сколько килограммов отличается суммарное количество вывезенных и привезенных Ивановым грузов. В ответе запишите только число.
✍ Решение:
- Задание можно выполнить использую опцию Фильтр в Excel.
- Выделим полностью первую строку и применим к ней фильтр (меню Данные — Фильтр).
- В фильтре для столбца
Bвыбираем сначала Выделить всё (чтобы отменить все выделения), а затем — значениеИванов. - Для столбца
Dаналогичным образом выбираемПривоз. - Полностью выделяем весь столбец
С(Объем груза) отфильтрованной таблицы. В нижней части окна Excel смотрим сведения по выделенным ячейкам: - Запоминаем сумму (то же самое можно сделать, выполнив действие автосумма, к примеру).
- Теперь для столбца
Dаналогичным образом выбираемВывоз. - Полностью выделяем весь столбец
Сотфильтрованной таблицы. В нижней части окна Excel смотрим сведения по выделенным ячейкам. Получаем значение 680096. - Вычитаем полученные значения с помощью калькулятора или формулы в Excel. В результате имеем:
680096 - 668372 = 11724
Ответ: 11724
3_3 new:
Задание выполняется с использованием прилагаемых файлов
В файле 3-1.xls приведён фрагмент базы данных «Рейсы» о движении грузов на базе. База данных состоит из одной таблицы. Таблица «Рейсы» содержит записи о водителе, объеме перевезенного груза в килограммах и характере перевозки («привоз» на базу или «вывоз» с базы). На рисунке приведена схема данных.
Используя информацию из приведённой базы данных, определите сколько раз Уточкин и Сидоров вывезли с базы грузы объемом не менее 1500 кг и не более 2000 кг. В ответе запишите только число.
✍ Решение:
- Задание можно выполнить использую опцию Фильтр в Excel.
- Выделим полностью первую строку и применим к ней фильтр (меню Данные — Фильтр).
- В фильтре для столбца
Bвыбираем сначала Выделить всё (чтобы отменить все выделения), а затем — значенияСидоровиУточкин. - Для столбца
Свыбираем в Фильтре Числовые фильтры — Между …. В открывшемся окне настраиваем диапазон: - Теперь для столбца
Dаналогичным образом выбираемВывоз. - Полностью выделяем весь столбец
С(Объем груза) отфильтрованной таблицы. В нижней части окна Excel смотрим сведения по выделенным ячейкам: - Результат 107.
Ответ: 107
3_4 new:
Задание выполняется с использованием прилагаемых файлов
В файле 3-4.xls приведён фрагмент базы данных «Родственники» о родственных отношениях между людьми. База данных состоит из двух таблиц. Таблица «Люди» содержит записи о людях — Фамилия ИО, пол («м» или «ж») и город рождения. Таблица «Родственные связи» содержит информацию о родительских связях — ID родителя из таблицы «Люди» и ID ребенка и той же таблицы. На рисунке приведена схема базы данных.
Используя информацию из приведённой базы данных, укажите количество людей, у которых в базе данных указан только один родитель. В ответе запишите только число.
✍ Решение:
-
✎ Решение в Excel с помощью фильтров:
- Если у ребенка только один родитель, то в таблице Родственные связи в столбце ID ребенка для него будет только одно значение (дважды не может быть).
- Таким образом, необходимо отфильтровать значения этого столбца, выделив только уникальные ячейки (не повторяющиеся). Для этого выделите полностью столбец
B, затем в меню Главная — Условное форматирование — выберите Правила выделения ячеек — Повторяющиеся значения. В открывшемся окошке в выпадающем списке выберите Уникальные. Щелкните Ок. Уникальные ячейки должны подсветиться указанным цветом. - Затем выберите Фильтр для этого же столбца (меню Данные — Фильтр). В окошке фильтра выберите Фильтр по цвету — указанный цвет. Остались только выделенные цветом ячейки.
- Выделите все ячейки столбца и в нижней части окна Excel смотрим сведения по выделенным ячейкам:
✎ Решение в Excel с помощью формул:
Ответ: 112
3_5 new:
Задание выполняется с использованием прилагаемых файлов
В файле 3-4.xls приведён фрагмент базы данных «Родственники» о родственных отношениях между людьми. База данных состоит из двух таблиц. Таблица «Люди» содержит записи о людях — Фамилия ИО, пол («м» или «ж») и город рождения. Таблица «Родственные связи» содержит информацию о родительских связях — ID родителя из таблицы «Люди» и ID ребенка и той же таблицы. На рисунке приведена схема базы данных.
Используя информацию из приведённой базы данных, укажите количество людей, родители которых родились в одном городе. В ответе запишите только число. В ответе запишите только число.
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
✍ Решение:
- Задача усложняется тем, что сведения по детям и их родителям мы имеем в одной таблице — Родственные связи, а города — в другой — Люди. То есть для вычисления необходимо
город рожденияродителя добавить в таблицуРодственные связи. - Для этого необходимо у каждого родителя смотреть ID_родителя в таблице Родственные связи и, затем, искать этот ID и соответствующий ему город в таблице Люди.
- Для поиска нам необходима функция
ИНДЕКС: - В нашем случае мы будем искать в массиве данных таблицы Люди ячейку Город рождения: по строке со значением
ID родителя(т.к. номер строки совпадает сID) и столбцу №4 в нашем массиве данных. Установите курсор в ячейкуD2таблицыРодственные связи:
ИНДЕКС — возвращает значение ячейки на пересечении конкретных строки и столбца.
=ИНДЕКС (Люди!A$2:D$1001;A2;4)
$, чтобы при копировании формулы значение не менялось.D.B, выделив только повторяющиеся ячейки (так как нам необходимо оставить только тех детей, у которых указаны оба родителя, а не один). Для этого выделите полностью столбец B, затем в меню Главная — Условное форматирование — выберите Правила выделения ячеек — Повторяющиеся значения. В открывшемся окошке в выпадающем списке выберите Повторяющиеся. Щелкните Ок. Повторяющиеся ячейки должны подсветиться указанным цветом.D будем выводить значение 1, если для родителей одного и того же ребенка совпадают, и 0 если не совпадают:Ячейка D3:
=ЕСЛИ(И(B3=B2;C3=C2);1;0)
Сумма: 16Ответ: 16
3_6 new: :
Задание выполняется с использованием прилагаемых файлов
В файле 3-4.xls приведён фрагмент базы данных «Родственники» о родственных отношениях между людьми. База данных состоит из двух таблиц. Таблица «Люди» содержит записи о людях — Фамилия ИО, пол («м» или «ж») и город рождения. Таблица «Родственные связи» содержит информацию о родительских связях — ID родителя из таблицы «Люди» и ID ребенка и той же таблицы. На рисунке приведена схема базы данных.
Используя информацию из приведённой базы данных, укажите максимальное количество детей у одного родителя. В ответе запишите только число.
✍ Решение:
-
Логика решения такова: сколько раз один и тот же родитель встречается в таблице
- В таблице
Родственные связииз диапазона ячеекID родителясчитаем количество повторов каждого родителя:
Родственные связи, соответственно, столько у него и детей. Таким образом, необходимо посчитать, сколько раз встречается каждый родитель; затем найти максимальное из этих значений.✎ Способ 1:
Ячейка D2:
=СЧЁТЕСЛИ(A:A;A2)
D.D:= МАКС(D:D)
✎ Способ 2:
Ячейка D2:
=МОДА(A:A)
ID родителя ищем значение 165 и считаем количество отфильтрованных строк.Ответ: 4
Задания прошлых лет для тренировки
3_6:
Ниже представлены две таблицы из базы данных. Каждая строка таблицы 2 содержит информацию о ребёнке и об одном из его родителей. Информация представлена значением поля ID в соответствующей строке таблицы 1.
Определите на основании приведённых данных фамилию и инициалы племянника Геладзе П.П.
Варианты ответа:
1) Вильямс С.П.
2) Геладзе П.И.
3) Леоненко М.С.
4) Леоненко С.С.
Подобные задания для тренировки
✍ Решение:
Подробное решение задания ГВЭ смотрите в видеоуроке:
📹 Видеорешение на RuTube здесь
3_1:
Ниже представлены две таблицы из базы данных. Каждая строка Таблицы 2 содержит информацию о ребенке и об одном из его родителей. Информация представлена значением поля ID в соответствующей строке Таблицы 1.
Определите на основании приведенных данных суммарное количество прямых потомков (т.е. детей, внуков, правнуков) Иоли А.Б.

Подобные задания для тренировки
✍ Решение:
- В первой таблице находим Иоли А.Б, ей соответствует ID 84
- Все остальное решение будет связано со второй таблицей: будем в ней искать ID родителя и соответствующего ему ID ребенка.
- Выполним задание при помощи дерева, подробно рассматривая каждый уровень иерархии: сначала детей родителя 84, затем по полученным ID — найдем внуков Иоли А.Б, затем правнуков и т.д.
- Посчитаем количество потомков: их 7
Результат: 7
Также можно посмотреть видео решения 3 задания ЕГЭ по информатике:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
3_2:
Ниже представлены две таблицы из базы данных, в которых собраны сведения о сотрудниках некоторой организации. Каждая строка Таблицы 2 содержит информацию о сотруднике структурного подразделения и о его непосредственном руководителе, который, в свою очередь, является непосредственным подчиненным руководителя более высокого уровня. Информация представлена значением поля ID в соответствующей строке Таблицы 1.
Определите на основании приведенных данных суммарное количество подчиненных (непосредственных и через руководителей более низкого уровня) Сидорова Т.И.

✍ Решение:
- В первой таблице находим Сидорова Т.И., ему соответствует ID 17
- Все остальное решение будет связано со второй таблицей: будем в ней искать ID руководителя и соответствующих ему ID подчиненных.
- Выполним задание при помощи дерева, подробно рассматривая каждый уровень иерархии: сначала непосредственных подчиненных руководителя 17, затем по полученным ID — найдем подчиненных подчиненных и т.д.
- Посчитаем количество подчиненных: 9
Результат: 9
Можете ознакомиться с решением данного 3 задания ЕГЭ по информатике из видеоурока:
📹 YouTube здесь
3_4: Демоверсия ЕГЭ 2018 информатика (ФИПИ):
Ниже представлены два фрагмента таблиц из базы данных о жителях микрорайона. Каждая строка таблицы 2 содержит информацию о ребёнке и об одном из его родителей. Информация представлена значением поля ID в соответствующей строке таблицы 1.
Определите на основании приведённых данных, у скольких детей на момент их рождения матерям было больше 22 полных лет. При вычислении ответа учитывайте только информацию из приведённых фрагментов таблиц.
Подобные задания для тренировки
✍ Решение:
- Из второй таблицы выпишем ID всех детей и соответствующих им ID родителей. Найдем выбранные ID родителей и детей в первой таблице и оставим только те ID родителей, которые соответствуют женскому полу. Выпишем также год рождения:
ID 23: 1968 - 1941 = 27 ! 24: 1993 - 1967 = 26 ! 32: 1960 - 1941 = 19 33: 1987 - 1960 = 27 ! 35: 1965 - 1944 = 21 44: 1990 - 1960 = 30 ! 52: 1995 - 1967 = 28 !
>22).Результат: 5
Подробное решение данного 3 (раньше № 4) задания из демоверсии ЕГЭ 2018 года смотрите на видео:
Задания для тренировки
Задания со сравнением строковых данных
Рассмотрим одно на первый взгляд простое, но с «ловушкой», задание ЕГЭ:
3_3:
В таблице представлены несколько записей из базы данных «Расписание»:
| № | Учитель | День недели | Номер урока | Класс |
|---|---|---|---|---|
| 1 | Айвазян Г.С. | понедельник | 3 | 8А |
| 2 | Айвазян Г.С. | понедельник | 4 | 9Б |
| 3 | Айвазян Г.С. | вторник | 2 | 10Б |
| 4 | Михальчук М.С. | вторник | 2 | 9А |
| 5 | Пай С.В. | вторник | 3 | 10Б |
| 6 | Пай С.В. | среда | 5 | 8Б |
Укажите номера записей, которые удовлетворяют условию
Номер_урока > 2 И Класс > ‘8А’
1) 1, 6
2) 2, 6
3) 2, 5, 6
4) 1, 2, 5, 6
С примером решения данного 3 задания ознакомьтесь из видеоурока:
📹 YouTube здесь
Задания с файлами и масками файлов
* тема с масками скорее всего не будет внесена в ЕГЭ 2021 года
3_5:
Для групповых операций с файлами используются маски имён файлов.
Символ «?» (вопросительный знак) означает ровно один произвольный символ.
Символ «*» (звёздочка) означает любую последовательность символов произвольной длины, в том числе «*» может задавать и пустую последовательность.
В каталоге находится 8 файлов:
declaration.mpeg delaware.mov delete.mix demo.mp4 distrib.mp2 otdel.mx prodel.mpeg sdelka.mp3
Определите, по какой из перечисленных масок из этих 8 файлов будет отобрана указанная группа файлов:
otdel.mx prodel.mpeg
Варианты ответа:
1) *de?.m*
2) ?de*.m?
3) *de*.mp*
4) de*.mp?
Подобные задания для тренировки
✍ Решение:
Решение задания 3 ГВЭ по информатике можно посмотреть на видео:
Валовая прибыль – это сумма рассчитана после вычитания расходов на себестоимость от доходов. Другими словами, общая прибыль – разница между выручкой и себестоимостью. В общую себестоимость товара включены разные виды расходов: на производство, на реализацию, операционные расходы и много других посреднических расходов. Чтобы рассчитать валовую прибыль, необходимо просто вычитать валовые расходы себестоимости от валового дохода.
Формула расчета валовой прибыли в процентах
Валовая прибыль в процентах рассчитывается путем деления валовой прибыли на общий доход и умножается на 100.
На рисунке представлен финансовый отчет определенной производственной фирмы:
Валовая прибыль находится в ячейке B4, а процентная валовая прибыль в ячейке C4: =B4/$B$2
Формула расчета валовой прибыли просто вычитает значение ячейки B3 от B2. В формуле вычисления валовой прибыли в процентах значение ячейки B4 разделено на значение в $B$2:
Обратите внимание здесь используется процентный формат ячеек – это значит не нужно умножать на 100. Такой же результат мы получим по выше описанной формуле =B4/B2*100, но здесь не используем процентный формат ячеек.
Важно отметить, что установлена абсолютная ссылка на ячейку $B$2 о чем свидетельствуют символы значка доллара в самой ссылке. Благодаря абсолютной ссылке можно свободно копировать формулу в другие строки отчета с целью расчета доли от общего дохода в процентах, которую занимает та или иная статья расходов и доходов. Так приблизительно выглядит поверхностный анализ расчета доходов и расходов фирмы.
Формула расчета процента наценки в Excel
Наценка очень часто отождествляется с процентной валовой прибылью, но является нечто другим. Наценка – это процентная сумма, добавленная к себестоимости продукта с целью рентабельного ценообразования для его реализации. Другими словами, сумма в процентах на которую повышена цена с целью получения прибыли и возмещения затрат не связанными с расходными на себестоимость. Ниже на рисунке представлен отчет по продажам товара с наценкой и рассчитанной валовой прибылью от продаж.
Наценка рассчитывается путем деления цены на расходы и от результата вычитается число 1:
Устанавливая наценку в размере 32% получаем валовую прибыль в процентах 24%. То есть как описано выше в предыдущем примере =B8/B6. Чтобы определить размер наценки покрывающую процентную валовую прибыль в 32% (как в столбце D) используйте следующую формулу:
Выше приведенная формула свидетельствует нам доказательством того, чтобы получить валовую прибыль равную 32% нам необходимо установить наценку в 47% с учетом всех доходов и расходов.
Интересный факт! Главное отличие процентной валовой прибыли от наценки заключается в формуле вычисления. Разницу очень легко заметить в этих двух показателях по их сути – валовая прибыль никогда не будет равна или превышать 100% в отличии от наценки. Для наглядного доказательства приведем простой пример, умножим цену на 10 000:
В те времена, когда все нужно было еще делать серым карандашом на белом листе бумаги уже тогда нашли свое применение вычислительные таблицы в бухгалтерской и финансовой деятельности. Хоть программа Excel в меру своего развития стала чем-то больше чем просто электронная вычислительная таблица ее табличные функции являются все еще незаменимым инструментом в бизнесе. Существует много формул в Excel часто используемых в бухгалтерии, финансах и других отраслях бизнеса.
Вариант задания
1. Создайте в табличном процессоре Excel таблицу 1 и заполните ее исходными данными. Автоматически пронумеруйте столбцы таблицы и показатели в столбце 1. Выполните следующие расчеты:
- Валовая прибыль = Торговые доходы – Торговые расходы;
- Общие затраты определяются как сумма расходов на зарплату, на рекламу и накладных расходов;
- Производственная прибыль = Валовая прибыль – Общие за-траты;
- Удельная валовая прибыль = Производственная прибыль / Торговые доходы;
- Итого за год определяется как сумма квартальных данных.
Таблица 1. Расчет прибыли фирмы, тыс. руб.
Расходы на зарплату
Расходы на рекламу
Удельная валовая прибыль
2. На втором листе создайте таблицу 2. Столбец 2 заполните на основании ссылки на соответствующую ячейку таблицы 1. На основании данных таблицы 1 Рассчитайте структуры затрат фирмы по кварталам и году в целом по следующей формуле: Расходы / Общие затраты * 100. Результаты расчетов округлить до одного знака после запятой.
Таблица 2. Структура затрат фирмы по кварталам, %
Расходы на зарплату
Расходы на рекламу
3. На отдельном листе по данным таблицы 1 (№ п/п 1, 2, 3 и столбцы 3, 4, 5 и 6) постройте объемную гистограмму с заголовком, легендой, названием осей. 4. На отдельном листе по данным таблицы 1 (№ п/п 2, 4, 5, 6 и столбец 7) постройте объемную разрезанную круговую диаграмму с заголовком, легендой и указанием долей. 5. Каждому листу присвойте имя, отражающее содержание таблицы, например, Лист1 назовите «Прибыль_руб.». 6. Введите в нижний колонтитул факультет, курс, номер группы, свою фамилию, дату и время, имя файла.
Как при помощи Excel создать таблицу для расчета прибыли
Очень часто предпринимателям приходится производить расчет эффективности будущих операций. Для автоматизации подобных расчетов можно составить электронную таблицу. Пример упрощенной таблицы представлен на рис. 1.
Рис. 1. Таблица расчета прибыли (с числовыми данными)
В данной таблице имеются четыре области:
- Ставки налогов (область А1:В2).
- Суммы реализованных товаров, издержек и дебетового НДС (область А4:В6).
- Расчет НДС, подлежащего уплате в бюджет (область А8:В9).
- Расчет прибыли и налогов на прибыль (область А11:В14).
Заметим, что первые две области предназначены для ввода информации, а последние — для ее дальнейшей обработки. Рассмотрим формулы, введенные в область расчета (рис. 2).
Рис. 2. Таблица расчета прибыли (с формулами)
Формула для расчета налогового обязательства по НДС описывалась в этой статье. Табличный вид этой формулы следующий: =ОКРУГЛ(B4*(B1/(1+B1));2).
Формула расчета НДС, подлежащего уплате в бюджет, определяется вычитанием суммы налогового кредита из суммы налоговых обязательств (находится в ячейке В10): =В8–В6.
Валовая прибыль без НДС (формула в ячейке В12) равна разности суммы реализации и суммы налоговых обязательств: =В4–В8.
Полученную в результате реализации прибыль можно определить путем вычитания издержек из суммы валовой прибыли: =В11–В5.
Налог на прибыль равен округленному до второго разряда (до копеек) произведению прибыли на действующую ставку налога на прибыль: =ОКРУГЛ(B12*B2;2).
Чистая прибыль в результате реализации равняется разности налогооблагаемой прибыли и суммы налога на прибыль: =В12–В13.
После доработки такую таблицу можно использовать для реальных проектов. Достоинством подобных таблиц является универсальность. Изменяя ставки налогов, таблицы можно подстраивать под действующее на момент расчета законодательство. При изменении суммы реализации и издержек сразу же виден фактический результат проведения будущей и прошедших операций. Это дает возможность моделировать предстоящую деятельность по принципу «а что произойдет, если…». Такая таблица наверняка пригодится также руководителю большого предприятия, на котором ведение бухгалтерского и налогового учета автоматизировано. С ее помощью можно осуществлять элементарное планирование и контроль правильности начисления налогов и использовать в качестве обоев для Windows Phone.
Приступая к разработке таблицы, надо выяснить, где она должна использоваться и кто с ней будет работать. Оперировать с таблицей будет удобнее, если вы подберете оптимальный масштаб ее представления на экране. Excel предоставляет в ваше распоряжение несколько методов ввода информации: при помощи клавиатуры, методы копирования, методы автоматического заполнения ячеек одинаковой информацией и т. д. Вы должны освоить эти методы, для того чтобы на практике быстро выбрать лучший с учетом конкретной ситуации.
Формулы и функции — это средства, которые превращают Excel из калькулятора в электронные таблицы. Поэтому ваш уровень владения этой программой определяется тем, насколько хорошо вы освоите работу с формулами. Таблица будет нагляднее и удобнее в работе, если вы оформите ее, воспользовавшись цветом и рамками. Для данных таблицы необходимо выбрать подходящий формат представления. Неудачный выбор формата может привести к неправильной трактовке данных. Что касается практического применения полученных знаний, то вы видите, что даже на этом этапе вы уже можете выполнить расчет НДС и налога на прибыль.
Точка безубыточности за 5 минут: формула расчёта и пример таблицы в Excel
Думаю, многие уже знают, что расчёт точки безубыточности является крайне важным мероприятием при старте любого бизнеса. В моем окружении это многие прекрасно понимают. Но недавно мне поступил вопрос от читателя. Вот как мне, говорит, в дни сезонных колебаний спроса да в дни тягостного кризисного застоя сбыт свой распланировать, чтобы и на плаву остаться и конкурентов перехитрить? Секунду поразмыслив, я его воодушевил названием вполне себе конкретного способа, который может помочь принять решение не только о том как сбыт подкорректировать, но и как цены установить наиболее оптимальные. Да и хорош этот способ не только и не столько в дни ослабления спроса, а ещё до момента выхода на рынок, когда особо остро встаёт вопрос ценообразования и осознания возможности выжить на рынке вообще. И как вы уже, наверное, догадались, связан этот способ с расчётом самой настоящей точки безубыточности вашего дела. Притом не важно, чем именно вы занимаетесь: у вас свой косметический салон в оффлайне или вы занимаетесь арбитражем трафика онлайн — она всегда готова прийти к вам на помощь и сохранить уйму вашего драгоценного времени и жизненной энергии, и уберечь от заранее предопределённого провала.
Итак, что же такое точка безубыточности? Вот что нам говорит экономический букварь:
Точка безубыточности — объём производства и реализации продукции, при котором расходы будут компенсированы доходами, а при производстве и реализации каждой последующей единицы продукции предприятие начинает получать прибыль. Точку безубыточности можно определить в единицах продукции, в денежном выражении или с учётом ожидаемого размера прибыли.
Глядя на это определение, мы уже можем понять, что в результате мы получим некий объём продукции или конкретную цифру денежного оборота, при котором мы, как минимум, ничего не потеряем и останемся на рынке. Ну, а как максимум — полетим на Гоа первым же рейсом обставлять свежекупленную виллу с видом на море.
Вроде всё просто. Но чтобы не сделать ложных выводов и понять наверняка каким образом расходы компенсируются доходами, давайте разберём структуру этих самых расходов (издержек). На самом деле именно в этом месте и таится весь секрет. Всё дело в том, что всё издержки, которые мы несём в течение расчётного периода делятся на постоянные и переменные.
Переменные издержки — издержки, которые появляются при производстве каждой новой единицы продукции (оказанной услуги).
Постоянные издержки — издержки, которые практически неизменны на протяжении всего расчётного периода.
Предположим, мы печатаем людям фотографии. Каждая распечатанная фотка будет включать в себя цену бумаги и краски, что вместе будет являться переменными издержками. При этом фотографии печатает сотрудник, которому мы платим зарплату, плоттер подключён к сети электропитания, а помещение мы снимаем в аренду. И всё это не зависит от объёма печати, а, стало быть, это постоянные издержки. Вне зависимости от рода бизнеса к ним можно отнести:
- Фонд оплаты труда.
- Социальные отчисления.
- Аренда помещения (если помещение не в собственности, естессно).
- Коммунальные услуги и охрана.
- Связь (телефон, хостинг, интернет).
- Реклама.
- Прочие раходы.
Таким образом, на данном этапе мы можем сделать 2 очень важных вывода:
- С увеличением объёма производства мы увеличиваем расходы исключительно за счёт переменных издержек.
- С увеличением объёма производства величина постоянных издержек на единицу продукции снижается. Это один из элементов т.н. эффекта масштаба.
Понимая данную структуру издержек, можно легко понять, где заканчивается убыток и начинается прибыль. А для более наглядного представления взгляните на эту картинку:
Как рассчитать доход по облигациям, используя функции Excel
Excel предлагает ряд функций, используемых для вычисления различных финансовых показателей облигаций. Облигацией называется финансовый инструмент, в котором покупатель выступает в роли заимодателя, а учреждение или государство, выпустившее облигации, — в роли заемщика. Однако многие функции, связанные с облигациями, выходят за рамки материала настоящей книги. В этой статье представлены примеры некоторых наиболее распространенных функций.
Некоторые свойства облигаций являются также и аргументами функций, связанных с облигациями.
- Расчетный день. Дата, в которую долговые обязательства переходят к покупателю.
- Срок погашения. Дата, в которую заем (представленный облигацией) возвращается покупателю.
- Ставка (также называемая купоном). Процентная ставка, которую выпустивший облигацию выплачивает покупателю.
- Доходность. Норма прибыли, получаемая покупателем. Включает в себя выплаты по процентам и дисконт.
- Погашение. Выкупная стоимость ценных бумаг за 100 долларов номинальной стоимости.
- Частота. Количество выплат дивидендов за год.
Оценка облигаций
Предприятия, выпускающие ценные бумаги, устанавливают перечисленные выше показатели, основываясь на текущей рыночной конъюнктуре. Когда конъюнктура меняется, стоимость облигаций тоже изменяется.
Для примера предположим, что некоторая компания выпустила облигации с номинальной стоимостью 100 долларов, сроком погашения 10 лет и 6%-ной ставкой, выплачиваемой дважды в год.
- Если процентная ставка по кредитам растет, ставка в 6% становится не такой уж и привлекательной. Покупатели уже не захотят платить 100 долларов за облигацию — они будут их покупать за меньшую сумму.
- Если процентная ставка по кредитам падает, ставка в 6% становится привлекательной. В данном случае покупатели готовы платить больше номинальной стоимости.
Функция ЦЕНА вычисляет сумму, которую покупатели потенциально готовы заплатить за облигацию в ожидании определенного дохода. Синтаксис этой функции таков: ЦЕНА(расчетный_день;срок_погашения;ставка;доходность;погашение;частота;базис). Учитывая приведенные выше факты, инвестор, желающий получить 7,5% годовых, должен использовать следующую формулу для вычисления приемлемой цены облигации, срок погашения которой наступает через 8 лет: =ЦЕНА(СЕГОДНЯ();СЕГОДНЯ()+ДАТА(8;1;0);,06;,075;100;2).
Результатом этой формулы будет 91,10 долларов — именно такую сумму стоит заплатить за облигацию номиналом в 100 долларов с шестью процентами годовых, чтобы прибыльность составила 7,5%. Каждый год инвестор будет получать 6%*100 долларов, плюс при погашении облигации он получит дополнительную прибыль в 8,90 долларов. Эти два компонента — проценты и дисконт — формируют доходность облигаций. Фактическая дата выпуска облигации может отличаться от даты ее покупки инвестором. Облигации выпускают многие организации, так производитель кондиционеров кватро клима имеет достаточно высокую ликвидность своих ценных бумаг, которая основывается на качестве продукции.
В рассмотренном примере облигации были выпущены за два года до их покупки, следовательно, инвестор будет получать за них проценты только в течение 8 лет. Если же процентная ставка упала с момента выпуска и инвестору достаточно 5,2%, формула слегка изменится: =ЦЕНА(СЕГОДНЯ();СЕГОДНЯ()+ДАТА(8;1;0);,06;,052;100;2). При этих обстоятельствах инвестор может заплатить за стодолларовую облигацию 105,18 долларов. На рис. 11.17 эти вычисления показаны на рабочем листе.
Вычисление доходности
В предыдущем примере инвестор знал необходимую ему доходность и вычислял такую цену облигации, чтобы получить ее. Если же, наоборот, он знает цену облигации, то функция ДОХОД поможет вычислить прибыльность инвестиций. Синтаксис этой функции следующий: ДОХОД (расчетный_день;срок_погашения;ставка;цена_покупки;номинал;частота;базис).
Рис. 1. Использование функции ЦЕНА
Инвестор все еще заинтересован в покупке десятилетней облигации с 6 процентами, выплачиваемыми дважды в год, однако на этот раз он хочет заплатить всего 93,95 долларов за стодолларовую облигацию. Следующая формула вычисляет процентную ставку за восемь лет, оставшихся до даты погашения: =ДОХОД(СЕГОДНЯ();СЕГОДНЯ()+ДАТА(8;1;0);,06;93,95;100;2). Если инвестор заплатит за облигацию 93,95 долларов, то получит от своих инвестиций 7%. Если бы он заплатил за облигацию больше ста долларов, то получил бы от инвестиций меньше 6% (рис. 2).
Рис. 2. Когда цена выше номинальной стоимости облигации, прибыльность ниже купона
Решение финансовых задач в Excel. Функции ДОХОД и ИНОРМА
Рассматривается возможность приобретения облигаций трех типов, каждая из которых с номиналом в 100 руб. и сроком погашения 9.10.2007 г. Курсовая стоимость этих облигаций на дату 25.07.2005 г. составила соответственно 90, 80 и 85 руб.
Годовая процентная ставка по купонам (размер купонных выплат) составляет:
для первой облигации 8 % при полугодовой периодичности выплат;
для второй облигации – 5 % при ежеквартальной периодичности выплат;
для третьей облигации – 10 % с выплатой 1 раз в год.
Расчеты ведутся в базисе фактический/фактический.
Провести анализ эффективности вложений в покупку этих облигаций, если требуемая норма доходности составляет 15% .
Алгоритм решения задачи.
Чтобы оценить эффективность вложений в покупку каждой из облигаций, рассчитаем их годовую доходность, используя функцию ДОХОД:
ДОХОД (дата_согл; дата_вступл_в_силу; ставка; цена; погашение; частота; базис)
Для решения задачи построим на листе Excel таблицу, в ячейки которой введем исходные данные и формулы расчета требуемых величин (рис. 4.27).
Выполним также расчет доходности, непосредственно задавая значения аргументов в функции ДОХОД.
Рис. 4.27. Применение функции ДОХОД для оценки доходности облигаций
Аргументы, содержащие даты, введем с помощью функции ДАТА (можно также указывать ссылки на ячейки, содержащие даты).
Для облигации первого типа:
=ДОХОД (ДАТА(2005;7;25);ДАТА(2007;10;9);8%;90;100;2;1)= 13,36%
Для облигации второго типа:
=ДОХОД (ДАТА(2005;7;25);ДАТА(2007;10;9);5%;80;100;4;1)= 15,93%
Для облигации третьего типа:
=ДОХОД (ДАТА(2005;7;25);ДАТА(2007;10;9);10%;85;100;1;1)= 18,83%
Результаты, полученные различными способами, совпадают.
Доходность по второй и третьей облигациям (15,93% и 18,83% соответственно) выше заданной нормы (15%), а по первой облигации (13,36%) – ниже. Следовательно, целесообразно покупать облигации второго и третьего типов.
Коммерческий банк предлагает свои сберегательные сертификаты номиналом 100 000 руб. сроком на 8 месяцев. Дата соглашения – 10.01.2005 г. Цена продажи составляет 85 000 руб. Способ вычисления дня – фактический/360. Необходимо определить доход за этот период.
Алгоритм решения задачи.
Для вычисления доходности данной финансовой операции, возвращающейся в виде годовой ставки, рассчитанной по простым процентам, используем функцию ИНОРМА, которая задается следующим образом:
ИНОРМА (дата_согл; дата_вступл_в_силу; инвестиция; погашение; базис)
Исходные данные задачи представим в виде таблицы. В соответствующую ячейку введем формулу, обеспечивающую вычисление доходности сберегательного сертификата (рис. 4.28).
Для проверки правильности результата в функцию ИНОРМА введем значения аргументов в непосредственном виде:
Очень часто предпринимателям приходится производить расчет эффективности будущих операций. Для автоматизации подобных расчетов можно составить электронную таблицу. Пример упрощенной таблицы представлен на рис. 1.
Рис. 1. Таблица расчета прибыли (с числовыми данными)
В данной таблице имеются четыре области:
- Ставки налогов (область А1:В2).
- Суммы реализованных товаров, издержек и дебетового НДС (область А4:В6).
- Расчет НДС, подлежащего уплате в бюджет (область А8:В9).
- Расчет прибыли и налогов на прибыль (область А11:В14).
Заметим, что первые две области предназначены для ввода информации, а последние — для ее дальнейшей обработки. Рассмотрим формулы, введенные в область расчета (рис. 2).
Рис. 2. Таблица расчета прибыли (с формулами)
Формула для расчета налогового обязательства по НДС описывалась в этой статье. Табличный вид этой формулы следующий: =ОКРУГЛ(B4*(B1/(1+B1));2) .
Формула расчета НДС, подлежащего уплате в бюджет, определяется вычитанием суммы налогового кредита из суммы налоговых обязательств (находится в ячейке В10): =В8–В6 .
Валовая прибыль без НДС (формула в ячейке В12) равна разности суммы реализации и суммы налоговых обязательств: =В4–В8 .
Полученную в результате реализации прибыль можно определить путем вычитания издержек из суммы валовой прибыли: =В11–В5 .
Налог на прибыль равен округленному до второго разряда (до копеек) произведению прибыли на действующую ставку налога на прибыль: =ОКРУГЛ(B12*B2;2) .
Чистая прибыль в результате реализации равняется разности налогооблагаемой прибыли и суммы налога на прибыль: =В12–В13 .
После доработки такую таблицу можно использовать для реальных проектов. Достоинством подобных таблиц является универсальность. Изменяя ставки налогов, таблицы можно подстраивать под действующее на момент расчета законодательство. При изменении суммы реализации и издержек сразу же виден фактический результат проведения будущей и прошедших операций. Это дает возможность моделировать предстоящую деятельность по принципу «а что произойдет, если…». Такая таблица наверняка пригодится также руководителю большого предприятия, на котором ведение бухгалтерского и налогового учета автоматизировано. С ее помощью можно осуществлять элементарное планирование и контроль правильности начисления налогов и использовать в качестве обоев для Windows Phone.
Приступая к разработке таблицы, надо выяснить, где она должна использоваться и кто с ней будет работать. Оперировать с таблицей будет удобнее, если вы подберете оптимальный масштаб ее представления на экране. Excel предоставляет в ваше распоряжение несколько методов ввода информации: при помощи клавиатуры, методы копирования, методы автоматического заполнения ячеек одинаковой информацией и т. д. Вы должны освоить эти методы, для того чтобы на практике быстро выбрать лучший с учетом конкретной ситуации.
Формулы и функции — это средства, которые превращают Excel из калькулятора в электронные таблицы. Поэтому ваш уровень владения этой программой определяется тем, насколько хорошо вы освоите работу с формулами. Таблица будет нагляднее и удобнее в работе, если вы оформите ее, воспользовавшись цветом и рамками. Для данных таблицы необходимо выбрать подходящий формат представления. Неудачный выбор формата может привести к неправильной трактовке данных. Что касается практического применения полученных знаний, то вы видите, что даже на этом этапе вы уже можете выполнить расчет НДС и налога на прибыль.
Практическая работа № 1
Тема: Организация расчетов в табличном процессоре MS Excel.
Цели: Изучение информационной технологии использования встроенных вычислительных функций Excel для финансового анализа.
Задание 1.1. Создать таблицу финансовой сводки за неделю, произвести расчеты, построить диаграмму изменения финансового результата, произвести фильтрацию данных.
Порядок работы:
1. Откройте папку со своей фамилией. Нажмите правую кнопку мыши → Создать → Лист Microsoft Excel. Введите название → Практическая работа №1.
2. Наведите курсор в ячейку A1 и введите заголовок таблицы «Финансовая сводка за неделю (тыс. руб.)».
3. Выделите ячейки A3:D11. На вкладке Главная группе Шрифт нажмите кнопку Границы и выберите Все границы.
4. Выделите ячейки на третьей строке A3:D3. Наведите курсор на выделенные ячейки, нажмите правую кнопку мыши, в контекстном меню выберите Формат ячеек, на вкладке Число выберите Числовой формат → Текстовой; на вкладке Выравнивание выберите Выравнивание по горизонтали и вертикали → по центру, Отображение → переносить по словам; на вкладке Заливка → любой цвет и нажмите ОК.
5. Выделите ячейки B4:D11, нажмите правую кнопку мыши, в контекстном меню выберите Формат ячеек , на вкладке Число выберите Числовой формат → Денежный, Отрицательные числа – красные и нажмите ОК.
6. На третьей строке введите названия колонок таблицы — «Дни недели», «Доход», «Расход», «Финансовый результат», далее заполните таблицу исходными данными:
Краткая справка. Для ввода дней недели наберите «Понедельник» и произведите автокопирование до «Воскресенья» (левой кнопкой мыши за маркер автозаполнения в правом нижнем углу ячейки).
7. Произведите расчеты в графе «Финансовый результат» по следующей формуле: Финансовый результат = Доход — Расход, для этого в ячейке D4 наберите формулу = В4-С4.
Краткая справка. Введите расчетную формулу только для расчета по строке «Понедельник», далее произведите автокопирование формулы (так как в графе «Расход» нет незаполненных данными ячеек, можно производить автокопирование двойным щелчком мыши по маркеру автозаполнения в правом нижнем углу ячейки).
8. Рассчитайте средние значения Дохода и Расхода. Установите курсор в ячейке B11. На вкладке Главная в группе Редактирование нажмите на стрелку рядом с кнопкой Сумма и выберите Среднее и нажмите клавишу Enter.
9. Установите курсор в ячейке C11. На вкладке Главная в группе Редактирование нажмите на стрелку рядом с кнопкой Сумма и выберите Среднее и нажмите клавишу Enter или выполните автокопирование.
10. В ячейке D13 выполните расчет общего финансового результата (сумма по столбцу «Финансовый результат»). На вкладке Главная в группе Редактирование нажмите на кнопку Сумма и нажмите клавишу Enter.
11. Проведите форматирование заголовка таблицы. Для этого выделите интервал ячеек от А1 до D1, нажмите правую кнопку мыши, в контекстном меню выберите Формат ячеек, на вкладке Выравнивание выберите Выравнивание по горизонтали и вертикали → по центру, Отображение → объединение ячеек и нажмите ОК.
12. Постройте диаграмму (линейчатого типа) изменения финансовых результатов по дням недели. Для этого выделите интервал ячеек с данными финансового результата от D4 до D10. На вкладке Вставка в группе Диаграмма нажмите кнопку Линейчатая и выберите Линейчатая с группировкой.
13. Перейдите на вкладку Конструктор и в группе Данные нажмите кнопку Выбрать данные, в Подписи горизонтальной оси (категории) нажмите кнопку Изменить, выделите диапазон A4:A10 и нажмите ОК.
14. Перейдите на вкладку Конструктор и в группе Стили диаграмм выберите любой стиль.
15. Произведите фильтрацию значений дохода, превышающих 4000 р.
Краткая справка. В режиме фильтра в таблице видны только те данные, которые удовлетворяют некоторому критерию, при этом остальные строки скрыты. В этом режиме все операции форматирования, копирования, автозаполнения, Автосуммирования и т.д. применяются только к видимым ячейкам листа.
16. Установите курсор в ячейке B3. Для установления режима фильтра перейдите на вкладку Данные и в группе Сортировка и фильтр нажмите кнопку Фильтр. В заголовках полей появятся стрелки выпадающих списков. Щелкните по стрелке в заголовке поля Доход → Числовый фильтры → больше… В появившемся окне введите 4000 нажмите ОК. Произойдет отбор данных по заданному условию. Проследите, как изменились вид таблицы и построенная диаграмма.
17. Сохраните созданную электронную книгу.
Задание 1.2. Перейдите на лист 2. Заполнить таблицу, произвести расчеты, выделить минимальную и максимальную суммы покупки; по результатам расчета построить круговую диаграмму суммы продаж.
Краткая справка. Формулы для расчета: Сумма = Цена * Количество; Всего = сумма значений колонки «Сумма». Для выделения максимального/минимального значений установите курсор в ячейке расчета, выберите встроенную функцию Excel Минимум (Максимум), в качестве первого числа выделите диапазон ячеек значений столбца «Сумма» (ячейки ЕЗ:Е10).
Задание 1.3. Перейдите на лист 3. Заполнить ведомость учета брака, произвести расчеты, выделить минимальную, максимальную и среднюю суммы брака, а также средний процент брака; произвести фильтрацию данных по условию процента брака < 8 %, построить график отфильтрованных значений изменения суммы брака по месяцам. Формула для расчета: Сумма брака = Процент брака * Сумма зарплаты.
Краткая справка. В колонке «Процент брака» установите процентный формат чисел (Формат/Ячейки/вкладка Число/формат — Процентный).
Задание 1.4. Перейдите на лист 4. Заполнить таблицу анализа продаж, произвести расчеты, выделить минимальную и максимальную продажи (количество и сумму); произвести фильтрацию по цене, превышающей 30000 р., построить гистограмму отфильтрованных значений изменения выручки по видам продукции.
Формулы для расчета: Всего = Безналичные платежи + Наличные платежи;
Выручка от продажи = Цена * Всего.