Как найти высот призмы по углу наклона

Два основания призмы могут определять ее форму, но высота призмы определяет ее размер. Призмы — это многогранники, трехмерные тела с двумя одинаковыми и параллельными многоугольными основаниями или концами. Высота призмы — это расстояние между двумя ее основаниями и является важным измерением при расчете объема призмы и площади поверхности. Работая в обратном направлении с общей формулой объем = базовая площадь * высота и площадь поверхности = периметр базы * высота + 2 * площадь базы, вы можете найти высоту любой призмы.

объем

Измерьте основание призмы. В этом примере основание призмы имеет квадратную форму со стороной 10 дюймов.

Найдите площадь базы по формуле площади конкретной фигуры. В этом примере формула для площади базы — это измерение одной стороны, умноженное на себя, или 10, умноженное на 10, что равно 100 квадратным дюймам.

Разделите объем призмы на площадь основания, чтобы найти высоту призмы. Завершая этот пример, пусть объем призмы составит 600 кубических дюймов. Разделив 600 кубических дюймов на 100 квадратных дюймов, вы получите высоту 6 дюймов.

Площадь поверхности

Измерьте основание призмы. Для этого примера, пусть основание будет прямоугольником с шириной 4 дюйма и длиной 6 дюймов.

Найдите площадь базы с формулой площади данной фигуры, затем умножьте площадь на 2. В этом примере формулой для площади базы будет ширина, умноженная на длину, или 4, умноженная на 6, что равно 24 квадратным дюймам, а 24 — умноженному на 2 результата в 48 квадратных дюймов.

Вычтите удвоенную базовую площадь из площади поверхности призмы. В этом примере пусть площадь поверхности будет 248 квадратных дюймов. Вычитание 48 из 248 дает 200 квадратных дюймов.

Рассчитайте периметр базы по формуле периметра фигуры. В этом примере формула для периметра базы равна 2 * ширина + 2 * длина или 2 * 4 + 2 * 6, что составляет 20 дюймов.

Разделите оставшуюся площадь поверхности от шага 3 по периметру основания, чтобы найти высоту призмы. Завершая этот пример, разделив 200 квадратных дюймов на 20 дюймов, получим высоту 10 дюймов.

подсказки

• Если призма является реальным объектом, измерьте расстояние между двумя ее основаниями с помощью измерительной ленты, чтобы определить ее высоту.

Сторона основания правильной четырехугольной призмы равна а .
Диагональ призмы наклонена к плоскости боковой грани под углом 30°

Найти высоту призмы и угол наклона диагонали призмы к плоскости основания.

Ясно, что угол  наклона диагонали к плоскости боковой грани  равен 30°.
Сделаем и смотрим рисунок.
ВС- высота призмы.
АВ- ее диагональ.
ВЕ- диагональ боковой грани.
АЕ=ЕС= а — стороны основания.
Призма правильная. Значит, в основании — квадрат.
Угол АВЕ=30°
Диагональ основания АС= а√2 по формуле диагонали квадрата.
Диагональ АВ призмы = АЕ:sin (30°)=2a
Диагональ ВЕ боковой грани=АЕ:tg(30°)=а:(1/√3)=а√3
Высота ВС= h призмы по т.Пифагора
h²=(а√3)²-а²=2а²
h=а√2
Треугольник АВС — прямоугольный, в котором катеты АС=ВС.
Отсюда угол  угол наклона диагонали призмы к плоскости основания 

∠ ВАС=45°

Советы к решению задач на призму

1. Если в условии задачи говорится диагональ боковой грани прямой призмы, то помните, что:

— Проекцией этой диагонали на плоскость основания будет соответствующая сторона основы призмы. Диагональ боковой грани прямой призмы, соответствующая ей сторона основания и боковое ребро призмы выходит с конца диагонали, образуют прямоугольный треугольник;

— Углом наклона диагонали боковой грани к плоскости основания будет угол между этой диагональю и соответствующей стороной основы призмы;

Если заданы или найдены диагональ боковой грани призмы и угол ее наклона к плоскости основания, или это диагональ и соответствующая ей сторона основы, то можно найти высоту призмы с помощью тригонометрических соотношений в прямоугольном треугольнике или последствий теоремы Пифагора.

2. Если в условии задачи говорится диагональ прямой призмы, то помните, что:

— Проекцией этой диагонали на плоскость основы будет соответствующая ей диагональ основания призмы. При этом большей диагонали основы соответствует большая диагональ призмы, меньшей — меньше диагональ призмы. Диагональ прямой призмы, соответствующая ей диагональ основания и боковое ребро призмы выходит с конца диагонали, образуют прямоугольный треугольник;

— Углом наклона диагонали прямой призмы к плоскости основания будет угол между этой диагональю и соответствующей диагональю основания призмы;

Если заданы или найдены диагональ прямой призмы и угол ее наклона к плоскости основания, или это диагональ и соответствующая ей диагональ основания основы, то можно найти высоту призмы с помощью тригонометрических соотношений в прямоугольном треугольнике или последствий теоремы Пифагора.

3. Если в условии задачи говорится сечение прямой призмы плоскостью, то помните, что:

— Если секущая плоскость проходит, например, через сторону основания прямой треугольной призмы и противоположную ей вершину призмы, принадлежащего другой основе, то сечением будет треугольник, ортогональной проекцией которого на плоскость основы будет треугольник, лежащий в основе призмы. Если известна площадь такого сечения и угол наклона плоскости сечения к плоскости основания, то можно найти площадь основания призмы. Площадь основания в таком случае будет равна площади сечения, помноженной на косинус угла между плоскостями сечения и основания. Соответственно площадь такого сечения будет равна площади основания, деленной на косинус угла между плоскостями сечения и основания.

Чтобы найти угол между плоскостью сечения и плоскостью основания, надо в одной из этих плоскостей провести перпендикуляр к общей прямой плоскостей и из основания перпендикуляра, во второй плоскости провести перпендикуляр к общей прямой плоскостей.

В случае правильной треугольной призмы угол наклона плоскости сечения, проходящей через сторону основания прямой треугольной призмы и противоположную ей вершину призмы к плоскости основания, будет угол между соответствующими высотами сечения и основы призмы.

 

Как построить пятиугольную наклонную призму?

Как построить пятиугольную наклонную призму?

Надо вычертить верхнее основание — это пятиугольник.

С каждой вершины под углом к вертикали опустить вниз боковые рёбра одинаковой длины.

Внизу параллельно верхнему основанию вычертить нижнее основание так, чтобы вершины совпадали с нижними концами рёбер.

Осталось выяснить, какие рёбра невидимы, и вычертить их пунктиром.

Расстояние между боковыми ребрами наклонной треугольной призмы равны?

Расстояние между боковыми ребрами наклонной треугольной призмы равны.

Определите двугранные при боковых ребрах призмы.

Чему равна площадь боковой поверхности прямой пятиугольной призмы со стороной основания 6см и высотой 5см?

Чему равна площадь боковой поверхности прямой пятиугольной призмы со стороной основания 6см и высотой 5см.

Сторона основания правильной шестиугольной призмы — а, наибольшая диагональ призмы наклонена к плоскости основания под углом α?

Сторона основания правильной шестиугольной призмы — а, наибольшая диагональ призмы наклонена к плоскости основания под углом α.

Определения : боковая поверхность наклонной призмы, боковая поверхность ( формула площади для правильной призмы, полная поверхность призмы?

Определения : боковая поверхность наклонной призмы, боковая поверхность ( формула площади для правильной призмы, полная поверхность призмы?

Дана наклонная треугольная призма боковое ребро длинной 8 см наклонено к плоскости основания под углом 45% определить высоту призмы?

Дана наклонная треугольная призма боковое ребро длинной 8 см наклонено к плоскости основания под углом 45% определить высоту призмы.

Боковое ребро наклонной призмы наклонена к плоскости основания под углом 30 , высота призмы = 15 см ?

Боковое ребро наклонной призмы наклонена к плоскости основания под углом 30 , высота призмы = 15 см .

Определите длину бокового ребра.

ОЧЕНЬ СРОЧНО боковое ребро наклонной призмы наклонено к плоскости основания под углом 45 и равна 2√2см?

ОЧЕНЬ СРОЧНО боковое ребро наклонной призмы наклонено к плоскости основания под углом 45 и равна 2√2см.

Сторона основания правильной четырехугольной призмы равна а?

Сторона основания правильной четырехугольной призмы равна а.

Диагональ призмы наклонена к плоскости боковой грани под углом в 30 градусов.

Найдите высоту призмы и угол наклона диагонали к плоскости.

Диагональ правильной четырёхугольной призмы наклонена к плоскости основания под углом в 30о?

Диагональ правильной четырёхугольной призмы наклонена к плоскости основания под углом в 30о.

Найдите площадь полной поверхности призмы, если высота этой призмы 12√2см.

В правильной пятиугольной призме сторона основания 4 см, высота призмы 11 см?

В правильной пятиугольной призме сторона основания 4 см, высота призмы 11 см.

Найти площадь боковой поверхности призмы.

На этой странице сайта, в категории Геометрия размещен ответ на вопрос Как построить пятиугольную наклонную призму?. По уровню сложности вопрос рассчитан на учащихся 5 — 9 классов. Чтобы получить дополнительную информацию по интересующей теме, воспользуйтесь автоматическим поиском в этой же категории, чтобы ознакомиться с ответами на похожие вопросы. В верхней части страницы расположена кнопка, с помощью которой можно сформулировать новый вопрос, который наиболее полно отвечает критериям поиска. Удобный интерфейс позволяет обсудить интересующую тему с посетителями в комментариях.

Средняя линия треугольника равна половине стороны, которой параллельна. Значит, наименьшая средняя линия треугольника будет напротив меньшего катета. Найдем длину меньшего катета по т. Пифагора х = ✓(29² — 21²) = ✓400 = 20 ½ * 20 = 10 см Ответ : 1..

AB + BC + CM + MD + DK = (AB + BC) + (CM + MD) + DK = AC + CD + DK = AK.

Теорема4. 1. Первый признак равенства треугольников. Если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны. Теорема4. 2. Второй признак равенс..

Середина сторони ВС є точка М, яка має координати М(1 ; 2), а відстань між точками А і М дорівнює 5 .

Источник

Как нарисовать пятиугольную призму? Объем и площадь поверхности фигуры

Пятиугольная призма при решении задач по геометрии встречается гораздо реже, чем такие призмы, как треугольная, четырехугольная или шестиугольная. Тем не менее полезно рассмотреть основные свойства этой фигуры, а также узнать, как ее можно нарисовать.

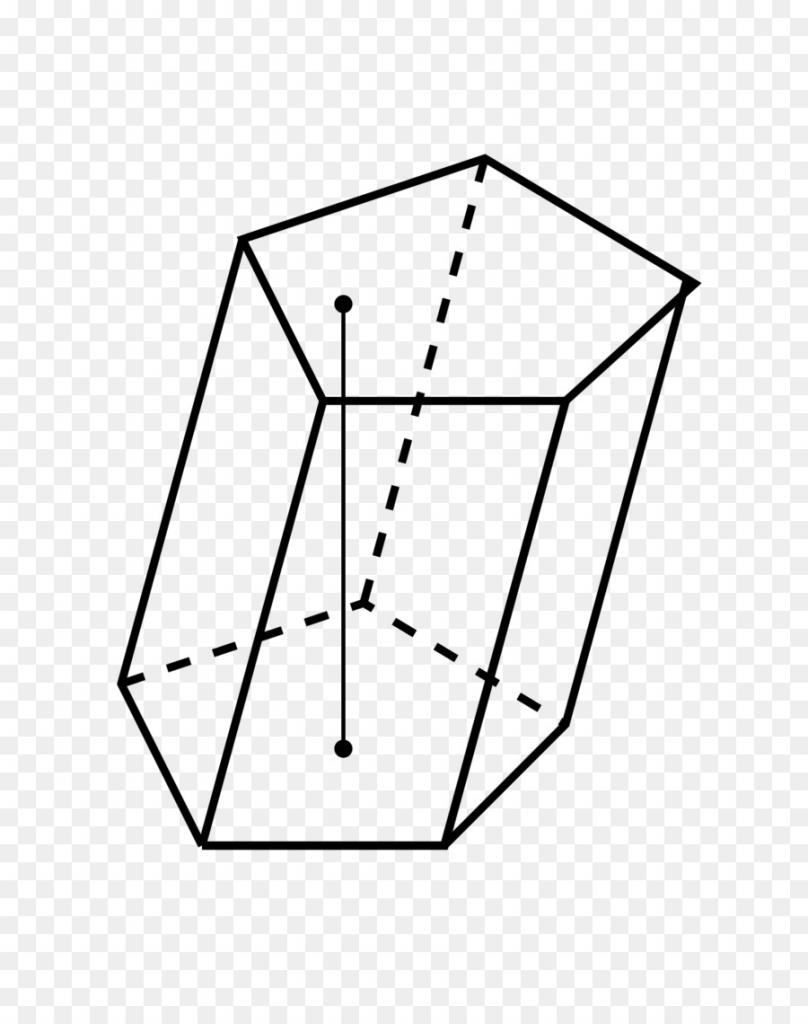
Что собой представляет пятиугольная призма?

Речь идет об объемной фигуре, основания которой являются пятиугольниками, а боковые стороны — параллелограммами. Если каждый из этих параллелограммов будет перпендикулярен параллельным основаниям, то такая призма называется прямоугольной. Боковая поверхность прямоугольной пятиугольной призмы составлена из пяти прямоугольников. Причем прилегающая к основанию сторона каждого из них равна соответствующей длине стороны пятиугольника.

Если пятиугольник будет правильным, то есть все его стороны и углы будут равны друг другу, тогда такая прямоугольная призма называется правильной. Далее в статье будем рассматривать свойства именно этой фигуры.

Элементы призмы

Для нее, как и для любой призмы, характерны следующие элементы:

• грани или стороны — это части плоскостей, ограничивающих фигуру в пространстве;
• вершины — точки пересечения трех сторон;
• ребра — отрезки пересечения двух сторон фигуры.

Числа всех названных элементов связаны друг с другом следующим равенством:

Число ребер = число вершин + число граней — 2

Это выражение носит название формулы Эйлера для полиэдра.

В пятиугольной призме количество сторон равно семи (два основания + пять прямоугольников). Число вершин составляет 10 (по пять для каждого основания). Число ребер в таком случае будет равно:

Десять ребер принадлежат основаниям призмы, а пять ребер образованы прямоугольниками.

Как начертить пятиугольную призму?

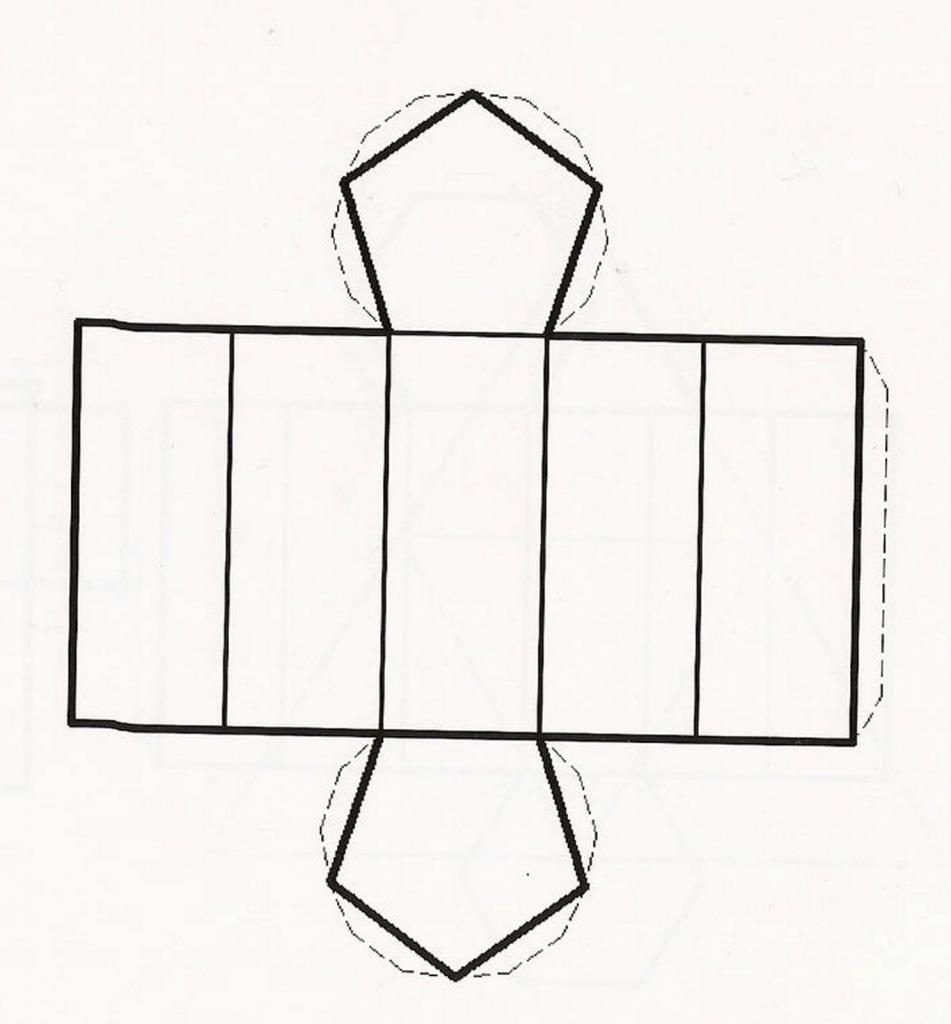
Ответ на этот вопрос зависит от конкретной задачи. Если необходимо начертить произвольную призму, тогда следует изобразить любой пятиугольник. После этого провести пять параллельных отрезков равной длины из каждой вершины пятиугольника. Затем, соединить верхние концы отрезков. Получилась пятиугольная произвольная призма.

Если же следует начертить правильную призму, тогда вся сложность задачи сводится к получению правильного пятиугольника. Существует несколько способов начертить этот многоугольник. Здесь мы рассмотрим только два способа.

Первый способ заключается в построении окружности с помощью циркуля. Затем проводится произвольный диаметр окружности и от него отсчитывается с помощью транспортира пять углов по 72 o (5*72 o = 360 o ). При отсчете каждого угла делается насечка на окружности. Для построения прямоугольника остается соединить прямыми отрезками отмеченные насечки.

Второй способ предполагает использование только циркуля и линейки. Он является несколько сложным в сравнении с предыдущим. Ниже приводится видео, где подробно объясняется каждый шаг такого построения.

Заметим, что пятиугольник легко нарисовать, если соединить концы звезды. Если нет необходимости чертить точно правильный пятиугольник, тогда можно использовать способ со звездой, нарисованной от руки.

Как только пятиугольник изображен, следует из каждой его вершины провести пять одинаковых параллельных отрезков и соединить их вершины. Получится пятиугольная призма.

Площадь фигуры

Теперь рассмотрим вопрос, как найти площадь пятиугольной призмы. На рисунке ниже приведена ее развертка. Видно, что искомая площадь образована двумя одинаковыми пятиугольниками и пятью равными друг другу прямоугольниками.

Площадь всей поверхности фигуры выразится формулой:

Здесь индексы o и p означают основание и прямоугольник соответственно. Обозначим длину стороны пятиугольника как a, а высоту фигуры как h. Тогда для прямоугольника запишем:

Чтобы вычислить площадь пятиугольника, воспользуемся универсальной формулой:

Где n — число сторон многоугольника. Подставляя n = 5, получаем:

Точность полученного равенства составляет 3 знака после запятой, что вполне достаточно для решения любых задач.

Теперь остается найти сумму полученных площадей основания и боковой поверхности. Имеем:

Следует помнить, что полученная формула справедлива только для прямоугольной призмы. В случае с косоугольной фигурой площадь ее боковой поверхности находят, исходя из знания периметра среза, который должен быть перпендикулярен всем параллелограммам.

Объем фигуры

Формула расчета объема пятиугольной призмы ничем не отличается от аналогичного выражения для любой другой призмы или цилиндра. Объем фигуры равен произведению ее высоты на площадь основания:

Если рассматриваемая призма является прямоугольной, тогда высота в ней является длиной ребра, образованного прямоугольниками. Площадь правильного пятиугольника была вычислена выше с высокой точностью. Подставим это значение в формулу для объема и получим необходимое выражение для пятиугольной правильной призмы:

Таким образом, вычисление объема и площади поверхности пятиугольной правильной призмы возможно, если известна сторона основания и высота фигуры.

Источник