Как найти высоту боковой поверхности правильной пирамиды - Исправление недочетов и поиск решений вместе с Examum.ru

Задача. Нахождение площади боковой поверхности и высоты пирамиды

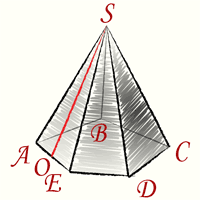
В правильной четырехугольной пирамиде сторона основания равна 10 см, а боковое ребро 13 см.

Найти площадь боковой поверхности и высоту пирамиды

Решение.
Исходя из свойств правильной пирамиды, каждая из ее сторон является равнобедренным треугольником.
Таким образом, площадь боковой поверхности правильной пирамиды будет равна сумме площадей каждой из граней, являющихся равнобедренными треугольниками.

Подставив значения из условия задачи в Формулу 1, получим:
S = 5 √ ( (13 + 5) (13 — 5) )
S = 5 √ 144 = 60

Поскольку граней у пирамиды четыре, то площадь боковой поверхности будет равна сумме всех четырех граней:

60 * 4 = 240 см²

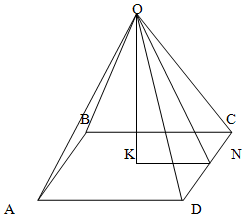
Так как по условию задачи, пирамида является правильной, то в основании ее лежит правильный многоугольник. Так как, согласно условию, она является четырехугольной, то данным многоугольником является квадрат.

Поскольку основанием пирамиды является квадрат, то:

Поскольку каждая грань правильной пирамиды представляет собой равнобедренный треугольник, а в равнобедренном треугольнике медиана, биссектриса и высота, проведенные к третьей стороне совпадают, то
CN = 10/2 = 5

Теперь найдем апофему пирамиды, исходя из свойств прямоугольного треугольника, образованного апофемой пирамиды, ребром и половиной основания (треугольником OCN).

ON² + CN² = OC²
ON² + 25 = 169
ON² = 144
ON = 12

Откуда уже несложно найти искомую высоту, исходя из свойств прямоугольного треугольника, образованного высотой пирамиды, ее апофемой и отрезком KN (треугольник ONK)

OK²+ KN²= ON²
OK² + 25 = 144
OK = √119

Ответ: √119, 240 см² .

Правильная пирамида с четырехугольником в основании |

Описание курса

| Правильная пирамида с четырехугольником в основании (часть 3)

Источник

Боковая поверхность правильной пирамиды, формула

Правильная пирамида — это многогранник, у которого одна грань — основание пирамиды — правильный многоугольник, а остальные — боковые грани — равные треугольники с общей вершиной. Высота опускается в центр основания из вершины.

Боковая поверхность правильной пирамиды равна произведению полупериметра основания на апофему:

[ S_{бок} = frac{1}{2} pa ]

p — периметр основания правильной пирамиды (ABCDE)
a — апофема правильной пирамиды (OS)

Вычислить, найти боковую поверхность правильной пирамиды по формуле(1)

Боковая поверхность правильной пирамиды	стр. 327

Источник

Определение

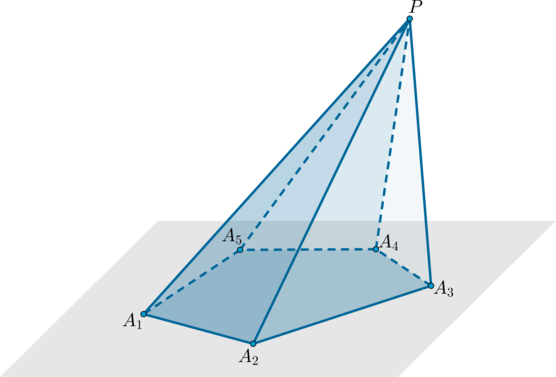
Пирамида – это многогранник, составленный из многоугольника (A_1A_2…A_n) и (n) треугольников с общей вершиной (P) (не лежащей в плоскости многоугольника) и противолежащими ей сторонами, совпадающими со сторонами многоугольника.
Обозначение: (PA_1A_2…A_n).
Пример: пятиугольная пирамида (PA_1A_2A_3A_4A_5).

Треугольники (PA_1A_2, PA_2A_3) и т.д. называются боковыми гранями пирамиды, отрезки (PA_1, PA_2) и т.д. – боковыми ребрами, многоугольник (A_1A_2A_3A_4A_5) – основанием, точка (P) – вершиной.

Высота пирамиды – это перпендикуляр, опущенный из вершины пирамиды на плоскость основания.

Пирамида, в основании которой лежит треугольник, называется тетраэдром.

Пирамида называется правильной, если в ее основании лежит правильный многоугольник и выполнено одно из условий:

((a)) боковые ребра пирамиды равны;

((b)) высота пирамиды проходит через центр описанной около основания окружности;

((c)) боковые ребра наклонены к плоскости основания под одинаковым углом.

((d)) боковые грани наклонены к плоскости основания под одинаковым углом.

Правильный тетраэдр – это треугольная пирамида, все грани которой – равные равносторонние треугольники.

Теорема

Условия ((a), (b), (c), (d)) эквивалентны.

Доказательство

Проведем высоту пирамиды (PH). Пусть (alpha) – плоскость основания пирамиды.

1) Докажем, что из ((a)) следует ((b)). Пусть (PA_1=PA_2=PA_3=…=PA_n).

Т.к. (PHperp alpha), то (PH) перпендикулярна любой прямой, лежащей в этой плоскости, значит, треугольники (PA_1H, PA_2H, PA_3H,…,
PA_nH) – прямоугольные. Значит, эти треугольники равны по общему катету (PH) и гипотенузам (PA_1=PA_2=PA_3=…=PA_n). Значит, (A_1H=A_2H=…=A_nH). Значит, точки (A_1, A_2, …, A_n) находятся на одинаковом расстоянии от точки (H), следовательно, лежат на одной окружности с радиусом (A_1H). Эта окружность по определению и есть описанная около многоугольника (A_1A_2…A_n).

2) Докажем, что из ((b)) следует ((c)).

Аналогично первому пункту треугольники (PA_1H, PA_2H, PA_3H,…,
PA_nH) прямоугольные и равны по двум катетам. Значит, равны и их углы, следовательно, (angle PA_1H=angle PA_2H=…=angle PA_nH).

3) Докажем, что из ((c)) следует ((a)).

Аналогично первому пункту треугольники (PA_1H, PA_2H, PA_3H,…,
PA_nH) прямоугольные и по катету и острому углу. Значит, равны и их гипотенузы, то есть (PA_1=PA_2=PA_3=…=PA_n).

4) Докажем, что из ((b)) следует ((d)).

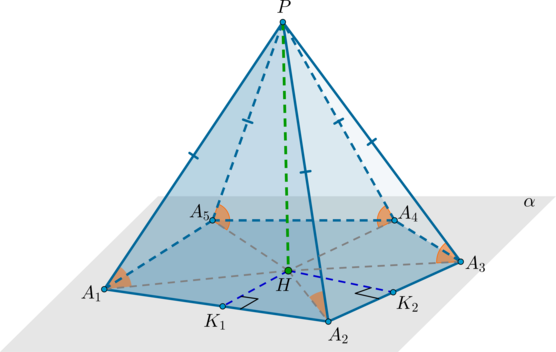
Т.к. в правильном многоугольнике совпадают центры описанной и вписанной окружности (вообще говоря, эта точка называется центром правильного многоугольника), то (H) – центр вписанной окружности. Проведем перпендикуляры из точки (H) на стороны основания: (HK_1,
HK_2) и т.д. Это – радиусы вписанной окружности (по определению). Тогда по ТТП ((PH) – перпендикуляр на плоскость, (HK_1, HK_2) и т.д. – проекции, перпендикулярные сторонам) наклонные (PK_1, PK_2) и т.д. перпендикулярны сторонам (A_1A_2, A_2A_3) и т.д. соответственно. Значит, по определению (angle PK_1H, angle PK_2H) равны углам между боковыми гранями и основанием. Т.к. треугольники (PK_1H, PK_2H, …) равны (как прямоугольные по двум катетам), то и углы (angle PK_1H, angle PK_2H, …) равны.

5) Докажем, что из ((d)) следует ((b)).

Аналогично четвертому пункту треугольники (PK_1H, PK_2H, …) равны (как прямоугольные по катету и острому углу), значит, равны отрезки (HK_1=HK_2=…=HK_n). Значит, по определению, (H) – центр вписанной в основание окружности. Но т.к. у правильных многоугольников центры вписанной и описанной окружности совпадают, то (H) – центр описанной окружности. Чтд.

Следствие

Боковые грани правильной пирамиды – равные равнобедренные треугольники.

Определение

Высота боковой грани правильной пирамиды, проведенная из ее вершины, называется апофемой.
Апофемы всех боковых граней правильной пирамиды равны между собой и являются также медианами и биссектрисами.

Важные замечания

1. Высота правильной треугольной пирамиды падает в точку пересечения высот (или биссектрис, или медиан) основания (основание – правильный треугольник).

2. Высота правильной четырехугольной пирамиды падает в точку пересечения диагоналей основания (основание – квадрат).

3. Высота правильной шестиугольной пирамиды падает в точку пересечения диагоналей основания (основание – правильный шестиугольник).

4. Высота пирамиды перпендикулярна любой прямой, лежащей в основании.

Определение

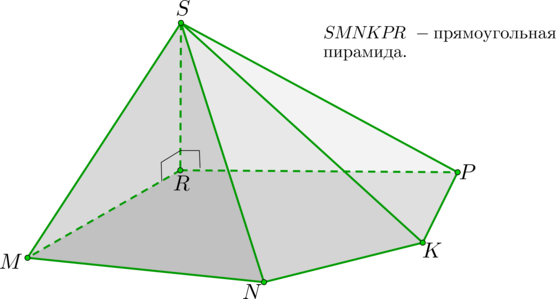
Пирамида называется прямоугольной, если одно ее боковое ребро перпендикулярно плоскости основания.

Важные замечания

1. У прямоугольной пирамиды ребро, перпендикулярное основанию, является высотой пирамиды. То есть (SR) – высота.

2. Т.к. (SR) перпендикулярно любой прямой из основания, то (triangle SRM, triangle SRP) – прямоугольные треугольники.

3. Треугольники (triangle SRN, triangle SRK) – тоже прямоугольные.
То есть любой треугольник, образованный этим ребром и диагональю, выходящей из вершины этого ребра, лежащей в основании, будет прямоугольным.

[{Large{text{Объем и площадь поверхности пирамиды}}}]

Теорема

Объем пирамиды равен трети произведения площади основания на высоту пирамиды: [V_{text{пирамиды}}=dfrac13 S_{text{осн}}cdot h]

Следствия

Пусть (a) – сторона основания, (h) – высота пирамиды.

1. Объем правильной треугольной пирамиды равен (V_{text{прав.треуг.пир.}}=dfrac{sqrt3}{12}a^2h),

2. Объем правильной четырехугольной пирамиды равен (V_{text{прав.четыр.пир.}}=dfrac13a^2h).

3. Объем правильной шестиугольной пирамиды равен (V_{text{прав.шест.пир.}}=dfrac{sqrt3}{2}a^2h).

4. Объем правильного тетраэдра равен (V_{text{прав.тетр.}}=dfrac{sqrt3}{12}a^3).

Теорема

Площадь боковой поверхности правильной пирамиды равна полупроизведению периметра основания на апофему.

[{Large{text{Усеченная пирамида}}}]

Определение

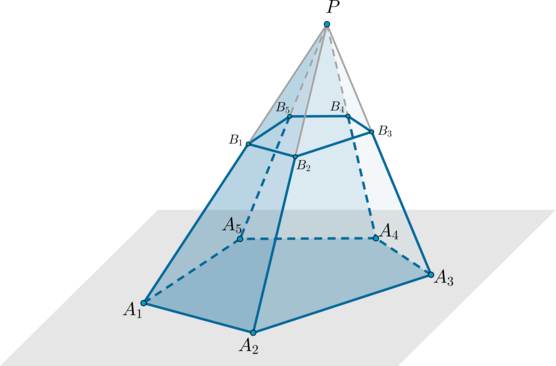
Рассмотрим произвольную пирамиду (PA_1A_2A_3…A_n). Проведем через некоторую точку, лежащую на боковом ребре пирамиды, плоскость параллельно основанию пирамиды. Данная плоскость разобьет пирамиду на два многогранника, один из которых – пирамида ((PB_1B_2…B_n)), а другой называется усеченная пирамида ((A_1A_2…A_nB_1B_2…B_n)).

Усеченная пирамида имеет два основания – многоугольники (A_1A_2…A_n) и (B_1B_2…B_n), которые подобны друг другу.

Высота усеченной пирамиды – это перпендикуляр, проведенный из какой-нибудь точки верхнего основания к плоскости нижнего основания.

Важные замечания

1. Все боковые грани усеченной пирамиды – трапеции.

2. Отрезок, соединяющий центры оснований правильной усеченной пирамиды (то есть пирамиды, полученной сечением правильной пирамиды), является высотой.

Источник

Геометрия, 10 класс

Урок № 15. Пирамида

Перечень вопросов, рассматриваемых в теме:

Понятие пирамиды;
Виды пирамид;
Элементы пирамиды: вершина, ребра, грани, основание;
Площадь боковой поверхности и полной поверхности пирамиды.

Глоссарий по теме

Пирамида – многогранник, составленный из n-угольника и n треугольников

Основание пирамиды – грань пирамиды, являющаяся n-угольником

Вершина пирамиды – общая точка всех треугольников, лежащих в боковых гранях.

Боковая грань – грань пирамиды, являющаяся треугольником

Боковые ребра – общие отрезки боковых граней

Высота – перпендикуляр, опущенный из вершины пирамиды на ее основание

Апофема – высота боковой грани правильной пирамиды

Правильная пирамида – пирамида, в основании которой лежит правильный многоугольник, а отрезок, соединяющий вершину и центр основания пирамиды, является высотой

Усеченная пирамида – многогранник, образованный двумя n-угольниками, расположенными в параллельных плоскостях (нижнее и верхнее основание) и n-четырехугольников (боковые грани).

Площадь полной поверхности пирамиды – сумма площадей всех граней пирамиды

Площадь боковой поверхности пирамиды – сумма площадей боковых граней пирамиды

Основная литература:

Потоскуев Е.В., Звавич Л. И. Геометрия. 11кл.: учеб. Для классов с углубл. и профильным изучением математики общеобразоват. Учреждений.. – М.: Дрофа, 2009. – 368 с.: ил. (117 с. – 121 с.)

Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. и др. Математика: алгебра и начала математического анализа, геометрия. Геометрия. 10–11 классы : учеб. Для общеобразоват. организаций : базовый и углубл. уровни – М. : Просвещение, 2014. – 255 с. (65 с. – 68 с.)

Открытые электронные ресурсы:

Многогранники.ru – сайт о создании моделей многогранников из бумаги https://www.mnogogranniki.ru/

Образовательный портал «Решу ЕГЭ». https://mathb-ege.sdamgia.ru/test?theme=177

Теоретический материал для самостоятельного изучения

Определение пирамиды

Рассмотрим многоугольник A₁A₂…A_n и точку Р, не лежащую в плоскости этого многоугольника (рис.1). Соединив точку Р с вершинами многоугольника, получим n треугольников: PA₁A₂, PA₂A₃,…, PA_nA₁.

Многогранник, составленный из n-угольника A₁A₂…A_nи n треугольников, называется пирамидой. Многоугольник A₁A₂…A_n называется основанием, а треугольники PA₁A₂, PA₂A₃,…, PA_nA₁– боковые грани пирамиды, отрезки PA₁, PA₂,…, PA_n – боковые ребра пирамиды, точка Р – вершина пирамиды. Пирамиду с основанием A₁A₂…A_n и вершиной Р называют n-угольной пирамидой и обозначают PA₁A₂…A_n.

Рисунок 1 — пирамида

Высота пирамиды

Перпендикуляр, проведенный из вершины пирамиды к плоскости основания, называется высотой пирамиды. На рисунке 1 PH является высотой. Обратите внимание, что высота может лежать и вне пирамиды (рис. 3) или быть одним из боковых ребер (рис. 4).

Рисунок 3 – высота вне пирамиды

Рисунок 4 – Высота пирамиды — боковое ребро

Правильная пирамида

Будем называть пирамиду правильной, если ее основание – правильный многоугольник, а отрезок, соединяющий вершину пирамиды с центром основания, является ее высотой. Напомним, что центром правильного многоугольника называется центр вписанной в него (или описанной около него) окружности (рис.5).

Рисунок 5 – Правильная пирамида

Правильная пирамида обладает несколькими хорошими свойствами. Давайте выясним, какими.

Рассмотрим правильную пирамиду PA₁A₂…A_n (рис. 5).

Пусть О – центр описанной около основания окружности, тогда РО – высота пирамиды, значит РО перпендикулярен любой прямой, лежащей в плоскости основания. Таким образом, высота РО перпендикулярна радиусам А₁О, А₂О,…А_nО.

Образованные высотой и радиусами треугольники являются прямоугольными. Причем, эти треугольники имеют общий катет – РО и равные катеты А₁О, А₂О,…А_nО (равны как радиусы). Значит, треугольники РОА₁, РОА₂,…РОА_n равны по двум катетам, значит равны гипотенузы PA_{1 ,}РA₂… РA_n, которые являются боковыми ребрами правильной пирамиды.

Боковые ребра пирамиды равны, значит боковые грани – равнобедренные треугольники. Основания этих треугольников равны друг другу, так как в основании лежит правильный многоугольник. Следовательно, боковые грани равны по третьему признаку равенства треугольников.

Таким образом, верны следующие утверждения:

Все боковые ребра правильной пирамиды равны.
Боковые ребра правильной пирамиды являются равными равнобедренными треугольниками.

Введем еще одно определение. Апофемой называется высота боковой грани правильной пирамиды, проведенная из ее вершины. На рисунке 5 PE – одна из апофем.

Все апофемы правильной пирамиды равны друг другу как высоты в равных треугольниках.

Усеченная пирамида

Возьмем произвольную пирамиду PA₁A₂…A_nи проведем секущую плоскость β, параллельную плоскости основания пирамиды α и пересекающую боковые ребра в точках В₁,В₂,…В_n (рис. 6). Плоскость β разбивает пирамиду на два многогранника. Многогранник, гранями которого являются n-угольники A₁A₂…A_n и В₁В₂…В_n (нижнее и верхнее основания соответственно), расположенные в параллельных плоскостях и n четырехугольников A₁A₂B₂B₁, A₂A₃B₃B₂, … A₁A_nB_nB₁ (боковые грани), называется усеченной пирамидой.

Рисунок 6 – Усеченная пирамида

Отрезки A₁B₁, A₂B₂, … A_nB_n называют боковыми ребрами усеченной пирамиды.

Усеченную пирамиду с основаниями A₁A₂…A_n и В₁В₂…В_n обозначают следующим образом: A₁A₂…A_nВ₁В₂…В_n.

Перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания называется высотой усеченной пирамиды. На рисунке 7 отрезки HH₁ и В1O –высоты усеченной пирамиды.

Рисунок 7 – Высота усеченной пирамиды

Площадь поверхности пирамиды

Площадью полной поверхности пирамиды называются сумма площадей всех ее граней, а площадью боковой поверхности пирамиды – сумма площадей ее боковых граней.

Для пирамиды, верно равенство S_полн= S_бок+S_осн.

Докажем теорему для площади боковой поверхности правильной пирамиды.

Теорема. Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.

Для площади боковой поверхности усеченной пирамиды верна следующая теорема

Теорема. Площадь боковой поверхности правильной усеченной пирамиды равна произведению полусуммы периметров оснований на апофему.

Примеры и разбор решения заданий тренировочного модуля

Задание 1. В пятиугольной пирамиде все боковые грани равны между собой. Площадь основания равна 42, а площадь боковой грани на 15 меньше. Чему равна площадь полной поверхности пирамиды?

Решение

Поскольку в пирамиде все боковые грани равны, то и площади их будут равны. Знаем, что площадь боковой грани на 15 меньше площади основания, значит она равна 27. В пятиугольной пирамиде боковых граней 5. Таким образом площадь полной поверхности равна 27*5+42 = 177.

Ответ: 177

Задание 2. В правильной пирамиде высота боковой грани равна 10, а в основании лежит квадрат со стороной 4. Чему равна площадь боковой поверхности?

Решение

Боковая грань пирамиды – это треугольник. Все боковые грани этой пирамиды равны между собой, так как пирамида правильная. Вычислим площадь треугольника: ½*4*10=20. В основании пирамиды лежит квадрат, значит боковых граней будет 4. Таким образом, площадь боковой поверхности равна 4* 20=80.

Ответ: 80

Источник

Пирамидой называют многогранник, одна грань которого – многоугольник, а остальные грани – треугольники с общей вершиной. Многоугольник называют основанием пирамиды, а треугольники – боковыми гранями.

Высотой пирамиды называют перпендикуляр, проведенный из вершины пирамиды к плоскости ее основания.

На рисунке 9.53 изображена четырехугольная пирамида с вершиной в точке . Четырехугольник – основание пирамиды, треугольники , , и – ее боковые грани. Отрезки , , и – боковые ребра пирамиды. Отрезок – высота пирамиды.

1. Если все боковые ребра пирамиды равны или наклонены к плоскости основания под одним и тем же углом, то основание высоты пирамиды, проведенной из ее вершины, совпадает с центром окружности, описанной около основания пирамиды.

2. Если боковые грани пирамиды наклонены к плоскости основания под одним и тем же углом (двугранные углы при основании равны), то основание высоты пирамиды, проведенной из ее вершины, совпадает с центром окружности, вписанной в основание пирамиды.

3. Если две боковые грани пирамиды перпендикулярны плоскости основания, то боковое ребро, содержащее эти грани, является высотой пирамиды.

Объем пирамиды высоты находят по формуле:

$LaTeX formula: V=frac{1}{3}S_{o.} cdot h$ , (9.11)

Площадь поверхности пирамиды находят по формуле:

$LaTeX formula: S_{n.}=S_{o.}+S_{delta .}$ . (9.12)

Пирамида называется правильной, если ее основанием является правильный многоугольник, а основание высоты пирамиды, проведенной из ее вершины, совпадает с центром окружности, вписанной в основание пирамиды (или описанной около основания пирамиды, так как центры этих окружностей совпадают).

На рисунке 9.54 изображена правильная четырехугольная пирамида, а на рисунке 9.55 – правильная треугольная.

Высоту боковой грани правильной пирамиды, проведенную из ее вершины, называют апофемой. На рисунке 9.54 отрезок – апофема правильной четырехугольной пирамиды.

Любую треугольную пирамиду называют тетраэдром.

Тетраэдр называется правильным, если все его ребра равны.

На рисунке 9.56 изображен правильный тетраэдр.

Площадь боковой поверхности правильной пирамиды находят по формуле:

$LaTeX formula: S_{delta .}=frac{1}{2}P_{o.} cdot h_{delta .}$ , (9.13)

где $LaTeX formula: h_{delta .}$ – апофема пирамиды.

Усеченной пирамидой называют многогранник, вершинами которого служат вершины основания пирамиды и вершины ее сечения плоскостью, параллельной основанию пирамиды.

Основания усеченной пирамиды – подобные многоугольники.

Высотой усеченной пирамиды называют перпендикуляр, заключенный между плоскостями ее оснований.

На рисунке 9.57 изображена треугольная усеченная пирамида, а на рисунке 9.58 – правильная четырехугольная усеченная пирамида.

Объем усеченной пирамиды находят по формуле:

$LaTeX formula: V=frac{1}{3}h(S_1+S_2+sqrt{S_1S_2})$ , (9.14)

где и – площади оснований, – высота усеченной пирамиды.

Пример 1. Основанием пирамиды является правильный треугольник со стороной дм, а две ее боковые грани перпендикулярны плоскости основания (рис. 9.59). Найдите объем пирамиды, зная, что ее высота равна дм.

Решение. Так как две боковые грани и пирамиды перпендикулярны плоскости ее основания, то их общее ребро является высотой пирамиды. Площадь основания пирамиды найдем по формуле $LaTeX formula: S=frac{sqrt{3}a^2}{4}$ . Получим: $LaTeX formula: S=frac{4sqrt{3}}{4}=sqrt{3}$ ( $LaTeX formula: _{partial M}\^3$ ).

Объем пирамиды найдем по формуле 9.11 . Получим: $LaTeX formula: V=frac{1}{3}cdot sqrt{3}cdot sqrt{3}=1$ ( $LaTeX formula: _{partial M}\^3$ ).

Ответ: $LaTeX formula: _{partial M}\^3$ .

Пример 2. Вычислите объем правильного тетраэдра с ребром, равным .

Решение. Так как тетраэдр правильный (рис. 9.60), то его высота опускается в центр треугольника : точку , точку пересечения высот, биссектрис и медиан этого треугольника.

Тогда $LaTeX formula: OA=frac{a }{sqrt{3}}$ – радиус окружности, описанной около ; – высота тетраэдра.

Найдем высоту тетраэдра. Рассмотрим треугольник . Из теоремы Пифагора: , , $LaTeX formula: h=sqrt{a^2-frac{a^2}{3}}=sqrt{frac{2a^2}{3}}=frac{sqrt{2}a}{sqrt{3}}$ .

Объем тетраэдра вычислим по формуле 9.11 , где $LaTeX formula: S_{o.}=frac{sqrt{3}a^2}{4}$ . Запишем: $LaTeX formula: V=frac{1}{3}cdot frac{sqrt{3}a^2}{4}cdot frac{sqrt{2}a}{sqrt{3}}=frac{sqrt{2}a^3}{12}$ .

Ответ: $LaTeX formula: frac{sqrt{2}a^3}{12}$ .

Пример 3. В основании пирамиды лежит прямоугольный треугольник с гипотенузой, равной , и острым углом $LaTeX formula: 30^{circ}$ . Боковые ребра пирамиды наклонены к плоскости основания под углом $LaTeX formula: 60^{circ}$ . Найдите объем пирамиды.

Решение. Основанием пирамиды является треугольник : $LaTeX formula: angle C=90^{circ}$ ; (рис. 9.61). Так как боковые ребра пирамиды наклонены к плоскости основания под одним и тем же углом, то высота пирамиды опускается в центр окружности, описанной около этого треугольника (на рисунке 9.61 точка ). Тогда $LaTeX formula: AO=R=frac{c}{2}$ и высота пирамиды .

Рассмотрим прямоугольный треугольник . Угол является углом наклона бокового ребра к плоскости основания, так как отрезок – проекция ребра на плоскость основания и $LaTeX formula: angle SAO=60^{circ}$ . Тогда $LaTeX formula: tg60^{circ}=frac{SO}{AO}$ и $LaTeX formula: SO=frac{sqrt{3}c}{2}=h$ .

Рассмотрим прямоугольный треугольник : $LaTeX formula: CB=frac{c}{2}$ по свойству катета, лежащего против угла $LaTeX formula: 30^{circ}$ ; $LaTeX formula: angle B=60^{circ}$ .

Найдем площадь треугольника:

$LaTeX formula: S_{triangle ABC}=frac{1}{2}ABcdot CBcdot sinangle B$ , $LaTeX formula: S_{triangle ABC}=frac{1}{2}ccdot frac{c}{2}cdot frac{sqrt{3}}{2}$ , $LaTeX formula: S_{triangle ABC}=frac{sqrt{3}c^2}{8}$ .

По формуле 9.11 найдем объем пирамиды: $LaTeX formula: V=frac{1}{3}cdot frac{sqrt{3}c^2}{8}cdot frac{sqrt{3}c}{2}=frac{c^3}{16}$ .

Ответ: $LaTeX formula: frac{c^3}{16}$ .

Пример 4. Основанием пирамиды служит треугольник со сторонами см, см и см. Боковые грани пирамиды образуют с ее основанием равные двугранные углы, содержащие по $LaTeX formula: 45^{circ}$ . Определите объем пирамиды.

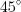
Решение. Основанием пирамиды (рис. 9.62) служит равнобедренный треугольник : см, см. Так как боковые грани образуют с плоскостью основания равные двугранные углы, то высота пирамиды опускается в центр окружности, вписанной в треугольник , то есть в точку , лежащую на высоте этого треугольника.

Тогда см; , где – радиус окружности, вписанной в основание пирамиды и $LaTeX formula: r=frac{2S}{a+b+c}$ .

Площадь треугольника найдем по формуле Герона $LaTeX formula: S_{triangle ABC}=sqrt{p(p-a)(p-b)(p-c)}$ , где $LaTeX formula: p=frac{5+6+6}{2}=8,5$ (см) и $LaTeX formula: S_{triangle ABC}=sqrt{8,5cdot (8,5-5)(8,5-6)^2}=frac{5sqrt{119}}{4}$ ( $LaTeX formula: _{CM}\^3$ ). Следовательно, $LaTeX formula: r=frac{5sqrt{119}}{2cdot 17}=frac{5sqrt{7}}{2sqrt{17}}$ (см).

Угол – линейный угол двугранного угла , так как и , и согласно условию задачи $LaTeX formula: angle SKB=45^{circ}$ . Значит, треугольник равнобедренный и $LaTeX formula: h=r=frac{5sqrt{7}}{2sqrt{17}}$ (см).

Согласно формуле 9.11 найдем объем пирамиды:

$LaTeX formula: V=frac{1}{3}cdot frac{5sqrt{119}}{4}cdot frac{5sqrt{7}}{2sqrt{17}}=frac{25cdot 7}{24}=frac{175}{24}$ ( $LaTeX formula: _{CM}\^3$ ).

Ответ: $LaTeX formula: frac{175}{24}$ $LaTeX formula: _{CM}\^3$ .

Пример 5. Апофема правильной четырехугольной пирамиды (рис. 9.63) равна и образует с высотой пирамиды угол $LaTeX formula: 30^{circ}$ . Найдите площадь боковой поверхности пирамиды.

Решение. Так как пирамида правильная, то четырехугольник – квадрат, а ее боковые грани – равнобедренные треугольники.

Точка – центр окружности, вписанной в основание пирамиды, следовательно, $LaTeX formula: OP=r=frac{DC}{2}$ .

Поскольку $LaTeX formula: angle SOP=90^{circ}$ , а $LaTeX formula: angle PSO=30^{circ}$ , то $LaTeX formula: OP=frac{sqrt{3}}{2}$ , тогда .

По формуле 9.13 найдем площадь боковой поверхности пирамиды: $LaTeX formula: S_{delta .}=frac{1}{2}cdot 4cdot sqrt{3}cdot sqrt{3}=6$ .

Ответ: .

Пример 6. Основание пирамиды – ромб с острым углом $LaTeX formula: 30^{circ}$ и стороной, равной . Найдите объем пирамиды, если известно, что ее вершина удалена от всех сторон основания на расстояние, равное .

Решение. Так как вершина пирамиды равноудалена от всех сторон ромба, то основание высоты пирамиды (точка ) совпадает с центром окружности, вписанной в ромб (рис. 9.64). По формуле найдем площадь ромба: $LaTeX formula: S=3^2sin30^{circ}=frac{9}{2}$ .

С другой стороны, площадь ромба можем найти и по формуле , откуда $LaTeX formula: h=frac{S}{a}$ , $LaTeX formula: h=frac{9}{2cdot 3}=frac{3}{2}$ .Тогда $LaTeX formula: OP=frac{h}{2}=frac{3}{4}$ .

Из теоремы Пифагора $LaTeX formula: OS=sqrt{SP^2-OP^2}$ , $LaTeX formula: OS=sqrt{3-frac{9}{16}}=frac{sqrt{39}}{4}$ .

По формуле 9.11 найдем объем пирамиды:

$LaTeX formula: V=frac{1}{3}cdot frac{9}{2}cdot frac{sqrt{39}}{4}=frac{3sqrt{39}}{8}$ .

Ответ: $LaTeX formula: frac{3sqrt{39}}{8}$ .

Пример 7. Боковое ребро правильной четырехугольной усеченной пирамиды наклонено к плоскости основания под углом 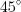$LaTeX formula: 45^{circ}$ , а длины ребер оснований соответственно равны см и см (рис. 9.65). Найдите объем пирамиды.

Решение. Так как основания усеченной пирамиды – квадраты со сторонами и см, то их площади соответственно равны:

$LaTeX formula: _{CM}\^2$ , $LaTeX formula: _{CM}\^2$ .

По теореме Пифагора найдем диагонали квадратов:

(см), (см).

Так как диагонали точкой пересечения делятся пополам, то см, а см.

Рассмотрим диагональное сечение пирамиды – трапецию . Так как , то имеем прямоугольник , в котором , а . Поскольку треугольник равнобедренный, то (см) и см. Следовательно, высота усеченной пирамиды см.

По формуле 9.14 найдем объем пирамиды:

$LaTeX formula: V=frac{1}{3}cdot sqrt{2}(16+4+sqrt{16cdot 4})=frac{sqrt{2}}{3}(20+4cdot 2)=frac{28sqrt{2}}{3}$ ( $LaTeX formula: _{CM}\^3$ ).

Ответ: $LaTeX formula: frac{28sqrt{2}}{3}$ $LaTeX formula: _{CM}\^3$ .

1. Решение задач, связанных с пирамидой, необходимо начинать с построения высоты пирамиды.

2. Различайте правильную треугольную пирамиду и правильный тетраэдр:

1) у правильной треугольной пирамиды основание – правильный треугольник, а боковые ребра хоть и равны между собой, но не обязательно, что они равны ребрам основания пирамиды;

2) правильный тетраэдр – это треугольная пирамида, у которой все ребра равны.

Источник