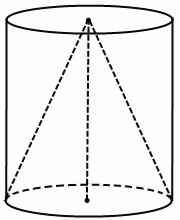
Конус вписан в цилиндр, если основание конуса совпадает с одним из оснований цилиндра, а вершина лежит в центре другого основания.
Оси цилиндра и вписанного в него конуса совпадают. Цилиндр и вписанный конус имеют равные высоты и радиусы.
Соответственно, в этом случае цилиндр описан около конуса.
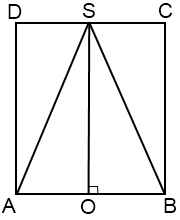
Рассмотрим осевое сечение комбинации тел. Оно представляет собой прямоугольник с вписанным в него равнобедренным треугольником.
Здесь SO=H — высота цилиндра и вписанного конуса, OA=OB=R — радиус цилиндра и радиус конуса, SB=SA= l — образующая конуса, AD — образующая цилиндра.
Найдем отношение объема конуса к объему описанного около него цилиндра:
Из прямоугольного треугольника SOA по теореме Пифагора
Теперь найдем отношение площади боковой поверхности конуса к площади боковой поверхности описанного цилиндра:
fioademior486
Вопрос по геометрии:
Конус с образующей равной 13 вписан в цилиндр с диаметром основания равным 10.
Найдите высоту цилиндра.
Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?
Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!
Ответы и объяснения 1
yortegadirer15
Построим осевое сечение: в результате у нас получится равнобедренный треугольник, вписанный в прямоугольник
Чтобы найти высоту цилиндра воспользуемся теоремой Пифагора.
H= sqrt(169-D/2)= sqrt(169-25)= 12.
Ответ: 12
Знаете ответ? Поделитесь им!
Гость ?
Как написать хороший ответ?
Как написать хороший ответ?
Чтобы добавить хороший ответ необходимо:
- Отвечать достоверно на те вопросы, на которые знаете
правильный ответ; - Писать подробно, чтобы ответ был исчерпывающий и не
побуждал на дополнительные вопросы к нему; - Писать без грамматических, орфографических и
пунктуационных ошибок.
Этого делать не стоит:
- Копировать ответы со сторонних ресурсов. Хорошо ценятся
уникальные и личные объяснения; - Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не
знаю» и так далее; - Использовать мат — это неуважительно по отношению к
пользователям; - Писать в ВЕРХНЕМ РЕГИСТРЕ.
Есть сомнения?
Не нашли подходящего ответа на вопрос или ответ отсутствует?
Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие
вопросы в разделе Геометрия.
Трудности с домашними заданиями? Не стесняйтесь попросить о помощи —
смело задавайте вопросы!
Геометрия — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения.
Задания
Версия для печати и копирования в MS Word
Тип 2 № 269377
i
Конус и цилиндр имеют общее основание и общую высоту (конус вписан в цилиндр). Вычислите объём цилиндра, если объём конуса равен 5.
Решение.
Это задание ещё не решено, приводим решение прототипа.
Конус и цилиндр имеют общее основание и общую высоту (конус вписан в цилиндр). Вычислите объём цилиндра, если объём конуса равен 5.
Поскольку
а конус и цилиндр имеют общую высоту и основание, имеем:
Ответ: 15.
Аналоги к заданию № 245350: 269369 269433 269437 … Все
Классификатор стереометрии: Комбинации круглых тел, Объём цилиндра, конуса, шара
Прототип задания
·
Видеокурс
Геометрия, 11 класс
Урок №10. Комбинации тел вращения
Перечень вопросов, рассматриваемых в теме:
- комбинации конуса и цилиндра, конуса и усеченного конуса, цилиндра и усеченного конуса, нескольких сфер;
- цилиндр, описанный около конуса, конус, описанный около цилиндра, усеченный конус, описанный около конуса и цилиндра;
- цилиндр, вписанный в конус, конус, вписанный в цилиндр, усеченный конус, вписанный в конус и цилиндр.
Глоссарий по теме
Определение
Цилиндр вписан в конус, если одно основание цилиндра лежит в плоскости основания конуса, а окружность другого основания — на боковой поверхности конуса. Конус, соответственно, в этом случае называется описанным около цилиндра.
Определение
Конус вписан в цилиндр, если основание конуса совпадает с основанием цилиндра, а вершина совпадает с центром другого основания цилиндра. Цилиндр, соответственно, в этом случае называется описанным около конуса.
Определение
Конус вписан в другой конус, если его вершина лежит в центре основания второго конуса, а основание лежит на боковой поверхности.
Основная литература:
Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. и др. Геометрия. 10–11 классы : учеб. для общеобразоват. организаций : базовый и углубл. уровни – М. : Просвещение, 2014. – 255, сс. 136-147.
Дополнительная литература:
Шарыгин И.Ф., Геометрия. 10–11 кл. : учеб. для общеобразоват. учреждений – М.: Дрофа, 2009. – 235, : ил., ISBN 978–5–358–05346–5, сс. 77-84.
Открытые электронные ресурсы:
Образовательный портал “Решу ЕГЭ”. https://mathb-ege.sdamgia.ru/test?theme=177
Теоретический материал для самостоятельного изучения
1. Комбинации цилиндра и конуса
Определение
Цилиндр вписан в конус, если одно основание цилиндра лежит в плоскости основания конуса, а окружность другого основания — на боковой поверхности конуса. Конус, соответственно, в этом случае называется описанным около цилиндра.
В любой конус можно вписать цилиндр.
Оси конуса и вписанного в него цилиндра совпадают. Верхнее основание цилиндра совпадает с сечением конуса плоскостью, параллельной основанию.
Осевое сечение цилиндра, вписанного в конус — представляет собой равнобедренный треугольник с вписанным в него прямоугольником.
SO=H — высота конуса
OA=OB=R — радиус конуса
OF=OM=r — радиус цилиндра
OO1=h — высота цилиндра
SA=SB=L — образующие конуса
NF=KM=h (l)— образующие цилиндра.
∆SOB и ∆KMB — прямоугольные
∆SOB
Поэтому:


Отношение боковой поверхности конуса к боковой поверхности вписанного цилиндра (через радиусы основания и образующие)


Таким образом:

Определение
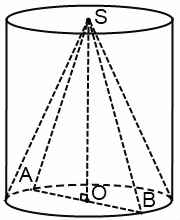
Конус вписан в цилиндр, если основание конуса совпадает с основанием цилиндра, а вершина совпадает с центром другого основания цилиндра. Цилиндр, соответственно, в этом случае называется описанным около конуса.
В любой цилиндр можно вписать конус.
OS — ось цилиндра и ось конуса, высота цилиндра и конуса
OA — радиус конуса и радиус цилиндра
SA=SB=L — образующие конуса,
CA=DB=l — образующие цилиндра
∆SOA, ∆SCA, ∆SDB и ∆SOB — прямоугольные
∆SOA=∆SCA, ∆SDB = ∆SOB, поэтому 2S∆ASB=2SACDB.
Отношение боковой поверхности конуса к боковой поверхности описанного около него цилиндра (через радиус основания и высоту)




2. Комбинация двух конусов
Определение
Конус вписан в другой конус, если его вершина лежит в центре основания второго конуса, а основание лежит на боковой поверхности.
OS — ось конусов, высота большого конуса
OH — высота малого конуса
OA — радиус большого конуса
CH — радиус малого конуса
AS=SB=L
OC=OD=l

Задача
В дне кашпо, имеющего форму конуса с площадью боковой поверхности 15π дм и радиусом основания 3 дм, сделано отверстие для того чтобы в него можно было вставить горшок для цветов, имеющий форму цилиндра. Определите радиус этого отверстия так, чтобы горшок для цветов был вписан в конус и имел форму равностороннего цилиндра.
Дано:
Цилиндр вписан в конус
Sб.п.к.=15π дм
R=3дм
dц =lц
Найти r.
Решение:

AS=L — образующая конуса
KC=l — образующая цилиндра
AO=R – радиус основания конуса
KO=r — радиус цилиндра
πRL=15π
L=15π: (3π)=5
Рассмотрим подобные треугольники AKC и AOS.
В них: 
АО=3 (по условию)
KA=3-r
OS=4 (из прямоугольного треугольника AOS с катетом 3 и гипотенузой 5.
KC=2r 
6r=4(3-r)
6r=12-4r
10r=12
r=1,2 (дм)
Ответ: r=1,2 (дм)
Примеры и разбор решения заданий тренировочного модуля
1. В конус, осевым сечением которого является прямоугольный треугольник, вписан равносторонний цилиндр. Найдите отношение площадей полных поверхностей конуса и цилиндра.
Решение:
Сделаем чертеж осевого сечения
Обозначим радиус цилиндра ЕО= r. Выразим через него все остальные элементы тел вращения.
Так как цилиндр равносторонний, то высота цилиндра равна h=СЕ=2r.
Так как сечение конуса ASB — прямоугольный треугольник и SO — его высота, то SO=OB. То есть высота конуса H равна радиусу R.
Образующая конуса равна L=SA=R
∆SHD

Радиус конуса R=OB=OK+KB.
OK=r, KB=h=2r.
Поэтому R=3r, образующая конуса равна SA=3r
Выразим площади полных поверхностей конуса и цилиндра.
Sп.п.ц. =2πr(r+h)= 2πr(r+2r)=6πr2.
Sп.п.к. =πR(R+L)= π3r(3r+3r

Теперь найдем отношение: 
Ответ: 
2. Усеченный конус вписан в цилиндр. Найдите площадь полной поверхности усеченного конуса, если радиус цилиндра равен 16, высота равна 6 а радиус меньшего основания усеченного конуса в два раза меньше радиуса цилиндра.
Решение:
Сделаем чертеж осевого сечения:
O1B — радиус меньшего основания усеченного конуса.
OC- радиус большего основания усеченного конуса и радиус цилиндра.
BH — высота цилиндра и высота усеченного конуса
По условию OC=2O1B, ОС=16, BH=6.
Так как OC=2O1B и ОС=16, то O1B=8.
Рассмотрим треугольник BHC.
В нем HC=OC-OH=8, BH=6. По теореме Пифагора BC=10.
Теперь нам известен радиус меньшего основания усеченного конуса: он равен 8, радиус большего основания усеченного конуса: он равен 16, образующая усеченного конуса: она равна 10.
Найдем площадь боковой поверхности:
Sб.п.у.к. =πL(r+R)
Sб.п.у.к. =10π(8+16)=240π
Площадь полной поверхности найдем, прибавив две площади оснований:
Sп.п.у.к. =240π+64π+256π=560π
Ответ: Sп.п.у.к. =560π