Как найти высоту куба через площадь

Содержание

  • — Как найти объем по площади и высоте?
  • — Как вычислить объем куба?
  • — Как найти площадь грани куба?
  • — Как найти объём куба с ребром?
  • — Как найти объем зная площадь поверхности?
  • — Как найти объем через площадь физика?
  • — Как вычислить объем прямоугольника?
  • — Как найти объем прямоугольного параллелепипеда формула 5 класс?
  • — Где находится грань кубика?
  • — Чему равны стороны куба?
  • — Как найти объем куба если известна сторона?
  • — Как найти площадь куба если известна длина ребра?

Как найти объем по площади и высоте?

площадь (S) — это произведение длинны и ширины (S= l*b), а объем – произведение длины, ширины и высоты. Подставьте в формулу вычисления объема вместо l*b площадь. Вы получите выражение V=S*h. Пример: Площадь одной из сторон параллелепипеда — 36 см², высота – 10 см.

Как вычислить объем куба?

Куб – это геометрическая фигура, которая представляет собой правильный многогранник, где каждая его грань является квадратом. Объем куба можно вычислить, зная только значение длины его ребра. Так как все его ребра между собой равны. Говоря проще объем куба приравнивается кубу длины его ребра.

Как найти площадь грани куба?

Площадь поверхности куба через сторону

Формула для нахождения площади поверхности куба через его сторону: S = 6 a 2 {S = 6 a^2} S=6a2, где a — сторона куба.

Как найти объём куба с ребром?

Объем = длина*ширина*высота. Ребро куба — это и есть его сторона, а все стороны в кубе равны. Следовательно, V= 1*1*1 = 1 кубический см.

Как найти объем зная площадь поверхности?

Выразите длину ребра через площадь поверхности (a = ³√V) и подставьте в формулу расчета объема: V = 6*(³√V)². Объем сферы (V) можно вычислить и по площади не полной поверхности, а лишь отдельного сегмента (s), высота которого (h) тоже известна.

Как найти объем через площадь физика?

По какой формуле можно найти объем?

  1. Зная массу и плотность V = m/ρ, где m — масса, а ρ — плотность
  2. Для геометрических фигур, например куб V = a^3 перемножить три стороны, а для цилиндра V = S*H площадь основания помножить на высоту

Как вычислить объем прямоугольника?

Объем прямоугольного параллелепипеда равен произведению его длины, ширины и высоты.

Как найти объем прямоугольного параллелепипеда формула 5 класс?

Решение: чтобы ответить на вопрос, нужно воспользоваться формулой для вычисления объёма прямоугольного параллелепипеда. V = а · b · c, где а – длина прямоугольного параллелепипеда. Ответ: объём увеличится в три раза.

Где находится грань кубика?

Глоссарий по теме: Куб — это многогранник, поверхность которого состоит из шести квадратов. Грани куба – это стороны куба, которые представляют собой квадрат. Ребра куба – это стороны граней куба.

Чему равны стороны куба?

Куб – правильный многогранник, каждая грань которого представляет собой квадрат. Все ребра куба равны.

Как найти объем куба если известна сторона?

Каждая сторона куба: длина, ширина и высота — равны между собой. Для вычисления объема куба необходимо длину его стороны возвести в третью степень. Найдите объем куба, если его сторона равна 2 см.

Как найти площадь куба если известна длина ребра?

Все ребра и грани куба равны. Площадь поверхности куба равна квадрату длины его грани умноженному на шесть. Формула для вычисления площади куба S = 6 a2 где S — площадь куба, a — длина грани куба.

Интересные материалы:

Чем подкормить морковь плохо растет?
Чем подкормить морковь во время роста?
Чем подкормить морковку для быстрого роста?
Чем подкормить огурцы чтобы они быстрее росли?
Чем подкормить огурцы чтобы пошли в рост?
Чем подкормить огурцы чтобы росли плоды?
Чем подкормить огурцы чтобы росли завязи?
Чем подкормить огурцы для роста плодов?
Чем подкормить огурцы для улучшения роста?
Чем подкормить огурцы в период роста?

Источник

Geometry and geometrical shapes play a pivotal role in our daily lives. Starting from a simple lunch box to a water tank, geometry surrounds us in different shapes and sizes. The shape and surface to be taken up by such shapes need to be calculated so as to store them without any difficulty, or to meet the needs of the people using them. Such study or computation is given a special name in the field of mathematics.

What is Mensuration?

Whenever the dimensions of various geometrical shapes are computed and their area or capacity is measured in mathematics, it is termed mensuration.

Cuboid 

Such a three-dimensional shape has 6 rectangular faces, 12 edges, and 8 vertices. It is convex in shape and not concave. As a 3D shape, it has a length, height, and width. In other words, when six rectangles are joined together in a certain manner, it forms a cuboid. In real life, we can see a lot of cuboidal shapes around us like tiffin boxes, books, shoebox, bricks, mattresses, etc.

Surface Area of Cuboid

  • Total Surface Area: Since a cuboid is formed by joining 6 rectangles in a definite fashion, the area of a cuboid would be equal to the surface area of all the rectangles combined together. Alternatively, the following formula can be used to calculate the surface area of a cuboid with its length being l, width being w, and height denoted by h.
  • Lateral Surface Area: It is obtained by finding the area of the given cuboid without including the area of the top and base. Thus, when the area of only the sideward faces is calculated, and not that of the top and the base, it amounts to the lateral surface area.

Formulas

Total surface area of a cuboid = 2(lb + bh + lh), where the products of lengths, breadths, heights represent the areas of two rectangles having identical dimensions.

Lateral surface area of a cuboid = 2h (l + b), where the products of lengths, breadths, heights represent the areas of two rectangles having identical dimensions.

How do you find the height of a cuboid when given the surface area?

  • Total Surface Area

Let the surface area be denoted by a, length, breadth and height with l, b, h respectively.

Hence, a = 2(lb + bh + lh)

⇒ a = 2lb + 2bh + 2lh

⇒ a = 2lb + 2h(l + b)

⇒ a − 2lb = 2h(l + b)

⇒ h(l + b) = frac{a − 2lb}{2}

⇒ h = frac{a-2lb}{2(l + b)}

  • Lateral Surface Area

Let the surface area be denoted by a, length, breadth and height with l, b, h respectively.

⇒ x = 2h (l + b)

⇒ 2h = frac{x}{(l + b)}

⇒ h = frac{x}{2(l + b)}

Sample Questions

Question 1. Find the height of a cuboid given that its total surface area is 108 sq. units, length 4 units, and breadth 6 units.

Solution:

Let the height be h units.

We know, h = frac{a-2lb}{2(l + b)}, whenever total surface area is given.

⇒ h = frac{108-2(4)(6)}{2(4+6)}

⇒ h = 60/20

⇒ h = 3 units

Question 2. Find the height of a cuboid given that its total surface area is 216 sq. units, length 4 units, and breadth 6 units.

Solution:

Let the height be h units.

We know, h = frac{a-2lb}{2(l + b)}, whenever total surface area is given.

⇒ h = frac{216-2(4)(6)}{2(4+6)}

⇒ h = 168/ 20

⇒ h = 8.4 units

Question 3. Find the height of a cuboid given that its lateral surface area is 216 sq. units, length 4 units, and breadth 6 units.

Solution:

Let the height be h units.

We know,  h = frac{x}{2(l + b)}, whenever lateral surface area is given.

⇒ h = frac{216}{2(4+6)}

⇒ h = 216/20

⇒ h = 10.8 units

Question 4. Find the height of a cuboid given that its lateral surface area is 108 sq. units, length 4 units, and breadth 6 units.

Solution:

Let the height be h units.

We know,  h = frac{x}{2(l + b)} , whenever lateral surface area is given.

⇒ h = frac{108}{2(4+6)}

⇒ h = 108/ 20

⇒ h = 5.4 units

Last Updated :
26 Oct, 2021

Like Article

Save Article

Источник

Как найти объем через площадь

Объем – мера вместимости, выраженная для геометрических фигур в виде формулы V=l*b*h. Где l – длина, b – ширина, h – высота объекта. При наличии только одной либо 2-х колляций вычислить объем в большинстве случаев невозможно. Впрочем при некоторых условиях представляется допустимым сделать это через площадь .

Инструкция

1. Задача первая: вычислить объем, зная высоту и площадь . Это самая простая задача, т.к. площадь (S) – это произведение длинны и ширины (S= l*b), а объем – произведение длины, ширины и высоты. Подставьте в формулу вычисления объема взамен l*b площадь . Вы получите выражение V=S*h.Пример: Площадь одной из сторон параллелепипеда – 36 см?, высота – 10 см. Обнаружьте объем параллелепипеда.V = 36 см? * 10 см = 360 см?.Результат: Объем параллелепипеда равен 360 см?.

2. Задача вторая: вычислить объем, зная только площадь

. Это допустимо, если вы вычисляете объем куба, зная площадь одной из его граней. Т.к. ребра куба равны, то извлекая из значения площади квадратный корень, вы получите длину одного ребра. Эта длина будет и высотой, и шириной.Пример: площадь одной грани куба – 36 см?. Вычислите объем.Извлеките квадратный корень из 36 см?. Вы получили длину – 6 см. Для куба формула будет иметь вид: V = a?, где а – ребро куба. Либо V = S*a, где S – площадь одной стороны, а – ребро (высота) куба.V = 36 см? * 6 см = 216 см?. Либо V = 6?см = 216 см?.Результат: Объем куба равен 216 см?.

3. Задача третья: вычислить объем, если вестима площадь и некоторые другие данные. Данные могут быть различные, помимо площади могут быть знамениты другие параметры. Длина либо ширина могут быть равны высоте, огромнее либо поменьше высоты в несколько раз. Также могут даваться добавочные данные о фигурах, которые помогут в вычислениях объема.Пример 1: обнаружьте объем призмы, если знаменито, что


площадь одной стороны 60 см?, длина 10 см, а высота равна ширине.S = l * b; l = S : bl = 60 см? : 10 см = 6 см – ширина призмы. Т.к. ширина равна высоте, вычислите объем:V=l*b*hV = 10 см * 6 см *6 см = 360 см?Результат:объем призмы 360 см?

4. Пример 2: обнаружьте объем фигуры, если площадь 28 см?, длина фигуры 7 см. Дополнительное условие: четыре стороны равны между собой, и объединены друг с ином по ширине.Для решения следует возвести параллелепипед. l = S : bl = 28 см? : 7 см = 4 см – ширинаКаждая сторона представляет собой прямоугольник, длина которого 7 см, а ширина 4 см. Если четыре таких прямоугольника объединить между собой по ширине, то получится параллелепипед. Длина и ширина в нем по 7 см, а высота 4 см. V = 7 см * 7 см * 4 см = 196 см?Результат: Объем параллелепипеда = 196 см?.

Онлайн калькулятор: Объем геометрических фигур

Данная статья содержит калькуляторы для расчета объема различных геометрических фигур. Основной источник формул: Spiegel, Murray R. Mathematical Handbook of Formulas and Tables. Schaum’s Outline series in Mathematics. McGraw-Hill Book Co., 1968.

Объем куба

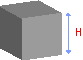
Размеры кубаРазмеры куба

Формула:

PLANETCALC, Объем куба

Объем куба

Длина ребра куба (H)

Точность вычисления

Знаков после запятой: 5

save Сохранить extension Виджет

Объем прямоугольной призмы

Размеры прямоугольной призмыРазмеры прямоугольной призмы

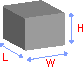
Формула:

PLANETCALC, Объем прямоугольной призмы

Объем прямоугольной призмы

Точность вычисления

Знаков после запятой: 5

save Сохранить extension Виджет

Объем пирамиды

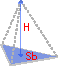
Размеры пирамидыРазмеры пирамиды

Формула:

PLANETCALC, Объем пирамиды

Объем пирамиды

Площадь основания

Точность вычисления

Знаков после запятой: 5

save Сохранить extension Виджет

Объем усеченной пирамиды

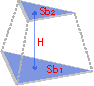
Размеры усеченной пирамидыРазмеры усеченной пирамиды

Формула:

PLANETCALC, Объем усеченной пирамиды

Объем усеченной пирамиды

Точность вычисления

Знаков после запятой: 5

Как найти объем через площадь

Объем – мера вместимости, выраженная для геометрических фигур в виде формулы V=l*b*h. Где l – длина, b – ширина, h – высота объекта. При наличии только одной или двух характеристик вычислить объем в большинстве случаев нельзя. Однако при некоторых условиях представляется возможным сделатьэто через площадь.Как найти объем через площадь

Задача первая: вычислить объем, зная высоту и площадь. Это самая простая задача, т.к. площадь (S) -это произведение длинны и ширины (S= l*b), а объем – произведение длины, ширины и высоты. Подставьте в формулу вычисления объема вместо l*bплощадь. Вы получитевыражение V=S*h.Пример: Площадь одной из сторон параллелепипеда — 36 см², высота – 10 см. Найдите объем параллелепипеда.V = 36 см² * 10 см = 360 см³.Ответ: Объем параллелепипеда равен 360 см³.

Задача вторая: вычислить объем, зная только площадь. Это возможно, если вы вычисляете объем куба, зная площадь одной из его граней. Т.к. ребра куба равны, то извлекая из значения площади квадратный корень, вы получите длину одного ребра. Эта длина будет и высотой, и шириной.Пример: площадь одной грани куба — 36 см². Вычислите объем.Извлекитеквадратный корень из 36 см². Вы получили длину – 6 см. Для куба формула будет иметь вид: V = a³, где а – ребро куба. Или V = S*a, где S – площадь одной стороны, а – ребро (высота) куба.V = 36 см² * 6 см = 216 см³. Или V = 6³см = 216 см³.Ответ: Объем куба равен 216 см³.

Задача третья: вычислить объем, если известна площадь и некоторые другие условия.Условия могут быть разные, помимо площади могут быть известны другие параметры. Длина или ширина могут быть равны высоте, больше или меньше высоты в несколькораз. Также могут даваться дополнительные сведения о фигурах, которые помогут в вычислениях объема.Пример 1: найдите объем призмы, если известно, что площадь одной стороны 60 см², длина 10 см, а высота равна ширине.S = l * b; l = S : b
l = 60 см² : 10 см = 6 см – ширина призмы. Т.к. ширина равна высоте, вычислите объем:

V=l*b*h
V = 10 см * 6 см *6 см = 360 см³Ответ:объем призмы 360 см³

Пример 2: найдите объем фигуры, если площадь 28 см², длина фигуры 7 см. Дополнительное условие: четыре стороны равны между собой, и соединены друг с другом по ширине.Для решения следует построить параллелепипед. l = S : b
l = 28 см² : 7 см = 4 см – ширинаКаждая сторона представляет собой прямоугольник, длина которого 7 см, а ширина 4 см. Если четыре таких прямоугольника соединить между собой по ширине, то получится параллелепипед. Длина и ширина в нем по 7 см, а высота 4 см. V = 7 см * 7 см * 4 см = 196 см³Ответ: Объем параллелепипеда = 196 см³.

Строительный объем здания: что это такое, как считается общий строительный объем

Например, длина двух параллельных зданий — 30 м, их ширина — 15 м. Размеры перехода — 2,5 на 6 м. Значит, сначала нужно найти площадь одинаковых зданий: умножаем 15 на 30, получаем 450 м². Площадь перехода — 15 м². Складываем три площади: 450 + 450 + 15, получается 915 м². Если высота здания составляет 3 м, то строительный объем будет 2745 м³.

Здания с чердачными перекрытиями

Если в здании есть чердачное перекрытие, то строительный объем надземной части считают по особой формуле:

X = S¹ × h.

В этом случае под S¹ понимают площадь горизонтального сечения здания. Ее измеряют на уровне первого этажа выше цоколя, по внешнему обводу здания. Чтобы найти площадь, нужно также умножить ширину на длину здания, как и в расчетах по другим формулам.

Высоту h измеряют от верха чистого пола на первом этаже до верха засыпки чердачного перекрытия.

Допустим, площадь горизонтального сечения здания на уровне первого этажа составляет 420 м². Высота составляет 25 м. В этом случае строительный объем будет равен 10500 м³.

Если у здания есть поздемная часть, ее объем считают так же, как и в предыдущих случаях, а затем оба значения складывают.

Дома без чердачного перекрытия

Строительный объем надземной части зданий без чердачных перекрытий считают по другой формуле:

X = S² × L

S² — тоже площадь поперечного сечения, но не горизонтального, а вертикального. Ее измеряют по наружным стенам, тоже с учетом слоя штукатурки и облицовки. В этом случае для определения площади нужна высота здания и его ширина.

L — это длина здания, перпендикулярная прямая относительно вертикального поперечного сечения. Ее измеряют от одного торца здания к другому, тоже с учетом штукатурки и облицовки, на уровне первого этажа либо цоколя.

Например, нужно рассчитать объем здания высотой 6 м, длиной 23 м и шириной 4 м. Площадь вертикального поперечного сечения в этом случае составит 24 м², а строительный объем — 552 м³.

Если у здания есть подземная часть, ее также считают отдельно, а потом полученные значения суммируют.

Если известна общая площадь

Детальные данные, например, длину, высоту до определенных перекрытий и другие, не всегда указывают в технической документации. Поэтому строительный объем можно посчитать по другим формулам.

Если известна общая площадь, можно использовать формулу:

X = S × H × К

В этом случае S — сумма площадей всех этажей, или общая площадь. Ее измеряют по внутренней обводке наружных стен, то есть не учитывается их толщина. Кроме того, замеряют также площадь подвала, поэтому отдельных расчетов для подземной части не нужно.

H в формуле — высота здания изнутри без учета перекрытий, так называемая высота в свету.

К — поправочный коэффициент, который учитывает толщину стен. Для жилых зданий он составляет 0,8.

То есть для расчета нужно знать всего два точных значения: общую площадь и высоту в свету. Допустим, площадь составляет 2 000 м², а высота в свету — 15 м. В этом случае показатель составит 24000 м³ с учетом поправочного коэффициента.

Если известна площадь застройки

Если известна площадь застройки, можно использовать другую формулу. В ней больше переменных, и выглядит она так:

X = S¹ × H¹ + S² × H²

S¹ в этом случае — площадь общей застройки. Ее можно найти, представив здание в виде геометрической фигуры или нескольких таких фигур, если постройка сложной формы. H¹ — высота дома, в которой можно не учитывать выступающие части крыши.

S² и H² — площадь и высота подвала соответственно. Площадь замеряют по внутренней обводке стен. Высоту — от верхней точки пола подвала до пола первого этажа.

Дома с мансардами

Мансарда — этаж в чердачном пространстве, фасад которого частично либо полностью образован поверхностями наклонной крыши. Обязательное условие — линия пересечения плоскости крыши и фасада должна находиться не больше, чем на высоте 1,5 м от уровня пола в мансарде. Согласно нормативам, строительный объем мансарды считается отдельно.

Чтобы найти строительный объем мансарды, нужно умножить площадь ее поперечного вертикального сечения на длину дома.

Ширину и высоту нужно измерять по внешнему обводу, вертикаль — до начала перекрытий. Все эти данные понадобятся для того, чтобы найти площадь вертикального сечения. Она равна половине произведения ширины, то есть основания, на высоту. Например, высота мансарды — 1,5 м, ширина, то есть основание — 6 м. Тогда площадь составит 9 м².

Полученное значение нужно умножить на длину дома. Например, она составляет 12 м. В этом случае строительный объем мансарды составит 108 м².

Оставшуюся надземную часть нужно считать по предыдущим формулам, но высоту измерять до начала основания мансарды, то есть до верхнего перекрытия. Объемы мансарды, надземной и подземной частей нужно просто сложить.

Если здание имеет сложную форму

Расчет строительного объема для зданий сложной формы — например, с мезонинами, башенками и различными пристроями — намного сложнее. В этом случае нужно сначала найти строительный объем каждого конструктивного элемента, а потом сложить полученные значения.

Полная формула расчета строительного объема зависит от исходных данных — есть ли подвал, предусмотрены ли чердачные перекрытия, построена ли мансарда. Чтобы получить точное значение, нужно провести тщательные замеры и использовать сложные схемы подсчета. Если не хотите тратить время на это, обратитесь к профессионалам — они посчитают все быстрее и точнее.

Как найти объем помещения. Как рассчитать, посчитать объем помещения

Как найти объем помещения фотоКак рассчитать, посчитать объем помещения.

Оценка объема помещений довольно часто требуется при производстве строительных и ремонтных работ. В большинстве случаев это требуется для уточнения количества материалов, необходимых для проведения ремонта, а также для подбора эффективной системы отопления или кондиционирования воздуха. Количественные характеристики, описывающие пространство, как правило, требуют проведения некоторых измерений и несложных вычислений.

1. Самый простой случай – когда требуется определить объем помещения правильной прямоугольной или квадратной формы. При помощи рулетки измерьте в метрах длину и ширину стен, а также высоту помещения. Удобнее всего проводить измерения по полу, вдоль плинтусов. Перемножьте полученные показатели длинны, ширины, высоты и вы получите искомый объем.

2. Если помещение имеет неправильную или сложную форму, задача немного усложняется. Разбейте площадь помещения на несколько простых фигур (прямоугольников, квадратов, полуокружностей и так далее) и вычислите площадь каждой из них, предварительно произведя замеры. Сложите полученные значения, суммируя площадь. Умножьте сумму на высоту помещения. Измерения необходимо проводить в одних и тех же единицах, например, в метрах.

3. При проведении строительных работ определение объема всего сооружения определяется по стандартам. Так называемый строительный объем наземной части здания с чердаком можно вычислить, умножив площадь горизонтального сечения по внешним обводам на уровне нижнего этажа. Измерьте полную высоту здания от уровня чистого пола до верхней части утеплителя чердачного перекрытия. Перемножьте оба показателя.

4. При наличии разных по площади этажей общий объем помещений в здании определите, сложив объемы всех частей. Таким же образом определяется объем, если помещения имеют разные очертания и конструкцию.

5. Отдельно вычислите объемы веранд, эркеров, тамбуров и иных вспомогательных элементов сооружения (за исключением крытых и открытых балконов). Включите эти данные в общий объем всех помещений здания. Таким образом можно легко найти объем любого помещения или здания, расчеты довольно просты, пробуйте и будьте внимательны.

Формула объема помещения

Формула

Пример расчета объема помещения по формуле

Калькулятор площади стены или пола

Вставьте размеры помещения и получите результат.

Как посчитать объем помещения в м3 калькулятор – площадь в метрах кубических

Как посчитать объем помещения

Объем – геометрический термин, позволяющий измерить количественные характеристики жилого и нежилого пространства.

Определить объемы помещения можно, обладая сведениями о его линейных размерах и характеристиками формы. Объем очень тесно переплетается с характеристиками вместимости. Наверняка каждому знакомы такие термины как внутренний объем сосуда или какой-либо тары.

Единица измерения объема классифицируется в соответствии с всемирными стандартами. Существует специальная система измерений – СИ, в соответствии с которой кубический метр, литр или сантиметр выступает метрической единицей объема.

Любое помещение, будь-то жилая комната или производственное помещение – имеет свои характеристики объема. Если рассматривать любое помещение с точки зрения геометрии, то комната сравнима с параллелепипедом. Это шестигранная фигура, в случае с комнатой грани ее – это стены, пол и потолок. Каждая из сторон комнаты – это прямоугольник. Как известно из геометрии, существует формула нахождения объема прямоугольного параллелепипеда. Объем данной фигуры вычисляется посредством умножения трех главных измерений параллелепипеда – длины, ширины и высоты граней. Также вычислить объем помещения можно по более простой формуле – площадь пола умножают на высоту комнаты.

Как узнать объём комнаты

Итак, каким же образом производят вычисления объема конкретной комнаты? Вначале измеряем длину стены, самой длинной в комнате. Затем определяем длину самой короткой стены в комнате. Все эти измерения проводятся на уровне пола, по линии пролегания плинтусов. При измерениях рулеточная лента должна располагаться ровно. Настал черед измерить и высоту потолка. Для этого необходимо провести рулетку от пола до потолка в одном из углов комнаты.

Все измерения необходимо записывать, с точностью до десятых частей. После этого можно приступить непосредственно к вычислению объемов комнаты. Берем длину самой большой стены, умножаем ее на длину самой маленькой стены, затем полученный результат умножаем на высоту комнаты. В итоге получаем необходимые цифры – объем комнаты.

Вычислить объем помещения бывает нужно в самых разных ситуациях. Так, объем комнаты нужно знать при установке секционного радиатора отопления. Количество секций в нем прямо зависит от объемов комнаты. Если устанавливается кондиционер, также нужно знать объемы помещения, поскольку отдельный кондиционер предназначен только для конкретного объема помещения.

Объём помещения сложной формы

В том случае, когда комната имеет неправильную форму, нужно исходить снова же, из фигуры параллелепипеда. В данном случае комната будет представлена большим и маленьким объемным телом. Так вот, объем нужно измерить отдельно у большого параллелепипеда, а затем – у маленького. После этого два объема складываются между собой. Бывает, что строение комнаты совершенно нестандартное, могут присутствовать арки и ниши полукруглой формации. В данном случае объемы нужно вычислять по другой формуле – объем цилиндра. Объем цилиндра всегда вычисляется по единой формуле – площадь его основания умножается на высоту цилиндрического тела. Полукруглые конструкции в комнате можно представить частью цилиндра, исходя из этого делаются расчеты полного объема цилиндра, а затем из них отнимается лишняя часть, в соответствии с размерами полукруглой ниши.

Как найти объем помещения

Оценка объема помещений довольно часто требуется при производстве строительных и ремонтных работ. В большинстве случаев это требуется для уточнения количества материалов, необходимых для проведения ремонта, а также для подбора эффективной системы отопления или кондиционирования воздуха. Количественные характеристики, описывающие пространство, как правило, требуют проведения некоторых измерений и несложных вычислений.

1. Самый простой случай – когда требуется определить объем помещения правильной прямоугольной или квадратной формы. При помощи рулетки измерьте в метрах длину и ширину стен, а также высоту помещения. Удобнее всего проводить измерения по полу, вдоль плинтусов. Перемножьте полученные показатели длинны, ширины, высоты и вы получите искомый объем.

2. Если помещение имеет неправильную или сложную форму, задача немного усложняется. Разбейте площадь помещения на несколько простых фигур и вычислите площадь каждой из них, предварительно произведя замеры. Сложите полученные значения, суммируя площадь. Умножьте сумму на высоту помещения. Измерения необходимо проводить в одних и тех же единицах, например, в метрах.

3. При проведении строительных работ определение объема всего сооружения определяется по стандартам. Так называемый строительный объем наземной части здания с чердаком можно вычислить, умножив площадь горизонтального сечения по внешним обводам на уровне нижнего этажа. Измерьте полную высоту здания от уровня чистого пола до верхней части утеплителя чердачного перекрытия. Перемножьте оба показателя.

4. При наличии разных по площади этажей общий объем помещений в здании определите, сложив объемы всех частей. Таким же образом определяется объем, если помещения имеют разные очертания и конструкцию.

5. Отдельно вычислите объемы веранд, эркеров, тамбуров и иных вспомогательных элементов сооружения. Включите эти данные в общий объем всех помещений здания. Таким образом можно легко найти объем любого помещения или здания, расчеты довольно просты, пробуйте и будьте внимательны.

Формула объема помещения

Как посчитать объем помещения

Объём — количественная черта места. Объём помещения определяется его формой и линейными размерами. С понятием объёма плотно сплетено понятие вместимость, другими словами объём внутреннего места сосуда, упаковочного ящика и т. п. Принятые единицы измерения — в ситме измерений СИ и производных от неё — кубический метр м3, кубический сантиметр, литр. Для вас понадобится Для измерения объема помещения для вас будет нужно рулетка, лист бумаги, калькулятор, ручка. 1 Каждое помещение, например комната, представляет собой, с геометрической точки зрения прямоугольный параллелепипед.

Параллелепипед — это большая фигура, у которой 6 граней. и неважно какая из их есть прямоугольником. Формула нахождения объёма прямоугольного параллелепипеда: V=abc. Количество прямоугольного параллелепипеда равен произведению 3-х его измерений. Не считая этой формулы может быть измерить количество помещения умножив площадь пола на высоту.

2 Итак приступайте к вычислениям объема помещения. Определите длину одной стены ,позже определите длину 2-ой стены. Измерения проводите по полу, на уровне плинтуса.Ленту рулетки держите ровно.

На данный момент определите высоту помещения, для этого подойдите к одному из его углов, и точно померьте высоту по углу от пола до потолка. Приобретенные данные запишите на листочек, чтоб не запамятовать.

Как посчитать объем в м3 бетона калькулятор

На данный момент приступайте к вычислениям: умножите длину длинноватой стены на длину недлинной стены, приобретенное произведение умножите на высоту и вы получите требуемый итог.

Объемы помещений вычисляют в различных случаях: 1) в случае приобретения кондюка воздуха, так как кондюки рассчитаны на определенный количество помещений; 2) с случае установки радиаторов отопления в комнатах, так как количество секций в радиаторе находится в зависимости от объема помещения. 3 Если у вас комната неверной формы, другими словами складывается из вроде бы огромного параллелепипеда и малеханького. В данном случае необходимо измерить количество каждого из их раздельно, а позже сложить. Если в вашей комнате есть альков. тогда его количество нужно высчитывать по формуле объема цилиндра. Количество всякого цилиндра равен произведению площади основания на высоту: V=? r2 h, где. – это число «пи» равное 3,14, r2 квадрат радиуса цилиндра, h – высота.

Представьте для себя ваш альков как часть цилиндра, вычислите количество вроде бы всего цилиндра, позже поглядите какую часть этого цилиндра занимает ваш альков,отымите от общего объема лишнюю часть.

Как рассчитать площадь комнаты?

Если комната с четырьмя стенами и имеет стандартную геометрическую фигуру с прямыми углами, тогда необходимо измерить две стенки и умножив полученные две цифры друг на друга мы получим площадь помещения, а для объёма нужно умножить полученный результат на высоту. но это только при правильных геометрических фигурах.

Сложнее находить площадь и размеры, когда форма комнаты неправильного размера, например такого.

Тогда нужно применять все знания геометрии, а именно — разделить комнату на несколько правильных фигур и в соответствии с формулами этих фигур найти их площадь, а потом все результаты сложить вместе, тогда получится общая площадь помещения. Для нахождения высоты необходимо полученный результат общей площади умножить на высоту.

Ещё хуже обстоят дела с нестандартными помещениями с неправильными углами стен и крыши. Тогда придётся переносить все размеры помещения на бумагу, разделять его на правильные фигуры и исходя из каждой фигуры находить её площадь и объём, а потом полученные результаты суммировать.

В площадь помещения не входят выступы окон и прочего, что выше пола, но они входят в расчёт объёма помещения.

Как посчитать площадь помещения

В случае измерения комнаты неправильной формы для более точного подсчета площади рекомендуется разбить ее на прямоугольники. Подсчитав площадь каждого такого участка, можно узнать общую площадь комнаты путем простого суммирования всех полученных результатов.

Если же разбить комнату на прямоугольные участки не представляется возможным, то можно попробовать такие фигуры как треугольник либо сектор круга. Площадь треугольника считается по формуле Герона: S=v**).

Р — полупериметр треугольника, который можно рассчитать таким образом: р=/2

http://denisyakovlev.com

Как посчитать кубатуру помещения зная площадь. Как посчитать объем помещения

Для многих, кто сталкивается с пиломатериалом, вопрос о том, как посчитать кубатуру необрезной и обрезной доски остаётся сложным заданием. В принципе, это довольно легко и просто. Ниже мы рассмотрим основные способы расчёта кубатуры доски.

На уроках геометрии довольно часто приходилось рассчитывать объём чего – либо. Ситуация точно также обстоит с обрезными пиломатериалами. Просто нужно перемножить ширину на высоту и на длину. Естественно, не нужно это делать на целой пачке бруса или доски. Достаточно будет, если вы посчитаете кубатуру одной доски (бруса), затем просто нужно пересчитать общее количество досок в пачке и кубатуру одной доски помножить на посчитанное количество досок. Ещё одно важно правило, при расчёте кубатуры одной доски, все размеры нужно привести к единому измерению, то есть или всё переводится в сантиметры, миллиметры или же в метры. А замеры мы проводим по следующим параметрам: толщина, ширина, длина.

При расчёте кубатуры необрезной доски, тоже измеряется ширина, длина и высота. Только в необрезных пиломатериалах невозможно рассчитать кубатуру одной доски, поэтому доску нужно уложить в пачку, обмерять и применить различные коэффициенты. Для более точного расчёта, лучше всего сложить доску в одну стопку, затем измерить посередине самую широкую и самую тонкую доски, далее сложить эти два показателя и разделить на два. В результате мы получим усреднённую ширину. А длину и высоту измеряем как обычно.

Далее нужно помножить толщину стопки на ширину и длину и применить понижающий коэффициент. По ГОСТу, для полубруса он составляет 0,5, а для необрезной доски 0,63. Но, очень часто, для упрощения расчётов, производители на пилорамах производят отгрузку пиломатериала, которые имеют коэффициент 0,7. Когда таким образом будет посчитана одна стопка, нужно переходить ко второй, третьей и так, до тех пор, пока не будет пересчитан весь пиломатериал.

Как посчитать кубатуру фундамента
  • столбчатый
  • ленточный
  • плитный

При расчёте кубатуры фундамента столбчатого типа, сначала нужно рассчитать кубатуру одного бетонного столбика. Для этого умножается длина на ширину. Если же применяются столбики круглого сечения, то умножается радиус квадрата на коэффициент «Пи – 3,14» и получившийся результат умножаем на высоту столбика. Далее результат перемножается на общее количество столбиков, которые размещены по территории. Это и будет общая кубатура фундамента. В тех случаях, когда столбики соединены раствором, то нужно воспользоваться формулой параллелепипеда.

При расчёте кубатуры фундамента ленточного типа сначала определяется вид сечения. Когда оно одинаковое, то периметр территории умножается на толщину и длину. В том случае, когда оно разное, необходимо просто рассчитать объёмы каждого участка по отдельности и в итоге, сложить все полученные результаты.

Объём — количественная характеристика пространства. Объём помещения определяется его формой и линейными размерами. С понятием объёма тесно связано понятие вместимость, то есть объём внутреннего пространства сосуда, упаковочного ящика и т. п. Принятые единицы измерения — в ситме измерений СИ и производных от неё — кубический метр м3, кубический сантиметр, литр.

Вам понадобится

  • Для измерения объема помещения вам потребуется рулетка, лист бумаги, калькулятор, ручка.

Инструкция

Каждое помещение, например комната, представляет собой, с геометрической точки зрения прямоугольный параллелепипед. Параллелепипед — это объемная фигура, у которой шесть граней (например комната: 4 стены, потолок, пол), и каждая из них является прямоугольником. Формула нахождения объёма прямоугольного параллелепипеда: V=abc. Объем прямоугольного параллелепипеда равен произведению трех его измерений. Кроме этой формулы можно измерить объем помещения умножив площадь пола на высоту.

Итак приступайте к вычислениям объема помещения. Измерьте длину одной стены (длинной стены),потом измерьте длину второй стены (короткой стены). Измерения проводите по полу, на уровне плинтуса.Ленту рулетки держите ровно. Теперь измерьте высоту помещения, для этого подойдите к одному из его углов, и точно померьте высоту по углу от пола до потолка. Полученные данные запишите на листочек, чтобы не забыть. Теперь приступайте к вычислениям: умножите длину длинной стены на длину короткой стены, полученное произведение (число)умножите на высоту и вы получите требуемый результат. помещений вычисляют в различных случаях: 1) в случае покупки кондиционера воздуха, так как кондиционеры рассчитаны на определенный объем помещений- 2) с случае установки радиаторов отопления в комнатах, так как количество секций в радиаторе напрямую зависит от объема помещения.

Если у вас комната неправильной формы, то есть состоит из как бы большого параллелепипеда и маленького. В данном случае необходимо измерить объем каждого из них отдельно, а потом сложить. Если в вашей комнате есть альков (ниша полукруглой формы), тогда его объем нужно высчитывать по формуле объема . Объем всякого цилиндра равен произведению площади основания на высоту: V=? r2 h, где? – это число «пи» равное 3,14, r2 квадрат радиуса цилиндра, h – высота. Представьте себе ваш альков как часть цилиндра, вычислите объем как бы всего цилиндра, потом посмотрите какую часть этого цилиндра занимает ваш альков,отнимите от общего объема лишнюю часть.

Оценка объема помещений довольно часто требуется при производстве строительных и ремонтных работ. В большинстве случаев это требуется для уточнения количества материалов, необходимых для проведения ремонта, а также для подбора эффективной системы отопления или кондиционирования воздуха. Количественные характеристики, описывающие пространство, как правило, требуют проведения некоторых измерений и несложных вычислений.

Инструкция

Самый простой случай – когда требуется определить объем помещения
 правильной прямоугольной или квадратной формы. При помощи рулетки измерьте в метрах длину и ширину стен, а также высоту помещения
. Удобнее всего проводить измерения по полу, вдоль плинтусов. Перемножьте полученные показатели и вы получите искомый объем.

Если помещение имеет неправильную или сложную форму, задача немного усложняется. Разбейте площадь помещения
 на несколько простых фигур (прямоугольников, квадратов, полуокружностей и так далее) и вычислите площадь каждой из них, предварительно произведя замеры. Сложите полученные значения, суммируя площадь. Умножьте сумму на высоту помещения
. Измерения необходимо проводить в одних и тех же единицах, например, в метрах.

При проведении строительных работ определение объема всего сооружения определяется по стандартам. Так называемый строительный объем наземной части здания с чердаком можно вычислить, умножив площадь горизонтального сечения по внешним обводам на уровне нижнего этажа. Измерьте полную высоту здания от уровня чистого пола до верхней части утеплителя чердачного перекрытия. Перемножьте оба показателя.

При наличии разных по площади этажей общий объем помещений в здании определите, сложив объемы всех частей. Таким же образом определяется объем, если помещения
 имеют разные очертания и конструкцию.

Отдельно вычислите объемы веранд, эркеров, тамбуров и иных вспомогательных элементов сооружения (за исключением крытых и открытых балконов). Включите эти данные в общий объем всех помещений здания.

Полезный совет

При измерения радиуса алькова, пользуйтесь ниткой с иголкой, иголку воткните в воображаемый центр цилиндра и тяните нитку до стены, потом измерьте её длину.

Расчетный объем | SkillsYouNeed

На этой странице объясняется, как рассчитать объем твердых объектов, то есть насколько вы можете поместиться в объекте, если, например, вы заполните его жидкостью.

Площадь — это мера того, сколько места находится внутри двухмерного объекта (подробнее см. Нашу страницу: Расчет площади).

Объем — это мера пространства внутри трехмерного объекта. Наша страница, посвященная трехмерным формам, объясняет основы таких форм.

В реальном мире вычисление объема, вероятно, не то, что вы будете использовать так часто, как вычисление площади.

Однако это все еще может быть важным. Возможность рассчитать объем позволит вам, например, определить, сколько у вас есть места для упаковки при переезде, сколько офисного пространства вам нужно или сколько варенья вы можете уместить в банку.

Это также может быть полезно для понимания того, что имеют в виду средства массовой информации, когда говорят о пропускной способности плотины или течении реки.

Calculating Area and Volume. Area is measured in units squared, how many squares will fit into a flat (two dimensional space)? Volume is measured in units cubed, how many cubes will fit into a solid (three-dimensional) object?

Примечание к агрегатам

Площадь выражается в квадратных единицах, потому что это два измерения, умноженные вместе.

Объем выражается в кубических единицах, потому что это сумма трех измерений (длина, ширина и глубина), умноженных вместе. Кубические единицы включают см 3 , м 3 и кубические футы.

ВНИМАНИЕ!

Объем также можно выразить как вместимость по жидкости.

Метрическая система

В метрической системе объем жидкости измеряется в литрах, что напрямую сопоставимо с кубическим размером, поскольку 1 мл = 1 см 3 .1 литр = 1000 мл = 1000 см 3 .

Британская / английская система

В британской / английской системе эквивалентными измерениями являются жидкие унции, пинты, кварты и галлоны, которые нелегко перевести в кубические футы. Поэтому лучше придерживаться жидких или твердых единиц объема.

Подробнее см. На нашей странице Системы измерения

Основные формулы для расчета объема

Объем твердых тел на основе прямоугольников

Area = Width x Length. Volume = Width x Length x Height.

В то время как основная формула для площади прямоугольной формы — длина × ширина, основная формула для объема — длина × ширина × высота.

То, как вы относитесь к различным размерам, не меняет расчет: вы можете, например, использовать «глубину» вместо «высоты». Важно то, что все три измерения умножаются. Вы можете умножать в любом порядке, поскольку это не изменит ответ (подробнее см. Нашу страницу о умножении ).

Коробка размером 15 см в ширину, 25 см в длину и 5 см в высоту имеет объем:
15 × 25 × 5 = 1875 см 3

Объем призм и цилиндров

Эта базовая формула может быть расширена для охвата цилиндров и призм .Вместо прямоугольного конца у вас просто другая форма: круг для цилиндров, треугольник, шестиугольник или любой другой многоугольник для призмы.

Фактически, для цилиндров и призм объем — это площадь одной стороны, умноженная на глубину или высоту формы.

Таким образом, основная формула для определения объема призм и цилиндров:

Площадь формы торца × высота / глубина призмы / цилиндра.

Объем конусов и пирамид

Тот же принцип, что и выше (ширина × длина × высота), выполняется для расчета объема конуса или пирамиды, за исключением того, что, поскольку они достигают точки, объем составляет лишь часть от общего количества, которое было бы, если бы они продолжались. в той же форме насквозь.

Объем конуса или пирамиды составляет ровно одну треть от объема коробки или цилиндра с таким же основанием.

Таким образом, формула:

Площадь основания или торца × высота конуса / пирамиды × 1 / 3

Вернитесь на нашу страницу Расчет площади , если вы не можете вспомнить, как рассчитать площадь круга или треугольника.

Например, чтобы вычислить объем конуса с радиусом 5 см и высотой 10 см:

Площадь внутри круга = πr2 (где π (пи) приблизительно равно 3.14 и r — радиус круга).

В этом примере площадь основания (круга) = πr 2 = 3,14
× 5 × 5 = 78,5 см 2 .

78,5 × 10 = 785

785 × 1/3 = 261,6667 см 3

Calculate the volume of a sphere. 4/3 x pi x radius cubed.

Объем сферы

Как и в случае с кругом, вам нужно π (пи), чтобы вычислить объем сферы.

Формула: 4/3 × π × радиус 3 .

Вам может быть интересно, как вычислить радиус шара.Если не протыкать через него спицу (эффективный, но конечный для мяча!), Есть более простой способ.

Вы можете измерить расстояние вокруг самой широкой точки сферы напрямую, например, с помощью рулетки. Этот круг является окружностью и имеет тот же радиус, что и сама сфера.

Длина окружности вычисляется как радиус 2 x π x.

Чтобы вычислить радиус из окружности, вы:

Разделите окружность на (2 x π) .

Рабочие примеры: расчет объема

Пример 1

Cylinder with length of 20cm and radius of 2.5cm

Вычислите объем цилиндра длиной 20 см, круговой конец которого имеет радиус 2,5 см.

Сначала обработайте площадь одного из круглых концов цилиндра.

Площадь круга равна πr 2 (π × радиус × радиус). π (пи) приблизительно равно 3,14.

Таким образом, площадь конца равна:

3.14 x 2,5 x 2,5 = 19,63 см 2

Объем — это площадь конца, умноженная на длину, и, следовательно, составляет:

19,63 см 2 x 20 см = 392,70 см 3

Sphere with a radius of 2cm and pyramid with a square base of 2.5cm and a height of 10cm.

Пример 2

Что больше по объему: сфера радиусом 2 см или пирамида с основанием 2,5 см в квадрате и высотой 10 см?

Сначала определим объем сферы .

Объем сферы равен 4/3 × π × радиус 3 .

Таким образом, объем сферы:

4 ÷ 3 x 3,14 × 2 × 2 × 2 = 33,51 см 3

Затем вычислите объем пирамиды .

Объем пирамиды 1/3 × площадь основания × высота.

Площадь основания = длина × ширина = 2,5 см × 2,5 см = 6,25 см 2

Объем, следовательно, равен 1/3 x 6,25 × 10 = 20.83см 3

Таким образом, сфера больше по объему, чем пирамида.

Расчет объема твердых тел неправильной формы

Точно так же, как вы можете вычислить площадь неправильных двумерных форм, разбив их на правильные, вы можете сделать то же самое для вычисления объема неправильных твердых тел. Просто разделите твердое тело на более мелкие части, пока не получите только твердые тела, с которыми вы сможете легко работать.

Рабочий пример

Рассчитайте объем водяного цилиндра общей высотой 1 м, диаметром 40 см и полусферической верхней частью.

Irregular solid. Circular base with a diameter of 40cm and with a total height of 1m. Top section is semi-spherical.

Сначала вы делите фигуру на две части: цилиндр и полусферу (полусферу).

Объем сферы равен 4/3 × π × радиус 3 . В этом примере радиус составляет 20 см (половина диаметра). Поскольку верхняя часть полусферической формы, ее объем будет вдвое меньше полной сферы. Таким образом, объем данного участка формы:

.

0,5 × 4/3 × π × 203 = 16,755,16 см 3

Объем цилиндра равен площади основания × высоте.Здесь высота цилиндра — это общая высота за вычетом радиуса сферы, которая составляет 1 м — 20 см = 80 см. Площадь базы 2 грн.

Таким образом, объем цилиндрического сечения данной формы составляет:

80 × π × 20 × 20 = 100 530,96 см 3

Таким образом, общий объем этого резервуара для воды составляет:
100 530,96 + 16 755,16 = 117 286,12 см 3 .

Это довольно большое число, поэтому вы можете преобразовать его в 117.19 литров путем деления на 1000 (поскольку в литре 1000 см 3 ). Однако вполне правильно выразить его как cm 3 , поскольку задача не требует, чтобы ответ был выражен в какой-либо конкретной форме.

В заключение…

Используя эти принципы, если необходимо, теперь вы сможете рассчитать объем практически всего в своей жизни, будь то упаковочный ящик, комната или водяной баллон.

,

Расчетная область | SkillsYouNeed

Площадь — это мера того, сколько места внутри фигуры. Вычисление площади формы или поверхности может быть полезно в повседневной жизни — например, вам может потребоваться знать, сколько краски нужно купить, чтобы покрыть стену, или сколько семян травы вам нужно, чтобы засеять газон.

На этой странице описаны основные сведения, которые необходимо знать для понимания и расчета площадей общих форм, включая квадраты и прямоугольники, треугольники и круги.

Расчет площади методом сетки

Когда фигура рисуется на масштабированной сетке, вы можете найти площадь, подсчитав количество квадратов сетки внутри фигуры.

В этом примере внутри прямоугольника 10 квадратов сетки.

Чтобы найти значение площади с помощью метода сетки, нам нужно знать размер, который представляет квадрат сетки.

В этом примере используются сантиметры, но тот же метод применяется к любой единице длины или расстояния.Например, вы можете использовать дюймы, метры, мили, футы и т. Д.

В этом примере каждый квадрат сетки имеет ширину 1 см и высоту 1 см. Другими словами, каждый квадрат сетки равен одному квадратному сантиметру.

Подсчитайте квадраты сетки внутри большого квадрата, чтобы найти его площадь.

Есть 16 маленьких квадратов, поэтому площадь большого квадрата составляет 16 квадратных сантиметров.

В математике мы сокращаем «квадратные сантиметры» до 2 . 2 означает «квадрат».

Каждый квадрат сетки равен 1 см 2 .

Площадь большого квадрата 16см 2 .

Подсчет квадратов на сетке для определения площади работает для всех форм — если известны размеры сетки. Однако этот метод становится более сложным, когда фигуры не точно соответствуют сетке или когда вам нужно подсчитать доли квадратов сетки.

В этом примере квадрат не точно помещается на сетке.

Мы все еще можем вычислить площадь, считая квадраты сетки.

  • Есть 25 квадратов полной сетки (заштрихованы синим).
  • 10 квадратов полусетки (заштрихованы желтым цветом) — 10 полуквадратов равны 5 полным квадратам.
  • Также есть 1 четверть квадрата (заштрихована зеленым) — (или 0,25 целого квадрата).
  • Сложите целые квадраты и дроби вместе: 25 + 5 + 0,25 = 30,25.

Таким образом, площадь этого квадрата составляет 30,25 см 2 .

Вы также можете записать это как 30¼см 2 .

Хотя использование сетки и подсчет квадратов внутри фигуры — очень простой способ изучения понятий площади, он менее полезен для нахождения точных областей с более сложными формами, когда можно сложить много частей квадратов сетки.

Площадь можно вычислить с помощью простых формул, в зависимости от типа фигуры, с которой вы работаете.

Остальная часть этой страницы объясняет и дает примеры того, как вычислить площадь фигуры без использования системы сеток.

Площади простых четырехугольников:
квадратов, прямоугольников и параллелограммов

Простейшие (и наиболее часто используемые) вычисления площади выполняются для квадратов и прямоугольников.

Чтобы найти площадь прямоугольника, умножьте его высоту на ширину.

Для квадрата вам нужно только найти длину одной из сторон (так как каждая сторона имеет одинаковую длину), а затем умножить это на себя, чтобы найти площадь. Это то же самое, что сказать длину 2 или длину в квадрате.

Рекомендуется проверять, является ли фигура квадратом, измерив две стороны. Например, стена в комнате может выглядеть как квадрат, но когда вы ее измеряете, вы обнаруживаете, что на самом деле это прямоугольник.

Часто в реальной жизни формы могут быть более сложными. Например, представьте, что вы хотите найти площадь пола, чтобы заказать нужное количество ковра.

Типовой план помещения не может состоять из простого прямоугольника или квадрата:

В этом и других подобных примерах фокус состоит в том, чтобы разделить фигуру на несколько прямоугольников (или квадратов).Неважно, как вы разделите фигуру — любое из трех решений даст один и тот же ответ.

Для решений 1 и 2 необходимо создать две фигуры и сложить их площади, чтобы найти общую площадь.

Для решения 3 вы создаете большую форму (A) и вычитаете из нее меньшую форму (B), чтобы найти площадь.

Другая распространенная проблема — найти область границы — фигуру внутри другой фигуры.

В этом примере показана дорожка вокруг поля — ширина дорожки 2 м.

Опять же, в этом примере есть несколько способов определить площадь пути.

Вы можете просмотреть путь как четыре отдельных прямоугольника, вычислить их размеры, а затем их площадь и, наконец, сложить области, чтобы получить итог.

Более быстрый способ — вычислить площадь всей формы и площадь внутреннего прямоугольника. Вычтите внутреннюю площадь прямоугольника из всего, оставив площадь пути.

  • Площадь всей формы составляет 16 м × 10 м = 160 м 2 .
  • Мы можем определить размеры средней секции, потому что знаем, что дорожка по краю имеет ширину 2 метра.
  • Ширина всей формы составляет 16 м, а ширина пути по всей форме — 4 м (2 м слева от формы и 2 м справа). 16 м — 4 м = 12 м
  • То же самое для высоты: 10м — 2м — 2м = 6м
  • Итак, мы подсчитали, что средний прямоугольник имеет размер 12 × 6 м.
  • Таким образом, площадь среднего прямоугольника составляет: 12 м × 6 м = 72 м 2 .
  • Наконец, мы убираем область среднего прямоугольника из области всей формы. 160 — 72 = 88м 2 .

Площадь тропы 88м 2 .

Параллелограмм представляет собой четырехстороннюю форму с двумя парами сторон равной длины — по определению прямоугольник является разновидностью параллелограмма. Однако большинство людей склонны думать о параллелограммах как о четырехсторонних фигурах с наклонными линиями, как показано здесь.

Площадь параллелограмма рассчитывается так же, как и для прямоугольника (высота × ширина), но важно понимать, что высота означает не длину вертикальных (или отклоненных от вертикали) сторон, а расстояние между сторонами.

Из диаграммы вы можете видеть, что высота — это расстояние между верхней и нижней сторонами фигуры, а не длина стороны.

Представьте себе воображаемую линию под прямым углом между верхней и нижней сторонами. Это высота.

Области треугольников

Может быть полезно думать о треугольнике как о половине квадрата или параллелограмма.

A triangle is half of a square or rectangle.

Если вы знаете (или можете измерить) размеры треугольника, то вы можете быстро вычислить его площадь.

Площадь треугольника (высота × ширина) ÷ 2.

Другими словами, вы можете вычислить площадь треугольника так же, как площадь квадрата или параллелограмма, а затем просто разделите свой ответ на 2.

Высота треугольника измеряется по прямой линии от нижней линии (основания) до «вершины» (верхней точки) треугольника.

Вот несколько примеров:

Calculating the area of a triangle

Площадь трех треугольников на диаграмме выше одинакова.

Каждый треугольник имеет ширину и высоту 3 см.

Площадь рассчитана:

(высота × ширина) ÷ 2

3 × 3 = 9

9 ÷ 2 = 4,5

Площадь каждого треугольника составляет 4,5 см 2 .

В реальных ситуациях вы можете столкнуться с проблемой, которая требует от вас найти площадь треугольника, например:

Вы хотите покрасить двускатный конец сарая. Вам нужно посетить магазин украшений только один раз, чтобы получить нужное количество краски.Вы знаете, что литр краски покроет 10 м 2 стены. Сколько краски нужно, чтобы покрыть фронтон?

Gable end (triangle)

Вам нужно три измерения:

A — Общая высота до вершины крыши.

B — Высота вертикальных стен.

C — Ширина здания.

В этом примере измерения:

A — 12,4 м

B — 6,6 м

C — 11,6 м

Следующий этап требует дополнительных расчетов.Представьте себе здание как две формы: прямоугольник и треугольник. По имеющимся у вас измерениям вы можете рассчитать дополнительное измерение, необходимое для определения площади фронтона.

Split the complex shape into simple shapes to calculate area

Размер D = 12,4 — 6,6

D = 5,8 м

Теперь вы можете определить площадь двух частей стены:

Площадь прямоугольной части стены: 6,6 × 11,6 = 76,56 м 2

Площадь треугольной части стены: (5.8 × 11,6) ÷ 2 = 33,64 м 2

Сложите эти две области вместе, чтобы получить общую площадь:

76,56 + 33,64 = 110,2 м 2

Как вы знаете, один литр краски покрывает 10 м 2 стены, поэтому мы можем рассчитать, сколько литров нам нужно купить:

110,2 ÷ 10 = 11,02 л.

На самом деле вы можете обнаружить, что краска продается только в 5-литровых или 1-литровых канистрах, результат — чуть более 11 литров. У вас может возникнуть соблазн округлить до 11 литров, но, если мы не будем разбавлять краску водой, этого будет недостаточно.Таким образом, вы, вероятно, округлите до следующего целого литра и купите две 5-литровые банки и две 1-литровые банки, что в сумме составит 12 литров краски. Это позволит избежать любых потерь и оставит большую часть литра для подкраски позднее. И не забывайте, что если вам нужно нанести более одного слоя краски, вы должны умножить количество краски для одного слоя на количество необходимых слоев!

Области кругов

Чтобы вычислить площадь круга, вам необходимо знать его диаметр или радиус .

Diameter and Radius of a circle

Диаметр круга — это длина прямой линии от одной стороны круга до другой, проходящей через центральную точку круга. Диаметр в два раза больше длины радиуса (диаметр = радиус × 2)

Радиус круга — это длина прямой линии от центральной точки круга до его края. Радиус составляет половину диаметра. (радиус = диаметр ÷ 2)

Вы можете измерить диаметр или радиус в любой точке окружности — важно измерять с помощью прямой линии, проходящей через (диаметр) или заканчивающейся в (радиусе) центра окружности.

На практике при измерении окружностей часто проще измерить диаметр, а затем разделить на 2, чтобы найти радиус.

Радиус нужен для вычисления площади круга, формула:

площадь круга = πR 2 .

Это означает:

π = Pi — постоянная, равная 3,142.

R = радиус окружности.

R 2 (радиус в квадрате) означает радиус × радиус.

Следовательно, круг с радиусом 5 см и имеет площадь:

3.142 × 5 × 5 = 78,55 см 2 .

Круг диаметром 3 м имеет площадь:

Сначала прорабатываем радиус (3м ÷ 2 = 1,5м)

Затем примените формулу:

πR 2

3,142 × 1,5 × 1,5 = 7,0695.

Площадь круга диаметром 3 м составляет 7,0695 м 2 .

Последний пример

В этом примере используется большая часть содержимого этой страницы для решения простых задач области.

Calculating Area - Bloomington Benjamin House example.

Это дом Рубена М. Бенджамина в Блумингтоне, штат Иллинойс, внесенный в Национальный реестр исторических мест США (номер записи: 376599).

Этот пример включает поиск области фасада дома, деревянной решетчатой ​​части — исключая дверь и окна. Вам нужны следующие размеры:

A — 9,7 м B — 7,6 м
C — 8,8 м D — 4,5 м
Е — 2.3 мес. F — 2,7 м
G — 1,2 м H — 1,0 м

Примечания:

  • Все размеры приблизительны.
  • Не стоит беспокоиться о границе вокруг дома — она ​​не учтена в измерениях.
  • Мы предполагаем, что все прямоугольные окна одинакового размера.
  • Размер круглого окна — это диаметр окна.
  • Размер двери включает ступеньки.

Какова площадь деревянной реечной части дома?

Работы и ответы ниже:

Ответы на пример выше

Во-первых, определите площадь основной формы дома — прямоугольника и треугольника, составляющих форму.

Главный прямоугольник (B × C) 7,6 × 8,8 = 66,88 м 2 .

Высота треугольника (A — B) 9,7 — 7,6 = 2,1.

Следовательно, площадь треугольника равна (2.1 × C) ÷ 2.
2,1 × 8,8 = 18,48. 18,48 ÷ 2 = 9,24 м 2 .

Общая площадь фасада дома равна сумме площадей прямоугольника и треугольника:

66,88 + 9,24 = 76,12 м 2 .

Затем проработайте площади окон и дверей, чтобы их можно было вычесть из всей площади.

Площадь двери и ступенек составляет (D × E) 4,5 × 2,3 = 10,35 м 2 .

Площадь одного прямоугольного окна составляет (G × F) 1.2 × 2,7 = 3,24 м 2 .

Есть пять прямоугольных окон. Умножьте площадь одного окна на 5.

3,24 × 5 = 16,2 м2. (общая площадь прямоугольных окон).

Круглое окно имеет диаметр 1 м и радиус 0,5 м.

Используя πR 2 , определите площадь круглого окна: 3,142 × 0,5 × 0,5 =. 0,7855м 2 .

Затем сложите площади двери и окон.

(зона двери) 10,35 + (прямоугольная зона окон) 16.2 + (площадь круглого окна) 0,7855 = 27,3355

Наконец, вычтите общую площадь окон и дверей из всей площади.

76,12 — 27,3355 = 48,7845

Площадь деревянного реечного фасада дома и ответ на проблему: 48,7845м 2 .

Вы можете округлить ответ до 48,8 м 2 или 49 м 2 .

См. Нашу страницу Оценка, приближение и округление .

,

класс — PHP: Как рассчитать объем, диаметр и площадь круга?

Переполнение стека

  1. Около
  2. Товары
  3. Для команд
  1. Переполнение стека
    Общественные вопросы и ответы
  2. Переполнение стека для команд
    Где разработчики и технологи делятся частными знаниями с коллегами
  3. работы
    Программирование и связанные с ним технические возможности карьерного роста
  4. Талант
    Нанимайте технических специалистов и создавайте свой бренд работодателя
  5. реклама
    Обратитесь к разработчикам и технологам со всего мира
  6. О компании

,

Объем сферы — Math Open Reference

Объем сферы — Открытый справочник по математике

Определение:
Количество кубических единиц, которые точно заполнят сферу.

Попробуй это
Перетащите оранжевую точку, чтобы настроить радиус сферы и обратите внимание на изменение объема.


Объем, заключенный в сфере, определяется формулой
Где r — радиус сферы. На рисунке выше перетащите оранжевую точку, чтобы изменить радиус сферы.
и обратите внимание, как формула используется для расчета объема.Поскольку 4, 3 и пи являются константами, это упрощается примерно до

Эта формула была открыта более двух тысяч лет назад греческим философом Архимедом. Он также понял, что объем сферы составляет ровно две трети объема описанной ею сферы.
цилиндр, который является самым маленьким цилиндром, который может содержать сферу.

Если известен объем

Переставив приведенную выше формулу, вы можете найти радиус:

где v — объем

Примечание Большинство калькуляторов не имеют кнопки кубического корня.Вместо этого используйте кнопку калькулятора «поднять до уровня мощности» и поднять внутреннюю часть до уровня мощности на одну треть.

Интересный факт

Для данной площади поверхности сфера — это одно твердое тело, имеющее наибольший объем. Вот почему он так часто появляется в природе, как капли воды, пузыри и планеты.

Что попробовать

    • На рисунке выше нажмите «скрыть детали».
    • Перетащите оранжевую точку, чтобы изменить размер сферы.
    • Рассчитать объем сферы
    • Нажмите «показать подробности», чтобы проверить свой ответ.
    • На рисунке выше нажмите «Сброс», затем снимите флажок «Показать радиус».
    • Перетащите оранжевую точку, чтобы изменить размер сферы.
    • Рассчитать радиус сферы по объему
    • Нажмите «показать радиус», чтобы проверить свой ответ.

Связанные темы

(C) Открытый справочник по математике, 2011 г.
Все права защищены.

,

Источник

Как найти объем через площадь

Объем – мера вместимости, выраженная для геометрических фигур в виде формулы V=l*b*h. Где l – длина, b – ширина, h – высота объекта. При наличии только одной или двух характеристик вычислить объем в большинстве случаев нельзя. Однако при некоторых условиях представляется возможным сделать это через площадь.

Как найти объем через площадь

Инструкция

Задача первая: вычислить объем, зная высоту и площадь. Это самая простая задача, т.к. площадь (S) — это произведение длинны и ширины (S= l*b), а объем – произведение длины, ширины и высоты. Подставьте в формулу вычисления объема вместо l*b площадь. Вы получите выражение V=S*h.Пример: Площадь одной из сторон параллелепипеда — 36 см², высота – 10 см. Найдите объем параллелепипеда.V = 36 см² * 10 см = 360 см³.Ответ: Объем параллелепипеда равен 360 см³.

Задача вторая: вычислить объем, зная только площадь. Это возможно, если вы вычисляете объем куба, зная площадь одной из его граней. Т.к. ребра куба равны, то извлекая из значения площади квадратный корень, вы получите длину одного ребра. Эта длина будет и высотой, и шириной.Пример: площадь одной грани куба — 36 см². Вычислите объем.Извлеките квадратный корень из 36 см². Вы получили длину – 6 см. Для куба формула будет иметь вид: V = a³, где а – ребро куба. Или V = S*a, где S – площадь одной стороны, а – ребро (высота) куба.V = 36 см² * 6 см = 216 см³. Или V = 6³см = 216 см³.Ответ: Объем куба равен 216 см³.

Задача третья: вычислить объем, если известна площадь и некоторые другие условия. Условия могут быть разные, помимо площади могут быть известны другие параметры. Длина или ширина могут быть равны высоте, больше или меньше высоты в несколько раз. Также могут даваться дополнительные сведения о фигурах, которые помогут в вычислениях объема.Пример 1: найдите объем призмы, если известно, что площадь одной стороны 60 см², длина 10 см, а высота равна ширине.S = l * b; l = S : b
l = 60 см² : 10 см = 6 см – ширина призмы. Т.к. ширина равна высоте, вычислите объем:
V=l*b*h
V = 10 см * 6 см *6 см = 360 см³Ответ:объем призмы 360 см³

Пример 2: найдите объем фигуры, если площадь 28 см², длина фигуры 7 см. Дополнительное условие: четыре стороны равны между собой, и соединены друг с другом по ширине.Для решения следует построить параллелепипед. l = S : b
l = 28 см² : 7 см = 4 см – ширинаКаждая сторона представляет собой прямоугольник, длина которого 7 см, а ширина 4 см. Если четыре таких прямоугольника соединить между собой по ширине, то получится параллелепипед. Длина и ширина в нем по 7 см, а высота 4 см. V = 7 см * 7 см * 4 см = 196 см³Ответ: Объем параллелепипеда = 196 см³.

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Источник


Загрузить PDF


Загрузить PDF

Объем трехмерной фигуры является величиной, которая характеризует пространство, занимаемое этой фигурой. Объем равен произведению длины фигуры на ее ширину и на высоту. Куб — это трехмерная фигура, у которой длина, ширина и высота одинаковые, то есть все ребра куба равны.[1]
 Поэтому вычислить объем куба довольно просто, если знать значение его ребра. А ребро можно найти по площади поверхности куба.

  1. Изображение с названием Find the Volume of a Cube from Its Surface Area Step 1

    1

    Запишите формулу для вычисления площади поверхности куба. Формула выглядит так: S=6x^{{2}}, где x — ребро куба.[2]

    • Чтобы вычислить объем куба, нужно перемножить значения трех его ребер (длину, ширину и высоту).[3]
       У куба длина, ширина и высота равны, поэтому нужно найти значение одного (любого) ребра, чтобы вычислить объем куба. Имейте в виду, что для вычисления площади поверхности куба нужно знать значение ребра; поэтому, если площадь поверхности куба дана, вы с легкостью найдете его ребро, а затем вычислите объем куба.

  2. Изображение с названием Find the Volume of a Cube from Its Surface Area Step 2

    2

    В формулу подставьте значение площади поверхности куба. Площадь поверхности должна быть дана в задаче.

  3. Изображение с названием Find the Volume of a Cube from Its Surface Area Step 3

    3

    Разделите значение площади поверхности куба на 6. Так вы найдете значение x^{{2}}.

  4. Изображение с названием Find the Volume of a Cube from Its Surface Area Step 4

    4

    Извлеките квадратный корень. Так вы найдете значение x, то есть значение ребра куба.

    Реклама

  1. Изображение с названием Find the Volume of a Cube from Its Surface Area Step 5

    1

    Запишите формулу для вычисления объема куба. Формула выглядит так: V=x^{{3}}, где V – объем куба, x — ребро куба.[4]

  2. Изображение с названием Find the Volume of a Cube from Its Surface Area Step 6

    2

    В формулу подставьте значение ребра куба. Это значение вы нашли по известной площади поверхности куба.

    • Например, если ребро куба равно 4 см, формула запишется так:
      V=4^{{3}}.

  3. Изображение с названием Find the Volume of a Cube from Its Surface Area Step 7

    3

    Возведите в куб (в третью степень) значение ребра куба. Сделайте это на калькуляторе или просто умножьте «x» на себя три раза. Так вы найдете объем куба в кубических единицах измерения.

    Реклама

Что вам понадобится

  • Карандаш/ручка
  • Бумага

Об этой статье

Эту страницу просматривали 33 350 раз.

Была ли эта статья полезной?

Источник

Понравилась статья? Поделить с друзьями:
  • Нашла социальную карту как найти хозяина
  • Как найти размах данных в алгебре
  • Как найти удаленные сообщения на телефоне ксиоми
  • Как найти сьерра мадре
  • Как составить уравнения для стороны треугольника