Изображение рельефа на топографических картах дает полное
и достаточно подробное представление о неровностях земной поверхности,
их форме и взаимном расположении, превышениях и абсолютных высотах
точек местности, преобладающей крутизне и протяженности скатов.
На современных топографических картах рельеф изображается горизонталями
в сочетании с условными знаками обрывов, скал, оврагов, промоин,
осыпей, оползней и т. д. Изображение рельефа дополняется подписями
абсолютных высот характерных точек местности, горизонталей, размеров
отдельных форм рельефа и указателями направления скатов.
Сущность изображения рельефа горизонталями. Горизонталь
— это замкнутая линия, изображающая на карте горизонтальный контур
неровностей, все точки которого на местности расположены на одной
высоте над уровнем моря. Горизонтали можно представить как линии,
полученные в результате сечения местности уровенными поверхностями,
то есть поверхностями, параллельными уровню воды в океанах.
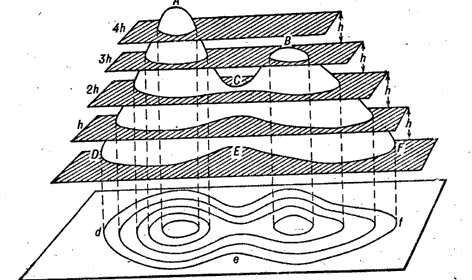
Рис.1 Сущность изображения рельефа горизонталями.
Рассмотрим сущность изображения рельефа горизонталями. На рис.1
изображен остров с вершинами А и Б и береговой линией D, Е, F. Замкнутая
кривая d e f представляет собой изображение береговой линии в плане.
Поскольку береговая линия является сечением острова уроненной поверхностью
океана, изображение этой линии на карте представляет собой нулевую
горизонталь, все точки которой имеют высоту, равную нулю. Допустим,
что уровень океана поднялся на высоту h, тогда образуется новое
сечение острова воображаемой секущей плоскостью h — h. Проектируя
это сечение с помощью отвесных линий, получим на карте изображение
первой горизонтали, все точки которой имеют высоту h. Точно так
же можно получить на карте изображение и других сечений, выполненных
на высотах 2h, Зh, 4h и т. д. В результате на карте будет иметь
место изображение рельефа острова горизонталями. При этом рельеф
острова изображается тремя горизонталями, — охватывающими остров
целиком, и двумя горизонталями, охватывающими отдельно каждую из
вершин. Вершина А несколько выше 4h, а вершина В несколько выше
Зh относительно уровня океана. Скаты возвышенности А круче, чем
скаты возвышенности В, поэтому в первом случае горизонтали на карте
расположены ближе друг к другу, чем во втором. Из рисунка видно,
что способ изображения рельефа горизонталями позволяет правильно
не только отображать формы рельефа, но и определять высоты отдельных
точек земной поверхности по высоте сечения рельефа и крутизне скатов.
Высота сечения рельефа — это разность высот двух смежных
секущих поверхностей. На карте она выражается разностью высот двух
смежных горизонталей. В пределах листа карты высота сечения рельефа,
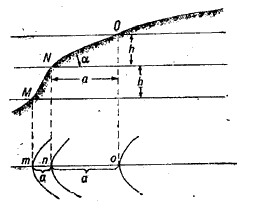
как правило, является постоянной. На рис.2 показан вертикальный
разрез (профиль) ската.
Рис.2 Профиль ската.
Через точки М, N, О проведены уровенные поверхности на расстоянии
друг от друга, равном высоте сечения Л. Пересекая поверхность ската,
они образуют кривые линии, ортогональные проекции которых в виде
трех горизонталей показаны нижней части рисунка. Расстояния mn и
no между горизонталями являются проекциями отрезков MN и NO ската.
Эти проекции называются заложениями горизонталей.
Определение высот точек. Абсолютную высоту какой-либо точки
местности, отметка которой на карте не подписана, определяют по
отметке ближайшей к ней горизонтали. Поэтому необходимо уметь определять
отметки горизонталей, используя отметки других горизонталей и характерных
точек местности, подписанных накарте.
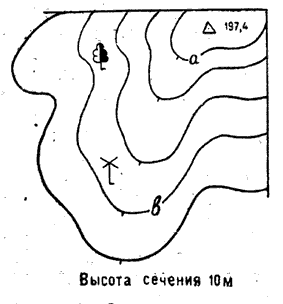
Например, отметку горизонтали а (рис.3) можно определить
по отметке высоты 197,4 и высоте сечения рельефа 10 м.
Рис.3 Определение отметки горизонтали по отметке
точки.
Отметка горизонтали а равна 190 м. Зная отметку горизонтали а, можно
легко определить отметки всех других горизонталей. Так, горизонталь
b будет иметь отметку 160 м, так как она расположена ниже
горизонтали а на величину, равную трем высотам сечения рельефа
(30 м). В случае когда точка расположена между горизонталями, находят
высоту ближайшей к ней горизонтали и к полученной высоте прибавляют
превышение данной точки над горизонталью, определенное на глаз.
Например, мельница, обозначение которой находится между горизонталями
(рис.3), имеет абсолютную высоту 162 м.
Определение взаимного превышения точек заключается в установлении
величины, указывающей, насколько одна точка выше или ниже другой.
При расположении точек на одной горизонтали их взаимное рис превышение
равно нулю, так как их высоты одинаковы. Если определяемые точки
совпадают с точками, высоты которых подписаны на карте, их взаимное
превышение равно разности этих высот.
В случае когда точки расположены на одном скате или на разных скатах
близко друг к другу, подсчитывают число промежутков между горизонталями
и. к целому числу добавляют их доли, которые оценивают на глаз.
Полученное число умножают на высоту сечения рельефа и таким образом
получают взаимное превышение указанных точек.
Когда точки расположены на значительном расстоянии друг от друга,
определяют их абсолютные высоты. Разность этих высот и будет взаимным
превышением точек.
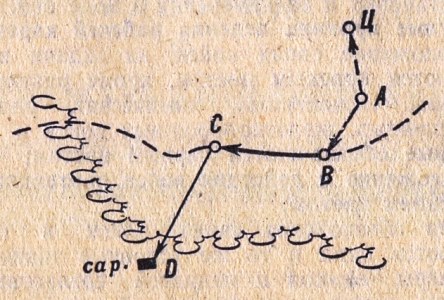
11. Определение по карте высот и взаимного превышения точек местности
Высоты
точек местности над уровнем моря
(абсолютные высоты) определяют по карте
с помощью отметок высот горизонталей
и принятой на карте высоты сечения
рельефа.
Если
точка расположена на горизонтали,
то ее абсолютная высота равна значению
отметки этой горизонтали. Например, на
рис. 19 горизонталь с отметкой 200 проходит
через сарай. Это значит, что сарай
расположен на высоте 200 м над уровнем
моря.
В
случае, когда горизонталь не имеет
подписанной отметки, ее значение
определяют по отметкам других горизонталей
или высот точек местности. Допустим,
требуется определить высоту точки
местности, на которой находится отдельный
камень (рис. 19). Условный знак отдельного
камня расположен на горизонтали без
отметки. Штрихи (указатели скатов) на
горизонталях показывают, что скат
понижается в сторону ручья. Слева от
горизонтали с отдельным камнем находится
утолщенная горизонталь с отметкой 200.
Высота сечения равна 10 м. Значит,
горизонталь, проходящая через условный
знак отдельного камня, имеет отметку
190, которая является высотой точки.
Если
точка находится между горизонталями,
то ее абсолютная высота определяется
по значению отметки высоты одной из
этих горизонталей. Для этого к значению
отметки высоты горизонтали прибавляют
или из нее вычитают (в зависимости от
положения точки относительно горизонтали)
ту часть высоты сечения, на которую
точка удалена от горизонтали.
Рис.
19. Определение по карте высот точек
местности
Например,
нужно определить высоту развилки полевых
дорог (см.
рис. 19). Точка расположена
примерно на 3/4 значения заложения от
нижней горизонтали, имеющей отметку
220, и на 1/4 – от верхней горизонтали с
отметкой 230. Высота сечения рельефа 10
м. Следовательно, поправка к нижней
горизонтали составит 7,5 м, а к верхней
горизонтали – 2,5 м. Прибавляя поправку
к значению отметки нижней горизонтали
или вычитая ее из значения отметки
верхней горизонтали, получим высоту
точки на развилке дорог:
220
м+7,5 м = 227,5 м ≈ 227 м
или
230
м – 2,5 м=227,5 м ≈ 227 м.
Взаимное
превышение точек местности
определяется как разность их абсолютных
высот. Например, превышение высоты с
отметкой 236,3 (см. рис. 19) над оз. Глубокое
(с отметкой 177,8) составляет
236,3
– 177,8 = 58,5 м.
Относительные
высоты скатов вершин и глубины лощин
удобно определять по числу промежутков
между горизонталями на них. Подсчитав
число промежутков между горизонталями
на скате, и умножив его на высоту сечения,
получим относительную высоту ската.
Например, на юго-западном скате высоты
с отметкой 236,3 (см. рис. 19) имеются три
промежутка между основными горизонталями
и один между основной и дополнительной
горизонталями. Высота сечения 10 м,
поэтому относительная высота ската
будет 3,5 *
10 м = 35 м.
Относительные
высоты (глубины) обрывов, оврагов,
промоин, насыпей, выемок определяются
с помощью подписей, стоящих рядом с
условными знаками.
Определение
по карте направления понижения и крутизны
скатов.
Направление
понижения скатов
определяется на карте по указателям
скатов на горизонталях, а также путем
сравнения отметок высот точек и
горизонталей: понижение ската будет
всегда в сторону меньшей отметки; цифры
отметок горизонталей своими основаниями
направлены в сторону понижения ската.
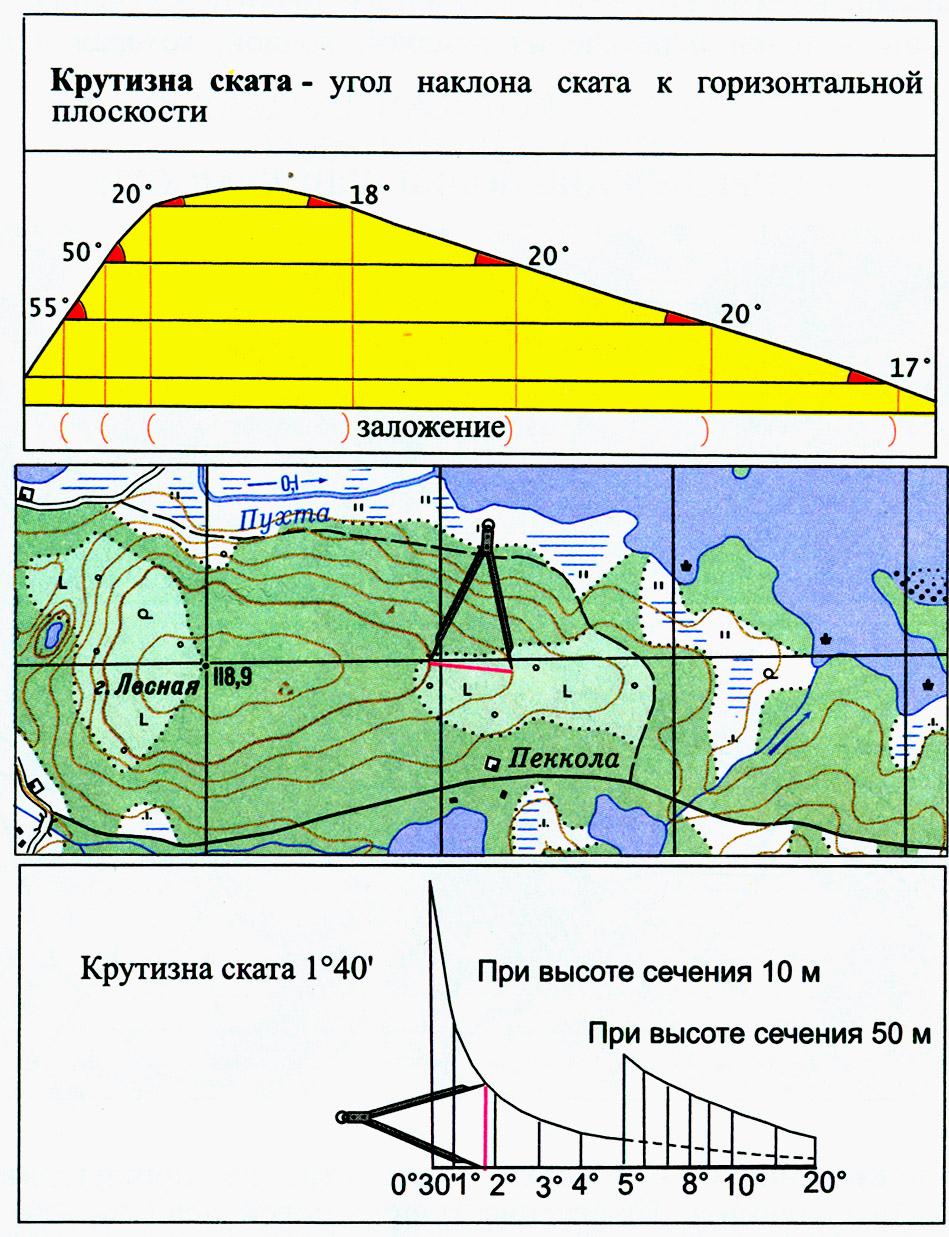
Крутизна
ската
определяется по значению заложения:
чем меньше значение заложения, тем скат
круче; чем больше значение заложения,
тем скат более пологий. На топографических
картах масштаба 1:25 000, 1:50 000 и
1:100 000 основная высота сечения рельефа
подобрана таким образом, что заложению
между основными горизонталями в 1 см
соответствует крутизна ската 1,2°
(округленно 1°).
Из
этой зависимости между заложением,
высотой сечения и крутизной ската можно
вывести следующее правило: во сколько
раз заложение меньше (больше) 1 см, во
столько раз крутизна ската больше
(меньше) 1°. Отсюда следует, что заложению
в 1 мм соответствует крутизна ската 12°
(округленно 10°), заложению в 2 мм – 6°
(округленно 5°), заложению в 5 мм – 2,4°
(округленно 2°) и т. д.
Более
точно крутизна ската может быть определена
с помощью специального графика,
называемого шкалой заложений (рис. 20),
которая располагается под южной стороной
рамки карты. Вдоль горизонтального
основания шкалы подписаны цифры,
обозначающие крутизну скатов в градусах.
На перпендикулярах к основанию отложены
соответствующие им заложения. Шкала
заложений дается для двух высот сечений:
одна – для заложений между основными
горизонталями, другая – для заложений
между утолщенными горизонталями.
Для
определения крутизны ската по шкале
заложений следует измерить расстояние
между двумя смежными сплошными
горизонталями в нужном направлении и
отложить его на шкале заложений так,
как показано на рис. 20. Отсчет внизу на
шкале против отложенного отрезка укажет
крутизну ската в градусах. В нашем
примере крутизна ската равна 1,8°. На
крутых скатах, где горизонтали проходят
близко одна от другой, крутизну удобнее
определять по утолщенным горизонталям.
Для этого измеряют отрезок между
соседними утолщенными горизонталями,
отложив его на правой части шкалы.
Рис.
20. Определение крутизны скатов.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Глава 1. Военная топография в допризывной подготовке молодежи
Раздел 4. Измерения на местности и целеуказание
§ 1.4.1. Угловые меры и формула тысячной
Градусная мера.
Основная единица — градус (1/90 прямого угла); 1° = 60′; 1’=60″.
Радианная мера.
Основная единица радиан — центральный угол, стягиваемый дугой, равной радиусу. 1 радиан равен приблизительно 57°, или, примерно, 10 больших делений
угломера (см.ниже).
Морская мера.
Основная единица — румб, равная 1/32 части окружности (10°1/4).
Часовая мера.
Основная единица — угловой час (1/6 прямого угла, 15°); обозначается буквой h, при этом: 1h = 60m, 1m = 60 s (m – минуты, s — секунды).
Артиллерийская мера.
Из курса геометрии известно, что длина окружности равна 2πR, или 6,28R (R – радиус окружности). Если окружность разделить на 6000 равных частей, то
каждая такая часть будет равна примерно одной тысячной длины окружности (6,28R/6000 = R/955 ≈ R/1000). Одна такая часть длины окружности называется тысячной (или делением угломера) и является основной единицей артиллерийской меры. Тысячная широко
используется в артиллерийских измерениях, поскольку позволяет легко переходить от угловых единиц к линейным единицам и обратно: длина дуги, соответствующая
делению угломера, на всех расстояниях равна одной тысячной длины радиуса, равного дальности стрельбы (рис.4.1).
Рис. 4.1
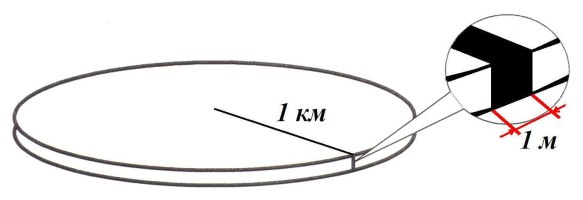
Формула, показывающая взаимосвязь дальности до цели, высоты (длины) цели и ее угловой величины называется формулой тысячной и применяется
не только в артиллерии, но и в военной топографии:
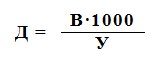
где Д — расстояние до предмета, м; В — линейный размер предмета (длина, высота или ширина), м;У — угловая величина предмета в тысячных. Запоминанию формулы тысячной способствуют такие образные выражения, как: « Дунул Ветер, Тысяча Упала», или: «
Веха высотой 1 м, удалённая от наблюдателя на 1 км, видна под
углом в 1 тысячную
».
Следует учитывать, что формула тысячных применима при не слишком больших углах — условной границей применимости формулы считается угол в 300 тысячных
(18?).
Углы, выраженные в тысячных, записываются через дефис и читаются раздельно: сначала сотни, а затем десятки и единицы; при отсутствии сотен или десятков
записывается и читается ноль. Например: 1705 тысячных записываются «17-05», читаются – «семнадцать ноль пять»; 130 тысячных записываются «1-30», читаются – « один тридцать»; 100 тысячных записываются «1-00», читаются – «один ноль»;
одна тысячная записывается «0-01», читается – «ноль ноль один».
Деления угломера, записанные до дефиса, иногда называют большими делениями угломера, а записанные после дефиса — малыми; одно большое деление угломера
равно 100 малым делениям.
Деления угломера в градусную меру и обратно можно перевести, пользуясь следующими соотношениями:
1-00 = 6°; 0-01 = 3,6′ = 216″; 0° = 0-00; 10′ ≈ 0-03; 1° ≈ 0-17; 360° = 60-00.
Единица измерения углов, подобная тысячной, существует и в вооружённых силах стран НАТО. Там она называется mil (сокращение от milliradian), но определяется как 1/6400 окружности. В армии Швеции, не входящей в НАТО, принято наиболее точное определение в 1/6300 окружности. Однако, делитель 6000, принятый в советской, российской и финской армиях, лучше подходит для устного счёта, так как он делится без остатка на 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 30, 40, 50, 60, 100, 150, 200, 250, 300, 400, 500 и т.д. вплоть до 3000, что позволяет быстро переводить в тысячные углы, полученные грубым измерением на местности подручными средствами.
§ 1.4.2. Измерение углов, расстояний (дальностей), определение высоты предметов
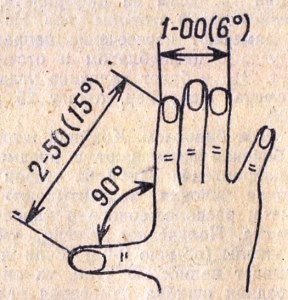
Рис. 4.2 Угловые величины между пальцами руки, вытянутой на 60 см от глаза
Измерение углов в тысячных может производиться различными способами:
глазомерно, с помощью циферблата часов, компаса, артиллерийской буссоли, бинокля, снайперского прицела, линейки, и т.д.
Глазомерное определение угла
заключается в сопоставлении измеряемого угла с известным. Углы определенной величины можно получить следующими способами. Прямой угол получается между
направлением рук, одна из которых вытянута вдоль плеч, а другая — прямо перед собой. От составленного таким приемом угла можно отложить какую-то часть его,
имея в виду, что 1/2 часть соответствует углу 7-50 (45°), 1/3 — углу 5-00 (30°) и т.д. Угол 2-50 (15°) получается путем визирования через большой и
указательный пальцы, расставленные под углом 90° и удаленные на 60 см от глаза, а угол 1-00 (6°) соответствует углу визирования на три сомкнутых пальца:
указательный, средний и безымянный (рис.4.2).
Определение угла по циферблату часов.
Часы держат перед собой горизонтально и поворачивают их так, чтобы штрих, соответствующий 12 часам на циферблате, совместился с направлением левой
стороны угла. Не меняя положения часов, замечают пересечение направления правой стороны угла с циферблатом и отсчитывают количество минут. Это и будет
величина угла в больших делениях угломера. Например, отсчет 25 минут соответствует 25-00.
Определение угла компасом.
Визирное приспособление компаса предварительно совмещают с начальным штрихом лимба, а затем визируют по направлению левой стороны измеряемого угла и, не
меняя положения компаса, против направления правой стороны угла снимают отсчет по лимбу. Это и будет величина измеряемого угла или его дополнение до 360°
(60-00), если подписи на лимбе идут против хода часовой стрелки.
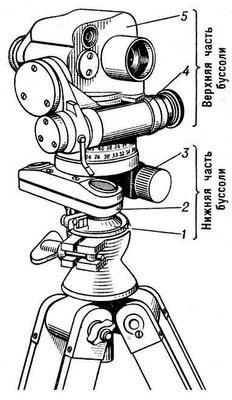
Рис. 4.3 Буссоль
Величину угла компасом можно определить более точно, измерив азимуты направлений сторон угла. Разность азимутов правой и левой сторон угла будет
соответствовать величине угла. Если разность получится отрицательной, то необходимо прибавить 360° (60-00). Средняя ошибка определения угла этим способом
составляет 3-4°.
Определение угла артиллерийской буссолью ПАБ-2А
(буссоль — прибор для топографической привязки и управления артиллерийским огнем, представляющий собою соединение компаса с угломерным кругом и оптическим
приспособлением, рис.4.3).
Для измерения горизонтального угла буссоль устанавливают над точкой местности, выводят пузырек уровня на середину и трубу последовательно наводят сначала
на правый, потом на левый предмет, точно совмещая вертикальную нить перекрестия сетки с точкой наблюдаемого предмета.
При каждом наведении снимают отсчет по буссольному кольцу и барабану. Затем выполняют второй прием измерений, для чего буссоль поворачивают на
произвольный угол и повторяют действия. В обоих приемах величина угла получается как разность отсчетов: отсчет на правый предмет минус отсчет на левый
предмет. За окончательный результат принимают среднее значение.
При измерении углов буссолью каждый отсчет складывается из отсчета больших делений буссольного кольца по указателю, отмеченному буквой Б, и малых делений
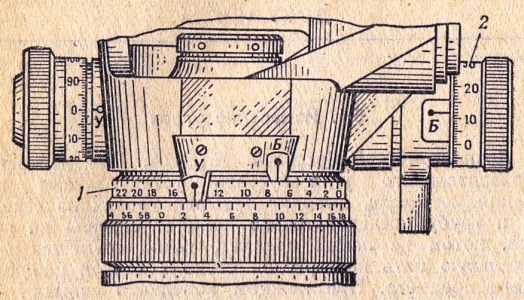
буссольного барабана, обозначенного той же буквой. Пример отсчетов на рис.4.4 по буссольному кольцу — 7-00, по буссольному барабану — 0-12; полный отсчет
— 7-12.
Рис. 4.4 Отсчетное устройство буссоли, используемое для измерения горизонтальных углов:
1 — буссольное кольцо;
2 — буссольный барабан
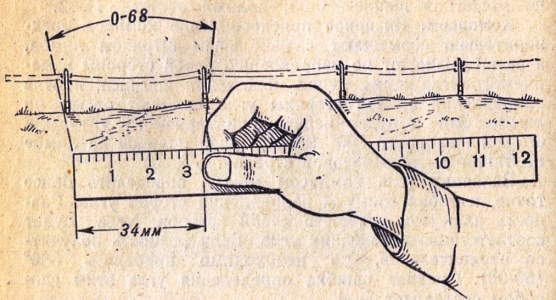
С помощью линейки
. Если линейку держать на расстоянии 50 см от глаз, то деление в 1 мм будет соответствовать 0-02. При удалении линейки от глаз на 60 см 1 мм соответствует
6′, а 1 см — 1°. Для измерения угла в тысячных линейку держат перед собой на расстоянии 50 см от глаз и подсчитывают число миллиметров между предметами,
обозначающими направления сторон угла. Полученное число умножают на 0-02 и получают величину угла в тысячных (рис.4.5). Для измерения угла в градусах
порядок действий тот же, только линейку необходимо держать на расстоянии 60 см от глаз.
Рис. 4.5 Измерение угла линейкой, удаленной на 50 см от глаза наблюдателя
Точность измерения углов с помощью линейки зависит от умения выносить линейку точно на 50 или на 60 см от глаз. В этой связи можно рекомендовать следующее:
к артиллерийскому компасу привязывается шнурок такой длины, чтобы линейка компаса, повешенного на шею и отнесенного вперед на уровень глаза наблюдателя,
оказывалась от него на расстоянии ровно 50 см.
Пример: зная, что среднее расстояние между столбами линии связи, изображенными на рис.1.4.5, составляет 55 м, вычисляем расстояние до них по формуле
тысячной: Д = 55 x 1000 / 68 = 809 м (линейные размеры некоторых предметов приведены в таблице 4.1)
.
| Объект | Размер |
| Расстояние между столбами линии связи | 50-60 м |
| Дом сельского типа (высота) | 6-7 м |
| Деревянный столб линии связи (высота) | 5-7 м |
| Один этаж жилого дома (высота) | 3-4 м |
| Железнодорожный вагон (высота) |
4 м |
| Танк (высота) | 2,5-3 м |
| Автомобиль грузовой (высота) | 2-2,5 м |
| Человек среднего роста |
1,7 м |
Таблица 4.1
Измерение угла биноклем
. Крайний штрих шкалы в поле зрения бинокля совмещают с предметом, расположенным в направлении одной из сторон угла, и, не меняя положения бинокля,
подсчитывают число делений до предмета, расположенного в направлении другой стороны угла (рис.4.6). Полученное число умножают на цену делений шкалы
(обычно 0-05). Если шкала бинокля не захватывает полностью угол, то он измеряется по частям. Средняя ошибка измерения угла биноклем составляет 0-10.
Рис. 4.6
Пример
(рис.4.6): угловая величина американского танка «Абрамс», определенная по шкале бинокля, составила 0-38, учитывая, что ширина танка составляет 3,7 м,
расстояние до него, вычисленное по формуле тысячной, Д = 3,7х1000 / 38 ≈ 97 м.
Рис. 4.7
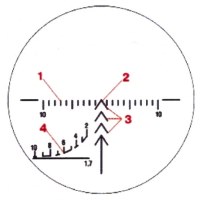
Измерение угла снайперским прицелом ПСО-1
. На сетке прицела нанесены (рис.4.7): шкала боковых поправок (1); основной (верхний) угольник для прицеливания при стрельбе до 1000 м
(2); дополнительные угольники (ниже шкалы боковых поправок по вертикальной линии) для прицеливания при стрельбе на 1100, 1200 и 1300 м (3); дальномерная
шкала в виде сплошной горизонтальной и кривой пунктирной линий (4).
Шкала боковых поправок обозначена снизу (влево и вправо от угольника) цифрой 10, что соответствует десяти тысячным (0-10). Расстояние между двумя
вертикальными черточками шкалы соответствует одной тысячной (0-01). Высота угольника и длинного штриха шкалы боковых поправок соответствует двум тысячным
(0-02). Дальномерная шкала рассчитана на высоту цели 1,7 м (средний рост человека). Это значение высоты цели указано под горизонтальной линией. Над верхней
пунктирной линией нанесена шкала с делениями, расстояние между которыми соответствует расстоянию до цели в 100 м. Цифры шкалы 2, 4, 6, 8, 10 соответствуют
расстояниям 200, 400, 600, 800, 1000 м. Определить дальность до цели с помощью прицела можно по дальномерной шкале (рис.4.8), а также по шкале боковых
поправок (см. алгоритм измерения углов биноклем).
Рис. 4.8
Зная расстояние до предмета в метрах и его угловую величину в тысячных можно вычислить его высоту по формуле В = Д x У / 1000, полученной
из формулы тысячных.
Пример: расстояние до башни 100 м, а ее угловая величина от основания до верха 2-20, соответственно, высота башни В = 100 x 220 / 1000
= 22 м.
Глазомерное определение расстояний
производится по признакам видимости (степени различаемости) отдельных предметов и целей (табл.4.2).
| Признаки видимости | Дальность |
| Видны дома сельского типа | 5 км |
| Различаются окна в домах | 4 км |
| Видны отдельные деревья, трубы на крышах | 3 км |
| Видны отдельные люди; танки от автомобилей (БТР, БМП) отличить трудно | 2 км |
| Танк можно отличить от автомобиля (БТР, БМП); видны столбы линий связи | 1,5 км |
| Виден ствол пушки; различаются стволы деревьев в лесу | 1 км |
| Заметны движения рук и ног идущего (бегущего) человека | 0,7 км |
| Видны командирская башенка танка, дульный тормоз, заметно движение гусениц | 0,5 км |
Таблица 4.2
Расстояние (дальность) глазомерно можно определить сравнением с другим, заранее известным расстоянием (н-р, с расстоянием до ориентира) или отрезками
100, 200, 500 м.
На точность глазомерного определения расстояний существенно влияют условия наблюдения:
- ярко освещенные предметы кажутся ближе слабо освещенных;
- в пасмурные дни, дождь, сумерки, туман все наблюдаемые предметы кажутся дальше, чем в солнечные дни;
- крупные предметы кажутся ближе мелких, находящихся на том же расстоянии;
- предметы яркой окраски (белой, желтой, оранжевой, красной) кажутся ближе темных (черных, коричневых, синих);
- в горах, а также при наблюдении через водные пространства предметы кажутся ближе, чем в действительности;
- при наблюдении лежа предметы кажутся ближе, чем при наблюдении стоя;
- при наблюдении снизу вверх предметы кажутся ближе, а при наблюдении сверху вниз — дальше;
- при наблюдении ночью светящиеся объекты кажутся ближе, а затемненные — дальше, чем в действительности.
Глазомерно определенное расстояние может быть уточнено следующими приемами:
-
расстояние мысленно делят на несколько равных отрезков (частей), затем возможно точнее определяют величину одного отрезка и путем умножения получают
искомую величину; - расстояние оценивается несколькими наблюдателями, а за окончательный результат принимается среднее значение.
Глазомерно расстояние до 1 км при достаточной опытности можно определить со средней ошибкой порядка 10—20% дальности. При определении больших расстояний
ошибка может доходить до 30—50%.
Определение дальности по слышимости звука
применяется в условиях плохой видимости, преимущественно ночью. Примерные дальности слышимости отдельных звуков при нормальном слухе и благоприятных
условиях погоды приведены в таблице 4.3.
| Объект и характер звука | Дальность слышимости |
| Негромкий разговор, кашель, негромкие команды, заряжание оружия и т.п. | 0,1-0,2 км |
| Забивка в землю кольев вручную (равномерно повторяющиеся удары) | 0,3 км |
| Рубка или пилка леса (стук топора, визг пилы) |
0,4 км |
| Движение подразделения в пешем строю (ровный глухой шум шагов) | 0,3-0,6 км |
| Падение срубленных деревьев (треск сучьев, глухой удар о землю) | 0,8 км |
| Движение автомобилей (ровный глухой шум мотора) | 0,5-1,0 км |
| Громкий крик, отрывка окопов (удары лопаты о камни) | 1,0 км |
| Гудки автомобилей, одиночные выстрелы из автомата | 2-3 км |
| Стрельба очередями, движение танков (лязг гусениц, резкий рокот моторов) | 3-4 км |
| Орудийная стрельба | 10-15 км |
Таблица 4.3
Точности определения расстояний по слышимости звуков невысокая. Она зависит от опытности наблюдателя, остроты и натренированности его слуха и умения
учитывать направление и силу ветра, температуру и влажность воздуха, характер сладок рельефа, наличие экранирующих поверхностей, отражающих звук, и другие
факторы, влияющие на распространение звуковых волн.
Определение дальности по звуку и вспышке (выстрела, взрыва)
. Определяют время от момента вспышке до момента восприятия звука и вычисляют дальность о формуле:
Д = 330·t
,
где Д — расстояние до места вспышки, м; t — время от момента вспышки до момента восприятия звука, с.
При этом средняя скорость распространения звука принимается равной 330 м/с (Пример: звук был услышан через 10 с после вспышки, соответственно, расстояние до места взрыва равно 3300 м).
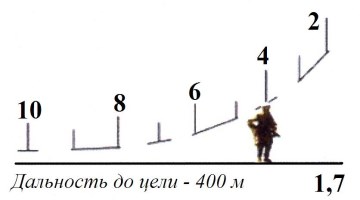
Определение дальности с помощью мушки АК
. Определение дальности до цели, сформировав соответствующий навык, можно осуществлять с помощью мушки и прорези прицела АК. При этом необходимо учитывать,
что мушка полностью покрывает мишень №6 (ширина мишени 50 см) на дистанции 100 м; мишень умещается в половине ширины мушки на дистанции 200 м;
мишень умещается в четверти ширины мушки на дистанции 300 м (рис.4.9).
Рис. 4.9 Определение дальности с помощью мушки АК
Определение дальности промером шагами
. При измерении расстояний шаги считают парами. Пару шагов можно принимать в среднем за 1,5 м. Для более точных подсчетов длину пары шагов определяют из
промера шагами линии не менее 200 м, длина которой известна из более точных измерений. При равном, хорошо выверенном шаге погрешность измерения не
превышает 5% пройденного расстояния.
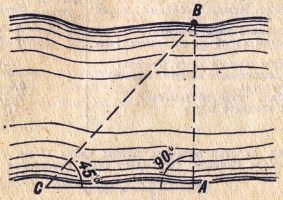
Определение ширины реки (оврага и других препятствий) построением равнобедренного прямоугольного треугольника
(рис.4.10).
Рис. 4.10 Определение ширины реки построением равнобедренного прямоугольного треугольника
У реки (препятствия) выбирают точку А так, чтобы на ее противоположной стороне был виден какой-либо ориентир В и, кроме того, вдоль реки возможно было бы измерить линию. В точке А восстанавливают
перпендикуляр АС к линии АВ и в этом направлении измеряют расстояние (шнуром, шагами
и т.п.) до точки С, в которой угол АСВ будет равен 45°. В этом случае расстояние АС
будет соответствовать ширине препятствия АВ. Точку С находят путем приближения, измеряя
несколько раз угол АСВ каким-либо доступным способом (компасом, с помощью часов или глазомерно).
Определение высоты предмета по его тени
. У объекта устанавливают в вертикальном положении веху (шест, лопату и т.п.), высота которой известна. Затем измеряют длину тени от вехи и от предмета.
Высоту предмета подсчитывают по формуле
h = d1·h1 / d ,
где h – высота предмета, м; d1 – высота тени от вехи, м;h1 – высота вехи, м; d – длина тени от предмета, м. Пример: длина тени от дерева 42 м, а от шеста высотой 2 м – 3 м, соответственно, высота дерева h = 42·2 / 3 = 28 м.
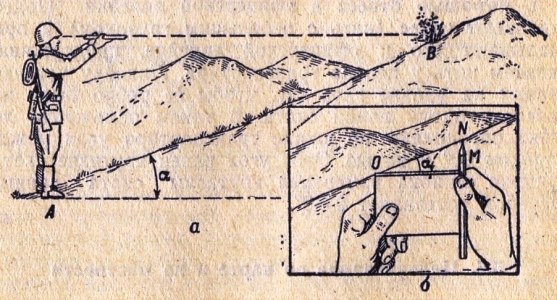
§ 1.4.3. Определение крутизны скатов
Горизонтальным визированием и промером шагами
. Располагаясь внизу ската в точке А (рис.4.11-а), устанавливают горизонтально на уровне глаз линейку, визируют вдоль нее и замечают на
скате точку В. Затем парами шагов измеряют расстояние АВ и определяют крутизну ската по формуле:
α = 60 / n ,
где α – крутизна ската, град; n – количество пар шагов. Данный способ применим при крутизне ската до 20-25°;
точность определения 2-3°.
Сравнением высоты ската с его заложением
. Становятся сбоку ската и, удерживая перед собой на уровне глаз горизонтально, ребро папки и вертикально карандаш, как показано на рис.4.11-б,
определяют на глаз или путем измерения число, показывающее, во сколько раз выдвинутая часть карандаша MN короче ребра папки ОМ.
Затем 60 делят на полученное число и в результате определяют крутизну ската в градусах.
Для большей точности определения соотношений высоты ската и его заложения рекомендуется измерить длину ребра папки, а вместо карандаша использовать линейку
с делениями. Способ применим при крутизне ската не более 25-30°; средняя ошибка определения крутизны ската составляет 3-4°.
Рис. 4.11 Определение крутизны ската:
а – горизонтальным визированием и промером шагами;
б – сравнением высот ската с заложением
Пример:
высота выдвинутой части карандаша равна 10 см, длина ребра папки 30 см; соотношение заложения и высоты ската равно 3 (30:10); крутизна ската будет 20°
(60:3).
С помощью отвеса и офицерской линейки
. Подготавливают отвес (нить с небольшим грузиком) и прикладывают его к офицерской линейке, придерживая пальцем нить у центра транспортира. Линейку
устанавливают на уровне глаз так, чтобы ее ребро было направлено вдоль линии ската. В таком положении линейки определяют по шкале транспортира угол
между штрихом 90° и нитью. Этот угол равен крутизне ската. Средняя ошибка измерения крутизны ската данным способом составляет 2-3°.
§ 1.4.4. Линейные меры
- Аршин = 0,7112 м
- Верста = 500 саженей = 1,0668 км
- Дюйм = 2,54 см
- Кабельтов = 0,1 морской мили = 185,3 м
- Километр = 1000 м
- Линия = 0,1 дюйма = 10 точек = 2,54 мм
- Лье (Франция) = 4,44 км
- Метр = 100 см = 1000 мм = 3,2809 фута
- Миля морская (США, Англия, Канада) = 10 кабельтовых = 1852 м
- Миля статутная (США, Англия, Канада) = 1,609 км
- Сажень = 3 аршина = 48 вершков = 7 футов = 84 дюйма = 2,1336 м
- Фут = 12 дюймов = 30,48 см
- Ярд = 3 фута = 0,9144 м
§ 1.4.5. Целеуказание по карте и на местности
Целеуказание – это краткое, понятное и достаточно точное указание местоположения целей и различных пунктов на карте и непосредственно на местности.
Целеуказание (указание пунктов) по карте
производится по квадратам координатной (километровой) или географической сетки, от ориентира, прямоугольными или географическими координатами.
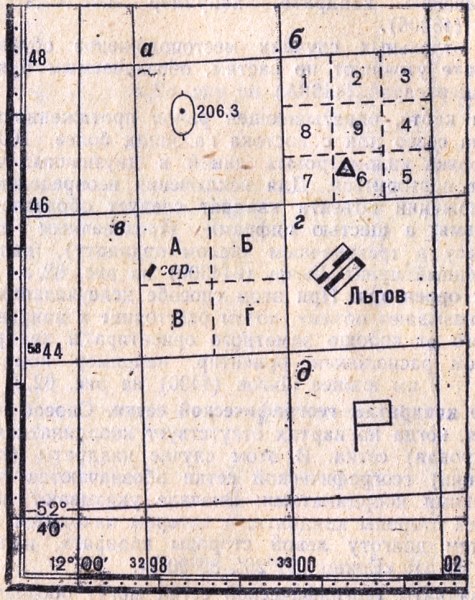
Рис. 4.12 Целеуказание по квадратам координатной (километровой) сетки
Целеуказание по квадратам координатной сетки
(рис.4.12-а). Квадрат, в котором находится объект, указывают подписями километровых линий. Вначале дается оцифровка нижней горизонтальной линии
квадрата, а затем левой вертикальной линии. В письменном документе квадрат указывают в скобках после наименования объект, например, выс. 206,3 (4698). При устном докладе вначале указывают квадрат, а затем наименование объекта: «Квадрат сорок шесть девяносто восемь, высота
двести шесть и три»
Для уточнения местоположения объекта квадрат мысленно делят на 9 частей, которые обозначают цифрами, как показано на рис.4.12-б. Цифру, уточняющую
положение объекта внутри квадрата, добавляют к обозначению квадрата, например наблюдательный пункт (46006).
В отдельных случаях местоположение объекта в квадрате уточняют по частям, обозначаемым буквами, например, сарай (4498А) на рис.4.12- в.
На карте, охватывающей район протяженностью с юга на север или с востока на запад более 100 км, оцифровка километровых линий в двузначных числах может
повториться. Для исключения неопределенности в положении объекта квадрат следует обозначать не четырьмя, а шестью цифрами (трехзначным числом абсциссу и
трехзначным числом ординату), например, населенный пункт Льгов (844300) на рис.4.12-г.
Целеуказание от ориентира
. При этом способе целеуказания вначале называют объект, потом расстояние и направление до него от хорошо заметного ориентира и квадрат, в котором
расположен ориентир, например командный пункт — 2 км южнее Льгов (4400) на рис.4.12-д.
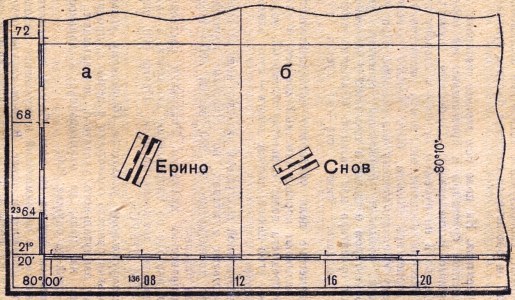
Целеуказание по квадратам географической сетки
. Способ применяется, когда на картах отсутствует координатная (километровая) сетка. В этом случае квадраты (точнее, трапеции) географической сетки
обозначаются географическими координатами. Вначале указывают широту нижней стороны квадрата, в котором находится пункт, а затем долготу левой стороны
квадрата, например (рис.4.13-а): «Ерино (21°20′, 80°00′)». Квадраты географической сетки могут обозначаться и оцифровкой ближайших
выходов километровых линий, если они показаны на сторонах рамки карты, например (рис.4.13-б): «Снов (6412)».
Рис. 4.13 Целеуказание по квадратам географической сетки
Целеуказание прямоугольными координатами
— наиболее точный способ; применяется для указания местоположения точечных целей. Цель обозначают полными или сокращенными координатами.
Целеуказание географическими координатами
применяется сравнительно редко — при использовании карт без километровых сеток для точного указания места нахождения отдельных удаленных объектов. Объект
обозначают географическими координатами: широтой и долготой.
Целеуказание на местности
выполняют различными способами: от ориентира, от направления движения, по азимутальному указателю и др. Способ целеуказания выбирают, сообразуясь с
конкретной обстановкой, так, чтобы он обеспечивал наиболее быстрое отыскание цели.
От ориентира
. На поле боя заранее выбирают хорошо заметные ориентиры и присваивают им номера или условные наименования. Ориентиры нумеруют справа налево и по рубежам
от себя в сторону противника. Местонахождение, вид, номер (наименование) каждого ориентира должны быть хорошо известны выдающему и принимающему
целеуказание. При указании цели называют ближайший ориентир, угол между ориентиром и целью в тысячных и удаление в метрах от ориентира или позиции: « Ориентир второй, вправо тридцать, ниже сто — в кустах пулемет».
Малозаметные цели указывают последовательно — вначале называют хорошо заметный предмет, а затем от этого предмета цель: « Ориентир четвертый, вправо двадцать — угол пашни, дальше двести — куст, влево — танк в окопе».
При визуальной воздушной разведке цель от ориентира указывают в метрах по сторонам горизонта: « Ориентир двенадцатый, юг 200, восток 300 — шестиорудийная батарея».
От направления движения
. Указывают расстояние в метрах вначале по направлению движения, а затем от направления движения до цели: «Прямо 500, вправо 200 — БМ ПТУРС».
Трассирующими пулями (снарядами) и сигнальными ракетами
. Для указания целей этим способом заранее устанавливают ориентиры, порядок и длину очередей (цвет ракет), а для приема целей назначают наблюдателя с
задачей наблюдать за указанным районом и докладывать о появлении сигналов.
§ 1.4.6. Нанесение на карту целей и других объектов
На глаз.
На ориентированной карте опознают ближайшие к объекту ориентиры или контурные точки; оценивают расстояния и направления от них до объекта и, соблюдая их
соотношения, наносят на карту точку, соответствующую местоположению объекта. Способ применяется при наличии вблизи объекта местных предметов, изображенных
на карте.
По направлению и расстоянию.
На исходной точке тщательно ориентируют карту и с помощью линейки прочерчивают направление на объект. Затем, определив расстояние до объекта, откладывают
его по прочерченному направлению в масштабе карты и получают положение объекта на карте. При невозможности графического решения задачи измеряют магнитный
азимут на объект и переводят его в дирекционный угол, по которому прочерчивают направление на карте, а затем на этом направлении откладывают расстояние до
объекта. Точность нанесения на карту объекта данным способом зависит от ошибок определения расстояния до объекта и прочерчивания направления на него.
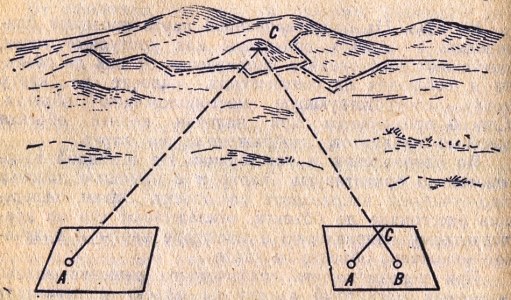
Рис. 4.14 Нанесение на карту объекта прямой засечкой
Прямой засечкой.
На исходной точке А (рис.4.14) тщательно ориентируют карту, визируют по линейке на определяемый объект и прочерчивают направление. Аналогичные
действия повторяют на исходной точке В. Точка пересечения двух направлений определит положение объекта С на карте.
В условиях, затрудняющих работу с картой, на исходных точках измеряют магнитные азимуты на объект, а затем азимуты переводят в дирекционные углы и по ним
прочерчивают направления на карте.
Этот способ применяется, если определяемый объект виден с двух исходных точек, доступных для наблюдения. Средняя ошибка положения на карте объекта,
нанесенного прямой засечкой, относительно исходных точек составляет 7-10% средней дальности до объекта при условии, что угол пересечения направлений
(угол засечки) находится в пределах 30-150°. При углах засечки менее 30? и более 150° ошибка положения объекта на карте будет значительно больше. Точность
нанесения объекта может быть несколько повышена путем засечки его с трех точек. В этом случае при пересечении трех направлений обычно образуется
треугольник, центральная точка которого принимается за положение объекта на карте.
Прокладкой хода.
Способ применяется в тех случаях, когда объект не виден ни с одной контурной (исходной) точки, например в лесу. На исходной точке, расположенной возможно
ближе к определяемому объекту, ориентируют карту и, наметив наиболее удобный путь к объекту, прочерчивают направление на какую-либо промежуточную точку.
На этом направлении откладывают соответствующее расстояние и определяют положение промежуточной точки на карте. С полученной точки такими же приемами
определяют положение на карте второй промежуточной точки и далее подобными действиями определяют все последующие точки хода до объекта.
В условиях, исключающих работу с картой на местности, вначале измеряют азимуты и длины всех линий хода, записывают их и одновременно чертят схему хода.
Затем в подходящих условиях по этим данным, преобразовав магнитные азимуты в дирекционные углы, наносят ход на карту и определяют положение объекта.
Рис. 4.15 Нанесение на карту объекта прокладкой компасного хода
При обнаружении цели в лесу или в других условиях, затрудняющих определение своего местоположения, ход прокладывают в обратном порядке (рис.4.15). Вначале
с точки наблюдения А определяют азимут и расстояние до цели Ц, а затем от точки А прокладывают ход до точки D, которую
можно безошибочно опознать на карте. В этом случае азимуты линий хода переводят в обратные, обратные азимуты — в дирекционные углы и по ним строят на карте
ход от твердой точки.
Средняя ошибка нанесения объекта на карту данным способом при определении азимутов компасом, а расстояний шагами составляет примерно 5% длины хода.
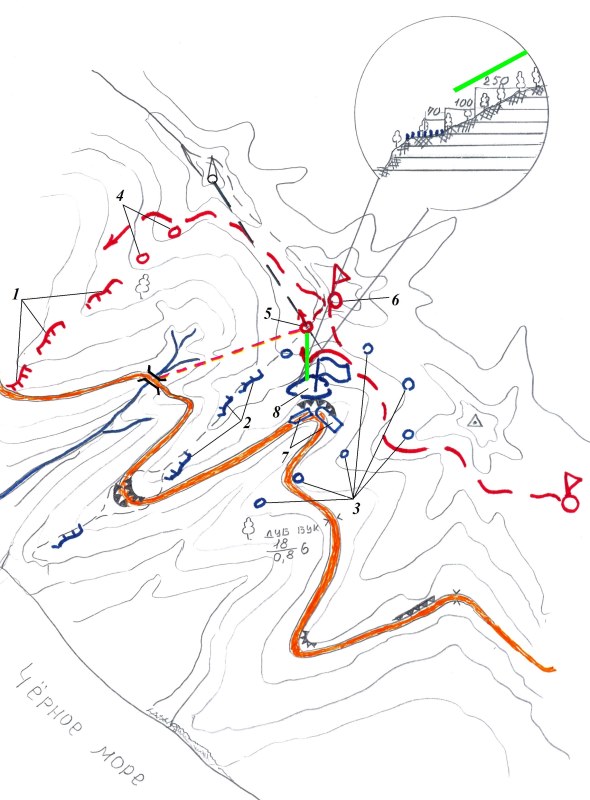
Примером комплексного использования вышеуказанных способов нанесения на карту целей может являться эпизод действий разведгруппы — схема действий приведена
на рис. 4.16.
Рис. 4.16 Схема действий разведгруппы
1 – расположение
абхазского ополчения;
2 – посты грузинских формирований;
3 – боевое охранение грузинских формирований;
4 — боевое охранение абхазских ополченцев;
5 – разведдозор группы в точке снятия координат;
6 – разведгруппа;
7 – техника грузинских формирований;
8 – расположение
грузинских
формирований
Пользуясь предрассветными сумерками, разведгруппа возвращалась после выполнения задачи на территорию, занятую абхазским ополчением. Неожиданно, при подходе
к передовым постам грузинских формирований, группа наткнулась на боевое охранение противника.
Просочившись за боевое охранение, командир группы принял решение провести доразведку данного участка. С этой целью был выделен разведдозор с задачей
обследовать участок местности, прилегающий к дороге на Батуми.
Выполняя задачу, разведдозор обнаружил скопление живой силы и техники противника на склоне выше дороги. Сержант (старший разведдозора), учитывая сложность
определения координат расположения противника в сложившихся условиях (местность резкопересеченная и поросшая густым лесом, плохая видимость в
предрассветных сумерках), определил координаты по следующей схеме. Находясь на расстоянии 80-90 м от расположения противника, и определив, что от центра
расположения до непосредственного охранения не более 50-70 м, сержант с дозором поднялся вверх по склону (примерный азимут — 0°), доведя свое расположение
до 100 м от непосредственного охранения. Затем, взяв азимут так, чтобы дирекционный угол при нанесении на карту был равен 0°, начал подъем по склону на
гребень отрога, отсчитывая пары шагов — при выходе на гребень получилось, что дозор прошел около 300 м. Учитывая крутизну ската, определил прямое
расстояние до центра расположения противника (рис. 4.16, изображение в круге): 250+100+70=420 м.
На гребне отрога в конце пройденного азимута было выбрано дерево, поднявшись на которое, сержант попытался определить точку своего стояния. К северо-западу
от этой точки на фоне светлеющего предрассветного неба четко проектировалась отмеченная на карте вышка, расположенная на одной из вершин хребта.
Понимая, что одного этого ориентира недостаточно для определения точки своего стояния, сержант принялся искать дополнительные ориентиры, обозначенные на
карте, и нашел ориентир в виде автомобильного моста к юго-западу. Взяв азимут на вышку, перевел его в дирекционный угол, и, отняв 180°, проложил его до
пересечения с гребнем отрога, тем самым получив достаточно точные координаты своей точки стояния. Оставалось проложить дирекционный угол 180° на
расположение противника и отложить уже вычисленное расстояние — 420 м.
Присоединившись к группе, сержант, доложил командиру вычисленные координаты цели. Командир, оценив достоверность информации и правильность расчетов, принял
решение на наведение огня своей артиллерии. После первого пристрелочного выстрела, расчет 120-мм миномета, имевшегося в распоряжении абхазского ополчения,
дал серию из 6 мин, четко поразив расположение противника.
Содержание конспекта
- 1. Системы координат, применяемые в топографии: географические, плоские прямоугольные, полярные и биполярные координаты, их сущность и использование
- 2. Определение географических координат и нанесение на карту объектов по известным координатам
- 3. Прямоугольная координатная сетка на топографических картах и ее оцифровка. Дополнительная сетка на стыке координатных зон
- 4. Определение прямоугольных координат точек. Нанесение на карту точек по их координатам
- 5. Точность определения координат на картах различных масштабов
- 6. Определение положения объектов (точек) в системах полярных и биполярных координат, нанесение на карту объектов по направлению и расстоянию, по двум углам или по двум расстояниям
- 7. Способы целеуказания по карте: в графических координатах, плоских прямоугольных координатах (полных и сокращенных), по квадратам километровой сетки (до целого квадрата, до 1/4, до 1/9 квадрата), от ориентира, от условной линии, по азимуту и дальности цели, в системе биполярных координат
- 8. Решение задач
1. Системы координат, применяемые в топографии: географические, плоские прямоугольные, полярные и биполярные координаты, их сущность и использование
Координатами называются угловые и линейные величины (числа), определяющие положение точки на какой-либо поверхности или в пространстве.
В топографии применяют, такие системы координат, которые позволяют наиболее просто и однозначно определять положение точек земной поверхности как по результатам непосредственных измерений на местности, так и с помощью карт. К числу таких систем относятся географические, плоские прямоугольные, полярные и биполярные координаты.
Географические координаты (рис.1) – угловые величины: широта (j) и долгота (L), определяющие положение объекта на земной поверхности относительно начала координат – точки пересечения начального (Гринвичского) меридиана с экватором. На карте географическая сетка обозначена шкалой на всех сторонах рамки карты. Западная и восточная стороны рамки являются меридианами, а северная и южная – параллелями. В углах листа карты подписаны географические координаты точек пересечения сторон рамки.
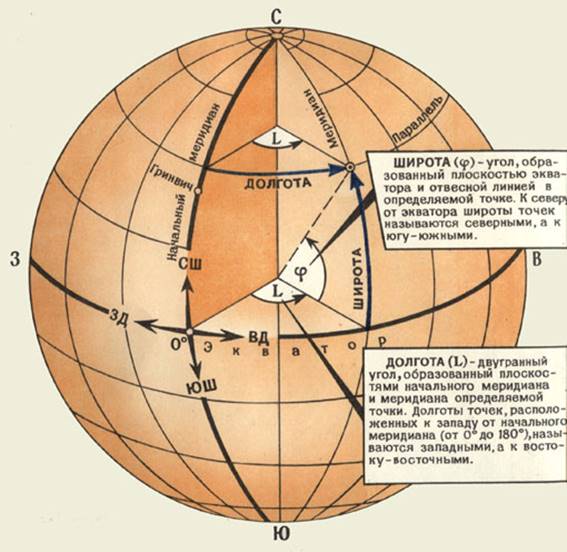
В системе географических координат положение любой точки земной поверхности относительно начала координат определяется в угловой мере. За начало у нас и в большинстве других государств принята точка пересечения начального (Гринвичского) меридиана с экватором. Являясь, таким образом, единой для всей нашей планеты, система географических координат удобна для решения задач по определению взаимного положения объектов, расположенных на значительных расстояниях друг от друга. Поэтому в военном деле эту систему используют главным образом для ведения расчетов, связанных с применением боевых средств дальнего действия, например баллистических ракет, авиации и др.
Плоские прямоугольные координаты (рис. 2) – линейные величины, определяющие положение объекта на плоскости относительно принятого начала координат – пересечение двух взаимно перпендикулярных прямых (координатных осей Х и Y).
В топографии каждая 6-градусная зона имеет свою систему прямоугольных координат. Ось Х — осевой меридиан зоны, ось Y – экватор, а точка пересечения осевого меридиана с экватором – начало координат.
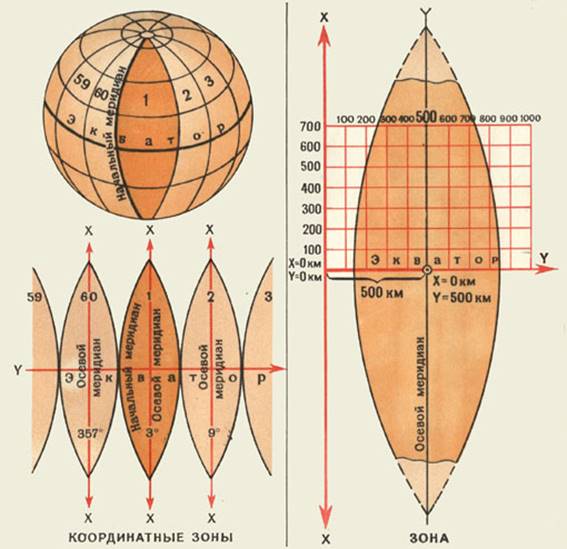
Система плоских прямоугольных координат является зональной; она установлена для каждой шестиградусной зоны, на которые делится поверхность Земли при изображении ее ни картах в проекции Гаусса, и предназначена для указания положения изображений точек земной поверхности на плоскости (карте) в этой проекции.
Началом координат в зоне является точка пересечения осевого меридиана с экватором, относительно которой и определяется в линейной мере положение всех остальных точек зоны. Начало координат зоны и ее координатные оси занимают строго определенное положение на земной поверхности. Поэтому система плоских прямоугольных координат каждой зоны связана как с системами координат всех остальных зон, так и с системой географических координат.
Применение линейных величин для определения положения точек делает систему плоских прямоугольных координат весьма удобной для ведения расчетов как при работе на местности, так и на карте. Поэтому в войсках эта система находит наиболее широкое применение. Прямоугольными координатами указывают положение точек местности, своих боевых порядков и целей, с их помощью определяют взаимное положение объектов в пределах одной координатной зоны или на смежных участках двух зон.
Системы полярных и биполярных координат являются местными системами. В войсковой практике они применяются для определения положения одних точек относительно других на сравнительно небольших участках местности, например при целеуказании, засечке ориентиров и целей, составлении схем местности и др. Эти системы могут быть связаны с системами прямоугольных и географических координат.
2. Определение географических координат и нанесение на карту объектов по известным координатам
Географические координаты точки, расположенной на карте, определяют от ближайших к ней параллели и меридиана, широта и долгота которых известна.
Рамка топографической карты разбита на минуты, которые разделены точками на деления по 10 секунд в каждом. На боковых сторонах рамки обозначены широты, а на северной и южной — долготы.
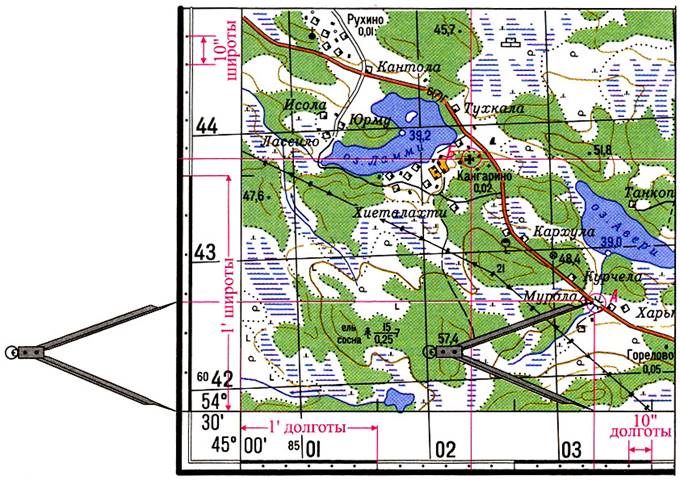
Пользуясь минутной рамкой карты можно:
1. Определить географические координаты любой точки на карте.
Например, координаты точки А (рис.3). Для этого необходимо с помощью циркуля-измерителя измерить кратчайшее расстояние от точки А до южной рамки карты, затем приложить измеритель к западной рамке и определить количество минут и секунд в измеренном отрезке, сложить полученное (измеренное) значение минут и секунд (0’27») с широтой юго-западного угла рамки — 54°30′.
Широта точки на карте будет равна: 54°30’+0’27» = 54°30’27».
Долгота определяется аналогично.
Измеряют с помощью циркуля-измерителя кратчайшее расстояние от точки А до западной рамки карты, прикладывают циркуль-измеритель к южной рамке, определяют количество минут и секунд в измеренном отрезке (2’35») складывают полученное (измеренное) значение с долготой юго-западного угла рамки — 45°00′.
Долгота точки на карте будет равна: 45°00’+2’35» = 45°02’35»
2. Нанести любую точку на карту по заданным географическим координатам.
Например, точку Б широта: 54°31 ’08», долгота 45°01 ’41».
Для нанесения на карту точки по долготе необходимо провести истинный меридиан через данную точку, для чего соединить одинаковое количество минут по северной и южной рамке; для нанесения на карту точки по широте необходимо провести параллель через данную точку, для чего соединить одинаковое количество минут по западной и восточной рамке. Пересечение двух прямых определит местоположение точки Б.
3. Прямоугольная координатная сетка на топографических картах и ее оцифровка. Дополнительная сетка на стыке координатных зон
Координатная сетка на карте представляет собой сетку квадратов, образованных линиями, параллельными координатным осям зоны. Линии сетки проведены через целое число километров. Поэтому координатную сетку называют также километровой сеткой, а ее линии километровыми.
На карте 1:25000 линии, образующие координатную сетку, проведены через 4 см, то есть через 1 км на местности, а на картах 1:50000-1:200000 через 2 см (1,2 и 4 км на местности соответственно). На карте 1:500000 наносятся лишь выходы линий координатной сетки на внутренней рамке каждого листа через 2 см (10 км на местности). При необходимости по этим выходам координатные линии могут быть нанесены на карту.
На топографических картах значения абсцисс и ординат координатных линий (рис. 2) подписывают у выходов линий за внутренней рамкой листа и девяти местах на каждом листе карты. Полные значения абсцисс и ординат в километрах подписываются около ближайших к углам рамки карты координатных линий и около ближайшего к северо-западному углу пересечения координатных линий. Остальные координатные линии подписываются сокращенно двумя цифрами (десятки и единицы километров). Подписи около горизонтальных линий координатной сетки соответствуют расстояниям от оси ординат в километрах.
Подписи около вертикальных линий обозначают номер зоны (одна или две первые цифры) и расстояние в километрах (всегда три цифры) от начала координат, условно перенесенного к западу от осевого меридиана зоны на 500 км. Например, подпись 6740 означает: 6 — номер зоны, 740 — расстояние от условного начала координат в километрах.
На внешней рамке даны выходы координатных линий (дополнительная сетка) системы координат смежной зоны.
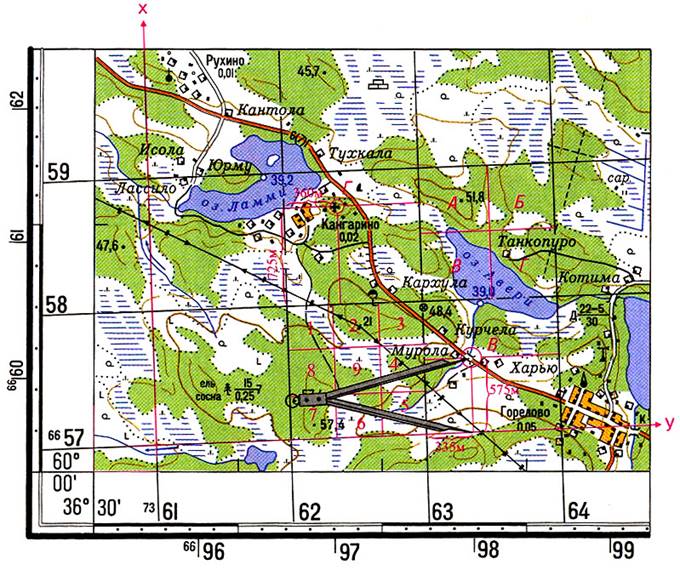
4. Определение прямоугольных координат точек. Нанесение на карту точек по их координатам
По координатной сетке с помощью циркуля (линейки) можно:
1. Определить прямоугольные координаты точки на карте.
Например, точки В (рис. 2).
Для этого надо:
- записать X — оцифровку нижней километровой линии квадрата, в котором находится точка В, т. е. 6657 км;
- измерить по перпендикуляру расстояние от нижней километровой линии квадрата до точки В и, пользуясь линейным масштабом карты, определить величину этого отрезка в метрах;
- сложить измеренную величину 575 м с значением оцифровки нижней километровой линии квадрата: X=6657000+575=6657575 м.
Определение ординаты Y производят аналогично:
- записать значение Y — оцифровку левой вертикальной линии квадрата, т.е.7363;
- измерить по перпендикуляру расстояние от этой линии до точки В, т. е.335 м;
- прибавить измеренное расстояние к значению оцифровки Y левой вертикальной линии квадрата: Y=7363000+335=7363335 м.
2. Нанести на карту цель по заданным координатам.
Например, точку Г по координатам: Х=6658725 Y=7362360.
Для этого надо:
- найти квадрат, в котором расположена точка Г по значению целых километров, т. е. 5862;
- отложить от левого нижнего угла квадрата отрезок в масштабе карты, равный разности абсциссы цели и нижней стороны квадрата — 725 м;
- от полученной точки по перпендикуляру вправо отложить отрезок, равный разности ординат цели и левой стороны квадрата, т. е. 360 м.
5. Точность определения координат на картах различных масштабов
Точность определения географических координат по картам 1:25000-1:200000 составляет около 2 и 10» соответственно.
Точность определения по карте прямоугольных координат точек ограничивается не только ее масштабом, но и величиной погрешностей, допускаемых при съемке или составлении карты и нанесении на нее различных точек и объектов местности
Наиболее точно (с ошибкой, не превышающей 0,2 мм) на карту наносятся геодезические пункты и. наиболее резко выделяющиеся на местности и видимые издали предметы, имеющие значение ориентиров (отдельные колокольни, фабричные трубы, постройки башенного типа). Поэтому координаты таких точек можно определить примерно с той же точностью, с которой они на карту наносятся, т. е. для карты масштаба 1:25000 — с точностью — 5-7 м, для карты масштаба 1:50000 — с точностью — 10-15 м, для карты масштаба 1:100000 — с точностью — 20-30 м.
Остальные ориентиры и точки контуров наносятся на карту, а, следовательно, и определяются по ней с ошибкой до 0,5 мм, а точки, относящиеся к нечетко выраженным на местности контурам (например, контур болота), с ошибкой до 1 мм.
6. Определение положения объектов (точек) в системах полярных и биполярных координат, нанесение на карту объектов по направлению и расстоянию, по двум углам или по двум расстояниям
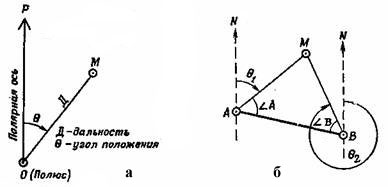
Система плоских полярных координат (рис. 3, а) состоит из точки О — начало координат, или полюса, и начального направления ОР, называемого полярной осью.
Положение точки М на местности или на карте в этой системе определяется двумя координатами: углом положения θ, который измеряется по ходу часовой стрелки от полярной оси до направления на определяемую точку М (от 0 до 360°), и расстоянием ОМ=Д.
В зависимости от решаемой задачи за полюс принимают наблюдательный пункт, огневую позицию, исходный пункт движения и т. п., а за полярную ось — географический (истинный) меридиан, магнитный меридиан (направление магнитной стрелки компаса) или же направление на какой-либо ориентир.
Этими координатами могут служить либо два угла положения, определяющих направления с точек А и В на искомую точку М, либо расстояния D1=АМ и D2=ВМ до нее. Углы положения при этом, как показано на рис. 1, б, измеряются в точках А и В или от направления базиса (т. е. угол А=ВАМ и угол В=АВМ) или от других каких-либо направлений, проходящих через точки А и В и принимаемых за начальные. Например, во втором случае место точки М определено углами положения θ1 и θ2, измеренными от направления магнитных меридианов.Система плоских биполярных (двухполюсных) координат (рис. 3, б) состоит из двух полюсов А и В и общей оси АВ, называемой базисом или базой засечки. Положение любой точки М относительно двух данных на карте (местности) точек А и В определяется координатами, которые измеряются на карте или на местности.
Нанесение обнаруженного объекта на карту
Это один из важнейших моментов в обнаружении объекта. От того, насколько точно объект (цель) будет нанесен на карту, зависит точность определения его координат.
Обнаружив объект (цель), необходимо сначала точно определить по различным признакам, что обнаружено. Затем, не прекращая наблюдение за объектом и не обнаруживая себя, нанести объект на карту. Для нанесения объекта на карту существуют несколько способов.
Глазомерно: объект наносится на карту, если он находится вблизи известного ориентира.
По направлению и расстоянию: для этого необходимо сориентировать карту, найти на ней точку своего стояния, свизировать на карте направление на обнаруженный объект и прочертить линию до объекта от точки своего стояния, затем определить расстояние до объекта, измерив это расстояние на карте и соизмерив его с масштабом карты.
Если таким образом графически невозможно решить задачу (мешает противник, плохая видимость и др.), то нужно точно измерить азимут на объект, затем перевести его в дирекционный угол и прочертить на карте из точки стояния направление, на котором отложить расстояние до объекта.
Чтобы получить дирекционный угол, надо к магнитному азимуту прибавить магнитное склонение данной карты (поправка направления).
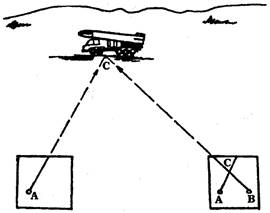
Прямой засечкой. Этим способом наносят объект на карту из 2-х-3-х точек, с которых можно вести наблюдение за ним. Для этого из каждой выбранной точки прочерчивается на ориентированной карте направление на объект, тогда пересечение прямых линий определяет местонахождение объекта.
7. Способы целеуказания по карте: в графических координатах, плоских прямоугольных координатах (полных и сокращенных), по квадратам километровой сетки (до целого квадрата, до 1/4, до 1/9 квадрата), от ориентира, от условной линии, по азимуту и дальности цели, в системе биполярных координат
Умение быстро и правильно указывать цели, ориентиры и другие объекты на местности имеет важное значение для управления подразделениями и огнем в бою или для организации боя.
Целеуказания в географических координатах применяется очень редко и только в тех случаях, когда цели удалены от заданной точки на карте на значительном расстоянии, выражающемся в десятках или сотнях километров. При этом географические координаты определяются по карте, как описано в вопросе № 2 настоящего занятия.
Местоположение цели (объекта) указывают широтой и долготой, например, высота 245,2 (40° 8′ 40″ с. ш., 65° 31′ 00″ в. д.). На восточную (западную), северную (южную) стороны топографической рамки наносят уколом циркуля отметки положения цели по широте и долготе. От этих отметок в глубину листа топографической карты опускают перпендикуляры до их пересечения (прикладывают командирские линейки, стандартные листы бумаги). Точка пересечения перпендикуляров и есть положение цели на карте.
Для приближенного целеуказания по прямоугольным координатам достаточно указать на карте квадрат сетки, в котором расположен объект. Квадрат всегда указывается цифрами километровых линий, пересечением которых образован юго-западный (нижний левый) угол. При указании квадрата карты придерживаются правила: сначала называют две цифры, подписанные у горизонтальной линии (у западной стороны), то есть координату «X», а затем две цифры у вертикальной линии (южная сторона листа), то есть координата «Y». При этом «X» и «Y» не говорятся. Например, засечены танки противника. При передаче донесения по радиотелефону номер квадрата произносят: «восемьдесят восемь ноль два».
Если положение точки (объекта) необходимо определить более точно, то пользуются полными или сокращенными координатами.
Работа с полными координатами. Например, требуется определить координаты указателя дорог в квадрате 8803 на карте масштаба 1:50000. Сначала определяют чему равно расстояние от нижней горизонтальной стороны квадрата до указателя дорог (например, 600 м на местности). Таким же образом измеряют расстояние от левой вертикальной стороны квадрата (например, 500 м). Теперь путем оцифровки километровых линий определяем полные координаты объекта. Горизонтальная линия имеет подпись 5988 (X), прибавив расстояние от этой линии до указателя дорог, получим: Х=5988600. Точно также определяем вертикальную линию и получаем 2403500. Полные координаты указателя дорог следующие: Х=5988600 м, У=2403500 м.
Сокращенные координаты соответственно будут равны: Х=88600 м, У=03500 м.
Если требуется уточнить положение цели в квадрате, то применяют целеуказание буквенным или цифровым способом внутри квадрата километровой сетки.
При целеуказании буквенным способом внутри квадрата километровой сетки квадрат условно разбивается на 4 части, каждой части присваивается заглавная буква русского алфавита.
Второй способ — цифровой способ целеуказания внутри квадрата километровой сетки (целеуказание по улитке). Этот способ получил свое название по расположению условных цифровых квадратов внутри квадрата километровой сетки. Они расположены как бы по спирали, при этом квадрат разбивается на 9 частей.
При целеуказании в этих случаях называют квадрат, в котором находится цель, и добавляют букву или цифру, уточняющую положение цели внутри квадрата. Например, высота 51,8 (5863-А) или высоковольтная опора (5762-2) (см. рис. 2).
Целеуказание от ориентира наиболее простой и распространенный способ целеуказания. При этом способе целеуказания вначале называют ближайший к цели ориентир, затем величину угла между направлением на ориентир и направлением на цель в делениях угломера (измеряется биноклем) и удаление до цели в метрах. Например: «Ориентир второй, вправо сорок, дальше двести, у отдельного куста – пулемет».
Целеуказание от условной линии обычно применяется в движении на боевых машинах. При этом способе по карте выбирают в направлении действий две точки и соединяют их прямой линией, относительно которой и будет вестись целеуказание. Эту линию обозначают буквами, разбивают на сантиметровые деления и нумеруют их начиная с нуля. Такое построение делается на картах как передающего, так и принимающего целеуказание.
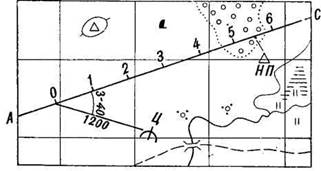
Целеуказание от условной линии обычно применяется в движении на боевых машинах. При этом способе по карте выбирают в направлении действий две точки и соединяют их прямой линией (рис. 5), относительно которой и будет вестись целеуказание. Эту линию обозначают буквами, разбивают на сантиметровые деления и нумеруют их начиная с нуля.
Такое построение делается на картах как передающего, так и принимающего целеуказание.
Положение цели относительно условной линии определяется двумя координатами: отрезком от начальной точки до основания перпендикуляра, опущенного из точки расположения цели на условную линию, и отрезком перпендикуляра от условной линии до цели.
При целеуказании называют условной наименование линии, затем число сантиметров и миллиметров, заключающихся в первом отрезке, и, наконец, направление (влево или вправо) и длину второго отрезка. Например: «Прямая АС, пять, семь; вправо ноль, шесть – НП».
Целеуказание от условной линии можно выдать, указав направление на цель под углом от условной линии и расстояние до цели, например: «Прямая АС, вправо 3-40, тысяча двести – пулемет».
Целеуказание по азимуту и дальности до цели. Азимут направления на цель определяют с помощью компаса в градусах, а дальность до нее – с помощью прибора наблюдения или глазомерно в метрах. Например: «Азимут тридцать пять, дальность шестьсот – танк в окопе». Этот способ чаще всего используют на местности, где мало ориентиров.
8. Решение задач
Определение координат точек местности (объектов) и целеуказание по карте отрабатывается практически на учебных картах по заранее подготовленным точкам (нанесенным объектам).
Каждый обучаемый определение географические и прямоугольные координаты (наносит на карту объекты по известным координатам).
Способы целеуказания по карте отрабатываются: в плоских прямоугольных координатах (полных и сокращенных), по квадратам километровой сетки (до целого квадрата, до 1/4, до 1/9 квадрата), от ориентира, по азимуту и дальности цели.
Скачать конспект
Определение высот и превышений
Виды и формы рельефа Проекция
рельефа на плоскость
Рельеф — совокупность неровностей земной поверхности, слагающихся из разнооб-разных элементарных форм различного порядка.
Горный рельеф слагается главным образом из линейно вытянутых, простирающихся на большие расстояния горных цепей с их отрогами, разделённых продольными долинами и другими межгорными понижениями. Глубина расчленения достигает: в низких горах (500-1000 м) — до 500 м, в средних горах (1000-2000 м) — до 1000 м, в высоких горах (свыше 2000 м) — более 1000 м.
Равнинный рельеф (равнины) характеризуется формами поверхности с малыми (в пре-делах 200 м) колебаниями высот. Чем выше над уровнем моря, тем сильнее может быть рас-членена поверхность. По общему характеру поверхности различают равнины горизонталь-ные, наклонные, выпуклые и вогнутые. Холмистый рельеф является одной из разновидно-стей равнинного рельефа. По форме и строению неровностей различают также плоскорав-нинный, волнистый, ступенчатый, овражно-балочный и другие разновидности равнинного рельефа.
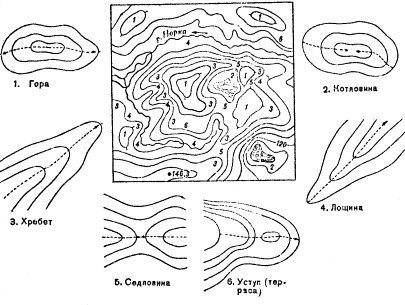
Всё многообразие неровностей, из которых слагается рельеф земной поверхности, можно в основном свести к следующим пяти элементарным формам:
1) Гора — значительное куполообразное или коническое возвышение с более или менее явно выраженным основанием — подошвой.
2) Котловина — замкнутая чашеобразная впадина обычно с пологими скатами.
3) Хребет — линейно вытянутое возвышение, постепенно понижающееся к одному или обоим своим концам.
4) Лощина — вытянутое углубление, понижающееся в одном направлении; имеет скаты с чётко выраженным верхним перегибом — бровкой. К разновидностям лощин относятся: долины, ущелья, овраги, балки, каньоны.
5) Седловина — понижение на гребне хребта между двумя смежными вершинами; к ней с двух противоположных направлений, поперечных хребту, подходят своими верховьями лощины.
На рис. 1 раздельно изображены горизонталями элементарные формы рельефа. На рисунке видно, что небольшая гора (холм) и котловина выглядят, в общем, одинаково — в виде системы замкнутых опоясывающих друг друга горизонталей. Схожи между собой и изображение хребта и лощины. Отличить их можно лишь по направлению скатов.
Рис.1 Изображение горизонталями элементарных форм рельефа.
Изображение рельефа на топографических картах дает полное и достаточно подробное представление о неровностях земной поверхности, их форме и взаимном расположении, превышениях и абсолютных высотах точек местности, преобладающей крутизне и протяженности скатов. На современных топографических картах рельеф изображается горизонталями в сочетании с условными знаками обрывов, скал, оврагов, промоин, осыпей, оползней и т. д. Изображение рельефа дополняется подписями абсолютных высот характерных точек местности, горизонталей, размеров отдельных форм рельефа и указателями направления скатов.
Сущность изображения рельефа горизонталями. Горизонталь — это замкнутая линия, изображающая на карте горизонтальный контур неровностей, все точки которого на местности расположены на одной высоте над уровнем моря. Горизонтали можно представить как линии, полученные в результате сечения местности уровенными поверхностями, то есть поверхностями, параллельными уровню воды в океанах.
Рис.1 Сущность изображения рельефа горизонталями.
Рассмотрим сущность изображения рельефа горизонталями. На рис.1 изображен остров с вершинами А и Б и береговой линией D, Е, F. Замкнутая кривая d e f представляет собой изображение береговой линии в плане. Поскольку береговая линия является сечением острова уроненной поверхностью океана, изображение этой линии на карте представляет собой нулевую горизонталь, все точки которой имеют высоту, равную нулю. Допустим, что уровень океана поднялся на высоту h, тогда образуется новое сечение острова воображаемой секущей плоскостью h — h. Проектируя это сечение с помощью отвесных линий, получим на карте изображение первой горизонтали, все точки которой имеют высоту h. Точно так же можно получить на карте изображение и других сечений, выполненных на высотах 2h, Зh, 4h и т. д. В результате на карте будет иметь место изображение рельефа острова горизонталями. При этом рельеф острова изображается тремя горизонталями, — охватывающими остров целиком, и двумя горизонталями, охватывающими отдельно каждую из вершин. Вершина А несколько выше 4h, а вершина В несколько выше Зh относительно уровня океана. Скаты возвышенности А круче, чем скаты возвышенности В, поэтому в первом случае горизонтали на карте расположены ближе друг к другу, чем во втором. Из рисунка видно, что способ изображения рельефа горизонталями позволяет правильно не только отображать формы рельефа, но и определять высоты отдельных точек земной поверхности по высоте сечения рельефа и крутизне скатов.
Высота сечения рельефа — это разность высот двух смежных секущих поверхностей. На карте она выражается разностью высот двух смежных горизонталей. В пределах листа карты высота сечения рельефа, как правило, является постоянной. На рис.2 показан вертикальный разрез (профиль) ската.
Рис.2 Профиль ската.
Через точки М, N, О проведены уровенные поверхности на расстоянии друг от друга, равном высоте сечения Л. Пересекая поверхность ската, они образуют кривые линии, ортогональные проекции которых в виде трех горизонталей показаны нижней части рисунка. Расстояния mn и no между горизонталями являются проекциями отрезков MN и NO ската. Эти проекции называются заложениями горизонталей.
Определение высот точек. Абсолютную высоту какой-либо точки местности, отметка которой на карте не подписана, определяют по отметке ближайшей к ней горизонтали. Поэтому необходимо уметь определять отметки горизонталей, используя отметки других горизонталей и характерных точек местности, подписанных накарте.
Например, отметку горизонтали а (рис.3) можно определить по отметке высоты 197,4 и высоте сечения рельефа 10 м.
Рис.3 Определение отметки горизонтали по отметке точки.
Отметка горизонтали а равна 190 м. Зная отметку горизонтали а, можно легко определить отметки всех других горизонталей. Так, горизонталь b будет иметь отметку 160 м, так как она расположена ниже горизонтали а на величину, равную трем высотам сечения рельефа (30 м). В случае когда точка расположена между горизонталями, находят высоту ближайшей к ней горизонтали и к полученной высоте прибавляют превышение данной точки над горизонталью, определенное на глаз. Например, мельница, обозначение которой находится между горизонталями (рис.3), имеет абсолютную высоту 162 м.
Определение взаимного превышения точек заключается в установлении величины, указывающей, насколько одна точка выше или ниже другой. При расположении точек на одной горизонтали их взаимное рис превышение равно нулю, так как их высоты одинаковы. Если определяемые точки совпадают с точками, высоты которых подписаны на карте, их взаимное превышение равно разности этих высот.
В случае когда точки расположены на одном скате или на разных скатах близко друг к другу, подсчитывают число промежутков между горизонталями и. к целому числу добавляют их доли, которые оценивают на глаз. Полученное число умножают на высоту сечения рельефа и таким образом получают взаимное превышение указанных точек.
Когда точки расположены на значительном расстоянии друг от друга, определяют их абсолютные высоты. Разность этих высот и будет взаимным превышением точек.