Как найти высоту опущенную на большую сторону

В общем виде решение данной задачи по планиметрии выглядит следующим образом:

где a – меньшая сторона, b – большая сторона, h – высота, опущенная на меньшую сторону, H – искомая высота.

Остается лишь подставить конкретные значения и подсчитать результат.

Поделитесь статьей с одноклассниками «Найдите длину высоты, опущенной на большую сторону параллелограмма – как решать».

При копировании материалов с сайта ссылка на источник обязательна. Уважайте труд людей, которые вам помогают.
Нашли ошибку? Выделите текст и нажмите Ctrl + Enter.

Формулы для нахождения высоты треугольника

В данной публикации мы рассмотрим формулы, с помощью которых можно найти высоту в различных видах треугольников, а также разберем примеры решения задач для закрепления материала.

Нахождение высоты треугольника

Напомним, высота треугольника – это отрезок, проведенный перпендикулярно из вершины фигуры к противоположной стороне.

Высота в разностороннем треугольнике

Высоту треугольника abc, проведенного к стороне a, можно найти по формулам ниже:

1. Через площадь и длину стороны

где S – площадь треугольника.

2. Через длины всех сторон

где p – это полупериметр треугольника, который рассчитывается так:

3. Через длину прилежащей стороны и синус угла

4. Через стороны и радиус описанной окружности

где R – радиус описанной окружности.

Высота в равнобедренном треугольнике

Длина высоты h_a, опущенной на основание a равнобедренного треугольника, рассчитывается по формуле:

Высота в прямоугольном треугольнике

Высота, проведенная к гипотенузе, может быть найдена:

1. Через длины отрезков, образованных на гипотенузе

2. Через стороны треугольника

Примечание: две остальные высоты в прямоугольном треугольнике являются его катетами.

Высота в равностороннем треугольнике

Для равностороннего треугольника со стороной a формула расчета высоты выглядит следующим образом:

Примеры задач

Задача 1
Найдите высоту треугольника, проведенную из вершины B к стороне AC, если известно, что AB = 7 см, а угол BAC = 45°.

Решение
В данном случае нам поможет формула для нахождения высоты через сторону и синус прилежащего угла:

Задача 2
Найдите длину основания равнобедренного треугольника, если высота, проведенная к нему, равняется 3 см, а боковые стороны – 5 см.

Решение
Вывести формулу для нахождения длины основания можно из формулы расчета высоты в равнобедренном треугольнике:

Найти наибольшую высоту треугольника

Как найти наибольшую или наименьшую высоту треугольника? Чем меньше высота треугольника, тем больше проведенная к ней высота. То есть наибольшая из высот треугольника — та, которая проведена к его наименьшей стороне. Наименьшая высота — та, которая проведена к наибольшей из сторон треугольника.

Чтобы найти наибольшую высоту треугольника, можно площадь треугольника разделить на длину стороны, к которой проведена эта высота (то есть на длину наименьшей из сторон треугольника).

Соответственно, для нахождения наименьшей высоты треугольника можно площадь треугольника разделить на длину его наибольшей стороны.

Найти наименьшую высоту треугольника, стороны которого равны 7 см, 8 см и 9 см.

AC=7 см, AB=8 см, BC=9 см.

Найти: наименьшую высоту треугольника.

Наименьшая из высот треугольника — та, которая проведена к его наибольшей стороне. Значит, нужно найти высоту AF, проведенную к стороне BC.

Для удобства записи введем обозначения

BC=a, AC=b, AB=c, AF=ha.

Высота треугольника равна частному от деления удвоенной площади треугольника на сторону, к которой эта высота проведена. Площадь треугольника по сторонам можно найти с помощью формулы Герона. Поэтому

Найти наибольшую сторону треугольника со сторонами 1 см, 25 см и 30 см.

AC=25 см, AB=11 см, BC=30 см.

наибольшую высоту треугольника ABC.

Наибольшая высота треугольника проведена к его наименьшей стороне.

Значит, нужно найти высоту CD, проведенную к стороне AB.

Способы нахождения высоты треугольника: теорема и формула

Определение высоты треугольника

Геометрия, являющаяся разделом математики, изучает структуры в пространстве и на плоскости. Одним из типов таких фигур являются геометрические фигуры. К ним можно отнести квадрат, прямоугольник, круг, пятиугольник, треугольник и другие. Из них можно делать более сложные фигуры или оставлять в первоначальном виде.

Треугольником является фигура, относящаяся к классу простых фигур, которая образована тремя точками, находящимися не на одной прямой, и соединенными между собой тремя отрезками.

Треугольники могут быть:

• разными по величине углов: прямоугольными, тупоугольными и остроугольными;
• разными по числу равных сторон: равносторонними, равнобедренными и разносторонними.

Помимо трех сторон, важными элементами треугольников являются медианы, высоты и биссектрисы.

Высотой треугольника является перпендикуляр, опущенный из угла треугольника вниз, на противоположную сторону.

В геометрии высота треугольника обозначается буквой h.

В зависимости от типа треугольника высота может:

• падать на противоположную сторону — у остроугольного треугольника;
• находиться вне треугольника — у тупоугольного треугольника;
• совпадать с одной из сторон — у прямоугольного треугольника.

Чтобы сделать высоту графически явной и понятной на рисунке, ее нередко выделяют красной линией.

Для того чтобы определить графическое начертание высоты треугольника, необходимо:

1. Найти вершину фигуры.
2. Опустить вниз перпендикулярную линию к противоположной стороне.
3. Продлить противоположную сторону до пересечения с высотой, если требуется.

Любой треугольник имеет 3 высоты — по числу углов. Их пересечение находится в точке ортоцентра, которая, в зависимости от типа треугольника, может находиться внутри треугольника, снаружи на пересечении продолжений высот или совпадать с вершиной прямого угла.

Все три высоты треугольника обратно пропорциональны сторонам, к которым опущены. Доказательством будет соотношение:

A × H A ÷ B × H B ÷ C × H C = 1 B C ÷ 1 A C ÷ 1 A B

Выглядеть графически это будет так:

Существует множество способов нахождения высоты треугольника в зависимости от имеющихся данных.

Через площадь и длину стороны, к которой опущена высота:

где S — уже известная площадь треугольника,

Через длины всех сторон:

h = 2 p p × a p × b p × c a

где a, b и c — стороны треугольника,

p — его полупериметр.

Данная формула подходит только для нахождения высоты разностороннего треугольника.

Через длину прилежащей стороны и синус угла:

s i n a — синус угла прилежащей стороны.

Данная формула подходит только для нахождения высоты разностороннего треугольника.

Через стороны и радиус описанной окружности.

Решать задачи с треугольником и описанной окружностью для нахождения высоты можно следующим образом:

где b, c — стороны разностороннего треугольника, к которым не опущена высота,

R — радиус описанной окружности.

Данная формула подходит только для нахождения высоты разностороннего треугольника.

Через длины отрезков, образованных на гипотенузе при проведении к ней высоты треугольника:

где C 1 и С 2 — длины отрезков, образованных на гипотенузе, проведенной к ней высотой.

Данная формула подходит только для нахождения высоты прямоугольного треугольника.

Нахождение высоты равнобедренного треугольника через основание и боковые стороны

Равнобедренным треугольником называют треугольник, имеющий одинаковые по длине катеты, которые образуют равные углы с основанием. В таком треугольнике высота будет опускаться ровно в середину основания, образуя с ним прямой угол.

Помимо высоты, проведенная линия будет являться также осью симметрии, биссектрисой вершинного угла и медианой.

Формула для нахождения высоты в этом случае:

где a — основание,

b — равные боковые стороны.

Свойства высоты в равностороннем треугольнике

Равносторонний треугольник — это треугольник, стороны которого, углы, высоты, медианы, оси симметрии и биссектрисы будут равны.

Такой треугольник является частным примером равнобедренного треугольника, но не наоборот.

Высоту в таком треугольнике можно найти с помощью следующей формулы:

где а — сторона равностороннего треугольника.

Главным свойством, которым обладает высота равностороннего треугольника, является тот факт, что она равна медиане и биссектрисе:

а — сторона правильного равностороннего треугольника.

Нахождение высоты прямоугольного треугольника через его катеты

Прямоугольным считается треугольник, у которого один из углов является прямым, то есть равным 90°. Высота, опущенная из такого угла, падает на гипотенузу треугольника и делит его на два прямоугольных треугольника, которые пропорциональны по отношению к большому треугольнику и друг к другу.

Важно отметить, что две другие высоты будут совпадать с катетами треугольника.

Найти высоту в прямоугольном треугольнике, можно через два его катета (a и b) и гипотенузу (c).

Причем гипотенуза также легко находится через катеты по теореме Пифагора:

Расчет высоты идет следующим образом:

где a, b и c — вышеупомянутые стороны треугольника.

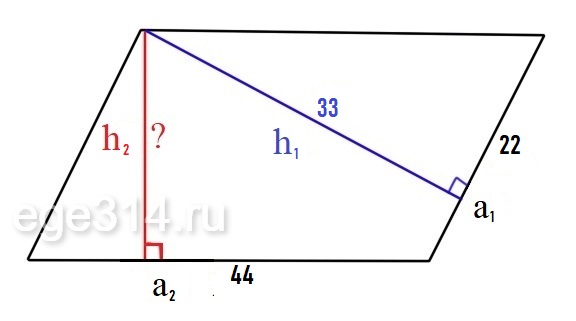
Стороны параллелограмма равны 22 и 44. Высота, опущенная на меньшую сторону, равна 33. Найдите высоту, опущенную на большую сторону параллелограмма.

---

Решение

Площадь параллелограмма находится по формуле (S=acdot h), где (a) – основание, (h) – высота.

Площадь можно найти на основании высоты равной (33) и на основании высоты равной (x) (которую нам и надо найти). Площадь должна быть одинаковой.

Найдем площадь при высоте равной (33) и меньшей стороной равной (22) (по условию, высота опущена на меньшую сторону): (S=33cdot22=726).

Зная площадь можно найти высоту, которая опущена на большую сторону параллелограмма (используя формулу площади параллелограмма): (726=xcdot44), отсюда (x=16,5).

Ответ: (16,5).

---

Источник: ЕГЭ 2023 Математика. Базовый уровень. Типовые экзаменационные варианты. 30 вариантов (вариант 21) (Купить книгу)

Нарисуем графический эскиз параллелограмма.![][­1]

Отметим, что AB = 27. BC = 24.

Высота DG = 18.

Необходимо найти высоту DH.

Известно, что площадь параллелограмма равна произведению высоты на основание, к которому она прилегает.

Получается справедливо равенство.

S (ABCD) = AB * DH = DG * BC.

Найдем площадь параллелограмма по известным данным: S (ABCD) = DG * BC = 24 * 18 = 432.

Тогда высота DH = S (ABCD) / AB = 432 / 27 = 16.