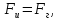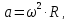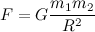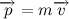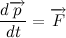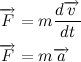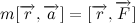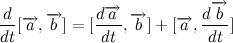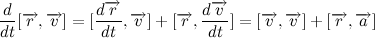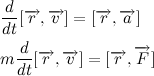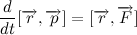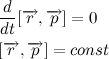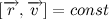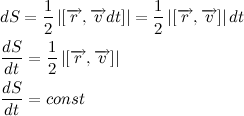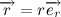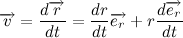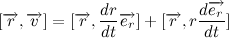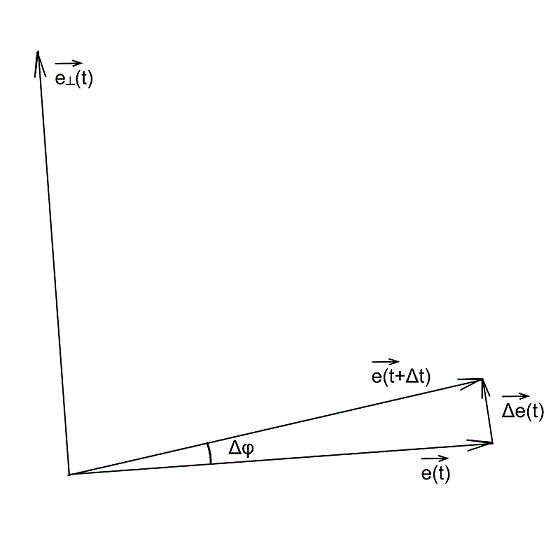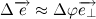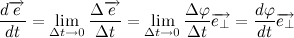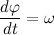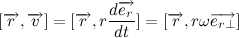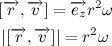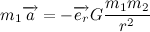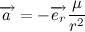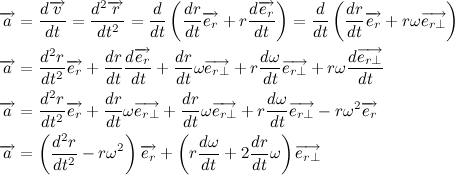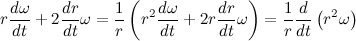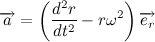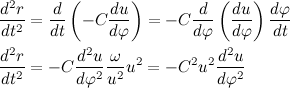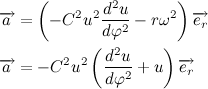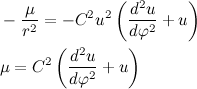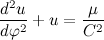Как найти высоту орбиты планеты

Высота орбиты
спутника

Помоги найти формулу высоты орбиты над поверхностью планеты, если известна масса (m), радиус(R), линейная скорость(v).

Вычисление параметров геостационарной орбиты Радиус орбиты и высота орбиты

На геостационарной
орбите спутник не приближается к Земле
и не удаляется от неё, и кроме того,
вращаясь вместе с Землёй, постоянно
находится над какой-либо точкой на
экваторе. Следовательно, действующие
на спутник силы гравитации и центробежная
сила должны уравновешивать друг друга.
Для вычисления высоты геостационарной
орбиты можно воспользоваться методами
классической механики и, перейдя в
систему отсчета спутника, исходить из
следующего уравнения:

где
– сила инерции, а в данном случае,
центробежная сила;– гравитационная сила. Величину
гравитационной силы, действующую на
спутник, можно определить по закону
всемирного тяготения Ньютона:

где
– масса спутника,– масса Земли в килограммах,– гравитационная постоянная, а– радиус орбиты (расстояние в метрах
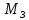
от спутника до центра Земли).

Величина центробежной
силы равна:

где
– центростремительное ускорение,
возникающее при круговом движении по
орбите.

Как можно видеть,
масса спутника присутствует в выражениях
и для центробежной силы, и для гравитационной
силы. То есть, высота орбиты не зависит
от массы спутника, что справедливо для
любых орбит и является следствием
равенства гравитационной и инертной
массы. Следовательно, геостационарная
орбита определяется лишь высотой, при
которой центробежная сила будет равна
по модулю и противоположна по направлению
гравитационной силе, создаваемой
притяжением Земли на данной высоте.

Центростремительное
ускорение равно:

где
– угловая скорость вращения спутника,
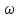
в радианах в секунду.

Исходя из равенства
гравитационной и центробежной сил,
получаем:

Отсюда
.

Угловая скорость
ωвычисляется делением угла,
пройденного за один оборот на период
обращения (время, за которое совершается
один полный оборот по орбите: один
сидерический день, или 86 164 секунды).
Получаем:рад/с

Расчетный радиус
орбиты составляет 42 164 км. Вычитая
экваториальный радиус Земли, 6 378 км,
получаем высоту ГСО 35 786 км.

Орбитальная скорость

Скорость движения
по геостационарной орбите вычисляется
умножением угловой скорости на радиус
орбиты:
км/с

Это примерно в 2.5
раза меньше, чем первая космическая
скорость равная 8 км/с для околоземной
орбиты (с радиусом 6400 км). Так как квадрат
скорости для круговой орбиты обратно
пропорционален её радиусу, то уменьшение
скорости по отношению к первой космической
достигается увеличением радиуса орбиты
более чем в 6 раз.

Длина орбиты

Длина геостационарной
орбиты:
.
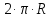
При радиусе орбиты 42 164 км получаем
длину орбиты 264 924 км. Длина орбиты
крайне важна для вычисления «точек
стояния» спутников.

Удержание спутника
в орбитальной позиции на геостационарной
орбите. Спутник, обращающийся на
геостационарной орбите, находится под
воздействием ряда сил (возмущений),
изменяющих параметры этой орбиты. В
частности, к таким возмущениям относятся
гравитационные лунно-солнечные
возмущения, влияние неоднородности
гравитационного поля Земли, эллиптичность
экватора и т.д. Деградация орбиты
выражается в двух основных явлениях:

1) Спутник смещается
вдоль орбиты от своей первоначальной
орбитальной позиции в сторону одной из
четырёх точек стабильного равновесия,
так называемых «потенциальных ям
геостационарной орбиты» (их долготы
75,3°E, 104,7°W, 165,3°E, и 14,7°W) над экватором
Земли;

2) Наклонение орбиты
к экватору увеличивается (от первоначального
=0) со скоростью порядка 0,85 градусов в
год и достигает максимального значения
15 градусов за 26,5 лет.

Для компенсации
этих возмущений и удержания спутника
в назначенной точке стояния спутник
оснащается двигательной установкой
(химической или электроракетной).
Периодическими включениями двигателей
малой тяги (коррекция «север-юг» для
компенсации роста наклонения орбиты и
«запад-восток» для компенсации дрейфа
вдоль орбиты) спутник удерживается в
назначенной точке стояния. Такие
включения производятся по нескольку
раз в несколько (10—15) суток. Существенно,
что для коррекции «север-юг» требуется
значительно большее приращение
характеристической скорости (около
45—50 м/с в год), чем для долготной коррекции
(около 2 м/с в год). Для обеспечения
коррекции орбиты спутника на протяжении
всего срока его эксплуатации (12—15 лет
для современных телевизионных спутников)
требуется значительный запас топлива
на борту (сотни килограммов, в случае
применения химического двигателя).
Химический ракетный двигатель спутника
имеет вытеснительную систему подачи
топлива (газ наддува – гелий), работает
на долгохранимых высококипящих
компонентах (обычно несимметричный
диметилгидразин и азотный тетраксид).
На ряде спутников устанавливаются
плазменные двигатели. Их тяга существенно
меньше, чем у химических, однако большая
эффективность позволяет (за счет
продолжительной работы, измеряемой
десятками минут для единичного маневра)
радикально снизить потребную массу
топлива на борту. Выбор типа двигательной
установки определяется конкретными
техническими особенностями аппарата.

Эта же двигательная
установка используется, при необходимости,
для маневра перевода спутника в другую
орбитальную позицию. В некоторых случаях
– как правило, в конце срока эксплуатации
спутника, для сокращения расхода топлива
коррекция орбиты «север-юг» прекращается,
а остаток топлива используется только
для коррекции «запад-восток». Запас
топлива является основным лимитирующим
фактором срока службы спутника на
геостационарной орбите.

Соседние файлы в папке 02-12-2014_07-07-59

• #
• #

Время на прочтение
7 мин

Количество просмотров 21K

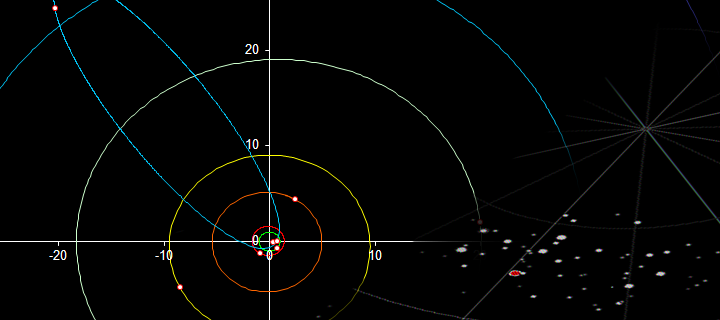
Не так давно очень активно обсуждалась тема Марса. В то время у меня возник вопрос от которого в силу своего наивного любопытства я никак не мог избавится: «Где Марс находится в данный момент, в какой стороне?» и смежный с ним: «Да и вообще, как определить положение остальных планет?». Очевидно, что траектории движения планет относительно земли будут весьма хитрыми. Конечно, можно воспользоваться планетариями, например таким, но как вы уже поняли, это не наш путь.

В данном цикле статей, я постараюсь максимально просто рассказать о сложном. В результате мы напишем простую программу, которая подскажет где искать планеты нашей Солнечной системы для любой заданной точки на поверхности земли в заданный момент времени. Своей целью я ставлю донести читателю суть того, что скрывается за Кеплеровой моделью орбиты, поэтому я не буду использовать никакие общеизвестные факты кроме законов Ньютона и закона всемирного тяготения.

Всех любопытных прошу под кат.

Стоит отметить, что дальнейшее изложение подразумевает, что читатель немного знаком с законами Ньютона, основными сведениями из геометрии, векторной алгебры и дифференциального исчисления.

Так как же движутся планеты?

В реальности, если учитывать взаимное влияние планет, смещение центра тяжести солнечной системы относительно центра тяжести солнца и т.д. движение планет окажется чрезвычайно сложным и не поддающимся строгому аналитическому определению. Стоит отметить что даже задача о движении трех тел не может быть решена аналитически. Поэтому давайте сразу оговорим в рамках каких моделей мы будем работать. Мы будем рассматривать Кеплерову модель орбиты. Существует большое множество других моделей, но все они являются полуаналитическими и в итоге большинство из них сводится к определению параметров Кеплеровой орбиты в интересующий момент времени. Другими словами, Кеплерова орбита является аппроксимацией сложного движения планеты в заданный момент времени. Кеплеровы параметры орбит планет можно посмотреть здесь nssdc.gsfc.nasa.gov/planetary/factsheet, там же указана эпоха (другими словами момент времени) в момент которой данные параметры Кеплеровой орбиты дают точное положение небесного тела. Обычно этим исходным моментом времени является эпоха J2000.0 (полдень 1 января 2000 года). Расчет движения тел на небольшой промежуток времени при помощи Кеплеровой модели является достаточно точным. Точности вполне хватит, чтобы не заметить ошибку визуально или в небольшой телескоп. Конечно, для расчета траектории полета к другой планете нужны более точные модели.

Кеплерова орбита

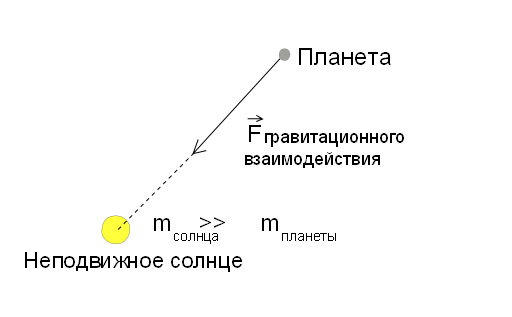
Итак, по порядку. Начнем с основных допущений данной модели. Предполагается, что масса Солнца много больше массы всех планет вместе взятых, откуда можно сделать вывод, что взаимодействие между планетой и планетой пренебрежимо мало по сравнению с взаимодействием между солнцем и планетой. Таким образом, поставленную задачу можно свети к задаче о взаимодействии двух тел (т.е. можно рассмотреть взаимодействии каждой планеты с солнцем отдельно). Более того предполагаем, что масса планеты много меньше массы Солнца, то взаимодействие получается одностороннее, т.е. планета никак не влияет на движение Солнца. Таким образом, мы можем рассматривать планету, как материальную точку, движущуюся в гравитационном поле, центр которого неподвижен. Примерно так:

Гравитационное взаимодействие

Что такое гравитационное взаимодействие? Это универсальное фундаментальное взаимодействие между всеми материальными телами. О гравитации можно говорить много и долго, но нам нужен только ключевой момент. Согласно классической теории тяготения Ньютона, сила гравитационного притяжения между двумя материальными точками массы m₁ и m₂, разделёнными расстоянием R, пропорциональна обеим массам и обратно пропорциональна квадрату расстояния между ними — то есть:

Здесь — G гравитационная постоянная (некий коэффициент пропорциональности). Нам важно отметить лишь то, что сила гравитации направлена от центра тяжести одного тела к центру тяжести другого и обратно пропорциональна квадрату расстояния между ними (закон обратных квадратов).
Отметим, что на нашу

сферическую планету в вакууме

материальную точку не действует никакая другая сила, кроме силы притяжения со стороны Солнца. В нашем случае, поле сил тяготения является центральным полем сил. В центральное поле сил, направление силы действующей на тело в любой точке такого поля, всегда проходит через центр этого поля (в нашем случае через центр тяжести солнца), а величина такой силы зависит только от расстояния до этого центра.

Второй закон Ньютона

Как движется тело под действием силы? На этот вопрос отвечает второй закон Ньютона. Вообще этот закон имеет несколько формулировок, наиболее распространенная из современных:

В инерциальных системах отсчёта ускорение, приобретаемое материальной точкой, прямо пропорционально вызывающей его силе, совпадает с ней по направлению и обратно пропорционально массе материальной точки.

Данная формулировка точная, но не слишком понятная. Сам Ньютон давал другую формулировку:

Изменение количества движения пропорционально приложенной движущей силе и происходит по направлению той прямой, по которой эта сила действует.

Такая формулировка хоть и менее точная (нужно сделать оговорки про системы отчета, но нас это пока не интересует), но куда более понятная. Под количеством движения здесь понимается так называемый импульс тела, равный произведению массы тела на его скорость:

Таким образом, запишем словесную формулировку в символьном виде:

Или же если мы распишем, чему равен импульс тела и вынесем массу как константу (масса не всегда константа, но в нашем случае это так) за знак дифференциала то получим следующую всем известную формулу:

Где вектор 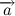— ускорении тела. Не забываем, что ускорение, импульс, скорость и сила величины векторные. Давайте условимся, что если над векторной величиной стоит знак вектора, то понимается именно вектор, в противном случае его модуль.

Второй закон Кеплера

Давайте для простоты, поместим начало координат в центре тяготения, т.е. в центре тяжести Солнца. Таким образом, вектор, проведенный из центра тяжести планеты к началу координат, совпадает по направлению с вектором силы притяжения.
Положение тела в пространстве описывается так называемым радиус-вектором — вектором, проведенным из начала координат к центру тяжести тела. Умножим векторно левую и правую часть выражения на радиус вектор:

Для дальнейших манипуляций, давайте распишем производную векторного произведения:

Тогда производная векторного произведения радиус вектора на скорость:

Напомню, что векторное произведение вектора самого на себя равно нулю, тогда:

Внесем массу под знак дифференциала, и с учетом выражения для импульса тела получим:

Так как вектор силы притяжения всегда направлен к центру тяготения, то векторное произведение радиус вектора на силу притяжения всегда равно нулю, отсюда делаем очень важный вывод:

Мы получили так называемый закон сохранения момента импульса. Изменение момента импульса тела пропорционально приложенному к нему моменту сил. Так как вектор силы притяжения всегда направлен к центру тяготения, то момент силы притяжения относительно центра тяготения всегда равен нулю. Отсюда следует, что момент импульса тела постоянен.
Так как мы договорились, что масса планеты постоянна, то также справедливо и следующее выражение:

Чтобы понять, что такое 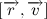, давайте обратимся к рисунку:

На рисунке изображен участок траектории. За время dt тело проходит расстояние vdt. Модуль векторного произведения векторов численно равен площади параллелограмма построенного на этих векторах. Получается, что:

Величина 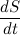есть площадь описываемая радиус вектором за единицу времени и называется она секториальной скоростью. Следовательно, секториальная скорость тела постоянна. Мы только что получили второй закон Кеплера который гласит:

Каждая планета движется в плоскости, проходящей через центр Солнца, причём за равные промежутки времени радиус-вектор, соединяющий Солнце и планету, описывает равные площади.

Да знаю, «получили закон» звучит не хорошо, но что поделаешь, он так называется. Причина в том, что Кеплер его не выводил, а интуитивно подобрал на основе своих наблюдений, т.е. получил его эмпирическим путем, в этом случае это действительно был закон.
Ниже приведена иллюстрация данного закона (рисунок взят из статьи на википедии).

Дифференциальное уравнение орбиты

Давайте все же подробнее рассмотрим векторное произведение радиус вектора на скорость. Радиус вектор можно представить в виде произведения модуля радиус вектора (расстояние от начала координат до точки) на вектор единичной длины, совпадающий по направлению с радиус вектором:


Тогда вектор скорости будет равен:

А векторное произведение радиус вектора на скорость в свою очередь:

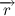
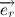
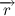
Учитывая тот факт, что вектора и совпадают по направлению, а следовательно совпадают по направлению и вектора и , получаем, что . Тогда:

Давайте разберем, что такое производная единичного вектора по времени:

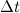
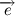
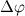
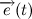
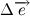
Из рисунка видно, что за время вектор поворачивается на угол . Разность векторов и равна вектору . Для малых углов справедливо следующее соотношение:

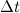
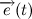
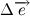
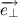
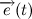
В пределе, когда устремляется к нулю, направления векторов и совпадают, а направление вектора перпендикулярно к ним. Введем единичный вектор , перпендикулярный к и совпадающий с направлением движения его конца, тогда:

Таким образом, переходя к пределу, получим:

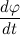
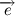
Где это угловая скорость вектора . Обозначим
Вернемся к нашему произведению радиус вектора на скорость, учитывая, что 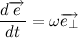получим:

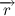
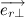
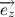
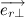
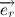
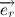
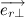
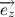
Несложно заметить, что вектора и взаимно перпендикулярны. Введем еще один единичный вектор , который перпендикулярен к векторам и . Таким образом, вектора , и образуют ортонормированный базис. Исходя из определения векторного произведения, получим:

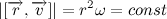
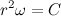
Следовательно, . Введем обозначение, . Так же стоит отметить, что:

Вернемся к второму закону ньютона. Вектор силы действующей на тело распишем сразу как величину гравитационной силы, умноженную на орт :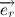

Где m₁ и m₂ — масса планеты и солнца соответственно.
Давайте на массу планеты сразу сократим, и нигде далее про массу планеты вспоминать не будем, так как она совершенно не влияет на траекторию движения. Будем считать, что мы работаем с телом единичной массы. Введем обозначение, , тогда:

Теперь давайте распишем вектор ускорения:

Рассмотрим содержимое второй скобки:

Но мы уже знаем, что , отсюда следует, что , тогда:

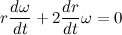
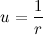
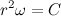
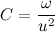
Введем обозначение . Напомню, что раннее мы ввели обозначение , очевидно, что .
Теперь распишем производную от модуля радиус вектора через С:

Теперь распишем вторую производную от модуля радиус вектора через С:

Учитывая полученный результат, перепишем выражение для вектора ускорения:

Тогда второй закон Ньютона примет вид:

Перепишем полученное дифференциальное уравнение в более привычный вид:

Я думаю многие из вас догадались, что представляет из себя полученное дифференциальное уравнение, но я пожалуй закончу на этом первую часть чтобы не перегружать читателя и себя.

Итог

Мы получили дифференциальное уравнение, описывающее траекторию движения материальной точки в гравитационном поле, которое вполне применимо для описания траектории планет и некоторых других небесных тел.

Что нам еще предстоит

В полученном дифференциальном уравнении отсутствует временной параметр, поэтому мы ничего не знаем о характере движения, поэтому необходимо как-то привязаться ко времени. Также далее будут рассмотрены различные системы координат и их преобразования для того чтобы получить координаты планет в системе привязанной к наблюдателю.

P.S.

Любая критика, замечания и дополнения приветствуются.