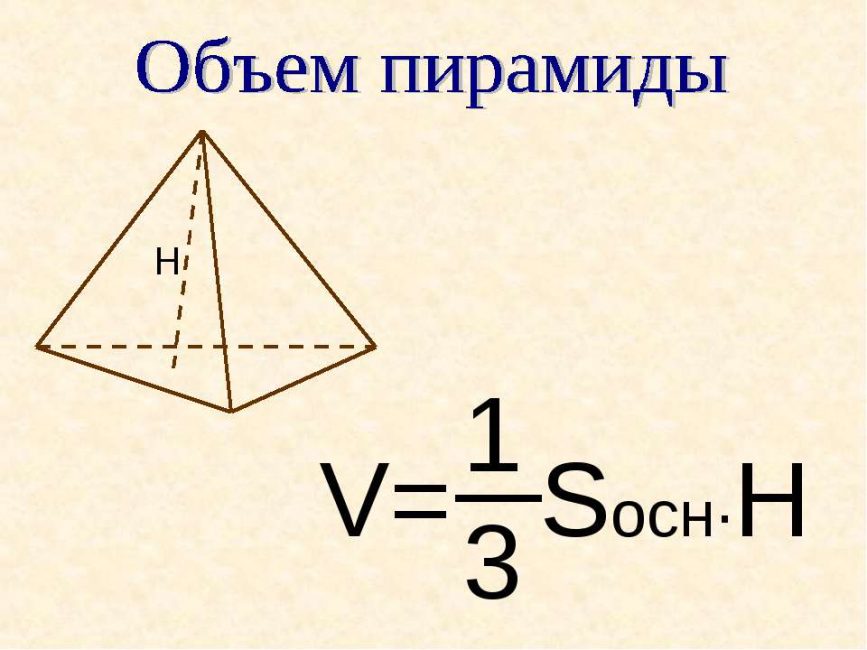
Высота правильной треугольной пирамиды.
Основание правильной пирамиды представляет собой правильный многоугольник. Так как мы имеем дело с треугольной пирамидой, то её основанием будет равносторонний треугольник.
Чтобы найти высоту пирамиды SO, достаточно вспомнить, что:
1) AO = BO = CO = R = a√3 / 3. (св-во равностороннего треугольника).
2) SB = AB. (боковое ребро равно длине стороны основания).
По теореме Пифагора высота SO равна:
SO = √(SB² — OB²) = √(a² — a²/3) = √(a²(1 — 1/3)) = √(a² * (2/3) = a√(2/3).
Итак, высота правильной треугольной пирамиды (H) равна произведению длины ребра (a) на корень из 2/3:
Высоту пирамиды также можно найти из формулы объёма:
V = 1 / 3 Sосн * H.
Так как основание пирамиды — это равносторонний треугольник, то Sосн = a² * √3 / 4.
Отсюда V = a² * √3 * H / 12 = a² * H / 4√3.
Остаётся выразить высоту:
V * 4√3 = a² * H.
H = V * (4√3 / a²).
Высота правильной треугольной пирамиды (H) равна дроби — в числителе произведение объёма пирамиды (V) на 4√3, в знаменателе — квадрат ребра (a).
Если же в условии задачи уже известна площадь основания, то высоту найти ещё проще:
H = 3 * V / Sосн.
Пример
Сторона основания правильной треугольной пирамиды равна 4 см, объём равен 10√3.
Нужно найти высоту пирамиды.
Воспользуемся вышеприведённой формулой:
H = V * (4√3 / a²) = 10√3 * 4√3 / 16 = 120 / 16 = 7,5 см.
Зная сторону основания правильной пирамиды, то есть пирамиды, в основании которой лежит правильный многоугольник, можно найти периметр основания, его площадь, радиус окружностей, которые можно вписать или описать около него, а также угол между сторонами многоугольника.
Периметр правильного многоугольника равен произведению длины его стороны на их удвоенное количество, а площадь представляет собой отношение количества сторон, умноженного на квадрат длины одной стороны, к четырем тангенсам 180 градусов, деленных на количество сторон.
P=n(a+b)
S=(na^2)/(4 tan〖(180°)/n〗 )
Чтобы найти радиус окружности, вписанной в основание правильной пирамиды, нужно разделить сторону основания на два тангенса из 180 градусов, деленных на количество сторон в основании. (рис.34.1)
r=a/(2 tan〖(180°)/n〗 )
Радиус окружности, описанной вокруг основания правильной пирамиды, равен отношению стороны основания к двум синусам того же угла.(рис.34.2)
R=a/(2 sin〖(180°)/n〗 )
Угол γ между сторонами правильного многоугольника, заложенного в основание пирамиды, легко найти, умножив 180 градусов на количество сторон многоугольника без двух, и деленное на полное количество сторон. (рис.34.3)
γ=180°(n-2)/n
Параметры самой пирамиды, как объемного тела, такие как боковое ребро и апофема пирамиды вычисляются через теорему Пифагора в прямоугольном треугольнике с высотой во внутреннем пространстве пирамиды. Вторым катетом прямоугольного треугольника с апофемой является радиус вписанной окружности, а катетом треугольника с боковым ребром – радиус описанной окружности основания. (рис.34.4,34.5)
l=√(h^2+r^2 )=√(h^2+(a/(2 tan〖(180°)/n〗 ))^2 )
b=√(h^2+R^2 )=√(h^2+(a/(2 sin〖(180°)/n〗 ))^2 )
Угол между апофемой и основанием рассчитывается как отношение синуса – высоты к радиусу вписанной окружности, а угол между боковым ребром и основанием аналогично – высоты к радиусу описанной окружности, из тех же прямоугольных треугольников.
sinα=h/r=(2h tan〖(180°)/n〗)/a
sinβ=h/R=(2h sin〖(180°)/n〗)/a
Зная апофему и сторону основания пирамиды, можно найти площадь боковой поверхности, а затем площадь полной поверхности пирамиды.
S_(б.п.)=lan/2
S_(п.п.)=an(l/2+a/(4 tan〖(180°)/n〗 ))
Объем пирамиды равен трети произведения площади основания на высоту, таким образом, зная высоту и сторону основания пирамиды, вычислить ее объем можно, подставив соответствующее выражение вместо площади основания.
V=1/3 S_(осн.) h=(na^2 h)/(12 tan〖(180°)/n〗 )
В любую правильную пирамиду (в основании которой лежит правильный многоугольник) можно вписать сферу, а также описать сферу около нее. Радиусы вписанной и описанной сфер зависят не только от высоты и стороны основания, но и от объема пирамиды, площади полной поверхности и бокового ребра пирамиды, поэтому для их вычисления необходимо произвести алгебраические преобразования формул. (рис.34.6,34.7)
r_1=3V/S_(п.п.) =ah/(tan〖(180°)/n〗 (2l+a/tan〖(180°)/n〗 ) )
R_1=b^2/2h=(h^2+(a/(2 sin〖(180°)/n〗 ))^2)/2h
Главная » Образование » Школа » Как найти высоту в пирамиде: треугольной, четырехугольной, правильной
Как найти высоту в пирамиде: треугольной, четырехугольной, правильной
35881 Просмотров 0
Высота основания в пирамиде – тема, на которую часто попадаются задачи на экзаменах и в старших классах. Решать такие задачи просто, если понимать принцип решения и знать формулы.
В нашей статье, вы без лишних формул и теории сможете понять, как решать задачи на нахождение высоты в пирамиде. Обратите внимание, что в разделе «формулы» отсутствуют все формулы правильной пирамиды, так как наша цель – научить решать задачи на нахождение высоты.
Содержание этой статьи:
- Теория
- Часто задаваемые вопросы
- Типичные ошибки на ЕГЭ
- Полезные советы
Теория
Это интересно: Как оформлять реферат в школе по ГОСТу + образец титульного листа 2019
Правильная пирамида
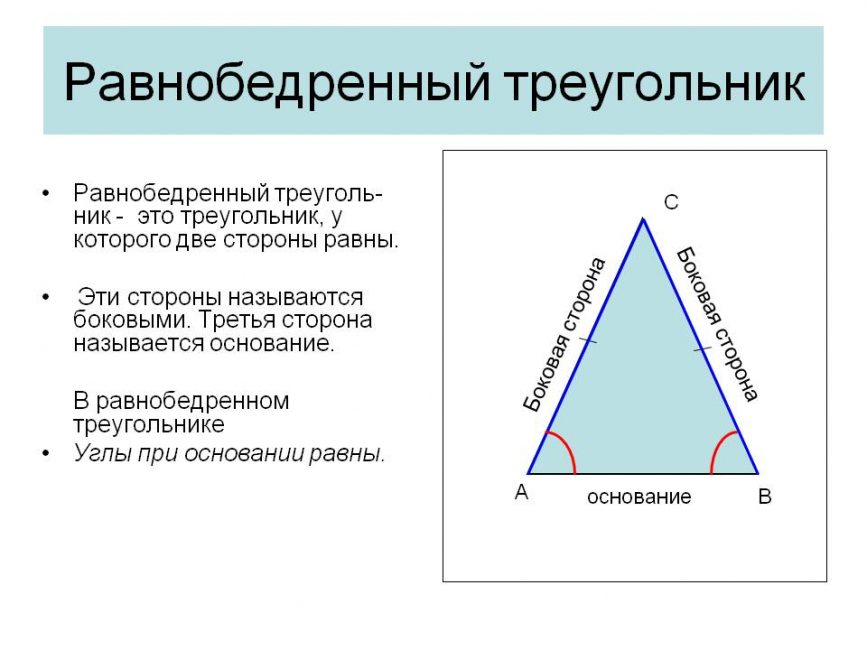
Правильная пирамида имеет в основании многоугольник, а высота проходит через центр основания. Боковые грани – равнобедренные треугольники. Напомним, что в равнобедренном треугольнике две стороны равны, следовательно, боковые ребра в правильной пирамиде тоже равны. Многоугольник в основании правильный, т.е. его стороны равны.
Для решения задач понадобится знать теоремы равнобедренного треугольника:
Равнобедренный треугольник
Основные свойства
1В правильную пирамиду можно вписать и описать сферу, так как при пересечении диагоналей, основание делится на равные части. Сферу нельзя вписать в любую фигуру.
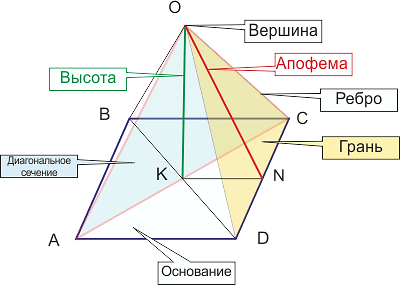
2Площадь боковой поверхности – половина произведения периметра основания на апофему. Апофема есть на каждой грани, а не только на одной.
Пирамида
Четырехугольная пирамида
В основании – многоугольник; остальные грани – треугольники, соединяющиеся в общей вершине.
Четырехугольная пирамида
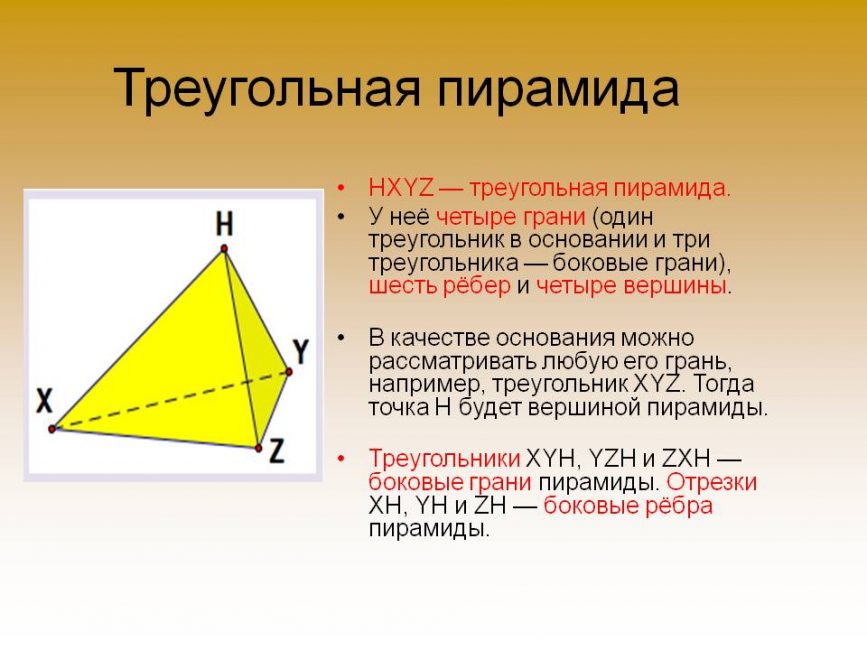
Треугольная пирамида
Читайте также: Как решать задачи по математике 5 класс
В качестве основания можно рассматривать любую грань. Вся фигура состоит из треугольников.
Треугольная пирамида
Необходимые знания для нахождения высоты
1Нужно понимать, что из себя представляют треугольники: свойства, формулы, определение. Большинство задач решается через треугольники (боковые грани).
2Понимать, что такое сечение и как оно влияет на геометрическую фигуру.
3Что такое правильные многоугольники: виды, свойства, формулы.
Когда теория закреплена, можно переходить к формулам.
Формулы для нахождения высоты
Формулы
Запомните, что маленькая буква h – это апофема, а большая H – высота.
В некоторых задачах, высоту можно найти через объем:
Объем пирамиды
ВИДЕО: Примеры решения задач
Нахождение высоты в правильной пирамиде
Нахождение высоты в правильной пирамиде
Ниже будут представлены текстовые решения часто встречающихся задач.
Треугольная пирамида
Треугольная пирамида
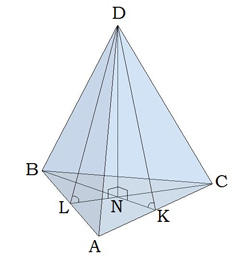
Задача 1
В правильной треугольной пирамиде DBAC с вершиной D биссектрисы треугольника BAC пересекаются в точке N. Площадь треугольника BAC равна 4; объем пирамиды равен 12. Найдите длину отрезка DN.
DN – высота, следовательно, объем фигуры можно выразить по формуле:
DN = 3V/S основания = 3*12/4 = 9
Ответ: 9
Задача 2
DBAC – медианы основания BAC. Они пересекаются в точке N. Площадь ΔBAC равна 18, V = 20; найдите высоту.
Пользуясь формулой объема, получается:
DN = 3V/S ΔBAC = 3*36/18 = 108/18 = 6
Ответ: 6
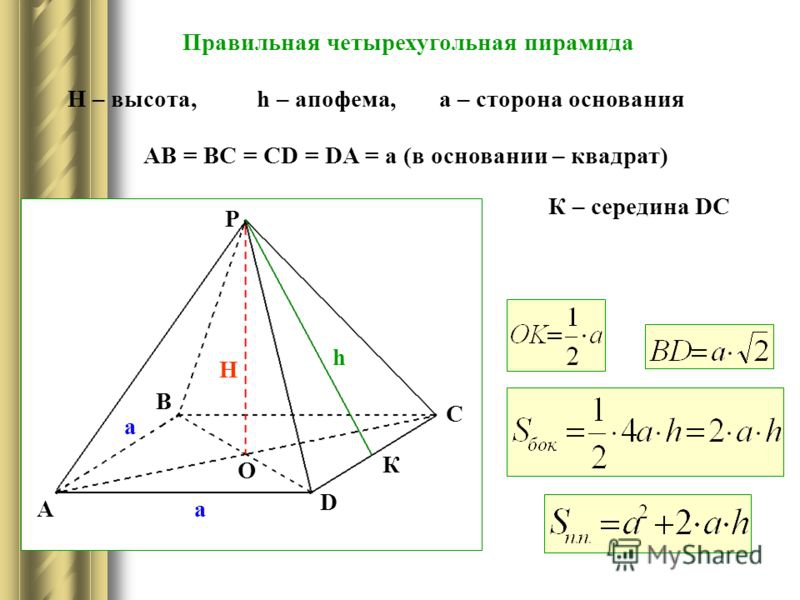
Четырехугольная пирамида
Четырехугольная пирамида
Задача 1
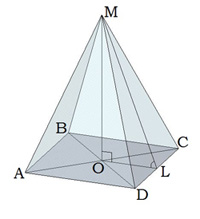
Найдите высоту пирамиды, если ML = 10, а DC = 12. В основании квадрат.
ML – это апофема, сторона нам известна, следовательно, можно применить формулу для нахождения OL:
OL = ½*12 = 6
Известно, что MOL – прямоугольный угол. Применим теорему Пифагора:
MO ² = √ML ² — √OL ² = √100- √36 = √64
MO = 8
Задача 2
Известно, что диагональ AC = 20, ML = 10, а сторона DC = 12; найдите MO правильной четырехугольной пирамиды.
Найдем OL
В основании фигуры – квадрат, стороны и углы которого равны. Значит, половина диагонали = 10. Рассмотрим треугольник LOC, он – прямоугольный. Из исходных данный ясно, что LC = 6 (в равнобедренном треугольнике, высота, проведенная из вершины, делит основание на 2 равные части – это свойство р/б треугольника).
Пользуясь теоремой Пифагора, находим OL:
OL² = √OC² — √LC² = √100 – √36 = √64 = 8
Задача 3
Ищем MO
Пользуясь той же теоремой, находим высоту:
MO² = √ML² – √OL² = 100 – 64 = 36
Ответ: 36
Задача 4
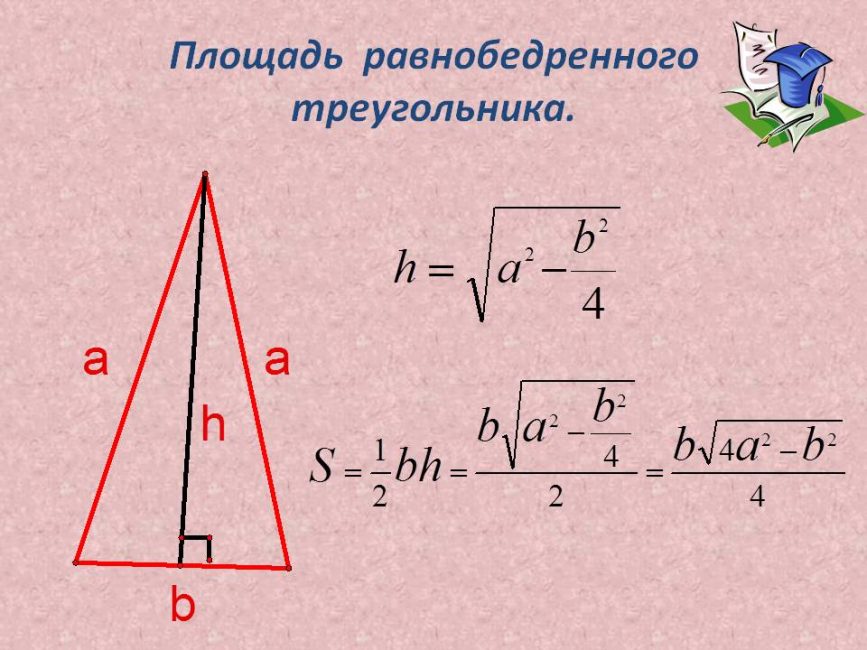
Известно, что в основании ABCD, AB=CD=BC=AD. Треугольник DMC имеет площадь 36см, DC = 4, OL = 6. Определите тип фигуры и найдите высоту.
Исходя из информации про основание, мы сделали вывод, что перед нами правильная пирамида – стороны основания равны. Следовательно, перед нами четырехугольная правильная пирамида.
Из первого вывода следует, что боковые грани – равнобедренные треугольники, а высота и медиана этих треугольников – апофема. Пользуясь формулами, найдем высоту.
Площадь равнобедренного треугольника
36 = ½ * 4 *h
36 = 2h
H = 18
Теперь у нас есть апофема, а OL нам было уже давно. MOL – прямоугольный треугольник, 2 стороны которого, мы уже знаем. Следовательно, мы можем посчитать высоту.
MO = ML – OL = 18 – 6 = 12
Ответ: 12
Часто задаваемые вопросы
1Как понять, что пирамида правильная, если в условии это не указано?
Часто в задании не указывают какой тип фигуры, чтобы человек сам догадался и применил нужные формулы. Понять какой тип фигуры легко – начните решение задачи с рассмотрения основания и заучивания свойств фигуры.
Зная определения и свойства, определить тип фигуры очень легко.
2Могут ли быть указаны в задании лишние данные?
Чтобы решать задачи, человек должен включать логику, а не подставлять исходные числа в знакомые формулы. С этим расчетом, в некоторых задачах умышленно добавляют лишние данные, которые могут даже не использоваться при решении. Чаще такое встречается в задачах на ЕГЭ.
3Обязательно ли оформлять высоту большой буквой H? Нужно ли выделять апофему?
Для удобства, человек может не выделять отдельно высоту, а сразу писать, например, BE (если B – вершина, а E – основание). То же с апофемой. Важно, чтобы сам человек осознавал, что это за линия и как ее использовать в решении.
4Как можно быстро изучить стереометрию?
Ключ к пониманию стереометрии – умение визуализировать объекты в пространстве. Если в дополнение к этому умению, знать формулы, свойства и теорию – задачи будут решаться быстро и безошибочно.
4Как искать высоту, если известен объем?
Если выразить высоту через формулу объема, то получится следующее:
H = (3*V)/ S;
Пример: объем пирамиды равен 70 куб. см., а площадь боковых граней – 30см²
H = 3*70/30 = 7см
Типичные ошибки на ЕГЭ
Незнание темы
Когда человек не знает, где находится апофема и что для нее есть определенные формулы, задачу может и можно решить, но тогда необходимо выполнить в 2 раза большей действий.То же обстоит с теорией – если человек не знает свойства многоугольников, то и решить задание он не сможет. Для того, чтобы понимать геометрию, не нужно обладать особенными способностями. Даже при отсутствии способностей к математике, зная теорию, вы будете понимать геометрию.
Отсутствие проверки
Хотите потерять балл на ЕГЭ? – не перепроверяйте решения. Часто, задания решаются хаотично и на листе бумаге разные решения намешаны в кучу. Когда приходит время написать ответ, человек по невнимательности либо забывает выполнить последнее действие, либо вписывает не тот ответ.Решайте задачи по действиям, проставляйте пункты и делайте проверку ответа, каким бы он ни был.
Задачи под копирку
Решая сотни аналогичных задач, человек настолько привыкает, что теряет бдительность, игнорируя многие исходные данные. Придя на экзамен, в задании может быть вопрос с подвохом и человек ошибается в теме, которую он знал идеально. Помните, к каждой задаче нужен индивидуальный подход, как бы хорошо вы в ней не разбирались.
Запись
Структурируйте решения, прописывая каждое действие и каждый полученный вывод. Это необходимо для того, чтобы не запутаться. Решая задания хаотично, можно легко записать неправильное число, не тот ответ, подставить не те числа, и задача уже решена неверно. Обидно получать низкий балл из-за невнимательности.
Подсчеты в уме
На экзамене все нервничают и переживают, а потому зарабатывают баллы ниже, чем планировалось изначально. Когда человек нервничает, уровень концентрации и внимания резко снижается. Он может упустить что-то важное, не поставить запятую или запутаться в ходе размышлений.Считая примеры в столбик, вы обезопасите себя от глупых ошибок.
Незнание структуры экзамена
Очень обидные ошибки допускают люди, пересдающие ЕГЭ через несколько лет, либо обучающиеся в экстернате. Как правило, они плохо знакомы с процедурой заполнения бланков и внесения ответов.Заполнение бланков для части А и С – различно. Внимательно посмотрите, как необходимо их заполнять, так как неправильное внесение ответа (например, запятая и число в одной клетке) будет приравниваться к ошибке и ответ будет не засчитан.Также, если вы самостоятельно готовитесь к экзамену, учитесь рассчитывать время на каждое задание.
Поспешные решения
В случае, если ответ был записан с ошибкой, его можно внести в графе ниже, заменив неправильный ответ на правильный. Однако, клетки для внесения результатов ограничены в количестве, а заданий в общей сложности 19!Несколько раз перепроверьте ответы, прежде чем внести их в бланк ответов.
Незнание степеней числа
В теореме Пифагора будут использованы не только маленькие числа (до 10). В профильной математике, могут быть крупные числа, которые тяжело посчитать в столбик.Также, степени числа могут понадобиться для других заданий. Выучите значение чисел в квадрате и кубе от 1 до 20. Помните, что на профильном экзамене, пользовать методической таблицей нельзя!
Полезные советы
- Если в задаче указан объем – ищите высоту через него.
- Делите равнобедренные треугольники на прямоугольные – так быстрее и проще решить задачу.
- Учите квадратные корни чисел – так, вы будете быстрее справляться с теоремой Пифагора.
- Не кидайтесь сразу к решению – изучите исходные данные и сделайте правильные выводы.
- Если в заданиях получаются слишком крупные числа (от 1000), то перепроверьте решение – вероятно, вы допустили ошибку. В заданиях в учебнике и на экзамене практически не используются крупные числа.
6.5 Total Score
Чтобы успешно решить задачу для нахождения высоты пирамиды, достаточно знать теорию и формулы. Добавив к своим знаниям немного практики и внимательности, вы легко и быстро будете решать подобные задачи!
Если вы не согласны с рейтингом статьи, то просто поставьте свои оценки и аргументируйте их в комментариях. Ваше мнение очень важно для наших читателей. Спасибо!
Достоверность информации
8.5
Актуальность информации
7.5
ПЛЮСЫ
- Благодаря доступной информации можно легко научиться решать задачи по геометрии
МИНУСЫ
- Необходимы знания математики
Добавить отзыв
Как найти высоту в правильной пирамиде
Пирамида представляет собой многогранник, в основании которого лежит многоугольник, а грани его представляют собой треугольники, обладающие общей вершиной. Для правильной пирамиды справедливо то же определение, но в основании ее лежит правильный многоугольник. Под высотой пирамиды подразумевается отрезок, который проведен от вершины пирамиды к основанию, и этот отрезок перпендикулярен ему. Найти высоту в правильной пирамиде очень легко.
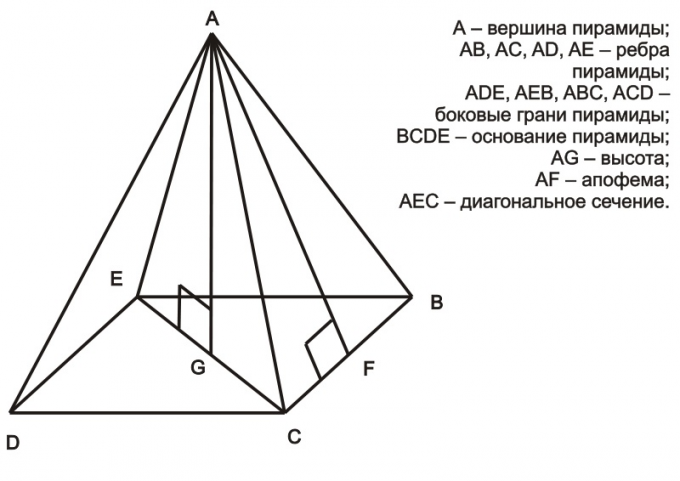
Вам понадобится
- В зависимости от ситуации, знать объем пирамиды, площадь боковых граней пирамиды, длину ребра, длину диаметра многоугольника в основании.
Инструкция
Одним из способов найти высоту пирамиды, и не только правильной — это выразить ее через объем пирамиды. Формула, с помощью которой можно узнать ее объем, выглядит так:
V = (S*h)/3, где S — площадь всех боковых граней пирамиды в сумме, h — высота данной пирамиды.
Тогда из этой формулы можно вывести другую, для нахождения высоты пирамиды:
h = (3*V)/S
К примеру, известно, что площадь боковых граней пирамиды 84 см², а объем пирамиды равен 336 куб.см. Тогда найти высоту можно так:
h = (3*336)/84 = 12 см
Ответ: высота данной пирамиды 12 см
Рассматривая правильную пирамиду, в основании которой лежит правильный многоугольник, можно прийти к выводу, что треугольник, образованный высотой, половиной диагонали и одной из граней пирамиды, представляет из себя прямоугольный треугольник (например, это треугольник АEG на рисунке выше). Согласно теореме Пифагора, квадрат гипотенузы равен сумме квадратов катетов (a² = b² + c²). В случае с правильной пирамидой, гипотенуза — это грань пирамиды, один из катетов — половина диагонали многоугольника в основании, а другой катет — высота пирамиды. В таком случае, зная длину грани и диагонали, можно вычислить и высоту. В качестве примера можно рассмотреть треугольник AEG:
AE² = EG²+GA²
Отсюда высоту пирамиды GA можно выразить так:
GA = √(AE²-EG²).
Чтобы было более понятно, как находить высоту правильной пирамиды, можно рассмотреть пример: в правильной пирамиде длина грани 12 см, длина диагонали многоугольника в основании — 8 см. Исходя из этих данных, требуется найти длину высоты этой пирамиды.Решение: 12² = 4² + c², где с — неизвестный катет (высота) данной пирамиды (прямоугольного треугольника).
144 = 16 + 128
Таким образом, высота данной пирамиды √128 или, приблизительно, 11.3 см
Источники:
- правильная четырехугольная пирамида найти высоту
- Решение заданий С2 ЕГЭ по математике
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Нахождение высоты пирамиды
Высоты любой треугольной пирамиды можно найти по формуле объема:
V = (1/3)*S*h,
где V — объем пирамиды; S — это площадь основания; h — высота пирамиды.
Из этой формулы высота пирамиды равна:
h = (3V)/S.
Основание треугольной пирамиды — это треугольник, если известны все три стороны треугольника ABC, то формула площади треугольника по трем сторонам:
S=[p-(p-a)*(p-b)*(p-c)]0.5
— выражение в квадратных скобках в степени 0,5 (или извлечь квадратный корень).
где: p – полупериметр треугольника, a, b, c – длины сторон треугольника.
полупериметр – это сумма длин всех сторон разделенная на 2.
p= (a+b+c)/2